Introduction

Wood is one of the most important and least polluting natural resources in the world. Currently, concern about greenhouse gas emissions is growing steadily. This results in sustainability policies strongly betting on the use of wood as a construction material and being interested in carrying out a sustainable exploitation of forests. In response, the research community is accompanying this change by developing products and tools that allow building in an environmentally friendly way, deepening the use of wood as a structural material.

Technological development and the better use of natural resources in recent years have sparked interest in the use of hardwood species in the building sector. Part of this concern is due to the high mechanical performance of hardwoods compared to softwoods. In this sense, one of the hardwood species that has recently gained a great deal of attention for structural purposes in Europe is beech (Fagus sylvatica L.) (Enders-Comberg et al. 2015; Kovryga et al. 2020; Ehrhart et al. 2021), on which this study will focus.

In the context of timber structures, there are common design situations where brittle failures can occur due to stress concentrations, for example, in beams with holes, joints, notched beams, etc. (Ardalany et al. 2016; Dourado et al. 2018; Majano-Majano et al. 2022) producing critical situations that require special attention. Therefore, it is necessary to establish adequate failure criteria and to accurately characterise the fracture properties of the material. In this context, conventional methods relying on the strength of materials and failure criteria have limitations. To overcome these drawbacks, fracture mechanics based approach can offer advantages, since this theory appeared as a tool to explain the failure mechanisms associated with the propagation of pre-existing cracks. The first model developed was only able to satisfactorily explain the behaviour of brittle materials such as glass (Inglis 1913; Griffith et al. 1921) and therefore did not arouse much enthusiasm in the research community. However, the theory underwent a great development after the Second World War (Irwin and Washington 1957; Dugdale 1960; Barenblatt 1962; Rice 1968; Bažant and Planas 1998) and managed to explain the failure of materials such as steel, concrete, or wood, which is characterised by the development of strain energy dissipation mechanisms before failure, such as plastic deformation around the crack tip, friction, microcracking, or fibre-bridging. These softening mechanisms in wood can be modelled with the concept of Fracture Process Zone (FPZ) ahead of the crack tip (de Moura et al. 2006). There is experimental research in the literature that suggests a quasi-brittle behaviour of wood, with fibre-bridging being the major crack tip toughening mechanism (Vasic and Smith 2002).

Numerical simulations using finite element analysis (FEA) are becoming a useful and powerful tool to better understand the fracture behaviour of many timber structural applications, such as end notched beams, beams with holes or bolted connections (Rautenstrauch et al. 2008; Caldeira 2011; Franke and Quenneville 2011, 2012; Ardalany et al. 2016; Dourado et al. 2018). In this sense, cohesive zone models (CZM) constitute one of the simplest methods to take into account the aforementioned toughening phenomena and whose precision has been sufficiently demonstrated (Dugdale 1960; Barenblatt 1962; Hillerborg et al. 1976; Petersson 1981; Boström 1992; Coureau et al. 2007; de Moura et al. 2009a; Dourado et al. 2013; de Moura et al. 2015; Pereira et al. 2018). The CZM applies a strength criterion based on limit stresses to determine the start of the damage, and later implements a traction-separation law to describe the progressive damage of the material according to a fracture mechanics criterion. However, the drawback of using CZM is that they must be associated with geometrically defined damage paths in the numerical model and, therefore, it is essential to know them previously. Moreover, knowledge of the different material properties is necessary to develop FEA models accurately. Relevant information on the properties of Fagus sylvatica L. can be found in the literature, such as the elastic orthotropic constants (Ozyhar et al. 2013a, c; Gómez-Royuela et al. 2021) and viscoelastic characterisation (Ozyhar et al. 2013b). However, CZMs also require the material fracture properties, such as the fracture energy and the cohesive law. These properties can be obtained experimentally by direct methods (Xavier et al. 2014b) or by inverse methods using numerical simulations (Dourado et al. 2012).

Various fracture test arrangements have been proposed to study pure fracture modes (mode I, mode II, mode III) (Cramer and Pugel 1987; Stanzl-Tschegg et al. 1995; Ehart et al. 1998; Frühmann et al. 2002b, a; Qiao et al. 2003; Yoshihara 2004; Brunner et al. 2008; Ardalany et al. 2012; Majano-Majano et al. 2019, 2012; Xavier et al. 2014a; Dourado et al. 2015; Luimes et al. 2018; Crespo et al. 2018). Although there is still no globally accepted method for each of them, the double cantilever beam (DCB) (Yoshihara and Kawamura 2006) and the three-point end notched flexure (ENF) (Yoshihara and Ohta 2000) tests are widely applied to pure modes I and II, respectively. Much research has focused mainly on the wood fracture behaviour under mode I, as it is considered to be the most predominant one. However, many elements are designed to withstand high shear loads, so knowing the fracture behaviour under mode II becomes an important key issue.

The objective of this work is to experimentally determine the main fracture properties in mode II loading of European beech wood (Fagus sylvatica L.) using ENF specimens for both tangential-longitudinal (TL) and radial-longitudinal (RL) crack propagation systems. For the first time, to the best of the authors' knowledge, the shear traction-separation laws of Fagus sylvatica L. are provided, which are derived directly from the relationship between the strain energy release rate (GII) obtained from the R-curves and the crack tip shear displacements (CTSD) monitored during testing by means of the 3D digital image correlation (DIC) technique. The compliance-based beam method (CBBM) is applied as a data reduction scheme, which is based on the beam theory and on the equivalent crack length (aeq) concept. It has the advantage that only the load–displacement curve is needed and does not require measuring crack growth during the test, which would be a complex task in wood, particularly under mode II loading. Numerical validation by FEA using cohesive zone models with exponential softening relationship of the shear traction–separation law is also performed.

Materials and methods

Raw material

Fagus sylvatica L. from Europe was the wood species tested in this work. The specimens were machined and carefully cut from knot-free boards and oriented according to the RL and TL crack propagation systems (Fig. 1). The material was stored in a climate chamber at 20 °C and 65% relative humidity until an equilibrium moisture content was reached. The density of each specimen was measured, resulting in average values of 721 kg/m3 and 708 kg/m3 for the batches corresponding to RL and TL systems, respectively. Main moisture contents of 10% and 9.9% were achieved for the RL and TL groups of specimens, respectively. Constant values for the shear modulus in LR plane, GLR = 1108 MPa, and the shear modulus in LT plane, GLT = 706 MPa, were taken from Gómez-Royuela et al. (2021).

Fig. 1
figure 1

RL and TL crack propagation systems of the specimens

Full size image

Three-point end notched flexure tests coupled with 3D digital correlation

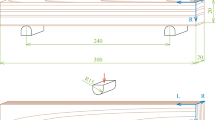
Twelve ENF specimens with RL orientation and fourteen with TL were tested according to the geometry schematically shown in Fig. 2. These are small rectangular-shaped beams with nominal dimensions 2L1 × 2h × B (500 mm × 20 mm × 20 mm). An initial crack was performed at mid-cross section height using a band saw. This procedure was carried out in two steps: first, a notch with an initial length a0 (161 mm) was machined, and just prior to testing this notch was lengthened 1 mm more using a very sharp thin blade. This delicate process was controlled using a universal testing machine (Fig. 3) with a cross-head speed of 10 mm/min, since the shape of the pre-crack surface plays an important role and could significantly influence the results, as reported in Dias et al. (2013). The pre-crack length was measured with a precision magnifying glass as shown in Fig. 4.

Fig. 2
figure 2

ENF geometry

Full size image
Fig. 3
figure 3

a Cutting setup: 1- ENF specimen, 2- sharp thin blade, 3- loading plate, 4- cutting support; b pre-crack

Full size image
Fig. 4
figure 4

Pre-crack measurement: measuring area marked in the highlighted square (left); measuring area viewed with a precision magnifying glass (right)

Full size image

The ENF specimens were subjected to three point bending tests using an electro-mechanical universal testing machine with a load cell of 5 kN maximum capacity (Fig. 5). The beam span was 2L (460 mm). The load was introduced at the mid-span under a constant crosshead speed of 2 mm/min. To avoid friction effects during the tests, two sheets of Teflon were introduced between the upper and lower sides of the crack at the support zone. The load displacement curves (P-δ) were recorded during the tests with a frequency of 1 Hz. The deflection of the specimen was obtained by means of a linear variable differential transformer (LVDT) measuring the loading plate displacement (element 4 in Fig. 5), as this LVDT was synchronised with both the 5 kN load cell and the DIC system. It should be noted that the loading nose did not produce any indentation on the specimens. An additional LVDT was used to verify that the supports showed no horizontal displacements (Fig. 5c). The maximum displacement recorded was approximately 0.01 mm, which was considered negligible. The initial test setup and the completed test result are shown in Figs. 5 and 6, respectively.

Fig. 5
figure 5

a ENF test set-up coupled with 3D DIC: (1) 300 kN load cell, (2) 5 kN load cell, (3) loading nose, (4) LVDT, (5) LVDT, (6) beech specimen, (7) speckle pattern, (8) supports, (9) DIC system equipment, (10) electro-mechanical testing machine frame; b detail of speckle pattern; c detail of the support

Full size image
Fig. 6
figure 6

a ENF specimen being tested; b detail of the fracture zone; c detail of the support

Full size image

3D DIC is an optical technique capable of measuring full field displacements of a speckled pattern, applied on the surface of interest (Sutton et al. 2009). An advantage of the 3D system over the 2D system is the ability to take measurements of an area within a volume, avoiding measurement errors arising from poor positioning of the specimen with respect to the cameras. The 3D DIC system ARAMIS® 3D (GOM mbH 2007) was used and coupled to the universal testing machine to record synchronized data of crack tip shear displacements with a frequency of 1 Hz. To ensure the accuracy of the measurements, a speckle pattern with appropriate contrast and granulometry was created on the surface of interest of the ENF specimens. This pattern was made in two stages: first, a thin, homogeneous layer of matte white paint was applied by spray, and then a pattern of black dots was projected on the surface using an airbrush. The optical system consisted of two front cameras with a resolution of 5 megapixels, coupled with 35 mm lenses. The optical system was calibrated according to the specifications described by the manufacturer (GOM mbH 2007). For this proposal, 13 images were taken and the calibration results were verified to be within the acceptable range established by GOM company. The calibration procedure was carried out using a CP20 according to the size of the study area. A subset size of 15 × 15 pixel2 and a subset step of 13 × 13 pixel2 were selected to improve the spatial resolution in a compromise with respect to accuracy. To achieve accurate measurements, the cameras were placed 400 mm from the surface of interest and set up for a field of view of 80 × 65 mm2. Consequently, an angle of 25° was established between the cameras. The separation between them and the reference axis was locked at 138 mm. In addition, to ensure the correct focus of the specimen surface, the device incorporated two white-light spotlights with adjustable light intensity to avoid insufficient or excessive light exposure. The spotlights and the shutter time were set to ensure adequate contrast and illumination of the specimen.

Experimental direct data reduction method

The shear traction–separation laws for pure mode II loading describe the relationship between the strain energy release rate (GII), the shear stresses (τ) and the crack tip shear displacements (CTSD) according to the following expression (Leffler et al. 2007)

$$G_{{{\text{II}}}} = \int\limits_{0}^{{\overline{u}}} \tau (u)du$$
(1)

where u is the CTSD, which was directly monitored during the test using the ARAMIS 3D DIC system. The differentiation of Eq. (1) provides directly the shear traction-separation law (τ = f(w)) as

$$\tau (u) = \frac{{dG_{{{\text{II}}}} }}{du}$$
(2)

To apply this equation, it is necessary to determine the evolution of GII during the test. However, nonlinear phenomena such as microcracks, cracks-branching and fibre-bridging appear in the area around the crack tip. These toughening mechanisms influence the fracture behaviour of wood and therefore cannot be neglected. This zone is known as FPZ and is located ahead of the crack tip. To overcome this difficulty, in this study, the GII was determined from the crack growth resistance curves (R-curves), which are a useful tool that allows quantifying the influence of the FPZ. The GIIc is given by the plateau value of these curves. According to this, GII can be obtained by the Irwin-Kies equation:

$$G_{{{\text{II}}}} = \frac{{P^{2} }}{2B}\frac{dC}{{da}}$$
(3)

where P, B, C and a are the applied load, the width of the specimen, the compliance (C = δ/P) and the crack length, respectively. In this work, dC/da was determined applying the CBBM (de Moura et al. 2006). This data reduction scheme is based on the equivalent crack length (aeq) concept and accounts for the energy dissipated due to the toughening mechanisms. These phenomena are developed in the FPZ and are not negligible in wood. In this context, considering the Timoshenko beam theory for the ENF test, the specimen compliance can be written as (de Moura et al. 2006)

$$C = \frac{{3a^{3} + 2L^{3} }}{{8Bh^{3} E_{L} }} + \frac{{3L}}{{10BhG_{{Li}} }},\,\,i = R,T$$
(4)

being EL and GLi the longitudinal and shear elastic moduli, respectively. In the last one, i can be either R or T and refer to the radial and tangential orthotropic directions. L, B, h and a are the dimensions of the specimens identified in Fig. 2. To take into account the effects that the inherent variability of wood has on the elastic properties, a corrected bending modulus Ef is considered instead of EL. For this purpose, the Ef value can be determined from Eq. (4) using the initial values of the crack length a = a0 and compliance C = C0. It should be clarified that C0 was estimated by linear regression of the P-δ curve applying the least-squares method. Consequently, Ef can be determined according to the following expression

$$E_{f} = \frac{{3a_{0}^{3} + 2L^{3} }}{{8Bh^{3} C_{{0,{\text{corr}}}} }}\,$$
(5)

where C0,corr is given by

$$C_{{0,{\text{corr}}}} = C_{0} - \frac{{3L}}{{10BhG_{{Li}} }},\,\,i = R,T$$
(6)

It should be highlighted that no significant errors are made when neglecting the influence of inherent variability of GLi on the result of C, as shown in de Moura et al. (2006). Therefore, in this research work, a typical value of GL summarized in “Raw material” section was considered in Eq. (6). On the other hand, accurate crack length measurements during the ENF test is a difficult task since crack tends to grow with their faces in close contact (Schuecker and Davidson 2000). Furthermore, the specimen compliance (C = δ/P) recorded during the test can be quite influenced by the effects that the FPZ causes in the vicinity of the crack tip. Because of this, an amount of energy can be dissipated that is not accounted for in GII, when real crack length is used as a calculation parameter. Consequently, important errors can occur in the characterisation of the fracture energy. To overcome these difficulties, an equivalent crack length (aeq) is used in Eq. (4) instead of the real one and can be written as (de Moura et al. 2006)

$$a_{{{\text{eq}}}} = a + \Delta a_{{{\text{FPZ}}}} = \sqrt[3]{{\frac{{C_{{{\text{corr}}}} }}{{C_{{0,{\text{corr}}}} }}a_{0}^{3} + \frac{2}{3}\left( {\frac{{C_{{{\text{corr}}}} }}{{C_{{0,{\text{corr}}}} }} - 1} \right)L^{3} }}$$
(7)

where Ccorr is given by

$$C_{{{\text{corr}}}} = C - \frac{{3L}}{{10BhG_{{{\text{L}}i}} }},\;i = R,T$$
(8)

Finally, combining Eqs. (3) and (7), the evolution of GII as a function of aeq can be determined as follows

$$G_{{{\text{II}}}} = \frac{{9P^{2} a_{{{\text{eq}}}}^{2} }}{{16B^{2} h^{3} E_{f} }}$$
(9)

In order to obtain the shear traction–separation law, CTSD were rigorously measured using the ARAMIS 3D DIC system. For this purpose, the pre-crack tip was identified in the first image and subsequently pairs of symmetrical facets to the expected fracture plane in the initial picture were carefully selected. According to this, each top subset (+ 1, + 2, + 3, …) was paired with its lower symmetrical subset (− 1, − 2, − 3, …) (Fig. 7). The displacements in the direction of the fracture plane were then post-processed for each loading step and for each selected pair of facets. It should be noted that the CTSD determination was always started considering the subsets pair closest to the crack tip (+ 1 and − 1). However, to avoid facets near discontinuities and damage areas, each subset of data was verified to be recognized successfully in each of the recorded images. A sensitivity analysis was therefore systematically performed. This validation process was carried out by observing if there were discontinuities in the u-δ curve. In addition, it was verified that each facet of a subset pair was on the opposite side of the crack during the test, as the crack propagation could place them on the same arm.

Fig. 7
figure 7

Scheme of the subsets pair location (squares) used for the determination of CTSD

Full size image

Finally, CTSD (u) was evaluated as the relative displacement between each set of facets as follows (Sousa et al. 2010, 2011)

$$u = \left\| {u^{ + } } \right. - \left. {u^{ - } } \right\|$$
(10)

where \(u^{ + }\) and \(u^{ - }\) are the displacement components parallel to the crack surface (Fig. 8) associated with the subsets described above and \(\left\| {\left. {\,\cdot\,} \right\|} \right.\) represents the Euclidean norm.

Fig. 8
figure 8

Scheme of the ENF test with the speckle pattern at the crack tip area of the specimen during testing

Full size image

In order to obtain τ, a continuous function was fitted to GII-u. There are different ways to address this problem adequately.

In this sense, relevant research available in the literature (Oliveira et al. 2021; Gómez-Royuela et al. 2022) has shown that a 4-parameter logistic model is a useful tool for fitting calibration curves of this shape. Therefore, in this study, a 4-parameter logistic function (Rodbard 1974; Rodbard and Hutt 1974) was fitted by least squares through successive approximations according to the following expression

$$G_{{{\text{II}}}} = \frac{{A_{1} - A_{2} }}{{1 + \left( {{u \mathord{\left/ {\vphantom {u {u_{0} }}} \right. \kern-\nulldelimiterspace} {u_{0} }}} \right)^{p} }} + A_{2}$$
(11)

where A1, A2, u0 and p are fitting constants by regression analysis. It should be noted that this function is used as a tool to smooth the noise before deriving Eq. (2). In this way, τ can be determined as follows

$$\tau = - \frac{{p(A_{1} - A_{2} )({u \mathord{\left/ {\vphantom {u {u_{0} )^{p - 1} }}} \right. \kern-\nulldelimiterspace} {u_{0} )^{p - 1} }}}}{{u_{0} \left( {1 + ({u \mathord{\left/ {\vphantom {u {u_{0} )^{p} }}} \right. \kern-\nulldelimiterspace} {u_{0} )^{p} }}} \right)^{2} }}$$
(12)

The A2 parameter in Eqs. (11) and (12) should provide an estimation of the critical strain energy release rate according to Eq. (13).

$$A_{2} = \mathop {\lim }\limits_{u \to \infty } G_{{{\text{II}}}} = G_{{{\text{IIc}}}}$$
(13)

On the other hand, this methodology has been successfully applied in other relevant research available in the literature (e.g. Pereira et al. 2018; Majano-Majano et al. 2020).

Numerical validation

In order to verify the appropriateness of the experimental procedure followed to determine the shear traction–separation law according to the direct method (Eq. (12)), a numerical law similar to the experimental one (Eq. (12)) was implemented in ABAQUS® v2021 (Abaqus 2021), a commercial finite element software. Since the fracture plane will remain the same throughout the thickness of the specimen, a 2D analysis was performed using CZM. To obtain accurate results, a refined mesh was performed in the crack growth region according to the scheme in Fig. 9. A total of 2070 8-node (CPS8R) quadratic plane stress elements were used to model the ENF specimen. 148 6-node quadratic cohesive surfaces were used to simulate fracture propagation at the plane located at half-height, as shown in Fig. 9. 73 of these 148 elements belong to the refined zone. The Newton–Cotes integration scheme was used in the elements (Gonçalves et al., 2000). The analyses were carried out considering nonlinear geometric behaviour. Implicit nonlinear analysis was considered and the Newton–Raphson convergence method was used to solve the systems of nonlinear equilibrium equations. The model was loaded applying 20 mm displacement (δ) at the mid-span of the specimen in increments no greater than 0.02 mm in order to obtain a smooth crack growth and accurate results.

Fig. 9
figure 9

Scheme of the numerical model with the refined mesh

Full size image
Table 1 Numerical parameters of the exponential shear traction–separation law. Maximum shear strength (τu), initial stiffness (k), ultimate displacement at which fibre breaks (uu), rate of damage evolution (α) and critical fracture energy in mode II (GIIc)
Full size table

Recent research available in the literature uses simple shapes to define the softening region of the shear traction–separation law, such as linear or bilinear softening, to simulate crack growth in wood (de Moura et al. 2009b; Xavier et al. 2014b; de Moura et al. 2018). In this study, an exponential softening relationship (Fig. 10) was implemented using standard items in ABAQUS to reproduce stable propagation of the crack in Mode II according to the experimental test. This shape provides very good fit to the experimental cohesive laws.

Fig. 10
figure 10

Exponential shear traction–separation law implemented in ABAQUS. Separation (u) and shear traction (τ)

Full size image

This fracture behaviour is characterised by an initial undamaged linear elastic branch until the maximum shear stress τu is reached at the peak of the curve, which is associated with the corresponding crack opening u0. This undamaged stage is defined by Eq. (14).

$$\tau = k\,u$$
(14)

where u is the CTSD and k is the initial interface stiffness considered by the user, usually known as the penalty parameter. It should be noted that being rigorous with the proposed data reduction scheme in “Experimental direct data reduction method” section the initial stiffness implemented in the numerical model could be taken directly from the second derivative of Eq. (11). However, this would lead to a greater consumption of computational resources and also in many situations to use unsound values of k, since the logistic curve shape leads to a stiffness close to zero in the first loading step, something that has no physical meaning in this material. According to this, the initial stiffness used in the numerical solution was the slope of the fitted line between the origin (u = 0 and τ = 0) and the peak of the curve given by Eq. (12) (u = u0 and τ = τu). The k values used are summarized in Table 1.

The second branch of the shear traction–separation law is a softening stage corresponding to the development of the FPZ. After achieving maximum local strength (τu), the material behaves in a nonlinear way and the largest slope zone (first descending branch) and the lowest slope zone represent microcracking and fibre-bridging, respectively. The ultimate crack growing (uu) is defined from the fracture energy GIIc. The shear traction–separation relationships at this part of the law are established according to Eq. (15):

$$\tau = \left( {1 - d} \right)k\,u$$
(15)

where d is the damage parameter, which is determined from the shear traction–separation law as a function of u according to Eq. (16). It varies between 0 and 1, with 0 if there is no material damage and 1 when the rupture is reached.

$$d = \frac{{1 - e^{{ - \alpha \left( {\frac{{u - u_{0} }}{{u_{u} - u_{0} }}} \right)}} }}{{1 - e^{ - \alpha } }}$$
(16)

being α a nondimensional parameter that defines the rate of damage evolution. A value of α = 6 was adopted, since it turned out to be a representative value that fits the damage branch given by Eq. (12). Knowing GIIc, the final CTSD (uu) can be obtained by integrating the area under the function given in Fig. 10. The values considered to determine the shape of the shear traction–separation law are listed in Table 1, which correspond to the average experimental values obtained in “Results and discussions” section. To consider the inherent variability of wood properties, two additional separation laws were implemented in the numerical validation, which are listed in Table 1 and represent the upper and lower limits of the shear traction–separation laws. These additional laws were derived by applying the standard deviation (St. Dev.) to the mean values, as detailed in “Shear traction-separation laws” section.

The mean values of the elastic constants of European beech used as input data in the numerical models were taken from previous work by the authors (Gómez-Royuela et al. 2021) and EL was altered in such a way that the initial slope of the experimental P-δ curves was correctly predicted. These values are summarized in Table 2.

Table 2 Elastic properties of Fagus sylvatica L. used in numerical validation (Gómez-Royuela et al. 2021)
Full size table

Results and discussions

R-curves

The experimental P-δ curves (in grey) obtained from the ENF tests for the RL and TL propagation systems are shown in Fig. 11. They also include the numerical P-δ curves using the exponential shear traction–separation laws and elastic constants specified in Tables 1 and 2. Likewise, numerical P-δ curves considering the upper and lower limits of the experimental shear traction–separation laws are represented (dotted and dashed lines, respectively), whose values are summarized in Table 1 and the laws can be seen in “Shear traction-separation laws” section.

Fig. 11
figure 11

Experimental and numerical P-δ curves from ENF tests in both RL (left) and TL (right) propagation systems

Full size image

The experimental curves of both crack propagation systems show consistent results despite the typical variability that surrounds a material such as wood. It should be noted that RL propagation system shows higher ultimate load and less scatter in the curves than the TL direction. In addition, the stiffness of both groups is quite similar. Initial compliance (C0) was calibrated using the straight branch of the experimental P-δ curves. This procedure was addressed by linear regression applying the least-squares method obtaining coefficients of determination R2 > 0.999. This value is used to fit Ef and thus avoid determining this property in each ENF test. The numerical curves obtained are consistent with the experimental ones. Furthermore, the numerical curves that represent the upper and lower limits of the shear traction-separation laws prove to be able to explain the variability of the wood.

In Fig. 11, it can be seen that both groups showed nonlinear behaviour before the curve reached the maximum load. This fact reveals that the influence of the FPZ developed ahead of the crack tip cannot be ignored. This is a typical behaviour of quasi-brittle materials such as wood. This phenomenon has also been observed by other authors for different wood species (Xavier et al. 2014b; Majano-Majano et al. 2020) and develops microcracks and fibre-bridging. This fact highlights the difficult task of accurately monitoring crack propagation during testing. In this sense, it seems appropriate to use the data reduction scheme based on an equivalent crack length concept to determine GII (de Moura et al. 2006). Typical macroscopic visualisation of the different stages during crack propagation and the absolute displacement fields (X,Y,Z) of the crack tip corresponding to the maximum load state (point 3) are shown in Fig. 12a, b, respectively.

Fig. 12
figure 12

a Macroscopic visualization of the different stages during crack propagation of the ENF TL 14 specimen and corresponding P-δ and P-CTSD curves; b absolute displacement fields (X,Y,Z) of the crack tip corresponding to point 3

Full size image

From Fig. 12b, it can be deduced that the relative displacements in the Y and Z directions are negligible. This fact verifies that the choice of an ENF test set-up is adequate to evaluate fracture mode II, since the relevant displacements occur in the X direction. Therefore, disregarding the displacements in the Y and Z directions does not imply a significant error.

The experimental and numerical R-curves obtained from both crack propagation systems are shown in Fig. 13. These curves describe the evolution of GII as a function of aeq and are a useful tool to determine the critical fracture energy. According to them, GII increases its value until it stabilizes, drawing a plateau. The transition between these two branches is not linear and, therefore, the influence of the FPZ can again be observed. However, in all cases, a horizontal branch is clearly evident, revealing stable crack growth. This fact verifies the suitability of the proposed method (CBBM).

Fig. 13
figure 13

R-curves from experimental and numerical ENF tests in both RL (left) and TL (right) crack propagation systems

Full size image

GIIc was determined as the average value of the points that belong to the horizontal branch. Numerical R-curves were obtained using the numerical P-δ curves. As can be observed, the numerical R-curves fit quite well with the experimental ones. In addition, the upper and lower limit curves encompass the dispersion of the experimental curves. These results justify the validity of the experimental procedure followed to obtain the fracture properties of Fagus sylvatica L.

The results of C0, Ef, maximum load (Pmax) and critical fracture energy (GIIc) obtained from each ENF test in both RL and TL crack propagation systems are listed in Tables 3 and 4, respectively. Additionally, the mean, St. Dev., and coefficient of variation (CoV) values are also shown in those tables. The average value of the critical fracture energy obtained in RL system is significantly higher than in TL system. In particular, GIIc in RL is twice that of GIIc in TL. Furthermore, it should be noted that RL system shows less variability than TL. This can also be observed in Fig. 13. The maximum load (Pmax) in RL is again higher than in TL but, in this case, the difference is only 32%. On the other hand, the differences of C0 and Ef between the two fracture propagation systems are negligible.

Table 3 Density (ρ), corrected flexural modulus (Ef), maximum load (Pmax), initial compliance (C0) and critical fracture energy (GIIc) obtained in RL crack propagation system from the R-curves
Full size table
Table 4 Density (ρ), corrected flexural modulus (Ef), maximum load (Pmax), initial compliance (C0) and critical fracture energy (GIIc) obtained in TL crack propagation system from the R-curves
Full size table

The average value of GIIc for Fagus sylvatica L. resulted in 2.29 N/mm (7.5% CoV) and 1.17 N/mm (22.1% CoV) in RL and TL crack propagation systems, respectively. This mean value in RL system is higher than that of other species such as Pinus pinaster, which according to Xavier et al. (2014b) has a GIIc value of 1.15 N/mm, or Eucalyptus globulus L., which according to Majano-Majano et al. (2020) shows a GIIc value of 1.54 N/mm.

Representative pictures of the specimen cross section and the fractured surface observed after crack propagation for both RL and TL propagation systems can be seen in Fig. 14. The fracture surface shows the rays crossing the wood in the radial direction, significantly affecting crack propagation in the RL system, which may explain the considerably higher values of fracture energy in RL with respect to the TL.

Fig. 14
figure 14

Representative ENF specimens after testing in RL (a) and TL (b) crack propagation systems: (1) cross section; (2) fracture surface of the two parts of the specimen; (3) oblique view of the fracture surface; (4) detail of the fracture surface

Full size image

Shear traction-separation laws

The shear traction-separation law describes the evolution of τ as a function of CTSD (u). The area under the τ-u curve corresponds to the GIIc value. To guarantee a correct characterization of the fracture properties in mode II, the presence of crack tip opening displacement (CTOD) during the test must be negligible, as otherwise part of the energy in mode I would be erroneously computed as fracture energy in mode II. This is a relevant aspect in the proposed data reduction scheme. To verify this, the influence of CTSD and CTOD was analysed as a function of the displacement (δ) applied to the ENF specimen. The CTOD measurement method is detailed in Gómez-Royuela et al. (2022). The results of a representative test in both RL and TL crack propagation systems are shown in Fig. 15.

Fig. 15
figure 15

Evaluation of normal CTOD (Mode I) and parallel CTSD (Mode II) with respect to applied displacement (δ) in both RL (left) and TL (right) crack propagation systems

Full size image

The results reveal that CTOD in Mode I is negligible, which means that the ENF test set-up followed is appropriate to determine GIIc, since the influence of Mode I on Mode II is very low. The evolution of GII as a function of u from the experimental tests is shown in Fig. 16. Such evolution of GII until reaching GIIc (plateau value in the R-curves) is smoother in the RL crack propagation system compared to TL, where the transition is more abrupt. This fracture behaviour reveals a greater influence of the FPZ in the RL system than in the TL, as a result of the toughening mechanisms such as microcracks and fibre-bridging.

Fig. 16
figure 16

Experimental GII-u relationship in both the RL (left) and TL (right) crack propagation systems

Full size image

With the main objective of reducing the noise from the experimental data and having a continuous and smooth function that can be derived to determine the shear traction–separation law, a logistic-type function (see “Experimental direct data reduction method” section) was fitted to each experimental GII-u curve. A representative example in both crack propagation systems is shown in Fig. 17, from which a good approximation can be observed. It should be noted that the same set of data points considered for determining GIIc according to “R-curves” section has been taken into account for this fitting procedure.

Fig. 17
figure 17

Logistic function fitting to the ENF RL 01 (left) and ENF TL 06 (right) test results

Full size image

All the experimental and the average shear traction-separation laws of both RL and TL fracture systems of Fagus sylvatica L. are shown in Fig. 18. Consistent results can be observed. The fitting parameters A1, A2, u0 and p of the logistic curves for the RL and TL systems are listed in Tables 5 and 6, respectively. It should be clarified that the fit parameter A2 is a direct estimate of GIIc. Furthermore, Glaw,II corresponds to the area under the logistic fit curve shown in Fig. 18. It should be noted that the mean curve (black line) shown in Fig. 18 is obtained using the average values of parameters A1, A2, u0 and p listed in Tables 5 and 6. However, this mean curve does not result in the mean values of Glaw,II, τu and uu. The average value of the maximum local shear stress (τu) in the RL direction resulted in 57% higher than in the TL.

Fig. 18
figure 18

Experimental (in grey) and average (in black) shear traction–separation laws in mode II for RL (left) and TL (right) crack propagation systems

Full size image
Table 5 Parameters of the logistic function (A1, A2, u0, p), maximum shear stress (τu), fracture energy of the shear traction–separation law (Glaw,II) and maximum relative displacement (uu) for RL crack propagation system
Full size table
Table 6 Parameters of the logistic function (A1, A2, u0, p), maximum shear stress (τu), fracture energy of the shear traction–separation law (Glaw,II) and maximum relative displacement (uu) for TL crack propagation system
Full size table

In order to explain the inherent variability of this wood species, three numerical laws (average, upper limit and lower limit) were fitted to the experimental ones by applying the St. Dev. to the average law. The three logistic experimental laws (dashed lines) and exponential numerical laws fitted to the logistic experimental laws (solid lines) are shown in Fig. 19. It should be noted that the numerical laws implemented in FEA have the same GIIc value as that determined according to the experimental method detailed in “Experimental direct data reduction method” section and obtained as follows: first, logistic curves (Eq. (12)) were obtained varying the values of parameters A1, A2, u0 and p so that the area under the curves obtained (average law, upper limit law and lower limit law) is equal to GIIc determined according to the experimental method. The average value of the parameters A1, A2, u0 and p coincides with the average values given in Tables 5 and 6. The upper and lower limits of these parameters were determined by adding or subtracting a percentage (55% in this research work) of the St. Dev. to the mean values. The average value of GIIc coincides with the average value shown in Table 3 and Table 4. Likewise, the upper and lower limits of GIIc were determined by adding and subtracting, respectively, the St. Dev. to the average value of GIIc (Tables 3, 4). Then, for simplicity in FEA, the logistic curves were simplified to exponential curves (see Fig. 10), so that the area under the exponential curve is equal to the area of the logistic curve, thus ensuring that the GIIc implemented in the FEA is the same as that obtained from the experimental test. Furthermore, as a design criterion of the exponential curve, it was imposed that the point located at the tip of the logistic curve coincides with the point where the damage of the exponential curve begins (coordinates u0, τu). The parameters defining each of the exponential laws are summarised in Table 1. The load–displacement curves and respective R-curves ensuing from the numerical laws were obtained and included for comparison with the experimental results in Figs. 11 and 13. Overall, it can be settled that the limiting curves define well the observed experimental range, which reinforces the suitability of the proposed methodology.

Fig. 19
figure 19

Shear traction–separation laws: experimental laws (in grey); average, upper limit and lower limit of the logistic experimental laws (dashed lines); and exponential numerical laws fitted to the logistic experimental laws (solid lines). RL (left) and TL (right) crack propagation systems

Full size image

Conclusion

The experimental shear traction–separation law was obtained by the direct method, and CTSD was analysed by 3D DIC technique. This data reduction scheme was validated by finite element analysis implementing an exponential softening relationship. A cohesive zone model was used to reproduce crack propagation. Two additional shear traction–separation laws were implemented in the numerical validation, representing the upper and lower limits of the average law determined by applying the standard deviation to the mean value of GIIc. These additional laws prove to be able to explain the variability of the wood.

The GII fracture energy of European beech was derived by applying the CBBM, a data reduction method based on beam theory and on the equivalent crack length concept that only requires the P-δ curves data and not the measurement of crack propagation during the test, which would be a difficult task in wood and in the ENF test.

The average GIIc values were approximately twice as high in the RL crack propagation system (2.29 N/mm) as in TL (1.17 N/mm). However, the maximum load reached in the RL direction only represented 32% more than in TL. The ultimate shear stress (τu) of the shear traction–separation law in the RL system resulting from a logistic curve fitting was 57% higher than in the TL direction.

The results of GIIc and the shear traction–separation laws presented in this work are of great interest for the design of timber structures made of beech with the possibility of brittle failure involving mode II (e.g. dowel connections loaded at an angle to the grain, or beams with holes or notches), both for use in analytical expressions based on energy approaches for the prediction of load carrying capacity, and in numerical FEM using cohesive zone models where damage initiation and propagation need to be analysed.