Contact problem of two punches in an elastic coating attached to a porous material

Abstract

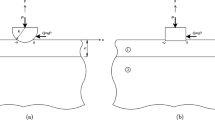
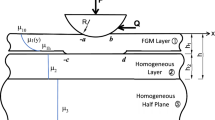
This paper investigates the contact problem of an elastic layer that is perfectly attached to a porous half-space by two rigid flat punches with collinear symmetry. Using integral transformation, the problem is condensed to a singular integral equation of the Cauchy type. Then, the exact expressions for the surface contact stress and surface interface displacement are provided. By using the Gauss–Chebyshev technique, the integral equations are solved numerically, and the variations of the unknown contact stresses and deformations for different parameters are addressed. The results indicate that stress concentration is typically higher on the outer edge of the contact area compared to the inner edge. This also explains why surface damage is more likely to occur on the outer edge in elastic and poroelastic materials. Due to the interaction between the two punches, there will be a superposition of normal displacements at the center. The deformation or bulging at the center can be managed by adjusting the parameter values, allowing the engineered material to fulfill its intended purpose. The potential applications of these research findings encompass safeguarding porous structures against contact-related deformation and damage.

Appendices

Appendix 1: Several lemmas and the proofs concerned

Lemma 1

The abnormal integral $\int_{0}^{\infty } {\sin (sx)} {\text{d}}s\;(x \ne 0)$ converges to $\frac{1}{x}(x \ne 0)$.

Proof

Let $\xi = sx$, then

$$ \int_{0}^{\infty } {\sin (sx)} {\text{d}}s = \left\{ {\begin{array}{*{20}c} {\int_{0}^{\infty } {\frac{s}{\xi }\sin \xi } {\text{d}}\xi ,} & {\xi > s}, \\ { - \int_{ - \infty }^{0} {\frac{s}{\xi }\sin \xi } {\text{d}}\xi }, & {\xi < s}. \\ \end{array} } \right. $$

By the accumulation of integral intervals $[0,\infty ) = [0,c] \cup [c,\infty ),( - \infty ,0] = ( - \infty , - c] \cup [ - c,0]$ and the Dirichlet discriminance, we know that $\int_{0}^{\infty } {\sin (sx)} {\text{d}}s\;(x \ne 0)$ is convergence. From the continuity of infinite integrals with parametric variables, we can obtain

$$ \int_{0}^{\infty } {\sin (sx)} {\text{d}}s = \int_{0}^{\infty } {\mathop {\lim }\limits_{{\delta \to 0^{ + } }} e^{ - \delta s} \sin (sx)} {\text{d}}s = \mathop {\lim }\limits_{{\delta \to 0^{ + } }} \int_{0}^{\infty } {e^{ - \delta s} \sin (sx)} {\text{d}}s, $$

then,

$$ \begin{gathered} I_{s} = \int_{0}^{\infty } {e^{ - \delta s} \sin (sx)} {\text{d}}s = - \frac{1}{\delta }\int_{0}^{\infty } {\sin (sx)} {\text{d}}(e^{ - \delta s} ) = \left. { - \frac{1}{\delta }\sin (sx)e^{ - \delta s} } \right|_{s = 0}^{\infty } + \frac{1}{\delta }\int_{0}^{\infty } {xe^{ - \delta s} \cos (sx)} {\text{d}}s \hfill \\ \;\;\; = - \frac{1}{{\delta^{2} }}\int_{0}^{\infty } {x\cos (sx)} {\text{d}}e^{ - \delta s} = \left. { - \frac{1}{{\delta^{2} }}x\cos (sx)e^{ - \delta s} } \right|_{s = 0}^{\infty } - \frac{1}{{\delta^{2} }}x^{2} \int_{0}^{\infty } {e^{ - \delta s} \sin (sx)} {\text{d}}s = \frac{1}{{\delta^{2} }}x - \frac{1}{{\delta^{2} }}x^{2} I_{s} . \hfill \\ \end{gathered} $$

So, we have

$$ I_{s} = \frac{x}{{\delta^{2} + x^{2} }} \Rightarrow \int_{0}^{\infty } {\sin (sx)} {\text{d}}s = \mathop {\lim }\limits_{{\delta \to 0^{ + } }} I_{s} = \frac{1}{x}. $$

□

Lemma 2

Cauchy convergence criterion: infinite integral $\int_{{m_{1} }}^{\infty } {f(x)} {\text{d}}x$ is convergence $\Leftrightarrow$$\forall \varepsilon > 0$, $\exists N > m_{1} \& N > 0$, $\forall p_{1} ,p_{2} > 0$, then $\left| {\int_{{p_{1} }}^{{p_{2} }} {f(x)} {\text{d}}x} \right| < \varepsilon$.

Lemma 3

Infinite integral $\int_{{m_{1} }}^{\infty } {f(x)} {\text{d}}x$ is convergence $\Leftrightarrow$$\forall m_{1} \ne m_{2}$, infinite integral $\int_{{m_{2} }}^{\infty } {f(x)} {\text{d}}x$ is convergence.

Appendix 2: Parameter values needed for plotting

Figure	Parameter value	Figure	Parameter value
Figure 4a	$\begin{aligned} & d = 1,N = 0.5,\nu _{e} = \nu _{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{P} = 0.5,\tilde{a} = 0,\tilde{b} = 1 \hfill \\ \end{aligned}$	Figure 4b	$\begin{aligned} & d = 0.25,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \mu = 1,\tilde{P} = 0.5,\tilde{a} = 0,\tilde{b} = 1 \hfill \\ \end{aligned}$
Figure 5a Figure 11 Figure 18 Figure 27	$\begin{aligned} & 2\tilde{a} = [0.05,0.1,0.5,1,5,10], \hfill \\ & d = 1,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{P} = 1,\tilde{b} = \tilde{a} + 2 \hfill \\ \end{aligned}$	Figure 5b Figure 12 Figure 19 Figure 28	$\begin{aligned} & \tilde{b} - \tilde{a} = [0.05,0.1,0.5,1,5,10], \hfill \\ & d = 1,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{P} = 1,\tilde{a} = 0.1 \hfill \\ \end{aligned}$
Figure 6a Figure 13 Figure 20 Figure 25	$\begin{aligned} & d = [0.001,0.01,0.1,1,5,10], \hfill \\ \tilde{P} = 1,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{a} = 0.1,\tilde{b} = 1 \hfill \\ \end{aligned}$	Figure 6b Figure 14 Figure 21 Figure 26	$\begin{aligned} & \mu = [0.5,1,2,5,8,10], \hfill \\ & d = 1,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \tilde{P} = 1,\tilde{a} = 0.1,\tilde{b} = 1 \hfill \\ \end{aligned}$
Figure 7a Figure 15 Figure 22 Figure 29	$\begin{aligned} & \nu_{e} = [0.01,0.05,0.1,0.3,0.4,0.5], \hfill \\ & d = 1,N = 0.5,\nu_{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{P} = 1,\tilde{a} = 0.1,\tilde{b} = 1 \hfill \\ \end{aligned}$	Figure 7b Figure 16 Figure 23 Figure 30	$\begin{aligned} & \nu_{p} = [0.01,0.05,0.1,0.3,0.4,0.5], \hfill & \\ d = 1,N = 0.5,\nu_{e} = 0.3, \hfill \\ & \mu = 0.5,\tilde{P} = 1,\tilde{a} = 0.1,\tilde{b} = 1 \hfill \\ \end{aligned}$
Figure 8a Figure 17 Figure 24 Figure 31	$\begin{aligned} & N = [0,0.001,0.01,0.1,0.5,0.7], \hfill \\ & d = 1,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{P} = 1,\tilde{a} = 0.1,\tilde{b} = 1 \hfill \\ \end{aligned}$	Figure 8b	$\begin{aligned} & \tilde{P} = [0.001,0.01,0.1,1,5,10], \hfill \\ & d = 1,N = 0.5,\nu_{e} = \nu_{p} = 0.3, \hfill \\ & \mu = 0.5,\tilde{a} = 0.1,\tilde{b} = 1 \hfill \\ \end{aligned}$