1 Introduction

A concentrated impact loading applied near a sharp edge of brittle materials can cause conchoidal fracture at the edge and permanently damage the materials. This mode of fracture, called edge chipping, is widely observed and well-known especially associated with the manufacturing process of cutting or machining brittle materials (Mohajerani and Spelt 2009). Edge chipping during the manufacturing process not only affects the geometric accuracy and surface finish of manufactured products but also could be the source of potential failure. Therefore, it is important to understand the conditions under which edge chipping occurs and to predict the damage states of materials.

The mechanism of edge chipping has been intensively studied by indentation experiments. In the early works, Almond and McCormick (1986) examined the chipping of various brittle materials using a conical diamond indenter and observed that the size of chip scars depended on the indentation distance d (distance between an indentation point and an edge). Also, several studies investigated the critical indent force F required for edge chipping. Chai and Lawn (2007b) found that F linearly relates to \(d^{1.5}\). Other studies show a linear correlation between F and d (Morrell and Gant 2001; Chai and Lawn 2007a; Gogotsi et al. 2007; Gogotsi and Mudrik 2009). The ratio of F to d is referred to as “edge toughness”. The edge toughness depends only on the investigated material and the indenter geometry (Danzer and Hangl 2001). Therefore, several attempts have been made to predict the fracture toughness \(K_c\) from the edge toughness whose value is given by the edge chipping test (Danzer and Hangl 2001; Morrell and Gant 2001; Chai and Lawn 2007b; Gogotsi et al. 2007; Gogotsi and Mudrik 2009; Gogotsi 2013). For example, Chai and Lawn (2007b) performed the edge chipping tests of soda-lime glass by Vickers indentation and reported that they were able to provide the value of \(K_c\) directly from the critical indent force F to within an accuracy of about 25%.

In addition to these analytical studies, the chip morphology has also been investigated in detail. The chipping process is quite different between sharp indenters (e.g., Vickers and Knoop indenters) and blunt spherical indenters (e.g., Rockwell indenters). Under quasi-static loading by the sharp indenter, median cracks from the tip of the indenter extend stably along the loading direction and form a penny-shaped crack (Chai and Lawn 2007b). This penny-shaped crack veers to the side wall of the specimen and removes a chip. On the other hand, cracks are not penny-shaped under quasi-static loading by the blunt spherical indenter. Instead, they form a Hertzian surface ring crack and grow downward to be conical shape; see Fig. 1. While its lateral expansion is stopped by intersecting the side wall, its downward extension continues in a curve path until it again intersects the side wall and removes a chip (Gogotsi and Mudrik 2010; Mohajerani and Spelt 2010; Chai 2011).

Most of these previous experimental studies on edge chipping have been limited to quasi-static loading. In spite of the fact that edge chipping commonly occurs under dynamic loading, a limited number of works deal with edge chipping by dynamic loading. For example, Chai and Ravichandran (2009) studied edge chipping of soda-lime glass by the impact of Vickers and spherical tip projectiles. They reported that the Vickers impactor formed median cracks from the contact point while the spherical impactor produced a cone crack starting from the contact point; these features are similar to those under quasi-static loading. However, as the impact force increased, the spherical blunt indenter formed cracks similar to penny-shaped median cracks as seen in sharp indentation. Morrell (2005) also studied edge chipping of brittle materials by the impact of a tungsten carbide WC ball. Although the crack pattern (i.e., penny shape or Hertzian cone) was not discussed in this study, the chip geometries shown in the results were rather penny-shaped cracks. In addition to these studies, Mohajerani and Spelt (2011) investigated edge chipping of borosilicate glass by the low-velocity impact of ceramic and steel balls and observed the Hertzian cone crack. Therefore, in the relatively high range of impact force, it is concluded that the blunt indenter also forms a penny-shaped median crack which is generally observed under the impact of sharp indenters.

Fig. 1
figure 1

Schematic model of chip scar: a penny-shaped crack, b Hertzian cone crack

Full size image

Although tremendous effort has been paid for experimental research on edge chipping, there have been very few numerical studies because of the complex 3D nature of edge chipping. Cao (2001) performed the finite element analysis to investigate the size of chip scars as related to loading conditions and intrinsic flaws of materials. Chai and Ravichandran (2007) also performed a brittle-fracture analysis in conjunction with the finite element analysis to elucidate the effect of the inclination angle of indenters on the chip morphology and the indentation force. However, these numerical analyses employed the idealized two-dimensional plane strain model. Also, many fracture analysis methods have been proposed in these two decades such as eXtended finite element method (XFEM) (Belytschko and Black 1999; Moës et al 1999; Belytschko et al. 2001), FEM with cohesive zone model (CZM) (Shet and Chandra 2002; Volokh 2004), Peridynamics (Silling 2000; Silling et al. 2007), and lattice model (Martín et al. 2000; Braun and Fernández-Sáez 2014, 2016; Braun and González-Albuixech 2019; Braun et al. 2021). These analysis methods have been successfully applied to a wide variety of fracture phenomena. Nevertheless, to the best of our knowledge, no previous studies have successfully simulated the complex 3D geometry of edge chipping.

In this study, we perform numerical analyses to reproduce the 3D crack morphology observed in edge chipping. The numerical analyses presented in this paper target edge chipping of glass by impact loading because edge chipping mostly occurs under impact loading. Since this type of problem involves dynamic loading accompanied by stress wave propagation and energy dissipation at collision, it is much more difficult to simulate than quasi-static loading. For the numerical analyses, we extend Particle Discretization Scheme Finite Element Method (PDS-FEM) (Hori et al. 2005; Oguni et al. 2009; Wijerathne et al. 2009; Hirobe et al. 2021a) developed by the authors to be able to simulate fracture due to impact loading. The crack morphologies given by our numerical analysis results are investigated with considerations of the impact force and the impact distance from the edge of the side wall of the specimen.

2 Numerical analysis method

In this study, we used the numerical analysis method based on PDS-FEM which was developed by the authors. PDS-FEM is one of the fracture analysis methods, and its detailed formulation has already been presented in the authors’ previous works (Hirobe et al 2021b; Hirobe et al. 2021a). For the simulations of edge chipping by impact loading, we extend PDS-FEM to analyze the fracture and the collision of two objects simultaneously. Here, we first introduce the overview of PDS-FEM formulations. Then, we present the impact analysis method using PDS-FEM formulation in Sect. 2.2. Einstein’s summation convention is employed for subscripts that describe indices in letters throughout this paper.

2.1 Overview of PDS-FEM

PDS-FEM applies the particle discretization to the field variables using a pair of conjugate geometries; see Fig. 2. The Delaunay tessellation becomes a set of triangles in the two-dimensional case and a set of tetrahedrons in the three-dimensional case. The field variables are discretized by using the following discontinuous shape functions defined on the respective Voronoi tessellations and the Delaunay tessellations.

$$\begin{aligned} \phi ^\alpha ({{\varvec{x}}})= \left\{ \begin{array}{ll} 1 &{} ({{\varvec{x}}} \in {\Phi }^\alpha ) \\ 0 &{} ({{\varvec{x}}} \notin {\Phi }^\alpha ) \end{array} \right. \end{aligned}$$
(1)
$$\begin{aligned} \psi ^\beta ({{\varvec{x}}})= \left\{ \begin{array}{ll} 1 &{} ({{\varvec{x}}} \in {\Psi }^\beta ) \\ 0 &{} ({{\varvec{x}}} \notin {\Psi }^\beta ) \end{array} \right. \end{aligned}$$
(2)

where \({{\varvec{x}}}\) is a position, \(\Phi ^\alpha \) is the \(\alpha \)-th Voronoi tessellation and \(\Psi ^\beta \) is the \(\beta \)-th Delaunay tessellation. The displacement field \(u_i ({{\varvec{x}}})\) is discretized on the Voronoi tessellations as

$$\begin{aligned} u_i ({{\varvec{x}}})= \sum ^{N}_{\alpha = 1}u_i^{\alpha } \phi ^\alpha ({{\varvec{x}}}) \end{aligned}$$
(3)

where N is the number of Voronoi tessellations. The physical quantities related to the spatial derivatives of the displacement field are discretized on the Delaunay tessellations as

$$\begin{aligned}{} & {} \epsilon _{ij} ({\varvec{x}})= \sum ^{M}_{\beta = 1}\epsilon _{ij}^{\beta } \psi ^\beta ({\varvec{x}}) \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \sigma _{ij} ({\varvec{x}})= \sum ^{M}_{\beta = 1}\sigma _{ij}^{\beta } \psi ^\beta ({\varvec{x}}) \end{aligned}$$
(5)

where \(\epsilon _{ij}^{\beta }\) and \(\sigma _{ij}^{\beta }\) are the strain tensor and the stress tensor, respectively. According to these discontinuous and non-overlapping shape functions, the displacement field can be regarded as the translational motion of the rigid body particles defined by the Voronoi tessellations. Such particle description enables the easy treatment of fracture.

Fig. 2
figure 2

The conjugate geometries used for discretization of field variables

Full size image

For the sake of simplicity, two-dimensional PDS-FEM formulation is provided here. The displacement–strain matrix \(B_i^{\beta \alpha }\) for the triangular element \({ \Psi }^{\beta }\) is given as

$$\begin{aligned}{} & {} B_i^{\beta \alpha } = \frac{1}{\Psi ^\beta } \int _{\Psi ^\beta } \phi _{,i}^\alpha \, \psi ^\beta dV \nonumber \\{} & {} \quad = \frac{1}{{ \Psi }^\beta } \left( \int _{\partial { \Phi }^{\alpha \gamma } \cap { \Psi }^\beta } n_i^{\alpha \gamma } dS + \int _{\partial { \Phi }^{\alpha \zeta } \cap { \Psi }^\beta } n_i^{\alpha \zeta } dS \right) \end{aligned}$$
(6)

where \(\partial { \Phi }^{\alpha \gamma }\) is the boundary of the \(\alpha \)-th Voronoi tessellation adjacent to the \(\gamma \)-th Voronoi tessellations (see Fig. 2), and \(n_i^{\alpha \gamma }\) is the outward unit normal vector of the \(\alpha \)-th Voronoi tessellation on \(\partial { \Phi }^{\alpha \gamma }\): likewise for \(\partial { \Phi }^{\alpha \zeta }\), and \(n_i^{\alpha \zeta }\). Then, the stiffness matrix \(K_{ik}^{\alpha \gamma }\) is defined as

$$\begin{aligned} K_{ik}^{\alpha \gamma }= & {} \sum _{\beta = 1}^{M}B_j^{\beta \alpha }c_{ijkl}^\beta B_l^{\beta \gamma }{ \Psi }^\beta \end{aligned}$$
(7)

where M is the number of Delaunay tessellations and \(c_{ijkl}^\beta \) is the material constant. Despite the discontinuous shape functions, the components of \(B_i^{\beta \alpha }\) and \(K_{ik}^{\alpha \gamma }\) are identical to those of the displacement–strain matrix for the conventional FEM of triangular elements with linear shape functions. According to this, PDS-FEM provides the rigorous particle description for the deformable solid continuum.

The particle description in PDS-FEM enables the definition of the Hamiltonian formulation for the solid continuum. The Hamiltonian H for the motion of the set of the Voronoi particles is given as

$$\begin{aligned} H = \sum _{\alpha = 1}^{N} \frac{1}{2m^\alpha } p_i^\alpha p_i^\alpha + \sum _{\alpha = 1}^{N} \sum _{\gamma = 1}^{N} \frac{1}{2} K_{ij}^{\alpha \gamma } q_i^\alpha q_j^\gamma \end{aligned}$$
(8)

where \(p_i^\alpha \) is the generalized momentum and \(q_i^\alpha \) is the generalized coordinates. Therefore, the dynamic behavior of the solid continuum is given by solving the following Hamilton’s equations.

$$\begin{aligned} \dot{q}_i^\alpha= & {} \frac{\partial H}{\partial p_i^\alpha } = \dot{u}_i^\alpha \end{aligned}$$
(9)
$$\begin{aligned} \dot{p}_i^\alpha= & {} -\frac{\partial H}{\partial q_i^\alpha } = -\sum _{\gamma = 1}^{N} K_{ij}^{\alpha \gamma } u_j^\gamma \end{aligned}$$
(10)

In PDS-FEM, the fracture is expressed as the loss of the interaction between two adjacent Voronoi tessellations; this is expressed as setting the surface integral in Eq. (6) on the fractured Voronoi boundary to zero. For example, when the boundary between the \(\alpha \)-th Voronoi particle \({ \Phi }^\alpha \) and the \(\gamma \)-th Voronoi particle \({ \Phi }^\gamma \) fractures,

$$\begin{aligned}{} & {} \int _{\partial { \Phi }^{\alpha \gamma } \cap { \Psi }^\beta } n_i^{\alpha \gamma } dS =0. \end{aligned}$$
(11)

2.2 Impact analysis

To analyze the edge chipping by impact loading, we incorporate the following impact analysis method in PDS-FEM. Here, for example, we consider the case in which the impactor collides with a glass material. The glass material is modeled as a set of Voronoi particles presented in section 2.1 and the impactor is set as a rigid body. When the \(\alpha \)-th Voronoi particle collides with the impactor, the velocities of the \(\alpha \)-th Voronoi particle and the impactor are changed to satisfy the momentum conservation law:

$$\begin{aligned} v_i^{\alpha \prime }= & {} \frac{ v_i^\alpha (m^\alpha -e^{ipt} M)+V_i(M-e^{ipt} M)}{m^\alpha +M} \end{aligned}$$
(12)
$$\begin{aligned} V_i^{\prime }= & {} \frac{ V_i(M-e^{ipt} m^\alpha )+v_i^\alpha (m^\alpha -e^{ipt} m^\alpha ) }{m^\alpha +M} \end{aligned}$$
(13)

where \(v_i^\alpha \) is the velocity of \(\alpha \)-th Voronoi particle, \(V_i\) is the velocity of the impactor, M is the mass of the impactor, \(e^{ipt}\) is the coefficient of restitution between the glass and the impactor, and the prime mark expresses the velocity after collision.

We should also consider the collision between Voronoi particles, whose boundary is fractured, in the glass material to avoid overlap of Voronoi particles. This is because the fractured Voronoi particles have no interaction with each other and the repulsive force does not work even when they mutually approach. When the boundary between the \(\alpha \)-th Voronoi particle \({ \Phi }^\alpha \) and the \(\gamma \)-th Voronoi particle \({ \Phi }^\gamma \) is fractured and also these two Voronoi particles collide with each other, the velocities of these Voronoi particles are changed to satisfy the momentum conservation law as the same manner as the collision between the glass and the impactor:

$$\begin{aligned} v_i^{\alpha \prime }= & {} \frac{ v_i^\alpha (m^\alpha -e^{gls} m^\gamma )+v_i^\gamma (m^\gamma -e^{gls} m^\gamma )}{m^\alpha +m^\gamma } \end{aligned}$$
(14)
$$\begin{aligned} v_i^{\gamma \prime }= & {} \frac{ v_i^\gamma (m^\gamma -e^{gls} m^\alpha )+v_i^\alpha (m^\alpha -e^{gls} m^\alpha )}{m^\alpha +m^\gamma } \end{aligned}$$
(15)

where \(e^{gls}\) is the coefficient of restitution between the glasses.

3 Numerical analysis setting

In this study, we perform numerical analyses for edge chipping by impact loading near the edge of brittle materials. As shown in Fig. 3, our numerical analyses intend to model the surface-normal impact loading on a rectangular soda-lime glass plate; glass is the ideal brittle material and also the most frequently used material in the experiment of edge chipping. The impactor is the rigid steel sphere. The impact point is located at (X/2, 0.0, \(Z-d\)) as shown in Fig. 3, where d is the distance between the impact point and the side wall of the glass plate. The displacement of \(x=0,\, X\) surfaces are constrained in x-direction, the displacement of \(z=0,\ Z\) surfaces is constrained in z-direction, and the displacement of \(y=0\) surface is constrained in y-direction. \(z=Z\) surface is referred to as “chipping wall” in this paper. The material properties of the soda-lime glass plate and the steel sphere are shown in Table 1. The value of the surface energy of the soda-lime glass was extracted from Wiederhorn (1969) at \(300\mathrm {\,Kelvin}\).

We prepared the finite element model with unstructured tetrahedral mesh for the soda-lime glass plate. In the numerical analyses, the diameter of the rigid sphere, the velocity of the spherical impactor at impact \(V_0\), and the impact distance d were varied. We performed two sets of numerical analyses: one was for analyzing the crack morphology of edge chipping and the other was for analyzing the chipping size.

The numerical analyses using PDS-FEM were performed with the constant time step \(\Delta t\) which satisfies the Courant-Friedrichs-Lewy (CFL) condition. We employed the fourth-order bilateral symplectic algorithm (Casetti 1995) for the time integration scheme to solve the Hamilton’s equations (Eqs. 9 and 10). At each time step, the collision determination with the spherical indenter was performed on all Voronoi particles of the glass plate. Also, the collision determination between Voronoi particles of the glass plate was performed on all fractured Voronoi particles. Then, if these collisions occur, the velocities of the spherical impactor and Voronoi particles are modified based on Eqs. 12–15. In addition to the collision determination, all the Voronoi boundaries adjacent to the already fractured boundaries were examined whether they satisfy the fracture criterion at each time step. For the fracture criterion, the Griffith energy criterion (Griffith 1921) was used. The detailed formulation of this criterion in the framework of PDS-FEM is shown in our previous researches (Hirobe et al. 2021a; Hirobe et al 2021b).

Fig. 3
figure 3

Schematic view of the analysis setting

Full size image
Table 1 Material properties of soda-lime glass and steel sphere
Full size table

4 Results

4.1 Mesh dependency

We performed the preliminary analysis to verify the mesh size dependency of the analysis results. The diameters of the spherical impactor was \(10{\,{\upmu }\hbox {m}}\) and the impact velocity \(V_0\) was \(2000\mathrm {\,m/s}\). The impact distance d was set as \(15{\,{\upmu }\hbox {m}}\). Here, we employed the small spherical impactor and the high impact velocity because this condition reproduces fine and complex crack patterns. We prepared two kinds of finite element models for the glass plate with different mesh sizes. For the coarse mesh, the number of nodes is 4,546,697, the number of elements is 27,613,669, and the average nodal distance \(l_{avg}\) is \(0.6{\,{\upmu }\hbox {m}}\). For the fine mesh, the number of nodes is 35,593,456, the number of elements is 219,872,596, and the average nodal distance \(l_{avg}\) is \(0.3{\,{\upmu }\hbox {m}}\). The dimension (\(X\times Y\times Z\)) of the finite element model for the glass plate was set as \(0.15\times 0.15\times 0.06\,\textrm{mm}\).

Figure 4 shows the comparison of the crack morphologies between two kinds of finite element models with different mesh sizes. In Fig. 4, the upper figure is a perspective view, the lower left figure is a front view, and the lower right figure is a side view; see view angles in Fig. 5. Though the rough shapes of the cracks agree with each other, the Hertzian cone crack (explained in sect. 4.2) is reproduced more clearly in the fine mesh than the coarse mesh. Therefore, we use the finite element models whose average nodal distance is \(0.3{\,{\upmu }\hbox {m}}\) hereafter.

Fig. 4
figure 4

Comparison of crack morphologies between two kinds of finite element model with different mesh size

Full size image
Fig. 5
figure 5

View angles for figures of numerical analyses results

Full size image

4.2 Crack morphology

Table 2 Numerical analysis cases for analyzing the crack morphology
Full size table

Table 2 shows the numerical analysis cases for analyzing the crack morphology of edge chipping; the analysis cases shown by round mark in Table 2 were performed. The diameters of the spherical impactor were set as \(25{\,{\upmu }\hbox {m}}\) and \(50{\,{\upmu }\hbox {m}}\). The impact distance d was set as \(1.0,\,2.5,\,5.0,\,10,\,15{\,{\upmu }\hbox {m}}\). The impact velocity \(V_0\) was varied between \(100-800\mathrm {\,m/s}\) in \(100\mathrm {\,m/s}\) increments. These analysis settings assume the edge chipping in the cutting process of glass. This edge chipping might be caused by the contact of very sharp points generated by folding and cutting of glass. Therefore, we employed the small spherical impactors and the short impact distances. In the numerical analysis cases shown in Table 2, the dimension (\(X\times Y\times Z\)) of the finite element model for the glass plate was set as \(0.15\times 0.15\times 0.06\,\textrm{mm}\) and \(0.2\times 0.2\times 0.08\,\textrm{mm}\) for the analyses with \(\phi \,25{\,{\upmu }\hbox {m}}\) and \(\phi \,50{\,{\upmu }\hbox {m}}\) spherical impactor, respectively. For the \(0.15\times 0.15\times 0.06\,\textrm{mm}\) finite element model, the number of nodes is 35,593,456 and the number of elements is 219,872,596. For the \(0.2\times 0.2\times 0.08\,\textrm{mm}\) finite element model, the number of nodes is 83,894,039 and the number of elements is 520,480,781. \(\Delta t\) was set as \(2.0\times 10^{-11}\,\textrm{sec}\) for both the models.

The computing resource is a dual CPU processor server with Intel Xeon Gold 6252. The computational time for each time step significantly depends on the number of fractured Voronoi boundaries because the impact analysis is not parallelized but performed by a single thread in our current code. Also, the total computational time depends on the number of time steps necessary for the termination of crack propagation. In the numerical analyses shown in Table 2, the maximum total computational time is about 360 h. The improvement of the efficiency of parallelization is our future work.

Fig. 6
figure 6

The relationship between the impact velocity \(V_0\) and the maximum impact force F

Full size image

The maximum impact force F depends on the impact velocity \(V_0\). F is predicted for the case of the impact of a rigid sphere on a semi-infinite elastic wall using Hertzian contact theory (Love A. E. 1934; Timoshenko and Goodier 1970) as

$$\begin{aligned} F=\left( \frac{4}{3}\frac{E}{1-\nu ^2}R^{1/2} \right) ^{2/5} \left( \frac{5}{4}V_0^2m\right) ^{3/5} \end{aligned}$$
(16)

where E is Young’s modulus of the wall, \(\nu \) is Poisson’s ratio of the wall, R is the radius of the rigid sphere, and m is the mass of the rigid sphere. This equation yields the relationship between the impact velocity \(V_0\) and the maximum impact force F in the analysis cases of Table 2 as shown in Fig. 6. It should be noted here that this analytical solution gives an upper limit for the impact force; since it does not take into account the energy dissipation due to impact, stress wave propagation, and possible cracking, the actual value of F during impact deviates from the analytical value.

Fig. 7
figure 7

Cracks formed by the impact of \(\phi \,25 {\,{\upmu }\hbox {m}}\) rigid sphere at impact distance \(d=1.0,\,2.5,\,5.0 {\,{\upmu }\hbox {m}}\) in the numerical analyses

Full size image
Fig. 8
figure 8

Cracks formed by the impact of \(\phi \,25 {\,{\upmu }\hbox {m}}\) rigid sphere at impact distance \(d=10,\,15 {\,{\upmu }\hbox {m}}\) in the numerical analyses

Full size image
Fig. 9
figure 9

Top view of the numerical analysis results: (a) impact of \(\phi \,25{\,{\upmu }\hbox {m}}\) rigid sphere, impact distance \(d=1.0{\,{\upmu }\hbox {m}}\); (b) impact of \(\phi \,25{\,{\upmu }\hbox {m}}\) rigid sphere, impact distance \(d=15{\,{\upmu }\hbox {m}}\)

Full size image

Figures 7 and 8 show the cracks formed by the impact of \(\phi \,25{\,{\upmu }\hbox {m}}\) rigid sphere. At each case in Figs. 7, 8, 11, 12, and 13, the upper figure is a perspective view, the lower left figure is a front view, and the lower right figure is a side view; see view angles in Fig. 5. At short impact distance \(d=1.0{\,{\upmu }\hbox {m}}\) shown in Fig. 7, the formation of a ring crack at the top surface of the glass plate is interrupted by the edge of the chipping wall; see also Fig. 9a. At relatively low impact force \(F=0.582\mathrm {\,N}\) (\(V_0=100\mathrm {\,m/s}\)), cracks are formed only on the impact surface. As impact force increases (\(F=1.337\mathrm {\,N}\), \(V_0=200\mathrm {\,m/s}\)), a ring crack grows downward to form a Hertzian cone crack. The ring crack and the Hertzian cone crack are indicated in Fig. 10. This Hertzian cone crack intersected the chipping wall and resulted in an incomplete cone crack at the short impact distance d. Upon the further increase of impact force (\(F\ge 2.176\mathrm {\,N}\), \(V_0\ge 300\mathrm {\,m/s}\)), the evolution of the Hertzian cone crack to the bottom of the glass plate is interrupted and it sharply deflected toward the chipping wall. When the deflected Hertzian cone crack reached the chipping wall, the conchoidal platelet of the glass was formed. This conchoidal platelet is the characteristic fracture pattern in edge chipping. Figure 9a shows the cracks on the top surface of the glass plate with impact distance \(d=1.0{\,{\upmu }\hbox {m}}\) and \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor. As impact force increases, the size of the ring cracks becomes larger. Also, at \(F=3.073, \, 4.016\mathrm {\,N}\) (\(V_0=400,\,500\mathrm {\,m/s}\)), it can be observed that radial cracks extended from the ring cracks to be perpendicular to the chipping wall.

In the analyses cases with \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor, these crack morphologies depending on the impact force F are also observed at relatively short impact distance d; see \(d=2.5{\,{\upmu }\hbox {m}}\) and \(d=5.0{\,{\upmu }\hbox {m}}\) in Fig. 7. However, the required impact force F for the crack growth is strongly affected by the impact distance d; the higher impact force is required at a longer impact distance to cause similar damage to a shorter impact distance. For example, at \(d=1.0{\,{\upmu }\hbox {m}}\), the Hertzian cone crack is formed by \(F=1.337\mathrm {\,N}\) (\(V_0=200\mathrm {\,m/s}\)) while it is formed by \(F=2.176\mathrm {\,N}\) (\(V_0=300\mathrm {\,m/s}\)) at \(d=2.5{\,{\upmu }\hbox {m}}\).

In Fig. 8, which is for relatively long impact distances \(d=10,\,15{\,{\upmu }\hbox {m}}\) with \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor, a ring crack at the top surface of the glass plate is completely formed. Then, as the impact force F increased, a ring crack grows downward and forms a Hertzian cone crack as seen in short impact distance. Simultaneously with that, radial cracks extend from the periphery of a ring crack; see Fig. 9 b in the case of \(d=15{\,{\upmu }\hbox {m}}\). At relatively low impact force (\(F=3.073\mathrm {\,N}\), \(V_0=400\mathrm {\,m/s}\)), the radial cracks are almost perpendicular to the chipping wall. However, at higher impact force (\(F\ge 4.016\mathrm {\,N}\), \(V_0\ge 500\mathrm {\,m/s}\)), the radial cracks start to extend in the direction parallel to the chipping wall edge and then bend toward the chipping wall. In the experimental results of Mohajerani and Spelt (2010), these crack arms are called “side cracks” and it is reported that these side cracks also grow stably downward and merge with the Hertzian cone crack into a single asymmetric cone crack. In our numerical analysis results, it is also difficult to distinguish the developed side cracks and the Hertzian cone crack; see also Fig. 10. As pointed out in Mohajerani and Spelt (2010), the side cracks are only observed at long impact distances where a ring crack is completely formed in our numerical analyses.

In addition to the growth of the side crack, the Hertzian cone crack sharply deflects toward the chipping wall at a high impact force. Upon further increase of the impact force, the Hertziain cone crack intersected the chipping wall and formed the conchoidal platelet of the glass as seen in short impact distance (\(d\le 5.0{\,{\upmu }\hbox {m}}\)). Here, at \(d=15{\,{\upmu }\hbox {m}}\), the analysis results seem to be affected by the other side walls because cracks reached the boundary of the analysis model (especially in the case with \(V_0=700,\,800\mathrm {\,m/s}\) ). Therefore, we performed the analyses by using the \(0.2\times 0.2\times 0.08\,\textrm{mm}\) finite element model for these cases. The analysis results are shown in Fig 11. Since the crack patterns become sharp and the extra cracks are not observed in the analyses with \(0.2\times 0.2\times 0.08\,\textrm{mm}\) finite element model, it is concluded that the chipping morphology is strongly affected by the specimen size when the specimen is not sufficiently large against the chipping size.

Fig. 10
figure 10

Location of characteristic crack pattern formed by the impact of \(\phi \,50{\,{\upmu }\hbox {m}}\) rigid sphere in the numerical analyses

Full size image
Fig. 11
figure 11

Cracks formed by the impact of \(\phi \,25{\,{\upmu }\hbox {m}}\) rigid sphere at impact distance \(d=15{\,{\upmu }\hbox {m}}\) in the numerical analyses with \(0.2\times 0.2\times 0.08\,\textrm{mm}\) finite element model

Full size image

Figures  12 and 13 show the cracks formed by the impact of \(\phi \,50{\,{\upmu }\hbox {m}}\) rigid sphere. The sequence of cracking such as the formation of the Hertizan cone crack, the side cracks, and the conchoidal platelet depending on the impact distance d and the impact force F is similar to that of the analysis cases with \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor. The different point is the multiple cracking. For example, at \(F\ge 12.29\mathrm {\,N}\) (\(V_0\ge 400\mathrm {\,m/s}\)) in Fig. 12, the multiple Hertizian cone cracks are observed. These multiple cone cracks are clearly observed in the experiments of Chai (2006), where quasi-static indentation tests of soda-lime glass bonded to a polycarbonate substrate were performed by using a spherical indenter made of W/C sphere. According to this study, the emergence of the different angles of cone cracks results from expansion of the contact radius during indentation. In our numerical analysis, since we also employed the spherical impactor, it is considered that the cause of the multiple cone cracks with different angles is the expansion of the contact radius during impact. Also, the multiple cone cracks are not observed at low impact force F. This tendency coincides with the experimental results of Mohajerani and Spelt (2010).

At higher impact force \(F=24.06,\,28.24\mathrm {\,N}\) (\(V_0=700,\,800\mathrm {\,m/s}\)) and longer impact distance \(d=10,\,15{\,{\upmu }\hbox {m}}\) in Fig. 13, the crack pattern becomes a penny-shaped crack rather than a conical crack. The penny-shaped crack is commonly observed under quasi-static loading of sharp indenters. However Chai and Ravichandran (2009); Morrell (2005) reported in their experimental studies that the blunt indenter forms a penny-shaped crack at a high range of the impact force. Our numerical analysis results agree with these experimental results.

Comparing the analysis cases with \(\phi \,25{\,{\upmu }\hbox {m}}\) and \(\phi \,50{\,{\upmu }\hbox {m}}\) spherical impactor at \(d=1.0{\,{\upmu }\hbox {m}}\), the Hertzian cone crack is sufficiently formed at \(F=2.176\mathrm {\,N}\) (\(V_0=300\mathrm {\,m/s}\)) with \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor and at \(F=2.329\mathrm {\,N}\) (\(V_0=100\mathrm {\,m/s}\)) with \(\phi \,50{\,{\upmu }\hbox {m}}\) spherical impactor. The edge chipping occurs at \(F=4.016\mathrm {\,N}\) (\(V_0=500\mathrm {\,m/s}\)) with \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor and at \(F=5.350\mathrm {\,N}\) (\(V_0=200\mathrm {\,m/s}\)) with \(\phi \,50{\,{\upmu }\hbox {m}}\) spherical impactor. Thus, the formation of the Hertzian cone crack occurs at around \(2\mathrm {\,N}\) and chipping force is 4–5N when the impact distance d is \(1.0{\,{\upmu }\hbox {m}}\), regardless of the impactor size. According to this, the chipping morphology could be determined only by the impact force F and the impact distance d. In this paper, since we performed limited numerical analysis cases, it requires more comprehensive analyses to determine the precise chipping force F and the relationship between the chipping force F and the impact distance d.

4.3 Chipping size

Fig. 12
figure 12

Cracks formed by the impact of \(\phi \,50{\,{\upmu }\hbox {m}}\) rigid sphere at impact distance \(d=1.0,\,2.5,\,5.0{\,{\upmu }\hbox {m}}\) in the numerical analyses

Full size image
Fig. 13
figure 13

Cracks formed by the impact of \(\phi \,50{\,{\upmu }\hbox {m}}\) rigid sphere at impact distance \(d=10,\,15{\,{\upmu }\hbox {m}}\) in the numerical analyses

Full size image

To analyze the size of edge chips, we performed the numerical analyses with two sizes of spherical impactor: the diameters were \(50{\,{\upmu }\hbox {m}}\) and \(100{\,{\upmu }\hbox {m}}\). The impact distance d was set as \(0.05\mathrm {\,mm}\). The velocity \(V_0\) was varied from \(100\mathrm {\,m/s}\) to \(2000\mathrm {\,m/s}\) in \(100\mathrm {\,m/s}\) increments in order for the impact force F to be under \(100\mathrm {\,N}\). It should be noted here that the analysis settings are not realistic but these are merely for numerical experiments. The relationships between the impact velocity and the impact force for \(\phi \,50{\,{\upmu }\hbox {m}}\) and \(\phi \,100{\,{\upmu }\hbox {m}}\) spherical impactor are shown in Fig. 6. The dimension (\(X\times Y\times Z\)) of the finite element model for the glass plate was set as \(4.0\times 2.5\times 1.0\,\textrm{mm}\). The number of nodes and elements of this analysis model were 110,560,806 and 686,110,789, respectively.

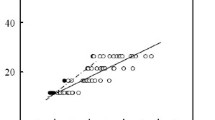
Using the crack patterns obtained from the numerical analyses, we measured the width (W) and the height (H) of chip scars; the definition of W and H is shown in Fig. 14. Figure 15 shows the plots of W and H versus impact force F. W and H are normalized by impact distance \(d=0.05\mathrm {\,mm}\). As impact force increases, the chip dimensions also increase. W and H are almost linearly increase until approximately \(40\mathrm {\,N}\) impact force however the gradient of increase becomes small over \(40\mathrm {\,N}\). While the width W of the analyses with \(\phi \,100{\,{\upmu }\hbox {m}}\) impactor is much larger than that of the analyses with \(\phi \,50{\,{\upmu }\hbox {m}}\) impactor, the height H has a slight difference between analyses with \(\phi \,50{\,{\upmu }\hbox {m}}\) impactor and \(\phi \,100{\,{\upmu }\hbox {m}}\) impactor.

Fig. 14
figure 14

The definition of chip dimensions in the case with \(\phi \,50{\,{\upmu }\hbox {m}}\) spherical impactor and \(V_0=800\mathrm {\,m/s}\). The upper figure is the perspective view of cracks and the lower figure is the front view of cracks

Full size image
Fig. 15
figure 15

Plots of normalized W and H versus impact force F by impact of \(\phi \,50{\,{\upmu }\hbox {m}}\) and \(\phi \,100{\,{\upmu }\hbox {m}}\) rigid sphere

Full size image

In the previous experiments of edge chipping due to quasi-static loading by a spherical indenter of different radii (Chai 2011), it is indicated that the chip dimensions are independent of indenter geometry. The tendency of the height H of our numerical analyses coincides with this previous experimental result while the tendency of the width W does not. Also, Chai and Lawn (2007b) shows that the chip dimensions are given by \(W/d=8\) and \(H/d=5.1\) through the experiments of edge chipping due to quasi-static loading by Vickers indenter. These equations are established regardless of the indented materials and the indent distances (i.e., chipping load) (Chai 2011). However, in our numerical analysis results, the ratios W/d and H/d are not constant and depend on the impact force. The disagreement of the tendency of the width W with the previous experimental observation and the dependency of W/d and H/d on the impact force could result from the difference in the loading condition (i.e., dynamic or quasi-static loading). However further investigation of this point is currently difficult because of the lack of experimental data about the chip dimensions under dynamic impact loading. More detailed discussions about the differences in the chip dimensions depending on loading conditions are our future work.

5 Conclusions

This paper proposes the numerical analysis method for edge chipping by impact loading. Our method is based on PDS-FEM developed by the authors and we extend PDS-FEM to be able to simulate impact loading. Using this method, we performed the numerical analyses of edge chipping of soda-lime glass caused by the impact of a rigid steel sphere. In the numerical analyses, the diameter of the rigid sphere, the impact velocity, and the impact distance were varied.

The numerical analyses successfully simulate the 3D complex crack morphology generally observed in edge chipping. In the numerical analyses with \(\phi \,25{\,{\upmu }\hbox {m}}\) spherical impactor, at relatively low impact force, the ring crack on the impact surface and the following Hertzian cone crack are formed. As impact force increases, the Hertzian cone crack deflects the chipping wall and a conchoidal chip is removed from the edge of the chipping wall. In addition to these Hertzian cone cracks, the radial cracks initiate from the ring crack at high impact force. Also, the critical chipping force is strongly affected by impact distance; a higher impact force is required for chipping at a longer impact distance. These Hertzian cone cracks and radial cracks reproduced in the numerical analyses are commonly observed in the experiments of edge chipping under quasi-static and dynamic loading of blunt (spherical) indenter. In the numerical analyses with \(\phi \,50{\,{\upmu }\hbox {m}}\) spherical impactor, the crack geometries become penny-shaped rather than conical with the increase of impact force. This formation of penny-shaped cracks at high-impact force also coincides with experimental observations reported in previous studies.

We also measured chip dimensions obtained from the numerical analysis with \(\phi \,50{\,{\upmu }\hbox {m}}\) and \(\phi \,100{\,{\upmu }\hbox {m}}\) spherical impactor. While the height of the chip scar has a very slight difference between the two sizes of impactors as long as the same impact force is applied, the width of chip scar of \(\phi \,100{\,{\upmu }\hbox {m}}\) impactor is larger than that of \(\phi \,50{\,{\upmu }\hbox {m}}\) impactor.

To the best of our knowledge, this is the first time that the 3D crack morphology of edge chipping has been simulated in detail. While the quantitative discussions of the precise critical chipping load and chip dimensions have yet to be provided, the numerical analyses studied here give insight into the complex mechanism of edge chipping. We anticipate that our method will help to predict the potential chipping even under complicated conditions and to improve the manufacturing techniques of cutting or machining brittle materials. In our future work, we will work on the improvement of the efficiency of parallelization and the detailed investigation of the effect of the specimen size for the practical application of our analysis method. Also, for quantitative comparison between numerical and experimental results, we will perform the numerical analysis for edge chipping under quasi-static loading which has more detailed experimental data than impact loading.