The systematic nature of regularization error in phase field modeling: implications for crack nucleation and propagation

Abstract

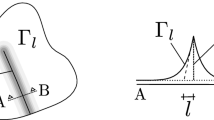
A critical issue in simulating the evolution of a crack using the phase field approach resides in the ability of the model to predict crack nucleation. In this work, we study the impact of the Ambrosio–Tortorelli regularized crack formulation on the phase field model’s ability to represent the phenomena of nucleation and early crack propagation in two-dimensional domains under generic boundary conditions. Through numerical experiments we study the nature of the errors introduced by the crack’s regularization at the early stages of crack propagation and its critical effects on the predictability of the nucleation phenomenon. We also show that the errors introduced through the regularization of the crack are systematic and can be predicted for a broad range of boundary conditions. Both external and internal crack cases are analyzed and the scalability of the error is verified. We then investigate the nature of the error and identify its localization with reference to the crack geometry. We conclude that the classical formulation of phase field is not designed to predict nucleation without affecting the early propagation of the crack.

Appendix A: Convergence studies

The numerical experiments shown in this section are conducted using the finite element software FEniCS (Alnæs et al. 2015). The goal of the convergence studies is two-fold. On the one hand, we wish to understand the impact of the choices made in our numerical experiments. On the other, we seek more insight into the interaction between the $\varGamma$-convergence of the regularized model and the finite element discretization. One of the parameters used in this appendix and in the body of this paper is the “mesh refinement factor” $n_h=\epsilon /h$, which links two types of approximation, the $\varGamma$-convergence and finite element discretization.

Study 1 We first compare the performances of three types of meshes (Fig. 21): structured-quadrilateral, structured-triangular and unstructured-triangular for various values of the mesh refinement factor $n_h$. We use model problem M1, described in Sect. 3, consisting of a unit square with a horizontal crack of length $\varGamma =0.5$. The mesh refinement factor is varied and the crack length $\varGamma _{\epsilon }$ is computed.

We define

$$\begin{aligned} \varGamma _{\epsilon }^{\infty }= \lim _{n_h\rightarrow \infty } \varGamma _{\epsilon ,h}. \end{aligned}$$

(19)

Fig. 21

Schematic representation of meshes used in this convergence study. From left to right, structured–quadrilateral, structured–triangular and unstructured–triangular

The results of the study, shown in Fig. 22, may be summarized as follows:

• For each fixed value of $\epsilon$ the regularized crack length $\varGamma _\epsilon$ converges to the same limit value $\varGamma _{\epsilon }^{\infty }$ independently of the type of mesh used.

• To reach the same level of accuracy toward the limit value $\varGamma _{\epsilon }^{\infty }$ different mesh types require different mesh refinement $n_h$.

• As expected quadrilateral meshes show faster convergence to $\varGamma _{\epsilon }^{\infty }$.

Note that for $\epsilon =0.2$ the asymptotic value $\varGamma _\epsilon ^\infty$ is approximately 0.595 instead of the 0.600 predicted by the proposed correction $\varGamma _\epsilon =\varGamma +0.5\epsilon$. The approximation is still very good even though the phase field for this case (shown in Fig. 4a) is clearly not fully developed toward the boundaries. This behavior is due to the size of $\epsilon$ compared the size of the domain and it is in line with the results plotted in Fig. 8. In fact, those results are normalized with respect to the error values at $n_y=2.5$, i.e., when the vertical distance between the crack and the top of the domain is 2.5 times $\epsilon$. These results show that at $n_y=2.5$ we need to expect a slight underestimation of the regularization error consistently at all crack lengths when compared to a domain geometry with $n_y>2.5$. Results are then in line with the “non-interacting distance” of $2.5\epsilon$ proposed in the present work since at $\epsilon =0.2$ the boundaries of the domain used for the convergence studies are exactly at $2.5\epsilon$ from the crack.

Study 2 With the same model problem as in the previous study (unit square sample with crack length $\varGamma =0.5$), we perform a set of numerical experiments to understand the interaction between the $\varGamma$-convergence of the regularized model and the finite element discretization.

Following the definition given in (19) it is clear that the value of $\varGamma _{\epsilon }^{\infty }$ at each value of $\epsilon$ characterizes the error in the crack length produced by the use of the regularized formulation. The value of $\varGamma _{\epsilon }^{\infty }$ can be estimated by refining the mesh and determining the mesh refinement factor ${n_h^\epsilon }$ at which the difference of the calculated $\varGamma _{\epsilon ,h}$ at two consecutive values of $n_h$ is less than a specific tolerance that we can call “relative convergence error” $R_{ce}$:

$$\begin{aligned} \left| \frac{[\varGamma _{\epsilon ,h}^{n_h}-\varGamma _{\epsilon ,h}^{(n-1)_h}]}{\varGamma _{\epsilon ,h}^{(n-1)_h}}\right| \le R_{ce} \end{aligned}$$

(20)

Thus ${n_h^\epsilon }$ represents the mesh refinement factor for which the discretization error is below the specified tolerance for a given $\epsilon$.

Fig. 22

Variation of $\varGamma _\epsilon$ as a function of the mesh refinement factor $n_h$ at $\epsilon =0.2$ and $\epsilon =0.1$ for different mesh types. For each value of $\epsilon$, all mesh types converge to the same limit value $\varGamma _{\epsilon }^{\infty }$

In Fig. 23, we plot the value of $n_h^{\epsilon }$ as a function of $\epsilon$ for the three different meshes using linear (Fig. 23a) and quadratic shape functions (Fig. 23b). The parameter $R_{ce}$ is set to $10^{-5}$ or $10^{-6}$ for linear shape functions and $10^{-4}$ or $10^{-5}$ for quadratic. The results lead to the following observations:

• The same level of accuracy can be achieved for a lower refinement factor ${n}_h^{\epsilon }$ when $\epsilon \rightarrow 0$.

• The relationship between $n_h^{\epsilon }$ and $\epsilon$ is approximately linear whether we use linear or quadratic finite elements.

• At constant relative convergence error $R_{ce}$, the value of $n_h$ decreases as $\epsilon \rightarrow 0$.

Fig. 23

Variation of ${n}_h^{\epsilon }$ as a function of $\epsilon$ at different values of relative convergence error $R_{ce}$ for a Linear shape functions and b quadratic shape functions. In both cases ${n}_h^{\epsilon }$ decreases linearly with $\epsilon$

Study 3 The $\varGamma$-convergence of discrete functionals $V_{\epsilon , h}$ has been demonstrated for scalar problems by Bellettini and Coscia (1994). In particular, they show that the $\varGamma$-convergence results holds for discrete functionals $V_{\epsilon , h}$ provided the characteristic length of the mesh h tends to zero faster than $\epsilon$.

In this study, we compare the ratio $\varGamma _{\epsilon ,h}/\varGamma$ for various values of $\epsilon$ and h using both triangular and quadrilateral meshes for model problem M1. These results are shown in Fig. 24.

Fig. 24

Variation of the ratio $\varGamma _\epsilon /\varGamma$ for model problem M1 as a function of $\epsilon$ at constant mesh size h for a quadrilateral mesh and b triangular mesh. In both cases we observe divergence approximately when $\epsilon <h$

At each fixed mesh size h the estimated crack length $\varGamma _\epsilon ,h$ clearly converges toward $\varGamma =0.5$ for $\epsilon \rightarrow 0$ but the rate of convergence decreases when $\epsilon$ approaches the value of h of the specific curve (vertical dash-dot lines identify visually these conditions).

Overall, the results of this study can be summarized as follows:

• The computational results are aligned with the findings of Bellettini and Coscia (1994) regarding the $\varGamma$-convergence of discrete functionals $V_{\epsilon , h}$ provided the characteristic length of the mesh tends to zero faster than $\epsilon$.

• The condition proposed by Miehe et al. (2010) of $n_h=\frac{\epsilon }{h}<2$ satisfies the convergence condition of the discrete functional of the Ambrosio–Tortorelli regularization.

• The mesh size h that optimizes the rate of convergence is a function of $\epsilon$.