Abstract
The realistic approximation of structural behavior in a post fracture state by the phase-field method requires information about the spatial orientation of the crack surface at the material point level. For the directional phase-field split, this orientation is specified by the crack orientation vector, that is defined perpendicular to the crack surface. An alternative approach to the determination of the orientation based on standard fracture mechanical arguments, i.e. in alignment with the direction of the largest principle tensile strain or stress, is investigated by considering the amount of dissipated strain energy density during crack evolution. In contrast to the application of gradient methods, the analytical approach enables the determination of all local maxima of strain energy density dissipation and, in consequence, the identification of the global maximum, that is assumed to govern the orientation of an evolving crack. Furthermore, the evaluation of the local maxima provides a novel aspect in the discussion of the phenomenon of crack branching. As the directional split differentiates into crack driving contributions of tension and shear stresses on the crack surface, a consistent relation to Mode I and Mode II fracture is available and a mode dependent fracture toughness can be considered. Consequently, the realistic simulation of rock-like fracture is demonstrated. In addition, a numerical investigation of \(\Gamma \)-convergence for an AT-2 type crack surface density is presented in a two-dimensional setup. For the directional split, also the issues internal locking as well as lateral phase-field evolution are addressed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A basic principle of structural design is the integrity and stability of load bearing components. Here, an important aspect is the prevention of crack evolution. From a continuum mechanical viewpoint, cracks are a separation of previously sound bulk material. In consequence, the material’s capacity to transfer tensile stresses is lost and the capability to transmit shear stresses is reduced to interlocking and frictional effects.
Approaches for the numerical approximation of a discrete crack topology via the method of b material forces, c eigenerosion and d phase-field
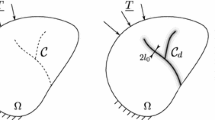
From the computational point of view, the continuous representation of a discrete crack’s topology, see Fig. 1a, by the phase-field, see Fig. 1d, is a rather novel approach. Previous approaches often involve the explicit representation of the crack schematically visualized in Fig. 1b, i.e. by means of an adaptive remeshing strategy and the duplication of nodes, e.g. Ingraffea and Saouma (1985), Miehe and Gürses (2007) and Ortiz and Pandolfi (1999). A comprehensive overview on the theory, implementation and analysis of this method in combination with a material force approach to evaluate dynamic crack propagation criteria is given in Özenç (2016). Another approach is denoted as extended finite element method (XFEM). Here, an enrichment of the displacement field ansatz functions is employed to account implicitly for the jump of displacements across the crack face without an explicit representation of the crack surface, see e.g. Belytschko et al. (2001) and Song and Belytschko (2009).
A variational description of brittle fracture is investigated in Francfort and Marigo (1998), considering the variation of the crack domain. Through the regularization of the fracture energy, inherent mesh dependency and challenging adaptive meshing strategies are overcome. An approach for the regularization is presented in Schmidt et al. (2009) as eigenfracture. In Pandolfi and Ortiz (2012), the method is implemented into an element deletion scheme for the finite element method (FEM) called eigenerosion, see Fig. 1c. The kinematics of a crack topology is obtained via the degradation of the stiffness of individual finite elements. Recently, an eigenfracture approach based on the framework of representative crack elements is shown in Storm et al. (2021) and a field crack mechanics approach in Morin and Acharya (2021), which also make use of a crack orientation vector.
Similar to eigenerosion, the phase-field method for fracture introduces a regularization for the fracture energy, which is related to the surface area of the crack
where \(G_\text {c}\) denotes the fracture toughness. The numerical approximation of Eq. (1), based on the ideas of Mumford and Shah on image segmentation in Mumford and Shah (1989), is discussed in Bourdin (2007) and Bourdin et al. (2000). In essence, the crack surface density \(\gamma _l\) is introduced in order to provide an approximation of the crack surface by
The crack surface density \(\gamma _l(p)\) is a function of an additionally introduced field variable—the phase-field p, which lends his name for the approach in general. In analogy to standard phase-transition problems, e.g. the evolution of austenite and martensite in metals or the transition of chemicals between the different physical states solid, fluid and gas, the crack is assumed to be a different “phase” of the material. More precisely, a sound solid is associated with \(p=0\) and the cracked state (or phase) is represented by \(p=1\), see Fig. 2. The numerical treatment of discontinuities is challenging and can lead to mesh dependency, localization and convergence problems, see e.g. Bažant and Pijaudier-Cabot (1988) and Pijaudier-Cabot and Bažant (1987) for a similar problem within the theory of damage and softening. A common approach to resolve the issue is gradient enhancement, see e.g. Zreid (2018). The question, whether the phase-field approach should be considered as a special type of a damage formulation, is discussed e.g. in de Borst and Verhoosel (2016) and Steinke et al. (2017).
Regularized crack approximation \(\Gamma _l\) of the sharp crack \(\Gamma \) in a 1D domain
The paper at hand is based on the developments, findings and discussions published in Steinke (2021). It aims at the further development of the phase-field method for crack approximation towards a realistic and reliable approach, not only for the prediction of crack patterns due to excessive loading, but also for the accurate simulation of the post fracture structural response. In Sect. 2, the basic theory of a phase-field method for brittle fracture is outlined. Section 3 is focused on the question, how the spatial orientation of the crack surface can be defined for the directional split. Section 4 is dedicated to numerical examples and the final section closes the paper with conclusions.
2 The phase-field approach to brittle fracture in the framework of the finite element method
2.1 Regularized crack surface
The phase-field method provides a regularized approximation \(\Gamma _l\) for the discrete crack \(\Gamma \) in terms of the volume integral given in Eq. (2) with a crack surface density
of AT-2 type (Ambrosio and Tortorelli 1990). An additional field variable p as well as the regularization length parameter l are considered. A fundamental feature of the crack set’s approximation by this elliptical functional is the continuous or smooth transition between the sound and broken regions of the solid shown in Fig. 2, that is governed by the gradient term in Eq. (3). In analogy to the gradient enhancement of damage, the regularization length parameter l governs the width of the transition zone. The relation of the regularization length to the discretization is discussed for instance in Hofacker and Miehe (2011), Linse et al. (2017) and Pandolfi et al. (2021).
AT-2 is a common choice in the computational mechanics community, see e.g. Borden et al. (2012), Hofacker et al. (2009) and Kuhn and Müller (2010), due to the straight forward implementation and onset of phase-field evolution at external loading. Nevertheless, the additional numerical effort to constrain the phase-field evolution in AT-1 is rewarded by an initial elastic phase before the phase-field evolution, which is a better approximation for brittle fracture than the softening behavior of AT-2 prior to the crack, see Alessi et al. (2018) and Tanné et al. (2018) for a discussion. Furthermore, higher order functionals can be used for the approximation of materials with anisotropic fracture toughness and an enhanced approximation of \(\Gamma _l\) at the expense of higher order gradients, see e.g. Borden et al. (2014).
By the continuous crack approximation, an explicit representation of the actual crack topology is lost. This results in additional effort necessary, if the position of the crack tip, the location of branching or the angle of kinking are required. A common strategy to visualize the crack surfaces is their representation by isosurfaces at a threshold value for the phase-field variable \(p_c\), e.g. \(p_\text {c}=0.95\), combined with the blanking out of elements where \(p> p_c\). Numerical approaches to evaluate the crack tip propagation speed are discussed e.g. in Steinke et al. (2016).
2.2 Crack driving force
According to Griffith, the formation of crack surface requires energy, that is dissipated from the strain energy stored in the deformation of the structure. In the initial considerations, a tensile force on the atomic structure is assumed. As soon as the distance between the atoms exceeds a critical value, the atomic bond is released and a separation of the initially continuous body, i.e. a crack, is obtained. In the framework of continuum mechanics, the counterpart to force and separation in the sense of Griffith are stresses and strains, respectively. Furthermore, the energy associated with forces acting along the separation distance has its local continuum mechanical counterpart in the strain energy density at the material point. Hence, in a similar way as \(\gamma _l\) is the representation of the regularized crack surface \(\Gamma _l\) at the material point level, the strain energy density \(\psi _\varepsilon \) is the local basis to obtain the phase-field analogue of the structural level quantity energy release rate \({\mathcal {G}}\). Assuming linear elasticity, the strain energy density
is written in terms of the Lamé coefficients \(\lambda \) and \(\mu \), the second order identity tensor \({\mathbf {1}}\) and the small strain tensor \(\varvec{\varepsilon }\). The additive decomposition of the strain energy density
into crack driving and persistent components, \(\psi ^+\) and \(\psi ^-\), respectively, is called the phase-field split. The phase-field split allows for a definition of the specific energetic components that drive the crack evolution. Furthermore, a thermodynamic consistent formulation of the phase-field results in a strong link between the split of the strain energy and the post fracture behavior of the phase-field crack.
When proposing variational fracture for the phase-field method in Francfort and Marigo (1998), Francfort and Marigo considered the total strain energy density to be available for the formation of the crack surface. In a strict sense, the proof of \(\Gamma \)-convergence for the phase-field functional, i.e. \(\Gamma \approx \Gamma _l\) for \(l\rightarrow 0\) is available for this split only. However, a \(\Gamma \)-convergence proof for eigenfracture exists in Schmidt et al. (2009), which takes a decomposition of the strain energy into account. The decomposition of the strain energy has turned out to be an essential part of phase-field and eigenfracture models in order to avoid nonphysical predictions for deformation kinematics of cracks, e.g. crack face interpenetration and lateral deformations in the post-fracture state. Thus, the split implicitly defines the traction transfer through a crack and the contact state of the crack surface. The energetic split further defines the contributions to the crack driving force. With such a split, nonphysical crack propagation at uniaxial or hydrostatic pressure is overcome, which is observed in the early phase-field formulations, see Bourdin et al. (2000).
Crack kinematics for ideal plane crack without friction or interlocking
The question on the correct split has appeared with its introduction to phase-field fracture. The most common volumetric deviatoric split and spectral decomposition are adopted and modified in many phase-field approaches. An overview on energy splits for phase-field can be found in Storm et al. (2020). The violation of the crack boundary conditions, reported for instance in May et al. (2015), Schlüter (2018) and others, inspired the stress based directional split published in Steinke and Kaliske (2018). The starting point is the set of basic crack kinematics. These are defined via the structural response of a body with an ideal plane crack without friction or interlocking on the surface at tensile, compression and shear loading, see Fig. 3. A perfectly plane and flawless crack surface of a closed crack subjected to compression loading perpendicular to the crack surface is assumed to transmit compression in a similar manner as if no crack is present at all. Reversing the sign of the loading to apply tensile loading yields the separation of the crack faces, i.e. crack opening. Here, no stresses are assumed to be transmitted and, therefore, no reaction force to a crack opening displacement is expected. Finally, also shear stresses vanish on the crack surface, if friction and interlocking effects are excluded. Hence, shearing of the crack faces against each other yields no resistance in terms of a reaction force.
Definition of the crack orientation vector \({\mathbf {r}}\), the crack coordinate system (CCS) and the decomposition of the stress tensor with respect to the CCS
The key feature of the stress based directional decomposition is the information about the orientation of the crack surface. This information is provided in a unique way by the crack orientation vector \({\mathbf {r}}\) perpendicular to the crack surface, see Fig. 4. In combination with vectors \({\mathbf {s}}\) and \({\mathbf {t}}\), both perpendicular to \({\mathbf {r}}\) and to each other, a Cartesian crack coordinate system (CCS) is established. The decomposition of a linear elastic ground stress tensor based on Eq. (4) with respect to the CCS is visualized in Fig. 4. In order to approximate the crack kinematics visualized in Fig. 3, the crack driving stress tensor
includes the shear components on the crack surface as well as the stress components perpendicular to the crack surface with tensile magnitude by \(\langle \bullet \rangle _\pm =(\bullet \pm \vert \bullet \vert )/2\). Furthermore, the continuum description of the crack kinematics originating from a discrete crack behavior requires an additional correction term to account for Poisson effects during crack opening, see Steinke and Kaliske (2018). It can be shown, that Eq. (6) is identical to the recent development of a representative crack element theory in case of isotropic linear elasticity at small strains, see Storm et al. (2020).
The persistent stress tensor, being the counterpart to the crack driving stress tensor, reads
containing the remaining components of the total stress tensor as well as the correction term with negative sign. This ensures, that linear elastic behavior is recovered in case of no phase-field crack is present. In reverse manner, the crack driving and persistent strain energy densities are obtained from the stress and strain tensors by
This ensures, that the amount of dissipated energy is directly linked to the post fracture behavior of the phase-field crack, which results in a thermodynamic consistent formulation.
With the measures of the crack surface as well as the crack driving strain energy in terms of their densities at hand, the energetic link to describe the dissipation of the latter into the evolution of the former is provided by the total energy
of the solid domain \(\Omega \), where \(G_\text {c}\) denotes the fracture toughness and the external forces are omitted for the sake of simplicity. This leads to the governing partial differential equations
and
for the two-field problem, a standard quadratic degradation function
is used in the following.
2.3 Crack irreversibility
From the macroscopic point of view, crack formation is an irreversible process and the irreversibility of fracture is a basic assumption in linear elastic fracture mechanics. A fundamental challenge of macroscopic irreversibility in the context of the phase-field method for fracture is the continuous approximation of the crack surface itself. While irreversibility of a discrete crack can be formulated as
in a straight forward manner, the question remains, whether this results in a similar constraint
on the phase-field degree of freedom as well as postulated in Miehe et al. (2010). Alternatively, a restriction on the global evolution of the regularized surface
could be required. It should be noted, that fulfilling Eq. (14) implicitly results in Eq. (15), but not vice versa. Furthermore, both conditions are not a strict representation of the original constraint of Eq. (13).
The implementation of the constraint Eq. (14) can be based on a history variable \({\mathcal {H}}\), that is used in Eq. (11) instead of the crack driving strain energy density \(\psi ^+\). While this approach is common in the theory of damage, its application in the context of the phase-field method for fracture is initially introduced by Miehe et al. (2010). The implementation of this approach is straight forward, as the history variable can be formulated in terms of the material point level value of the crack driving strain energy density \(\psi ^+\). However, the analysis of Linse et al. (2017) indicates, that the amount of crack surface area is overestimated by this method.
An alternative approach is published by Bourdin et al. (2000). They propose an additional boundary condition on the phase-field degree of freedom, as soon as a critical value is exceeded. In consequence, the local ”healing” of the phase-field value is allowed and the phase-field profile at the end of the evolution closely resembles the analytical solution, see Linse et al. (2017). Therefore, the final amount of crack surface obtained in their setup is very close to the expected value. However, this result can be obtained only by the violation of Eq. (14). In consequence, the energetic counterpart of the crack surface, i.e. the strain energy, that is dissipated locally for the higher phase-field value, can increase due to the increase of the degradation function for the decreasing phase-field value. From the energetic point of view, strain energy is created from crack surface locally. While the global energy balance is not violated in this case due to the equivalence of energetic contributions from strain and crack surface in Eq. (9), a different problem arises. The energy is a scalar value without direction. In contrast, the degradation function affects a second order tensor in the definition of the effective stress tensor in Eq. (10). As the crack evolution is reversed locally, the energy of the crack surface, that is without direction, is transformed into an increase in the effective stress tensor. Let us assume a volumetric deviatoric split. Furthermore, assume volumetric expansion triggered the phase-field evolution in the first place. Now, local healing permits the transformation of this initial ”volumetric” strain energy into deviatoric components. For a directional split, the same applies to the interchange of tension and shear as well as a change of the crack orientation during evolution. However, a study on this issue is a non-trivial challenge, that may have not been tackled yet, as the phase-field community seems to be totally unaware of this hardly realistic process. Nevertheless, this issue is not investigated in this paper any further.
In this work, the combination of both approaches, that is already published in Steinke and Kaliske (2018), is applied in order to benefit from the elegant simplicity of a formulation with a damage-like history while obtaining a proper profile for fully evolved cracks. A critical value for the phase-field \(p_\text {c}\) is defined. Based on this value, a history variable \({\mathcal {H}}(t)\) is introduced, that depends on the current solution time \(t_n\) as well as on a previous step of the simulation at time \(t_{n-1}\). The history variable reads
and is used in the modified evolution equation for the phase-field
2.4 Finite element aspects
The solution of multifield finite element equations systems based on the governing equations Eqs. (10) and (17) is obtained within the parallel version of FEAP 8.5 (parFEAP) documented in Taylor (2017). ParFEAP’s solution is based on a METIS Karypis and Kumar (1998) partitioning of the discretization and the application of parallel solvers provided by PETSC Balay et al. (2019). Within this paper, the generalized minimal residual algorithm published in Saad and Schultz (1986) with a Jacobi preconditioner and a modified conjugate gradient approach published in van der Vorst (1992) are applied.
A multifield equation system can be solved in a monolithic or staggered scheme. In the monolithic scheme, the increments of all DOF are obtained simultaneously. Therefore, the stiffness coupling terms are of major importance. The staggered solution scheme is based on an alternated solution for specific DOF. In terms of the phase-field method, the increments of the displacements are obtained at frozen phase-field values and the increments of the phase-field are computed for a frozen state of deformation. The alternated solution is performed iteratively, until a convergence criterion is met. Convergence criteria are e.g. no further changes in the increments are obtained for all DOF or the norm obtained for a post-processed monolithic residuum is below the tolerance limit.
The application of the staggered solution scheme to phase-field simulations is required for static crack propagation, as the monolithic solution cannot obtain convergence in the case of brutal phase-field evolution, see Miehe et al. (2010). Instead, a staggered solution is proposed in Miehe et al. (2010). Originally, a single solution for each increment of the mechanical field and the phase-field is motivated by very small load steps during the crack evolution, which is replaced by the staggered iterations in later phase-field approaches. In transient simulations, the inertia, which is not affected by the phase-field, acts as a stabilization to the solution and the monolithic solution scheme is applicable, see e.g. Borden (2012) and Steinke et al. (2016).
3 Crack orientation vector
A major ingredient of the directional split is a realistic definition of the crack orientation vector \({\mathbf {r}}\). The explicit definition of the crack orientation forms further the basis of the generalization of the directional split in the framework of representative crack elements, see e.g. (Storm and Kaliske 2021; Storm et al. 2020, 2021; Yin et al. 2021). The definition \({\mathbf {r}}=\nabla {p}/\vert \nabla {p}\vert \) proposed in Strobl and Seelig (2015) seems an intuitive approach. It results in a realistic orientation in the special case of the through crack discussed by Strobl and Seelig. However, this definition fails both at the crack tip as well as within fully degraded elements. At the crack tip, the gradient of the phase-field does not represent the actual orientation of the crack, see Fig. 5. While this is the critical region, where crack propagation is expected, the phase-field evolution is affected by a wrong decomposition of the stresses. Furthermore, the stress free boundary of the crack surface requires an approximation by at least one row of connected fully degraded elements, see Steinke et al. (2016). However, in a fully degraded element, i.e. all nodes having \(p=1\), the gradient of the phase-field is not specified properly. While this region is critical for the proper approximation of the crack kinematics, again the gradient definition fails to deliver a realistic approximation of the crack.
Representation of the crack orientation \({\mathbf {r}}\) at the crack tip by the gradient type definition \({\mathbf {r}}=\nabla {p}/\vert \nabla {p}\vert \)
In the following, two approaches to define the orientation of a phase-field crack are proposed. The focus during the development is on a realistic approximation of the actual crack orientation of the represented discrete crack, especially during crack propagation. At first, a definition based on an evaluation of the principal stresses is proposed, that resembles closely to the principal stress failure criterion of early fracture mechanics theory. The second approach is based on an analytical evaluation of the crack driving strain energy density at the material point level.
3.1 Principal direction
The evaluation of the principal direction of stresses or strains is well established in early approaches to model fracture. Furthermore, it sustains a significant influence on damage and failure simulation, see Gross and Seelig (2011). Indeed, the formation of a crack surface perpendicular to the largest tensile strain or stress is an intuitively realistic approach based on everyday life’s observation.
In an isotropic linear elastic material, the principal directions of strains and stresses are identical. A similar conclusion is obtained for the strains and the effective stress tensor for special cases, e.g. the spectral and volumetric deviatoric split, see Steinke (2021) for a detailed investigation of the spectral split on this issue. However, an analogous derivation is hardly possible for the directional split. The reason is the composition of the stress tensors in Eqs. (6) and (7), which depend on the crack orientation vector \({\mathbf {r}}\), as well as the dependence on the specific value of the degradation function. In consequence, analytical conclusions on the principal directions of the effective stress tensor of the directional split, i.e. whether or not they are identical to the principal directions of the strain tensor, are not available. Rather, the principal directions of the strains are evaluated and employed.
A general definition of the crack orientation vector by a principal (strain) direction criterion can be provided by
where \({\mathbf {n}}_1\) is the direction of the largest principal strain, i.e. \(\hat{\varepsilon }_1>\hat{\varepsilon }_2\) holds. In combination with the irreversibility approach, the change of the crack orientation is formulated in an explicit scheme by
This enables the change of the crack orientation during the evolution of the crack, while keeping the orientation of the evolved crack in unloading and reloading situations.
3.2 Energetic crack orientation in two dimensions
The fracture toughness \(G_\text {c}\) is a measure for the material inherent energetic barrier against crack evolution. In combination with the crack surface density \(\gamma _l\), the resistance against crack propagation is quantitatively specified at the material point level. In the phase-field method, the crack driving component of the local strain energy density is the energetic counterpart to that resistance. Crack evolution is a result on the global level, that is based on the local formulation and evaluation of driving force and resistance by Eq. (17). The specific amount of crack driving strain energy density depends on the state of strain. Furthermore, it strongly depends on the orientation of the crack surface. In the previous section, an intuitive alignment of the crack orientation vector, i.e. along the direction of the largest principal strain, is postulated. It can be shown, that in the majority of possible strain states, this approach yields the maximum driving force for isotropic elastic material due to maximization of the crack driving strain energy density with respect to the crack orientation vector. However, certain states of strain exhibit the maximum in the crack driving strain energy density for a crack orientation, that is at a specific angle to the principle direction. Also recent experimental observations in Rozen-Levy et al. (2020) support the hypothesis that the principal of maximum energy dissipation also applies to the propagation of cracks.
Relation between the reference coordinate system (RCS), the principal direction coordinate system (PCS) and the crack coordinate system (CCS)
In this section, an analytical approach to obtain the maximum crack driving component of the strain energy density is proposed and evaluated for a linear elastic material in a 2D setup. At the basis of known eigenvectors \({\mathbf {n}}_1\) and \({\mathbf {n}}_2\) of the 2D strain tensor \(\varvec{\varepsilon }\), a principal direction coordinate system (PCS) is established. The representation of both eigenvectors in the RCS and the PCS reads
and
where the RCS and the PCS are indicated by subscripts \({\mathbf {x}}\) and \({\mathbf {n}}\), respectively. The representation of the base vectors of the CCS in terms of the PCS reads
and
Here, an angle \(\alpha \) between the principal direction \({\mathbf {n}}_1\) and the crack orientation vector \({\mathbf {r}}\) is considered according to Fig. 6.
In analogy to the base vectors, the strain tensor is rewritten as
A relation between the principal strains \({\hat{\varepsilon }}_1\) and \({\hat{\varepsilon }}_2\) is introduced based on the local strain magnitude \(\hat{\varepsilon }\) by
By definition,
holds, i.e. \({\hat{\varepsilon }}_1\) is the major principal strain, \({\mathbf {n}}_1\) is the major principal strain direction and the spatial orientation of \({\mathbf {r}}\) is defined in an unique manner, see Fig. 6.
The linear elastic ground stress tensor \(\varvec{\sigma }_0\) of a linear elastic material with strain energy density provided in Eq. (4) is given in PCS representation by
The tensor bases specified in Eqs. (6) and (7) are given with respect to the representation of \({\mathbf {r}}\) and \({\mathbf {s}}\) in the PCS by
and
The stress tensor components, relevant for the crack driving strain energy density, read
and
The crack driving stress tensor \(\varvec{\sigma }^+\) contains components related to tension on the crack surface
and contributions related to shear on the crack surface
in an additive decomposition, that reads
where \(k=\lambda /(\lambda +2\mu )\). For brevity of notation, the trigonometric functions are abbreviated by \(\text {s}=\text {sin}(\alpha )\) as well as \(\text {c}=\text {cos}(\alpha )\).
Beside the comprehensive study of all possible states of strain, the concept of a modified F-criterion, see e.g. Shen and Stephansson (1994), is considered as well, i.e. a mode dependent fracture toughness is analyzed. Therefore, also the crack driving energetic counterpart has to be decomposed into components associated with Mode I and Mode II. An application in the framework of the phase-field method is published in Zhang et al. (2017), where a volumetric deviatoric split is employed. Thus, Mode I is associated with volumetric expansion and Mode II is related to a deviatoric deformation. While this results in a realistic approximation of wing cracks and secondary cracks in pre-notched sandstone specimens, the connection of the continuum measures of volumetric and deviatoric strains to the representation of Mode I and Mode II deformation is ambiguous. In contrast, an association of the components in a directional decomposition to the modes of crack opening is much more straight forward. Here, tensile components in \({\mathbf {r}}\otimes {\mathbf {r}}\) direction can be associated with Mode I and shear components in \({\mathbf {r}}\otimes {\mathbf {s}}\) and \({\mathbf {s}}\otimes {\mathbf {r}}\) direction are related to Mode II. Thus, \(\psi ^+\) is decomposed into the Mode I crack driving strain energy density
and a Mode II crack driving strain energy density
A reference fracture toughness \(\hat{G}_\text {c}\) is introduced in order to specify the relations
Furthermore, the range of relations n investigated is restricted to materials characterized by
Then, in analogy to the modified F-criterion, mode dependent driving forces are introduced via
and
The total driving force for phase-field evolution reads
For short notation, two additional material parameters are introduced as
and
which are bounded due to the range of Poisson’s ratio \(0\le \nu <0.5\) by \(0\le q\) and \(0 \le k \le 1\), respectively, see Fig. 7 for a visualization of the valid ranges for q and k in logarithmic scale.
Material parameter q und k
The individual crack driving strain energy density components are weighted by their corresponding fracture toughnesses. Therefore, the phase-field evolution equation Eq. (17) is rewritten as
where the history variable in Eq. (16) is adjusted by
The mode dependent driving force \({\mathcal {F}}\) for the phase-field evolution equation according to Eq. (42) is a function of the angle \(\alpha \). The application of the modified F-criterion within the framework of the phase-field method is based on the postulate ”phase-field evolution due to local maximum of driving force at the material point level governs the global energy dissipation realistically”. Thus, an analytical discussion of the function is necessary to find its maximum value and to obtain the proper driving force for phase-field evolution at each material point. To this end, the condition for an extremum
is analyzed in order to determine all possible \(\alpha _0\). Then, the second derivative condition
is used in order to evaluate, whether \({\mathcal {F}}(\alpha _0)\) is a maximum. The discussion of equations, that contain trigonometric functions, results in an infinite number of possible solutions. However, in terms of the orientation of the crack orientation vector \({\mathbf {r}}\), the range for \(\alpha _0\) can be restricted to \(-90^\circ \le \alpha _0\le 90^\circ \). In other words, \(\alpha _0=0^\circ \) represents the case, where the evolving crack is aligned to the major principal strain and \(\alpha _0=\pm 90^\circ \) represents the case, where the evolving crack is aligned to the minor principal strain. Detailed information on the derivations are provided in Steinke (2021). In the following, the results of the discussion are summarized for the main aspects.
The investigation of small strain linear elasticity with isotropic material behavior and fracture toughnesses results in the noteworthy aspect, that the energetic level of the driving force for phase-field evolution according to Eq. (42) at an angle \(\alpha _0\) is exactly the same as for its negative counterpart, i.e.
In this case, an energetical branching point is obtained, i.e. the kinking angle of the crack is not well defined due to the continuum mechanical approximation of the discrete kinematics of the crack. At the level of the crack driving stress tensor, the sign of the shear components in its PCS representation is the opposite, i.e.
This is a direct consequence of a basic assumption of the directional split, i.e. the decomposition of the stress tensor with respect to the orientation of a single crack. In fact, having identified a point of branching energetically, also the kinematics of a branched configuration should be considered. First ideas to develop a suitable approach are based on the framework of the representative crack element introduced in Storm et al. (2020). However, a final solution is not available yet. Instead, the intrinsic capability of the phase-field method to obtain crack branching on a global level is exploited and a unique local orientation of the crack is chosen.
In general, it should be noted, that the update of the crack orientation vector is based on an explicit scheme in this context. Furthermore, an interesting yet undiscussed aspect is the actual meaning of a change of crack orientation during its evolution. Due to the continuous representation of the phase-field, intermediate states between sound (\(p=0\)) and broken (\(p=1\)) are possible at the material point level. The local evolution of the phase-field is a contribution to the global crack approximation \(\Gamma _l\). However, it is always linked to a local crack orientation vector \({\mathbf {r}}\).
On the one hand, this results in the possibility, that the orientation of the crack, which is a uniquely defined property of every point on the surface of a discrete crack, can vary over the profile of its continuous representation. This could be interpreted as an actual violation of a proper approximation scheme. However, if two or three dimensions are considered, it is hardly possible to associate every point in the phase-field profile to the discrete point on the crack surface it represents. Furthermore, a major role for the realistic approximation of the crack kinematics is played by the fully degraded state at \(p=1\) and the influence of the transition zone is of only minor degree.
On the other hand, the local orientation may change during the local evolution of the phase-field. The fundamental question is, whether the energy dissipated for the local evolution in a specific direction can be transferred to the updated direction without modification. From the viewpoint of a discrete crack, the answer is definitely no, as a different crack orientation at the same location more likely represents another crack at another orientation, e.g. a point of crack branching. Therefore, in the case of a discrete crack, tearing apart the material in a different direction requires additional energy because a different atomic bond has to be broken. It could be concluded that the energy dissipated for the initial direction in the first place cannot contribute to the second crack with a different orientation.
Nevertheless, as already stated, kinematics for a branched crack at the material point is not available yet and only single cracks are considered. Furthermore, the number of possible crack orientations at a single material point is infinite and the computation and storage of individual driving forces for each orientation is not feasible.
Therefore, the level of energy dissipated in the initial direction is considered as the starting point for the evolution in the new direction. If an energetic branching point is obtained, e.g. in the sense of Eq. (49), then the new crack orientation is chosen such that the previous orientation has a minimum angle to the new crack orientation. The same holds, if multiple energetically equivalent orientations are obtained. Furthermore, the change of crack orientation is allowed for the transition zone only, i.e. as long as the phase-field is below a critical value \(p_\text {c}\). Together with the modified history variable approach proposed in Eq. (46), a realistic approximation of the crack kinematics is obtained at the global level with this approach.
Instead of a general analysis of Eq. (42) for an arbitrary state of strain, the strain state is categorized into characteristics based on the magnitudes of the principal values and the analysis is realized in terms of a case study. A positive local strain magnitude \(\hat{\varepsilon }>0\) specifies a strain state, where the major principal strain \({\hat{\varepsilon }}_1\) is a tensile strain. Then, based on the value of m, the strain state can be verbally described as
-
\({\hat{\varepsilon }}_2>0 \leftrightarrow 0 < m \le 1\) - biaxial tension,
-
\(m=1\)—volumetric tension,
-
\(m<1\)—dominant tension in \({\mathbf {n}}_1\) direction,
-
-
\({\hat{\varepsilon }}_2=0 \leftrightarrow m=0\)—uniaxial tension in \({\mathbf {n}}_1\) direction,
-
\({\hat{\varepsilon }}_2<0 \leftrightarrow m<0\)—biaxial tension compression,
-
\(m>-1\)—dominant tension (in \({\mathbf {n}}_1\) direction),
-
\(m=-1\)—pure shear and
-
\(m<-1\)—dominant compression (in \({\mathbf {n}}_2\) direction).
-
Principal strains for a local strain magnitude of \(\hat{\varepsilon }=0\) cannot be determined and the relation according to Eq. (25) cannot be applied. Due to \(\hat{\varepsilon }={\hat{\varepsilon }}_1\ge {\hat{\varepsilon }}_2\), only uniaxial compression in \({\mathbf {n}}_2\) direction is possible in this case.
A negative local strain magnitude \(\hat{\varepsilon }<0\) specifies a strain state, where the major principal strain \({\hat{\varepsilon }}_1\) is a compressive strain. Then, based on the value of m, the following strain states are possible
-
\({\hat{\varepsilon }}_2={\hat{\varepsilon }}_1 \rightarrow m=1\) - volumetric compression and
-
\({\hat{\varepsilon }}_2<{\hat{\varepsilon }}_1 \rightarrow m>1\) - biaxial compression.
Volumetric tension A state of volumetric tension yields a constant driving force of
for phase-field crack evolution, which is independent on the angle \(\alpha \), see Fig. 8.
Phase-field driving force for a state of volumetric tension
Biaxial tension A state of biaxial tension with dominant tension in \({\mathbf {n}}_1\) direction yields a maximum driving force of
for phase-field crack evolution at an angle of \(\alpha =0^\circ \), see Fig. 9.
Phase-field driving force and components for a state of biaxial tension
Uniaxial tension A state of uniaxial tension in \({\mathbf {n}}_1\) direction yields the maximum finite amount of driving force of
for phase-field evolution at an angle of \(\alpha =0^\circ \), see Fig. 10 with \(n=1\).
Phase-field driving force and components for a state of uniaxial tension at \(n=1\)
Biaxial tension compression with dominant tension A state of biaxial tension compression with dominant tension in \({\mathbf {n}}_1\) direction yields a maximum driving force for phase-field evolution of
at \(\alpha =0^\circ \), if \(m>m_\text {dt} \vee \left( m=m_\text {dt}\wedge n<n_\text {dt} \right) \), where
In addition, a maximum driving force for phase-field evolution of
is obtained at an angle of
in the case of \( m< m_\text {dt} \wedge n<n_\text {dt}\). The visualization of the single and double maxima, that depend on the combination of m and n, are given in Figs. 11 and 12, respectively.
Phase-field driving force and components for a state of biaxial tension compression with dominant tension in \({\mathbf {n}}_1\) direction for \(m>m_\text {dt}\)
Phase-field driving force and components for a state of biaxial tension compression with dominant tension in \({\mathbf {n}}_1\) direction for \(m<m_\text {dt}\)
Pure shear A state of pure shear yields a maximum driving force for phase-field evolution of
at \(\alpha =0^\circ \wedge n>n_\text {dt}\), see Fig. 13.
Phase-field driving force and components for a state of pure shear for \(n>n_\text {dt}\)
For \(n = n_\text {dt}\), a constant driving force identical to Eq. (59) is obtained for the whole range of \(0^\circ \le \alpha \le 45^\circ \), see Fig. 14.
Phase-field driving force and components for a state of pure shear for \(n=n_\text {dt}\)
In the case of \(n < n_\text {dt}\), which is visualized in Fig. 15, the maximum driving force is obtained at \(\alpha =45^\circ \) with
Phase-field driving force and components for a state of pure shear for \(n<n_\text {dt}\)
Biaxial tension compression with dominant compression A state of biaxial tension compression with dominant compression in \({\mathbf {n}}_2\) direction yields a maximum driving force for phase-field evolution of
at \(\alpha =0^\circ \) for \(m>m_\text {dc}\) with
An energetic branching point is obtained at \(\alpha =\pm 45^\circ \) for \(m<m_\text {dc}\). In this case, the maximum driving force reads
An energetic triple branching point is obtained for \(m=m_\text {dc}\), i.e. the driving forces are identical at \(\alpha =0^\circ \) and \(\alpha =\pm 45^\circ \) and can be computed according to Eqs. (61) or (63), see Fig. 16 for a visualization.
Phase-field driving force and components for a state of biaxial tension compression with dominant tension in \({\mathbf {n}}_2\) direction with \(m=m_\text {dc}\)
Uniaxial compression A state of uniaxial compression in \({\mathbf {n}}_2\) direction yields the maximum finite amount of driving force
for phase-field evolution at an angle of \(\alpha =\pm 45^\circ \), see Fig. 17.
Phase-field driving force and components for a state of uniaxial compression in \({\mathbf {n}}_2\) direction
Volumetric compression A state of volumetric compression yields no driving force for phase-field crack evolution.
Biaxial Compression A state of biaxial compression with dominant compression in \({\mathbf {n}}_2\) direction yields the maximum finite amount of driving force
for phase-field evolution at an angle of \(\alpha =45^\circ \), see Fig. 18.
Phase-field driving force and components for a state of biaxial compression
4 Numerical examples
4.1 Crack surface approximation
The approximation of the discrete crack surface \(\Gamma \) by its regularized approximation \(\Gamma _l\) is governed by Eq. (2). In the following, characteristic 2D crack patterns are studied with respect to the quality of this approximation. The focus is on the relation between the regularization length l and the characteristic size of the finite element discretization h, that is necessary for an adequate approximation.
4.2 Single through crack
Geometry and position of the initial crack for single through crack example
A rectangular patch of dimensions \(1.0\text { m}\times 1.0\text { m}\) with a discrete, horizontal through crack \(\Gamma \) is investigated, see Fig. 19. The crack’s approximation by \(\Gamma _l\) is based on a finite element solution with phase-field boundary conditions at nodes located at the discrete crack. In principle, the phase-field approximation of \(\Gamma \) can be represented in two ways, i.e. as a single row of nodes with \(p=1\) or as a row of elements, i.e. two rows of nodes with \(p=1\), see e.g. Steinke (2021) and Steinke et al. (2016) for a transient analysis of the realistic approximation of crack kinematics as well as the discussion in Sect. 4.5 for the static case. Furthermore, finite element discretizations with triangular and quadrilateral elements with characteristic size \(h=5\text { mm}\) are studied. The guidelines of the crack approximation based on a row of nodes and details of the discretization with triangles (SST) and quadrilaterals (SSQ) are shown in Fig. 20a. The guidelines for the crack approximation based on a row of elements and the details of the discretization with triangles (SDT) and quadrilaterals (SDQ) are given in Fig. 20b.
Discretization for a row of nodes and b row of elements
The phase-field distributions obtained by the finite element simulation for SST and SDT are visualized in Fig. 21 for different regularization length parameters l. The differences between the representation of the crack by a row of nodes or a row of elements is restricted to the location of the crack and the transition zone between \(p=1\) and \(p=0\) is not affected.
Phase-field for straight through crack with respect to discretization and l
A more detailed investigation is possible based on a plot of the phase-field profile in y-direction, provided in Figs. 22 and 23 for SST and SDT, respectively. First of all, it should be noted, that negative phase-field values are observed at the nodes directly adjacent to the node with the phase-field boundary \(p=1\) with \(l=h/5\). This is due to the fact, that the discretization with 2D finite elements, which are based on linear shape functions, is not fine enough to resolve the phase-field gradient properly. In consequence, the nodes along the profile exhibit oscillating positive and negative phase-field values with fast decreasing amplitude. Furthermore, due to the AT-2 functional studied here, the profile of the phase-field is rather wide and does not fit into the patch of height \(1\text { m}\) for \(l> 20h(=10\text { cm})\). The close up view on the profile for SDT in Fig. 23 also visualizes the plateau of the phase-field values at \(p=1\) for the row of elements. However, this does not influence the gradient of the profile, which is entirely governed by the value of the regularization length l.
Phase-field profile for SST with respect to the regularization length l
Phase-field profile for SDT with respect to the regularization length l
The length of the discrete crack in this example is given by \(\Gamma =1.0\text { m}\). The amount of regularized crack surface \(\Gamma _l\) is computed based on Eq. (2) for an integration over the whole finite element domain. The result of the study of the regularization length \(l=h/5\dots 40h\) is provided in Fig. 24. It should be noted, that a good approximation of \(\Gamma /\Gamma _l\approx 1.0\) is obtained both for SST and SSQ at \(l>2h\). On the one hand, this indicates, that the use of triangular or quadrilateral elements is equivalent in terms of the regularized crack approximation. On the other hand, this result confirms the conclusions obtained in Hofacker (2013), i.e. the lower limit for the regularization length \(l>2h\). In contrast, the results obtained for the crack approximation based on a row of elements, i.e. SDT and SDQ, are converging much slower to the upper limit. Furthermore, the upper limit in this case cannot be \(\Gamma /\Gamma _l=1.0\) in principle, as the plateau contribution is a fundamental violation of the theoretical framework of crack approximation by the phase-field. Nevertheless, the impact of the plateau on the value of \(\Gamma _l\) is decreasing with increasing l. In detail, the error decreases from \(\Gamma /\Gamma _l=79.5\%\) at \(l=2h\) to \(\Gamma /\Gamma _l=97.5\%\) at \(l=20h\). A further increase of the regularization length is not possible in this study due to the excess width of the phase-field profile with respect to the size of the specimen, see Fig. 22.
Quality of the crack surface approximation of a single through crack with respect to the ratio between element size h and regularization length l
4.3 Crack tip approximation
Geometry and position of the initial crack for the half crack example with a left alignment and b center alignment
A rectangular patch of dimensions \(1.0\text { m}\times 1.0\text { m}\) with a discrete, horizontal crack of length \(\Gamma =0.5\text { m}\) is investigated, see Fig. 25. Two alignments of the crack are studied, i.e. an alignment to the left edge of the specimen and an alignment at the center of the specimen, in order to investigate the influence of one and two crack tip approximations, respectively. The phase-field approximation of the discrete crack is obtained by phase-field boundary conditions \(p=1\) at the location of the crack. The left aligned crack is studied for a regularized crack approximated by a row of nodes with triangular elements (HLST) and quadrilateral elements (HLSQ) as well as for an approximation by a row of fully degraded triangular elements (HLDT) and quadrilateral elements (HLDQ). Accordingly, these cases are studied for the centered alignment of the crack as well, that are referred to by the abbreviations HCST, HCSQ, HCDT and HCDQ, respectively. The finite element discretization of the single through crack example discussed in Sect. 4.2 is used, see Fig. 20.
The phase-field distribution for HCST and HLST is visualized in Fig. 26. It should be noted, that for the center aligned crack, the width available for the phase-field profile of the crack tip is limited and the study should be restricted to \(l\le 10h\) in this case.
Phase-field for half crack with respect to alignement and l
Quality of the crack surface approximation of a half crack at left alignment with respect to the ratio between element size h and regularization length l
Quality of the crack surface approximation of a half crack at center alignment with respect to the ratio between element size h and regularization length l
Given the amount of discrete crack surface \(\Gamma =0.5\text { m}\) to be approximated in both cases of this example, the quality of the crack surface approximation can be analyzed with respect to the regularization length parameter l, see Figs. 27 and 28. First of all, the discretization with triangular and quadrilateral elements is identical in all cases. Thus, the choice of the element type is of minor relevance for the approximation of the crack surface again. Furthermore, a limit value of \(\Gamma /\Gamma _l\) cannot be observed. In contrast, the influence of the crack tip approximation increases with increasing regularization length. A conclusion of the example discussed in Sect. 4.2 is the fact, that the discrete length of the crack is already represented by the phase-field profile in vertical direction with a very good accuracy. In contrast, the crack tip does not have a finite length. However, it is approximated by a phase-field profile with semicircle shape, see Fig. 26, that increases in radius with increasing regularization length. Therefore, increasing the regularization length parameter increases the error due to the semicircle crack tip approximation. Interestingly, the approximation based on a single row of nodes yields the most accurate result at \(l=2h\) with \(\Gamma /\Gamma _l=96.7\%\) and \(\Gamma /\Gamma _l=98\%\) for HCST and HLST, respectively. In contrast, if the crack is approximated by a row of fully degraded elements, the most accurate results are obtained at \(l=8h\), where \(\Gamma /\Gamma _l=86.2\%\) for HCDT, and at \(l=10h\), where \(\Gamma /\Gamma _l=90.1\%\) for HLDT. Nevertheless, it should be noted, that the profile of the crack tip is usually small compared to an evolved crack and the impact of its semicircle profile approximation decreases with increasing total length of the crack.
4.4 Branched crack approximation
Geometry of the branched crack example and guidelines of the finite element discretization for different branching angles \(\alpha \)
A branched crack configuration is examined in the last example on the quality of the crack surface approximation by the phase-field method. A rectangular patch of dimensions \(0.5\text { m}\times 1.0\text { m}\) is joined to a semicircle patch with radius \(0.5\text { m}\), see Fig. 29. The discrete crack to be approximated consists of a horizontal straight component of length \(0.5\text { m}\) and two branches of length \(0.5\text { m}\) each, i.e. the total length of the discrete crack is \(\Gamma =1.5\text { m}\). The angle between both branches is specified by \(2\alpha \) and studied for \(\alpha =5\dots 85^\circ \) in steps of \(5^\circ \). The semicircle shape is chosen in order to minimize edge effects on the profile of the crack branches. As already observed in the previous examples, the profile perpendicular to the crack surface is essential for a correct approximation. Hence, the semicircle shape can decrease the impact of the edges on the profile for small regularization length parameters by ensuring a \(90^\circ \) angle between the discrete crack and the specimen edges. However, especially for large l, the profile is trimmed, which results in an underestimation of the regularized crack surface in general. In this example, only the crack approximation by a single row of nodes and a discretization with triangular finite elements is investigated. The guidelines of the meshing are the outer boundary of the specimen as well as the location of the discrete crack. Furthermore, exemplary discretizations of the branching point are visualized in Fig. 29 for \(\alpha =10^\circ \), \(\alpha =45^\circ \) and \(\alpha =80^\circ \).
Phase-field contour plots wrt \(\alpha \) and l
As already discussed, the phase-field profile perpendicular to the crack is crucial for a correct representation of the discrete crack \(\Gamma \) by its regularized approximation \(\Gamma _l\). Therefore, the optimal case for a phase-field crack approximation is given by the initial example of the straight through crack in Sect. 4.2. On the one hand, the through crack does not have any crack tip that yields a significant error for the regularized crack surface \(\Gamma _l\), see Sect. 4.3. On the other hand, the phase-field profile is not disturbed, e.g. by edges or neighboring cracks, and can form a flawless transition from the broken to the sound region of the specimen, which results in a very accurate approximation of the discrete crack surface. In contrast, if a branched configuration is investigated, the vicinity of the branching point is a location of multiple supports of phase-field profiles overlapping and influencing each other. Starting at the branching point along the crack path in direction of the edges, the influence of the neighboring cracks on the phase-field profile decreases. However, the decreased influence strongly depends on the angle between the branches, see Fig. 30 for a visualization of phase-field profiles at \(\alpha =5^\circ \), \(\alpha =30^\circ \) and \(\alpha =50^\circ \) for exemplary regularization lengths. While the individual branches can be identified clearly for \(\alpha \ge 30^\circ \) even for large values of l, the branches are merged and represented by a single fat phase-field profile for small branching angles. The overlapping results in an underestimation of the crack surface in principle, see Fig. 31. The underestimation is strongly influenced by the branching angle. Furthermore, a pronounced change is observed for \(\alpha \ge 30^\circ \), i.e. the influence of the branching angle is decreasing significantly for this range. This also has an impact on the choice of l/h for the best approximation of \(\Gamma \). In the range of \(\alpha \ge 30^\circ \), an exact approximation with \(\Gamma /\Gamma _l=100\%\) is obtained for \(l=2h\). For smaller branching angles \(\alpha <30^\circ \), the optimal choice of the regularization length is decreasing as well until \(l=h\) for \(\alpha =5^\circ \), which yields \(\Gamma /\Gamma _l=99.5\%\).
Quality of the crack surface approximation of a half crack at center alignment with respect to the ratio between element size h and regularization length l
4.5 Kinematics of ideal plane cracks without friction
The crack kinematics for the special case of an ideal plane crack surface without frictional effects is discussed in Sect. 2.2 and encompasses the three types of structural deformation crack closure, crack opening and crack face sliding. A realistic approximation of cracks by the phase-field method must be able to reproduce these features in a numerical setting. The quality of the approximation is evaluated based on the numerically obtained reaction forced at the structural level as well as the local values of the stress tensor. In the following, benchmark examples with initial phase-field cracks at static and dynamic loading are presented and analyzed in order to evaluate different phase-field splits with respect to a realistic post fracture behavior. The focus of the last two examples is on the specific challenges arising from the implementation of a directional split in the framework of FEM.
Load specification function for the static investigation of crack kinematics
4.5.1 Static investigation of crack kinematics
In the first example, a 2D single through crack is investigated, that is similar in geometry to the example studied in Sect. 4.1, i.e. a rectangular patch of dimensions \(1.0\text { m}\times 1.0\text { m}\) with a discrete, horizontal through crack \(\Gamma \) halfway up in vertical direction is examined, see Fig. 19. The through crack is approximated by an initial phase-field crack represented by phase-field boundary conditions \(p=1\) at a row of nodes or all nodes of a row of elements, see the discretizations in Fig. 20 for SST and SDT, respectively, where the nodes with a phase-field boundary condition are indicated by a horizontal thick line. In addition to the nodal phase-field boundaries at the location of the initial crack, displacement boundaries \(\hat{u}_\text {x}({\bar{t}})=\hat{u}\cdot f_\text {x}({\bar{t}})\) and \(\hat{u}_\text {y}({\bar{t}})=\hat{u}\cdot f_\text {y}({\bar{t}})\) are applied at the top edge of the specimen. Furthermore, the displacements at the lower edge are fixed in x- and y-direction. The magnitude of the displacement is \(\hat{u}=1\text { mm}\) and the pseudo time dependent scaling functions are visualized in Fig. 32. Initially, a horizontal displacement is applied to investigate crack face sliding. Then, the subsequent displacement in vertical direction results in crack opening followed by crack closing.
The structural response is evaluated by a homogenized stiffness
that is computed based on the mean value of the displacement U and the sum of the numerically obtained reaction forces F at the upper edge in the specific direction. The material parameters \(\lambda =7.15\text { GPa}\) and \(\mu =12.71\text { GPa}\) are used and lead to \(K_\text {s}=8.184\text { GN/m}\) and \(K_\text {c/o}=31.432\text { GN/m}\), for shear deformation and a compressive/tensile (closing/opening) deformation in vertical direction, respectively. It should be noted, that these values are obtained with the SDT mesh, but without a phase-field crack, i.e. they describe the linear elastic behavior of a bulk rectangular patch with displacement boundaries as mentioned above. These homogenized stiffnesses provide a measure for the structural response of the rectangular patch with respect to the material parameters and serve as a comparative value for the evaluation of the phase-field approximation. According to the considerations on crack kinematics visualized in Fig. 3 of Sect. 2.2, the stiffnesses are estimated as \(K_\text {s}=0\text { GN/m}\), \(K_\text {c}=31.432\text { GN/m}\) and \(K_\text {o}=0\text { GN/m}\) for an actual discrete horizontal through crack. The results for the homogenized stiffnesses are summarized in Tab. 1 for the split and discretizations investigated in this example.
Structural deformation of SDT by a volumetric deviatoric split with deformation scaling factor 50: a \({\bar{t}}=1\), b \({\bar{t}}=3\), c \({\bar{t}}=5\) and d close up view on the crack at \({\bar{t}}=3\)
The structural deformations obtained with the volumetric deviatoric split are visualized with a deformation scaling factor of 50 in Fig. 33 and 34 for discretizations SDT and SST, respectively. The homogenized stiffnesses obtained are included in Tab. 1. It should be noted, that the opening and sliding is possible without reaction forces for the volumetric deviatoric split in SDT only, i.e. a realistic post fracture behavior is obtained, if the phase-field crack is approximated by a row of elements with each node having \(p=1\). The explanation of this phenomenon is obtained by a detailed investigation of the finite element implementation of the phase-field method for a crack opening, see Fig. 35. Let A and B the two parts of the rectangular patch, that are separated by the horizontal through crack. In the FEM discretization, these parts are connected via finite elements with modified stiffness according to the local phase-field values, that may be simplified as stiffness k in vertical direction, which is actually a combination of components of the elemental stiffness matrices. For a crack opening deformation, the split affects the correct identification of the strain and stress components associated with the structural opening direction. However, it is the degradation function g(p), that defines the amount of degradation of this specific stiffness. As a fundamental aspect of finite element implementation, the elemental stiffness is a result of the numerical integration of the element volume, i.e. the summation of contributions at the Gauss points of the element according to basic finite element theory. If the crack is approximated by a single row of nodes with \(p=1\), then the Gauss point value of the phase-field for the elements connected to those nodes is always lower than one. Therefore, the element stiffness is only partially degraded by \(g(p<1)>0\) and a realistic behavior cannot be simulated. While the explanation and visualization of this feature in Fig. 35 is provided for the crack opening deformation, an analogous argumentation applies to the stiffness component for shear deformation. Furthermore, it should be noted, that this is a fundamental aspect of the phase-field implementation. Although the Gauss point value of the phase-field is more close to \(p=1\) for an increased regularization length l, a Gauss point value of \(p=1\) can only be obtained, if all nodes associated with an element exhibit \(p=1\).
Structural deformation of SST by a volumetric deviatoric split with deformation scaling factor 50: a \({\bar{t}}=1\), b \({\bar{t}}=3\) and c \({\bar{t}}=5\)
Structural behavior influenced by the finite element implementation of the phase-field method
The homogenized stiffness for crack closure is only \(93.3\%\) of the expected value for the volumetric deviatoric split. The reason is visualized in Fig. 33d and is directly related to the volumetric deviatoric decomposition of the strains. Lets assume the local strain for crack closure is an uniaxial compressive strain in vertical direction of magnitude \(\hat{\varepsilon }_\text {yy}\), which would be the case if the horizontal displacement of the upper and lower edge of the specimen is free. According to the considerations on crack kinematics visualized in Fig. 3, no degradation should be applied in this case. However, the volumetric deviatoric decomposition of a uniaxial strain in vertical direction reads
The volumetric component is compressive, i.e. it is not associated with degradation in the volumetric deviatoric split. In contrast, degradation is always applied to components related to the deviatoric part of the strain. Therefore, a finite component of the initial uniaxial strain is associated with degradation and a wrong homogenized stiffness for crack closure is obtained. While this is a fundamental feature of the volumetric deviatoric split and applies to every element, an additional aspect is observed at the edge of the specimen, see Fig. 33d. The degradation of the deviatoric component results in a degraded stiffness in horizontal direction as well and the uniaxial strain becomes biaxial with a horizontal strain magnitude \(\hat{\varepsilon }_\text {xx}\). Then, volumetric deviatoric decomposition reads
i.e. the amount of deviatoric strain is increased. This results in increased degradation of the horizontal stiffness, which eventually yields an increase in the horizontal strain up to the point of \(\hat{\varepsilon }_\text {xx}=\hat{\varepsilon }_\text {yy}\), i.e. the non-degraded volumetric components vanish totally. While this is the reason for the defective horizontal displacement shown in Fig. 33d, it also results in non-convergent results for large amounts of crack closure deformations for the volumetric deviatoric split.
Structural deformation of SDT by a spectral split with deformation scaling factor 50: a \({\bar{t}}=1\text { s}\), b \({\bar{t}}=3\text { s}\), c \({\bar{t}}=5\text { s}\) and d phase-field evolution for increased shear loading
The structural deformations obtained by the spectral split are visualized with a deformation scaling factor of 50 in Figs. 36 for the SDT discretization. The results with SST discretization are omitted, as they suffer from the same fundamental deficiency discussed above for the volumetric deviatoric split. The spectral split exhibits realistic post fracture behavior in the case of crack closure and crack opening, where the homogenized stiffnesses are identical to the expected ones within the tolerances of a numerical approximation, see Tab. 1. However, significant reaction forces are obtained in the case of crack face sliding, that result in a homogenized stiffness for shear deformation that amounts to \(91\%\) of linear elastic behavior without a crack. Again, the reason to the unrealistic post fracture behavior is given by the decomposition of the strain tensor. Let the structural shear deformation be simplified by a strain tensor, that consists exclusively of shear components of magnitude \(\hat{\varepsilon }_\text {xy}\). Its decomposition according to the spectral split reads
i.e. it is considered to be a combination of a tensile principal strain of magnitude \(\hat{\varepsilon }_1\) and a compressive principal strain of magnitude \(\hat{\varepsilon }_2\). Furthermore, pure shear results in \(\hat{\varepsilon }_1=\hat{\varepsilon }_2\). In the spectral split, tensile principal strains are associated with degradation and compressive principal strains are related to persistent components of stress and strain energy density. Therefore, the decomposition of the shear strain, that should be totally degraded for a realistic post fracture behavior, results in a significant amount of non-degraded contributions to the elemental stiffness and the global structural response.
Structural deformation of SDT by a directional split with deformation scaling factor 50: a \({\bar{t}}=1\,\text {s}\), b \({\bar{t}}=3\text { s}\), c \({\bar{t}}=5\,\text {s}\)
The structural deformations obtained with the directional split are visualized with a deformation scaling factor of 50 in Fig. 37 for the SDT discretization. Due to the explicit design of the split to approximate a realistic post fracture behavior, both the structural deformations are in good agreement with the expected behavior and the homogenized stiffnesses provide values within the tolerances of a numerical approximation, see Tab. 1. It should be noted, that the fundamental deficiency regarding a proper crack approximation within an SST discretization is observed for the directional split as well, as this is an aspect of the FEM implementation rather than the phase-field split. In consequence, a row of fully degraded elements is a basic requirement for the approximation of an initial phase-field crack.
4.5.2 Type and orientation of finite elements
The realistic post fracture behavior of a 2D rectangular patch with an initial phase-field crack and a directional split is investigated with a special focus on the type and the orientation of the finite elements applied for the discretization. An initial crack \(\Gamma \) with orientation \({\mathbf {r}}=[0,1]^\text {T}\) divides the specimen into two separate bodies A and B. Three types of discretization are analyzed, see Fig. 38. Two discretizations are based on quadrilateral elements with quadratic shape. In ETQ90, the element edges are aligned with the surface of the initial crack. In ETQ45, the element edges are at an angle of \(45^\circ \) to the surface of the initial crack. It should be noted, that a continuous sequence of fully degraded elements along the location of the initial crack requires a zig-zag pattern of totally degraded elements, which results in a significantly larger plateau of \(p=1\) in the phase-field profile. The discretization ETT is based on triangular elements. According to the results of previous examples in Sect. 4.5, a row of fully degraded elements is considered to obtain a realistic post fracture behavior. The elements investigated are indicated by thick black lines in Fig. 38, where some nodes belong to body A and some nodes to body B. The characteristic element size is \(h=5\text { mm}\) and material parameter \(\lambda =8.89\text { GPa}\) and \(\mu =13.33\text { GPa}\) are assumed.
Setup of the 2D benchmark considering element type and orientation for a realistic post fracture behavior
The numerical integration of field quantities in finite elements is based on Gaussean quadrature formulas and is discussed in more detail e.g. in Zienkiewicz (1977). A 2D quadrilateral element with linear shape functions requires four Gauss points at the local coordinates \(\xi \approx \pm 0.577\) and \(\eta \approx \pm 0.577\), see Figs. 39 and 40. The summation over the Gauss point contributions is the basis for the computation of elemental quantities in the FEM framework like the residual vector and the stiffness matrix, where the definition of the crack driving component of the stress tensor \(\varvec{\sigma }^+\) is crucial. The elements under consideration in this example are indicated by a thick line in Fig. 38. They are analyzed as representatives of all elements that link the two bodies A and B separated by the initial crack. The residual at the nodes of these elements describes the local reaction forces against a specific structural deformation at the position of the specific element. The reaction force at the structural level is the result of all the local reaction forces obtained for the fully degraded elements. A realistic post fracture behavior at crack opening and crack face sliding deformation is characterized by no reaction forces. Therefore, the contributions of the fully degraded elements to the nodal residual in these cases must be zero. This implies a similar constraint on all Gauss points, as the residual vector is a result of the summation over all Gauss point contributions of the element.
Gauss point locations and element deformation in ETQ90
The orientation of quadrilateral elements in ETQ90 is characterized by the element edges being parallel to both the plane of the initial crack as well as the crack orientation. Therefore, the crack opening and crack face sliding deformation at the global level are represented by a vertical and horizontal deformation of the upper edge of the element, respectively, see Fig. 39. In consequence, a uniform state of strain is obtained, that is identical for all Gauss points and reads
for a vertical displacement \(u_\text {y}=1\text { mm}\) and a horizontal displacement \(u_\text {x}=1\text { mm}\), respectively. The directional decompositions of the associated ground stress tensors read
In both cases, the total stress is associated with the crack driving component of the stress tensor \(\varvec{\sigma }^+\). Thus, at full degradation, i.e. \(g(p)=0\), the reaction forces at the element level are zero and a realistic structural behavior is obtained, see the example in Sect. 4.5.1.
Gauss point locations and element deformation in ETQ45
Due to the discretization in ETQ45, nodes 1, 2 and 4 belong to the body A and node 3 belongs to body B. Therefore, crack opening and crack face sliding deformations result in a displacement of node 3 only, see Fig. 40. A crack opening deformation yields the strain tensors
at the Gauss points \(G_1\) to \(G_4\), respectively, which results in the directional decompositions of the associated ground stress tensors as
As the persistent stress tensor contributions \(\varvec{\sigma }^-\) are zero at all Gauss points, the residual vector is zero as well and a realistic structural response is obtained. For a crack face sliding deformation, the strain tensors read
and the directional decompositions of the associated ground stress tensors are explicitly written as
For Gauss points 2 and 4, non-zero persistent stress tensor contributions \(\varvec{\sigma }^-\) are obtained, which causes non-zero components in the residual vector of the element. In consequence, a global crack face sliding deformation, that is actually without resistance for an ideal crack, results in significant reaction forces in the finite element approximation. It should be noted, that this behavior can be observed in every discretization, that deviates from the perfect alignment of element edges and crack orientation discussed as ETQ90. It is a direct consequence of the bi-linear approximation of the field variables inside the quadrilateral elements, that is already pointed out in Sect. 2.4.
Gauss point location and element deformation in ETT
Linear shape functions within finite triangular elements result in a constant field of strain all over the domain of the finite element. Thus, the numerical integration of the function with respect to the strain field can be obtained by a single Gauss point, see Fig. 41. However, it should be noted, that in a transient simulation, the field of acceleration is not constant and the higher order function requires additional Gauss points for a proper numerical integration. Nevertheless, the strain tensors due to crack opening and crack face sliding deformations are constant all over the element and read
respectively. As they are similar to the strains obtained in ETQ90, again, the realistic post fracture behavior is obtained. Furthermore, the orientation of the triangular element does not affect the strain field, as the strain field is constant. Therefore, in contrast to discretizations with quadrilateral elements, a realistic post fracture behavior can be obtained regardless the discretization. It should be noted, that this issue is present for 3D simulations as well, where brick element discretizations exhibit a tri-linear field of strain and tetrahedral elements provide a constant field of strain. Nevertheless, a constant approximation of strain results in a poor accuracy of the numerical results and a comparable accuracy to the bi- and tri-linear approximation of quadrilaterals and bricks, respectively, can be obtained only by an increase of the discretization density. Fortunately, the phase-field crack approximation requires a very high discretization density as well and the application of triangular and tetrahedral elements is a suitable approach to obtain a realistic post fracture behavior in principle.
4.5.3 Distortion of the crack orientation vector
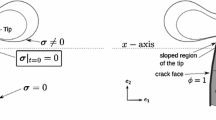
A rectangular patch of dimensions \(1.0\text { m}\times 1.0\text { m}\) with an initial horizontal through crack \(\Gamma \), dividing the specimen into bodies A and B, is investigated. The initial crack is approximated by a row of fully degraded elements and the whole specimen is discretized by a mapped meshing with triangular elements with characteristic size \(h\approx 1\text { mm}\), see Fig. 42. The crack orientation vector of all elements is set to \({\mathbf {r}}=[0,1]^\text {T}\), except for one fully degraded element indicated by a thick edge in Fig. 42. For this specific element, the crack orientation vector is deviated from the vertical direction by the angle \(\phi \). Material parameters \(\lambda =8.89\text { GPa}\) and \(\mu =13.33\text { GPa}\) are assumed.
Setup of the distortion of the crack orientation vector benchmark example
Crack orientation vector \({\mathbf {r}}\) deviated by a \(\phi =5^\circ \), b \(\phi =40^\circ \) and c \(\phi =70^\circ \)
The investigations are focused on the impact of a deviation of the crack orientation of a single element on the post fracture behavior of the structure at crack opening and crack face sliding deformations. During the evolution of phase-field cracks, a deviation of the crack orientation between neighboring elements is essential to approximate crack kinking or branching. Furthermore, the deviation is observed as a result of the stress field around the crack tip, see e.g. Steinke and Kaliske (2018).
The phase-field profile is computed once at the beginning of each simulation and the subsequent computations are restricted to the mechanical DOF with fixed crack orientation vectors for each element. A crack opening deformation is obtained by a displacement boundary of the upper edge in vertical direction with a magnitude of \(u_\text {y}=1\text { cm}\). Analogously, the crack face sliding deformation is studied for a displacement boundary of the upper edge in horizontal direction with a magnitude of \(u_\text {x}=1\text { cm}\). It should be noted, that both cases result in a rigid body movement of body B, regardless of the deviation angle \(\phi \), i.e. the impact on the displacement fields are minor and a contour plot of the displacements is omitted. In contrast, the impact on the stress fields and the reaction forces is significant. Deviation angles of \(0^\circ \le \phi \le 90^\circ \) are analyzed and three representative examples with \(\phi =5^\circ \), \(\phi =40^\circ \) and \(\phi =70^\circ \) are discussed in more detail, see Fig. 43 for a visualization of the neighborhood of the element with deviated crack orientation and Figs. 45, 46 and 47 for the contour plot of the stresses, respectively. The structural response is evaluated based on the homogenized stiffness according to Eq. (66).
Homogenized stiffness \(K_\text {o/s}\) with respect to the deviation of the crack orientation
A summary of the results with respect to the deviation angle \(\phi \) is visualized in Fig. 44. It is recapitulated from Sect. 4.5.1, that the homogenized stiffnesses of a linear elastic specimen without a crack are \(K_\text {o}=31.43 \times 10^9\text { N/m}\) and \(K_\text {s}=8.19 \times 10^9\text { N/m}\) for crack opening and crack face sliding deformation, respectively. These values are employed for an evaluation of the numerical results with deviated crack orientations. Furthermore, it should be considered, that the actual discrete crack kinematics discussed in Sect. 2.2 require zero stiffness in both cases. At the structural level, the homogenized stiffnesses obtained due to a deviation of the crack orientation of a single element are small for a crack opening deformation with a maximum of \(2.67\%\) of the linear elastic value at \(\phi \approx 70^\circ \), which is a very large angle of deviation anyway. In contrast, the homogenized stiffnesses for a crack face sliding deformation amount to \(13.43\%\) of the linear elastic value at \(\phi \approx 40^\circ \).
In the following, the stress fields for three representative angles of deviation \(\phi \) are evaluated. Again, the linear elastic response of the specimen without a crack are considered for the evaluation of the stress field magnitudes. Due to the displacement boundary conditions in horizontal and vertical direction at the upper and lower edge of the specimen, the linear elastic results for the stress fields are not homogeneous. Thus, the local linear elastic stress tensor in the element with the deviation of the crack orientation are employed for an evaluation and are computed as
for crack opening and crack face sliding deformation with magnitude \(1\text { cm}\) each, respectively.
Stress field contour plot for crack distortion angle \(\phi =5^\circ \) with crack opening deformation: a \({\hat{\sigma }}_\text {xx}\), b \({\hat{\sigma }}_\text {yy}\) and c \({\hat{\sigma }}_\text {xy}\) and with crack face sliding deformation: d \({\hat{\sigma }}_\text {xx}\), e \({\hat{\sigma }}_\text {yy}\) and f \({\hat{\sigma }}_\text {xy}\)
A deviation angle of \(\phi =5^\circ \) results in homogenized stiffnesses \(K_\text {o}=0.47 \times 10^6\text { N/m}\) and \(K_\text {s}=62.51 \times 10^6\text { N/m}\) for crack opening and crack face sliding deformation, respectively. Both values are small in comparison to the stiffnesses obtained for a linear elastic specimen without a crack, i.e. \(0.0015\%\) and \(0.76\%\) for opening and sliding, respectively. Nevertheless, the peak stress magnitude for \({\hat{\sigma }}_\text {xx}\) amounts to more than three times the linear elastic value for a crack opening deformation, see Fig. 45a. Interestingly, a tensile peak is observed at the left upper edge of the element with the deviation of the crack orientation vector and a peak compressive stress of identical magnitude is observed at the right lower edge below the element with the deviation of the crack orientation vector. At a first guess, this looks like an inclusion of stresses, where the positive and the negative magnitude neutralize each other. However, the non-zero amount of homogenized stiffness indicates a significant impact on the structural level, which is in contrast to a self-eliminating inclusion of stress. A similar combination of positive and negative peak values is observed for \({\hat{\sigma }}_\text {yy}\) and \({\hat{\sigma }}_\text {xy}\) at different positions, see Figs. 45b and c. While the shear stress component \({\hat{\sigma }}_\text {xy}\) is significantly higher than the linear elastic reference value, too, the stresses in vertical direction are negligible. It should be noted, that the combination of tension and compression gives rise to a significant amount of crack driving strain energy density at the position of the tensile peak, that eventually leads to phase-field evolution perpendicular to the initial crack, if the deformation is increased and phase-field evolution is allowed. The results of an additional simulation for crack opening deformation with non-fixed crack orientation and phase-field evolution is shown in Fig. 48a. The lateral growth of the phase-field is located at the position of the tensile peak. Furthermore, the modified crack orientation vector in the elements around the additional phase-field evolution is provided. Instead of an explicit additional branch, the phase-field crack widens and a diffusive pattern of irregular crack orientations is obtained, that leads to further stress inclusions. The crack face sliding deformation gives rise to a very high amount of normal stress in x-direction, see Fig. 45d, while the amount of \({\hat{\sigma }}_\text {yy}\) and \({\hat{\sigma }}_\text {xy}\) is rather small. Nevertheless, the combinations of positive and negative peak stresses in adjacent elements seem to be a characteristic pattern for a deviation angle of \(\phi =5^\circ \).
Stress field contour plot for crack distortion angle \(\phi =40^\circ \) with crack opening deformation: a) \({\hat{\sigma }}_\text {xx}\), a) \({\hat{\sigma }}_\text {yy}\) and c) \({\hat{\sigma }}_\text {xy}\) and with crack face sliding deformation: d) \({\hat{\sigma }}_\text {xx}\), e) \({\hat{\sigma }}_\text {yy}\) and f) \({\hat{\sigma }}_\text {xy}\)
The deviation angle of \(\phi =40^\circ \) results in homogenized stiffnesses \(K_\text {o}=0.4 \times 10^9\text { N/m}\) and \(K_\text {s}=1.1 \times 10^9\text { N/m}\) for crack opening and crack face sliding deformation, respectively. The homogenized stiffness for crack opening deformation is already at \(1.27\%\) of the comparative value. However, the homogenized stiffness for crack face sliding deformation exhibits its maximum value of \(13.43\%\) in this case. In contrast to the small deviation angle of \(\phi =5^\circ \), the combination of tensile and compressive peaks in adjacent elements is not observed for a crack opening deformation. Instead, large peak stresses are obtained for the normal stress in x-direction \({\hat{\sigma }}_\text {xx}\), i.e. \(\approx 28\) times the comparative value, and for the shear stress \({\hat{\sigma }}_\text {xy}\), i.e. \(\approx 10^4\) times the comparative value, see Figs. 46a and c, respectively. Furthermore, the vertical stress in y-direction \({\hat{\sigma }}_\text {yy}\) amounts to approximately the linear elastic comparative value, see Fig. 46b, which results in additional phase-field evolution for a very small crack opening deformation at the position of the maximum tensile peak, if phase-field evolution is considered, see Fig. 48b. For the crack face sliding deformation, a stress inclusion with a minor tensile stress is observed for the stress component \({\hat{\sigma }}_\text {xx}\), see Fig. 46d, that exhibits a peak value of \(\approx -10^4\) time the linear elastic comparative value. Furthermore, the vertical stresses \({\hat{\sigma }}_\text {yy}\) rise to \(\approx 1.5 \times 10^4\) of the comparative value, see Fig. 46e. Additionally, the shear stresses \({\hat{\sigma }}_\text {xy}\) amounts to \(\approx 4.2\) of the comparative value. It should be noted, that the deformation applied for crack opening and crack face sliding are similar for Figs. 46 and 45. Nevertheless, the peak stress values of crack driving stress components, i.e. tensile and shear stresses, are significantly higher in the case of an increased deviation angle of \(\phi \). Therefore, additional phase-field evolution is triggered at smaller deformation, when the deviation angle is higher.
The deviation angle of \(\phi =70^\circ \) results in homogenized stiffnesses \(K_\text {o}=0.83 \times 10^9\text { N/m}\) and \(K_\text {s}=0.34 \times 10^9\text { N/m}\) for crack opening and crack face sliding deformation, respectively. Thus, this deviation angle results in the highest homogenized stiffness for crack opening deformation with \(2.67\%\) of the linear elastic comparative value. Compared to the previous results, the homogenized stiffness for crack face sliding deformation reduces to \(4.15\%\) of the linear elastic comparative value. The horizontal stresses \({\hat{\sigma }}_\text {xx}\), visualized in Fig. 47a, and the shear stresses \({\hat{\sigma }}_\text {xy}\), shown in Fig. 47c, exhibit reduced magnitudes of \(\approx 26\) and \(\approx -6 \times 10^3\) times of the linear elastic comparative values. However, the peak tensile stress in vertical direction \({\hat{\sigma }}_\text {yy}\) amounts to \(\approx 1.9\) times of comparative values, see Fig. 47b. While this results in a high amount of crack driving strain energy density in the case of crack opening deformations, it should be noted, that it also coincides with the maximum amount of homogenized stiffness. The result of an additional simulation with phase-field evolution is visualized in Fig. 48c in this case. It should be noted, that in this case the additional phase-field evolves above the initial crack because of the fact, that the tensile peak of the vertical stresses \({\hat{\sigma }}_\text {yy}\) is above the initial crack, too, see Fig. 47b. The peak stress values of horizontal and vertical stresses \({\hat{\sigma }}_\text {xx}\) and \({\hat{\sigma }}_\text {yy}\), respectively, are both compressive in the case of a crack face sliding deformation. Furthermore, the peak shear stress \({\hat{\sigma }}_\text {xy}\) is only a relatively small \(\approx 1.4\) times of the comparative linear elastic value. Thus, a high angle \(\phi \) of crack orientation deviation is less significant in this case of deformation.
Stress field contour plot for crack distortion angle \(\phi =70^\circ \) with crack opening deformation: a \({\hat{\sigma }}_\text {xx}\), b \({\hat{\sigma }}_\text {yy}\) and c \({\hat{\sigma }}_\text {xy}\) and with crack face sliding deformation: d \({\hat{\sigma }}_\text {xx}\), e \({\hat{\sigma }}_\text {yy}\) and f \({\hat{\sigma }}_\text {xy}\)
Crack orientation vector \({\mathbf {r}}\) after phase-field evolution for an initial deviation by a \(\phi =5^\circ \) at \(u_\text {y}=15\text { cm}\), b \(\phi =40^\circ \) at \(u_\text {y}=1\text { mm}\) and c \(\phi =70^\circ \) at \(u_\text {y}=1\text { mm}\)
4.6 Wing crack evolution
The major difference between a directional split with a crack orientation aligned to the principal direction and an energetically obtained crack orientation occurs for states of strain, where the phase-field driving force is dominated by shear stresses on the crack surface. The experimental investigation of a pre-notched gypsum specimen at compressive loading published in Bobet and Einstein (1998) is an example, where the impact of mode dependent fracture toughnesses can be demonstrated, see e.g. Bryant and Sun (2018). The geometry, boundary conditions and the location of the initial notches are shown in Fig. 49. A horizontal deformation \(u_\text {x}\) is applied on the left edge in negative x-direction in order to apply a compressive loading on the structure with initial cracks \(\Gamma \). In consequence, so-called wing cracks evolve perpendicular to the initial notches at first. The wing cracks are driven by tensile stresses and exhibit Mode I crack opening deformation. However, due to the change of the load bearing structure by the wing crack evolution, the shear stresses at the tip of the initial cracks increase and result in a secondary crack evolution as a straight extension of the initial cracks. By the application of a mode dependent fracture toughness, Bryant and Sun demonstrate in (2018), that the wing cracks only evolve for a Mode II fracture toughness significantly higher than the fracture toughness for Mode I.
Setup of the wing crack benchmark experiment
The material parameters are \(\lambda =1.111\text { GPa}\), \(\mu =2.591\text { GPa}\), \(\rho =2300\text { kg/m}^3\) and \(G_\text {c}=50\text { J/m}^2\). The geometry is discretized by 758982 2D triangular elements with characteristic size \(h=0.2\text { mm}\). The initial cracks are represented by a discrete gap of width \(0.1\text { mm}\) at the location of the initial cracks and the regularization length is specified as \(l=1\text { mm}\). A horizontal displacement \(u_\text {x}(t)=\hat{u}_\text {x}\cdot f_\text {x}\) of magnitude \(\hat{u}_\text {x}=0.5\text { mm}\) and time dependency \(f_\text {x}\) according to Fig. 32 is applied at the upper edge of the specimen. The pseudo time step for the static simulation is constant with \(\Delta {\bar{t}} =10^{-2}\). The crack propagation is investigated for the directional split with energetic crack orientation with \(n=1{-}100\). The linear elastic result at displacement of \(u_\text {x}=50\, \mu \hbox {m}\) is provided in Fig. 50 in terms of contour plots for the stresses with a close up on the edge of an initial crack. Significant shear stresses are observed at the tip of the initial crack in Fig. 50c. In addition, large tensile stresses in x- and y-direction are obtained along the side of the initial crack surface, see Figs. 50a and b.
Stress contour plot at \(u_\text {x}=50\, \mu \text {m}\) for a \(\hat{\sigma }_\text {xx}\), b \(\hat{\sigma }_\text {yy}\) and c \(\hat{\sigma }_\text {xy}\)
Phase-field profile and close up on crack tip for a \(n=1\) and b \(n=100\)
Iso-mode fracture toughness results with \(n=1\) are provided in Fig. 51a. The larger shear stress at the tip of the initial cracks results in phase-field evolution as a straight extension of the initial crack. In between the two initial cracks, their extensions propagate towards each other and merge. From the structural point of view, the specimen loses its structural integrity due to the shear crack propagating through the whole specimen at \(\approx 45^\circ \) and a subsequent crack surface sliding deformation. The relation between the reaction force \(F_\text {x}\) and the displacement at the edge of the specimen is provided in Fig. 52. With the shear stress contributions at maximum with \(n=1\), the lowest peak reaction force is obtained. It should be noted, that the crack orientation is highly distorted around the phase-field cracks and significant convergence problems are observed in the numerical simulation for further phase-field evolution and post-fracture deformation analysis. In contrast, decreasing the amount of phase-field driving force from shear stress contribution by a large Mode II fracture toughness with \(n=100\) prevents the shear crack evolution. Instead, the typical wing cracks perpendicular to the initial cracks, as observed in the experiments, are obtained, see Fig. 51b. It should be noted, that the highly distorted crack orientation results in a significant widening of the wing cracks, see the close up for \({u}_\text {x}=0.53\text { mm}\) and \({u}_\text {x}=0.57\text { mm}\) in Fig. 51b. In consequence, no further propagation of the phase-field can be obtained due to non-convergence of the results beyond \({u}_\text {x}=0.58\text { mm}\). Nevertheless, the aspect of wing crack evolution is demonstrated in principle as a consequence of considering a mode dependent fracture toughness in the phase-field model. Furthermore, increasing the Mode II fracture toughness yields a decrease in phase-field driving force for this specific example, where shear stresses are dominated. Therefore, also the peak reaction force increases with increasing n, see Fig. 52.
Relation between reaction force \(F_\text {x}\) and displacement \(u_\text {x}\) at \(x=152.4\,\text {mm}\)
5 Conclusion
The phase-field method is a powerful approach with the potential to become the most comprehensive numerical technique for a realistic approximation of fracture evolution and post fracture behavior. The elegant combination of the spatial description of the crack surface with the governing physical principle of crack surface formation, i.e. strain energy dissipation, already provides an approach, that can model and predict the propagation of cracks along realistic and experimentally validated paths. Additional effort is necessary for the further development towards a general description of post fracture behavior close to reality. The analysis and discussion provided in this paper are intended to contribute to this development, both via the development of the directional split as well as providing benchmark simulations for the numerical evaluation of future phase-field approaches.
The following developments and findings are presented and discussed:
-
A modified irreversibility formulation combines the straight forward implementation of a history variable approach and the recovery of a crack-like phase-field profile after phase-field evolution similar to the application of additional phase-field boundary conditions during the simulation.
-
Three basic kinematics are formulated for the simplification of an ideal plane and frictionless crack. The compression of the crack faces against each other results in contact force transmission. In contrast, crack opening and crack face sliding deformations are possible without reaction forces. A realistic phase-field model for crack approximation needs to be able to model these features. A suitable approach is based on the identification of stress and strain components normal to the crack surface and shearing components on the crack surface. For components perpendicular to the crack surface, a further distinction between compressive and tensile components is necessary.
-
Standard phase-field splits, i.e. the volumetric deviatoric and the spectral split, exhibit deficiencies for a realistic post fracture behavior. The introduction of the directional split, that is based on a local vector describing the spatial orientation of the crack, provides a phase-field split, that can approximate the post fracture behavior of an idealized crack close to reality.
-
The alignment of the crack orientation vector along the direction of the largest tensile principal strain is a suitable approach for most of the strain states.
-
The amount of crack driving strain energy density depends on the local orientation of the crack orientation vector. The decomposition of the crack driving strain energy density into components related to Mode I and Mode II fracture and a relation with mode dependent fracture toughnesses provide a measure of the phase-field driving force. The phase-field driving force can be formulated with respect to the crack orientation for 2D and 3D strain states. A maximization of the phase-field driving force with respect to the crack orientation under consideration of a mode dependent fracture toughness is derived analytically for a 2D state of strain.
-
The maximum of the phase-field driving force exhibits a non-unique definition of the crack orientation vector for specific states of strain. A non-unique crack orientation vector is considered as energetically branching. The constitutive behavior is different for the energetically equal crack orientations. Thus, the new crack orientation is specified such, that the previous orientation is at the smallest angle with the new orientation.
-
The quality of the crack surface approximation in 2D is best, when the crack is straight and the regularization length l is small compared to the size of the domain. For straight cracks, a good approximation is obtained for \(l\ge 2h\), where h is the characteristic size of the finite elements. The phase-field profile of a crack tip yields an additional artificial amount of regularized crack surface. The impact of this overestimation increases with increasing l and is negligible, if l is small in comparison to the domain and the overall length of the crack. The regularized approximation of branching results in overlapping phase-field profiles and an underestimation of the regularized crack surface. Increasing l yields more overlapping and increased underestimation of the crack surface. Again, the impact of overlapping is negligible, if l is small in comparison to the domain and the overall length of the crack.
-
For an initial straight crack, the volumetric deviatoric split, the spectral split and the directional split are analyzed with respect to the approximation of the three basic crack kinematics of an idealized crack. The volumetric deviatoric split fails in modeling crack closing deformation in a realistic and numerically stable manner. The spectral split cannot model crack face sliding deformations realistically. The directional split exhibits perfect agreement with the expected behavior, if the crack orientation is constantly perpendicular to the crack surface over the whole phase-field profile.
-
The directional decomposition of stresses in a 2D element with bi-linear shape functions yields persistent components at the material point level in case of a crack face sliding deformation, if the element edges are not aligned to both the crack surface and the crack orientation vector. A similar defect is expected for 3D simulations with tri-linear shape functions. A solution can be the application of constant strain elements, i.e. triangles in 2D and tetrahedrals in 3D.
-
The distortion of the crack orientation vector yields artificial stress inclusions for crack opening and crack face sliding deformations, that increase in magnitude with increasing distortion angle. The stress inclusions of tensile and shear kind can trigger additional phase-field evolution, that results in a lateral widening of the phase-field profile. In consequence, artificial stiffnesses against the reaction free crack kinematics crack opening and crack face sliding are obtained and the convergence behavior of the solution is affected in a negative manner.
-
Experimentally observed wing cracks in rock-like material require mode dependent fracture toughnesses \(G_\text {c,I}\) and \(G_\text {c,II}\), where \(G_\text {c,II}\) must be significantly larger than \(G_\text {c,I}\). The directional split is suitable for the simulation of wing crack formation in principle. However, the distortion of the crack orientation vector and the evolution of lateral widening for the phase-field profile remain open issues in this case.
Several recent approaches of fracture mechanics make use of an explicit representation of the crack normal, for instance (Morin and Acharya 2021; Storm et al. 2020, 2021, 2022). Thus, there is a demand for realistic predictions of the crack orientation in ongoing research activities. The presented concept to determine the crack orientation based on the principle of maximum energy dissipation is supported by the experimental findings in Rozen-Levy et al. (2020).
References
Alessi R, Ambati M, Gerasimov T, Vidoli S, De Lorenzis L (2018) Comparison of phase-field models of fracture coupled with plasticity. In: Oñate E, Peric D, de Souza Neto E, Chiumenti M (eds) Advances in computational plasticity, vol 46. Computational Methods in Applied Sciences, pp 1–21. Springer, Cham (2018)
Ambrosio L, Tortorelli VM (1990) Approximation of functional depending on jumps by elliptic functional via t-convergence. Commun Pure Appl Math 43:999–1036. https://doi.org/10.1002/cpa.3160430805
Balay S, Abhyankar S, Adams MF, Brown J, Brune P, Buschelman K, Dalcin L, Dener A, Eijkhout V, Gropp WD, Karpeyev D, Kaushik D, Knepley MG, May DA, McInnes LC, Mills RT, Munson T, Rupp K, Sanan P, Smith BF, Zampini S, Zhang H, Zhang H (2019) PETSc Web page. https://www.mcs.anl.gov/petsc
Bažant ZP, Pijaudier-Cabot G (1988) Nonlocal continuum damage, localization instability and convergence. J Appl Mech 55:287–290
Belytschko T, Moës N, Usui S, Parimi C (2001) Arbitrary discontinuities in finite elements. Int J Numer Methods Eng 50:993–1013
Bobet A, Einstein H (1998) Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int J Rock Mech Min Sci 35:863–888. https://doi.org/10.1016/S0148-9062(98)00005-9
Borden MJ (2012) Isogeometric analysis of phase-field models for dynamic brittle and ductile fracture. PhD Thesis, University of Texas at Austin, Austin (2012)
Borden MJ, Hughes TJ, Landis CM, Verhoosel CV (2014) A higher-order phase-field model for brittle fracture: formulation and analysis within the isogeometric analysis framework. Comput Methods Appl Mech Eng 273:100–118. https://doi.org/10.1016/j.cma.2014.01.016
Borden MJ, Verhoosel CV, Scott MA, Hughes TJ, Landis CM (2012) A phase-field description of dynamic brittle fracture. Comput Methods Appl Mech Eng 217–220:77–95. https://doi.org/10.1016/j.cma.2012.01.008
Bourdin B (2007) Numerical implementation of the variational formulation for quasi-static brittle fracture. Interfaces Free Bound 9:411–430. https://doi.org/10.4171/IFB/171
Bourdin B, Francfort G, Marigo JJ (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48:797–826. https://doi.org/10.1016/S0022-5096(99)00028-9
Bryant EC, Sun W (2018) A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics. Comput Methods Appl Mech Eng 342:561–584. https://doi.org/10.1016/j.cma.2018.08.008
de Borst R, Verhoosel CV (2016) A discussion on gradient damage and phase-field models for brittle fracture. In: Naumenko K, Aßmus M (eds) Advanced methods of continuum mechanics for materials and structures, vol 60. Advanced Structured Materials, pp 263–277. Springer Singapore, Singapore (2016). https://doi.org/10.1007/978-981-10-0959-4_14
Francfort G, Marigo JJ (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46:1319–1342. https://doi.org/10.1016/S0022-5096(98)00034-9
Gross D, Seelig T (2011) Bruchmechanik. Springer, Berlin. https://doi.org/10.1007/978-3-642-10196-0
Hofacker M (2013) A thermodynamically consistent phase field approach to fracture. PhD Thesis, Universität Stuttgart, Stuttgart
Hofacker M, Miehe C (2011) A phase field model for three-dimensional dynamic fracture and its efficient numerical implementation. Proc Appl Math Mech 11:153–154. https://doi.org/10.1002/pamm.201110068
Hofacker M, Welschinger F, Miehe C (2009) A variational-based formulation of regularized brittle fracture. Proc Appl Math Mech 9:207–208. https://doi.org/10.1002/pamm.200910078
Ingraffea AR, Saouma V (1985) Numerical modeling of discrete crack propagation in reinforced and plain concrete. In: Sih GC, DiTommaso A (eds) Fracture Mechanics of Concrete: Structural Application and Numerical Calculation, pp. 171–225. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-009-6152-4_4
Karypis G, Kumar V (1998) A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J Sci Comput 20:359–392. https://doi.org/10.1137/S1064827595287997
Kuhn C, Müller R (2010) A continuum phase field model for fracture. Eng Fract Mech 77:3625–3634. https://doi.org/10.1016/j.engfracmech.2010.08.009
Linse T, Hennig P, Kästner M, de Borst R (2017) A convergence study of phase-field models for brittle fracture. Eng Fract Mech 184:307–318. https://doi.org/10.1016/j.engfracmech.2017.09.013
May S, Vignollet J, de Borst R (2015) A numerical assessment of phase-field models for brittle and cohesive fracture: \(\gamma \)-convergence and stress oscillations. Eur J Mech A Solids 52:72–84. https://doi.org/10.1016/j.euromechsol.2015.02.002
Miehe C, Gürses E (2007) A robust algorithm for configurational-force-driven brittle crack propagation with R-adaptive mesh alignment. Int J Numer Methods Eng 72:127–155. https://doi.org/10.1002/nme.1999
Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199:2765–2778. https://doi.org/10.1016/j.cma.2010.04.011
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int J Numer Methods Eng 83:1273–1311. https://doi.org/10.1002/nme.2861
Morin L, Acharya A (2021) Analysis of a model of field crack mechanics for brittle materials. Comput Methods Appl Mech Eng 386. https://doi.org/10.1016/j.cma.2021.114061
Mumford D, Shah J (1989) Optimal approximations by piecewise smooth functions and associated variational problems. Commun Pure Appl Math 42:577–685. https://doi.org/10.1002/cpa.3160420503
Ortiz M, Pandolfi A (1999) Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int J Numer Methods Eng 44:1267–1282
Özenç K (2016) Approaches to model failure of materials by configurational mechanics: theory and numerics. PhD Thesis, Technische Universität Dresden
Pandolfi A, Ortiz M (2012) An eigenerosion approach to brittle fracture: an eigenerosion approach to brittle fracture. Int J Numer Methods Eng 92:694–714. https://doi.org/10.1002/nme.4352
Pandolfi A, Weinberg K, Ortiz M (2021) A comparative accuracy and convergence study of eigenerosion and phase-field models of fracture. Comput Methods Appl Mech Eng 386. https://doi.org/10.1016/j.cma.2021.114078
Pijaudier-Cabot G, Bažant ZP (1987) Nonlocal damage theory. J Eng Mech 113:1512–1533
Rozen-Levy L, Kolinski JM, Cohen G, Fineberg J (2020) How fast cracks in brittle solids choose their path. Phys Rev Lett 125. https://doi.org/10.1103/PhysRevLett.125.175501
Saad Y, Schultz MH (1986) GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J Sci Stat Comput 7:856–869. https://doi.org/10.1137/0907058
Schlüter A (2018) Phase field modeling of dynamic brittle fracture. PhD Thesis, Technische Universität Kaiserslautern, Kaiserslautern
Schmidt B, Fraternali F, Ortiz M (2009) Eigenfracture: an eigendeformation approach to variational fracture. Multiscale Model Simul 7:1237–1266. https://doi.org/10.1137/080712568
Shen B, Stephansson O (1994) Modification of the G-criterion for crack propagation subjected to compression. Eng Fract Mech 47:177–189. https://doi.org/10.1016/0013-7944(94)90219-4
Song JH, Belytschko T (2009) Cracking node method for dynamic fracture with finite elements. Int J Numer Methods Eng 77:360–385. https://doi.org/10.1002/nme.2415
Steinke C (2021) On the numerical approximation of brittle fracture evolution at impact loading and realistic post-fracture behavior by the phase-field method. PhD Thesis, Technische Universität Dresden
Steinke C, Kaliske M (2018) A phase-field crack approximation approach based on directional stress decomposition. Comput Mech. https://doi.org/10.1007/s00466-018-1635-0
Steinke C, Özenç K, Chinaryan G, Kaliske M (2016) A comparative study of the r-adaptive material force approach and the phase-field method in dynamic fracture. Int J Fract 201:97–118. https://doi.org/10.1007/s10704-016-0125-7
Steinke C, Zreid I, Kaliske M (2017) On the relation between phase-field crack approximation and gradient damage modelling. Comput Mech 59:717–735. https://doi.org/10.1007/s00466-016-1369-9
Storm J, Kaliske M (2021) Phase-field fracture with representative crack elements for non-linear material behaviour. Proc Appl Math Mech. https://doi.org/10.1002/pamm.202000207
Storm J, Supriatna D, Kaliske M (2020) The concept of representative crack elements for phase-field fracture: anisotropic elasticity and thermo-elasticity. Int J Numer Methods Eng 121:779–805. https://doi.org/10.1002/nme.6244
Storm J, Qinami A, Kaliske M (2021) The concept of representative crack elements applied to eigenfracture. Mech Res Commun. https://doi.org/10.1016/j.mechrescom.2021.103747
Storm J, Yin B, Kaliske M (2022) The concept of representative crack elements (RCE) for phase-field fracture: transient thermo-mechanics. Comput Mech. https://doi.org/10.1007/s00466-021-02135-w
Strobl M, Seelig T (2015) A novel treatment of crack boundary conditions in phase field models of fracture: a novel treatment of crack boundary conditions in phase field models of fracture. Proc Appl Math Mech 15:155–156. https://doi.org/10.1002/pamm.201510068
Tanné E, Li T, Bourdin B, Marigo JJ, Maurini C (2018) Crack nucleation in variational phase-field models of brittle fracture. J Mech Phys Solids 110:80–99. https://doi.org/10.1016/j.jmps.2017.09.006
Taylor RL (2017) FEAP—finite element analysis program. http://www.ce.berkeley/feap
van der Vorst HA (1992) Bi-CGSTAB: a fast and smoothly converging variant of bi-CG for the solution of nonsymmetric linear systems. SIAM J Sci Stat Comput 13:631–644. https://doi.org/10.1137/0913035
Yin B, Storm J, Kaliske M (2021) Viscoelastic phase-field fracture using the framework of representative crack elements. Int J Fract. https://doi.org/10.1007/s10704-021-00522-1
Zhang X, Sloan SW, Vignes C, Sheng D (2017) A modification of the phase-field model for mixed mode crack propagation in rock-like materials. Comput Methods Appl Mech Eng 322:123–136. https://doi.org/10.1016/j.cma.2017.04.028
Zienkiewicz OC (1977) The Finite Element Method. Methode der finiten Elemente, vol 3. VEB Fachbuchverlag Leipzig, Altenburg
Zreid I (2018) Regularized damage and plasticity microplane models for concret. PhD Thesis, Technische Universität Dresden, Dresden
Acknowledgements
The authors would like to acknowledge the financial support of the German Research Foundation under grants KA 1163/19 and KA 1163/40 as well as the technical support of ZIH of TU Dresden for providing access to the Bull HPC-Cluster.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Steinke, C., Storm, J. & Kaliske, M. Energetically motivated crack orientation vector for phase-field fracture with a directional split. Int J Fract 237, 15–46 (2022). https://doi.org/10.1007/s10704-022-00633-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-022-00633-3