Mode II fracture characterization of toughened epoxy resin composites

Abstract

Epoxy resin used commonly as a matrix for polymer composite materials has good handling properties, but is too brittle. That is why various modifiers are used to increase the flexibility of products based on epoxy resin. This leads to two issues: how to efficiently increase the toughness of the resin without impacting significantly other properties, as well as how to measure the toughness in composite materials. The work aimed to show how the addition of a reactive rubber modifier will affect the fracture toughness of the obtained laminates during the longitudinal shear test (Mode II fracture). In total, three epoxy-glass laminates with different matrices were made and subjected to the End-Notched Flexure test according to ASTM D7905/D7905M standard: (1) the basic matrix of Epidian 6 resin, (2) Epidian 6 modified with the addition of 10% of Albipox 1000 reactive liquid rubber and (3) Epidian 6 modified with the addition of 10% of Hypro 1300X16 ATBN reactive liquid rubber. Based on the obtained results, it can be seen that the modulus of elasticity for the modified laminates was decreased compared to the laminate of pure epoxy resin (by ~ 25%). However, the addition of reactive rubbers increased the fracture toughness of the modified epoxy-glass laminates in the Mode II longitudinal shear test (G_IIc) by ~ 40–60%. Thus the benefits of modification outweigh the drawbacks if fracture toughness is an important designing consideration in a given application. The applicability of ENF method is successfully tested, but potential drawbacks are indicated—careful control of specimen thickness is necessary.

Introduction

Polymer composite materials, also known as fiber-reinforced plastics (FRP) are nowadays widely used construction materials. They typically consist of reinforcing fibers (e.g. glass, carbon, aramid) embedded in a thermosetting matrix (e.g. unsaturated polyester or epoxy resin). The main advantages of FRP are high specific strength and modulus, as well as the ability to tailor the properties throughout the element to suit local needs. Thermosetting resins are used predominantly because of their ease of manufacture, as well as better temperature and creep resistance.

Epoxy resins are a widely used material in the industry, including in everyday life as adhesives or sealants, as well as in composite materials as a matrix. Apart from numerous advantages, they also have significant disadvantages—they are brittle and have a relatively low impact strength. This excludes them from many applications that require significant fracture toughness, i.e. impact and fatigue strength. Therefore, resin modifying additives (various polymers, often elastomers) were used to improve the fracture toughness and dynamic properties. One of the most commonly used methods to improve the fracture toughness parameters of resins is the addition of reactive liquid rubbers (RLR, also called reactive liquid polymers—RLP), which at the same time do not deteriorate the processing properties, nor final properties after curing (see, inter alia, Sultan and McGarry 1973; Ozturk et al. 2001; Chikhi et al. 2002; Kinloch et al. 2005; Unnikrishnan and Thachil 2006; Abadyan et al. 2011; Szymańska et al. 2018; Guo et al. 2019; Chae et al. 2020; Januszewski et al. 2021). Nowadays, it is a common method of increasing the efficiency of epoxy resins in the industry. Acrylonitrile-butadiene rubbers (NBR) are the most commonly used. An important aspect is the very good miscibility of the elastomer with liquid resin. Rubbery particles precipitate on curing, leading to the formation of a second phase due to an increase in the molecular weight of the resin. To obtain stable elastomer dispersions in epoxy resin, rubbers with the amine (ATBN), carboxyl (CTBN), and hydroxyl (HTBN) end groups are used. The elastomer particles should not be too small, as they prevent the propagation of microcracks. This has a significant impact on the impact strength of the resin composition. The disadvantages of rubber elastomers include the presence of structures with places susceptible to oxidizing agents and high temperature.

This success led to trials of using RLR for modification of other types of resins: phenolic (Kaynak and Cagatay 2006) as well as vinyl ester and unsaturated polyester (e.g. Kostański and Królikowski 1985; Crosbie and Phillips 1985a, b; McBain 1996; Ullet and Chartoff 1996; Barcikowski and Królikowski 2013; Barcikowski et al. 2017). Despite that long-term use, neither the specifics of its mechanism nor fracture mechanics are fully understood (Unnikrishnan and Thachil 2006; Ullet and Chartoff 1996).

Destruction of materials made of layered composites, i.e. laminates, is often associated with the development of an interlaminar crack, called delamination. They are one of the most dangerous types of damage to structural elements. They happen suddenly and violently, and they can be associated with huge material and non-material losses. Cracking in fiber-reinforced laminates generally occurs between the individual layers. It begins in the matrix of the composite and leads to the weakening of the interaction between the polymer and the fibers. The fibers are the last to be destroyed, which leads to further propagation of delamination (Ochelski 2004). Characterization of the resistance to delamination often follows the Fracture Mechanics approach (Davies et al. 1998; Tay 2003).

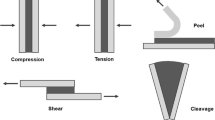
Due to the behavior of the crack under load, three main modes of fracture can be distinguished: Mode I—clean tearing (crack opening)—stretching of the joint surfaces in opposite directions, perpendicular to the crack plane, Mode II—longitudinal shear—the fracture surfaces slide together as a result of the shear action applied parallel to the fracture plane, Mode III—transverse shear—the joint surfaces slide in a direction parallel to the front of the joint (Irwin 1957). In practice, they rarely occur independently, so mixed modes, e.g I + II, are more often encountered (Pereira and de Morais 2006).

During the brittle fracture of the laminate, i.e. during the propagation of the created gap, the potential energy of the system changes. The rate at which energy is released is called the energy release rate, G_α, where α is the way the sample is loaded. The fracture will propagate until the energy release rate, G_α, is equal to or greater than the critical value of fracture energy (toughness), G_αc. The critical energy release rate, G_αc, is a material constant that determines the resistance of a material to brittle fracture (Zehnder 2012; Gdoutos 2020).

The Double Cantilever Beam (DCB) test is nowadays standardized for the measurement of the mode I critical strain energy release rate, G_Ic, of unidirectional (UD) laminates (JIS K 7086:1993, ASTM D 5528-94a, ISO 15024:2001, Beckermann and Pickering 2015; Li et al. 2020; Cheng et al. 2020; Dadian et al. 2020). For mode II, various experiments have been proposed but it is not clear which is the best one (Davies et al. 1990, 1999), though the End-Notched Flexure (ENF, Fig. 2) test has been used the most (see e.g. Saidpour et al. 2003; Pereira et al. 2004; Campilho et al. 2010; Dourado et al. 2012; Beckermann and Pickering 2015; Cheng et al. 2020; Dadian et al. 2020; Shin et al. 2020). Although the ENF method has been designed for UD composites, it has been successfully applied to multidirectional (e.g. textile-reinforced) laminates (Pereira and Morais 2004; Rzeczkowski 2020).

Though RLR modifiers are available on the market and recommended by their manufacturers, there is a distinctive lack of information on the exact effects of the modifiers in a quantifiable manner. ENF is hereby tested as a method for quantifying the fracture toughness of toughened textile-reinforced epoxy laminates. This paper presents an investigation into Mode II fracture toughness, as measured by the ENF method, for glass–epoxy laminates modified with 2 different RLR modifiers. The aim is to assess in an objective and quantifiable manner the effect of resin modification by two of the RLR modifiers available on the market. Verification of the suitability of the ENF method and energy release coefficient approach in general is the primary goal, while the supply of data for fracture toughness of two specific combinations of resin and RLR is secondary to that. The primary innovation of the study is the appraisal of the suitability of the use of ENF test for the assessment of toughening efficacy in GFRP prepared from RLP-modified epoxy resin by way of the Mode II fracture toughness.

Materials and methods

Resin and hardener

The work uses epoxy resin Epidian 6 produced by CIECH Sarzyna S.A., Poland. Epidian 6 (bisphenol A diglycidyl ether) is a popular, inexpensive, versatile resin used for the production of laminates, adhesives, linings, coatings etc., cured at room or at elevated temperature. In the study, the Z-1 hardener from CIECH Sarzyna S.A., Poland, was used. It consists of triethylenetetramine (TETA), which is an aliphatic polyamine that reacts only with epoxy groups contained in the resin. Z-1 is used for room-temperature curing with the optional post-curing at elevated temperatures. Epidian 6 is by default mixed with the Z-1 hardener in 100:13 proportion (13 phr of hardener).

Modifiers

Two types of rubber modifiers were used in the work. Recommended amounts of 10% of each were mixed with epoxy resin to obtain a homogeneous solution.

The first of the modifiers used was ALBIPOX® 1000 by Evonik Nutrition & Care GmbH. It is a resin based on bisphenol A, modified with elastomer, free of silicones. The used acrylonitrile-butadiene elastomer (NBR) is a special nitrile rubber chemically bonded to epoxy resin. During the curing of the resin, phase separation occurs, resulting in elevated properties for the final product.

The second used modifier is Hypro® 1300X16 ATBN, which is a low molecular weight acrylonitrile-butadiene (NBR) rubber terminated with an amino group. The modifier dissolves in the epoxy resin. During its hardening, discrete rubber particles precipitate, which absorbs the energy stored in the material during deformation. The amine structure in this modifier is based on N-aminoethylpiperazine (N-AEP).

Laminates preparation

Three resin compositions were prepared. One of them consists of neat epoxy resin—Epidian 6—with a hardener, while the other two have been modified with appropriate additives (Chap. 2.2). The individual compositions are summarized in Table 1. First the modifier is added to neat resin in the amount of 10% of the resin-mixture. Just before laminate manufacturing, the hardener is added in the amount of 13 parts per hundred parts resin or resin-modifier mixture.

Table 1 Resin and modifier compositions used in this study

The reinforcement of each laminate consisted of 6 layers of STR 024-500-110/125 woven roving (Krossglass S.A., Poland) stacked with the same orientation ([0°]₆). The fabric used is a balanced, plain-weave woven roving with universal surface treatment.

Three laminates 230 × 310 mm in size were manufactured following the guidelines of ASTM D7905/D7905M standard, one with each of the three resin compositions. Laminates were manufactured on glass plates using a hand lay up method, followed by vacuum bagging consolidation for increased fiber content in the composite.

Polyethylene insert was placed in the middle of the laminate thickness along the longer side. The inserts, which facilitated delamination under loading, were cut from a 30 µm thick polyethylene foil. According to the standard, the thickness of the insert should not exceed 13 µm. However, it was impossible to obtain such a thin release film in the time available. The insert was folded in half along the longer side to obtain straight and even edge.

Specimen preparation

Before starting the test, the obtained laminates were sectioned into proper specimens. The ASTM D7905/D7905M standard indicates that the part of the sample without the insert should be a minimum of 115 mm, while the part with the insert minimum 45 mm. From each of them, 5 specimens with approximate dimensions of 200 × 25 mm and an insert length of about 70 mm were cut with a diamond saw. Then, on the long sides of the specimens, three vertical lines were marked perpendicular to the plane of the laminate at a distance of 20, 30, and 40 mm from the beginning of the gap, respectively. They indicate the places where the force was applied during the calibration and the actual test. The prepared specimen is shown in Fig. 1.

Fig. 1

End-Notched Flexure (ENF) specimen and loading method. a Schematics. 2 h—specimen thickness; a₀ = 30 mm—initial delamination length used in the fracture test; a_j = 20 mm and 40 mm—crack length for compliance calibration; L = 50 mm—distance between the bottom support and the loading pin; R = 100 mm—support span. b Photograph of an actual specimen

Determination of elastic modulus

ASTM D7905/D7905M standard contain detailed instructions for procedures to be followed, as well as equations (Eqs. 1 through 6) to be used for calculations at each step. In order to determine the values of the flexural modulus, E_f, and the theoretical critical force, P_c (the force at which the specimen should delaminate further when the axis of the lower support coincides with the corresponding line on the sample at a distance from the start of the insert of a₀), needed for further tests, a 3-point bending test, carried out in accordance with the ISO 178:2019 standard is performed on one sample from each laminate using an MTS Bionix® Servohydraulic Test Systems machine (support span 100 mm, test speed 3 mm/min). The measurements were carried out until the linear dependence of the deformation on the applied force was obtained, consistent with Hooke’s law. Flexural stresses (Eq. 1 after ASTM D7905/D7905M) and flexural strains (Eq. 2 after ASTM D7905/D7905M) are calculated:

$$ \sigma_{f} = \frac{3PR}{{2B\left( {2h} \right)^{2} }} $$

(1)

where σ_f flexural stress (MPa), P applied load (N), R support span (mm), B specimen width (mm), 2 h specimen thickness (mm).

$$ \varepsilon_{f} = \frac{{6s\left( {2h} \right)}}{{R^{2} }} $$

(2)

where ε_f flexural strain, s deflection (mm), 2 h specimen thickness (mm), R support span (mm).

The flexural modulus, E_f, was calculated from the Eq. (3) after ASTM D7905/D7905M:

$$ E_{f} = \frac{{\sigma_{f2} - \sigma_{f1} }}{{\varepsilon_{f2} - \varepsilon_{f1} }} $$

(3)

where σ_f1 flexural stress measured at ε_f1 = 0.0005 (MPa), σ_f2 flexural stress measured with ε_f2 = 0.0025 (MPa).

The theoretical critical force, P_c, was calculated from the Eq. (4) after ASTM D7905/D7905M:

$$ P_{c} = \frac{4B}{{3a_{0} }}\sqrt {G_{IIc} E_{f} h^{3} } $$

(4)

where P_c theoretical critical force (N), B sample width (m), a₀ initial delamination length used in the fracture test (m), G_IIc energy release factor (from the literature) (J/m²), E_f flexural modulus (N/m²), h half the sample thickness (m).

Non-precracked toughness

The measurement is in essence a 3-point bending test, with the difference that the placement of the specimen was variable (Fig. 2). The distance between the lower supports remained the same, i.e. 100 mm. For compliance calibration (NPC-CC), the specimen was placed so that the axis of one lower support was aligned with the line on the side of the specimen representing a distance of 20 mm from the start of the insert in the first test, and 40 mm in the second test. Specimens were loaded to 50% of the P_c, then unloaded. For the proper non-pre-cracked fracture test (NPC) axis of the lower support coincides with the distance of 30 mm from the beginning of the insert. In all cases loading and unloading was performed at a speed of 0.5 mm/min.

Fig. 2

Specimen in non-pre-cracked test. a during compliance calibration (NPC-CC) for a₀ = 40 mm, b during fracture test. Note the position of left lower support in relation to the marks on the edge of the specimen

The first crack in the specimen during the actual test can be observed in two ways: visually and by force drop on the plot. The visual method of determining the maximum force, P_max, could not be considered reliable. The better method is the one in which the crack was observed as a visible decrease in force on the recorded diagram (Fig. 3). Ideally, the line corresponding to the loading should grow linearly so that it drops off sharply in the course of the fracture. This is, however, often not the case because of the complicated nature of crack growth in polymeric materials (e.g. crazing, see Ehrenstein 2011).

Fig. 3

Force–displacement relationship for one specimen example during the NPC fracture test (loading and unloading)

To calculate the energy release factor, G_IIc, plot the displacement versus applied force during compliance calibration. Compliance, C₀, is reciprocal to the slope of the plot (Fig. 4). This is made thrice—for a_j = 20 mm.and a_j = 40 mm, and in the actual fracture test.

Fig. 4

Force–displacement relationship for compliance calibration of a specimen at a_j = 20 mm

The compliance, C₀, was plotted against the delamination length cubed (Fig. 5). Linear regression of the plot yields calibration coefficients A (y-intercept) and m (slope).

Fig. 5

Compliance dependence on delamination length

The flexural modulus of elasticity E_lf was calculated from Eq. (5) after ASTM D7905/D7905M:

$$ E_{lf} = \frac{{L^{3} }}{{4ABh^{3} }} $$

(5)

where E_lf flexural modulus (MPa), L distance between the bottom support and the loading pin (mm), A calibration factor (mm/N), B sample width (mm), h half of the sample thickness (mm).

The energy release coefficient, G_IIc, for the specimen is calculated (Eq. 6 after ASTM D7905/D7905M):

$$ G_{IIc} = \frac{{3mP_{max}^{2} a_{0}^{2} }}{2B} $$

(6)

where G_IIc energy release coefficient (N/mm), m calibration coefficient (1/Nmm²), P_max force at which the fracture occurred (N), a₀ delamination length used in the actual test (mm), B sample width (mm).

Results and discussion

Table 2 presents the calculated values of the flexural modulus and the theoretical critical force, P_c, for tested specimens.

Table 2 Flexural modulus of elasticity and theoretical critical force values for specimens of tested compositions

Figures 6 and 7 present a comparison of the mean values of the energy release coefficients, G_IIc, forces at break, P_max, and flexural modulus, E_lf of non-pre-cracked specimens of the tested laminates.

Fig. 6

Flexural modulus E_lf for each composition

Fig. 7

Energy release coefficients G_IIc and maximum forces (forces at break) P_max for each composition

It is visible, both in Table 2 and Fig. 6, that the addition of 10% of RLR modifiers significantly (by about 22–26%, T test returns p values of 0.000815 and 0.000282 for Abipox 1000 and Hypro ATBN modified compositions, respectively) reduced the flexural modulus of elasticity of laminates made with the modified composition. That is contrary to what might generally be expected from both the literature and suppliers’ promotional materials, though Unnikrishnan and Thachil (2006) do report examples of such reduction. The drop in modulus might be attributed to incomplete phase separation. Some of the rubber may remain dissolved in the resin, acting as an active (taking part in the curing-crosslinking reaction) plasticizer. That topic in itself is worth further investigation. As Unnikrishnan and Thachil (2006) note, both the modulus and strength reduction, as well as the toughening effect depend greatly on the chemistry of both the rubber and the resin (e.g. epoxy number and crosslinking density).

Figure 7 present the G_IIc energy release coefficients calculated from the experiment. Both modifiers considerably increased the toughness of the composites of modified resins, by 39% and 58% for Albipox 1000 and Hypro 1300X16 ATBN, respectively. It is worth noting that the maximum force P_max also increased significantly (by 16% and 29%, respectively; p values 0.0386 and 0.0183) despite the reduction in the modulus. This demonstrates that modified materials can withstand significantly more deformation without initiation or propagation of cracks.

Surprisingly enough, the energy release coefficients themselves do not breach the significance thresholds. T test yields p values of 0.284 and 0.070 for compositions modified with Albipox 1000 and Hypro ATBN, respectively, when compared to composites of neat Epidian 6 resin. The most probable cause for low significance of G_IIc when compared to the P_max is the variability of thickness between the specimens in case of laminates manufactured not in a stiff closed mold, while the specimen thickness is a significant input in the calculations. In case of testing the interlaminar fracture toughness of composites, it is effectively the matrix that undergoes fracture, while the majority of load in the composite (dictated by the moduli of fibers and matrix, which are an order of magnitude different) is carried by the reinforcing fibers, the amount of which do not differ. What differs is the volume fraction of fibers, which is lower in the thicker laminate with excessive resin content. This is also seen in the case of flexural strength of laminates, which is overly reliant on the thickness of the specimens, thus is susceptible to differences caused by the excess of resin in the composite. It is worth noting that majority of technologies for composite manufacturing control the amount of fibers being emplaced, not the amount of resin or the thickness of the element. This indicates a potential drawback of the energy release coefficient approach (originally devised for homogenous materials) for the quantification of the fracture toughness of composite materials, especially the Mode II fracture toughness as measured by the ENF method. Careful control of the thickness of laminates used in for this method is highly advisably to obtain meaningful results.

Overall, the toughness increase of modified materials is greater than the decrease in modulus, thus warranting the industrial use of such modifying agents to increase the dynamical properties of used materials.

Conclusions

A very important aspect when designing a machine or structure is its fracture resistance. Epoxy resin used commonly as a matrix for polymer composite materials has good handling properties but is too brittle. That is why various modifiers are used to increase the flexibility of products based on epoxy resin. This leads to two issues: how to efficiently increase the toughness of the resin without impacting significantly other properties, as well as how to measure the toughness in composite materials. This work presents the investigation of the use of the End-Notched Flexure test as a method for the assessment of toughening efficacy of RLP modification of glass–epoxy laminated composites. The laminates in question were prepared both with and without the addition of modifiers to the epoxy resin. The Mode II interlaminar fracture test is appraised as a potential standardized method for evaluating different toughening agents.

• The work has demonstrated a successful application of the ASTM D7905/D7905M standard End-Notched Flexure test to the measurement of the interlaminar toughness (here approximated by the energy release coefficient G_IIc) of multidirectionally reinforced layered composites. This method has the potential to become a useful comparative measure for the toughness of various laminates.

• Potential drawbacks of the End-Notched Flexure for the assessment of laminated composites are however indicated. Most laminated composites are manufactured in ways that control for the amount of fibers used, not the thickness of the laminate, while the results in ENF method, as in all flexural methods, are over-reliant on thickness of specimens.

• The results of the experiment demonstrated some of the drawbacks of reactive liquid rubber modification of epoxy resins, namely the reduction of the modulus of elasticity (flexural modulus in this case, though there is no reason to expect the tensile modulus to behave differently). The reduction is significant (on the order of 25%).

• However, the experiment demonstrates also the benefits of the modification—toughness of the composites as measured by the G_IIc energy release coefficient increased by ca. 40–60%. The increase in toughness potentially outweighs the reduction of the modulus (and thus stiffness), thus warranting the use of such modifiers when necessary.

• The results are one addition to a greater database of modification results of various epoxy resins by various modifying agents. The effect depends greatly on the specific chemistry and properties of both the rubber and the resin, thus one set of results may not be universally applied to every modifier and every resin.