1 Introduction

A lot of structures or materials exhibit stress relaxation and creep. To describe this behavior, viscoelastic material models are employed. In the literature, many publications present approaches to characterize the behavior of linear viscoelastic solids. The foundation of linear viscoelastic models started with the works of Boltzmann (1878). The stress at a particle within a viscoelastic solid depends on both history and temperature at the particle. Further information regarding thermomechanical analysis of linear viscoelastic solids can be found in the work of Taylor et al. (1970). In the study of Holzapfel and Reiter (1995), a fully coupled thermomechanical finite element formulation of viscoelastic solids is derived. Further studies related to viscoelastic solids can be found in the work of Kaliske and Rothert (1997), Park and Kim (1999), Lakes (1998), Wineman (2009) and in many others. However, in the study at hand, we limit us to small strain linear viscoelastic solids using Prony series with n-Maxwell elements. Analysis of fracture of structures is of high interest for engineers because crack propagation leads to the failure of the structure at loads that are smaller than their real bearing capacity. The analysis of stress fields in linear elastic continua with a sharp crack is carried out in the work of Westergaard (1939), Sneddon (1946) and others. Although a lot of studies investigate cracks in elastic continua, however, the first who presented a proper application of the stress intensity factor is Irwin (1957). The stress intensity factor derived by Irwin (1957) is limited to problems with small yielding zones around the crack tip, or, in other words, to cases where the theory of linear elastic fracture mechanics is governing. The analysis of crack propagation in viscoelastic solids started earlier in the works of Schapery (1964), Knauss (1963) and others. The crack speed is defined as a criterion for unstable crack propagation in Knauss (1966). The stability of crack propagation is investigated by Knauss (1969). Furthermore, an energetic fracture criterion to characterize initiation and propagation of cracks in viscoelastic media is derived in the work of Williams (1965). Moreover, an appropriate crack growth law in Maxwell solids subjected to small-scale and large-scale yielding, based on energy and crack opening displacement fracture criteria, is derived in the study of McCartney (1979). A Barenblatt fracture criterion is used in the work of Willis (1967) to characterize crack propagation in viscoelastic solids.

Configurational forces or material forces are known as non-Newtonian forces that act on an inhomogeneity within a homogeneous body. These inhomogeneities can be either inclusions, voids or even cracks. The theory of material forces arises from Eshelby’s thought experiment Eshelby (1951). In the aforementioned study, Eshelby considers that the energy variation within a homogeneous elastic body due to the movement of the inclusion is equal to the product between the material force vector, that is acting on the inclusion, and the displacement vector. In the framework of fracture mechanics, the inclusion can be considered as a crack. The material force acting on the crack tip is considered as the crack driving force. In linear elasticity, the component of the material force in crack direction is nothing else but the J-integral derived by Rice (1968). The use of material forces in the field of the finite element method starts with the work of Braun (1997) and Mueller and Maugin (2002). The formulation of material forces in viscoelastic materials can be found in the publications of Kaliske et al. (2005), Näser et al. (2009) and others. In the work Nguyen et al. (2005), material forces are derived for small strain linear viscoelastic solids, that are characterized by the Prony term with one Maxwell element.

At cyclic loading, the pioneering law that describes crack growth is Paris’ law introduced by Paris and Erdogan (1963). This law correlates the cyclic stress intensity factor \(\varDelta K\) to the crack growth rate per cycle \(\frac{da}{dN}\). However, the cyclic stress intensity factor is limited to the cases, where the theory of linear elastic fracture mechanics (LEFM) is applicable. To overcome the limitation of LEFM, Dowling and Begley (1976) derived the cyclic J-integral \(\varDelta J\), which is appropriate for gross plasticity. Moreover, Ochensberger and Kolednik (2014) derived the elasto-plastic cyclic J-integral \(\varDelta J^{ep}\) using configurational forces, that is appropriate for fatigue crack growth at non-proportional loading. In a further work of Ochensberger and Kolednik (2015), an appropriate parameter known as the active plastic zone elasto-plastic cyclic J-integral \(\varDelta J^{ep}_{\text {actPZ}}\) is derived. This parameter is able to depict the overload effect in elasto-plastic materials. However, this parameter is path-dependent and requires to know in advance the active plastic zone around the crack tip. In our previous study Khodor et al. (2021), a path-independent domain integral based on cyclic material forces is introduced. The domain-integral is able to characterize the overload effect in small strain elastic-plastic materials without any need to identify the active plastic zone.

The aim of the study at hand is to derive a path-independent domain integral to describe fatigue crack growth in viscoelastic solids at cyclic loading. The method has been previously introduced for elastic-plastic materials in Khodor et al. (2021). The approach is based on cyclic material forces. These forces are similar to conventional material forces used at monotonic loading, however, they are derived using the cyclic free energy density.

The paper at hand is structured as follows. In Sect. 2, the constitutive equations used to characterize the viscoelastic solids are presented. Moreover, the balance of energy momentum and the balance cyclic energy momentum for n-Maxwell elements are derived in Sects. 3 and 4, respectively. Furthermore, the numerical computations of nodal material forces and cyclic nodal material forces are shown in Sect. 5. Path-independence of the domain integrals using both material forces and cyclic material forces as well as the proof of the existence of the balance of energy momentum and cyclic energy momentum are presented in Sect. 6. Furthermore, the cyclic material force approach is validated in Sect. 6 by comparing it to experimental data. Finally, concluding remarks are drawn in Sect. 7.

2 Material description

Small strain linear viscoelasticity in the subsequent derivations is characterized by Prony series. The Cauchy stress tensor is obtained as

$$\begin{aligned} \varvec{\sigma }=\int _0^t2G(t-\tau )\frac{d\varvec{e}}{d\tau }d\tau +\varvec{I}\int _0^t K(t-\tau )\frac{d\varDelta }{d\tau }d\tau , \end{aligned}$$
(2.1)

where \(\tau \), \(\varvec{e}\) and \(\varDelta \) are the past time, deviatoric strain and volumetric strain, respectively. The parameters G(t) and K(t) are the Prony series shear-relaxation and bulk-relaxation moduli, respectively. The shear-relaxation and the bulk-relaxation moduli are formulated as

$$\begin{aligned} G(t)=&\,G_0\left[ \alpha _{eq}^G+\sum _{i=1}^{n_G}\alpha _i^G exp\left( -\frac{t}{\tau _i^G}\right) \right] , \end{aligned}$$
(2.2)
$$\begin{aligned} K(t)=&\,K_0\left[ \alpha _{eq}^K+\sum _{i=1}^{n_K}\alpha _i^K exp\left( -\frac{t}{\tau _i^K}\right) \right] , \end{aligned}$$
(2.3)

where \(\tau _i^G\) and \(\tau _i^K\) are the shear relaxation time and bulk relaxation time, respectively. \(G_0\) and \(K_0\) are the shear and bulk moduli at \(t=0\). More details regarding the constitutive equations can be seen in the paper of Kaliske and Rothert (1997). \(n_G\) and \(n_K\) are the number of shear Maxwell elements and bulk Maxwell elements, respectively. The total number of Maxwell elements is equal to the maximum of \(n_G\) and \(n_K\). \(\alpha _i^G\) and \(\alpha _i^K\) are the relative moduli. Using the relative moduli, \(\alpha ^G_{eq}\) and \(\alpha ^K_{eq}\) can be obtained as

$$\begin{aligned} \alpha _{\mathrm {eq}}^G=&\,1-\sum _{i=1}^{n_G}\alpha _i^G, \end{aligned}$$
(2.4)
$$\begin{aligned} \alpha _{\mathrm {eq}}^K=&\,1-\sum _{i=1}^{n_K}\alpha _i^K. \end{aligned}$$
(2.5)

The linear viscoelastic material model can be described using a generalized Maxwell solid as shown in Fig. 1. The model consists of a set of n-Maxwell elements in parallel to a spring that is the equilibrium spring. Each Maxwell element consists of a spring and a dashpot, each spring within this element is a non-equilibrium spring.

Fig. 1
figure 1

Generalized Maxwell model

Full size image

Due to infinitesimal strain, the total total strain tensor \(\varvec{\varepsilon }\) is an additive decomposition of the elastic strain and the viscous strain within each Maxwell element and can be written as

$$\begin{aligned} \varvec{\varepsilon }=\varvec{\varepsilon }^e_i+\varvec{\varepsilon }^v_i\qquad \text {for}\, i=1,\ldots ,n , \end{aligned}$$
(2.6)

where \(\varvec{\varepsilon }^e_i\) and \(\varvec{\varepsilon }^v_i\) are the elastic strain tensor in the ith Maxwell element. The total Cauchy stress tensor is a sum of the stress tensors in the equilibrium spring and the non-equilibrium springs and can therefore be obtained as

$$\begin{aligned} \varvec{\sigma }=\varvec{\sigma }^{\mathrm {eq}}+\sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i, \end{aligned}$$
(2.7)

where \(\varvec{\sigma }^{\mathrm {eq}}\) and \(\varvec{\sigma }^{\mathrm {neq}}_i\) are the Cauchy stress tensors in the equilibrium spring and the non-equilibrium spring of the ith Maxwell element. The free energy is also the summation of the free energies in the equilibrium and non-equilibrium springs and can be calculated as

$$\begin{aligned} \psi (\varvec{\varepsilon },\varvec{\varepsilon }^e_1,\ldots ,\varvec{\varepsilon }^e_n)=\psi ^{\mathrm {eq}}(\varvec{\varepsilon })+\sum _{i=1}^{n}\psi ^{\mathrm {neq}}_i(\varvec{\varepsilon }^e_i), \end{aligned}$$
(2.8)

where \(\psi ^{\mathrm {eq}}\) and \(\psi ^{\mathrm {neq}}_i\) are the contributions to the free energy of the equilibrium spring and non-equilibrium spring in the ith Maxwell element, respectively. Let \(\mathbb {C}^{\mathrm {eq}}\) and \(\mathbb {C}^{\mathrm {neq}}_i\) be the fourth order elasticity tensors in the equilibrium spring and the non-equilibrium spring of the ith Maxwell element. In isotropic material, the fourth order elasticity tensor is obtained using Young’s modulus E and Poisson’s ratio \(\nu \) or using the bulk modulus K and shear modulus G. Therefore, \(\mathbb {C}^{\mathrm {eq}}\) is obtained using \(G^{\mathrm {eq}}=\alpha _{\mathrm {eq}}^GG_0\) and \(K^{\mathrm {eq}}=\alpha _{\mathrm {eq}}^KK_0\). On the other hand, \(G^{\mathrm {neq}}_i=\alpha ^G_iG_0\) and \(K^{\mathrm {neq}}_i=\alpha ^K_iK_0\) are taken to compute \(\mathbb {C}^{\mathrm {neq}}_i\). By \(\mathbb {C}^{\mathrm {eq}}\) and \(\mathbb {C}^{\mathrm {neq}}_i\), the free energy and the Cauchy stress tensors reformulate into

$$\begin{aligned}&\psi =0.5\,\varvec{\varepsilon }:\mathbb {C}^{\mathrm {eq}}:\varvec{\varepsilon }+\sum _{i=1}^n 0.5\,\varvec{\varepsilon }^e_i:\mathbb {C}^{\text {neq}}_i:\varvec{\varepsilon }^e_i, \end{aligned}$$
(2.9)
$$\begin{aligned}&\varvec{\sigma }^{\mathrm {eq}}=\frac{\partial {\psi ^{\mathrm {eq}}}}{\partial {\varvec{\varepsilon }}}=\mathbb {C}^{\mathrm {eq}}:\varvec{\varepsilon }, \end{aligned}$$
(2.10)
$$\begin{aligned}&\varvec{\sigma }^{\mathrm {neq}}_i=\frac{\partial {\psi ^{\mathrm {neq}}_i}}{\partial {\varvec{\varepsilon }^e_i}}=\mathbb {C}^{\mathrm {neq}}_i:\varvec{\varepsilon }^e_i. \end{aligned}$$
(2.11)

3 Balance of energy momentum

In Nguyen et al. (2005), the local balance of energy momentum is derived for small strain linear viscoelastic solids with one Maxwell element, in other words \(n=1\). In this section, the local balance of energy momentum is derived for n Maxwell elements. The inertia effects will be neglected and, therefore, the balance of linear momentum is expressed as

$$\begin{aligned}&\nabla _{\varvec{X}}\cdot \varvec{\sigma }+\varvec{b}=\varvec{0}, \end{aligned}$$
(3.1)
$$\begin{aligned}&\sigma _{jk,k}+b_j=0 \qquad \text {for}\,j,k=1,2,3\,, \end{aligned}$$
(3.2)

where \(\nabla _{\varvec{X}}\cdot (\bullet )\) is the divergence operator, and \(\varvec{b}\) are body forces. The starting point to obtain the balance is by calculating the gradient of the free energy density, which can be written as

$$\begin{aligned} \begin{aligned}&\nabla _{\varvec{X}\,}\psi (\varvec{\varepsilon },\varvec{\varepsilon }^e_1,\ldots ,\varvec{\varepsilon }^e_n,\varvec{X})\\&\quad =\frac{\partial {\psi ^{\mathrm {eq}}}}{\partial {\varvec{\varepsilon }}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }+ \sum _{i=1}^n\frac{\partial {\psi ^{\mathrm {neq}}_i}}{\partial {\varvec{\varepsilon }^e_i}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^e_i\\&\qquad +\,\frac{\partial {\psi }}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}, \end{aligned} \end{aligned}$$
(3.3)

where the operator \(\nabla _{\varvec{X}\,}(\bullet )\) is the gradient operator and the term \(\frac{\partial {{\psi }}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}\) is the explicit dependence of the free energy on the position \(\varvec{X}\). This term is used when for instance the Young’s modulus is a function of the position \(\varvec{X}\), \(E:=E(\varvec{X})\). Inserting Eqs. (2.10) and (2.11) into the above equation yields

$$\begin{aligned} \begin{aligned} \nabla _{\varvec{X}\,}\psi =&\,\varvec{\sigma }^{\mathrm {eq}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }+ \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^e_i\\ {}&+ \frac{\partial {\psi }}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}. \end{aligned} \end{aligned}$$
(3.4)

Using the additive decomposition of the strain tensor, Eq. (3.4) can be recast into

$$\begin{aligned} \begin{aligned} \nabla _{\varvec{X}\,}\psi =&\,\varvec{\sigma }^{\mathrm {eq}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }+ \left( \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i\right) :\nabla _{\varvec{X}\,}\varvec{\varepsilon }\\&- \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_i+ \frac{\partial {\psi }}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}\\ =&\,\varvec{\sigma }:\nabla _{\varvec{X}\,}\varvec{\varepsilon }- \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_i+ \frac{\partial {\psi }}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}. \end{aligned}\nonumber \\ \end{aligned}$$
(3.5)

By the balance of linear momentum and due to the fact that \(\varvec{\varepsilon }=\frac{1}{2}\left( \nabla _{\varvec{X}\,}\varvec{u}+\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \right) \), the term \(\varvec{\sigma }:\nabla _{\varvec{X}\,}\varvec{\varepsilon }\) can be written as

$$\begin{aligned} \begin{aligned} \varvec{\sigma }:\nabla _{\varvec{X}\,}\varvec{\varepsilon }&=\nabla _{\varvec{X}}\cdot \left( \left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{\sigma }\right) -\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \nabla _{\varvec{X}}\cdot \varvec{\sigma }\\&=\nabla _{\varvec{X}}\cdot \left( \left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{\sigma }\right) +\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{b}, \end{aligned} \end{aligned}$$
(3.6)

where \(\nabla _{\varvec{X}\,}\varvec{u}\) is the gradient of the displacement field and \(\left( {\bullet }\right) ^\intercal \) denotes the transpose operator. The insertion of Eq. (3.6) into Eq. (3.5) yields

$$\begin{aligned} \begin{aligned} \nabla _{\varvec{X}\,}\psi =&\,\nabla _{\varvec{X}}\cdot (\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{\sigma })- \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i:\varvec{\varepsilon }^v_i\\&+ \left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{b}+ \frac{\partial {\psi }}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}. \end{aligned} \end{aligned}$$
(3.7)

The gradient of the free energy can take the form \(\nabla _{\varvec{X}\,}\psi =\nabla _{\varvec{X}}\cdot (\psi \varvec{I})\), and, therefore, leads to the balance of energy momentum that can be written as

$$\begin{aligned} \nabla _{\varvec{X}}\cdot \varvec{\Sigma }+\varvec{B}=\varvec{0}, \end{aligned}$$
(3.8)

where \(\varvec{\Sigma }=\psi \varvec{I}-\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{\sigma }\) is the Eshelby stress tensor and \(\varvec{B}=\sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_i:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_i-\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{b}-\frac{\partial {\psi }}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}\) are the configurational volume forces.

4 Balance of cyclic energy momentum

In case of fatigue crack propagation, a continuum is subjected to cyclic loading, therefore, a new balance of energy momentum is derived in our previous work Khodor et al. (2021) and is called balance of cyclic energy momentum. In the aforementioned work, the balance of cyclic energy momentum is appropriate for elastic-plastic materials at cyclic loading. In the study at hand, this balance law will be derived for small strain linear viscoelastic solids. This balance is a combination of the balance of energy momentum at maximum load and minimum load. The starting point to obtain the balance of cyclic energy momentum is to evaluate the cyclic free energy \(\psi _{\mathrm {cycle}}\) that is defined as

$$\begin{aligned} \begin{aligned} \psi _{\mathrm {cycle}}=&\psi ^{\mathrm {eq}}_{\mathrm {cycle}}+\sum _{i=1}^n\psi ^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\\ =&\int _{\varvec{\varepsilon }_{\mathrm {min}}}^{\varvec{\varepsilon }_{\mathrm {max}}}(\varvec{\sigma }^{\mathrm {eq}}-\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {min}}):d\varvec{\varepsilon }\\&+ \sum _{i=1}^n\int _{\varvec{\varepsilon }^e_{i_{\mathrm {min}}}}^{\varvec{\varepsilon }^e_{i_{\mathrm {max}}}}(\varvec{\sigma }^{\mathrm {neq}}_i-\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {min}}}):d\varvec{\varepsilon }^e_i, \end{aligned} \end{aligned}$$
(4.1)

where \(\psi ^{\mathrm {eq}}_{\mathrm {cycle}}\) and \(\psi ^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\) are the cyclic free energies of the equilibrium spring and the non-equilibrium spring in the ith Maxwell element, respectively. The subscripts \((\bullet )_{\mathrm {max}}\) and \((\bullet )_{\mathrm {min}}\) designate the value of a specific parameter at maximum and minimum load, respectively. For instance, \(\varvec{\varepsilon }_{\mathrm {max}}\) is defined as the value of the total strain tensor at maximum load and this notation applies for all other quantities. To better understand the calculation of the cyclic energy, the reader is referred to Appendix B. Developing the terms of Eq. (4.1), the cyclic free energy takes the form

$$\begin{aligned} \psi _{\mathrm {cycle}}&=\,\psi ^{\mathrm {eq}}_{\mathrm {max}}-\psi ^{\mathrm {eq}}_{\mathrm {min}}-\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {min}}:(\varvec{\varepsilon }_{\mathrm {max}}-\varvec{\varepsilon }_{\mathrm {min}})\nonumber \\&\quad +\sum _{i=1}^n(\psi ^{\mathrm {neq}}_{i_{\mathrm {max}}}-\psi ^{\mathrm {neq}}_{i_{\mathrm {min}}}-\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {min}}}:(\varvec{\varepsilon }^e_{i_{\mathrm {max}}}-\varvec{\varepsilon }^e_{i_{\mathrm {min}}}))\nonumber \\&=\,\frac{1}{2}(\varvec{\varepsilon }_{\mathrm {max}}-\varvec{\varepsilon }_{\mathrm {min}}):\mathbb {C}^{\mathrm {eq}}:(\varvec{\varepsilon }_{\mathrm {max}}-\varvec{\varepsilon }_{\mathrm {min}})\nonumber \\&\quad +\sum _{i=1}^{n}\frac{1}{2}(\varvec{\varepsilon }^e_{i_{\mathrm {max}}}-\varvec{\varepsilon }^e_{i_{\mathrm {min}}}):\mathbb {C}^{\mathrm {neq}}_i:(\varvec{\varepsilon }^e_{i_{\mathrm {max}}}-\varvec{\varepsilon }^e_{i_{\mathrm {min}}})\nonumber \\&=\,\frac{1}{2}(\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {max}}-\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {min}}):(\varvec{\varepsilon }_{\mathrm {max}}-\varvec{\varepsilon }_{\mathrm {min}})\nonumber \\&\quad +\sum _{i=1}^n\frac{1}{2}(\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {max}}}-\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {min}}}):(\varvec{\varepsilon }^e_{i_{\mathrm {max}}}-\varvec{\varepsilon }^e_{i_{\mathrm {min}}}) . \end{aligned}$$
(4.2)

The gradient of the cyclic free energy can be expressed as

$$\begin{aligned} \begin{aligned}&\nabla _{\varvec{X}\,}\psi _{\mathrm {cycle}}(\varvec{\varepsilon }_{\mathrm {cycle}},\varvec{\varepsilon }^e_{1_{\mathrm {cycle}}},\ldots ,\varvec{\varepsilon }^e_{n_{\mathrm {cycle}}})\\&\quad =\frac{\partial {\psi _{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }_{\mathrm {cycle}}}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }_{\mathrm {cycle}}+\sum _{i=1}^n\frac{\partial {\psi _{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}\\&\qquad \quad +\, \frac{\partial {{\psi _{\mathrm {cycle}}}}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}, \end{aligned} \end{aligned}$$
(4.3)

where \(\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}=\varvec{\varepsilon }^e_{i_{\mathrm {max}}}-\varvec{\varepsilon }^e_{i_{\mathrm {min}}}\), \(\varvec{\varepsilon }_{\mathrm {cycle}}=\varvec{\varepsilon }_{\mathrm {max}}-\varvec{\varepsilon }_{\mathrm {min}}\) and \(\frac{\partial {{\psi _{\mathrm {cycle}}}}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}\) is the explicit dependence of the cyclic free energy on the position \(\varvec{X}\). The partial derivatives \(\frac{\partial {\psi _{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }_{\mathrm {cycle}}}}\) and \(\frac{\partial {\psi _{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}}}\) can be evaluated as

$$\begin{aligned} \begin{aligned} \frac{\partial {\psi _{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }_{\mathrm {cycle}}}}&=\frac{\partial {\psi ^{\mathrm {eq}}_{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }_{\mathrm {max}}}}:\left( \frac{\partial {\varvec{\varepsilon }_{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }_{\mathrm {max}}}}\right) ^{-1}\\ {}&=\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {max}}-\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {min}}=\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {cycle}}, \end{aligned} \end{aligned}$$
(4.4)
$$\begin{aligned} \begin{aligned} \frac{\partial {\psi _{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}}}&=\frac{\partial {\psi ^{\mathrm {neq}}_{i_{\mathrm {cycle}}}}}{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {max}}}}}:\left( \frac{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}}}{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {max}}}}}\right) ^{-1}\\&=\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {max}}}-\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {min}}}=\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}, \end{aligned} \end{aligned}$$
(4.5)

where \(\frac{\partial {\varvec{\varepsilon }_{\mathrm {cycle}}}}{\partial {\varvec{\varepsilon }_{\mathrm {max}}}}=\frac{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}}}{\partial {\varvec{\varepsilon }^e_{i_{\mathrm {max}}}}}=\mathbb {I}\) and \(\mathbb {I}\) is the fourth order identity tensor. Neglecting inertia effects, the balance of linear momentum at maximum and at minimum load is written as

$$\begin{aligned}&\nabla _{\varvec{X}}\cdot \varvec{\sigma }_{\mathrm {max}}+\varvec{b}_{\mathrm {max}}=\varvec{0}, \end{aligned}$$
(4.6)
$$\begin{aligned}&\nabla _{\varvec{X}}\cdot \varvec{\sigma }_{\mathrm {min}}+\varvec{b}_{\mathrm {min}}=\varvec{0}. \end{aligned}$$
(4.7)

The subtraction of Eq. (4.7) from Eq. (4.6) leads to the modified form of linear momentum at cyclic loading, that can be expressed as

$$\begin{aligned} \nabla _{\varvec{X}}\cdot \varvec{\sigma }_{\mathrm {cycle}}+\varvec{b}_{\mathrm {cycle}}=\varvec{0}, \end{aligned}$$
(4.8)

where \(\varvec{\sigma }_{\mathrm {cycle}}=\varvec{\sigma }_{\mathrm {max}}-\varvec{\sigma }_{\mathrm {min}}\) is the cyclic Cauchy stress tensor and \(\varvec{b}_{\mathrm {cycle}}=\varvec{b}_{\mathrm {max}}-\varvec{b}_{\mathrm {min}}\) are the cyclic body forces. The cyclic Cauchy stress tensor can be calculated as \(\varvec{\sigma }_{\mathrm {cycle}}=\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {cycle}}+ \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\). The total cyclic strain tensor can be additively decomposed into \(\varvec{\varepsilon }_{\mathrm {cycle}}=\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}+\varvec{\varepsilon }^v_{i_{\mathrm {cycle}}}\), where \(\varvec{\varepsilon }^e_{i_{\mathrm {cycle}}}\) is the cyclic elastic strain and \(\varvec{\varepsilon }^v_{i_{\mathrm {cycle}}}\) is the cyclic viscous strain. Using the additive decomposition of the cyclic strain tensor and inserting Eqs. (4.4) and (4.5) in Eq.(4.3) yields

$$\begin{aligned} \begin{aligned} \nabla _{\varvec{X}\,}\psi _{\mathrm {cycle}}=&\,\varvec{\sigma }^{\mathrm {eq}}_{\mathrm {cycle}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }_{\mathrm {cycle}}\\ {}&+ \left( \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\right) :\nabla _{\varvec{X}\,}\varvec{\varepsilon }_{\mathrm {cycle}}\\&-\sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_{i_{\mathrm {cycle}}}+\frac{\partial {{\psi _{\mathrm {cycle}}}}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}\\ =&\,\varvec{\sigma }_{\mathrm {cycle}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }_{\mathrm {cycle}}\\ {}&- \sum _{i=1}^n\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_{i_{\mathrm {cycle}}}\\ {}&+ \frac{\partial {{\psi _{\mathrm {cycle}}}}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}. \end{aligned} \end{aligned}$$
(4.9)

Defining the cyclic gradient of the displacement field \(\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}=\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {max}}-\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {min}}\), the total cyclic strain tensor can be written as \(\varvec{\varepsilon }_{\mathrm {cycle}}=\frac{1}{2}\left( \nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}+\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal \right) \). Analogously to \(\varvec{\sigma }:\nabla _{\varvec{X}\,}\varvec{\varepsilon }\), the term \(\varvec{\sigma }_{\mathrm {cycle}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }_{\mathrm {cycle}}\) is computed as

$$\begin{aligned} \begin{aligned} \varvec{\sigma }_{\mathrm {cycle}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }_{\mathrm {cycle}}=&\,\nabla _{\varvec{X}}\cdot \left( \left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal \varvec{\sigma }_{\mathrm {cycle}}\right) \\&+\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal {\varvec{b}_{\mathrm {cycle}}}. \end{aligned} \end{aligned}$$
(4.10)

Knowing that \(\nabla _{\varvec{X}\,}\psi _{\mathrm {cycle}}=\nabla _{\varvec{X}}\cdot \left( \psi _{\mathrm {cycle}}\varvec{I}\right) \) and inserting Eq. (4.10) into Eq.(4.9) results in

$$\begin{aligned} \begin{aligned}&\,\nabla _{\varvec{X}}\cdot \left( \psi _{\mathrm {cycle}}\varvec{I}-\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal \varvec{\sigma }_{\mathrm {cycle}}\right) \\&+\sum _{i=1}^{n}\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_{i}{_{\mathrm {cycle}}}\\&-\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal {\varvec{b}}_{\mathrm {cycle}}-\frac{\partial {{\psi _{\mathrm {cycle}}}}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}=\varvec{0}. \end{aligned} \end{aligned}$$
(4.11)

Introducing the cyclic Eshelby stress tensor \(\varvec{\Sigma }_{\mathrm {cycle}}=\psi _{\mathrm {cycle}}\varvec{I}-\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal \varvec{\sigma }_{\mathrm {cycle}}\) and the cyclic configurational volume forces \(\varvec{B}_{\mathrm {cycle}}=\sum _{i=1}^{n}\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_{i_{\mathrm {cycle}}}-\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal {\varvec{b}}_{\mathrm {cycle}}-\frac{\partial {{\psi _{\mathrm {cycle}}}}}{\partial {\varvec{X}}}\Big \vert _{\text {exp}}\), the balance of cyclic energy momentum is defined as

$$\begin{aligned} \nabla _{\varvec{X}}\cdot \varvec{\Sigma }_{\mathrm {cycle}}+\varvec{B}_{\mathrm {cycle}}=\varvec{0}. \end{aligned}$$
(4.12)

It should be noted from the above equation that \(\varvec{\Sigma }_{\mathrm {cycle}}\ne \varvec{\Sigma }_{\mathrm {max}}-\varvec{\Sigma }_{\mathrm {min}}\) and \(\varvec{B}_{\mathrm {cycle}}\ne \varvec{B}_{\mathrm {max}}-\varvec{B}_{\mathrm {min}}\).

Fig. 2
figure 2

Cracked body with domain around the crack tip

Full size image

5 Nodal material forces and cyclic nodal material forces

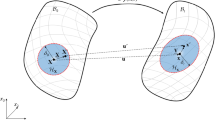
Consider a cracked body \(\mathcal {B}\) with traction free crack surfaces, volume V and boundary \(\partial \mathcal {B}\), as shown in Fig. 2. A finite element discretization over the whole body domain results in a body denoted by \(\mathcal {B}^h\). \(\mathcal {B}^h =\bigcup \nolimits _{e=1}^{N_e}\mathcal {B}_e\), where \(\mathcal {B}_e\) is a finite element with volume \(V_e\) and \(N_e\) is the total number of elements in \(\mathcal {B}^h\). The nodal material forces are equivalent to the internal nodal forces, however, the only difference is that the nodal material forces are obtained using the balance of energy momentum. More details related to nodal material forces can be found in Mueller and Maugin (2002). Carrying out a finite element discretization over the balance of energy momentum, shown in Eq. (3.8), yields the nodal material force

$$\begin{aligned} \varvec{F}^{\text {mat}}_{\mathrm {node}}&= -\sum _{e=1}^{k}\int _{\mathcal {B}_e}\varvec{\Sigma }\cdot \nabla _{\varvec{X}\,}\varvec{N}^{I}dV_e +\sum _{e=1}^k\int _{\mathcal {B}_e}\varvec{B}\varvec{N}^IdV_e\nonumber \\&\quad \,+\sum _{e=1}^{ksur}\int _{\partial \mathcal {B}_e} (\varvec{\Sigma }\tilde{\varvec{N}})\varvec{N}^I dA_{e}, \end{aligned}$$
(5.1)

where \(\varvec{N}^I\) are the shape functions, k is the total number of elements connected to the node whereas ksur is the number of surface elements connected to the node. Let \(\varvec{F}^{\Sigma }_{\text {node}}\), \(\varvec{F}^{diss}_{\text {node}}\) and \(\varvec{F}^{sur}_{\text {node}}\) be the Eshelby, dissipative and surface parts of the nodal material force, respectively. These parts can be written as

$$\begin{aligned} \varvec{F}^{\Sigma }_{\mathrm {node}}&=-\sum _{e=1}^{k}\int _{\mathcal {B}_e}\varvec{\Sigma }\cdot \nabla _{\varvec{X}\,}\varvec{N}^{I}dV_e, \end{aligned}$$
(5.2)
$$\begin{aligned} \varvec{F}^{diss}_{\mathrm {node}}&=\sum _{e=1}^k\int _{\mathcal {B}_e}\varvec{B}\varvec{N}^IdV_e, \end{aligned}$$
(5.3)
$$\begin{aligned} \varvec{F}^{sur}_{\mathrm {node}}&=\sum _{e=1}^{ksur}\int _{\partial \mathcal {B}_e} (\varvec{\Sigma }\tilde{\varvec{N}})\varvec{N}^I dA_{e}, \end{aligned}$$
(5.4)

where \(V_e\) is the volume of the element and \(A_e\) is the area of the element’s outer surface. At small strain, the dissipation in \(\mathcal {B}\) according to Gurtin and Podio-Guidugli (1996) can be written as

$$\begin{aligned} \begin{aligned} \Psi (\mathcal {B})=&\,\int _{\mathcal {B}}\left[ \varvec{\sigma }:\dot{\varvec{\varepsilon }}-\dot{\psi }\right] dV\\ {}&+ \dot{\varvec{a}}\cdot \lim \limits _{r\rightarrow 0} \int _{\partial \mathcal {C}}\left[ \psi \varvec{I}-\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{\sigma }\right] \tilde{\varvec{N}} dS, \end{aligned} \end{aligned}$$
(5.5)

where \(\dot{\varvec{a}}\) is the crack tip velocity. The second term in Eq. (5.5) is the dissipation due to crack propagation, which leads to the crack driving force

$$\begin{aligned} \varvec{F}^{\text {crack}}=-\lim \limits _{r\rightarrow 0} \int _{\partial \mathcal {C}}\left[ \psi \varvec{I}-\left( {\nabla _{\varvec{X}\,}\varvec{u}}\right) ^\intercal \varvec{\sigma }\right] \tilde{\varvec{N}} dS. \end{aligned}$$
(5.6)

According to Runesson et al. (2009) and Tillberg et al. (2010), the crack driving force, for the traction free crack surfaces, is obtained from the weak form of the balance of energy momentum in a cracked body and is defined as

$$\begin{aligned} \varvec{F}^{\text {crack}}\cdot \dot{\varvec{a}}=&\,\int _{\mathcal {B}}\left[ -\varvec{\Sigma }:\nabla _{\varvec{X}\,}\delta \dot{\varvec{X}}+\varvec{B}\cdot \delta \dot{\varvec{X}}\right] dV\nonumber \\ {}&+ \int _{\partial \mathcal {B}}\left[ \left( \varvec{\Sigma }\tilde{\varvec{N}}\right) \cdot \delta \dot{\varvec{X}}\right] dS, \end{aligned}$$
(5.7)

where \(\delta \dot{\varvec{X}}=\dot{\varvec{a}}\). After carrying out a finite element discretization over the whole domain, a discrete form of Eq. (5.7) recasts into

$$\begin{aligned} \varvec{F}^{\text {crack}}&=\int _{\mathcal {B}^h}-\varvec{\Sigma }\cdot \nabla _{\varvec{X}\,}\varvec{N}^IdV +\int _{\mathcal {B}^h}\varvec{B}\varvec{N}^IdV\nonumber \\ {}&\quad + \int _{\partial \mathcal {B}}\left( \varvec{\Sigma }\tilde{\varvec{N}}\right) \varvec{N}^I dS\nonumber \\&= \sum _{i=1}^{\mathcal {N_B}^h}\varvec{F}^{\mathrm {mat}}_i, \end{aligned}$$
(5.8)

where \(\mathcal {N_B}^h\) is the total number of nodes in \(\mathcal {B}^h\). Consider the domain \(\mathcal {P}\) around the crack tip and its discretized form \(\mathcal {P}^h\), the crack driving force, in case of traction free crack surfaces, can be obtained by carrying out a domain integral over \(\mathcal {P}\) and its discretized form \(\mathcal {P}^h\) as

$$\begin{aligned}&\varvec{F}^{\text {crack}}\cdot \dot{\varvec{a}}=\,\int _{\mathcal {P}}\left[ -\varvec{\Sigma }:\nabla _{\varvec{X}\,}\delta \dot{\varvec{X}}+\varvec{B}\cdot \delta \dot{\varvec{X}}\right] dV, \end{aligned}$$
(5.9)
$$\begin{aligned}&\varvec{F}^{\text {crack}}=\int _{\mathcal {P}^h}-\varvec{\Sigma }\cdot \nabla _{\varvec{X}\,}\varvec{N}^IdV +\int _{\mathcal {P}^h}\varvec{B}\varvec{N}^IdV\nonumber \\ {}&\qquad \quad = \sum _{i=1}^{\mathcal {N_P}^h}\varvec{F}^{\mathrm {mat}}_i \end{aligned}$$
(5.10)

where \(\mathcal {N_P}^h\) is the number of nodes in \(\mathcal {P}^h\). In the subsequent sections, the crack driving force will be called global material force. The global material force is divided into Eshelby \(\varvec{F}^\Sigma \) and \(\varvec{F}^{diss}\) dissipative contributions. These contributions are obtained as

$$\begin{aligned}&\varvec{F}^{\Sigma }=\sum _{i=1}^{\mathcal {N_P}^h}\varvec{F}^{\Sigma }_{\mathrm {i}}=\int _{\mathcal {P}^h}-\varvec{\Sigma }\cdot \nabla _{\varvec{X}\,}\varvec{N}^IdV, \end{aligned}$$
(5.11)
$$\begin{aligned}&\varvec{F}^{diss}=\sum _{i=1}^{\mathcal {N_P}^h}\varvec{F}^{diss}_{\mathrm {i}}=\int _{\mathcal {P}^h}\varvec{B}\varvec{N}^IdV. \end{aligned}$$
(5.12)

Analogously to nodal material force, the cyclic nodal material force is obtained from the discrete form of Eq. (4.12)

$$\begin{aligned} \varvec{F}^{\text {mat}}_{\mathrm {node,cycle}}=&\, -\sum _{e=1}^{k}\int _{\mathcal {B}_e}\varvec{\Sigma }_{\mathrm {cycle}}\cdot \nabla _{\varvec{X}\,}\varvec{N}^{I}dV_e\nonumber \\&+\sum _{e=1}^k\int _{\mathcal {B}_e}\varvec{B}_{\mathrm {cycle}}\varvec{N}^IdV_e\nonumber \\&+\sum _{e=1}^{ksur}\int _{\partial \mathcal {B}_e} (\varvec{\Sigma }_{\mathrm {cycle}}\tilde{\varvec{N}})\varvec{N}^I dA_{e}. \end{aligned}$$
(5.13)

Let \(\varvec{F}^{\Sigma }_{\text {node,cycle}}\), \(\varvec{F}^{diss}_{\text {node,cycle}}\) and \(\varvec{F}^{sur}_{\text {node,cycle}}\) be the Eshelby, dissipative and surface parts of the cyclic nodal material force, respectively. The contributions of the cyclic nodal material forces can be written as

$$\begin{aligned} \varvec{F}^{\Sigma }_{\mathrm {node,cycle}}&=-\sum _{e=1}^{k}\int _{\mathcal {B}_e}\varvec{\Sigma }_{\mathrm {cycle}}\cdot \nabla _{\varvec{X}\,}\varvec{N}^{I}dV_e, \end{aligned}$$
(5.14)
$$\begin{aligned} \varvec{F}^{diss}_{\mathrm {node,cycle}}&=\sum _{e=1}^k\int _{\mathcal {B}_e}\varvec{B}_{\mathrm {cycle}}\varvec{N}^IdV_e, \end{aligned}$$
(5.15)
$$\begin{aligned} \varvec{F}^{sur}_{\mathrm {node,cycle}}&=\sum _{e=1}^{ksur}\int _{\partial \mathcal {B}_e} (\varvec{\Sigma }_{\mathrm {cycle}}\tilde{\varvec{N}})\varvec{N}^I dA_{e}. \end{aligned}$$
(5.16)

In our previous work Khodor et al. (2021), the derived cyclic crack driving force is defined as

$$\begin{aligned} \begin{aligned}&\varvec{F}^{\text {crack}}_{\mathrm {cycle}}\\&= -\lim \limits _{r\rightarrow 0} \int _{\partial \mathcal {C}}\left[ \psi _{\mathrm {cycle}}\varvec{I}-\left( {\nabla _{\varvec{X}\,}\varvec{u}_{\mathrm {cycle}}}\right) ^\intercal \varvec{\sigma }_{\mathrm {cycle}}\right] \tilde{\varvec{N}} dS. \end{aligned} \end{aligned}$$
(5.17)

Using the weak form of balance of cyclic energy momentum in a cracked body, the cyclic crack driving force is computed as

$$\begin{aligned} \varvec{F}^{\text {crack}}_{\mathrm {cycle}}\cdot \dot{\varvec{a}}&= \int _{\mathcal {B}}\left[ -\varvec{\Sigma }_{\mathrm {cycle}}:\nabla _{\varvec{X}\,}\delta \dot{\varvec{X}}+\varvec{B}_{\mathrm {cycle}}\cdot \delta \dot{\varvec{X}}\right] dV\nonumber \\&\quad +\,\int _{\partial \mathcal {B}}\left[ \left( \varvec{\Sigma }_{\mathrm {cycle}}\tilde{\varvec{N}}\right) \cdot \delta \dot{\varvec{X}}\right] dS, \end{aligned}$$
(5.18)
$$\begin{aligned} \varvec{F}^{\text {crack}}_{\mathrm {cycle}}&=\,\int _{\mathcal {B}^h}-\varvec{\Sigma }_{\mathrm {cycle}}\cdot \nabla _{\varvec{X}\,}\varvec{N}^IdV\nonumber \\&\quad +\,\int _{\mathcal {B}^h}\varvec{B}_{\mathrm {cycle}}\varvec{N}^IdV\nonumber \\&\quad +\, \int _{\partial \mathcal {B}}\left( \varvec{\Sigma }_{\mathrm {cycle}}\tilde{\varvec{N}}\right) \varvec{N}^I dS = \sum _{i=1}^{\mathcal {N_B}^h}\varvec{F}^{\mathrm {mat}}_{i,\mathrm {cycle}}. \end{aligned}$$
(5.19)

The cyclic crack driving force is called cyclic global material force in the subsequent sections. The cyclic global material force can be computed in the domain \(\mathcal {P}^h\) as

$$\begin{aligned} \varvec{F}^{\text {crack}}_{\mathrm {cycle}}&=\int _{\mathcal {P}^h}-\varvec{\Sigma }_{\mathrm {cycle}}\cdot \nabla _{\varvec{X}\,}\varvec{N}^IdV +\int _{\mathcal {P}^h}\varvec{B}_{\mathrm {cycle}}\varvec{N}^IdV\nonumber \\&=\sum _{i=1}^{\mathcal {N_P}^h}\varvec{F}^{\mathrm {mat}}_{i,\mathrm {cycle}}. \end{aligned}$$
(5.20)

The path-independence of material forces and cyclic material forces is proved in Appendix A. Let \(\varvec{F}^{\Sigma }_{\mathrm {cycle}}\) and \(\varvec{F}^{diss}_{\mathrm {cycle}}\) be the Eshelby and dissipative components of the cyclic material force, respectively. These contributions can be written as

$$\begin{aligned} \varvec{F}^{\Sigma }_{\mathrm {cycle}}&=\sum _{i=1}^{\mathcal {N}_{\mathcal {P}^{h}}}\varvec{F}^{\Sigma }_{i,\mathrm {cycle}}=\,\int _{\mathcal {P}^h}-\varvec{\Sigma }_{\mathrm {cycle}}\cdot \nabla _{\varvec{X}\,}\varvec{N}^IdV, \end{aligned}$$
(5.21)
$$\begin{aligned} \varvec{F}^{diss}_{\mathrm {cycle}}&=\sum _{i=1}^{\mathcal {N_P}^h}\varvec{F}^{diss}_{i,\mathrm {cycle}}=\int _{\mathcal {P}^h}\varvec{B}_{\mathrm {cycle}}\varvec{N}^IdV. \end{aligned}$$
(5.22)

6 Numerical examples

In this section, several numerical investigations are discussed. At first, an investigation on the path-independency of the domain integral using the material force approach is carried out for a specimen at monotonic loading. Furthermore, the path-independency of the domain integral obtained using cyclic material forces is investigated for a specimen at cyclic loading. Furthermore, the existence of the balance of energy momentum and cyclic energy momentum is shown. Finally, the cyclic material force approach is validated by experimental results. It should be noted that all the studies are carried out in pure Mode I of fracture. This means that the component of the cyclic global material force perpendicular to the crack vanishes. The simulations are performed using the finite element code ANSYS.

6.1 Path-independency of material forces at monotonic loading

In this section, a numerical study is presented to illustrate the path-independent behavior of material forces. The study is carried out on a two-dimensional precracked disc at plane strain conditions. The specimen used is similar to that in Nguyen et al. (2005) and Özenç et al. (2014). The disc is subjected to prescribed displacements at its boundaries that are consistent with a Mode I K-field. The applied displacements at the boundary in x- and y-direction are calculated as

$$\begin{aligned} \begin{aligned}&u_x(r,\theta )=\\ {}&\frac{K_I}{2\mu _{\infty }}\sqrt{\frac{r}{2\pi }}\cos \left( \frac{\theta }{2}\right) \left[ \kappa _{\infty }-1+2\sin ^2\left( \frac{\theta }{2}\right) \right] , \end{aligned} \end{aligned}$$
(6.1)
$$\begin{aligned} \begin{aligned}&u_y(r,\theta )=\\ {}&\frac{K_I}{2\mu _{\infty }}\sqrt{\frac{r}{2\pi }}\sin \left( \frac{\theta }{2}\right) \left[ \kappa _{\infty }+1-2\sin ^2\left( \frac{\theta }{2}\right) \right] , \end{aligned} \end{aligned}$$
(6.2)

where \(\kappa _{\infty }=3-4\nu _{\infty }\), \(\mu _{\infty }\) is the shear modulus at the relaxed state, \(E_{\infty }\) is Young’s modulus and \(\nu _{\infty }\) is Poisson’s ratio at the relaxed state. The material properties at the relaxed state are obtained as

$$\begin{aligned}&\mu _\infty =G_{\mathrm {eq}}=\alpha ^G_{\mathrm {eq}}G_0, \end{aligned}$$
(6.3)
$$\begin{aligned}&K_{\mathrm {eq}}=\alpha ^K_{\mathrm {eq}}K_0, \end{aligned}$$
(6.4)
$$\begin{aligned}&E_\infty =\frac{9K_{\mathrm {eq}}G_{\mathrm {eq}}}{3K_{\mathrm {eq}}+G_{\mathrm {eq}}}, \end{aligned}$$
(6.5)
$$\begin{aligned}&\nu _\infty =\frac{3K_{\mathrm {eq}}-2G_{\mathrm {eq}}}{2\left( 3K_{\mathrm {eq}}+G_{\mathrm {eq}}\right) }, \end{aligned}$$
(6.6)

where \(K_0=\) 16666 Nmm\(^{-2}\) and \(G_0=\) 23076 Nmm\(^{-2}\). In this numerical example, two Maxwell elements are used to characterize the viscoelastic behavior. The bulk and shear relaxation times as well as the shear and bulk ratio of each Maxwell element are shown in Table 1.

Table 1 Material parameters used to describe viscoelastic behavior
Full size table
Fig. 3
figure 3

Cracked disc having the crack located at \(y=0\) and \(x\le 0\)

Full size image

The finite element mesh of the disc is shown in Fig. 3). The disc radius is \(R_\text {disc}=4000h\), where h is the element size of the mapped mesh surrounding the crack tip as depicted in Fig. 3). A pre-crack is located at \(y=0\) and \(x\le 0\), with the crack tip located at the centre of the disc at \(x=0\) and \(y=0\). In this example, the disc is subjected to an energy release rate \(G=10\) Nmm\(^{-1}\), where

$$\begin{aligned} G=\frac{K_I^2}{E'_\infty }\quad \text {and}\quad E'_\infty =\frac{E_\infty }{1-\nu ^2_\infty }. \end{aligned}$$
(6.7)

Since viscoelastic solids are time-dependent, therefore, the load is applied in the following sequence: at \(t=0\), \(K_I=0\) and for \(t\ge 10\) s, \(K_I=\sqrt{GE'_\infty }\). t represents the time. Let \(F^{\mathrm {mat}}_1\), \(F^\Sigma _1\) and \(F^{diss}\) be the components in crack direction of the global material force, the Eshelby part of the global material force and the dissipative part of the global material force, respectively. The path-independent feature is illustrated by evaluating the value of the material forces using different domain integrals surrounding the crack tip. The domain integrals are shown in Fig. 4.

Fig. 4
figure 4

Contours surrounding the crack tip

Full size image

In this example and the subsequent examples, \(\Gamma _1\) is considered as the first contour that includes only the crack tip node. Moreover, the global material force evaluated on the second contour \(\Gamma _2\) is a summation of the crack tip nodal material force and the nodal material forces of the first set of nodes surrounding the crack tip. Furthermore, the global material forces evaluated at the third contour \(\Gamma _3\) are equal to the summation of the crack tip nodal material forces and the nodal material forces of the first and second set of nodes surrounding the crack tip. The result obtained by the evaluation of material force components in crack direction using different contours at \(t=10\) s and at \(t=300\) s are shown in Fig. 5.

Fig. 5
figure 5

Evaluation of material forces for different contours at a \(t=10\) s and b \(t=300\) s

Full size image

It can be seen from Fig. 5 that the material forces are path-independent. It can be noticed that the value of the global material forces at \(t=300\) s reaches a value of 10 Nmm\(^{-1}\). The variations with respect to time of the global material force and the dissipative part of the global material force, evaluated at Contour 10, are plotted in Fig. 6.

Fig. 6
figure 6

Variation with respect to time of a the global material force and b the dissipative part of the global material force evaluated at contour number 10

Full size image

To better understand this behavior of material forces, the \(\sigma _{yy}\)-component of the total Cauchy stress tensor as well as the \(\sigma _{yy}\)-components of the \(\varvec{\sigma }^{\mathrm {neq}}_i\) of each Maxwell element at a Gauss point next to the crack tip are plotted versus time in Fig. 7. Stress relaxation occurs in the Maxwell element which leads to \(\varvec{\sigma }^{\mathrm {neq}}_i\approx \varvec{0}\). Since \(\varvec{\sigma }^{\mathrm {neq}}_i\approx \varvec{0}\), therefore, the configurational volume forces in each Maxwell element \(\varvec{B}_i=\varvec{\sigma }^{\mathrm {neq}}_i:\nabla _{\varvec{X}\,}\varvec{\varepsilon }^v_i\) and the dissipative material force \(\varvec{F}^{diss}\) tend to zero.

Fig. 7
figure 7

Variation with respect to time of the \(\sigma _{yy}\)-component of a the total Cauchy stress tensor and b \(\varvec{\sigma }^{\mathrm {neq}}_i\) of each Maxwell element

Full size image

The reason behind the material forces reaching a value almost equal to 10 Nmm\(^{-1}\) is due to the fact that the total Cauchy stress tensor after relaxation is equal to the stress in the equilibrium spring \(\varvec{\sigma }^{\mathrm {eq}}\). Since after relaxation, stress is only in the equilibrium spring, therefore, the model at \(t=300\) s acts like a linear elastic material model with a Young’s modulus \(E_\infty \) and a Poisson’s ratio \(\nu _\infty \). To verify the previous explanation, the same boundary conditions are prescribed to the same disc but using a linear elastic material model instead of the viscoelastic material. The linear elastic material model exhibits \(E_\infty \) and \(\nu _\infty \) as material properties. The global material force value obtained using this model is equal to 10 Nmm\(^{-1}\). The nodal material forces and the dissipative parts of nodal material forces are depicted in Figs. 8 and 9, respectively.

Fig. 8
figure 8

Nodal material forces at \(t=10\) s and \(t=300\) s

Full size image
Fig. 9
figure 9

Dissipative part of nodal material forces at \(t=10\) s and \(t=300\) s

Full size image

6.2 Path-independency of cyclic material forces at cyclic loading

The purpose of the cyclic material force approach is to yield a path-independent integral, therefore, the path-independency of cyclic material forces is illustrated by subjecting the same crack disc with the same material parameters represented in Sect. 6.1 to cyclic displacements. The cyclic displacements are applied with a load ratio \(R_\text {load}=\frac{u_{\mathrm {min}}}{u_{\mathrm {max}}}=0.4\), where \(u_{\mathrm {max}}\) and \(u_{\mathrm {min}}\) are the maximum and minimum applied displacements, respectively. \(u_{\mathrm {max}}\) is equivalent to a prescribed energy release rate \(G=10\) Nmm\(^{-1}\) and is therefore calculated using Eqs. (6.1) and (6.2) in x- and y-direction, respectively. In this study, the disc is subjected to 50 cycles. The cyclic global material force is evaluated at the end of each cycle. The cycles are applied for 1000 s, the application of cycles is plotted in Fig. 10.

Fig. 10
figure 10

Application of cyclic displacements and definition of cycles according to time

Full size image

Considering the second cycle as shown in Fig. 10, \(u_{\mathrm {max}}\) is applied at \(t=30\) s and \(u_{\mathrm {min}}\) at \(t=40\) s. Let \(N_{\mathrm {cycle}}\) be the number of a specific cycle. In terms of \(N_{\mathrm {cycle}}\), \(u_{\mathrm {max}}\) and \(u_{\mathrm {min}}\) are applied at \(t=(2N_{\mathrm {cycle}}-1)\times 10\) whereas \(u_{\mathrm {min}}\) is applied at \(t=(2N_{\mathrm {cycle}})\times 10\). The evaluation of the cyclic global material force at different contours at \(N_{\mathrm {cycle}}=2\) and \(N_{\mathrm {cycle}}=50\) is shown in Fig. 11. In Fig. 11, the component in crack direction of \(\varvec{F}^{\mathrm {mat}}_{\mathrm {cycle}}\) is denoted by \(F^{\mathrm {mat}}_{1_\mathrm {cycle}}\).

Fig. 11
figure 11

Evaluation of the cyclic global material force for different contours at a \(N_{\mathrm {cycle}}=2\) and b \(N_{\mathrm {cycle}}=50\)

Full size image

It can be seen from Fig. 11, that the cyclic material force approach results in a path-independent domain integral. The cyclic nodal material forces and their dissipative parts are depicted in Figs. 12 and 13, respectively.

Fig. 12
figure 12

Cyclic nodal material forces at \(N_{\mathrm {cycle}}=2\) and \(N_{\mathrm {cycle}}=50\)

Full size image
Fig. 13
figure 13

Dissipative part of nodal material forces at \(N_{\mathrm {cycle}}=2\) and \(N_{\mathrm {cycle}}=50\)

Full size image

The variations with respect to cycles of \(\varvec{F}^{\mathrm {mat}}_{\mathrm {cycle}}\), \(\varvec{F}^{\mathrm {mat}}_{\mathrm {max}}\) and \(\varvec{F}^{\mathrm {mat}}_{\mathrm {min}}\) in crack direction are depicted in Fig. 14. \(\varvec{F}^{\mathrm {mat}}_{\mathrm {max}}\) and \(\varvec{F}^{\mathrm {mat}}_{\mathrm {min}}\) are the values of the global material force, which is calculated using Eq. (5.10), at maximum and minimum displacements, respectively. It should be noted that the values are obtained on Contour 10.

Fig. 14
figure 14

Variation of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\), \(F^{\mathrm {mat}}_{1_{\mathrm {max}}}\) and \(F^{\mathrm {mat}}_{1_{\mathrm {min}}}\) with respect to cycles

Full size image

It can be seen from Fig. 14 that the cyclic global material force reaches almost a constant value after 5 cycles. To clarify this behavior, the variations of the \(\sigma _{yy}\)-components with respect to cycles of \(\varvec{\sigma }_{\mathrm {cycle}}\) and \(\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\) (of each Maxwell element) are depicted in Fig. 15. It can be seen from Fig. 15, that beyond the fifth cycle, \(\varvec{\sigma }_{\mathrm {cycle}}\) and \(\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\) do not vary and keep almost a constant value. In the work of Ochensberger and Kolednik (2014), they derive a domain integral to calculate the cyclic energy release rate using the value of the elastic-plastic J-integral \(J^{ep}\) at maximum and minimum loads as

$$\begin{aligned} \varDelta J^{ep}=J^{ep}_{\mathrm {max}}+J^{ep}_{\mathrm {min}}-2\sqrt{J^{ep}_{\mathrm {max}}J^{ep}_{\mathrm {min}}}. \end{aligned}$$
(6.8)

It should be noted that Eq. (6.8) cannot be used to calculate the cyclic global material force if \(J^{ep}_{\mathrm {max}}\) and \(J^{ep}_{\mathrm {min}}\) are replaced by \(F^{\mathrm {mat}}_{1_{\mathrm {max}}}\) and \(F^{\mathrm {mat}}_{1_{\mathrm {min}}}\). The reason of Eq. (6.8) being not appropriate to calculate \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) is that \(F^{\mathrm {mat}}_{1_{\mathrm {min}}}\) yields negative values. The cyclic material force approach overcomes the issue of negative material forces at unloading stages. Moreover, the cyclic material force results in a path-independent domain integral and, therefore, it can be used as a fatigue crack growth criterion. In linear elastic materials, the cyclic global material force is nothing else as the cyclic J-integral derived in Tanaka (1983).

Fig. 15
figure 15

Variation of the \(\sigma _{yy}\)-component with respect to cycles a of the cyclic Cauchy stress tensor and b of \(\varvec{\sigma }^{\mathrm {neq}}_{i_{\mathrm {cycle}}}\) of each Maxwell element

Full size image

6.3 Balance of energy momentum and cyclic energy momentum

Mueller and Maugin (2002) derived the weak form of the balance of energy momentum. The weak form states that the internal nodal material force within a homogeneous body, where no prescribed displacements or applied forces are present, is equal to zero. Moreover, the summation of all nodal material forces over the body should be equal to zero. To prove the existence of the balance of energy momentum in small strain viscoelastic solids, a 10 mm \(\times \) 10 mm block at plane strain conditions is subjected to prescribed displacements. The material parameters used are shown in Table 1.

Fig. 16
figure 16

Block at plane strain conditions subjected to prescribed displacements

Full size image

The lower boundary of the block is fixed in both x- and y-direction, whereas at the upper boundary the x-direction is fixed and a displacement u is prescribed in y-direction. The prescribed displacement is time-dependent, where \(u(t=0)=0\) and \(u(t\ge 10)=0.1\) mm. The nodal material force distribution within the block at \(t=10\) s and \(t=300\) s are depicted in Fig. 17. It can be seen from Fig. 17 that the nodal material forces at internal nodes are negligible. Furthermore, the summation of all nodal material forces is zero and, therefore, the balance of energy momentum at monotonic loading is fulfilled.

Fig. 17
figure 17

Distribution of nodal material forces in the block at \(t=10\) s and \(t=300\) s

Full size image

The aim now is to show the existence of the balance of cyclic of energy momentum, represented by Eq. (4.12). The validation is carried out by subjecting the block to a cyclic displacement with ratio \(R=\frac{u_{\mathrm {min}}}{u_{\mathrm {max}}}=-1\) and the same cyclic pattern as shown in Fig. 10. The cyclic nodal material force distribution at \(N_{\mathrm {cycle}}=2\) and \(N_{\mathrm {cycle}}=50\) are depicted Fig. 18. It can be seen from the sketch, that the cyclic nodal material forces at the internal nodes are zero. Furthermore, the summation of all cyclic nodal material forces within the block is zero. It can be therefore concluded that the balance of cyclic energy momentum exists.

Fig. 18
figure 18

Distribution of cyclic nodal material forces in the block at \(N_{\mathrm {cycle}}=2\) and \(N_{\mathrm {cycle}}=50\)

Full size image

6.4 Cyclic material forces as a fatigue crack growth criterion

Paris’ pioneering law characterizes fatigue crack propagation. This law correlates the rate of crack length per cycle to the cyclic stress intensity factor \(\varDelta K\) as

$$\begin{aligned} \frac{da}{dN_{\mathrm {cycle}}}=C(\varDelta K)^m, \end{aligned}$$
(6.9)

where a is the crack length, C and m are material parameters that are obtained experimentally. \(\varDelta K\) is however limited to the case of LEFM, therefore, Dowling and Begley (1976) introduced the cyclic J-integral for gross plasticity. In viscoelastic fracture mechanics, an analytical cyclic J-integral is derived in Kuai et al. (2009) and Lee et al. (2015) in order to model fatigue crack growth in asphalt concretes. The aforementioned cyclic J-integral is denoted in this study by \(\varDelta J^{\text {visc}}\). \(\varDelta J^{\text {visc}}\) is the difference between the generalized J-integral derived by Schapery (1984) at maximum and minimum load. \(\varDelta J^{\text {visc}}\) is derived using the cyclic stress intensity factor and the creep compliance. Moreover, it requires in advance to have the cyclic stress intensity factor as an explicit function of the crack length a. In a complex geometry, \(\varDelta K\) cannot be obtained as an explicit function of a and, therefore, \(\varDelta J^{\text {visc}}\) is not valid for the case of complex geometries. The purpose of this example is to illustrate that the cyclic global material force can be used as a fatigue crack growth criterion, leading to the new form of Paris’ law

$$\begin{aligned} \frac{da}{dN_{\mathrm {cycle}}}={C'}(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}})^{m'}, \end{aligned}$$
(6.10)

where \(C'\) and \(m'\) are material parameters. To validate that Eq. (6.10) exists, a numerical study is conducted on the same specimen as presented in the work of Kuai et al. (2009). In the aforementioned study, a fatigue crack growth test is carried out on an asphalt concrete specimen. Asphalt concrete is a very complex material that exhibits relaxation and creep. A simplified description of the asphalt concrete is obtained using a small strain viscoelastic material model. The specimen has a thickness \(t=50\) mm with an initial crack length

\(a_0=30\) mm and width \(W=110\) mm. The specimen is subjected to a periodic load P that is defined as

$$\begin{aligned} P(t)=P_0+P_0\sin \left( 2\pi ft-\frac{\pi }{2}\right) , \end{aligned}$$
(6.11)

where \(P_0\) is the load amplitude and f is the load frequency. Numerically, only half of the specimen is used due to symmetric boundary conditions. The specimen dimensions and finite element mesh are shown in Fig. 19. A mapped mesh with an element size of 1 mm \(\times \) 1 mm along the crack path is used. The specimen is simulated at plane stress conditions with 50 mm thickness. One volumetric Maxwell element and one isochoric Maxwell element with \(\alpha _1^G=0.4\), \(\tau ^G_1=0.02\) s, \(\alpha _1^G=0.5\) and \(\tau ^K_1=0.05\) s have been assigned to the specimen. The initial shear modulus \(G_0\) and initial bulk modulus \(K_0\) are obtained from the initial Young’s modulus \(E=2000\) Nmm\(^-2\) and initial Poisson’s ratio \(\nu =0.3\). The cyclic global material forces are evaluated at the end of each cycle. From Eq. (6.11), it can be noticed that the load reaches its maximum value \(P_{\mathrm {max}}\) and its minimum value \(P_{\mathrm {min}}\) at \(t_{\mathrm {max}}=\frac{2N_{\mathrm {cycle}}-1}{2f}\) and \(t_{\mathrm {min}}=\frac{N_{\mathrm {cycle}}}{f}\), respectively. The cycle ends at \(t_{\mathrm {min}}\), therefore, the quantities needed to evaluate the cyclic global material force are obtained from \(t_{\mathrm {max}}\) and \(t_{\mathrm {min}}\) of each cycle.

Fig. 19
figure 19

Representation of a the specimen geometry and dimensions and b the finite element mesh and symmetric boundary conditions

Full size image

Viscoelastic materials are time-dependent which means that the loading frequency or rate have an impact on the behavior of the material. Different material behavior stands for different states of stresses and strains and, therefore, different values of the cyclic global material forces. Therefore, the starting point in this study is to evaluate the effect of the load frequency and the load amplitude on the cyclic global material force. The behavior of the cyclic global material force is investigated by applying the load for 50 cycles at different loading frequencies and at a fixed loading amplitude \(P_0=200\) N.

Fig. 20
figure 20

Representation of a the load function at different loading frequencies and b the effect of loading frequency on the cyclic global material force

Full size image

The variation of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) at different frequencies is depicted in Fig. 20. It can be seen from this figure that the value of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) decreases with increasing the frequencies. This means that for higher frequency the fatigue life of the material increases. In the experimental work of Lee et al. (2015), it has been shown that the fatigue life of asphalt concrete increases with increasing the loading frequency. Therefore, it can be concluded that the cyclic global material force takes into consideration the effects of loading frequency. Moreover, the effect of the loading amplitude on the cyclic global material force is investigated by varying the loading amplitude and fixing the loading frequency to \(f=10\) Hz. The results of this investigation are plotted in Fig. 21. It can be seen from the obtained results that the cyclic global material force values increase with increasing the loading amplitude. Higher values of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) means that the fatigue life of the specimen is shorter. It is also observed in the work of Lee et al. (2015), that higher loading amplitudes resulted in shorter fatigue life. Therefore, the cyclic global material force characterizes the effect of the loading amplitudes.

Fig. 21
figure 21

Representation of a the load function at different loading amplitudes and b the effect of loading amplitudes on the cyclic global material force

Full size image

It can be seen from Figs. 20 and 21 that the cyclic global material force reaches a constant value after the fifth cycle. An additional study is carried out in order to review the variation of the cyclic global material force with crack propagation. The specimen is subjected to the same periodic load \(P_0=200\) N at \(f= 10\) Hz. The crack propagation is achieved by applying a node release algorithm with a crack increment \(\varDelta a=1\) mm. The crack propagates at the end of the fifth cycle of each crack tip. The reason behind releasing the node at the end of the fifth cycle is that the cyclic global material force reaches a constant values after 5 cycles as shown in Fig. 21. This behavior is also observed in the previous example, see Fig. 14. Moreover, the values of the cyclic global material force are plotted against the experimental crack growth rate \(\frac{da}{dN_{\mathrm {cycle}}}\). \(\frac{da}{dN_{\mathrm {cycle}}}\) is calculated using the crack length at different cycles obtained from the experimental work of Kuai et al. (2009). The experimental crack length increase with respect to cycles as well as the best-fit function are plotted in Fig. 22.

Fig. 22
figure 22

Crack length values at different cycles obtained from experimental data and best-fit function

Full size image

The best-fit function of the crack length and the crack crack growth rate per cycle are defined as

$$\begin{aligned}&a(N_{\mathrm {cycle}})=\,10^{-16}N_{\mathrm {cycle}}^3-6\times 10^{-11}N_{\mathrm {cycle}}^{2}\nonumber \\ {}&\qquad \qquad \qquad +\,2\times 10^{-5}N_{\mathrm {cycle}}+29.5, \end{aligned}$$
(6.12)
$$\begin{aligned}&\frac{da}{dN_{\mathrm {cycle}}}=\,3\times 10^{-16}N_{\mathrm {cycle}}^2-12\times 10^{-11}N_{\mathrm {cycle}}\nonumber \\ {}&\qquad \qquad \qquad +2\times 10^{-5}. \end{aligned}$$
(6.13)

The variation of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) is depicted in Fig. 23, it can be seen that the value of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) increases when the crack

propagates. Figure 23 is a double logarithmic plot of the values of \(\frac{da}{dN_{\mathrm {cycle}}}\) versus the values of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) at different crack lengths. The data of this plot are obtained by calculating \(\frac{da}{dN_{\mathrm {cycle}}}\) as well as \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) at the same crack length. It can be noted from Fig. 23 that the relation between \(\frac{da}{dN_{\mathrm {cycle}}}\) and \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) is the same as Paris’ law and can be expressed as

$$\begin{aligned} \frac{da}{dN_{\mathrm {cycle}}}=3.21\times 10^{-5}(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}})^{0.55}. \end{aligned}$$
(6.14)

Using Eq. (6.14), the Paris’ parameters of Eq. (6.10) are obtained, where \(C'=3.21\times 10^{-5}\) and \(m'=0.55\). Therefore, it can be concluded that the cyclic global material force can be used as fatigue crack growth parameter in Paris’ law instead of the cyclic J-integral and cyclic stress intensity factor.

Fig. 23
figure 23

Representation of a the dependency of \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\) on the crack length as well as b the correlation between \(\frac{da}{dN_{\mathrm {cycle}}}\) and \(F^{\mathrm {mat}}_{1_{\mathrm {cycle}}}\)

Full size image

7 Conclusions

The focus of the study at hand is mainly on small strain viscoelastic solids, that are characterized by Prony series with n-Maxwell elements. The main aim of this paper is to present a path-independent domain integral using cyclic material forces in viscoelastic solids to evaluate the cyclic energy release rate. As a starting point, the local balance of energy momentum for n-Maxwell is derived using the free energy density. Furthermore, at cyclic loading, the free energy density is replaced by the cyclic free energy of a cycle. The cyclic free energy is computed from the cyclic stresses and the cyclic strains. The balance of cyclic energy momentum is obtained using the gradient of the cyclic free energy.

In the framework of numerical methods, a finite element discretization is carried out leading to nodal material forces and cyclic nodal material forces in viscoelastic solids. The crack driving force at monotonic loading is obtained by evaluating a domain integral around the crack tip. Numerically, the crack driving force is computed by summing up all the nodal material forces within a region surrounding the crack tip. Analogously to the crack driving force at monotonic load, the cyclic crack driving force is evaluated numerically by performing a summation of cyclic nodal material forces within a region surrounding the crack tip.

Several numerical studies are carried out in this research. At first, it has been shown that the domain integral obtained using material forces at monotonic loading is path-independent, in other words the results obtained using two different domains are equal. Moreover, it has been shown that after relaxation, the value of the global material force in crack direction is equal to the prescribed energy release rate on a linear elastic material having the relaxed Young’s modulus \(E_\infty \) and Poisson’s ratio \(\nu _\infty \) as material parameters. Furthermore, path-independency of the domain integral using cyclic material forces is validated. The cyclic global material force overcomes the problem of negative values obtained using the global material force at minimum load. Moreover, the existence of the balance of energy momentum and cyclic energy momentum is shown. Furthermore, the cyclic material force approach is validated using experimental results. It has been shown, that the cyclic global material force characterizes the effects of both the loading frequency and the loading amplitude. Finally, the relation between the crack growth rate per cycle and the cyclic global material force illustrates that the cyclic material force approach can characterize fatigue crack growth.