Observation of cracking and measurement of fracture toughness in graphite

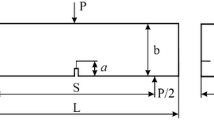
Abstract

The dominant mechanical failure mechanism in brittle or quasi-brittle materials is cracking, and the parameters that characterize the fracture process of a given material are the extension of cracked region as a function of externally applied load and the resistance of the deforming material to the advance of cracking, also known as fracture toughness. In the present investigation we develop and demonstrate a technique for observing and studying the process of macroscopic crack initiation and propagation, and for determining the fracture toughness of the brittle or quasi-brittle materials. We will address issues such as specimen design using only small amount of material, loading configuration that can generate stable crack growth in brittle solids, diagnostics for identifying crack initiation and quantifying the extent of crack growth, and scheme for extracting the stress intensity factor at the tip of a growing crack. The technique described is applied to the brittle material graphite.

Appendices

Appendix A: Verification of the numerical scheme: a virtual test

For determining the stress intensity factor at the crack tip, or the fracture toughness of the tested material, we have described a numerical scheme that combines the crack-tip field representation and the DIC measurement of the displacement field. In this section, we consider a “virtual” test shown in Fig. 19, where a crack with the length of $2\ell$ is situated in an infinite two-dimensional domain. At the midpoint of the crack surface, a pair of concentrated force P is applied and tends to open the crack.

Fig. 19

A “virtual” experiment configuration

For this idealized configuration, the displacement field within the unbounded domain has the closed form expression (Muskhelishvili 1953; Rice 1968):

$$\begin{aligned} u_{1} + i\,u_{2} = \frac{1}{2\mu } \Bigl \{ \kappa \,\phi (z) - z\,\overline{\phi }'(\overline{z}) - \overline{\psi }(\overline{z}) \Bigr \}, \end{aligned}$$

(6)

where $z = x_{1} + i\,x_{2}$ and

$$\begin{aligned} \kappa = {\left\{ \begin{array}{ll} \dfrac{3 - \nu }{1 + \nu }, &{} \text { for plane stress,} \\ 3 - 4\nu , &{} \text { for plane strain.} \end{array}\right. } \end{aligned}$$

The two potential functions $\phi (z)$ and $\psi (z)$ are given by

$$\begin{aligned}&\phi (z) = \frac{P}{2\pi }\cos ^{-1}\Bigl (\frac{\ell }{z}\Bigr ), \quad \psi (z) \nonumber \\&\quad = \frac{P}{2\pi }\Bigl \{\cos ^{-1}\Bigl (\frac{\ell }{z}\Bigr ) - \frac{\ell }{\sqrt{z^{2} - \ell ^{2}}}\Bigr \}. \end{aligned}$$

(7)

Now the “measurable” displacement field has the expression

$$\begin{aligned}&u_{1} + i\,u_{2} = \frac{P}{4\pi \mu } \Bigl \{ \kappa \,\cos ^{-1}\Bigl (\frac{\ell }{z}\Bigr ) \nonumber \\&\quad - \cos ^{-1}\Bigl (\frac{\ell }{\overline{z}}\Bigr ) + \frac{\ell }{\sqrt{\overline{z}^{2} - \ell ^{2}}} \Bigl (1 - \frac{z}{\overline{z}}\Bigr ) \Bigr \}. \end{aligned}$$

(8)

The mode-I stress intensity factor, $K_{\text {I}}$, at the crack tip of this “virtual” test is given by

$$\begin{aligned} K_{\text {I}} = \frac{P}{\sqrt{\pi \ell }}. \end{aligned}$$

(9)

The verification scheme is that based on the displacement “measurement” of Eq. (8), the least-square scheme should give the result of Eq. (9). A side result is that we can also study the number of terms in the asymptotic expansion of the displacement field required for accurately determining the stress intensity factor $K_{\text {I}}$.

For a fixed crack length $2\ell$ and a given applied load P, the displacement fields of the “virtual” test are shown in Fig. 20, where the two coordinates x and y have been normalized by the half crack length $\ell$. Note that the coordinates x and y are measured from the crack tip. By fitting the displacement data, shown in Fig. 20, to the asymptotic expression of the displacement field and by applying the least-square scheme, we can determine the stress intensity factors $K_{\text {I}}$ and $K_{\text {II}}$, at the crack tip. Since the “virtual” test configuration is pure mode-I, we focus on the stress intensity factor $K_{\text {I}}$ only. However, we will treat the number of terms used in the asymptotic expression, N, as a free parameter in the least-square scheme.

Fig. 20

Displacement fields associated with the “virtual” test configuration

The result from the least-square fitting is presented in Fig. 21, where the “measured” mode-I stress intensity factor $K_{\text {I}}$ is plotted as a function of the number of terms used in the asymptotic expansion N. The mode-I stress intensity factor $K_{\text {I}}$ is normalized by the theoretical value $P/\sqrt{\pi \ell }$, therefore, if the “measured” mode-I stress intensity factor $K_{\text {I}}$ matches the correct value, the plotted value $K_{\text {I}}/(P/\sqrt{\pi \ell })$ should be 1. Meanwhile, results of two different regions, from which the displacement data is used in the fitting, are also shown in Fig. 21. In one case, displacement data is taken from the region, where $r/\ell \leqslant 3/4$, while in another case, displacement data is taken from a smaller region $r/\ell \leqslant 1/2$, i.e., more closer to the crack tip.

Fig. 21

Mode-I stress intensity factor, $K_{\text {I}}$, determined using the displacement data and the least-square scheme on the “virtual” test configuration. The number of terms, N, in the asymptotic expansion is treated as a free parameter

From Fig. 21, we see that a single term or couple of terms in the asymptotic expansion will never accurately determine the stress intensity factor. Using only the most singular term gives the stress intensity factor 20% higher than the correct value. By including the second term, or the so-called T-stress term, the result is even worst. Including three terms seems yield a better result, but we also see that with 4 or 5 terms, the least-square fitting under estimate the stress intensity factor. Only when sufficient number of terms is used, for case $r/\ell \leqslant 3/4$, $N > 11$, and for $r/\ell \leqslant 1/2$, $N > 6$, the numerical fitting scheme is able to obtain the correct value of the crack-tip stress intensity factor. Meanwhile, taking displacement data closer to the crack tip will make the convergence of the stress intensity factor faster. However, in reality, the displacement data very close to the crack tip should be avoided due to the three-dimensional effect, since the asymptotic representation of the deformation field near the crack tip assumes planar deformation.

Appendix B: Elastic constants extraction from fracture specimen compression

Consider the situations shown in Fig. 22, where the specimen on the right has the geometry for the fracture toughness measurement test specimen. The specimen on the left has exactly the same overall dimensions as the fracture test specimen and made of the same material, but without the cavity in the center. Now if we apply the same compressive load P to the two specimens and assume that the deformation of the specimen is both elastic and two-dimensional. Then the relation between the applied load P and the overall displacement $\delta$ can be written for the two samples shown in Fig. 22, as

$$\begin{aligned} \frac{P}{WB} = E\Bigl (\frac{\delta }{H}\Bigr ), \quad \frac{P}{WB} = E^{*}\Bigl (\frac{\delta }{H}\Bigr ), \end{aligned}$$

(10)

where W, B, and H are the width, the thickness, and the height of the rectangular sample, respectively. Here E is the Young’s modulus of the material and $E^{*}$ is the apparent stiffness of the fracture test specimen.

Fig. 22

Rectangular compression specimens with and without cavity

In general, we have

$$\begin{aligned} E^{*} < E. \end{aligned}$$

(11)

Based on dimensional analysis, we can write that

$$\begin{aligned} E^{*} = \eta \Bigl (\nu ,\, \frac{d}{W},\, \frac{W}{H}\Bigr )\,E, \end{aligned}$$

(12)

where $\eta$ represent the reduction in stiffness due to the presence of cavity. Except the Poisson’s ratio $\nu$, the factor $\eta$ only depends on the non-dimensional ratios of those geometric quantities listed in the parentheses. Now, the slope of the linear portion of the applied load P versus overall displacement $\delta$ curve, or the apparent stiffness $E^{*}$, can be determined very accurately from the fracture test. If we know the value of factor $\eta$ for the geometries of each fracture specimen, then the Young’s modulus E becomes readily available.

Fig. 23

a Overall response of graphite specimen C4 and sample stiffness. b Correction factor $\eta$ as function of Poisson’s ratio $\nu$

Figure 23a shows the response of the graphite specimen C4, where the onset of cracking is also indicated. We see that prior to the crack initiation, the majority of the response is quite linear and the stiffness of the specimen, $E^{*}$ can thus be accurately determined. Through a simple finite element analysis (FEA), we compute the non-dimensional factor $\eta$ for given geometric parameters d/W and W/H. The Young’s modulus of the specimen material E is determined according to Eq. (12). This step can be done for each individual specimen, where the dimensions d, W, and H are measured, so that variations in sample dimensions can be accounted for when converting the apparent stiffness of the specimen to the Young’s material. The other elastic constant is the Poisson’s ratio $\nu$. From the literature, the Poisson’s ratio $\nu$ is within the range from 0.2 to 0.3. However, from finite element analysis, we found that the dependence of factor $\eta$ on Poisson’s ratio $\nu$ is rather weak, as shown in Fig. 23b. In all the calculations in getting the factor $\eta$ and the extraction of the stress intensity factor, $K_{\text {I}}$ and $K_{\text {II}}$, we choose that $\nu = 0.25$.