A low constraint center cracked Brazilian disk specimen for ductile FCC single crystal

Abstract

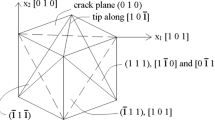
In this work, the center cracked Brazilian disk (BD) geometry is proposed as a possible small-scale low crack tip constraint fracture specimen for ductile FCC single crystals. These low crack tip constraint conditions are frequently encountered where shallow cracks are present. The effect of in-plane and out-of-plane crack tip constraint on crack tip fields in a Brazilian disk geometry was analyzed for an aluminum single crystal. A simple stress difference method is proposed to evaluate the in-plane crack tip constraint, T-stress for any anisotropic FCC crystal. The magnitude of T-stress for the center cracked BD specimen was calculated to be much lower than that in other standard fracture specimens. Besides, the energy release rate, J-integral was also evaluated for this specimen using the domain integral method. Results obtained from the full 3D crystal plasticity finite element analysis agreed well with previously reported modified boundary layer analysis with negative crack tip constraint. The study primarily considered the specific crack orientation, $\{ 010\} \left\langle {101} \right\rangle$. Two other crack orientations were also studied to analyze the different nature of strain localization in ductile single crystal. The forward localization band was observed to be significantly dominant over the other possible localization bands for all the crack orientations. However, the nature of localization varied from slip to kink in the forward band depending on the crack orientation. Under mixed mode I–II loading, localization bands not aligned with slip directions were observed with high local lattice rotation, suggesting possible existence of kink shear bands. Additionally, some important specimen details are reported, which would help in designing the small scale experiment on ductile single crystal, to measure crack tip constraint, and fracture toughness under low constraint condition.

Appendix

1.1 A1: Simulations with different BD configurations

Several simulations with different combinations of a/R ratios, crack lengths, 2a, and applied LPD were performed to figure out the suitable BD geometry. Here, the contour plots of maximum logarithmic plastic strain, $\log \left( {\lambda _1^p} \right)$ obtained in some of these simulations are plotted. The idea was to have a low magnitude of a/R ratio to obtain a BD geometry with high negative T-stress. In Fig. 21a, it was noticed that for a BD geometry with $a/R=0.05$, magnitude of LPD = 0.2 mm was not sufficient enough to cause any significant plasticity at the crack tip. Then, some trial simulations were performed with higher values of LPD. Still, it was observed that the plasticity at the crack tip for this central crack was not so significant though, plastic deformation at the contact of the loading platen and the specimen was noticeable (results are not included). So, to have prominent localization bands at the crack tip, magnitude of the applied LPD was further increased to LPD = 0.5 mm. But, the deformation fields emanating from the contact area interacted with the crack tip fields as shown in Fig. 21b. Next, a larger central crack with higher a/R ratio was chosen, and the combination of LPD = 0.2 mm, $a/R=0.1$, and $2a=2.4$ mm was found to be a suitable BD geometry with prominent localization bands at the crack tip without any interaction with the deformation fields from the contact area (Fig. 21c). Here, all these simulations were performed with radius, $R=12$ mm.

Fig. 21

Maximum principal logarithmic plastic strain, $\log \left( {\lambda _1^p} \right)$ with different configurations and loading conditions

1.2 A2: Crystal plasticity model and computational tools (Deka and Jonnalagadda 2019)

The kinematics of the elasto-plastic deformation of the single crystal was modeled utilizing the multiplicative decomposition of the deformation gradient, F into elastic, $F_e$, and plastic, $F_p$, components (Marin and Dawson 1998; Marin 2006). The elastic deformation gradient, $F_e$ was again decomposed into elastic left stretch tensor, $V_e$, and rotation tensor, $R_e$.

The flow rule was defined by a non-linear viscous constitutive law in the form of a power law as (Marin 2006),

$$\begin{aligned} { {{\dot{\gamma }}} ^\alpha = {{\dot{\gamma }}} _0 \left| {\frac{{\tau ^\alpha }}{{g^\alpha }}} \right| ^{\frac{1}{m}} \,\,sign\,\,\left( {\tau ^\alpha } \right) } \end{aligned}$$

(9)

where, ${g ^\alpha }$ and ${\tau ^\alpha }$, are the strength and resolved shear stress of the slip system $\alpha$, respectively; ${{{\dot{\gamma }}} _0}$ is the reference strain rate, and m controls the slip rate sensitivity.

Evolution of slip system strength, ${g^\alpha }$ is given as (Bassani and Wu 1991),

$$\begin{aligned} {\dot{g} ^\alpha = \sum \limits _{\beta = 1}^{12} {{h_{\alpha \beta }}\left| {{{{{\dot{\gamma }}} }^\beta }} \right| } } \end{aligned}$$

(10)

where, the matrix ${h_{\alpha \beta }}$ comprises instantaneous hardening moduli which include both self and latent hardening.

The diagonal terms of the matrix, ${h_{\alpha \beta }}$ was represented as,

$$\begin{aligned} { h_{\alpha \alpha } = L(\gamma ^\alpha )\,.\,M\left( {\gamma ^\beta ;\, \beta = 1, N} \right) \,\,\,\,\,\,\left( {{\mathrm{no}}\,\,{\mathrm{sum}}\,\,\,{\mathrm{on}}\,\,{\mathrm{\alpha }}} \right) } \end{aligned}$$

(11)

where, the instantaneous hardening modulus under single slip, L, was implemented as,

$$\begin{aligned} { L(\gamma ^\alpha ) = \left( {h_0 - h_s } \right) {\mathrm{sech}}^2 \left[ {\frac{{\left( {h_0 - h_s } \right) \gamma ^\alpha }}{{\left( {\tau _1 - \tau _0 } \right) }}} \right] + h_s } \end{aligned}$$

(12)

here, $\tau _1$, is the stage I stress, $\tau _0$, is the initial critical resolved shear stress, $h_0$, is the hardening modulus just after initial yield, and $h_s$, is the hardening modulus during easy glide.

In Eq. 11, the scalar term, M is associated with interactive (cross) hardening. The term M has no effect on the hardening of the $\alpha$-th slip system when ${\gamma ^\beta } = 0$. The magnitude of M is unity when all its arguments are zero, i.e., $M\left( {\gamma ^\beta =0 ;\beta = 1, N, \beta \ne \alpha } \right) =1$. When shear strain, $\gamma ^\beta$ is large, for $\beta \ne \alpha$, the term M has a finite value, which is given as,

$$\begin{aligned} {M\left( {\gamma ^\beta ;\beta = 1, N, \beta \ne \alpha } \right) = 1 + \mathop \sum \limits _{\begin{array}{c} \scriptstyle \beta = 1 \\ \scriptstyle \beta \ne \alpha \end{array}}^N {f_{\alpha \beta } \tanh \left( {\frac{{\gamma ^\beta }}{{\lambda _0 }}} \right) } } \end{aligned}$$

(13)

In Eq. 13, ${\lambda _0}$ represents the amount of slip after which the interaction between slip systems $\alpha$ and $\beta$ attains its maximum strength. The interaction coefficients, $f_{\alpha \beta }$, signify the magnitude of the strength of a particular slip interaction as mentioned in Table 3 (Bassani and Wu 1991).

Table 3 Strength amplitude factors $f_{\alpha \beta }$ for 12 FCC slip system (Bassani and Wu 1991)

The notations for different interactions of slip systems were assumed from Bassani and Wu (1991). For FCC single crystal, there are five independent components of $f_{\alpha \beta }$, and they are categorized as follows: N= no junction: $f_{\alpha \beta }= a_1$; H=Hirth lock: $f_{\alpha \beta }= a_2$; C=coplaner junction: $f_{\alpha \beta }= a_3$; G=glissile junction: $f_{\alpha \beta }= a_4$; S=sessile junction: $f_{\alpha \beta }= a_5$; with $a_1 \le a_2 \le a_3 \le a_4 \le a_5$. For Al single crystal, these coefficients were chosen as, $a_1=a_2=a_3=1.75$, $a_4=2$, $a_5=2.25$ (Lu et al. 2011).

The hardening of the system $\beta$, caused by the slip on the system $\alpha$, which represents the latent hardening if the system $\beta$ is inactive, was considered to be a fraction of the modulus, $h_{\alpha \alpha }$ through the latent hardening ratio (LHR), q as Eq. 14,

$$\begin{aligned} { h_{\beta \alpha } = qh_{\alpha \alpha } ,\,\,\,\beta \ne \alpha \,\,\,\,\left( {{\mathrm{no}}\,\,{\mathrm{sum}}\,\,\,{\mathrm{on}}\,\,{\mathrm{\alpha }}} \right) } \end{aligned}$$

(14)

where, q is the ratio of the latent-hardening rate to the self-hardening rate of a slip system.