Numerical investigation of crack tip strain localization under cyclic loading in FCC single crystals

Abstract

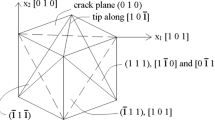
In this work, the crack tip strain localization in a face centered cubic single crystal subject to both monotonic and cyclic loading was investigated. The effect of constraint was implemented using T-stress and strain accumulation was studied for both isotropic and anisotropic elastic cases with the appropriate application of remote displacement fields in plane strain. Modified boundary layer simulations were performed using the crystal plasticity finite element framework. The consideration of elastic anisotropy amplified the effect of constraint level on stress and plastic strain fields near the crack tip indicating the importance of its use in fracture simulations. In addition, to understand the cyclic stress and strain behavior in the vicinity of the crack tip, combined isotropic and kinematic hardening laws were incorporated, and their effect on the evolution of yield curves and plastic strain accumulation were investigated. With zero-tension cyclic load, the evolution of plastic strain and Kirchhoff stress components showed differences in magnitudes between isotropic and anisotropic elastic cases. Furthermore, under cyclic loading, ratcheting was observed along the localized slip bands, which was shown to be affected by T-stress as well as elastic anisotropy. Negative T-stress increased the accumulation of plastic strain with number of cycles, which was further amplified in the case of elastic anisotropy. Finally, in all the cyclic loading simulations, the plastic strain accumulation was higher near the $55^0$ slip band.

Appendices

Appendix 1: Plastic strain field under monotonic load

Contour plots of maximum principal logarithmic plastic strain, $\log \left( {\lambda _1^p} \right)$ for various levels of T-stress are presented respectively with the consideration of elastic isotropy and anisotropy. The plots in Fig. 14a show an excellent agreement with Patil et al. (2008) results. Similar occurrence of slip shear band and kink shear band were observed for different levels of T-stress. Mainly, activation of the slip systems caused the appearance of shear bands and they governed the shape of the plastic zone. For $T = 0$, three shear bands (two slip shear bands and a kink shear band) were observed in agreement with the analytical results of Rice (1987). By contrast, for $\frac{T}{{{\tau _0}}} = 2$ the slip band sited at an angle of ${125^0}$ to crack direction was more prominent though a small but visible kink shear band took place at ${90^0}$ along with slip shear band at ${55^0}$. For $\frac{T}{{{\tau _0}}} = -2$, the contour was inclined at an angle of ${55^0}$ and the slip band (shear) at ${125^0}$ was disappeared in contour plots. Effect of elastic anisotropy was observed in the shape and spread of the plastic zone for different T-stress values as shown in plots Fig. 14b.

Appendix 2: Kirchoff stress components under monotonic load with elastic isotropy formulation

The normalized Kirchhoff stresses $\frac{{{\tau _{11}}}}{{{\tau _0}}}$,$\frac{{{\tau _{22}}}}{{{\tau _0}}}$,$\frac{{{\tau _{12}}}}{{{\tau _0}}}$ and their angular variation at $\frac{r}{{(J/\tau _0 )}} = 4$ from notch center are presented in Fig. 15 with consideration of elastic isotropy of aluminum single crystal. Similar angular variation of stress components and yield locus were observed as the results of elastic anisotropy formulation (Fig. 2) with slight variation in the magnitudes only.

Fig. 16

Maximum principal logarithmic plastic strain fields after 20 cycles for a $T = -\tau _0$, b $T =0$ and c $T = \tau _0$ at $\frac{K}{{\left( {\tau _0 \sqrt{b_0 } } \right) }} = 80$ with elastic isotropy formulation

Appendix 3: Plastic strain field under cyclic load with elastic isotropy formulation

Contour plots of $\log \left( {\lambda _1^p} \right)$ after 20 cycles are shown in Fig. 16 for different levels of T-stress with the assumption of elastic isotropy. Discontinuities observed in these plots were almost same as the ones presented in Fig. 9 obtained with elastic anisotropy formulation but with slight variation in the spreads of plastic zones.