1 Introduction

The J-integral is an expression for calculating the strain energy release rate in a cracked body, or the energy available at the tip of a crack to form new crack surfaces as the crack extends (Rice 1968). It is a firmly established parameter that can advantageously be applied both to linear and nonlinear elastic materials. In its original formulation, the J-integral is expressed as a contour integral. However, in finite element (FE) analysis, the J-integral may vary depending on the fracture, mesh design and integration method. One point of concern is that coordinates and displacements are calculated at element nodes, while stresses and strains are obtained at Gaussian integration points. Other points of concern are crack tip element specification, domain of integration and numerical errors. Therefore, the more objective J-area integral is commonly used in FE software, as its integration area dependence is less than the path dependence of a corresponding J-contour integral in integration regions close to a crack tip (Li et al. 1985; Banks-Sills and Sherman 1992; Kuna 2013). As an example of a FE implementation, using quadrilateral elements, the contour integral may be evaluated along a line of three Gaussian points in each element along the integration path, while the area integral includes the area of an element and all of its nine Gaussian points (Banks-Sills and Sherman 1986, 1992; Khoei 2015). The J-area integral is generally also simpler to implement in FE codes (Anderson 2005). Nevertheless, the first ring-shaped areas close to and around the crack tip of the J-area integral usually still display path dependency (Khoei 2015, Fig. 7.23; Simulia 2014; Ansys 2019).

The peridynamic theory is a nonlocal formulation of solid mechanics, introduced for handling crack initiation, extension and final failure of a body, without the need of supplementary methods (Silling 2000; Silling and Askari 2005). Peridynamics is based upon integral equations, thereby avoiding spatial derivatives, which are not defined at discontinuities, such as crack surfaces.

A peridynamic nonlocal J-integral has been derived by Silling and Lehoucq (2010) for state-based peridynamics, based on an energy balance approach. Later, Hu et al. (2012) presented a bond-based peridynamic J-integral, using an infinitesimal virtual crack extension method. These nonlocal J-integral formulations include displacement derivatives and force interactions over inner and outer regions associated with the contour integral. The width of these regions depends on the degree of nonlocality of the peridynamic model.

Fig. 1
figure 1

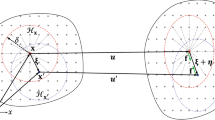
Uniformly discretized peridynamic body \(\Omega \), showing point \(\mathbf {x}\)’s interaction with one of its neighbors \(\mathbf {x}^\prime \), within horizon \(\mathcal {H}_\mathbf {x}\) of radius \(\delta \). \(\varvec{\xi } = \mathbf {x}^\prime - \mathbf {x}\) is the relative position of the points, \(\varvec{\eta } = \mathbf {u}^\prime - \mathbf {u}\) is the relative displacement and \(\varvec{f}\) is the pairwise force

Full size image

The displacements are the principal unknowns in peridynamics, from which other quantities subsequently can be obtained. A general expression of the J-contour integral as a function of displacement derivatives was derived by Bruck (1989). The expression can also be found in Sutton et al. (1992), Hamam et al. (2007) and Hart and Bruck (2021). Since the J-area integral is common in classical solid mechanics, we implement in this paper the J-area integral in peridynamics as an alternative to the J-contour integral. Our treatment of J is simpler than Bruck’s, due to rectangular integration paths.

For assessing the accuracy of the proposed J-area integral, we apply it to the exact analytical stress-strain-displacement solution of an infinite plate with a central crack loaded in mode I and compare the result to the corresponding analytical solution \(J_0=K_I^2/E\). The stresses or displacements of the exact solution on a contour away from the crack tip can be used as input boundary conditions in a peridynamic model of the same crack problem. To allow comparison with previous work (Hu et al. 2012; Stenström and Eriksson 2019), stresses are used as boundary conditions in the peridynamic model in this work. The J-area formulation will then be evaluated for the peridynamic model, to test for discrepancy between the analytical J-area integral and the peridynamic solution.

Our approach can be seen as a two-step process. In the first step, the displacement of a body may be obtained with any suitable method. In the second step, the J-integral is calculated from displacements obtained in the first step. The method is in principle thus not limited to be used jointly with just peridynamics, but allows also other methods that obtain displacements of a body, analytical, numerical or experimental. In particular, the method is equally applicable to bond-based as well as state-based peridynamics. At present, however, peridynamic J-integral works are foremost bond-based. Therefore, in this work only comparisons with bond-based peridynamic J-integral applications are made.

In the next section, we briefly introduce the bond-based peridynamic theory; for the state-based peridynamic theory, the reader is referred to Silling et al. (2007). The sections thereafter will, in order, deal with: derivation of the J-area integral on displacement formulation, derivation of the exact analytical solution of the crack problem, description of the discretization for implementation, and algorithm for calculating the J-area integral. The accuracy of the method is then investigated by comparing the peridynamic solution with the exact analytical solution of the crack problem, followed by studying conformity when the peridynamic discretization method is changed. Thereafter, the results are discussed and conclusions are given in the last sections.

2 Bond-based peridynamic theory

The peridynamic equation of motion of the material point at position \(\mathbf {x}\) at time t is given as (Silling 2000; Silling and Askari 2005)

$$\begin{aligned} \rho (\mathbf {x})\ddot{\mathbf {u}}(\mathbf {x},t)= & {} \int _{\mathcal {H}_{\mathbf {x}}}^{} \mathbf {f}\Big ( \mathbf {u}\left( \mathbf {x}^\prime , t \right) - \mathbf {u}\left( \mathbf {x}, t \right) , \mathbf {x}^\prime - \mathbf {x} \Big ) \, \text {d}V_{\mathbf {x}^\prime } \nonumber \\&\quad + \, \mathbf {b}(\mathbf {x},t) \; \forall \mathbf {x} \in \Omega \end{aligned}$$
(1)

where \(\Omega \) is the domain of the body, \(\mathbf {u}\) is the displacement vector field, \(\rho \) is the mass density and \(\mathbf {b}\) is a prescribed body force field. \(\mathbf {f}\) is the pairwise force function (a vector) per unit volume squared, denoting the force the material point at \(\mathbf {x}^\prime \) exerts on the material point at \(\mathbf {x}\). This interaction between pairs of material points is called bond, or spring in case of a linear elastic material. The integral is defined over a region \(\mathcal {H}_\mathbf {x}\), called the horizon, of radius \(\delta \), Fig. 1. The horizon can be seen as a sphere, disk or range, for 3D-, 2D- and 1D-models, respectively. A suitable horizon size is chosen and the material body discretized in accordance with problem geometry, loading and desired accuracy of the results. Convergence studies may be performed to justify the selection of horizon and discretization. The relative grid density factor \(m = \delta /\Delta x\), where \(\Delta x\) is the uniform grid spacing, should in a plane square lattice arrangement have a ratio of at least 3 (Silling and Askari 2005; Madenci and Oterkus 2014) and in many cases 4 or higher (Ha and Bobaru 2010; Henke and Shanbhag 2014; Dipasquale et al. 2016), to provide grid independent crack growth patterns. Studying the effect of increasing m is a so-called m-convergence study, introduced by Bobaru et al. (2009).

A material is called microelastic if the pairwise force between material points is derivable from a micropotential \(\omega \) (Silling 2000):

$$\begin{aligned} \mathbf {f}(\varvec{\eta }, \varvec{\xi }) = \frac{\partial \omega (\varvec{\eta }, \varvec{\xi })}{\partial \varvec{\eta }} \end{aligned}$$
(2)

where \(\varvec{\xi } = \mathbf {x}^\prime - \mathbf {x}\) is the relative position of two material points in the reference configuration, and \(\varvec{\eta } = \mathbf {u}\left( \mathbf {x}^\prime , t \right) - \mathbf {u}\left( \mathbf {x}, t \right) = \mathbf {u}^\prime - \mathbf {u}\) is the corresponding relative displacement in the deformed configuration. A linear microelastic material results in the micropotential

$$\begin{aligned} \omega ( \varvec{\eta }, \varvec{\xi } ) = \frac{ c(||\varvec{\xi }||) s^2 ||\varvec{\xi }|| }{2} \end{aligned}$$
(3)

where s is the relative elongation of a bond:

$$\begin{aligned} s = \frac{|| \varvec{\xi } + \varvec{\eta } || - || \varvec{\xi } ||}{|| \varvec{\xi } ||} \end{aligned}$$
(4)

Differentiation of (3) according to (2) gives

$$\begin{aligned} \mathbf {f} (\varvec{\eta }, \varvec{\xi }) = \frac{\partial \omega (\varvec{\eta }, \varvec{\xi })}{\partial \varvec{\eta }}= & {} c(||\varvec{\xi }||) s \frac{\partial || \varvec{\xi } + \varvec{\eta } ||}{\partial \varvec{\eta }} \nonumber \\= & {} \frac{\varvec{\xi } + \varvec{\eta }}{|| \varvec{\xi } + \varvec{\eta } ||} c(||\varvec{\xi }||)s \end{aligned}$$
(5)

where \((\varvec{\xi } + \varvec{\eta })/|| \varvec{\xi } + \varvec{\eta } || = \mathbf {e}\),

is a unit vector along a line through the two points of a bond in the deformed configuration. As we assume that a material point \(\mathbf {x}\) does not interact with material points outside its horizon, \(\mathbf {f} = \mathbf {0}\) for \(||\varvec{\xi }|| > \delta \). The particular kernel of the integrand in Eq. (1), here the ratio \(c(||\varvec{\xi }||) / ||\varvec{\xi }||\), is common in peridynamic mechanical problems. Other kernels are possible and the selection influences the nonlocality, convergence, and thus the the discretization applied (Chen et al. 2016).

2.1 Micromodulus

The elastic stiffness of a bond is determined by the micromodulus function \(c(||\varvec{\xi }||)\), which is found by calibrating the peridynamic strain energy density against the classical strain energy density, for a homogeneous body under a) isotropic (dilatational) deformation and b) pure shear (distortional) deformation. The micropotential \(\omega \) is the energy in a single bond with dimension ‘energy per unit volume squared’. The strain energy density of a single point is therefore

$$\begin{aligned} W = \frac{1}{2} \int _{\mathcal {H}_{\mathbf {x}}}^{} \omega (\varvec{\eta }, \varvec{\xi }) \, \text {d}V_{\xi } \end{aligned}$$
(6)

The factor \(\nicefrac {1}{2}\) appears as the points in a bond shares the bond energy between them equally. For a 2D body

$$\begin{aligned} W = \frac{1}{2} \int \displaylimits _{\mathcal {H}_{\mathbf {x}}} \omega (\varvec{\eta }, \varvec{\xi }) \, \text {d}V_{\xi } = \frac{c_1s^2t}{4} \int \displaylimits _{0}^{2\pi } \int \displaylimits _{0}^{\delta } \xi \xi \, \text {d} \xi \, \text {d} \theta = \frac{\pi c_1 s^2 t \delta ^3}{6}\nonumber \\ \end{aligned}$$
(7)

where t is the thickness of the body, and \(c_1\) comes from assuming a constant micromodulus \(c(||\varvec{\xi }||) = c_1\). Isotropic deformation and plane stress give the classical strain energy density \(W_0 = \nicefrac {1}{2}\, \sigma _{ij} \epsilon _{ij} = E\epsilon ^2/(1-\nu )\). Setting \(W = W_0\) yields the corresponding micromodulus:

$$\begin{aligned} c(||\varvec{\xi }||) = c_1 = \frac{6E}{\pi t \delta ^3 (1 - \nu )} \end{aligned}$$
(8)

The isotropic and pure shear deformations must result in the same \(c_1\), which in 2D plane stress restricts Poisson’s ratio to \(\nicefrac {1}{3}\), and to \(\nicefrac {1}{4}\) in 2D plane strain and 3D models (Silling 2000; Gerstle et al. 2005). This is because the forces within a bond depend only on the two material points of a bond (and no other points). This restriction was overcome in state-based peridynamics by letting each bond depend on the collective deformation within the horizon (Silling et al. 2007). The forces do not necessarily have to be pairwise equal in magnitude and opposite to each other as in bond-based peridynamics. However, an advantage of bond-based peridynamics is that it is computationally less expensive.

Equation (8) is derived under the assumption of a constant micromodulus for plane stress in 2D (in which case \(\nu = \nicefrac {1}{3}\)), and it holds also for plane strain (\(\nu = \nicefrac {1}{4}\)) (Gerstle et al. 2005). Other types of micromoduli (triangular, conical, higher degree polynominal) are derived in a similar fashion and are available for 1D (Bobaru et al. 2009), 2D (Ha and Bobaru 2010) and 3D (Silling and Askari 2005). Note that these micromoduli are calculated assuming a continuous body, i.e., an infinite number of points inside the horizon. For a finite number of points in this region, the micromodulus is, depending upon the type, more or less dependent upon the number of points there (Eriksson and Stenström 2020, 2021). Depending on the desired accuracy, and with respect to the type of micromodulus and the relative grid density factor (m), the dependence of the micromodulus upon the number of points inside the horizon might be necessary to take into account.

In this study, both c derived from assuming an infinite and finite number of material points within the horizon will be applied, i.e. \(c_{\infty }\) (Eq. (8)) and c(m). Approximate values of \(c(m=3)\) and \(c(m=5)\) have been derived in Appendix A and are \(c_{m=3}=1.1507c_{\infty }\) and \(c_{m=5}=1.0697c_{\infty }\). It is seen here that the approximation error decreases as the grid density is increased from 3 to 5.

2.2 Skin effect

Each material point \(\mathbf {x}\) interacts with its neighboring points, the family of \(\mathbf {x}\), within a radius \(\delta \). Therefore, material points at a distance smaller than \(\delta \) from a free surface will experience a truncated horizon, resulting in a smaller domain of integration. This skin effect (Ha and Bobaru 2011) leads to a softer material and larger strains near boundaries. Various correction methods exist, and have conveniently been reviewed and compared by Le and Bobaru (2018).

In this study, ‘the energy method’ method by Madenci and Oterkus (2014) will be used for skin effect correction; see Appendix B.

2.3 Constraint conditions and stresses

The peridynamic equation of motion is a nonlinear integro-differential equation in time and space, without spatial derivatives, and therefore does not lead to any classical boundary constraints. Instead volume constraints can be applied through a nonzero volume rather than on a surface (Silling and Askari 2005; Du et al. 2012), commonly introduced within a layer of thickness \(\Delta x\) or \(\delta \) (Hu et al. 2012).

The treatment of stresses at boundaries also differ from that in classical continuum mechanics. Instead of introduced as traction forces, stresses at boundaries are introduced in peridynamics as body forces \(\mathbf {b}\) within a layer \(\Delta x\) (Madenci and Oterkus 2014) or \(\delta \) (Silling and Askari 2005). In practice, to prescribe a stress \(\sigma \) to a material point \(\mathbf {x}\), one divides with the grid spacing \(\Delta x\), to attain force per unit volume.

2.4 Volume correction

The numerical integration of a material point \(\mathbf {x}\) over its horizon \(\mathcal {H}_\mathbf {x}\) includes the entire volume of each material point \(\mathbf {x}^\prime \) within the horizon radius \(\delta \) (Fig. 13). Therefore, the integration area will be larger than the area of the disc-shaped horizon, and thus, a correction factor is introduced, commonly as a linear variation between 1 and \(\nicefrac {1}{2}\) (Parks et al. 2010):

$$\begin{aligned} V_{\mathbf {x}^\prime } (||\varvec{\xi }||) = \left\{ \begin{array}{ll} \left( \frac{\delta - ||\varvec{\xi }||}{2r} + \frac{1}{2}\right) V_{\mathbf {x}^\prime }&{} if \quad (\delta -r)< ||\varvec{\xi }||< \delta \\ V_{\mathbf {x}^\prime } &{} if \quad ||\varvec{\xi }|| < (\delta -r) \end{array} \right. \end{aligned}$$
(9)

where \(r = \Delta x / 2\), and a uniform cubic lattice is assumed. Eq. (9) will be used in this study and called LAMMPS method. Other correction methods exist and can be found in Seleson (2014) and Seleson and Littlewood (2018).

2.5 Evaluation of the peridynamic equation of motion

For numerical implementation, the integral in the peridynamic equation of motion, Eq. (1), is replaced by a summation. For dynamic or quasi-static modeling, the common implementation in practice is by time integration through a finite number of small time steps and looping over the equilibrium equations of the material points. Detailed algorithms are found in Littlewood (2015) and Madenci and Oterkus (2014), and a supportive flowchart can be found in Javili et al. (2019).

For further reading, reviews are offered by Javili et al. (2019) and Diehl et al. (2019). For peridynamic modeling of Mode I loading, which is used in the present study, see Diehl et al. (2016) for investigation on convergence and crack initiation.

3 The J-area integral as a function of displacement derivatives

The J-integral of a plane homogeneous body is defined as (Rice 1968)

$$\begin{aligned} J = \int _{\Gamma }^{} \left( W \, \text {d} y - T_i u_{i,x} \, \text {d}s \right) \end{aligned}$$
(10)

where \(x = x_1\), \(y = x_2\) and \(u_{i,x} = \frac{\partial u_i}{\partial x} = \frac{\partial u_i}{\partial x_1} = u_{i,1}\). The body contains a straight through crack parallel to the x-axis. J is a contour integral evaluated counterclockwise along an arbitrary path \(\Gamma \) enclosing the crack tip. \(T_i = \sigma _{ij}n_j\) is (the components of) the traction vector along \(\Gamma \), with the outward unit normal vector \(n_j\) and \(\sigma _{ij}\) stress. \(u_i\) is a displacement vector and \(\text {d}s\) is a segment of arc length along \(\Gamma \), the inner contour in Fig. 2.

3.1 From path to area integral

By using the identity \(\text {d}y = \delta _{j1}n_j \, \text {d}s\) and Eshelby’s energy momentum tensor \(P_{jk} = W\delta _{jk} - \sigma _{ij}u_{i,k}\) (Eshelby 1975), Eq. (10) can be written as

$$\begin{aligned} J = \int _{\Gamma }^{} \left( W \delta _{j1} - \sigma _{ij} u_{i,1} \right) n_j \, \text {d}s = \int _{\Gamma }^{} P_{j1} n_j \, \text {d}s \end{aligned}$$
(11)

Now, we add another path \(S_2\) outside \(\Gamma \), enclosing the crack tip and traversed counterclockwise so that \(S_2\), the crack surfaces \(S_u\) and \(S_l\) and \(-\Gamma \) together enclose an area A (see Fig. 2).

Fig. 2
figure 2

Region A enclosed by the contour \(S_2+S_u-\Gamma +S_l\) with outward unit normal \(m_i\). Adapted from Li et al. (1985)

Full size image

We now introduce a weight function q that takes unit value on \(\Gamma \) and vanishes on \(S_2\), and is a differentiable function of position in A, including its boundaries. Then J can be written as

$$\begin{aligned} J= & {} - \!\!\!\!\!\!\! \int \limits _{ S_2+S_u-\Gamma +S_l }^{} \!\!\!\!\!\!\!\!\!\!\!\! P_{j1} m_i q \, \text {d}s \end{aligned}$$
(12)

Note that J vanishes on unloaded, stress free crack surfaces, that is, J vanishes on \(S_u\) and \(S_l\), as both \(\text {d}y\) and \(T_i\) vanish on \(S_u\) and \(S_l\).

The region enclosed by A does not contain any crack tip singularity and is therefore regular. The theorem of Gauss applied on Eq. (12) then yields

$$\begin{aligned} J = - \int _A ( P_{j1} q)_{,j} \, \text {d}A = - \int _A P_{j1} q_{,j} \, \text {d}A \end{aligned}$$
(13)

as \(P_{j1,j}=0\), due to absence of body forces. This is the same expression as in Li et al. (1985).

Denoting the integrand in Eq. (13) I and expanding yields

$$\begin{aligned}&I = P_{j1} q_{,j}= P_{11} q_{,1} + P_{21} q_{,2} \nonumber \\&\quad = \left( W-\sigma _{i1} u_{i,1} \right) q_{,1} - \sigma _{i2} u_{i,1} q_{,2}\nonumber \\&\quad = [ W- ( \sigma _{11} u_{1,1} + \sigma _{21} u_{2,1} )] q_{,1} - ( \sigma _{12} u_{1,1} \nonumber \\&\qquad + \sigma _{22} u_{2,1} ) q_{,2} \end{aligned}$$
(14)

which is the desired result.

3.2 Weight function

Let the weight function q be a truncated square pyramid with base corners at r and s, see Figs. 3 and 4. \(d_i = a\) gives a full (untruncated) pyramid, while \(a< d_i < d_y\) gives a truncated pyramid, and \(d_i=d_y\) gives a single contour, i.e. the J-integral contour.

Fig. 3
figure 3

The weight function q forming a pyramid truncated at \(d_i\), and integration region divided into \(\textcircled {1}\)–\(\textcircled {3}\)

Full size image
Fig. 4
figure 4

The weight function q in profile. \(h=d_y/(d_y-d_i)\)

Full size image

Before integration of the three regions (\(\textcircled {1}\)–\(\textcircled {3}\)) of Fig. 3, we need to write the strain energy density and stresses as functions of displacement derivatives.

3.3 Displacement derivatives

For a linear elastic material, assumed in this work, the strain energy density

$$\begin{aligned} W = \frac{1}{2} \sigma _{ij} \epsilon _{ij} \end{aligned}$$
(15)

Hooke’s law provides the following plane stress versus strain relationships in 2D:

$$\begin{aligned} \sigma _{11}= & {} \frac{E}{1-\nu ^2} (\epsilon _{11} + \nu \epsilon _{22}) \end{aligned}$$
(16a)
$$\begin{aligned} \sigma _{22}= & {} \frac{E}{1-\nu ^2} (\epsilon _{22} + \nu \epsilon _{11}) \end{aligned}$$
(16b)
$$\begin{aligned} \sigma _{12}= & {} \sigma _{21} = \frac{E}{1+\nu } \epsilon _{12} \end{aligned}$$
(16c)

The strain-displacements relationships are

$$\begin{aligned} \epsilon _{ij} = \frac{1}{2} (u_{i,j} + u_{j,i}) \end{aligned}$$
(17)

Substitution of Eq. (17) in Eqs. (16a–c) provides the stress-displacements derivative relationships

$$\begin{aligned} \sigma _{11}= & {} \frac{E}{1-\nu ^2} (u_{1,1} + \nu u_{2,2}) \end{aligned}$$
(18a)
$$\begin{aligned} \sigma _{22}= & {} \frac{E}{1-\nu ^2} (u_{2,2} + \nu u_{1,1}) \end{aligned}$$
(18b)
$$\begin{aligned} \sigma _{12}= & {} \sigma _{21} = \frac{E}{2(1+\nu )} (u_{1,2} + u_{2,1})\nonumber \\= & {} \frac{E}{1-\nu ^2} \frac{1-\nu }{2} (u_{1,2} + u_{2,1}) \end{aligned}$$
(18c)

Substitution of Eq. (18a–c) in Eq. (15) yields W as a function of displacement derivatives:

$$\begin{aligned} W= & {} \frac{E}{2(1-\nu ^2)} \left[ u_{1,1}^2 + u_{2,2}^2 + 2\nu u_{1,1} u_{2,2}\right. \nonumber \\&\left. \quad +\, \frac{1 - \nu }{2} (u_{1,2} + u_{2,1})^2 \right] \end{aligned}$$
(19)

where E and \(\nu \) are Young’s modulus and Poisson’s ratio, respectively.

The second term in Eq. (10) is expanded to

$$\begin{aligned} \sigma _{ij} n_j u_{i,1} = (\sigma _{11}n_1 + \sigma _{12}n_2)u_{1,1} + (\sigma _{21}n_1 + \sigma _{22}n_2)u_{2,1} \end{aligned}$$
(20)

By taking the integration contour as a square around the crack tip, as in Fig. 3, Eq. (20) can be separated into three parts; \(\textcircled {1}\) right hand side, \(\textcircled {2}\) top and \(\textcircled {3}\) left hand side contours:

$$\begin{aligned}&{\textcircled {1}},~n = (1,0){:} \;\; \sigma _{ij}n_j u_{i,1} = \sigma _{11} u_{1,1} + \sigma _{21} u_{2,1} \end{aligned}$$
(21a)
$$\begin{aligned}&{\textcircled {2}},~n = (0,1){:} \;\; \sigma _{ij}n_j u_{i,1} = \sigma _{12} u_{1,1} + \sigma _{22} u_{2,1}\end{aligned}$$
(21b)
$$\begin{aligned}&{\textcircled {3}},~n = (-1,0){:} \;\; \sigma _{ij}n_j u_{i,1} = -\sigma _{11} u_{1,1} - \sigma _{21} u_{2,1}\nonumber \\ \end{aligned}$$
(21c)

Substitution of Eqs. (18a–c) in Eqs. (21a–c) yields

$$\begin{aligned} w_1= & {} \frac{E}{1-\nu ^2} \bigg \{\left( u_{1,1} \right) ^2 + \nu u_{1,1} u_{2,2} \nonumber \\&+ \frac{1-\nu }{2} \left[ u_{1,2} u_{2,1} + \left( u_{2,1} \right) ^2 \right] \bigg \} \end{aligned}$$
(22a)
$$\begin{aligned} w_2= & {} \frac{E}{1-\nu ^2} \Big \{ \frac{1-\nu }{2} u_{1,1} u_{1,2} \nonumber \\&+ \frac{1+\nu }{2} u_{1,1} u_{2,1} + u_{2,1} u_{2,2} \Big \} \end{aligned}$$
(22b)
$$\begin{aligned} w_3= & {} -w_1 \end{aligned}$$
(22c)

where \(w_1\), \(w_2\) and \(w_3\) are calculated on the right, top and left sides of the contour, respectively. Substitution of Eqs. (22a–c) in Eq. (14) yields

$$\begin{aligned} I = (W-w_1)q_{,1} - w_2 q_{,2} \end{aligned}$$
(23)

3.4 Integration of regions

The three regions of Fig. 3 (\(\textcircled {1}\)–\(\textcircled {3}\)) are now ready for integration. The q and I for each region is given in Table 1. The J-area integral, henceforth \(J_A\), is then given by:

$$\begin{aligned} J_A= & {} J_1+J_2+J_3 = \int \limits _{d_i}^{d_y}\int \limits _0^{x_1-a} I_1(x_1,x_2) \, \text {d}x_2 \text {d}x_1 \nonumber \\&\quad +\, \int \limits _{d_i-a}^{d_y-a}\int \limits _{a-x_2}^{a+x_2} I_2(x_1,x_2) \, \text {d}x_1 \text {d}x_2 \nonumber \\&\quad +\,\int \limits _{2a-d_y}^{2a-d_i}\int \limits _0^{a-x_1} I_1(x_1,x_2) \, \text {d}x_2 \text {d}x_1 \end{aligned}$$
(24)
Table 1 Weight function q and integrand I per region
Full size table

We will now go to finding an exact analytical solution of the center cracked specimen for benchmarking, followed by discretization and the algorithm for \(J_A\).

4 Exact analytical solution of the center cracked specimen

Exact analytical solutions of stresses and displacements for an infinite plate with a straight crack, under uniform, uniaxial remote stress perpendicular to the crack, have been derived by Unger et al. (1983). In-plane (or Mode I) stresses and displacements can be expressed in terms of the real and imaginary parts of the complex potential of Westergaard (1939)

$$\begin{aligned} Z_I(z) = \frac{\sigma _{\infty }z}{\sqrt{z^2-a^2}} \end{aligned}$$
(25)

where \(\sigma _{\infty }\) is the remotely applied tensile stress, a is half the crack length, and \(z = x + iy\) is a complex coordinate. Unger et al. derived the expressions for stresses and displacements under plane strain conditions by making use of the complex identity of Aifantis and Gerberich (1978):

$$\begin{aligned} \sqrt{c+id}= & {} \pm \Bigg [ \left( \frac{c+\sqrt{c^2+d^2}}{2} \right) ^{\nicefrac {1}{2}} \nonumber \\&+ i \, \text {sgn}(d) \left( \frac{-c+\sqrt{c^2+d^2}}{2} \right) ^{\nicefrac {1}{2}} \Bigg ] \end{aligned}$$
(26)

The real and imaginary parts of Eq. (25) can then be found, from which in turn closed form stress and displacement expressions can be derived. We have in an analogue manner derived the stresses and displacements under plane stress conditions

$$\begin{aligned}&\begin{matrix} \sigma _x \\ \sigma _y \end{matrix} = \frac{\sigma _{\infty }}{\sqrt{2}} \left( \frac{X\sqrt{C} + Y\sqrt{D}}{B} \begin{matrix} - \\ + \end{matrix} Y\frac{A\sqrt{D} + 2XY\sqrt{C}}{B^3} \right) \end{aligned}$$
(27a)
$$\begin{aligned}&\sigma _{xy} = \frac{\sigma _{\infty }}{\sqrt{2}} Y \frac{A\sqrt{C} - 2XY\sqrt{D}}{B^3} \end{aligned}$$
(27b)
$$\begin{aligned}&\begin{matrix} u \\ v \end{matrix} = \frac{\sigma _{\infty }a }{\sqrt{2} E} (1+\nu ) \left[ \begin{matrix} \alpha \sqrt{C} - (Y^2\sqrt{C} - XY\sqrt{D})/B \\ \beta \sqrt{D} - (Y^2\sqrt{D} + XY\sqrt{C})/B \end{matrix} \right] \end{aligned}$$
(27c)

where X, Y and A–C are dimensionless variables, \(\alpha \) and \(\beta \) are constants for plane stress and plane strain, respectively. The dimensionless variables are given as

$$\begin{aligned} X= & {} x/a, \end{aligned}$$
(28a)
$$\begin{aligned} Y= & {} y/a \end{aligned}$$
(28b)
$$\begin{aligned} A= & {} X^2 - Y^2 - 1, \end{aligned}$$
(28c)
$$\begin{aligned} B= & {} \sqrt{A^2 + 4X^2Y^2} \end{aligned}$$
(28d)
$$\begin{aligned} C= & {} A + B, \end{aligned}$$
(28e)
$$\begin{aligned} D= & {} B - A \end{aligned}$$
(28f)

\(\alpha \) and \(\beta \) are given by:

$$\begin{aligned} \alpha= & {} \frac{\kappa -1}{2}, \end{aligned}$$
(29a)
$$\begin{aligned} \beta= & {} \frac{\kappa +1}{2} \end{aligned}$$
(29b)
$$\begin{aligned} \kappa= & {} \bigg \{ \begin{array}{lll} (3-\nu )/(1+\nu ) &{}\text {for plane stress} \\ 3-4\nu &{}\text {for plane strain} \end{array} \end{aligned}$$
(29c)

x and y in Eq. (28a,b) are the spatial coordinates. With Eq. (27) the stresses and displacements can be calculated at any point in the infinite plate.

The benefit of this exact solution is that the stresses or displacements can be used as input to peridynamic modeling, or more precisely, as boundary conditions for finite models of the infinite geometry problem.

5 Discretization of the J-area integral for numerical implementation

The material domain is discretized uniformly to allow for a midpoint integration scheme (one-point Gaussian quadrature) (Silling and Askari 2005). The J-area integral of Eq. (24) can then be recast for numerical implementation by using the trapezoidal rule as follows:

$$\begin{aligned} J_1= & {} \int \limits _{d_i}^{d_y}\int \limits _0^{x_1-a} I_1(x_1,x_2) \, \text {d}x_2 \text {d}x_1 \nonumber \\= & {} \frac{-1}{\Delta d} \sum _{j=1}^N \left[ \sum _{i=1}^{n_j} \left( W^i-w_1^i \right) \Delta x_2 \right] \Delta x_1 \end{aligned}$$
(30a)
$$\begin{aligned} J_2= & {} \int \limits _{d_i-a}^{d_y-a}\int \limits _{a-x_2}^{a+x_2} I_2(x_1,x_2) \, \text {d}x_1 \text {d}x_2 \nonumber \\= & {} \frac{1}{\Delta d} \sum _{j=1}^N \left( \sum _{i=1}^{n_j} w_2^i \Delta x_1 \right) \Delta x_2 \end{aligned}$$
(30b)
$$\begin{aligned} J_3= & {} \int \limits _{2a-d_y}^{2a-d_i}\int \limits _0^{a-x_1} I_3(x_1,x_2) \, \text {d}x_2 \text {d}x_1 \nonumber \\= & {} \frac{-1}{\Delta d} \sum _{j=1}^N \left[ \sum _{i=1}^{n_j} \left( W^i-w_1^i \right) \Delta x_2 \right] \Delta x_1 \end{aligned}$$
(30c)

where: i: Material point \(i=1,\dots ,n_j\), \(n_j\): Number of material points in the x/y direction of contour j, j: Contour \(j=1,\dots ,N\), N: Number of contours.

Following the uniformly discretized material domain, \(\Delta x_1\) and \(\Delta x_2\) refer to the constant grid spacing \(\Delta x\). Moreover, \(\Delta d\) equals \(d_y-d_i\), as given in Table 1. Last, \(W^i\), \(w_1^i\) and \(w_2^i\) are given by Eqs. (19) and (22a–c)

The strains in Eqs. (19) and (22a–c) are approximated by applying the central difference scheme on the displacement field. For a material point i, the strains are given as follows:

$$\begin{aligned} u_{1,1} = \frac{\partial u_1(x_1^i,x_2^i)}{\partial x_1^i} \approx \frac{ u_1(x_1^i + \Delta x,x_2^i) - u_1(x_1^i - \Delta x,x_2^i) }{2\Delta x} \nonumber \\\end{aligned}$$
(31a)
$$\begin{aligned} u_{1,2} = \frac{\partial u_1(x_1^i,x_2^i)}{\partial x_2^i} \approx \frac{ u_1(x_1^i, x_2^i + \Delta x) - u_1(x_1^i, x_2^i - \Delta x) }{2\Delta x} \nonumber \\\end{aligned}$$
(31b)
$$\begin{aligned} u_{2,1} = \frac{\partial u_2(x_1^i,x_2^i)}{\partial x_1^i} \approx \frac{ u_2(x_1^i + \Delta x,x_2^i) - u_2(x_1^i - \Delta x,x_2^i) }{2\Delta x} \nonumber \\\end{aligned}$$
(31c)
$$\begin{aligned} u_{2,2} = \frac{\partial u_2(x_1^i,x_2^i)}{\partial x_2^i} \approx \frac{ u_2(x_1^i, x_2^i + \Delta x) - u_2(x_1^i, x_2^i - \Delta x) }{2\Delta x}\nonumber \\ \end{aligned}$$
(31d)

6 Algorithm for evaluating the J-area integral

Recall that the exact solution is of an infinite specimen and the peridynamic counterpart is of a finite one. Thus, exact stresses are calculated at coordinates that corresponds to the boundary of the finite peridynamic specimen and then imposed as boundary conditions in the peridynamic model.

Within the algorithm, evaluation on the exact solution is indicated with a prime, e.g. \(J_A^{\prime }\). The algorithm for calculating \(J_A\) is as follows:

  1. 1.

    Specify input parameters:

    • Material body width and height

    • Material properties \(\nu \) and E

    • Grid spacing \(\Delta x\)

    • Remote loading \(\sigma _0 = \sigma _{\infty }\)

    • Integration interval \(d_y-d_i\) for \(J_A\)

  2. 2.

    Discretize the material body into spatial coordinates x and y.

  3. 3.

    Set-up the peridynamic model:

    • Calculate the exact stresses \(\sigma _x^{\prime }\), \(\sigma _y^{\prime }\) and \(\sigma _{xy}^{\prime }\) (or the \(u^{\prime }\) and \(v^{\prime }\)) at x- and y-coordinates that corresponds to the outer most contour of the discretized material body of Step 2. Eq. (27)

    • Impose the exact stresses \(\sigma _x^{\prime }\), \(\sigma _y^{\prime }\) and \(\sigma _{xy}^{\prime }\) as boundary conditions at the outer most contour N in the peridynamic model, as equivalent body forces by dividing with \(\Delta x\).

    • Integrate the peridynamic equation of motion at all nodes x and y, by rewriting Eq. (1) as a summation and use of time integration.

    • Integrate a finite number of time steps to reach quasi-static equilibrium and obtain displacements u and v.

  4. 4.

    Calculate \(J_A^{\prime }\):

    • Calculate the exact displacements \(u^{\prime }\) and \(v^{\prime }\) at nodes x and y within the interval \(d_y-d_i\). Eq. (27)

    • Approximate strains at nodes x and y within the interval \(d_y-d_i\). Eqs. (31a–d)

    • Calculate \(J_A^\prime \) on the selected interval \(d_y-d_i\). Eqs. (30a–c)

  5. 5.

    Calculate \(J_A\):

    • Approximate strains at nodes x and y, using the obtained u and v (Step 3), within the interval \(d_y-d_i\). Eqs. (31a–d)

    • Calculate \(J_A\) on the selected interval \(d_y-d_i\). Eqs. (30a–c)

We use Fortran language for peridynamic modeling and Matlab software for pre- and post-processing. Fortran example codes for peridynamic modeling are provided by Madenci and Oterkus (2014).

7 Validation of \(J_A\) with study of PD discretization methods

Validation of \(J_A\) will be carried out by comparing it to the analytical solution \(J_0=K_I^2/E\), and to the J-contour integral as they should give similar results. Thereafter, we will study the \(J_A\) near and remote to the crack tip, to see the impact of the tip and skin effect. \(J_A\) should be less sensitive to disturbances. Here, we will also study the influence of the ‘corner points’ of the rectangular integration domain. Finally, we will make changes to the discretization parameters and evaluate \(J_A\)’s conformity. As J is evaluated on a contour or region enclosing the crack tip, it can be used as a tool to test the accuracy of peridynamic discretizations, which is demonstrated.

7.1 Problem set-up

To facilitate comparison with previous results, e.g. of Stenström and Eriksson (2019) and Hu et al. (2012), we will use a Young’s modulus of 72 GPa, a Poisson’s ratio of \(\nicefrac {1}{3}\), a 10 cm by 10 cm specimen, and we will impose boundary conditions within a layer \(\Delta x\), as suggested by Hu et al. (2012). Prescribing the body force within a layer \(\Delta x\) also maximizes the skin effect.

Fig. 5
figure 5

The center cracked specimen with crack length a, analytical stresses at the boundary (i.e. equivalent body forces thereof), and symmetry boundary conditions

Full size image

The stresses are imposed along the boundaries at the top, bottom and right hand side of the test specimen, and symmetry conditions of zero horizontal displacement are imposed on the left hand side of the specimen (Fig. 5).

To avoid peridynamic skin effects along the symmetry line, i.e. along the x-axis, the peridynamic model is taken as a square, and not as a symmetry half (Fig. 5).

For a center crack in an infinite plate with a remote loading of \(\sigma _0 = 1\) MPa perpendicular to the crack, and a half crack length \(a = 0.05\) m, \(J_0 = K_I^2/E = (\sigma \sqrt{\pi a})^2/E = 2.1817\) Pa m. The relative difference of the \(J_A\) a on displacement formulation can then be calculated as \((J_A-J_0)/J_0\).

By inserting the remote loading \(\sigma _0\) in the exact solution of the center crack problem, we can calculate the stresses corresponding to the boundary of the specimen shown in Fig. 5; see Fig. 6.

Fig. 6
figure 6

Analytical stresses at the boundary corresponding to remote constant stress \(\sigma _0\) in the exact analytical solution. Calculated using Eq. (27) and used as boundary conditions in the peridynamic model; see Step 3 in the algorithm

Full size image

7.2 Peridynamic discretization

For validation of \(J_A\), we use the discretization method of the code provided by Madenci and Oterkus (2014), here called method PD1. Thereafter we will vary the grid density factor m, the micromodulus c, neighbor volume correction (partial volume, PV) and skin effect / surface correction. See Table 2.

Table 2 Discretization methods and their parameters
Full size table

In the table, \(c_{\infty }\) is given by Eq. (8), c(m) is given by Eqs. (A.5) and (A.6) in Appendix A, ‘\(c_{\infty }\) with \(W_0\)’ refers to the correction given by Eq. (B.2) in Appendix B, and PV refer to LAMMPS volume correction given by Eq. (9). All four methods can be complemented with skin effect correction but the default value is that it is turned off.

As described in Sect. 2, the micromodulus c is commonly calculated assuming a infinite number of neighbor points within the horizon region \(\mathcal {H}_{\mathbf {x}}\), whose circumference, in turn, divides neighbor elements located at the horizon radius \(\delta \) into two parts, one part inside of the horizon and one part outside. In method PD0, non of these discretization effects are corrected. In PD1, \(c=c_{\infty }\) is corrected by calibration with the classical strain energy density \(W_0\) and partial volumes are corrected using LAMMPS method. In PD2, c is calculated assuming a finite number of neighbor points and calibrated with use of \(W_0\). The only difference between c(m) and ‘\(c_{\infty }\) with \(W_0\)’ is how \(W_0\) is expressed (see Appendix B). Volumes are corrected in PD2 using LAMMPS method. PD3 differ from PD2 by an increased grid density, \(\delta =5\Delta x\).

PD1 will be used in the next section, and all four methods will be used in the section there after.

7.3 Validation of \(J_A\)

PD1 is used for the validation. There is no skin effect correction and the 10 cm by 10 cm specimen is discretized into \(50^2\) or \(500^2\) material points.

An example of integration region (contours no. 8–11) is shown in Fig. 7. The integration domain’s ‘corner points’ are colored orange. The first contour (at the crack tip) comprises four material points and the second twelve. Thus, the contours nearest to the crack tip for which \(J_A\) can be calculated are contours no. 1 and 2. Further, Fig. 7 shows the deformed configuration of the peridynamic model with displacements magnified 3000 times and color corresponding to the the strain energy density.

Fig. 7
figure 7

Contours marked out on the deformed configuration of the peridynamic model with \(50^2\) material points. Along contour 25 are applied body forces equivalent to boundary stresses in Fig. 6

Full size image
Fig. 8
figure 8

The J-contour evaluated for contour 2–24 for analytical and peridynamic (PD) models of \(50^2\) material points. At contour 14, analytical error \(\nicefrac {(J_C^{'}-J_0)}{J_0} = 0.032\%\) and PD error \(\nicefrac {(J_C-J_0)}{J_0} = 15\%\). \(J_0 = 2.1817\)

Full size image
Fig. 9
figure 9

The J-contour evaluated for contour 2–249 for analytical and peridynamic (PD) models of \(500^2\) material points. At contour 126, analytical error \(\nicefrac {(J_C^{'}-J_0)}{J_0} = 0.005\%\) and PD error \(\nicefrac {(J_C-J_0)}{J_0} = 0.38\%\). \(J_0 = 2.1817\)

Full size image
Fig. 10
figure 10

The \(J_A\) based on five contours evaluated for contour 2–6, 3–7,\(\dots \), 20–24, for \(50^2\) analytical and peridynamic models

Full size image

For evaluating the \(J_A\), we start by plotting the J-contour integral (\(J_C\)) from the second contour from the crack tip to the second last contour; see Figs. 8, 9. The discretization is of \(50^2\) and \(500^2\) material points, respectively. The skin effect that is apparent in the results of the peridynamic model has two origins. The first is the skin effect at the crack faces, which effect all \(J_C\) results. The second origin is the skin effect at the outer boundary of the peridynamic model, which affects the outer-most contours.

Fig. 11
figure 11

Displacement errors of methods PD0–PD3, of a square plate under uniaxial normal stress in the y-direction. Name of method followed by a ‘b’ means skin effect correction. The error \(e = \nicefrac {(u_{PD}-u_0)}{u_0}\). L and R stands for left and right hand side, E stands for end node, and ‘An.’ stands for analytical solution, i.e. \(u_x=\nu \epsilon x\) and \(u_y=\epsilon y\)

Full size image

Recalling \(J_0 = 2.1817\), the relative error of the analytical \(J_C\) at contour 14 in Fig. 8 is 0.032% and that of the corresponding peridynamic model 15%. In Fig. 9, the corresponding errors at contour 126 are \(0.005\%\) and 0.38%; the skin effect has less influence on the result. These results are in line with the convergence study presented in the previous article (Stenström and Eriksson 2019). Keeping the number of material points covered by the horizon (m) constant, while decreasing the horizon radius \(\delta \), i.e. increases the total number of material points of the model, is called \(\delta \)-convergence (Bobaru et al. 2009).

The skin effect can also be reduced by use of correction methods (Le and Bobaru 2018) or by using the state-based peridynamic method. In 1D, it is possible, in certain situations, to altogether eliminate the skin (i.e. end) effect (Eriksson and Stenström 2020, 2021).

The \(J_A\) gives the same result and error as \(J_C\) when evaluated at the middle contours; see Fig. 10 for the \(50^2\) model results. \(d_y-d_i\) is set to \(5\Delta x\) for simplicity, i.e. five contours. It is seen that \(J_A\) is less sensitive to local disturbances, or in this case, the skin effect.

Considering the contour corners points, it is favorable to include the corner points in the side contours instead of the top contour in the peridynamic model, as slightly more accurate J values are obtained.

As \(J_A\) has been shown to give similar results as \(J_C\), we will now move on to changing the PD discretization method and study \(J_A\)’s correspondence.

7.4 \(J_A\) and changing PD discretization methods

For studying the discretization methods PD0–3, the methods are first applied to a defect free 10 cm by 10 cm specimen in uniaxial normal stress of 1 MPa, applied on the opposite boundaries in the y-direction. The stress is prescribed as a body force in a layer \(\Delta x\). Material parameters are kept the same as for the center cracked specimen. Modeling a defect free specimen allows the study of the stiffness in the bulk of the specimen and at its boundary, and consequently relates it to the discretization method and \(J_A\).

Modeling results of the defect free specimen is shown in Fig. 11. The error in displacement between the methods PD0-3 are calculated as \(e = \nicefrac {(u_{PD}-u_0)}{u_0}\). PD1–3 (Fig. 11b–e) give errors between 0–3%. PD0 (Fig. 11a) gives an error of 7–13%, which can be expected as c and volume corrections are not applied and m is the lowest advisable at 3. Increasing m reduces the error. The difference between PD2 and PD3 is that the m is increased to 5. However, both give similar errors despite the increased m, which is explained by the increased skin effect as the number of material points are kept constant at \(50^2\). In PD3, the stiffness in a layer \(5\Delta x\) from the boundary is lowered, which propagates throughout the whole model.

Boundary nodes error in displacement is 4% for PD2 and 18% for PD3 (Fig. 11c–e). When skin effect correction is applied in PD2b and PD3b, theses values become 0.13% and 5.6% (Fig. 11d and f). However, the error in the bulk increases. Better performing skin effect correction methods are found in Le and Bobaru (2018).

In Fig. 12, the methods PD0–PD3 are applied to the cracked specimen and \(J_A\) is calculated. The PD1 curve is exact to Fig. 10, i.e. no difference in the problem set-up or discretization. PD1 and PD2 give almost the same \(J_A\), which is because the correction factors for c differ only in how \(W_0\) is expressed. PD0 gives a \(J_A\) closest to the analytical curve; however, in a \(\delta \)-convergence, when the number of material points increases, PD0 will not converge to \(J_0=2.1817\) as the other methods. PD3 gives the highest \(J_A\) which is a result of the increased skin effect and a low number of material points (\(50^2\)). When the skin effect procedure is applied, both curves of PD2b and PD3b are shifted down. The whole curves are shifted down as the skin effect on the crack faces are present at all contours 1–25.

8 Conclusion

The J-area integral is an alternative to the corresponding J-contour integral for evaluating the J-integral in peridynamics, or for any other method where the displacements are the principal unknowns, or when a displacement formulation is appealing.

The area integral was found to be less sensitive to local errors, which in this case are due to the skin effect.

Lastly, including the corner points of the integration domain in the side contours somewhat improved the accuracy of the area integral.

Fig. 12
figure 12

\(J_A\) of methods PD0–PD3 with ‘b’ indicating skin correction. Based on five contours evaluated for contour 2–6, 3–7,\(\dots \), 20–24, for \(50^2\) discretization

Full size image

A possible future work is to include Mode II loading by comparing peridynamics and FEM, and/or possibly study convergence towards the stress intensity factor \(K_{II}\) of a slanted crack in a biaxial stress field of an infinite plate.