Crack channelling mechanisms in brittle coating systems under moisture or temperature gradients

Abstract

Crack channelling is predicted in a brittle coating-substrate system that is subjected to a moisture or temperature gradient in the thickness direction. Competing failure scenarios are identified, and are distinguished by the degree to which the coating-substrate interface delaminates, and whether this delamination is finite or unlimited in nature. Failure mechanism maps are constructed, and illustrate the sensitivity of the active crack channelling mechanism and associated channelling stress to the ratio of coating toughness to interfacial toughness, to the mismatch in elastic modulus and to the mismatch in coefficient of hygral or thermal expansion. The effect of the ratio of coating to substrate thickness upon the failure mechanism and channelling stress is also explored. Closed-form expressions for the steady-state delamination stress are derived, and are used to determine the transition value of moisture state that leads to unlimited delamination. Although the results are applicable to coating-substrate systems in a wide range of applications, the study focusses on the prediction of cracking in historical paintings due to indoor climate fluctuations, with the objective of helping museums developing strategies for the preservation of art objects. For this specific application, crack channelling with delamination needs to be avoided under all circumstances, as it may induce flaking of paint material. In historical paintings, the substrate thickness is typically more than ten times larger than the thickness of the paint layer; for such a system, the failure maps constructed from the numerical simulations indicate that paint delamination is absent if the delamination toughness is larger than approximately half of the mode I toughness of the paint layer. Further, the transition between crack channelling with and without delamination appears to be relatively insensitive to the mismatch in the elastic modulus of the substrate and paint layer. The failure maps developed in this work may provide a useful tool for museum conservators to identify the allowable indoor humidity and temperature fluctuations for which crack channelling with delamination is prevented in historical paintings.

1 Introduction

The prediction of the fracture response of a bilayer composed of a brittle coating adhering to a substrate is highly relevant to the structural integrity of micro-electronics components (van Gils et al. 2004), thermal barrier coatings (Choi et al. 1999; Hille et al. 2009), ceramic multi-layers (Sørensen et al. 2012), road pavements (Timm et al. 2003), natural phenomena (surface layers in dry soils (Velde 1999)), and also to the failure and preservation of cultural heritage objects including historical oak wood cabinets (Luimes et al. 2018a) and historical paintings (Giorgiutti-Dauphiné and Pauchard 2016; Léang et al. 2017). This study is mainly motivated from observations of surface crack development in historical paintings, as driven by indoor climate variations.

Historical paintings typically consist of one or more layers of paint adhering to a canvas or wooden substrate, and their degradation is sensitive to environmental changes associated with moisture fluctuations, and to a lesser extent to temperature changes (Mecklenburg and Tumosa 1991). Degradation originates from differential swelling and shrinkage across the layers: indoor climate variations, along with differential mechanical and hygro-thermo-expansive properties of the paint and substrate materials, result in tensile self-stresses in the paint layer. If the tensile stress at some location of the paint layer attains the fracture strength, then paint cracking will occur. The most common mechanism of paint cracking is crack channelling, as observed at the surface of panel and canvas paintings, and is usually denoted as craquelure. The network of these cracks is complex, and generally depends on the geometry and materials used and on the environmental conditions to which the painting is exposed (Bucklow 1997). Moisture-driven channelling cracks in wooden panel paintings have been analysed (Bratasz 2013; Krzemień et al. 2016; Bratasz and Vaziri Sereshk 2018), and the sensitivity of crack stability to micro-climate variations, and to the thickness of layers have been reported. A channelling crack may kink at the interface between the paint layer and the substrate, generating interfacial delamination. This mechanism has also been identified in paintings (Crook and Learner 2000; Young 2007), and its occurrence under the influence of relative humidity cycles has been investigated in Tantideeravit et al. (2013), Wood et al. (2018). If the delamination is unstable such that it grows without limit, it may ultimately lead to spallation or flaking of the paint material, as reported in Brewer and Forno (1997), O’Donoghue et al. (2006). Flaking degrades the visual appearance of the painting, and needs to be understood in detail for museums to adequately regulate their indoor climate control and safely preserve their objects.

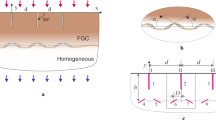
An illustrative overview of the three crack channelling mechanisms as described above is given in Fig. 1. In the lower left corner of the painting displayed in Fig. 1a, a fine network of channelling cracks can be observed at the paint surface, see Fig. 1b. This may lead to crack deflection at the paint-substrate interface, characterized by two opposite delaminations, see Fig. 1c. A delamination crack may advance without limit, thereby triggering paint flaking, see Fig. 1d.

Fig. 1

a Still life with flowers, Anonymous Italian, circa 1850, Oil on canvas, Private collection. The rectangle in the lower left corner indicates the area from which the detailed pictures shown in figures b–d have been taken. b–d Qualitative overview of failure mechanisms occurring in historical paintings: b fine network of cracks channelling through the paint layer; c channelling crack that has kinked at the interface between the substrate and the paint layer, thereby introducing two opposite delaminations; d unlimited delamination that has led to flaking of the paint material. Pictures courtesy of Matteo Rossi Doria

From a more general perspective, the study of cracking in coating-substrate systems has been the topic of various investigations, as follows. The channelling behaviour of a single mode I crack in a brittle, isotropic elastic layer subjected to residual tension and bonded either to a semi-infinite or finite-thickness substrate has been analysed in Beuth (1992) and Vlassak (2003), respectively. These analyses show that the reduction in film stress associated with elastic deformation of the substrate may have a significant effect on the energy release rate for crack propagation. The channelling of a series of parallel cracks in a surface layer has been addressed in Thouless (1990), Thouless et al. (1992), and the crack spacing has been predicted as a function of the stress in the surface layer, its thickness, and the toughness of the layer. A similar problem has been studied for the case of thermal loading in Timm et al. (2003). Several studies have focussed on crack path selection (He and Hutchinson 1989a, b), whereby conditions were identified such that a brittle mode I crack in the surface layer penetrates the underlying substrate, or kinks along the layer interface and generates delamination. Various aspects of crack deflection at the interface between the coating and the substrate have been investigated, including the formation of multi-fissures and debonding (León Baldelli et al. 2013), the origin of crack spacing (Lazarus and Pauchard 2011; Lazarus 2017; Ma et al. 2019), the contribution of residual stresses in relation to bending (Charalambides et al. 1990; Delette et al. 2012; Forschelen et al. 2016), and the influence of a thermal misfit between the coating and substrate (Lee et al. 2006). When delamination is absent, brittle mode I cracks may channel through both the coating and substrate; depending upon the stiffness mismatch, the depth of the channelling crack may be an order of magnitude larger than the coating thickness (Thouless et al. 2011). An extensive overview of studies on crack channelling, interfacial delamination and substrate damage is provided in the reference works Hutchinson and Suo (1992), Freund and Suresh (2004).

Inspired by the failure mechanisms observed in historical paintings, see Fig. 1, the present study addresses the behaviour of a brittle crack channelling in a bilayer under a moisture (or temperature) gradient in the thickness direction. The moisture gradient originates from a jump in humidity across the thickness of the system, with diffusion in steady-state, such that time transients do not play a role. The mode I channelling crack may deflect at the coating-substrate interface into two opposite delaminations of equal length, leading to the doubly deflected crack as sketched in Fig. 2.

Fig. 2

A doubly deflected crack in a brittle elastic coating bonded to an elastic substrate of finite thickness. In historical paintings the coating is representative of the paint layer and the substrate reflects a wooden or canvas support

Since the delamination length can vary, in principle, over the full range from zero to infinity, this configuration is representative of all three crack channelling scenarios as illustrated in Fig. 1b–d for a historical painting. The coating and substrate are characterized by two isotropic, linear elastic solids of dissimilar hygroscopic and mechanical properties. The assumption of elastic isotropy is acceptable for most paints; the substrate, however, is anisotropic in the case of wood or canvas, and this will lead to some inaccuracy in the predicted fracture response as computed herein. However, as demonstrated in a recent study on the fracture of both historic and new oak wood samples (Luimes et al. 2018b), the error is minor if the crack face normal aligns with a specific material direction, and the assumed value of Young’s modulus for the isotropic elastic solid equals the anisotropic stiffness in the direction of the crack face normal.

Crack channelling is investigated by considering the three distinct fracture scenarios as summarized in Fig. 3a–c. These scenarios are: (i) channelling of a mode I crack in the coating with delamination absent (mechanism 1), (ii) channelling of a doubly deflected crack with finite delamination length (mechanism 2), and (iii) channelling of a mode I crack with unlimited delamination in all directions (mechanism 3). It is emphasised that these three mechanisms are representative of the cracking scenarios that are regularly observed in historical paintings, recall Fig. 1b–d.

The 3D failure mechanisms sketched in Fig. 3 are analysed by making use of the results from finite element calculations of steady-state crack channelling and plane-strain delamination. The critical remote stress for steady-state crack channelling may be determined from a plane-strain elasticity solution of a doubly deflected crack, whereby the difference in strain energy upstream and downstream of the channelling crack front is equated to the work of fracture of the doubly deflected crack (Hutchinson and Suo 1992; Beuth 1992; Suiker and Fleck 2004). The delamination toughness is taken to be constant and independent of the mode-mix; this assumption is acceptable, as the mode-mix attains a steady-state value at a relatively short delamination length for all configurations investigated. This modelling strategy for the analysis of 3D crack channelling mechanisms is similar to that used in Fleck and Zhao (2000) for microbuckle tunnelling in fibre composites and in Suiker and Fleck (2004), Cox and Marshall (1996), Suiker and Fleck (2006) for crack tunnelling in layered solids. The numerical results are used in the construction of failure mechanism maps, which illustrate the sensitivity of the active fracture mechanism and corresponding critical channelling stress to the ratio of layer interface to coating toughness, and to the mismatches in stiffness and in coefficient of hygral expansion. In the analysis of the results, the moisture content profile driving the fracture process is idealised by the superposition of a uniform contribution and a contribution that varies linearly across the thickness of the bilayer. In accordance with this decomposition, the remote stresses generated in the coating and substrate may be decomposed into constant and linear parts. These two stress contributions can be conveniently combined to construct the overall critical remote stress for crack channelling. Results are presented in terms of the hygral boundary conditions, but, from the analogy between hygral diffusion and thermal conduction, they can be immediately applied to channelling cracks under thermal boundary conditions.

Fig. 3

Three possible crack channelling mechanisms for a bilayer system consisting of two dissimilar, isotropic materials and subjected to a moisture content gradient across the thickness. a Mechanism 1: Channelling of a mode I crack in the coating with delamination absent; b Mechanism 2: Channelling of a doubly deflected crack with finite delamination length; c Mechanism 3: Channelling of a mode I crack with unlimited delamination in all directions

The study considers a coating-substrate system containing a single crack. In historical paintings, however, multiple cracks can develop, with the typical crack spacing ranging between 10 and 50 times the coating thickness (Giorgiutti-Dauphiné and Pauchard 2016). It has been verified from the results of the numerical simulations that, for almost all the configurations analysed (with the exception of systems with a thick but compliant substrate), the stress field in the coating approaches the value of the remote stress at a distance from the delamination tip of less than six times the coating thickness. Since the crack spacing in historical painting typically exceeds the coating thickness by an order of magnitude, the cracks may be treated as isolated defects. Hence, the results of this study can also be applied to systems containing multiple parallel cracks. This conclusion is consistent with that reported in Thouless (1990). Although the present study has been motivated from observations of crack patterns in historical paintings, the modelling approach applies to the general case in which a surface layer on a substrate experiences channelling cracks under moisture and/or temperature gradients.

The paper is organized as follows. The problem is defined in Sect. 2. In Sect. 3 the governing equations for steady-state crack channelling and plane-strain delamination are presented. Section 4 gives the numerical results for a bilayer system composed of layers of equal thickness. The influence of the relative substrate thickness upon the failure response is then studied in Sect. 5. The main conclusions of the study are summarised in Sect. 6.

Fig. 4

Plane-strain cracking in a bilayer system. Doubly deflected crack at the interface between the coating and the substrate as a result of the applied moisture content profile $\Delta m(y)$. Bending and vertical deformations of the system are prevented through the fixed and roller supports at the bottom of the substrate. The remote stress profile depends on the system geometry, the moisture content profile, and the mismatch in hygro-mechanical properties of the individual layers

2 Definition of the problem

The three channelling mechanisms of Fig. 3 shall be predicted by considering the plane-strain crack as detailed in Fig. 4. Consider a bilayer system composed of a coating of thickness $h_1$ bonded to a substrate of thickness $h_2$, with $h = h_1 + h_2$ the total thickness of the bilayer. Assume that a crack-like flaw develops across the coating thickness and subsequently deflects at the interface with the substrate into two opposite delaminations, each of length $\ell$, see Fig. 4. The location of the crack is described by means of a Cartesian coordinate system (x, y) , with the x-axis located along the interface between the coating and the substrate, and the y-axis coinciding with the vertical symmetry axis at the centre of the system. The coating and substrate are isotropic elastic solids, of Young’s modulus $E_i$, Poisson’s ratio $\nu _i$, hygral expansion coefficient $\beta _i$, and moisture diffusion coefficient $D_i$, with $i=1$ designating the coating and $i=2$ denoting the substrate. There is choice in the assumed boundary condition on the bottom of the substrate. Here, roller supports are imposed to allow for horizontal displacements and to prevent vertical displacements (and consequently impose zero curvature on the system). The bilayer is subjected to plane-strain conditions, and experiences a steady-state hygroscopic loading as defined by a moisture content $\Delta m$ that varies as a function of vertical coordinate y in the thickness direction.

The moisture content variation depends on the moisture diffusion coefficients of the coating, $D_1$, and substrate, $D_2$, and on the changes in moisture content at the top, $\Delta m_1 = m_1 - m_0$, and at the bottom bottom, $\Delta m_2 = m_2 - m_0$, where $m_0$ is a reference value of moisture content. For a steady-state diffusion process, the moisture content $\Delta m(y)$ across the thickness is bi-linear,¹ and each linear branch can be split into a uniform part (with magnitude at $y=0$) and a part that scales linearly with y as given by

$$\begin{aligned}&\Delta m (y) \nonumber \\&\quad = \left\{ \begin{array}{l} \displaystyle {\frac{\Delta m_1D_1 h_2 + \Delta m_2D_2h_1}{D_1h_2 + D_2 h_1} + y \frac{D_2(\Delta m_1- \Delta m_2)}{D_1h_2 + D_2 h_1} }\quad \mathrm {if}\quad y\ge 0 \\ \displaystyle {\frac{\Delta m_1D_1 h_2 + \Delta m_2D_2h_1}{D_1h_2 + D_2 h_1} + y \frac{D_1(\Delta m_1- \Delta m_2)}{D_1h_2 + D_2 h_1} }\quad \mathrm {if}\quad y< 0 ~. \end{array}\right. \nonumber \\ \end{aligned}$$

(1)

The in-plane, axial stresses $\sigma _1$ and $\sigma _2$ that are generated in the coating and substrate by the moisture content profile follow from the constitutive equations as

$$\begin{aligned}&\sigma _1(x,y) = \bar{E}_1 \left( \varepsilon _1(x,y) - \bar{\beta }_1 \Delta m(y) \right) ~ ,\nonumber \\&\sigma _2(x,y) = \bar{E}_2 \left( \varepsilon _2(x,y) - \bar{\beta }_2 \Delta m (y)\right) ~ , \end{aligned}$$

(2)

where $\bar{E}_{i} = E_i/(1-\nu _i^2)$ and $\bar{\beta }_i = \beta _i(1+\nu _i)$ are the plane-strain elastic modulus and coefficient of hygral expansion of layer $i \in \{1,2\}$, and $\varepsilon _i(x,y)$ and $\bar{\beta }_i \Delta m (y)$ are the total strain and hygroscopic strain, respectively.

Fig. 5

Bilayer system subjected to moisture content variation. Remote stress components $\bar{\sigma }_1$ and $\Sigma _1$ presented by Eqs. (6)$_1$ and (6)$_2$, as a function of the relative thickness $h_2/h_1$, for a selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$. The stress component $\bar{\sigma }_1$ is associated with a uniform moisture content profile equal to the moisture content at the coating-substrate interface, and the stress component $\Sigma _1$ is associated with a linear moisture content profile that vanishes at the coating-substrate interface. The layers have the same diffusion coefficient, $D_2/ D_1=1$. The mismatch in the coefficient of hygroexpansion is a $\bar{\beta }_2/\bar{\beta }_1 = 0.1$ and b $\bar{\beta }_2/\bar{\beta }_1 = 10$

Closed-form expressions for the remote, moisture-induced layer stresses that drive fracture can be derived from force equilibrium on an upstream cross-section remote from the crack. The total force on the cross-section vanishes. Upon expressing the upstream remote stresses in the coating and substrate as $\sigma _1(x\rightarrow \infty , y)= \sigma ^{\infty }_1(y)$ and $\sigma _2(x\rightarrow \infty , y)= \sigma ^{\infty }_2(y)$, respectively, this leads to

$$\begin{aligned} \int _0^{h_1} \sigma ^{\infty }_1(y)\mathrm {d}y + \int _{-h_2}^{0} \sigma ^{\infty }_2(y)\mathrm {d}y = 0 ~. \end{aligned}$$

(3)

Now substitute the moisture content profile (1) into the constitutive relations (2)$_1$ and (2)$_2$, and insert the result into (3). Also, enforce the compatibility statement that the total axial strain is uniform across the upstream cross-section:

$$\begin{aligned}&\varepsilon ^{\infty }_1 = \varepsilon ^{\infty }_2 \qquad \text{ where } \quad \varepsilon ^{\infty }_i = \varepsilon _i(x \rightarrow \infty ,y)\nonumber \\&\qquad \text{ with } \qquad i \in \{ 1,2 \} \, . \end{aligned}$$

(4)

Consequently, the remote stress distributions $\sigma ^{\infty }_1(y)$ and $\sigma ^{\infty }_2(y)$ become

$$\begin{aligned} \sigma ^{\infty }_1(y)= & {} \bar{\sigma }_1 + \Sigma _1 \displaystyle {\left( 1+ \frac{y D_2}{ \eta _1(D_1 h_2+D_2h_1)}\right) } ~,\nonumber \\ \sigma ^{\infty }_2(y)= & {} \bar{\sigma }_2 + \Sigma _2 \displaystyle { \left( 1 +\frac{y D_1}{ \eta _2(D_1h_2+D_2h_1)}\right) } ~, \end{aligned}$$

(5)

where

$$\begin{aligned} \bar{\sigma }_1= & {} \displaystyle {{\frac{\bar{E}_1 \bar{E}_2 ( \bar{\beta }_2 - \bar{\beta }_1) h_2}{\bar{E}_1 h_1 + \bar{E}_2 h_2}\frac{ \Delta m_1 D_1 h_2 + \Delta m_2 D_2 h_1 }{D_1h_2+D_2h_1} }} ~,\nonumber \\ \Sigma _1= & {} \bar{E}_1\bar{\beta }_1\eta _1(\Delta m_2-\Delta m_1) ~,\nonumber \\ \eta _1= & {} \displaystyle {\frac{ \bar{E}_2 D_1 h_2^2 (\bar{\beta }_2/\bar{\beta }_1) -\bar{E}_1 D_2 h_1^2 }{2(D_1h_2+D_2h_1 )(\bar{E}_1 h_1 + \bar{E}_2 h_2)}} ~,\nonumber \\ \bar{\sigma }_2= & {} - \displaystyle {\frac{h_1}{h_2}\bar{\sigma }_1} ~ ,\nonumber \\ \Sigma _2= & {} \displaystyle {\frac{\bar{E}_2}{\bar{E}_1}\Sigma _1} ~,\nonumber \\ \eta _2= & {} \displaystyle {\frac{\bar{\beta }_1}{\bar{\beta }_2}\eta _1} ~. \end{aligned}$$

(6)

Note from Eq. (5) that, in each layer i, the remote stress $\sigma ^{\infty }_i$ is characterized by the sum of constant and linear stress contributions across the thickness. The constant stress contribution $\bar{\sigma }_i$ is defined by Eqs. (6)$_1$ and (6)$_4$, and is due to the first term on the right end side of Eq. (1): it is the contribution to $\sigma ^{\infty }_i$ from a uniform moisture content $\Delta m= \Delta m (0) = { (\Delta m_1 D_1h_2 + \Delta m_2 D_2h_1)/ }{(D_1h_2 + D_2 h_1)}$ that equals the moisture content value at the coating-substrate interface. The linear stress is quantified by the stress measure $\Sigma _i$ as defined by Eqs. (6)$_2$ and (6)$_5$, and is due to the linear moisture profile as stated by the second term on the right end side of Eq.(1). It is emphasised that this linear moisture content variation vanishes at the coating-substrate interface.

The coating stress contributions $\bar{\sigma }_1$ and $\Sigma _1$ as given by Eqs. (6)$_1$ and (6)$_2$ are depicted in Fig. 5 as a function of the relative thickness $h_2/h_1$, for the case of vanishing moisture content at the bottom face of the bilayer, $\Delta m_2 = 0$. It is further assumed that the layers have equal diffusion coefficients, $D_2/ D_1=1$. The stresses in the coating are given in dimensionless form for selected stiffness mismatches $\bar{E}_2/\bar{E}_1 = [0.1, 1, 10]$, and for mismatches in hygroexpansion coefficient of $\bar{\beta }_2/\bar{\beta }_1=0.1$, see Fig.  5a, and of $\bar{\beta }_2/\bar{\beta }_1=10$, see Fig.  5b. It is clear from Fig. 5a that, for a low coefficient of hygroexpansion of the substrate $\bar{\beta }_2/\bar{\beta }_1=0.1$, the stresses $\bar{\sigma }_1$ and $\Sigma _1$ asymptote under increasing substrate thickness to a compressive stress that is independent of stiffness mismatch $\bar{E}_2/\bar{E}_1$. For a coating and substrate of equal thickness, $h_2/h_1 = 1$, a coating of moderate to high stiffness, $0.1 \le \bar{E}_2/\bar{E}_1 \le 1$, experiences tensile stresses $\Sigma _1$ that may induce cracking. Conversely, the constant stress contribution $\bar{\sigma }_1$ is compressive, irrespective of the value of the stiffness mismatch $\bar{E}_2/\bar{E}_1$ and the relative coating thickness $h_2/h_1$. Figure 5b illustrates that for a relatively high coefficient of hygroexpansion of the substrate $\bar{\beta }_2/\bar{\beta }_1=10$, the stress $\bar{\sigma }_1$ unconditionally lies in the tensile regime, while $\Sigma _1$ lies in the compressive regime. Both stress parameters increase in magnitude with increasing substrate thickness, eventually approaching a limit value. It is emphasised that the above discussion relates to the case of hygroscopic swelling, with the imposed change in moisture content being positive, $\Delta m_1 >0$. In the case of hygroscopic shrinkage such that the moisture content variation is negative, $\Delta m_1 <0$, the stresses along the vertical axes of Fig. 5a, b change sign, and consequently “tension” and “compression” in the above discussion are interchanged. It is concluded that the constant and linear stresses in the coating may either lay in the compressive or tensile regime, depending on the moisture profile, stiffness mismatch, hygroexpansion coefficient mismatch and substrate-to-coating thickness ratio.

Consider first the case of a uniform moisture content profile that generates a uniform stress distribution within the coating, such that $\Sigma _1=0$. Mode I fracture in the coating can only occur if the constant remote stress $\bar{\sigma }_1$ in the coating is tensile, i.e.,

$$\begin{aligned} \bar{\sigma }_1 > 0 ~. \end{aligned}$$

(7)

Referring to the remote stress definition (6)$_1$, under hygroscopic swelling, $\Delta m = (\Delta m_1 D_1 h_2 + \Delta m_2 D_2 h_1)/ ( D_1 h_2 + D_2 h_1) > 0$, this condition is met for a hygroexpansion coefficient mismatch $\bar{\beta }_2/\bar{\beta }_1 > 1$, independent of the value of the stiffness mismatch and the relative substrate thickness. Conversely, for the case of hygroscopic shrinkage, $\Delta m < 0$, the coating is in tension for a mismatch in hygroexpansion coefficient $\bar{\beta }_2/\bar{\beta }_1 < 1$.

Next consider the case of a linear moisture content variation that vanishes at the layer interface, along with $\bar{\sigma }_1 = 0$. For simplicity, it is assumed that the linear stress distribution in the coating that follows from Eq. (5)$_1$ as $\Sigma _1(1 + {y D_2}/({\eta _1(D_1h_2+D_2h_1)}))$, is tensile across the entire coating thickness. This condition is satisfied for the choice:

$$\begin{aligned} \left\{ \begin{array}{l} \Sigma _1> 0 \qquad \mathrm {and} \\ \displaystyle {1+ \frac{y D_2}{ \eta _1(D_1 h_2+D_2 h_1)}} > 0 \qquad \mathrm {for} \qquad 0\le y \le h_1 ~. \end{array}\right. \end{aligned}$$

(8)

Note from the remote stress definition (6)$_2$ that requirement (8)$_1$ is met if the function $\eta _1$ and the moisture content difference $\Delta m_2- \Delta m_1$ have the same sign. For the choice $\Delta m_1 - \Delta m_2 > 0$, this implies that $\eta _1 < 0$, and, upon referring to the definition (6)$_3$, this is equivalent to $\bar{E}_2D_1 \bar{\beta }_2h_2^2/(\bar{E}_1 D_2 \bar{\beta }_1 h_1^2) <1$. Conversely, for $\Delta m_1 - \Delta m_2 < 0$, the remote stress $\Sigma _1$ is tensile if $\eta _1 > 0$, leading to $\bar{E}_2 D_1 \bar{\beta }_2h_2^2/(\bar{E}_1 D_2 \bar{\beta }_1 h_1^2) > 1$. Additionally, condition (8)$_2$ holds when it is satisfied at its most critical location, which is at the top surface of the coating, $y = h_1$. Note that (8)$_2$ depends solely on the hygro-mechanical and geometrical properties of the bilayer system, and is independent of the moisture content profile imposed. The material parameters and geometrical properties of the bilayer systems analysed in Sects. 4 and 5 are selected such that condition (8)$_2$ is satisfied at $y = h_1$, when condition (8)$_1$ holds. Specifically, the selected elastic mismatches between the coating and substrate are $\bar{E}_2/\bar{E}_1 = \left[ 0.1, 0.3, 1, 3, 10\right]$, with their Poisson’s ratios being taken equal, $\nu _1 =\nu _2 = 0.3$. Further, the diffusion coefficient is chosen to be equal for the two layers, $D_2/ D_1=1$. If the thicknesses of the coating and substrate are in the same range, i.e., $h_2/h_1 < 10$, for the range of stiffness ratios mentioned above, condition (8)$_2$ is unconditionally satisfied at $y= h_1$ for hygroexpansion coefficient mismatches $\bar{\beta }_2/\bar{\beta }_1 \ge 10$. Hence, as an illustrative case, in the numerical analyses the mismatch in hygroexpansion coefficients will be taken as $\bar{\beta }_2/\bar{\beta }_1 = 10$.

Note finally that the above model may be also used for thermo-mechanical loading, whereby Eq. (1) refers to a temperature variation and the coefficients $D_1$ and $D_2$ are substituted by the thermal conductivities of the coating and substrate, respectively. Further, the coefficients $\bar{\beta }_1$ and $\bar{\beta }_2$ in the constitutive equations (2)$_1$ and (2)$_2$ are replaced by the thermal expansion coefficients of the coating and substrate, respectively.

3 Steady-state crack channelling and plane-strain delamination

The governing equations for steady-state crack channelling and plane-strain delamination in a coating-substrate system under a moisture gradient can be derived from a framework similar to that employed for microbuckle tunnelling in fibre composites in Fleck and Zhao (2000) and that developed for crack tunnelling in layered solids (Cox and Marshall 1996; Suiker and Fleck 2004, 2006). Accordingly, it is assumed that the channelling crack has nucleated from an initial flaw in the coating and develops as a result of a moisture-induced tensile remote stress $\sigma ^{\infty }_1(y)$ given by Eq. (5)$_1$. During steady-state channelling, the channelling front has a constant shape, whereby the energy release rate does not depend on the channelling length in the out-of-plane direction of the crack. Hence, the energy released per unit advance of crack channelling can be calculated as the difference in the elastic strain energy $\Delta W$ upstream and downstream of the channelling front (Hutchinson and Suo 1992; Beuth 1992; Fleck and Zhao 2000; Suiker and Fleck 2004), which equals the difference between the strain energy stored in the uncracked plane-strain solid and in the cracked plane-strain solid. For the channelling crack shown in Fig. 4, this energy difference equals

$$\begin{aligned} \Delta W = \frac{1}{2}\int _0^{h_1} \sigma ^{\infty }_1(y) \delta (y) \mathrm {d}y ~, \end{aligned}$$

(9)

where $\delta (y)$ is the opening displacement across the crack faces within the coating. For convenience, this crack opening displacement $\delta (y)$ is decomposed as

$$\begin{aligned} \delta (y) = \delta _{\bar{\sigma }}(y)+ \delta _\Sigma (y) ~, \end{aligned}$$

(10)

where the contribution $\bar{\delta }_{\bar{\sigma }}(y)$ represents the crack opening displacement when the remote stress in the coating is constant and equal to $\bar{\sigma }_1$, while $\bar{\delta }_\Sigma (y)$ is the crack opening displacement associated with a linear remote stress, characterized by the stress measure $\Sigma _1$, see Eq. (5)$_1$. Insert Eqs. (2)$_1$ and (10) into Eq. (9), and apply Betti’s reciprocity principle; then, the elastic strain energy can be decomposed into three contributions, in a similar way to that done in Vlassak (2003). The first contribution $\Delta W_{\bar{\sigma }}$ relates to the stress $\bar{\sigma }_1$ that is constant across the coating thickness, the second contribution $\Delta W_\Sigma$ is associated with a linear stress profile described by the stress measure $\Sigma _1$, and the third contribution $\Delta W_{{\bar{\sigma }\Sigma }}$ results from the coupling between the constant stress and linear stress distributions,² i.e.,

$$\begin{aligned} \Delta W = \Delta W_{\bar{\sigma }} + \Delta W_\Sigma + \Delta W_{{\bar{\sigma }\Sigma }} ~, \end{aligned}$$

(11)

where

$$\begin{aligned} \Delta W_{\bar{\sigma }}= & {} \displaystyle {\frac{1}{2} \bar{\sigma }_1 \bar{\delta }_{\bar{\sigma }} h_1} ~,\nonumber \\ \Delta W_\Sigma= & {} \displaystyle { \frac{1}{2}\Sigma _1 \bar{D}_\Sigma h_1} ~, \nonumber \\ \Delta W_{{\bar{\sigma }\Sigma }}= & {} \displaystyle {\Sigma _1 \bar{D}_{\bar{\sigma }} h_1 } ~, \end{aligned}$$

(12)

with the corresponding average displacement parameters as

$$\begin{aligned} \bar{\delta }_{\bar{\sigma }}= & {} \displaystyle {\frac{1}{h_1}\int _0^{h_1} \delta _{\bar{\sigma }}(y) \mathrm {d}y~} ,\nonumber \\ \bar{D}_\Sigma= & {} \displaystyle {\frac{1}{h_1}\int _0^{h_1} \delta _\Sigma (y)\left( \displaystyle {1+ \frac{y D_2}{\eta _1(D_1h_2+D_2h_1)}}\right) \mathrm {d}y } ~,\nonumber \\ \bar{D}_{\bar{\sigma }}= & {} \displaystyle {\frac{1}{h_1}\int _0^{h_1} \delta _{\bar{\sigma }}(y)\left( \displaystyle {1+ \frac{y D_2}{\eta _1(D_1h_2+D_2h_1)}}\right) } \mathrm {d}y ~.\nonumber \\ \end{aligned}$$

(13)

3.1 Steady-state crack channelling with a finite delamination length

In accordance with the decomposition of the strain energy as stated by Eq. (11), steady-state channelling of the doubly deflected crack can be analysed by separately considering the constant and linear stress distributions in the coating. Hence, the contribution $\Delta W_{\bar{\sigma }}$ associated with the constant stress $\bar{\sigma }_1$ alone, from a uniform moisture content variation, is considered first. Based on dimensional considerations, the corresponding average displacement $\bar{\delta }_{\bar{\sigma }}$ is expressed in the form

$$\begin{aligned} \bar{\delta }_{\bar{\sigma }} = \frac{h_1 \bar{\sigma }_1}{\bar{E}_1} f \left( \frac{\ell }{h_1},\frac{\bar{E}_2}{\bar{E}_1}, \frac{\bar{\beta }_2}{\bar{\beta }_1},\frac{D_2}{D_1}\right) ~, \end{aligned}$$

(14)

where the dimensionless function f depends on the aspect ratio $\ell /h_1$ of the doubly deflected crack, the stiffness mismatch $\bar{E}_2/\bar{E}_1$, the mismatch in hygroexpansion coefficients $\bar{\beta }_2/\bar{\beta }_1$ and the ratio between the moisture diffusion coefficients $D_2/D_1$. Upon substituting Eq. (14) into Eq. (12)$_1$, the energy drop per unit crack length becomes

$$\begin{aligned} \Delta W_{\bar{\sigma }}= \frac{ \bar{\sigma }_1^2}{2\bar{E}_1}h_1^2 f \left( \frac{\ell }{h_1},\frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1}, \frac{D_2}{D_1}\right) ~. \end{aligned}$$

(15)

Under a uniform moisture content, the moisture content profile (1)$_1$ becomes $\Delta m(y) =\Delta m_1 = \Delta m_2$, and the remote stress $\sigma ^{\infty }_1$ coincides with the constant stress contribution $\bar{\sigma }_1$, see Eq. (5)$_1$. The corresponding average energy release rate per unit advance of a channelling crack $G_{c,{\bar{\sigma }}}$ is directly related to the elastic energy drop via the expression (Hutchinson and Suo 1992; Beuth 1992; Fleck and Zhao 2000; Suiker and Fleck 2004)

$$\begin{aligned} G_{c,{\bar{\sigma }}} = \frac{\Delta W_{\bar{\sigma }}}{h_1 +2\ell } ~. \end{aligned}$$

(16)

The energy drop $\Delta W_{\bar{\sigma }}$ reflects the energy necessary to form a mode I crack of length $h_1$ in the coating and two delamination cracks of length $\ell$. Write the mode I toughness of the coating as $\Gamma _{I}$ and the delamination toughness as $\Gamma _{d}$; then, the energy drop can be written as

$$\begin{aligned} \Delta W_{\bar{\sigma }} = G_{c,{\bar{\sigma }}}(h_1 +2\ell ) =\Gamma _{I}h_1 + 2 \Gamma _{d}\ell ~. \end{aligned}$$

(17)

In general, the delamination toughness $\Gamma _{d}$ is a function of the mode-mix $\Psi$ of the interfacial crack, as will be discussed in more detail in Sect. 3.2. The critical remote stress for steady state channelling $\bar{\sigma }_1 = \bar{\sigma }_c$ can be computed by combining Eqs. (17) and (15), leading to

$$\begin{aligned} \bar{\sigma }_{c} = \left( \frac{2\bar{E}_1\left( \Gamma _{I}h_1 + 2 \Gamma _{d}\ell \right) }{h_1^2 \, f \left( {\ell }/{h_1},{\bar{E}_2}/{\bar{E}_1},{\bar{\beta }_2}/{\bar{\beta }_1}, D_2/D_1\right) }\right) ^{\frac{1}{2}} ~. \end{aligned}$$

(18)

Now consider the second term $\Delta W_\Sigma$ of the energy drop given by Eq. (11), which is related to the linear stress measure $\Sigma _1$. Analogous to Eq. (14), the average displacement $\bar{D}_\Sigma$ associated with $\Sigma _1$ can be written as

$$\begin{aligned} \bar{D}_\Sigma = \frac{h_1 \Sigma _1}{\bar{E}_1} g \left( \frac{\ell }{h_1}, \frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1},\frac{D_2}{D_1}\right) ~. \end{aligned}$$

(19)

Here, the non-dimensional function g characterizes the doubly deflected crack, and is a dimensionless function of the aspect ratio $\ell /h_1$, the stiffness mismatch $\bar{E}_2/\bar{E}_1$, the mismatch in hygroexpansion coefficient $\bar{\beta }_2/\bar{\beta }_1$ and the ratio between the moisture diffusion coefficients ${D_2}/{D_1}$. Substituting Eq. (19) into Eq. (12)$_2$, the energy drop $\Delta W_\Sigma$ can be expressed as

$$\begin{aligned} \Delta W_\Sigma = \frac{ \Sigma _1^2}{2\bar{E}_1}h_1^2 g \left( \frac{\ell }{h_1},\frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1}, \frac{D_2}{D_1}\right) ~. \end{aligned}$$

(20)

For a linear profile in moisture content, with a vanishing value at the coating-substrate interface, Eq. (1)$_1$ reduces to $\Delta m(y) = y {D_2(\Delta m_1- \Delta m_2)}/{(D_1h_2} {+ D_2 h_1)}$, and the remote stress in Eq. (5)$_1$ reduces to the linear distribution, $\sigma _1^{\infty }(y)= \Sigma _1 (1 +yD_2/(\eta _1 (D_1h_2 + D_2h_1)) )$. The corresponding average energy release rate for unit advance of a channelling crack $G_{c,\Sigma }$ is expressed as

$$\begin{aligned} G_{c,\Sigma } = \frac{\Delta W_\Sigma }{h_1 +2\ell } ~. \end{aligned}$$

(21)

The critical remote stress for steady-state channelling, $\Sigma _{1} = \Sigma _{c},$ is obtained by combining Eqs. (21) and (20), and by assuming that the energy drop $\Delta W_{\Sigma }$ is related to the mode I toughness $\Gamma _{I}$ and the delamination toughness $\Gamma _{d}$ in a similar manner to that given in (17), such that

$$\begin{aligned} \Sigma _{c} = \left( \frac{2\bar{E}_1\left( \Gamma _{I}h_1 + 2 \Gamma _{d}\ell \right) }{h_1^2 \, g \left( {\ell }/{h_1},{\bar{E}_2}/{\bar{E}_1},{\bar{\beta }_2}/{\bar{\beta }_1},{D_2}/ {D_1}\right) } \right) ^{\frac{1}{2}}~. \end{aligned}$$

(22)

Consider finally the energy drop contribution $\Delta W_{{\bar{\sigma }\Sigma }}$ in Eq. (11) that is associated with the coupling between the constant and linear parts of the stress field. From dimensional considerations, the corresponding displacement $\bar{D}_{\bar{\sigma }}$ defined by relation (13)$_3$ can be written in the form

$$\begin{aligned} \bar{D}_{\bar{\sigma }} = \frac{h_1 \bar{\sigma }_1}{\bar{E}_1} k \left( \frac{\ell }{h_1}, \frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1},\frac{D_2}{D_1}\right) ~. \end{aligned}$$

(23)

Here, k is a dimensionless function that depends upon the aspect ratio of the crack $\ell /h_1$, the stiffness mismatch $\bar{E}_2/\bar{E}_1$, the mismatch in hygroexpansion coefficient $\bar{\beta }_2/\bar{\beta }_1$ and the ratio between the moisture diffusion coefficients ${D_2}/{D_1}$. Substituting Eq. (23) into Eq. (12)$_3$, the energy drop $\Delta W_{{\bar{\sigma }\Sigma }}$ follows as

$$\begin{aligned} \Delta W_{{\bar{\sigma }\Sigma }}= \frac{ \Sigma _1\bar{\sigma }_1}{\bar{E}_1}h_1^2 k \left( \frac{\ell }{h_1},\frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1}, \frac{D_2}{D_1}\right) ~. \end{aligned}$$

(24)

The remote channelling stress $\sigma ^{\infty }_c(y)$ associated with the general moisture content profile as given by (1) can be computed from the total energy drop $\Delta W$ in Eq. (11) for the doubly deflected crack, such that

$$\begin{aligned} \Delta W = G_c (h_1 +2\ell ) =\Gamma _{I}h_1 + 2 \Gamma _{d}\ell ~, \end{aligned}$$

(25)

where $G_c$ is the average energy release rate for crack channelling. Inserting the energy components $\Delta W_{\bar{\sigma }}, \Delta W_{\Sigma }$ and $\Delta W_{{\bar{\sigma }\Sigma }}$ as given by Eqs. (15), (20) and (24), respectively, into Eq. (11), and combining the result with Eq. (25), leads to the general result

$$\begin{aligned} \Gamma _{I}h_1 + 2 \Gamma _{d}\ell = \frac{ \bar{\sigma }_1^2}{2\bar{E}_1}h_1^2 f +\frac{ \Sigma _1^2}{2\bar{E}_1}h_1^2 g + \frac{ \Sigma _1\bar{\sigma }_1}{\bar{E}_1}h_1^2 k ~. \end{aligned}$$

(26)

The above relation gives a failure locus in $\bar{\sigma }_1$ versus $\Sigma _1$ space for any assumed delamination length $\ell$. In order to determine the operative mechanism 1, 2 or 3 of Fig. 3, assume that $\bar{\sigma }_1$ is specified, and solve (26) for $\Sigma _1$ as a function of $\ell$. If $\Sigma _1$ is smallest for $\ell =0$ then mechanism 1 operates, if $\Sigma _1$ is smallest for a finite but non-vanishing value of $\ell$ then mechanism 2 operates and if $\Sigma _1$ is smallest for $\ell \rightarrow \infty$ then mechanism 3 operates. In particular, to calculate $\Sigma _1$ from relation (26), first write $\bar{\sigma }_c$ as the uniform remote stress $\bar{\sigma }_1$ for steady-state channelling such that $\Sigma _1 =0$, recall (18). Next, assume that $\bar{\sigma }_1$ is prescribed as $\bar{\sigma }_1 = \alpha \bar{\sigma }_c$, where the weighting factor $\alpha$ lies within the range $0 \le \alpha \le 1$. Since the sign of $\bar{\sigma }_c$ is positive, the range chosen for $\alpha$ ensures that the uniform remote stress $\bar{\sigma }_1$ corresponds to a tensile stress, consistent with condition (7) that enables mode I crack development in the coating. The quadratic equation (26) is then solved for $\Sigma _1$, giving a positive and a negative solution for the corresponding remote stress measure for steady-state crack channelling. In accordance with condition (8)$_1$, the positive solution is assumed for the critical channelling stress, $\Sigma _1= \Sigma _c^\alpha$. Then, upon substituting $\bar{\sigma }_1 = \alpha \bar{\sigma }_c$ and $\Sigma _1=\Sigma _c^\alpha$ into Eqs. (6)$_1$ and (6)$_2$, the critical moisture content values $\Delta m_1$ and $\Delta m_2$ at the top and bottom surfaces of the system are determined, and the corresponding moisture profile for steady-state crack channelling via Eq. (1), for the assumed value of $\ell$. Furthermore, the selected value for $\alpha \bar{\sigma }_c$ and the associated value of $\Sigma _c^\alpha$ can be substituted into Eq. (5)$_1$ in order to obtain the remote stress profile for crack channelling, $\sigma _c^{\infty , \alpha }(y)$. Note that the limit $\alpha =1$ results in the uniform remote channelling stress, $\sigma _c^{\infty , \alpha } (y) = \bar{\sigma }_c$, with $\bar{\sigma }_c$ given by Eq. (18), and the limit $\alpha =0$ leads to the linear remote channelling stress, $\sigma _c^{\infty , \alpha }(y) = \Sigma _c (1+{y D_2}/({ \eta _1(D_1h_2+D_2 h_1))})$, with $\Sigma _c$ following from (22).

3.2 Plane-strain crack with a finite delamination length

In addition to analysing the problem of crack channelling with a finite delamination length, it is of interest to consider delamination growth from the tip of a plane-strain crack that exists across the thickness of the coating, recall Fig.  4. The plane-strain crack problem is closely related to the channelling problem, and helps in the identification of mechanisms 1, 2 or 3 for crack channelling. The details are as follows.

First, characterize the plane-strain delamination crack between two elastic isotropic but dissimilar materials, by introducing the Dundurs’ parameters A and B that quantify the elastic mismatch between the two solids (Dundurs 1969). They are defined by

$$\begin{aligned} A= & {} \displaystyle { \frac{\bar{E}_1 - \bar{E}_2}{\bar{E}_1 + \bar{E}_2}} ~,\nonumber \\ B= & {} \displaystyle {\frac{1}{2} \frac{(1-2\nu _2)/G_2 - (1-2\nu _1)/G_1 }{(1-\nu _2)/G_2 + (1-\nu _1)/G_1 }} ~, \end{aligned}$$

(27)

where $G_j = E_j/(2(1+\nu _j))$ is the shear modulus of layer j. In general, the singular stress field at the tip of an interfacial crack is characterized by a complex stress intensity factor $K=K_1 +i K_2$, with $i = \sqrt{-1}$ and $K_1, K_2$ the real and the imaginary parts of the stress intensity factor, respectively. The singular normal $\sigma _{yy}$ and shear $\sigma _{xy}$ stress components at a distance r from the tip in the asymptotic limit read (Hutchinson et al. 1987; Rice 1988)

$$\begin{aligned} \sigma _{yy} + i \sigma _{xy} = \frac{K}{\sqrt{2\pi r}}r^{i \epsilon }~, \end{aligned}$$

(28)

where $r =e^{i\epsilon \mathrm {ln} r} = \cos (\epsilon \mathrm {ln}r) + i \sin (\epsilon \mathrm {ln}r)$, and the oscillatory index $\epsilon$ is defined as

$$\begin{aligned} \epsilon = \frac{1}{2\pi } \mathrm {ln}\left( \frac{1-B}{1+B}\right) ~, \end{aligned}$$

(29)

in terms of the second Dundurs’ parameter B as introduced in Eq. (27)$_2$. The phase angle $\Psi$ is directly related to the ratio of shear stress to normal stress on the crack plane immediately ahead of the crack tip, as follows. This ratio is dependent on the distance r from the tip, and consequently it is necessary to evaluate the mode-mix at an arbitrary, but specified, reference length $\hat{l}$, ahead of the crack tip. As a consequence of the oscillatory stress behaviour at the tip of an interfacial crack between two dissimilar solids, the classical definition of the mode-mix is extended to the form (Rice 1988)

$$\begin{aligned} \tan (\Psi ) = \frac{\sigma _{xy} (r = \hat{l})}{\sigma _{yy} (r = \hat{l})} =\frac{\mathrm {Im}(K \hat{l}^{i\varepsilon })}{\mathrm {Re} (K \hat{l}^{i\varepsilon })} ~. \end{aligned}$$

(30)

The choice of the reference length $\hat{l}$ has only a minor effect on the value of the angle $\Psi$ for commonly encountered values of the oscillatory index, $|\epsilon | \ll 1$ (Rice 1988).

The plane-strain energy release rate per unit advance of delamination along a bi-material interface is given by (Hutchinson and Suo 1992)

$$\begin{aligned} G_d = \frac{1 - B^2}{E_*}\left( K_1^2 + K_2^2\right) ~, \end{aligned}$$

(31)

where $E_*= 2(\bar{E}_1^{-1} + \bar{E}_2^{-1})^{-1}$. Delamination will occur when the energy release rate as defined in (31) equals the delamination toughness at the appropriate mode-mix $\Gamma _{d}(\Psi (\hat{l}))$, i.e.,

$$\begin{aligned} G_d = \Gamma _{d}(\Psi (\hat{l}))~. \end{aligned}$$

(32)

The plane-strain energy release rate for delamination can be further related to the energy drop $\Delta W$, given by relation (9). For the doubly deflected crack sketched in Fig. 4, the energy release rate for each delamination can be calculated as

$$\begin{aligned} G_d = \frac{1}{2}\frac{\partial \Delta W}{\partial \ell }~, \end{aligned}$$

(33)

where the factor of 2 is due to the fact that there are two delamination tips. Similar to the decomposition of the energy drop $\Delta W$ as given by Eq. (11), the energy release rate may be decomposed into

$$\begin{aligned} G_d = G_{d,{\bar{\sigma }}} + G_{d,{\Sigma }} + G_{d,{{\bar{\sigma }\Sigma }}} ~. \end{aligned}$$

(34)

Upon inserting expression (15) into (33), the first term in the right-hand side of Eq. (34) becomes

$$\begin{aligned} G_{d,{\bar{\sigma }}} = \frac{1}{2}\frac{\partial \Delta W_{\bar{\sigma }}}{\partial \ell } =\frac{ \bar{\sigma }_1^2}{4\bar{E}_1}h_1 f' \left( \frac{\ell }{h_1},\frac{\bar{E}_2}{\bar{E}_1}, \frac{\bar{\beta }_2}{\bar{\beta }_1},\frac{D_2}{D_1}\right) ~, \end{aligned}$$

(35)

with $f'$ representing the partial derivative $f' = \partial f / \partial \ell$. Hence, if the coating-substrate system is subjected to a uniform moisture content with $\Delta m(y) ~ =\Delta m_1 =\Delta m_2$, then it follows from Eq. (34) that $G_d = G_{d,{\bar{\sigma }}}$, so that the critical remote stress for plane-strain delamination, $\bar{\sigma }_1 = \bar{\sigma }_d$, is obtained by combining Eq. (32) with Eq. (35), to give

$$\begin{aligned} \bar{\sigma }_{d} = \left( \frac{4\bar{E}_1 \Gamma _{d}}{h_1 f' \left( \ell / h_1, \bar{E}_2 / \bar{E}_1, \bar{\beta }_ / \bar{\beta }_1 , {D_2}/{D_1}\right) }\right) ^{\frac{1}{2}} ~. \end{aligned}$$

(36)

In an analogous fashion, the energy release rate per unit advance of delamination $G_{d,\Sigma }$, which is related to the stress measure $\Sigma _1$, is derived from expression (20), such that

$$\begin{aligned} G_{d,\Sigma } = \frac{1}{2}\frac{\partial \Delta W_\Sigma }{\partial \ell } =\frac{ \Sigma _1^2}{4\bar{E}_1}h_1 \, g' \left( \frac{\ell }{h_1}, \frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1},\frac{D_2}{D_1}\right) ~, \end{aligned}$$

(37)

where $g'$ represents the partial derivative $g' = \partial g / \partial \ell$. Accordingly, in the case of a linear moisture content profile of vanishing value at the coating-substrate interface, $\Delta m(y) = y {D_2(\Delta m_1- \Delta m_2)}/{(D_1h_2 + D_2 h_1)}$, the energy release rate for plane-strain delamination follows from relation (34) as $G_d = G_{d,\Sigma }$. Now combine Eq. (32) with Eq. (37); then, the critical remote stress for delamination, $\Sigma _1 = \Sigma _d$, follows as

$$\begin{aligned} \Sigma _{d} = \left( \frac{4\bar{E}_1 \Gamma _d}{h_1 \, g' \left( \ell / h_1, \bar{E}_2 / \bar{E}_1, \bar{\beta }_2 / \bar{\beta }_1 , {D_2}/{D_1} \right) }\right) ^{\frac{1}{2}} ~. \end{aligned}$$

(38)

Consider finally the energy drop $\Delta W_{{\bar{\sigma }\Sigma }}$ associated with the coupling between the constant and the linear parts of the stress field, as given by Eq. (24). The corresponding energy release rate $G_{d,{{\bar{\sigma }\Sigma }}}$ for plane-strain delamination is computed as

$$\begin{aligned} G_{d,{{\bar{\sigma }\Sigma }}} = \frac{1}{2}\frac{\partial \Delta W_{{\bar{\sigma }\Sigma }}}{\partial \ell } =\frac{\bar{\sigma }_1\Sigma _1}{2\bar{E}_1}h_1 \, k' \left( \frac{\ell }{h_1}, \frac{\bar{E}_2}{\bar{E}_1},\frac{\bar{\beta }_2}{\bar{\beta }_1}, \frac{D_2}{D_1}\right) ~, \end{aligned}$$

(39)

in terms of the partial derivative $k' = \partial k / \partial \ell$. Substituting expressions (35), (37) and (39) into relation (34) then leads to the energy release rate for plane-strain delamination under the arbitrarily linear moisture content profile given by relation (1). Now equate this value of energy release rate to the delamination toughness, upon recalling Eq. (32), to obtain

$$\begin{aligned} \Gamma _{d} = \frac{ \bar{\sigma }_1^2}{4\bar{E}_1}h_1 f' +\frac{ \Sigma _1^2}{4\bar{E}_1}h_1 g' + \frac{ \bar{\sigma }_1\Sigma _1}{2\bar{E}_1}h_1 k' ~. \end{aligned}$$

(40)

The remote delamination stress under the moisture content profile (1)$_1$ is finally found in a similar way to that demonstrated at the end of Sect. 3.1 for the channelling stress. Relation (40) represents a failure locus in $\bar{\sigma }_1$ versus $\Sigma _1$ space. It is assumed that $\bar{\sigma }_1$ is specified, and Eq. (40) is solved with respect to $\Sigma _1$. In particular, first take $\bar{\sigma }_d$ as the uniform remote stress $\bar{\sigma }_1$ for plane-strain delamination, with $\Sigma _1 =0$, in accordance with (36). Next, the value of $\bar{\sigma }_1$ is prescribed as $\bar{\sigma }_1 = \alpha \bar{\sigma }_d$, with $\alpha$ a weighting factor in the range $0 \le \alpha \le 1$. The positive sign of $\bar{\sigma }_d$, along with the selected range for $\alpha$, guarantees that the uniform remote stress $\bar{\sigma }_1$ is tensile, in accordance with condition (7). Further, Eq. (40) is solved for $\Sigma _1$, providing a positive and a negative solution for the corresponding remote stress for plane-strain delamination. The positive solution is taken as the critical delamination stress, $\Sigma _1= \Sigma _d^\alpha$, consistent with requirement (8)$_1$. Next, the critical moisture content values $\Delta m_1$ and $\Delta m_2$ at the top and bottom surfaces of the system can be determined, by inserting $\bar{\sigma }_1 = \alpha \bar{\sigma }_d$ and $\Sigma _1=\Sigma _d^\alpha$ into Eqs. (6)$_1$ and (6)$_2$. Using the values of $\Delta m_1$ and $\Delta m_2$, the corresponding moisture profile for plane-strain delamination can be calculated through Eq. (1). Finally, by substituting into Eq. (5)$_1$ the assumed value for $\alpha \bar{\sigma }_d$ and the corresponding value of $\Sigma _d^\alpha$, the remote stress distribution for plane-strain delamination $\sigma _d^{\infty , \alpha }(y)$ can be determined. Analogous to the mechanism of crack channelling, for $\alpha = 1$ the remote delamination stress becomes uniform, $\sigma _d^{\infty , \alpha }(y) = \bar{\sigma }_d$, with $\bar{\sigma }_d$ in accordance with (36), whereas for $\alpha = 0$ it reduces to the linear stress profile $\sigma _d^{\infty , \alpha }(y) = \Sigma _d (1 + yD_2/(\eta _1(D_1h_2 + D_2 h_1)))$, with $\Sigma _d$ given by Eq. (38).

3.3 Unlimited delamination

When the delamination length exceeds the thickness of the coating, $\ell / h_1 > 1$, the energy release rate for delamination typically approaches an asymptotic steady-state value, $G_{d,ss} = G_d(\ell / h_1 \rightarrow \infty )$, see also Hutchinson and Suo (1992), Freund and Suresh (2004), Suiker and Fleck (2004), Forschelen et al. (2016). This value can be derived analytically by computing the difference in the elastic strain energy downstream and upstream of the delamination tip. For this purpose, the geometry depicted in Fig. 4 is considered, whereby the system is subjected to the arbitrarily linear moisture content profile (1). Recall that the remote stresses $\sigma _1^{\infty } (y)$ and $\sigma _2^{\infty } (y)$, as specified by (5)$_1$ and (5)$_2$, respectively, have been computed via relations (2)$_1$ and (2)$_2$ in combination with force equilibrium of the intact, upstream cross-section via Eq. (3). In a similar fashion, force equilibrium at the fractured, down-stream cross-section $x = 0$ may be expressed as

$$\begin{aligned} \int _{-h_2}^{0} \sigma _2^0(y)\mathrm {d}y = 0 ~, \end{aligned}$$

(41)

where, in correspondence with Eq. (2)$_2$, the stress $\sigma _2^0(y) = \sigma _2(x=0,y)$ is evaluated at $x=0$. Inserting the moisture content profile (1)$_2$ into the constitutive relation (2)$_2$, and substituting the result into relation (41) allows one to solve for the strain $\varepsilon _2(x=0,y)$. Substituting this result back into Eq. (2)$_2$ yields for the stress $\sigma _2^0$:

$$\begin{aligned} \sigma _2^0(y) = -\Sigma _2 \frac{D_1(h_2+2y)}{2\eta _2 (D_1 h_2 + D_2 h_1) } ~. \end{aligned}$$

(42)

Note that $\sigma _2^0$ is described solely by the stress contribution associated with the linear moisture content variation in the substrate, and the contribution from the uniform moisture content variation vanishes, i.e., $\bar{\sigma }_2^0 = 0$.

The steady-state energy release rate at an individual delamination tip can be obtained from the difference between the energies upstream and downstream of the delamination tip, i.e.,

$$\begin{aligned} G_{d,ss}= & {} \frac{1}{2}\int _{0}^{h_1} \sigma ^{\infty }_1(y) \varepsilon _1^{e,\infty }(y)\mathrm {d}y \nonumber \\&+\frac{1}{2}\int _{-h_2}^{0} \sigma ^{\infty }_2(y)\varepsilon _2^{e,\infty }(y)\mathrm {d}y\nonumber \\&-\frac{1}{2}\int _{-h_2}^{0} \sigma _2^{0}(y)\varepsilon _2^{e,0}(y)\mathrm {d}y~, \end{aligned}$$

(43)

with $\varepsilon _i^{e,\infty }(y)$ the remote, upstream elastic strain of layer i and $\varepsilon _2^{e,0}(y)$ the downstream elastic strain in the substrate. Now insert expressions (5)$_1$, (5)$_2$ and (42) for the upstream and downstream stresses into (43), and invoke the constitutive relation $\sigma _i = \bar{E}_i \varepsilon _i^e$ with $i \in \{1,2\}$, to obtain

$$\begin{aligned} G_{d,ss} = G_{ss,{\bar{\sigma }}} + G_{ss,\Sigma } + G_{ss, {{\bar{\sigma }\Sigma }}} ~, \end{aligned}$$

(44)

where

$$\begin{aligned} G_{ss,{\bar{\sigma }}}= & {} \displaystyle {\frac{1}{2} \frac{\bar{\sigma }_1^2 h_1}{\bar{E}_1 } \left( 1+\frac{\bar{E}_1}{\bar{E}_2}\frac{h_1}{h_2}\right) }~,\nonumber \\ G_{ss,\Sigma }= & {} \displaystyle \frac{1}{2} \frac{\Sigma _1^2 h_1}{\bar{E}_1} \left[ 1 +\frac{D_2h_1}{ \eta _1 (D_1h_2 + D_2h_1)} \right. \nonumber \\&+\, \frac{D_2^2h_1^2}{3 \eta _1^2 (D_1h_2 + D_2h_1)^2} \nonumber \\&+\, \displaystyle \frac{\bar{E}_2 h_2}{\bar{E}_1h_1} \left( 1 -\frac{D_1h_2}{ \eta _2 (D_1h_2 + D_2h_1)}\right. \nonumber \\&\left. \left. +\,\frac{D_1^2h_2^2}{4\eta _2^2 (D_1h_2 + D_2h_1)^2 }\right) \right] ~,\nonumber \\ G_{ss,{{\bar{\sigma }\Sigma }}}= & {} - \displaystyle \frac{\bar{\sigma }_1 \Sigma _1 h_1}{\bar{E}_1} \left[ \frac{D_2h_1}{\eta _1 (D_1h_2 + D_2h_1)}\right. \nonumber \\&\left. +\, \frac{D_1h_2}{\eta _2 (D_1h_2 + D_2h_1)}\right] ~. \end{aligned}$$

(45)

Here, the sub-index “d” has been dropped in the above energy release rate, as the steady-state value is representative of both plane-strain delamination and crack channelling, i.e., $G_{ss} = G_{d}(\ell / h_1 \rightarrow \infty ) = G_{c}(\ell / h_1 \rightarrow \infty )$. Specifically, the equality between the crack channelling and delamination energy release rates occurs at any point of the $G_{c}$ versus $\ell / h_1$ curve for which $\partial G_{c} /\partial \ell = 0$ (Beuth 1992; Fleck and Zhao 2000; Suiker and Fleck 2004). It will be demonstrated in Sect. 4 that the finite element results confirm this condition when $\ell / h_1 \rightarrow \infty$.

During unlimited delamination the energy release rate equals the delamination toughness $\Gamma _{d}$ at the appropriate mode-mix, see Eq. (32). Upon substituting expression (45)$_1$ into relation (32) allows to solve for the steady-state stress value $\bar{\sigma }_{ss} = \bar{\sigma }_{d}(\ell / h_1 \rightarrow \infty ) = \bar{\sigma }_{c}(\ell / h_1 \rightarrow \infty )$ corresponding to a uniform moisture content profile $\Delta m(y) ~(=\Delta m_1 =\Delta m_2 )$, with $\Sigma _{1} =0$. Similarly, substituting expression (45)$_2$ into (32) leads to the steady-state stress $\Sigma _{ss} = \Sigma _{d}(\ell / h_1 \rightarrow \infty ) = \Sigma _{c}(\ell / h_1 \rightarrow \infty )$ associated with a linear moisture content profile, $\Delta m(y) =(\Delta m_1 - \Delta m_2) D_2 y/(D_1h_2 + D_2h_1)$, where $\bar{\sigma }_{1} =0$. Hence, the expressions for the stresses $\bar{\sigma }_{ss}$ and $\Sigma _{ss}$ in the coating are

$$\begin{aligned} \bar{\sigma }_{ss}= & {} \left( 2\bar{E}_1 \Gamma _{d}\right) ^{\frac{1}{2}} \left[ h_1\left( 1+ \displaystyle {\frac{\bar{E}_1 h_1}{\bar{E}_2 h_2} } \right) \right] ^{-\frac{1}{2}} ~,\nonumber \\ \Sigma _{ss}= & {} \left( 2\bar{E}_1 \Gamma _{d}\right) ^{\frac{1}{2}} \left[ h_1\displaystyle \left[ 1 +\frac{D_2h_1}{\eta _1 (D_1h_2 + D_2h_1)}\right. \right. \nonumber \\&+\,\frac{D_2^2h_1^2}{3 \eta _1^2 (D_1h_2 + D_2h_1)^2} \nonumber \\&+\, \displaystyle \frac{\bar{E}_2 h_2}{\bar{E}_1 h_1} \left( 1 -\frac{D_1h_2 }{ \eta _2 (D_1h_2 + D_2h_1)} \right. \nonumber \\&\left. \left. \left. + \frac{D_1^2h_2^2}{4\eta _2^2 (D_1h_2 + D_2h_1)^2} \right) \right] \right] ^{-\frac{1}{2}} ~. \end{aligned}$$

(46)

with the parameters $\eta _1$ and $\eta _2$ in Eq. (45)$_2$ provided by Eqs. (6)$_3$ and (6)$_6$, respectively. Note that expression (46)$_1$ for the critical steady-state stress under a uniform moisture content distribution is independent of both the mismatch in coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$ and the mismatch in diffusion coefficient, $D_2/D_1$.

Fig. 6

Steady-state critical stress $\sigma ^{\infty , \alpha }_{ss}(0)$ in the coating versus stiffness mismatch $\bar{E}_2/\bar{E}_1$ for different weighting factors $\alpha$, see Eq. (47). The stress is computed for a bilayer system with layers of equal thickness, $h_2/h_1=1$, equal diffusion coefficient, $D_2/D_1=1$, and for a mismatch in coefficient of hygral expansion $\bar{\beta }_2/\bar{\beta }_1=10$

The remote critical steady-state stress value corresponding to an arbitrary moisture profile can be finally obtained, as follows. For a given value of $\alpha$, the contribution $\bar{\sigma }_1$ is $\bar{\sigma }_1 = \alpha \bar{\sigma }_{ss}$, and upon equating the energy release rate to the delamination toughness $\Gamma _{d}$ in (44), the steady-state stress $\Sigma _1 =\Sigma _{ss}^\alpha$ is calculated. The steady-state stress profile $\sigma _{ss}^\alpha (y)$ follows immediately as

$$\begin{aligned} \sigma _{ss}^{\infty , \alpha }(y) =\alpha \bar{\sigma }_{ss} + \Sigma _{ss}^\alpha \left( 1 + \frac{yD_2}{ \eta _1(D_1 h_2 + D_2 h_1 )}\right) ~. \end{aligned}$$

(47)

Figure 6 depicts the steady-state stress, Eq. (47), for arbitrary moisture profiles, evaluated at the interface between the coating and substrate with $y=0$, i.e. $\sigma _{ss}^{ \infty ,\alpha }(0)$, as a function of the stiffness mismatch, $\bar{E}_{2}/\bar{E}_{1}$, for a selection of weighting factors, $\alpha = [0, 0.5, 0.7, 0.9, 1]$. The stress is computed for a system characterized by equal layer thicknesses, $h_1=h_2$, by equal diffusion coefficients, $D_1=D_2$, and by a mismatch in the coefficients of hygral expansion $\bar{\beta }_2/\bar{\beta }_1=10$, in order to satisfy condition (8)$_2$. The stress is obtained from expression (47), for which the limit values $\alpha = 0$ and $\alpha =1$ respectively reduce to the linear $\sigma ^{\infty ,\alpha }_{ss}(0) = \Sigma _{ss}$ and uniform $\sigma ^{\infty , \alpha }_{ss}(0) = \bar{\sigma }_{ss}$ steady-state stress measures given in Eq. (46). It can be seen that for all values of $\alpha$ the steady-state stress grows monotonically with an increasing stiffness ratio. The response envelope is indeed provided by the cases $\alpha =0$ and $\alpha =1$, from which it is concluded that the corresponding stress measures $\bar{\sigma }_{ss}$ and $\Sigma _{ss}$ may respectively serve as lower and upper bounds in the practical design against plane-strain delamination.

4 Cracking in a bilayer system with layers of equal thickness

4.1 Geometry and modelling features

Crack channelling and plane-strain delamination are studied first for a system in which the coating and substrate have the same thickness, i.e., $h_1/h_2=1$. The stress state is analysed using the commercial finite element program ABAQUS Standard.³ Due to symmetry, only half of the domain is considered. Roller and fixed supports impose the required symmetry and prevent rigid body motions, and vertical supports at the bottom edge prevent bending of the bilayer. The geometry is taken to be sufficiently long in order for boundary effects to be negligible, in accordance with a horizontal system length equal to $200 h_1$. The fracture response has been analysed for a crack with a delamination length within the range $\ell / h_1 \in \left[ 0.015, 20\right]$. For each delamination length a different finite element mesh was used. The finite element configurations contain 2500 to 3600 plane-strain 8-nodes iso-parametric elements, equipped with $3 \times 3$ Gauss quadrature. At the delamination tip, the mid-side nodes on the crack faces are moved to the 1/4 point nearest to the crack tip, in order to represent the square root singularity of the stress field. Further, for each tip element, three neighbouring nodes are collapsed to the crack tip.

As already discussed in Sect. 2, the elastic mismatch between the coating and substrate is taken to be $\bar{E}_2/\bar{E}_1 = \left[ 0.1, 0.3, 1, 3, 10\right]$, and the Poisson’s ratio of the coating and substrate is $\nu _1 =\nu _2 =0.3$. Consequently, the Dundurs’ parameters as given by Eq. (27) take the values $A = [0.81, 0.53, 0, -0.5, -0.82]$ and $B =[0.23, 0.15, 0, -0.14, -0.23]$. The hygroexpansion coefficient mismatch is chosen as $\bar{\beta }_2/\bar{\beta }_1 =10$, and for all analyses performed the coating is fully loaded in tension. The diffusion coefficients of the layers are considered to be equal, i.e., $D_2/D_1=1$. The system is subjected to the moisture profile as given by Eq. (1), whereby the moisture content at the top surface of the system equals $\Delta m_1$ and at the bottom surface is $\Delta m_2 = 0$. Although the coating-substrate system is subjected to a specific moisture content profile, the FEM results for steady-state crack channelling and plane-strain delamination can be generalized to a wide range of critical moisture content profiles, which are obtained by varying the value of the weighting factor $\alpha$ introduced in relation to the solution of Eqs. (26) and (40), see also the discussion below.

The FEM data required for the calculation of the critical remote stresses for steady-state crack channelling and plane-strain delamination are (i) the displacement profile $\delta (y)$ of the nodes at the mode I crack faces, (ii) the energy release rate per unit advance of delamination $G_d$ at the delamination tip, which for a crack in an elastic solid equals the path-independent J-integral, $G_d=J$ (Rice 1968), and (iii) the complex stress intensity factor at the delamination tip, $K = K_1 + i K_2$. The real and imaginary parts of the stress intensity factor, $K_1$ and $K_2$, are calculated via an embedded routine within ABAQUS using an interaction integral method: the mode I and mode II stress intensity factors $K_1$ and $K_2$ are extracted from the energy release rate $G_d$ for plane-strain delamination by combining the solution of the actual crack tip field with that of an auxiliary field (Matos et al. 1989). In accordance with the modelling framework presented in Sect. 3, the critical remote stresses for steady-state crack channelling and plane-strain delamination are characterized by constant ($\bar{\sigma }_c$ and $\bar{\sigma }_d$) and linear ($\Sigma _c$ and $\Sigma _d$) stress contributions, which can be derived from two separate FEM simulations that respectively consider (i) only the constant part of a simulated moisture content profile, and (ii) the total moisture content profile. Considering a system with specific stiffness and toughness properties, first a FEM simulation is performed in which only a constant moisture content part is applied. For the moisture content profile and geometry considered, with $D_2/D_1 =1$, the value of the constant moisture content follows from Eq. (1) as $\Delta m = \Delta m(0) = \Delta m_1/2$. The constant moisture content induces a constant remote stress in the coating, $\sigma _1^{\infty }(y)=\bar{\sigma }_{1}$, and in the substrate, $\sigma _2^{\infty }(y) =\bar{\sigma }_{2}$, see Eq. (5). The generated displacements $\delta _{\bar{\sigma }}(y)$ of the mode I crack faces provide the average crack opening displacement $\bar{\delta }_{\bar{\sigma }}$ via relation (13)$_1$, and its non-dimensional value f by means of Eq. (14). Subsequently, the drop in strain energy $\Delta W_{\bar{\sigma }}$ follows from Eq. (12)$_1$, and this is substituted into (16) to give the energy release rate $G_{c,{\bar{\sigma }}}$ for steady-state crack channelling. The function f further results in the constant remote stress $\bar{\sigma }_{c}$ for crack channelling via Eq. (18). In addition, the J-integral leads to the energy release rate for plane-strain delamination, $G_{d,{\bar{\sigma }}}=J$, and thereby to the derivative $f'$ through relation (35). The constant remote stress $\bar{\sigma }_d$ for plane-strain delamination follows from Eq. (36).

As a next step, the same coating-substrate system is subjected to the total moisture content profile, which, for the moisture content profile and geometry considered, with $D_2/D_1 =1$, follows from Eq. (1) as $\Delta m(y)=\Delta {m}_1/2 + \Delta {m}_1 \, y/h$. The mode I crack opening displacement $\delta (y)$ calculated for the total moisture content profile is combined in Eq. (10) with the displacement function $\delta _{\bar{\sigma }}(y)$ for a constant moisture content to obtain the mode I crack opening displacement under the linear moisture content profile, $\delta _\Sigma (y) = \delta (y) -\delta _{\bar{\sigma }}(y)$. Subsequently, the average crack opening displacement parameters $\bar{D}_\Sigma$ and $\bar{D}_{\bar{\sigma }}$ related to the linear and constant moisture contributions are calculated from Eqs. (13)$_2$ and (13)$_3$, and the non-dimensional values g and k are thereby obtained via relations (19) and (23), respectively. The corresponding drops in elastic energy, $\Delta W_\Sigma$ and $\Delta W_{{\bar{\sigma }\Sigma }}$, result from Eqs. (12)$_2$ and (12)$_3$, respectively, and consequently the total drop in elastic energy $\Delta W$ is determined via (11), and the energy release rate $G_{c,\Sigma }$ per unit advance of steady-state crack channelling through (21). Subsequently, by choosing a value for $\alpha$, the fraction of the constant channelling stress experienced by the coating becomes $\bar{\sigma }_1=\alpha \bar{\sigma }_{c}$. This stress value is inserted into (26) to give the corresponding linear stress measure for crack channelling, $\Sigma _1 = \Sigma _c^\alpha$, which via (5)$_1$ leads to the total stress for steady-state crack channelling, $\sigma _c^{\infty ,\alpha }(y)$.

Furthermore, the energy release rate for plane-strain delamination generated under the total moisture content profile is obtained from the J-integral as $G_{d}=J$. From the corresponding values of the mode I and mode II stress intensity factors at the delamination tip, $K_1$ and $K_2$, the stress intensity factors $K_{1,\Sigma }$ and $K_{2,\Sigma }$ due to a linear moisture content profile are calculated as

$$\begin{aligned} K_{1,\Sigma }= & {} K_{1} - K_{1,\bar{\sigma }}~, \nonumber \\ K_{2,\Sigma }= & {} K_{2} - K_{2,\bar{\sigma }}~, \end{aligned}$$

(48)

where $K_{1,\bar{\sigma }}$ and $K_{2,\bar{\sigma }}$ are the delamination stress intensity factors for a constant moisture content profile. The values of $K_{1,\Sigma }$ and $K_{2,\Sigma }$ are inserted into Eq. (31) to give the delamination energy release rate $G_{d,\Sigma }$ under a linear moisture content profile. In accordance with (34), the coupling term for the delamination energy release rate can now be calculated as $G_{d,{{\bar{\sigma }\Sigma }}} =G_d-G_{d,{\bar{\sigma }}}-G_{d,\Sigma }$, and the corresponding derivative $k'$ follows from Eq. (39). The value chosen for $\alpha$ specifies the fraction of the constant delamination stress present in the coating, $\bar{\sigma }_1=\alpha \bar{\sigma }_d$, which, after substitution into (40), leads to the critical linear stress measure for plane-strain delamination, $\Sigma _1 =\Sigma _d^\alpha$. The total stress for plane-strain delamination, $\sigma _d^{\infty , \alpha }(y)$, is obtained from Eq. (5)$_1$.

Fig. 7

Cracking in a bilayer system with layers of equal thickness ($h_2/h_1=1$). a Mode-mix $\Psi _{\bar{\sigma }}=\mathrm {atan} (\mathrm {Im}(\mathrm{K}_{\bar{\sigma }} \mathrm{h}_1^{i \epsilon })/\mathrm {Re(K}_{\bar{\sigma }} \mathrm{h}_1^{i \epsilon }))$ as a function of the delamination length $\ell /h_1$, for a constant moisture content profile. The results are independent of the mismatch in coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$. Energy release rate for b plane-strain delamination $G_{d,{\bar{\sigma }}}$, Eq. (35), and c steady-state crack channelling $G_{c,{\bar{\sigma }}}$, Eq. (16), as a function of the delamination length $\ell /h_1$, for a constant moisture content profile. The normalized results are independent of the mismatch in coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$, and mismatch in diffusion coefficient $D_2/D_1$. The depicted steady-state values $G_{ss,\bar{\sigma }}$ are computed with Eq. (45)$_1$

As pointed out above, the value of $\alpha$ specifies the relative contributions of the constant and linear remote stress measures $\bar{\sigma }_1$ and $\Sigma _1$ to the activation of steady-state crack channelling and plane-strain delamination. For any given value of $\alpha$, the critical moisture contents $\Delta m_1$ and $\Delta m_2$ for steady-state crack channelling and plane-strain delamination at the top and bottom surfaces of the coating-substrate system can be obtained from the corresponding constant and linear stress measures via relations (6)$_1$ and (6)$_2$. By varying the factor $\alpha$ in the range $0\le \alpha \le 1$, the two FEM simulation results above thus provide a family of critical linear moisture content profiles for both steady-state crack channelling and plane-strain delamination, with the limit value $\alpha =1$ reflecting the uniform moisture content distribution and $\alpha =0$ representing the linear moisture content distribution with a vanishing value at the coating-substrate interface.

4.2 Cracking due to a uniform moisture content distribution ($\alpha =~1$)

For the coating-substrate system described in Sect. 4.1, the failure mechanisms of steady-state crack channelling and plane-strain delamination are first examined for a uniform moisture content distribution, $\Delta m(y) = \Delta m_1 = \Delta m_2$. Accordingly, the weighting factor $\alpha$ is set to unity, $\alpha =1$: the remote stresses for crack channelling and plane-strain delamination are uniform, such that $\sigma _c^{\infty , \alpha }(y) = \bar{\sigma }_c$ and $\sigma _d^{\infty , \alpha }(y) = \bar{\sigma }_d$. All numerical results will be presented using appropriate dimensionless parameters. For the case of a uniform moisture content contribution, the obtained mode-mix and critical stresses turn out to be independent of both the mismatch in the coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$, and the mismatch in diffusion coefficient, $D_2/D_1$. The normalization selected for the energy release rates makes these results also independent of the hygroscopic coefficient mismatch, $\bar{\beta }_2/\bar{\beta }_1$, and diffusion coefficient mismatch, $D_2/D_1$.

4.2.1 Mode-mix and energy release rate

For the considered configuration, the mode-mix $\Psi _{\bar{\sigma }}$ associated with a uniform moisture content is illustrated in Fig. 7a as a function of the relative delamination length $\ell / h_1$, for selected values of the stiffness mismatch $\bar{E}_2/\bar{E}_1$. In correspondence with Eq. (30), the phase angle of mode-mix is calculated as $\Psi _{\bar{\sigma }} = \mathrm {atan}({\mathrm {Im(K}_{\bar{\sigma }}} {\hat{l}^{i \epsilon })}/{\mathrm {Re(K}_{\bar{\sigma }} \hat{l}^{i \epsilon })})$, where the complex stress intensity factor $K_{\bar{\sigma }}$ is defined by $K_{\bar{\sigma }} = K_{1,\bar{\sigma }}+i K_{2,\bar{\sigma }}$, in terms of the mode I and mode II stress intensity factors for interfacial delamination, $K_{1,\bar{\sigma }}$ and $K_{2,\bar{\sigma }}$, respectively. The reference length at which the mode-mix is evaluated is set equal to the thickness of the coating, $\hat{l} =h_1$. For all stiffness mismatches considered, the mode-mix $\Psi _{\bar{\sigma }}$ varies over a relatively small range, and a steady-state value is attained when the delamination length approaches the coating thickness, i.e., when $\ell /h_1 \ge 0.8$. The values of the phase angle at steady-state lies within the range $52^ \circ$ to $57^ \circ$. The evolution of the mode-mix with delamination length is comparable to that computed in Suiker and Fleck (2004) for a doubly deflected crack generated under a remote tensile stress in the two outer layers of a layered solid, see Figure 16a in Suiker and Fleck (2004).

Fig. 8

Crack channelling and plane-strain delamination in a bilayer system with layers of equal thickness ($h_2/h_1=1$). Remote stress $\bar{\sigma }_1$ versus delamination length $\ell /h_1$ for a constant moisture content profile, considering a stiffness mismatch of a $\bar{E}_2/\bar{E}_1 = 0.1$, b $\bar{E}_2/\bar{E}_1 =1$ and c $\bar{E}_2/\bar{E}_1 =10$. The dark blue lines represent the crack channelling stress $\bar{\sigma }_1 = \bar{\sigma }_c$ for selected toughness ratios $\Gamma _{d}/\Gamma _{I}$. The light blue line reflects the plane-strain delamination stress $\bar{\sigma }_1 =\bar{\sigma }_d$. The results are independent of the mismatch in coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$, and the mismatch in diffusion coefficient, $D_2/D_1$. The depicted steady-state value $\bar{\sigma }_{ss}$ is computed with Eq. (46)$_1$

Figure 7b, c depict the energy release rates for plane-strain delamination $G_{d,\bar{\sigma }}$ and steady-state crack channelling $G_{c,\bar{\sigma }}$, respectively, as a function of the delamination length $\ell /h_1$, generated under a constant moisture content. The energy release rate for plane-strain delamination is strongly sensitive to the delamination length for $\ell /h_1<1$, whereby in the asymptotic limit $\ell /h_1 \rightarrow 0$ it becomes equal to zero for stiffness mismatches $\bar{E}_2/\bar{E}_1<1$, and goes to infinity for $\bar{E}_2/\bar{E}_1>1$. This behaviour has also been reported in other studies on interfacial delamination (He and Hutchinson 1989b; Ye et al. 1992; Lu 1996; Suiker and Fleck 2004). For $\bar{E}_2/\bar{E}_1=1$ the energy release rate at zero delamination is finite, and is slightly less than the corresponding value for a doubly-deflected crack in the two outer layers of a multi-layered solid (Suiker and Fleck 2004). For $l/h_1>1$ the energy release rate $G_{d,\bar{\sigma }}$ for plane-strain delamination has almost attained a steady state, and the values for the range of stiffness mismatches are in close agreement with the analytical steady-state energy release rate, $G_{ss,\bar{\sigma }} = G_{d,\bar{\sigma }} (l/h_1 \rightarrow \infty )$, as given by Eq. (45)$_1$.

The energy release rate $G_{c,\bar{\sigma }}$ for crack channelling, shown in Fig. 7c, decreases monotonically with increasing delamination length $\ell / h_1$ for all values of stiffness mismatch $\bar{E}_2/\bar{E}_1$. Compared to the energy release rate for plane-strain delamination, the steady-state energy release rate $G_{ss,\bar{\sigma }}$ is reached at a substantially larger delamination length. Moreover, the steady-state value is reached at a smaller delamination length with increasing stiffness mismatch $\bar{E}_2/\bar{E}_1$. These two features have also been observed for the crack tunnelling mechanisms studied in Suiker and Fleck (2004).

4.2.2 Failure mechanisms

The crack channelling stress $\bar{\sigma }_{c}$ and plane-strain delamination stress $\bar{\sigma }_{d}$ associated with a uniform moisture content profile in the coating-substrate system are shown in dimensionless form in Fig. 8 as a function of delamination length $\ell /h_1$. Figures 8a–c contain the numerical results for stiffness mismatches $\bar{E}_2/\bar{E}_1 = 0.1$, $\bar{E}_2/\bar{E}_1 = 1$ and $\bar{E}_2/\bar{E}_1 = 10$, respectively. The channelling stress $\bar{\sigma }_{c}$ has been computed using Eq. (18) and is indicated by the dark blue lines for a selection of toughness ratios $\Gamma _{d}/\Gamma _{I} = \left[ 0.05, 0.1, 0.2, 0.5, 1, 10 \right]$.

Although the delamination toughness $\Gamma _{d}$ is, in principle, a function of the mode-mix $\Psi _{\bar{\sigma }}$, for the calculation of the channelling stress $\bar{\sigma }_{c}$ a constant delamination toughness is assumed. This assumption is reasonable since the mode-mix typically has only a small variation and reaches a steady-state value at relatively short delamination length, $\ell /h_1 \approx 0.8$, see Fig. 7a. Since the stresses are normalized with respect to the delamination toughness $\Gamma _{d}$, a channelling stress $\bar{\sigma }_{c}$ associated with a larger toughness ratio $\Gamma _{d}/\Gamma _{I}$ corresponds to a smaller mode I toughness of the coating material. The curve for the delamination stress $\bar{\sigma }_{d}$, plotted by the light blue line, is obtained from Eq. (36), and may be interpreted as a crack-growth resistance curve (R-curve). The depicted analytical steady-state stress, $\bar{\sigma }_d(\ell /h_1 \rightarrow \infty ) = \bar{\sigma }_{c}(\ell /h_1 \rightarrow \infty ) =\bar{\sigma }_{ss}$, follows from Eq. (46)$_1$, and adequately reflects the asymptotic limit to which the $\bar{\sigma }_{c}$- and $\bar{\sigma }_{d}$-curves converge under increasing delamination.

In accordance with the procedure presented in Cox and Marshall (1996), Fleck and Zhao (2000), Suiker and Fleck (2004), from the results in Fig. 8 the three main failure scenarios sketched in Fig. 3 can be distinguished, which depend on the toughness ratio $\Gamma _{d}/\Gamma _{I}$ and the elastic mismatch $\bar{E}_2/\bar{E}_1$. Consider first the crack channelling and delamination stresses for the case of a stiffness mismatch $\bar{E}_2/\bar{E}_1 = 0.1$ as depicted in Fig. 8a. The delamination stress has an initial, rising branch (R-curve behaviour) for relatively short delamination lengths, $\ell /h_1 \le 0.45$; subsequently, after having reached its maximum value, it drops slightly under growing delamination in order to reach the steady-state stress $\bar{\sigma }_{ss}$. Since stable plane-strain delamination is characterized by an increasing stress $\bar{\sigma }_{d}$ versus delamination length $\ell /h_1$, channelling of a doubly deflected crack with stable delamination corresponds to a crack channelling curve intersecting with the rising branch of the delamination curve, which occurs for $\Gamma _d/\Gamma _I \ge 0.58$, up to some maximum value that is discussed below. At the intersection between the actual $\bar{\sigma }_c (\ell /h_1)$ curve and the $\bar{\sigma }_d (\ell /h_1)$ curve, the corresponding delamination length $\ell /h_1$ can be read off along the horizontal axis of Fig. 8a. Further, the corresponding value of the channelling stress is represented by a minimum (extremum), which becomes clear when applying the condition $\partial \bar{\sigma }_c/\partial \ell = 0$ to expression (18) for the channelling stress, leading to $\bar{\sigma }_{c,min} = \bar{\sigma }_d$ with $\bar{\sigma }_d$ given by Eq. (36). The above fracture scenario is denoted in Fig. 3 as mechanism 2.

In contrast, for toughness ratios $\Gamma _d/\Gamma _I < 0.58$, the channelling stress $\bar{\sigma }_c$decreases monotonically with increasing delamination $\ell /h_1$, as a result of which the critical, minimum channelling stress coincides with the steady-state value at infinite delamination, $\bar{\sigma }_{c,min} =\bar{\sigma }_{c}(\ell /h \rightarrow \infty ) = \bar{\sigma }_{ss}$. Hence, crack channelling is characterized by unlimited delamination in all directions, as visualized in Fig. 3 by mechanism 3. Finally, it can be observed from Fig. 8a that for values of $\Gamma _d/\Gamma _I$ towards 10 the crack channelling curve $\bar{\sigma }_{c}(\ell /h_1)$ drops below the delamination curve $\bar{\sigma }_{d} (\ell /h_1)$, as a result of which there are no intersection points between the two curves. The precise value of the toughness ratio at which this transition happens appears to be $\Gamma _d/\Gamma _I=2.16$. Accordingly, for $\Gamma _d/\Gamma _I \ge 2.16$ delamination remains absent during crack channelling, which is in agreement with the observation that the minimum value of the crack channelling curve in this range occurs at zero delamination, $\ell / h_1=0$, see Fig. 8a. In Fig. 3 this fracture scenario is designated as mechanism 1. In summary, from the numerical results presented in Fig. 8a, it is concluded that crack channelling with delamination absent (mechanism 1) is operational for toughness ratios in the range $\Gamma _{d}/\Gamma _{I} \ge 2.16$, crack channelling with constant delamination (mechanism 2) occurs for $0.58 \le \Gamma _d/\Gamma _I <2.16$, and crack channelling with unlimited delamination in all directions (mechanism 3) is operational for $\Gamma _d/\Gamma _I < 0.58$. Note that the corresponding value of the minimum crack channelling stress in the coating, $\bar{\sigma }_{c,min}$, can be translated to a critical value for the uniform moisture content via Eq. (6)$_1$, upon substituting for the condition $\Delta m_1=\Delta m_2$.

Consider now a stiffness mismatch $\bar{E}_2/\bar{E}_1 = 1$ for which the numerical results are illustrated in Fig. 8b. The peak value for the delamination stress $\bar{\sigma }_d$ is found at relatively small delamination length $\ell /h_1 \approx 0.15$, after which the delamination curve rapidly decreases towards its steady-state value $\bar{\sigma }_{ss}$. Due to the small rising part of the delamination curve $\bar{\sigma }_d (\ell /h_1)$, mechanism 2 only appears for a small range of toughness ratios, $0.44 \le \Gamma _d/\Gamma _I <0.49$, and is characterized by small delamination lengths, $\ell /h_1 \le 0.15$. For $\Gamma _d/\Gamma _I \ge 0.49$ and $\Gamma _d/\Gamma _I < 0.44$, mechanism 1 and mechanism 3 are operational, respectively. Figure 8c finally refers to a stiffness mismatch $\bar{E}_2/\bar{E}_1 = 10$. Observe that, after a minor oscillation at $\ell /h_1 = 0.03$, the delamination stress $\bar{\sigma }_d$ drops monotonically towards its steady-state value $\bar{\sigma }_{ss}$ upon increasing delamination. Neglecting the initial, local oscillation in the delamination stress, from the decreasing trend of the delamination curve $\bar{\sigma }_d (\ell /h_1)$ it follows that mechanism 2 does not occur. Accordingly, for low toughness ratios $\Gamma _d/\Gamma _I \le 0.43$mechanism 3 is operational, while the bilayer system may fail in accordance with mechanism 1 when $\Gamma _d/\Gamma _I > 0.43$.

From the above identification procedure of the three crack channelling mechanisms, a failure mechanism map can be constructed in which the minimum crack channelling stress $\bar{\sigma }_{c,min}$ in the coating is plotted as a function of the toughness ratio $\Gamma _{d}/\Gamma _{I}$ for a selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$, see Fig. 9. This failure map thus provides an estimate of the critical crack channelling stress, given the values of the toughness ratio $\Gamma _{d}/\Gamma _{I}$ and the elastic stiffness mismatch $\bar{E}_2/\bar{E}_1$. The three failure mechanisms are represented by the regions defined by the dotted orange lines. For coating-substrate systems characterized by a relatively low toughness ratio $\Gamma _{d}/\Gamma _{I} \le 0.43$, mechanism 3 prevails for any of the stiffness mismatches considered. For higher toughness ratios $\Gamma _d/\Gamma _I > 0.43$, mechanism 1 operates at higher stiffness mismatches, $\bar{E}_2/\bar{E}_1 \ge 3$, while for moderate to low stiffness mismatches $\bar{E}_2/\bar{E}_1 < 3$mechanism 3 gradually turns into mechanism 2, and finally into mechanism 1 under increasing toughness ratio $\Gamma _d/\Gamma _I$. Note that the transitions in failure mechanism occur at a larger toughness ratio $\Gamma _d/\Gamma _I$ if the stiffness ratio $\bar{E}_2/\bar{E}_1$ is lower.

Fig. 9

Failure mechanism map for a bilayer system with layers of equal thickness ($h_2/h_1=1$). Minimum crack channelling stress $\bar{\sigma }_{c,min}$ in the coating versus toughness ratio $\Gamma _{d}/\Gamma _{I}$ for a constant moisture content profile, considering a broad selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$. The dotted orange lines define the regions corresponding to the three failure mechanisms presented in Fig. 3. The results are independent of the mismatch in coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$, and the mismatch in diffusion coefficient, $D_2/D_1$

4.3 Influence of the moisture profile on the cracking response via the parameter $\alpha$

This section discusses the influence of the considered moisture profile on the predicted fracture response, by exploring the effect of the weighting factor $\alpha$. For the bilayer system described in Sect. 4.1, the fracture scenarios are first analysed corresponding to a linear moisture content distribution with a vanishing moisture content value at the layer interface, which, for the case $D_2/D_1=1$, is defined via Eq. (1)$_1$ as $\Delta m (y) = (\Delta m_1 -\Delta m_2)y/h$. Correspondingly, the weighting factor $\alpha$ is set to zero, $\alpha =0$, yielding the remote stresses for crack channelling and plane-strain delamination as $\sigma _c^{\infty , \alpha }(y) =\Sigma _c(1+ y/(h\eta _1))$ and $\sigma _d^{\infty , \alpha }(y) =\Sigma _d(1+ y/(h\eta _1))$, respectively. Next, an arbitrary linear moisture content profile, as represented by relation (1), is considered. The corresponding remote channelling and plane-strain delamination stresses $\sigma _c^{\infty , \alpha }(y) = \alpha \bar{\sigma }_c +\Sigma _c(1+y/(h\eta _1))$ and $\sigma _d^{\infty , \alpha }(y) =\alpha \bar{\sigma }_d +\Sigma _d(1+ y/(h\eta _1))$, respectively, are computed by assuming a weighting factor $\alpha =0.5$, and are evaluated at the interface between the coating and substrate, i.e. at $y=0$. Note that the numerical results are now dependent on the mismatch in the coefficient of hygral expansion, $\bar{\beta }_2/\bar{\beta }_1$, and the mismatch in the diffusion coefficient, $D_2/D_1$, which quantify the remote stress measure $\Sigma _1$, and thus $\sigma _1^{\infty }(y)$, via the parameter $\eta _1$, see Eqs. (6)$_{2,3}$. The mismatch in coefficient of hygral expansion has been chosen as $\bar{\beta }_2/\bar{\beta }_1=10$, so that condition (8)$_2$ is satisfied for the full range of selected stiffness mismatches, $\bar{E}_2/\bar{E}_1 \in [ 0.1, 10 ]$.

Fig. 10

Failure mechanism map for a bilayer system with layers of equal thickness ($h_2/h_1=1$). Minimum crack channelling stress $\Sigma _{c,min}$ in the coating versus toughness ratio $\Gamma _{d}/\Gamma _{I}$ for a linear moisture content profile related to a weighting factor $\alpha =0$, considering a broad selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$. The dotted orange lines define the regions corresponding to the three failure mechanisms presented in Fig. 3. The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1=10$, and the ratio of diffusion coefficients is $D_2/D_1=1$

4.3.1 Failure mechanisms for a linear moisture content distribution with a vanishing value at the layer interface ($\alpha =0$)

Similarly to that done in Sect. 4.2, the mode-mix $\Psi _{\Sigma }$, the energy release rates $G_{c,\Sigma }, G_{d,\Sigma }$ and the channelling $\Sigma _{c}$ and plane-strain delamination $\Sigma _{d}$ stresses are predicted in the case of a linear moisture content distribution with a vanishing value at the layer interface ($\alpha =0$), as a function of the delamination length $\ell /h_1$. The obtained results present trends that are qualitatively comparable to those discussed for a uniform moisture profile ($\alpha =1$), and are presented in detail in Appendix 1. These results can be summarized in the failure mechanism map shown in Fig. 10, illustrating the regions in which the three crack channelling mechanisms depicted in Fig. 3 are active. In Fig. 10, the minimum channelling stress $\Sigma _{c,min}$ in the coating is plotted as a function of the toughness ratio, $\Gamma _d/\Gamma _I$, for selected values of the stiffness mismatch, $\bar{E}_2/\bar{E}_1$. In the range of toughness ratios $0.4 \le \Gamma _d/\Gamma _I < 0.52$, mechanism 1 directly converts into mechanism 3 for moderate to large values of the stiffness mismatch $\bar{E}_2/\bar{E}_1 \ge 1$, while for low stiffness mismatch values $\bar{E}_2/\bar{E}_1 < 1$mechanism 2 intervenes. However, since the corresponding values of constant delamination length are relatively small, with a maximum value of $\ell /h_1 = 0.3$ for $\bar{E}_2/\bar{E}_1 = 0.1$, in practice it may be difficult to distinguish mechanism 2 from mechanism 1.

Fig. 11

Cracking in a bilayer system with layers of equal thickness ($h_2/h_1=1$). Possible failure mechanisms as a function of the elastic mismatch $\bar{E}_2/\bar{E}_1$ and toughness ratio $\Gamma _d/\Gamma _I$. The light blue dotted lines and the dark blue dashed lines define the regions corresponding to the three failure mechanisms depicted in Fig. 3 under linear ($\alpha =0$) and uniform ($\alpha =1$) moisture content profiles, respectively. The results obtained under a linear moisture content profile relate to a mismatch in coefficient of hygral expansion of $\bar{\beta }_2/\bar{\beta }_1=10$, and a ratio of diffusion coefficients $D_2/D_1=1$

4.3.2 Crack channelling mechanisms under linear ($\alpha = 1$) versus uniform ($\alpha = 0$) moisture profiles

The regimes of dominance of the three crack channelling scenarios depicted in Figs. 9 and 10 differ somewhat under uniform and linear moisture content profiles. In order to clearly illustrate these differences, Fig. 11 summarizes the failure scenarios activated under the two types of moisture variations in a single failure map in material property space, by plotting on a log-linear scale the elastic stiffness mismatch $\bar{E}_2/\bar{E}_1$ as a function of the toughness ratio $\Gamma _d/\Gamma _I$. Here, the light blue dotted lines delineate the failure regions under the presence of a linear moisture content profile (whereby the weighting factor $\alpha =0$), and the dark blue dashed lines delineate failure regions under a uniform moisture content profile (whereby the weighting factor $\alpha =1$). It can be clearly seen that for stiffness mismatches $\bar{E}_2/\bar{E}_1 \ge 1$mechanism 2 is (virtually) absent, with the transition from mechanism 1 to mechanism 3 under uniform and linear moisture content profiles occurring at similar values of the toughness ratio $\Gamma _{d}/\Gamma _{I}$. Conversely, for $\bar{E}_2/\bar{E}_1 < 1$mechanism 2 intervenes, although, as discussed previously, the corresponding constant delamination length remains limited to a fraction of the coating thickness, $\ell /h_1 < 1$. At the lowest value of the stiffness mismatch, $\bar{E}_2/\bar{E}_1=0.1$, the range of toughness ratios across which mechanism 2 operates under a linear moisture content profile is substantially smaller than under a uniform moisture content profile. Hence, for the experimental identification of mechanism 2 it is recommended to use a bilayer specimen with a relatively compliant substrate that is exposed to a uniform moisture content profile.

4.3.3 Failure mechanisms for an arbitrarily linear moisture content profile ($0<\alpha <1$)

The failure scenario corresponding to an arbitrarily linear moisture content profile is next analysed. Observe first from Fig. 6, illustrating the dependence of the steady-state stress $\sigma _{ss}^{\infty , \alpha }(0)$ on the parameter $\alpha$, that the failure response for arbitrarily linear moisture profiles ($0<\alpha <1$) is bounded by the cases $\alpha =0$ and $\alpha =1$. In the following, the crack channelling stress $\sigma _{c}^{\infty , \alpha }(0)$ and delamination stress $\sigma _{d}^{\infty , \alpha }(0)$ are thus calculated based on an intermediate value of the weighting factor $\alpha$, i.e., $\alpha =0.5$. This is done by repectively substituting the results from Eqs. (26) and (40) in Eq. (5)$_1$. The obtained plots for the remote crack channelling stress and delamination stress as a function of the delamination length result to be qualitatively comparable to those shown in Fig. 8 for a constant moisture profile related to $\alpha =1$, and therefore are omitted here. The failure mechanism map depicted in Fig. 12 for $\alpha =0.5$ also is comparable to those in Fig. 9 for $\alpha =1$ and in Fig. 10 for $\alpha =0$. However, for relatively low stiffness ratios $\bar{E}_2/\bar{E}_1 < 0.3$, the transition from mechanism 1 to mechanism 2 in Fig. 12 with $\alpha =0.5$ and in Fig. 9 for $\alpha =1$ clearly occurs at a larger toughness ratio $\Gamma _{d}/\Gamma _{I}$ than in Fig. 10 with $\alpha =0$.

Fig. 12

Failure mechanism map for a bilayer system with layers of equal thickness ($h_2/h_1=1$). Minimum crack channelling stress $\bar{\sigma }_{c,min}^{\infty ,\alpha }(0)$ in the coating versus toughness ratio $\Gamma _{d}/\Gamma _{I}$ for a linear moisture content profile related to a weighting factor $\alpha =0.5$, considering a broad selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$. The dotted orange lines define the regions corresponding to the three failure mechanisms presented in Fig. 3. The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1=10$, and the ratio of the diffusion coefficients is $D_2/D_1=1$

Fig. 13

Influence of the relative substrate thickness $h_2/h_1$ on the steady-state coating stress for unlimited plane-strain delamination, considering a broad selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$. a Constant delamination stress $\bar{\sigma }_{ss}$ ($\alpha =1$), Eq. (46)$_1$, whereby the results are independent of the ratios $\bar{\beta }_2/\bar{\beta }_1$ and $D_2/D_1$; b Linear delamination stress $\Sigma _{ss}$ ($\alpha =0$), Eq. (46)$_2$, for $\bar{\beta }_2/\bar{\beta }_1=10$ and $D_2/D_1=1$, and c Total delamination stress $\sigma ^{\infty , \alpha }_{ss}(0)$ (with $\alpha =0.5$), Eq. (47), for $\bar{\beta }_2/\bar{\beta }_1=10$ and $D_2/D_1=1$

5 Influence of the relative layer thickness upon cracking

5.1 Steady-state delamination under varying relative substrate thickness

The influence of the relative layer thickness $h_2/h_1$ on the steady-state delamination stress is studied by varying the substrate thickness $h_2$ in the range $h_2 = [h_1, 1000 h_1]$. The steady-state stresses $\bar{\sigma }_{ss}$, $\Sigma _{ss}$ and $\sigma ^{\infty ,\alpha }_{ss}(0)$ generated in the coating under uniform and linear moisture profiles are respectively shown in Fig. 13a–c as a function of the relative layer thickness $h_2/h_1$. The constant and linear stress measures, $\bar{\sigma }_{ss}$ ($\alpha =1$) and $\Sigma _{ss}$ ($\alpha =0$), are calculated from Eq. (46), and the total stress $\sigma ^{\infty , \alpha }_{ss}(0)$ is computed from expression (47), with the weighting factor set equal to $\alpha = 0.5$. The constant steady-state delamination stress $\bar{\sigma }_{ss}$ in the coating is associated with a uniform moisture content distribution, and is independent of the mismatch in the coefficient of hygral expansion, $\bar{\beta }_{2}/\bar{\beta }_{1}$, see also expression (46)$_1$. Figure 13a illustrates that its magnitude increases with increasing stiffness mismatch $\bar{E}_{2}/\bar{E}_{1}$. In addition, the delamination stress grows monotonically with increasing relative layer thickness $h_2/h_1$, and asymptotes to a limit value $\bar{\sigma }_{ss}(h_2/h_1\rightarrow \infty ) = \sqrt{2\bar{E}_1 \Gamma _{d}/h_1}$ that is independent of the stiffness mismatch. Note that under increasing relative layer thickness $h_2/h_1$ the limit value is reached earlier for a larger stiffness ratio $\bar{E}_{2}/\bar{E}_{1}$.

Fig. 14

Crack channelling and plane-strain delamination in a bilayer system with a relatively thick substrate ($h_2 /h_1=10$). The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1 = 10$ and the ratio of the diffusion coefficients is $D_2/D_1=1$. Remote stress $\sigma ^{\infty , \alpha }_{1}(0)$ (related to $\alpha = 0.5$) versus the delamination length $\ell /h_1$, considering a stiffness mismatch of a $\bar{E}_2/\bar{E}_1 = 0.1$, b $\bar{E}_2/\bar{E}_1 =1$ and c $\bar{E}_2/\bar{E}_1 =10$. The dark blue lines represent the crack channelling stress $\sigma _1^{\infty , \alpha }(0) = \sigma _{c}^{\infty , \alpha }(0) = \sigma _c$, derived from Eqs. (26) and (5)$_1$ for selected toughness ratios $\Gamma _{d}/\Gamma _{I}$. The light blue line reflects the plane-strain delamination stress $\sigma ^{\infty , \alpha }_1(0) = \sigma _{d}^{\infty , \alpha }(0)= \sigma _d$, derived from Eqs. (40) and (5)$_1$. The depicted steady-state value $\sigma _{ss}^{\infty , \alpha }(0)$ is computed with Eq. (47)

Figure 13b, c shows that the steady-state delamination stress $\Sigma _{ss}$ ($\alpha =0$) and the total stress $\sigma ^{\infty ,\alpha }_{ss}(0)$ ($\alpha =0.5$) in the coating follow a similar trend as the constant stress depicted in Fig. 13a. Although $\Sigma _{ss}$ and $\sigma ^{\infty ,\alpha }_{ss}(0)$ are computed for a mismatch in the coefficient of hygral expansion of $\bar{\beta }_{2}/\bar{\beta }_{1}=10$ and a ratio of the diffusion coefficients of $D_2/D_1=1$, the effect of these specific values on the fracture response vanishes for a large substrate thickness. Specifically, at large values of the relative thickness, $h_2/h_1 \ge 5$, it can be observed that the failure stresses $\bar{\sigma }_{ss}$, $\Sigma _{ss}$ and $\sigma ^{\infty ,\alpha }_{ss}(0)$ are almost identical, irrespective of the value of the stiffness mismatch $\bar{E}_{2}/\bar{E}_{1}$. As can be confirmed from the second term in Eq. (5)$_1$, this implies that for a large substrate the linear variation in stress across the coating becomes relatively small, such that the stress within the coating is approximately uniform and thus independent of the values of $\bar{\beta }_{2}/\bar{\beta }_{1}$ and $D_2/D_1$. Conversely, when the coating and substrate have a comparable thickness, $h_2/h_1 < 5$, the linear variation in stress has a substantial effect on the total stress $\sigma ^{\infty ,\alpha }_{ss}(0)$, and needs to be explicitly accounted for in the failure analysis. Note again that under these circumstances the constant and linear stress measures $\bar{\sigma }_{ss}$ and $\Sigma _{ss}$ respectively serve as upper and lower bounds for the total steady-state stress $\sigma ^{\infty ,\alpha }_{ss}(0)$ for any value of the stiffness mismatch $\bar{E}_{2}/\bar{E}_{1}$. Observe further that the linear failure stress $\Sigma _{ss}$ approaches zero for a bilayer system with layers of equal thickness, $h_2/h_1=1$, and a stiffness mismatch equal to $\bar{E}_{2}/\bar{E}_{1}=0.1$, see Fig. 13b. This means that under a linear moisture content profile with a vanishing value at the layer interface this system has no resistance against delamination, and will fail spontaneously. However, the practical relevance of this particular case is small, since a linear moisture content profile in general will also induce a constant stress contribution (i.e., in practice $\alpha \ne 0$), for which the resistance against delamination is finite, see Fig. 13a.

5.2 Failure mechanisms for a bilayer system with a thick substrate ($h_2/h_1=10$)

Consider now a bilayer system with a relatively thick substrate characterized by $h_2/h_1=10$. Under the application of a linear moisture profile associated with $\alpha =0.5$, the generated remote crack channelling and delamination stresses $\sigma _1^{\infty , \alpha }(0)=\sigma _c^{\infty , \alpha }(0)$ and $\sigma _1^{\infty , \alpha }(0)=\sigma _d^{\infty , \alpha }(0)$, as obtained by respectively inserting the results from Eqs. (26) and (40) into Eq. (5)$_1$, are shown in Fig. 14a–c as a function of the delamination length $\ell /h_1$ for stiffness mismatches $\bar{E}_2/\bar{E}_1=0.1$, 1 and 10, respectively.

As argued in the previous section, for such a thick substrate the normalized failure stresses are mainly governed by the uniform part of the moisture content distribution. It is interesting to observe that for the stiffness mismatches $\bar{E}_2/\bar{E}_1 = 0.1$ and $\bar{E}_2/\bar{E}_1 = 1$ the rising part of the delamination curve $\sigma _d^{\infty , \alpha }(l/h_1)$ is more prominent than for the case of a bilayer system with layers of equal thickness discussed in Sect. 4; for both stiffness mismatches the increase of the delamination stress continues up to a stable delamination length of $\ell /h_1 \approx 4$, which is sufficiently large to adequately identify mechanism 2 in practical applications. The range of toughness mismatches for which mechanism 2 is operational is $0.10 \le \Gamma _d/\Gamma _I < 0.73$ for $\bar{E}_2/\bar{E}_1 = 0.1$ and $0.22 \le \Gamma _d/\Gamma _I < 0.41$ for $\bar{E}_2/\bar{E}_1 = 1$. Above and below these ranges crack channelling occurs by means of mechanism 1 and mechanism 3, respectively. For $\bar{E}_2/\bar{E}_1 = 10$ the toughness range related to mechanism 2 is minor and corresponds to relatively small delamination lengths, $\ell /h_1 < 0.1$; hence, under an increasing toughness ratio mechanism 3 more or less directly converts into mechanism 1 at a value $\Gamma _d/\Gamma _I \approx 0.4$. The above-mentioned regions of the three failure mechanisms are designated in more detail in the failure mechanism map presented in Fig. 15; the figure clearly shows that mechanism 2 indeed becomes a distinguished failure mechanism at lower values of the stiffness ratio $\bar{E}_2/\bar{E}_1$, i.e., for a bilayer system with a relatively compliant substrate.

Fig. 15

Failure mechanism map for a bilayer system with a relatively thick substrate ($h_2 /h_1=10$). The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1 = 10$ and the ratio of the diffusion coefficients is $D_2/D_1=1$. Minimum crack channelling stress $\sigma _{c,min}^{\infty , \alpha }(0)$ in the coating versus toughness ratio $\Gamma _{d}/\Gamma _{I}$ for a linear moisture content profile related to a weighting factor $\alpha =0.5$, considering a broad selection of stiffness mismatches $\bar{E}_2/\bar{E}_1$. The dotted orange lines define the regions corresponding to the three failure mechanisms presented in Fig. 3

5.3 Comparison of failure response for bilayer systems with $h_2/h_1=10$ and $h_2/ h_1=1$

The results obtained in Figs. 12 and 15 are summarized in Fig. 16, illustrating the operative failure mechanisms as a function of the elastic stiffness mismatch $\bar{E}_2/\bar{E}_1$ and toughness ratio $\Gamma _{d}/\Gamma _{I}$. Dark blue dashed lines refer to a system with layers of equal thickness ($h_2/ h_1=1$) and light blue dotted lines refer to a system characterized by a relatively thick substrate ($h_2/ h_1=10$). It can be seen that the toughness range $\Gamma _d/\Gamma _I$ within which mechanism 2 is active generally corresponds to lower values when the substrate is thicker. Also, at larger stiffness ratios $\bar{E}_2/\bar{E}_1 >1$ (i.e., for systems with a relatively stiff substrate) mechanism 2 vanishes for a bilayer with $h_1=h_2$, while for the case with $h_2=10h_1$ it remains present.

Fig. 16

Cracking in a bilayer system for different relative layer thicknesses and a linear moisture content profile related to a weighting factor $\alpha =0.5$. The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1 = 10$ and the ratio of the diffusion coefficients is $D_2/D_1=1$. Possible failure mechanisms as a function of the elastic mismatch $\bar{E}_2/\bar{E}_1$ and toughness ratio $\Gamma _{d}/\Gamma _{I}$. The dark blue dashed lines and the light blue dotted lines define the regions corresponding to the three failure mechanisms depicted in Fig. 3 for $h_2/h_1=1$ and $h_2/h_1=10$, respectively

It is further instructive to display the critical total stress for crack channelling $\sigma _{c,min}^{\infty , \alpha }(0)$ (using a weighting factor $\alpha =0.5$) for mechanisms 1 and 3 as a function of the stiffness mismatch $\bar{E}_2/\bar{E}_1$, considering the two relative layer heights, $h_2/h_1=1$ and $h_2/h_1=10$, see Fig. 17.

Fig. 17

Cracking in a bilayer system for different relative layer thicknesses and a linear moisture content profile related to a weighting factor $\alpha =0.5$. The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1 = 10$ and the ratio of the diffusion coefficients is $D_2/D_1=1$. Critical channelling stress $\sigma _{c,min}^{\infty , \alpha }(0)$ in the coating for mechanism 1 and mechanism 3 as a function of the elastic mismatch $\bar{E}_{2}/\bar{E}_{1}$. The dark blue thin lines and the light blue thick lines refer to the relative layer heights $h_2/h_1=1$ and $h_2/h_1=10$, respectively. In the normalization of the minimum channelling stress along the vertical axis, for mechanisms 1 and 3 the toughness parameter is taken as $\Gamma _c = \Gamma _{I}$ and $\Gamma _c = \Gamma _d$, respectively

The critical channelling stress in the coating is normalized by the term $\sqrt{(\bar{E}_1 \Gamma _c)/h_1}$, where $\Gamma _c = \Gamma _{I}$ when referring to mechanism 1 (indicated by the solid lines) and $\Gamma _c = \Gamma _{d}$ when denoting mechanism 3 (indicated by the dashed lines). The critical channelling stress for mechanism 1 is calculated from the FEM results presented in Sects. 4.3.3 and 5.2, by taking the limit $\sigma _{c,min}^{\infty , \alpha }=\sigma _{c}^{\infty , \alpha }(\ell /h_1\rightarrow 0 )$, while for mechanism 3 it follows from inserting $\bar{\sigma }_1 =\alpha \bar{\sigma }_{ss}$, together with the fracture criterion (32), into Eq. (44), and solving for $\Sigma _1$, after which the solution is substituted into expression (47). In all cases the critical channelling stress monotonically increases with increasing value of the stiffness mismatch. It can be further observed that for both mechanisms the corresponding critical channelling stress is lower for the system with the smaller relative substrate thickness, $h_2/h_1=1$. The figure may serve as a design graph provided the failure mechanism is known. Note that mechanism 2 can intervene, depending on the value of the toughness mismatch $\Gamma _d/\Gamma _I$, as demonstrated by the failure mechanism maps depicted in Figs. 12 and 15.

6 Conclusions

Crack channelling is addressed for a brittle coating-substrate system subjected to a moisture (or temperature) gradient in the thickness direction. Three distinct failure scenarios have been identified: (i) channelling of a mode I crack in the coating with delamination absent, (ii) channelling of a doubly deflected crack with constant delamination length, and (iii) channelling of a mode I crack with unstable, unlimited delamination in all directions. Failure mechanism maps have been constructed, illustrating the dependence of the active crack channelling mechanism and the corresponding critical channelling stress to the ratio of layer interface to coating toughness, and to the mismatches in stiffness and in coefficient of hygral expansion. The influence of the thickness ratio of the coating and substrate on the critical channelling stress and failure mechanism has also been explored. Closed-form expressions are derived for the steady-state delamination stresses, which allow one to determine the critical moisture conditions that lead to unlimited delamination. Due to the general character of the study, the results can be applied to coating-substrate systems in various applications. Specifically, the study serves to predict cracking phenomena generated in historical paintings under indoor climate fluctuations, thereby helping museums to preserve their art objects. In particular, failure mechanisms 2 and 3 (crack channelling with finite and unlimited delamination, respectively) are the most critical for a painting and must be avoided, while mechanism 1 (crack channelling with no delamination) is the preferential failure regime. From the proposed failure maps, it is possible to derive (i) the material property range in which mechanism 1 is active; (ii) the stress level at which it occurs and (iii) the corresponding critical moisture content values. This information may thus provide museums guidelines on appropriate conservation interventions.

Appendix 1: Cracking due to a linear moisture content distribution with a vanishing value at the layer interface (\(\alpha =0\))

The results for the bilayer system presented in Sect. 4.1, characterized by equal diffusion coefficients $D_1 = D_2$, and subjected to a linear moisture content distribution with a vanishing moisture content value at the layer interface, i.e., $\Delta m (y) = (\Delta m_1 -\Delta m_2)y/(h_1+h_2)$, are presented in detail in the following.

Fig. 18

Cracking in a bilayer system with layers of equal thickness ($h_2/h_1=1$). The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1=10$ and the ratio of diffusion coefficients is $D_2/D_1=1$. a Mode-mix $\Psi _{\Sigma } = \mathrm {atan}(\mathrm {Im(K_{\Sigma } h_1^{i \epsilon })}/\mathrm {Re(K_{\Sigma } h_1^{i \epsilon })})$ as a function of the delamination length $\ell /h_1$, for a linear moisture content profile with a vanishing value at the layer interface. Energy release rate for b plane-strain delamination $G_{d,{\Sigma }}$, Eq. (37), and c steady-state crack channelling $G_{c,{\Sigma }}$, Eq. (21), as a function of the delamination length $\ell /h_1$, for a linear moisture content profile that vanishes at the layer interface. The depicted steady-state values $G_{ss,\Sigma }$ are computed with Eq. (45)$_2$

Fig. 19

Crack channelling and plane-strain delamination in a bilayer system with layers of equal thickness ($h_2/h_1=1$). The mismatch in coefficient of hygral expansion equals $\bar{\beta }_2/\bar{\beta }_1=10$, and the ratio of diffusion coefficients is $D_2/D_1=1$. Remote stress $\Sigma _1$ versus delamination length $\ell /h_1$ for a linear moisture content profile, considering a stiffness mismatch of a $\bar{E}_2/\bar{E}_1 = 1$ and b $\bar{E}_2/\bar{E}_1 =10$. The dark blue lines represent the crack channelling stress $\Sigma _1 = \Sigma _c$, equation (22), for selected toughness ratios $\Gamma _{d}/\Gamma _{I}$. The light blue line reflects the plane-strain delamination stress $\Sigma _1 = \Sigma _d$, equation (38). The depicted steady-state value $\Sigma _{ss}$ is computed with Eq. (46)$_2$

1.1 A1.1 Mode-mix and energy release rate

The phase angle $\Psi _{\Sigma }$ generated by the linear moisture content variation is depicted in Fig. 18a as a function of the delamination length $\ell /h_1$. In alignment with Eq. (30), the mode-mixity is calculated as $\Psi _{\Sigma } = \mathrm {atan}({\mathrm {Im(K}_{\Sigma } \hat{l}^{i \epsilon })}/{\mathrm {Re(K}_{\Sigma } \hat{l}^{i \epsilon })})$, whereby the complex stress intensity factor $K_{\Sigma }$ is defined by $K_{\Sigma } = K_{1,\Sigma }+i K_{2,\Sigma }$, with $K_{1,\Sigma }$ and $K_{2,\Sigma }$ as given by relation (48). The reference length at which the mode-mix is evaluated is taken equal to the layer height $\hat{l} =h_1$. The phase angle attains a steady state at a delamination length $\ell /h_1 \approx 0.8$ for all stiffness mismatches selected, with the asymptotic value lying within the range $[46^\circ , 54^\circ ]$. The phase angle at steady-state typically decreases with increasing stiffness mismatch $\bar{E}_2/\bar{E}_1$, with the exception being the slightly lower steady-state value for $\bar{E}_2/\bar{E}_1 = 0.3$ compared to $\bar{E}_2/\bar{E}_1 = 0.1$.

The normalized energy release rates for plane-strain delamination $G_{d,\Sigma }$ and crack channelling $G_{c,\Sigma }$ are shown respectively in Fig. 18b, c, as a function of the delamination length $\ell /h_1$. The results for $\bar{E}_2/\bar{E}_1 = 0.1$ have been omitted in this figure, due to the relatively large values found for this case. The trends observed for the energy release rates are comparable to those calculated for the constant moisture profile, see Fig. 7b, c, and asymptote to the analytical steady-state value $G_{ss,\Sigma }$ as given by Eq. (45)$_2$

1.2 A1.2 Failure mechanisms

Figure 19 contains plots of the stresses $\Sigma _d$ for plane-strain delamination and $\Sigma _c$ for steady-state crack channelling as a function of the delamination length $\ell /h_1$, for a linear moisture distribution. Figure  19a, b respectively refer to stiffness mismatches $\bar{E}_2/\bar{E}_1 = 1$ and 10. The results for a stiffness mismatch of $\bar{E}_2/\bar{E}_1 = 0.1$ are not depicted here, since the remote stress values calculated for this case almost vanishes. The channelling stress $\Sigma _{c}$, indicated in Fig. 19 by the dark blue lines, has been computed using Eq. (22) for the following selected values of toughness ratio, $\Gamma _{d}/\Gamma _{I} = \left[ 0.05, 0.1, 0.2, 0.5, 1, 10 \right]$. The delamination stress $\Sigma _{d}$, designated by the light blue line, has been calculated by means of Eq. (38). For a system characterized by a mismatch in elastic stiffness of $\bar{E}_2/\bar{E}_1 =1$, mechanism 2 operates along the small rising part of the $\Sigma _c (\ell /h_1)$ curve, see Fig. 19a. The toughness range over which this occurs is limited, $0.40 \le \Gamma _d/\Gamma _I < 0.44$, whereby the constant delamination length remains relatively small, $\ell /h_1 \le 0.1$. For toughness values above and below this range mechanism 1 and mechanism 3 become active, respectively. At a large value of the stiffness mismatch, $\bar{E}_2/\bar{E}_1 =10$, apart from a minor, local oscillation the delamination curve is monotonically decreasing, see Fig. 19b, so that a transition from mechanism 1 to mechanism 3 takes place under an increasing toughness ratio at a value $\Gamma _d/\Gamma _I = 0.45$.