Skip to main content
SpringerLink
Log in

Singular elastic solutions in corners with spring boundary conditions under anti-plane shear

  • Original Paper
  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

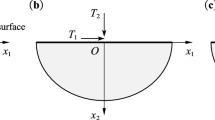
A new analytical procedure is developed for the deduction of the asymptotic series of the singular solutions in displacements and stresses near the vertex of the linear elastic isotropic corners with the Dirichlet–Robin (fixed-spring) and Neumann–Robin (free-spring) boundary conditions. Under the assumption of antiplane shear loading, the corresponding elastic problem reduces to the Laplace equation for the out-of-plane displacement. In the deduction of such singular solution, the complex variable is used to propose a harmonic function in the form of an asymptotic series including both power and logarithmic terms. This original procedure is suitable for its implementation in a computer algebra software which makes all the necessary symbolic computing, simplifications and rearrangements. This is a key issue due to the fact that the complexity of terms in these series may increase with increasing order of terms. These series are composed by the main terms (also called main singularities), solutions of the corresponding Dirichlet–Neumann or Neumann–Neumann problems, and the associated finite or infinite series of the so-called shadow terms (also called shadow singularities). These terms are determined by solving systems of recursive inhomogeneous Dirichlet–Neumann or Neumann–Neumann problems, respectively. A general classification of the behaviours of the asymptotic series covering all the considered corner problems is introduced. A few examples of the asymptotic series for corners with Dirichlet–Robin and Neumann–Robin boundary conditions are presented to illustrate the capabilities of this procedure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Notes

  1. The following subsets of real numbers will be used in this work: \({\mathbb {Z}}\) the set of integer numbers, \({\mathbb {N}}\) the set of natural numbers, \({\mathbb {Q}}\) the set of rational numbers, and \({\mathbb {N}}_{0}={\mathbb {N}}\cup \{0\}\) the set of non-negative integers.

  2. The authors thank to Professor Serge Nicaise (Université Polytechnique Hauts-de-France, Valenciennes) for calling their attention to this non-uniqueness issue.

References

  • Antipov YA, Avila-Pozos O, Kolaczkowski ST, Movchan AB (2001) Mathematical model of delamination cracks on imperfect interfaces. Int J Solids Struct 38(36–37):6665–6697

    Google Scholar 

  • Barber JR (2010) Elasticity. Springer, Dordrecht

    Google Scholar 

  • Barroso A, Mantič V, París F (2003) Singularity analysis of anisotropic multimaterial corners. Int J Fract 119(1):1–23

    Google Scholar 

  • Benveniste Y, Miloh T (2001) Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech Mater 33:309–323

    Google Scholar 

  • Cornetti P, Corrado M, Lorenzis LD, Carpinteri A (2015) An analytical cohesive crack modeling approach to the edge debonding failure of FRP-plated beams. Int J Solids Struct 53:92–106

    Google Scholar 

  • Costabel M, Dauge M (1993) Construction of corner singularities for Agmon–Douglis–Nirenberg elliptic systems. Mathematische Nachrichten 162(1):209–237

    Google Scholar 

  • Costabel M, Dauge M (1996) A singularly perturbed mixed boundary value problem. Commun Partial Differ Equ 21(11–12):1919–1949

    Google Scholar 

  • Costabel M, Dauge M (2002) Crack singularities for general elliptic systems. Mathematische Nachrichten 235(1):29–49

    Google Scholar 

  • Costabel M, Dauge M, Yosibash Z (2004) A quasi-dual function method for extracting edge stress intensity functions. SIAM J Math Anal 35(5):1177–1202

    Google Scholar 

  • Dempsey JP, Sinclair GB (1979) On the stress singularities in the plane elasticity of the composite wedge. J Elast 9(4):373–391

    Google Scholar 

  • Dillard DA, Mukherjee B, Karnal P, Batra RC, Frechette J (2018) A review of Winkler’s foundation and its profound influence on adhesion and soft matter applications. Soft Matter 14:3669–3683

    CAS  Google Scholar 

  • Erdogan F (1997) Fracture mechanics of interfaces. In: Rossmanith HP (ed) Damage and failure of interfaces. Balkema Publishers, Rotterdam, pp 3–36

    Google Scholar 

  • Geymonat G, Krasucki F, Lenci S (1999) Mathematical analysis of a bonded joint with a soft thin adhesive. Math Mech Solids 4:201–225

    Google Scholar 

  • Goland M, Reissner E (1944) The stresses in cemented joints. J Appl Mech 11:A17–A27

    Google Scholar 

  • Grisvard P (1985) Elliptic problems in nonsmooth domains. Pitman, Boston

    Google Scholar 

  • Grisvard P (1992) Singularities in boundary value problems. Springer, London

    Google Scholar 

  • Hashin Z (2002) Thin interphase/imperfect interface in elasticity with application to coated fiber composites. J Mech Phys Solids 50:2509–2537

    Google Scholar 

  • Hwu C, Omiya M, Kishimoto K (2003) A key matrix N for the stress singularity of the anisotropic elastic composite wedges. JSME Int J Ser A 46:40–50

    Google Scholar 

  • Kashiwabara T, Colciago C, Dedè L, Quarteroni A (2015) Well-posedness, regularity, and convergence analysis of the finite element approximation of a generalized Robin boundary value problem. SIAM J Numer Anal 53(1):105–126

    Google Scholar 

  • Kondratiev VA (1967) Boundary-value problems for elliptic equations in domains with conical or angular points. Trans Moscow Math Soc 16:227–313

    Google Scholar 

  • Leguillon D, Sanchez-Palencia E (1987) Computation of singular solutions in elliptic problems and elasticity. Masson, Paris

    Google Scholar 

  • Lenci S (2001) Analysis of a crack at a weak interface. Int J Fract 108:275–290

    Google Scholar 

  • Mantič V, París F, Berger J (2003) Singularities in 2D anisotropic potential problems in multi-material corners. Real variable approach. Int J Solids Struct 40:5197–5218

    Google Scholar 

  • Mantič V, Barroso A, París F (2014) Singular elastic solutions in anisotropic multimaterial corners. Applications to composites. In: Mantič V (ed) Mathematical methods and models in composites. Imperial College Press, London, pp 425–495

    Google Scholar 

  • Mantič V, Távara L, Blázquez A, Graciani E, París F (2015) A linear elastic-brittle interface model: application for the onset and propagation of a fibre-matrix interface crack under biaxial transverse loads. Int J Fract 195:15–38

    Google Scholar 

  • Mazya V, Rossmann J (1992) On a problem of Babuška (Stable asymptotics of the solution to the Dirichlet problem for elliptic equations of second order in domains with angular points). Mathematische Nachrichten 155(1):199–220

    Google Scholar 

  • Medková D (2018) The Laplace equation boundary value problems on bounded and unbounded Lipschitz domains. Springer, Cham

    Google Scholar 

  • Mghazli Z (1992) Regularity of an elliptic problem with mixed Dirichlet-Robin boundary conditions in a polygonal domain. Calcolo 29(3–4):241–267

    Google Scholar 

  • Mishuris G (2001) Interface crack and nonideal interface concept (Mode III). Int J Fract 107:279–296

    Google Scholar 

  • Mishuris GS, Kuhn G (2001) Asymptotic behaviour of the elastic solution near the tip of a crack situated at a nonideal interface. ZAMM Zeitschrift für Angewandte Mathematik und Mechanik 81(12):811–826

    Google Scholar 

  • Nicaise S, Li H, Mazzucato A (2017) Regularity and a priori error analysis of a Ventcel problem in polyhedral domains. Math Methods Appl Sci 40(5):1625–1636

    Google Scholar 

  • Omer N, Yosibash Z, Costabel M, Dauge M (2004) Edge flux intensity functions in polyhedral domains and their extraction by a quasidual function method. Int J Fract 129(2):97–130

    Google Scholar 

  • Paggi M, Carpinteri A (2008) On the stress singularities at multimaterial interfaces and related analogies with fluid dynamics and diffusion. Appl Mech Rev 61:020801-1–22

    Google Scholar 

  • Prandtl L (1933) Ein Gedankenmodell für den Zerreißvorgang spröder Körper (A thought model for the fracture of brittle solids). Zeitschrift für Physik Angenwandte Mathematik und Mechanik 13(2):129–133, Translation: Knauss W. G. Int J Fract (2011) 171:105–109

  • Sinclair GB (1996) On the influence of cohesive stress-separation laws on elastic stress singularities. J Elast 44:203–221

    Google Scholar 

  • Sinclair GB (1999) A note on the removal of further breakdowns in classical solutions of Laplace’s equation on sectorial regions. J Elast 56:247–252

    Google Scholar 

  • Sinclair GB (2004) Stress singularities in classical elasticity–I: Removal, interpretation and analysis, –II: Asymptotic identification. Appl Mech Rev 57(4):251–297, 385–439

  • Sinclair GB (2009) A note on the influence of cohesive stress-separation laws on elastic stress singularities in antiplane shear. J Elast 94:87–93

    Google Scholar 

  • Sinclair GB (2015) On the influence of adhesive stress-separation laws on elastic stress singularities. J Elast 118:187–206

    Google Scholar 

  • Steigemann M (2015) Power-law solutions of anisotropic multi-material elasticity problems. J Elast 118:63–87

    Google Scholar 

  • Ting TCT (1997) Stress singularities at the tip of interfaces in polycrystals. In: Rossmanith HP (ed) Damage and failure of interfaces. Balkema Publishers, Rotterdam, pp 75–82

    Google Scholar 

  • Valoroso N, Champaney L (2006) A damage-mechanics-based approach for modelling decohesion in adhesively bonded assemblies. Eng Fract Mech 73:2774–2801

    Google Scholar 

  • Vasilopoulos D (1988) On the determination of higher order terms of singular elastic stress fields near corners. Numer Math 53(1–2):51–95

    Google Scholar 

  • Volkersen O (1938) Die Nietkraftverteilung in Zugbeanspruchten Nietverbindungen mit Konstanten Laschen-querschnitten. Luftfahrtforschung 15:41–47

    Google Scholar 

  • Wang CH, Rose LRF (1999) A crack bridging model for bonded plates subjected to tension and bending. Int J Solids Struct 36:1985–2014

    Google Scholar 

  • Wieghardt K (1907) Über das Spalten und Zerreissen elastischer Körper (On splitting and cracking of elastic bodies). Zeitschrift für Mathematik und Physik 55(1-2):60–103, Translation: Rossmanith H.P. Fatigue Fract Eng Mater Struct (1995) 12:1371–1405

  • Williams ML (1952) Stress singularities resulting from various boundary conditions in angular corners of plates in extension. J Appl Mech 19:526–528

    Google Scholar 

  • Winkler E (1867) Die Lehre von der Elasticität und Festigkeit mit besondere Rücksicht auf ihre Anwendung in der Technik, für polytechnische Schulen, Bauakademien, Ingenieure, Maschienenbauer, Architecten, etc. Verlag von H, Dominicus, Prag

  • Wolfram S (1991) Mathematica. A system for doing mathematics by computer. Addison-Wesley, Redwood City

    Google Scholar 

  • Yin WL (2003) Anisotropic elasticity and multi-material singularities. J Elast 71:263–292

    Google Scholar 

  • Yosibash Z (2012) Singularities in elliptic boundary value problems and elasticity and their connection with failure. Springer, New York

    Google Scholar 

Download references

Acknowledgements

The authors thank to Professor Serge Nicaise (Université Polytechnique Hauts-de-France, Valenciennes) for calling their attention to the issue of non-uniqueness of shadow terms. The research was conducted with the support of the Spanish Ministry of Science, Innovation and Universities and European Regional Development Fund (Project PGC2018-099197-B-I00), and the Junta de Andalucía and European Regional Development Fund (Projects US-1266016 and P18-FR-1928).

Author information

Author notes

  1. Víctor Villalba

    Present address: Section Space Systems Engineering, Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HS, Delft, The Netherlands

Authors and Affiliations

  1. Grupo de Elasticidad y Resistencia de Materiales, Escuela Técnica Superior de Ingeniería, Universidad de Sevilla, Camino de los Descubrimientos, s/n, 41092, Sevilla, Spain

    Sara Jiménez-Alfaro, Víctor Villalba & Vladislav Mantič

Authors
  1. Sara Jiménez-Alfaro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Víctor Villalba
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vladislav Mantič
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vladislav Mantič.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiménez-Alfaro, S., Villalba, V. & Mantič, V. Singular elastic solutions in corners with spring boundary conditions under anti-plane shear. Int J Fract 223, 197–220 (2020). https://doi.org/10.1007/s10704-020-00443-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10704-020-00443-5

Keywords

Search

Navigation