A hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress: II. An isogeometric discretization method for incompressible materials

Abstract

This is Part II of a multipart article on a hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress. We introduce an isogeometric discretization method for incompressible materials and present test computations. Accounting for the out-of-plane normal stress distribution in the out-of-plane direction affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the shell. The return is more than what we get from accounting for the out-of-plane deformation mapping. The traction acting on the shell can be specified on the upper and lower surfaces separately. With that, the model is now free from the “midsurface’ location in terms of specifying the traction. In dealing with incompressible materials, we start with an augmented formulation that includes the pressure as a Lagrange multiplier and then eliminate it by using the geometrical representation of the incompressibility constraint. The resulting model is an extended one, in the Kirchhoff–Love category in the degree-of-freedom count, and encompassing all other extensions in the isogeometric subcategory. We include ordered details as a recipe for making the implementation practical. The implementation has two components that will not be obvious but might be critical in boundary integration. The first one is related to the edge-surface moment created by the Kirchhoff–Love assumption. The second one is related to the pressure/traction integrations over all the surfaces of the finite-thickness geometry. The test computations are for dome-shaped inflation of a flat circular shell, rolling of a rectangular plate, pinching of a cylindrical shell, and uniform hydrostatic pressurization of the pinched cylindrical shell. We compute with neo-Hookean and Mooney–Rivlin material models. To understand the effect of the terms added in the extended model, we compare with models that exclude some of those terms.

1 Introduction

This is Part II of a multipart article on a hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress. In Part I [1], we presented the formulation. Here we introduce an isogeometric discretization method for incompressible materials and present test computations. Because the method description and test computations would be rather extensive otherwise, we will cover compressible materials in future work.

1.1 History of related shell formulations and examples

We include this subsection from Part I to reiterate the significance of this work compared to earlier related work. A good number of shell models were presented earlier in the finite element context (see, for example, [2,3,4,5,6,7,8]), with significant effort in bending representation. The model in [5] is based on a mixed formulation. The model in [8] is based on a discontinuous-Galerkin type approximation to weakly enforce $C^1$ continuity. The model in [7] is a TUBA family element, which has displacement derivatives as unknowns to attain $C^1$ continuity in the displacement. The model we are introducing here is similar to the model in [2], which uses only one parameter to represent the out-of-plane deformation. Most of the other shell formulations, including some based on the Reissner–Mindlin theory, use the plane-stress assumption. The models in [3, 4], based on the Reissner–Mindlin theory, are, however, without the plane-stress assumption, in the finite element context.

1.2 Accounting for the out-of-plane normal stress: summary

The isogeometric Kirchhoff–Love shell models have the advantage of not requiring rotational degrees of freedom. Within this category of the models, the extended method presented in this article encompasses all other extensions. We list what the method accounts for beyond the Kirchhoff–Love shell theory

• out-of-plane deformation in the constitutive laws

• out-of-plane deformation in the out-of-plane integration

• curvature effects in the undeformed configuration

• quadratic terms in the metric tensor

• quadratic terms in the virtual work

• out-of-plane normal stress

• separate tractions acting on the upper and lower surfaces

• moment generated by the separate shear tractions on the upper and lower surfaces

• improved rotational kinematics

We reiterate, from [1], what motivated the development of the method introduced in Part I. The level of accuracy we are striving for in representing the tractions on the upper and lower surfaces would be meaningful in an fluid–structure interaction computation only if the flow solution method can deliver those tractions with a comparable level of accuracy. That level of flow solution accuracy, especially in representing the shear stress, requires moving-mesh methods [9], where the high mesh resolution near solid surfaces follows the fluid–solid interface as it moves. That is now possible even in flow computations with actual contact between solid surfaces or some other topology change. The Space–Time Topology Change method [10] enabled that. We can both represent the actual contact and have high-fidelity, moving-mesh flow solution near the solid surfaces.

1.3 Focus in Part II

We start with an augmented formulation that includes the pressure as a Lagrange multiplier and then eliminate it by using the geometrical representation of the incompressibility constraint. The resulting model is an extended one, in the Kirchhoff–Love category in the degree-of-freedom count, and encompassing all other extensions in the isogeometric subcategory. The vector form of the equations used in Part I provides good physical intuition about the formulation, and the tensor-coefficients form helps with efficient implementation. We include ordered details as a recipe for making the implementation practical. The implementation has two components that will not be obvious but might be critical in boundary integration. The first one is related to the edge-surface moment created by the Kirchhoff–Love assumption. The second one is related to the pressure/traction integrations over all the surfaces of the finite-thickness geometry. It will give us divergence-theorem-consistent representation in the integrations when the basis functions have $C^2$ continuity.

1.4 Outline of the remaining sections

In Sect. 2, we briefly provide the kinematics, including some of the crucial definitions, from Part I, mass conservation, and the incompressibility constraint. In Sect. 3, we present an augmented variational formulation that includes the pressure as a Lagrange multiplier. In Sect. 4, we eliminate the pressure by using the geometrical representation of the incompressibility constraint. We describe the isogeometric discretization method in Sect. 5, including the path to the tangent stiffness matrix, and key methods in the boundary integrations. The test computations are presented in Sect. 6, and the concluding remarks are given in Sect. 7. The notation rules and some operator definitions are given in Appendix A, complete expressions for the symbols, used in putting the equations in a compact form, detailed derivations, and range of acceptable shell thickness in Appendices B and C, and the constitutive models in Appendix D.

2 Hyperelastic incompressible shell model

2.1 Kinematics

2.1.1 Overview of geometry concepts introduced in Part I

The spatial domain $\varOmega _t= \overline{\varGamma }_t{\times }(h_\textrm{th})_t\in \mathbb {R}^{{n_{\textrm{sd}}}}$, where $\overline{\varGamma }_t$ represents the “midsurface.” The midsurface quantities are identified by an overbar. The undeformed configuration is denoted by subscript 0; $\varOmega _0= \overline{\varGamma }_0{\times }(h_\textrm{th})_0$, or by capital letters.

The position $\overline{{\textbf {x}}} \in \overline{\varGamma }_t$, its covariant basis vector is $\overline{{\textbf {g}}}_{\alpha }$, and $\xi ^{\alpha }$ represents the parametric space. The thickness direction is $\overline{{\textbf {n}}}$, and the parametric coordinate across the thickness is $\xi ^3$. The basis vectors depend on $\xi ^3$, and they are ${\textbf {g}}_{\alpha }$, while the normal direction remains the same. The counterparts in the undeformed configuration are $\overline{{\textbf {X}}} \in \overline{\varGamma }_0$, $\overline{{\textbf {G}}}_{\alpha }$, $\xi ^{\alpha }$, $\overline{{\textbf {N}}}$, $\xi ^3_0$, and ${\textbf {G}}_{\alpha }$. We note that

$$\begin{aligned} \textrm{d}\xi ^3 = \lambda _3 \textrm{d}\xi ^3_0, \end{aligned}$$

(1)

where $\lambda _3$ is the stretch in the thickness direction, and this parametrization was introduced in [11] to account for the out-of-plane deformation. We use the dual basis system, and the covariant metric tensor components for the current and undeformed configurations are

$$\begin{aligned} g_{\alpha \beta }&= \overline{g}_{\alpha \beta } + 2 \overline{\kappa }_{\alpha \beta } \xi ^3 + \overline{\omega }_{\alpha \beta } \left( \xi ^3\right) ^2, \end{aligned}$$

(2)

$$\begin{aligned} G_{\alpha \beta }&= \overline{G}_{\alpha \beta } + 2 \overline{K}_{\alpha \beta } \xi ^3_0 + \overline{\varOmega }_{\alpha \beta } \left( \xi ^3_0\right) ^2. \end{aligned}$$

(3)

With that, the deformation gradient tensor ${\textbf {F}}$, its determinant $J$, Cauchy–Green deformation tensor ${\textbf {C}}$, and Green–Lagrange strain tensor ${\textbf {E}}$ can be expressed. We also define the areas

$$\begin{aligned} A&= \sqrt{\left| g_{\bullet \bullet } \right| }, \end{aligned}$$

(4)

$$\begin{aligned} A_0&= \sqrt{\left| G_{\bullet \bullet } \right| }, \end{aligned}$$

(5)

and they depend on $\xi ^3$ and $\xi ^3_0$. We note that $\bullet$ serves as an index position indicator for whether the tensor components are covariant or contravariant. This simplifies the notation for the matrix operators, such as the determinant, reduces the dummy indices used, and reduces, the confusion that may arise from repeated usage of indices. For details of our notation, see Appendix A.

2.1.2 Areas and mass conservation

We introduce ratios that are independent of the parametrization and, for convenience, alternate notations z and $z_0$ for $\xi ^3$ and $\xi ^3_0$:

$$\begin{aligned} \frac{A}{~\overline{A}}&=\hat{A}(\xi ^3) =\hat{A}(z), \end{aligned}$$

(6)

$$\begin{aligned} \frac{A_0}{~\overline{A}_0}&=\hat{A}_0(\xi ^3_0)=\hat{A}_0(z_0), \end{aligned}$$

(7)

where $z = z_0 = 0$ at the midsurface.

Remark 1

The areas given by Eqs. (6) and (7) are represented by quadratic functions with coefficients that are the mean and Gaussian curvatures at the midsurface of the current and undeformed configurations.

The mass conservation law can be written as

$$\begin{aligned} \rho \hat{A}(z) \overline{A} \textrm{d}\xi ^3&= \rho _0 \hat{A}_0(z_0) \overline{A}_0 \textrm{d}\xi ^3_0, \end{aligned}$$

(8)

where z is a function of $z_0$, and using $\rho _0 = \rho J$, we get

$$\begin{aligned} \hat{A}(z) \textrm{d}\xi ^3 \frac{ \overline{A} }{ \overline{A}_0 }&= J\hat{A}_0(z_0) \textrm{d}\xi ^3_0. \end{aligned}$$

(9)

Integrating both sides of Eq. (9) in corresponding parametric coordinates, and defining the two functions

$$\begin{aligned} \hat{V} (\xi ^3)&= \int _{0}^{\xi ^3} \hat{A} (z) \textrm{d}z, \end{aligned}$$

(10)

$$\begin{aligned} \hat{V}_0(\xi _0^3)&= \int _{0}^{\xi _0^3}J\hat{A}_0 (z_0) \textrm{d}z_0, \end{aligned}$$

(11)

we get

$$\begin{aligned} \overline{A} \hat{V} (\xi ^3) = \overline{A}_0 \hat{V}_0(\xi _0^3). \end{aligned}$$

(12)

This relationship will represent the functional form

$$\begin{aligned} \xi ^3 = z(\xi ^3_0). \end{aligned}$$

(13)

The alternate form given by Eq. (12) is what we will use instead of Eq. (1).

We now take variation of both sides of Eq. (12) holding $\xi ^3_0$ constant at a given $\xi ^3_0$. The left-hand side is

$$\begin{aligned} \delta \left( \overline{A} \hat{V} \right)&= \left. \frac{\partial \left( \overline{A} \hat{V} \right) }{\partial \xi ^3} \right| _{A} \delta \xi ^3 + \left. \frac{\partial \left( \overline{A} \hat{V} \right) }{\partial A} \right| _{\xi ^3} \delta A \end{aligned}$$

(14)

$$\begin{aligned}&= \overline{A} \hat{A} \delta \xi ^3 + \int _{0}^{\xi ^3} \left. \delta A \right| _{\xi ^3} \textrm{d}z. \end{aligned}$$

(15)

By using Eq. (188) from Appendix B.3 and $\left. \delta {\textbf {g}}_{\alpha }\right| _{\xi ^3} = \delta \overline{{\textbf {g}}}_{\alpha } + \delta \overline{{\textbf {n}}}_{,\alpha } \xi ^3$, we get

$$\begin{aligned} \delta \left( \overline{A} \hat{V} \right)&= \overline{A} \hat{A} \delta \xi ^3 + \int _{0}^{\xi ^3} {\textbf {g}}^{\alpha } \cdot \left. \delta {\textbf {g}}_{\alpha } \right| _{\xi ^3} A \textrm{d}z \nonumber \\&= A \delta \xi ^3 + \overline{A} \int _{0}^{\xi ^3} {\textbf {g}}^{\alpha } \hat{A} \textrm{d}z \cdot \delta \overline{{\textbf {g}}}_{\alpha } \nonumber \\&\quad + \overline{A} \int _{0}^{\xi ^3} z {\textbf {g}}^{\alpha } \hat{A} \textrm{d}z \cdot \delta \overline{{\textbf {n}}}_{,\alpha } . \end{aligned}$$

(16)

The variation of the right-hand side of Eq. (12) is

$$\begin{aligned} \delta \left( \overline{A}_0 \hat{V}_0 \right)&= \overline{A}_0 \int _{0}^{\xi ^3_0} \delta J\hat{A}_0 \textrm{d}z_0 . \end{aligned}$$

(17)

We convert the integration to the current configuration as

$$\begin{aligned} \delta \left( \overline{A}_0 \hat{V}_0 \right)&= \int _{0}^{\xi ^3} \delta J\underbrace{A_0 \frac{1}{\lambda _3}}_{=J^{-1} A} \textrm{d}z \end{aligned}$$

(18)

$$\begin{aligned}&= \overline{A} \int _{0}^{\xi ^3} \delta \ln J\hat{A} \textrm{d}z . \end{aligned}$$

(19)

Thus, we obtain

$$\begin{aligned} \delta \xi ^3&= \underbrace{ - \frac{1}{\hat{A}} \int _{0}^{\xi ^3} {\textbf {g}}^{\alpha } \hat{A} \textrm{d}z }_{=\hat{{\textbf {q}}}_0^{\alpha }} \cdot \delta \overline{{\textbf {g}}}_{\alpha } \underbrace{ - \frac{1}{\hat{A}} \int _{0}^{\xi ^3} z {\textbf {g}}^{\alpha } \hat{A} \textrm{d}z }_{=\hat{{\textbf {q}}}_1^{\alpha }} \cdot \delta \overline{{\textbf {n}}}_{,\alpha } \nonumber \\ {}&\quad + \underbrace{ \frac{1}{\hat{A}} \int _{0}^{\xi ^3} \delta \ln J\hat{A} \textrm{d}z }_{ =\delta \hat{J} } . \end{aligned}$$

(20)

For notational convenience, we introduce $\hat{{\textbf {q}}}_0^{\alpha }$, $\hat{{\textbf {q}}}_1^{\alpha }$, and $\delta \hat{J}$, and write as

$$\begin{aligned} \delta \xi ^3&= \hat{{\textbf {q}}}_0^{\alpha } \cdot \delta \overline{{\textbf {g}}}_{\alpha } + \hat{{\textbf {q}}}_1^{\alpha } \cdot \delta \overline{{\textbf {n}}}_{,\alpha } + \delta \hat{J} . \end{aligned}$$

(21)

2.1.3 Incompressibility constraint

With the incompressibility constraint $J= 1$, Eq. (11) becomes

$$\begin{aligned} \hat{V}_0(\xi _0^3)&= \int _{0}^{\xi _0^3}\hat{A}_0 (z_0) \textrm{d}z_0. \end{aligned}$$

(22)

This and Eq. (10) can be integrated independently. With that, Eq. (13) becomes a cubic function relating $\xi ^3$ and $\xi ^3_0$, and satisfying this equation makes $J= 1$ pointwise along the thickness direction for any midsurface deformation.

3 Variational formulation augmented by pressure

3.1 Strain-energy density and stress tensor

We assume that the strain-energy density function can be separated into the isovolumetric and volumetric parts as

$$\begin{aligned} \varphi = \varphi _\textrm{iso}+ \varphi _\textrm{vol}. \end{aligned}$$

(23)

For incompressible material, the volumetric part can be represented with pressure as the Lagrange multiplier:

$$\begin{aligned} \varphi _\textrm{vol}= p (1 - J), \end{aligned}$$

(24)

and $\varphi _\textrm{iso}$ does not depend on p. The second Piola–Kirchhoff tensor can also be separated into two parts:

$$\begin{aligned} {\textbf {S}}&= S^{\alpha \beta }{\textbf {G}}_{\alpha }{\textbf {G}}_{\beta } + S^{33}\overline{{\textbf {N}}}~\overline{{\textbf {N}}}\end{aligned}$$

(25)

$$\begin{aligned}&= S_\textrm{iso}^{\alpha \beta }{\textbf {G}}_{\alpha }{\textbf {G}}_{\beta } + S^{33}_\textrm{iso}\overline{{\textbf {N}}}~\overline{{\textbf {N}}}+ S_\textrm{vol}^{\alpha \beta }{\textbf {G}}_{\alpha }{\textbf {G}}_{\beta } + S^{33}_\textrm{vol}\overline{{\textbf {N}}}~\overline{{\textbf {N}}}, \end{aligned}$$

(26)

where

$$\begin{aligned} S_\textrm{iso}^{\alpha \beta }&= \frac{\partial \varphi _\textrm{iso}}{\partial E_{\alpha \beta }}, \end{aligned}$$

(27)

$$\begin{aligned} S^{33}_\textrm{iso}&= \frac{\partial \varphi _\textrm{iso}}{\partial E_{3 3}}, \end{aligned}$$

(28)

$$\begin{aligned} S_\textrm{vol}^{\alpha \beta }&= \frac{\partial \varphi _\textrm{vol}}{\partial E_{\alpha \beta }}, \end{aligned}$$

(29)

$$\begin{aligned} S^{33}_\textrm{vol}&= \frac{\partial \varphi _\textrm{vol}}{\partial E_{3 3}}. \end{aligned}$$

(30)

This is based on writing the Green–Lagrange strain tensor as ${\textbf {E}}= E_{\alpha \beta } {\textbf {G}}^{\alpha }\,{\textbf {G}}^{\beta } + E_{33} \overline{{\textbf {N}}}\, \overline{{\textbf {N}}}.$ The volumetric parts can further be rewritten as

$$\begin{aligned} S_\textrm{vol}^{\alpha \beta }&= - p \frac{\partial J}{\partial E_{\alpha \beta }} = -p Jg^{\alpha \beta }, \end{aligned}$$

(31)

$$\begin{aligned} S^{33}_\textrm{vol}&= - p \frac{\partial J}{\partial E_{3 3}} = -p \frac{J}{\lambda _3^2}. \end{aligned}$$

(32)

3.2 Internal virtual work

We repeat here Eq. (74) from Part I:

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \int _{(h_\textrm{th})_0} {\textbf {g}}_{\beta } S^{{\alpha } \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,{\alpha }} \cdot \int _{(h_\textrm{th})_0} \xi ^3 {\textbf {g}}_{\beta } S^{{\alpha } \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \overline{{\textbf {n}}}_{,{\alpha }} \cdot \int _{(h_\textrm{th})_0} \delta \xi ^3 {\textbf {g}}_{\beta } S^{{\alpha } \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \overline{{\textbf {n}}}\cdot \int _{(h_\textrm{th})_0} \delta \lambda _3 \lambda _3 \overline{{\textbf {n}}}S^{33} \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta p\left( 1 - J\right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(33)

We consider the following equations:

$$\begin{aligned} \overline{{\textbf {n}}}_{,{\alpha }} \cdot {\textbf {g}}_{\beta }&= \underbrace{ \overline{\kappa }_{\alpha \beta } + \overline{\omega }_{\alpha \beta } \xi ^3 }_{\kappa _{\alpha \beta }}, \end{aligned}$$

(34)

$$\begin{aligned} \delta \lambda _3&= \frac{\textrm{d}\delta \xi ^3}{\textrm{d}\xi ^3_0} = \lambda _3 \frac{\textrm{d}\delta \xi ^3}{\textrm{d}\xi ^3}. \end{aligned}$$

(35)

Substituting them into Eq. (33), we get

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \int _{(h_\textrm{th})_0} {\textbf {g}}_{\beta } S^{{\alpha } \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,{\alpha }} \cdot \int _{(h_\textrm{th})_0} \xi ^3 {\textbf {g}}_{\beta } S^{{\alpha } \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \xi ^3 \kappa _{{\alpha } \beta } S^{{\alpha } \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \frac{\textrm{d}\delta \xi ^3}{\textrm{d}\xi ^3} \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta p\left( 1 - J\right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(36)

The along-the-thickness part of the fourth integral can be rearranged as

$$\begin{aligned} \int _{(h_\textrm{th})_0} \frac{\textrm{d}\delta \xi ^3}{\textrm{d}\xi ^3} \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3&= \int _{(h_\textrm{th})_0} \frac{ 1 }{\hat{A}} \frac{\textrm{d}\left( \delta \xi ^3 \hat{A}\right) }{\textrm{d}\xi ^3} \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \nonumber \\&\quad - \int _{(h_\textrm{th})_0} \delta \xi ^3 \underbrace{ \frac{ 1 }{\hat{A}} \frac{\textrm{d}\hat{A}}{\textrm{d}\xi ^3} }_{ =\frac{\textrm{d}\ln \hat{A}}{\textrm{d}\xi ^3} } \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 . \end{aligned}$$

(37)

Using

$$\begin{aligned} \frac{\textrm{d}\ln A}{\textrm{d}\xi ^3}&= \frac{1}{2} g^{\alpha \beta } \underbrace{ \frac{\textrm{d}g_{\alpha \beta }}{\textrm{d}\xi ^3} }_{ { = 2\left( \overline{\kappa }_{\alpha \beta } + \overline{\omega }_{\alpha \beta } \xi ^3 \right) } } \end{aligned}$$

(38)

$$\begin{aligned}&= g^{\alpha \beta } \kappa _{\alpha \beta } \end{aligned}$$

(39)

and

$$\begin{aligned} \frac{\textrm{d}\left( \delta \xi ^3 \hat{A}\right) }{\textrm{d}\xi ^3}&= - \delta \overline{{\textbf {g}}}_{\alpha } \cdot {\textbf {g}}^{\alpha } \hat{A} - \delta \overline{{\textbf {n}}}_{,\alpha } \cdot \xi ^3 {\textbf {g}}^{\alpha } \hat{A} + \delta \ln J\hat{A} , \end{aligned}$$

(40)

which can be obtained from Eq. (20), we get

$$\begin{aligned} \int _{(h_\textrm{th})_0} \frac{\textrm{d}\delta \xi ^3}{\textrm{d}\xi ^3} \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3&= - \delta \overline{{\textbf {g}}}_{\alpha } \cdot \int _{(h_\textrm{th})_0} {\textbf {g}}^{\alpha } \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \nonumber \\&\quad - \delta \overline{{\textbf {n}}}_{,\alpha } \cdot \int _{(h_\textrm{th})_0} \xi ^3 {\textbf {g}}^{\alpha } \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \nonumber \\&\quad + \int _{(h_\textrm{th})_0} \delta \ln J\lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \nonumber \\&\quad - \int _{(h_\textrm{th})_0} \delta \xi ^3 g^{\alpha \beta } \kappa _{\alpha \beta } \lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 . \end{aligned}$$

(41)

Substituting this into Eq. (36), we obtain

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \int _{(h_\textrm{th})_0} {\textbf {g}}_{\beta } \left( S^{{\alpha } \beta } - \lambda _3^2 S^{33} g^{\alpha \beta } \right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,{\alpha }} \cdot \int _{(h_\textrm{th})_0} \xi ^3 {\textbf {g}}_{\beta } \left( S^{{\alpha } \beta } - \lambda _3^2 S^{33} g^{\alpha \beta } \right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \xi ^3 \kappa _{{\alpha } \beta } \left( S^{{\alpha } \beta } - \lambda _3^2 S^{33} g^{\alpha \beta } \right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \ln J\lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta p\left( 1 - J\right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(42)

We introduce

$$\begin{aligned} \tilde{S}^{\alpha \beta }&= S^{\alpha \beta } - \lambda _3^2 g^{\alpha \beta } S^{33} \end{aligned}$$

(43)

for notational convenience and substitute Eq. (20) into Eq. (42), obtaining

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \int _{(h_\textrm{th})_0} \left( {\textbf {g}}_{\beta } \tilde{S}^{{\alpha } \beta } + \hat{{\textbf {q}}}_0^{\alpha } \kappa _{{\gamma } \delta } \tilde{S}^{{\gamma } \delta } \right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,{\alpha }} \cdot \int _{(h_\textrm{th})_0} \left( \xi ^3 {\textbf {g}}_{\beta } \tilde{S}^{{\alpha } \beta } + \hat{{\textbf {q}}}_1^{\alpha } \kappa _{{\gamma } \delta } \tilde{S}^{{\gamma } \delta } \right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \hat{J} \kappa _{{\gamma } \delta } \tilde{S}^{{\gamma } \delta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \ln J\lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta p\left( 1 - J\right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(44)

As in Part I, we define the first Piola–Kirchhoff tensor $\tilde{{\textbf {p}}}^{\alpha } {\textbf {G}}_{\alpha }$ as

$$\begin{aligned} \tilde{{\textbf {p}}}^{\alpha }&= {\textbf {g}}_{\beta } \tilde{S}^{{\alpha } \beta }\hat{A}_0 , \end{aligned}$$

(45)

and its integral over $(h_\textrm{th})_0$ as

$$\begin{aligned} \hat{\tilde{{\textbf {p}}}}_0^{\alpha }&= \int _{(h_\textrm{th})_0} \tilde{{\textbf {p}}}^{\alpha } \textrm{d}\xi ^3 , \end{aligned}$$

(46)

and its first moment as

$$\begin{aligned} \hat{\tilde{{\textbf {p}}}}_1^{\alpha }&= \int _{(h_\textrm{th})_0} \xi ^3 \tilde{{\textbf {p}}}^{\alpha } \textrm{d}\xi ^3 . \end{aligned}$$

(47)

With those, we obtain

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \left( \hat{\tilde{{\textbf {p}}}}_0^{{\alpha }} + \int _{(h_\textrm{th})_0} \hat{{\textbf {q}}}_0^{\alpha } \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,{\alpha }} \cdot \left( \hat{\tilde{{\textbf {p}}}}_1^{\alpha } + \int _{(h_\textrm{th})_0} \hat{{\textbf {q}}}_1^{\alpha } \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \hat{J} \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta \ln J\lambda _3^2 S^{33} \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta p\left( 1 - J\right) \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(48)

We also note that the volumetric part of $\tilde{S}^{\gamma \delta }$ is canceled as follows:

$$\begin{aligned} \tilde{S}^{\gamma \delta }&= S^{\gamma \delta }_\textrm{iso}- p Jg^{\gamma \delta } - \lambda _3^2 g^{\gamma \delta } \left( S^{33}_\textrm{iso}- p \frac{J}{\lambda _3^2} \right) \end{aligned}$$

(49)

$$\begin{aligned}&= S^{\gamma \delta }_\textrm{iso}- \lambda _3^2 g^{\gamma \delta } S^{33}_\textrm{iso} . \end{aligned}$$

(50)

3.3 External virtual work

The external virtual work is given by Eq. (103) in Part I. From Part I, we expand Eq. (108) by using Eq. (21):

$$\begin{aligned} \delta W_{\textrm{exsurf}}&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {x}}} \cdot \left( \hat{{\textbf {h}}}_{0}^- + \hat{{\textbf {h}}}_{0}^+ \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}\cdot \left( \hat{{\textbf {h}}}_{1}^- + \hat{{\textbf {h}}}_{1}^+ \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \left( \left. \left( \hat{{\textbf {q}}}_0^{\alpha } \hat{p}^- \right) \right| _{(\xi ^3_0)^-} - \left. \left( \hat{{\textbf {q}}}_0^{\alpha } \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,\alpha } \cdot \left( \left. \left( \hat{{\textbf {q}}}_1^{\alpha } \hat{p}^- \right) \right| _{(\xi ^3_0)^-} - \left. \left( \hat{{\textbf {q}}}_1^{\alpha } \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \left( \left. \left( \delta \hat{J} \hat{p}^- \right) \right| _{(\xi ^3_0)^-} - \int _{\overline{\varGamma }_0} \left. \left( \delta \hat{J} \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} \right) \textrm{d}\varGamma , \end{aligned}$$

(51)

and write Eq. (147) from Part I:

$$\begin{aligned} \delta W_\textrm{exedge}&= \int _{\overline{S}_0} \delta \overline{{\textbf {x}}}\cdot \hat{{\textbf {h}}}_0^\textrm{e} \textrm{d}S + \int _{\overline{S}_0} \delta \overline{{\textbf {n}}}\cdot \hat{{\textbf {h}}}_1^\textrm{e} \textrm{d}S. \end{aligned}$$

(52)

Here $\hat{{\textbf {h}}}_{0}^\textrm{e}$ and $\hat{{\textbf {h}}}_{1}^\textrm{e}$ are the traction and its first moment (see Eqs. (144) and (145) in Part I).

Remark 2

We note that $\hat{p}^-$ and $\hat{p}^+$ are defined by Eqs. (113) and (114) in Part I. They are the normal tractions, not the pressure.

4 Variational formulation with the pressure eliminated

For any midsurface deformation, we construct $\delta U$ using $J= 1$ (see Sect. 2.1.3), and the Lagrange multiplier p is eliminated completely.

4.1 Internal virtual work

With $J=1$ and $\delta J= 0$ in Eq. (48), we get

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \left( \hat{\tilde{{\textbf {p}}}}_0^{{\alpha }} + \int _{(h_\textrm{th})_0} \hat{{\textbf {q}}}_0^{\alpha } \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,{\alpha }} \cdot \left( \hat{\tilde{{\textbf {p}}}}_1^{\alpha } + \int _{(h_\textrm{th})_0} \hat{{\textbf {q}}}_1^{\alpha } \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \right) \textrm{d}\varGamma . \end{aligned}$$

(53)

As seen in Eq. (50), the integration does not involve the pressure.

4.2 External virtual work

With $\delta J=0$ in Eq. (51), we get

$$\begin{aligned} \delta W_{\textrm{exsurf}}&= \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {x}}} \cdot \left( \hat{{\textbf {h}}}_{0}^- + \hat{{\textbf {h}}}_{0}^+ \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}\cdot \left( \hat{{\textbf {h}}}_{1}^- + \hat{{\textbf {h}}}_{1}^+ \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {g}}}_{\alpha } \cdot \left( \left. \left( \hat{{\textbf {q}}}_0^{\alpha } \hat{p}^- \right) \right| _{(\xi ^3_0)^-} - \left. \left( \hat{{\textbf {q}}}_0^{\alpha } \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{{\textbf {n}}}_{,\alpha } \cdot \left( \left. \left( \hat{{\textbf {q}}}_1^{\alpha } \hat{p}^- \right) \right| _{(\xi ^3_0)^-} - \left. \left( \hat{{\textbf {q}}}_1^{\alpha } \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} \right) \textrm{d}\varGamma , \end{aligned}$$

(54)

and there is no change in Eq. (52):

$$\begin{aligned} \delta W_{\textrm{exedge}}&= \int _{\overline{S}_0} \delta \overline{{\textbf {x}}} \cdot \hat{{\textbf {h}}}_{0}^\textrm{e} \textrm{d}S + \int _{\overline{S}_0} \delta \overline{{\textbf {n}}}\cdot \hat{{\textbf {h}}}_{1}^\textrm{e} \textrm{d}S . \end{aligned}$$

(55)

4.3 Internal force and moment

We see the internal force $\left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _0^{\alpha }$ and moment $\left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha }$ as the factors of $\delta \overline{{\textbf {g}}}_{\alpha }$ and $\delta \overline{{\textbf {n}}}_{,{\alpha }}$ in the integrals over $\overline{\varGamma }_0$:

$$\begin{aligned} \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _0^{\alpha }&= \hat{\tilde{{\textbf {p}}}}_0^{{\alpha }} + \int _{(h_\textrm{th})_0} \hat{{\textbf {q}}}_0^{\alpha } \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \nonumber \\ {}&\quad + \left. \left( \hat{{\textbf {q}}}_0^{\alpha } \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} - \left. \left( \hat{{\textbf {q}}}_0^{\alpha } \hat{p}^- \right) \right| _{(\xi ^3_0)^-} , \end{aligned}$$

(56)

$$\begin{aligned} \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha }&= \hat{\tilde{{\textbf {p}}}}_1^{\alpha } + \int _{(h_\textrm{th})_0} \hat{{\textbf {q}}}_1^{\alpha } \kappa _{\gamma \delta } \tilde{S}^{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \nonumber \\&\quad + \left. \left( \hat{{\textbf {q}}}_1^{\alpha } \hat{p}^+ \right) \right| _{(\xi ^3_0)^+} - \left. \left( \hat{{\textbf {q}}}_1^{\alpha } \hat{p}^- \right) \right| _{(\xi ^3_0)^-} . \end{aligned}$$

(57)

Remark 3

We note that in the strong-form representation, $\left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _0^{\alpha }$ and $\left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha }$ are the same as $\hat{{\textbf {p}}}_0^{\alpha }$ and $\hat{{\textbf {p}}}_1^{\alpha }$ in the Part I; but not in the discrete form.

The moment $\left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha }$ with respect to the midsurface may need to be converted to moment with respect to a surface of our choice, $\breve{\xi }^3$, in the deformed configuration. We do that by first writing

$$\begin{aligned} \breve{\hat{\tilde{{\textbf {p}}}}}_1^{\alpha }&= \int _{(h_\textrm{th})_0} \left( \xi ^3 - \breve{\xi }^3 \right) \tilde{{\textbf {p}}}^{\alpha } \textrm{d}\xi ^3 \end{aligned}$$

(58)

$$\begin{aligned}&= \hat{\tilde{{\textbf {p}}}}_1^{\alpha } - \breve{\xi }^3 \hat{\tilde{{\textbf {p}}}}_0^{\alpha } , \end{aligned}$$

(59)

and

$$\begin{aligned} \breve{\hat{{\textbf {q}}}}_1^{\alpha }&= - \frac{1}{\hat{A}} \int _0^{\xi ^3} {\textbf {g}}^{\alpha } (z - \breve{\xi }^3) \hat{A} \textrm{d}z \end{aligned}$$

(60)

$$\begin{aligned}&= \hat{{\textbf {q}}}_1^{\alpha } - \breve{\xi }^3 \hat{{\textbf {q}}}_0^{\alpha } , \end{aligned}$$

(61)

and then using those in Eq. (57). With that and Eq. (56), the conversion becomes

$$\begin{aligned} \left( \breve{\hat{{\textbf {p}}}}_{\textrm{tot}}\right) _1^{\alpha }&= \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha } - \breve{\xi }^3 \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _0^{\alpha } . \end{aligned}$$

(62)

Remark 4

Most shell formulations do not take into account the deformation in the thickness direction, and the moment center is typically at the midsurface, resulting in

$$\begin{aligned} \breve{\xi }^3&= \frac{\left( \xi ^3\right) ^- + \left( \xi ^3\right) ^+}{2} , \end{aligned}$$

(63)

and that corresponds to the undeformed-configuration midsurface

$$\begin{aligned} \breve{\xi }^3_0&= \frac{\left( \xi ^3_0\right) ^- + \left( \xi ^3_0\right) ^+}{2} . \end{aligned}$$

(64)

In our formulation here, the thickness-direction centers of in the undeformed and deformed configurations may not correspond to each other. In addition, a more physically meaningful location would be the centroid, which would give zero moment under uniform pressure. We note that in many applications, the undeformed configuration is a flat plate or we may not be taking the curvature effects into account. In those cases, Eq. (64) represents the centroid. In our formulation, if we chose $\breve{\xi }^3$ to be the centroid, from

$$\begin{aligned} \int _{(h_\textrm{th})_t} \left( \xi ^3 - \breve{\xi }^3 \right) \frac{L}{\overline{L}~} \textrm{d}\xi ^3 =0 , \end{aligned}$$

(65)

we get

$$\begin{aligned} \breve{\xi }^3&= \frac{ \int _{(h_\textrm{th})_t} \xi ^3 L\textrm{d}\xi ^3 }{ \int _{(h_\textrm{th})_t} L\textrm{d}\xi ^3 } . \end{aligned}$$

(66)

We can also express this at the undeformed configuration:

$$\begin{aligned} \breve{\xi }^3&= \frac{ \int _{(h_\textrm{th})_0} \xi ^3 \lambda _\textrm{T} L_0\lambda _3 \textrm{d}\xi ^3 }{ \int _{(h_\textrm{th})_0} \lambda _\textrm{T} L_0\lambda _3 \textrm{d}\xi ^3 } . \end{aligned}$$

(67)

See the definition of $L$, $\overline{L}$, $L_0$, $\overline{L}_0$, and $\lambda _\textrm{T}$ in Section 3.4 of Part I.

5 Computational method

In this section, we describe the full method for the isogeometric discretization, including the linearization needed in the Newton–Raphson iterations. We also describe a method for reducing the effect of the edge-surface moment creation by the Kirchhoff–Love assumption in arbitrary midsurface selection. Furthermore, we describe a divergence-theorem consistent pressure/traction integration method to overcome the difficulty due to the finite-thickness geometry.

5.1 Geometrical representation of the incompressibility constraint

We start with the geometrical-constraint equation given by Eq. (12). The area ratios in both the current and undeformed configurations can be expressed using the mean and Gaussian curvatures:

$$\begin{aligned} \hat{A}(z)&= 1 + 2 \overline{\kappa }_\textrm{M} z + \overline{\kappa }_\textrm{G} z^2, \end{aligned}$$

(68)

$$\begin{aligned} \hat{A}_0(z_0)&= 1 + 2 \overline{K}_\textrm{M} z_0 + \overline{K}_\textrm{G} z^2_0. \end{aligned}$$

(69)

See the definitions and usable expressions for the mean and Gaussian curvatures in Appendix B.1. When the midsurface deformation is given, the midsurface quantities are given. Therefore, we can integrate the above equations as

$$\begin{aligned} \hat{V}(z)&= z + \overline{\kappa }_\textrm{M} z^2 + \frac{1}{3}\overline{\kappa }_\textrm{G} z^3, \end{aligned}$$

(70)

$$\begin{aligned} \hat{V}_0(z_0)&= z_0 + \overline{K}_\textrm{M} z_0^2 + \frac{1}{3}\overline{K}_\textrm{G} z^3_0. \end{aligned}$$

(71)

With those, for a given $z_0 = \xi ^3_0$, using Eq. (12), we can obtain the current position $z = \xi ^3$ in the functional form of Eq. (13) by solving, with Newton–Raphson iterations, a cubic function for z. We note that there is a restriction on acceptable solutions for z. The restriction comes from not having overlapping material points due to high curvatures or large thicknesses. The range of acceptable z can be predetermined. We use that information to disallow going beyond that range in the Newton–Raphson solution of the cubic equation.

Remark 5

This is a limitation of the formulation here; if three is overlapping, the computation cannot proceed with the discretization used.

5.2 Variational formulation for isogeometric discretization

In many other shell implementations, we see the thickness integrations done term by term. In the formulation here, it is significantly more efficient to evaluate all the terms together at each thickness position. For that, we use quadrature points in the undeformed configuration and the corresponding points in the deformed configuration can be obtained as described in Sect. 5.1. Consequently, in our method, we evaluate the residuals using a rather simple expression of the form

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta E_{\alpha \beta } \tilde{S}^{\alpha \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(72)

Here $\tilde{S}^{\alpha \beta }$ is obtained, at each thickness integration point, from Eq. (50), using the Green–Lagrange strain tensor or Cauchy–Green deformation tensor, and

$$\begin{aligned} \delta E_{\alpha \beta }&= \delta \overline{\varepsilon }_{\alpha \beta } + \delta \overline{\kappa }_{\alpha \beta } \xi ^3 + \frac{1}{2} \delta \overline{\omega }_{\alpha \beta } \left( \xi ^3\right) ^2 + \delta \xi ^3 \kappa _{\alpha \beta } . \end{aligned}$$

(73)

Here $\kappa _{\alpha \beta }$ is not an independent variable (see Eq. (34)), and $\delta \overline{\omega }_{\alpha \beta }$ and $\delta \xi ^3$ are also not independent from the midsurface quantities and $\delta \overline{\varepsilon }_{\alpha \beta }$ and $\delta \overline{\kappa }_{\alpha \beta }$. Those variations can be expressed as

$$\begin{aligned} \delta \overline{\omega }_{\alpha \beta }&= 2 \delta \overline{\varepsilon }_{\gamma \delta } \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta } + 2 \delta \overline{\kappa }_{\gamma \delta } \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta } , \end{aligned}$$

(74)

$$\begin{aligned} \delta \xi ^3&= \delta \overline{\varepsilon }_{\alpha \beta } Q_\varepsilon ^{\alpha \beta } + \delta \overline{\kappa }_{\alpha \beta } Q_\kappa ^{\alpha \beta } . \end{aligned}$$

(75)

Here $\left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta }$ and $\left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta }$ are given by Eqs. (223) and (224) of Appendix B.5.1, and $Q_\varepsilon ^{\alpha \beta }$ and $Q_\kappa ^{\alpha \beta }$ are given by Eqs. (251) and (254) of Appendix B.6.2.

5.3 Linearization for the Newton–Raphson iterations

The variation with subscript a is associated with the variational formulation, and the variation with subscript b is associated with the iteration linearization:

$$\begin{aligned} \delta _a \delta _b U&= \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta _a E_{\alpha \beta } \delta _b \tilde{S}^{\alpha \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta _a \delta _b E_{\alpha \beta } \tilde{S}^{\alpha \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \end{aligned}$$

(76)

$$\begin{aligned}&= \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta _a E_{\alpha \beta } {\tilde{\mathbb {C}}}^{ \alpha \beta \gamma \delta } \delta _b E_{\gamma \delta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \int _{(h_\textrm{th})_0} \delta _a \delta _b E_{\alpha \beta } \tilde{S}^{\alpha \beta } \hat{A}_0 \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(77)

The elastic moduli ${\tilde{\mathbb {C}}}^{\alpha \beta \gamma \delta }$, which include the effect of the thickness-direction deformation, are given by Eq. (282) of Appendix C. For the second integral, which is the geometric stiffness, we need the second variation of $E_{\alpha \beta }$:

$$\begin{aligned} \delta _a \delta _b E_{\alpha \beta }&= \left( \delta _a \overline{\kappa }_{\alpha \beta } + \delta _a \overline{\omega }_{\alpha \beta } \xi ^3 \right) \delta _b \xi ^3\nonumber \\&\quad + \delta _a \xi ^3 \left( \delta _b \overline{\kappa }_{\alpha \beta } + \delta _b \overline{\omega }_{\alpha \beta } \xi ^3 \right) \nonumber \\ {}&\quad + \overline{\omega }_{\alpha \beta } \delta _a \xi ^3 \delta _b \xi ^3 + \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } + \delta _a \delta _b \overline{\kappa }_{\alpha \beta } \xi ^3 \nonumber \\ {}&\quad + \frac{1}{2} \delta _a \delta _b \overline{\omega }_{\alpha \beta } {\left( \xi ^3\right) }^2 + \delta _a \delta _b \xi ^3 \kappa _{\alpha \beta } . \end{aligned}$$

(78)

We already mentioned that $\kappa _{\alpha \beta }$, $\delta \overline{\omega }_{\alpha \beta }$, and $\delta \xi ^3$ are not independent, and here $\delta _a \delta _b \overline{\omega }_{\alpha \beta }$ and $\delta _a \delta _b \xi ^3$ are also not independent. We see $\delta _a \delta _b \overline{\omega }_{\alpha \beta }$ only in the double contraction $\frac{1}{2} \delta _a \delta _b \overline{\omega }_{\alpha \beta } \tilde{S}^{\alpha \beta }$, and that can be written as

$$\begin{aligned} \frac{1}{2} \delta _a \delta _b \overline{\omega }_{\alpha \beta } \tilde{S}^{\alpha \beta }&= \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon }+ \delta _a \delta _b \overline{\kappa }_{\alpha \beta }\nonumber \\&\quad \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon }- \delta _a \overline{\varepsilon }_{\alpha \beta } \nonumber \\&\quad {\left[ 4 \left( \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\bullet \bullet }_{\quad \bullet \bullet } : \tilde{S}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\varepsilon }_{\alpha \beta } {\left[ 2 \left( \overline{g}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \cdot \tilde{S}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\kappa }_{\alpha \beta } \left[ 2 \left( \tilde{S}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \cdot \overline{g}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \left[ \tilde{S}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } . \end{aligned}$$

(79)

The derivation is given in Appendix B.5.2. The other dependent second variation can be expressed as

$$\begin{aligned} \delta _a \delta _b \xi ^3&= \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } Q_\varepsilon ^{\alpha \beta } + \delta _a \delta _b \overline{\kappa }_{\alpha \beta } Q_\kappa ^{\alpha \beta } \nonumber \\ {}&\quad + \delta _a \overline{\varepsilon }_{\alpha \beta } \mathbb {Q}_{\varepsilon \varepsilon }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } + \delta _a \overline{\varepsilon }_{\alpha \beta } \mathbb {Q}_{\varepsilon \kappa }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \mathbb {Q}_{\kappa \varepsilon }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } + \delta _a \overline{\kappa }_{\alpha \beta } \mathbb {Q}_{\kappa \kappa }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } . \end{aligned}$$

(80)

The derivation can be found in Appendix B.6.2, together with the expressions for $\mathbb {Q}_{\varepsilon \varepsilon }^{\alpha \beta \gamma \delta }$, $\mathbb {Q}_{\varepsilon \kappa }^{\alpha \beta \gamma \delta }$, and $\mathbb {Q}_{\kappa \kappa }^{\alpha \beta \gamma \delta }$ (see Eqs. (261),(263) and (264)), and $\mathbb {Q}_{\kappa \varepsilon }^{\alpha \beta \gamma \delta } = \mathbb {Q}_{\varepsilon \kappa }^{\gamma \delta \alpha \beta }$.

5.4 Implementation details

Based on the earlier subsections, we introduce some new tensors and express $\delta U$ and $\delta _a \delta _b U$ as

$$\begin{aligned} \delta U&= \int _{\overline{\varGamma }_0} \delta \overline{\varepsilon }_{\alpha \beta } \left( \int _{(h_\textrm{th})_0} \left( \mathbb {B}_{\varepsilon }(z(\xi ^3_0)) \right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \right) \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta \overline{\kappa }_{\alpha \beta } \left( \int _{(h_\textrm{th})_0} \left( \mathbb {B}_{\kappa }(z(\xi ^3_0)) \right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \right) \textrm{d}\varGamma \end{aligned}$$

(81)

and

$$\begin{aligned}&\delta _a \delta _b U= \int _{\overline{\varGamma }_0} \delta _a \overline{\varepsilon }_{\alpha \beta } \int _{(h_\textrm{th})_0} \left( \mathbb {D}_{\varepsilon \varepsilon } (z(\xi ^3_0)) \right) ^{ \alpha \beta \gamma \delta }\nonumber \\&\quad \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \delta _b \overline{\varepsilon }_{\gamma \delta } \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta _a \overline{\varepsilon }_{\alpha \beta } \int _{(h_\textrm{th})_0} \left( \mathbb {D}_{\varepsilon \kappa } (z(\xi ^3_0)) \right) ^{ \alpha \beta \gamma \delta } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \delta _b \overline{\kappa }_{\gamma \delta } \textrm{d}\varGamma \nonumber \\ {}&\quad + \int _{\overline{\varGamma }_0} \delta _a \overline{\kappa }_{\alpha \beta } \int _{(h_\textrm{th})_0} \left( \mathbb {D}_{\kappa \varepsilon } (z(\xi ^3_0)) \right) ^{ \alpha \beta \gamma \delta } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \delta _b \overline{\varepsilon }_{\gamma \delta } \textrm{d}\varGamma \nonumber \\&\quad + \int _{\overline{\varGamma }_0} \delta _a \overline{\kappa }_{\alpha \beta } \int _{(h_\textrm{th})_0} \left( \mathbb {D}_{\kappa \kappa } (z(\xi ^3_0)) \right) ^{ \alpha \beta \gamma \delta } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \delta _b \overline{\kappa }_{\gamma \delta } \textrm{d}\varGamma \nonumber \\ {}&\quad + \int _{\overline{\varGamma }_0} \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } \int _{(h_\textrm{th})_0} \left( \mathbb {B}_{\varepsilon }(z(\xi ^3_0)) \right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \textrm{d}\varGamma \nonumber \\ {}&\quad + \int _{\overline{\varGamma }_0} \delta _a \delta _b \overline{\kappa }_{\alpha \beta } \int _{(h_\textrm{th})_0} \left( \mathbb {B}_{\kappa }(z(\xi ^3_0)) \right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon } \hat{A}_0(\xi ^3_0) \textrm{d}\xi ^3 \textrm{d}\varGamma . \end{aligned}$$

(82)

The tensors introduced above are also evaluated at each thickness position. They are expressed as

$$\begin{aligned} {\left( \mathbb {B}_{\varepsilon }(z) \right) }^{\alpha \beta }_{\quad \chi \epsilon }&= {{\left[ {\delta ^{\bullet }}_{\bullet } \odot {\delta ^{\bullet }}_{\bullet } \right] }^{\alpha \beta }}_{\chi \epsilon } + z^2 \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\alpha \beta }_{\quad \chi \epsilon } + Q_\varepsilon ^{\alpha \beta } \kappa _{\chi \epsilon } , \end{aligned}$$

(83)

$$\begin{aligned} {\left( \mathbb {B}_{\kappa }(z) \right) }^{\alpha \beta }_{\quad \chi \epsilon }&= z {{\left[ {\delta ^{\bullet }}_{\bullet } \odot {\delta ^{\bullet }}_{\bullet } \right] }^{\alpha \beta }}_{\chi \epsilon } + z^2 \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\alpha \beta }_{\quad \chi \epsilon } + Q_\kappa ^{\alpha \beta } \kappa _{\chi \epsilon } , \end{aligned}$$

(84)

and

(85)

(86)

(87)

(88)

where

(89)

(90)

(91)

(92)

Remark 6

We note that all second-order tensors have symmetry and all fourth-order tensors have at least minor symmetry. We can express these by using the Voigt notation.

Remark 7

The double contraction operator “ : ” between fourth-order tensors is defined by Eq. (143) of Appendix A.6, and the transpose “” for a fourth-order tensor with minor symmetry is defined by Eq. (144) of Appendix A.7.

Remark 8

The curvature at a thickness position differs from the one at midsurface, as can be seen in Eq. (34). The tensors $Q_\varepsilon ^{\alpha \beta }$, $Q_\kappa ^{\alpha \beta }$, $\mathbb {Q}_{\varepsilon \varepsilon }^{\alpha \beta \gamma \delta }$, $\mathbb {Q}_{\varepsilon \kappa }^{\alpha \beta \gamma \delta }$, $\mathbb {Q}_{\kappa \varepsilon }^{\alpha \beta \gamma \delta }$, and $\mathbb {Q}_{\kappa \kappa }^{\alpha \beta \gamma \delta }$ are also functions of z. In fact, they are rational functions. This is why in this formulation it is more efficient to do the integrations by evaluating all the terms together at each thickness-integration point, rather than doing the integrations as in a typical Kirchhoff–Love shell implementation.

5.5 Moment at the edge

As mentioned in Remark 21 in Part I, the $\overline{{\textbf {b}}}^\star$ component of the moment (see the definition of $\overline{{\textbf {b}}}^\star$ in Eq. (139) or Figure 6 of Part I) is predetermined in the Kirchhoff–Love shell model, with a dependence on the midsurface selection. Here we propose a method that makes the midsurface selection less consequential. To do that, we add to Eq. (55) the integral

$$\begin{aligned} - \int _{\overline{S}_0} \delta \overline{{\textbf {n}}}\cdot \overline{{\textbf {b}}}\, \overline{{\textbf {b}}}^\star \cdot \left( \left( \breve{\hat{{\textbf {p}}}}_{\textrm{tot}}\right) _1^{\alpha } - \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha } \right) \overline{{\textbf {G}}}_{\alpha }\cdot \overline{{\textbf {B}}}\textrm{d}S, \end{aligned}$$

(93)

which makes $\left( \breve{\hat{{\textbf {p}}}}_{\textrm{tot}}\right) _1^{\alpha }$ zero instead of $\left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _1^{\alpha }$. Currently our choice for $\breve{\xi }^3$ is as given by Eq. (67). Substituting Eq. (62) into Eq. (93), we get

$$\begin{aligned} \breve{\xi }^3 \int _{\overline{S}_0} \delta \overline{{\textbf {n}}}\cdot \overline{{\textbf {b}}}\, \overline{{\textbf {b}}}^\star \cdot \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _0^{\alpha } \overline{{\textbf {G}}}_{\alpha }\cdot \overline{{\textbf {B}}}\textrm{d}S. \end{aligned}$$

(94)

Thus, the new form of Eq. (55) is

$$\begin{aligned} \delta W_{\textrm{exedge}}&= \int _{\overline{S}_0} \delta \overline{{\textbf {x}}} \cdot \hat{{\textbf {h}}}_{0}^\textrm{e} \textrm{d}S + \int _{\overline{S}_0} \delta \overline{{\textbf {n}}}\cdot \hat{{\textbf {h}}}_{1}^\textrm{e} \textrm{d}S \nonumber \\ {}&\quad + \breve{\xi }^3 \int _{\overline{S}_0} \delta \overline{{\textbf {n}}}\cdot \overline{{\textbf {b}}}\, \overline{{\textbf {b}}}^\star \cdot \left( \hat{{\textbf {p}}}_{\textrm{tot}}\right) _0^{\alpha } \overline{{\textbf {G}}}_{\alpha }\cdot \overline{{\textbf {B}}}\textrm{d}S. \end{aligned}$$

(95)

5.6 Surface integration

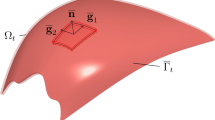
We now examine the implications of performing the upper- and lower-surface integrations based on the midsurface normal vectors (see Fig. 1). The implications include the effect on having a conservative form and therefore on the consistency with the divergence theorem. As we do our analysis, we describe a different way of doing the integrations.

We do the analysis for the upper surface, but it is straightforward to apply that also to the lower surface. First we introduce a global thickness parameter $0 \le \vartheta \le 1$, such that

Fig. 1

The true normal and the midsurface normal $\overline{{\textbf {n}}}$. The bottom curve represents the midsurface, and the upper surface, located at ${(\xi ^3)}^+$, is obtained by setting $\vartheta = 1$. For a given point on the midsurface, the area change from $\vartheta = 0$ to 1 is $\overline{A}$ to A, and is the inclined area

$$\begin{aligned} \xi ^3_0 = (\xi ^3_0)^+ \vartheta , \end{aligned}$$

(96)

and $\vartheta = 1$ represents the upper surface in the undeformed and current configurations. We define the following variables:

$$\begin{aligned} (\xi ^3_0)_{, \alpha }&= \left. \frac{\partial \xi ^3_0}{\partial \xi ^\alpha } \right| _\vartheta , \end{aligned}$$

(97)

$$\begin{aligned} \xi ^3_{, \alpha }&= \left. \frac{\partial \xi ^3 }{\partial \xi ^\alpha } \right| _\vartheta . \end{aligned}$$

(98)

With that, we have new coordinate systems:

(99)

(100)

If we integrate over the current configuration, we do not need to use the basis vectors in the undeformed configuration. Therefore, here we focus on the current configuration. See Appendix B.7 for the derivation of $\xi ^3_{,\alpha }$. We define as

(101)

and its normal vector is

(102)

With that, can also be written as

(103)

(104)

We expand the cross product as

(105)

Because the second and third terms on the right-hand side are orthogonal to $\overline{{\textbf {n}}}$, we get

(106)

(107)

which means

(108)

From that,

(109)

We write the modified versions of Eqs. (109)–(114) of Part I as

(110)

(111)

(112)

(113)

(114)

(115)

where is the traction acting on the curved current configuration, and use these tractions in Eq. (54).

Remark 9

With being the physical traction, and defining $\hat{{\textbf {h}}}$ by

(116)

performing the integrations over the upper and lower surfaces represented the way A represents a surface would give the same result.

If the traction is given in terms of pressure, we need to form the traction vector by using the true normals. Therefore, doing the integrations over the upper and lower surfaces using the true normals will bring us closer to a conservative form.

Remark 10

When the traction is given in terms of pressure, we will have consistency with the divergence theorem when $(\xi ^3)^-$ and $(\xi ^3)^+$ are continuous across element boundaries. Otherwise, even if we use the true normals in forming the traction vector, we will not be in a conservative form. Then, a uniform pressure over all the boundaries, for example, may produce a net force. For $(\xi ^3)^-$ and $(\xi ^3)^+$ to have that continuity, the midsurface representation needs to have $C^2$ continuity.

6 Test computations

In the Kirchhoff–Love category in the degree-of-freedom count, the extended model in this article is encompassing all other extensions in the isogeometric subcategory. The other extensions can be obtained by excluding certain terms. The set of methods compared will be described in Sect. 6.1. We conduct four test computations, with multiple cases in the first three.

• 1. Dome-shaped inflation of a flat circular shell The circular shell is inflated with a uniform pressure and simply-supported edges. As the pressure is increasing, the bending deformation is dominant at first, but at the end, we have mostly in-plane deformation. From this perspective, the response to bending and in-plane deformations is validated. Similar tests were conducted in [12, 13].

• 2. Rolling of a rectangular plate One edge of the plate is clamped, and the angle along the opposing edge is increased in a sequence of steady-state solutions. As the angle increases, the required moment increases. The pure bending response is validated.

• 3. Pinching of a cylindrical shell While the bottom longitudinal line being simply-supported, a uniform vertical force is applied along the top longitudinal line. This is also a bending-dominant deformation, and it involves normal-curvature change of sign. In this problem, we are doing a verification study. Similar tests were conducted in [14,15,16,17].

• 4. Uniform hydrostatic pressurization of the pinched cylindrical shell The uniform pressure is applied to the pinched cylindrical shell to validate the consistency with the divergence theorem.

In these studies, the number of elements is denoted by $n_{\textrm{el}}$, and the polynomial order of the B-splines by p. As integration with Gaussian quadratures, we use $(p+1){\times }(p+1)$ points over the midsurface and 8 points in the thickness direction. All test problems are with steady-state computations. We use Eq. (95) on all midsurface edges. For the pressure loading, we use the true normal of the surface, as described in Sect. 5.6. For the visualization of the deformed shapes, we calculate the positions of the upper and lower surfaces. In all test computations, we will be working with nondimensional numbers.

6.1 Methods compared

We focus on two aspects of the methods. The first one (see Fig. 2) is about the out-of-plane normal stress ($S^{33}$). If we assume $S^{33} \ne 0$, there are two options, whether we include the out-of-plane deformation in representing the bending effect ($\xi ^3\ne \xi ^3_0$) or not. From those scenarios, we consider three cases, identified as “M1,” “M2,” and “M3,” and with the level of assumptions decreasing in that order. The second aspect (see Fig. 3) is about the metric tensors. Omitting the quadratic terms, $\overline{\omega }_{\alpha \beta }$ and $\overline{\varOmega }_{\alpha \beta }$, in Eqs. (2) and (3) is the common practice. When we do not omit them, there are two options, whether we include $\delta \overline{\omega }_{\alpha \beta }$ in Eq. (73) or not. For those scenarios, we consider three cases, identified as “A,” “B,” and “C,” and with the level of assumptions decreasing in that order.

The two aspects are independent and we identify their combinations with labels like “M3-C.” For example, the combination M3-B includes $S^{33}$, and $\delta \xi ^3$ in Eq. (73) is also included but $\delta \overline{\omega }_{\alpha \beta }$ is not included. We also note that in comparing the methods, all other aspects of the formulations, such as those explained in Sects. 5.5 and 5.6, remain the same.

Remark 11

The method introduced in [15] is close to M1-A. In performing the integrations over the undeformed configuration, we take into account the curvature effects, which was introduced in [11].

Remark 12

The method introduced in [11] is close to M2-B.

Remark 13

From the set of methods proposed here, the one used in the comparisons is M3-C.

Fig. 2

Models compared. Out-of-plane deformation and stress. Model identifications are “M1,” “M2,” and “M3”

Fig. 3

Models compared. Metric-tensor approximation. Model identifications are “A,” “B,” and “C”

Fig. 4

Dome-shaped inflation of a flat circular shell. Problem setup. We note that $p_\text {ext}$ is applied on the lower surface, and not on the midsurface

Table 1 Dome-shaped inflation of a flat circular shell. Parameters

6.2 Dome-shaped inflation of a flat circular shell

6.2.1 Problem setup

A flat circular shell with radius $r_0$ and thickness $(h_\textrm{th})_0$ shown in Fig. 4 is inflated with a uniform pressure and simply-supported edges as shown in Fig. 5. The vertical displacement of the plate center point is denoted by d.

6.2.2 Computational conditions

The Mooney–Rivlin material model given by Eq. (284) is used. The parameters are given in Table 1. With the symmetry condition, we compute only one fourth of the shell. The exact geometry is represented by using a quadratic NURBS mesh, with control points coalescing at the plate center. We start with the mesh shown in Fig. 6. Using order elevation and knot insertion techniques, we obtain a mesh with $p = 4$ and $n_{\textrm{el}}= 64$. We place the midsurface at the center in the undeformed configuration.

Fig. 5

Dome-shaped inflation of a flat circular shell. Boundary condition

Fig. 6

Dome-shaped inflation of a flat circular shell. The control mesh with $p=2$ and $n_{\textrm{el}}= 1$. The physical shape in green

6.2.3 Results

Fig. 7

Dome-shaped inflation of a flat circular shell. M3-C. $p=4$, $n_{\textrm{el}}=64$. Deformed shapes colored by $\lambda _3$. $p_\text {ext}=12$ (upper left), 24 (upper right), 36 (lower left), and 48 (lower right)

Fig. 8

Dome-shaped inflation of a flat circular shell. M3-C. $p=4$, $n_{\textrm{el}}=64$. Deformed shapes colored by $\lambda _3$. Two views of the superimposed shapes for $p_\text {ext}={0,12,24,36, \,\,{\hbox {and}}\,\, 48}$

Figures 7 and 8 show the deformed shapes at different $p_\text {ext}$ values. Figure 9 shows the solutions from M1-A, M2-B, and M3-C. Figure 10 shows $p_\text {ext}$ as a function of d. For each of M1, M2, and M3, the A and B solutions are essentially indistinguishable from the C solution. However, the computations with M3-A and M3-B could not be continued beyond $p_\text {ext}= 30\,\, {\hbox {and}}\,\, 26$. We show those solutions in Fig. 11, together with the M2-B solution as a reference.

Fig. 9

Dome-shaped inflation of a flat circular shell. $p=4$, $n_{\textrm{el}}=64$. Deformed shapes at $p_\text {ext}=48$. Superimposed shapes from M1-A (red), M2-B (blue), and M3-C (orange)

Fig. 10

Dome-shaped inflation of a flat circular shell. $p=4$, $n_{\textrm{el}}=64$. $p_\text {ext}$ as a function of d. We note that the A and B solutions are essentially indistinguishable from the C solutions

Fig. 11

Dome-shaped inflation of a flat circular shell. $p=4$, $n_{\textrm{el}}=64$. $p_\text {ext}$ as a function of d. We show how far it was possible to compute with M3-A and M3-B and how close those solutions are to the M2-B solution

Fig. 12

Rolling of a rectangular plate. Problem setup

6.2.4 Discussion of the results

The performances of M1, M2, and M3 are different. At low values of $p_\text {ext}$, M2 is closer to M1, and at high values, closer to M3. That is because the bending stiffness plays greater role at lower $p_\text {ext}$ values, and the out-of-plane deformation plays greater role at high $p_\text {ext}$ values. The out-of-plane deformation plays greater role at higher $p_\text {ext}$ values because the shape of the lower surface plays greater role.

When the A and B solutions are computable, they are essentially indistinguishable from the C solution. We get full robustness and computability range by including all the quadratic terms in the metric-tensor representation.

6.3 Rolling of a rectangular plate

6.3.1 Problem setup

A straight rigid rod is attached to a rectangular plate of $\ell _0{\times }w_0$ as shown in Fig. 12. One edge of the plate is clamped, and the angle $\theta$ along the opposing edge is increased in a sequence of steady-state solutions. The required moment M supplied by the rod is obtained by integrating over the edge. We note that at both ends, the midsurface tangent angle is given, but the rotation around the normal direction is free.

6.3.2 Computational conditions

The Mooney–Rivlin material model is used. The parameters are given in Table 2. With symmetry along the $x_1$ axis, we compute only half of the plate. The half-domain mesh is made of uniform B-splines with $p=4$ and $16{\times }4$ elements, as shown in Fig. 13.

Table 2 Rolling of a rectangular plate. Parameters

Fig. 13

Rolling of a rectangular plate. Mesh with $p=4$, $n_{\textrm{el}}= 16{\times }4$

Fig. 14

Rolling of a rectangular plate. M3-C. $(h_\textrm{th})_0=0.1$. Deformed shape, colored by $\lambda _3$, at $\theta =0$, $\frac{\pi }{2}$, $\pi$, $\frac{3\pi }{2}$, and $2\pi$. Three different views, (a–c), and we see in (d) the half-plate with version of (b)

6.3.3 Results: $(h_\textrm{th})_0=0.1$

Figure 14 shows the deformed shape at different values of $\theta$, and Fig. 15 shows M as a function of $\theta$.

Fig. 15

Rolling of a rectangular plate. $(h_\textrm{th})_0=0.1$. M as a function of $\theta$

6.3.4 Results: $(h_\textrm{th})_0=0.2$

Figure 16 shows the deformed shape at different values of $\theta$, and Fig. 17 shows M as a function of $\theta$.

Fig. 16

Rolling of a rectangular plate. M3-C. $(h_\textrm{th})_0=0.2$. Deformed shape, colored by $\lambda _3$, at $\theta =0$, $\frac{\pi }{2}$, $\pi$, $\frac{3\pi }{2}$, and $2\pi$. Three different views, (a–c), and we see in (d) the half-plate with version of (b)

Fig. 17

Rolling of a rectangular plate. $(h_\textrm{th})_0= 0.2$. M as a function of $\theta$

6.3.5 Discussion of the results

The trend is the same for $(h_\textrm{th})_0= 0.1 \,\,{\hbox {and}}\,\, 0.2$.  From  Figs. 15 and 17, M1 is stiffer than M3. M2 is stiffer than M1 for A and B, and they are almost the same for C. We also see that A is stiffer than B, and B is stiffer than C. The difference between M3 and M1 is more than the difference between M1 and M2 for all of A, B, and C. This implies that in bending-dominant problems, the out-of-plane normal stress has larger impact than the out-of-plane deformation. In fact, in this example, just accounting for the out-of-plane deformation makes the response stiffer.

6.4 Pinching of a cylindrical shell

6.4.1 Problem setup

Figure 18 shows the cylindrical shell, with midsurface radius $r_0$ and length $\ell _0$, and how a uniform vertical force is applied along the top longitudinal line, with the bottom longitudinal line simply-supported. The uniform vertical force per unit length is $F/\ell _0$. As F is increased, the midsurface displacement in the $-x_3$ direction, d, measured as shown in Fig. 18, increases.

Fig. 18

Pinching of a cylindrical shell. Problem setup

6.4.2 Computational conditions

The neo-Hookean material model given by Eq. (283) is used. There are two different thickness values. The parameters are given in Table 3. With the symmetry condition, we compute only one-fourth of the cylinder. The mesh is made of uniform B-splines in both the circumferential and longitudinal directions. The mesh is built in the circumferential direction by starting with full-circle periodic B-splines with equally spaced control points and splitting that into half by knot insertions. We do that for each $n_{\textrm{el}}$, to reduce the difference from the exact arc. Our coarsest mesh has 8 elements in the circumferential direction and 3 in the $x_1$ direction. The meshes used have various combinations of $n_{\textrm{el}}$ and p, coming from $n_{\textrm{el}}= 8{\times }3, 16{\times }6, 24{\times }9, 32{\times }12, {\hbox {and}}\,\, 48{\times }18$, and $p = 2,3, {\hbox {and}}\,\, 4$. Figures 19, 20, and 21 show, as three examples, meshes with 8 elements in the circumferential direction and$p = {2,3, {\hbox {and}}\,\, 4}$. The figures also show the radius of curvature, which of course should be constant in the exact representation. Except for the mesh with 8 elements in the circumferential direction and $p=2$, the deviation from the exact radius of curvature is not noticeable. The radius of curvature with $p=2$ is continuous in the figure, but that is just for the undeformed configuration, and it can be discontinuous in the deformed configuration.

Table 3 Pinching of a cylindrical shell. Parameters

Fig. 19

Pinching of a cylindrical shell. Control mesh, physical mesh, and radius of curvature. Mesh with $p=2$ and 8 elements in the circumferential direction. The radius of curvature is plotted over the surface, in the normal direction

Fig. 20

Pinching of a cylindrical shell. Control mesh, physical mesh, and radius of curvature. Mesh with $p=3$ and 8 elements in the circumferential direction. The radius of curvature is plotted over the surface, in the normal direction

Fig. 21

Pinching of a cylindrical shell. Control mesh, physical mesh, and radius of curvature. Mesh with $p=4$ and 8 elements in the circumferential direction. The radius of curvature is plotted over the surface, in the normal direction

6.4.3 Results: $(h_\textrm{th})_0=0.01$

Figures 22,  23, 24, and 25 show, for M3-C and $p=4$, $n_{\textrm{el}}=96$, the deformed shapes for different F values. Figure 26 shows, for $p=4$, $n_{\textrm{el}}=96$, and $F=8{\times }10^{-5}$, the deformed shapes for M1-A, M2-B, and M3-C. Figure 27 shows, for $p=4$, $n_{\textrm{el}}=96$, F as a function of d for all combinations of the methods. Figure 28 shows, for M3-C, mesh refinement studies with $F=4{\times }10^{-5}\,\,{\hbox {and}}\,\,8{\times }10^{-5}$. Figure 29 shows, for the purpose of validating M1-A and M2-B, mesh refinement studies for M1-A, M2-B, and M3-C, again with $F=4{\times }10^{-5}\,\, {\hbox {and}}\,\,8{\times }10^{-5}$.

Fig. 22

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.01$. $p=4$, $n_{\textrm{el}}=96$. Deformed shape, colored by $\lambda _3$, when $F={0}$

Fig. 23

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.01$. $p=4$, $n_{\textrm{el}}=96$. Deformed shape, colored by $\lambda _3$, when $F=4{\times }10^{-5}$

Fig. 24

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.01$. $p=4$, $n_{\textrm{el}}=96$. Deformed shape, colored by $\lambda _3$, when $F=8{\times }10^{-5}$

Fig. 25

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.01$. $p=4$, $n_{\textrm{el}}=96$. Superimposed views of the deformed shapes, colored by $\lambda _3$, when $F=0,2{\times }10^{-5},4{\times }10^{-5},6{\times }10^{-5}, {\hbox {and}}\,\,8{\times }10^{-5}$

Fig. 26

Pinching of a cylindrical shell. $(h_\textrm{th})_0=0.01$. $p=4$, $n_{\textrm{el}}=96$. Superimposed views of the deformed shapes when $F=8.0{\times } 10^{-5}$. M1-A (red), M2-B (blue), and M3-C (orange)

Fig. 27

Pinching of a cylindrical shell. $(h_\textrm{th})_0=0.01$. $p=4$, $n_{\textrm{el}}=96$. F as a function of d

Fig. 28

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.01$. $L^2$-norm of the difference compared to the mesh with $p=4$ and $n_{\textrm{el}}={864}$. $F={4{\times }10^{-5}}$ (top) and ${8{\times }10^{-5}}$ (bottom)

Fig. 29

Pinching of a cylindrical shell. $(h_\textrm{th})_0=0.01$. Validation of M1-A and M2-B. Mesh with $p=4$ compared to M3-C with $p=4$ and $n_{\textrm{el}}={864}$. We also show M3-C as a reference. $F={4{\times }10^{-5}}$ (top) and ${8{\times }10^{-5}}$ (bottom)

6.4.4 Results: $(h_\textrm{th})_0=0.02$

Figures 30, 31, 32, and 33 show, for M3-C and $p=4$, $n_{\textrm{el}}= 96$, the deformed shapes for different F values. Figure 34 shows, for $p=4$, $n_{\textrm{el}}=96$, and $F={6.0{\times }10^{-4}}$, the deformed shapes for M1-A, M2-B, and M3-C. Figure 35 shows, for $p=4$, $n_{\textrm{el}}=96$, F as a function of d for all combinations of the methods.

Fig. 30

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.02$. $p=4$, $n_{\textrm{el}}=96$. Deformed shapes, colored by $\lambda _3$, when $F={0}$

Fig. 31

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.02$. $p=4$, $n_{\textrm{el}}=96$. Deformed shapes, colored by $\lambda _3$, when $F={3.0{\times }10^{-4}}$

Fig. 32

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.02$. $p=4$, $n_{\textrm{el}}=96$. Deformed shapes, colored by $\lambda _3$, when $F={6.0{\times }10^{-4}}$

Fig. 33

Pinching of a cylindrical shell. M3-C. $(h_\textrm{th})_0=0.02$. $p=4$, $n_{\textrm{el}}=96$. Superimposed views of the deformed shapes, colored by $\lambda _3$, when $F=0,1.5{\times }10^{-4}, 3.0{\times }10^{-4}, 4.5{\times }10^{-4}, {\hbox {and}}\,\, 6.0{\times }10^{-4}$

Fig. 34

Pinching of a cylindrical shell. $(h_\textrm{th})_0=0.02$. $p=4$, $n_{\textrm{el}}=96$. Superimposed views of the deformed shapes when $F={6.0{\times }10^{-4}}$. M1-A (red), M2-B (blue), and M3-C (orange)

Fig. 35

Pinching of a cylindrical shell. $(h_\textrm{th})_0=0.02$. $p=4$, $n_{\textrm{el}}=96$. F as a function of d

6.4.5 Discussion of results

From Figs. 27 and 35, M2 is stiffer than M1, and M1 is stiffer than M3. We also see that A is stiffer than B, and B is stiffer than C. The difference between M3 and M1 is more than the difference between M1 and M2 for all of A, B, and C. Again, this implies the out-of-plane normal stress has large impact.

From Fig. 28, we see that the convergence rate for M3-C is roughly pth order. From Figs. 26 and 34, we see that the differences between methods for $(h_\textrm{th})_0= {0.01}$ are not as significant as they are for $(h_\textrm{th})_0= {0.02}$. However, what we see in Fig. 29 is that, even the converged solution from M1-A and M2-B can be obtained with M3-C using the coarsest mesh.

6.5 Uniform hydrostatic pressurization of the pinched cylindrical shell

6.5.1 Problem setup

A uniform hydrostatic pressure $p_\infty$ is applied to the pinched cylindrical shell from Sect. 6.4. We integrate $p_\infty$ over all the physical surfaces. Because of the symmetry assumed in the computations, for the purpose of evaluating the surface-integration accuracy, we can only check the $x_3$ component of the force. We use the deformed shapes obtained for $(h_\textrm{th})_0= 0.01$, with $n_{\textrm{el}}=96$ and $p=2,3, {\hbox {and}}\,\, 4$.

The total surface area for the full cylindrical shell in the undeformed configuration is $S_0 = 4 \pi r_0 \left( \ell _0 + (h_\textrm{th})_0\right)$. We computed only with one-fourth of the cylindrical shell. The symbol ${\textbf {f}}_{\frac{1}{4}}$ will represent the force obtained by integrating $p_\infty$ over the physical surfaces of the one-fourth cylindrical shell. Due to the symmetry, we can write

$$\begin{aligned} \left\| {\textbf {f}} \right\|&= 4 \left| \smash {{\textbf {f}}_{\frac{1}{4}}} \cdot {\textbf {e}}_3 \right| , \end{aligned}$$

(117)

where ${\textbf {e}}_3$ is the Cartesian basis vector.

We will use $n_\textrm{quad}$ as a parameter representing the level of integration effort. On the upper and lower surfaces, we will have $n_\textrm{quad}{\times }n_\textrm{quad}$ integration points in the 2D parametric space. On the edge surfaces, we will have $n_\textrm{quad}{\times }n_\textrm{quad}$ integration points in the tangential parametric space and thickness direction.

6.5.2 Results and discussion

Figures 36 and 37 show $\left\| {\textbf {f}} \right\| / (p_\infty S_0)$ and $4 \left\| \smash {{\textbf {f}}_\frac{1}{4}} \right\| /(p_\infty S_0)$. From Fig. 36, we see that, with sufficient integration effort, the machine accuracy can be reached with $p= 3\,\, {\hbox {and}}\,\, 4$, but not with $p=2$. From Fig. 37, we see that the force value that is not expected to be zero is reaching almost high enough accuracy with $n_\textrm{quad} = 3$. That is less than or equal to the typical integration accuracy requirement in solving the structural mechanics equations.

Fig. 36

Uniform hydrostatic pressurization of the pinched cylindrical shell. $\left\| {\textbf {f}} \right\| / (p_\infty S_0)$

Fig. 37

Uniform hydrostatic pressurization of the pinched cylindrical shell. $4 \Vert \smash {{\textbf {f}}_\frac{1}{4}} \Vert /(p_\infty S_0)$

7 Concluding remarks

This was Part II of a multipart article on a hyperelastic extended Kirchhoff–Love shell model with out-of-plane normal stress. We start with an augmented formulation that includes the pressure as a Lagrange multiplier and then eliminate it by using the geometrical representation of the incompressibility constraint. The resulting model is an extended one, in the Kirchhoff–Love category in the degree-of-freedom count, and encompassing all other extensions in the isogeometric subcategory. The vector form of the equations used in Part I provides good physical intuition about the formulation, and the tensor-coefficients form helps with efficient implementation. We included ordered details as a recipe for making the implementation practical. The implementation has two components that are not be obvious but might be critical in boundary integration. The first one is related to the edge-surface moment created by the Kirchhoff–Love assumption. The second one is related to the pressure/traction integrations over all the surfaces of the finite-thickness geometry. It gives us divergence-theorem-consistent representation in the integrations when the basis functions have $C^2$ continuity.

We have presented test computations for dome-shaped inflation of a flat circular shell, rolling of a rectangular plate, pinching of a cylindrical shell, and hydrostatic pressurization of the pinched cylindrical shell. We computed with neo-Hookean and Mooney–Rivlin material models. We evaluated the effect of the terms added in the extended model. In-plane stress is already represented well in all other extensions of the isogemetric Kirchhoff–Love shell model. However, if we have pressure acting on the upper or lower surface, a good representation of the out-of-plane deformation is required. In bending representation, both the out-of-plane deformation and out-of-plane normal stress are important, and the out-of-plane normal stress has a larger impact. In terms of the robustness of the computation, the quadratic term in the metric tensor plays a significant role when we account for the out-of-plane normal stress. With uniform hydrostatic pressurization of the pinched cylindrical shell, we demonstrated the divergence-theorem-consistency when using a midsurface representation with $C^2$ or higher continuity. To have machine accuracy exactness in that consistency, the integration accuracy needs to be high. However, a level of accuracy comparable to the overall solution accuracy might be sufficient.

Appendices

Tensor notation and operators

We explain the basics of our notation in the context of second-order tensors. We assume that all tensors can be represented by the dual basis system. We use the symbols ${\textbf {A}}$, ${\textbf {B}}$, ${\textbf {C}}$, and ${\textbf {D}}$ to represent the second-order tensors. A tensor can be represented as

$$\begin{aligned} {\textbf {A}}&= A^{\alpha \beta } {\textbf {g}}_{\alpha } {\textbf {g}}_{\beta } \end{aligned}$$

(118)

$$\begin{aligned}&= A_{\alpha \beta } {\textbf {g}}^{\alpha } {\textbf {g}}^{\beta }, \end{aligned}$$

(119)

where ${\textbf {g}}_{\alpha }$ and ${\textbf {g}}^{\alpha }$ are the covariant and contravariant basis vectors. When the basis vectors are obvious or assumed, we will use the representation $A^{\bullet \bullet },$ where $\bullet$ serves as an index position indicator for whether the tensor components are covariant or contravariant. We note that this is just for representing the components, but it also represents, if needed, the tensor by imagining the omitted basis vectors. After an operation, if we need to use any of the remaining indices as a dummy index, we do that by placing that index outside a pair of brackets. For example,

$$\begin{aligned} {\textbf {A}} \cdot {\textbf {B}}&= A_{\alpha \beta } B^{\beta \gamma } {\textbf {g}}^{\alpha } {\textbf {g}}_{\gamma } \end{aligned}$$

(120)

$$\begin{aligned}&= \left[ A_{\bullet \bullet } \cdot B^{\bullet \bullet } \right] _{\alpha }^{\,\,\gamma } {\textbf {g}}^{\alpha } {\textbf {g}}_{\gamma }. \end{aligned}$$

(121)

With Eq. (121), we do not need to use the dummy index $\beta$, and the notation provides more physical intuition than Eq. (120).

1.1 Determinant

The determinant of a tensor can be written as

$$\begin{aligned} \det {\textbf {A}}&= \left| A^{\bullet \bullet } \right| \left| g_{\bullet \bullet } \right| , \end{aligned}$$

(122)

where $g_{\bullet \bullet }$ represents the covariant metric tensor.

1.2 Trace

The vector-notation trace will be interpreted as

$$\begin{aligned} \textrm{tr}{\textbf {A}} = A^{\alpha \beta } g_{\alpha \beta }, \end{aligned}$$

(123)

and the matrix-form is interpreted as

$$\begin{aligned} \textrm{tr}A^{\bullet \bullet }&= A^{\alpha \alpha }. \end{aligned}$$

(124)

1.3 Symmetries of a fourth-order tensor

We denote the components of a fourth-order tensor as $\mathbb {X}_{\alpha \beta \gamma \delta }$. There are two types of symmetry. The major symmetry is

$$\begin{aligned} \mathbb {X}_{\alpha \beta \gamma \delta }&= \mathbb {X}_{\gamma \delta \alpha \beta }. \end{aligned}$$

(125)

The minor symmetry is

$$\begin{aligned} \mathbb {X}_{\alpha \beta \gamma \delta }&= \mathbb {X}_{\alpha \beta \delta \gamma },&\mathbb {X}_{\alpha \beta \gamma \delta }&= \mathbb {X}_{\beta \alpha \gamma \delta } . \end{aligned}$$

(126)

1.4 Fourth-order tensor products

Putting two tensors together without an operator in between generates a fourth-order tensor:

$$\begin{aligned} \pmb {\mathbb {X}}&= {\textbf {A}} {\textbf {B}}. \end{aligned}$$

(127)

With the index notation, we can write this as

$$\begin{aligned} \mathbb {X}_{\alpha \beta \gamma \delta }&= A_{\alpha \beta } B_{\gamma \delta } . \end{aligned}$$

(128)

We can also write it as

$$\begin{aligned}&\mathbb {X}_{\alpha \beta \gamma \delta }= \left[ A_{\bullet \bullet } B_{\bullet \bullet } \right] _{\alpha \beta \gamma \delta } . \end{aligned}$$

(129)

We also define the following fourth-order tensor:

$$\begin{aligned} \pmb {\mathbb {Y}}&= {\textbf {A}} \odot {\textbf {B}} = {\textbf {B}} \odot {\textbf {A}} . \end{aligned}$$

(130)

With the index notation, we can write this as

$$\begin{aligned} \mathbb {Y}_{\alpha \beta \gamma \delta }&= \frac{ A_{\alpha \gamma } B_{\beta \delta } + B_{\alpha \gamma } A_{\beta \delta } + A_{\alpha \delta } B_{\beta \gamma } + B_{\alpha \delta } A_{\beta \gamma } }{4} . \end{aligned}$$

(131)

Remark 14

This operation brings minor symmetry. If ${\textbf {A}}$ and ${\textbf {B}}$ are both symmetric, we will then have also major symmetry.

We can also express the fourth-order tensor of Eq. (130) as

$$\begin{aligned} \mathbb {Y}_{\alpha \beta \gamma \delta } = \left[ A_{\bullet \bullet } \odot B_{\bullet \bullet } \right] _{\alpha \beta \gamma \delta } . \end{aligned}$$

(132)

1.5 Double contraction between fourth- and second-order tensors

We define the double contractions between fourth- and second-order tensors as

$$\begin{aligned} \left[ \mathbb {X}_{\bullet \bullet \bullet \bullet } : A^{\bullet \bullet } \right] _{\alpha \beta } = \mathbb {X}_{\alpha \beta \gamma \delta } A^{\gamma \delta } , \end{aligned}$$

(133)

$$\begin{aligned} \left[ A^{\bullet \bullet } : \mathbb {X}_{\bullet \bullet \bullet \bullet } \right] _{\gamma \delta } = A^{\alpha \beta } \mathbb {X}_{\alpha \beta \gamma \delta } . \end{aligned}$$

(134)

We have the following identities:

(135)

(136)

In general, the operation $\odot$ has priority over the double contraction. We note that the following relationship holds:

(137)

(138)

Because of Eq. (138), we can omit the parentheses; i.e.,

$$\begin{aligned} {\textbf {D}} :\left( {\textbf {A}}\odot {\textbf {B}} : {\textbf {C}} \right) = \left( {\textbf {D}}: {\textbf {A}}\odot {\textbf {B}}\right) : {\textbf {C}} = {\textbf {D}}: {\textbf {A}}\odot {\textbf {B}}: {\textbf {C}} . \end{aligned}$$

(139)

When ${\textbf {C}}$ and ${\textbf {D}}$ are symmetric, we can reduce the operations to

(140)

(141)

We can also express the operation given by Eq. (135) as

$$\begin{aligned}&\left[ A^{\bullet \bullet } \odot B^{\bullet \bullet } \right] ^{ \alpha \beta \gamma \delta } {C}_{\gamma \delta }\nonumber \\&\quad = \frac{ A^{\alpha \gamma } \left( {C}_{\gamma \delta } + {C}_{\delta \gamma } \right) B^{\beta \delta } + B^{\alpha \gamma } \left( {C}_{\gamma \delta } + {C}_{\delta \gamma } \right) A^{\beta \delta } }{4} . \end{aligned}$$

(142)

1.6 Double contraction between fourth-order tensors

The double contraction between two fourth-order tensors is defined as

$$\begin{aligned} \left[ \mathbb {X}_{\bullet \bullet \bullet \bullet } : \mathbb {Y}^{\bullet \bullet \bullet \bullet } \right] _{\alpha \beta }^{\,\,\,\,\,\gamma \delta }&= \mathbb {X}_{\alpha \beta \chi \epsilon } \mathbb {Y}^{\chi \epsilon \gamma \delta } . \end{aligned}$$

(143)

1.7 Transpose of a fourth-order tensor with minor symmetry

The transpose of a fourth-order tensor with minor symmetry is

(144)

Geometrical concepts

The concepts we cover here are applicable to both undeformed and deformed configurations, but we explain them for the deformed configuration. The position in the thickness direction is z.

1.1 Midsurface curvature tensor

We define the curvature tensor as

$$\begin{aligned} \overline{\pmb {\kappa }}&= \overline{\kappa }_{\alpha \beta } \overline{{\textbf {g}}}^{\alpha } \overline{{\textbf {g}}}^{\beta } . \end{aligned}$$

(145)

The principal curvatures are $\overline{\kappa }_1$ and $\overline{\kappa }_2$, and the corresponding normalized eigenvectors $\overline{{\textbf {t}}}_1$ and $\overline{{\textbf {t}}}_2$. With that, we define

$$\begin{aligned} \overline{\kappa }_\textrm{M}&= \frac{1}{2} \left( \overline{\kappa }_1 + \overline{\kappa }_2 \right) , \end{aligned}$$

(146)

$$\begin{aligned} \overline{\kappa }_\textrm{G}&= \overline{\kappa }_1 \overline{\kappa }_2 . \end{aligned}$$

(147)

Then we can write

$$\begin{aligned} \overline{\pmb {\kappa }}&= \overline{\kappa }_1 \overline{{\textbf {t}}}_1 \overline{{\textbf {t}}}_1 + \overline{\kappa }_2 \overline{{\textbf {t}}}_2 \overline{{\textbf {t}}}_2 , \end{aligned}$$

(148)

and write

$$\begin{aligned} \overline{\pmb {\kappa }}^2&= \overline{\kappa }_1^2 \overline{{\textbf {t}}}_1 \overline{{\textbf {t}}}_1 + \overline{\kappa }_2^2 \overline{{\textbf {t}}}_2 \overline{{\textbf {t}}}_2 . \end{aligned}$$

(149)

From the four equations above,

$$\begin{aligned} \overline{\kappa }_\textrm{G} {\textbf {I}}_2&= \underbrace{ \overline{\pmb {\kappa }} : {\textbf {I}}_2 }_{= 2 \overline{\kappa }_\textrm{M} } \overline{\pmb {\kappa }} - \overline{\pmb {\kappa }}^2 , \end{aligned}$$

(150)

where

$$\begin{aligned} {\textbf {I}}_2 = {\textbf {I}}- {\textbf {n}}{\textbf {n}}. \end{aligned}$$

(151)

The principal curvatures come from the solution of the characteristic equation

$$\begin{aligned} \overline{\kappa }^2 - 2 \overline{\kappa }_\textrm{M} \overline{\kappa }+ \overline{\kappa }_{G} = 0, \end{aligned}$$

(152)

and they are

$$\begin{aligned} \overline{\kappa }_1&= \overline{\kappa }_\textrm{M} - \sqrt{\overline{\kappa }_\textrm{M}^2 - \overline{\kappa }_\textrm{G}}, \end{aligned}$$

(153)

$$\begin{aligned} \overline{\kappa }_2&= \overline{\kappa }_\textrm{M} + \sqrt{\overline{\kappa }_\textrm{M}^2 - \overline{\kappa }_\textrm{G}}, \end{aligned}$$

(154)

where $\overline{\kappa }_1 \le \overline{\kappa }_2$. When $\overline{\kappa }_k z = -1$, the integration arclength in the kth principal direction is zero. From that, we have the restriction $\overline{\kappa }_k z > -1$. Then, we have the range limitations

$$\begin{aligned} -\frac{1}{\overline{\kappa }_2} <&z&\text {if }\,\, \overline{\kappa }_2 > 0, \end{aligned}$$

(155)

$$\begin{aligned}&z< -\frac{1}{\overline{\kappa }_1}&\text {if} \,\,\overline{\kappa }_1 < 0. \end{aligned}$$

(156)

We note that if $\overline{\kappa }_\textrm{G} < 0$, then we have both range limits:

$$\begin{aligned} -\frac{1}{\overline{\kappa }_2}< z < -\frac{1}{\overline{\kappa }_1}. \end{aligned}$$

(157)

1.2 Area

By definition, the ratio between the areas at $\xi ^3$ and midsurface is

$$\begin{aligned} \frac{A}{ ~\overline{A}~} = \frac{\sqrt{\left| g_{\bullet \bullet } \right| }}{\sqrt{\left| \overline{g}_{\bullet \bullet } \right| }}. \end{aligned}$$

(158)

This can be obtained from the tensor

$$\begin{aligned} \hat{{\textbf {A}}} = g_{\alpha \beta } \overline{{\textbf {g}}}^{\alpha } \overline{{\textbf {g}}}^{\beta }, \end{aligned}$$

(159)

and we get

$$\begin{aligned} \left( \frac{A}{ ~\overline{A}~} \right) ^2 = \det \hat{{\textbf {A}}} . \end{aligned}$$

(160)

Because we are in a 2D parametric space, the determinant, the third principal invariant, is equal to the second principal invariant:

$$\begin{aligned} \det \hat{{\textbf {A}}}&= \frac{1}{2} \left( \left( \hat{{\textbf {A}}} : {\textbf {I}}_2 \right) ^2 - \hat{{\textbf {A}}}^2 : {\textbf {I}}_2 \right) \end{aligned}$$

(161)

$$\begin{aligned}&= \hat{{\textbf {A}}} : \underbrace{ \frac{1}{2} \left( {\textbf {I}}_2 {\textbf {I}}_2 - {\textbf {I}}_2 \odot {\textbf {I}}_2 \right) }_{\equiv \pmb {\mathbb {D}}_2} : \hat{{\textbf {A}}} . \end{aligned}$$

(162)

From Eq. (159),

$$\begin{aligned} \hat{{\textbf {A}}}&= \left( \overline{g}_{\alpha \beta } + 2 \overline{\kappa }_{\alpha \beta } z + \overline{\omega }_{\alpha \beta } z^2 \right) \overline{{\textbf {g}}}^{\alpha } \overline{{\textbf {g}}}^{\beta } \end{aligned}$$

(163)

$$\begin{aligned}&= {\textbf {I}}_2 + 2 \overline{\pmb {\kappa }} z + \overline{\pmb {\kappa }}^2 z^2 . \end{aligned}$$

(164)

Rearranging Eq. (150), we get

$$\begin{aligned} \overline{\pmb {\kappa }}^2&= 2 \overline{\kappa }_\textrm{M} \overline{\pmb {\kappa }} - \overline{\kappa }_\textrm{G} {\textbf {I}}_2 , \end{aligned}$$

(165)

and we can express $\hat{{\textbf {A}}}$ as

$$\begin{aligned} \hat{{\textbf {A}}}&= \left( 1 - \overline{\kappa }_\textrm{G} z^2 \right) {\textbf {I}}_2 + 2 \left( 1+ \overline{\kappa }_\textrm{M} z \right) z \overline{\pmb {\kappa }} . \end{aligned}$$

(166)

We also note the following identities:

$$\begin{aligned} \pmb {\mathbb {D}}_2 : {\textbf {I}}_2&= \frac{1}{2} {\textbf {I}}_2 , \end{aligned}$$

(167)

$$\begin{aligned} \pmb {\mathbb {D}}_2 : \overline{\pmb {\kappa }}&= \frac{1}{2} \left( 2 \overline{\kappa }_\textrm{M} {\textbf {I}}_2 - \overline{\pmb {\kappa }} \right) , \end{aligned}$$

(168)

$$\begin{aligned} {\textbf {I}}_2 : \pmb {\mathbb {D}}_2 : {\textbf {I}}_2&= 1, \end{aligned}$$

(169)

$$\begin{aligned} {\textbf {I}}_2 : \pmb {\mathbb {D}}_2 : \overline{\pmb {\kappa }}&= \overline{\pmb {\kappa }} : \pmb {\mathbb {D}}_2 : {\textbf {I}}_2 = \overline{\kappa }_\textrm{M} , \end{aligned}$$

(170)

$$\begin{aligned} \overline{\kappa }_\textrm{G}&= \overline{\pmb {\kappa }} : \pmb {\mathbb {D}}_2 : \overline{\pmb {\kappa }} . \end{aligned}$$

(171)

We can express $\det \hat{{\textbf {A}}}$ as

$$\begin{aligned} \det \hat{{\textbf {A}}}&= \hat{{\textbf {A}}} : \pmb {\mathbb {D}}_2 : \hat{{\textbf {A}}} \end{aligned}$$

(172)

$$\begin{aligned}&= \left( 1- \overline{\kappa }_\textrm{G} z^2 \right) ^2 +4 \left( 1-\overline{\kappa }_\textrm{G }z^2\right) \left( 1 + \overline{\kappa }_\textrm{M} z \right) \overline{\kappa }_\textrm{M} z \nonumber \\&\quad + 4 \overline{\kappa }_\textrm{G} z^2 \left( 1 + \overline{\kappa }_\textrm{M} z \right) ^2 \end{aligned}$$

(173)

$$\begin{aligned}&= \left( 1+ 2 \overline{\kappa }_\textrm{M} z + \overline{\kappa }_\textrm{G} z^2 \right) ^2 . \end{aligned}$$

(174)

Thus, we obtain

$$\begin{aligned} \hat{A}(z) = 1+ 2 \overline{\kappa }_\textrm{M} z + \overline{\kappa }_\textrm{G} z^2 . \end{aligned}$$

(175)

We now investigate about $\hat{A}$ for $\overline{\kappa }_\textrm{G} = 0$ or $\overline{\kappa }_\textrm{G} \ne 0$.

When $\overline{\kappa }_\textrm{G} = 0$, Eq. (175) is linear. If $\overline{\kappa }_\textrm{M}$ is also zero, the area is a constant value. If $\overline{\kappa }_\textrm{M} \ne 0$, the minimum area is zero, at $z = -\frac{1}{2 \overline{\kappa }_\textrm{M}}$, which will be one of the limits in Eqs. (155) and (156).

When $\overline{\kappa }_\textrm{G} \ne 0$, by setting $\hat{A}(z) = 0$, we obtain

$$\begin{aligned} z&= \frac{-\overline{\kappa }_\textrm{M} \pm \sqrt{\overline{\kappa }_\textrm{M}^2 - \overline{\kappa }_\textrm{G}}}{\overline{\kappa }_\textrm{G}} \end{aligned}$$

(176)

$$\begin{aligned}&= \frac{-2 \overline{\kappa }_\textrm{M} \pm \left( \overline{\kappa }_2 - \overline{\kappa }_1\right) }{2 \overline{\kappa }_\textrm{G}}. \end{aligned}$$

(177)

We will call the two solutions $z_1$ and $z_2$, and with that,

$$\begin{aligned} z_1&= \frac{-2 \overline{\kappa }_\textrm{M} - \left( \overline{\kappa }_2 - \overline{\kappa }_1\right) }{2 \overline{\kappa }_\textrm{G}} =-\frac{1}{\overline{\kappa }_1}, \end{aligned}$$

(178)

$$\begin{aligned} z_2&= \frac{-2 \overline{\kappa }_\textrm{M} + \left( \overline{\kappa }_2 - \overline{\kappa }_1\right) }{2 \overline{\kappa }_\textrm{G}} =-\frac{1}{\overline{\kappa }_2}. \end{aligned}$$

(179)

The local extremum is at $z = - \frac{\overline{\kappa }_\textrm{M}}{\overline{\kappa }_\textrm{G}}$ and

$$\begin{aligned} \hat{A} \left( - \frac{\overline{\kappa }_\textrm{M}}{\overline{\kappa }_\textrm{G}} \right)&= 1 - \frac{\overline{\kappa }_\textrm{M}^2}{\overline{\kappa }_\textrm{G}} = -\frac{\left( \overline{\kappa }_2 - \overline{\kappa }_1\right) ^2}{4 \overline{\kappa }_\textrm{G}}. \end{aligned}$$

(180)

If $\overline{\kappa }_\textrm{G} > 0$, then either $z_2 < z$ and $\overline{\kappa }_2 > 0$ or $z < z_1$ and $\overline{\kappa }_1 < 0$. If $\overline{\kappa }_\textrm{G} < 0$, then $z_1< z < z_2$ and the maximum area is at $z = - \frac{\overline{\kappa }_\textrm{M}}{\overline{\kappa }_\textrm{G}}$.

Remark 15

What is stated in the above paragraph is equivalent to the statements in Eqs. (155) and (156).

1.3 Variations of A and $\overline{A}$

We derive $\delta A$ first and set the location to the midsurface to obtain $\delta \overline{A}$. We start with

$$\begin{aligned} A = \left| g_{\bullet \bullet } \right| ^{\frac{1}{2}}, \end{aligned}$$

(181)

and take logarithmic variation of this:

$$\begin{aligned} \delta \ln A = \frac{1}{2 A^2} \delta \left| g_{\bullet \bullet } \right| . \end{aligned}$$

(182)

Because metric tensors are invertible, their variations can be obtained by the Jacobi’s formula:

$$\begin{aligned} \delta \left| g_{\bullet \bullet } \right|&= \left| g_{\bullet \bullet } \right| g^{\alpha \beta } \delta g_{\alpha \beta } \end{aligned}$$

(183)

$$\begin{aligned}&= A^2 g^{\alpha \beta } \delta g_{\alpha \beta } . \end{aligned}$$

(184)

With that, Eq. (182) becomes

$$\begin{aligned} \delta \ln A&= \frac{1}{2} g^{\alpha \beta } \delta g_{\alpha \beta } . \end{aligned}$$

(185)

This can be expressed with the basis vectors. By using the identity

$$\begin{aligned} \delta g_{\alpha \beta } = \delta {\textbf {g}}_{\alpha } \cdot {\textbf {g}}_{\beta } + {\textbf {g}}_{\alpha } \cdot \delta {\textbf {g}}_{\beta } \end{aligned}$$

(186)

and the symmetry of the metric tensors, we get

$$\begin{aligned} \delta \ln A&= g^{\alpha \beta } \delta {\textbf {g}}_{\alpha } \cdot {\textbf {g}}_{\beta } \end{aligned}$$

(187)

$$\begin{aligned}&= \delta {\textbf {g}}_{\alpha } \cdot {\textbf {g}}^{\alpha } . \end{aligned}$$

(188)

For the second variation, we start from Eq. (185), and obtain

$$\begin{aligned} \delta _a \delta _b \ln A&= \frac{1}{2} \delta _b g^{\alpha \beta } \delta _a g_{\alpha \beta } + \frac{1}{2} g^{\alpha \beta } \delta _a \delta _b g_{\alpha \beta } \end{aligned}$$

(189)

$$\begin{aligned}&= - \frac{1}{2} \delta _a g_{\alpha \beta } \left[ g^{\bullet \bullet } \odot g^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b g{_{\gamma \delta }} + \frac{1}{2} g^{\alpha \beta } \delta _a \delta _b g_{\alpha \beta } . \end{aligned}$$

(190)

The midsurface versions are

$$\begin{aligned} \delta \ln \overline{A}&= \frac{1}{2} \overline{g}^{\alpha \beta } \delta \overline{g}_{\alpha \beta } \end{aligned}$$

(191)

$$\begin{aligned}&= \overline{g}^{\alpha \beta } \delta \overline{\varepsilon }_{\alpha \beta } \end{aligned}$$

(192)

and

$$\begin{aligned} \delta _a \delta _b \ln \overline{A}&= - \frac{1}{2} \delta _a \overline{g}_{\alpha \beta } \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{g}_{\gamma \delta } + \frac{1}{2} \overline{g}^{\alpha \beta } \delta _a \delta _b \overline{g}_{\alpha \beta } \end{aligned}$$

(193)

$$\begin{aligned}&= - 2 \delta _a \overline{\varepsilon }_{\alpha \beta } \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } + \overline{g}^{\alpha \beta } \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } . \end{aligned}$$

(194)

1.4 Variations of $\overline{\kappa }_\textrm{M}$ and $\overline{\kappa }_\textrm{G}$

We first write $\overline{\kappa }_\textrm{M}$ and $\overline{\kappa }_\textrm{G}$ as

$$\begin{aligned} \overline{\kappa }_\textrm{M}&= \frac{1}{2} \overline{\pmb {\kappa }}: {\textbf {I}}, \end{aligned}$$

(195)

$$\begin{aligned} \overline{\kappa }_\textrm{G}&= \det \overline{\pmb {\kappa }} \end{aligned}$$

(196)

$$\begin{aligned}&= \overline{\pmb {\kappa }}: \mathbb {D}_2 : \overline{\pmb {\kappa }} \end{aligned}$$

(197)

$$\begin{aligned}&= 2 \overline{\kappa }_\textrm{M}^2 - \frac{1}{2} \overline{\pmb {\kappa }} : \overline{\pmb {\kappa }} . \end{aligned}$$

(198)

The variation of $\overline{\kappa }_\textrm{M}$ is

$$\begin{aligned} \delta \overline{\kappa }_\textrm{M}&= \frac{1}{2} \delta \overline{\pmb {\kappa }}: {\textbf {I}}\end{aligned}$$

(199)

$$\begin{aligned}&=\delta \left( \overline{\kappa }_{\alpha \beta } \overline{g}^{\alpha \beta } \right) \end{aligned}$$

(200)

$$\begin{aligned}&= \underbrace{ - \frac{1}{2} \overline{\kappa }^{\alpha \beta } }_{=\frac{\partial \overline{\kappa }_\textrm{M}}{\partial \overline{g}_{\alpha \beta }} } \delta \overline{g}_{\alpha \beta } + \underbrace{ \frac{1}{2} \overline{g}^{\alpha \beta } }_{=\frac{\partial \overline{\kappa }_\textrm{M}}{\partial \overline{\kappa }_{\alpha \beta }}} \delta \overline{\kappa }_{\alpha \beta } \end{aligned}$$

(201)

$$\begin{aligned}&= 2 \frac{\partial \overline{\kappa }_\textrm{M}}{\partial \overline{g}_{\alpha \beta }} \delta \overline{\varepsilon }_{\alpha \beta } + \frac{\partial \overline{\kappa }_\textrm{M}}{\partial \overline{\kappa }_{\alpha \beta }} \delta \overline{\kappa }_{\alpha \beta } . \end{aligned}$$

(202)

The variation of $\overline{\kappa }_\textrm{G}$ is

$$\begin{aligned} \delta \overline{\kappa }_\textrm{G}&= 4 \overline{\kappa }_\textrm{M} \delta \overline{\kappa }_\textrm{M} - \frac{1}{2} \delta \left( \overline{\kappa }_{\alpha \beta } \overline{\kappa }^{\alpha \beta } \right) \end{aligned}$$

(203)

$$\begin{aligned}&= 4 \overline{\kappa }_\textrm{M} \delta \overline{\kappa }_\textrm{M} - \frac{1}{2} \overline{\kappa }^{\alpha \beta } \delta \overline{\kappa }_{\alpha \beta } - \frac{1}{2} \overline{\kappa }_{\alpha \beta } \delta \overline{\kappa }^{\alpha \beta } \end{aligned}$$

(204)

$$\begin{aligned}&= 4 \overline{\kappa }_\textrm{M} \delta \overline{\kappa }_\textrm{M} - \frac{1}{2} \overline{\kappa }^{\alpha \beta } \delta \overline{\kappa }_{\alpha \beta } + \overline{\kappa }_{\alpha \beta } {\left[ \overline{g}^{\bullet \bullet } \odot \overline{\kappa }^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta \overline{g}_{\gamma \delta } \nonumber \\ {}&\quad - \frac{1}{2} \overline{\kappa }_{\alpha \beta } { \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta \overline{\kappa }_{\gamma \delta } \end{aligned}$$

(205)

$$\begin{aligned}&= \underbrace{ \left( \overline{\omega }^{\alpha \beta } - 2 \overline{\kappa }_\textrm{M} \overline{\kappa }^{\alpha \beta } \right) }_{=-\overline{\kappa }_\textrm{G} \overline{g}^{\alpha \beta }} \delta \overline{g}_{\alpha \beta } + \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta } - \overline{\kappa }^{\alpha \beta } \right) \delta \overline{\kappa }_{\alpha \beta } \end{aligned}$$

(206)

$$\begin{aligned}&= \underbrace{ -\overline{\kappa }_\textrm{G} \overline{g}^{\alpha \beta } }_{=\frac{\partial \overline{\kappa }_\textrm{G}}{\partial \overline{g}_{\alpha \beta }}} \delta \overline{g}_{\alpha \beta } + \underbrace{ \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta } - \overline{\kappa }^{\alpha \beta } \right) }_{=\frac{\partial \overline{\kappa }_\textrm{G}}{\partial \overline{\kappa }_{\alpha \beta }}} \delta \overline{\kappa }_{\alpha \beta } \end{aligned}$$

(207)

$$\begin{aligned}&= 2 \frac{\partial \overline{\kappa }_\textrm{G}}{\partial \overline{g}_{\alpha \beta }} \delta \overline{\varepsilon }_{\alpha \beta } + \frac{\partial \overline{\kappa }_\textrm{G}}{\partial \overline{\kappa }_{\alpha \beta }} \delta \overline{\kappa }_{\alpha \beta } . \end{aligned}$$

(208)

The second variation of $\overline{\kappa }_\textrm{M}$ is

$$\begin{aligned} \delta _a \delta _b \overline{\kappa }_\textrm{M}&= \delta _a \overline{\varepsilon }_{\alpha \beta } \frac{4 \partial ^2 \overline{\kappa }_\textrm{M}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{g}_{\gamma \delta } } \delta _b \overline{\varepsilon }_{\gamma \delta } + \delta _a \overline{\varepsilon }_{\alpha \beta } \frac{2 \partial ^2 \overline{\kappa }_\textrm{M}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \frac{2 \partial ^2 \overline{\kappa }_\textrm{M}}{ \partial \overline{\kappa }_{\alpha \beta } \partial \overline{g}_{\gamma \delta } } \delta _b \overline{\varepsilon }_{\gamma \delta } + \delta _a \overline{\kappa }_{\alpha \beta } \underbrace{ \frac{\partial ^2 \overline{\kappa }_\textrm{M}}{ \partial \overline{\kappa }_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } } }_{=0} \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\&\quad + 2 \frac{\partial \overline{\kappa }_\textrm{M}}{ \partial \overline{g}_{\alpha \beta } } \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } + \frac{\partial \overline{\kappa }_\textrm{M}}{ \partial \overline{\kappa }_{\alpha \beta } } \delta _a \delta _b \overline{\kappa }_{\alpha \beta } ,\end{aligned}$$

(209)

where

$$\begin{aligned} \frac{\partial ^2 \overline{\kappa }_\textrm{M}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{g}_{\gamma \delta }}&= - \frac{1}{2} \frac{\partial \overline{\kappa }^{\alpha \beta }}{ \partial \overline{g}_{\gamma \delta } } = \left[ \overline{g}^{\bullet \bullet } \odot \overline{\kappa }^{\bullet \bullet }\right] ^{\alpha \beta \gamma \delta } , \end{aligned}$$

(210)

$$\begin{aligned} \frac{\partial ^2 \overline{\kappa }_\textrm{M}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } }&= \frac{1}{2} \frac{\partial \overline{g}^{\alpha \beta }}{ \partial \overline{g}_{\gamma \delta } } = - \frac{1}{2} \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } . \end{aligned}$$

(211)

With that,

$$\begin{aligned} \delta _a \delta _b \overline{\kappa }_\textrm{M}&= \delta _a \overline{\varepsilon }_{\alpha \beta } 4 \left[ \overline{g}^{\bullet \bullet } \odot \overline{\kappa }^{\bullet \bullet }\right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\&\quad - \delta _a \overline{\varepsilon }_{\alpha \beta } \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\kappa }_{\alpha \beta } \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } - \overline{\kappa }^{\alpha \beta } \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } \nonumber \\&\quad + \frac{1}{2} \overline{g}^{\alpha \beta } \delta _a \delta _b \overline{\kappa }_{\alpha \beta } . \end{aligned}$$

(212)

The second variation of $\overline{\kappa }_\textrm{G}$ is

$$\begin{aligned} \delta _a \delta _b \overline{\kappa }_\textrm{G}&= \delta _a \overline{\varepsilon }_{\alpha \beta } \frac{4 \partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{g}_{\gamma \delta } } \delta _b \overline{\varepsilon }_{\gamma \delta } + \delta _a \overline{\varepsilon }_{\alpha \beta } \frac{2 \partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \frac{2 \partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{\kappa }_{\alpha \beta } \partial \overline{g}_{\gamma \delta } } \delta _b \overline{\varepsilon }_{\gamma \delta } + \delta _a \overline{\kappa }_{\alpha \beta } \frac{\partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{\kappa }_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad + 2 \frac{\partial \overline{\kappa }_\textrm{G}}{ \partial \overline{g}_{\alpha \beta } } \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } + \frac{\partial \overline{\kappa }_\textrm{G}}{ \partial \overline{\kappa }_{\alpha \beta } } \delta _a \delta _b \overline{\kappa }_{\alpha \beta } , \end{aligned}$$

(213)

where

$$\begin{aligned} \frac{\partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{g}_{\gamma \delta } }&= - \overline{g}^{\alpha \beta } \frac{\partial \overline{\kappa }_\textrm{G}}{ \partial \overline{g}_{\gamma \delta }} - \overline{\kappa }_\textrm{G} \frac{\partial \overline{g}^{\alpha \beta } }{ \partial \overline{g}_{\gamma \delta }} \nonumber \\&= \overline{\kappa }_\textrm{G} \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } + \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } , \end{aligned}$$

(214)

$$\begin{aligned} \frac{\partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{g}_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } }&= - \overline{g}^{\alpha \beta } \frac{\partial \overline{\kappa }_\textrm{G}}{ \partial \overline{\kappa }_{\gamma \delta }} = -2 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta } \overline{g}^{\gamma \delta } + \overline{g}^{\alpha \beta } \overline{\kappa }^{\gamma \delta } , \end{aligned}$$

(215)

$$\begin{aligned} \frac{\partial ^2 \overline{\kappa }_\textrm{G}}{ \partial \overline{\kappa }_{\alpha \beta } \partial \overline{\kappa }_{\gamma \delta } }&= 2 \overline{g}^{\alpha \beta } \frac{\partial \overline{\kappa }_\textrm{M}}{ \partial \overline{\kappa }_{\gamma \delta } } - \frac{\partial \overline{\kappa }^{\alpha \beta }}{ \partial \overline{\kappa }_{\gamma \delta }} \nonumber \\&= \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } - \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } . \end{aligned}$$

(216)

Thus,

$$\begin{aligned} \delta _a \delta _b \overline{\kappa }_\textrm{G}&= \delta _a \overline{\varepsilon }_{\alpha \beta } 4 \overline{\kappa }_\textrm{G} \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } + \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\varepsilon }_{\alpha \beta } \overline{g}^{\alpha \beta } \left( 4 \overline{\kappa }_\textrm{M} \overline{g}^{\gamma \delta } - 2 \overline{\kappa }^{\gamma \delta } \right) \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\kappa }_{\alpha \beta } \left( 4 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta } - 2 \overline{\kappa }^{\alpha \beta } \right) \overline{g}^{\gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } - \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad - 2\overline{\kappa }_\textrm{G} \overline{g}^{\alpha \beta } \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } + \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta } - \overline{\kappa }^{\alpha \beta } \right) \delta _a \delta _b \overline{\kappa }_{\alpha \beta } . \end{aligned}$$

(217)

1.5 Variations of $\overline{\omega }_{\alpha \beta }$

We define $\overline{\omega }_{\alpha \beta }$ as the covariant components of $\overline{\pmb {\kappa }}^2$:

$$\begin{aligned} \overline{\omega }_{\alpha \beta } = \overline{\pmb {\kappa }}^2 : \overline{{\textbf {g}}}_{\alpha } \overline{{\textbf {g}}}_{\beta } . \end{aligned}$$

(218)

We show the variations of $\overline{\omega }_{\alpha \beta }$ in terms of variations of $\overline{\varepsilon }_{\alpha \beta }$ and $\overline{\kappa }_{\alpha \beta }$.

1.5.1 $\delta \overline{\omega }_{\alpha \beta }$

We take variation on Eq. (218) as follows:

(219)

(220)

(221)

(222)

For notational convenience, we introduce the symbols:

$$\begin{aligned} \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta }&= - {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{\kappa }_{\bullet \bullet } \odot \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } , \end{aligned}$$

(223)

$$\begin{aligned} \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta }&= {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{g}_{\bullet \bullet } \odot \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } , \end{aligned}$$

(224)

and we write

$$\begin{aligned} \delta \overline{\omega }_{\alpha \beta }&= 2 \delta \overline{\varepsilon }_{\gamma \delta } \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta } + 2 \delta \overline{\kappa }_{\gamma \delta } \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta } . \end{aligned}$$

(225)

1.5.2 $\delta _a \delta _b \overline{\omega }_{\alpha \beta }$

The second variation of $\overline{\omega }_{\alpha \beta }$ is obtained by taking the variation of Eq. (225):

$$\begin{aligned} \delta _a \delta _b \overline{\omega }_{\alpha \beta }&= 2 \delta _a \delta _b \overline{\varepsilon }_{\gamma \delta } \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta } + 2 \delta _a \delta _b \overline{\kappa }_{\gamma \delta } \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta } \nonumber \\ {}&\quad + 2 \delta _a \overline{\varepsilon }_{\gamma \delta } \delta _b \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta } + 2 \delta _a \overline{\kappa }_{\gamma \delta } \delta _b \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta } , \end{aligned}$$

(226)

where

$$\begin{aligned} \delta _b \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\gamma \delta }_{\quad \alpha \beta }&= - 2 {\left[ \delta _b \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{\kappa }_{\bullet \bullet } \odot \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } \nonumber \\ {}&\quad - 2 {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \delta _b \overline{\kappa }_{\bullet \bullet } \odot \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } \end{aligned}$$

(227)

$$\begin{aligned}&= 4 {\left[ \left( \overline{g}^{\bullet \bullet } \cdot \delta _b \overline{\varepsilon }_{\bullet \bullet } \cdot \overline{g}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } : \overline{\kappa }_{\bullet \bullet } \odot \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } \nonumber \\ {}&\quad - 2 {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \delta _b \overline{\kappa }_{\bullet \bullet } \odot \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } \end{aligned}$$

(228)

$$\begin{aligned}&= - 4 {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{g}_{\bullet \bullet } \odot \delta _b \overline{\varepsilon }_{\bullet \bullet } : \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\bullet \bullet }_{\quad \bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } \nonumber \\ {}&\quad - 2 {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{\kappa }_{\bullet \bullet } \odot \delta _b \overline{\kappa }_{\bullet \bullet } \right] }^{\gamma \delta }_{\quad \alpha \beta } , \end{aligned}$$

(229)

$$\begin{aligned} \delta _b \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta }&= \left[ \delta ^{\bullet }_{\quad \bullet } \odot \left( \delta _b \overline{g}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } + \overline{g}^{\bullet \bullet } \cdot \delta _b \overline{\kappa }_{\bullet \bullet } \right) \right] ^{\gamma \delta }_{\quad \alpha \beta } \end{aligned}$$

(230)

$$\begin{aligned}&= -2 \left[ \delta ^{\bullet }_{ \bullet } \odot \left( \overline{g}^{\bullet \bullet } \cdot \delta _b \overline{\varepsilon }_{\bullet \bullet } \cdot \overline{g}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \right) \right] ^{\gamma \delta }_{\quad \alpha \beta } \nonumber \\ {}&\quad + \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{g}_{\bullet \bullet } \odot \delta _b \overline{\kappa }_{\bullet \bullet } \right] ^{\gamma \delta }_{\quad \alpha \beta } \end{aligned}$$

(231)

$$\begin{aligned}&= -2 \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{g}_{\bullet \bullet } \odot \left( \delta _b \overline{\varepsilon }_{\bullet \bullet } \cdot \overline{g}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \right) \right] ^{\gamma \delta }_{\quad \alpha \beta } \nonumber \\ {}&\quad + \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } : \overline{g}_{\bullet \bullet } \odot \delta _b \overline{\kappa }_{\bullet \bullet } \right] ^{\gamma \delta }_{\quad \alpha \beta } . \end{aligned}$$

(232)

We will see these terms only as part of the contractions with $\tilde{S}^{\alpha \beta }$. We write those contractions as

(233)

(234)

(235)

(236)

(237)

Then, we obtain

$$\begin{aligned}&\delta _a \overline{\varepsilon }_{\gamma \delta } \delta _b {\left( \overline{\mathbb {W}}_{\varepsilon }\right) }^{\gamma \delta }_{\quad \alpha \beta } \tilde{S}^{\alpha \beta }\nonumber \\&\quad = - \delta _a \overline{\varepsilon }_{\alpha \beta } {\left[ 4 \left( {\left( \overline{\mathbb {W}}_{\varepsilon }\right) }^{\bullet \bullet }_{\quad \bullet \bullet } : \tilde{S}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\varepsilon }_{\alpha \beta } {\left[ 2 \left( \overline{g}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \cdot \tilde{S}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } , \end{aligned}$$

(238)

$$\begin{aligned}&\delta _a \overline{\kappa }_{\gamma \delta } \delta _b \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\gamma \delta }_{\quad \alpha \beta } \tilde{S}^{\alpha \beta }\nonumber \\&\quad = - \delta _a \overline{\kappa }_{\alpha \beta } \left[ 2 \left( \tilde{S}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \cdot \overline{g}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \left[ \tilde{S}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } . \end{aligned}$$

(239)

Thus, we can write

$$\begin{aligned} \frac{1}{2} \delta _a \delta _b \overline{\omega }_{\alpha \beta } \tilde{S}^{\alpha \beta }&= \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon } + \delta _a \delta _b \overline{\kappa }_{\alpha \beta } \left( \overline{\mathbb {W}}_{\kappa }\right) ^{\alpha \beta }_{\quad \chi \epsilon } \tilde{S}^{\chi \epsilon } \nonumber \\ {}&\quad - \delta _a \overline{\varepsilon }_{\alpha \beta } {\left[ 4 \left( \left( \overline{\mathbb {W}}_{\varepsilon }\right) ^{\bullet \bullet }_{\quad \bullet \bullet } : \tilde{S}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\varepsilon }_{\alpha \beta } {\left[ 2 \left( \overline{g}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \cdot \tilde{S}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } \nonumber \\ {}&\quad - \delta _a \overline{\kappa }_{\alpha \beta } \left[ 2 \left( \tilde{S}^{\bullet \bullet } \cdot \overline{\kappa }_{\bullet \bullet } \cdot \overline{g}^{\bullet \bullet } \right) \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \left[ \tilde{S}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } . \end{aligned}$$

(240)

1.6 Variations of $\xi ^3$

We express the variations of $\xi ^3$ in terms of variations of $\overline{\varepsilon }_{\alpha \beta }$ and $\overline{\kappa }_{\alpha \beta }$.

1.6.1 $\delta \xi ^3$

We take the variation of Eq. (12) and obtain

$$\begin{aligned} \overline{A} \delta \hat{V} + \delta \overline{A} \hat{V} = 0 , \end{aligned}$$

(241)

which gives us

$$\begin{aligned} \delta \hat{V} = - \hat{V} \delta \ln \overline{A} . \end{aligned}$$

(242)

By definition, $\delta \hat{V}$ and $\delta \hat{A}$ can be expressed as

$$\begin{aligned} \delta \hat{V}&= \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \delta \overline{\kappa }_\textrm{M} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \delta \overline{\kappa }_\textrm{G} + \hat{A} \delta \xi ^3, \end{aligned}$$

(243)

$$\begin{aligned} \delta \hat{A}&= \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \delta \overline{\kappa }_\textrm{M} + \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \delta \overline{\kappa }_\textrm{G} + \frac{\partial \hat{A}}{\partial z} \delta \xi ^3 . \end{aligned}$$

(244)

Rearranging Eq. (242), we get

$$\begin{aligned} -\hat{V} \delta \ln \overline{A}&= \left( \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \delta \overline{\kappa }_\textrm{M} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \delta \overline{\kappa }_\textrm{G} + \hat{A} \delta \xi ^3 \right) . \end{aligned}$$

(245)

With that, $\delta \xi ^3$ can be expressed as

$$\begin{aligned} \delta \xi ^3&= - \frac{ 1 }{ \hat{A} } \left( \hat{V} \delta \ln \overline{A} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \delta \overline{\kappa }_\textrm{M} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \delta \overline{\kappa }_\textrm{G} \right) . \end{aligned}$$

(246)

Equation (246) is expressed in terms of the variations of $\overline{\varepsilon }_{\alpha \beta }$ and $\overline{\kappa }_{\alpha \beta }$ as follows:

$$\begin{aligned} \delta \xi ^3&= \delta \overline{\varepsilon }_{\alpha \beta } Q_\varepsilon ^{\alpha \beta } + \delta \overline{\kappa }_{\alpha \beta } Q_\kappa ^{\alpha \beta } , \end{aligned}$$

(247)

where $Q_\varepsilon ^{\alpha \beta } = Q_\varepsilon ^{\alpha \beta } (\xi ^3)$ and $Q_\kappa ^{\alpha \beta } = Q_\kappa ^{\alpha \beta } (\xi ^3)$, which are expressed as

$$\begin{aligned} Q_\varepsilon ^{\alpha \beta } (z)&= -\frac{1}{\hat{A}} \Bigg ( \hat{V} \overline{g}^{\alpha \beta } - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } -2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \Bigg ) \end{aligned}$$

(248)

$$\begin{aligned}&= -\frac{1}{\hat{A}} \Bigg ( \Bigg ( z + \overline{\kappa }_\textrm{M} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} +\overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \Bigg ) \overline{g}^{\alpha \beta }\nonumber \\&\quad - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } - 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \Bigg ) \end{aligned}$$

(249)

$$\begin{aligned}&= -\frac{1}{\hat{A}} \left( \left( z + \overline{\kappa }_\textrm{M} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} - \overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \right) \overline{g}^{\alpha \beta } - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } \right) \end{aligned}$$

(250)

$$\begin{aligned}&= -\frac{1}{\hat{A}} \left( \left( 1 + z \overline{\kappa }_\textrm{M} - \frac{1}{3} \overline{\kappa }_\textrm{G} z^2 \right) \overline{g}^{\alpha \beta } - z \overline{\kappa }^{\alpha \beta } \right) z , \end{aligned}$$

(251)

$$\begin{aligned} Q_\kappa ^{\alpha \beta } (z)&= -\frac{1}{\hat{A}} \left( \frac{1}{2} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \overline{g}^{\alpha \beta } + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta } - \overline{\kappa }^{\alpha \beta } \right) \right) \end{aligned}$$

(252)

$$\begin{aligned}&= -\frac{1}{\hat{A}} \left( \frac{1}{2} \left( \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} + 4 \overline{\kappa }_\textrm{M} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \right) \overline{g}^{\alpha \beta } - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \overline{\kappa }^{\alpha \beta } \right) \end{aligned}$$

(253)

$$\begin{aligned}&= -\frac{1}{\hat{A}} \left( \frac{1}{6} \left( 3 + 4 \overline{\kappa }_\textrm{M} z \right) \overline{g}^{\alpha \beta } - \frac{1}{3} z \overline{\kappa }^{\alpha \beta } \right) z^2 . \end{aligned}$$

(254)

Remark 16

$\hat{A} = 1$ at $z=0$, and it is possible to have $\hat{A} < 1$ (see Appendix B.2). $Q_\varepsilon ^{\alpha \beta }$ is of order z to $z^3$, and $Q_\kappa ^{\alpha \beta }$ is of order $z^2$ to $z^3$.

1.6.2 $\delta _a \delta _b \xi ^3$

We rearrange Eq. (246) as

$$\begin{aligned} \hat{A} \delta \xi ^3&= - \hat{V} \delta \ln \overline{A} - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \delta \overline{\kappa }_\textrm{M} - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \delta \overline{\kappa }_\textrm{G} . \end{aligned}$$

(255)

We take another variation and obtain

(256)

Substituting Eqs. (242) and (244) into this and rearranging the terms, we get

$$\begin{aligned} \hat{A} \delta _a \delta _b \xi ^3&= \hat{V} \delta _a \ln \overline{A} \delta _b \ln \overline{A} - \hat{V} \delta _a \delta _b \ln \overline{A} - \delta _a\xi ^3 \frac{\partial \hat{A}}{\partial z} \delta _b\xi ^3 \nonumber \\ {}&\quad - \delta _a \overline{\kappa }_\textrm{M} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \delta _b \xi ^3 - \delta _a \xi ^3 \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \delta _b \overline{\kappa }_\textrm{M} \nonumber \\ {}&\quad - \delta _a \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \delta _b \xi ^3 - \delta _a \xi ^3 \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \delta _b \overline{\kappa }_\textrm{G} \nonumber \\ {}&\quad - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \delta _a \delta _b \overline{\kappa }_\textrm{M} - \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \delta _a \delta _b \overline{\kappa }_\textrm{G} . \end{aligned}$$

(257)

Thus,

$$\begin{aligned} \delta _a \delta _b \xi ^3&= \frac{\hat{V}}{\hat{A}} \left( \delta _a \ln \overline{A} \delta _b \ln \overline{A} - \delta _a \delta _b \ln \overline{A} \right) - \delta _a\xi ^3 \frac{1}{\hat{A}} \frac{\partial \hat{A}}{\partial z} \delta _b\xi ^3 \nonumber \\ {}&\quad - \frac{1}{\hat{A}} \left( \delta _a \overline{\kappa }_\textrm{M} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} + \delta _a \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \right) \delta _b \xi ^3 \nonumber \\ {}&\quad - \delta _a \xi ^3 \frac{1}{\hat{A}} \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \delta _b \overline{\kappa }_\textrm{M} + \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \delta _b \overline{\kappa }_\textrm{G} \right) \nonumber \\ {}&\quad - \frac{1}{\hat{A}} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \delta _a \delta _b \overline{\kappa }_\textrm{M} - \frac{1}{\hat{A}} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \delta _a \delta _b \overline{\kappa }_\textrm{G} . \end{aligned}$$

(258)

By arranging the terms, we obtain

$$\begin{aligned} \delta _a \delta _b \xi ^3&= \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } Q_\varepsilon ^{\alpha \beta } + \delta _a \delta _b \overline{\kappa }_{\alpha \beta } Q_\kappa ^{\alpha \beta } + \delta _a \overline{\varepsilon }_{\alpha \beta } \mathbb {Q}_{\varepsilon \varepsilon }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\ {}&\quad + \delta _a \overline{\varepsilon }_{\alpha \beta } \mathbb {Q}_{\varepsilon \kappa }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } + \delta _a \overline{\kappa }_{\alpha \beta } \mathbb {Q}_{\kappa \varepsilon }^{\alpha \beta \gamma \delta } \delta _b \overline{\varepsilon }_{\gamma \delta } \nonumber \\&\quad + \delta _a \overline{\kappa }_{\alpha \beta } \mathbb {Q}_{\kappa \kappa }^{\alpha \beta \gamma \delta } \delta _b \overline{\kappa }_{\gamma \delta } , \end{aligned}$$

(259)

where

$$\begin{aligned} \mathbb {Q}_{\varepsilon \varepsilon }^{\alpha \beta \gamma \delta }&= \frac{1}{\hat{A}} \left( \hat{V} \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } +2 \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } - \frac{\partial \hat{A}}{\partial z} Q_\varepsilon ^{\alpha \beta } Q_\varepsilon ^{\gamma \delta } \right) \nonumber \\ {}&\quad + \frac{1}{\hat{A}} \left( \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } + 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \right) Q_\varepsilon ^{\gamma \delta } \right. \nonumber \\ {}&\quad \left. + Q_\varepsilon ^{\alpha \beta } \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\gamma \delta } + 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\gamma \delta } \right) \right) \nonumber \\ {}&\quad - \frac{4}{\hat{A}} \Bigg ( \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \left[ \overline{g}^{\bullet \bullet } \odot \overline{\kappa }^{\bullet \bullet } \right] ^{ \alpha \beta \gamma \delta } \nonumber \\&\quad + \overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \Bigg [ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } + \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \Bigg ]^{ \alpha \beta \gamma \delta } \Bigg ) \end{aligned}$$

(260)

$$\begin{aligned}&= \frac{1}{\hat{A}} \left( \left( \hat{V} -4 \overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \right) \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \right. \nonumber \\ {}&\quad \left. +2 \left( \hat{V} -2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \right) \left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } \right. \nonumber \\&\quad \left. - 4 \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \left[ \overline{g}^{\bullet \bullet } \odot \overline{\kappa }^{\bullet \bullet } \right] ^{ \alpha \beta \gamma \delta } \right) \nonumber \\ {}&\quad - \frac{1}{\hat{A}} \left( \frac{\partial \hat{A}}{\partial z} Q_\varepsilon ^{\alpha \beta } Q_\varepsilon ^{\gamma \delta } - \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } + 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \right) Q_\varepsilon ^{\gamma \delta } \right. \nonumber \\ {}&\quad \left. - Q_\varepsilon ^{\alpha \beta } \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\gamma \delta } + 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\gamma \delta } \right) \right) , \end{aligned}$$

(261)

$$\begin{aligned} \mathbb {Q}_{\varepsilon \kappa }^{\alpha \beta \gamma \delta }&= -\frac{1}{\hat{A}} \left( \frac{\partial \hat{A}}{\partial z} Q_\varepsilon ^{\alpha \beta } - \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } + 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \right) \right) Q_\kappa ^{\gamma \delta } \nonumber \\ {}&\qquad - \frac{1}{\hat{A}} Q_\varepsilon ^{\alpha \beta } \left( \frac{1}{2} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{g}^{\alpha \beta } + \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\gamma \delta } - \overline{\kappa }^{\gamma \delta } \right) \right) \nonumber \\ {}&\qquad + \frac{1}{\hat{A}} \left( \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } {+} 2 \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\gamma \delta } {-} \overline{\kappa }^{\gamma \delta } \right) \right) \end{aligned}$$

(262)

$$\begin{aligned}&= \frac{1}{\hat{A}} \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{\kappa }^{\alpha \beta } + 2 \overline{\kappa }_\textrm{G} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \right) Q_\kappa ^{\gamma \delta } \nonumber \\ {}&\quad -\frac{1}{\hat{A}} Q_\varepsilon ^{\alpha \beta } \left( \frac{\partial \hat{A}}{\partial z} Q_\kappa ^{\gamma \delta } + \frac{1}{2} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \overline{g}^{\gamma \delta } \right) \nonumber \\ {}&\quad -\frac{1}{\hat{A}} \left( \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} Q_\varepsilon ^{\alpha \beta } - 2 \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \overline{g}^{\alpha \beta } \right) \left( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\gamma \delta } - \overline{\kappa }^{\gamma \delta } \right) \nonumber \\ {}&\quad + \frac{1}{\hat{A}} \left( \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} {\left[ \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } \right) , \end{aligned}$$

(263)

$$\begin{aligned} \mathbb {Q}_{\kappa \kappa }^{\alpha \beta \gamma \delta }&= -\frac{1}{\hat{A}} \left( \frac{\partial \hat{A}}{\partial z} Q_\kappa ^{\alpha \beta } Q_\kappa ^{\gamma \delta } + \frac{1}{2} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{M}} \left( \overline{g}^{\alpha \beta } Q_\kappa ^{\gamma \delta } + Q_\kappa ^{\alpha \beta } \overline{g}^{\gamma \delta } \right) \right) \nonumber \\ {}&\quad -\frac{1}{\hat{A}} \frac{\partial \hat{A}}{\partial \overline{\kappa }_\textrm{G}} \Bigg ( \Bigg ( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\alpha \beta }- \overline{\kappa }^{\alpha \beta } \Bigg ) Q_\kappa ^{\gamma \delta } \nonumber \\&\quad + Q_\kappa ^{\alpha \beta } \Bigg ( 2 \overline{\kappa }_\textrm{M} \overline{g}^{\gamma \delta } - \overline{\kappa }^{\gamma \delta } \Bigg ) \Bigg ) \nonumber \\ {}&\quad - \frac{1}{\hat{A}} \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \left[ \overline{g}^{\bullet \bullet } \overline{g}^{\bullet \bullet } - \overline{g}^{\bullet \bullet } \odot \overline{g}^{\bullet \bullet } \right] ^{\alpha \beta \gamma \delta } . \end{aligned}$$

(264)

1.7 Spatial derivatives of $\xi ^3$

We take the logarithmic derivative of Eq. (12) with respect to $\xi ^{\alpha }$ and multiply Eq. (12) on each side:

$$\begin{aligned} \overline{A} \left( \hat{V} \frac{\partial \ln \overline{A} }{\partial \xi ^{\alpha }} + \frac{ \partial \hat{V} }{\partial \xi ^{\alpha }} \right) = \overline{A}_0 \left( \hat{V}_0 \frac{\partial \ln \overline{A}_0 }{\partial \xi ^{\alpha }} + \frac{ \partial \hat{V} _0 }{\partial \xi ^{\alpha }} \right) , \end{aligned}$$

(265)

where

$$\begin{aligned} \frac{\partial \hat{V}}{\partial \xi ^{\alpha }}&= \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \frac{\partial \overline{\kappa }_\textrm{M}}{\partial \xi ^{\alpha }} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \frac{\partial \overline{\kappa }_\textrm{G}}{\partial \xi ^{\alpha }} + \hat{A} \xi ^3_{,\alpha }, \end{aligned}$$

(266)

$$\begin{aligned} \frac{ \partial \hat{V}_0}{\partial \xi ^{\alpha }}&= \frac{\partial \hat{V}_0}{\partial \overline{K}_\textrm{M}} \frac{\partial \overline{K}_\textrm{M}}{\partial \xi ^{\alpha }} + \frac{\partial \hat{V}_0}{\partial \overline{K}_\textrm{G}} \frac{\partial \overline{K}_\textrm{G}}{\partial \xi ^{\alpha }} + \hat{A}_0 \left( \xi ^3_0\right) _{,\alpha } , \end{aligned}$$

(267)

where $\overline{K}_{\textrm{M}}$ and $\overline{K}_{\textrm{G}}$ are the undeformed-configuration versions of $\overline{\kappa }_\textrm{M}$ and $\overline{\kappa }_\textrm{G}$. The left-hand side of Eq. (265) is

$$\begin{aligned}&\overline{A} \left( \hat{V} \frac{\partial \ln \overline{A} }{\partial \xi ^{\alpha }} + \frac{ \partial \hat{V} }{\partial \xi ^{\alpha }} \right) \nonumber \\&\quad = A \left( \frac{ 1 }{\hat{A}} \left( \hat{V} \frac{\partial \ln \overline{A} }{\partial \xi ^{\alpha }} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \frac{\partial \overline{\kappa }_\textrm{M}}{\partial \xi ^{\alpha }} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \frac{\partial \overline{\kappa }_\textrm{G}}{\partial \xi ^{\alpha }} \right) + \xi ^3_{,\alpha } \right) . \end{aligned}$$

(268)

From Eqs. (246) and (247), we can write

$$\begin{aligned}&\frac{ 1 }{\hat{A}} \left( \hat{V} \frac{\partial \ln \overline{A} }{\partial \xi ^{\alpha }} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{M}} \frac{\partial \overline{\kappa }_\textrm{M}}{\partial \xi ^{\alpha }} + \frac{\partial \hat{V}}{\partial \overline{\kappa }_\textrm{G}} \frac{\partial \overline{\kappa }_\textrm{G}}{\partial \xi ^{\alpha }} \right) \nonumber \\&\quad = - \frac{1}{2} Q_\varepsilon ^{\gamma \delta } \overline{g}_{\gamma \delta , \alpha } - Q_\kappa ^{\gamma \delta } \overline{\kappa }_{\gamma \delta , \alpha } . \end{aligned}$$

(269)

Thus, we get

$$\begin{aligned}&\overline{A} \left( \hat{V} \frac{\partial \ln \overline{A} }{\partial \xi ^{\alpha }} + \frac{ \partial \hat{V} }{\partial \xi ^{\alpha }} \right) \nonumber \\&\quad = A \left( - \frac{1}{2} Q_\varepsilon ^{\gamma \delta } \overline{g}_{\gamma \delta , \alpha } - Q_\kappa ^{\gamma \delta } \overline{\kappa }_{\gamma \delta , \alpha } + \xi ^3_{,\alpha } \right) . \end{aligned}$$

(270)

The right-hand side of Eq. (265) can be written as the undeformed-configuration version of the left-hand side:

$$\begin{aligned}&\overline{A}_0 \left( \hat{V}_0 \frac{\partial \ln \overline{A}_0 }{\partial \xi ^{\alpha }} + \frac{ \partial \hat{V} }{\partial \xi ^{\alpha }} \right) \nonumber \\&= A_0 \left( - \frac{1}{2} \left( Q_\varepsilon \right) _0^{\gamma \delta } \overline{G}_{\gamma \delta , \alpha } - \left( Q_\kappa \right) _0^{\gamma \delta } (z_0) \overline{K}_{\gamma \delta , \alpha } + \left( \xi ^3_0\right) _{,\alpha } \right) , \end{aligned}$$

(271)

where

$\left( Q_\varepsilon \right) _0^{\gamma \delta } = \left( Q_\varepsilon \right) _0^{\gamma \delta } (\xi ^3_0)$ and $\left( Q_\kappa \right) _0^{\gamma \delta } = \left( Q_\kappa \right) _0^{\gamma \delta } (\xi ^3_0)$, which are expressed as

$$\begin{aligned}&\left( Q_\varepsilon \right) _0^{\gamma \delta } (z_0)\nonumber \\&= -\frac{1}{\hat{A}_0} \Bigg ( \Bigg ( z_0 + \overline{K}_\textrm{M} \frac{\partial \hat{V}_0}{\partial \overline{K}_\textrm{M}} \quad - \overline{K}_\textrm{G} \frac{\partial \hat{V}}{\partial \overline{K}_\textrm{G}} \Bigg ) \overline{G}^{\gamma \delta } - \frac{\partial \hat{V}}{\partial \overline{K}_\textrm{M}} \overline{K}^{\gamma \delta } \Bigg ) \end{aligned}$$

(272)

$$\begin{aligned}&= -\frac{1}{\hat{A}_0} \left( \left( 1 + z_0 \overline{K}_\textrm{M} - \frac{1}{3} \overline{K}_\textrm{G} z^2_0 \right) \overline{G}^{\gamma \delta } - z_0 \overline{K}^{\gamma \delta } \right) z_0 , \end{aligned}$$

(273)

$$\begin{aligned}&\left( Q_\kappa \right) _0^{\gamma \delta } (z_0)\nonumber \\&= -\frac{1}{\hat{A}_0} \left( \frac{1}{2} \left( \frac{\partial \hat{V}_0}{\partial \overline{K}_\textrm{M}} + 4 \overline{K}_\textrm{M} \frac{\partial \hat{V}_0}{\partial \overline{K}_\textrm{G}} \right) \overline{G}^{\gamma \delta } - \frac{\partial \hat{V}_0}{\partial \overline{K}_\textrm{G}} \overline{K}^{\gamma \delta } \right) \end{aligned}$$

(274)

$$\begin{aligned}&= -\frac{1}{\hat{A}_0} \left( \frac{1}{6} \left( 3 + 4 \overline{K}_\textrm{M} z_0 \right) \overline{G}^{\gamma \delta } - \frac{1}{3} z_0 \overline{K}^{\gamma \delta } \right) z^2_0 . \end{aligned}$$

(275)

Remembering that $\lambda _3 = \frac{A_0}{A}$, we get

$$\begin{aligned}&- \frac{1}{2} Q_\varepsilon ^{\gamma \delta } \overline{g}_{\gamma \delta , \alpha } - Q_\kappa ^{\gamma \delta } \overline{\kappa }_{\gamma \delta , \alpha } + \xi ^3_{,\alpha } \nonumber \\&= \lambda _3 \left( - \frac{1}{2} \left( Q_\varepsilon \right) _0^{\gamma \delta } \overline{G}_{\gamma \delta , \alpha } - \left( Q_\kappa \right) _0^{\gamma \delta } \overline{K}_{\gamma \delta , \alpha } + \left( \xi ^3_0\right) _{,\alpha } \right) . \end{aligned}$$

(276)

Thus,

$$\begin{aligned} \xi ^3_{,\alpha }&= \frac{1}{2} Q_\varepsilon ^{\gamma \delta } \overline{g}_{\gamma \delta , \alpha } + Q_\kappa ^{\gamma \delta } \overline{\kappa }_{\gamma \delta , \alpha } \nonumber \\ {}&\quad - \lambda _3 \left( \frac{1}{2} \left( Q_\varepsilon \right) _0^{\gamma \delta } \overline{G}_{\gamma \delta , \alpha } + \left( Q_\kappa \right) _0^{\gamma \delta } \overline{K}_{\gamma \delta , \alpha } - \left( \xi ^3_0\right) _{,\alpha } \right) . \end{aligned}$$

(277)

Using Eq. (96), we get

$$\begin{aligned} \left( \xi ^3_0\right) _{,\alpha }&= {\left\{ \begin{array}{ll} \frac{\xi ^3_0}{ \left( \xi ^3_0\right) ^-} \left( \xi ^3_0\right) ^-_{,\alpha } &{}{(\xi ^3_0 < 0)} \\ 0 &{}{(\xi ^3_0 = 0)} \\ \frac{\xi ^3_0}{ \left( \xi ^3_0\right) ^+} \left( \xi ^3_0\right) ^+_{,\alpha } &{}{(\xi ^3_0 > 0)} \end{array}\right. } . \end{aligned}$$

(278)

The elastic moduli considering thickness deformation

The variation of the $\tilde{S}^{\alpha \beta } = S_{\textrm{iso}}^{\alpha \beta } - \lambda _3^2 S_{\textrm{iso}}^{3 3} g^{\alpha \beta }$ is

(279)

(280)

(281)

From that, we get

$$\begin{aligned} {\tilde{\mathbb {C}}}^{\alpha \beta \gamma \delta }&= \mathbb {C}_{\textrm{iso}}^{\alpha \beta \gamma \delta } - \lambda _3^2 \left( \mathbb {C}_{\textrm{iso}}^{\alpha \beta 3 3} g^{\gamma \delta } + g^{\alpha \beta } \mathbb {C}_{\textrm{iso}}^{3 3 \gamma \delta } \right) \nonumber \\ {}&\quad + \lambda _3^4 \mathbb {C}_{\textrm{iso}}^{3 3 3 3} g^{\alpha \beta } g^{\gamma \delta } \nonumber \\&\quad + 2 \lambda _3^2 S_{\textrm{iso}}^{3 3} \left( {\left[ g^{\bullet \bullet } \odot g^{\bullet \bullet } \right] }^{\alpha \beta \gamma \delta } + g^{\alpha \beta } g^{\gamma \delta } \right) . \end{aligned}$$

(282)

Constitutive models

We test two constitutive models: neo-Hookean and Mooney–Rivlin materials. The strain-energy density functions are

$$\begin{aligned} \varphi _\textrm{NH} \left( {\textbf {C}}\right)&= \frac{1}{2} \mu \left( \textrm{tr}{\textbf {C}}- 3\right) , \end{aligned}$$

(283)

$$\begin{aligned} \varphi _\textrm{MR} \left( {\textbf {C}}\right)&= C_{10}\left( \textrm{tr}{\textbf {C}}- 3\right) + C_{01}\left( \frac{1}{2}\left( \left( \textrm{tr}{\textbf {C}}\right) ^2-\textrm{tr}\left( {\textbf {C}}\cdot {\textbf {C}}\right) \right) - 3\right) , \end{aligned}$$

(284)

where $\mu$ is the shear modulus, and $C_{10}$ and $C_{01}$ are the coefficients of the Mooney–Rivlin material model. The shear modulus in the undeformed configuration is $\mu _0 = \mu$ for the neo-Hookean material and $\mu _0 = 2\left( C_{10}+C_{01}\right)$ for the Mooney–Rivlin material. In this article, we use these models in their incompressible-material forms.