Analytical Solutions for an Isotropic Elastic Half-Plane with Complete Surface Effects Subjected to a Concentrated/Uniform Surface Load

Abstract

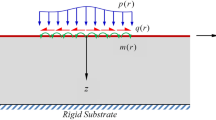
Within the context of Gurtin–Murdoch surface elasticity theory, closed-form analytical solutions are derived for an isotropic elastic half-plane subjected to a concentrated/uniform surface load. Both the effects of residual surface stress and surface elasticity are included. Airy stress function method and Fourier integral transform technique are used. The solutions are provided in a compact manner that can easily reduce to special situations that take into account either one surface effect or none at all. Numerical results indicate that surface effects generally lower the stress levels and smooth the deformation profiles in the half-plane. Surface elasticity plays a dominant role in the in-plane elastic fields for a tangentially loaded half-plane, while the effect of residual surface stress is fundamentally crucial for the out-of-plane stress and displacement when the half-plane is normally loaded. In the remaining situations, combined effects of surface elasticity and residual surface stress should be considered. The results for a concentrated surface force serve essentially as fundamental solutions of the Flamant and the half-plane Cerruti problems with surface effects. The solutions presented in this work may be helpful for understanding the contact behaviors between solids at the nanoscale.

Appendices

Appendix A: Expressions of a Series of $f_{n}$ and $g_{n}$ Functions

For brevity, the expressions of $f_{n}$ and $g_{n}$ functions will be given here only for the cases of n = − 1, 0, 1, and 2, which are directly used in analytical solutions. $x_{2} \ge 0$ holds throughout the paper and the appendices.

Firstly, $f_{n} \left( {x_{1} ,x_{2} } \right)$ and $g_{n} \left( {x_{1} ,x_{2} } \right)$, as the inverse Fourier transforms of $F_{n} \left( {\xi ,x_{2} } \right)$ and $G_{n} \left( {\xi ,x_{2} } \right)$ in Eq. (26), respectively, are

$$ \begin{aligned}& f_{ - 1} \left( {x_{1} ,x_{2} } \right) = - \ln \left( {x_{1}^{2} + x_{2}^{2} } \right) - 2\gamma \\& f_{0} \left( {x_{1} ,x_{2} } \right) = \, \frac{{2x_{2} }}{{x_{1}^{2} + x_{2}^{2} }} \\& f_{1} \left( {x_{1} ,x_{2} } \right) = \, - \frac{{2\left( {x_{1}^{2} - x_{2}^{2} } \right)}}{{\left( {x_{1}^{2} + x_{2}^{2} } \right)^{2} }} \\& f_{2} \left( {x_{1} ,x_{2} } \right) = \,- \frac{{4x_{2} \left( {3x_{1}^{2} - x_{2}^{2} } \right)}}{{\left( {x_{1}^{2} + x_{2}^{2} } \right)^{3} }} \\& g_{ - 1} \left( {x_{1} ,x_{2} } \right) = 2\arctan \frac{{x_{1} }}{{x_{2} }} \\& g_{0} \left( {x_{1} ,x_{2} } \right) = \, \frac{{2x_{1} }}{{x_{1}^{2} + x_{2}^{2} }} \\& g_{1} \left( {x_{1} ,x_{2} } \right) = \frac{{4x_{1} x_{2} }}{{\left( {x_{1}^{2} + x_{2}^{2} } \right)^{2} }} \\& g_{2} \left( {x_{1} ,x_{2} } \right) = \frac{{4x_{1} \left( {3x_{2}^{2} - x_{1}^{2} } \right)}}{{\left( {x_{1}^{2} + x_{2}^{2} } \right)^{3} }} \\ \end{aligned} $$

(A1)

where $\gamma$ is Euler’s constant.

According to definitions in Eq. (8), the inverse Fourier transforms of $F_{0} \left( {\xi ,x_{2} ;a} \right)$ and $G_{0} \left( {\xi ,x_{2} ;a} \right)$ in Eq. (25) are

$$ \begin{aligned} f_{0} \left( {x_{1} ,x_{2} ;a} \right) & = \frac{1}{a}\left[ {\text{e}}^{{\left( {x_{2} + {\text{i}}x_{1} } \right)/a}} E_{1} \left( {\frac{{x_{2} + {\text{i}}x_{1} }}{a}} \right) \right.\\ &\quad\left.+ {\text{e}}^{{\left( {x_{2} - {\text{i}}x_{1} } \right)/a}} E_{1} \left( {\frac{{x_{2} - {\text{i}}x_{1} }}{a}} \right) \right] \hfill \\ g_{0} \left( {x_{1} ,x_{2} ;a} \right) &= \frac{{\text{i}}}{a}\left[ {\text{e}}^{{\left( {x_{2} + {\text{i}}x_{1} } \right)/a}} E_{1} \left( {\frac{{x_{2} + {\text{i}}x_{1} }}{a}} \right) \right.\\ &\quad\left.- {\text{e}}^{{\left( {x_{2} - {\text{i}}x_{1} } \right)/a}} E_{1} \left( {\frac{{x_{2} - {\text{i}}x_{1} }}{a}} \right) \right] \hfill \\ \end{aligned}$$

(A2)

where

$$ E_{1} \left( z \right) = \int_{1}^{ + \infty } {\frac{{{\text{e}}^{ - zt} }}{t}{\text{d}}t} $$

(A3)

is the exponential integral function of a complex argument $z$ with ${\text{Re}} \left( z \right) > 0$. From Eqs. (25) and (26), we notice the following recurrence relations in the transform space

$$ \begin{gathered} F_{n} \left( {\xi ,x_{2} ;a} \right) = \frac{1}{a}\left[ {F_{n - 1} \left( {\xi ,x_{2} } \right) - F_{n - 1} \left( {\xi ,x_{2} ;a} \right)} \right] \hfill \\ G_{n} \left( {\xi ,x_{2} ;a} \right) = \frac{1}{a}\left[ {G_{n - 1} \left( {\xi ,x_{2} } \right) - G_{n - 1} \left( {\xi ,x_{2} ;a} \right)} \right] \hfill \\ \end{gathered} $$

(A4)

So there exist similar recurrence relations as

$$ \begin{gathered} f_{n} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}\left[ {f_{n - 1} \left( {x_{1} ,x_{2} } \right) - f_{n - 1} \left( {x_{1} ,x_{2} ;a} \right)} \right] \hfill \\ g_{n} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}\left[ {g_{n - 1} \left( {x_{1} ,x_{2} } \right) - g_{n - 1} \left( {x_{1} ,x_{2} ;a} \right)} \right] \hfill \\ \end{gathered} $$

(A5)

by virtue of which we have

$$ \begin{aligned} & f_{ - 1} \left( {x_{1} ,x_{2} ;a} \right) = f_{ - 1} \left( {x_{1} ,x_{2} } \right) - af_{0} \left( {x_{1} ,x_{2} ;a} \right) \\& f_{1} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}f_{0} \left( {x_{1} ,x_{2} } \right) - \frac{1}{a}f_{0} \left( {x_{1} ,x_{2} ;a} \right) \\& f_{2} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}f_{1} \left( {x_{1} ,x_{2} } \right) - \frac{1}{{a^{2} }}f_{0} \left( {x_{1} ,x_{2} } \right) + \frac{1}{{a^{2} }}f_{0} \left( {x_{1} ,x_{2} ;a} \right) \\& g_{ - 1} \left( {x_{1} ,x_{2} ;a} \right) = g_{ - 1} \left( {x_{1} ,x_{2} } \right) - ag_{0} \left( {x_{1} ,x_{2} ;a} \right) \\& g_{1} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}g_{0} \left( {x_{1} ,x_{2} } \right) - \frac{1}{a}g_{0} \left( {x_{1} ,x_{2} ;a} \right) \\& g_{2} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}g_{1} \left( {x_{1} ,x_{2} } \right) - \frac{1}{{a^{2} }}g_{0} \left( {x_{1} ,x_{2} } \right) + \frac{1}{{a^{2} }}g_{0} \left( {x_{1} ,x_{2} ;a} \right) \\ \end{aligned} $$

(A6)

where $f_{n} \left( {x_{1} ,x_{2} } \right)$, $g_{n} \left( {x_{1} ,x_{2} } \right)$ and $f_{0} \left( {x_{1} ,x_{2} ;a} \right)$, $g_{0} \left( {x_{1} ,x_{2} ;a} \right)$ are given in Eqs. (A1) and (A2), respectively. Equations (A1), (A2), and (A6) constitute a series of $f_{n}$ and $g_{n}$ functions that facilitate the expression of analytical solutions for a half-plane subjected to a concentrated surface force.

$f_{0} \left( {x_{1} ,x_{2} ;a} \right)$ and $g_{0} \left( {x_{1} ,x_{2} ;a} \right)$ are two key functions to express the closed-form analytical solutions in the present paper. They are composed properly of the exponential and the exponential integral functions. Similar solutions invoking the exponential integral functions were proposed by Huang and Yu [11], and were subsequently used in Zhao and Rajapakse [12]. Chen and Zhang [15] presented a detailed discussion on the properties of two functions closely related to $f_{0} \left( {x_{1} ,x_{2} ;a} \right)$ and $g_{0} \left( {x_{1} ,x_{2} ;a} \right)$. Koguchi [26] employed another special function, namely the incomplete Gamma function ${\Gamma }\left( {0,z} \right)$, which is equivalent to $E_{1} \left( z \right)$, to express their solutions. There are other choices of special functions, for example, according to definitions in Eq. (8), the inverse Fourier transforms of $F_{n} \left( {\xi ,x_{2} ;a} \right)$ in Eq. (25) can also be written as

$$ \begin{aligned} f_{n} \left( {x_{1} ,x_{2} ;a} \right) & = \frac{{{\Gamma }\left( {n + 1} \right)}}{{a^{n + 1} }}\left[ U\left( {n + 1,n + 1,\frac{{x_{2} + {\text{i}}x_{1} }}{a}} \right)\right.\\ &\quad\left.+ U\left( {n + 1,n + 1,\frac{{x_{2} - {\text{i}}x_{1} }}{a}} \right) \right]\end{aligned} $$

(A7)

where ${\Gamma }\left( n \right)$ is the Gamma function and $U\left( {p,q,z} \right) = \frac{1}{{{\Gamma }\left( p \right)}}\int_{0}^{ + \infty } {\frac{{\eta^{p - 1} {\text{e}}^{ - \eta z} }}{{\left( {1 + \eta } \right)^{1 + p - q} }}{\text{d}}\eta }$ is the Tricomi function, i.e., the confluent hypergeometric function of the second kind [33].

Appendix B: Several Limit and Differential Relations among $f_{n}$ and $g_{n}$ Functions

By taking limit analyses to $f_{n}$ and $g_{n}$ functions in Eqs. (28), (A1), (A2), and (A6), it is found that

$$ \begin{aligned} &\mathop {\lim }\limits_{{a_{2} \to 0}} f_{n} \left( {x_{1} ,x_{2} ;a_{1} ,a_{2} } \right) = f_{n} \left( {x_{1} ,x_{2} ;a_{1} } \right) \, \\ &\mathop {\lim }\limits_{{a_{1} \to 0}} f_{n} \left( {x_{1} ,x_{2} ;a_{1} } \right) = f_{n} \left( {x_{1} ,x_{2} } \right) \hfill \\ &\mathop {\lim }\limits_{{a_{2} \to 0}} g_{n} \left( {x_{1} ,x_{2} ;a_{1} ,a_{2} } \right) = g_{n} \left( {x_{1} ,x_{2} ;a_{1} } \right) \,\\ &\mathop {\lim }\limits_{{a_{1} \to 0}} g_{n} \left( {x_{1} ,x_{2} ;a_{1} } \right) = g_{n} \left( {x_{1} ,x_{2} } \right) \hfill \\ \end{aligned} $$

(B1)

They are consistent with those limit relations between corresponding transformed functions $F_{n}$ and $G_{n}$ in Eqs. (24)–(26).

From definitions in Eqs. (24)–(26), it is obvious that

$$ F_{n} = \left| \xi \right|F_{n - 1} = - \frac{{\partial F_{n - 1} }}{{\partial x_{2} }}, \, G_{n} = \left| \xi \right|G_{n - 1} = - \frac{{\partial G_{n - 1} }}{{\partial x_{2} }} $$

(B2)

therefore,

$$ f_{n} = - \frac{{\partial f_{n - 1} }}{{\partial x_{2} }}, \, g_{n} = - \frac{{\partial g_{n - 1} }}{{\partial x_{2} }} $$

(B3)

From Eqs. (24)–(26), it is also clear that

$$ F_{\text{n}} = - \text{i}\xi G_{\text{n} - 1} , \, G_{\text{n}} = \text{i}\xi F_{\text{n} - 1} $$

(B4)

thus by virtue of the differential properties of the Fourier integral transforms defined in Eq. (8), we have

$$ f_{n} = \frac{{\partial g_{n - 1} }}{{\partial x_{1} }}, \, g_{n} = - \frac{{\partial f_{n - 1} }}{{\partial x_{1} }} $$

(B5)

Combining Eqs. (B3) and (B5), there exist another group of differential relations

$$ \frac{{\partial f_{n} }}{{\partial x_{1} }} = \frac{{\partial g_{n} }}{{\partial x_{2} }}, \, \frac{{\partial f_{n} }}{{\partial x_{2} }} = - \frac{{\partial g_{n} }}{{\partial x_{1} }} $$

(B6)

which are exactly the Cauchy–Riemann equations in complex analysis, indicating that $f_{n}$ and $g_{n}$ can be taken as the real and imaginary parts of a holomorphic complex function.

In view of the differential relations among $f_{n}$ and $g_{n}$ functions discussed above, it is possible to re-write the analytical solutions in Eqs. (29) and (30) in terms of only two functions $f_{ - 1}$ and $g_{ - 1}$, as well as their partial derivatives. However, we decide not to go further along this line here due to space constraints.

Appendix C: Expressions of a Series of $f_{n}^{c}$ and $g_{n}^{c}$ Functions

$f_{n}^{c} \left( {x_{1} ,x_{2} } \right)$ and $g_{n}^{c} \left( {x_{1} ,x_{2} } \right)$, as the inverse Fourier transforms of $F_{n}^{c} \left( {\xi ,x_{2} } \right)$ and $G_{n}^{c} \left( {\xi ,x_{2} } \right)$ in Eq. (37), respectively, are

$$ \begin{aligned} & f_{ - 1}^{c} \left( {x_{1} ,x_{2} } \right) = \frac{1}{c}\left\{ {x_{2} \left[ {{\text{atan2}}\left( {x_{2} ,x_{1} + c} \right) - {\text{atan2}}\left( {x_{2} ,x_{1} - c} \right)} \right]} \right. \\ & \qquad \left. { - \left[ {\left( {x_{1} + c} \right)\ln \sqrt {\left( {x_{1} + c} \right)^{2} + x_{2}^{2} } - \left( {x_{1} - c} \right)\ln \sqrt {\left( {x_{1} - c} \right)^{2} + x_{2}^{2} } } \right]} \right\} + 2\left( {1 - \gamma } \right) \\ & f_{0}^{c} \left( {x_{1} ,x_{2} } \right) = - \frac{1}{c}\left[ {{\text{atan2}}\left( {x_{2} ,x_{1} + c} \right) - {\text{atan2}}\left( {x_{2} ,x_{1} - c} \right)} \right] \\ & f_{1}^{c} \left( {x_{1} ,x_{2} } \right) = \frac{1}{c}\left[ {\frac{{x_{1} + c}}{{\left( {x_{1} + c} \right)^{2} + x_{2}^{2} }} - \frac{{x_{1} - c}}{{\left( {x_{1} - c} \right)^{2} + x_{2}^{2} }}} \right] \\ & f_{2}^{c} \left( {x_{1} ,x_{2} } \right) = \frac{{2x_{2} }}{c}\left\{ {\frac{{x_{1} + c}}{{\left[ {\left( {x_{1} + c} \right)^{2} + x_{2}^{2} } \right]^{2} }} - \frac{{x_{1} - c}}{{\left[ {\left( {x_{1} - c} \right)^{2} + x_{2}^{2} } \right]^{2} }}} \right\} \\ & g_{ - 1}^{c} \left( {x_{1} ,x_{2} } \right) = - \frac{1}{c}\left\{ {x_{2} \left( {\ln \sqrt {\left( {x_{1} + c} \right)^{2} + x_{2}^{2} } - \ln \sqrt {\left( {x_{1} - c} \right)^{2} + x_{2}^{2} } } \right)} \right. \\ & \left. { + \left[ {\left( {x_{1} + c} \right){\text{atan2}}\left( {x_{2} ,x_{1} + c} \right) - \left( {x_{1} - c} \right)\text{a}{\text{tan2}}\left( {x_{2} ,x_{1} - c} \right)} \right]} \right\} + \pi \\ & g_{0}^{c} \left( {x_{1} ,x_{2} } \right) = \frac{1}{c}\left( {\ln \sqrt {\left( {x_{1} + c} \right)^{2} + x_{2}^{2} } - \ln \sqrt {\left( {x_{1} - c} \right)^{2} + x_{2}^{2} } } \right) \\ & g_{1}^{c} \left( {x_{1} ,x_{2} } \right) = - \frac{{x_{2} }}{c}\left[ {\frac{1}{{\left( {x_{1} + c} \right)^{2} + x_{2}^{2} }} - \frac{1}{{\left( {x_{1} - c} \right)^{2} + x_{2}^{2} }}} \right] \\ & g_{2}^{c} \left( {x_{1} ,x_{2} } \right) = \frac{1}{c}\left\{ {\frac{{\left( {x_{1} + c} \right)^{2} - x_{2}^{2} }}{{\left[ {\left( {x_{1} + c} \right)^{2} + x_{2}^{2} } \right]^{2} }} - \frac{{\left( {x_{1} - c} \right)^{2} - x_{2}^{2} }}{{\left[ {\left( {x_{1} - c} \right)^{2} + x_{2}^{2} } \right]^{2} }}} \right\} \\ \end{aligned} $$

(C1)

where ${\text{atan2}}\left( {x_{1} ,x_{2} } \right)$ denotes the “2-argument arctangent” function, computing the principal value of the argument function applied to the complex number $x_{1} + \text{i}x_{2}$ in the range $\left( { - \pi ,\pi } \right]$.

According to definitions in Eq. (8), the inverse Fourier transforms of $F_{1}^{c} \left( {\xi ,x_{2} ;a} \right)$ and $G_{1}^{c} \left( {\xi ,x_{2} ;a} \right)$ in Eq. (36) are

$$ \begin{gathered} f_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) = \frac{{g_{0} \left( {x_{1} + c,x_{2} ;a} \right) - g_{0} \left( {x_{1} - c,x_{2} ;a} \right)}}{2c} \hfill \\ g_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) = - \frac{{f_{0} \left( {x_{1} + c,x_{2} ;a} \right) - f_{0} \left( {x_{1} - c,x_{2} ;a} \right)}}{2c} \hfill \\ \end{gathered} $$

(C2)

where $f_{0} \left( {x_{1} ,x_{2} ;a} \right)$ and $g_{0} \left( {x_{1} ,x_{2} ;a} \right)$ are given in Eq. (A2). According to the recurrence relations similar to Eq. (A5), we have

$$ \begin{aligned} & f_{ - 1}^{c} \left( {x_{1} ,x_{2} ;a} \right) = f_{ - 1}^{c} \left( {x_{1} ,x_{2} } \right) - af_{0}^{c} \left( {x_{1} ,x_{2} } \right) + a^{2} f_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) \\ & f_{0}^{c} \left( {x_{1} ,x_{2} ;a} \right) = f_{0}^{c} \left( {x_{1} ,x_{2} } \right) - af_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) \\ & f_{2}^{c} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}f_{1}^{c} \left( {x_{1} ,x_{2} } \right) - \frac{1}{a}f_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) \\ & g_{ - 1}^{c} \left( {x_{1} ,x_{2} ;a} \right) = g_{ - 1}^{c} \left( {x_{1} ,x_{2} } \right) - ag_{0}^{c} \left( {x_{1} ,x_{2} } \right) + a^{2} g_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) \\ & g_{0}^{c} \left( {x_{1} ,x_{2} ;a} \right) = g_{0}^{c} \left( {x_{1} ,x_{2} } \right) - ag_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) \\ & g_{2}^{c} \left( {x_{1} ,x_{2} ;a} \right) = \frac{1}{a}g_{1}^{c} \left( {x_{1} ,x_{2} } \right) - \frac{1}{a}g_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right) \\ \end{aligned} $$

(C3)

where $f_{n}^{c} \left( {x_{1} ,x_{2} } \right)$, $g_{n}^{c} \left( {x_{1} ,x_{2} } \right)$ and $f_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right)$, $g_{1}^{c} \left( {x_{1} ,x_{2} ;a} \right)$ are given in Eqs. (C1) and (C2), respectively. Equations (C1)–(C3) and Eq. (A2) constitute a series of $f_{n}^{c}$ and $g_{n}^{c}$ functions that facilitate the expression of analytical solutions for a half-plane subjected to a uniform surface traction.

In addition, it is worth noting that the limit and differential relations established in Eqs. (B1)–(B6) can entirely apply to functions with a superscript ‘c’ as seen in Eqs. (34)–(37) and Eqs. (C1)–(C3).