Dynamic response of ductile materials containing cylindrical voids

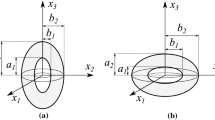
Abstract

The goal of this paper is to characterize the dynamic behavior of porous materials containing parallel cylindrical voids. Unlike static approaches, micro-inertia effects are accounted for in the modeling which infer a strong dependence of the dynamic response upon void geometry. Since cylindrical voids are considered, the void radius and void length both play a crucial role in the overall response of the porous material. A theoretical approach is developed, founded on the dynamic homogenization scheme proposed by Molinari and Mercier (J Mech Phys Solids 49:1497–1516, 2001) for spherical voids embedded in a viscoplastic matrix material. Considering a cylindrical unit cell, a constitutive response of porous material containing cylindrical void is developed for general homogeneous boundary conditions. For illustrative purpose, the analysis focuses on axisymmetric loadings considering a perfectly plastic matrix material. Micro-inertia effects are exemplified considering various loading conditions such as, among others, spherical loading and plane strain loading. In particular, the peculiar effect of the length of the cylindrical void is revealed. Indeed, particular attention has been paid to the response of short and elongated cylindrical voids. All predictions of the present model are verified against numerical simulations developed for various axisymmetric loading paths. Our findings can be used in several applications such as thick wall honeycomb structures or additively manufactured materials submitted to dynamic loading.

Appendices

Appendix

Formulation of the macroscopic dynamic stress tensor

1.1 General formulation

The macroscopic dynamic stress tensor ${\varvec{\varSigma }}^\text {dyn}$ is evaluated in this section with use of the following kinematic boundary condition:

$$\begin{aligned} {\mathbf{v}}={\mathbf{L}}\cdot {\varvec{x}} \quad \text {on} \quad \partial V\,, \end{aligned}$$

(47)

with ${\varvec{x}}=x_1{\mathbf{e}_1}+x_2{\mathbf{e}_2}+x_3{\mathbf{e}_3}$ being the position vector.

$\mathbf{L}$ is the macroscopic velocity gradient tensor, related to the macroscopic strain rate $\mathbf{D}$ and spin tensor ${\varvec{\varOmega }}$ by the following relationships:

$$\begin{aligned} \mathbf{D}=\frac{\mathbf{L}+\,^\text {t}\mathbf{L}}{2}\,,\quad {\varvec{\varOmega }}=\frac{\mathbf{L}-\,^\text {t}\mathbf{L}}{2}\,. \end{aligned}$$

(48)

With the boundary condition (47), Eqs. (3) and (9) become:

$$\begin{aligned} \varvec{\varSigma }:{^\text {t}}\mathbf{L}= & {} \langle \varvec{\sigma }:\mathbf{d}\rangle +\frac{1}{2}\left\langle \rho \frac{\text {d}{|\mathbf{v}|^2}}{\text {d}{t}}\right\rangle \,, \end{aligned}$$

(49)

$$\begin{aligned} {\varvec{\varSigma }}:{^\text {t}}{\delta }{{\mathbf{L}}}= & {} \frac{\partial \langle {\hat{\varPhi }}\rangle }{\partial {\mathbf{D}}}:\delta {\mathbf{D}}+ {\varvec{\varSigma }}^\text {dyn}:{^\text {t}}{\delta }{{\mathbf{L}}}\,, \end{aligned}$$

(50)

with

$$\begin{aligned} {\varvec{\varSigma }}^\text {dyn}:{^\text {t}}{\delta }{{\mathbf{L}}}=\langle \rho {{\varvec{\gamma }}}\cdot \delta {\mathbf{v}}\rangle =\frac{1}{|V|}\int \limits _V \rho \varvec{\gamma }\delta \mathbf{v}dV\,. \end{aligned}$$

(51)

More information can be found in Molinari and Mercier (2001).

The dynamic stress tensor ${\varvec{\varSigma }}^\text {dyn}$ is evaluated considering that the porous material is represented by the hollow cylinder and that the approximate velocity field is of the form:

$$\begin{aligned} {\mathbf{v}}={\hat{\mathbf{L}}}\cdot {\varvec{x}}+ B {\tilde{\varvec{x}}} \end{aligned}$$

(52)

where $B=\frac{\text {tr}(\mathbf{D})}{2} \left( \frac{b}{r}\right) ^2-\frac{\mathbf{D}_{33}}{2}$ and ${\hat{\mathbf{L}}}$ is defined as in Eq. (21) replacing $\mathbf{D}$ by $\mathbf{L}$. The adopted velocity field satisfies the kinematic condition (47) together with the matrix incompressibility condition. From Eq. (52), the variation of the velocity $\delta {\mathbf{v}}$ due to the change $\delta \mathbf{L}$ of $\varvec{\mathbf{L}}$ at the boundary and the acceleration are:

$$\begin{aligned} \delta {\mathbf{v}}= & {} \delta {\hat{\mathbf{L}}}\cdot {\varvec{x}}+ \delta B {\tilde{\varvec{x}}}\,, \end{aligned}$$

(53)

$$\begin{aligned} \varvec{\gamma }= & {} \dot{\hat{\mathbf{L}}}\cdot {\varvec{x}}+{\hat{{\mathbf{L}}}}\cdot \mathbf{v}+\dot{B}{\tilde{\varvec{x}}}+B{\tilde{\mathbf{v}}}\,, \end{aligned}$$

(54)

where ${\tilde{\mathbf{v}}}=v_1{\mathbf{e}_1}+v_2{\mathbf{e}_2}$. Combining Eqs. (52–54), the integral term $I=\frac{1}{|V|}\int _V \rho \varvec{\gamma }\delta \mathbf{v}$ of Eq. (51) can be written as:

$$\begin{aligned} I= & {} \frac{1}{|V|}\int \limits _V \rho \varvec{\gamma }\delta \mathbf{v}dV=\frac{1}{|V|}\int \limits _V\rho ({\varvec{x}}\cdot {{^t}{\dot{\hat{\mathbf{L}}}}}\cdot {\delta {\hat{\mathbf{L}}}}\cdot {\varvec{x}}\nonumber \\&+\,{\mathbf{v}}\cdot {{^t}{\hat{\mathbf{L}}}}\cdot {\delta {\hat{\mathbf{L}}}}\cdot {\varvec{x}}\nonumber \\&+\,{\dot{B}}{\delta {B}}{\tilde{\varvec{x}}}\cdot {\tilde{\varvec{x}}}\nonumber \\&+\,B{\delta {B}}{\tilde{\mathbf{v}}}\cdot {\tilde{\varvec{x}}} +{\dot{B}}{\tilde{\varvec{x}}}\cdot {\delta {\hat{\mathbf{L}}}}\cdot {\varvec{x}}+B{\tilde{\mathbf{v}}}\cdot {\delta {\hat{\mathbf{L}}}}\cdot {\varvec{x}}\nonumber \\&+\,{\delta B}{\tilde{{\varvec{x}}}}\cdot {\dot{\hat{\mathbf{L}}}}\cdot {\varvec{x}}+{\delta B}{\tilde{\varvec{x}}}\cdot {\hat{\mathbf{L}}}\cdot {\mathbf{v}})dV \end{aligned}$$

(55)

The volume |V| of the RVE is $2l\pi b^2$. Note that particles are present only for $a\le r\le b$. After some calculations leading to an explicit relation for $I=\frac{1}{|V|}\int _V \rho \varvec{\gamma }\delta \mathbf{v}dV$, the use of Eq. (51) provides the components of the dynamic stress tensor. ${\varSigma }^\text {dyn}_{11}$, ${\varSigma }^\text {dyn}_{22}$ and ${\varSigma }^\text {dyn}_{33}$ are given by Eqs. (23–25) while the other components are expressed as:

$$\begin{aligned} {\varSigma }^\text {dyn}_{12}= & {} \frac{\rho a^2}{4}\left[ \left( f^{-1}-f\right) ({\dot{{L}}_{12}}+{C}_{12}-{D}_{33}{{L}_{12}})\right. \nonumber \\&\left. +\,6\left( f^{-1}-1\right) {D}_\text {m}{{L}_{12}}\right] \end{aligned}$$

(56)

$$\begin{aligned} {\varSigma }^\text {dyn}_{21}= & {} \frac{\rho a^2}{4}\left[ \left( f^{-1}-f\right) ({\dot{{L}}_{21}}+{C}_{21}-{D}_{33}{{L}_{21}})\right. \nonumber \\&\left. +\,6\left( f^{-1}-1\right) {D}_\text {m}{{L}_{21}}\right] \end{aligned}$$

(57)

$$\begin{aligned} \varSigma ^\text {dyn}_{13}= & {} \frac{\rho l^2}{3}\left[ \left( 1-f\right) \left( \dot{{L}}_{13}+C_{13}-\frac{D_{33}}{2}{{L}}_{13}\right) \right. \nonumber \\&\left. +\frac{3}{2}\ln \left( \frac{1}{f}\right) D_\text {m}{{L}_{13}}\right] \end{aligned}$$

(58)

$$\begin{aligned} \varSigma ^\text {dyn}_{23}= & {} \frac{\rho l^2}{3}\left[ \left( 1-f\right) \left( \dot{{L}}_{23}+C_{23}-\frac{D_{33}}{2}{{L}}_{23}\right) \right. \nonumber \\&\left. +\frac{3}{2}\ln \left( \frac{1}{f}\right) D_\text {m}{{L}_{23}}\right] \end{aligned}$$

(59)

$$\begin{aligned} \varSigma ^\text {dyn}_{31}= & {} \frac{\rho a^2}{4}\left[ \left( f^{-1}-f\right) ({\dot{{L}}_{31}}+{C}_{31}-\frac{{D}_{33}}{2}{{L}_{31}})\right. \nonumber \\&\left. +\,3\left( f^{-1}-1\right) {D}_\text {m}{{L}_{31}}\right] \end{aligned}$$

(60)

$$\begin{aligned} \varSigma ^\text {dyn}_{32}= & {} \frac{\rho a^2}{4}\left[ \left( f^{-1}-f\right) ({\dot{{L}}_{32}}+{C}_{32}-\frac{{D}_{33}}{2}{{L}_{32}})\right. \nonumber \\&\left. +\,3\left( f^{-1}-1\right) {D}_\text {m}{{L}_{32}}\right] \end{aligned}$$

(61)

where ${\mathbf{C}}=\hat{\mathbf{D}}\cdot \hat{\mathbf{D}}$ and ${\hat{\mathbf{C}}}$ is defined as in Eq. (21) replacing $\mathbf{D}$ by $\mathbf{C}$.

The dynamic stress tensor reveals particular aspects that are commented in the main text, see Sect. 3.1.

1.2 Case where ${\varvec{\varOmega }}=\mathbf{0}$

The case where $\mathbf{L}$ is symmetric corresponds to the velocity field (20) of Sect. 2.2. The dynamic stress tensor components $\varSigma ^\text {dyn}_{11}$, $\varSigma ^\text {dyn}_{22}$ and $\varSigma ^\text {dyn}_{33}$ are still given by Eqs. (23), (24) and (25) respectively. Since ${\mathbf{C}}=\hat{\mathbf{D}}\cdot \hat{\mathbf{D}}$ in this case is symmetric, the other components are obtained directly from Eqs. (56–61), leading to Eqs. (26–30). As also stated in Sect. 2.1, the dynamic stress tensor is not symmetric even when spin effects are disregarded. For spherical voids, without spin contribution the dynamic stress tensor is symmetric, Molinari and Mercier (2001). The results are due to the geometrical configuration of the RVE which is not isotropic.

1.2.1 Axisymmetric case

For an axisymmetric configuration without shear contributions, the velocity field used by Tracey (1971) is of the form of Eq. (20) with $\mathbf{D}$ expressed as:

$$\begin{aligned} {\mathbf{D}}= \begin{bmatrix}D_{11} &{} 0 &{} 0 \\ 0 &{} D_{11} &{} 0 \\ 0 &{} 0 &{} D_{33} \end{bmatrix} \,, \end{aligned}$$

(62)

From Eqs. (23–30), the only non zero components of ${\varvec{\varSigma }}^\text {dyn}$ are:

$$\begin{aligned} {\varSigma }^\text {dyn}_{11}= & {} {\varSigma }^\text {dyn}_{22}=\rho a^2F,\nonumber \\ {\varSigma }^\text {dyn}_{33}= & {} \rho a^2G+\frac{\rho l^2}{3}\left( 1-f\right) \left( \dot{D}_{33}+D_{33}^2\right) \end{aligned}$$

(63)

with

$$\begin{aligned} F= & {} \frac{1}{4}\left\{ 2f^{-1}\ln \left( \frac{1}{f}\right) \dot{D}_{11} \nonumber \right. \\&\left. +\,\left[ 1-f^{-1}+f^{-1}\ln \left( \frac{1}{f}\right) \right] \dot{D}_{33}\right. \nonumber \\&-\,2\left[ f^{-2}-f^{-1}-2f^{-1}\ln \left( \frac{1}{f}\right) \right] D_{11}^2\nonumber \\&-\,\frac{1}{2}\left( 1-f\right) ^{2}f^{-2}D_{33}^2\nonumber \\&\left. -\,2\left[ f^{-2}-f^{-1}-f^{-1}\ln \left( \frac{1}{f}\right) \right] D_{11}D_{33}\right\} \nonumber \\\end{aligned}$$

(64)

$$\begin{aligned} G= & {} \frac{1}{4}\left\{ 2\left[ 1+f^{-1}\ln \left( \frac{1}{f}\right) -f^{-1}\right] \dot{D}_{11}\right. \nonumber \\&+\,\left[ f^{-1}\ln \left( \frac{1}{f}\right) -\frac{1}{2}\left( f^{-1}-1\right) \left( 3-f\right) \right] \dot{D}_{33}\nonumber \\&-\,2\left[ \left( 1+f\right) f^{-2}-3f^{-1}\nonumber \right. \\&\left. \ln \left( \frac{1}{f}\right) -2\right] D_{11}^2\nonumber \\&-\,\frac{1}{4}\left[ f^{-2}\left( 1-f\right) ^3+f^{-2}-1-2f^{-1}\nonumber \right. \\&\left. \ln \left( \frac{1}{f}\right) \right] D_{33}^2\nonumber \\&\left. -\,2\left[ f^{-2}-1-2f^{-1}\ln \left( \frac{1}{f}\right) \right] D_{11}D_{33}\right\} \end{aligned}$$

(65)

Note that the case of uniaxial extension considered in Molinari et al. (2015) for the dynamic coalescence of cylindrical unit cell is retrieved from Eqs. (63–65) by setting $D_{11}=\dot{D}_{11}=0$.

In addition to the previous axisymmetric configuration, under plane strain conditions, $D_{33}=0$, the following relationships are obtained:

$$\begin{aligned} {\varSigma }^\text {dyn}_{11}= & {} {\varSigma }^\text {dyn}_{22} =\frac{\rho a^2}{2}\Bigg \{f^{-1}\ln \left( \frac{1}{f}\right) \dot{D}_{11}\nonumber \\&-f^{-1}\left[ f^{-1}-2\ln \left( \frac{1}{f}\right) -1\right] D_{11}^2\Bigg \} \end{aligned}$$

(66)

$$\begin{aligned} {\varSigma }^\text {dyn}_{33}= & {} \frac{\rho a^2}{2}\Bigg \{\left[ f^{-1}\ln \left( \frac{1}{f}\right) -f^{-1}+1\right] \dot{D}_{11}\nonumber \\&-\left[ \left( 1+f\right) f^{-2}-3f^{-1}\ln \left( \frac{1}{f}\right) -2\right] \nonumber \\&\quad D_{11}^2\Bigg \} \end{aligned}$$

(67)

Note that when $D_{33}=0$ (i.e. the length of the cylinder remains constant, $l=l_0$), the porosity evolution is solely governed by $D_{11}$ through $\dot{f}=2(1-f) D_{11}$. Using in addition Eq. (66) and $\dot{a}/a=D_{11}/f$ (matrix incompressibility), since the static stress is expressed in terms of $D_{11}$ and f, it appears that under imposed in plane stress (i.e. $\varSigma _{11}$ is known), the radial strain rate component $D_{11}$ can be obtained. As a consequence, when $D_{33}=0$, one can determine the porosity evolution from the stress components in the ($\mathbf{e}_1, \mathbf{e}_2$) plane. But, interestingly, inertia effects related to radial expansion are transferred also to $\varSigma _{33}^\text {dyn}$. This implies that limiting the analysis to the 2D plane configuration may leave aside substantial information on the role played by micro-inertia. As a matter of fact, the axial stress needed to constrain the length of the cylinder in a dynamic problem cannot be captured by such 2D in plane approach.

Finite element modeling

To validate the proposed constitutive model, dynamic micromechanical computations have been carried out with the finite element code ABAQUS/Explicit. Various axisymmetric models have been developed to depict the dynamic response under (i) plane strain condition (ii) hydrostatic loading conditions and (iii) other loading cases considered in the paper. Since the matrix material is taken as rigid (elastically undeformable), a large value of the Young’s modulus has been adopted (6000 GPa) in all finite element calculations. In addition, to approach the incompressibility condition for the matrix, a value of 0.499 for the Poisson’s ratio has been used.

Recall that for all configurations addressed in the paper, the proposed analytical approach has been accurately compared to results obtained from numerical simulations. Here, only some examples have been selected to bring the comparison.

1.1 Plane strain configuration

Fig. 15

Finite element cylindrical unit cell of length l, inner radius a and external radius b used for various loading cases. The mesh is made with 4 node axisymmetric elements (CAX4R) of element size of 20 $\upmu$m $\times$ 40 $\upmu$m

For this case, the unit cell, illustrated on Fig. 15, is meshed with 4 nodes axisymmetric elements with reduced integration (CAX4R). The initial element size is about 20 $\upmu$m  $\times$ 40 $\upmu$m. Since the unit cell is expanded in the radial direction, elements are initially elongated in the axial direction, so as to prevent the element aspect ratio from excessive values during the deformation process. Kinematic conditions of the following form are considered:

$$\begin{aligned} v_3({\varvec{x}},t)=0 \text { on } \partial B_0,\ v_3({\varvec{x}},t)=0 \text { on } \partial B_l \end{aligned}$$

(68)

which account for the condition of symmetry at $\partial B_0$ and ensure the plane strain condition at $\partial B_l$. In addition, the following stress boundary conditions prevail (expressed in the cylindrical coordinate system):

$$\begin{aligned} \varSigma _{r3}({\varvec{x}},t)=\varSigma _{\theta 3}({\varvec{x}},t)=0 \text { on } \partial B_l \end{aligned}$$

(69)

and

$$\begin{aligned} \varSigma _{rr}({\varvec{x}},t)=\dot{p} t,\ \varSigma _{\theta r}({\varvec{x}},t)=\varSigma _{3 r}({\varvec{x}},t)=0 \text { on } \partial B_b \nonumber \\ \end{aligned}$$

(70)

An example has been selected to illustrate the agreement between the analytical modeling and the numerical simulations. The case corresponds to the configuration of Sect. 4.1, Fig. 2a, with $\dot{p}$ =  10 MPa/ns. For the reference material of Table 1, Fig. 16 shows that analytical results (solid line) coincide with Finite Element simulations (dots). In particular, the reduction of the axial stress $\varSigma _{33}$ occurring at large deformation while the lateral stress is still increasing, is reproduced by both approaches, as observed in Fig. 16b. Note that $\varSigma _{33}$ is evaluated from the ratio of the axial force on $\partial B_l$ divided by the current area $\pi b^2$.

Fig. 16

FEM calculations and analytical result comparison for plane strain loading. Time evolution of a the porosity and b the axial stress. The stress rate is $\dot{p}$ = 10 MPa/ns. The reference material with parameters listed in Table 1 is considered

1.2 Hydrostatic loading

There is no difficulty to prescribe $\varSigma _{11}=\varSigma _{22}$ at the external boundary of the unit cell ($r=b$). Imposing $\varSigma _{33}$ on the top surface ($0\le r \le b$) where a void is present for $0\le r\le a$ is not straightforward. To overcome this difficulty, two strategies have been developed aiming at defining a model able to verify the proposed approach in case of hydrostatic loading. They give identical results and for completeness purpose, both will be presented in this appendix.

1.2.1 Boundary conditions inherited from the analytical model

The first approach relies on a two-step formalism. The solution of the considered configuration (prescribed hydrostatic loading condition) is searched by using the analytical approach presented in this paper. The resulting velocity field in the axial direction, denoted by $v_3^{\text {th.}}$, is collected and used as a boundary condition in the finite element model of Fig. 15. Including the condition of symmetry, the set of kinematic boundary conditions is expressed as:

$$\begin{aligned} v_3({\varvec{x}},t)=0 \text { on }\partial B_0,\quad v_3({\varvec{x}},t)=v_3^{\text {th.}} \text { on } \partial B_l \end{aligned}$$

(71)

complemented with the stress boundary conditions expressed by Eqs. (69–70).

It has been shown that under intense imposed velocity $v_3^{\text {th.}}$, the shape of the unit cell can strongly deviate from its cylindrical shape. As a consequence, a supplementary constraint turned out to be necessary to prevent the unit cell from unexpected shape change. Specifically, the nodes located at the inner and outer vertical boundaries of the cylindrical void ($\partial B_a$ and $\partial B_b$ in Fig. 15) are linked through a set of linear multi-point constraints so that, at each time of the deformation process, these surfaces remain vertical.

Fig. 17

Closed cylindrical unit cell of length l, inner radius a and external radius b having a thin plate of thickness $t_p$ on the top. CAX4R elements with initial size of 20 $\upmu$m $\times$ 40 $\upmu$m are used

1.2.2 Closed unit-cell

The second approach consists of adopting a closed unit cell composed of a thin layer added at the top of the cylindrical void, see Fig. 17. If the top layer thickness, denoted by $t_p$ in Fig. 17, is sufficiently small, and the additional domain is of negligible mass, it should not affect the overall response of the unit cell under dynamic loading. Thus, imposing the macroscopic stress tensor component at the top layer is immediate. This strategy however requires additional kinematic constraints in order to prevent the unit cell from excessive and unexpected distortion. Specifically, the inner surfaces identified by $\partial B_a$ and $\partial B_{t_p}$ on Fig. 17 as well as the outer surfaces $\partial B_l$ and $\partial B_{b}$ remain planar. In addition, the condition of symmetry (70) still prevails. The lateral stress $\dot{p} t$ is prescribed according to Eq. (70), and the axial stress $\varSigma _{33}=\dot{p} t$ is imposed at the top surface.

1.2.3 Validation on the reference case

The two strategies are compared against analytical results of Fig. 5 obtained for $\dot{p}$ = 10 MPa/ns, $l_0$ = 2000 $\upmu$m and other material parameters listed in Table 1. In our calculation, the thickness of the top layer was 10 $\upmu$m and it was confirmed that a lower value does not affect the response of the unit cell. Fig. 18 shows the evolution of the porosity versus time and serves at verifying the analytical approach. Fig. 18 also illustrates the equivalence between the two finite element models of Sects. B.2.1 and B.2.2.

Fig. 18

Time evolution of the porosity for a porous medium with cylindrical void under the stress rate $\dot{p}$ = 10 MPa/ns and considering the reference material with $l_0$ = 2000 $\upmu$m and other parameters listed in Table 1. Comparison between analytical results and FEM calculations for spherical loading. The approach using the analytically inherited velocity field and the closed unit cell give comparable results