Abstract
The objective of this paper is to develop the implicit integration scheme and calibration method for a recently developed cohesive zone model (CZM), for improved predictive capabilities in interlaminar delamination. The concept of string-based CZM is briefly introduced. An associated implicit integration scheme, which can handle complex separation paths and mixed-mode fracture, is developed, and the implicit CZM is implemented in an implicit solver via a user subroutine, for structural analysis. The constant interface parameters are identified from a thermodynamic perspective, and a systemic method for model calibration is subsequently developed. The present CZM is validated by calibrating its constant parameters via a series of flexural tests. The integration scheme is found to produce improved convergence and accuracy. The calibration method is found to provide a reliable guide to model calibration. The present CZM can be modified to accommodate other types of debonding or fracture.



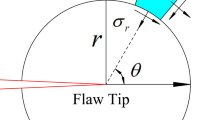
(adapted from Hui et al. (2011))













Similar content being viewed by others
References
ASTM (2013a) Astm d552813 standard test method for mode i interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites
ASTM (2013b) Astm d6671/d6671m13e1 standard test method for mixed mode i–mode ii interlaminar fracture toughness of unidirectional fiber reinforced polymer matrix composites
ASTM (2014) Astm d7905/d7905m14 standard test method for determination of the mode ii interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites
Balzani C, Wagner W (2008) An interface element for the simulation of delamination in unidirectional fiber-reinforced composite laminates. Eng Fract Mech 75:2597–2615
Benzerga AA, Besson J (2001) Plastic potentials for anisotropic porous solids. Eur J Mech A 20:397–434
Blaysat B, Hoefnagels JP, Lubineau G, Alfano M, Geers MG (2015) Interface debonding characterization by image correlation integrated with double cantilever beam kinematics. Int J Solids Struc 55:79–91
Borg R, Nilsson L, Simonsson K (2002) Modeling of delamination using a discretized cohesive zone and damage formulation. Compos Sci Technol 62:1299–1314
Camanho PP, Dávila CG (2002) Mixed-mode decohesion finite elements for the simulation of delamination in composite materials
Cordebois J, Sidoroff F (1982) Anisotropic damage in elasticity and plasticity. Journal de Mécanique Théorique et Appliquée 45–60
Dávila CG, Camanho PP, Turon A (2008) Effective simulation of delamination in aeronautical structures using shells and cohesive elements. J Aircraft 45:663–672
Elmarakbi AM, Hu N, Fukunaga H (2009) Finite element simulation of delamination growth in composite materials using ls-dyna. Compos Sci Technol 69:2383–2391
Gao Z, Zhang L, Yu W (2015) Simulating the mixed-mode progressive delamination in composite laminates. In: American Society of composites-30th technical conference
Gent AN, Petrich RP (1969) Adhesion of viscoelastic materials to rigid substrates. In: Proceedings of the royal society of London a: mathematical, physical and engineering sciences, The Royal Society. pp. 433–448
Harper PW, Hallett SR (2008) Cohesive zone length in numerical simulations of composite delamination. Eng Fract Mech 75:4774–4792
Hill BC, Giraldo-Londoño O, Paulino GH, Buttlar WG (2017) Inverse estimation of cohesive fracture properties of asphalt mixtures using an optimization approach. Exp Mech 57:637–648
Hui CY, Ruina A, Long R, Jagota A (2011) Cohesive zone models and fracture. J Adhes 87:1–52
Luo Y (2010) A local multivariate lagrange interpolation method for constructing shape functions. Int J Num Methods Biomed Eng 26:252–261
Mosler J, Scheider I (2011) A thermodynamically and variationally consistent class of damage-type cohesive models. J Mech Phys Solids 59:1647–1668
Overgaard LC, Lund E, Camanho PP (2010) A methodology for the structural analysis of composite wind turbine blades under geometric and material induced instabilities. Comput Struct 88:1092–1109
Park K, Paulino GH (2011) Cohesive zone models: a critical review of traction-separation relationships across fracture surfaces. Appl Mech Rev 64:060802
Pinho ST, Iannucci L, Robinson P (2006) Formulation and implementation of decohesion elements in an explicit finite element code. Compos A 37:778–789
Press WH, Flannery BP, Teukolsky SA, Vetterling WT (1992) Numerical recipes in C: the art of scientific computing. Cambridge University Press, Cambridge
Reeder JR (1992) An evaluation of mixed-mode delamination failure criteria
Reeder JR, Crews JH (1990) Mixed-mode bending method for delamination testing. AIAA J 28:1270–1276
Sarrado C, Turon A, Renart J, Urresti I (2012) Assessment of energy dissipation during mixed-mode delamination growth using cohesive zone models. Compos A 43:2128–2136
Scalet G, Auricchio F, Hartl DJ (2016) Efficiency and effectiveness of implicit and explicit approaches for the analysis of shape-memory alloy bodies. J Intell Mater Syst Struct 27:384–402
Shen B, Paulino GH (2011) Direct extraction of cohesive fracture properties from digital image correlation: a hybrid inverse technique. Exp Mech 51:143–163
Simo JC, Hughes TJR (1998) Computational inelasticity of volume 7 interdisciplinary applied mathematics. Springer, New York
Simulia (2013) Abaqus 6.13 documentation
Turon A, Camanho PP, Costa J, Dávila C (2006) A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech Mater 38:1072–1089
Turon A, Camanho PP, Costa J, Renart J (2010) Accurate simulation of delamination growth under mixed-mode loading using cohesive elements: definition of interlaminar strengths and elastic stiffness. Compos Struct 92:1857–1864
Turon A, Davila CG, Camanho PP, Costa J (2007) An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng Fract Mech 74:1665–1682
Xie D, Waas AM (2006) Discrete cohesive zone model for mixed-mode fracture using finite element analysis. Eng Fract Mech 73:1783–1796
Zhang L, Gao Z, Yu W (2017) A string-based cohesive zone model for interlaminar delamination. Eng Fract Mech 180:1–22
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Path dependence function
In this appendix, the construction of the path dependence function, \(J\left( {\hat{\varvec{\gamma }}} \right) \), will be briefly introduced [see Zhang et al. (2017) for more details]. Borg et al. (2002) expressed the total energy release rate as
where t denotes the current time. Clearly, G is a path-dependent line integral whose integration path is the separation path along which a cohesive element is deformed. Let
denote the energy release rate vector such that
Combining Eqs. (46) and (47) gives
where
with \({{{\varvec{e}}}_i}\) denoting the \({i^{{\mathrm{th}}}}\) local unit vector. Let
denote the mode mixture vector. The following assumption is invoked in Sect. 4: during each test, each element experiences the same proportional separation path. This assumption is the equivalent of setting \(\dot{\hat{\varvec{\gamma }}} = {{\varvec{0}}}\) everywhere. Setting \(\dot{\hat{\varvec{\gamma }}} = {{\varvec{0}}}\) in Eqs. (45) and (48) gives
Substituting Eqs. (51) into Eq. (50) gives
Clearly, \(\dot{\hat{\varvec{\gamma }}} = {{\varvec{0}}}\) is a sufficient condition of \(\dot{\varvec{\beta }} = {{\varvec{0}}}\). Let \({t_c}\) denote the time when delamination occurs. \({G_c}\) and \({{{\varvec{G}}}_c}\) can then be obtained as
respectively, where \({\left( {{\varPsi _e}} \right) _c} \rightarrow 0\) is assumed.
Given a set of n data points \(\left( {{{\hat{\varvec{\gamma }}}_i},{J_i}} \right) \)’s mentioned in Sect. 2, one can construct a multivariate Lagrange polynomial, \(J\left( {\hat{\varvec{\gamma }}} \right) \), such that each \({J_i}\) makes \({G_c}\) take a designated value. Introduce the Hadamard power of a vector, \({\left( \cdot \right) ^{ \circ 2}}\), e.g.,
Also introduce Lagrange basis polynomials (Luo 2010)
and normalized Lagrange basis polynomials
Let \(J\left( {\hat{\varvec{\gamma }}} \right) \) take the form of
so that it is a subjective (and possibly injective) function of \({\varvec{\beta }}\) when \(\dot{\hat{\varvec{\gamma }}} = {{\varvec{0}}}\). \({{\partial J} / {\partial \hat{\varvec{\gamma }}}}\) can then be obtained from Eq. (57) as
where
with
In Sect. 4, a cohesive element is assumed to have the same properties in all directions in the \({x_2}{x_3}\) plane. In this case, J degenerates to a univariate Lagrange polynomial of \({{\hat{\gamma }} _1}\). Introduce Lagrange basis polynomials
\(J\left( {{{\hat{\gamma }} _1}} \right) \) is then given by
and
where
B UMAT algorithm
Figure 17 depicts a flowchart of the UMAT algorithm. The algorithm can be described as follows:
- 1.
Read \({{\varvec{\tau }}_n}\) and \(\varDelta {\varvec{\gamma }}\) passed in by Abaqus/Standard, while read \({{\varvec{\gamma }}_n}\), \({d_n}\), and \({\alpha _n}\) saved for the present element.
- 2.
Check if damage initiates or evolves (see Eq. (10)).
- 3.
If yes, (a) compute \(\varDelta \alpha \), (b) update \(\alpha \), d, and \({\varvec{\tau }}\), and (c) compute \({{{\varvec{L}}}^ * }\).
- 4.
Otherwise, (a) update \({\varvec{\gamma }}\), (b) set \(\alpha = {\alpha _n}\) and \(d = {d_n}\), and (c) compute \({{{\varvec{L}}}^ * }\) (here \({{{\varvec{L}}}^ * } = K{{{{\varvec{I}}}^ + } + {{{{\tilde{K}}}}_c}\left( {{{\varvec{I}}} - {{{\varvec{I}}}^ + }} \right) }\)) and \({\varvec{\tau }}\).
- 5.
Save \({\varvec{\gamma }}\), d, and \(\alpha \) for the present element, while return \({\varvec{\tau }}\) and \({{{\varvec{L}}}^ * }\) to Abaqus/Standard.
Once \(d = {d_c}\), UMAT will set \(K = 0\) and mark the present element as failed hereafter. More details on Abaqus/Standard and UMAT can be found in Simulia (2013).
C Method of nonlinear least squares
In this appendix, the method of NLLSQ, along with Monte Carlo experiments and Powell’s methods, will be briefly introduced. Unless otherwise specified, let the “local” variables defined in this appendix override the “global” variables defined in Sects. 2–5, having the same names.
Suppose that N data points \(\left( {{x_i},{y_i}} \right) \)’s are to be fitted to a nonlinear model depending on M adjustable parameters \(a_j\)’s (\(N \ge M\)). Let
and let the nonlinear model take the general form of \(y = f\left( {x;{{\varvec{a}}}} \right) \). Further suppose that each \(\left( {{x_i},{y_i}} \right) \) has its respective, known standard deviation \({\sigma _i}\), and introduce the so-called chi-square merit function,
which is the sum of N squares of normalized, distributed residuals. The method of NLLSQ involves finding \({{\varvec{a}}}\) minimizing \({\chi ^2}\). An NLLSQ problem is therefore an optimization problem whose objective function is \({\chi ^2}\left( {{\varvec{a}}} \right) \).
The Rastrigin function is frequently used for performance testing of optimization methods. Figure 18 shows its 3D surface and contour plots. As can be seen, the function has a global minimum at \(\left( {0,0} \right) \) and numerous local minima. When handling such a function, an optimization method itself is not guaranteed to converge to the global minimum and often gets “lost” if started far from the solution. Fortunately, setting the guessed values close to the solution greatly improves the convergence. In this paper, such guessed values are obtained through Monte Carlo experiments consisting of the following steps:
- 1.
Estimate the domains of \(a_j\)’s.
- 2.
Create a lot of different combinations of \(a_j\)’s over these domains.
- 3.
Compute the values of \({\chi ^2}\) for these combinations.
- 4.
Find as many neighborhoods of local minima (i.e., where an optimization method converges to these local minima) as possible.
The global minimum can be found first by carrying out an optimization procedure at each of these neighborhoods and then by identifying the local minimum yielding the smallest \({\chi ^2}\). In this paper, each set of Monte Carlo experiments include less than \(20 \cdot M\) (M the number of \(a_j\)’s) numerical tests of a single cohesive element, taking about 20 ms each.
Optimization methods can be classified into (1) those only requiring evaluations of the objective functions (e.g., Powell’s method) and (2) those also requiring evaluations of the derivatives of the objective functions (e.g., Newton’s method). In this paper, Powell’s method is chosen due to the following reasons:
Newton’s method often fails to converge if an \(a_j\) is an exponent.
In iterative optimization, it is difficult to compute the derivatives of \({\chi ^2}\) through finite element analysis.
Given good initial guesses, Powell’s method produces good convergence and high efficiency.
Powell’s method involves successively minimizing the objective function along M mutually non-interfering directions (see Fig. 19 for the case of \(M = 2\)). These directions are defined so that Powell’s method converges quadratically (see Press et al. (1992) for more details). The procedure is repeated until the objective function effectively stops decreasing, or mathematically speaking, until
where \(\chi _k^2\) and \(\chi _{k - 1}^2\) are the values of \({\chi ^2}\) in the current and the previous iteration, respectively, and \({\varepsilon _1}\) and \({\varepsilon _2}\) are two prescribed tolerances.

(adapted from Press et al. (1992))
Successive minimizations in a long, narrow “valley”
In Sect. 4, the method of NLLSQ is used (1) when estimating Q and b, (2) when estimating \(J_i\)’s, and (3) in iterative optimization (see also Fig. 6). In the first two cases, both Monte Carlo experiments and Powell’s method are needed, while in the last case, only Powell’s method is needed thanks to the initial guess previously created (see Fig. 11, where the estimated curves are already close to the experimental ones). Still suppose that there were n flexural tests, and let subscript i denote the \({i{{\mathrm{th}}}}\) test, e.g., \({\left( {{G_c}} \right) _i}\) denotes the \({i{{\mathrm{th}}}}\) estimated value of \(G_c\). Let \({P_{i\max }}\) and \({u_{i\max }}\) denote the \({i{{\mathrm{th}}}}\) peak load and its corresponding displacement, respectively, so that \(\left( {{u_{i\max }},{P_{i\max }}} \right) \) is the peak point of the \({i{{\mathrm{th}}}}\) load–displacement curve. Table 6 lists the information required to generate \({\chi ^2}\) in each case. Here each nonlinear model is a black box only whose inputs and outputs are of interest. For simplicity’s sake, each \(x_i\) in Table 6 is set to be a sequence number. Setting \({\sigma _i} = {y_i}\) (\({y_i} \ne 0\)) makes \({\chi ^2}\) the sum of N squares of percentage errors made in fitting, and \(a_j\)’s minimizing this measure of percentage errors are the best possible fitted parameters.
Rights and permissions
About this article
Cite this article
Zhang, L., Du, H. & Yu, W. String-based cohesive zone model: implicit integration scheme and calibration method. Int J Fract 222, 53–74 (2020). https://doi.org/10.1007/s10704-020-00431-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-020-00431-9