Abstract
Stress rupture is a time-dependent failure mode occurring in unidirectional fiber composites under sustained tensile loads, resulting in highly variable lifetimes. Stress-rupture is of particular concern in composite overwrapped pressure vessels (COPVs) since it is unpredictable, and has catastrophic consequences. At the micromechanical level, stress rupture begins with the breakdown of individual fibers at random flaws, followed by local load-transfer to intact neighbors through shear stress in the matrix. Over time, the matrix creeps in shear causing lengthening overload zones around fiber breaks, resulting in even more fiber breaks, and eventually, formation of a catastrophically unstable break cluster. Current reliability models are direct extensions of classic stochastic breakdown models for a single fiber, and do not reflect such micromechanical activity. These models are adequate for modeling composite stress rupture under a constant load, however, they may be unrealistic under more complex loading profiles, such as a constant load that follows a brief ‘proof test’ at a load level up to 1.5 times this constant load. For carbon fiber/epoxy COPVs, current models predict a reliability, conditioned on survival of a proof test, that is always higher than the reliability without such a proof test. Concern exists that this is incorrect, and that a proof test may result in reduced reliability over time. While the failure probability during a proof test may be very low, overwrap damage occurs nonetheless in the form of a large number of fibers breaks that would not occur otherwise based on fiber Weibull strength statistics. This phenomenon of increased fiber breakage during a proof test is captured in the model we develop and that specifically builds on the micromechanical failure process described above. For typical proof-test load ratios, the model predicts conditional reliabilities for lifetime that are typically much lower than those calculated in the absence of a proof test.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Stress rupture is a time dependent failure mode that affects unidirectional continuous fiber composites, such as composite overwrapped pressure vessels (COPVs). It is catastrophic and occurs without warning under sustained loading at typical operating temperatures and pressures. In stress-rupture failures, individual fibers fail successively, some forming clusters of broken fibers. The overall composite fails when one such cluster becomes too large and is unstable.
On the micromechanical level, individual fibers inherently have high variability in strength, with flaws randomly spaced along their length. On initial loading of the composite, fibers fail if they have flaws weaker than the applied load. The load that was carried by a now broken fiber is transferred onto its neighbors through matrix shear, thus causing higher loads in these neighboring fibers in the region near a break. These neighbors may then break, creating a cluster of broken fibers that further overload the fibers surrounding the cluster, perhaps causing even more failures.
A second feature is that the matrix shear load around a fiber break causes the matrix to creep over time, or possibly debond progressively along the fiber-matrix interface, thus lengthening the regions that are overloaded on the neighboring fibers. Ultimately the growing overload region encounters further flaws in neighboring fibers, which may cause those to break, adding to the cluster. Eventually a cluster will grow to a size that becomes unstable.
To understand the process by which stress rupture occurs, one must first have a robust model for the statistics of fiber strength and failure at small length scales. Current models, as reviewed by Phoenix and Beyerlein (2000) and Beyerlein and Phoenix (1996a), build on a Poisson process framework to represent the occurrence and severity of flaws along a fiber. Assuming a power law for the cumulative frequency of flaws having strengths below a given stress level leads to a Weibull distribution for fiber strength that exhibits the usual size (length) effect. The associated Weibull parameters can be estimated separately from tension tests on individual fibers at a suitable gage length. Such fiber strength models indicate that, under typical load levels in composite, large numbers of individual fiber failures are to be expected.
There has been extensive research, including theoretical (Hedgepeth 1961; Hikami and Chou 1990; Hedgepeth and Van Dyke 1967; Beyerlein and Phoenix 1996b; Beyerlein et al. 1996), experimental (Beyerlein and Landis 1999; Beyerlein et al. 1998a; McCarthy et al. 2015) and with simulations (Mahesh and Phoenix 2004a; Mahesh et al. 1999; Ibnabdeljalil and Curtin 1997; Iyengar and Curtin 1997), into how the matrix transfers the load from a broken fiber to its intact neighbors. Matrix creep in shear has been modeled and experimentally verified (Zhou et al. 2002, 2003, 2004), and the overall process of cluster formation has been numerically simulated (Mahesh et al. 1999, 2002; Mahesh and Phoenix 2004a; Ibnabdeljalil and Curtin 1997). Lacking is a coherent framework incorporating micromechanical knowledge of fiber-to-fiber stress redistribution over time, and a statistical framework for fiber breakage to yield a realistic and robust model for stress rupture. Models currently used (Phoenix 1979; Coleman 1956, 1957; Coleman and Knox 1957; Coleman 1958a, b; Tobolsky and Eyring 1943; Glasstone et al. 1941; Kelly and McCartney 1981; Christensen 1984; and Reeder 2012) all fit the same 1979 functional form by Phoenix (1979) and are typically rooted in the breakdown process in a single fiber, yet these models, when using experimentally-determined parameter values from testing composite specimens, often describe the stress-rupture behavior of composite materials under a given sustained load (Engelbrecht-Wiggans and Phoenix 2018). One such model involves a classic power-law in a Weibull framework (CPL-W), wherein composite lifetime follows a power law in terms of stress level, and both strength and lifetime follow separate Weibull distributions (Coleman 1956, 1957; Coleman and Knox 1957; Coleman 1958a, b; Tobolsky and Eyring 1943; and Glasstone et al. 1941).
There is concern, however, that these models become overly optimistic for load profiles other than a simple sustained load. Of particular concern is ‘proof testing’, whereby a virgin structure, such as a COPV, is subjected for a short ‘proof time’, to a ‘proof load’ much higher than its later ‘service load’ in use. Such proof testing, soon after COPV fabrication, is conceptually viewed as a process of weeding out inferior vessels, thus improving overall reliability in service. However, a vessel is typically weeded out because of liner leakage, rather than failure of the composite overwrap. Nevertheless, unlike with all metal pressure vessels, proof testing can do considerable damage to the overwrap in terms of breaking fibers and possibly epoxy-impregnated yarns or tows. This is clear from acoustic emission data generated during proof testing and should be expected based on strength data on individual fibers and tows at fiber stress levels comparable to that in the overwrap. Thus, it is possible that excessive proof pressure levels above the long-term service pressure may degrade the long-term reliability rather than improve it.
There is anecdotal evidence of such a possibility from proof tests on carbon fiber/epoxy COPVs where broken strands have been found on the outer surfaces of COPVs after proof testing. Furthermore, NASA, a key user of COPVs, was concerned enough about the possible degradation of long-term reliability to specifically adjust the proof testing guidelines away from higher proof tests, and to lower pressures on COPVs already in service such that the fiber strains do not exceed 50% of the original fiber strains at burst (ANSI S-081B 2018).
Despite the possibility that proof testing can degrade the long-term reliability, current stress-rupture models cannot predict such degradation. Models, such as the CPL-W model mentioned above, are largely phenomenological. When applied to carbon fiber/epoxy materials, their mathematical form is such that the conditional reliability upon surviving a proof test is virtually always predicted to be higher than the reliability under a simple sustained load absent a proof test.
These models more accurately describe the behavior of composites where the dominant driver of stress-rupture is fibers that degrade in time rather than a matrix that creeps in shear. However, carbon fiber/epoxy matrix composites have primarily time-independent fibers of variable strength due to flaws, so matrix creep in shear becomes important.
Thus, in this paper we develop a model that explicitly accounts for the micromechanical and statistical failure processes in a unidirectional composite consisting of carbon fibers in an epoxy matrix. This model will be called the stochastic fiber breakage (SFB) model. It will build on the previously-mentioned research into the micromechanics of stress-rupture in the context of statistical modeling of the local failure process, which involves local fiber load-sharing among broken and intact fibers in the vicinity of any composite cross-section. While actual loads in service are our main interest in applications, throughout we will commonly refer a ‘strength test’ or a ‘lifetime test’ with and without a proof test so as to focus our thinking on failure mechanisms in the model and associated probabilities of failure in a composite structure such as a COPV.
In developing the model, the following basic assumptions have been made: The fibers are assumed stiff, brittle and elastic, and possess randomly distributed flaws whose strengths can be characterized by a Poisson–Weibull model; that is, fiber elements have strengths following a Weibull distribution exhibiting the usual size (length) effect. The fibers themselves exhibit no time-dependent creep, and do not suffer strength degradation. The fibers and matrix are well bonded to each other. The matrix has an instantaneous shear modulus that is one to two orders of magnitude less than the tensile modulus of the fiber. Time dependence in the model enters through the matrix, which obeys power-law creep under a shear stress. This shear creep comes into play in the vicinity of broken fibers where the length scale of load-transfer to neighboring survivors grows over time, thus exposing increasing numbers flaws to stress levels that may result in their failure despite having survived up to that time. As the analysis in subsequent sections develops, additional assumptions will become necessary, and will err on the side of being conservative.
In Sect. 5, we present results for several cases of interest (involving wide ranging sets of parameter values) where we compare stress-rupture lifetime predictions from our new SFB model versus the well-known CPL-W model. Results are generated and compared under conditions involving an initial proof test versus having no true proof test, i.e., the proof stress level over a short proof time is less than or equal to the stress level in later service. Specifically, we compare probabilities of failure over time under fixed load levels where high reliability is desired. Despite having very different underlying assumptions and mathematical structure, the two models predict virtually the same behavior absent a true proof test. However, once the stress level in a proof test significantly exceeds that in later service, the two models diverge in their predictions, wherein the SFB model reveals a loss in reliability resulting from breakage of fibers that otherwise would not have occurred. Overall, we show that the SFB model generates far more complex behavior following a proof test than previous models such as the CPL-W model, and the long-term benefits and drawbacks of a proof test are very different for the two models.
Lastly, in a model of this type, fully investigating the ramifications of the various assumptions on the predicted stress-rupture lifetime of a composite is a major topic all by itself. Over the past few years much numerical and experimental work has appeared in the literature that could shed light on the robustness of certain assumptions, and how they might be improved or relaxed. The authors are presently collecting and interpreting this body of work for this purpose and intend to present the findings in a future publication.
2 Idealized composite
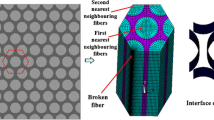
The model we develop is for an idealized composite structure, consisting of an array of n parallel continuous, brittle, elastic fibers embedded in a flexible polymer matrix. The stiffness of the matrix is one to two orders of magnitude less than that of the fibers. The role of the matrix is not only to bind the fibers together, but also to locally transfer load from broken to intact fibers, through shear, when the composite is under tensile load. Three fiber configurations are considered, as shown in Fig. 1: a planar array mimicking tapes used in winding COPVs, a hexagonal array that is a fair approximation of a 3D composite, and a square array, which is used for illustrative purposes.
2.1 The fibers
We assume that the occurrence of flaws along a fiber is well described by a Poisson–Weibull model. In this model the key parameter is \(\lambda \left( \sigma \right) =\left( {\sigma /{\sigma _{\ell _0 } }} \right) ^{\zeta }\), where \(\sigma \) is the stress level, \(\sigma _{\ell _0 } \) is a reference strength corresponding to the reference length \(\ell _0 \), and \(\zeta \) is a positive exponent (Phoenix and Beyerlein 2000). One interpretation is that \(\lambda \left( \sigma \right) \) is the average number of flaws per length \(\ell _0 \) with strength \(\le \sigma \). As a result, the number of flaws in a given length \(\ell \) that have strength \(\le \; \sigma \) follows a Poisson distribution with parameter \(\lambda \left( \sigma \right) \left( {\ell /{\ell _0 }} \right) \). The Poisson distribution implies that the probability that the number of flaws is zero in a given length, \(\ell \), i.e. no flaws occur, is given by \(\exp \left( {-\lambda \left( \sigma \right) \left( {\ell /{\ell _0 }} \right) } \right) \). Then the probability that at least one flaw with strength less than or equal to \(\sigma \) occurs in length \(\ell \) is one minus this probability, which is also the probability that the fiber will fail. Letting \(F_\ell \left( \sigma \right) \) be the probability of fiber failure due to at least one flaw, we obtain:
This is the classic Weibull distribution for fiber strength, whereby the strength of a fiber is equal to that of its worst defect. Furthermore, this Weibull distribution for the strength of a fiber has weakest link scaling in terms of length \(\ell /{\ell _0 }\).
In later modeling, we are interested in the strength distribution for a short fiber element of length \(\delta _e \), which is the initial effective length for load transfer (from a statistical point of view) around a fiber break, as is described in Sect. 2.2. This ‘statistical’ length \(\delta _e \) is typically much less than \(\ell _0 \), which in practice is a reference length, typically the tension test gage length for fiber testing (e.g., 1 cm). Over time the lengths of interest grow to exceed \(\delta _e \), as a result of matrix creep.
For the short length, \(\delta _e \), the Poisson–Weibull model still applies, giving:
Tension tests are used to estimate the Weibull scale parameter, \(\sigma _{\ell _0 } \), and shape parameter, \(\zeta \). Then \(\sigma _{\delta _e } \), the Weibull scale parameter for the strength of a fiber element of length \(\delta _e \), becomes:
This scaling is consistent with the fact that fibers typically follow Weibull weakest-link statistics (Phoenix and Beyerlein 2000). Also, \(\sigma _{\delta _e } \gg \sigma _{\ell _0 } \) as \(\left( {{\delta _e }/{\ell _0 }} \right) ^{{-1}/\zeta }\approx \left( {1/{20}} \right) ^{{-1}/5}\approx 1.82\), and a ratio of 1/20 for \({\delta _e }/{\ell _0 }\) is conservative, so that typically \(\sigma _{\delta _e } \sim 2\sigma _{\ell _0 } \).
In a large composite approaching failure, the far field applied stress on fiber elements, \(\sigma \), is small relative to \(\sigma _{\delta _e } \), or even, \(\sigma _{\ell _0 } \). Thus the failure probability for each individual fiber element is very small, and the lower tail of Eq. (2) can be accurately approximated by:
2.2 The matrix
The matrix, being much less stiff than the fibers, supports negligible tensile load. However, around fiber breaks the matrix becomes loaded in shear as it acts to locally transfer load from broken fibers to their nearest intact neighbors over some effective length, proportional to \(\delta _e \). In a planar array the load from a broken fiber is shared mainly across its two nearest neighbors, while in a hexagonal array the load is shared mainly across its six nearest neighbors.
The load transfer process has been successfully described using the classic shear-lag model developed by Hedgepeth (1961) and co-workers (Hikami and Chou 1990; and Hedgepeth and Van Dyke 1967). Extensions and refinements have been developed to improve the accuracy and realism in certain circumstances, (Goree and Gross 1980; Rossettos and Shishesaz 1987; Nairn 1988a, b, 1992; Rossettos and Olia 1993; Nairn and Wagner 1996; Nairn 1997) however, for the purposes of modeling time dependence in this paper, we have chosen to work with the simplest versions based on the shear-lag models of Hedgepeth (1961) in planar fiber arrays, and Hedgepeth and Van Dyke (1967) for hexagonal fiber arrays.
Over time the matrix creeps, giving rise to an increase in the effective length over which load transfer occurs. To model this matrix creep within the shear lag model, we use the power-law creep model, a common and useful creep law, whereby the creep compliance takes the form:
where \(J_{m,e} \) is the instantaneous creep compliance (\(J_{m,e} =1/{G_{m,e} }\), where \(G_{m,e} \) is the instantaneous elastic shear modulus), \(t_c \) is the characteristic time for creep to occur (at which time the compliance \(J_m \left( t \right) \) has roughly doubled), and \(\theta \) is the creep exponent. This creep compliance was used by Lagoudas et al. (1989). Beyerlein et al. (1998b) used a slightly different version, which in simplified form, was used by Mahesh and Phoenix (2004a). The creep exponent is a crucial parameter that governs the growth of the effective length for load transfer over time and depends on such factors as the matrix and adhesion chemistry, fiber volume fraction, and temperature—to name perhaps the most important influences (Beyerlein et al. 1998b). Typically, \(0.1<\theta <0.5\) for epoxies, (Brinson and Brinson 2015) and we note that, as a reference point, the value \(\theta =1\) corresponds to a Maxwell viscoelastic material, which has Newtonian viscous behavior at long times, \(t>>t_c \).
Overload on adjacent fibers, in a planar array, for three times \(t_1<t_2 <t_3 \), as a function of the distance from the break. Lengths shown for the step overloads are approximate for a fiber scale parameter \(\zeta =5\) using the values from Phoenix and Beyerlein (2000). Approximately triangular overload profiles are replaced by mathematically simpler, step overload profiles
One characteristic of the power-law creep model in the shear-lag framework is that there is an initial elastic characteristic length, \({\hat{\delta }}_e \), for load transfer (including regions on both sides of the break along the fiber). This length depends on both mechanical and geometric quantities: the fiber diameter, \(d_f \); the fiber cross sectional area, \(A_f \), (approximately \({\pi d_f^2 }/4\)); the fiber Young’s modulus, \(E_f \); the matrix shear modulus, \(G_m \); and the fiber volume fraction, \(V_f \), which is manifest in the effective matrix width between fiber surfaces, \(w_m \), and the effective matrix thickness, h, (which is of order \(d_f \)). The latter two quantities depend on the nature of the fiber packing as for instance in Fig. 1.
For fully elastic behavior, \({\hat{\delta }}_e \) is given in terms of these parameters by Phoenix and Beyerlein (2000), Hikami and Chou (1990) and Beyerlein et al. (1996) as:
The strongest influences on \({\hat{\delta }}_e \) are the fiber diameter, \(d_f \), and the square root of the fiber to matrix stiffness ratio, \(\sqrt{{E_f }/{G_m }}\). The remaining parameters above have a more modest influence through the fiber volume fraction.
Assuming linear viscoelastic behavior and solving the shear lag model under the power-law creep function, Eq. (5), Lagoudas et al. (1989) found that the characteristic load transfer length grows in time and is accurately approximated by:
An import aspect of the model considered in more detail later is the overload profile and stress state for a fiber neighboring a broken fiber (or a small cluster of transversely aligned breaks). This overload profile is roughly triangular in shape, as illustrated in Fig. 2, and with a certain magnitude at its peak that is characterized later. When calculating the probability of failure of such an overloaded neighbor, this profile can be modeled with an appropriately scaled, ‘rectangular’ overload profile over a certain effective length, denoted \(\delta \left( t \right) \), which as time passes increases in proportion to \({\hat{\delta }}\left( t \right) \) of Eq. (7). Figure 2 illustrates the assumed rectangular overload profile of effective length, termed \(\delta \left( t \right) \), in comparison to the actual, more triangular, load profile with its characteristic length \({\hat{\delta }}\left( t \right) \).
In Fig. 2, the effective length, \(\delta \left( t \right) \), is specifically chosen such that the actual triangular profile and the rectangular approximation are essentially equivalent with respect to fiber failure probability calculations in the model. The proportionality between \(\delta \left( t \right) \) and \({\hat{\delta }}\left( t \right) \) is governed by the relationship between the initial elastic, statistical effective length, earlier denoted as \(\delta _e \), and the initial elastic, characteristic length, denoted \({\hat{\delta }}_e \), which is approximately given by:
As discussed in Phoenix and Beyerlein (2000), this modification results from the fact that the higher the Weibull shape parameter for strength, \(\zeta \), the lower the variability in strength. Lower variability is due to a sparser distribution of weaker flaws, such that only the higher stresses near the peak of the triangular overload region are likely to cause failure, which also effectively narrows the overloaded region as \(\zeta \) increases, thus also reducing the ‘staggering’ of breaks around a cross-sectional plane.
Another important point is that while the lengths of the overload regions grow in time, the magnitudes of the overloads on the neighboring intact fibers do not change, as was shown by Lagoudas et al. (1989) and Beyerlein et al. (1998b) for the linearly viscoelastic matrix we consider here. This is true for immediate neighbors to a single break or to a small cluster of transversely aligned breaks. These authors also showed that next-nearest and more distant neighbors, are also overloaded but to a much lesser extent than the nearest neighbors. For aligned break clusters the magnitudes of these overloads also do not change. Thus, in calculating probabilities for new fiber failures, only the nearest neighbors and their overload profiles are considered. This approach has been found to work well, as shown in Mahesh et al. (2002) and Mahesh and Phoenix (2004a), some aspects of which are revisited later.
Based on these observations, and using Eqs. (7) and (8), we then obtain the time dependent relationship for the effective overload length:
or in normalized form as:
Thus, the length depends approximately as the \(\theta /2\) root of time, and significantly, the length is independent of stress level, assuming the stress level remains constant over time. This approximation will be used extensively in later analysis.
Note that in the case of a composite with a nonlinear, power-law creeping matrix, whereby the matrix creep rate is also dependent on shear stress to some power, various stress profiles around a fiber break were studied by Mason et al. (1992). In this case, the growing lengths of the overload regions on fibers next to a fiber break are similar to those shown in Fig. 2, except they are longer for higher composite stress levels. This leads to time-dependency similar to that in Eq. (9b), except there is also a modest dependence on overall composite stress level to some power. Phoenix et al. (1988) discussed the effects of this stress dependence on the overall composite lifetime distribution. It was argued that the effects are minor, being similar to those resulting from at most a unit increase in \(\zeta \), the Weibull shape parameter for fiber strength, and thus, the effects on the predictions of the current model are expected to be minimal.
2.3 Idealized failure process
In a strength test, failure is assumed to be triggered when a large enough cluster of broken fibers has formed somewhere in the composite at some stress level, such that the failure probability for overloaded neighbors reaches of order 1/2, whereby instability then becomes very likely. This process occurs roughly as follows: Upon initial loading, some fibers will break, even when the load is relatively low. These initial failures tend to be isolated and far apart but do create some level of stress concentration on their neighbors. Upon further increasing of the applied load, the overloaded neighbors of some of these isolated breaks can also fail, creating small clusters. Further increasing of the load leads to additional failed neighbors to these clusters, increasing their size, and thus, the stress concentration level on newly exposed neighbors. Eventually one or more of these clusters grows to a critical, unstable size in terms of the number of broken fibers, triggering overall composite failure.
A strength test, as just described, is quasi-static, i.e., the loading is presumed to take place quickly enough that we can ignore the time component in the composite failure process, resulting from matrix creep or time dependent breakdown in the fibers themselves or even overloading from dynamic recoil at the break (Hedgepeth 1961), which otherwise would result in additional failures without further increasing the load. In our stress-rupture modeling, however, the applied load is held fixed over time (after initial loading or proof testing), but the overloaded region in fibers neighboring break clusters is allowed to grow over time through matrix creep and/or time dependent debonding. This results in changes to the failure process as described below.
Suppose the idealized composite is loaded under a sudden, far-field tensile stress such that each fiber has been exposed to stress \(\sigma \ll \sigma _{\delta _e } \), and the overall tensile load on the composite is approximately \(\sigma n A_f \). Since the composite strength will turn out to be a small fraction of \(\sigma _{\delta _e } \), and the load under consideration smaller still, the probability of failure of a given fiber element is small, and thus the breaks, though numerous, tend to be widely separated.
When such a fiber element breaks, its load is redistributed locally onto its nearest neighbors over an initial effective length for load transfer, \(\delta _e \). In lifetime testing the effective load transfer length grows from \(\delta _e \) to become \(\delta \left( t \right) \), following Eq. (9). In either case, this local load redistribution is modeled as an equivalent uniform overload, over the effective load transfer length, on each of the neighboring fibers, as illustrated in Fig. 2.
If all such overloaded fiber elements have strength greater than the overload stress, then no additional fibers fail, and the composite is temporarily stable. In strength testing a stable cluster is made unstable only by increasing the load, whereas in lifetime testing under a constant load, an increase in the effective load transfer length can expose new flaws, causing additional fiber breaks.
When additional fiber breaks occur around isolated breaks, whether by an increase in applied composite load or growth over time of overload lengths, small clusters of broken fibers form, and all fibers adjacent to these clusters now become more severely overloaded. Once again, if all these newly overloaded fiber elements happen to be strong enough, the composite is stable. Otherwise even more fibers break, thus causing even more severe overloads on previously surviving neighbors. If these neighbors withstand the overloads, then further fiber breakage will occur either due to an increase in load (as in a strength test) or further passage of time (in a lifetime test), and the process repeats itself.
Eventually, catastrophic failure of the composite will occur if at least one cluster reaches a certain critical size, \({\hat{k}}\), for instability, which we define more precisely later. Except in special circumstances, the same critical size, \({\hat{k}}\), can be applied for both quasi-static strength and for time dependent lifetime behaviors. The process of cluster growth is illustrated in Fig. 3.
Initial fiber failures, upon first loading a composite, will occur at stress levels far below \(\sigma _{\delta _e } \), the Weibull scale parameter for the strength of a fiber element of length, \(\delta _e \). For instance, even if \(\sigma \) is just one tenth of \(\sigma _{\delta _e } \) and \(\zeta \approx 5\), the probability of an arbitrary fiber element failing is about \(10^{-5}\), meaning that one in a hundred thousand fiber elements fails. However, the volume of the composite, V, expressed as the number of fiber elements of length, \(\delta _e \), is easily on the order of \(10^{12}\) for COPVs. Thus, there can be around \(10^{12}10^{-5}=10^{7}\) initial fiber breaks. Once again, these initial breaks are typically widely spaced, and for \(\delta _e =0.1~\hbox {mm}\) as is typical in carbon/epoxy systems, the distance along a fiber between breaks would be around 10 meters on average. If, on the other hand, the stress level \(\sigma \) is doubled to one fifth of \(\sigma _{\delta _e } \) and if \(\zeta \approx 5\), then the probability of an arbitrary fiber element failing is considerably larger at about \(3\times 10^{-4}\), and fiber breaks are now much more closely spaced at 30 cm apart, or 3000 fiber elements apart, which is still a wide spacing compared to \(\delta _e \).
While there are large numbers of single fiber breaks at stresses far less than the characteristic element strength \(\sigma _{\delta _e } \), there are far fewer clusters of two breaks, and even fewer clusters of three breaks and so on, as we shortly show. To fail the composite at some combination of stress level and loading time, only one such cluster needs to reach critical size, \({\hat{k}}\), at which point the cluster becomes unstable and failure is sudden. Paradoxically, failure of the composite from a critical cluster that starts with failure of a given fiber element under stress \(\sigma \), is by nature an extremely rare event, even when failure of the entire composite under \(\sigma \) is likely, as there are an extremely large number of possible triggering fiber elements. At the same time, failure of the composite due to two smaller joining clusters to form a cluster larger than \({\hat{k}}\) at the point of instability is also a rare event compared to failure from just one reaching criticality.
In determining the probability of overall composite failure in the case of a quasi-static strength test, we first focus on a quantity \(W_k \left( \sigma \right) \), which is the probability of a cluster of k fiber breaks forming at a particular location in the composite, and at arbitrary stress \(\sigma \), and where k is arbitrary. These results are used later in connection with a specific value of \(k={\hat{k}}\), the critical cluster size. Any group of k adjacent fiber elements has the potential to become a cluster of k breaks, despite being a rare event for a given group of size k. However, the probability of obtaining at least one cluster of size k somewhere in the composite is much larger, and takes the weakest-link form:
where again V is the volume, i.e. the number of fiber elements of length \(\delta _e \) in the composite. This is true even though two nearby groups of k fiber elements can overlap each other and might ostensibly be viewed as statistically dependent. In reality, they satisfy the concept of k-dependence and essentially act independently [see Smith et al. (1983) for theorems on the concept of k-dependence associated with rare events].
A useful fact is:
and letting \(x=-VW_k \left( \sigma \right) \) we get:
Since V is large we have:
and Eq. (10) is well approximated by:
reminiscent of the Weibull form (see Smith et al. 1983).
3 Model for strength and lifetime testing
In developing our model for stress rupture, it is instructive to first focus on strength testing, where the loading increases relatively rapidly until failure, e.g., in 30 s. Thus, we first consider the process of failure, ignoring time dependence, as was described in Sect. 2.3. After developing a model for strength, we will continue with modeling stress-rupture lifetime behavior.
3.1 Strength testing
As a first step towards calculating the failure probability for the overall composite in a strength test, we calculate the probability, \(W_k \left( \sigma \right) \), that a given group of k fiber elements fails. In so doing we treat the neighbors of this final group of k fiber elements as having infinite strength, as shown in the various illustrations of configurations in the Online Resource, and thus do not participate in the failure progression, other than accepting the load of failed fibers at the edge of the resulting cluster, as would occur in the actual composite having exactly k such failed elements in a cluster.
In general, for small clusters of size k, \(W_k \left( \sigma \right) \) can be written down exactly. For example, if \(k=1\), we simply have \(W_1 \left( \sigma \right) =F_{\delta _e } \left( \sigma \right) \). In the case where \(k=2\), and assuming a planar array of fibers such as in Fig. 3a, we obtain:
where \(F_{\delta _e } \left( \sigma \right) \), \(\sigma \ge 0\) is the probability of failure of a fiber with effective length, \(\delta _e \), as given in Eq. (2) or Eq. (4), and where \(K_i \) is the stress concentration on a fiber element caused by a cluster of i adjacent broken fibers. In Eq. (15) the first term is the probability that both fibers fail under their applied load, \(\sigma \). The second term is the probability that only one fiber fails under load \(\sigma \), and the second fiber, while surviving load \(\sigma \), fails subsequently under the overload \(K_1 \sigma \), there being two ways this can happen as shown in the illustration of configurations for \(k=2\) in the Online Resource. Otherwise, the bundle of two fibers survives.
In the case \(k=3\), and again assuming a planar array of fibers such as in Fig. 3a, a more elaborate sequential fiber failure analysis can be carried out as shown in the illustration of configurations for \(k=3\) in the Online Resource. Summing all probabilities for specific failure sequences, expanding various products and then collapsing by summing similar terms, we obtain:
In the case \(k=4\), and again assuming the planar fiber array in Fig. 3a, a failure sequence analysis can be performed, as shown in the illustration of configurations for \(k=4\) in the Online Resource. Summing and collapsing all associated probability terms results in:
Finally, in the case \(k=5\), and again assuming a planar array of fibers as in Fig. 3a, a similar analysis for all possible failure sequences is shown in the illustration of configurations for \(k=5\) in the Online Resource. Summing and collapsing all the associated probability terms results in:
Clearly as k increases, the complexity of the calculation and the number of resulting terms increases drastically, but fortunately we are able to establish an accurate approximation for \(W_k \left( \sigma \right) \). Before doing so, we give an intuitive explanation of the structure of the results.
In the case where \(k=4\), Eq. (17) is the result of expanding and adding together the failure probabilities for all 31 distinct sequences in which a given contiguous group of four fibers can break, as shown in the illustration of configurations for \(k=4\) in the Online Resource. Only the first term in Eq. (17) involves a sequence whereby one fiber fails according to applied stress, \(\sigma \), a second fiber fails under the first overload, \(K_1 \sigma \), a third fails due to the second overload, \(K_2 \sigma \), and the final fiber fails due to the third overload, \(K_3 \sigma \). Note however, that the actual probabilities for such failure sequences are more complicated than simply this first term of Eq. (17). The constant 8 in front of the first term of Eq. (17) arises because for a given group of \(k=4\) adjacent failures in a planar array, there are \(2^{k-1}=2^{3}=8\) different ways in which a progressive sequence involving \(K_1 \), \(K_2 \), and \(K_3 \) can occur, as seen in lines 5 and 6 of the illustration of configurations for \(k=4\) in the Online Resource.
An important feature of the various product terms that occur in Eq. (17) is the magnitude progression \(F_{\delta _e } \left( {K_3 \sigma } \right)>F_{\delta _e } \left( {K_2 \sigma } \right)>F_{\delta _e } \left( {K_1 \sigma } \right) >F_{\delta _e } \left( \sigma \right) \), typically by more than a factor of two in each overload step. Thus, any sequence where two or more fibers fail at once, such as depicted in all lines in the illustration of configurations for \(k=4\) in the Online Resource other than lines 5 and 6, involves duplicating one of the lower stress concentrations thus reducing the magnitude of the product.
This sequential argument has a further implication. As was alluded to earlier, a cluster of more than k adjacent failed fibers in the composite can result from two (or more) clusters growing independently and then joining at the end to create a cluster of more than k breaks. However, this requires (i) at least two fibers to fail under the applied load, \(\sigma \), (ii) more than k fibers to fail, and (iii) that the clusters are close enough together that they can join.
Two fibers failing under the applied load, as discussed above, results in a lower probability than when the fibers fail sequentially in a single cluster. Furthermore, the initial fiber failure is a low probability event, and for each additional broken fiber in a cluster beyond size k, the failure probability becomes much smaller. Thus, the probability of two smaller clusters forming and joining to form a cluster of size larger than k, is much less than that of forming a cluster of exactly size k.
Returning to Eq. (17), the first term turns out to be the dominant term due to the combination of the higher stress concentrations and the large combinatorial factor. Thus, the first term can be used to approximate \(W_k \left( \sigma \right) \) very accurately, as we will show, and Eq. (17) can be approximated by:
The remaining terms in Eq. (17) have positive and negative signs, resulting in cancellation effects.
To illustrate, if we substitute Eq. (4) into Eq. (17), letting \(K_1 =3/2\), \(K_2 =2\), and \(K_3 =5/2\), as well as choosing \(\zeta =5\), as might be the case in an average quality carbon fiber, we get:
In comparison, our approximation in Eq. (19) gives:
A comparison of 0.550 from Eq. (20) to 0.545 from Eq. (21) shows that there is less than 1% difference in load required to achieve the same probability of failure. Comparing these two numbers is apt, as any inaccuracies in the approximation are comparable in magnitude to small changes or inaccuracies in the scale parameter \(\sigma _{\delta _e } \). This comparison is also shown in Fig. 4, where the ratio of the predicted failure probabilities is about 1.2, however on the scaling of Fig. 4, in the lower tail this is barely more than the thickness of the plotted lines.
As stated earlier, as k gets larger the exact expression for \(W_k \left( x \right) \) becomes increasingly complex. Fortunately, for the same reasons that Eq. (17) is well approximated by Eq. (19), the general expression for the strength of a cluster of k fibers, namely \(W_k \left( x \right) \), is well approximated by:
where \(c_k \) is a combinatorial factor capturing all the possible configurations (in terms of a growing sequence of fiber breaks) that a cluster can have, and \(K_i \) is the stress concentration on a fiber caused by a cluster of i broken fibers.
Weibull plot comparison of the exact expression for \(W_k \left( \sigma \right) \), Eqs. (15) through Eq. (18), with the approximation used in this paper, Eq. (22), where \(K_1 =3/2\), \(K_2 =2\), \(K_3 =5/2\) and \(K_4 =3\), and where \(\zeta =5\), using the exact expression for \(F_{\delta _e } \left( \sigma \right) \), i.e., Eq. (2)
Figure 5 compares approximation Eq. (22) with the exact expressions for \(W_k \left( \sigma \right) \) for \(k=1, 2,3,4~\hbox {and}~ 5\), as given by Eqs. (15–18) and noting again that \(W_1 \left( \sigma \right) =F_{\delta _e } \left( \sigma \right) \). Of special importance is the behavior of the respective lower tails, which tend to fold down on a single limiting characteristic distribution function curve as k increases, as is important later. Note, however, that the upper tails for \(\sigma >2{\sigma _{\delta _e } }/3\) will not superimpose onto a single curve, namely \(F_{\delta _e } \left( \sigma \right) \) for a single fiber, but will lie above it. This is because in the group of k fibers the first fiber to fail essentially fails the group since \(K_1 =3/2\) and there are k possible first fiber failures rather than one. At such high stress levels, we see that \(W_k \left( \sigma \right) \approx 1-\left[ {1-F_{\delta _e } \left( \sigma \right) } \right] ^{k}=F_{k\delta _e } \left( \sigma \right) \), the distribution function for strength of a chain of k fiber elements, i.e., of a fiber k times as long.
The form of Eq. (22) reflects the fact that, for a cluster to grow, a neighboring fiber element must fail. There are \(N_k \) neighboring fibers around a cluster of k breaks. Each of these fiber elements is exposed to the overload \(K_k \sigma \), which increases as k grows. For planar arrays of fibers:
but for other arrays \(N_k \) also increases as k grows. In particular, for a hexagonal fiber array (Mahesh et al. 2002) find that
where \(\eta \) and \(\gamma \) are parameters with ranges \(2.5\le \eta \le 6\) and \(0\le \gamma \le 1/2\). Taking \(\eta =\sqrt{4\pi }\approx 3.54\) and \(\gamma =1/2\) has the interpretation that \(N_k \) is the number of neighbors around a circular cluster of diameter, D, and containing \(k\approx {\pi D^{2}}/4\) breaks. However, this effectively over counts the number of severely overloaded neighbors, as some of the actual neighbors tend to be shielded and loaded significantly less than others as discussed in Mahesh et al. (2002) and Smith et al. (1983). For \(1\le \zeta \le 5\), it appears that \(\eta =6\) and \(\gamma =0\) work well, which indicates that the number of significantly overloaded fibers around a cluster is about six irrespective of cluster size. For larger \(5<\zeta \), smaller values in the vicinity of \(\eta \approx 4\) work better along with \(\gamma \approx 0.25\). In using the model, we leave these two parameters as free, though suggest that when applying the model, they should have values approximately as suggested.
Generally, the expression:
captures the fact that, except for the failure of the first fiber element, there are \(N_k \) overloaded neighbors next to the growing cluster at any growth step. Since the first failure is the trigger, it is excluded from that count, i.e., there are \(k-1\) additional growth steps to get a cluster of size, k.
Thus, for a planar array of fibers where \(N_k =2\), we get that:
In a hexagonal array \(c_k \) will grow more rapidly than in the planar case and will involve products of increasing numbers of fibers. In light of the discussion following Eq. (24) we have:
where again, \(j\approx {\pi D^{2}}/4\) is approximately the number of fiber breaks in a cluster of diameter, D, measured in number of fibers.
The stress concentrations also depend on the fiber arrangement. Henceforth we use the Hedgepeth versions described in Hedgepeth (1961), Hedgepeth and Van Dyke (1967) and Phoenix and Beyerlein (2000). For planar fiber array in Fig. 1a, it can be shown that:
In contrast to the planar case, for the hexagonal case the values of \(K_1 ,~K_2 ,\ldots ,~ K_k ,\ldots \) grow more slowly. In fact, it has been shown that (Mahesh et al. 1999, 2002):
again where D is approximately the cluster diameter measured in number of fibers.
By assuming the lower tail approximation, Eq. (4), for fiber failure probability, Eq. (22) becomes:
For the approximation in Eq. (4) to be accurate, we must be in the lower tail of the strength distribution. This may not be the case when the stress concentration factor is occasionally high, however any error induced in this approximation turns out to have a negligible impact on the overall value of \(W_k \left( \sigma \right) \) in Eq. (30) (this behavior of Eq. (30) is manifest as straight lines in the lower tails in Fig. 5).
Combining Eqs. (14) and (30), and taking \(k={\hat{k}}\), results in an approximation for the failure probability of the composite at a stress level \(\sigma \), i.e., the strength distribution, which can be written in Weibull distribution form as:
where \(H_V \left( \sigma \right) \equiv \left. {H_{V, k} \left( \sigma \right) } \right| _{k={\hat{k}}} \), and where:
is the effective Weibull scale parameter for strength and:
is the corresponding effective Weibull shape parameter. In these expressions, \({\hat{k}}\) is again the critical cluster size, at a particular applied stress, \(\sigma \), but also in the stress region where composite specimens are likely to fail (in a strength test). Thus, this \({\hat{k}}\) value satisfies:
Using Eq. (34) with Eq. (28) for the planar case, we find that \({\hat{k}}\) satisfies:
and with Eq. (29) for the hexagonal array, \({\hat{k}}\) satisfies:
where ‘\(\left\lceil \bullet \right\rceil \)’ corresponds to the ceiling function, i.e., rounding up the argument to the next integer, since instability requires going to the next highest cluster size.
It is important to note that at applied stress levels, \(\sigma \), considerably lower than the effective Weibull scale parameter for composite strength, \({\hat{\sigma }}_V \), which is the setting in stress-rupture lifetime discussed next, the cluster size needed to fail the composite initially is actually a considerably larger value, \(k_\sigma \), than \({\hat{k}}\) and satisfying:
However, the probability of forming this significantly larger cluster at \(\sigma <{\hat{\sigma }}_V \) is even smaller than forming one of size \({\hat{k}}\), defined by Eq. (34) in terms of the Weibull scale parameter for composite strength. Our approach of defining a single \({\hat{k}}\) value for all stress levels \(\sigma <{\hat{\sigma }}_V \) yields a Weibull distribution for composite strength, which is both convenient and conservative since the true distribution for composite strength, \(H_V \left( \sigma \right) \), tends to curve downward in the lower tail compared to the Weibull approximations. This is clear from studying the behavior of the governing lower tails of the distribution functions \(W_k \left( \sigma \right) \) in Fig. 5, as k increases with decreasing \(\sigma \). Picking a reference stress value, say \(\tilde{\sigma }\), and reference \(k_{\tilde{\sigma }} \) where a particular characteristic distribution function, \(W_{k_{\tilde{\sigma }} } \left( \sigma \right) \), is tangent to the limiting characteristic curve (as k grows large), one can see that lowering \(\sigma \) requires a higher \(k_\sigma \), and hence a different \(W_{k_\sigma } \left( \sigma \right) \) corresponding to a lower probability of failure than implied by the previous Weibull lower tail.
It is important to appreciate that the mathematical characterization and calculation of \(W_{{\hat{k}}} \), as well as the appropriate \({\hat{k}}\) value for a given material volume and probability of failure, is a mathematically deep and difficult topic. The approach we have used above is largely qualitative and strictly valid only for large Weibull strength shape parameter, \(\zeta \), (i.e., greater than 15). Surprisingly, it has worked very well in many instances for much smaller \(\zeta \), (i.e. for 5 and less) as supported using numerical analysis and Monte Carlo simulations (see for instance: Mahesh et al. 2002; Phoenix and Beyerlein 2000). A more rigorous version of this argument for the case of \(\zeta \rightarrow \infty \) can be found in Sec. 5 of Smith (1980), and for all values of \(\zeta \) in Mahesh and Phoenix (2004b). Also, Kuo and Phoenix (1987) provide a characterization of the problem in terms of a recursive system of equations where \(W_{{\hat{k}}} \) has an eigenvalue interpretation.
In the setting of a stress-rupture lifetime test, while early on, a larger value \(k_\sigma \), would be needed to fail the composite at stress \(\sigma \), significantly less than \({\hat{\sigma }}_V \), (say 1/3 to 2/3 of \({\hat{\sigma }}_V \)) the probability of the occurrence of even one such cluster of size \(k_\sigma \) larger than \({\hat{k}}\) is extremely small (orders of magnitude less than unity) and even more remote than forming one of exactly size \({\hat{k}}\), which is already extremely small. However, as time goes on, the situation changes as the smaller, more likely forming clusters begin to grow, as is discussed next. Nevertheless, in the model, failure is defined as occurring once a cluster of size \({\hat{k}}\) has formed irrespective of stress level.
3.2 Lifetime testing
Lifetime testing consists of loading the composite to a specified load or stress level, and then sustaining that load until the composite fails, presuming that the composite did not already fail during initial loading (an unlikely event, as the lifetime load level is typically a modest fraction of the mean strength of a typical specimen). Stress rupture, the dominating failure mode, arises in the model due to the matrix creeping and/or progressive debonding in shear around fiber breaks, thus increasing the length of the overloaded region on neighboring fibers (in this paper we do not explicitly model debonding through the effects are similar). Earlier we assumed the classic power-law creep model Eq. (5), in a shear-lag framework (Mason et al. 1992), and obtained the characteristic load transfer length, Eq. (9a), which increases with time. Below we use the normalized version Eq. (9b), and where applicable, its approximate power-law form.
Materials with high variability in fiber strength, as indicated by low values for the Weibull shape parameter, \(\zeta \), (i.e., \(\zeta \ll 1\)) are particularly susceptible to such stress-rupture failures. This is because, as the overloaded region increases in length, the probability that it will encounter a very weak flaw also increases due to the high variability in both the strengths of flaws and their locations. Carbon fibers particularly have high variability in strength from one segment of length \(\delta _e \) to the next, meaning that an unusually strong portion of a fiber is unlikely to be followed by an equally strong portion (this is not the situation with Kevlar fibers, for instance). This means that Weibull weakest flaw behavior tends to persist down to the length scale of load transfer. Even though the individual fibers themselves are virtually immune to stress rupture, i.e. single carbon fibers under constant stress essentially fail on loading or never fail, carbon/epoxy composites are much more sensitive in comparison. As mentioned, the driving mechanism in the stress rupture of carbon/epoxy composites is the increasing overload length around individual fiber breaks and clusters, thus promoting cluster growth.
To model stress rupture at a fixed stress level, \({\bar{\sigma }}<{\hat{\sigma }}_V \), assuming exactly \({\bar{\sigma }}\) is applied for all \(t\ge 0\) (i.e., no proof test occurs at some \(\sigma _{\mathrm{p}} >{\bar{\sigma }})\) the lifetime distribution function can be derived as a modification of the strength distribution Eq. (31) above. Using similar arguments, the distribution function for composite lifetime follows:
analogous to Eq. (14), where \(W_{{\hat{k}}} \left( {t;{\bar{\sigma }}} \right) \) is a characteristic distribution function analogous to Eq. (22), but with an added time component:
where \({\hat{k}}\) is again defined by Eq. (34), and \(F_{\delta _e } \left( {{\bar{\sigma }}} \right) \) is defined by Eq. (2) yielding:
which in the lower tail is approximated following Eq. (4) as:
Substituting Eq. (9) into Eq. (41) gives:
Using Eq. (42), the characteristic distribution function for stress rupture, Eq. (39), becomes:
For sufficiently large times, i.e. when \(t\gg t_c \), Eq. (43) can be further simplified using Eq. (9) to become:
Throughout these results, from Eqs. (38) to (44), we assume that \({\hat{k}}>1\), since otherwise, the problem is trivial; that is, if \({\hat{k}}=1\), the composite would either fail on loading should any fiber fail, or last indefinitely since no initial fiber breaks would mean no further failures could occur in time.
Note also that \({\hat{k}}\) for lifetime is taken to be the same as the \({\hat{k}}\) used in modeling the strength, and thus is given by either Eq. (35) in the planar case, or Eq. (36) for a hexagonal fiber array. The reasonableness of using the same \({\hat{k}}\) value in lifetime settings has been demonstrated in some detailed analysis in related earlier work (Phoenix et al. 1988). The basic idea is that early on in time under stress level \({\bar{\sigma }}<{\hat{\sigma }}_V \), being say 1/3 to 2/3 of \({\hat{\sigma }}_V \), the probability of formation of at least one cluster of size \({\hat{k}}\) is initially extremely small (and one of larger initial size \(k_\sigma \) is even more remote), so the composite survives with high probability. This situation changes, however, as time passes and initially formed small clusters grow as \(\delta \left( t \right) \) expands relative to the initial value \(\delta _e \) following Eq. (9).
The form of Eq. (44) again reflects the fact that, for the cluster to grow, a neighboring fiber element must fail. As in the strength distribution, there are again \(N_k \) neighboring fiber elements to a cluster of size k, but unlike for the strength distribution, these elements are now nominally of length \(\delta \left( t \right) >\delta _e \). As before, each of these longer fiber elements is exposed to the overload \(K_k {\bar{\sigma }}\), which increases as k grows. But now, additional flaws are exposed, and additional fiber breaks occur to add to the existing cluster. Ultimately the length over which the search for flaws occurs grows to the point where \({\hat{k}}\) breaks are critical (more breaks are less likely and having fewer breaks is insufficient since an even longer \(\delta \left( t \right) \) would be necessary).
An assumption implicit in this description is that when a fiber breaks, the overloaded region on the next fiber is not \(\delta _e \) but instead jumps quickly to \(\delta _e \sqrt{1+\left( {t/{t_c }} \right) ^{\theta }}\). In reality, fiber breaks occur sequentially, and thus, there is typically time between breaks, and certainly much time between when the initial fiber, \(k=1\), broke and when the final fiber, \(k={\hat{k}}\), breaks. Because of this difference in failure times there is actually some time lag for growth of the new overload length at each new fiber failure site, but this is not reflected in the above formula where the time over which the overload length grows is taken as the original time, t, thus artificially speeding up exposure to new flaws. Simulations show, however, that the effect of this assumption is small in light of the long timescales involved (Beyerlein et al. 1998b). This is in large measure the result of the fact that the power law exponent \(\theta \) is typically much less than 1, such that, in relative terms, there is rapid growth in \(\delta \left( t \right) \) right after failure, as is clear from Eq. (9). By comparison, the effect of this assumption is also smaller than the effect of small changes in stress level, \({\bar{\sigma }}\), or small errors in \(\sigma _{\delta _e } \). These have a larger effect on lifetime and failure probabilities, which are usually viewed using log scales. In practice, stress level is the key driver and the quantity easiest to control.
The resulting Weibull approximation for longer times, \(t\gg t_c \), is:
where \({\hat{\sigma }}_V \) is as given in Eq. (32), where:
is the Weibull shape parameter, and where:
is the power-law exponent for lifetime versus stress level, and where typically \({\hat{\rho }}>>10\). Equation Eq. (45) can be re-written in the Weibull form:
where:
is the effective Weibull scale parameter for lifetime, and once again \({\hat{\beta }}\) is the associated Weibull shape parameter, where typically \({\hat{\beta }}<1\), and often \({\hat{\beta }}<<1\).
To summarize, in lifetime testing the failure probability on loading is very small, as the applied stress, \({\bar{\sigma }}\), is much smaller than the scale parameter for tensile strength, \({\hat{\sigma }}_V \) (this, of course, assumes there are no ‘manufacturing defects’ not reflected by the model). Instead the concern is for failure at long times, \(t\gg t_c \), even though the fibers themselves may not suffer time dependent degradation. This is because there are initial fiber failures on loading, causing immediate overloads onto neighboring fiber elements of elastic length \(\delta =\delta _e \). Over time these overloaded regions increase in length, and thus, the remaining \({\hat{k}}-1\) fibers (required to create a critical cluster of size \({\hat{k}})\) eventually fail due to time dependency through matrix creep.
Three assumptions are implicit in the above discussion: The first is that any other initial fiber failures are automatically accounted for in the time dependent failures. The second is that \({\hat{k}}\) for stress rupture at long times is virtually the same as \({\hat{k}}\) for strength at times near zero (of course requiring a much higher stress level), and the associated stress concentrating \(K_j \) values themselves are also preserved, as a result of assuming linear viscoelastic creep behavior. Lastly \({\hat{k}}>1\) since otherwise the composite would fail on loading with the first fiber to break or survive indefinitely if no such fiber breaks occurred.
Finally, in deriving Eqs. (43) and (44), we have assumed that fiber breaks form a common transverse plane. Thus, we have ignored the potential consequences of staggering of breaks in significantly reducing the stress concentrations on intact neighbors, and thus, their probabilities of subsequent failure. However, as mentioned earlier, the degree to which significant staggering takes place decreases with increasing fiber Weibull shape parameter for strength, \(\zeta \). Also, as time goes on, the increase in the overload length, \(\delta \left( t \right) \), effectively reduces the effect of staggering so that fiber breaks increasingly act as though they are aligned. This effect can be seen in Figure 8 of Mahesh and Phoenix (2004a), and was shown to be an important factor in achieving agreement between theoretical and Monte Carlo simulated lifetime distributions.
4 Modeling effect of proof testing on the probability of composite failure
Proof testing consists of loading the composite to some proofing stress, \(\sigma _{\mathrm{p}} \), before reducing the stress to a lifetime maintenance level, \({\bar{\sigma }}\). For the purposes of this paper we will assume the simplified load profile:
where \(t_{\mathrm{p}} \) is the proof hold time; that is, the effects of the short times spent ramping the load level up to \(\sigma _{\mathrm{p}}\) and then back down to \({\bar{\sigma }}\) are assumed negligible in comparison to \(t_{\mathrm{p}} \).
Proof tests are often applied to COPVs with the implicit goal of filtering out weak vessels. For metal pressure vessels, and many homogeneous materials in general, this process can be argued to be all beneficial with no drawbacks, i.e., the lifetime failure probability conditional on surviving the proof test is reduced compared to the lifetime failure probability without the proof test. In ductile materials this can be due to crack blunting, and in brittle materials this can be due to weeding out all specimens with flaws or cracks above a critical length, without introducing new ones. In composites, however, the benefits are far less clear.
In reality, proof testing of a COPV may serve the purpose of exposing and weeding out vessels with manufacturing defects such as flawed liners or some gross manufacturing irregularity in the overwrap, such as missing tows or even a wrap, or the use of carbon/epoxy prepreg beyond its expiration date for proper resin flow and curing. These important aspects of proof testing are not reflected in our modeling, and by ignoring such possibly defective tanks in a manufacturing setting, the probability of failure of a freshly manufactured COPV, during the proof test, may actually be much higher than our models would initially suggest. That said, our analysis is more focused on whether proof testing of an otherwise ‘good tank’, i.e., one with no such gross manufacturing defects, induces unintentional damage to the composite.
From the point of view of our modeling, it is clear that, because of the proof test, many fiber elements will fail at the higher proof stress level, \(\sigma _{\mathrm{p}} \), that would not have failed under the lower lifetime stress level, \({\bar{\sigma }}\), as used in service. These additional fiber failures from the proof test provide many additional locations for subsequent time dependent cluster growth, potentially accelerating the stress-rupture process.
For instance, the number, \(n\left( {\sigma _{\mathrm{p}} } \right) \), of fiber breaks at the proof stress level \(\sigma _{\mathrm{p}} \), divided by the number, \(n\left( {{\bar{\sigma }}} \right) \), at the lifetime load level, \({\bar{\sigma }}\), is given by:
For the carbon fiber value, \(\zeta =5\), and for \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}=1.5\), we obtain \({n\left( {1.5{\bar{\sigma }}} \right) }/{n\left( {{\bar{\sigma }}} \right) }=7.6\). Thus, there are 7.6 times as many single fiber breaks or ‘singlets’ due to the proof test than without the proof test. These additional singlets provide many more seeds for stress rupture than would have occurred without the proof test. The situation is made worse, however, as the proof test will not only cause singlets, but could also form clusters of two or more broken fibers, according to Eqs. (15) through (18). In this way the proof test creates a larger number of broken fiber clusters of all sizes that would not have otherwise occurred on loading (nor later on unless eventually subsumed by another nearby cluster), potentially making later stress-rupture failure more likely.
At the same time, a proof test to stress level \(\sigma _{\mathrm{p}} \) would eliminate any vessels in the lower tail of the strength distribution, which is beneficial, at least in the short run (certainly in potentially eliminating tanks with defective liners, or missing tows, etc.). This raises the potential for trade-offs whereby there are time regimes where proof testing is beneficial and other time regimes (shorter or longer) where it is not. With the appropriate proof level this feature could be exploited.
Note that the fiber itself benefits in some respects from the proof test. This is because any fiber flaws weaker than \(\sigma _{\mathrm{p}} \), irrespective of their location, will fail in the proof test, and possibly be involved in various clusters. However, the remaining unbroken fiber flaws will then have strength greater than \(\sigma _{\mathrm{p}} \). Furthermore, for a stable cluster to grow after the proof test, i.e., after time \(t_{\mathrm{p}} \), the overloaded region must expand along the adjacent fibers. This is because the overloaded fiber elements directly adjacent to the cluster already have strength greater than \(K_j \sigma _{\mathrm{p}} \) where j is the cluster size (otherwise they would have also failed in the proof test), and under the subsequent lower, lifetime service stress, \({\bar{\sigma }}<\sigma _{\mathrm{p}} \), the overload has been lowered to \(K_j {\bar{\sigma }}\). When this overload expansion along neighboring fiber regions occurs, one of two situations may happen as follows:
Situation one This situation occurs when the cluster formed in proof testing is large enough such that the overload, \(K_j {\bar{\sigma }}\), created on the neighboring fiber regions expanding longitudinally over time after time, \(t_{\mathrm{p}} \), is greater than the proof stress level, \(\sigma _{\mathrm{p}} \), to which all fiber elements were previously exposed. These expanded regions were not themselves exposed to overloads from the cluster during the proof test, and therefore, have only been exposed thus far to a stress level of \(\sigma _{\mathrm{p}} \). Thus, new failures after the proof hold are caused by the overload \(K_j {\bar{\sigma }}>\sigma _{\mathrm{p}} \) in these newly expanded regions along neighboring fibers to the cluster.
Situation two This situation occurs when the cluster is small enough after proof testing such that over-load stresses after time \(t_{\mathrm{p}} \) are less than or equal to the proof stress, that is, \(K_j {\bar{\sigma }}\le \sigma _{\mathrm{p}} \). Thus, as the overload length increases, cluster growth can continue only by encountering previous fiber breaks resulting from flaws that already failed under \(\sigma _{\mathrm{p}} \), rather than by creating new failures from flaws of strength of \(K_j {\bar{\sigma }}\) or less, since these would have already failed under the applied load \(\sigma _{\mathrm{p}} \). Note that when \(K_j {\bar{\sigma }}\) is significantly less than \(\sigma _{\mathrm{p}} \), it may take several previously broken flaws, say i, to be encountered in succession in order to grow the cluster to where we eventually have \(K_{j+i} {\bar{\sigma }}>\sigma _{\mathrm{p}} \).
For situation one to occur, there is a minimum cluster size, denoted \(k_{\mathrm{p}} =k_{\mathrm{p}} ({{\bar{\sigma }}}/{\sigma _{\mathrm{p}} })\), satisfying:
For a planar array, where \(K_j \) is given in Eq. (28) as \(K_j \approx \sqrt{1+{\pi j}/4}\), this minimum cluster size is:
while for a hexagonal array, with \(K_j \) given in Eq. (29) as \(K_j \approx \sqrt{1+\sqrt{{4j}/{\pi ^{3}}}}\), the minimum size is determined to be:
Depending on the ratio \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}\), and the values of various model parameters, it is theoretically possible to obtain a minimum size, \(k_{\mathrm{p}} \), satisfying Eq. (52), that actually exceeds \({\hat{k}}\), the critical cluster size satisfying Eq. (34), i.e. \(K_{{\hat{k}}-1}<{\sigma _{\delta _e } }/{{\hat{\sigma }}_V }<K_{{\hat{k}}} \). This threshold in the model would be exceeded if the ratio of the proof test stress to the long-term service stress level exceeds the ratio of the fiber element strength to the Weibull scale parameter for composite strength, that is, \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}>{\sigma _{\delta _e } }/{{\hat{\sigma }}_V }\).
The probabilities for the various cluster formation paths resulting from a proof test must be assessed and summed systematically, and any potential sequences only ruled out when it is clear they are dominated by probabilities of occurrence of other, far more likely sequences. In the current case we have conservatively defined the occurrence of a cluster of \({\hat{k}}\) breaks as equivalent to failure.
The following analysis is subdivided into considering two cases and associated probabilities of failure. Overall, we seek the cumulative distribution function for failure, denoted, \(H_V \left( {t;{\bar{\sigma }},\sigma _{\mathrm{p}} } \right) \) covering all times \(t>0\), both during the proof hold time up to time \(t_{\mathrm{p}} \), and afterwards. The first is where failure occurs during the proof test itself, specifically during time \(0<t<t_{\mathrm{p}} \). For this case the analysis is straightforward, and it is easy to arrive at this portion of the cumulative distribution function for failure. The second case is where failure occurs at some longer time, \(t\ge t_{\mathrm{p}} \), when the composite is now under lower service load, \(\sigma \left( t \right) ={\bar{\sigma }}\). This analysis is more complicated, requiring consideration of many possible events for both \(0<t<t_{\mathrm{p}} \) and \(t\ge t_{\mathrm{p}} \), and related quantities, \(W_{{\hat{k}},k_{\mathrm{p}} } \). Determining the distribution function for failure requires summing the probabilities for all such events.
The first step in investigating what happens for \(t\ge t_{\mathrm{p}} \) is to consider the state of the composite at time \(t_{\mathrm{p}} \). Again, we assume \({\hat{k}}\ge 2\) since otherwise the composite would fail on loading with the first fiber to break or survive indefinitely if no such fiber break occurred.
4.1 Probability of forming a cluster of size \({\hat{k}}\ge 2\) during proof hold time, \(t_{\mathrm{p}} \), causing failure
We now consider failure probabilities under an initial proof test to stress \(\sigma _{\mathrm{p}} \) over \(0<t<t_{\mathrm{p}} \), where \(t_{\mathrm{p}} \) is termed the ‘proof holding time’, and after which the stress is lowered to \({\bar{\sigma }}\) for \(t\ge t_{\mathrm{p}} \). This is the stress profile \(\sigma \left( t \right) \) described by Eq. (50). For failure to occur during the proof test, \(0<t<t_{\mathrm{p}} \), a critical cluster of size at least \({\hat{k}}\) must form (which is failure by definition), and in that event we have:
analogous to Eq. (38), where:
The right hand side of Eq. (56) is simply Eq. (43) upon taking \(\sigma =\sigma _{\mathrm{p}} \).
4.2 Probability of forming a cluster of exactly size \({\hat{k}}-1\) during proof hold time, \(t_{\mathrm{p}} \), but eventually growing to critical size, \({\hat{k}}\ge 2\)
Next we consider times, \(t\ge t_{\mathrm{p}} \), and suppose that an initial cluster of exactly \({\hat{k}}-1\) breaks occurs under the proof hold to \(t_{\mathrm{p}} \), that is, the cluster size is one short of that required to fail the composite, (since by definition, the occurrence of a cluster of \({\hat{k}}\) breaks implies failure). To reach a cluster of critical size \({\hat{k}}\) at some later time, \(t\ge t_{\mathrm{p}} \), requires failure of at least one nearest neighbor. In the degenerate case where \(\sigma _{\mathrm{p}} ={\bar{\sigma }}\), (i.e., not a true proof test), then for failure to occur after \(t\gg t_{\mathrm{p}} \), the overload length need only grow until \(F_{\delta _e } \left( {K_{{\hat{k}}} {\bar{\sigma }},t} \right) \approx 1/2\). However, when \({\bar{\sigma }}<\sigma _{\mathrm{p}} \), the analysis is more complicated, and we must look closely at the two situations described above regarding the cluster size after the proof test, and specifically its relation to the critical proof threshold size, \(k_{\mathrm{p}} \). Thus we investigate first the case where a cluster of exactly \({\hat{k}}-1\) breaks forms during \(0<t<t_{\mathrm{p}} \), and where \(k_{\mathrm{p}} \le {\hat{k}}-1\). We then consider other possibilities for \(k_{\mathrm{p}} \) relative to \({\hat{k}}\).
4.2.1 Cluster of size \({\hat{k}}-1\) forms during proof hold time, \(t_{\mathrm{p}} \), where \(1\le k_{\mathrm{p}} \le {\hat{k}}-1\) and \({\hat{k}}\ge 2\)
In considering the formation of a cluster of \({\hat{k}}-1\) breaks during the proof test, we first consider situation one above, whereby the cluster size must satisfy \(1\le k_{\mathrm{p}} \le {\hat{k}}-1\), the critical proof threshold size. In this case, the overloads caused by the cluster after time \(t_{\mathrm{p}} \) are larger than the previously applied load \(\sigma _{\mathrm{p}} \), and new flaws are encountered once the neighboring fiber regions lengthen in time following \(\delta \left( t \right) \). The characteristic distribution function for this event takes the form:
where, as before, \(N_{{\hat{k}}-1} \) is the number of nearest neighbors around a cluster of \({\hat{k}}-1\) breaks. As written, Eq. (57) assumes \({\hat{k}}>2\), however, if the product term in square parentheses is omitted (i.e., only one break occurs during proof up to time \(t_{\mathrm{p}} )\) then the formula applies also to \({\hat{k}}\ge 2\).
To understand the structure of Eq. (57) we note that exactly\({\hat{k}}-1\) breaks occur over time \(t_{\mathrm{p}} \), and afterwards one of the \(N_{{\hat{k}}-1} \) nearest neighbors fails, causing composite failure, since the cluster is now of critical size, \({\hat{k}}\). Since this additional fiber did not fail by time \(t_{\mathrm{p}} \), the portion of the fiber exposed to this overload is stronger than \(K_{{\hat{k}}-1} \sigma _{\mathrm{p}} >K_{{\hat{k}}-1} {\bar{\sigma }}\). Thus, when calculating the probability for the fiber’s subsequent failure, we need only consider lengths that are newly exposed. For each of the \(N_{{\hat{k}}-1} \) overloaded fibers, this is captured by the incremental probability:
a quantity easier to appreciate when Eq. (41) is substituted into Eq. (58), resulting in:
Finally, the term in the second line of Eq. (57) accounts for the probability of survival of all the neighboring fiber elements up to the end of the proof hold time, \(t_{\mathrm{p}} \), over overload length \(\delta \left( {t_{\mathrm{p}} } \right) \):
since only \({\hat{k}}-1\) breaks occur during the proof test itself, thus no neighbors failed during \(t_{\mathrm{p}} \).
From Eqs. (59) and (60), and using Eq. (41) on the remaining terms in Eq. (57), we reduce Eq. (57) to:
where, recalling Eq. (25), we have \(c_1 =1\), and \(c_{{\hat{k}}} =N_{{\hat{k}}-1} c_{{\hat{k}}-1} ,~{\hat{k}}>1.\)
Taking \({\delta \left( t \right) }/{\delta _e }=\sqrt{1+\left( {t/{t_c }} \right) ^{\theta }}\), as in Eq. (9), and rearranging the result, we can rewrite Eq. (61) as:
As mentioned, Eq. (61) required \({\hat{k}}>2\), however, in light of the associated comment, Eq. (62) is also valid for \({\hat{k}}\ge 2\) and \({1}\le k_{\mathrm{p}} \le {\hat{k}}-1\) as indicated, whereupon the term in the second line is unity.
4.2.2 Cluster of size \({\hat{k}}-1\) forms during proof hold time, \(t_{\mathrm{p}} \), where \(1\le k_{\mathrm{p}} -1={\hat{k}}-1\) and \({\hat{k}}\ge 2\)
Equations (55) through (62) assumed that \(k_{\mathrm{p}} \le {\hat{k}}-1\), i.e. the overloads, caused by the cluster after time \(t_{\mathrm{p}} \), were larger than the previously applied load \(\sigma _{\mathrm{p}} \). If, instead, we have \(k_{\mathrm{p}} ={\hat{k}}\), and a cluster of size \({\hat{k}}-1\) has already resulted from the proof test, we have situation two described above whereby all overloads during the subsequent sustained loading, \({\bar{\sigma }}\), will now be less than \(\sigma _{\mathrm{p}} \), and thus no new fiber breaks can occur due to the expanding overload length. However, the proof load \(\sigma _{\mathrm{p}} \) will still have resulted in broken fibers, so we simply must wait for the overload region to grow in length until it engulfs a previously broken fiber at a flaw that was weaker than \(\sigma _{\mathrm{p}} \) in order to finally grow the cluster to size \({\hat{k}}\), the failure size. As such, the characteristic distribution function for this event takes the form:
As written, Eq. (63) assumes \({\hat{k}}>2\). However, as with Eq. (57), if the product term in square parentheses is omitted (since only one break occurs up to time \(t_{\mathrm{p}} )\) then the formula applies also to \({\hat{k}}\ge 2\). The key difference between Eqs. (57) and (63) is that instead of searching for newly exposed flaws that are weaker than \(K_{{\hat{k}}-1} {\bar{\sigma }}\), and calculating the associated probability of finding them, we instead search for flaws weaker than \(\sigma _{\mathrm{p}} \), i.e. flaws that already failed during the proof test. Thus only the last term in Eq. (57) changes, becoming \(F_{\delta _e } \left( {\sigma _{\mathrm{p}} ,t} \right) -F_{\delta _e } \left( {\sigma _{\mathrm{p}} ,t_{\mathrm{p}} } \right) \).
Substituting Eq. (41) into Eq. (63) and again using Eq. (9), we manipulate Eq. (63) into the convenient form:
Note that Eq. (64) is also valid for \({2}\le k_{\mathrm{p}} ={\hat{k}}\) and \({\hat{k}}\ge 2\) since the last factor in the second line vanishes when \({\hat{k}}-1=1\). Also Eq. (64) no longer involves \(k_{\mathrm{p}} \) as a parameter but only \(\sigma _{\mathrm{p}} \) itself.
4.2.3 Cluster of size \({\hat{k}}-1\) forms during proof hold time, \(t_{\mathrm{p}} \), where \(2\le {\hat{k}}<k_{\mathrm{p}}\)
Having considered cases \(k_{\mathrm{p}} \le {\hat{k}}\) after having \({\hat{k}}-1\) breaks form up to time \(t_{\mathrm{p}} \), we also may have \(2\le {\hat{k}}<k_{\mathrm{p}} \). This occurs if one has an excessively high proof ratio, \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}\), and a value of \({\hat{k}}\) such that \({K_{{\hat{k}}-1} \sigma _{\mathrm{p}} }/{\sigma _{\delta _e } }\) is of order unity or larger whereby \(F_{\delta _e } \left( {K_{{\hat{k}}-1} \sigma _{\mathrm{p}} ,t_{\mathrm{p}} } \right) \rightarrow 1\). This case also happens to be covered by Eqs. (63) and (64), which again no longer involves \(k_{\mathrm{p}} \) as a parameter.
4.3 Cluster of size k forms during proof hold time, \(t_{\mathrm{p}}\), where \(1\le k<{\hat{k}}-1\) and \({\hat{k}}\ge 2\)
Suppose that during time \(1<t<t_{\mathrm{p}} \) a cluster of k fiber breaks forms, but this time \(k<{\hat{k}}-1\), i.e., two or more additional breaks are needed to reach critical size \({\hat{k}}\) occurring during \(t\ge t_{\mathrm{p}} \). In Sect. 4.3.1 we study situation one where \(k_{\mathrm{p}} \le k\), and in Sect. 4.3.2 we study situation two, where \(k<k_{\mathrm{p}} \le {\hat{k}}\). Lastly, in Sect. 4.3.3 we address the case where \({\hat{k}}<k_{\mathrm{p}} \).
4.3.1 Cluster of size k forms during proof hold time, \(t_{\mathrm{p}} \), with \(1\le k_{\mathrm{p}} \le k\le {\hat{k}}-2\) and \({\hat{k}}\ge 2\)
When a cluster of \(k<{\hat{k}}-1\) fiber breaks forms by time \(t_{\mathrm{p}} \), then composite failure by some time, t, after the proof test (which requires a cluster of \({\hat{k}}\) breaks) is caused by a sequence of at least \({\hat{k}}-k>1\) additional failures, beginning with the failure of a fiber flanking the stalled k cluster. Since \(k_{\mathrm{p}} \le k\), the overloads, for \(t_{\mathrm{p}} \le t\), are larger than the previously applied load \(\sigma _{\mathrm{p}} \). In the case, \(1<k_{\mathrm{p}} \le k\le {\hat{k}}-2\) and \({\hat{k}}>3\), the characteristic distribution function thus takes the form:
As written, this equation assumes \({\hat{k}}>3\). However, as with (57), if the first product term in square parentheses is omitted (i.e., only one break occurs up to time \(t_{\mathrm{p}} )\) then the formula applies also to \({\hat{k}}\ge 3\) (further reductions to allow \({\hat{k}}\ge 2\) are discussed below).
The first two lines in Eq. (65) results from arguments similar to those made in connection with Eqs. (57) and (63) but with k less than \({\hat{k}}-1\), while the third line in Eq. (65) results from similar arguments associated with Eq. (58). The quantity, \(c_k F_{\delta _e } \left( {\sigma _{\mathrm{p}} } \right) \left[ \prod \nolimits _{i=1}^{k-1} F_{\delta _e } \left( {K_i \sigma _{\mathrm{p}} ,t_{\mathrm{p}} } \right) \right. \Big ]\), in the first line is the probability that exactlykfibers failed during the proof time, \(t_{\mathrm{p}} \). The term, \(\left( {1-F_{\delta _e } \left( {K_k \sigma _{\mathrm{p}} ,t_{\mathrm{p}} } \right) } \right) ^{N_k }\), is the probability that, by assumption, none of the \(N_k \) neighboring fibers failed during time up to \(t_{\mathrm{p}} \) as a result of the overload of the k broken fibers to that point. The term, \(N_k \left( {F_{\delta _e } \left( {K_k {\bar{\sigma }},t} \right) -F_{\delta _e } \left( {K_k {\bar{\sigma }},t_{\mathrm{p}} } \right) } \right) \), is the approximate probability of failure of at least one of the newly exposed portions of the \(N_k \) neighboring fibers.
Once such a neighboring fiber has failed, new fiber lengths become exposed to \(K_{k+1} {\bar{\sigma }}\), whose previous maximum load was simply \(\sigma _{\mathrm{p}} \). Since \(\sigma _{\mathrm{p}} <K_{k+1} {\bar{\sigma }}\), we must search the whole overloaded region for flaws to fail and calculate the associated probability. The final product term in Eq. (65) reflects this, though it does not differentiate between the remaining fibers that were neighbors to the stalled cluster versus neighbors newly created by the \(k+1\), \(k+2\)... \({\hat{k}}-1\) breaking fibers. Thus, this term corresponds to the failure probability of the remaining \(k+2\) through \({\hat{k}}\) fibers, with the growth of the overload length starting at time \(t_{\mathrm{p}} \). Thus, this final term approximates the desired quantity.
Taking Eq. (65) and substituting in Eq. (41) to approximate the failure probability of a fiber element, and using Eq. (9) for \(\delta \left( t \right) \), we can manipulate Eq. (65) into the form:
which, as indicated, also happens to be valid for \({1}\le k_{\mathrm{p}} \le k\le {\hat{k}}-2\) and \({\hat{k}}\ge 3\). Note that when \({1}=k_{\mathrm{p}} =k\), the two terms in the second line vanish. If we take \(k={\hat{k}}-1\) allowing \({\hat{k}}\ge 2\), the last quantity in the last line vanishes and this result collapses to (62) and does not depend on \(k_{\mathrm{p}} \).
4.3.2 Cluster of size k forms during proof hold time, \(t_{\mathrm{p}} \), with \(1<k<k_{\mathrm{p}} \le {\hat{k}}\) and \({\hat{k}}\ge 3\)
Again, suppose that during time \(t_{\mathrm{p}} \) a smaller cluster of \(1<k<{\hat{k}}-1\) fiber breaks forms but this time we also have \(k<k_{\mathrm{p}} \le {\hat{k}}\). Here, all initial overloads during the sustained loading will now be less than \(\sigma _{\mathrm{p}} \), and thus, no new fibers will break until the cluster size reaches \(k_{\mathrm{p}} \). Once the cluster has reached size \(k_{\mathrm{p}} \), and the load is thus greater than the proof load, \(\sigma _{\mathrm{p}} \), new breaks will occur until the critical cluster size, \({\hat{k}}\), is reached and the composite fails. In the case, \(1<k<k_{\mathrm{p}} \le {\hat{k}}\), and \({\hat{k}}>4\), the characteristic distribution function takes the general form:
If only one break occurs during proof up to time \(t_{\mathrm{p}} \), i.e. \(k=1\), then the product term in square parentheses in the first line can be omitted, and the formula applies also to \({\hat{k}}\ge 4\). Additionally, if \(1=k=k_{\mathrm{p}} -1<{\hat{k}}-1\) the product term in square parentheses in the fourth line also vanishes, thus allowing \({\hat{k}}\ge 3\). Finally, if \(k=k_{\mathrm{p}} -1={\hat{k}}-1\) the product term in square parentheses in the last line also vanishes and allows \({\hat{k}}\ge 2\). In this case Eq. (67) reduces to Eq. (63).
The first two lines in Eq. (67) are the same as in Eq. (65) and the arguments are the same. However, we now have \(k<k_{\mathrm{p}} \), so all overloads during the sustained loading from cluster size k up to cluster size \(k_{\mathrm{p}} \) will still be less than \(\sigma _{\mathrm{p}} \). Thus, no new fibers will break even as the overload lengths expand following \(\delta \left( t \right) \), and the cluster grows only by encountering breaks that occurred earlier under stress, \(\sigma _{\mathrm{p}} \). Thus, the third and fourth lines use \(\sigma _{\mathrm{p}} \) as the applied stress instead of \(K_i {\bar{\sigma }}\), as in Eq. (65). After that, for cluster sizes \(k_{\mathrm{p}} \le i\) up to the critical size \({\hat{k}}-1\), there emerge new fiber breaks due to the overloads from the steady stress, \(K_i {\bar{\sigma }}\), and where from a probability of failure point of view, fibers are taken as essentially ‘fresh’ and unaffected by the previous proof test stress, \(\sigma _{\mathrm{p}} \) (i.e., they would be broken anyway). The term in the last line reflects that probability.
Using Eq. (41) to approximate the failure probability of a fiber element, and using Eq. (9) to describe the growing length of the overload, Eq. (67) can be factored and rearranged into the form:
and in light of the comments following Eq. (67), the above form also happens to be valid for the cases \({1}\le k\le k_{\mathrm{p}} -1\le {\hat{k}}-1\) and \({\hat{k}}\ge 3\), as indicated. Note that when \(k=1\), the two terms in the second line vanish, and when \(k_{\mathrm{p}} ={\hat{k}}\), the first factor in last line vanishes. Lastly, in the special case \(k=k_{\mathrm{p}} -1={\hat{k}}-1\), then the last line and the last term in the second line disappear and the result collapses to Eq. (64) with \({\hat{k}}\ge 2\).
4.3.3 Cluster of size k forms during proof hold time, \(t_{\mathrm{p}} \), with \(1\le k\le {\hat{k}}-1<k_{\mathrm{p}} -1\)
Having just considered the cases where \(k_{\mathrm{p}} \le {\hat{k}}\), we also must consider \(k\le {\hat{k}}-1<k_{\mathrm{p}} -1\). For this to occur one must have a very high proof ratio, \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}\), and a value of \({\hat{k}}\) such that \({K_{{\hat{k}}} \sigma _{\mathrm{p}} }/{\sigma _{\delta _e } }\) may be of order unity or larger. This case is also covered by Eqs. (67) and (68) upon replacing \(k_{\mathrm{p}} \) with \({\hat{k}}\), giving \(W_{{\hat{k}},k\le \;{\hat{k}}-1 < k_{\mathrm{p}} \;-1 } \left( {t;{\bar{\sigma }},\sigma _{\mathrm{p}} } \right) \). The result no longer involves \(k_{\mathrm{p}} \) as a parameter, but only \(\sigma _{\mathrm{p}} \).
4.4 Summation of mutually exclusive events to obtain characteristic distribution function for composite failure
Here we obtain the general characteristic distribution function, denoted, \(W_{{\hat{k}},k_{\mathrm{p}} } \left( {t;\sigma _{\mathrm{p}} ,{\bar{\sigma }}} \right) \) for failure after a proof test for the case \(t\ge t_{\mathrm{p}} \). This involves summing probabilities for all possible values of \(1\le k\le {\hat{k}}\), which is the number of fiber breaks occurring over time \(0<t<t_{\mathrm{p}} \) on the way to forming an eventual critical cluster of size \({\hat{k}}\) during later time \(t\ge t_{\mathrm{p}} \).
In view of all the cases and equations described in Sects. 4.1, 4.2.1, 4.2.2, 4.2.3, 4.3.1, 4.3.2 and 4.3.3, and summing the first equations in each section but rearranged in order of related cases, we obtain the following: For the case \(1\le k_{\mathrm{p}} <{\hat{k}}\) and \({\hat{k}}\ge 2\), and summing on both \(1\le k<k_{\mathrm{p}} <\;{\hat{k}}\) and \(1\le k_{\mathrm{p}} \le k\;<\;{\hat{k}}\) we obtain:

where for any function \(g_i \), and any non-negative integers p, q and i we define:

where the quantity in double-square parentheses is the usual product unless \(q<p\) where it is unity. We also define a left-continuous version of the ‘Heaviside function’, (i.e., \(\mathrm{H}\left( 0 \right) \equiv 0\), instead of equaling ‘1’):
We similarly obtain \(W_{{\hat{k}},k_{\mathrm{p}} \ge {\hat{k}}} \left( {t;\sigma _{\mathrm{p}} ,{\bar{\sigma }}} \right) \), covering the case \(2\le {\hat{k}}\le k_{\mathrm{p}} \), which involves summing over \(1\le k\le {\hat{k}}-1\). This results in an overall result covering both cases, which is:

where we have introduced \(\mathrm{H}\left( {k-k_{\mathrm{p}} +1} \right) \) in the first sum rendering the terms ‘zero’ when \(k<k_{\mathrm{p}} \). Also \(k_{1} \vee k_2 \equiv \min \left( {k_1 ,k_2 } \right) \), is the minimum of \(k_{1} \) and \(k_2 \). Thus, in covering the case \(2\le {\hat{k}}\;\le k_{\mathrm{p}} \), the first sum vanishes in deference to the second sum whose upper limit becomes \({\hat{k}}-1\), and in this case, the upper limits of all products over index i cannot exceed \({\hat{k}}-1\), the critical cluster size in Sects. 4.2.3 and 4.3.3.
Using the special versions for the various terms in Sects. 4.1, 4.2.1, 4.2.2, 4.2.3, 4.3.1, 4.3.2 and 4.3.3 (final equation in each), we get the following: For the case \(1\le k_{\mathrm{p}} <{\hat{k}}\) and \({\hat{k}}\ge 2\) we have:
On the other hand, for the case \(1\le k<{\hat{k}}\le k_{\mathrm{p}} ~\hbox {and}~{\hat{k}}\ge 2\), we instead obtain:
As was done in deriving Eq. (72), the results Eqs. (73) and (74) can also be combined and collapsed to yield:
Note that in both the general version Eq. (72) and the special version (75) of \(W_{{\hat{k}},k_{\mathrm{p}} } \left( {t;{\bar{\sigma }},\sigma _{\mathrm{p}} } \right) \), the quantity, \(c_{{\hat{k}}} \), is given by Eqs. (26) and (27):
and the quantity, \(N_k \), is given by Eqs. (23) and (24):
where guidelines for choosing the parameters, \(\eta \) and \(\gamma \), were described following Eq. (24).
4.5 Distribution function for composite failure for times following a proof test
In the time range of the proof loading itself, \(0<t<t_{\mathrm{p}} \), we derived the probability of failure at time, t, and thus, the portion of the cumulative distribution function for failure corresponding to \(0<t<t_{\mathrm{p}} \), during the proof test as given in Sect. 4.1 by Eqs. (55) and (56). Continuing on to longer times \(t\ge t_{\mathrm{p}} \), the probability of overall composite failure (i.e., the distribution function) is given by Eq. (38), and upon inserting Eq. (75) and slightly rearranging the result we obtain:
where:
4.6 Conditional reliability following a proof test
Of special interest is the reliability of a structure, \(R_{\mathrm{p}} \left( {\left. {t } \right| t\ge t_{\mathrm{p}} } \right) \), conditional on surviving a proof test. This is calculated in general terms using Bayes theorem:
First, we consider the conditional reliability for lifetime, \(R_{{\hat{k}},{\mathrm{p}}} \left( {\left. t \right| t_{\mathrm{p}} ,{\bar{\sigma }}} \right) \), under a sustained load, \({\bar{\sigma }}\), and for times \(t\ge t_{\mathrm{p}} \), and conditioned on surviving to time \(t_{\mathrm{p}} \) under the initial proof loading, \(\sigma _{\mathrm{p}} ={\bar{\sigma }}\) (i.e., no elevation in the proof load relative the ‘service’ load). From Eqs. (48) and (49) this is just:
On the other hand, for the case of surviving a proof test with elevated proof load, \(\sigma _{\mathrm{p}} >{\bar{\sigma }}\), the conditional reliability, \(R_{{\hat{k}},k_{\mathrm{p}} } \left( {\left. t \right| t_{\mathrm{p}} ,\sigma _{\mathrm{p}} ,{\bar{\sigma }}} \right) \), is calculated using Eqs. (55) and (78), in Eq. (80), yielding:
and written this way for later convenience. This expression is used in the next section to assess the effects on COPV reliability due to a proof test.
5 Discussion and examples
In this section we present results for several cases of interest (involving wide ranging sets of parameter values) where we compare stress-rupture lifetime predictions from our new SFB model versus the CPL-W model described in detail above. Results are generated and compared under conditions involving an initial proof test versus having no true proof test, i.e., the proof stress level over the proof time is less than or equal to the stress level in later service. Specifically, we compare probabilities of failure over time under fixed load levels where high reliability is desired.
5.1 Determining model parameters
In characterizing experiment results from stress-rupture testing of composites, such as epoxy-impregnated yarns or laboratory scale COPVs, there are four independent parameters most commonly involved. These are \({\hat{\sigma }}_V \) and \({\hat{\alpha }}\), the Weibull scale and shape parameters, respectively, for strength for a given volume, V, the power-law exponent, \({\hat{\rho }}\), for sensitivity of lifetime to stress level, \({\bar{\sigma }}\), and \(t_c \), a characteristic lifetime parameter also involved in controlling the Weibull scale parameter for lifetime at a given stress ratio, \({{\bar{\sigma }}}/{{\hat{\sigma }}_V }\). An additional parameter is the Weibull shape parameter for lifetime, \({\hat{\beta }}\), which in this stochastic fiber breakage (SFB) model follows \({\hat{\beta }}={{\hat{\alpha }}}/{{\hat{\rho }}}\), and so is a dependent parameter. Using the maximum likelihood estimation method, as is described in Engelbrecht-Wiggans and Phoenix (2018) and Engelbrecht-Wiggans and Phoenix (2017a, b), estimates of these parameters can be determined from a comprehensive data set containing both strength and lifetime observations, that have been replicated at several stress levels.
For the SFB model of this paper, the structure of the strength and lifetime distributions are parametrically similar in key respects to those of the model involving a classic power-law in a Weibull framework (CPL-W) (Coleman 1956, 1957, 1958a, b; Tobolsky and Eyring 1943; Coleman and Knox 1957; Glasstone et al. 1941), with the exception that, in the CPL-W model \(\beta =\alpha /{( {\rho +1} )}\), whereas in the SFB model, \({\hat{\beta }}={{\hat{\alpha }}}/{{\hat{\rho }}}\), as just mentioned. Also, the CPL-W model involves a constraint on the reference time parameter, \(t_{{\mathrm{ref}}} \), (analogous to \(t_c \) in the current model), such that \(t_{{\mathrm{ref}}} \) can be written in terms of the other model parameters, as well as the strength loading rate, R, used in determining the Weibull strength parameters, and on which the scale parameter depends. This constraint gives the CPL-W model three independent parameters, rather than four.
Since the value of \({\hat{\rho }}\) is typically quite large, there is little numerical difference between \({\hat{\rho }}\) and \({\hat{\rho }}+1\), and thus, the CPL-W model and the SFB model are very similar for similar values of \(t_c \) and \(t_{{\mathrm{ref}}} \). Given a set of CPL-W model parameters \(\left\{ {\sigma _{{\mathrm{ref}}} ,\alpha ,\rho } \right\} \), for a given material volume, V, and loading rate, R, used in strength testing, the corresponding strength and lifetime parameters for the SFB model are as follows:
However, when considering a proof test in the SFB model, where \(\sigma _{\mathrm{p}} \) is initially applied over \(0<t<t_{\mathrm{p}} \), additional parameters are required to describe the subsequent failure probability at times, \(t\ge t_{\mathrm{p}} \), when the subsequent long term applied stress is less than the proof stress, \({\bar{\sigma }}<\sigma _{\mathrm{p}} \), as described by Eqs. (78) and (79). Beyond the phenomenologically motivated parameters of the CPL-W model, the additional parameters are based on fiber and matrix properties and the micromechanics of stress redistribution around fiber breaks, these being \(\sigma _{\delta _e } \), \(\zeta \), \(\theta \), \({\hat{k}}\), and \(k_{\mathrm{p}} \).
Typically, \(\zeta \), the Weibull shape parameter for fiber strength, is known based on fiber strength tests. For single carbon fibers for instance, \(\zeta \) is typically around 5. The parameter \(k_{\mathrm{p}} \) is determined from Eq. (53) for the 2D planar case and Eq. (54) for the 3D hexagonal packing case. The parameter \(\sigma _{\delta _e } \), the Weibull scale parameter for fiber strength corresponding to the characteristic elastic length, \(\delta _e \), for immediate fiber-to-fiber load transfer, can be calculated indirectly given \({\hat{k}}\), \(\zeta \), \({\hat{\sigma }}_V \) and the volume V, using Eq. (32). Also, from Eq. (47), we have \({\hat{\rho }}={2\zeta {\hat{k}}}/{( {\theta ( {{\hat{k}}-1} )} )}\), and thus, if \({\hat{\rho }}\) is known, we can calculate \(\theta \) in terms of \({\hat{k}}\), knowing that \({\hat{\alpha }}={\hat{k}}\zeta \). This results in:
Note that some of these parameters, such as \(\theta \) and \(\delta _e \), could be determined, in principle, from special micromechanical tests involving thin specimens under tension that have fiber breaks driving matrix creep or time dependent debonding of the matrix from the fiber, all of which would have to be observable. However, most are difficult to determine and must be interpreted from strength and stress-rupture data for the system of interest.
Finally, an expression for \({\hat{k}}\) can be obtained solely in terms of \(\zeta \) and the volume, V. In the 2D planar case, we obtain such a result by combining Eqs. (26), (28), (32), (35) and (84), and carrying out a sequence of manipulations as follows:
This last expression is an implicit relationship for solving for \({\hat{k}}\) in the 2D planar case.
Likewise for the 3D hexagonal fiber packing case, combining Eqs. (27), (29), (32), (36) and (84), we obtain an implicit expression for \({\hat{k}}\) solely in terms of \(\zeta \) and the volume V:
In some circumstances Eqs. (85) and (86) may not uniquely identify one value of \({\hat{k}}\), however, we are typically interested in the smallest value of \({\hat{k}}\) that satisfies them, and in addition \({\hat{k}}\), \(\zeta \), and \({\hat{\alpha }}\) should satisfy Eq. (33), namely \({\hat{\alpha }}={\hat{k}}\zeta \).
Thus, we now have a method for calculating all five additional parameters, namely \({\hat{k}}\), \(\theta \), \(\zeta \), \(\sigma _{\delta _e } \), and \(k_{\mathrm{p}} \), assuming we know the volume V, the three CPL-W parameters, \(\sigma _{{\mathrm{ref}}} \), \(\alpha \), and \(\rho \), based on MLE estimation of a strength and lifetime data set where strength was obtained under loading rate, R.
First, we use the known value of \(\zeta \) to determine \({\hat{k}}\) dependent on V using Eq. (85) in the planar case, and Eq. (86) for the hexagonal case. Then \(\theta \) may be determined using \(\alpha \), \(\rho \), and Eq. (84). The parameter \(\sigma _{\delta _e } \) can be calculated next, given \({\hat{k}}\), \(\zeta \), \({\hat{\sigma }}_V \), V, and Eq. (32). Finally the parameter \(k_{\mathrm{p}} \) is given by Eq. (53) for the planar case and Eq. (54) for the hexagonal case. Of course, the set of parameter values should be consistent with any obtained from experimental micromechanical observations.
5.2 Conditional lifetime distributions following a proof test for both the SFB and CPL-W models
For the CPL-W model the conditional reliability for times \(t>t_{\mathrm{p}} \) is given by:
Thus, for the CPL-W model the failure probability conditional on surviving a proof test is unity minus the reliability in Eq. (87):
Likewise, for the SFB model the conditional failure probability following a proof test is obtained from Eq. (82) as:
These are the key results of the paper for which comparisons are to be made.
Plots of the SFB model conditional lifetime distribution following a proof test, Eq. (89), versus that for the CPL-W model, Eq. (88), and the unconditional lifetime distribution (no proof test), Eq. (45), for a planar fiber array and the key parameter values, \(\alpha =36,\rho =360~\hbox {and} \;\beta =0.1\)
Plots of the SFB model conditional lifetime distribution following a proof test, Eq. (89), versus that for the CPL-W model, Eq. (88), and the unconditional lifetime distribution (no proof test), Eq. (45), for a planar fiber array and the key parameter values, \(\alpha =36, \rho =144~\hbox {and} \;\beta =0.25\)
Plots of the SFB model conditional lifetime distribution following a proof test, Eq. (89), versus that for the CPL-W model, Eq. (88), and the unconditional lifetime distribution (no proof test), Eq. (45), for a planar fiber array and the key parameter values \(\alpha =36, \rho =72~\hbox {and} \;\beta =0.5\)
Plots of the SFB model conditional lifetime distribution following a proof test, Eq. (89), versus that for the CPL-W model, Eq. (88), and the unconditional lifetime distribution (no proof test), Eq. (45), for a planar fiber array and the key parameter values \(\alpha =36, \rho =48\) and \(\beta =0.75\)
Plots of the SFB model conditional lifetime distribution following a proof test, Eq. (89), versus that for the CPL-W model, Eq. (88), and the unconditional lifetime distribution (no proof test), Eq. (45), for a planar fiber array and with the key parameter values \(\alpha =36, \rho =36\) and \(\beta =1.0\)
Plots of the SFB model conditional lifetime distribution following a proof test, Eq. (89), versus that for the CPL-W model, Eq. (88), and the unconditional lifetime distribution (no proof test), Eq. (45), for a planar fiber array and with the key parameter values \(\alpha =36, \rho =24\) and \(\beta =1.5\)
5.3 Graphical comparisons of lifetime distributions in the SFB and CPL-W models with and without a proof test
For the SFB model, Figs. 6, 7, 8, 9, 10 and 11 show plots of the conditional distribution function for lifetime (conditional probability of failure vs. time t) following survival of a proof test, Eq. (89), as well as plots for the corresponding lifetime distribution function in the CPL-W model, Eq. (88). Also shown is the unconditional distribution function for lifetime (i.e., without having applied a proof test), which is virtually the same for both the SFB model and the CPL-W model, as given by Eq. (45). The results are all for a composite where fibers form a planar array.
The cases shown in Figs. 6, 7, 8, 9, 10 and 11, begin with Fig. 6 corresponding to a very low Weibull shape parameter for lifetime, \(\beta =0.1\), and correspondingly very high power-law exponent value, \(\rho =360\) (governing the dependence of lifetime on stress level), to the opposite in Fig. 11, where \(\beta =1.5\) is a relatively high value and \(\rho =24\) is relatively low. Throughout the figures, the Weibull shape parameter for strength is kept at \(\alpha =36\), the Weibull scale parameter for strength is normalized to unity, i.e., \(\sigma _V =1\), and the overall composite volume is taken as \(V=10{,}000\) elements. The characteristic time in all cases is taken as \(t_c =0.01\), and the proof hold time \(t_{\mathrm{p}} =1\), is 100 times larger. Other parameter values specific to the SFB model are kept fixed throughout, namely the respective Weibull shape and scale parameters for fiber strength, \(\zeta =4\) and \(\sigma _\delta =2.83\), where the latter is 2.83 times the overall composite value, \(\sigma _V \), and the critical cluster size is \({\hat{k}}=9\). Otherwise, the creep exponent, \(\theta \), varies among Figs. 6, 7, 8, 9, 10 and 11 in keeping with the inverse relationship of \(\theta \) and \(\rho \), as seen in Eq. (84). The various panels in each figure vary in terms of stress ratio, \({{\bar{\sigma }}}/{\sigma _V }\), and proof ratio, \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}\), which also affects, \(k_{\mathrm{p}} \), a specific cluster size associated with the proof stress ratio, \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}\), as described in Eqs. (52)–(54).
A general observation in Figs. 6, 7, 8, 9, 10 and 11, is that the SFB model has a conditional failure probability greater than for the CPL-W model. When the proof ratio is unity, i.e. \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}=1\), then initially both the CPL-W model and the SFB model have a conditional failure probability that is less than the unconditional failure probability over time in service. That is, there is a short-term benefit from the ‘proof test’, as we would expect. In essence, placing freshly manufactured structures (e.g., COPVs) in a proof test device, where they are loaded to the service load, \({\bar{\sigma }}\), over a proof hold time \(0\le t<t_{\mathrm{p}} \), still amounts to a ‘weeding out’ process before placing such structures in service, however small their probability of failure in the proof test itself. However, for the SFB model, the short-term benefit is less than for the CPL-W model, since the SFB model lifetime distribution with a proof test reverts to the lifetime distribution without a proof test earlier in time than in the CPL-W model.
When the proof ratio is greater than unity, i.e., \({\sigma _{\mathrm{p}} }/{{\bar{\sigma }}}>1\), then the conditional failure probability over time from the SFB model is higher than the corresponding unconditional failure probability, (i.e. without a proof test). Furthermore, the difference between the SFB conditional and unconditional failure probabilities is much more pronounced for small \(\beta \) and large \(\rho \) combinations, and can span several orders of magnitude.
For instance, Fig. 6, where \(\beta =0.1\) and \(\rho =360\), shows the largest such difference, and Fig. 7 where \(\beta =0.25\) and \(\rho =144\), is similar. However, Fig. 11 for \(\beta =1.5\) and \(\rho =24\) shows only a small difference between the conditional and unconditional failure probabilities. Very small values of \(\beta \), as in Figs. 6, 7 and 8, typically correspond to carbon fiber based composites, whereas values of \(\beta \) satisfying \(\beta \ge 1\) as in Figs. 10 and 11, corresponds to polymeric fiber composites, like Kevlar, Vectran and PBO with other parameters adjusted accordingly to give similar strength distributions, as are often seen in practice.
The CPL-W model also exhibits the largest difference between the conditional lifetime failure probability and the unconditional lifetime failure probability for smaller \(\beta \) and higher \(\rho \) combinations, especially in Figs. 6, 7 and 8, but in contrast to the SFB model, the CPL-W model predicts much lower values for conditional failure probability for lifetime (higher reliabilities), not the higher values predicted by the SFB model (lower reliabilities), when \(\beta <1\). This difference is a key aspect of the results in this paper, namely that proof testing in the SFB model can result in composite damage in terms of reduced reliability later in time, where the classic CPL-W model predicts just the opposite. The difference is especially pronounced in Figs. 6 and 7, where a stress ratio of 0.6 followed by a high proof ratio is detrimental to later reliability.
In fact, the conditional failure probabilities for lifetime in the CPL-W model in such circumstances are so small, that they cannot be plotted on the chosen scale for the higher proof ratios in Figs. 6 and 7, where \(\beta \ll 1\), since the probability values are orders of magnitude less than the unconditional lifetime failure probabilities. However, when \(\beta >1\) (corresponding to an increasing composite ‘hazard’ or failure rate in time in classical reliability theory, that begins at zero at \(t=0\)), and thus, \(\rho \) is relatively small (as is the case for Kevlar/epoxy composites), the reliability behavior is reversed. That is, the CPL-W model predicts a slight increase in the conditional failure probability versus time, relative to the unconditional failure probability (no proof test), as illustrated in Fig. 11. This occurs because the lower tail of the failure rate becomes truncated such that the failure rate now begins at a positive value.
However, when \(\beta \ll 1\), as occurs in carbon fiber-epoxy composite structures such as COPVs, decreased failure probability (increased reliability) predictions of the CPL-W model after a proof test are very unrealistic when applied to a fiber/matrix composite with complex micromechanical failure processes, which the CPL-W does reflect. This is true also of models adapted from single fiber, stress rupture based on crack growth, as described in Christensen (1984), Reeder (2012) and Engelbrecht-Wiggans and Phoenix (2018).
Carbon fiber composite have become the primary material for COPVs in aerospace and commercial (e.g., automotive) applications. The plotted results in this section confirm what some practitioners in the field suspect, namely that an excessive proof ratio applied to a carbon/epoxy COPV can result in fiber damage that significantly reduces longer-term, stress-rupture reliability. This may seem obvious, in light of typically low Weibull shape parameter values for single carbon fiber strength, coupled to their resistance to stress-rupture, however, mapping the failure process to show reduced reliability thereafter is clearly a complex calculation.
Note also that the calculations were ‘sample calculations’ performed for \(V=10{,}000\) whereas a real COPV is likely to have of the order of \(V=10^{10}\) fiber elements, so a larger number by six orders of magnitude. If one thinks of the 10,000 elements as acting like one super-element in a weakest- link system of \(10^{6}\) such elements, then if the absolute stresses remained the same, all the failure probabilities in Figs. 6, 7, 8, 9, 10 and 11 would necessarily be increased by a factor of \(10^{6}\), which would render them unacceptable in an actual application. This does not, however, reflect the true situation, since, the strength, \(\sigma _V \), would be reduced by the factor \(10^{{-6}/\alpha }=10^{-1/6}=0.681\), and thus, all stress levels, \(\sigma _{\mathrm{p}} \) and \({\bar{\sigma }}\) must also be reduced.
If the model were applied directly to the larger volume, \(V=10^{10}\), then other changes would result such as a larger critical cluster size, \({\hat{k}}\), and associated increases in \(\alpha \) and \(\beta \), as well as a milder reduction in \(\sigma _V \) relative to the case \(V=10^{4}\). Reliabilities would likely improve for the adjusted stress and proof ratios, but the drawbacks of an excessive proof ratio would remain.
While the choice of \(\zeta =4\) is useful for demonstrating the richness in behavior of the model, it is borderline in terms of the accuracy of the sequential fiber failure approach we have used in calculating probabilities of failure. That is, the behavior of the approximations in connection with Figs. 4 and 5 (where \(\zeta =5\)) may begin to break down for smaller \(\zeta \). That said, Mahesh et al. (2002), and to a lesser extent Mahesh and Phoenix (2004a), show that while the failure configurations begin to deviate from the idealization in Fig. 3 the resulting calculated probabilities themselves match those from Monte Carlo simulations surprising well, even down to \(\zeta =2\). Although beyond the scope of this paper, we mention there are newer models for cluster growth, valid down to \(\zeta =1\), and which could be adapted to the current setting. See for instance the work of Gupta et al. (2017).
Finally, when considering parametric cases studied in Mahesh and Phoenix (2004a) and that reasonably match up with the model and parameters here, it was found that predictions from their theoretical model were in strong agreement with results from their Monte Carlo simulations. Their theoretical model had assumptions similar to ours on both collapsing failure time sequences in fiber load-sharing, and on assuming transverse alignment of fiber breaks rather than staggering. Their Monte Carlo simulations did not suffer from these simplifying assumptions. Thus we have good reason to believe that the model we have built that includes the effects of proof testing will be accurate and have realistic behavior. While not applicable to the circumstances of proof testing, their model allows consideration of time dependent failure of fibers under constant stress through a power-law/Weibull breakdown mechanism that is at the heart of the CPL-W model. This is an important avenue to pursue in the future, i.e., combining both mechanisms for fiber failure over time.
6 Conclusions
In this paper we have developed the SFB model, which involves the breakage of individual fibers with increasing stress, load redistribution from failed to surviving fibers, and most important, matrix creep in shear, which progressively lengthens overload regions along fiber, thus resulting increasing numbers of fibers even when the overall applied stress is held fixed. The model exhibits richness in mathematical form as compared to the CPL-W model, and thus the SFB model can predict different outcomes in the case of a proof test. This is, perhaps unsurprising, as the SFB model has a very different form than the CPL-W model, or any model of the 1979 functional form. At the same time, under linearly increasing loads as in a strength test, or under constant load in the absence of a proof test, the SFB model and CPL-W model yield essentially the same strength and lifetime distributions.
All current phenomenological models, including those motivated by time-dependent crack growth in fibers, predict that the conditional reliability following such a proof test in carbon fiber/epoxy COPVs is higher than that for a simple sustained load even when conditioned on surviving the initial step load for some small time. The SFB model indicates that many practically important situations of proof testing, following certain protocols frozen into standards or considered as ‘best practices’, may in fact be detrimental.
There are many reasons not addressed in this paper for performing a proof test all connected in some way or another to screening out anomalous COPVs, such as those with seriously flawed liners or using fiber that came, say, from an inferior lot. The implication of the results in this paper is that there are inevitably tradeoffs in proof testing, and proof levels much be chosen carefully with that in mind.
References
ANSI, AIAA S-081B-2018 (2018) American National Standard, space systems—composite overwrapped pressure vessels. American Institute of Aeronautics and Astronautics, Reston
Beyerlein IJ, Landis CM (1999) Shear-lag model for failure simulations of unidirectional fiber composites including matrix stiffness. Mech Mater 31:331–350
Beyerlein IJ, Phoenix SL (1996a) Statistics for the strength and size effects of microcomposites with four carbon fibers in epoxy resin. Compos Sci Technol 56:75–92
Beyerlein IJ, Phoenix SL (1996b) Stress concentrations around multiple fiber breaks in an elastic matrix with local yielding or debonding using quadratic influence superposition. J Mech Phys Solids 44:1997–2039
Beyerlein IJ, Phoenix SL, Sastry AM (1996) Comparison of shear-lag theory and continuum fracture mechanics for modeling fiber and matrix stresses in an elastic cracked composite lamina. Int J Solids Struct 33:2543–2574
Beyerlein IJ, Amer M, Schadler LS, Phoenix SL (1998a) New methodology for determining in situ fiber, matrix and interface stresses in damaged multifiber composites. Sci Eng Compos Mater 7:151–204
Beyerlein IJ, Phoenix SL, Raj R (1998b) Time evolution of stress redistribution around multiple fiber breaks in a composite with viscous and viscoelastic matrices. Int J Solids Struct 35:3177–3211
Brinson HF, Brinson LC (2015) Polymer engineering science and viscoelasticity: an introduction. Springer, Boston
Christensen RM (1984) Interactive mechanical and chemical degradation in organic materials. Int J Solids Struct 20:791–804
Coleman BD (1956) Time dependence of mechanical breakdown phenomena. J Appl Phys 27:862–866
Coleman BD (1957) A stochastic process model for mechanical breakdown phenomena. Trans Soc Rheol 1:153–168
Coleman BD (1958a) Time dependence of mechanical breakdown in bundles of fibers. III. The power law break-down rule. Trans Soc Rheol 2:195–218
Coleman BD (1958b) Statistics and time dependence of mechanical breakdown in fibers. J Appl Phys 29:968–983
Coleman BD, Knox AG (1957) The interpretation of creep failure in textile fibers as a rate process. Text Res J 27:393–399
Engelbrecht-Wiggans A, Phoenix SL (2017a) Analysis of stress rupture data on fiber composites: part 1—a unified maximum likelihood method. J Space Saf Eng 4:9–14
Engelbrecht-Wiggans A, Phoenix SL (2017b) Analysis of stress rupture data on fiber composites: part 2—determining uncertainty and removing bias in estimates. J Space Saf Eng 4:83–94
Engelbrecht-Wiggans A, Phoenix SL (2018) Comparison of probabilistic models for stress rupture failure in continuous unidirectional fiber composite structures. J Mater Sci 53:7431–7452
Glasstone S, Laidler KJ, Erying H (1941) The theory of rate processes. McGraw-Hill, New York
Goree JG, Gross RS (1980) Stresses in a three-dimensional unidirectional composite containing broken fibers. Eng Fract Mech 13:395–405
Gupta A, Mahesh S, Keralavarma SM (2017) Strength distribution of large unidirectional composite patches with realistic load sharing. Phys Rev E 96:043002
Hedgepeth JM (1961) Stress concentrations in filamentary structures. NASA TN D-882
Hedgepeth JM, Van Dyke P (1967) Local stress concentration in imperfect filamentary composite materials. J Compos Mater 1:294–309
Hikami F, Chou T-W (1990) Explicit crack problem solutions of unidirectional composites—elastic stress concentrations. AIAA J 28:499–505
Ibnabdeljalil M, Curtin WA (1997) Strength and reliability of fiber-reinforced composites: localized load-sharing and associated size effects. Int J Solids Struct 34:2649–2668
Iyengar N, Curtin WA (1997) Time-dependent failure in fiber-reinforced composites by matrix and interface shear creep. Acta Mater 45:3419–3429
Kelly A, McCartney LN (1981) Failure by stress corrosion of bundles of fibres. Proc R Soc Lond A 374:475–489
Kuo CC, Phoenix SL (1987) Recursions and limit theorems for the strength and lifetime distributions of a fibrous composite. J Appl Probab 24:137–159
Lagoudas DC, Hui C-Y, Phoenix SL (1989) Time evolution of overstress profiles near broken fibers in a composite with a viscoelastic matrix. Int J Solids Struct 25:45–66
Mahesh S, Phoenix SL (2004a) Lifetime distributions for unidirectional fibrous composites under creep-rupture loading. Int J Fract 127:303–360
Mahesh S, Phoenix SL (2004b) Absence of a tough-brittle transition in the statistical fracture of unidirectional composite tapes under local load sharing. Phys Rev E 69:026102
Mahesh S, Beyerlein IJ, Phoenix SL (1999) Size and heterogeneity effects on the strength of fibrous composites. Physica D 133:371–389
Mahesh S, Phoenix SL, Beyerlein IJ (2002) Strength distributions and size effects for 2D and 3D composites with Weibull fibers in an elastic matrix. Int J Fract 115:41–85
Mason DD, Hui C-Y, Phoenix SL (1992) Stress profiles around a fiber break in a composite with a nonlinear, power-law creeping matrix. Int J Solids Struct 26:2829–2854
McCarthy ED, Kim JH, Heckert NA, Leigh SD, Gilman JW, Holmes GA (2015) The fiber break evolution process in a 2-D epoxy/glass multi-fiber array. Compos Sci Technol 121:73–81
Nairn JA (1988a) Fracture mechanics of unidirectional composites using the shear-lag model I: theory. J Compos Mater 22:561–588
Nairn JA (1988b) Fracture mechanics of unidirectional composites using the shear-lag model II: experiment. J Compos Mater 22:589–600
Nairn JA (1992) A variational mechanics analysis of the stresses around breaks in embedded fibers. Mech Mater 13:131–154
Nairn JA (1997) On the use of shear-lag methods for analysis of stress transfer in unidirectional composites. Mech Mater 26:63–80
Nairn JA, Wagner HD (1996) A revised shear-lag analysis of an energy model for fiber-matrix debonding. Adv Compos Lett 5:131–135
Phoenix SL (1979) The asymptotic distribution for the time to failure of a fiber bundle. Adv Appl Probab 11:153–187
Phoenix SL, Beyerlein IJ (2000) Statistical strength theory for fibrous composite materials, Chapter 19. In: Chou TW, Zweben C (eds) Comprehensive composite materials, vol 1. Elsevier Ltd., New York
Phoenix SL, Schwartz P, Robinson HH III (1988) Statistics for the strength and lifetime in creep-rupture of model carbon/epoxy composites. Compos Sci Technol 32:81–120
Reeder J (2012) Composite stress rupture: a new reliability model based on strength decay. Report NASA/TM-2012-217566, L-20122, NF1676L-14234
Rossettos JN, Olia M (1993) Stress concentration and post matrix yield at fiber breaks in hybrid composites. In: Chou SC, Bartlett FD, Wright TW, Iyer K (eds) Proceedings of the 13th army symposium on solid mechanics, Plymouth, MA, August 17–19, 1993, pp 201–212. http://www.dtic.mil/dtic/tr/fulltext/u2/a327004.pdf. Accessed 6 Apr 2019
Rossettos JN, Shishesaz M (1987) Stress concentration in fiber composite sheets including matrix extension. ASME J Appl Mech 54:722–724
Smith RL (1980) A probability model for fibrous composites with local load sharing. Proc R Soc Lond Ser A 372:539–553
Smith RL, Phoenix SL, Greenfield MR, Henstenburg RB, Pitt RE (1983) Lower-tail approximations for the probability of failure of three-dimensional fibrous composites with hexagonal geometry. Proc R Soc Lond A 388:353–391
Tobolsky A, Eyring H (1943) Mechanical properties of polymeric materials. J Chem Phys 11:125–134
Zhou CH, Schadler LS, Beyerlein IJ (2002) Time-dependent micromechanical behavior in graphite/epoxy composites under constant load: a combined experimental and theoretical study. Acta Mater 50:365–377
Zhou CH, Beyerlein IJ, Schadler LS (2003) Time-dependent micromechanical behavior in graphite/epoxy composites under constant load at elevated temperatures. J Mater Sci 8:877–884
Zhou CH, Schadler LS, Beyerlein IJ (2004) Stress concentrations in graphite/epoxy model composites during creep at room temperature and elevated temperatures. J Compos Mater 38:417–433
Acknowledgements
Funding for this work was provided under National Institute of Standards and Technology (NIST) Agreement ID 70NANB14H323.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Engelbrecht-Wiggans, A., Phoenix, S.L. A stochastic model based on fiber breakage and matrix creep for the stress-rupture failure of unidirectional continuous fiber composites. Int J Fract 217, 1–34 (2019). https://doi.org/10.1007/s10704-019-00359-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-019-00359-9