Abstract
When synthesizing a system from a given specification, there is room for automatically adding various requirements, hence improving the resulting system. One such requirement covered extensively in past literature is that of robustness. In particular, the system can fail to read the inputs correctly from the environment, and the environment can fail to satisfy our assumptions about its behavior. Nevertheless, we want the system to still satisfy the specification even under these failures, in some limited way. It has to be limited because it is typically too strong of a requirement to realize the property regardless of the inputs and the environment’s assumptions. In this work, we propose a simple and flexible framework for synthesizing robust systems, where the user defines the required robustness via a temporal robustness specification. For example, the user may specify that the environment is eventually reliable, or input misreadings cannot occur more than \(k\) consecutive steps and synthesize a system under this assumption. Furthermore, our framework enables us to specify a temporal recovery specification, which describes how the designer expects the system to recover after a failure of the environment assumptions. We show examples of robust systems that we synthesized with this method using our synthesis tool Party.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The problem of reactive synthesis is to generate a system M such that \(M\models \mathrm {\Phi }\), where \(\mathrm {\Phi }\) is often defined as
Here \(\varphi _s(I,O)\) is a temporal specification over the inputs I and outputs O of M, and \(\varphi _e(I,O)\) a temporal assumption about the environment’s behavior. When solving the synthesis problem is computationally possible, it may save labor compared to the more traditional route of manually constructing M and then verifying that it satisfies \(\mathrm {\Phi }\) via model-checking.
In practice, it is difficult to fully specify a system, i.e., specify the exact behavior in reaction to any input sequence from the environment. As a result, there can be many such systems M that satisfy \(\varphi _s\), and hence it is desirable to define default criteria for the quality of the synthesized system, e.g., [1, 10, 15], which can guide us in the synthesis process. In this sense, it is like an optimization problem without an explicit objective function. In [10], for example, the implicit objective is to minimize the synthesized system’s circuit size. In [7], it is to synthesize a system that satisfies the input property in a non-vacuous way. Another implicit objective directly related to the current article is robustness. This term was used with multiple meanings in the synthesis literature (e. g., [2, 3, 5, 9, 26, 27]), system testing [23], and software verification literature [29]. Informally, robustness measures the degree to which a system can function correctly in the presence of erroneous input or stressful environmental conditions [14]. Indeed it is common to expect M to operate under an environment whose behavior is not fully specified, cannot be modeled in a precise way (e. g., if it is a physical environment), or cannot be fully trusted. Hence when possible, \(M\) should satisfy \(\varphi _s\) even when \(\varphi _e\) does not hold,Footnote 1 or when some inputs are misread by the system or misreported by the environment. These additional requirements may depend on the type of system and the expected environment in which it operates and, accordingly, on the selected definition of robustness.
We are aware of four prior works that considered robustness as an implicit objective for synthesis. In [3], the main idea is to build a special game graph that ensures that a winning strategy satisfies the liveness guarantees, even if \(\varphi _e\) is violated infinitely often. In [9], the main idea is a new synthesis algorithm based on a generalized Rabin automaton ensuring that even if the environment violates \(\varphi _e\) a finite number of times, eventually the system returns to satisfy its guarantees \(\varphi _s\) (here \(\varphi _e\) and \(\varphi _s\) are restricted to be invariants; namely they are of the form \({\textbf {G}}\psi\) where \(\psi\) is propositional). In [17], a synthesis algorithm is presented for the case that not all inputs are available (in their terminology: there is ‘incomplete information’). Although the term ‘robustness’ is not mentioned there, implicitly, the goal is to make the synthesized system satisfy \(\varphi _s\) even when some of the inputs are not available. Finally, a recent article [2] proposed a new temporal logic called rLTL (for robust LTL), in which the robustness level is measured by the levels of violations of the temporal operators, forming a partial order of robustness. Specifically, the paper suggests evaluating LTL properties in systems over a 5-valued logic, according to the property’s degree of violation, leading to a finer-grained model-checking procedure that outputs the robustness degree of a given system w.r.t. an rLTL specification. This approach results in three-valued GR(1) formulae for synthesis, falling into one of the robustness categories we introduce in Sect. 3. Note that all four prior works suggested a new synthesis algorithm tailored to a particular robustness definition.
This leads us to this article’s main contribution: a unified method of reducing the problem of robust synthesis, for many definitions of robustness, to the problem of ‘normal’ synthesis. Hence, there is no need for a specialized algorithm to cope with this problem with our method. The reduction is simple and amounts to synthesis from a conjunction of \(\mathrm {\Phi }\) and a new LTL formula that we denote by \(\mathrm {\Theta }\). This formula combines \(\varphi _e, \varphi _s\) and a user-specified robustness specification \(\upchi\) in LTL. The conjunction with \(\mathrm {\Phi }\) guarantees that the synthesis is of a formula implied by \(\mathrm {\Phi }\) itself.
We further offer another level of flexibility in the framework by allowing the user to write a recovery specification in LTL, defining how the system recovers from failures. Our method accommodates any off-the-shelf synthesizer that supports synthesis with incomplete information [17], by merely modifying the specification. We implemented an even easier route in Party [16] (via bounded synthesis) where in addition to \(\varphi _e,\varphi _s\), we only need to add the robustness and recovery specifications.
This article extends an earlier proceedings article [8] with several examples, clarifications, and extended explanations. It also uses quantified propositional temporal logic (QPTL) as the underlying formalism.
2 Preliminaries
Notation Let A, B be two finite sets of signals over some alphabet. By \({\mathcal{S}} ({A})\) we denote \((2^A)^\omega\), the set of all infinite sequences (also called ‘traces’) over assignments to A. For a sequence \(\pi = \pi _0, \pi _1, \dots\), we will write \(\pi ^{k\dots } = \pi _k, \pi _{k+1}, \dots\) for the suffix starting at position k. Given two sequences \(\pi \in {\mathcal{S}} ({A})\), and \(\rho \in {\mathcal{S}} ({B})\), we define their composition as \((\pi _1 \cup \rho _1, \pi _2 \cup \rho _2, \dots ) \in {\mathcal{S}} ({A \cup B})\) and denote it by \((\pi \,\Vert \,\rho )\). For two sequences \(\pi\), \(\rho\) over A and a subset \(C \subseteq A\), we write \(\pi \simeq _{C} \rho\) if for all i, \(\pi _i \cap C = \rho _i \cap C\).
Mealy machines We model systems by Mealy machines [19]. Mealy machines are formally defined as tuples \(M = \langle Q, q_0, \Sigma , \Lambda , T, G \rangle\), where
-
Q is a finite set of states,
-
\(q_0\) is the initial state,
-
\(\Sigma\) is the input alphabet,
-
\(\Lambda\) is the output alphabet,
-
\(T: Q\times \Sigma \rightarrow Q\) is a transition function,
-
\(G: Q\times \Sigma \rightarrow \Lambda\) is an output function.
If \(\Sigma = 2^I\) and \(\Lambda = 2^O\), which will be our usual case, we will sometimes write M(I, O) to make the inputs and outputs explicit.
We will focus on the infinitary behavior of Mealy machines. An input sequence \(\pi \in \Sigma ^{\omega }\) induces a run \(\rho \in\) in M, defined as \(\rho _0 = q_0\) and \(\rho _{i+1} = T(\rho _i, \pi _i)\) for \(i\ge 0\). The corresponding output word \(\sigma \in \Lambda ^{\omega }\) is defined as \(\sigma _i = G(\rho _i,\pi _i)\) and is denoted by \(M(\pi )\).
Temporal logic We will use Linear Temporal Logic as a specification formalism [21]. We will also occasionally use Quantified Propositional Temporal Logic (QPTL) [25]. We will first define QPTL since it is an extension of LTL with temporal quantifiers.
Definition 1
Given a set \({\text {AP}}\) of atomic propositions and a set X of variables, any atomic proposition \(p \in {\text {AP}}\) and any variable \(x \in X\) are QPTL formulas. If \(\phi\) and \(\psi\) are QPTL formulas and x is a variable, then \(\lnot \phi\), \(\phi \wedge \phi\), \({{\textbf {X}}}\phi\), \(\phi \mathbin {\textbf{U}}\psi\), and \(\exists x. \phi\) are also QPTL formulas. An LTL formula is a QPTL formula that does not contain any occurrence of variables or quantifiers.
The semantics of QPTL are given over pairs of infinite traces \(\pi\) over \({\text {AP}}\) and \(\rho\) over X. We have that
As usual, other propositional connectives can be defined as abbreviations:
We say that a variable x is free in a QPTL formula if it does not occur in the scope of a quantifier. For clarity, we will sometimes denote \(\phi\) by \(\phi (X')\) where \(X'\) is the set of free variables in \(\phi\). If the formula \(\phi\) does not contain free variables, it is closed and the assignments to X do not matter. So, instead of \(\pi , \rho \models \phi\), we can just write \(\pi \models \phi\). Note that the atomic propositions are never bound by quantifiers and that LTL formulas are closed by definition.
For a Mealy machine M with input alphabet \(2^I\) and output alphabet \(2^O\) and a QPTL formula \(\phi\) with atomic propositions \(I \cup O\), we say that M satisfies \(\phi\) (denoted by \(M \models \phi\)) if for all \(\pi \in {\mathcal{S}} ({I})\), we have that \(\left( \pi ~\Vert ~M(\pi )\right) \models \phi .\)
As an example, take the QPTL formula
This formula is satisfied by any trace over \(\{p\}\) in which p is true in every even step. This property is omega-regular, but not expressible in LTL.
Synthesis The realizability problem is to decide whether there exists a system (a Mealy machine) that satisfies an LTL property; the synthesis problem is to find one such system. For this question to make sense, we partition our atomic propositions into inputs I and outputs O. Thus, given an LTL specification \(\phi (I,O)\), synthesis tries to find a Mealy machine M(I, O) that satisfies the property. We can also assume that some inputs are hidden from the system, asking for a system \(M(I',O)\) that satisfies \(\phi\), where \(I' \subset I\). This is the problem of synthesis with incomplete information. Both problems are 2EXPTIME complete [17, 22].
3 Definitions of robustness
We will distinguish between two classes of robustness definitions. The first is robustness against ‘corrupted’ inputs, which means that the system fails to read some of the environment’s signals or they are unavailable, as in [17]; The second is robustness against cases in which the environment does not satisfy the assumption \(\varphi _e\).
Let us now survey various definitions of robustness in these two classes. Those that are described below without a reference are novel to this work.
Definitions of robustness against corrupted inputs:
-
(R1)
A robust system satisfies \(\varphi _s\) even if some of the inputs can be misread (‘corrupted’) in a finite number of steps.
-
(R2)
k-robustness (inputs): A robust system satisfies \(\varphi _s\) even if it misreads some of the inputs up to k times consecutively.
-
(R3)
A system is robust if it satisfies \(\varphi _s\) even if some or all the inputs are occasionally corrupted.
Definitions of robustness against violations of the assumptions:
-
(R4)
A system is robust if despite a finite number of violations of the assumptions, it still satisfies the guarantees \(\varphi _s\).
-
(R5)
According to Ehlers [9] a robust system eventually stabilizes and returns to satisfy \(\varphi _s\) after a finite number of violations of \(\varphi _e\)’s safety assumptions. A similar definition also appeared in [26]: ‘bounded disturbances lead to bounded deviations from nominal behavior,’ and ‘the effect of a sporadic disturbance disappears in finitely many steps’.Footnote 2
-
(R6)
According to Bloem [3], a robust system satisfies its liveness guarantees, even if \(\varphi _e\) is violated infinitely often.
-
(R7)
k-robustness (\(\varphi _e\)): a robust system satisfies \(\varphi _s\) even if the environment violates \(\varphi _e\) up to k consecutive times.
There are also definitions of metric robustness in the literature [11, 13, 24], but since LTL cannot accommodate such specifications, it is outside the scope of our suggested method. This is also true about [5]’s definition of robustness, which is based on a quantitative measure.
The above definitions of robustness can be further generalized by adding a dimension of a recovery specification, which is an LTL formula that defines how the system recovers from failures, as follows. For example, (R5) with the dimension of recovery can specify that the system should recover within 5 steps after each failure of the environment to satisfy \(\varphi _e\). We denote the extensions of the above robustness definitions with recovery by replacing R with C, e.g., (R5) becomes (C5).
We note that the informal definitions in (R5) and (R7) generally cannot be applied to environment assumptions in LTL because such formulas are interpreted over infinite traces w.r.t. the initial state. For example, if \(\varphi _e = {\textbf {G}}{\textbf {F}}r\), then we can say whether a given path satisfies it or not, but there is no meaning to saying that it violates \(\varphi _e\) k times or even a finite number of times. The same problem exists if the guarantees are in general LTL: it is meaningless to say that they are violated a finite number of times.
We, therefore, interpret these informal definitions as relevant only for assumptions and guarantees of the form \({\textbf {G}}\psi\), where \(\psi\) is a propositional formula, and the failure count refers to the number of locations along the path that satisfy \(\lnot \psi\).
The following two sections present our suggested method for synthesizing robust systems against corrupted inputs and assumption violations.
4 Robustness against corrupted signals
This section describes how to synthesize systems that react appropriately when the input is not quite trustworthy. Initially, we will insist that the system behaves correctly regardless, and in Sect. 4.3 we will look at ways to relax this requirement.
4.1 Closeness of traces
For maximal flexibility in the types of robustness we consider, we use a “synchronization bit” that indicates when signals may be corrupted. Using such a synchronization bit, the user can specify a temporal formula \(\upchi\) when to trust a signal’s value. We call \(\upchi\) the robustness specification. It can be viewed as a temporal fault model for signals. We will later distinguish between the corruption of inputs and outputs, and correspondingly refer to two separate such bits: \(\varvec{sb_{in}}\) and \(\varvec{sb_{out}}\). However, since the definitions that follow are common to both cases, we will use a single symbol \(\varvec{sb}\). We will assume that the robustness specification refers to the whole set of signals (all inputs, or all outputs) at every given step, i.e., either all or none of them can be trusted. It is not hard to extend the technique to work with finer granularity, specifying that certain inputs are always correct whereas other signals can be corrupted.
We now define when two sequences over A and \(A'\), where \(A'\) is the set of primed signals from A, are close.
Definition 2
(\(\varvec{\upchi }\)-Close) For sequences \(\pi \in {\mathcal{S}} ({A})\), \(\pi ' \in {\mathcal{S}} ({A'})\), and an LTL formula \(\upchi (\varvec{sb})\) (i.e., \(\upchi\) over the single variable \(\varvec{sb}\)), we say that \(\pi\) and \(\pi '\) are \(\upchi\)-close (with witness \(\tau\)) (denoted by \(\pi \approx _{\upchi } \pi '\)) if there exists a \(\tau \in {\mathcal{S}}( {\{\varvec{sb}\}})\) such that \(\tau \models \upchi\) and for all i, if \(\tau _i = \{\varvec{sb}\}\) then \((\pi _i)' = \pi _i'\), where \((\pi _i)'\) stands for \(\pi _i\) with all variables in A replaced by their primed versions.
Less formally, \(\pi\) and \(\pi '\) are \({\upchi }\)-close if there exists a trace \(\tau\) over \(\varvec{sb}\) that satisfies \(\upchi\), such that \(\pi\) and \(\pi '\) are equal in time steps in which \(\varvec{sb}\) is true in \(\tau\). We will use the notion of \({\upchi }\)-closeness in the subsections that follow.
4.2 Input robustness
In this subsection, we will consider the case of corrupted inputs. Here, \(\varvec{sb_{in}}\) denotes the synchronization bit for the inputs. This signal can either be visible to the synthesized system or not, depending on whether the environment can produce such information.
For a set of input signals I and output signals O, let \(\mathrm {\Phi }\) be the specification that we want the system to satisfy robustly, that is, even if it receives inputs \(I'\) that are not identical to the original inputs I. In what follows, we denote a system over the original inputs I by M and a system over the possibly corrupted inputs \(I'\) by \(M'\).
Definition 3
(\(\varvec{\upchi _{in}}\)-Robust system) A system \(M'(I', O)\) is \(\upchi _{in}\)-robust for \(\mathrm {\Phi }\) if for any sequences \(\pi \in {\mathcal{S}}( {I})\) and \(\pi ' \in {\mathcal{S}} ({I'})\) such that \(\pi \approx _{\upchi _{in}} \pi '\), we have that \(\left( \pi ~\Vert ~M'(\pi ')\right) \models \mathrm {\Phi }\).
Intuitively, even if a \(\upchi _{in}\)-robust system \(M'\) is fed with a corrupted input sequence \(\pi '\), its output sequence \(\sigma\) still fulfills the specification when taken together with the original inputs \(\pi\). Note that robustness satisfaction is a stronger notion than satisfaction. In the extreme case, \(M'(I', O)\) is only \({\textbf {G}}\lnot \varvec{sb_{in}}\)-robust for \(\mathrm {\Phi }\) if \(\mathrm {\Phi }\) allows the outputs to be chosen independently of the inputs, which implies that \(M'\) satisfies \(\Phi\).
We define
which states that traces over I and \(I'\) are \(\upchi\)-close.
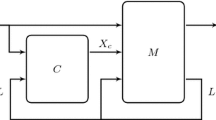
Let \(\mathrm {\Theta }\) denote \(\upchi _{in}'(\varvec{sb_{in}}) \rightarrow \mathrm {\Phi }\). The following theorem forms the basis of our reduction of synthesizing a \(\upchi _{in}\)-robust system to synthesis with incomplete information. The intuition is that the system does not see the original inputs I but rather the corrupted inputs \(I'\), which are constrained to be close to I by the specification \(\mathrm {\Theta }\). A graphical representation can be seen in Fig. 1.
Theorem 1
A system \(M'(I',O)\) is \(\upchi _{in}\)-robust for \(\mathrm {\Phi }\) iff
Proof
(\(\Rightarrow\)) Suppose \(M'(I',O)\) is \(\upchi _{in}\)-robust for \(\mathrm {\Phi }\). Let \(\pi \in {\mathcal{S}} ({I})\), \(\pi ' \in {\mathcal{S}} ({I'})\), and \(\tau \in {\mathcal{S}}( {\varvec{sb_{in}}})\) and suppose \((\pi \,\Vert \,\pi '\,\Vert \,\tau ) \models \upchi _{in}'(\varvec{sb_{in}})\). Then, \(\pi \approx _{\upchi _{in}}\!\pi '\) and since \(M'\) is \(\upchi _{in}\)-robust, we have \(\left( \pi \,\Vert \,M'(\pi ')\right) \models \mathrm {\Phi }\); hence, (3) holds.
(\(\Leftarrow\)) Suppose \(M'(I',O) \models \mathrm {\Theta }(I,I',\varvec{sb_{in}},O)\) and suppose that \(\pi \approx _{\upchi _{in}} \pi '\). Then there is a \(\tau \in {\mathcal{S}}( {\{\varvec{sb_{in}}\}})\) such that \((\pi \,\Vert \,\pi '\,\Vert \,\tau ) \models \upchi _{in}'(\varvec{sb_{in}})\) and hence by (3), \(M'(I',O) \models \mathrm {\Phi }\) and is thus \(\upchi _{in}\)-robust. \(\square\)
Note that if we make \(\varvec{sb_{in}}\) visible to the system, the theorem still holds as the proof does not depend on the fact that \(M'\) cannot observe \(\varvec{sb_{in}}\). This setting would be appropriate if the environment knows when the inputs are reliable or not. According to this theorem, if realizable, (3) gives us a \(\upchi _{in}\)-robust system.
We will now give an example of an input robust system.
Example 1
(\(\upchi _{in}\)-Robust arbiter) The example is inspired by the arbiter of Bloem et al. [4]. The system has a single request input r and a single grant output g. The requirement is that g stays low as long as r is low. When r goes high, g eventually goes high. g should then remain high until r goes down again, after which g eventually goes down. The assumption on the environment is that the request r will not be withdrawn until it is granted with g, and not raised again until g is low.
A system that fulfills \(\mathrm {\Phi }\) can be seen in Fig. 2a.
Now consider the following robustness specification in which the inputs can be erroneously flipped at most one out of every three-time steps.
Note that this is a primitive error-correcting code. By considering three consecutive steps, we can reconstruct whether r was high in all three or low in all three: If r is high (low) thrice consecutively, then \(r'\) is high (low) at least twice. Figure 3 demonstrates a trace that distinguishes the robust behavior of the system shown in Fig. 2b from the arbiter in Fig. 2a.
An example of a \(\upchi _{in}\)-robust arbiter for this robustness specification, synthesized from the spec by our tool PARTY, can be found in Fig. 2b. The robust arbiter does not react to changes in \(r'\) immediately. Rather, it waits until the input remains the same for two consecutive time steps before taking action. This means that the system may take two steps to react to a change in r: if r goes high, the robustness specification allows \(r'\) to remain low for one step, and when \(r'\) goes high, the system waits for one more step to react.
An arbiter alongside a \(\upchi _{in}\)-robust version for Example 1
A distinguishing trace for the systems demonstrated in Fig. 2
4.3 Recovery specifications
If the inputs to a system are not reliable, it may not be possible to produce outputs satisfying the specification. It thus makes sense to relax the requirements on the outputs a little, stating, in effect, that if the inputs are close to what they should be, then so are the outputs. For instance, if the specification is \({\textbf {G}}(r \leftrightarrow g)\) and the input can be misread once every ten ticks, then the output cannot always conform to the original input, but may also be incorrect once in every ten-time steps. A more interesting example showing that a specification may not always be \(\upchi _{in}\)-robust-realizable follows.
Example 2
(\(\upchi _{in}\)-Robust arbiter) To continue Example 1, suppose that we have the additional requirement that the grant signal g must be true if the request signal r was true in the previous step. Hence, if \(\mathrm {\Phi }(r,g)\) denotes the specification from Example 1, then the new specification is
This specification is realizable by a system that replies to a request in the step after the request is raised.
The arbiter in Fig. 2a satisfies the specification in (4)a, but it is not robust w.r.t. (5). The arbiter in Fig. 2b is robust w.r.t. (5), but is not robust w.r.t. the new specification \(\Phi '\) in (6).
In fact, given the robustness specification (5) from Example 1, there is no system that is \(\upchi _{in}(\varvec{sb_{in}})\)-robust for \(\mathrm {\Phi }'\). The reason is that two scenarios are not distinguishable to the system: (1) r remains low, but \(r'\) goes up incorrectly, and the system must leave g low, and (2) r goes up, \(r'\) follows one tick later, and the system must raise g immediately. The question is whether a system exists that almost fulfills \(\mathrm {\Phi }\).
We let the user define a recovery specification \(\upchi _{out}\) over \(\varvec{sb_{out}}\) describing when the outputs can deviate from what the specification prescribes. We define
in analogy to \(\upchi _{in}'(\varvec{sb_{in}})\) [see (2)]. In the following, we present two alternative definitions. We will start with a trace-based view of what correct behavior is and then present a system-based view.
4.3.1 \({\upchi _{in}}\)-\({\upchi _{out}}\) trace robustness
Definition 4
(\(\varvec{\upchi _{in}}\)-\(\varvec{\upchi _{out}}\) Trace robust system) A system \(M'(I', O')\) is \(\upchi _{in}\)-\(\upchi _{out}\) trace robust for \(\mathrm {\Phi }\) if for any sequences \(\pi \in {\mathcal{S}} ({I})\), \(\pi ' \in {\mathcal{S}} ({I'})\) such that \(\pi \approx _{\upchi _{in}}\pi '\), there is a \(\sigma \in {\mathcal{S}} ({O})\) such that \(\sigma \approx _{\upchi _{out}}M'(\pi ')\) and \(\left( \pi ~\Vert ~\sigma \right) \models \mathrm {\Phi }(I,O)\).
Intuitively, if the input is close to the intended input, then the output must also be close to a correct output. The definition is illustrated in Fig. 4a, where the \(\approx\) boxes denote the closeness of traces. Note that in general, the notion of \(\upchi _{in}\)-\(\upchi _{out}\) trace robustness is neither stronger nor weaker than the regular notion of satisfaction. For instance, in general, \(({\textbf {G}}\lnot \varvec{sb_{in}})\)-\(({\textbf {G}}\varvec{sb_{out}})\)-robustness for \(\Phi\) is harder to satisfy than the specification \(\Phi\) without any robustness requirements, as argued in the paragraph following Definition 3. On the other hand, any system is \(({\textbf {G}}\varvec{sb_{in}})\)-\(({\textbf {G}}\lnot \varvec{sb_{out}})\)-robust for \(\Phi\), as long as \(\Phi\) allows for some correct output for any input. (See also Example 4.)
Before explaining how synthesis can be performed for \(\upchi _{in}\)-\(\upchi _{out}\) trace robust systems, let us first give an example.
Example 3
[\(\upchi _{in}\)-Robust Arbiter] Continuing from Example 2, we can introduce the recovery specification
which states that the output can be disregarded for two ticks starting at a rising edge of r.
We can express \(\upchi _{in}\)-\(\upchi _{out}\) trace robustness as a formula in quantified temporal logic. We will use existential quantification to express that a correct output \(\sigma\) exists that is close to the actual output \(\sigma '\).
Theorem 2
A system \(M'(I', O')\) is \(\upchi _{in}\)-\(\upchi _{out}\) trace robust for \(\mathrm {\Phi }(I,O)\) iff M satisfies the QPTL formula
Proof
(\(\Rightarrow\)) Suppose \(M'(I', O')\) is \(\upchi _{in}\)-\(\upchi _{out}\) trace robust for \(\mathrm {\Phi }\). Let \(\pi \in {\mathcal{S}} ({I})\), \(\pi ' \in {\mathcal{S}} ({I'})\), and \(\tau _{in} \in {\mathcal{S}}( {\{\varvec{sb_{in}}\}})\). If \(\pi \not \approx _{\upchi _{in}}\pi '\) or \(\tau _{in}\) is not a witness for \(\pi \approx _{\upchi _{in}}\pi '\), then the left-hand side of the implication in Eq. (2) does not hold, and hence the formula holds for any \(\sigma \in {\mathcal{S}} ({O})\) and \(\tau _{out} \ {\mathcal{S}} ({\{\varvec{sb_{out}}\}})\). Otherwise (that is, \(\pi \approx _{\upchi _{in}}\pi '\) and \(\tau _{in}\) is a witness for the \(\upchi _{in}\)-closeness of \(\pi\) and \(\pi '\)), by Definitions 2 and 4 there exists \(\sigma \in {\mathcal{S}} ({O})\) and a \(\tau _{out} \in {\mathcal{S}}( {\{\varvec{sb_{out}}\}})\) such that \(\sigma \approx _{\upchi _{out}}M'(\pi ')\) with witness \(\tau _{out}\) and \(\left( \pi ~\Vert ~\sigma \right) \models \mathrm {\Phi }(I,O)\). Therefore,
Since the equation holds for all \(\pi\), \(\pi '\), and \(\tau _{in}\), we have
(\(\Leftarrow\)) Suppose that
Let \(\pi \in {\mathcal{S}} ({I})\), \(\pi ' \in {\mathcal{S}} ({I'})\), and \(\pi \approx _{\upchi _{in}}\pi '\) with witness \(\tau _{in} \in {\mathcal{S}} ({\{\varvec{sb_{in}}\}})\). Then \(\pi \Vert \pi ' \Vert \tau _{in} \models \upchi _{in}'(\varvec{sb_{in}}, I, I')\) and therefore there exist \(\sigma \in {\mathcal{S}} ({O})\) and \(\tau _{out} \in {\mathcal{S}} ({\{\varvec{sb_{out}}\}})\) such that \(\sigma , \tau _{out} \models \upchi _{out}'(\varvec{sb_{out}}, O, O') \wedge \mathrm {\Phi }(I,O)\). This implies that \(\sigma \approx _{\upchi _{out}}M'(\pi ')\) with witness \(\tau _{out}\) and that \(\pi \Vert \sigma \models \Phi (I,O)\), and therefore \(M'(I', O')\) is \(\upchi _{in}\)-\(\upchi _{out}\) trace robust for \(\mathrm {\Phi }\) by Definition 4. \(\square\)
Complexity The synthesis procedure for QPTL formulas with an \(\forall \exists\) quantifier prefix is doubly-exponential. We can first build a nondeterministic Büchi word automaton with exponentially many states from the formula \(\left[ \,\upchi _{in}'(\varvec{sb_{in}}) \rightarrow \upchi _{out}'(\varvec{sb_{out}}) \wedge \mathrm {\Phi }\,\right]\) [28]. From this automaton, we can existentially quantify O and \(\varvec{sb_{out}}\) without an additional blowup [25]. Viewing the word automaton as a tree automaton, we can then apply the construction for partial observability from [17], which yields an alternating tree automaton of the same size. This alternating tree automaton can be turned into a Mealy machine using the construction of Kupferman and Vardi [17, Theorem 4.6]. The last step incurs another exponential blowup. The double-exponential complexity of this algorithm is optimal because LTL synthesis (which is double-exponential) can be reduced to the synthesis of \(\upchi _{in}\)-\(\upchi _{out}\) trace-robust systems, with \(\upchi _{in}\) and \(\upchi _{out}\) defined as identities.
4.3.2 \(\upchi _{in}\)-\(\upchi _{out}\) tree robustness
We will now present a stronger definition to \(\upchi _{in}\)-\(\upchi _{out}\) robustness. Definition 4 requires that every actual output trace is close to a correct output trace. It does not require that there exists a correct system that produces these traces. We can take exactly that criterion as a definition and require that such a “witness” system exists.
Definition 5
(\(\varvec{\upchi _{in}}\)-\(\varvec{\upchi _{out}}\) Tree robust system) A system \(M'(I',O')\) is \(\upchi _{in}\)-\(\upchi _{out}\)-tree robust for \(\mathrm {\Phi }\) if there exists a system \(W(I \cup I',O \cup \{\varvec{sb_{out}}\})\) such that for all sequences of \(\varvec{sb_{in}}\),
or, developing according to (2) and (7),
We refer to this definition as “tree” robustness since it refers to the computation tree of a system rather than to a single trace. Thus, instead of requiring the output to be close to a correct trace, as we did in the last section, we now ask for a system that is “close” to a correct system W in the sense that its output traces are always close to the outputs of W. This definition is illustrated in Fig. 4b.
In some ways, Trace Robustness and Tree Robustness are similar. For instance, if we set \(\upchi _{out}= {\textbf {G}}\varvec{sb_{out}}\), then \(\upchi _{in}\)-\(\upchi _{out}\) Tree Robustness for \(\Phi\) requires the system to produce correct outputs even if the input is adulterated according to \(\upchi _{in}\), which is a stronger notion than plain adherence to \(\Phi\). Similarly, the notion can be weakened by choosing a \(\upchi _{out}\) that allows \(\varvec{sb_{out}}\) to be false.
\(\upchi _{in}\)-\(\upchi _{out}\) trace robustness vs. \(\upchi _{in}\)-\(\upchi _{out}\) tree robustness. In both subfigures, we have that the trace defined by I and O satisfies \(\mathrm {\Phi }\). To generate an \(\upchi _{in}\)-\(\upchi _{out}\) tree-robust system (\(M'\) in the right diagram), we synthesize \(M'\) and W according to (10), which guarantees that \(M'\) satisfies the recovery specification
However, the notions of Trace and Tree Robustness do not coincide. For any output trace of \(M'\), system W witnesses the existence of a trace that is close to it. Thus, tree robustness implies trace robustness, but not vice versa, as the following example illustrates.
Example 4
(Trace robustness vs. tree robustness) To see that the definitions of tree and trace robustness are not the same, suppose that r is an input, and g is an output. Let \(\mathrm {\Phi }= {\textbf {G}}({{\textbf {X}}}r \leftrightarrow g)\), \(\upchi _{in}= {\textbf {G}}\varvec{sb_{in}}\), and \(\upchi _{out}= {\textbf {G}}({{\textbf {X}}}r \rightarrow \varvec{sb_{out}})\). It should be clear that \(\mathrm {\Phi }\) is not realizable and thus \(\mathrm {\Phi }\) is not \(\upchi _{in}\)-\(\upchi _{out}\) tree-realizable. However, \(\mathrm {\Phi }\) is \(\upchi _{in}\)-\(\upchi _{out}\) trace-realizable (by a system that always outputs a g). Thus, one might see tree-realizability as a more interesting notion as it precludes the possibility that a specification that is not realizable in the first place is realized “robustly”.
Synthesis of tree-robust systems is a distributed synthesis problem of constructing \(M'\) and W. The proof that the distributed synthesis problem is decidable is given in the next theorem. The theorem depends on the notion of an information fork [12]. Intuitively, a component in a distributed synthesis setting receives information when it has an input. An information fork occurs when the information for each component is not fully ordered. In other words, there are components P and \(P'\) so that P receives information that \(P'\) does not receive and \(P'\) receives information that P does not receive.
In our case, W receives all information that \(M'\) receives: W has inputs \(I'\) and I, whereas \(M'\) only receives I. Thus, the information is fully ordered (\(\{I',I\} \supseteq \{I\}\)) and an information fork does not exist. Since there is no information fork, distributed synthesis is decidable following the construction in [12].
Theorem 3
Given \(\upchi _{in}\) and \(\upchi _{out}\) and \(\mathrm {\Phi }\), we can decide whether a \(\upchi _{in}\)-\(\upchi _{out}\)-tree robust system \(M'(I',O')\) for \(\mathrm {\Phi }\) exists in 3EXP time, and if so, we can build one in the same time complexity.
Proof
The proof goes along the lines of the synthesis procedure shown in [12]. Our architecture is ordered in an information sense: W has all information that \(M'\) has. Whereas [12] assumes that the specification is given as a \(\upmu\)-a specification in LTL. While \(\upmu\)-calculus formulas can be translated into alternating tree automata in polynomial time [12, Theorem 4.4], [18], for LTL the translation into a tree automaton (a game) results in an exponential blowup [6]. The rest of the construction outlined in [12] can be followed as is, resulting in a triply exponential bound. \(\square\)
4.4 Examples of robust specifications
We begin by showing several robustness specifications, corresponding to the definitions (R1)–(R3).
Recall that (R1) defines a system to be robust if it satisfies \(\varphi _s\) even if the inputs are corrupted for a finite number of steps. We can translate this definition into an LTL robustness specification:
Similarly, R2 is captured by the robustness specification
i. e., the inputs are corrupted up to k steps consecutively. (R3) is the most general definition and therefore as a special case can be (12) or (13), but also other specifications such as
(the inputs will be corrupted infinitely often) or
(we trust the inputs only if they are equal). A plausible scenario is when the relationship between the inputs is an indication of whether they can be trusted. For example, when using error-correcting code, the relation between bits in a packet and a parity bit at its end determines whether to trust the packet.
5 Robustness against unreliable environments
In the previous section, we focused on robustness against corrupted signals; Let us now focus on robustness against environmental assumptions that cannot always be trusted.
5.1 Assumption robustness
As explained in Sect. 3, the number of times that a specification is violated, as prescribed by (R7), is generally not well-defined, because temporal formulas are either satisfied by a path or not (but see [5]). We can, however, restrict ourselves to invariant properties, i.e., formulas of the form \({\textbf {G}}\psi\) where \(\psi\) is propositional. We then interpret ‘failure’ as a temporary failure of the invariant (this is the same interpretation of robustness taken by Ehlers [9]). Hence the failure count refers to the number of time frames in which \(\psi\) is false. We denote by \(\upchi _{e}\) a robustness specification that relates to an assumption failure. It is defined over a synchronization bit \(\varvec{sb_{e}}\).
As explained before, our approach is more general than the one in [9] because we have the freedom to specify the robustness specification, whereas [9] suggested an algorithm tailored for systems that are eventually reliable. In the case of Ehlers [9], \(\upchi _{e}\) can be thought of as being fixed to \({\textbf {F}}{\textbf {G}}\varvec{sb_{e}}\). In addition, our method works with any existing synthesizer, whereas [9] requires a tailored algorithm based on a generalized Rabin(1) automaton.
Let our specification \(\mathrm {\Phi }= \varphi _e \rightarrow \varphi _s\) be defined by \(\varphi _e \equiv {\textbf {G}}\psi _e\) and \(\varphi _s \equiv {\textbf {G}}\psi _s\), where \(\psi _e,\psi _s\) are propositional.
To synthesize a system that is robust against environmental failures, we repeat the same pattern that we used in the previous sections. We first define
That is, \(\upchi _{e}'\) is true for paths that satisfy \(\upchi _{e}\), and each time \(\varvec{sb_{e}}\) is true, then the assumption \(\psi _e\) holds.
We define robust systems as follows.
Definition 6
(\(\upchi _{e}\)-Assumption-robust system) A system \(M'(I,O)\) is \(\upchi _{e}\)-assumption-robust for \(\mathrm {\Phi }\) if
Intuitively, every path in \(M'\) must satisfy \({\textbf {G}}\psi _s\) if in every time step either \(\varvec{sb_{e}}\) is false or \(\psi _e\) is true. This is of course a stronger requirement than satisfying \(\mathrm {\Phi }\) itself because the latter is trivially satisfied once there is a time step in which the environment assumption is violated. Thus, every \(\upchi _{e}\)-assumption-robust system is correct. As an example of using (17), synthesizing the following formula yields a system that is robust according to (R4):
We continue with an example of a formula that has to be synthesized according to a robustness specification relating to its assumptions.
Example 5
Consider the specification
Fig. 5a shows a system realizing \(\Phi\). Once the assumption fails, the system transits to a ‘sink’ state in which it does not satisfy \(\varphi _s\).
Systems for (19). The value of \(\varvec{sb_{e}}\) is omitted from the drawings
Suppose that (19) works in an adversarial environment, and we want it to start trusting the inputs only after it receives some password confirming the identity of the environment. This pattern can be specified with
where pwd is the password. For this example assume that \(pwd = \overline{r}_1 \wedge r_2\). The systems depicted in Fig. 5b are the result of synthesizing (17). Note that as long as \(\varvec{sb_{e}}\) is down (at state 0, before the password was given) violating the assumption does not lead us to a sink state, and the guarantee still holds.
Similarly, for (R7), which defines robustness as the requirement that the guarantee \(\psi _s\) holds even if the environment violates (\(\psi _e\)) up to k consecutive steps, we can use once again the pattern of (17) while defining \(\upchi _{e}\) as follows:
Indeed this definition guarantees that every path that satisfies \(\psi _e\) at least once in every window of size k, satisfies the guarantee \({\textbf {G}}\psi _s\) as well.
5.2 Recovery specifications for environment failures
Similar to Sect. 4.3, we now consider the problem of synthesis with a recovery specification.
Example 6
Suppose that we allow the system to provide an arbitrary output for k time steps after a failure of the environment to satisfy \(\psi _e\). We will denote by \(\upchi _{s}\) the recovery specification, and it will operate over a synchronization bit \(\varvec{sb_{s}}\). Hence, for our example we will specify
It is left to specify the behavior of \(\varvec{sb_{s}}\) in the first k steps. We may require that in step \(i \le k\), the synchronization bit \(\varvec{sb_{s}}\) is high if in all previous steps the assumption \(\psi _e\) is true. In this case we conjoin \(\upchi _{s}(\varvec{sb_{s}})\) with
We can now define \(\upchi _{s}\)-robustness and again, we have the choice between defining a trace variant (cf. Definition 4) and a tree variant (cf. Definition 5). For simplicity, we will only define the tree variant here.
Definition 7
(\(\upchi _{s}\)-Tree-robustness) A system \(M'(I',O')\) is \(\upchi _{s}\)-tree-robust for \(\mathrm {\Phi }\) if there exists a system W(I, O) such that
Interestingly, this definition does not refer to \(\upchi _{e}\). \(\upchi _{s}\) in itself can refer to \(\psi _e\), as can be seen in (22). In other words, here we synthesize a system that satisfies \(\psi _s\) based on the satisfaction of \(\psi _e\). In contrast, in Definition 6, we required that \({\textbf {G}}\psi _s\) holds [see (17)] if the environment assumption holds according to \(\upchi _{e}\). It should be possible to combine the two definitions, i.e., the specification will be vacuously satisfied if \(\varvec{sb_{e}}\wedge \lnot \psi _e\). A different direction is to replace the recovery specification \(\psi _e\) with \(\psi _e \vee \lnot \varvec{sb_{e}}\), and hence strengthen the recovery requirement. We leave such directions for future research.
The following example demonstrates the result of adding the recovery specification (22) with \(k=1\).
Example 7
Continuing Example 5, suppose we add the recovery specification
Figure 6 shows a system satisfying the resulting specification. The system satisfies \(\Phi\) from (19), with the robustness specification \(\upchi _{e}(\varvec{sb_{e}})\) (where again \(pwd = \overline{r}_1 \wedge r_2\)) from (20) and the recovery specification (25). Note that after a violation of the assumption with \(r_1r_2\) at state 0, the system transits to state \(0'\) with an arbitrary output and then has an additional transition with an arbitrary output (in this case party chose as arbitrary output \(\bar{g}_1\bar{g}_2\)).
6 Conclusion
The incompleteness of most specifications gives a certain freedom to the synthesis algorithm. It is left for the designer of the synthesis algorithm to set criteria for what system is preferable from the large set of options. Several previous publications suggested using this freedom to synthesize a robust system. Each publication had its definition of robustness, and each suggested a synthesis method to achieve a robust system accordingly. This article showed a general framework that enables specifying with LTL formulas \(\upchi _{in}\) and \(\upchi _{e}\) the expected robustness. From there on, it reduces the robust synthesis problem to that of normal synthesis. Furthermore, with LTL formulas, we enable to specify a recovery specification. Our framework is flexible and easy to use with existing reactive synthesizers. As we showed, it covers most of the previously published definitions of robustness and several new ones that we introduced here. Our tool Party, which implements our method, is available for download from Party [20].
Notes
When we do not explicitly write the parameters of \(\mathrm {\Phi }, \varphi _e,\varphi _s\) the meaning is that it is over the inputs and outputs I, O, respectively.
Tabuada et al. [26] did not deal with LTL specifications, however, instead with systems specified as sets of differential equations.
References
Almagor S, Boker U, Kupferman O (2013) Formalizing and reasoning about quality. In: ICALP, pp. 15–27
Anevlavis T, Philippe M, Neider D, Tabuada P (2022) Being correct is not enough: efficient verification using robust linear temporal logic. ACM Trans Comput Log 23(2):8:1-8:39. https://doi.org/10.1145/3491216
Bloem R, Hofferek G, Könighofer B, Könighofer R (2012) Synthesizing robust systems with RATSY. In: Peled DA, Schewe S (eds) Proceedings 1st workshop on synthesis, SYNT 2012, Berkeley, California, USA, 7th and 8th July 2012, EPTCS, vol 84, pp 47–53. https://doi.org/10.4204/EPTCS.84.4
Bloem R, Jobstmann B, Piterman N, Pnueli A, Sa’ar Y (2012) Synthesis of reactive(1) designs. J Comput Syst Sci 78(3):911–938
Bloem R, Chatterjee K, Greimel K, Henzinger TA, Hofferek G, Jobstmann B, Könighofer B, Könighofer R (2014) Synthesizing robust systems. Acta Informat 51(3–4):193–220
Bloem R, Chatterjee K, Jobstmann B (2018) Graph games and reactive synthesis. In: Clarke EM, Henzinger TA, Veith H, Bloem R (eds) Handbook of model checking, pp 921–962. Springer
Bloem R, Chockler H, Ebrahimi M, Strichman O (2017) Synthesizing non-vacuous systems. Verification. Model checking, and abstract interpretation (VMCAI). Springer, Berlin, Heidelberg, pp 55–72
Bloem R, Chockler H, Ebrahimi M, Strichman O (2019) Synthesizing reactive systems using robustness and recovery specifications. In: FMCAD. IEEE, pp 147–151
Ehlers R (2011) Generalized Rabin(1) synthesis with applications to robust system synthesis. In: Bobaru MG, Havelund K, Holzmann GJ, Joshi R (eds) NASA formal methods—3rd international symposium, NFM 2011, Pasadena, CA, USA, April 18–20, 2011. Proceedings, Lecture notes in computer science, vol 6617. Springer, pp 101–115
Ehlers R, Könighofer R, Hofferek G (2012) Symbolically synthesizing small circuits. In: Cabodi G, Singh S (eds) Formal methods in computer-aided design, FMCAD 2012, Cambridge, UK, October 22–25, 2012. IEEE, pp 91–100
Fainekos GE, Pappas GJ (2009) Robustness of temporal logic specifications for continuous-time signals. Theor Comput Sci 410(42):4262–4291. https://doi.org/10.1016/j.tcs.2009.06.021
Finkbeiner B, Schewe S (2005) Uniform distributed synthesis. In: 20th IEEE symposium on logic in computer science (LICS 2005), 26–29 June 2005, Chicago, IL, USA, Proceedings. IEEE Computer Society, pp 321–330. https://doi.org/10.1109/LICS.2005.53
Huang C, Peled DA, Schewe S, Wang F (2016) A game-theoretic foundation for the maximum software resilience against dense errors. IEEE Trans Softw Eng 42(7):605–622
ISO/IEC JTC 1/SC 7 Committee: Systems and Software Engineering—Vocabulary. ISO/IEC/IEEE 24765:2017 (2017)
Jing G, Ehlers R, Kress-Gazit H (2013) Shortcut through an evil door: optimality of correct-by-construction controllers in adversarial environments. In: 2013 IEEE/RSJ international conference on intelligent robots and systems, Tokyo, Japan, November 3–7, 2013. IEEE, pp 4796–4802. https://doi.org/10.1109/IROS.2013.6697048
Khalimov A, Jacobs S, Bloem R (2013) PARTY parameterized synthesis of token rings. In: Sharygina N, Veith H (eds) CAV, LNCS, vol 8044. Springer, pp 928–933
Kupferman O, Vardi M (1997) Synthesis with incomplete information. In: 2nd international conference on temporal logic. Manchester, pp 91–106
Kupferman O, Vardi M (2000) \(\mu\)-calculus synthesis. In: Proc. 25th international symp. on mathematical foundations of computer science, LNCS, vol 1893. Springer, pp 497–507
Mealy GH (1955) A method for synthesizing sequential circuits. Bell Syst Tech J 34(5):1045–1079
party. https://extgit.iaik.tugraz.at/scos/scos.sources/party-eris
Pnueli A (1977) The temporal logic of programs. In: Proc. 18th IEEE symp. on foundation of computer science, pp 46–57
Pnueli A, Rosner R (1989) On the synthesis of a reactive module. In: POPL. Austin, pp 179–190
Saad-Khorchef F, Berrada I, Rollet A, Castanet R (2010) Automated robustness testing for reactive systems: application to communicating protocols. In: Eichler G, Kropf PG, Lechner U, Meesad P, Unger H (eds) I\({}^{\text{2}}\)CS, LNI, vol P-165. GI, pp 409–421. https://dl.gi.de/20.500.12116/19036
Samanta R, Deshmukh JV, Chaudhuri S (2013) Robustness analysis of string transducers. In: Hung DV, Ogawa M (eds) ATVA, Lecture notes in computer science, vol 8172. Springer, pp 427–441 (2013). https://doi.org/10.1007/978-3-319-02444-8_30
Sistla AP, Vardi MY, Wolper P (1987) The complementation problem for Büchi automata with applications to temporal logic. Theor Comput Sci 49:217–237. https://doi.org/10.1016/0304-3975(87)90008-9
Tabuada P, Balkan A, Caliskan SY, Shoukry Y, Majumdar R (2012) Input-output robustness for discrete systems. In: EMSOFT, pp 217–226
Topcu U, Ozay N, Liu J, Murray RM (2012) On synthesizing robust discrete controllers under modeling uncertainty. In: Dang T, Mitchell IM (eds) Hybrid systems: computation and control (part of CPS Week 2012), HSCC’12, Beijing, China, April 17–19, 2012. ACM, pp 85–94
Vardi M, Wolper P (1994) Reasoning about infinite computations. Inf Comput 115(1):1–37
Zhang C, Garlan D, Kang E (2020) A behavioral notion of robustness for software systems. In: Devanbu P, Cohen MB, Zimmermann T (eds) ESEC/FSE. ACM, pp 1–12. https://doi.org/10.1145/3368089.3409753
Acknowledgements
This work was supported by the Austrian Research Promotion Agency (FFG) through Project TRUSTED (867558) and the Graz University of Technology’s LEAD project “Dependable Internet of Things in Adverse Environments”. It was also partially supported by the Coleman-Cohen Foundation, by the Royal Society grant IES\R2\170021, the UKRI Trust-worthy Autonomous Systems Hub (EP/V00784X/1) the UKRI Strategic Priorities Fund to the UKRI Research Node on Trustworthy Autonomous Systems Governance and Regulation (EP/V026607/1), and by the European Union (IMMORTAL, Grant 644905), and by the ECSEL Joint Undertaking (ENABLE-S3, Grant 692455).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bloem, R., Chockler, H., Ebrahimi, M. et al. Specifiable robustness in reactive synthesis. Form Methods Syst Des 60, 259–276 (2022). https://doi.org/10.1007/s10703-023-00418-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10703-023-00418-x