On the Growing Universe of Causal Set Theory—An Order-Type Approach

Abstract

We investigate a model of becoming—classical sequential growth (CSG)—that has been proposed within the framework of causal sets (causets), with the latter defined as order types of certain partial orderings. To investigate how causets grow, we introduce special sequences of causets, which we call “csg-paths”. We prove a number of results concerning relations between csg-paths and causets. These results paint a highly non-trivial picture of csg-paths. There are uncountably many csg-paths, all of them sharing the same beginning, after which they branch. Every infinite csg-path achieves in the limit an infinite causet, and vice versa, every infinite causet is achieved in the limit by an infinite csg-path. However, coalescing csg-paths, i.e., ones that achieve the same causet even after forking off at some point, are ubiquitous.

1 Introduction

The focus of this paper is the theory of Classical Sequential Growth (CSG) in the “causal sets” (henceforth “causets”) program in quantum gravity.¹² CSG was put forward by Rideout and Sorkin [1] and Rideout [2], and the causets program was launched by Raphael Sorkin and his collaborators.³ The program’s salient hypothesis is that on the fundamental level the reality is discrete; continuous features, ever-present in general relativistic models of space-time and extant physics, are only an approximation of the fundamentally discrete reality of causets. Continuity vs. discreteness has been the predominant topic in the early development of the program. With CSG came a novel feature of the program, the evolution of causets. The theory’s emphasis on discreteness and on the emergent character of space-time introduces significant mathematical and conceptual challenges to analysing evolutions: since the background is not continuous, the standard approach of writing down a Hamiltonian and solving the evolution equation cannot be applied.

An answer is provided by growth models (cf. [4]). Putting it generally, in the context of causets a growth model is a collection of causets—with a successor relation such that each causet has at least one successor—plus a probability measure on some structures defined on the set of causets. This probability measure is intended to answer physically meaningful questions. Also, as the successor relation induces maximal chains of causets, naturally interpreted as possible histories of a universe, the idea is that the probability measure would produce a distribution of histories, with physically non-reasonable histories receiving negligible probability only. CSG models of Rideout and Sorkin form a sub-species of growth models, distinguished by several physically-motivated conditions. These models are advertised by their authors as models of indeterministic becoming. To quote,

[The CSG dynamics] can be regarded as a process of “cosmological accretion” or “growth”. At each step of this process an element of the causal set comes into being as the “offspring” of a definite set of the existing elements—the elements that form its past. ([1], p. 2)

[Causal Sets offer] the complete departure from determinism - even at the fundamental scale, when all aspects of the “state of the system” are “known”, the classical limit of the theory is postulated to be stochastic in nature. (As opposed to the philosophical attitude of kinetic theory, which assumes that only the incomplete knowledge of the state leads to indeterminism ...). ([2], p. 109)

The CSG models are thus a rare treat for philosophers of physics and metaphysicians, since proponents of becoming (a metaphysically-loaded notion) form a slim minority in these fields. Our ultimate aim is thus to display how possible histories of CSG grow. To this end we need first to decide on the adequate formal representations of causets, and then to gain clarity about the formal features of the theory. Our main decision in this paper is to define causets as order types, and focus on the consequences of this definition. This definition is not novel, as a few authors assumed it as well. Sorkin and Rideout state that they use isomorphism equivalence classes of finite causal sets, i.e., order types. Results in order type frameworks have been obtained by Brightwell et al. ([5], p. 3), Gudder ([6], p. 6), Dowker et al. ([7], p. 4), and others. However, a typical path to causets as order types begins with the so-called labeled posets, with the labels being abstracted from at a later stage. Our paper attempts a different tactics: from the start we work with causets as order types, and attempt a reconstruction of the already known, or popularly accepted claims of CSG. As a consequence, in this approach we will occasionally prove claims that are already established or at least believed to be true in the community. We take it that nevertheless the tactics pays off: by developing the framework in purely order type terms one will get a more complete picture of CSG, possibly pointing to some limitations or oddities of this way of thinking as well.

The paper is organized in the following manner. Section 2 informally introduces causets together with some related notions, and explains our approach. Section 3 defines causets as order types and translates into the framework of order types all the notions needed to express the causets’ growth, the most important of those being csg-paths. Section 4 investigates the rationales behind the identification of causets with order types. Section 5 contains the bulk of our formal results, which are divided into four kinds. First, in Sect. 5.1 we offer some results concerning the class of causets. Next, in Sect. 5.2 we put forward our main theorems, to the effect that every causet is achievable by a csg-path and vice versa (that is, any order type achievable by a csg-path is a causet). In Sect. 5.3 come results concerning branching, coalescing, and crossing of infinite csg-paths. Our final formal results (given in Sect. 5.4) focus on what csg-paths look like locally, i.e., “at” a given causet.

2 Setting the Stage: on Causets, Labeling, Probabilities, and Covariant Questions

To introduce causets, we start with the concept of a countable set with a non-reflexive, anti-symmetric and transitive relation <. Following the usual practice of causal set theoreticians, we call a set with such an ordering a poset. (In mathematicians’ parlance, < is a strict partial ordering, whereas partial order is reflexive, anti-symmetric, and transitive).

To define causets, one adds a local finiteness condition, to ensure discreteness. In this text we employ the past finiteness condition: for every element x of a poset $\mathcal {A} = \langle A, <\rangle$, its past $\{ y \in A \mid y < x\}$ is finite. The ordering < is supposed to be an analogue in discrete contexts of the strict partial ordering definable by causal connectibility relation in General Relativistic space-times that admit no closed, future-directed smooth causal curves. Accordingly, any two elements of a causet that are incomparable by < are interpreted as “space-like”.

CSG dynamics prescribes that causets grow: an n-element causet gives rise to an $(n+1)$-element causet, the new element being placed anywhere but below an element of the former causet; a causet thus typically has multiple immediately succeeding causets. This dynamics induces a numbering of elements of each causet in accord with how the causet has been produced, starting from the causet based on the empty set. This numbering of a causet’s elements is called “labeling”. Given the above prohibition of placing a new element below an existing element, we get the condition of natural labeling: for $x, y \in A$, if $x < y$, then $l(x) < l(y)$, where $l: A \mapsto N$ is a labeling function. The resulting object, a causet with a natural labeling, is called a “labeled causet” in the literature, and is contrasted with unlabeled causets.

Although natural labelings come with the dynamics, for space-like (i.e., incomparable by <) elements of a causet, the numbers assigned to them by a natural labeling do not carry any physically meaningful information, if relativistic physics is at least approximately right. The labeling of incomparable elements is merely a mathematical surplus posited by CSG dynamics. This observation brings us to the task of finding a mathematical representation of causets that would capture only (what one may think as) physically significant information. The well-tried recipe suggests “gauge ’em out”.

Consider the set X of all labeled causets (countable past-finite posets). We define unlabeled causets, following the literature, as equivalence classes on X with respect to the relation of order isomorphism, i.e., as order types. Clearly, an order type does not contain the information on the identity of elements of posets it comprises, or their labelings. This concept tallies nicely with the arguments from General Relativity (see below) that suggest the identity of the elements of causets should not be physically meaningful. As one slogan has it, “Order and Number” [7] provide all of the physically meaningful information about space-times. Needless to say, mathematical objects that encode exactly this information are order types.

Turning to CSG dynamics, it requires labeling, as it is based on an order of creation, the important notion for Rideout and Sorkin being “transitions”, i.e., pairs consisting of a labeled causet together with its immediate succeeding causet ([1], p. 3). The authors’ decision is to assign probabilities to such transitions. Formally, this is equivalent to assigning probabilities to sets of maximal elements of a labeled causet taken together with their pasts (aka “partial stems”). Derivatively, probabilities are assigned as well to paths of labeled causets by multiplying probabilities of all the transitions involved. Importantly, Rideout and Sorkin assume some physically-motivated constraints, which permit the derivation of the general form of a probability assignment in CSG (see [1], Eq. 12).

Since CSG dynamics fails to accommodate quantum effects, it is considered “classical”; yet, it still offers an important testing ground, informing what the growth of causets looks like. It turns out that the general form of CSG probability of transition ([1], Eq. 12), depends on a few parameters. By choosing particular values of these parameters one might produce special models of CSG, for instance, a model in which the only non-zero transition probabilities are to elements space-like related to every element of the parent. By equating zero probability transitions with impossible transitions, one thus gets a CSG model containing anti-chains only. Despite this possibility of circumscribing CSG models by a choice of parameters governing the transition probabilities, most researchers assume that all transitions have non-zero probability (they call such models “generic”). Generic models are significant for our aims in this paper.

An unwelcome feature of constructing CSG dynamics in terms of labeled causets is that it assigns probabilities to questions relative to labelings. A question like “Do the four first elements of a causet form an anti-chain?” has different answers, depending on the labeling. In contrast, it is independent of labeling whether the growth produces an infinite causet with the so-called “post”, i.e., an element, different from the empty set, that is comparable to every other element of the causet (a causet with a post stands for a re-collapsing universe). The former question is an example of “non-covariant” questions, whereas the latter is “covariant”. Since labelings carry no physical significance other than the causal ordering < of a labeled causet, the questions of the first type are of little interest, in contrast to the latter, covariant, questions. An important task, taken up by a few papers, is thus to produce, within the framework of labeled causets, a representation of covariant questions that will allow for assigning probabilities to them.

The ingenuity of this program notwithstanding, there is a hint of a schism in the approach. On the one hand, causets (which are the basic entities of the program) should be abstract, in the sense of encoding no information about the order of birth of its elements, or the identity thereof. Mathematically, order types of countable past finite posets look thus like an adequate choice. On the other hand, CSG dynamics assign probabilities in the first place to transitions between labeled causets. There is thus a schism between the labeled causets and causets as order types, which is bridged to some extent by the concepts of covariant questions and stem events: despite the labelings, one can ask physically meaningful questions and expect probabilistic answers to them. Despite this maneuver, the tension remains and calls for the creation of “manifestly covariant formulation of growth dynamics” ([8], p. 43). We believe that such a formulation should dispense of the labelings from the start. And, if causets as order type are the real McCoy, one had better learn what structures they admit and how they grow.

With this last observation we return to the objectives of this paper. As we said, our main theme is to make contact between CSG and modal metaphysics. In the last decades the latter has developed theories of possible worlds (histories), and used them in various applications. CSG comes with the notion of possible histories as well, with a novel feature: they grow.⁴ It is thus interesting to learn what new insights for modal metaphysics CSG might have, given the latter’s commitment to becoming and indeterminism.

In contrast to the existing literature, in our study we will ignore the probabilistic aspect of CSG. This might sound as a blasphemy since the probability assignment is the very essence of CSG. However, in generic CSG models (which are the focus of the literature as well as ours), all transition probabilities are non-zero. Thus, no legitimate transition between causets is excluded by having zero probability. In a similar vein, no sequence of causets is excluded on probabilistic grounds. This justifies, we think, our focus on sequences of causets, ignoring their probabilities. Our aim is to investigate the features of causet growth which are independent of the probability of the given growth process.

We now introduce the basic notions of CSG, following the definitions of Sorkin and Rideout, but taking care to always formulate them in the order type framework. Our plan is to learn as much as possible about CSG in the framework that is explicitly developed, from (as close as possible to) start to end, in terms of order types.

3 Defining Past-Finite Posets, Causets, and csg-paths

Following authors such as Rideout and Sorkin [1] as well as Dowker et al. [7], we define causets as order types of special posets:

Definition 1

(order type, past-finite, causet) The order type $\textsf{A}$ of the order $\mathcal {A} = \langle A, < \rangle$ is the class of all orders isomorphic to $\mathcal {A}$. If $\mathcal {A} \in \textsf{A}$, then we say that $\mathcal {A}$ is a realization of $\textsf{A}$.

A poset $\langle A, < \rangle$ is past-finite iff for any $x \in A$ the set $\{ y \in A \; | \; y < x\}$ is finite.

A causet is defined as the order type of a countable past-finite poset.

To differentiate objects of different categories, we adopt the following typographical convention: for order types we use the sans-serif letterform ($\textsf{A}$), for partially ordered sets (posets) we use the calligraphic ($\mathcal {A}$), and for base sets of posets we use the normal font (A). The “$\setminus$” symbol denotes set-theoretic complement.

Note that elements of an order type might have different base sets⁵; the exception is the order type of the empty order $\langle \varnothing , \varnothing \rangle$. Whenever it is more convenient, we use the weak companion $\le$ to the strict partial order relation <, standardly defined by: $x \le y$ iff ($x < y$ or $x = y$). As a matter of convenience, while talking about elements of posets we use the notation “$x < \!\! \cdot \, y$” for x being immediately below y,⁶ and “$x \text { inc } y$” for x and y being incomparable by $\le$.

In requiring past-finiteness we follow Dowker et al. ([7], p. 3); the earlier literature required Alexandroff-set finiteness instead, i.e., it demanded that if $x < y$, then $\{z \mid x< z < y\}$ should be finite. Past-finiteness implies Alexandroff-set finiteness, but not vice versa.⁷

The poset $\langle \varnothing , \varnothing \rangle$ is the unique realization of the smallest causet $\overline{\varnothing }:= \{\langle \varnothing , \varnothing \rangle \}$. Apart from the smallest causet, all causets have infinitely many elements (these elements are posets, differentiated by different base sets or different orderings of the same base set). In what follows, however, we need the locutions “infinite / finite causet” and “n-element causet”. Far from redefining cardinality, we define these locutions in terms of realisations (using a simple fact that all realisations of a given causet have the same cardinality):

Definition 2

(infinite/finite causet, n-element causet) $\textsf{G}$ is an infinite causet iff its every realisation $\mathcal {G}$ is infinite and $\textsf{G}$ is a finite causet iff its every realisation $\mathcal {G}$ is finite. $\mathcal {G}$ is an n-element causet iff the cardinality of its every realisation $\mathcal {G}$ is n.

Next, we turn to the notions relating to the “growth” of causets. The crucial thing here is that the growth is discrete: step-wise. The notion of “link” captures the relationship between two causets such that one has outgrown the other by a single step, that is, between a “parent” and its “child”.⁸ A chain of such successive links forms a “path”; of special interest will be those paths which start from the smallest possible causet, which we will label “csg-paths”. The notions of link, parent, child, and csg-path were introduced by Sorkin and Rideout, though they did not use our name for the last notion. We give the following definitions:

Definition 3

(link, parent, child, path, csg-path) For finite causets $\textsf{A}$ and $\textsf{B}$, we say that there is a link from $\textsf{A}$ to $\textsf{B}$—symbolically: $\textsf{A} \prec \textsf{B}$—if there are realizations $\mathcal {A} = \langle A, <_A \rangle$ and $\mathcal {B} = \langle B, <_B \rangle$ such that $B {\setminus } A = \{ y\}, \; <_{B\; \mid A}\; = \; <_A$, and $\forall x \in A \; y \not <_B x$. We call $\textsf{A}$ a parent of $\textsf{B}$ and $\textsf{B}$ – a child of $\textsf{A}$.

A path is a finite or countably infinite sequence of causets $( \mathsf {A_0}, \mathsf {A_1}, \ldots )$ whose any two successive elements form a link: for any $\mathsf {A_k}, \mathsf {A_{k+1}}$ belonging to the sequence it is the case that $\mathsf {A_k} \prec \mathsf {A_{k+1}}$.

We will call a path a csg-path iff its first element is the smallest causet $\overline{\varnothing }:= \{\langle \varnothing , \varnothing \rangle \}$.

To comment on the concept of link, the $\prec$ relation is thought of as constraining how a child is related to its parent in a link. A realisation of the child is larger than the realisation of the parent by exactly one element, and this element cannot be below (in the sense of <) any element of the realisation of the parent. In somewhat loose talk, one might say that what has become is fixed, or that the past is settled. (Note also that the process of causal sequential growth never removes any links.) But, given the emergent character of space-times in the causet theory, such uses of tenses are highly disputable. To illustrate how this idea restricts csg-paths, consider the three-element “$\bigwedge$”-shaped causet and ask what its parent is. Clearly, its parent must be a two-element causet. By the definition of links above, the two-element “|”-shaped causet is excluded, so the only option is the causet based on two incomparable elements. Note also that the smallest causet $\overline{\varnothing }$ is the parent of a unique child, which is the causet based on one-element posets: the realization of the former is $\langle \varnothing , \varnothing \rangle$ and any one-element poset $\langle \{a\}, \varnothing \rangle$ is a realization of the latter. Thus, there is a single link starting from $\overline{\varnothing }$.

Turning to paths, if a causet $\mathsf {A_i}$ is an element of a path we will say that the path passes through $\mathsf {A_i}$. We will compare in a natural way causets from a given path, saying that one causet is above (below) another causet in a given path. If a causet is an element of two paths, then we say that these paths coincide at that causet. In a similar way, we say that two csg-paths branch at a causet $\textsf{K}_0$ if they coincide at $\textsf{K}_0$ and do not coincide at any causet above $\textsf{K}_0$ (“above” from the perspective of any of the two paths).⁹ Note that infinite csg-paths can branch while achieving the same limit, as the limit is not their element (for an example of this see p. 23 below). We also say that two csg-paths coalesce at a causet $\textsf{K}_0$ if they coincide at $\textsf{K}_0$ and do not coincide immediately below¹⁰$\textsf{K}_0$. Finally, two csg-paths cross at a causet $\textsf{K}_0$ if they coincide at $\textsf{K}_0$ but coincide neither immediately below $\textsf{K}_0$ nor immediately above $\textsf{K}_0$. Observe that if two csg-paths cross at $\textsf{K}_0$, then $\textsf{K}_0$ is finite. Note that since elements of csg-paths are finite causets, csg-paths coincide, branch, coalesce, and cross at finite causets (if they do). In the limit, however, they can achieve the same or different countably infinite causets.

As you can see, the notion of paths crossing at a causet is more demanding than that of paths coinciding at a causet. Here come two facts relevant to this issue. First, if a causet is the $n^{\text {th}}$ element of a csg-path, it is the $n^{\text {th}}$ element of every csg-path to which it belongs—that is because causets grow by their realizations getting larger by one element at each step. Second, observe that in contrast to paths, all csg-paths coincide at the same two initial causets (based on the empty-set and on one-element posets).

The final notion to be defined here is “achievability by a path”. An important distinction is between achievability by a path simpliciter and achievability by CSG dynamics, i.e., by a csg-path.

Definition 4

(achievable by a path) We say that an order type A is achievable by the path $( \mathsf {A_0}, \mathsf {A_1}, \ldots )$ of causets if there is a sequence $( \mathcal {A}_0, \mathcal {A}_1, \ldots )$, with $\mathcal {A}_i = \langle A_i, <_i \rangle$, of realizations of the corresponding elements of the path such that, if we define:

• $A = \bigcup A_i$;

• for $x,y \in A$, $x < y$ iff there exists an $i \in \mathbb {N}$ such that $x,y \in A_i$ and $x <_i y$;

then $\textsf{A}$ is the order type of $\langle A, < \rangle$.

We say that A is achievable in the limit if A is is achievable by an infinite csg-path.

Note that this Definition is posed in the general context of order types. As it will emerge in Theorem 2 on p. 20, order types achievable in the limit are (infinite) causets. When a causet is achievable by a path, we will say that that path is a path to that causet. We will also say that a path $(\textsf{A}, \ldots , \textsf{B})$ is a path from $\textsf{A}$ to $\textsf{B}$.

To get an inkling of paths, consider the following example:

• Let $\textsf{L}$ be the order type of $\langle L, <_L\rangle$ where $L = \mathbb {N} \cup \{a\}$, $a \not \in \mathbb {N}$, and $<_L = <_{\mathbb {N}}$ (that is, $\forall n \in \mathbb {N}$, $a \not <_{L} n$ and $n \not <_{L} a$ and $a \ne n$).

• Let $\textsf{K}_n$ be the order type of $\langle K_n, <_n \rangle$, where $K_n = \{0, \ldots , n\} \cup \{ a \}$ and $<_n = <_{\mathbb {N}\; \mid \{ 0, \ldots , n\}}$.

• Let $\textsf{N}_0$ be the order type of the poset $\langle \{ 0 \}, \varnothing \rangle$; that is, $\textsf{N}_0$ is the unique one-element causet.

• Let $\textsf{N}_1$ be the order type of the poset $\langle \{ 0,1 \}, \{ \langle 0, 1 \rangle \} \rangle$.

Achievability by finite paths is not interesting as a causet can be achieved in a single step (the path is then the singleton of the causet in question). Observe that, for instance, the causet $\textsf{K}_1$ is achievable by the path $(\textsf{N}_0, \textsf{N}_1, \textsf{K}_1)$, but also of course just by the path $(\textsf{K}_1)$. What is of interest, though, is achievability by csg-paths, for studying the possible processes of achieving the given causet “ex nihilo” by sequential growth. We can then see that there are two csg-paths to $\textsf{K}_1$: $(\overline{\varnothing }, \textsf{N}_0, \textsf{K}_0, \textsf{K}_1)$ and $(\overline{\varnothing }, \textsf{N}_0, \textsf{N}_1, \textsf{K}_1)$. Notice also that both $(\overline{\varnothing }, \textsf{N}_0, \textsf{K}_0, \textsf{K}_1, \textsf{K}_2, \ldots )$ and $(\overline{\varnothing }, \textsf{N}_0, \textsf{N}_1, \textsf{K}_1, \textsf{K}_2, \ldots )$ are infinite csg-paths by which $\textsf{L}$ is achievable. These csg-paths both pass through $\textsf{K}_1$. It is clear that $\textsf{L}$ is achievable by infinitely many infinite csg-paths, as the sub-sequence $\textsf{N}_i, \textsf{K}_i, \textsf{K}_{i+1} \ldots$ may begin arbitrarily late.¹¹

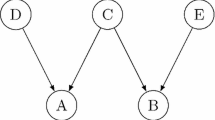
If we focus, then, on how all csg-paths have to start, note that each one starts at the smallest causet $\overline{\varnothing }$, which has a single child—the order type of a one-element poset. This one has two children—two order types of two-element posets. Then five order-types of three-elements posets follow (see Fig. 1). Four of these are achievable by just one csg-path; one, $\textsf{K}_1$ from the example just given, is achievable by two different csg-paths.

Fig. 1

How CSG starts. The figure is a part of Figure from Rideout and Sorkin [1]

These simple observations uncover some features of csg-paths. Separate csg-paths might converge to one and the same causet. Also, one finite causet belongs to multiple csg-paths. But there are more questions we will soon address. Are order types achievable in the limit identifiable with causets? Are there causets which are not achievable by a csg-path? More specifically, are there infinite causets which are not achievable by a csg-path in the limit? These and a few more questions concerning csg-paths, as well as the characterization of the class of all causets, are the subject of Sect. 5. Before we turn to it, we need a short interlude to justify our identification of causets with order types.

4 Why Order Types?

We owe the readers a discussion of why we take the basic elements of causal set theory to be the order types of posets rather than posets themselves. To this end, we will focus on the arguments of causets theorists for picking causets, identified with special order types, as the main objects of their theory. Ultimately, these arguments attempt to establish that “Order and Number” [7] provide all of the physically meaningful information. From a mathematical perspective, the structures that encode exactly this information, on order and on number, and on nothing else, are order types. Causet theorists usually invoke two arguments in this context: one invoking general covariance and the other related to the theorems of Malament [10], Kronheimer and Penrose [11], and Hawking [12]. To begin with the former, General Relativity is viewed as an approximation to the theory of causets and the former is generally covariant—thus the theory of causets should recover (perhaps as an approximation) general covariance. Now, general covariance is the idea that the theory’s equations do not change their form if all objects in the theory’s model are transformed by an arbitrary diffeomorphism. (The precise meaning of general covariance is somewhat contentious—see [13]). However, since diffeomorphisms are continuous maps between differential manifolds, they are not applicable to causets, and hence we loose grip of general covariance, as a feature of the theory of causets. One need thus reflect on general covariance asking what meaning or aims it has, and apply this idea to the theory of causets. As Sorkin [14] suggests, the core idea is that “only diffeomorphism-invariant quantities possess physical meaning”. In the context of causets, he claims that “what has physical meaning is only the isomorphism equivalence class of the given poset C. General covariance for causets can thus be interpreted as invariance under relabeling, in analogy to the interpretation of general covariance as coordinate-invariance in the continuum.”¹² To clarify the terminology, in the phrase “the isomorphism equivalence class of a given poset”, one must mean “order-isomorphism” (in a poset there is no other structure than order). The phrase thus means “the order type of a given poset”. Causets as order types are indeed similar to classes of diffeomorphic space-times, as diffeomorphic space-times might have different base sets and, of course, differently labeled elements of a shared base set. That is, for each, neither the identity of the underlying set nor the labeling of the set’s elements is relevant. Although this might be a minor point, this stands in contrast to an invariant of relabelings (a set of labeled posets based on a given poset) since it is based on a particular poset (and hence, a particular set).

We have more substantial qualms, however, with what we read as the second claim above, namely, that order types of posets can be interpreted as invariants of relabeling transformations. It is one thing that order isomorphisms preserve natural labelings, and the other that order types are invariants of relabeling transformations. The proper context for the former notion is a pair of two equi-numerous posets, $\langle A, <_A \rangle$ and $\langle B, <_B \rangle$, each with their set of labelings (both natural and not). Then, given a bijection $\phi : A \mapsto B$ and a natural labeling l of A, $l \circ \phi$ is a natural labeling of B iff $\phi$ is an order isomorphism. Yet, the talk of invariants of transformations calls for a different context, which is provided by a set of objects, identified with labelings of a given poset, and their transformations, i.e., relabelings. The issue then is whether the relabelings that leave intact natural labelings correspond, in some sense, to the order type of a poset at hand. Focusing on relabelings that preserve natural labelings, for some posets we get a troubling mismatch between the set of naturally labeled posets and invariants of relabeling transformations (see the Appendix for details).

The moral from this discussion is that generally, order types are different from invariants of relabeling transformations that preserve natural labelings, defined on the set of labeled posets. A theory that takes order types as its basic objects is thus mathematically different from a theory that takes the mentioned invariants as its basic objects. Causets as order types and as invariants of relabelings might thus embody some different senses of general covariance.

To return to the motivations for identifying the basic objects of the theory with order types, a yet another motivation comes from the theorems of Kronheimer and Penrose [11], Malament [10], and Hawking [12].¹³ These theorems indicate that “the space-time causal order together with space-time volume are sufficient [...] to provide the full geometry of a Lorentzian spacetime for a very large class including all globally hyperbolic spacetimes” ([7], p. 2). Since in the discrete settings with local finiteness, “volume” translates into “number”, the theorems are seen as the evidence that Order and Number provide all the information about Lorentzian geometrical features. However, as Dowker makes clear, these theorems are about recovering a space-time’s metric from volume and order, and do not imply that the information about matter and other fields could be recovered in this way. This should not be read as an objection to the causet program: after all, the appeal to the mentioned theorems serves as a heuristic argument rather than a proof. Yet, this brings to the fore a significant interpretational decision concerning the relation between causets and phases of becoming: does any difference between phases of becoming supervene on a difference between Order and Number?

This question links to an intriguing feature of CSG, known as pseudosimilarity (see chapter 6.4 of [9], in particular Figure 6.4.2., p. 361; the idea is attributed to Brendan McKay).¹⁴ In the poset framework, it is sometimes possible to add to a poset a new element in one “location” and, alternatively, in another “location”, obtaining isomorphic posets.¹⁵ Although we seem to have two different additions, the parent–child link is the same. Furthermore, the notion of location can be made precise in terms of the embedding of a parent poset into a child poset. This underlies a feeling that a difference between such two additions might have a physical meaning. Pseudosimilarity can be accounted for in the framework of posets. We concede, however, that, as we present it, the framework of causets as order types cannot accommodate pseudosimilarity: although it is present at the level of realisations, is washed out once one moves to order types.

We believe that understanding pseudosimilarity, in particular its physical meaning (if any), has a crucial bearing on what an adequate framework for causal sets is: unlabeled posets, order types, or still some subtler framework. We leave this issue for future research, returning to our main task of presenting CSG theory as formulated in terms of order types.

5 Facts About the Set of Causets and csg-paths

5.1 Some Results About the Class of Causets

We would like now to present a few facts about the class of causets, which is our candidate for the state-space for the Causal Sets theory. We will first define some auxiliary notions.

Definition 5

(generalized diamond, braid, broom) A generalized diamond of width n is a poset isomorphic to $\langle \{ a, b_1, \ldots , b_n, c \}, < \rangle$ with the ordering given by, for any i, $a < b_i$, $b_i < c$, and $a<c$.

A braid is the order type of a past-finite poset which is either a (possibly infinite) chain or is obtained from one by choosing some its (possibly infinite) subset D and, for any $d \in D$, substituting for it a generalized diamond of some finite width.

A broom is the order type of a poset $\langle A, < \rangle$ which has a nonempty set C of maximal elements and is such that $A {\setminus } C$ has a unique maximal element b (note that it follows that for any $c \in C$, $b <c$) such that the order type of $\langle b\downarrow , <|_{b\downarrow } \rangle$ is a braid (Fig. 2).

Fig. 2

A generalized diamond of width 4, a braid, and a broom

An informal commentary. Braids are causets which may be nonlinear but are nonetheless similar to linear ones in some respects: first, there is no real branching, in the sense that any upward splits are countered as the causet reconverges; second, in the underlying poset for any four elements $a<b$, $c<d$ it holds that a or b are below or identical to c or d; third, any two maximal chains in the poset underlying a braid share, roughly, at least every second element.

Note that brooms might be infinite (i.e. they might be order types of posets of the above type where the set C is an infinite antichain). In our approach, brooms are positioned with the broomstick down.

Our first Fact concerns cardinalities:

Fact 1

There are uncountably many infinite causets. There are uncountably many infinite csg-paths.

Proof

Consider decimal expansions of real numbers from the (0, 1) segment. Each of these naturally corresponds to a different infinite braid involving generalized diamonds of widths from 1 to 10. (For a number $0.xyz(\ldots )$, put a diamond of width x at the bottom of your poset, stack a diamond of width y on top of it, then one of width z on top of the previous two diamonds, etc.; treat 0 as 10. The braid in question will be the order type of your poset.) Therefore there are uncountably many infinite causets. Since one csg-path cannot achieve more than one causet in the limit, there are uncountably many infinite csg-paths. $\square$

This information about the cardinalities can be extracted from earlier discussions in the literature —see, e.g., Dribus’ ([9], pp. 173–174) argument concerning countable acyclic directed sets.

An unwelcome feature of the class of causets is that it admits no partial ordering on the class of causets that respects links. This result goes against one strand in formal metaphysics that begins with a partial order of all possibilities and aims to carve “possible histories” from it by means of some criterion (see [16]). By the result below, no procedure of this sort is going to work, if one (naturally) requires that the ordering respect the links:

Fact 2

There is no relation $\sqsubset$ on the class of all causets (as order types) satisfying the following desiderata:

• 1. $\sqsubset$ is a strict partial ordering (and so is, in particular, asymmetric);

• 2. if $\textsf{A} \prec \textsf{B}$, then $\textsf{A} \sqsubset \textsf{B}$;

• 3. if $\textsf{A}$ is obtained in the limit from $\{ \mathsf {A_0}, \mathsf {A_1}, \ldots \}$, then for any $i \in \mathbb {N}$ $\textsf{A}_i \sqsubset \textsf{A}$.

Proof

The argument relies on the following example by Andrzej Wroński. This is a scheme for constructing 3 posets whose base set is some countable set:

• $\mathcal {A}_0$ consists of chains, one of each finite cardinality, such that all elements of distinct maximal chains are incomparable;

• $\mathcal {B}$ which we obtain from $\mathcal {A}_0$ by appending a novel element to each of the aforementioned chains (so that again all elements of distinct maximal chains are incomparable);

• $\mathcal {A}_1$ which we obtain from $\mathcal {B}$ by adding a single novel element incomparable with any element from $\mathcal {B}$.

Note that in $\mathcal {B}$ each maximal chain contains more than one element. Observe that $\mathcal {A}_0$ and $\mathcal {A}_1$ are isomorphic, belonging to the order type $\textsf{A}$, which is different from $\textsf{B}$.

Assume for reductio that a relation $\sqsubset$ satisfying the three above desiderata exist. Observe that $\textsf{B} \prec \textsf{A}$ due to the way in which $\mathcal {A}_1$ is obtained from $\mathcal {B}$. And so by desideratum 2 above $\textsf{B} \sqsubset \textsf{A}$. Note further that the description of obtaining $\mathcal {B}$ from $\mathcal {A}_0$ allows us to define an infinite family of causets $\{ \textsf{A}, \mathsf {A'}, \mathsf {A''}, \ldots \}$ from which $\textsf{B}$ is obtained in the limit, therefore by desideratum 3 $\textsf{A} \sqsubset \textsf{B}$. But $\textsf{A} \sqsubset \textsf{B}$ and $\textsf{B} \sqsubset \textsf{A}$ violates asymmetry: a contradiction. $\square$

If we restrict our attention to the class of finite causets (ie., order types of finite posets), there is a partial ordering relation on this class—see Dowker et al. ([7], p. 5 and 9). Furthermore, Gudder [17] shows that one can define a partial ordering in terms of links for posets, but the resulting order is not a lattice, i.e., some pairs of finite causets do not have least upper bounds / greatest lower bounds. The existence of least upper bounds is essential for some formal theories of metaphysics, e.g., Branching Time.

5.2 Two Theorems About Achievability

We now turn to the main theorems in this paper. (They will serve as the formal bedrock for the philosophical claims made in the sequel to the current paper.) We know that finite csg-paths achieve causets. But what order types are achievable in the limit, i.e., by infinite csg-paths? The answer that the theorem yields is: causets as well. For the proof we need auxiliary definitions:

Definition 6

(witness to a link, witness to a path) If $\textsf{A} \prec \textsf{B}$, then any pair of realizations $\mathcal {A} = \langle A, <_A \rangle$ and $\mathcal {B} = \langle B, <_B \rangle$ such that there exists a y satisfying the two conditions:

• $A \subsetneq B$;

• $B \setminus A = \{ y\}$; and

• $\forall x \in A \; y \not <_B x$,

is a witness to the link from $\textsf{A}$ to $\textsf{B}$.

Take a path $( \mathsf {A_0}, \mathsf {A_1}, \ldots )$. A witness to that path is any sequence $( \mathcal {A}_0, \mathcal {A}_1, \ldots )$ of realizations of the corresponding elements of the path such that for any i, the pair consisting of $\mathcal {A}_i$ and $\mathcal {A}_{i+1}$ is a witness to the link from $\mathsf {A_i}$ to $\mathsf {A_{i+1}}$.

So: a witness to the link from one causet to another is a pair of realizations; a witness to a path to a causet is a sequence of realizations. Notice that in the first case the witness is a witness for the link; in the second case, one causet might be achievable by different paths, and so a witness to one path might not be a witness to a different path to the same causet.

Theorem 1

Every causet is achievable by a csg-path.

Proof

Recall that causets are the order types of countable past-finite posets. Given a causet $\textsf{K}$, we take its realization $\mathcal {K} = \langle K, < \rangle$. To find a csg-path to $\textsf{K}$, we will construct a witness to this path, i.e., ($\dagger$) a sequence of past-finite countable posets $(\mathcal {A}_0, \mathcal {A}_1, \ldots )$, with each $\mathcal {A}_i = \langle A_i, <_i\rangle$, $<_i = <_{\mid A_i}$, and such that (i) $K = \bigcup _i A_i$ and (ii) $A_{i+1}\setminus A_i = \{y\}$ and $\forall x \in A_i\; y \not <_{i+1} x$. In our proof we will number the elements of K in a way that delivers the sought-after sequence of posets.

To this end we divide, not necessarily in an exhaustive manner, the set of natural numbers $\mathbb {N}$ into a countable family of countable sets $N_1, N_2,\ldots$, for instance by taking $N_k = \{(2k +1) 2^s | s \in \mathbb {N} \cup \{0\} \}$. We will number the elements of K in stages. At stage 1 we pick the set $M_1$ of all minimal elements of $\mathcal {K}$ (note that $M_1$ might happen to be infinite), we arrange $M_1$ arbitrarily into a sequence, and then enumerate this sequence by elements of $N_1$. We move then to stage 2, at which we consider the poset $\mathcal {K}_1 = \langle K{\setminus } M_1, <_{\mid K{\setminus } M_1} \rangle$. Like above, we pick the set $M_2$ of all minimal elements $\mathcal {K}_1$, arrange $M_2$ arbitrarily into a sequence, and enumerate this sequence by elements of $N_2$, subject to the following condition: we assign to $x\in M_2$ the smallest element from $N_2$ that has not been used as a label yet, and which is greater from the labels of all $y \in K$ such that $y < x$ (as there are only finitely many ys below x, thanks to $\mathcal {K}$ being past-finite, we do not run out of labels).¹⁶ Generally, for $m \ge 1$ we take at stage m the set $M_m$ of minimal elements of $\mathcal {K}_{m-1} = K \setminus (\bigcup _{i = 0}^{m-1} M_i)$, arrange $M_m$ into a sequence, and enumerate this sequence by $N_m$ subject to the condition that the label assigned to $x \in M_m$ is the smallest number from $N_{m}$ that has not been used as a label yet, and which is greater from the labels of all $y \in K$ such that $y < x$. Every element $x \in K$ is above finitely many elements of K, and hence there is some set $M_i$ to which x belongs. Elements of $M_i$ are then labeled by elements of $N_i$, so x has some label assigned to it. Thus, every element of K has a label, and moreover, by this construction, labels respect the poset ordering, i.e., if $x < y$ for $x, y \in K$, then the label of x is smaller than the label of y.

The result of this construction is that K can be written as a set of labeled elements, $K = \{x_{l_1}, x_{l_2}, x_{l_3}, \ldots \}$. This gives rise to the sequence of posets $\mathcal {A}_0, \mathcal {A}_1, \mathcal {A}_2, \mathcal {A}_3, \ldots$, where $\mathcal {A}_0$ is the poset based on the empty set, and for $i > 0$: $\mathcal {A}_i = \langle \{x_{l_1}, x_{l_2}, \ldots , x_{l_i} \}, <_{\mid \{x_{l_1}, x_{l_2}, \ldots , x_{l_i} \}} \rangle$. It is immediately obvious that this sequence satisfies conditions ($\dagger$), so it is a witness to a csg-path leading to causet $\textsf{K}$, indeed.¹⁷$\square$

Next comes a theorem concerning the opposite relation.

Theorem 2

For any csg-path there is a causet achieved by it.

Proof

Pick a csg-path $\gamma$. If $\gamma$ is finite, it has a last element, $\textsf{A}_n$ and $\gamma$ achieves $\textsf{A}_n$. If $\gamma$ is infinite, we recall that every two consecutive elements of it form a link. By the definition of link, we obtain a sequence of realizations $(\mathcal {A}_0, \mathcal {A}_1, \mathcal {A}_2, \ldots )$ of $(\textsf{A}_0, \textsf{A}_1, \textsf{A}_2, \ldots )$, respectively, such that $A_{i} \subsetneq A_{i+1}$, $A_{i+1} {\setminus } A_i = \{y_i\}$, and $\forall x \in A_i [y_i \not <_{i+1} x]$, where $\mathcal {A}_k = \langle A_k, <_k\rangle$. We claim that the order type $\textsf{K}$ of $\langle K, <\rangle$, with $K = \bigcup A_i$ and < defined by $x < y$ iff $\exists A_i\; [ x, y \in A_i \; \wedge x <_i y]$, is a causet. For an argument, two observations must suffice. (1) The union of countably many countable sets is countable; (2) For past-finiteness of $\langle K, <\rangle$ pick an arbitrary $x \in K$ and consider $B_{<x} = \{y \in K \mid y < x \}$. Hence $x \in A_i$ for some $A_i$. Then $B_{<x} \subseteq A_i$ as every element of $B_{<x}$ must have occurred in a poset below $\mathcal {A}_i$. Thus, since < and $<_i$ agree on $A_i$, we get $B_{<x} = \{y \in K \mid y <_i x \}$; since $A_i$ is past-finite, $B_{<x}$ is finite, hence $\langle K, <\rangle$ is past-finite. A final thing to note is that, by our definitions, $\gamma = (\textsf{A}_0, \textsf{A}_1, \textsf{A}_2, \ldots )$ is a csg-path to $\textsf{K}$, and $(\mathcal {A}_0, \mathcal {A}_1, \mathcal {A}_2, \ldots )$ is a witness to $\gamma$. $\square$

The two theorems above assure a perfect match between csg-paths and causets. This result crucially depends on the assumption of past-finiteness. For: consider a countably infinite anti-chain with some other element immediately above each element of the anti-chain (see Fig. 3). The order type of this poset is not achievable in the limit. Notice, however, that we can see this poset as resulting from adding a single element to the antichain so that no element of the antichain is above the new element. It is, then, only due to the fact that by our choice Definition 3 pertains exclusively to causets—and not to the more general class of order types—that the causet displayed in Fig. 3 is not formally a child of the infinite anti-chain causet.

Similar ideas or findings have been obtained in the literature. Brightwell and Luczak ([4], p. 18) state our Theorem 2 without proof. Dribus’s Theorem 4.6.3, stated in a different and more general framework, appears to achieve a similar result. We believe, however, that presenting proofs done in an order type framework may lead us to a better insight into the theory.

Fig. 3

This order type is not a causet, since past-finiteness fails. It is Alexandroff-set finite, however (see Sect. 3). Were the definition of “achievable in the limit” reformulated so as it apply to order types of Alexandroff-set finite posets, this order type would not be achievable in the limit

5.3 On Infinite csg-paths and Causets Achievable in the Limit

Let $\textsf{K}$ be a causet achievable in the limit, and $P_{\textsf{K}}$ be the set of csg-paths leading to $\textsf{K}$. We say that $\gamma , \gamma ' \in P_\textsf{K}$ are branching if they branch at some causet. Our next Lemma uncovers a fact about causets achievable in the limit by branching paths.

Lemma 1

Let $\textsf{K}$ be a causet achievable in the limit. If $\textsf{K}$ is achievable by two branching csg-paths, then $\textsf{K}$ is achievable by infinitely many csg-paths.

For a proof of this Lemma we need one definition and one auxiliary fact.

Definition 7

(composition of two causets from paths in $P_{\textsf{K}}$) Let $\textsf{A} \in \gamma$ and $\textsf{B} \in \gamma '$, where $\gamma , \gamma ' \in P_{\textsf{K}}$, and $\langle K, < \rangle$ be a realization of $\textsf{K}$. Let furthermore $\langle A, <_A \rangle$, $\langle B, <_B \rangle$ be realizations of $\textsf{A}$ and $\textsf{B}$, resp., and elements of witnesses to $\gamma$ and $\gamma '$, respectively, where these witnesses are built on the same set K.

We define the composition $\textsf{A} \otimes \textsf{B}$ as the order-type of $\langle A \cup B, <_{AB} \rangle$, where the ordering $<_{AB}$ is the restriction of < to $A \cup B$, i.e., $<_{AB} \; =\; <_{\mid A\cup B}$.

Fact 3

Let $\textsf{A}$ and $\textsf{B}$ be causets from paths in $P_{\textsf{K}}$. Then $\textsf{A} \otimes \textsf{B}$ is a causet.

Proof

Let $\textsf{A} \in \gamma$ and $\textsf{B} \in \gamma '$ for $\gamma , \gamma ' \in P_{\textsf{K}}$. Pick witnesses to $\gamma$ and $\gamma '$ that are built on the same set K, and take from these witnesses the realizations $\langle A, <_A \rangle$ and $\langle B, <_B \rangle$ of $\textsf{A}$ and $\textsf{B}$, resp. Then $\langle A \cup B, <_{AB} \rangle$ is a finite poset (by the definition of $<_{AB}$ since a restriction of a partial order is a partial order). Further, since each $\langle A, <_A \rangle$ and $\langle B, <_B \rangle$ is countable and past-finite, so is $\langle A \cup B, <_{AB} \rangle$. Thus, its order-type is a causet. $\square$

We now return to the proof of Lemma 1.

Proof

We show that given two branching csg-paths to $\textsf{K}$, there are infinitely many csg-paths to $\textsf{K}$. Consider two branching paths $\gamma _1 = \textsf{A}(0), \textsf{A}(1), \textsf{A}(2) \ldots$ and $\gamma _2 = \textsf{B}(0), \textsf{B}(1), \textsf{B}(2), \ldots$ from $P_{\textsf{K}}$, where the numbers in the parentheses indicate the cardinality of the underlying posets, so $\textsf{A}(0)$ is the order-type of the empty poset, $\textsf{A}(1)$ is the order-type of some one-element past-finite poset, etc. Suppose first there are infinitely many paths joining $\gamma _1$ and $\gamma _2$, that is, paths from $\textsf{A}(m)$ to $\textsf{B}(n)$ or from $\textsf{B}(m)$ to $\textsf{A}(n)$, where $m < n$. Then there are infinitely many csg-paths to $\textsf{K}$ and our lemma is proven. Let us thus suppose that there are only finitely many paths joining $\gamma _1$ and $\gamma _2$. It follows that there is a stage k above which the elements of the two paths are not joined, i.e. there are no paths from $\textsf{A}(m)$ to $\textsf{B}(n)$ and from $\textsf{B}(m)$ to $\textsf{A}(n)$ if $n> m > k$. We will now show that this supposition leads to a contradiction. Consider a witness $\mathcal {A}(0), \mathcal {A}(1), \mathcal {A}(2) \ldots$ to $\gamma _1$ and a witness $\mathcal {B}(0), \mathcal {B}(1), \mathcal {B}(2) \ldots$ to $\gamma _2$ that are based on the same set K, i.e., $\bigcup A(i) = \bigcup B(j) = K$. Pick some $n > k$ and note that for realization $\mathcal {A}(n) = \langle A(n), <_{A(n)}\rangle$ of $\textsf{A}(n)$ there is a causet $\textsf{B}(m^*)$ with the realization $\mathcal {B}(m^*) = \langle B(m^*), <_{B(m^*)}\rangle$ such that $A(n) \subseteq B(m^*)$ and $\textsf{B}(m^*)$ is the smallest causet satisfying this condition. [Such a $\textsf{B}(m^*)$ exists because $\bigcup A(i) = \bigcup B(j) = K$ and each A(i), B(j) is finite.] Now consider the sequence of causets

$$\begin{aligned}{} & {} \textsf{A}(n), \textsf{A}(n) \otimes \textsf{B}(1), \textsf{A}(n) \otimes \textsf{B}(2), \ldots \textsf{A}(n) \otimes \textsf{B}(n), \textsf{A}(n) \otimes \textsf{B}(n+1), \\{} & {} \quad \ldots , \textsf{A}(n) \otimes \textsf{B}(m^* ) = \textsf{B}(m^* ). \end{aligned}$$

By the construction, $n < m^*$. Some consecutive elements of this sequence might be identical. Yet, its first element and the last element, $\textsf{A}(n)$ and $\textsf{B}(m^* )$, cannot be identical because $k< n < m^*$ and our two paths cannot coincide above k. Thus, some consecutive elements are not identical; we now claim that consecutive non-identical elements of the above sequence form a link. Consider realizations $\mathcal {A}(n), \mathcal {B}(m)$, and $\mathcal {B}(m+1)$. If $B(m+1) \setminus B(m) \subseteq A(n)$, then $\textsf{A}(n) \otimes \textsf{B}(m) = \textsf{A}(n) \otimes \textsf{B}(m+1)$. Let thus $B(m+1) {\setminus } B(m) \not \subseteq A(n)$, which implies that there is a $b \in (B(m+1) \cup A(n)) {\setminus } (B(m) \cup A(n))$. Furthermore, we have $\forall b' \in B(m)\; b \not <_{B(m+1)} b'$ since $\textsf{B}(m) \prec \textsf{B}(m+1)$. Hence $\forall b' \in B(m)\; b \not <_{A(n) \cup B(m+1)} b'$. Analogously, $\forall a' \in A(n)\; b \not <_{A(n) \cup B(m+1)} a'$. For, since $\bigcup A(i) = \bigcup B(j)$, there must be some $A(m')$, first one among As to which b belongs. Thus, $\forall a' \in A(m')\; b \not <_{A(m')} a'$. Since $A(n) \subseteq A(m')$ and $b \in B(m+1)$, we get $\forall a' \in A(n)\; b \not <_{A(n) \cup B(m+1)} a'$. To sum up, $\forall a' \in (A(n) \cup B(m) \; b \not <_{A(n) \cup B(m+1)} a'$. We thus showed that $\textsf{A}(n)\otimes \textsf{B}(m) \prec \textsf{A}(n)\otimes \textsf{B}(m+1)$. Accordingly, every two consecutive elements of the sequence above are either identical, or form a link, so the sequence is a path from $\textsf{A}(n)$ to $\textsf{B}(m^*)$. This is a contradiction, since $m^*> n > k$ and, by our assumption, there are no such connecting paths. $\square$

Let us now discuss a few natural questions regarding paths and causets. The first two are not directly related to the main results of the paper, but we hope that they will make the notions more familiar to the Reader.

Is it true for a causet ${\textsf{K}}$ achievable in the limit by multiple csg-paths, that for any two $\gamma , \gamma ' \in P_{\textsf{K}}$ and any natural number n, $\gamma$ and $\gamma '$ coincide at some causet above the nth stage?

The answer is “no”. The argument is provided by the order type of the poset consisting of an infinite chain and an infinite anti-chain, both “starting” from a common base element (we may visualize it as an infinite letter L). To be more specific, let the chain be given by odd natural numbers starting with 0, and the anti-chain by even natural numbers, starting with 0 as well. Now, there is a csg-path $\gamma$ to our causet, a witness of which is given by the sequence of posets whose universes are produced by the recipe: begin with $\{ 0 \}$, then add 1, then 2, then 3, etc. (That is, the universes will be $\{ 0\}, \{0, 1\}, \{0,1, 2\}$, etc.) There is also a different csg-path $\gamma '$ to our causet with a witness constructed according to the following recipe: start with $\{ 0 \}$, add consecutively two first numbers from the chain, then one number from the anti-chain, then two numbers from the chain, then one number from the ani-chain. etc. So, the universes of posets constituting that witness to $\gamma '$ will be $\{0\}, \{0, 1\}, \{0, 1, 3\}, \{0, 1, 3, 2\}, \{0, 1, 3, 2, 5\}, \{0, 1, 3, 2, 5, 7\}, \{0, 1, 3, 2, 5, 7, 4\}$, etc. These two paths, $\gamma$ and $\gamma '$, coincide only at the two first elements, i.e., at the order type of $\{0\}$ and at the order type of the (0, 1)-chain. Moreover, this example shows that one can produce infinitely many paths like $\gamma$ and $\gamma '$ by which that causet is achievable.

Is it true that “every two csg-paths from $P_{\textsf{K}}$  coincide at some stage $n > 1$” implies “there is a stage $m> 1$  at which all csg-paths from $P_{\textsf{K}}$ coincide”?

The answer here is “no” as well. The order type $\textsf{K}$ of a poset consisting of an infinite chain $\{a_1, a_2, \ldots \}$ with a single element b incomparable to any $a_i$ from the chain is a counterexample (see the right causet in Fig. 4). Each csg-path to this causet is determined by a number n such that for every witness to that path, at the nth step b is added,¹⁸ so we may refer to paths in $P_{\textsf{K}}$ by natural numbers. Note then that if $k < l$, then the k csg-path coincides with the l csg-path at step l (and not earlier), i.e., the element of the path l which is the order type of a poset containing exactly l elements belongs to both l and k, and the same is not true for elements of l that are order types of posets of lower cardinality. Accordingly, every two csg-paths from $P_{\textsf{L}}$ coincide. However, there is no step at which all the csg-paths from $P_{\textsf{K}}$ coincide, because for any natural number n there is a csg-path to $\textsf{K}$ in which b is added after the nth step.

Fig. 4

Two causets, $\textsf{A}$ (left) and $\textsf{B}$ (right). $\textsf{A}$ is achievable in the limit, $\textsf{B}$ is achievable in the limit, and $\textsf{B}$ is not a child of $\textsf{A}$

This leaves us with one thornier question:

What are the necessary and sufficient conditions for a causet achievable in the limit to be achievable by a unique csg-path?

To address this query, we first need some definitions (recalling definition of $< \!\! \cdot \,$ and $\text { inc }$ on p. 8 will help).

Definition 8

(one-way causet) A one-way causet is a causet achievable in the limit and by a unique csg-path.

A poset $\langle A, < \rangle$ is an $\shortmid \! \centerdot$-poset iff $A = \{a_0, a_1, a_2\}$ such that (i) $a_0$ is immediately before $a_1$, $a_0 < \!\! \cdot \, a_1$, (ii) $a_0 \text { inc } a_2$, and $a_1 \text { inc } a_2$.

A crucial observation is that a diamond does not contain an $\shortmid \! \centerdot$-subposet (recall that what we call “diamond” is a poset $\langle \{a_0, a_1, a_2, a_3\}, <\rangle$ such that $a_0< \!\! \cdot \, a_1 < \!\! \cdot \, a_2$ and $a_0< \!\! \cdot \, a_3 < \!\! \cdot \, a_2$, with $a_1 \text { inc } a_3$).¹⁹ Posets containing diamonds behave weirdly: a diamond preceded by a chain and followed by an infinite chain yields an order type which is a one-way causet. If we “rotate it by 90 degrees”, however, i.e., if we consider a diamond with an infinite anti-chain attached to the diamond’s incomparable elements, the resulting poset can be enumerated in an infinite number of non-equivalent ways, yielding infinitely many csg-paths; by all these paths the causet based on “a single diamond + an infinite anti-chain” is achievable. Furthermore, the order type of an infinite chain with one incomparable element (which is a poset with an $\shortmid \! \centerdot$- subposet; see the right causet in Fig. 4 again), is a causet achievable in the limit by multiple csg-paths. These observations lie behind our concept of $\shortmid \! \centerdot$- subposet.

Lemma 2

Let $\textsf{K}$ be a causet achievable in the limit. Then $\textsf{K}$ is a one-way causet iff $\textsf{K}$ has a realization $\mathcal {K}$ that contains no $\shortmid \! \centerdot$-subposet.

Proof

$\Leftarrow \;$ Consider a causet $\textsf{K}$ and its realization $\mathcal {K} = \langle K, < \rangle$ that contains no $\shortmid \! \centerdot$-subposet. We will argue that $\textsf{K}$ is a one-way causet, i.e., achievable by one csg-path only. In other words, all witnesses to csg-paths from $P_{\textsf{K}}$ must be pointwise-isomorphic. We aim to establish this last claim. To this end, let us first reflect on what $\mathcal {K}$ must be like if it contains no $\shortmid \! \centerdot$ - subposets. If $\mathcal {K}$ contains only anti-chains consisting of one element, then $\mathcal {K}$ is an infinite chain, so it is achievable by one csg-path only. Suppose thus that $\mathcal {K}$ contains an anti-chain l with at least 2 elements and assume first that l is infinite. Then there is no element immediately above any element of l. Otherwise, if there were b such that $a < \!\! \cdot \, b$ and $a \in l$, it had to be that $a' < \!\! \cdot \, b$ for every $a' \in l$, by the absence of $\shortmid \! \centerdot$-subposets; however, an infinite anti-chain with a common upper bound is not past-finite, and thus its order type is not a causet (see Fig. 3). So, if l is infinite, no element of it is followed by an element of K.

Let us next turn to finite anti-chains. Let l be a maximal anti-chain in $\mathcal {K}$ that contains at least two elements. We argue that there must be an element of K that is above some element of l, and hence – some element of K that is immediately above some element of l. Let us assume to the contrary and let $M_k$ be the highest stage to which an element of l belongs, and $a \in l \cap M_k$. Since l is a maximal anti-chain, if $l \subseteq M_k$, then $l = M_k$, so $M_k$ is finite. On the other hand, if there is $b \in M_k \setminus l$, then by our reductio assumption, b is incomparable to every element of l; hence $M_k \cup l$ is an anti-chain; by maximality of l, $M_k \cup l = l$, and hence – $M_k$ is finite. As $a \in M_k$, there must be then $a' \in M_{k-1}$ such that $a' < \!\! \cdot \, a$. $M_{k-1}$ is an anti-chain, and since $a' <a$, it must be finite (by the above). There is then $a'' \in M_{k-2}$, with $a'' < \!\! \cdot \, a'$. By the same observation, $M_{k-2}$ is finite. Since k is finite and every $M_1, \ldots , M_k$ is finite, and by the assumption, there are no higher stages in $\mathcal {K}$, we get that K is finite; contradiction with $\textsf{K}$ being achievable in the limit. Thus, for a finite and maximal anti-chain l there are $a \in l$ and $b \in K$ such that $a< \!\! \cdot \, b$. However, by the absence of $\shortmid \! \centerdot$-subposets, b must be immediately above every element of l. Note that b need not be a unique common bound of l immediately above all elements of l.

Now, if $l = \{a_1, a_2, \ldots \, a_n\}$ has multiple upper bounds $\{b_1, b_2, \ldots \}$ immediately above it, then either (i) there are finitely many such bounds and all these bounds have a (possibly non-unique) common upper bound immediately above them, or (ii) there are infinitely many such bounds and none of them is followed by an element of K. The case (i) is continued in a similar manner: the next “layer” of immediate upper bounds is considered, and so on.

Putting these observations together, consider the stages of $\mathcal {K}$. Stage $M_1$ consists of minimal elements of $\mathcal {K}$; if it is infinite, it is the final stage. Otherwise there is the stage $M_2$ that consists of the common upper bounds of the elements of $M_1$. If that stage is infinite, it is the final stage. Otherwise there is the stage $M_3$ that consists of the common upper bounds of the elements of $M_2$. If that stage is infinite, ..., etc.

Now, although the elements of each stage can typically be ordered in many ways, with these orderings giving rise to different witnesses to csg-paths in $P_{\textsf{K}}$, so we may have, e.g., say, $(\mathcal {A}_0, \mathcal {A}_1, \mathcal {A}_2, \ldots )$ and $(\mathcal {A}'_0, \mathcal {A}'_1, \mathcal {A}'_2, \ldots )$, the order types of corresponding elements, $\mathcal {A}_i$ and $\mathcal {A}'_i$, must be the same: and hence these sequences are witnesses to one and the same csg-path in $P_{\textsf{K}}$. [This can be elaborated further, using labeling – a crucial fact here is that labels of all elements of $M_i$ are lower than the labels of all elements of $M_{i+1}$, so a reordering of a stage does not produce different csg-paths.]

$\Rightarrow$ We argue for the contraposition; accordingly, we assume there is a realization $\mathcal {K}$ of $\textsf{K}$ that contains a $\shortmid \! \centerdot$-subposet and aim to construct multiple csg-paths to $\textsf{K}$. Let the $\shortmid \! \centerdot$-subposet of $\mathcal {K}$ be given by $\{a_0, a_1, a_2\}$ and $a_0 < \!\! \cdot \, a_1$, $a_0 \text { inc } a_2$, and $a_1 \text { inc } a_2$. Clearly, for some k, $a_0 \in M_k$ and $a_1 \in M_{k+1}$.²⁰ There are then four options as to where $a_2$ is located: (i) $a_2 \in M_k$ (ii) $a_2 \in M_{k+1}$, (iii) $a_2 \in M_i$ with $i < k$, and (iv) $a_2 \in M_i$ with $i > (k+1)$. As case (iii) involves case (i), and case (iv) involves case (ii),²¹ we may restrict our attention to cases (i) and (ii) only. We discuss in detail only case (i), leaving (ii) to the Reader.

The idea is to construct two different labelings l and $l'$ of $\mathcal {K}$, such that they induce different sequences of countable past-finite posets, which in turn yield different csg-paths in $P_{\textsf{K}}$. For the labeling, we use the the grouping of natural numbers given by the formula $N_k = \{(2k +1) 2^s | s \in \mathbb {N} \cup \{0\} \}$ for $k \in \mathbb {N}$. We first require that l and $l'$ agree on all $M_i$ for $1 \le i < k$, i.e., for $b \in \bigcup _{i =1}^{k-1} M_{i}$: $l(b) = l'(b)$. To further describe the working of l: we order $M_k$ such that first come all the predecessors $b_1, b_2, \ldots b_n$ of $a_1$ (so $a_0 = b_i$ for some $1 \le i \le n$); these are followed by $a_2$, and then go the remaining elements of $M_k$. The last predecessor $b_n$ of $a_1$ receives the label $(2k +1) 2^s$, where s depends on the number and the location of the elements of K below $a_1$; by the rules of labeling then $l(a_2) = (2k +1) 2^{s+1}$. Turning to $M_{k+1}$, we take care to order it so as it start with $a_1$, so $a_1$ gets the label $l(a_1) = (2(k+1) +1) 2^{s} = (2k +3)2^s$. As required, $l(a_1)$ is the smallest number of the required form that is larger than any $l(b_i)$, as $(2k +1) 2^s < (2k +3)2^s$ but $(2k +1) 2^s \not < (2k +3)2^{s-1}$. Furthermore, $l(a_1) < l(a_2)$, as $(2k +3)2^s < (2k +1) 2^{s+1}$. In sum, l yields this ordering of labels:

$$\begin{aligned} l(b_1)< l(b_2)< \ldots< l(b_n)< l(a_1) < l(a_2). \end{aligned}$$

As for the labeling $l'$, it diverges from l at stage k only, as it assumes that $M_k$ is ordered in a way that starts with sequence $(a_2, b_1, \ldots , b_n)$. Now, $b_n$ receives the label $l'(b_n) = (2k+1) 2^{s+1}$; since there are n $b_i$’s, $l'(a_2) = (2k +1) 2^{s-n+1}$, and $l'(a_1) = (2(k+1) +1) 2^{s +1}$, so as $l'(a_1)$ be the smallest number of the required form that is larger than $l'(b_n)$. We thus get the following ordering of labels:

$$\begin{aligned} l'(a_2)< l'(b_1)< l'(b_2)< \ldots< l'(b_n) < l'(a_1). \end{aligned}$$

Now, each labeling, l or $l'$, yields a sequence of posets – a witness to a csg-path in $P_{\textsf{K}}$. To be specific, let l yield the sequence $(\mathcal {A}_0, \mathcal {A}_1, \mathcal {A}_2, \ldots )$ and $l'$ — the sequence $(\mathcal {A}'_0, \mathcal {A}'_1, \mathcal {A}'_2, \ldots )$. Consider now $A_{l(a_1)}$. By the construction, $A_{l(a_1)}$ has exactly one element in $M_{k+1}$ and exactly n elements in $M_{k}$. Note now that among the posets induced by the labeling $l'$, there are no posets isomorphic to $A_{l(a_1)}$: if $A_m'$ has one element in $M_{k+1}$, it must have at least $(n+1)$ elements in $M_{k}$. Thus, the two sequences of posets are not point-wise isomorphic, and hence they induce two different csg-paths from $P_{\textsf{K}}$.

Finally, we give a hint about case (ii). For both l and $l'$ we order $M_k$ by putting first all the predecessors $b_1, \ldots , b_n$ of $a_1$, then all the predecessors $b'_1, \ldots , b_m'$ of $a_2$, and then the remaining elements of $M_k$. Note that the sets $\{b_1, \ldots , b_n\}$ and $\{b'_1, \ldots , b_m'\}$ are not identical, thanks to the ordering in case (ii). Then we order $M_{k+1}$ for l such that it starts with $(a_1, a_2)$ whereas for $l'$ – such that it starts with $(a_2, a_1)$. Now among the posets induced by the labeling l there is one A that has exactly one element in $M_{k+1}$ and exactly n elements in $M_k$. There is no isomorphic poset to A among posets induced by $l'$: if a poset of the latter kind has has exactly one element in $M_{k+1}$, then it must have at least $m+n$ elements in $M_k$. By the observation above, $n \ne m+n$, so indeed l and $l'$ induce sequences of posets that are not point-wise isomorphic; such sequences are witnesses to different csg-paths to $\textsf{K}$. $\square$

To comment on the Lemma above, intuitively speaking, causets achievable in the limit whose realizations do not contain $\shortmid \! \centerdot$ subposets are particular. But there are uncountably many of them:

Fact 4

There are uncountably many infinite causets whose realizations contain no $\shortmid \! \centerdot$-subposets.

Proof

Note that neither brooms nor braids contain $\shortmid \! \centerdot$-subposets. The result follows from the fact that there are uncountably many infinite braids (see proof of Fact 1). $\square$

Fact 5

There are uncountably many infinite causets whose realizations contain $\shortmid \! \centerdot$-subposets.

Proof

Take an at least two-element realization of a braid. Add to it an element incomparable with all other elements. The resulting poset contains an $\shortmid \! \centerdot$-subposet. This can be done for any of the uncountably many infinite braids, in each case resulting in a different causet.

The moral of the story told by our above result is that, with the exception of causets whose realizations do not contain $\shortmid \! \centerdot$-subposets, a causet achievable in the limit is achievable by multiple csg-paths. Furthermore, if it is achievable by two branching csg-paths, it is achievable by infinitely many csg-paths.

We end the topic of one-way causets with a corollary on the above Lemma:

Corollary 1

Let $\textsf{K}$ be a causet achievable in the limit by a csg-path $= (\textsf{A}_0, \textsf{A}_1, \ldots )$ such that for some $n \in \mathbb {N}$, $\textsf{A}_n, \textsf{A}_{n-2} \in p$ and a realization $\mathcal {A}_n$ contains an $\shortmid \! \centerdot$-subposet $\langle \{a_0, a_1, a_2\}, <\}$, with $a_0 < \!\! \cdot \, a_1, a_0 \text { inc } a_2$, $a_1 \text { inc } a_2$, whereas $\{ a_1, a_2\} \cap A_{n-2} = \varnothing$ for any realization $\mathcal {A}_{n-2} = \langle A_{n-2}, <\rangle$ of $\textsf{A}_{n-2} \in p$. Then there are at least two csg-paths in $P_{\textsf{K}}$ that coincide at $\textsf{A}_{m} \in p$, for any $0 \le m \le n-2$.

Proof

There is a realization of $\textsf{K}$ that contains $a_0, a_1, a_2$. Assume $a_0, a_2 \in M_k$ for some k (the case with $a_1, a_2 \in M_k$ is analogous – see the proof of Lemma 2 above). Consider next two labelings, l and $l'$, that agree on stages below $M_k$, but disagree on $M_k$. For l, the stage $M_k$ is ordered starting with $(a_0, a_2)$, whereas for $l'$ – $M_k$ is ordered starting with $(a_2, a_0)$. As argued in the Lemma above, l and $l'$ induce different csg-paths in $P_{\textsf{K}}$. As l and $l'$ below $M_k$, these paths agree up to (inclusive) a causet whose realization has exactly one element in stage $M_k$– this is $\textsf{A}_{n-2}$. $\square$

5.4 What Happens at a Causet?

The final topic is the behavior of causets other than those achievable in the limit (all such causets are finite, i.e. are order types of finite past-finite posets). Two questions loom large: how many csg-paths coincide at an arbitrary finite causet? And, how many csg-paths cross at an arbitrary causet? The first question is answered by this Fact:

Fact 6

Every finite causet belongs to uncountably many csg-paths.

Proof

We modify the proof of Fact 1. Let $\textsf{A}$ be a finite causet. To produce uncountably many csg-paths through $\textsf{A}$, we “conjoin” $\textsf{A}$ with all infinite braids that represent decimal expansions of real numbers from the (0, 1) segment, in the following sense. We take a realization $\mathcal {A}$ of $\textsf{A}$, pick a maximal element a of $\mathcal {A}$, and add above a an infinite sequence of generalized diamonds, in the sense of Definition 5. We take the decimal expansion of a number $x \in (0, 1)$ and make sure that the widths of consecutive generalized diamonds are the same as consecutive digits in the expansion of x. The result is a countably infinite past-finite poset, so its order type is an infinite causet, so it is achievable in the limit by csg-paths. Among these paths there are ones that contain $\textsf{A}$. Next consider all infinite causets resulting from conjoining $\textsf{A}$ with braids representing decimal expansions of any number from (0, 1). Clearly, there are uncountably many such infinite causets. As distinct infinite causets must be achievable by distinct csg-paths, by picking for each causet of that sort a csg-path containing $\textsf{A}$, we get that there are uncountably many csg-paths containing $\textsf{A}$. $\square$

Recall the notion of csg-paths crossing at a causet: two csg-paths cross at a causet $\textsf{A}$ if they coincide at $\textsf{A}$ but coincide neither immediately below $\textsf{A}$ nor immediately above $\textsf{A}$. The next Fact contains two observations relevant to this issue.

Fact 7

• (1) For any finite and non-empty causet $\textsf{A}$, there are csg-paths that coincide at $\textsf{A}$, but do not coincide immediately above it.

• (2) For any finite causet $\textsf{A}$, if a realization $\mathcal {A}$ of $\textsf{A}$ contains two maximal elements that belong to different stages $M_k, M_l$, $k \ne l$, then there are csg-paths that coincide at $\textsf{A}$, but not immediately below it.

Proof

• (1) As a realization $\mathcal {A}$ of $\textsf{A}$ has a non-empty base set A, we construct two witnesses to the csg-paths in question, which we will call “vertical” and “horizontal”. For the vertical sequence of countable past-finite posets, we pick a maximal element a of $\mathcal {A}$, and keep adding elements above a producing a single infinite chain above a. For the horizontal sequence, we add, stepwise, an infinite anti-chain to $\mathcal {A}$. The two sequences have an identical element, $\mathcal {A}:= \mathcal {A}_n$, but their $(n+1)$th elements are non-isomorphic.

• (2) Let a realization $\mathcal {A} = \langle A, <\rangle$ of $\textsf{A}$ contain two maximal elements $a_1 \in M_k$ and $a_2 \in M_l$, where $k \ne l$. Then there are two countable past-finite posets $\mathcal {A}' = \langle A', <'\rangle$ and $\mathcal {A}'' = \langle A'', <''\rangle$, where $A':= A{\setminus } \{a_1\}$, $A'':= A{\setminus } \{a_2\}$, $<':= <_{\mid A'}$, and $<'':= <_{\mid A''}$. The two posets give rise to different causets $\textsf{A}'$ and $\textsf{A}''$ as $\mathcal {A}'$ and $\mathcal {A}''$ are different at $M_k$ and $M_l$, so they are non-isomorphic. Moreover, $(\textsf{A}', \textsf{A})$ forms a link and $(\textsf{A}'', \textsf{A})$ forms a link, so each pair is contained in a different csg-path. These paths coincide at $\textsf{A}$ but not immediately below it.

$\square$

By the definition of crossing, since infinite causets are achievable in the limit only, no csg-paths cross at an infinite causet. By this observation and the Fact above, we obtain the following Lemma:

Lemma 3

If $\textsf{A}$ is finite and its realization $\mathcal {A}$ contains two maximal elements that belong to different stages $M_k, M_l$, $k \ne l$, then some csg-paths cross at $\textsf{A}$.

Proof

Pick an $\textsf{A}$ as in the premise. Consider two csg-paths $\gamma$ and $\gamma '$ that end with $\textsf{A}$, but do not coincide below $\textsf{A}$ – they exist by Fact 7 (2). Consider then some two csg-paths coinciding at $\textsf{A}$ but not immediately above it, guaranteed to exist by Fact 7 (1). Take their upper segments $\tau$ and $\tau '$ that start immediately above $\textsf{A}$, and adjoin $\tau$ to $\gamma$ and $\tau '$ to $\gamma '$. As a result, we get two csg-paths crossing at $\textsf{A}$. $\square$

Lemma 3 states a sufficient condition for csg-paths crossing at a causet. Note, however, that this is not a necessary condition, and a counterexample is the four-element causet of the N shape. Two csg-paths cross at this causet, yet its realization has two maximal elements, both at stage 2.

We end this topic with a statement of the necessary condition for csg-paths crossing at a causet. To this end we need the intuitive notion of a subposet in the past of a given element:

Lemma 4

Let $\textsf{A}$ be a causet at which csg-paths cross. Then there is a realization $\mathcal {A}$ of $\textsf{A}$ that contains two maximal elements $a_1$ and $a_2$ and such that the subposet of $\mathcal {A}$ in the past of $a_1$ is not isomorphic to the subposet of $\mathcal {A}$ in the past of $a_2$.

Proof

We leave the proof to the Reader, hinting that it needs to be shown that $\mathcal {A}' = \langle A', <'\rangle$ and $\mathcal {A}'' = \langle A'', <''\rangle$ are non-isomorphic, where $A':= A{\setminus } \{a_1\}$, $A'':= A{\setminus } \{a_2\}$, $<':= <_{\mid A'}$, and $<'':= <_{\mid A''}$. Note also that since at $\textsf{A}$ csg-paths cross, $\textsf{A}$ is finite, i.e., it is based on finite posets. $\square$

6 Discussion and Conclusions

We defined causets as the order types of past finite countable posets. We introduced paths of classical sequential growth (csg-paths) and proved a number of their properties. Such paths can be viewed as possible evolutions of a system, which (given the intentions of causet theorists) might be identified with our physical universe. To sum up our findings:

By definition, all csg-paths begin with the causet based on the empty set. There are uncountably many infinite causets and uncountably many infinite csg-paths (Fact 1). There is no strict partial ordering on the class of all causets that meshes naturally with the link relation on causets (Fact 2). Every causet is achievable by a csg-path (Theorem 1) and every csg-path achieves a (unique) causet (Theorem 2). If a causet is achievable in the limit by two branching csg-paths, then it is achievable by infinitely many csg-paths (Lemma 1). We give sufficient and necessary conditions for a causet achievable in the limit to be achievable by exactly one csg-path (Lemma 2). The consequence of these conditions is that there are uncountably many infinite causets achievable by exactly one csg-path, and there are also uncountably many infinite causets achievable by at least two csg-paths, and hence, by infinitely many csg-paths (Facts 4 and  5). Each finite causet belongs to uncountably many csg-paths (Fact 6). In Lemmas 3 and 4 we give sufficient and necessary conditions for csg-paths crossing at a causet.

The picture that emerges from these results looks somewhat disorderly. Although many csg-paths continue separately, many others coalesce, then branch or cross at later phases. Since CSG is supposed to accommodate indeterministic becoming, the branching of csg-paths is to be expected, as it is naturally read as describing alternative possible evolutions following a given causet. It is the coalescing, i.e., two or more csg-paths achieving the same causet, that might be somewhat troublesome. Although in our everyday talk we readily acknowledge that a state of affairs might be achieved by different alternative processes, we equally readily acknowledge that once a state of affairs is given, it has been achieved by exactly one way, and it is a matter of fact what this way is.

Providing an interpretation of coalescing csg-paths (and csg-paths themselves) presents a major challenge for CSG. The goal is to propose an objective and mind-independent interpretation of such paths, understood as alternative paths. As the word “alternative” suggests, such paths are incompatible, that is, they correspond to growth processes such that the occurrence of one implies the nonoccurrence of all the others, while “coalescing” means that they achieve numerically the same (not merely qualitatively the same) object. In a nutshell, the problem is this: how can two incompatible paths achieve one and the same object?

The challenge is analogous to that of understanding Borges’s The Garden of Forking Paths. The climax of that story is the murder of one Stephen Albert in England during WWI, a keen researcher of a time labyrinth allegedly left by a Chinese scholar, Ts’ui Pên, some centuries before. The scholar was murdered by an unknown perpetrator, and what was left of his work was considered of little import by his contemporaries and forgotten. While contemplating the further details of Borges’s story, the reader likely develops the feeling that the murder of Stephen Albert and the murder of Ts’ui Pên were one and the same event. But how can that be? There were different paths (literally) that led to the death of Stephen Albert / Tsui Pên, one passing through England in 1916, and the other through China some centuries before. Could these paths really coalesce in a single event?

We leave these philosophical issues for our future work.²²

Appendix

In this appendix we attempt to clarify the notion of invariance under relabeling. Standardly, invariance under transformations requires a set S of objects together with a class of transformations C from S to S that forms a group. A subset $S' \subseteq S$ is an invariant of C iff C preserves $S'$, i.e., for every $f \in C$ and every $x \in S'$: $f(x) \in S'$. We synonymously say that $S'$ is invariant under transformations C in this case. To speak about relabeling invariance, we thus need to specify what S, $S'$, and C are in our case.

The context for this Appendix is the relation between order types and the invariants of relabelings that preserve natural labeling, discussed above on p. 13. We will argue that there are labeled posets such that their order type (i.e. their isomorphism equivalence class) does not correspond in any natural way to any class of posets invariant under some class of relabelings. We should thus keep these two notions apart. Since it is enough to use finite posets to make our point, we assume from now on that all posets under discussion are finite.

We begin with labelings of posets. Although there are a few ways to make this concept precise, a labeling l should assign consecutive natural numbers to all elements of a poset, starting with 1. We intend our approach to allow us to impose—when needed—the formal condition of natural labeling (see Sect. 2), i.e., ($\dagger$) $x< y \Rightarrow l(x) <_{\mathbb {N}} l(y)$, where $<_{\mathbb {N}}$ is the standard ordering on the set of natural numbers $\mathbb {N}$.

Let $\mathbb {N}_n :=\{1, \ldots , n\}$. A labeling l of the poset $\langle A, <\rangle$ is a bijection $A \mapsto \mathbb {N}_{|A|}$. A natural labeling l of $\langle A, < \rangle$ additionally satisfies the condition $(\dagger )$ for every x, y $\in A$. Note that a labeling does not bear the property of being natural in itself: one and the same l might be a natural labeling of $\langle A, < \rangle$, and not be a natural labeling of some $\langle A, <' \rangle$.

A labeled poset is then defined as a poset together with one of its labelings (natural or not), i.e., a tuple $\langle \langle A, <\rangle , l \rangle$. A naturally labeled poset is a tuple consisting of a poset together with one of its natural labelings.

A relabeling of a poset $\langle A, < \rangle$ is a bijection $\phi$: $\mathbb {N}_{|A|} \mapsto \mathbb {N}_{|A|}$, that is, it is a permutation of the set of the first |A| natural numbers. If $\langle \langle A, < \rangle , l \rangle$ is a labeled poset, then so is $\langle \langle A, < \rangle , \phi \circ l \rangle$. Note that the identity function is a (trivial) relabeling.

Some nontrivial relabelings may preserve the naturalness of some labeled posets. It might even happen that, given some poset $\langle A, < \rangle$, the set of all naturally labeled posets $\langle \langle A, < \rangle , l \rangle$ is invariant under some non-singleton set of relabelings (i.e., a set consisting of something more than just the identity permutation). An example of that is depicted in Fig. 5. The two-element set of all naturally labeled posets based on some “V”-poset (situated to the left of the vertical bar) is invariant under the two-element set of relabelings consisting of the permutations (1)(2)(3) and (1)(23): these two relabelings do not take us outside the set of the naturally labeled posets, and trivially form a group under $\circ$. In a sense, then, we can abstract away from the details of the two natural labelings and perhaps Sorkin would indeed be justified in saying that the order type of the “V”-poset somehow corresponds to the class consisting of the two labeled posets to the left of the vertical bar (i.e. to the class of all naturally labeled “V”’s made from some particular three elements).

Fig. 5

Labeled posets based on the V-poset. The subset of naturally labeled posets is on the left: it is invariant under the class of relabelings consisting of the permutations (1)(23) and (1)(2)(3)

However, we cannot count on this in general. Consider some $\shortmid \! \centerdot$-poset $\mathcal {B}$ (see Definition 8 above) and its 6 possible labelings, depicted in Fig. 6. The leftmost three are the natural ones. Note that for any non-trivial relabeling $\phi$ of $\mathcal {B}$ there is a natural labeling l of $\mathcal {B}$ such that $\phi \circ l$ is not a natural labeling of $\mathcal {B}$. The immediate conclusion is that the three-element set of all naturally labeled posets based on $\mathcal {B}$ is not invariant under any class of relabelings that includes anything more than the identity permutation.

Fig. 6

All labeled posets based on some $\shortmid \! \centerdot$-poset $\mathcal {B}$. All the naturally labeled ones are to the left of the vertical bar. The only relabeling under which the set consisting of them is invariant is the identity permutation (1)(2)(3)

It looks as if, then, the order type of $\mathcal {B}$, i.e. its isomorphism class, does not correspond to any class of labeled posets based on $\mathcal {B}$ that would be invariant under some class of relabelings (comprising more than the identity transformation).