Abstract
Existing causal discovery algorithms are often evaluated using two success criteria, one that is typically unachievable and the other which is too weak for practical purposes. The unachievable criterion—uniform consistency—requires that a discovery algorithm identify the correct causal structure at a known sample size. The weak but achievable criterion— pointwise consistency—requires only that one identify the correct causal structure in the limit. We investigate two intermediate success criteria—decidability and progressive solvability—that are stricter than mere consistency but weaker than uniform consistency. To do so, we review several topological theorems characterizing which discovery problems are decidable and/or progressively solvable. These theorems apply to any problem of statistical model selection, but in this paper, we apply the theorems only to selection of causal models. We show, under several common modeling assumptions, that there is no uniformly consistent procedure for identifying the direction of a causal edge, but there are statistical decision procedures and progressive solutions. We focus on linear models in which the error terms are either non-Gaussian or contain no Gaussian components; the latter modeling assumption is novel to this paper. We focus especially on which success criteria remain feasible when confounders are present.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction: varieties of success
Shimizu et al. (2006) inaugurated a new era in causal discovery by demonstrating that if functional relationships are linear, noise terms are independent and non-Gaussian, and there are no unobserved confounders, then all causal relationships are uniquely identified from observational data, even without assuming faithfulness. The LiNGAM framework, as it was henceforth known, is significantly more friendly to causal discovery than the previously well-studied linear Gaussian regime, which drops the requirement of non-Gaussianity. When noise terms are Gaussian, only the Markov equivalence class of the structure generating the data is identifiable (Spirtes et al. 2000). Although some non-trivial causal information can be extracted from observational data, one would usually not be able to uniquely identify the full causal structure. Prior to the introduction of the LiNGAM framework, theorists of causal discovery had been focused on the hardest case: although the assumption of Gaussian noise made the subject analytically tractable, it made learning causal structure from observational data very difficult. Since then, many new and exciting identifiability results have been proven under a variety of modeling assumptions (for example, Hoyer et al. (2009) and Zhang and Hyvärinen (2009). See Glymour et al. (2019) for a review). These are significant theoretical developments, but an identifiability result is only the first step towards characterizing the difficulty of a learning problem.
An identifiability result suggests that a learning problem is not hopeless, but it does not mean that the problem is easy—in fact, it does not even mean that the problem can be solved by empirical means.Footnote 1 For this reason, it is necessary to go beyond identifiability results and analyze in what sense, if any, a causal discovery problem can be solved. For the most part, these discussions orient themselves around two solution concepts: pointwise and uniform consistency. The latter is a very strong notion of success which is achievable only if there exists a discovery method and a sample size n such that, no matter which causal structure is generating the data, the output of the method is correct with high probability for samples larger than n. The former is a very weak notion of success which requires only that there exists a discovery method such that, for every causal structure that may be generating the data, there is some sample size n after which the output of the discovery method is correct with high probability. The crucial difference between the two cases is whether the sample size n depends on (or is “uniform over") the causal structure generating the data. If there is no such dependence, then the output of the method is reliable so long as the sample is large enough. Otherwise, the situation is much worse: not only do we not know a priori how large a sample size is “large enough" for the method to be reliable, but we may get no sign from the method that the crucial sample size has been achieved.
If we are lucky, the problem we are interested in admits of a uniformly consistent solution. Unfortunately, typical causal discovery problems do not. It is possible to strengthen standard assumptions to allow for uniformly consistent solutions (Zhang and Spirtes 2003; Bühlmann et al. 2014), but these stronger assumptions are unattractive in that they rule out geometrically large sets of causal structures (Uhler et al. 2013). Uniform consistency, it seems, comes only at the cost of implausibly strong assumptions. On the other hand, weaker assumptions are sufficient to admit pointwise solutions. But the essentially asymptotic nature of this latter success concept leaves a lot to be desired from pointwise consistent methods. One such method always gives rise to another in the following way: while the sample size is less than \(10^5\), pick your output out of a hat; and after sample size \(10^5\), do as the original method recommends. Both the original method and the silly new one are both pointwise consistent—this success concept does not give us the resources to praise the one and condemn the other.
The trouble is that pointwise consistency is compatible with perverse finite-sample performance. In the linear Gaussian paradigm, Kelly and Mayo-Wilson (2010) show that, even when a causal orientation is identified, any pointwise consistent method can be forced to “flip" its judgement about the direction of the arrow, i.e. there are causal structures in which the method outputs one orientation with high probability at sample size \(n_1<n_2\), only to output the opposite orientation with high probability at \(n_2>n_1.\) See Fig. 1. The number of such flips that the method can be forced into is bounded only by the number of variables in the model. Moreover, there must be intermediate sample sizes at which the output of the method is essentially the outcome of a fair coin-flip. Note that this is not a failing of the method, but merely a reflection of the inherent difficulties which present themselves in the linear Gaussian setting—any consistent method can be made to exhibit the same behavior.
Causal “Flipping”—for any pointwise consistent method, there is a linear Gaussian parametrization of model \({\mathcal {M}}_3\) that will force the method first to conjecture model \({\mathcal {M}}_1\) at some sample size \(n_1\) and then conjecture model \({\mathcal {M}}_2\) at some sample size \(n_2 > n_1\). In other words, in the linear Gaussian setting, the probability that a consistent method outputs a model with an \(X \rightarrow Y\) edge vs. a \(Y \rightarrow X\) edge can be forced to alternate between arbitrarily close to one and arbitrarily close to zero, as shown in the lower right graph. See Kelly and Mayo-Wilson (2010)
In the linear Gaussian setting, “flipping" is the price of consistency; is the same true for (unconfounded) LiNGAM? Once again, the non-Gaussian setting is significantly friendlier to causal discovery: Genin and Mayo-Wilson (2020) show that, even though uniformly consistent methods do not exist, there are pointwise consistent discovery methods that avoid flipping. In other words, although uniform consistency is too strong a success concept to be feasible and pointwise consistency is too weak to be satisfactory, there are intermediate success concepts that are weak enough to be feasible in the LiNGAM regime and strong enough to rule out flipping behavior. For example, we say that a method is an \(\alpha\)-decision procedure if it is pointwise consistent and, at every sample size, the probability that it outputs an incorrect orientation is bounded by \(\alpha .\) So long as \(\alpha\) is small, such a method cannot exhibit flipping behavior since flipping requires that there is some sample size at which the method outputs an incorrect orientation with high probability. Genin and Mayo-Wilson (2020) show that in the unconfounded LiNGAM regime, \(\alpha\)-decision procedures for causal orientation exist for every \(\alpha >0.\) In broad strokes, such decision procedures succeed by suspending judgement until they discern a clear signal in the data that allows them to (with high probability) correctly orient an edge. Since the signal only becomes clearer with larger samples, flipping is avoided.
The preceding discussion conceals an ambiguity. It is clear that a method which outputs \(X\leftarrow Y\) when in fact \(X\rightarrow Y\) has made an incorrect orientation. The results of Genin and Mayo-Wilson (2020) show that we can construct methods that bound the probability of such misorientations to be arbitrarily small. But what about a method which omits an edge between X and Y when, in fact, such an edge exists? Unfortunately, it is not possible to bound the probability of such false negatives since weaker and weaker edges can approximate the absence of an edge arbitrarily well. However, it is still possible to prevent flipping behavior. Say that a method is \(\alpha\)-progressive if it is pointwise consistent and, for any two sample sizes, \(n_1<n_2\) the probability of correctly inferring the presence and orientation of an edge decreases by no more than \(\alpha .\) This is yet another success notion intermediate between poinwise and uniform consistency. Genin and Mayo-Wilson (2020) show that in the unconfounded LiNGAM regime, \(\alpha\)-progressive methods exist for the problem of inferring the presence and orientation of an edge, where \(\alpha\) can be chosen to be arbitrarily small (though not zero). In broad strokes, progressive methods infer that no edge exists until they detect a clear signal in the data that allows them to (with high probability) correctly orient an edge. They can be fooled into false negatives by weak edges, but one can bound the probability with which they flip between the absence and presence of an edge, or between competing orientations.
To summarize: in the (unconfounded) LiNGAM regime, although uniformly consistent methods do not exist, it is possible to do better than mere pointwise consistency. The precise sense of “better" depends on how much causal information you are willing to presuppose. The question of causal orientation is decidable, presupposing that some edge exists. On the other hand, the question of the presence and orientation of an edge is progressively solvable, though not decidable. Both senses of success are better than mere pointwise consistency and preclude flipping between competing answers.
The preceding naturally raises the question of what happens when we allow for the presence of unobserved latent variables. Hoyer et al. (2008) and, more recently, Salehkaleybar et al. (2020) demonstrate that if, in addition to the usual LiNGAM assumptions, we assume causal faithfulness, then causal ancestry relationships between observed variables are identified even in the presence of unobserved latents. In other words: if two faithful, confounded LiNGAM models generate the same distribution over the observed variables, then for every pair of observed variables X, Y, the models must agree on whether X is causally upstream of Y, Y is upstream of X, or neither is upstream of the other. Note that the models do not have to agree on which variables are direct causes of which others, only on which variables are ancestors of which others. Moreover, although all models generating the same distribution over the observed variables must agree on the causal ancestry relations between them, they may disagree on the strength of the causal effects.
But, as we have emphasized, identifiability results are only the first step in understanding the inherent difficulty of a causal discovery problem. As one might expect, allowing for confounders makes learning orientations more difficult. Genin (2021) shows that, although there exist pointwise consistent methods for learning the presence and orientation of causal ancestry relationships, causal ancestry is no longer decidable in the presence of unobserved latents. In other words: flipping between orientations returns once we allow for the presence of confounders. However, this disappointing result suggests several adjustments to the LiNGAM model that would recover decidability. In particular, Genin (2021) proposes that the standard assumptions might be strengthened to preclude exogenous noise terms with Gaussian components.Footnote 2 In this paper, we investigate a slightly stronger adjustment: no linear combination of noise terms can have a Gaussian component. We call the resulting regime the FLAMNGCo (“flamingo") model, for “Faithful Linear Acyclic Model with No Gaussian Components". This adjustment recovers decidability, even in the presence of unobserved confounders.
The methods used to prove these results are largely topological and draw heavily from Kagan et al. (1973). Many of the theorems stated here are already proven elsewhere, with the exception of the results in Sect. 7. We suppress the proofs of most lemmas and provide only the proofs that we take to be most illuminating, as befits an introduction. We attempt to collect here the most elementary proofs and provide all necessary prerequisites for understanding the key moves. Reader beware: although the results here suggest discovery algorithms, they do not, on their own, provide any. The results here stand to causal discovery as complexity theory stands to the design of algorithms. They reveal the inherent difficulty of causal discovery problems under various assumptions, which sets the standard for what counts as a good solution. Of course, that is not the same as actually furnishing such a solution, which we do not attempt here. What we do here is provide refinements of identifiability results which, ideally, would guide the design of future algorithms.
We emphasize that the discovery concepts that we investigate—and the topological theorems that characterize them—are applicable in other cases of model selection. In such cases (e.g., polynomial regression), uniform consistency is unattainable and pointwise consistency is too lenient. So although we focus exclusively on causal discovery, our results, we hope, will inspire researchers in other areas of model selection to develop algorithms that possess the intermediate success concepts that we investigate.
The rest of the paper is organized as follows. In the next section, we give mathematical definitions for the various success notions we have discussed in this introduction. In Sect. 3 we introduce the topological concepts and results that are invoked in the following. Section 4 introduces a menagerie of linear causal models. Section 5 states and proves the decidability and progressive solvability results for LiNGAMs with no latent variables. Section 6 shows that, although pointwise consistent solutions exist, the problem of causal orientation is no longer decidable when we allow for potential confounders. The final section shows how decidability (and progressive solvability) are recovered when the LiNGAM assumptions are strengthened to rule out linear combinations of exogenous terms with Gaussian components.
2 Varieties of success: mathematical definitions
Let \({\mathcal {M}}\) be a set of statistical models. Let \({\mathcal {O}}\) be the set of all random vectors taking values in \(\mathbb {R}^p,\) the space of observable outcomes. We assume there is a function \(P:M \mapsto P_M\) that maps each model in \({{\mathcal {M}}}\) to a random vector in \({\mathcal {O}},\) although we often equivocate between the random variable and the probability measure it induces on the Borel algebra over \(\mathbb {R}^p.\) In other words: the function P specifies a measurement model which maps the models in \({\mathcal {M}}\) to observable random vectors. We lift \(P(\cdot )\) to sets of models in the obvious way: if \({{\mathcal {A}}}\subseteq {\mathcal {M}}\), let \(P[{{\mathcal {A}}}] = \{ P(M) : M \in {{\mathcal {A}}}\}.\) We write \(P_M^k\) for the k-fold product measure.
A question \({\mathfrak {Q}}\) is a countable set of disjoint subsets of \({\mathcal {M}}.\) The elements of \({\mathfrak {Q}}\) are called answers. Note that the answers do not have to cover all of the models in \({\mathcal {M}}.\) For all \(M\in \cup {\mathfrak {Q}},\) let \({\mathfrak {Q}}_M\) denote the unique answer in \({\mathfrak {Q}}\) containing M. The answer to question \({\mathfrak {Q}}\) is identified iff \(P(M)\ne P(M')\) whenever \({\mathfrak {Q}}_M\ne {\mathfrak {Q}}_{M'}.\)
Given a question \({{\mathfrak {Q}}}\), we define a method \(\lambda = \langle \lambda _n \rangle _{n \in \mathbb {N}}\) to be a sequence of measurable functions \(\lambda _n:\mathbb {R}^{np} \rightarrow {{\mathfrak {Q}}}\cup \{{{\mathcal {M}}}\}\), where \(\lambda _n\) maps samples of size n to answers to the question; a method may also take the value \({{\mathcal {M}}}\) to indicate that the data do no fit any particular answer sufficiently well, and so we call \({{\mathcal {M}}}\) the uninformative answer. We require that the boundary region \(\partial \lambda _n^{-1}({{\mathcal {A}}})\) has Lebesgue measure zero for all n and every answer \({{\mathcal {A}}}\) in the range of \(\lambda _n\), as otherwise the method \(\lambda\) will be impossible to implement in practice.Footnote 3
Method \(\lambda\) is pointwise consistent for \({\mathfrak {Q}}\) if for all \(\epsilon >0\) and \(M\in \cup {\mathfrak {Q}},\) there is n such that \(P_M^k(\lambda _k={\mathfrak {Q}}_M)>1-\epsilon\) for all \(k\ge n.\) We say that \({\mathfrak {Q}}\) is decidable in the limit iff there is a pointwise consistent method for \({\mathfrak {Q}}.\) Method \(\lambda\) is uniformly consistent for \({\mathfrak {Q}}\) if for all \(\epsilon >0\) there is n such that for all \(M\in \cup {\mathfrak {Q}},\) \(P_M^k(\lambda _k={\mathfrak {Q}}_M)>1-\epsilon\) for all \(k\ge n.\) We say that \({\mathfrak {Q}}\) is uniformly decidable iff there is a uniformly consistent method for \({\mathfrak {Q}}.\)
For \(\alpha >0,\) method \(\lambda\) is an \(\alpha\)-decision procedure for \({\mathfrak {Q}}\) if (1) \(\lambda\) is pointwise consistent for \({\mathfrak {Q}}\) and (2) \(P_M^n(M\notin \lambda _n)\le \alpha\) for all \(M\in \cup {\mathfrak {Q}}\) and all sample sizes n. A question is statistically decidable (or simply decidable) if there is an \(\alpha\)-decision procedure for \(\alpha >0.\) For a summary of the varieties of decidability, see Table 1.
For \(\alpha >0,\) method \(\lambda\) is an \(\alpha\)-progressive solution for \({\mathfrak {Q}}\) if (1) \(\lambda\) is pointwise consistent for \({\mathfrak {Q}}\) and (2) \(P_M^{n_2}(\lambda _{n_2}={\mathfrak {Q}}_M)+\alpha >P_M^{n_1}(\lambda _{n_1}={\mathfrak {Q}}_M)\) for all \(M\in \cup {\mathfrak {Q}}\) and all sample sizes \(n_2>n_1.\) A question is progressively solvable if it has an \(\alpha\)-progressive solution for all \(\alpha >0.\)
Clearly, uniform decidability implies statistical decidability. Further, statistical decidability implies progressive solvability: if the chance of conjecturing the wrong answer is never greater than \(\alpha\), then the chance of producing the right answer can never drop by more than \(\alpha\). As the toy example in the next section shows, the converse of both those implications fails.
3 Topology, or the geometry of success
Topology is often described as the study of geometric properties conserved by stretching, but not cutting or gluing. That makes it sound remote from our concerns here. But topology is a kind of qualitative geometry, abstracting from numerical/metrical measures of distance, in favor of qualitative notions of “separation” and “arbitrary closeness.” These qualitative notions are just as important for understanding what can be learned from data as they are for understanding the geometry of cutting and gluing.Footnote 4 Statistical models that are “arbitrarily close/similar" are difficult to distinguish by observation. In contrast, models that are “separated" are more easily distinguished by data. In this section, we introduce some general topological definitions and explain how they can be used to characterize which statistical inference problems are hard and which are easier to solve.
In topology, a point w is a limit point of a region A if there are points lying in A that get arbitrarily close to w. These points may never arrive at w, but they are said to approximate w arbitrarily well. Roughly speaking, two regions are separated if neither contains limit points of the other. Two separated regions can become connected if you “glue” them together. And two connected regions can become separated if you “cut” them apart. So cutting and gluing fail to preserve qualitative relations of separation. As we shall see, this rough notion of separation can be refined in various ways.
Suppose we have two coins, either of which may be biased. We want to answer the question “Which (if either) of the coins are biased?”, but we are not interested in how far the coins deviate from fairness nor whether they are biased towards heads or tails. We can plot the degrees of bias of the coins on the X and Y axes of the plane, as shown in Fig. 2. In each quadrant, regions of different colors represent different possible answers/hypotheses to our question, and both the number of answers and the difficulty of answering the question depend upon how rich our background knowledge is.
Figure 2i, for example, depicts the situation in which background knowledge determines that (1) exactly one coin is biased and that (2) there is a known lower bound \(\epsilon > 0\) for the degree (if any) to which a given coin deviates from fairness. In other words, this quadrant represents a case in which the question “Which coin is biased?” has precisely two possible answers/hypotheses: (1) “Only coin 1 is biased, and its bias deviates from 1/2 by at least \(\epsilon _1 > 0\)” and (2) “Only coin 2 is biased, and its bias deviates from 1/2 by at least \(\epsilon _2 > 0\)”. Those two hypotheses are represented by the red and blue lines. This is a fortunate situation because there exists a uniformly consistent method for deciding between the red and blue hypotheses. Using \(\min \{\epsilon _1, \epsilon _2\}\), we can compute the smallest sample size by which a standard confidence region would allow us to, with high probability, correctly decide the question.
Figure 2ii depicts the situation in which exactly one of the coins is biased but there is no known lower bound on how much that coin deviates from fairness. Again, there are two possible answers to our question: “Only coin 1 is unfair” and “Only coin 2 is unfair.” And again, those two hypotheses are represented by the red and blue lines. However, notice the red and blue lines become arbitrarily close; although they do not intersect, they share a common limit point, the white dot, which represents the case that both coins are perfectly fair (a case that is, by assumption, ruled out by background knowledge).
In this case, uniform solutions no longer exist. Why? Roughly, both coins may be arbitrarily close to fairness. That is, no matter how large of a sample size n you name, there is a possible coin of bias \(M = 1/2 + \epsilon\) that would be indistinguishable from a fair coin after only n many flips. Thus, one cannot distinguish (a) the case in which coin 1 is fair and coin 2 has some tiny bias \(\epsilon\) from (b) the case in which coin 2 is fair but coin 1 has some tiny bias.
In this case, one cannot name a sample size a priori by which one is guaranteed, with high probability, to be able to answer the question. However, using a standard confidence region procedure, we could suspend judgement until the region excludes either the red or the blue hypothesis. By collecting larger and larger independent samples, we will eventually decide the question, without exposing ourselves to a high probability of inferring an incorrect hypothesis at any stage. In other words: the question in Fig. 2ii is decidable, although it is not uniformly decidable.
Figure 2iii depicts the situation in which background knowledge determines only that at most one of the coins is biased. There are now three possible answers: only coin 1 is unfair; only coin 2 is unfair, and neither is unfair. The new third possible answer is represented by the yellow dot at the hinge of the two lines.
If we ever want to converge to the right answer in the yellow (both fair) possibility, we must expose ourselves to a high chance of error in nearby blue and red possibilities. Thus, the problem is not decidable in the above sense: we cannot bound the chance of error.
However, progressive convergence to the truth is still possible. The intuitive way of achieving this is to conjecture “yellow” so long as a standard confidence region is consistent with yellow. Otherwise, conjecture a disjunction of all remaining hypotheses compatible with the confidence region.
What about the fourth quadrant? Here, background knowledge determines nothing about the coins: the bias of either coin may take any value. We ask: are an even (\(\textsf{yellow}\)) or an odd (\(\textsf{black}\)) number of coins biased? This question is not even progressively solvable. The way to see this is to notice that the distribution at the origin is arbitrarily well approximated by distributions on the axis; and, in turn, any axis distribution is arbitrarily well approximated by distributions in the sector. Thus, for any consistent method, there are sufficiently subtle sector possibilities in which the method can be made to flip from even to odd and then back to even (See Kelly and Mayo-Wilson (2010) and Genin and Kelly (2019) for more on the topology of flipping).
Figure 2 suggests that the topological relationships of the competing hypotheses determine in which sense the question is solvable. But how, exactly do they determine this? To illuminate this, we need a few more topological concepts. The topological closure of a region A, which we write \(\textsf{cl}(A)\), is the result of adding to A all of its missing limit points, if any. A region is topologically closed if it is identical with its closure. It is open if its complement is closed. Finally, it is clopen if it is both closed and open.
In the first quadrant, the blue and red hypotheses are both closed. In this case, the two hypotheses are not only disjoint, but their closures are also disjoint, i.e. \(\textsf{cl}(\textsf{red})\cap \textsf{cl}(\textsf{blue})=\varnothing .\) In the second quadrant, neither the blue nor the red hypothesis is closed since they are missing a limit point at the origin. Since they are both missing the same limit point, their closures intersect: \(\textsf{cl}(\textsf{red})\cap \textsf{cl}(\textsf{blue})\ne \varnothing .\) On the other hand, each is disjoint from the closure of the other: \(\textsf{red}\cap \textsf{cl}(\textsf{blue})=\varnothing\) and \(\textsf{blue}\cap \textsf{cl}(\textsf{red})=\varnothing .\) In the third quadrant, some answers intersect the closures of other answers, since \(\textsf{yellow}\subseteq \textsf{cl}(\textsf{red})\) and \(\textsf{yellow}\subseteq \textsf{cl}(\textsf{blue}).\) However, it is possible to order the answers \(\textsf{yellow}, \textsf{red}, \textsf{blue}\) such that each answer is disjoint from the closures of the answers that precede it. In the fourth quadrant, there is no such ordering of the answers: however we enumerate \(\textsf{yellow}\) and \(\textsf{black}\), the second answer will be consistent with the closure of the first. In what follows we shall see that it is these topological relations that turn out to be decisive for whether a question is decidable, or progressively solvable.
The example in Fig. 2 is rather simple; the relevant distributions are completely characterized by a parameter in the unit square. Moreover, our ordinary intuitions about the topology of the unit square are reliable guides to how difficult the various possibilities are to distinguish. However, it is unclear how to represent causal hypotheses in a standard Euclidean space and, even if we managed to do it, why should the standard Euclidean metric be informative about how hard causal models are to distinguish from each other? Indeed, we cannot rely on our usual Euclidean intuitions. However, there is a topology on probability distributions that does reliable capture this: the weak topology. We define the weak topology in what follows, but first we state the theorem characterizing decidability. The theorem is a minor modification of Theorem 3.2.4 in Genin and Kelly (2017).
Theorem 1
Let \(\textsf{cl}(\cdot )\) bet the closure operator induced by the weak topology. Suppose that every element of \(P_{{\mathcal {M}}}\) is absolutely continuous with Lebesgue measure. Then, \({{\mathfrak {Q}}}\) is decidable iff \(P_{{{\mathcal {A}}}}\cap \textsf{cl}(P_{{\mathcal {B}}})=\varnothing\) for each \({{\mathcal {A}}},{{\mathcal {B}}}\in {{\mathfrak {Q}}}.\)
Note that this condition entails that the question is identified, i.e. that \(P_{{\mathcal {A}}}\cap P_{{\mathcal {B}}}= \varnothing\) for each \({{\mathcal {A}}},{{\mathcal {B}}}\in {{\mathfrak {Q}}}.\) To ensure this paper is self-contained, we define the weak topology below. But what is important is that, by the above theorem (and others below) the weak topology captures the sense in which distinct sets of probability measures can be distinguished by finite samples. The above theorem says that if \(P_n\Rightarrow P\) in the weak topology, then the question \({{\mathcal {A}}}_1 =\{P_n: n \in \mathbb {N}\}\) vs. \({{\mathcal {A}}}_2 = \{P\}\) is not decidable. Conversely, if \({{\mathcal {A}}}_1\) does not contain a sequence of measures \(P_1, P_2, \ldots\) converging to P in the weak topology, then the question \({{\mathcal {A}}}_1\) vs. \({{\mathcal {A}}}_2= \{P\}\) is decidable. In our running example, the map \(x \mapsto P_x\) from parameters endowed with the Euclidean topology to probability distributions endowed with the weak topology enjoys a special property: a parameter x in the square is in the closure of a set of parameters A iff the distribution \(P_x\) induced by x is in the weak topological closure of the set of distributions \(P_A.\)Footnote 5 That is why our ordinary Euclidean intuitions track the relevant properties in this simple example.
To define the weak topology, let \({{{\mathcal {P}}}}={{{\mathcal {P}}}}_{{\mathcal {M}}}\) denote the set of all probability measures induced by models in \({{\mathcal {M}}}.\) The weak topology on \({{{\mathcal {P}}}}\) is defined by letting a sequence of Borel measures \(P_n\) converge weakly to P, written \(P_n\Rightarrow P\) iff \(P_n(A)\rightarrow P(A),\) for every A such that \(P(\partial A)=0\), where \(\partial (\cdot )\) is the boundary operator in the usual topology on \(\mathbb {R}^p.\) Henceforth, we write \(\textsf{cl}(\cdot )\) for the closure operator in the weak topology.
As promised, we give a topological condition that is sufficient for progressive solvability; necessary conditions are currently unknown. For a proof see, Theorem 3.6.3 in Genin (2018).
Theorem 2
Suppose that every element of \(P_{{\mathcal {M}}}\) is absolutely continuous with Lebesgue measure. If there exists an enumeration \({{\mathcal {A}}}_1, {{\mathcal {A}}}_2, \ldots\) of the answers to \({{\mathfrak {Q}}}\) such that \({{\mathcal {A}}}_j\cap \textsf{cl}({{\mathcal {A}}}_i)=\varnothing\) for \(i<j\), then \({{\mathfrak {Q}}}\) is progressively solvable.
Theorem 2 has important implications for causal discovery. It implies, for example, that there is a progressive solution to the question “To which Markov equivalence class does the unknown causal model belong?” if one assumes the underlying model is either discrete or linear Gaussian. See (Genin 2018, Theorem 3.6.5) for a proof.
Limiting decidability also has a topological characterization, first stated by Dembo and Peres (1994) and simplified somewhat in Genin and Kelly (2017).
Theorem 3
Suppose that every element of \(P_{{\mathcal {M}}}\) is absolutely continuous with Lebesgue measure. Suppose that (1) \({{\mathfrak {Q}}}\) is identified and (2) each element of \({{\mathfrak {Q}}}\) is a countable union of sets closed in the weak topology, then \({{\mathfrak {Q}}}\) is decidable in the limit.
Unfortunately, we know no purely-topological condition that is both necessary and sufficient for a problem to be uniformly decidable. Nonetheless, the simple example involving two coins above motivates a necessary condition for uniform decidability. Recall, the problem depicted in the upper-left quadrant of Fig. 2 is uniformly decidable, but the problem in the upper-right quadrant is not. The difference between the two problems is that, in the upper left quadrant, the topological closures of the two possible answers are disjoint, whereas in the upper right, the two answers have overlapping closures.
Theorem 4
Suppose every element of \(P_{{{\mathcal {M}}}}\) is absolutely continuous with respect to Lebesgue measure. If there are two distinct answers \({{\mathcal {A}}}, {{\mathcal {B}}}\in {\mathfrak {Q}}\) such that \(\textsf{cl}(P_{{{\mathcal {A}}}}) \cap \textsf{cl}(P_{{{\mathcal {B}}}}) \ne \emptyset\), then \({\mathfrak {Q}}\) is not uniformly decidable.
Proof of Theorem 4
Let \(P_M \in \textsf{cl}(P_{{{\mathcal {A}}}}) \cap \textsf{cl}(P_{{{\mathcal {B}}}})\). Hence, there are sequences \(M_1, M_2 \ldots \in P_{{{\mathcal {A}}}}\) and \(N_1, N_2 \ldots \in P_{{{\mathcal {B}}}}\) such that \(P_{M_j}, P_{N_j} \Rightarrow P_M\).
Suppose for the sake of contradiction that \({\mathfrak {Q}}\) is uniformly decidable, and let \(\lambda\) be a uniformly consistent method.
Then there is some sample size k such that \(P^j_{M_n}(\lambda _j = {{\mathcal {A}}}) > 1/2\) and \(P^j_{N_n}(\lambda _j = {{\mathcal {B}}}) > 1/2\) for all n and all \(j \ge k\).
By assumption \(P_M \in P_{{{\mathcal {M}}}}\) is absolutely continuous with respect to Lebesgue measure, and thus, so is \(P_M^k\). Because \(\lambda\) is a method, it follows that \(P^k_M(\partial \lambda _k^{-1} {{\mathcal {A}}}) = 0\), i.e., \(P^k_M(\partial (\lambda _k= {{\mathcal {A}}})) = 0\). By definition of convergence in the weak topology, we know that \(P^k_{M_j}(\lambda _k = {{\mathcal {A}}}), P^k_{N_j}(\lambda _k = {{\mathcal {A}}}) \Rightarrow P^k_{M}(\lambda _k = {{\mathcal {A}}})\) as j approaches infinity. Thus, for any \(\epsilon > 0\), there is some large j such that
But by choice of k, we have \(P^k_{M_n}(\lambda _k = {{\mathcal {A}}}) > 1/2\) for all n. So if we choose \(\epsilon = P^k_{M_j}(\lambda _k = {{\mathcal {A}}}) - 1/2\), then it follows that \(P^k_{N_j}(\lambda _k = {{\mathcal {A}}}) > 1/2\). Since \({{\mathcal {A}}}\ne {{\mathcal {B}}}\), that contradicts that fact that \(P^k_{N_j}(\lambda _k = {{\mathcal {B}}}) > 1/2\). \(\square\)
4 Linear causal models
An acyclic linear causal model in d variablesFootnote 6M is a triple \(\langle \textbf{X}, \textbf{e}, A \rangle ,\) where \(\textbf{X} = \langle X_i \rangle\) is a vector of d random variables, \(\textbf{e} = \langle e_1, e_2, \ldots , e_d\rangle\) is a random vector of d exogenous noise terms, and A is a \(d\times d\), properly lower-triangular matrix such that
-
1.
Each variable \(X_i\) is a linear function of variables earlier in the order, plus an unobserved noise term \(e_i\):
$$\begin{aligned} X_i = \sum _{j<i} A_{ij}X_j + e_i; \end{aligned}$$ -
2.
the noise terms \(e_1, \ldots , e_d\) are mutually independent.
On our definition, the variables in a linear causal models are enumerated in agreement with their causal order. This simplifies the presentation somewhat, although we have to take care to distinguish between the causal model and the vector of observed variables that it gives rise to. The latter is some subset of the variables in \(\textbf{X}\) that arrives correctly ordered only in exceptional cases.
In matrix notation, we can write a linear causal model as \(\textbf{X} = A \textbf{X}+ \textbf{e}.\) Because no \(X_i\) causes itself, A has only zeroes along its diagonal. By virtue of the causal order, A is lower triangular, i.e. all elements above the diagonal are zero. The random vector \(\textbf{X}\) also admits a “dual” representation: \(\textbf{X} = B\textbf{e}\), where \(B = (I-A)^{-1}.\) Since the inverse of a lower triangular matrix is lower triangular, the matrix B is also lower triangular, although its diagonal elements are all equal to one. For any linear causal model \(M=\langle \textbf{X}, \textbf{e}, A \rangle ,\) we write |M| for the length of the vector \(\textbf{X}.\) Moreover, we let \(\textbf{X}(M),\textbf{e}(M), A(M)\) and B(M) be \(\textbf{X}, \textbf{e}, A\) and \((I-A)^{-1},\) respectively.
Every linear causal model M gives rise to a direct cause relation \(\rightarrow _M\) by setting \(j\rightarrow _M i\) iff \(A_{ij}(M)\ne 0.\) In turn, the direct cause relation gives rise to a directed acyclic graph G(M) over the vertices \(\{1,\ldots , |M|\}.\) A causal path of length m from i to j in G(M) is a sequence of vertices \(\pi = (v_1, \ldots , v_m)\) such that \(v_1=i,\) \(v_m=j\) and \(v_i\rightarrow _M v_{i+1}.\) Let \(\Pi ^n_{ij}(M)\) be the set of all causal paths of length n from i to j in G(M). Let \(\Pi _{ij}(M)\) be the set of all causal paths from i to j in G(M). Let \(\Pi (M)\) be the set of all causal paths in G(M). Write \(i\rightsquigarrow _M j\) as a shorthand for \(\Pi _{ij}(M)\ne \varnothing .\) Write \(j\circ _M i\) when  and
and  If \(\pi = (v_1, \ldots , v_n)\) is a sequence of vertices in \(\{1, \ldots , |M|\},\) let the path product
If \(\pi = (v_1, \ldots , v_n)\) is a sequence of vertices in \(\{1, \ldots , |M|\},\) let the path product  be the product of all causal coefficients along the path \(\pi\) in G(M), i.e.
be the product of all causal coefficients along the path \(\pi\) in G(M), i.e.  . Note that \(\pi \in \Pi (M)\) iff
. Note that \(\pi \in \Pi (M)\) iff  It is easy to verify thatFootnote 7
It is easy to verify thatFootnote 7
In other words \(A^k_{ij}(M)\) is the sum of all path products for paths of length k from i to j. So \(A_{ij}^k(M)\ne 0\) implies \(j\rightsquigarrow _M i.\) By a classic result of Carl Neumann’s, \(B(M)=\sum _{k=0}^{|M|} A^k(M).\)Footnote 8 The spectral radius \(\rho (A)\) of a square matrix A is the largest absolute value of its eigenvalues. Neumann’s result states that if \(\rho (A)<1\) then \((I-A)^{-1}\) exists and is equal to \(\sum _{k=0}^\infty A^k.\) Since the eigenvalues of a triangular matrix are exactly its diagonal entries, \(\rho (B(M))=0\) for any acylic linear causal model M. By acyclicity, there are no paths longer than |M|, so \(\sum _{k>d} A^k=0.\) So  In other words \(B_{ij}(M)\) is the sum of all path products for paths from i to j. So \(B_{ij}(M)\ne 0\) implies \(j\rightsquigarrow _M i.\) The converse does not necessarily hold since non-zero path products may sum to zero. We say that model M is faithful if the total causal effect from \(X_i\) to \(X_j\) is nonzero if there is a causal path from \(X_i\) to \(X_j.\) In other words: M is faithful if \(B_{ij}(M)\ne 0\) whenever \(j\rightsquigarrow _M i.\)
In other words \(B_{ij}(M)\) is the sum of all path products for paths from i to j. So \(B_{ij}(M)\ne 0\) implies \(j\rightsquigarrow _M i.\) The converse does not necessarily hold since non-zero path products may sum to zero. We say that model M is faithful if the total causal effect from \(X_i\) to \(X_j\) is nonzero if there is a causal path from \(X_i\) to \(X_j.\) In other words: M is faithful if \(B_{ij}(M)\ne 0\) whenever \(j\rightsquigarrow _M i.\)
An acyclic linear causal model M is non-Gaussian (a LiNGAM) if in addition to satisfying (1) and (2), each of the noise terms is non-Gaussian. A LiNGAM has no Gaussian components if there is no linear combination of its noise terms \(\sum b_i e_i\) such that \(\sum b_i e_i = Y + Z,\) where Y and Z are independent random variables and Z is Gaussian. Let \(\textsc {Lin}_d\) be the class of all acyclic linear causal models on d variables, and let \(\textsc {Lng}_d, \textsc {Flng}_d,\textsc {Flngco}_d\), respectively, denote the classes of non-Gaussian models, faithful non-Gaussian models and faithful non-Gaussian models with no Gaussian components in d variables. Let \(\textsc {Lin}_{\le d} = \bigcup _{p \le d} \textsc {Lin}_p\) denote the classes of linear models in d or fewer variables, and define \(\textsc {Lng}_{\le d}, \textsc {Flng}_{\le d},\textsc {Flngco}_{\le d}\) similarly. Finally, \(\textsc {Lin}, \textsc {Lng}\) and \(\textsc {Flng},\textsc {Flngco}\) respectively represent the classes of all acyclic linear causal models, all acyclic linear non-Gaussian models, and all faithful acyclic linear non-Gaussian models over some finite number of variables.
It is sometimes reasonable to introduce a priori constraints on the maximum size of a coefficient in a LiNGAM model. For example, if c is the current number of particles in the universe, let \(\textsc {Flng}^c\) be the set \(\{M \in \textsc {Flng}: \max _{i,j}|B_{ij}(M)|<c\}.\) Let \(\textsc {Flng}^c_d\) be \(\textsc {Flng}^c\cap \textsc {Flng}_d.\) For any \({{\mathcal {M}}}\subseteq \textsc {Lin},\) let \({{\mathcal {M}}}^{i\rightarrow j}\) be the set \(\{M\in {{\mathcal {M}}}: i\rightarrow _M j\}\). Define \({{\mathcal {M}}}^{i\rightsquigarrow j}\) and \({{\mathcal {M}}}^{i\circ j}\) similarly.
What justifies assuming the true causal model is non-Gaussian, or more strongly, that it lacks Gaussian components? In most applications, the variables under investigation are bounded: mass, velocity, gross domestic product, population size, etc. are all bounded either from above or below, and therefore, cannot contain Gaussian components.
4.1 Parsimonious models
Let \({\mathcal {O}}\) be the set of all probability distributions on \(\mathbb {R}^p\). We are interested in when a vector of observed random variables could have arisen from a linear causal model. Accordingly, say that a random vector \(\textbf{O}=(O_1,\ldots ,O_p)\in {\mathcal {O}}\) admits a linear causal model \(M \in \textsc {Lin}_d\) if there is a permutation \(\alpha\) of \((1,\ldots , d)\) such that \(O_i=X_{\alpha ^{-1}(i)}(M)\) for \(1\le i \le p.\) In other words: \(\textbf{O}=(O_1,\ldots ,O_p)\) admits M if there is a way to order the d variables of X(M) such that the first p are identical with \(O_1,\ldots , O_p.\) We say that the permutation \(\alpha\) embeds \(\textbf{O}\) into M. If \(\alpha\) embeds \(\textbf{O}\) into M, then
Here, \(B_\textbf{O}(M)\) is the first p rows of \(P_\alpha B(M) P_\alpha\), and \(\textbf{e}_\textbf{O}(M)\) is \(P_\alpha \textbf{e}(M)\), and \(P_\alpha\) is the permutation matrix corresponding to \(\alpha\). Given an embedding \(\alpha\), we can extend the causal order over the elements of M to the \(O_i\) by setting \(O_i\rightsquigarrow _M O_j\) if \(\alpha ^{-1}(i)\rightsquigarrow _M \alpha ^{-1}(j)\) and \(O_i \circ _M O_j\) if \(\alpha ^{-1}(i)\circ _M \alpha ^{-1}(j).\) We shall see that, if we restrict attention to models in \(\textsc {Flng},\) only one such order can arise for any vector \(\textbf{O}\).
Say that \(\textbf{O}\) admits a LiNGAM model if there is d such that \(\textbf{O}\) admits \(M\in \textsc {Lng}_d.\) Trivially, if \(\textbf{O}\) admits a LiNGAM model in \(\textsc {Lng}_d,\) then it also admits some model in \(\textsc {Lng}_f\) for \(f>d.\) However, we say that a model \(M\in \textsc {Lng}_d\) is parsimonious (in \(\textsc {Lng}\)) for \(\textbf{O}\) if \(\textbf{O}\) admits M and \(\textbf{O}\) admits no \(M'\) in \(\textsc {Lng}_f\) with \(f<d.\) It is immediate that if \(\textbf{O}\) admits a LiNGAM model, it admits some parsimonious LiNGAM model. Similar remarks apply if \(\textbf{O}\) admits a model in \(\textsc {Lng}^c_d, \textsc {Flng}_d,\) or \(\textsc {Flng}_d^c\).
Thus, for \({{\mathcal {M}}}\in \{\textsc {Lin}_d, \textsc {Lng}_d, \textsc {Lng}^c_d, \textsc {Flng}_d, \textsc {Flng}_d^c\}\), define:
For \({{\mathcal {M}}}\in \{\textsc {Lin}, \textsc {Lng}, \textsc {Lng}^c, \textsc {Flng}_d, \textsc {Flng}^c\}\), let \({\mathcal {O}}_{{{\mathcal {M}}}_{\le d}}=\cup _{j\le d}~ {\mathcal {O}}_{{{\mathcal {M}}}_j}\) and \({\mathcal {O}}_{{{\mathcal {M}}}_{\ge d}} = \cup _{j\ge d} ~{\mathcal {O}}_{{{\mathcal {M}}}_j}.\) Let \({\mathcal {O}}_{{{\mathcal {M}}}_{<d}}, {\mathcal {O}}_{{{\mathcal {M}}}_{>d}}\) be defined similarly. Finally, let \({\mathcal {O}}_{{\mathcal {M}}}={\mathcal {O}}_{{{\mathcal {M}}}_{\ge p}}.\) We can characterize the parsimonious models by a simple condition on the matrix \(B_\textbf{O}(M).\) For a proof, see Theorem 4.3 in Genin (2021).
Theorem 5
Suppose that \(M\in \textsc {Lng}_d\) is faithful. Then, M is parsimonious for \(\textbf{O}=(O_1, \ldots , O_p)\) iff no column of \(B_\textbf{O}(M)\) is proportional to any other.
The following theorem allows us to work with a “canonical" model for every \(\textbf{O}\) that admits a faithful LiNGAM. For a proof, see Corollary 4.4 in Genin (2021).
Theorem 6
Suppose that \(\textbf{O}\) admits \(M\in \textsc {Flng}.\) Then there is \(M'\in \textsc {Flng}\) such that (i) \(\textbf{O}\) admits \(M'\) (ii) \(M'\) is parsimonious for \(\textbf{O}\) and (iii) \(O_i \rightsquigarrow _M O_j\) iff \(O_i \rightsquigarrow _{M'} O_j.\)
Theorem 6 remains true if we substitute \(\textsc {Flngco}\) everywhere for \(\textsc {Flng}.\) The following variation can be proven with the same means.
Lemma 1
Suppose that \(\textbf{O}\) admits \(M\in \textsc {Lin}.\) Then there is \(M'\in \textsc {Lin}\) such that (i) \(\textbf{O}\) admits \(M'\) (ii) no column of \(B_\textbf{O}(M')\) is proportional to any other (iii)  implies
implies 
5 LiNGAM: the unconfounded case
One would expect that if two linear causal models have similar causal structure, then they induce similar distributions over the observable variables. That is the import of the following theorem, whose proof is a straightforward application of Slutsky’s theorem. In a slogan: similar causal models have similar observational consequences.
Theorem 7
Let \({{\mathcal {M}}}={\textsc {Lin}}\) and let P map each \(M\in {{\mathcal {M}}}\) to a random vector admitting M. Let \((M_n)\) be a sequence of models in \({{\mathcal {M}}}.\) If \(A(M_{n})\rightarrow A(M)\) and \(\textbf{e}(M_n)\Rightarrow \textbf{e}(M),\) then \(P(M_n)\Rightarrow P(M).\)
But what about the converse? We know it cannot be true in general, but is it true that unconfounded LiNGAMs that have similar observational consequences must have similar causal structures? That is the more significant question—an affirmative answer implies that the observational distribution is a reliable guide to the causal structure, at least for LiNGAMs with no unobserved latent variables. In this section, we prove the following partial converse to Theorem 7.
Theorem 8
Let \({{\mathcal {M}}}\subseteq {\textsc {Lng}^c_p}\) and let P map each \(M\in {{\mathcal {M}}}\) to a p-dimension random vector admitting M. Let \((M_n)\) be a sequence of models in \({{\mathcal {M}}}.\) If \(P(M_n)\Rightarrow P(M),\) then there is a subsequence \((M_{n_i})\) such that \(A(M_{n_i})\rightarrow A(M)\) and \(\textbf{e}(M_{n_i})\Rightarrow \textbf{e}(M).\)
To get a feeling for this theorem, note that it implies the full identifiability of the unconfounded LiNGAM model. For suppose that two fully observed \(M,M'\in \textsc {Lng}^c_p\) induce identical distributions \(P(M)=P(M').\) Letting \((M_n)\) be the constantly M sequence, Theorem 8 implies that \(A(M)=A(M')\) and \(\textbf{e}(M)=\textbf{e}(M').\) In other words: If M and \(M'\) give rise to the same observational distribution, they must have identical causal structures and their exogenous terms must be identically distributed.
In fact, much more follows from Theorem 8. It implies rather directly that (1) the problem of learning the orientation of a direct edge, presupposing that some edge exists, is statistically decidable and (2) the problem of learning the presence and orientation of an edge is progressively solvable, though not decidable. In other words: these two problems are the causal analogues of the second and third quadrants in Fig. 2.
Theorem 9
Let \({{\mathcal {M}}}\subseteq \textsc {Lng}^c_p\) and let P map each \(M \in {{\mathcal {M}}}\) to an absolutely continuous p-dimension random vector admitting M. Then,
-
1.
\({\mathfrak {Q}}=\{{{\mathcal {M}}}^{i\rightarrow j},{{\mathcal {M}}}^{i\leftarrow j}\}\) is decidable, but not uniformly decidable;
-
2.
\({\mathfrak {Q}}=\{{{\mathcal {M}}}^{i\circ j},{{\mathcal {M}}}^{i\rightarrow j},{{\mathcal {M}}}^{i\leftarrow j}\}\) is progressively solvable, but not decidable.
The proof of Theorem 9 follows straightforwardly from the topological characterizations in Section 3 and Theorem 8.
Proof of Theorem 9
-
(1)
By Theorem 1, showing that \(P({{\mathcal {M}}}^{i\rightarrow j})\cap \textsf{cl}({{\mathcal {M}}}^{i\leftarrow j}) = \varnothing\) in the weak topology on \({{\mathcal {M}}}\) suffices to demonstrate decidability. Let \(M\in {{\mathcal {M}}}^{i\rightarrow j}\). Suppose for a contradiction that there are \((M_n)\) in \({{\mathcal {M}}}^{i\leftarrow j}\) such that \(P(M_n)\rightarrow P(M).\) By Theorem 9, \(A_{ji}(M_{n_i})\rightarrow A_{ji}(M)\) for some subsequence \((M_{n_i})\). But, since the \(M_{n_i}\) are all in \({{\mathcal {M}}}^{i\leftarrow j},\) acyclicity implies that \(A_{ji}(M_{n_i})=0,\) whereas \(A_{ji}(M)\ne 0.\) So the constantly zero sequence \(A_{ji}(M_{n_i})\) converges to a non-zero limit. Contradiction. To show that the question is not uniformly decidable, it is enough to observe that models with weak edges of either orientation can approximate the absence of an edge arbitrarily well and, therefore, that \({{\mathcal {M}}}^{i\circ j}\subseteq \textsf{cl}({{\mathcal {M}}}^{i \rightarrow j})\cap \textsf{cl}({{\mathcal {M}}}^{i \leftarrow j})\). Appealing to Theorem 4, the question is not uniformly decidable.
-
(2)
By Theorem 2, the question is progressively solvable if every element in the enumeration \({{\mathcal {M}}}^{j\circ i},{{\mathcal {M}}}^{i\rightarrow j},{{\mathcal {M}}}^{j\rightarrow i}\) is disjoint from the closures of the previous elements. By (1), it suffices to show that \({{\mathcal {M}}}^{i\rightarrow j},{{\mathcal {M}}}^{j\rightarrow i}\) are disjoint from \(\textsf{cl}({{\mathcal {M}}}^{j\circ i})\). Arguing by contradiction as in (1), it is straightforward to show that this must be the case. Undecidability follows by Theorem 1 and the observation that \({{\mathcal {M}}}^{i\circ j}\subseteq \textsf{cl}({{\mathcal {M}}}^{i\rightarrow j}).\)
To prove Theorem 8, we first have to collect some lemmas. The first is the Lukacs–King theorem (1954), which is perhaps not so well known as its consequence, the Darmois–Skitovich theorem (1953; 1953).
Theorem 10
Let \(X_1, \ldots , X_m\) be independent random variables, \(X' = \sum _i \alpha _i X_i\) and \(X'' = \sum _i \beta _i X_i\). Then, \(X', X''\) are independent iff (a) each \(X_i\) such that \(\alpha _i\beta _i\ne 0\) is Gaussian; and (b) \(\sum _{i} \alpha _i\beta _i \text {Var}(X_i)=0.\)
The second lemma illuminates how weak convergence of random variables interacts with marginal dependence. For an elementary proof, see Genin and Mayo-Wilson (2020).
Lemma 2
Suppose that the random vector (X, Y) is absolutely continuous with Lebesgue measure and that X, Y are dependent. Then, if \((X_i,Y_i) \Rightarrow (X,Y)\) all but finitely many of the \(X_i,Y_i\) are dependent.
Finally, say that a matrix is a mixing matrix if and only if some column has two non-zero entries. The following is proven by Genin and Mayo-Wilson (2020), Lemma 2.1.
Lemma 3
Suppose that A, B are square matrices of the same dimension having unit diagonals. Suppose that B is lower triangular and the result of the matrix multiplication AB is not a mixing matrix. Then \(A=B^{-1}.\)
We now have all the ingredients we need to give a proof of 8. The proof has the virtue of being rather elementary and not relying on facts about the ICA algorithm as is typical for work on the LiNGAM model.
Proof of Theorem 8
Suppose \(P(M_n)\Rightarrow P(M).\) Let \(A=A(M), \textbf{e}=\textbf{e}(M)\) and \(A_n=A(M_n), \textbf{e}_n = \textbf{e}(M_n).\) It follows that
Since we have assumed that the \(A_n\) are bounded, it follows by the Bolzano–Weierstrass theorem that there must be some subsequence \((A_{n_i})\) converging in the Euclidean metric to a matrix \(A'\). It follows by Slutsky’s theorem that
The matrix \((I-A')\) has unit diagonal since each of \((I-A_n)\) does. \((I-A)^{-1}\) also has unit diagonal. Moreover, \((I-A)^{-1}\) is lower triangular.
Suppose that \((I-A')(I-A)^{-1}\) is a mixing matrix. Let
By Theorem 10, there must be two elements of \(\mathbf{e'}\) that are dependent. By Lemma 2, the same elements of \(\mathbf{e_{n_i}}\) must also be dependent for at least one i (and, in fact, for all but finitely many i). Contradiction. Therefore, \((I-A')(I-A)^{-1}\) is not a mixing matrix. By Lemma 3, \(A=A'\) and \(\textbf{e}'=\textbf{e}\). Therefore, the \({A_{n_i}}\) are converging to A and the \(\textbf{e}_{n_i}\) are converging to \(\textbf{e}\).
6 LiNGAM: the confounded case
Unsurprisingly, learning causal structure becomes significantly more difficult in the presence of hidden variables. The confounded LiNGAM setting does not enjoy anything like the total identifiability of the unconfounded case, even if we assume faithfulness. For one, structures which differ on the strength, though not the direction, of direct edges between observed variables can generate identical distributions over the observed variables (see Fig. 3). Furthermore, the number of hidden variables cannot be identified: models with fewer latents can always be perfectly mimicked by models with more, potentially causally disconnected, latents. Moreover, models with latent “mediators" can be perfectly imitated by models with only exogenous latents (see Fig. 4). For this reason, causal relations involving latents are not identified and we cannot even identify direct edges among observed variables. The good news is that the causal ancestry relation among observed variables is identified so long as we assume faithfulness. In other words if two faithful, but not necessarily fully-observed, LiNGAMs generate the same observational distribution, then they must agree on which observed variables are causally upstream of which others. As a warm-up we prove this identifiability result, elsewhere given by Hoyer et al. (2008) and Salehkaleybar et al. (2020). We attempt to keep things elementary, and we do not appeal to any facts about the ICA algorithm.
Note that the exogenous noise terms \(\epsilon _1, \epsilon _3\) switch places. Although the left and right-hand models generate the same distribution over \((X_1,X_2)\) they disagree on the total causal effect of \(X_1\) on \(X_2\) whenever \(b\ne 0.\) When \(ac=-b\), the lhs model is unfaithful and the models disagree, not only on the size of the effect, but on the presence of an edge
The left and right-hand models generate the same distribution over \((X_1,X_2)\) although they differ in the number of latents. The hidden mediator L can be “absorbed" into the exogenous noise term for \(X_2\). When \(c=0,\) but \(ab\ne 0,\) the two models differ on whether \(X_1\) is a direct cause of \(X_2\), or merely an ancestor
Theorem 11
Let \({{\mathcal {M}}}=\textsc {Flng}\) and let P map each \(M\in {{\mathcal {M}}}\) to a p-dimensional random vector \((O_1, \ldots , O_p)\) admitting \({{\mathcal {M}}}\). If \(P(M)=P(M'),\) then \(O_i\rightsquigarrow _M O_j\) iff \(O_i\rightsquigarrow _{M'} O_j\).
We need only one additional resource for this result, due to Kagan et al. (1973). For a proof, see their Lemmas 10.2.2 and 10.2.4.
Theorem 12
Suppose that \(\textbf{X}=A\textbf{e}=B\textbf{f},\) where A and B are \(p\times r\) and \(p\times s\) matrices and \(\textbf{e}=(e_1,\ldots , e_r),\) \(\textbf{f}=(f_1,\ldots , f_s)\) are random vectors with independent components. Suppose that no two columns of A are proportional to each other. If the ith column of A is not proportional to any column of B, then \(e_i\) is normally distributed.
Proof of Theorem 11
Suppose that \(\textbf{O}=(O_1,\ldots ,O_p)\) admits \(M,M'\in \textsc {Flng}.\) We show that \(O_i\rightsquigarrow _M O_j\) iff \(O_i\rightsquigarrow _{M'} O_j.\) By Theorem 5 and 6, there are \(F,F'\in \textsc {Flng}\) such that 1. \(\textbf{O}\) admits \(F,F';\) 2. \(O_i\rightsquigarrow _M O_j\) iff \(O_i\rightsquigarrow _F O_j\); 3. \(O_i\rightsquigarrow _{M'} O_j\) iff \(O_i\rightsquigarrow _{F'} O_j\) and 4. no two columns of \(B_{\textbf{O}}(F)\) are proportional; 5. no two columns of \(B_{\textbf{O}}(F')\) are proportional. By (1) and (2), it suffices to prove that \(O_i\rightsquigarrow _F O_j\) iff \(O_i\rightsquigarrow _{F'} O_j.\) But since the situation is symmetrical, it suffices to prove that \(O_i\rightsquigarrow _F O_j\) only if \(O_i\rightsquigarrow _{F'}O_j\).
Suppose for a contradiction that \(O_i\rightsquigarrow _F O_j\) but  Let \(\alpha\) be a permutation embedding \(\textbf{O}\) in F. Let B, C be \(B_\textbf{O}(F),B_\textbf{O}(F'),\) respectively. Let \(\textbf{e},\textbf{f}\) be \(\textbf{e}_\textbf{O}(F),\textbf{e}_\textbf{O}(F'),\) respectively. Then
Let \(\alpha\) be a permutation embedding \(\textbf{O}\) in F. Let B, C be \(B_\textbf{O}(F),B_\textbf{O}(F'),\) respectively. Let \(\textbf{e},\textbf{f}\) be \(\textbf{e}_\textbf{O}(F),\textbf{e}_\textbf{O}(F'),\) respectively. Then
Since  \(C_{ji}=0.\) Moreover, \(C_{ii}=1\). By faithfulness of F, \(O_i\rightsquigarrow _F O_j\) implies that \(B_{ji} \ne 0.\) By Theorem 12, there must be a column \(k\ne i\) and real number \(a\ne 0\) such that \(B_{ik}=aC_{ii}\ne 0\) but \(B_{jk}=aC_{ji}=0.\) Since \(B_{ik}\ne 0,\) it follows that \(\alpha ^{-1}(k)\rightsquigarrow _F \alpha ^{-1}(i).\) Since \(O_i\rightsquigarrow _F O_j\) by assumption, it follows that \(\alpha ^{-1}(i)\rightsquigarrow _F \alpha ^{-1}(j).\) By transitivity of \(\rightsquigarrow _F,\) \(\alpha ^{-1}(k)\rightsquigarrow _F \alpha ^{-1}(j).\) However, \(B_{jk}=0.\) So F is unfaithful. Contradiction. \(\square\)
\(C_{ji}=0.\) Moreover, \(C_{ii}=1\). By faithfulness of F, \(O_i\rightsquigarrow _F O_j\) implies that \(B_{ji} \ne 0.\) By Theorem 12, there must be a column \(k\ne i\) and real number \(a\ne 0\) such that \(B_{ik}=aC_{ii}\ne 0\) but \(B_{jk}=aC_{ji}=0.\) Since \(B_{ik}\ne 0,\) it follows that \(\alpha ^{-1}(k)\rightsquigarrow _F \alpha ^{-1}(i).\) Since \(O_i\rightsquigarrow _F O_j\) by assumption, it follows that \(\alpha ^{-1}(i)\rightsquigarrow _F \alpha ^{-1}(j).\) By transitivity of \(\rightsquigarrow _F,\) \(\alpha ^{-1}(k)\rightsquigarrow _F \alpha ^{-1}(j).\) However, \(B_{jk}=0.\) So F is unfaithful. Contradiction. \(\square\)
The bad news is that the orientation of the ancestry relation is no longer decidable in the potentially confounded LiNGAM setting, even assuming faithfulness.
Let \(Z_1, Z_2, U_1, U_2, W_1, W_2\) be mutually independent, absolutely continuous random variables. \(Z_1, Z_2\) are Gaussian with identical variance, while the others are non-Gaussian. Let \(V_1=Z_1+Z_2\) and \(V_2=Z_1-Z_2.\) Note that \(V_1, V_2\) are independent by Theorem 10. Let \(J_{1,n}=Z_1 + \frac{1}{n}W_1\) and \(J_{2,n}=Z_2+\frac{1}{n}W_2\). Then, the \((X_{1,m},X_{2,m}),\) which lie in \({\mathcal {O}}_{\textsc {Flng}_4^c}^{1 \leftarrow 2},\) converge in probability to \((X_1,X_2),\) lying in \({\mathcal {O}}_{\textsc {Flng}_2^c}^{1 \rightarrow 2}\). Note that although error terms approach Gaussianity and the model approaches unfaithfulness, no term in the sequence is unfaithful and no noise term is Gaussian. For more detail, see the proof of Theorem 13
Theorem 13
Let \({{\mathcal {M}}}=\textsc {Flng}^c\) and let P map each \(M\in {{\mathcal {M}}}\) to a 2-dimensional random vector admitting \({{\mathcal {M}}}\). Then the question  is not decidable.
is not decidable.
Proof of Theorem 13
Let \(Z_1, Z_2, U_1, U_2, W_1, W_2\) be mutually independent, absolutely continuous random variables. Assume that \(Z_1, Z_2\) are Gaussian with identical variance, while the others are non-Gaussian. Let \(V_1=Z_1+Z_2\) and \(V_2=Z_1-Z_2.\) By Theorem 10, \(V_1,V_2\) are independent and, therefore, so are \(U_1+V_1\) and \(U_2+V_2\). Let \(J_{1,n}=Z_1 + \frac{1}{n}W_1\) and \(J_{2,n}=Z_2+\frac{1}{n}W_2\). Let M be the faithful, fully observed LiNGAM on the lhs of Fig. 5. Let \(M_n\) be defined as the faithful, but confounded, LiNGAMs on the rhs of Fig. 5, where the \(X_{1,n}\) and \(X_{2,n}\) are the observable variables. Then the \(P(M_n)=(X_{1,n},X_{2,n})\) converge weakly to \(P(M)=(X_1,X_2)\). By Theorem 1, \({{\mathfrak {Q}}}\) is not decidable.
In fact, “flipping" returns in this potentially confounded LiNGAM setting: it is no longer possible to converge to the right orientation without exposing yourself to a high chance of mis-orienting the causal relation. Although we omit the details of this construction, for appropriate choices of noise terms \(U_1,U_2,V_1,V_2,\) it is possible to approximate each model in the sequence of models on the rhs of Fig. 5 by a sequence of models, this time with four hidden variables, and in which the orientation is once again reversed. That means that for any pointwise consistent method for learning the causal ancestry relation, there are faithful but confounded LiNGAM models in which the method can be forced to flip between a high probability of outputting one orientation at sample size \(n_1<n_2\) and a high probability of outputting the opposite orientation at sample size \(n_2>n_1,\) where the number of such flips is limited only by the number of hidden variables. The good news, such as it is, is that the presence and orientation of the causal ancestry relation remains decidable in the limit. For a proof, see Sections 6 and 7 in Genin (2021).
Theorem 14
Let \({{\mathcal {M}}}=\textsc {Flng}^c\) and let P map each \(M\in {{\mathcal {M}}}\) to a p-dimensional random vector admitting \({{\mathcal {M}}}\). Then, the question  is decidable in the limit.
is decidable in the limit.
7 The Flamingo model, or decidability returns
The results of the previous section show that learning causal orientation in faithful, but not fully observed, LiNGAM models is a difficult problem. Not so difficult that it is impossible to construct pointwise consistent methods, but difficult enough that no consistent method can guarantee a finite-sample bound on the probability of orientation errors.
In view of the positive results for the unconfounded setting, this negative result for potentially confounded models is something of a disappointment. However, the example in Fig. 5 suggests several different adjustments to the framework that may recover decidability. The first is the relatively well-trodden path of strong faithfulness. As m grows, the direct path from \(U_2\) to \(X_{1,m}\) comes closer and closer to canceling the path via \(X_{2,m}.\) Strengthening faithfulness would preclude this possibility. But faithfulness is already a controversial assumption and strengthenings would do nothing to appease its critics.Footnote 9 While precisely canceling paths would be a miracle, approximate cancellations are to be expected from equilibrated systems. Moreover, Uhler et al. (2013) show that strong versions of faithfulness can rule out a topologically large set of models. The second path of escape is to strengthen the assumption of non-Gaussianity. As m grows, \(J_{1,m}\) and \(J_{2,m}\) converge to the Gaussians \(Z_1\) and \(Z_2.\) Assuming that noise terms are bounded away from Gaussianity would preclude this possibility. But although precisely Gaussian noise terms would be a kind of miracle, approximate Gaussianity is often plausible: noise terms may be sums of many different independent variables, and such sums will tend towards normality by the central limit theorem and its generalizations (Gnedenko and Kolmogorov 1968).
We pursue a different possibility. A random variable X has a Gaussian component if it can be expressed as the sum \(Y+Z\) where Y, Z are independent and Z is Gaussian. It is clear that the error terms in Fig. 5 violate this condition — indeed properties of the Gaussian are essential to ensuring that \(V_1\) and \(V_2,\) and therefore \(U_1+V_1\) and \(U_2+V_2\) are independent. In light of uniqueness results by Kagan et al. (1973), we require that no linear combination of the exogenous noise terms has a Gaussian component. We do not assess whether this assumption is less plausible than the assumption of non-Gaussianity itself, however we note that so long as all the noise terms are bounded, the assumption is satisfied.Footnote 10 We also require that there is a known, potentially very large, upper bound d on the number of hidden variables. For example, let d be the current number of particles in the universe.
Theorem 15
Let \({{\mathcal {M}}}=\textsc {Flngco}^c_{\le d}\) and let P map each \(M\in {{\mathcal {M}}}\) to some absolutely continuous p-dimensional random vector admitting \({{\mathcal {M}}}.\) Then,
-
1.
 is decidable, but not uniformly decidable;
is decidable, but not uniformly decidable; -
2.
 is progressively solvable, but not decidable.
is progressively solvable, but not decidable.
To prove this theorem, we first need to collect some lemmas. For a proof of the following, see Corollary 6.4 in Genin (2021).
Lemma 4
Suppose the k-dimensional random vectors \(\textbf{e}_n\) have independent components. Consider a sequence of p-dimensional random vectors \(\textbf{X}_n=B_n\textbf{e}_n,\) where the \(B_n\) are \(p\times k\) matrices and \(B_n\rightarrow B\). If the \(\textbf{X}_n\) converge in distribution to \(\textbf{X},\) then \(X=B\textbf{e},\) where \(\textbf{e}\) is a k-dimensional random vector with independent components.
Kagan et al. (1973) prove the following, see their Theorem 10.3.7.
Theorem 16
Suppose that \(\textbf{X}=A\textbf{e}=B\textbf{f},\) where A and B are \(p\times r\) and \(p\times s\) matrices and \(\textbf{e}=(e_1,\ldots , e_r),\) \(\textbf{f}=(f_1,\ldots , f_s)\) are random vectors with independent components. Suppose that no two columns of A are proportional to each other and no two columns of B are proportional to each other. Moreover, suppose that no linear combination of variables in \(\textbf{e}\) has a Gaussian component. Then every column of A is proportional to some column of B and vice versa.
Proof of Theorem 15
(1) Let \(p\le f \le d\) and suppose \(M\in {{\mathcal {M}}}^{i\rightsquigarrow j}.\) Let \(\textbf{O}=P(M)\). Let \(M^*\in \textsc {Flngco}^c_{f}\) be parsimonious for \(\textbf{O}\). Let \(A=B_\textbf{O}(M^*)\) and \(\textbf{e}=\textbf{e}_\textbf{O}(M^*).\) Then, \(\textbf{O}=A\textbf{e},\) where no linear combination of \(\textbf{e}\) has a Gaussian component and (by parsimony) no column of A is proportional to any other.
Let \(p\le g \le d\) and let \((M_n)\) lie in  Let \(\textbf{O}_n=P(M_n).\) Let \(B_n=B_{\textbf{O}_n}(M_n)\) and \(\textbf{e}_n=\textbf{e}_{\textbf{O}_n}(M_n)\). Suppose for a contradiction that \(\textbf{O}_n \Rightarrow \textbf{O}\). Each of the \(B_n\) are \(p\times g\) matrices. By the Bolzano–Weierstrass theorem, since the \(B_n\) are uniformly bounded, there is a \(p\times g\) matrix B and a convergent subsequence \(B_{n_m}\rightarrow B.\) By assumption, \(B_{n_m}\textbf{e}_{n_m}\) converge in distribution to \(\textbf{O}.\) By Corollary 4, \(\textbf{O}=B\textbf{f}\) where \(\textbf{f}\) is a vector of independent components. Therefore \(\textbf{O}=A\textbf{e}=B\textbf{f}.\)
Let \(\textbf{O}_n=P(M_n).\) Let \(B_n=B_{\textbf{O}_n}(M_n)\) and \(\textbf{e}_n=\textbf{e}_{\textbf{O}_n}(M_n)\). Suppose for a contradiction that \(\textbf{O}_n \Rightarrow \textbf{O}\). Each of the \(B_n\) are \(p\times g\) matrices. By the Bolzano–Weierstrass theorem, since the \(B_n\) are uniformly bounded, there is a \(p\times g\) matrix B and a convergent subsequence \(B_{n_m}\rightarrow B.\) By assumption, \(B_{n_m}\textbf{e}_{n_m}\) converge in distribution to \(\textbf{O}.\) By Corollary 4, \(\textbf{O}=B\textbf{f}\) where \(\textbf{f}\) is a vector of independent components. Therefore \(\textbf{O}=A\textbf{e}=B\textbf{f}.\)
Since the \(g\times g\) matrices \(A(M_{n_m})\) are bounded, there must be a converging subsequence \(A(M_{n_j})\). Letting D be the limit of this subsequence and \(\textbf{X}=D\textbf{f},\) we have that \(M'=\langle \textbf{X}, \textbf{f}, D \rangle\) is a model in \(\textsc {Lin}_g\) admitting \(\textbf{O}.\) By analysis of zeroes in the matrices \(A(M_{n_j}),\) it must be that  By Lemma 1 there is \(M^\dagger \in \textsc {Lin}_{\le g}\) such that (1) \(M^\dagger\) admits \(\textbf{O}\); (2)
By Lemma 1 there is \(M^\dagger \in \textsc {Lin}_{\le g}\) such that (1) \(M^\dagger\) admits \(\textbf{O}\); (2)  and (3) no two columns of \(B^{\dagger }=B_\textbf{O}(M^\dagger )\) are proportional. Letting \(\textbf{e}^{\dagger }=\textbf{e}_\textbf{O}(M^{\dagger }),\) we have that \(\textbf{O}=A\textbf{e}=B^{\dagger }\textbf{e}^{\dagger }.\)
and (3) no two columns of \(B^{\dagger }=B_\textbf{O}(M^\dagger )\) are proportional. Letting \(\textbf{e}^{\dagger }=\textbf{e}_\textbf{O}(M^{\dagger }),\) we have that \(\textbf{O}=A\textbf{e}=B^{\dagger }\textbf{e}^{\dagger }.\)
By (2), \(B^{\dagger }_{ji}=0\) and \(B^{\dagger }_{ii}=1.\) By Theorem 16, there must be a column \(k\ne i\) of A proportional to column i of \(B^\dagger .\) So \(A_{ik}\ne 0\) and \(A_{jk}=0.\) It follows that \(O_k \rightsquigarrow _{M^*} O_i\) and \(O_{i} \rightsquigarrow _{M^*} O_j.\) By transitivity of the ancestry relation \(O_{k} \rightsquigarrow _{M^*} O_j.\) But since \(A_{jk}=0,\) faithfulness implies  Contradiction.
Contradiction.
We have shown that  Since g was arbitrary, it follows that there are open sets \(O_g\) containing \({{{\mathcal {M}}}^{i\rightsquigarrow j}}\) and disjoint from
Since g was arbitrary, it follows that there are open sets \(O_g\) containing \({{{\mathcal {M}}}^{i\rightsquigarrow j}}\) and disjoint from  for each g with \(p\le g \le d.\) Therefore, the finite intersection \(O=\bigcap _{p\le g\le d} O_g\) is an open set containing \({{{\mathcal {M}}}^{i\rightsquigarrow j}}\) and disjoint from
for each g with \(p\le g \le d.\) Therefore, the finite intersection \(O=\bigcap _{p\le g\le d} O_g\) is an open set containing \({{{\mathcal {M}}}^{i\rightsquigarrow j}}\) and disjoint from  In other words:
In other words:  Since
Since 
 By symmetry,
By symmetry,  Decidability follows by Theorem 1. The argument for failure of uniform decidability is unchanged from that in Theorem 9.
Decidability follows by Theorem 1. The argument for failure of uniform decidability is unchanged from that in Theorem 9.
(2) Consider the enumeration of the answers  . By (1),
. By (1),  . Since
. Since  . By identical reasoning,
. By identical reasoning,  and
and  . Progressive solvability follows by Theorem 2. The argument for the failure of solvability is unchanged from that in Theorem 9. \(\square\)
. Progressive solvability follows by Theorem 2. The argument for the failure of solvability is unchanged from that in Theorem 9. \(\square\)
8 Conclusion
Researchers in causal discovery continue to produce many new and exciting identifiability results. But demonstrating identifiability proves only that discovery is not completely hopeless — it is only the first step in understanding how difficult discovery is. Success notions intermediate between uniform decidability and decidability in the limit can guide the search for modeling assumptions that are neither so weak as to preclude short-run error bounds nor so strong as to secure uniform convergence. In this paper we propose two such notions: decidability and progressive solvability. We show that they are feasible in the fully observed LiNGAM setting, even without assuming faithfulness, and infeasible in the confounded LiNGAM setting, even if we assume faithfulness. In light of this latter result, we propose an adjustment to the LiNGAM framework that recovers decidability and progressive solvability even when hidden variables may be present. It is our hope that the success concepts we propose, as well as the topological methods we adopt, prove fruitful in the future development of causal discovery.
Notes
For an artificial but illustrative example, suppose we wanted to learn whether the mean of a continuous random variable were rational or irrational. The problem is identified, since rational-valued possibilities cannot induce precisely the same distribution as irrational-valued ones, but it is hopeless from a learning perspective so long as our observations are recorded with finite precision.
X has a Gaussian component if \(X=Y+Z\), for Gaussian Z and Y independent of Z.
The basic idea is that, so long as recorded measurements have finite precision, it is impossible to tell whether a random sample is precisely on the boundary of an acceptance zone. So we assume that methods are designed so that this situation arises only with measure zero. See “feasible tests” in Genin and Kelly (2017, p. 239) for further explanation.
We acquire this perspective on topology from Kelly (1996) and subsequent work by Kelly and his students.
The technical term for a map which preserves closures in this way is a homeomorphism.
In the following d refers to the total number of (potentially hidden) variables and \(p\le d\) to the number of observed variables.
Of course, it is the matrix product that is intended here.
To see this, suppose that X is a linear combination of noise terms and that X has a Gaussian component. Then, X must be unbounded. But then one of the noise terms must be unbounded.
References
Bühlmann P, Peters J, Ernest J (2014) CAM: causal additive models, high-dimensional order search and penalized regression. Ann Stat 42(6):2526–2556
Cartwright N (2007) Hunting causes and using them: approaches in philosophy and economics. Cambridge University Press
Darmois G (1953) Analyse générale des liaisons stochastiques: etude particulière de l’analyse factorielle linéaire. Revue de l’Institut international de statistique, JSTOR, pp 2–8
Dembo A, Peres Y (1994) A topological criterion for hypothesis testing. Ann Stat 22(1):106–117
Genin K (2018) The Topology of Statistical Inquiry. Doctoral Dissertation, Carnegie Mellon University, Pittsburgh, PA
Genin K (2021) Statistical undecidability in linear, non-gaussian causal models in the presence of latent confounders. In: Advances in Neural Information Processing Systems, p 34
Genin K, Kelly KT (2017) The Topology of Statistical Verifiability. In: Proceedings of Theoretical Aspects of Rationality and Knowledge (TARK). URL https://arxiv.org/abs/1707.09378v1
Genin K, Kelly KT (2019) Theory choice, theory change, and inductive truth-conduciveness. Studia Logica 107(5):949–989
Genin K, Mayo-Wilson C (2020) Statistical decidability in linear, non-Gaussian models. In: NeurIPS 2020:Workshop on Causal Discovery and Causality-Inspired Machine Learning
Glymour C, Zhang K, Spirtes P (2019) Review of causal discovery methods based on graphical models. Front Genet 10:524
Gnedenko BV, Kolmogorov AN (1968) Limit distributions for sums of independent random variables. Addison-Wesley, pp ix+293 (Translated from the Russian, annotated Translated from the Russian, annotated by J.~L. Doob and P.~L. Hsu. MR:0233400)
Hoover Kevin D et al (2001) Causality in macroeconomics. Cambridge University Press
Hoyer PO, Shimizu S, Kerminen AJ, Palviainen M (2008) Estimation of causal effects using linear non-Gaussian causal models with hidden variables. Int J Approx Reason 49(2):362–378
Hoyer PO, Janzing D, Mooij JM, Peters J, Schölkopf B (2009) Nonlinear causal discovery with additive noise models. In: Advances in Neural Information Processing Systems, pp 689–696
Kagan A M, Linnik YV, Rao CR (1973) Characterization problems in mathematical statistics. John Wiley & Sons
Kelly KT (1996) The logic of reliable inquiry. Oxford University Press, New York
Kelly KT, Mayo-Wilson C (2010) Causal conclusions that flip repeatedly and their justification. In: Proceedings of the Twenty Sixth Conference on Uncertainty in Artificial Intelligence (UAI), pp 277–286
Lukacs E, King EP (1954) A property of the normal distribution. Ann Math Stat 25(2):389–394
Salehkaleybar S, Ghassami A, Kiyavash N, Zhang K (2020) Learning linear non-Gaussian causal models in the presence of latent variables. J Mach Learn Res 21(39):1–24
Shimizu S, Hoyer PO, Hyvarinen A, Kerminen AJ (2006) A linear non-Gaussian acyclic model for causal discovery. J Mach Learn Res 7:2003–2030
Skitivic VP (1953) On a property of the normal distribution. Doklady Akademii Nauk SSSR 89:217–219
Spirtes P, Glymour CN, Richard S (2000) Prediction, and search. The MIT Press, Causation
Uhler C, Raskutti G, Bühlmann P, Bin Y (2013) Geometry of the faithfulness assumption in causal inference. Ann Stat 41(2):436–463
Zhang J, Spirtes P (2003) Strong faithfulness and uniform consistency in causal inference. In: Proceedings of the Nineteenth conference on Uncertainty in Artificial Intelligence (UAI), pp 632–639
Zhang K, Hyvärinen A (2009) On the identifiability of the post-nonlinear causal model. In: 25th Conference on Uncertainty in Artificial Intelligence (UAI 2009), AUAI Press, pp 647–655
Acknowledgements
On behalf of all authors, the first author states that there is no conflict of interest. The first author is funded by the German Research Foundation, EXC number 2064/1 - Project number 390727645. The manuscript has no associated data.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose. The first author is funded by the German Research Foundation, EXC number 2064/1 - Project number 390727645. The manuscript has no associated data.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Genin, K., Mayo-Wilson, C. Success concepts for causal discovery. Behaviormetrika 51, 515–538 (2024). https://doi.org/10.1007/s41237-022-00188-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41237-022-00188-6



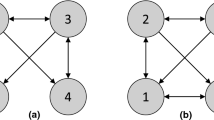






 is decidable, but not uniformly decidable;
is decidable, but not uniformly decidable; is progressively solvable, but not decidable.
is progressively solvable, but not decidable.