1 Introduction

In 2022 we celebrated the centenary of the famous Stern–Gerlach experiment [1] establishing that the intrinsic magnetic moments of atomic systems are quantized. Stern and Gerlach established this for silver atoms [2], for which the magnetic moment is created by the intrinsic magnetic moment of an unpaired 5 s electron. We capture this quantization of the magnetic moment by introducing the internal variable spin of elementary particles, in this case for the electron spin \(s= 1/2\). In standard quantum mechanics we reduce our description of the magnetic moment to one of the spin, representing it by a unitary matrix \({\hat{\sigma }}\in \text {SU}({2})\) and its wave function space by \({\mathbb {C}}^2\). A particle beam of unpolarized atoms is then described by a random mixture of spin-up and spin-down states which get deflected into two separate spots on the measurement screen. Input and output statistics are related using the Pauli equation.

The Einstein–Podolsky–Rosen (EPR) thought experiment [3] was suggested to argue that the description of a quantum system via a wave function can not be considered complete. In 1951, Bohm [4] formulated an equivalent thought experiment considering measurement of discrete spin variables. He considered a system of two initially anticorrelated spins in a singlet state which fly apart in opposite directions. This singlet state ensures that spin measurements on the particle pair using two SG setups will always yield antiparallel results, irrespective of the measurement axis chosen for the SG experiments. Measuring the spin A, \(s^A_z\), along the z-axis determines or “unveils” \(s^B_z\) immediately, even when the particles are space-like separated. A “paradox” arises when a different measurement axis for \(s^B\) is chosen, for example, when measuring the x component of B, \(s^B_x\), simultaneously with \(s^A_z\). Then we would assign a certain value for \(s^B_z\) as well as for \(s^B_x\) which would not be derivable from the wave function description. Bell generalized this to correlations between different orientations of the measurement axis and derived inequalities that are violated by quantum mechanics but are supposed to hold for local hidden-variable theories. The ability of quantum states to be entangled lies at the heart of the violation of Bell’s inequalities and the experimental proof of this behavior has been awarded the noble prize in physics in 2022 [5].

In the rest of this manuscript we will present a hidden variable theory where the instantaneous position of a particle and the orientation of its magnetic moment are the hidden variables undergoing conservative Brownian motion [6]. Faris [7] used diffusion processes on \({\mathbb {R}}^{}\times \text {SU}({2})\) following Dankel’s discussion [8], to perform an analysis of the SG experiment within stochastic mechanics. We will analyze the quantum Hamilton equations [9,10,11] which have been derived for this dynamic model to describe the measurement process in the SG apparatus in a time-resolved fashion. We will then consider the EPRB setup and show that we can correctly predict the correlations between the spin measurements on the two particles and the violation of Bell’s inequalities. We can trace the ability of this hidden variable theory to successfully do that to the fact that it is Bell non-separable (often called non-local) in the same way as standard quantum theory is. We argue that this non-locality supports Bohr’s view [12, 13], that the description of a quantum system with a wave function is epistemological in nature and not ontological, i.e., the wave function itself has no physical reality.

2 Quantum Hamilton Equations

The article is built upon the work presented in [11], which derived quantum Hamilton equations for the particle spin using the Bopp–Haag model [14]. We consider a time-reversible stochastic process \(Y_t = (\varvec{X}_t, R_t)\in M={\mathbb {R}}^3\times {SO}({3})\) for position and orientation variables of a particle. Here, \({\varvec{X}}_t\) denotes the position of its center of mass in space, and \(R_t\) represents the orientation of the particle’s magnetic moment. This model assumes an extended spherical particle with moment of inertia \({I_{\textrm{m}}}>0\)  as illustrated in Fig. 1.

Fig. 1
figure 1

The figure illustrates the combination of a stochastic process regarding position and orientation. A quantum object with mass m and moment of inertia \({I_{\textrm{m}}}\) is subjected to random perturbations with diffusion constants \(\sigma ^2_m=\hbar /m\) and \(\sigma ^2_I=\hbar /{I_{\textrm{m}}}\)

Full size image

The conservative diffusion in \({\mathbb {R}}^3\times {SO}({3})\) may be described by the following forward-backward stochastic differential equations (FBSDEs)

$$\begin{aligned} \text {d}\varvec{X}_t&= \left[ \varvec{v}(t,Y_t)\pm \varvec{u}(t,Y_t)\right] \text {d}t + \sigma _m \text {d}\varvec{W}_{\pm ,t} \end{aligned}$$
(1)
$$\begin{aligned} \text {d}\varvec{R}_t&= \varvec{R}_t \times \left[ (\varvec{\omega }_v(t,Y_t) \pm \varvec{\omega }_u(t,Y_t))\text {d}t + \sigma _I \text {d}{\tilde{W}}_{\pm ,t} \right] \,, \end{aligned}$$
(2)

where we parameterize an element of \({SO}({3})\) as a vector \(\varvec{R}_t\in {\mathbb {R}}^ 3\) representing the orientation of the particle. In these equations \(\varvec{W}_{\pm ,t}\) and \({\tilde{W}}_{\pm ,t}\) are forward and backward Wiener processes.Footnote 1

The stochastic process is characterized by the velocity fields \(\varvec{v},\varvec{\omega }_v\) for the current (angular) velocities, and \(\varvec{u}, \varvec{\omega }_u\) for the osmotic (angular) velocities. The diffusion constant is split into \(\sigma _m\) and \(\sigma _I\), representing diffusion in \({\mathbb {R}}^3\) and rotation in SO(3), \(\sigma _I=\sqrt{\nicefrac \hbar {I_{\textrm{m}}}}\) being analogous to Nelson’s definition for the translation diffusion constant \(\sigma _m = \sqrt{\nicefrac {\hbar }{m}}\).

The translation part of the quantum Hamilton equations (see [11]), is given by

$$\begin{aligned} \text {d}\varvec{X}_t&= [\varvec{v}\pm \varvec{u}]\text {d}t + \sqrt{\frac{\hbar }{m}} \text {d}\varvec{W}_{\pm ,t} \end{aligned}$$
(3)
$$\begin{aligned} \text {d}\varvec{P}_{t}&= \big [\varvec{F}^{\text {Lor}} - \gamma {I_{\textrm{m}}}\nabla ([\varvec{\omega }_v+{\varvec{\omega }_u}]\cdot \varvec{B}) \big ] \text {d}t +q \text {d}\varvec{A} +\Pi ^{x}_{t}\text {d}W_{-,t} \,. \end{aligned}$$
(4)

Here \(W_{-,t} = (\varvec{W}_{-,t}, {\tilde{W}}_{-,t})\) is a six-dimensional backward Wiener process. The stochastic processes \(\varvec{P}_t\in {\mathbb {R}}^3\) and \(\Pi ^x_t \in {\mathbb {R}}^{3\times 6}\) represent the co-state of the stochastic control problem associated with the position. Specifically, \(\varvec{P}_t=m(\varvec{v}+\varvec{u})+q\varvec{A}\) is the canonical stochastic momentum [10]. Additionally, \(\varvec{F}^{\text {Lor}}=-\nabla V -q\partial _t\varvec{A} - q(\varvec{v}+\varvec{u})\times \varvec{B}\) is the Lorentz force, \(\varvec{A}\) the vector potential and \(\varvec{B} = \nabla \times \varvec{A}\) the magnetic field.

We will use \(z-x-z\) Euler angles \(\theta = (\vartheta ,\varphi ,\chi )\) as generalized coordinates to represent the orientation degree of freedom. The quantum Hamilton equations for the orientation \(\theta _t\) have the form (see Sect. 5 of [11])

$$\begin{aligned} \text {d}\theta ^j_t&= \left[ \omega _{v}^j\pm \omega _{u}^j {\mp } \frac{\sigma _I^2}{2}\Gamma ^j_{kl}g^{kl}\right] \text {d}t + \sqrt{\frac{\hbar }{{I_{\textrm{m}}}}} {h}^j_k \text {d}\tilde{W}^k_{\pm ,t} \end{aligned}$$
(5)
$$\begin{aligned} \text {d}s_{\vartheta ,t} =&\bigg [ {\partial _\vartheta V^\text {rot}_\text {eff}(\vartheta _t, s_{\varphi ,t}, s_{\chi ,t}) + \frac{\gamma }{\sin ^2\vartheta _t}( s_{\varphi ,t}-\cos \vartheta _ts_{\chi ,t})(B_x\cos \varphi _t-B_y\sin \varphi _t)} \end{aligned}$$
(6)
$$\begin{aligned}&+ \frac{\hbar s_{\vartheta ,t}}{2{I_{\textrm{m}}}\sin ^2\vartheta _t} \bigg ]\text {d}t +\Pi ^\theta _{\vartheta k}\text {d}W^k_- \end{aligned}$$
(7)
$$\begin{aligned} \text {d}s_{\varphi ,t} =&{\gamma [\varvec{s}_t\times \varvec{B}]_z} \text {d}t +\Pi ^\theta _{\varphi k}\text {d}W^k_- \end{aligned}$$
(8)
$$\begin{aligned} \text {d}s_{\chi ,t} =&\Pi ^\theta _{\chi k}\text {d}W^k_-\,. \end{aligned}$$
(9)

Here the canonical angular momenta \(s_{j,t}=g_{kj}(\omega _{v}^k+\omega _{u}^k)+\gamma {I_{\textrm{m}}}B_j\) are identified with the stochastic spin components of the particle and \(\Pi ^\theta _t \in {\mathbb {R}}^{3\times 6}\) is the second co-state process in form of a matrix. In equation (5), the Cristoffel symbols of the second kind \(\Gamma ^j_{kl}\), the metric \(g^{kl}\) and \(h^k_jh^l_j=g^{kl}\) occur. These are additional second-order terms that follow from the stochastic calculus and vanish in the classical limit \(\sigma _{I},\sigma _m\rightarrow 0\), see equation (12) in Ref. [11]. The rotational effective potential

$$\begin{aligned} V^\text {rot}_\text {eff}(\vartheta ,s_\varphi ,s_\chi ) = \frac{1}{2{I_{\textrm{m}}}\sin ^2\vartheta }( s_\varphi ^2 + s_\chi ^2 -2 \cos \vartheta \,s_\chi s_\varphi ) \end{aligned}$$
(10)

in (6) is due to the metric.

From the QHE (3–9) the Madelung equations on the configuration manifold can be derived using Itô calculus, which in turn can be transformed into the Schrödinger equation [8, 11]. In [11] it was shown that the quantum Hamilton equations for a freely spinning particle lead to stochastic processes reproducing the expectation values of spin in standard quantum mechanics. In the next section we will extend the analysis of the QHE to describe the SG experiment.

3 Stern–Gerlach Experiment

Our numerical analysis will employ the geometry and parameters close to Stern and Gerlach’s experiment, given in Table 1. At \(t=0\) a beam of silver atoms with a Gaussian width (in the y and z directions) of \(\sigma _0\) moves in the y direction. At \(t=0\) the beam enters the SG magnet which creates an inhomogeneous magnetic field \(\varvec{B} = (B_0 + b\,z)\varvec{e}_z\). The gradient term \(b z \ll B_0\) in the magnetic field introduces a momentum gain in the z direction based on the particle’s magnetic moment, resulting in the separation of particles at a detector after passing through the magnet.Footnote 2 The Gaussian fixes the width of the initial distribution in the y and z directions, such that the osmotic velocity is given by \(\varvec{u}(t=0, \varvec{x}) = \frac{1}{\tau _0}(0,-y,-z)\), where \(\tau _0 = \frac{m\sigma ^2_0}{\hbar }\). The momentum in the y direction is assumed to follow from a Maxwell-Boltzmann distribution, with the root mean square velocity \(v_y= \sqrt{\frac{4 k_B T}{m}}\) serving as the semi-classical propagation velocity. The other components of v are initially set to 0. We assume that the current velocity \(v_y\) remains constant throughout the experiment, disregarding potential spreading effects from the beam’s distribution along the propagation path. The length \(d_1\) of the magnet results in an interaction time of the beam with the inhomogeneous magnetic field given by \(T_m= \frac{d_1}{v_y}\). After this time, the magnetic field is assumed to vanish, and the motion becomes field-free.

Table 1 The table presents the experimental data used in the numerical simulation
Full size table

Classically, the deflection of a particle is determined by the orientation of its magnetic moment with respect to the inhomogeneous magnetic field, therefore we would expect a broad distribution on the screen for randomly oriented magnetic moments at the high temperature of the experiment. Experimentally, however, one only observes two sharp spots. How does this come about within the stochastic framework, utilizing the quantum Hamilton equations of motion above?

The force term coupling the translation to the orientation of the magnetic moment in Eq. (4) is given by

$$\begin{aligned} \varvec{F}_{\textrm{mag}}= - \gamma \nabla ({I_{\textrm{m}}}(\varvec{\omega }_v+\varvec{\omega }_u)\cdot \varvec{B})=-\gamma {I_{\textrm{m}}}( {\omega }_{v,z}+ {\omega }_{u,z}) b\,\varvec{e}_z. \end{aligned}$$
(11)

The QHE (4) for the z component of the momentum then read

$$\begin{aligned} m\text {d}[v_z+u_z] =&\gamma {I_{\textrm{m}}}({\omega }_{v,z}+\omega _{u,z})b \,\text {d}t + \Pi _{zj,t} \text {d}W^j_{-,t}\,. \end{aligned}$$
(12)

The other components of the momentum equations have vanishing drift terms, while the QHE for the spin in the Euler angles (6–9) show no contribution of the external field term B,

$$\begin{aligned} \text {d}s_{\vartheta ,t} =&\left[ \partial _\vartheta V^\text {rot}_\text {eff} + \frac{\hbar s_{\vartheta ,t}}{2{I_{\textrm{m}}}\sin ^2\vartheta _t} \right] \text {d}t + \Pi _{\vartheta j}\text {d}W^j_{-,t} \end{aligned}$$
(13)
$$\begin{aligned} \text {d}s_{\varphi ,t} =&\Pi _{\varphi j}\text {d}W^j_{-,t} \end{aligned}$$
(14)
$$\begin{aligned} \text {d}s_{\chi ,t} =&\Pi _{\chi j}\text {d}W^j_{-,t}\,. \end{aligned}$$
(15)

Hence, the backward SDEs concerning the angular momenta in this case yield the drift terms of a freely spinning particle. The coupling of the particle’s position to its orientation in the QHE is then due to the matrix \(\Pi _t\). Considering the canonical momenta \(\varvec{P}_t\) as feedback momenta, i.e., \(\varvec{P}_{t}=\varvec{p}(t, \varvec{x},\theta )\), in general they depend on all variables. This implies a dependence of \(\Pi _{jk,t}(t,\varvec{x},\theta )\) \(\propto \partial _j p_k(t,\varvec{x},\theta )\) on all configuration coordinates. Similarly, this holds for the canonical angular momenta considered as fields \(\varvec{s}_t = \varvec{s} (t,\varvec{x},\theta )\). Such a coupling follows in the stochastic picture if the expectation values of the spins are not aligned with the measurement setup, as will be shown later.

3.1 Solutions to Constant \(s_z\) Expectation

To obtain some understanding of the dynamics in the SG apparatus, we consider at first a simplified version of constant spin projection. We assume that the orientation variables decouple from the motion in space. The discussion of the solutions to the angular momentum Eq. (14) then follows the section regarding the freely spinning particle in [11]. For spin \(\frac{1}{2}\) particles the stochastic processes fulfill \(\text {E}\left[ s ^2\right] =\frac{3\hbar ^2}{4}\) and \(\text {E}[\varvec{s}]=\pm \frac{\hbar }{2} e_z\) for the two eigenstates. The feedback controls for the angular momenta read \(s^v_\varphi = s^v_\chi =\frac{\hbar }{2}\) and \(s^u_\vartheta = -\frac{\hbar }{2}\tan \frac{\vartheta }{2}\) for the spin up particle, and \(s^v_\varphi =- s^v_\chi =-\frac{\hbar }{2}\), \(s^u_\vartheta = -\frac{\hbar }{2}\cot \frac{\vartheta }{2}\) for the spin down state, respectively. Hence, in the case of a spin decoupled from the position we find constants for the \(\varphi\) and \(\chi\) components. In terms of the spin vector in the reference frame, e.g., the spin up vector, there is

$$\begin{aligned} \varvec{s}= \varvec{s}_v+\varvec{s}_u = \frac{\hbar }{2}(\tan \nicefrac {\vartheta }{2}(\cos \varphi +\sin \varphi ), -\tan \nicefrac {\vartheta }{2}(\cos \varphi -\sin \varphi ), 1)^T\,. \end{aligned}$$
(16)

It follows that the feedback field of the spin along the measurement axis z is constant. The solutions to (12) are approximated, as the coupling is primarily due to the z component of the magnetic field and angular velocity. With that, the force acting on the particle in the magnetic field is constant, simplifying the search for a solution of the quantum velocity with the help of the QHE.

In the inhomogeneous field, the particle with constant \(s_z= \pm \frac{\hbar }{2}\) gains a transverse momentum which leads to a time-dependent z-component of the quantum velocity, i.e., \(v^q_u = v_z -\text {i}u_z\),

$$\begin{aligned} v^{q,m}_z(t,z)= v_{{\textrm{cl}}}(t) - \frac{\text {i}}{\tau _0\sigma _t} \left( -z +z_{\textrm{cl}}(t)\right) \end{aligned}$$
(17)

with the definition of a classical velocity \(v_{\textrm{cl}}(t) = \frac{\gamma s_z b}{m}t\) and a classical displacement \(z_{\textrm{cl}}(t)=\frac{\gamma s_z b}{2\,m}t^2\,.\) The quantum velocity given in (17) is a solution to the QHE for a constant spin projection \(s_z\). Spreading effects of the distribution depend on the timescale of the experiment, where \(\tau _0=\frac{m\sigma _0^2}{\hbar }\) depends on \(\sigma _0\) and m and \(\sigma _t=1+\text {i}\frac{t}{\tau _0}\).

At the exit of the magnet at time \(t=T_m\) the current velocity has an additional contribution in the z direction \(v_m=v_{\textrm{cl}}(T_m)=\frac{\gamma s_z b}{m}T_m\) and the probability distribution is displaced by \(z_m=z_{\textrm{cl}}(T_m)=\frac{\gamma s_z b}{2\,m}T_m^2\). This leads to a quantum velocity after the interaction with the magnet in the field free region

$$\begin{aligned} v^{q,f}_z(t',z)= v_m - \frac{\text {i}}{\tau _0\sigma _{t'}} \left( -z + z_m + v_m t'\right) \end{aligned}$$
(18)

where \(t'=t-T_m\). The spreading of the distribution is again related to \(\frac{t}{\tau _0}\) and higher orders terms in

$$\begin{aligned} \frac{1}{\sigma _t}= 1-\text {i}\frac{t}{\tau _0}+{\mathcal {O}}\left( \left( \frac{t}{\tau _0}\right) ^2\right) \end{aligned}$$
(19)

are neglected since the change in transversal momentum is large compared to the spreading of the distribution.Footnote 3 The feedback solutions given in (17 and 18) may be verified by applying the complex Itô formula, e.g., see [16] or [11], to the quantum velocities \(v^{q,\cdot }_z\) and comparing the drift terms in the momentum equations of the QHE.

On average, the particles pick up a transversal momentum in the magnet according to their initial spin projection \(s_z\) which can be read from the real part in Eqs. (17 and 18). This is the current velocity. The osmotic velocity encoded in the imaginary part of these equations, ensures that the particle stays close to the classically expected path. Hence, in the special cases of constant spin projections, i.e., the spin states are aligned with the direction of the field gradients, the stochastic mechanics’ description is similar to that expected from classical mechanics. The same interpretation is used in the superposition of the spin eigenstates with Pauli spinors where from a semiclassical point of view each component is deflected as if the spins are either aligned up or down w.r.t. the magnetic field. The conceptual differences to the classical picture and the ordinary treatment in quantum mechanics appear when the spins are randomly oriented before the interaction with the magnetic field.

3.1.1 Randomly Oriented Initial Spins

For particles with spin-\(\frac{1}{2}\), when the z projections satisfy \(\left| \text {E}[s_z]\right| <\frac{\hbar }{2}\), the expected spin is given by \(\text {E}[ \varvec{s}] = \pm \frac{\hbar }{2} \varvec{e}_{\delta }\). Here, \(\varvec{e}_\delta\) is a unit vector representing the new spin projection axis, tilted at an angle \(\delta\) with respect to the measurement axis. Regardless of this, the second moment of the expectation, \(\text {E}\left[ {\varvec{s}}^2\right]\), remains constant at \(\frac{3\hbar ^2}{4}\). Stochastic processes that yield these expectation values and satisfy the QHE for a freely spinning particle can be formulated using a combination of the known solutions given in [11].

The associated calculation can be found in appendix A. This calculation presents the rotated canonical angular momenta as feedback controls for the Euler angles, and read

$$\begin{aligned} \begin{aligned} s_\vartheta&= \frac{\hbar }{2\rho } (\text {i}\cos \delta \sin \vartheta + \sin \delta (\cos \varphi - \text {i}\cos \vartheta \sin \varphi ))\\ s_\varphi&= {\frac{\hbar }{2\rho }} (\cos \delta + \cos \vartheta - \text {i}\cos \varphi \sin \delta \sin \vartheta )\\ s_\chi&= \frac{\hbar }{2} \end{aligned} \end{aligned}$$
(20)

with \(\rho =(1 + \cos \delta \cos \vartheta + \sin \delta \sin \vartheta \sin \varphi )\). The intrinsic rotation \(s_\chi\) in (20) is unaffected, whereas the z projection, i.e., the component \(s_\varphi\), is no longer constant. The corresponding spin vector in the reference frame is thus given by

$$\begin{aligned} s = \frac{\hbar }{2\rho } \begin{pmatrix} \sin \delta + \sin \vartheta (\text {i}\cos \delta \cos \varphi + \sin \varphi ) \\ -\text {i}\cos \vartheta \sin \delta - \sin \vartheta (\cos \varphi - \text {i}\cos \delta \sin \varphi ) \\ (\cos \delta + \cos \vartheta - \text {i}\cos (\varphi ) \sin \delta \sin \vartheta ) \end{pmatrix}. \end{aligned}$$
(21)

The z-component of the spin \(s_\varphi =s_z(\theta ,\delta )\) depends in general on the Euler angles \(\theta = (\vartheta ,\varphi ,\chi )\), while the expectation along the z axis is \(\text {E}[s_z]=\frac{\hbar }{2}\cos \delta\). Thus, \(s_z\) is not a constant field, so the description of the SG experiment has to include the coupling of the random orientation variables to the translation motion due to the classical force term \(- \gamma s_zb(t,\varvec{x}, \theta ,\delta )\). It is not trivial to derive solutions to the QHE in an analytic form for position and orientation in space. It is, however, possible to describe the present experiment using the solutions for the cases with \(\text {E}[s_z]=\pm \frac{\hbar }{2}\) discussed earlier in this section.

The constant spin projection solutions determine the velocity fields both within and after the magnet, as derived in Eqs. (17 and 18). Depending on the spin projections for a spin-\(\frac{1}{2}\) particle, there are two known solutions to the QHE: one for spin up and the other for the down state. These solutions may be combined to describe solutions in the stochastic picture for random orientations of spin expectations according to (20 or 21). This combination of the corresponding spin-\(\frac{1}{2}\) particles gives a velocity in the magnetic field of

$$\begin{aligned} v^{q,m}_{z}(t,z,s^{q,m}_z(t))= \frac{2}{\hbar }v_{\textrm{cl}}(t) s^{q,m}_{z}(t) - \frac{\text {i}}{\tau _0 \sigma _t}\left( -z+\frac{2}{\hbar }z_{\textrm{cl}}(t)s^{q,m}_{z}(t)\right) \,. \end{aligned}$$
(22)

Here the feedback angular momentum \(s^{q,m}_{z}(t)=s^{q,m}_{z} (t,z,\theta )\) is written in short-hand notation. The expressions for the angular momenta \(s^{q,m}_{j}(t)=s^{q,m}_{j} (t,z,\theta )\) can also be written explicitly, e.g. see [17]. We do not present them here in detail because we will approximate them due to the different timescales of the problem.

Consider a situation where the initial spin component \(s^{q}_{z}\) is treated as a continuous random variable with a zero expected value. After interacting with the apparatus, the spin-\(\frac{1}{2}\) particle should have equal probabilities for both upward and downward motion. The initial random value of that spin component at \(t=0\) influences the direction the particle is moving as given in Eq. (17). Thus, the probability of ending up in one of the two channels, depends on the direction of the spin. This will be shown in the following subsection w.r.t. the spin average in more detail.

Note that the field equations for the angular momenta, e.g., given in Eq. (22), have no counterpart in the spinor description of quantum mechanics since \(s^q_j(t,z,\theta )\) depend on the orientation variables. Hence, the stochastic description offers additional information on the change in the particle’s orientation. However, the detailed information on \(\theta\) and the associated stochastic spin is not necessary to reproduce known quantum behavior in the stochastic picture, which is due to the different timescales of the stochastic processes in position and orientation which will discussed for the explicit numerical solution of the stochastic processes in the following.

3.1.2 Numerical Solution

Consider the forward SDEs given by (3 and 5). Within the magnetic field, these describe the stochastic processes related to position \(\varvec{x}=(y,z)\) and orientation \(\theta =(\vartheta ,\varphi ,\chi )\), and can be solved with the velocity fields given in (22).

To obtain a numerical solution, we select specific values for characteristic time \(t_c\) and length \(l_c\). As mentioned earlier, the moment of inertia \({I_{\textrm{m}}}\approx m R^2\), depending on the radius of the modeled extended mass distribution, fixes the time scale \(t^\text {rot}_c = \frac{{I_{\textrm{m}}}}{\hbar }\) of the rotational diffusion. Compared to the time scale \(t_c = \frac{m}{\hbar }d_1^2\) for translation over the length of the magnet (or fractions thereof)

$$\begin{aligned} t^\text {rot}_c \approx \frac{m}{\hbar }R^2 \ll \frac{m}{\hbar }d_1^2 = t_c\,, \end{aligned}$$
(23)

the change of the orientation is rapid compared to the motion in space. Therefore, during a time step \(\Delta t \gg t^{\text {rot}}_c\) (but \(\Delta t \ll t_c\)) in the simulation of the atoms in the SG experiment, all reachable orientation angles are visited according to their current probability distribution. E.g., for the spin field \(s(t, \varvec{x},\theta )\) the average

$$\begin{aligned} \langle s(t, \varvec{X}_t, \theta _t)\rangle _{\Delta t} = \frac{1}{\Delta t} \int _t^{t+\Delta t} s(t, \varvec{X}_t, \theta _t) \text {d}t \end{aligned}$$
(24)

corresponds approximately to the expectation of the spin at \((t, \varvec{x})\), if \(\varvec{X}_t\approx \varvec{X}_{t+\Delta } = \varvec{x}\) is assumed to be constant during the time span \(\Delta t\). Consequently, we can simplify the diffusion process, going from the complex space \({\mathbb {R}}^3 \times {SO}({3})\) to the simpler \({\mathbb {R}}^ 3\) space, by taking the orientation averages of the considered quantities. For example,

$$\begin{aligned} {\bar{f}}(t, \varvec{x}) = \frac{1}{{\bar{\rho }} (t, \varvec{x})} \int f(t, \varvec{x}, \theta ) \rho (t, \varvec{x},\theta ) \text {d}\theta \end{aligned}$$
(25)

where \({\bar{\rho }} (t, \varvec{x})= \int \rho (t,\varvec{x},\theta ) \text {d}\theta\) and the integral is meant to cover the whole configuration space concerning the orientation.Footnote 4 The averaging simplifies the numerical solution of the stochastic differential equations for the position by averaging the spin dynamics. From here on, averages concerning the orientation variables will be used. Hence,

$$\begin{aligned} \begin{aligned} \text {d}{\bar{Y}}_t&= \left[ v_0 + \frac{v_0 t - {\bar{Y}}_t}{\tau _0} \right] \text {d}t + \sqrt{\frac{\hbar }{m}}\text {d}W^y_+\\ \text {d}{\bar{Z}}_t&= \left[ \frac{2}{\hbar }\left( v_{\textrm{cl}}(t)+\frac{z_{\textrm{cl}}(t)}{\tau _0}\right) \bar{s}^{v+u}_\varphi -\frac{{\bar{Z}}_t}{\tau _0}\right] \text {d}t + \sqrt{\frac{\hbar }{m}}\text {d}W^z_+ . \end{aligned} \end{aligned}$$
(26)

Considering the z-direction, the orientation average of the spin angular momentum \({\bar{s}}^{m,v+u}_z(t,z) = {\bar{s}}^{m,v+u}_\varphi (t,z)\) can be calculated analytically. In the magnet, and, similarly for the field-free region, we have

$$\begin{aligned} {\bar{s}}^{m,v+u}_\varphi (t,z)&= \frac{1}{{\bar{\rho }}(t,z)} \int s^{m,v+u}_\varphi (t,z, \theta ) \rho (t,z,\theta ) \text {d}\theta \nonumber \\&= -\frac{\hbar }{2}\left( 1- \frac{{2}(1+\cos \delta )}{1+\exp \left( \nicefrac {4 z_{cl}(t) z }{\sigma _t \sigma _0^2}\right) (1-\cos \delta )+\cos \delta } \right) \,. \end{aligned}$$
(27)

This implies that the spin average is influenced by the initial spin expectation, particularly via the incident angle \(\delta\). The two cases of spin up (\(\delta = 0\)) and down (\(\delta = \pi\)) lead to \({\bar{s}}^{m,v+u}_z(t,z) = \pm \nicefrac {\hbar }{2}\).

3.1.3 Results

The experiment by Stern–Gerlach can be recovered in the stochastic picture of a spinning particle by randomly choosing the incident spin projection \(\delta\) of each simulated particle. Figure 2 illustrates that the beam of particle paths diverges into two channels regardless of initial spin expectations, and spin expectations change accordingly. This behavior sharply contrasts with the classical predictions, represented by the dashed lines in Fig. 2. Here, deflection relies solely on the initial magnetic moment on the measurement axis.

Fig. 2
figure 2

Spin-\(\frac{1}{2}\) particles entering the magnet of length 3 cm with random spin expectation values are depicted. Eight numerically determined stochastic trajectories in the \(y-z\) plane are shown as solid lines. The attached arrows at selected positions represent the direction of the mean orientation of the spin vector \(\bar{\varvec{s}}\). The dashed lines show the classically expected paths depending on the initial position and spin expectation. The right plot shows the paths and spins throughout the proposed SG device, where the vertical dashed line separates the field-free region from the magnet. The left plot depicts a zoomed-in version of the right plot, focusing only on the inside of the magnet

Full size image

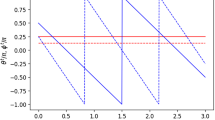
The averaged spins \(\bar{ \varvec{s}}(t)\) for each particle are represented as arrows in the same graph. For a detailed view of the orientation average of the z component, \({\bar{s}}_z(t)\), in a numerical simulation refer to Fig. 3. Finally, the spins will be fully aligned along the measurement axis.

Fig. 3
figure 3

The graph depicts the same color-coded stochastic realizations as in Fig. 2 for \(\bar{s}_z(t)\) as a function of time. The vertical dashed line indicates the transition from the inhomogeneous field to a vanishing field. \(T_m\) is the time spent in the magnet

Full size image

It’s important to emphasize that the averaged spins, represented by \({\bar{s}}_z(t)\), typically do not align perfectly with the external field already within the magnetic. Figure 3 reveals that some spins are not yet fully aligned when they enter the field free region (right of the dashed vertical line). The osmotic contribution to the velocity and the spin are responsible for the change in the field-free region. In more detail, the osmotic velocity (and the current velocity) ensures that the diffusion is conservative. Under expectation, there is an additional torque \(\bar{\varvec{T}}_u = \bar{\varvec{s}}\times \left( \nicefrac {\hbar }{2\,m}\Delta \bar{ \varvec{s}} + (\bar{\varvec{u}}\cdot \nabla )\bar{ \varvec{s}} \right)\) acting on the spin averages

$$\begin{aligned} \text {d}\bar{ \varvec{s}} = \left( \gamma \bar{ \varvec{s}}\times \varvec{B} + \bar{ \varvec{T}}_u\right) \text {d}t \,. \end{aligned}$$
(28)

This implies nontrivial changes of the expectation value of the spin even in the absence of a magnetic field. Equation (28) follows by comparing the drift terms of the Itô formula applied to \(\bar{ \varvec{s}}(t, \varvec{x})\) to the classically expected precession \(\gamma \bar{ \varvec{s}}\times \varvec{B} \text {d}t\).

As long as the beams are not separated, the stochastic particle has a non-vanishing probability of changing the beam it enters. Hence, the assignment of a particle having a momentum pointing (anti-)parallel to the field in the experiment can only be made when the beams are disjoint, i.e., the distance of the recording screen to the magnet is big enough. The same applies to the particle’s spin expectation. Thus, separation of probability distributions implies distinct spin expectations.

3.1.4 Polarization of the Initial Spin Expectations

What would be the outcome of the SG experiment when consecutive measurements are executed? Or, put differently, what if the spins are polarized before being introduced into the SG apparatus? The answers to these questions are significantly determined by two initial conditions: the position \(z(t=0)\) and the spin orientation \(\bar{\varvec{s}}_z (t=0)\). This is illustrated in the left column of Fig. 4 for two different incident angles \(\delta\).

When the spins are aligned with the measurement axis (\(\delta = 0\)) in the considered measurement setting, every particle goes up, irrespective of its initial position. For angles \(0< \delta < \pi\), the dependence on the initial position correlates with the outcome of the spin measurement. For example, consider the plot for \(\delta =\nicefrac {\pi }{4}\) in the top right of Fig. 4. The two particles in that sub-ensemble which are measured to be in a spin-down state are the ones with the lowest initial position \(z(t=0)\). A similar conclusion is drawn by looking at \(\delta =\nicefrac {\pi }{2}\).

Fig. 4
figure 4

The left column depicts stochastic paths of two different spin polarizations at the entrance of the SG magnet. These plots illustrate the (z, y)-plane of 8 stochastic realizations entering the inhomogeneous magnetic field at \(t=0\) and leaving the magnetic field of length 0.03 m at \(t=T_m\). The insets show the associated spin averages \({\bar{s}}_z(t)\). The chosen polarization incident angles are \(\delta = \nicefrac {\pi }{4}\) (top left) and \(\delta = \nicefrac {\pi }{2}\) (bottom left). The plot on the right depicts the normalized probabilities for z polarized spin-\(\frac{1}{2}\) particles entering a SG device to choose one of the two possible beams depending on the measurement angle \(\delta\). The probabilities following from the Pauli-equation (dashed) are compared to the approximated probabilities from the numerical simulations based on the quantum Hamilton equations (dots)

Full size image

We can compare the probabilistic approach to the predictions derived using the standard Pauli spinor approach. Generally, the two-component spinor in the basis \(\Psi _{z'}\) (where the \(z'\) axis is inclined at angle \(\delta\) relative to the z axis) can be expressed as

$$\begin{aligned} \Psi _{z'} = \begin{pmatrix} \cos \frac{\delta }{2}\,e^{-\text {i}\nicefrac {\phi _0}{2}}\psi _+ \\ \sin \frac{\delta }{2}\,e^{\text {i}\nicefrac {\phi _0}{2}}\psi _- \end{pmatrix}\,. \end{aligned}$$
(29)

In this formulation, the probabilities of a spin entering the up (down) channel are given by \(\rho ^{QM}_+=\cos ^2\nicefrac {\delta }{2}\) (\(\rho ^{QM}_-=\sin ^2\nicefrac {\delta }{2}\)). The comparison with the stochastic picture is shown on the right side of Fig. 4. The probabilities \(\rho _\pm\) are approximated by the proportion of particles moving up/down, i.e., \(\rho _\pm \approx \frac{N_\pm }{N_{total}}\). For all measurement angles, the number of particles was \(N_{total}=10^{6}\). Hence, the stochastic model agrees perfectly with the predictions of the Pauli theory.

The stochastic model including an internal orientation coordinate as a dynamic variable thus offers a more detailed view on the phenomena associated with the magnetic moment of an elementary particle. From that point of view, spin as a discrete internal degree of freedom as described by the Pauli equation is the minimal amount of structure added to the ordinary Schrödinger equation which is able to describe the statistical phenomena related to measurements of these magnetic moments.

3.1.5 Other Treatments

Scully et al. [18] presented an analysis of the SG experiment based on operator theory. Our discussion of the Stern–Gerlach experiment shows similarities to the explanations given in the pilot wave theory [19]. In [20], deterministic paths are analyzed for fixed initial spin expectations. There the incident position \(z_0=z(t=0)\) of the particle determines the outcome of the measurement, i.e., \(z_0\) is the hidden variable. In the stochastic picture, the velocity v has the same properties as in Bohmian mechanics. The hidden variables, however, are stochastic. Hence, the initial position \(z_0\) of the process does not predetermine the outcome but is rather an indicator of the probability of the measurement outcome. From the numerical simulations, one can deduce that the conditional probability of moving up depends—in the case of the spin averages—on the initial position. The particles with \({\bar{Z}}_{t=0} > 0\) are more likely to end up in the upper channel for spin expectation values perpendicular to the measurement axis, for example. From the plots in the left row if Fig. 4 on the other hand, we know that the initial spin orientation in general has an impact on the movement of the particle, too. Hence, there is an interplay of the random initial positions and spins of the particle giving rise to the probabilities of ending up being measured as spin up of spin down particle.

A completely different approach has been followed by de Raedt et al. [21]. Following a similar analysis of other foundational experiments for quantum mechanics, they showed that a combination of Newtonian dynamics with an event driven step involving some random choice for the orientation of the spin allows to reproduce the experimental SG results without invoking quantum mechanics. However, here the event dynamics has to be introduced by hand, whereas our approach is based on the general formulation of microscopic dynamics of conservative diffusion processes, applied to a specific physical model, in this case the Bopp–Haag model.

The following section deals with the stochastic description of two simultaneous spin measurements based on the results given here. This allows to describe one of the well-known entanglement phenomena in quantum mechanics, namely the Einstein–Podolsky–Rosen–Bohm thought experiment.

4 Einstein–Podolsky–Rosen–Bohm

The EPRB thought experiment considers two non-interacting anti-parallel spins which are in contact at time \(t=0\) and then fly apart in opposite directions to enter two SG experiments. Standard quantum theory describes the anti-parallel spins in a singlet state using Dirac notation as

$$\begin{aligned} {|{\Psi }\rangle } = \frac{1}{\sqrt{2}}\left( {|{\uparrow \downarrow }\rangle }- {|{\downarrow \uparrow }\rangle } \right) \,. \end{aligned}$$
(30)

here, the spatial part of the wave function is often omitted. Within this framework, measuring the spin of particle A along some direction a will cause the wave function to collapse to one of the two-state vectors in eq. (30). There is a perfect anti-correlation for the spin expectation values if B measures the same axis \(b = a\). However, if the second measurement axis is different, i.e., \(b\ne a\), the expected correlation yields

$$\begin{aligned} \frac{4}{\hbar ^2}\langle ( s^A\cdot a)\ ( s^B\cdot b)\rangle _{\Psi _-} = - a\cdot b\,. \end{aligned}$$
(31)

This correlation caught the attention of Bell [22], who demonstrated that no local hidden variable theory could match the predictions of quantum mechanics. Generalized versions [23] of the Bell inequality underwent experimental testing in the following decades, and led to the common conclusion that quantum mechanics is “non-local”. Hall [24] proposed “Bell non-separability” as a more appropriate term in the context of the EPRB experiment. His discussion is centered around the joint probability density, which represents the statistical correlations observed from repeated measurement outcomes.

If hidden variables exist, the joint probability density can be expressed as the integral of the product of conditional probability densities and the probability density of the hidden variables. The properties that a probabilistic model must satisfy to obey Bell’s inequality are statistical completeness, statistical locality, and measurement independence. Quantum mechanics violates statistical completeness, as non-factorizable probability densities arise from entangled states. This leads to non-local velocity fields in stochastic mechanics. Here, non-locality can occur in the sense that the measurement of one particle can affect the velocity of another particle that is space-like separated. Other interpretations of quantum mechanics, such as Everett’s many worlds interpretation [25, 26] or the idea of super-determinism [27,28,29], and super-measured theories [30], also preserve local realism but may involve multiple realities or the relaxation of measurement independence.

In the following we will address the EPRB problem within stochastic mechanics by using the previously outlined solutions to the QHE from the Stern–Gerlach section.

4.1 Stochastic Description

An idealized anti-parallel two-particle spin state in quantum mechanics—in the sense that the quantum expectations \(\langle {\hat{s}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle =-\langle {\hat{s}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle\)—can be described by the superposition

$$\begin{aligned} {|{\psi }\rangle }_{\epsilon ,\phi } = \frac{1}{\sqrt{2}}\left( \cos \frac{\epsilon }{2}{|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }-e^{\text {i}\phi }\sin \frac{\epsilon }{2}{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\right) \end{aligned}$$
(32)

where \({|{\pm _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}}\rangle }\) denotes the spin-up/down eigenstate of particle k in the z basis. For \(\epsilon = 0\) and \(\epsilon = \pi\), state (32) reduces to the Bell separable two particles states \({|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\) and \({|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\).

For \(\epsilon \in (0,\pi )\) the state \({|{\psi }\rangle }_{\epsilon ,\phi }\) does not fulfill the properties of Bell separability. These states are entangled, i.e., they cannot be written as a tensor product of single particle states. Maximally entangled states are described for \(\epsilon = \nicefrac \pi 2\). For example, Bell’s original inequality [22] addresses a singlet state (\(\epsilon =\nicefrac \pi 2,\phi =0\))

$$\begin{aligned} {|{\psi _s}\rangle } = {|{\psi }\rangle }_{\frac{\pi }{2},0} = \frac{1}{\sqrt{2}}\left( {|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }-{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\right) \,, \end{aligned}$$
(33)

which is one of the four so-called Bell states for a two-level system. Another Bell state is described by \({|{\psi }\rangle }_{\nicefrac \pi 2,\pi }\) which is the triplet state.Footnote 5

The specific property of an entangled spin state is related to the fact that these states cannot be understood only from the viewpoint of individual particles. For example, the expectation values w.r.t. to the state (32) of the total spin operator \({\hat{s}} = {\hat{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} + {\hat{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}\) read

$$\begin{aligned} \langle {\hat{s}}\rangle = 0 \qquad \langle {\hat{s}}^2 \rangle = \hbar ^2 (1-\cos \phi )\, \end{aligned}$$
(34)

while for the single spin operators

$$\begin{aligned} \langle {\hat{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\rangle = 0 \qquad \langle {\hat{s}}^2_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} \rangle = \frac{3\hbar ^2}{4}\,. \end{aligned}$$
(35)

The expectation of the single particle spin is zero, although the magnitude of the single particle spin does not vanish. Hence, each spin-\(\frac{1}{2}\) particle has an undefined quantization axis in these entangled states.

Consider the singlet state where \(\phi = 0\) in more detail. The magnitude of the total spin in (34) is zero under expectation. In the stochastic picture this translates to the ensemble expectations \(\text {E}[s_{{\textrm{tot}}}] = 0\) and \(\text {E}[s_{\textrm{tot}}^2] = 0\) where

$$\begin{aligned} 0=\text {E}[s_{{\textrm{tot}}}^2]= \text {E}[s^2_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}]+\text {E}[s^2_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]+2\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]=\frac{3\hbar ^2}{2}+2\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]\,. \end{aligned}$$
(36)

The dot product of the two spins thus has to fulfill \(\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]= -\frac{3\hbar ^2}{4}\). Within stochastic mechanics this implies that the angular velocity fields of the particles have to be dependent of each other’s orientation variables.

Going back to the quantum Hamilton equations for a simplified system of two spins, we have

$$\begin{aligned} \text {d}p_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}&= -\gamma {I_{\textrm{m}}}\nabla _{_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}} \left( {\omega _q}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\cdot B_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\right) \text {d}t +q_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\text {d}A_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}+ \Pi ^p_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\text {d}W_- \end{aligned}$$
(37)
$$\begin{aligned} \text {d}s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}&= \left[ \gamma s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} \times B_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} + \frac{\hbar }{{I_{\textrm{m}}}}T_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\right] \text {d}t + s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\times \Pi ^s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} \text {d}W_-\,, \end{aligned}$$
(38)

where \(p_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} = m v^q_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}+q_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}A_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\) and \(s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} = {{I_{\textrm{m}}}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} \omega ^q_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}+{{I_{\textrm{c}}}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}B_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\) are the canonical momenta of particle k, \(B_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\) are the magnetic fields generated by the SG devices for each particle and \(T_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\) is a purely quantum torque term which vanishes in the classical limit. The coupling of the particle’s orientation degrees of freedom to their motion in space is apparent in Eq. (37), which includes an inhomogeneity in the magnetic field. In the absence of a magnetic field, i.e., before and after the particles interact with the SG magnets, the classical force \(\nabla _{_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}} ({\omega _q}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\cdot B_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}})\) vanishes.

In the spin QHE (38), the spins may be correlated depending on the preparation of the initial state. This correlation is manifested in the momentum QHE (38) through the stochastic matrices \(\Pi ^s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\). Written as feedback controls \({\tilde{\Pi }}^s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} (t,\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}},\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})\) they generally depend on both orientation variables which allows correlated random changes of the spin directions.

For example, take \(\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]=-\text {E}[s^2_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}]=-\text {E}[s^2_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]\). Then, \(\text {E}[s_{{\textrm{tot}}}] = 0\) leads to \(\text {E}[s^v_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}]=-\text {E}[s^v_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]\) since \(\text {E}[s^u_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}]=0\). These expectations state that the spins along all possible stochastic orientation trajectories have to be antiparallel \(s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}=-s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}\) for \(t>0\) until one of them enters a measurement device. Hence, there is perfect anticorrelation without any decorrelation in the stochastic setting, which is generated through the matrices \({\tilde{\Pi }} ^s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} =- {\tilde{\Pi }}^s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}\).

It is possible to construct the singlet state with the solutions to the QHE for a freely spinning particle first, neglecting the position for now. According to the definition in (32), the singlet (and triplet state) in the field free regime can be derived by a combination of two solutions to a pair of spin-\(\frac{1}{2}\) particles with antiparallel expectations along the z axis. The state \((\pm )\) is a solution to two decoupled spins with \(\mu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} = -\mu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} = \nicefrac {1}{2}\), \(\nu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} = \nu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}= \nicefrac {1}{2}\), such that \(\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}]= -\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]= \frac{\hbar }{2}e_z\). Similarly, we denote \(({\mp })\) for the solution to the free spin QHE with \(\mu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} = -\mu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} = \nicefrac {1}{2}\), \(\nu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} = \nu _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}= \nicefrac {1}{2}\), such that \(\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}]= -\text {E}[s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}]= \frac{\hbar }{2}e_z\).

Both two-particle states are Bell-separable, as they are product states of spin-up and spin-down particles with distributions \(\rho _{(\pm )}(t,\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}},\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})=\rho _+(\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}})\rho _-(\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})\) and \(\rho _{({\mp })}(t,\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}},\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})=\rho _-(\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}})\rho _+(\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})\) and can be seen as the stochastic analog to \({|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\) and \({|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\).

Similar to (A1) in the appendix, the combination of the 2 two-particle solutions \((\pm )\) and \(({\mp })\) with the constants \(c_1=\frac{1}{\sqrt{2}}\cos \frac{\epsilon }{2}\) and \(c_2=\frac{-e^{i\phi }}{\sqrt{2}}\sin \frac{\epsilon }{2}\) in reference to Eq. (32) yields spin fields for the two entangled particles. E.g., the spin field of particle 1 for a maximally entangled state (\(\epsilon =\nicefrac \pi 2\)) reads

$$\begin{aligned} s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}= \frac{1}{\rho }\begin{pmatrix} -2\text {i}A\left( e^{\text {i}(\phi +\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})} \text {c} \frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}{2} \text {s} \frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}{2}+e^{\text {i}\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}} \text {s} \frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}{2} \text {c}\frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}{2}\right) \left( A^*\text {c} \frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}{2} \text {c} \frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}{2}-\text {s} \frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}{2} \text {s}\frac{\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}{2}\right) \\ -\text {s} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} (\text {c} (\phi +\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})+\text {i}\text {c} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} \text {s} (\phi +\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}))+\text {s} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} (\text {c} \varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}+\text {i}\text {c} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} \text {s} \varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}) \\ -\text {i}\text {s} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} \text {s} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} \text {s} (\phi -\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}+\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})+\text {c} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}-\text {c} \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} \end{pmatrix} \end{aligned}$$
(39)

with shorthand notations \(\text {c}=\cos\) and \(\text {s}=\sin\), the definition of \(A=e^{-i \left( \phi +\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}+\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}\right) }\) and the probability distribution \(\rho =\frac{1}{8} (2 \sin \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}} \sin \vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} \cos (\phi -\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}+\varphi _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})-\cos (\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}-\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})-\cos (\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}+\vartheta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})+2)\).

In the singlet state (\(\phi =0\)), the spin fields \(s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}} (\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}},\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})= -s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}(\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}},\theta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})\) are perfectly anti-parallel. Note that the stochastic process of the total spin \(s_t = s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}t} + s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}t}\) as a critical feedback process to the spin QHE necessarily leads to \(\text {d}s_t = 0\). I.e., the drift and the stochastic terms vanish in the SDE. In terms of the single spin QHE we have \(\text {d}s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}t}=-\text {d}s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}t}\).

For the triplet state (\(\phi = \pi\)) the x, y components of the feedback fields coincide and \({s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}_z=-{s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}_z\). Note that these quantities are not ensemble expectations but the drift fields of the stochastic processes depending on both orientations. This is also manifested in the corresponding spin correlation matrix of the spin pair. The expected correlation depending on \(\epsilon ,\phi\) reads

$$\begin{aligned} \text {E}\left[ {s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}_i{s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}_j\right] = \frac{\hbar ^2}{4} \begin{pmatrix} -\sin \epsilon \cos \phi &{} \sin \epsilon \sin \phi &{} 0\\ \sin \epsilon \sin \phi &{} -\sin \epsilon \cos \phi &{} 0\\ 0 &{} 0&{} -1 \end{pmatrix}\, \end{aligned}$$
(40)

where \(i,j\in \{x,y,z\}\). As expected, the uncoupled spins (\(\epsilon =0\)) can be maximally (anti-)correlated for one axis, the z axis in the example. The entangled states (\(0<\epsilon < \pi\)), on the other hand, show additional correlations between other components, e.g., the triplet (singlet) state shows perfect (anti-)correlation under expectation w.r.t. to the x, y components. One can conclude that the stochastic spin fields for the singlet state violate Bell’s inequality (before the measurement) but not a generalized Schwarz inequality

$$\begin{aligned} -\text {E}[(a\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}})(b\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})]-\text {E}[(a\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}})(c\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})]\le \frac{3\hbar ^2}{8}-\text {E}[(b\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}})(c\cdot s_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}})] \end{aligned}$$
(41)

for continuous random variables. This follows the discussion in chapter 6 of [7], where it was pointed out that Bell’s inequality only holds for discrete random variables. The treatment after the particles couple to the position in the measurement process is analyzed in what follows.

4.1.1 Simultaneous Measurement

The coupling of spin or orientation to space also shows up in the description of the measurement procedures for the EPRB pair. Here we consider two uncoupled particles entering two space-like separated inhomogeneous magnets. The Bell separable \((\pm )\) and \(({\mp })\) pairs are augmented to describe the coupling to the position with the corresponding (angular) velocities \(v^\pm _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}q} = v^+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}q}\), \(v^\pm _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}q} = v^-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}q}\) and \(v^{\mp }_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}q} = v^-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}q}\), \(v^{\mp }_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}q} = v^-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}q}\). Since these models are still product states, the velocity field of each particle can be described independently in analogy to the SG description in section 3. To describe entangled states, the velocity fields for each particle k, namely \(v^\pm _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\) and \(v^\pm _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\), are now combined with the same coefficients \(c_1, c_2\) as before.

Fig. 5
figure 5

The plot depicts a sample of 5 numerically calculated particle pairs (each pair has a distinct color) prepared in a singlet state entering the magnets simultaneously with measurement angles \(\delta _1=\delta _2=\frac{\pi }{4}\)

Full size image

The Eq. (26) given in section 3 were used for each particle k with the corresponding orientation averages of the forward drift fields

$$\begin{aligned} {\bar{v}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} (t,z_1, z_2,{\bar{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}\varphi })+{\bar{u}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} (t,z_1, z_2,{\bar{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}\varphi }) \end{aligned}$$

depending on the \(\varphi\) component of the spin angular average. E.g., for particle 1 in the magnet, denoted by the superscript m, the averaged spin along the measurement direction \(z^{\delta _1}\) reads

$$\begin{aligned} {\bar{s}}^m_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}z} =\,&{\bar{s}}^m_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}\varphi }(t,z_1, z_2)\nonumber \\ =&-\frac{\hbar }{2{\bar{\rho }}} \bigg (\cos ^2\frac{\epsilon }{2} \left( -\cos \delta _1-(\cos \delta _1+1) A(z_1)+1\right) \left( -\cos \delta _2+(\cos \delta _2-1) A(z_2)-1\right) \nonumber \\&-\sin ^2\frac{\epsilon }{2} \left( \cos \delta _1+(\cos \delta _1-1) A(z_1)+1\right) \left( -\cos \delta _2+(\cos \delta _2+1) A(z_2)+1\right) \nonumber \\&-\sin \epsilon \cos \phi \sin \delta _1 \sin \delta _2 \left( A(z_1)-1\right) \left( A(z_2)-1\right) \bigg ) \end{aligned}$$
(42)

where \(A(z_k) = \exp \left( -\frac{4\,m z_k z_\text {cl}(t)}{\tau _0 \hbar }\right)\) and

$$\begin{aligned} {\bar{\rho }}^m =&\cos ^2\frac{\epsilon }{2} (A(z_1) (\cos \delta _1+1)-\cos \delta _1+1) (A(z_2) (\cos \delta _2-1)-\cos \delta _2-1)\nonumber \\&+\sin ^2\frac{\epsilon }{2} (A(z_1) (\cos \delta _1-1)-\cos \delta _1-1) (A(z_2) (\cos \delta _2+1)-\cos \delta _2+1)\nonumber \\&+2\sin \delta _1 \sin \delta _2 \sin \epsilon \cos \phi (A(z_1)-1) (A(z_2)-1)\,. \end{aligned}$$
(43)

E.g., the SDE for the z component of particle k given by the stochastic process \({\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}t}\) in the magnet (\(t<T_m\)) reads

$$\begin{aligned} \text {d}{\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}t}&= \left[ \frac{2}{\hbar }\left( v_{\textrm{cl}}(t)+\frac{z_{\textrm{cl}}(t)}{\tau _0}\right) \bar{s}^{m}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}\varphi }(t,{\bar{Z}} _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}t},{\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}t})-\frac{{\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}t}}{\tau _0}\right] \text {d}t + \sqrt{\frac{\hbar }{m}}\text {d}W_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}t} \end{aligned}$$
(44)

where \(v_{\textrm{cl}}(t) = \frac{\gamma \hbar b}{2m}t\) and \(z_{\textrm{cl}}(t)=\frac{\gamma \hbar b}{4m}t^2\) denote the classical velocity and displacement of a magnetic moment in an gradient field. After the magnet, the spin average \({\bar{s}}^a_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}z}\) is a copy of (42) with terms including \(z_{\textrm{cl}}(t)\) being replaced by \(z_m+v_m t\). Note that the drift terms including \({\mathcal {O}} \left( (\frac{1}{\tau _0})^2\right)\) have been neglected as in section 3.

For measurement angles \(\delta _1=\delta _2=0\), anti-correlated coincidences would be measured for the entangled states and the unentangled separable model, e.g., \((\pm )\). The spin fields (42) in the magnet in z direction are independent of the phase \(\phi\). They simplify to

$$\begin{aligned} {\bar{s}}^m_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}z\hspace{-1pt}),}1} = -{\bar{s}}^m_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}z\hspace{-1pt}),}2} = \frac{\hbar }{2}\tanh \left( \frac{2 m (z_1-z_2)z_{\textrm{cl}}(t)}{\tau _0\hbar }\right) . \end{aligned}$$
(45)

In contrast to the single-particle SG experiment, e.g., see Fig. 2, the averaged spin components in the singlet state for each spin are 0 before entering the magnet due to \(z_\text {cl}(0)=0\) and acquire \(z_l\) components for \(t>0\). If \({\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}t} > {\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}t}\), the first of the two drift terms in Eq. (44) are positive for particle 1 while negative for the other. Eventually, \(s^m_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}z\hspace{-1pt}),}l}\) approaches \(\pm \nicefrac \hbar 2\) for large times depending on the difference \({\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}t}-{\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}t}\) of both particle positions, which leads to an opposite deflection for the two-particle positions in the direction of measurement. Although the positions \({\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt}),}t}\ne -{\bar{Z}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt}),}t}\) for each particle pair are not exactly anti-correlated, the spin averages are, which is a feature of the entangled states considered here. The averaged x and y components of the spins remain 0 throughout the experiment.

A sample of trajectories for 5 particle pairs moving in opposite directions and entering a magnetic field is shown in Fig. 5 for the singlet pairs. The measurement angles for the SG devices are \(\delta _1=\delta _2=\frac{\pi }{4}\) in these figures. The spin averages of the individual particles along the measured \(z_k (\ne z)\) axes are also 0 at the entrance of the magnets according to (35) independent of the measurement angles. Eventually, each particle ends up in one of the two possible spin channels following the alignment of its magnetic moment. In the moment of the measurement of a particle at a detector after the magnet, one can assign a spin state for a single particle. Hence, the particles gradually disentangle in the stochastic picture until they choose one of the two distinct channels where the particle properties in terms of expectations can be described for uncoupled particles again. This mechanism is the counterpart to the collapse of the state function in the Copenhagen interpretation given in (32) to one of the two states \({|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\) or \({|{-_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}1\hspace{-1pt})}}}\rangle }{|{+_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}2\hspace{-1pt})}}}\rangle }\).

Fig. 6
figure 6

The plot compares the joint probability distributions as calculated from the singlet state wave function in standard quantum mechanics (solid) to the numerically calculated probabilities associated with the singlet spin model (circles) depending on the angle \(\delta\) as defined in Eq. (47). The non-local velocity fields in the QHE model lead to the violation of Bell’s inequality \(\rho ^{A{\bar{B}}}+\rho ^{B{\bar{C}}}\ge \rho ^{A{\bar{C}}}\) for \(\delta < \nicefrac {\pi }{2}\). Since \(\rho ^{A{\bar{B}}}_Q = \rho ^{B{\bar{C}}}_Q\) the pink dotted line is not visible

Full size image

For the singlet state, the spin pairs in Fig. 5 give anti-correlated outcomes since the measurement angles are the same \(\delta _1=\delta _2\). This agrees with the state’s definition of perfect anti-correlation independent of the measurement axis where the probability of (positively) correlated outcomes, i.e., measuring \(++\) or \(--\) coincidences, only depends on the difference of the measurement angles \(\delta _1-\delta _2\). Figure 6 shows the joint probabilities in magenta and green

$$\begin{aligned} \rho ^{A{\bar{B}}}(\delta _1=0,\delta _2=\delta ) \approx \rho ^{B\bar{C}}(\delta _1=\delta ,\delta _2=2\delta )\, \end{aligned}$$
(46)

where the joint probabilities are defined as

$$\begin{aligned} \rho ^{A{\bar{B}}}(\delta _1,\delta _2):=\rho \left( A=+,\bar{B}=-\Big |a=z^{\delta _1}_1,b=z^{\delta _2}_2\right) \,. \end{aligned}$$
(47)

The correlation of the particles can be compared to the inequality for local hidden variable theories given by the Bell inequality

$$\begin{aligned} \rho ^{A{\bar{B}}}(0,\delta )+\rho ^{B{\bar{C}}}(\delta ,2\delta )\ge \rho ^{A{\bar{C}}}(0,2\delta )\,. \end{aligned}$$
(48)

Following Fig. 6, the stochastic model (circles) agrees with the predictions from quantum mechanics and violates Bell’s inequality. This is not surprising since the model is based on the definition of the singlet wave function with the corresponding expected values. Moreover, the stochastic model’s drift fields are non-local, allowing us to describe the strong correlations between the two particles. This is a result of the non-separability of the probability distribution, violating the requirement of Bell separability.

In summary, the stochastic model of a spinning top allows a consistent description of the EPRB with spins as continuous random variables in contrast to the picture of an intrinsic property of a constant and discrete spin in standard quantum mechanics. Before the measurement, the spin fields of entangled particles depend on the configuration of the two-particle system. The measurement leads to joint spin distributions, which depend on the chosen measurement axes and the configuration variables of both particles. This leads to a clear violation of the Bell (CHSH) inequality. Finally, we note that the spin components along the measured axes approach discrete values for sufficiently large distances to the SG magnet.

5 Discussion and Conclusion

We have shown that the Bopp–Haag model of a rotating charge undergoing a conservative diffusion process in its translation and rotation degrees of freedom can be used to get a dynamic understanding of the measurement process in a Stern–Gerlach experiment. The orientation degree of freedom is associated with the magnetic moment of the particle, which is the physical observable which can be experimentally addressed. In this theory, spin is the canonical angular momentum belonging to this orientation degree of freedom. The description therefore contains position and orientation of the particels as hidden variables. It offers a more detailed understanding of spin dynamics than the standard approach in quantum mechanics, where spin is no longer a physical object in real space but an internal degree of freedom of a particle. However, for most experimental situations, the dynamics of the orientation motion can be averaged out, because it is much faster than the translation motion, and with this one recovers the results from the standard analysis using the Pauli equation.

For the EPRB experiment, we have seen that although the second particle is locally separated from the first particle, its spin is changed in reaction to the measurement of particle 1. The position of particle 2 is unaffected, but its spin changes over the course of the measurement of particle 1 due to the non-local quantum torque

$$\begin{aligned} \bar{\varvec{T}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt}),}u} = \bar{ \varvec{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}}\times \sum _l\left( \frac{\hbar }{2m}\Delta _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}l\hspace{-1pt})}} \bar{ \varvec{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} + (\bar{ \varvec{u}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}l\hspace{-1pt})}}\cdot \nabla _{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}l\hspace{-1pt})}})\bar{ \varvec{s}}_{\hspace{-.5pt}\scriptscriptstyle {(\hspace{-1pt}k\hspace{-1pt})}} \right) \end{aligned}$$
(49)

which depends on the configuration variables of both particles.

If this is interpreted as a physical effect from particle 1 on particle 2, we would have what Einstein called a spooky action at a distance. This is understood in contrast to non-spooky action at a distance which comes about by an instant interaction at a distance typical for Galilean physics as encoded in an interaction potential. Such a non-spooky interaction at a distance is present in the Hamilton-Jacobi theory of classical mechanics, where the action field S(x, t) depends on the positions \(x=\{x_n(t)\}\) of all particles through their interaction potentials. A measurement on particle k, which affects its position, instantaneously changes the field S(x, t) which in turn instantaneously changes the paths we would predict for all particles from this time on. The field S(x, t) encodes everything we know about a classical mechanical system at a given time t, but is has no physical existence, it is purely epistemological. The same is true for the wave function \(\psi (x,t)= \sqrt{\rho (x,t)}\exp \{i/\hbar S(x,t)\}\) as Niels Bohr always stressed (see [31] for an insightful discussion of the different points of view of Einstein and Bohr). After all, Schrödinger derived his equation with the goal of constructing a Hamilton-Jacobi formulation for quantum dynamics. The wave function, \(\psi (x,t)\), and by construction \(\rho (x,t)\) and S(x, t) of the Madelung equations, and v(x, t) and u(x, t) of our quantum Hamilton equations, encode everything we know about a quantum system. When we perform a measurement on particle 1 in an EPRB experiment, we update this information conditioned on the outcome, and consequently predict a different dynamical behavior of particle 2 from this time on. There is no physical interaction involved and the speed of light is of no importance. The hidden variables in this description are position and orientation of the particles and their magnetic moments and for all quantum states \(\psi\) the allowed set of hidden variables is always \({\mathbb {R}}^3\times {SO}({3})\). Our description therefore belongs to the class of \(\psi\)-epistemic theories in the nomenclature of Harrigan and Spekkens [32]. This epistemological view of the meaning of the wave function makes it a tool for inference about our expectations for experimental results for a given preparation procedure [33, 34].

Only when we pick a starting point and let a particle position evolve deterministically along the gradient of the action field, S(x, t), in classical mechanics, does the epistemological content of the action field give rise to an ontological particle path. In the same way, the epistemological content of the velocity fields, v(x, t) and u(x, t), or, equivalently, the wave function, \(\psi (x,t)\), gives rise to a stochastic path when we choose a starting position for a quantum particle. This is the ontological content of quantum mechanics Einstein was demanding.