Causal Lie Products of Free Fields and the Emergence of Quantum Field Theory

Abstract

All causal Lie products of solutions of the Klein-Gordon equation and the wave equation in Minkowski space are determined. The results shed light on the origin of the algebraic structures underlying quantum field theory.

1 Introduction

In this note we analyze the structure of causal Lie products (brackets) of solutions of the Klein-Gordon equation in Minkowski space with mass $m \ge 0$. This problem was studied in the Wightman framework of quantum field theory by several people: for massive free fields by Jost [1], Schroer [2], Federbush, Johnson [3], and for massless fields by Pohlmeyer [4]. It revealed the fact that free fields must have c-number commutators. However, these results depend crucially on the assumptions of some underlying Hilbert space structure and spectral properties of a Hamiltonian (the existence of a vacuum sector). It is the aim of the present note to establish the properties of free fields in a more general framework, shedding some light on the origin of the algebraic structures underlying quantum field theory.

2 Framework and Results

Let ${{{\mathcal {S}}}}({\mathbb {R}}^d)$ be the Schwartz space of real scalar test functions on Minkowski space ${\mathbb {R}}^d$, $d > 2$, with its standard metric. We consider a Lie algebra $\varvec{\Phi }$ over ${\mathbb {R}}$ that is generated by symbols $\phi (f)$ which are real linear with regard to $f \in {{{\mathcal {S}}}}({\mathbb {R}}^d)$. Thus we have for their Lie products the standard relations (anti-symmetry and Jacobi identity), $f_1,f_2,f_3 \in {{{\mathcal {S}}}}({\mathbb {R}}^d)$,

$$\begin{aligned}&[\phi (f_1), \phi (f_2)] = - [\phi (f_2), \phi (f_1)] \nonumber \\&[[\phi (f_1), \phi (f_2)],\phi (f_3)] + [[\phi (f_3), \phi (f_1)],\phi (f_2)] + [[\phi (f_2), \phi (f_3)],\phi (f_1)] = 0 \, . \end{aligned}$$

(1)

In addition, we assume that $\phi$ is a solution of the Klein-Gordon equation (including the wave equation for mass $m=0$) and that its Lie products comply with the condition of Einstein causality (locality). Thus we have the additional relations for $f_1, f_2 \in {{{\mathcal {S}}}}({\mathbb {R}}^d)$, $K := \square + m^2$ being the Klein-Gordon operator and $\perp$ denoting spacelike separation,

$$\begin{aligned}&\phi (Kf_1) = 0 \, , \nonumber \\&[\phi (f_1), \phi (f_2)] = 0 \quad \text {if} \quad \text {supp} \, f_1 \perp \text {supp} \, f_2 \, . \end{aligned}$$

(2)

We assume that there exist (multi)linear forms on $\varvec{\Phi }$ which are tempered distributions with regard to the underlying test functions. We also assume that the collection of all such forms on $\varvec{\Phi }$ is faithful, i.e. the intersection of their kernels is trivial. (Frobenius Lie algebras are examples with this property.) Given any such form l, we want to show that

$$\begin{aligned} l([[\phi (f_1), \phi (f_2)], \phi (f_3)]) = 0 \, , \quad f_1,f_2,f_3 \in {{{\mathcal {S}}}}({\mathbb {R}}^d) \, . \end{aligned}$$

(3)

Since the collection of all functionals is faithful, this implies that the Lie products $[\phi (f_1), \phi (f_2)]$ lie in the center of $\varvec{\Phi }$.

We begin by noting that by the Schwartz kernel (nuclear) theorem, the distribution (3) extends by continuity in $f_1 \otimes f_2 \otimes f_3$ to arbitrary test functions $f \in {{{\mathcal {S}}}}({\mathbb {R}}^{3d})$. Thus it is sufficient to consider for any $h \in {{{\mathcal {S}}}}({\mathbb {R}}^d)$ the distributions

$$\begin{aligned} x,y \mapsto l_h([[\phi (x),\phi (y)], \phi (0)]) := \int \! dz \, h(z) \, l([[\phi (x +z),\phi (y + z)], \phi (z)]) \, , \end{aligned}$$

(4)

from which the original l can be recovered. Because of locality, $l_h$ vanishes for $(x-y)^2 < 0$ and, by the Jacobi identity, this also obtains if, both, $x^2 < 0$ and $y^2 < 0$. Picking any fixed spacelike y, it follows that the distribution vanishes if $x^2 < 0$ or $(x - y)^2 < 0$. Thus it vanishes with regard to x in some open time slice. Since it is a solution in x of the Klein-Gordon equation, it vanishes for all x.

With this information we pick now any x. According to the preceding step, the distribution then vanishes in y for $y^2 < 0$ and, again by locality, for $(x - y)^2 < 0$. If x is spacelike, the preceding step implies that the distribution vanishes for all y.

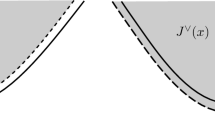
If x is positive timelike, the distribution vanishes for y in the interior of the complement of $(V_+ + x) \cup V_- \cup D$, where $V_\pm$ are the forward and backward lightcones, respectively, and D is the double cone fixed by the timelike line segment from 0 to x. We pick now any timelike line segment L in this complement which does not touch D and the boundaries of $(V_+ + x)$ and $V_-$, cf. Fig. 1. Since L is localized in the interior of this complement, the solution of the Klein-Gordon equation with regard to y vanishes in a timelike tube and hence in the double cone fixed by it; this is a consequence of standard theorems on solutions of hyperbolic differential equations with constant coefficients [5] or of Borchers’ double cone theorem [6]. Performing this step for all such line segments, we find that the distribution vanishes for all y with support in the interior of the complement of $(V_+ + x) \cup V_-$. Making again use of the fact that the distribution is a solution of the Klein-Gordon equation in y, this implies that it vanishes for all y. A similar argument applies if x is negative timelike.

Fig. 1

Initial support of the Lie product (gray), which is further restricted by the existence of timelike line segments L in its complement and the Klein-Gordon equation

We finally discuss the case that x is positive lightlike. As in the preceding step, the distribution vanishes with regard to y in the interior of the complement of the region $(V_+ + x) \cup V_- \cup D$, where D now denotes the degenerate double cone consisting of the lightlike line segment connecting 0 and x. At this point it matters that the dimension d of spacetime is larger than 2. If $d=2$ and the field is massless, that complement cannot be enlarged. This follows from the observation that in the quantum field theoretic example of local chiral fields their normal ordered products still satisfy the wave equation, but their double commutators do not vanish. Yet if $d > 2$, there exist timelike line segments L in the interior of the above complement that cross the characteristic hyperplane defined by the lightlike line segment at an arbitrarily small distance from it. The corresponding double cones fixed by L then intersect the lightlike segment in some open interval. Hence the distribution vanishes again in y in some time slice and consequently vanishes everywhere. A similar argument works if x is negative lightlike. We summarize these results in a first proposition.

Proposition 2.1

Let $\varvec{\Phi }$ be a Lie algebra with properties given above. Then the Lie product of any two elements lies in the center of this algebra.

It remains to determine the possible form of the Lie products. To this end we consider the distribution, canonically extended to complex test functions h,

$$\begin{aligned} x \mapsto l_h([\phi (x), \phi (0)]) := \int \! dz \, h(z) \, l([\phi (x +z),\phi (z)]) \, . \end{aligned}$$

(5)

It is a solution of the Klein-Gordon equation which vanishes because of locality if $x^2 < 0$. So its Cauchy data at time 0 are tempered distributions on space which are localized at the origin. Hence they are finite sums of derivatives of the Dirac measure, supported at 0. It follows that

$$\begin{aligned} l_h([\phi (x), \phi (0)]) = \int \! dp \, P_h(p) \, \varepsilon (p_0) \delta (p^2 - m^2) \, e^{ipx} \, , \end{aligned}$$

(6)

where $P_h$ is a polynomial in the zero and spatial components of p of the form $p \mapsto P_h(p) = p_0 \, Q_h(\varvec{p}) + R_h(\varvec{p})$; it depends in a complex linear and tempered manner on h. In order to determine the dependence of $P_h$ on h, we exploit the fact that the second field in this distribution also satisfies the Klein-Gordon equation and proceed to

$$\begin{aligned} x \mapsto l_h([\phi (x), \phi (0)]) = \int \! dz \, h(z-x) \, l([\phi (z),\phi (z - x)]) \, . \end{aligned}$$

(7)

Applying the Klein-Gordon operator, we get

$$\begin{aligned}&0 = \int \! dz \, (\square _x h(z - x) + 2 \, \partial _{x \mu } h(z -x) \, \partial _x^\mu ) \, l([\phi (z),\phi (z - x)]) \nonumber \\&\quad = - \int \! dz \, (\square h)(z) \, l([\phi (x + z),\phi (z)]) - 2 \, \partial _x^\mu \int \! dz \, (\partial _\mu h)(z) \, l([\phi (x + z),\phi (z)]) \nonumber \\&\quad = - 2 \, \partial _x^\mu \, l_{\, \partial _\mu h}([\phi (x), \phi (0)]) - l_{\, \square h}([\phi (x), \phi (0)]) \, . \end{aligned}$$

(8)

Making use of the preceding result (6) on the structure of $l_h$, we obtain for the resulting polynomials the equality on the mass shell $p^2 = m^2$

$$\begin{aligned} 2i p^\mu P_{\, \partial _\mu h}(p) + P_{\, \square h}(p) = P_{(2i p^\mu \partial _\mu + \square )h}(p) = 0 \, . \end{aligned}$$

(9)

Thus we have for arbitrary test functions h

$$\begin{aligned} P_h(p) = \int \! dq \, (A(p) \delta (q) + B(p) \delta (q^2 + 2qp)) {\widetilde{h}}(q) \, , \end{aligned}$$

(10)

where the tilde $\tilde{ \ \ }$ denotes Fourier transforms. Since this expression is to be a polynomial in the components of p for arbitrary h, it follows that $B=0$ and that A is a polynomial. Hence $p \mapsto P_h(p) = {\widetilde{h}}(0) A(p)$, where A is of the special form given above. Summarizing these observations, we have arrived at our second proposition.

Proposition 2.2

Let $\varvec{\Phi }$ be a Lie algebra with properties given above. Then one has for any tempered functional l the equality in the sense of distributions

$$\begin{aligned} l([\phi (x), \phi (y)]) = \int \! dp \, A_l(p) \, \varepsilon (p_0) \delta (p^2 - m^2) \, e^{ip(x-y)} \, , \end{aligned}$$

(11)

where $A_l$ is some even (as a consequence of the antisymmetry of the Lie product) polynomial.

In view of the preceding results one can fix the central elements of the Lie algebra $\varvec{\Phi }$. This is accomplished by first extending the algebra by complex multiples of an identity 1 and then taking the quotient with regard to the ideal generated by

$$\begin{aligned}{}[\phi (f), \phi (g)] - l([\phi (f), \phi (g)]) \, 1 \, , \quad f,g \in {{{\mathcal {S}}}}({\mathbb {R}}^d) \, . \end{aligned}$$

(12)

In this manner, the Lie products are identified with multiples of the identity with the concrete numerical factors, given by Proposition 2.2. Let us emphasize that the polynomial $A_l$ in this proposition depends on the choice of the functional l. Its specific form is not encoded in the Lie algebra $\varvec{\Phi }$. As a matter of fact, every even polynomial A defines by equation  (11) some admissible functional on $\varvec{\Phi }$ and thereby some “primary” non-commutative Lie algebra whose center consists of multiples of 1.

3 Conclusions

Starting from the assumption that the action induced by free fields on each other can be described by a Lie algebra, in analogy to the Poisson brackets in classical physics, we have determined the possible realizations of these algebras which are compatible with Einstein causality. It turned out that the Lie products of the fields are elements of the center of the algebra with very specific properties: all functionals on the Lie products are invariant under simultaneous translations of the fields and they are finitely covariant with regard to Lorentz transformations, i.e. they transform like components of a tensor field [7]. Any such functional determines a primary Lie algebra with c-number commutation relations.

The best known examples which are compatible with these results are the scalar free fields $\phi _0$ in quantum field theory, where the polynomial $A_0$ appearing in the Lie product is some positive constant, depending on the dimension d. In that case the Lie-algebra can consistently be extended to a non-commutative *-algebra which is faithfully represented on Fock space and where the Lie product is given by the commutator of the field operators.

It turns out that any other “primary” Lie algebra for a given even polynomial A is obtained from $\phi _0$ by a real linear map

$$\begin{aligned} \phi _0(f) \mapsto \phi _0(B f) \, , \quad f \in {{{\mathcal {S}}}}({\mathbb {R}}^d) \, . \end{aligned}$$

(13)

Here B is a multiplication operator in momentum space. The underlying function $p \mapsto B(p)$ has the following properties: it is even with regard to momentum, its square equals A, and it is continuous almost everywhere on ${\mathbb {R}}^d$, cf. the appendix. The corresponding fields are faithfully represented on Fock space as well. Since $\phi _0(B f)^* \supset \phi _0(\overline{B f})$, these operators are not symmetric, however, unless B is real in momentum space. This can only happen if A is positive and hence the value of the commutator (11) is purely imaginary. In the general case, the fields and also their adjoints have local commutators on Fock space, but they are not relatively local. Alternatively, these cases can be realized by components of tensor fields on indefinite Fock spaces.

So we conclude that the appearance of the familiar algebraic structures of quantum field theory can be traced back in the case of free fields to Einstein causality. Results pointing into a similar direction were also established in [8], but the existence of a $*$-operation (of a complex structure) was assumed there from the outset. As we have seen here, this feature is a consequence of the representation theory of the specific Lie algebras, which emerge from our assumptions. They have faithful representations by Hilbert space operators as a consequence of Einstein causality.

Appendix

For completeness, we give here a proof of the elementary fact, used in the main text, that any complex polynomial A on ${\mathbb {R}}^d$ (which is not necessarily of the special type considered here) has a square root B which is continuous almost everywhere. We proceed from the principal square root $z \mapsto \sqrt{z}$ on the complex plane, which is defined for $- \pi < \arg z \le \pi$ and vanishes at 0. It is continuous along the real axis. In the complement of the (closed) negative axis it is analytic and it is discontinuous across the cut at the negative reals.

With this choice, we put $p \mapsto B(p) := \sqrt{A(p)}$. If A is symmetric in p, as in the present investigation, it is clear that B is symmetric as well since the principal square root does not depend on p. Discontinuities of B can only appear at points where the values of A cross the cut at the negative reals from imaginary directions. Defining the set

$$\begin{aligned} S := \{ p \in {\mathbb {R}}^d : A(p) \le 0 \} \, , \end{aligned}$$

(14)

there are the following possibilities: (i) $S = \emptyset$. Then B is continuous (even real analytic). (ii) $S = {\mathbb {R}}^d$. Then A is real, hence B is continuous. (iii) $S \subset {\mathbb {R}}^d$ is a proper subset. If the imaginary part $\, \text {Im} A$ of A vanishes on ${\mathbb {R}}^d$, then A is real again and B is continuous. If $\, \text {Im} A$ varies on ${\mathbb {R}}^d$, then, being a polynomial, it can vanish only on sets of zero Lebesgue measure, cf. [9]. Thus S, being a closed subset, has zero measure as well. Only in the latter case it can happen that B is discontinuous on such negligible sets of ${\mathbb {R}}^d$.