Skip to main content
SpringerLink
Log in

The Twofold Role of Observables in Classical and Quantum Kinematics

  • Published:
Foundations of Physics Aims and scope Submit manuscript

Abstract

Observables have a dual nature in both classical and quantum kinematics: they are at the same time quantities, allowing to separate states by means of their numerical values, and generators of transformations, establishing relations between different states. In this work, we show how this twofold role of observables constitutes a key feature in the conceptual analysis of classical and quantum kinematics, shedding a new light on the distinguishing feature of the quantum at the kinematical level. We first take a look at the algebraic description of both classical and quantum observables in terms of Jordan–Lie algebras and show how the two algebraic structures are the precise mathematical manifestation of the twofold role of observables. Then, we turn to the geometric reformulation of quantum kinematics in terms of Kähler manifolds. A key achievement of this reformulation is to show that the twofold role of observables is the constitutive ingredient defining what an observable is. Moreover, it points to the fact that, from the restricted point of view of the transformational role of observables, classical and quantum kinematics behave in exactly the same way. Finally, we present Landsman’s general framework of Poisson spaces with transition probability, which highlights with unmatched clarity that the crucial difference between the two kinematics lies in the way the two roles of observables are related to each other.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. Sometimes, these transformations are also called canonical transformations.

  2. A diffeomorphism \(\phi : S \longrightarrow S\) induces a map \({\varPhi }: {\mathscr {C}}^\infty (S, {\mathbb {R}}) \longrightarrow {\mathscr {C}}^\infty (S, {\mathbb {R}})\) defined by:

    $$\begin{aligned} \forall f \in {\mathscr {C}}^\infty (S, {\mathbb {R}}), ({\varPhi }f)(p) = f(\phi (p)). \end{aligned}$$

    This in turn allows one to define the push-forward \(\phi _*\) of vector fields and the pull-back \(\phi ^*\) of n-forms by:

    $$\begin{aligned} \forall v \in {\varGamma }(TS),&\,\, (\phi _*v)[f]:= v[{\varPhi }f],\\ \forall \alpha \in {\varOmega }^n(S),&\,\, (\phi ^*\alpha )(v_1, \ldots , v_n):= \alpha (\phi _*v_1, \ldots ,\phi _*v_n ). \end{aligned}$$

  3. For a given two-form \(\alpha \in {\varOmega }^2(S)\), the Lie derivative with respect to the vector field \(v \in {\varGamma }(TS)\) is given by the so-called “Cartan’s magic formula”: \({\mathscr {L}}_v \alpha = (\iota _v d + d\iota _v)\alpha \), where \(\iota _v \alpha := \alpha (v, \cdot ) \in {\varOmega }^1(S)\).

  4. A real Jordan algebra \(({\mathscr {A}}, \bullet )\) is a commutative algebra such that, moreover, \(F \bullet (G \bullet F^2) =( F \bullet G) \bullet F^2\) for all \(F, G \in {\mathscr {A}}\). This concept was introduced by the German theoretical physicist Pascual Jordan in 1933 [26].

  5. Recall that, given a vector space V and a linear operator A acting on V, the spectrum of A is defined as \(spec(A):=\big \{\alpha \in {\mathbb {R}}\,\big |\, (A-\alpha \, \text {Id}_V) \text { is not invertible}\big \}.\)

  6. \(v_f\) and \(v_g\) being linear operators on the real vector space \({\mathscr {A}}^C\), one can consider their composition \(v_f \circ v_g\). This fails to be a derivative operator (and hence a vector field), but the commutator \(v_f \circ v_g-v_g \circ v_f\) is again a derivative operator.

  7. Here, we suppose that the space of state is a simply connected manifold. In the general case, the kernel of \(v_{-}\) is the center of \(({\mathscr {A}}^C, \star )\), that is, the set of locally constant functions.

  8. As it will later become clearer, Fig. 2 should by no means be regarded as the intrinsic and indisputable conceptual structure governing classical Hamiltonian kinematics, but simply as the underlying structure of the most standard narrative.

  9. For finite-dimensional Hilbert spaces, this is clear: any operator \(A \in {\mathscr {B}}_{i{\mathbb {R}}}\) defines a one-parameter group of unitary operators through exponentiation: \(e^{tA} \in U({\mathscr {H}}),\, t \in {\mathbb {R}}\). The situation is more subtle in the infinite-dimensional case for two reasons. First, \(U({\mathscr {H}})\) is not a Lie group (it is infinite-dimensional) and thus the notion of an associated Lie algebra is problematic. However, by Stone’s theorem we know there is a one-to-one correspondence between anti-self-adjoint operators and continuous one-parameter unitary groups. In this sense, one is still allowed to claim that anti-self-adjoint operators are the generators of unitary transformations. The second problem is that, without further restrictions, anti-self-adjoint operators do not form a Lie algebra (in fact, they do not even form a vector space). This is the reason why we restrict attention here to bounded anti-self-adjoint operators. The question of how to deal with the more general case allowing for unbounded operators is delicate and certainly deserves further conceptual investigation. For a precise mathematical treatment of these issues, see [2].

  10. It is important to stress that these are the two natural structures present on the set of self-adjoint operators. For example, the composition of operators is not a well-defined operation on this set (the composition of self-adjoint operators is not self-adjoint). One should also notice that the Lie product on bounded self-adjoint operators is not the commutator: the multiplication by the complex number i in the definition is a necessary one. This is because the commutator of two self-adjoint operators yields an anti-self-adjoint operator. On the other hand, the two factors \(\frac{1}{2}\) are only a convenient normalization in order to obtain the associator rule as written in axiom v) but other choices are possible. For instance, another normalization is \(F\star G := \frac{i}{\hbar }[F, G]\), which forces \(\kappa = \frac{\hbar ^2}{4}\) (cf. Definition 5), but allows one to write the canonical commutation relations between position and momentum operators as \(P \star X = 1\).

  11. Given a unital commutative \(C^*\)-algebra \({\mathscr {U}}\), its Gelfand spectrum \(spec_G({\mathscr {U}})\) is the set of all positive linear functionals \(\rho : {\mathscr {U}}\longrightarrow {\mathbb {C}}\) such that \(\rho ({\mathbb {I}})=1\) [34]. The fact that \(spec_G(C^*(F))\) is isomorphic to the spectrum of F (in the usual sense) justifies the use of the word “spectrum" in Gelfand’s theory [11].

  12. Indeed, \(C^*(F)\) consists of all polynomials in F and \(F^*\). Then, \(C^*(F)\) will be non-commutative if and only if \([F, F^*]\ne 0\).

  13. The same word of caution raised about Fig. 2 applies here. As it will be explained in the next sections, alternative approaches to the standard Hilbert space formulation of quantum kinematics can be perceived as attempts to change the conceptual structure described in Fig. 3.

  14. This confusion was there since the very beginning of Quantum Mechanics. For example, in their second paper of 1926, Born, Heisenberg and Jordan write:

    We introduce the following basic quantum-mechanical relation: \(\varvec{pq} - \varvec{qp} = \frac{h}{2\pi i} \varvec{1}\). [...] One can see from [this equation] that in the limit \(h=0\) the new theory would converge to classical theory, as is physically required. [9, 327]

    It is clear that they were comparing the commutator in quantum mechanics with point-wise multiplication in Classical Mechanics (despite the fact that, by the time of the second quoted paper, Dirac had already shown in [17] that the quantum commutator should be compared to the classical Poisson bracket).

  15. A \(C^*\)-algebra \(({\mathscr {U}}, \circ , *, \Vert \cdot \Vert )\) is a complex associative algebra \(({\mathscr {U}}, \circ )\) equipped with an involution \(^*\) and a norm \(\Vert \cdot \Vert \) such that: (i) \(({\mathscr {U}}, \Vert \cdot \Vert )\) is a complex Banach space, (ii) \(\forall A, B \in {\mathscr {U}}, \Vert A \circ B \Vert \le \Vert A \Vert \Vert B \Vert \), and (iii) \(\forall A \in {\mathscr {U}}, \Vert A^* \circ A \Vert = \Vert A \Vert ^2\).

  16. To be more precise: given any \(C^*\)-algebra \(({\mathscr {U}}, \circ )\), its real part \({\mathscr {U}}_{{\mathbb {R}}}:=\big \{A \in {\mathscr {U}}\big | A=A^*\big \}\) equipped with the operations \(A\bullet B= \frac{1}{2}(A\circ B+ B\circ A)\) and \(A\star B= \frac{i}{2}(A\circ B- B\circ A)\) is a Jordan–Lie–Banach algebra. Conversely, given any real JLB-algebra \(({\mathscr {U}}_{{\mathbb {R}}}, \bullet , \star )\), its complexification \(({\mathscr {U}}_{{\mathbb {R}}})_{\mathbb {C}}\) can be turned into a \(C^*\)-algebra by first defining the operation \(A \circ B := A \bullet B -i A \star B\) on \({\mathscr {U}}_{{\mathbb {R}}}\) and then extending it by \({\mathbb {C}}\)-linearity to \({\mathscr {U}}\). In this sense, \(C^*\)-algebras are equivalent to JLB-algebras. Moreover, a \(C^*\)-algebra \({\mathscr {U}}\) is commutative if and only if the associated JLB-algebra \({\mathscr {U}}_{{\mathbb {R}}}\) is associative. However, not all Jordan–Lie algebras can be equipped with a norm so that they become JLB-algebras, and, in fact, no non-trivial Poisson algebra can be normed in such a way that the bracket is defined in the norm-completion of the algebra. Therefore, non-trivial Poisson algebras do not fall under the theory of \(C^*\)-algebras. For details, see [34, Chapter I.1].

  17. Because of Heisenberg’s famous uncertainty relations, the definition of compatible observables is perhaps more often stated in terms of the product \({\varDelta }_\rho (F) {\varDelta }_\rho (G)\) rather than the sum. However, as Strocchi points out in [42], this is wrong since for any two bounded operators, one has \(\inf \limits _\rho ({\varDelta }_\rho (F) {\varDelta }_\rho (G)) =0\).

  18. It is important to clearly distinguish the program of a geometric reformulation of quantum mechanics from the program of ‘geometric quantization’ which we will not discuss here and is completely unrelated. The first aims at a reformulation of quantum mechanics which avoids Hilbert spaces. The second is geared towards an explicit construction of the quantum description of a system for which the classical description is given. But the resulting quantum description is still based on Hilbert spaces. What is ‘geometric’ about geometric quantization is the means by which the Hilbert space is constructed: roughly, one starts with the symplectic manifold describing the classical system, considers a complex line bundle over it and defines the Hilbert space as a particular class of sections of this bundle. The program of geometric quantization was started by Jean-Marie Souriau and Bertram Kostant [31, 41]. A standard reference is [47].

  19. Associated to the Riemannian metric, there is a unique torsion-free metric compatible affine connection \(\nabla \) (the so-called Levi-Civita connection). An almost complex structure J is said to be invariant if \(\nabla J = 0\) [28].

  20. Given \((\phi , \psi ) \in {\mathscr {H}}\times {\mathscr {H}}\), define \(V_\phi \in T_\psi {\mathscr {H}}\) by

    $$\begin{aligned} \forall f \in {\mathscr {C}}^\infty ({\mathscr {H}},{\mathbb {R}}), V_\phi [f](\psi )= \frac{d}{ds}f(\psi + s \phi )\Big |_{s=0}. \end{aligned}$$

  21. Of course, one needs to be sure that such a 2-form does exist. A cleaner way of defining the symplectic form is by means of the so-called Marsden–Weinstein symplectic reduction [37]. Therein, one considers the natural action of U(1) on \({\mathscr {H}}\). This is a strongly Hamiltonian action and the momentum map \(\mu : {\mathscr {H}}\longrightarrow u(1)^* \simeq {\mathbb {R}}\) is given by \(\mu (\phi )=\langle \phi , \phi \rangle \). Then, \({\mathbb {P}}{\mathscr {H}}\simeq \mu ^{-1}(1)/U(1)\) and the general theory insures this is a symplectic manifold. For the details, I refer the reader to [34].

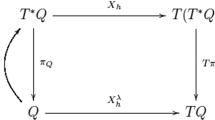
  22. Two examples of this are the canonical commutation relations \(\{p,q\}=1\) (which state that linear momentum is the generator of space translations) and Hamilton’s equations of motion \(\frac{d}{dt}=\{H, \cdot \}\) (which state that the Hamiltonian is the generator of time evolution).

  23. The reader will recognise here the question raised by Heisenberg in his 1925 seminal paper that definitely launched the development of quantum mechanics [24].

  24. An heuristic argument in the direction of this claim is the following. Given an observable \(\texttt {f}\), the observable \(\texttt {f}^2\) is operationally defined as the observable associated with squaring each result of a measurement of \(\texttt {f}\). Suppose now that \(\texttt {f}\) is represented by the abstract element \(f \in {\mathscr {U}}\), where \({\mathscr {U}}\) is the abstract mathematical structure used to describe observables. Since \(\texttt {f}^2\) is defined solely in terms of \(\texttt {f}\), then, by the same token, \(\texttt {f}^2\) should be represented by an element \(k \in {\mathscr {U}}\) which should also be defined solely in terms of f. But the Lie product of f with itself vanishes, so we are left with \(f \bullet f\) as the only option.

  25. As a side remark, notice that, in the same way that the Riemannian and symplectic structures of the quantum space of states arise then from the real and imaginary parts of the Hermitian product of \({\mathscr {H}}\) respectively, at the algebraic level the quantum Jordan and Lie products \(\bullet : \frac{1}{2}[\cdot , \cdot ]_+\) and \(\star : \frac{i}{2}[\cdot , \cdot ]\) may also be seen as the real and imaginary parts of the composition of operators:

    $$\begin{aligned} \text {for } A, B \in {\mathscr {B}}_{{\mathbb {R}}}({\mathscr {H}}), \, A \circ B = A \bullet B - i A\star B. \end{aligned}$$

  26. Recall that the distance between two points p and \(p'\) of a Riemannian manifold with metric g is given by:

    $$\begin{aligned} d_g(p,p') := \text {inf}\,\bigg \{\int \limits _{\varGamma }\sqrt{g(v_{\varGamma }(t), v_{\varGamma }(t))}dt \, \big | \, {\varGamma }\in \text {Path}(p,p')\bigg \}. \end{aligned}$$

  27. A Poisson manifold is a manifold P for which the algebra of smooth functions \({\mathscr {C}}^\infty (P, {\mathbb {R}})\) is a Poisson algebra. An important theorem in Poisson geometry states that any such manifold can always be written as a disjoint union of symplectic manifolds—the so-called symplectic leaves of the Poisson manifold [34, Theorem I.2.4.7, p. 71].

  28. This notion was introduced for the first time by Landsman in [33, p. 38]. His definition differs slightly from the one given here, for it also includes a linear subspace \({\mathscr {U}}_{{\mathbb {R}}}({\mathscr {P}}) \subset {\mathscr {C}}^\infty _L({\mathscr {P}}, {\mathbb {R}})\) which separates points and is closed under the Poisson bracket: \(\{f, g\}_{{\mathscr {P}}}(\iota _\alpha (q)) := \{\iota ^*_\alpha f, \iota ^*_\alpha g\}_{S_\alpha }(q)\), where \(q \in S_\alpha \). I nonetheless find the inclusion of this subspace somewhat unnatural at this point. This subspace \({\mathscr {U}}_{{\mathbb {R}}}({\mathscr {P}})\) will only become important when defining the key notion of a Poisson space with transition probability.

  29. This concept was introduced for the first time in 1937 by von Neumann in a series of lectures delivered at the Pennsylvania State College. The manuscript was only published posthumously in 1981 [45].

  30. These function spaces are defined as follows. First, \({\mathscr {C}}^\infty _{Pois}({\mathscr {P}}, {\mathbb {R}})\) is the set of all \(f \in {\mathscr {C}}({\mathscr {P}}, {\mathbb {R}})\) such that their restrictions to any \(S_\alpha \) are smooth: \(\iota ^*_\alpha f \in {\mathscr {C}}^\infty (S_\alpha , {\mathbb {R}})\). On the other hand, the definition of \({\mathscr {C}}_{Prob}({\mathscr {P}}, {\mathbb {R}})\) is more involved. One considers first the functions \(\mathrm {Pr}_\rho : {\mathscr {P}}\rightarrow {\mathbb {R}}\) such that \(\mathrm {Pr}_\rho (\sigma ) := \mathrm {Pr} (\rho , \sigma )\), and defines \({\mathscr {C}}_{Prob}^{00}({\mathscr {P}})\) as the real vector space generated by these functions. Then \({\mathscr {C}}_{Prob}({\mathscr {P}},{\mathbb {R}}):= \overline{{\mathscr {C}}_{Prob}^{00}({\mathscr {P}})}^{**}\). It remains unclear to the author of this article why this specific definition of \({\mathscr {C}}_{Prob}({\mathscr {P}},{\mathbb {R}})\) yields indeed “the function space intrinsically associated to a Poisson space” as Landsman claims. See [34, pp. 76–84] for more details.

  31. Given a transition probability space \(({\mathscr {P}}, \mathrm {Pr})\), two subsets \({\mathscr {S}}_1\) and \({\mathscr {S}}_2\) are said to be orthogonal if, for any \(p \in {\mathscr {S}}_1\) and any \(p' \in {\mathscr {S}}_2\), \(\mathrm {Pr}(p, p') = 0\). A subset \({\mathscr {S}}\subset {\mathscr {P}}\) is said to be a component if \({\mathscr {S}}\) and \({\mathscr {P}}\setminus {\mathscr {S}}\) are orthogonal. Finally, a sector is a component which does not have any non-trivial components.

  32. Given a subset \({\mathscr {S}}\subset {\mathscr {P}}\), the orthoplement \({\mathscr {S}}^\bot \) is defined by

    $$\begin{aligned} {\mathscr {S}}^\bot :=\big \{ p \in {\mathscr {P}}\,\big |\, \forall s \in {\mathscr {S}}, \text { Pr}(p, s) =0\big \}. \end{aligned}$$

    In turn, a subset is called orthoclosed whenever \({\mathscr {S}}^{\bot \bot } = {\mathscr {S}}\).

  33. To be more precise, this holds only for well-behaved transition probability spaces. A transition probability space is said to be well-behaved if every orthoclosed subset \({\mathscr {S}}\subset {\mathscr {P}}\) has the property that any maximal orthogonal subset of \({\mathscr {S}}\) is a basis of it. See [34, Definition I.2.7.5 and Proposition I.2.7.6].

  34. As stated, the theorem is only valid for finite-dimensional \(C^*\)-algebras. In the infinite-dimensional case, two more technical axioms are necessary:

    1. (QM 3)

      The space \({\mathscr {C}}({\mathscr {P}},{\mathbb {R}})_{\mathscr {K}}\) is closed under the Jordan product defined by Eqs. (22) and (23).

    2. (QM 4)

      The pure state space of \({\mathscr {C}}({\mathscr {P}},{\mathbb {R}})_{\mathscr {K}}\), seen as a Jordan–Lie–Banach algebra, coincides with \({\mathscr {P}}\).

    See [34, Theorem I.3.9.2. and Corollary I.3.9.2. pp 105–106] for the details and proofs.

  35. Indeed, in its core, the quantum superposition principle is a claim about the ability to generate new possible states from the knowledge of just a few: given the knowledge of states \(p_1\) and \(p_2\), one can deduce the existence of an infinite set \(S_{p_1,p_2}\) of other states which are equally accessible to the system. In the standard Hilbert space formalism, the superposition principle is described by the canonical association of a two-dimensional complex vector space to any pair of states: for two different states \(\psi _1, \psi _2 \in {\mathscr {H}}\), any superposition of them can be written as \(\phi = a \psi _1 + b \psi _2\), with \(a,b \in {\mathbb {C}}\). In other words, it is captured by the existence of a map

    $$\begin{aligned} V: {\mathscr {H}}\times {\mathscr {H}}\longrightarrow \text {Hom}({\mathbb {C}}^2, {\mathscr {H}}) \end{aligned}$$

    where the linear map \(V_{\psi _1, \psi _2}: {\mathbb {C}}^2 \rightarrow {\mathscr {H}}\) is an injection iff \(\psi _1\) and \(\psi _2\) are linearly independent vectors. The geometric reformulation is then found simply by taking the projective analogue of this. Therein, the superposition principle is now seen as the existence of a map

    $$\begin{aligned} S: {\mathbb {P}}{\mathscr {H}}\times {\mathbb {P}}{\mathscr {H}}\longrightarrow \text {Hom}({\mathbb {P}}{\mathbb {C}}^2 \simeq S^2, {\mathbb {P}}{\mathscr {H}}) \end{aligned}$$

    where, for \(p_1 \ne p_2\), the map \(S_{p_1,p_2}\) is an injection. Axiom (QM 1) is the generalization of this for any Poisson space with transition probability.

References

  1. Abraham, R., Marsden, J.E.: Foundations of Mechanics, 2nd edn. Addison-Wesley Publishing Company, Redwood City (1978)

    MATH  Google Scholar 

  2. Abraham, R., Marsden, J.E., Ratiu, T.S.: Manifold, Tensor Analysis, and Applications, 2nd edn. Springer, New York (1988)

    Book  MATH  Google Scholar 

  3. Alfsen, E.M., Shultz, F.W.: Non-commutative spectral theory for affine function spaces on convex sets. Mem. Am. Math. Soc. 172, 1–120 (1976)

    MathSciNet  MATH  Google Scholar 

  4. Alfsen, E.M., Shultz, F.W.: State Spaces of Operator Algebras. Birkhäuser, Boston (2001)

    Book  MATH  Google Scholar 

  5. Arnold, V.I.: Mathematical Methods of Classical Mechanics, vol. 60, 2nd edn. Springer, New York (1989)

    Book  Google Scholar 

  6. Ashtekar, A., Schilling, T.A.: Geometrical formulation of quantum mechanics. In: Harvey, A. (ed.) On Einstein’s Path: Essays in Honor of Engelbert Schücking, pp. 23–65. Springer, New York (1997)

    Google Scholar 

  7. Bargmann, V.: On unitary ray representations of continuous groups. Ann. Math. 59(1), 1–46 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bell, J.S.: On the Einstein–Podolsky–Rosen paradox. Physics 1(3), 195–200 (1964)

    Article  MathSciNet  Google Scholar 

  9. Born, M., Heisenberg, W., Jordan, P.: On quantum mechanics II. In: Van der Waerden, B. (ed.) Sources of Quantum Mechanics, pp. 321–384. Dover Publications Inc, New York (1967)

    Google Scholar 

  10. Brody, D.C., Hughston, L.P.: Geometric quantum mechanics. J. Geom. Phys. 38(1), 19–53 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Cartier, P.: Notion de spectre. In: Première école d’été : Histoire conceptuelle des mathématiques - Dualité Algèbre-Géométrie, pp. 232–242. Maison des Sciences de l’Homme, Universidade de Brasilia (2008)

  12. Catren, G.: On classical and quantum objectivity. Found. Phys. 38(5), 470–487 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Catren, G.: Quantum ontology in the light of gauge theories. In: de Ronde, S.A.C., Aerts, D. (eds.) Probing the Meaning of Quantum Mechanics: Physical, Philosophical, and Logical Perspectives. World Scientific, Singapore (2014)

    Google Scholar 

  14. Chernoff, P.R., Marsden, J.E.: Properties of Infinite Dimensional Hamiltonian Systems. Lecture Notes in Mathematics. Springer, Heidelberg (1974)

    Book  MATH  Google Scholar 

  15. Cirelli, R., Gatti, M., Manià, A.: On the nonlinear extension of quantum superposition and uncertainty principles. J. Geom. Phys. 29(1), 64–86 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Cirelli, R., Gatti, M., Manià, A.: The pure state space of quantum mechanics as hermitian symmetric space. J. Geom. Phys. 45(3), 267–284 (2003)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Dirac, P.A.M.: The fundamental equations of quantum mechanics. Proc. R. Soc. Lond. A109, 642–653 (1925)

    Article  ADS  MATH  Google Scholar 

  18. Dirac, P.A.M.: The Principles of Quantum Mechanics, 4th edn. Oxford University Press, Oxford (1958)

    MATH  Google Scholar 

  19. Gelfand, I., Naimark, M.: On the imbedding of normed rings into the ring of operators in Hilbert space. Matematicheskii Sbornik 12, 197–213 (1943)

    MathSciNet  MATH  Google Scholar 

  20. Geroch, R.: A method for generating solutions of Einstein’s equations. J. Math. Phys. 12(6), 918–924 (1971)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Gleason, A.M.: Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 6, 885–894 (1957)

    MathSciNet  MATH  Google Scholar 

  22. Grgin, E., Petersen, A.: Duality of observables and generators in classical and quantum mechanics. J. Math. Phys. 15(6), 764–769 (1974)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Guillemin, V., Sternberg, S.: Variations on a Theme by Kepler, vol. 42. American Mathematical Society, Providence (2006)

    MATH  Google Scholar 

  24. Heisenberg, W.: Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Zeitschrift für Physik 33, 879–893 (1925)

    Article  ADS  MATH  Google Scholar 

  25. Iglesias-Zemmour, P.: Aperçu des origines de la géométrie symplectique. In: Actes du colloque “Histoire des géométries”, vol. 1. Maison des Sciences de l’Homme, Paris (2004)

  26. Jordan, P.: Über Verallgemeinerungsmöglichkeiten des Formalismus der Quantenmechanik. Nachr. Akad. Wiss. Göttingen 41, 209–217 (1933)

    MATH  Google Scholar 

  27. Kibble, T.: Geometrization of quantum mechanics. Commun. Math. Phys. 65(2), 189–201 (1979)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry, vol. 2. Wiley, New York (1969)

    MATH  Google Scholar 

  29. Kochen, S.B., Specker, E.: The problem of hidden variables and physical measurements. J. Math. Mech. 17(59–67) (1967)

  30. Kosmann-Schwarzbach, Y.: The Noether Theorems: Invariance and Conservations Laws in the Twentieth Century. Sources and Studies in the History of Mathematics and Physical Sciences. Springer, New York (2011)

    Book  MATH  Google Scholar 

  31. Kostant, B.: Quantization and Unitary Representations. Lectures in Modern Analysis and Applications III, Lecture Notes in Mathematics. Springer, New York (1970)

    Book  MATH  Google Scholar 

  32. Landsman, N.P.: Classical and quantum representation theory (1994). arXiv:hep-th/9411172

  33. Landsman, N.P.: Poisson spaces with a transition probability. Rev. Math. Phys. 9(1), 29–57 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  34. Landsman, N.P.: Mathematical Topics Between Classical and Quantum Mechanics. Springer, New York (1998)

    Book  MATH  Google Scholar 

  35. Landsman, N.P.: Simple new axioms for quantum mechanics. Int. J. Theor. Phys. 37, 343–348 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  36. Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry. A Basic Exposition of Classical Mechanical Systems, 2nd edn. Springer, New York (1999)

    Book  MATH  Google Scholar 

  37. Marsden, J.E., Weinstein, A.: Reduction of symplectic manifolds with symmetry. Rep. Math. Phys. 5(1), 121–130 (1974)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Puta, M.: Hamiltonian Mechanical Systems and Geometric Quantization. Kluwer Academic Publishers, Dordrecht (1993)

    Book  MATH  Google Scholar 

  39. Schilling, T.A.: Geometry of Quantum Mechanics. Ph.D. thesis, The Pennsylvania State University (1996)

  40. Shultz, F.W.: Pure states as dual objects for \(C^*\)-algebras. Commun. Math. Phys. 82, 497–509 (1982)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Souriau, J.M.: Structure des systèmes dynamiques. Dunod, Paris (1970)

    MATH  Google Scholar 

  42. Strocchi, F.: An Introduction to the Mathematical Structure of Quantum Mechanics, 2nd edn. World Scientific, Singapore (2008)

    Book  MATH  Google Scholar 

  43. Townsend, J.S.: A Modern Approach to Quantum Mechanics. University Science Books, Sausalito (2000)

    Google Scholar 

  44. von Neumann, J.: Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton (1955)

    MATH  Google Scholar 

  45. von Neumann, J.: Continuous Geometries with a Transition Probability, vol. 252. American Mathematical Society, Providence (1981)

    MATH  Google Scholar 

  46. Wigner, E.P.: Group Theory and Its Applications to the Quantum Mechanics of Atomic Spectra. Academic Press, New York (1959)

    MATH  Google Scholar 

  47. Woodhouse, N.: Geometric Quantization, 2nd edn. Clarendon Press, Oxford (1991)

    MATH  Google Scholar 

Download references

Acknowledgements

This work has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013 Grand Agreement No. 263523, ERC Project PhiloQuantumGravity). I would like to thank Gabriel Catren, Mathieu Anel, Christine Cachot, Julien Page, Michael Wright, Fernando Zalamea and the anonymous reviewer for helpful discussions and comments on earlier drafts of this paper.

Author information

Authors and Affiliations

  1. Laboratoire SPHERE - UMR 7219, 4 Rue Elsa Morante, 75013, Paris, France

    Federico Zalamea

  2. EFREI Paris, 30–32 Avenue de la République, 94800, Villejuif, France

    Federico Zalamea

  3. Basic Research Community for Physics, Leipzig, Germany

    Federico Zalamea

Authors
  1. Federico Zalamea
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Federico Zalamea.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zalamea, F. The Twofold Role of Observables in Classical and Quantum Kinematics. Found Phys 48, 1061–1091 (2018). https://doi.org/10.1007/s10701-018-0194-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10701-018-0194-8

Keywords

Search

Navigation