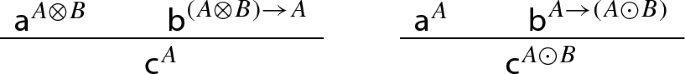Molecular Biology Meets Logic: Context-Sensitiveness in Focus

Abstract

Some real life processes, including molecular ones, are context-sensitive, in the sense that their outcome depends on side conditions that are most of the times difficult, or impossible, to express fully in advance. In this paper, we survey and discuss a logical account of context-sensitiveness in molecular processes, based on a kind of non-classical logic. This account also allows us to revisit the relationship between logic and philosophy of science (and philosophy of biology, in particular).

1 Introduction

Starting from Neopositivism, the interplay between logic and philosophy of science has been punctuated by divergences and convergences about the very role of logic in analyzing the structure and the development of empirical sciences (van Benthem 2012). However, fruitful and lively debates have been focussing almost exclusively on physical theories, due to the highly sophisticated mathematical language in which they are written. At the other extreme of the spectrum of empirical sciences there is biology, displaying a dramatic imbalance between the richness and complexity of the subject and the relative poverty of its own mathematical tools.

In the Twentieth Century the few attempts to consider biology from a logical point of view received often merciless criticisms. Suffice it to mention the dismissive comments of Ruse (1975) and Hull (2000) on the 1937 seminal book by Woodger, The Axiomatic Method in Biology (Woodger 1937; Nicholson and Gawne 2014). It is true that Woodger’s approach was still entrenched in the logical tradition of Hilbert’s Axiomatisches Denken (Hilbert 1917; Hubert and Bernays 1934), which champions a too rigid conceptual platform for tackling a broad range of problems arising in empirical (and mathematical) theories. However, the claim that logic is irrelevant to biological and biomedical sciences sounds utterly uncharitable and anachronistic in the age of major achievements in computational biology and bioinformatics (Calzone et al. 2006; Dini and Schreckling 2008; Watterson et al. 2008; Tamaddoni-Nezhad et al. 2004; Bernot and Comet 2010; Monteiro et al. 2008; Rosselló and Valiente 2005).

In spite of the still persisting misunderstandings about the role of logic in biology among a number of philosophers of biology and biomedicine, a decade ago some of us put forward Zsyntax, a multifaceted project concerning a logical language for molecular biology and originally designed to deal with text mining (Boniolo et al. 2010). Zsyntax was later developed and refined so as to cover also crucial aspects such as non-monotonicity, resource awareness, and automated deduction (Boniolo et al. 2013; D’Agostino et al. 2014; Boniolo et al. 2015; Sestini and Crafa 2018). The whole project relies on a a simple but intriguing idea: representing biochemical types as logical formulae and, consequently, molecular processes as formal derivations. This move allowed for the analysis of elementary molecular transitions in terms of inferential steps, leading to a proto-formalism of the family of non-classical resource-aware systems, called substructural logics (Dosen and Schroeder-Heister 1994; Piazza and Castellan 1996; D’Agostino et al. 1999; Restall 2000, 2008). In this way, the Zsyntax formalism stands as the core of a research program where logic becomes the formal counterpart of what occurs at the empirical level of molecular biology, or, from a dual perspective, logic becomes the specific syntax having molecular processes as the most natural semantic counterpart.

The aim of this paper is to describe and discuss the context sensitiveness phenomenon, as it emerges in molecular reactions and processes, through the lenses of our logical approach. This means we shall be touching issues such as biological networks—in particular those concerning molecular interactions—as well as control mechanisms (Boniolo and Campaner 2018). Needless to say, context sensitiveness is an aspect of utmost relevance, since all biochemical reactions and processes always occur in specific molecular environments. As the environment changes, biochemical reactions and processes may not occur anymore and let new outcomes to take place. This phenomenon is very well-known and stressed from the pathological and therapeutical viewpoints insofar as a change in a molecular pathway can be the (con)cause of a disease or even a (co)way of treating it.

A suspicious reader might object at this point that Zsyntax just consists in a mere linguistic exercise that boils down to formalizing molecular pathways given an initial list of molecular components. In response to this objection, let us highlight the main motivations of our formalism by raising and answering two questions:

• 1. Is Zsyntax useful and meaningful for philosophy?

• 2. Is Zsyntax useful and meaningful for theoretical biology?

Our answer to (1) is straightforward: Zsyntax is worth being investigated from a philosophical point of view because it allows us to shed new light on the logic of empirical theories. As such, this is a contribute to philosophy of science tout court. In a Quinean spirit, we conceive of logic as revisable according to our up-to-date knowledge of the (biological) empirical world (Quine 1976). Zsyntax is then an example of a logical framework governed by empirical constrains. In short, we defend the view that logic has an important part to play in framing conceptual issues in theoretical biology: molecular context-sensitiveness is a case in point.

As regards (2), Zsyntax could be seen as one of the many languages employed to formally address certain biological domains, in particular molecular biology and system biology. However, the salience of Zsyntax lies in its strong connections with proof-theory: it represents molecular pathways as logical proofs, so as to analyze basic molecular transitions as inferential steps. Zsyntax has also the capacity to combine at the same level of logical analysis, and in a well-structured way, both the pure logical layer (namely, tautological statements and truth-preserving inference laws) and the biological layer (i.e., the extra-logical information coming from the labs). Of course, we cannot foresee whether potential outcomes (data mining, prediction, and construction of rigorous databases) will be successfully realized. After all, quantum logic as the logic of quantum mechanics was conceived of in 1936 but it is only in recent times that physicists have begun to use it (for example, within the domain of quantum computation). For many years, quantum logic has been studied by logicians and philosophers, regardless of its utility for physics. We think that the same attitude should be maintained towards the many logics now applied in the biological field and in particular towards Zsyntax.

The paper is organised as follows. In Sect. 2, we give an overview of the molecular context dependency, focusing on the control mechanisms phenomenon. In Sect. 3, we outline Zsyntax with respect to this issue, and then we discuss how thinking about the (biological) empirical world constrains the construction of Zsyntax. In Sect. 4, we will adapt what said in the previous sections to represent both control loop mechanisms and the node-edge structure in biological networks expressing interactions. Then, Sect. 5 presents our conclusions. Finally, an “Appendix” (Sect. 1) will compare Zsyntax with one of the formal languages currently employed in biology, that is, the System Biology Markup Language (Hucka et al. 2003).

2 Molecular Interactions and Molecular Control Mechanisms

The complexity of molecular interactions and pathways (or processes) can be represented through graphs, the so-called biological networks. Their nodes and edges stand, respectively, for molecules (proteins, DNA, RNA, etc.) and interactions between molecules producing new ones (i.e. new nodes). Which direction a given process takes depends on the molecular context in which it is embedded and very often on the molecular control mechanisms governing interactions. It should be noticed that control mechanisms are evolutionary outcomes governing functioning of both gene expression and of more or less any intra- and infra-cellular pathway. Such mechanisms, previously studied in detail by engineers, have entered molecular biology in particular thanks to the 1961 work by Jacob and Monod on the ‘Genetic regulatory mechanisms in the synthesis of proteins’ (Jacob and Monod 1961).

According to their main function, and thus to their logical structure, control mechanisms can be divided into activation and inhibition controls. For example, consider enzymology, where molecular control mechanisms are more pervasive. An enzyme inhibitor ${\mathsf {I}}$ is a molecule that binds to an enzyme ${\mathsf {E}}$ to decrease or even eliminate its activity. In absence of ${\mathsf {I}}$, it can be assumed that ${\mathsf {E}}$ always binds to its substratum ${\mathsf {S}}$, i.e., the reaction starting with ${\mathsf {E}}$ and ${\mathsf {S}}$ and ending in their bonding ${\mathsf {E}}\odot {\mathsf {S}}$ is empirically allowed. However, if the cellular environment includes the inhibitor ${\mathsf {I}}$, we have that the compound ${\mathsf {E}}\odot {\mathsf {S}}$ cannot be delivered due to the fact that ${\mathsf {I}}$ and ${\mathsf {E}}$ bind together, thus precluding the bonding between ${\mathsf {E}}$ and ${\mathsf {S}}$. In other words, there exists a molecular mechanism controlling the activation of the enzyme according to the absence/presence of a molecule capable of inhibiting the reaction. Activation cases work similarly.

Logical monotonicity is the principle according to which, if some A can be derived from a certain cluster of premises $\varGamma$, then A can be also derived from any extended set of premises $\varGamma \cup \varDelta$. According to this view, information has always an ampliative character in the sense that new premises cannot erase what follows from older ones. Coming back to control mechanisms, in order to be formally expressed, they have to be represented by means of non-monotonic logical inferences. If we consider again the concurrent enzyme inhibition phenomenon, monotonicity proves infringed to the extent that the ‘deducibility’ of ${\mathsf {E}}\odot {\mathsf {S}}$ from ${\mathsf {E}}$ and ${\mathsf {S}}$ is blocked by the introduction of a specific third element ${\mathsf {I}}$ that forces the reaction towards another issue. In more formal terms, in case ${\mathsf {I}}\notin \varGamma$ we are allowed to claim the following:

$$\begin{aligned} \varGamma ,{\mathsf {E}},{\mathsf {S}}\Rightarrow \varGamma , {\mathsf {E}}\odot {\mathsf {S}} \end{aligned}$$

(1)

The comma here intuitively means ‘and’ on both sides of the arrow.

However, in case ${\mathsf {I}}$ is added to $\varGamma$ the previous derivation is no longer empirically allowed. As a matter of fact, what we actually have is the transition reported below:

$$\begin{aligned} \varGamma ,{\mathsf {I}},{\mathsf {E}},{\mathsf {S}}\Rightarrow \varGamma ,{\mathsf {S}},{\mathsf {E}}\odot {\mathsf {I}} \end{aligned}$$

(2)

which produces the compound ${\mathsf {E}}\odot {\mathsf {I}}$ leaving the substratum ${\mathsf {S}}$ as a residual element.

It is worth recalling that the two kinds of controls mentioned before (activation and inhibition) turn out to be at the core of two classes of non-Boolean molecular loops:

• The feed forward loop control mechanisms (FFL) take into account the inputs and, in function of them, modify future states of the system—i.e. they are activation controls—, even if they do not consider the output. To illustrate this point, we can mention the Escherichia coli as well as the Saccharomyces cerevisiae mechanisms where a transcription factor ${\mathsf {X}}$ regulates the expression of a second transcription factor ${\mathsf {Y}}$. Both of them bind the regulatory region of a gene ${\mathsf {Z}}$ and, thus, in combination, they regulate its expression.

• The feedback loop control mechanisms (FbL) can either stop (or downregulate ) the system in function of the output, or boost (or upregulate) it. In the first case, we have inhibition controls, in the second activation controls. The main biological case of FbL was described by Jacob and Monod in the already mentioned paper. It regards a feedback inhibition in the regulation of the lactose catabolism in Escherichia coli. In these species, there is an operon, the Lac operon, that is, a cluster of three genes ($\mathsf {lacZ, lacY, lacA}$) under the control of a single promoter. These three genes code the three enzymes $\beta$ -galactosidase, lactose permease, and $\beta$ -galactoside transacetylase, respectively. The $\mathsf {lactose permease}$ transports the lactose (a sugar) into the cell. Then, $\beta$ -galactosidase cleaves the lactose into glucose and galactose. If there is no lactose to cleave, there is no point in expressing the operon. Thus a control mechanism enters the scene: the protein $\mathsf {Lac\, repressor}$ binds the DNA close to the beginning of the Lac operon, so inhibiting its expression. In presence of lactose, allolactose (a lactose metabolite) binds the $\mathsf {Lac\, repressor}$ changing its conformation and inhibiting its bonding with DNA. This results in permitting the Lac operon expression.

A prototypical example of inhibition/activation process is represented by the functioning mechanism of drugs. Drugs can be thought of as elements of control mechanisms which are ad hoc introduced in the organism with the aim of controlling a ‘non-normal’ or even ‘pathological’ situation and, in so doing, have an inhibiting function. Let us consider thermoregulation in humans. We know that it is a feedback control mechanism to maintain the temperature around 37 C. It could happen, for several reasons, that the temperature increases perilously. In this case we take paracetamol (a drug) to control it. Paracetamol is an inhibitor; in particular, it inhibits cyclooxygenase, which is responsible for the formation of prostanoids. Therefore, it can be considered as an ad hoc external part of an already existing internal mechanism of thermoregulation based on a feedback. Generally speaking, a drug is an ad hoc external control molecule (and, thus, it is a part of a control mechanism) which interrupts in some way the ‘non-normal’ or ‘pathological’ behaviour (pathway) of a cell (or of a cell population) by attempting to divert it from its ‘natural history’.

By the way, drugs do not exhaust the class of ad hoc inhibitors. Insecticides, herbicides and disinfectants are all produced by stressing the very same inhibition mechanisms, and therefore with the same underlying logical structure. For instance, malathion binds cholinesterases (a class of enzymes whose function is essential to allow cholinergic neurons to return to their resting state after activation) in order to inhibit their function. Malathion can thus be used as the active ingredient of insecticides to kill, for example, the parasites infesting sheep. Another molecule of this kind is glyphosate that inhibits the enzymes involved in the synthesis of aromatic amino acids (tyrosine, tryptophan, phenylalanine) and is used in herbicides to eliminate weeds and grasses competing with crops. As a third example, we could mention triclosan, which is used in antibacterial disinfectants (e.g., it is present in some toothpastes), because it inhibits an enzyme involved in the building of bacterial (but not human) membranes.

To conclude this section, it is worth mentioning the so-called ‘natural poisons’ (the biotoxins, or natural toxins). Such inhibiting molecules are evolutionary outcomes by means of which some species attack other species or defend themselves depending on whether they are predators (e.g., spiders, snakes, scorpions, and jellyfishes) or not (e.g. bees, ants, termites, wasps, and frogs). Interesting enough, in several cases they are used also by humans to construct lethal weapons as it happens with the biotoxin naturally produced in the skin cells by a species of frogs (the poison dart frogs which belong to the family Dendrobatidae). These ‘batrachotoxins’, used by some Amerindias to poison their blowdart tips, are neurotoxins that bind the sodium channels of nerve cells. Consequently, the neurons cannot longer work properly resulting in paralysis of the unfortunate living being in question. Unlike drugs, poisons are clearly not introduced voluntarily in the organism. However, they can be regarded as ‘negative’ drugs interrupting somehow the ‘normal’ or ‘non-pathological’ behaviour of a cell by attempting to divert it from its ‘natural history’. Thus, a poison can be thought of as an ad hoc external control molecule (and hence a part of a control mechanism) which, in many cases, works exactly like an inhibitor.

3 The Logic of Molecular Control Mechanisms

3.1 The Zsyntax Operators

The family of logical calculi forming the whole picture of the Zsyntax project have been designed with the aim of formally representing biochemical pathways in terms of deductive processes (Boniolo et al. 2010, 2013, 2015) and, more in general, to deal with extra-logical information (Piazza and Pulcini 2016, 2017; Sestini and Crafa 2018). According to this pathway-as-deduction paradigm, aggregates of molecules are interpreted as logical types (formulas) and biochemical pathways/processes are formally shaped as logical deductions, i.e., chains or trees of inferences performed according to the rules of a logical system.

Empirically, we start from a given initial set of aggregates of molecules ${\mathsf {a}}_1,\ldots ,{\mathsf {a}}_n$ and, by means of a suitable number of reactions, a certain final aggregate c is produced. In Zsyntax, such a pathway/process is interpreted as a proof starting from a multiset of types $A_1,\ldots ,A_n$ (the premises where $A_i$ is the type of the aggregate ${\mathsf {a}}_i$¹) and, by means of a suitable number of inferences, we arrive at the final type C (the conclusion). From now on, we will write ${\mathsf {a}}^A$ to mean that the type A is associated with the aggregate a. The key point here is that this is meant to establish a sort of analogous of the Curry-Howard correspondence by linking reactions and their logical counterpart to the effect that, if ${\mathsf {a}}^{A_1}_1,\ldots ,{\mathsf {a}}^{A_n}_n$, then ${\mathsf {c}}^C$.

$$\begin{aligned} \begin{array}{ll} {\mathsf {a}}_1,\ldots ,{\mathsf {a}}_n\leadsto {\mathsf {c}} &{} \textit{process} \\ {A_1},\ldots ,{A_n}\Rightarrow C &{} \textit{formal derivation} \end{array} \end{aligned}$$

In Zsyntax, atomic formulas stand for the type of a given molecule such as the Tumor Suppressor Protein ($\mathsf {TP53}$) or the Caretaker Gene Brest Cancer Type 1 ($\mathsf {BRAC1}$). Complex well-formed formulae are recursively built out of the atomic formulae by means of the three binary operators illustrated below: Z-interaction, Z-conditional and and Z-conjunction.

• Z-conjuntion ($\otimes$). An aggregate c of type $A\otimes B$ indicates the type of the union—without or before any kind of interaction—of two disjoint aggregates ${\mathsf {a}}^A$ and ${\mathsf {b}}^B$. Z-conjunction can be iterated so as to produce longer aggregates $A_{1}\otimes A_{2}\otimes \cdots \otimes A_{n}$. Accordingly, we write $A_{1}\otimes A_{2}\otimes \cdots \otimes A_{n}$ to mean that n aggregates ${\mathsf {a}}_{1}, {\mathsf {a}}_{2},\dots , {\mathsf {a}}_{n}$ of type $A_{1}, A_{2},\dots , A_{n}$, respectively, are simultaneously present in the same environment and ready to interact together (if empirically allowed).

Example 1

Z-conjucntion can be used to rewrite the formal expressions (1) and (2) as follows:

$$\begin{aligned}&\varGamma ,{\mathsf {E}}\otimes {\mathsf {S}}\Rightarrow \varGamma , {\mathsf {E}}\odot {\mathsf {S}} \end{aligned}$$

(3)

$$\begin{aligned}&\varGamma ,{\mathsf {E}}\otimes {\mathsf {S}}\otimes {\mathsf {I}}\Rightarrow \varGamma , ({\mathsf {E}}\odot {\mathsf {I}})\otimes {\mathsf {S}} \end{aligned}$$

(4)

• Z-interaction ($\odot$). We write that an aggregate c is of type $A\odot B$ to mean that there has been an effective interaction between the aggregates ${\mathsf {a}}^A$ and ${\mathsf {b}}^B$ that consumed both a and b, and delivered a third element ${\mathsf {c}}^{A\odot B}$. We use the Z-interaction operator to represent any interaction of two or more molecules. Clearly, Z-interaction expresses a stronger form of conjunction insofar as the presence at the time $t_{n}$ of an element of type $A\odot B$ presupposes the presence of an element of type $A\otimes B$ at a certain time $t_{m}$ with $m<n$.

Example 2

It is known that the interaction of D-Glucose-6-phosphate with Glucose-6-phosphate isomerase delivers D-Fructose-6-phosphate. So, if the types A and B are associated with D-Glucose-6-phosphate and Glucose-6-phosphate isomerase, respectively, then we will associate the type $A\odot B$ with the aggregate $\mathsf{D-Fructose-6-phosphate}$.

• Z-conditional ($\rightarrow$). We say that that an aggregate c is of type $A\rightarrow B$ in case there is a well-established reaction delivering another aggregate ${\mathsf {b}}^B$ once ${\mathsf {c}}^{A\rightarrow B}$ and ${\mathsf {a}}^A$ interact with each other. Mathematically speaking, a Z-conditional-type $A\rightarrow B$ should be thought of as a function that returns the type B once A is applied to $A\rightarrow B$. The nature of this interaction clearly depends on the types attached to the elements ${\mathsf {a}}$ and ${\mathsf {b}}$. Consider, for instance, these two cases:

  

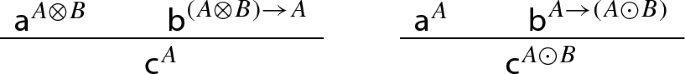
  The inference on the left clearly expresses a mere logical interaction, whereas the one on the right is meant to formalize some specific biochemical reaction.

Example 3

Consider the interaction between TP53 and the gene MDM2 which returns the protein MDM2. As already seen, this can be formally expressed as follows:

(5)

Now, Z-conditional allows us to encode the empirical information expressed in (5) by assigning the type $A\rightarrow (A\odot B)$ to $\mathsf { MDM2 }\,(gene)$ or the type $B\rightarrow (A\odot B)$ to A, as displayed in (6) and (7), respectively.

(6)

(7)

Z-interaction, Z-conjuntion and Z-conditional show some important non-classical features essentially dictated by their empirical meaning. First, Z-interaction does not necessarily enjoy associativity, this is, the type $(A\,\odot \,B)\,\odot \,C$ is not necessarily equivalent to $A\,\odot \,(B\,\odot \,C)$. The reason is simple: even if A interacts with B and the resulting product $A\odot B$ interacts, in turn, with C, it does not automatically follow that B interacts with C, or that $B\odot C$ interacts with A.

Example 4

(Non-associativity of $\odot$) In the case of the Trp Operon of Escherichia  coli, the Trp-repressor does not bind it if not already bound to Tryptophan. Formally speaking, given $\mathsf {Tryptophan}^A$, $\mathsf{Trp-repressor}^B$ and $\mathsf {Trp\,Operon}^C$, we have that $(A\odot B)\odot C$ does not entail $A\odot (B\odot C)$.

Second, Z-conjuntion and Z-interaction are not idempotent operators, that is, both $A \otimes A$ and $A\odot A$ are not necessarily equivalent to A. This sort of resource-sensitivity (having two items or more of the element A is clearly not the same as having only one item of A) is a basic feature borrowed from some substructural logics which is needed to represent the obvious fact that, in a molecular process, we often need more tokens of the same molecular type, sometimes intervening at different moments of the reaction chain.

Example 5

(Non-idempotency of $\odot$ and $\otimes$) Trivially enough, having two molecules of ATP is not biochemically the same as having only one of them, that is, $ATP\odot ATP \ne ATP$. Analogously having a molecular compound produced by two molecules of hydrogen is not the same as having just one of it, namely $H\otimes H$ is not logically equivalent to H.

Finally, Z-conditional fails in fulfilling some properties characterizing the behaviour of the conditional operator in the best known logical systems. The two following logical laws are intended to express the kind of resource-insensitivity typically holding in both classical and intuitionistic logic.

$$\begin{aligned}&A\rightarrow (B \rightarrow A) \end{aligned}$$

(8)

$$\begin{aligned}&(A \rightarrow (A \rightarrow B)) \rightarrow (A \rightarrow B) \end{aligned}$$

(9)

On the one hand, (8) formally expresses the fact that, if A is derivable, then it is also derivable when some additional information B is assumed. On the other, (9) establishes the fact that, if B is derivable from n-copies of A, then it is also derivable from just one occurrence of the same resource A. To provide a counterexample to (8), it suffices to resort again to the concurrent enzyme inhibition phenomenon and instantiate (8) as follows.

$$\begin{aligned} (\mathsf {E}\otimes \mathsf {S}\rightarrow \mathsf {E}\odot \mathsf {S})\rightarrow (\mathsf {I}\rightarrow (\mathsf {E}\otimes \mathsf {S}\rightarrow \mathsf {E}\odot \mathsf {S})) \end{aligned}$$

(10)

3.2 The Zsyntax Inference Rules

Having introduced the language of Zsyntax, we shall now be concerned with its inference rules. They constitute the deductive engine of the system since they allow the user to produce derivations made by several successive inference steps. The general pattern of an inference rule that licenses the transition from an aggregate of type A to another aggregate of type B is the following:

(11)

Here $\varGamma$ is a variable ranging over arbitrary multisets of aggregates which represents the molecular context in which the reaction is supposed to take place. It is to note that this is extremely relevant if we want to capture by a formal representation real biological processes, since the context (in particular the molecular context) plays a fundamental role in allowing or hindering reactions. We indicate with ${\mathbf {S}}$ a (possibly empty) set of side conditions on $\varGamma$ specifying some negative or positive information regulating the biochemical transition from A to B. On the one hand, negative side conditions encode the molecular contexts $\varGamma$ in which the given reaction is known to be ‘blocked’. On the other, positive conditions specify the molecular context in which the reaction is boosted.

Fig. 1

The logical rules

Rules in our system can be classified as logical (LR) or empirical (ER). On the one hand, LRs (and more specifically, following a tradition that dates back to Gentzen 1935) establish the meaning of the two logical operators $(\otimes )$, and ($\rightarrow$) in the way reported in Fig. 1. On the other hand, ERs are expected to formally encode the empirical information coming from the lab and, thus, determine the correct use of the Z-interaction operator ($\odot$).

To take a clear example of an ER, consider the synthesis of the $\mathsf {ATP}$ consisting in the transitions from the adenosine diphosphate ($\mathsf {ADP}$), inorganic phosphate (${{\mathsf {P}}}{{\mathsf {h}}}$), and the enzyme catalyzing the reaction ($\mathsf {ATPsynthase}$) to the adenosine triphosphate ($\mathsf {ATP}$). In more formal terms:

(12)

In (12), $\mathsf {ATP}$ abridges the type $\mathsf {ATPsynthase}\odot \mathrm {ADP}\odot {{\mathsf {P}}}{{\mathsf {h}}}$. Moreover, the side condition ${\mathbf {S}}$ allows us take into account the very fact that there are inhibitors of the $\mathsf {ATP}$ synthesis, such as $\mathsf {Oligomycin}$ (typically used as an antibiotic) which binds the $\mathsf {ATPsynthase}$, thus preventing the synthesis. Therefore, in the rule above, ${\mathbf {S}}$ encodes the information telling us that the reaction occurs if there is no $\mathsf {Oligomycin}$ in the context represented by $\varGamma$.

There can be, however, overlaps between LRs and ERs. The Z-conditional elimination rule reported in Fig. 1 can be simply read as the Zsyntax version of the classical Modus Ponens. Nonetheless, its correct application may well depend on the empirical information associated with the transition from A to B. For example, the rule (12) reported above can be ‘internalized’ in the formalism and thus written as the following conditional:

$$\begin{aligned}(\mathsf {ATPsyn.}\otimes \mathrm {ADP} \otimes {{\mathsf {P}}}{{\mathsf {h}}})\rightarrow \mathsf{ATP}. \end{aligned}$$

This conditional can be used as major premise of Modus Ponens only if the context of its application complies with the empirical information about the contexts that may inhibit or boost the transition from the antecedent to the consequent. Hence the following inference step

(13)

is clearly an instance of Modus Ponens. However, in order to be performed correctly, it needs to meet the side condition expressed by S. This can be formally expressed by associating each conditional of the form $A \rightarrow B$ with a side condition ${\mathbf {S}}_{A \rightarrow B}$ that depends on the actual content of A and B and “controls” the application of $\rightarrow$-${\mathscr {E}}$. On the other hand, the rule, as such, is a logical rule in that it is content independent. By contrast, the side conditions do depend on the content of A and B.

The dual rule for Z-implication has to be read as follows: if there is a derivation leading from the aggregate $\varGamma ,A$ to the aggregate $B,\varDelta$, then this same derivation can be prolonged by inferring the aggregate $A\rightarrow B,\varDelta$ while A is removed (in the jargon of proof theory, one says that the hypothesis A has been discharged) from the initial aggregate $\varGamma ,A$, i.e.,

In other words, the rule tells us that any instance of the aggregate $\varGamma$ is ipso facto an instance of the aggregate $A\rightarrow B,\varDelta$, whenever it can be shown that any instance of $\varGamma$ is of type $A\rightarrow B,\varDelta$. As an illustrative example, we can consider the specific application of the $\rightarrow {\mathscr {I}}$-rule reported below:

The duality between introduction ($\rightarrow {\mathscr {I}}, \otimes \,{\mathscr {I}}$) and elimination ($\rightarrow {\mathscr {E}}, \otimes \,{\mathscr {E}}$) rules sheds light on the twofold nature of our formalism that can be used to grasp reactions, as well as to represent and systematize information. On the one hand, molecular processes can be formally reproduced by means of a chain of inferences essentially eliminating operators. On the other hand, introduction rules allow the user to formally encode into formulas the history of such reactions so as to get a kind of ready-to-share information.

The validity of LRs is purely formal and this is what distinguishes them from the ERs, whose validity is empirically grounded and content-dependent. However, as explained above, the Z-conditional elimination may well include a side condition corresponding to the empirical information that needs to be used in order to introduce the conditional (see also the next section for further examples). Otherwise the introduction rule and the elimination rule would not be in “harmony”: the elimination of a formula should not allow us to obtain any transformation that was forbidden by some side-condition in the process that led to its introduction.

3.3 Context Sensitive Rules

We have already seen that the general format of an inference pattern from an initial aggregate of type $A_{i}$ to a final aggregate of type $A_{f}$ is

(14)

$\varGamma$, as said, represents the molecular context in which $A_{i}$ and $A_{f}$ are assumed to interact and ${\mathbf {S}}$ expresses the side condition about $\varGamma$ which determines which process can occur and which cannot.

To better illustrate the case, let us resort again to the process of enzymatic inhibition involving an enzyme $\mathsf {E}$, its substratum $\mathsf {S}$, and, possibly, an inhibitor $\mathsf {I}$. The process is an if-then-else: if no inhibitor is present in the environment at the very moment of reaction, we can assume that $\mathsf {E}$ binds to $\mathsf {S}$ so as to deliver the compound $\mathsf {E\odot S}$. Otherwise, if $\mathsf {I}$ is one of the elements forming $\varGamma$, the transition expressed in (4) proves empirically hindered since $\mathsf {I}$ binds to $\mathsf {E}$ delivering $\mathsf {E\odot I}$ instead of $\mathsf {E\odot S}$ (cfr. Fig. 2).

Fig. 2

The flow chart representing the concurrent enzyme inhibition phenomenon

This specific phenomenon can be formalized in our system as follows. The following rule expresses the fact that $\mathsf {E}$ and $\mathsf {I}$ always bind when they are present in the same environment.

(15)

This second rule regulate the binding of $\mathsf {E}$ with $\mathsf {S}$:

(16)

Going back to (14), we can now observe that the role side conditions play in implementing ERs consists in constraining substitutions on $\varGamma$. In case of concurrent enzyme inhibition, the specific side conditions regulating the transition from $E\otimes S$ to $E\odot S$ allows for the replacement of $\varGamma$ with any multiset of biochemical elements provided that the multiset does not contain the inhibitor I.²

Similar constraints may also come into play to regulate the Z-conditional elimination rule ($\rightarrow {\mathscr {E}}$). Consider, for instance, the following derivation:

Here, the same information expressed at the meta-level by (16) is ‘internalized’ in the proof itself by including among the initial premises the formula $({\mathsf {E}}\otimes {\mathsf {S}})\rightarrow ({\mathsf {E}}\odot {\mathsf {S}})$. In order to rule out empirically unsound inferences, the specific $\rightarrow {\mathscr {E}}$-application delivering the type ${\mathsf {E}}\odot {\mathsf {S}}$ has to come accompanied by the following side condition:

As already observed, the logical nature of Z-conditional elimination rule is not affected by the presence of side conditions. Indeed, they just reflect what happens in the corresponding empirical rule. In the case in question, we know that the above inference is empirically valid:

This one-step derivation can be prolonged by means of a $\rightarrow {\mathscr {I}}$-application as follows

In this longer proof, the type ${\mathsf {E}}\otimes {\mathsf {S}}$ is removed (discharged) from the set of initial premises and the side condition is still active: it just migrates one step below. Thus, if the context $\varGamma$ contains at least one instance of ${\mathsf {E}}\otimes {\mathsf {S}}$, then the type ${\mathsf {E}}\odot {\mathsf {S}}$ can be produced, provided that the inhibitor ${\mathsf {I}}$ is not included in $\varGamma '$:

Side conditions may also constrain context replacements by expressing positive conditions. This is the case of activation processes, which require the presence of some specific elements in $\varGamma$ to be actually carried out. This can be exemplified by the enzyme activators, which are chemical compounds that have the function of increasing the velocity, or render it possibile, an enzymatic reaction. Among activators there could be ions, peptides, proteins, lipids and other small organic molecules. They can act in different ways, but in each case their presence is necessary to speed up, or make it possible, a specific reaction. That is, if we have E and S in the same environment but there is not the activator A, we have:

(17)

otherwise, in the presence of the activator:

(18)

4 Control Loops and Biological Networks

In the introduction we planned to show that Zsyntax allows us to formally represent both the control loop mechanisms and the node-edge structure which is necessarily pervasive in any molecular interaction network. Now, it is time to engage ourselves on this task by discussing some paradigmatic cases which also exemplify the adopted language.

4.1 Control Loops and Context Sensitiveness

It is well-know that a FFL is a kind of control where one or more molecules act in the same direction as the pathway. Only if those molecules are timely present, the pathway at stake occurs and properly develops (see, Berka 2012). There are many ways in which a molecular FFL is instantiated, but to exemplify how our formalism works, we limit ourselves to a case shown in Fig. 3 and discussed by Mangan and Alon (2003).

This is a FFL realized by three-genes (X, Y, Z) and by two input transcription factors ($\mathsf {S}_{\mathsf {x}}$ and $\mathsf {S}_{\mathsf {y}}$) one of which regulates the other, both jointly regulating a target gene. We may easily apply our formalism to represent it through a formal derivation. In particular, as we can see in the Fig. 3, effective interactions introducing the bonding operator $\odot$ are represented by the solid line, whereas dotted lines just express renaming steps (for instance, in the first dotted line replaces ${\mathsf {S}}_{x}\odot {\mathsf {X}}$ by ${\mathsf {x}}$). The binding ${\mathsf {S}}_{x}\odot {\mathsf {X}}$ expresses the fact that the inducer ${\mathsf {S}}_{x}$ activates the transcription factor ${\mathsf {X}}$ so as to deliver the protein ${\mathsf {x}}$. Likewise, the factor ${\mathsf {S}}_{y}$ binds to ${\mathsf {Y}}$, and then, in a next step, to ${\mathsf {x}}$. The complete interaction between ${\mathsf {S}}_{y}, {\mathsf {Y}}$, and ${\mathsf {x}}$ is expressed by the formula ${\mathsf {x}} \odot S_{y}\odot Y$, i.e., the protein ${\mathsf {y}}$. Finally, the three elements ${\mathsf {x}}, {\mathsf {y}}$, and ${\mathsf {Z}}$ bind all together in a way to deliver ${\mathsf {z}}$. Along the whole deduction, $\varGamma$ is taken to represent the generic context in which the reaction leading from ${\mathsf {S}}_{x}\otimes {\mathsf {S}}_{x}\otimes {\mathsf {S}}_{y}\otimes {\mathsf {X}}\otimes {\mathsf {X}}\otimes {\mathsf {Y}}\otimes {\mathsf {Z}}$ to ${\mathsf {z}}$ takes place.

Fig. 3

Zsyntax Graphical (on the left) and formal (on the right) respresentations of the FFL under analysis

It is worth observing that logic can directly take into account the specific kind of context-sensitiveness here involved by handling it in terms of resource-awareness. The whole reaction can be carried out only on condition that the transcription factor $\mathsf {X}$ occurs at least twice in the initial aggregate. This kind of condition can be fully expressed in a resource-aware setting such as the one proposed here by explicitly displaying two tokens of the type $\mathsf {X}$ in the list of types formally representing the starting stage. Similar considerations can be made for the other components of the reaction.

If we like to write it by using our general pattern of an inference rule, we have

(19)

where ${\mathbf {S}}$ represents the molecular context in which there are no inhibitors of the FFL.

As far as the FbL is concerned, instead of discussing the lac operon case presented in the introduction, we prefer to exemplify it by means of the Tryptophan synthesis (for a biological discussion see Yanofsky 2001).

In Escherichia coli there is a gene cluster which is transcribed by the RNA-polymerase into a set of enzymes, which allow for the biosynthesis of an amino acid: the Tryptophan. Actually, here we have four elements involved: i) the Tryptophan (Try); ii) the Tryptophan Repressor (TryR); iii) the Cluster Gene (C); and iv) the RNA Polymerase (RNAp). In this case, there is a strong control mechanism acting in the molecular context in which the reaction takes place. To be more precise, so that the expression of the C begins, a molecule of RNAp must bind its promoter. If this succeeds, the enzymes are coded and the Try synthesis begins. Nevertheless, it can occur that the Try produced is already sufficient within the Escherichia coli. Or it could happen that there is already a sufficient quantity of Try since it has entered the cell from the medium in which it lives. In these cases there is no need of other Try, and its expression must stop. This happens because, within the promoter, there is a short nucleotide sequence, the operator, which is recognized by a gene regulatory protein: the TryR. If this latter binds the operator, then the RNAp cannot bind the promoter and the expression of the enzymes cannot begin. This is what happens when the Try level is high and a molecule of Try binds the TryR. At this point the compound binds, in turn, the operator and the expression is blocked. As soon as the Try level drops, the TryR releases the Try and it can detach from the operator. Now the promoter is free to accept the RNA-polymerase and the enzymes expression starts again (cfr. Fig. 4).

Analogously to the FFL case, also the FbL could be synthesized by means of our general pattern of inference, that is,

(20)

where $\varGamma$ represents the molecular context in which there is no sufficient Try to stop its biosynthesis.

Fig. 4

The if-then-else structure of the Escherichia coli control mechanism

4.2 Biological Networks and Context Sensitiveness

As said, there are biological networks representing sets of molecular interactions occurring intra- and infra cells. These networks are usually represented by means of oriented graphs whose geometrical complexity parallels the interactional complexity of the molecules at issue. In such a graph-like representation, nodes and edges stand for molecules and interactions, respectively. Edges may represent simple interactions but also single pieces of a potentially extremely long molecular pathway or process. Each node may allow for several incident and emerging edges. The number of incident and emerging edges depends on the interactional relevance of the molecule represented by the node, that is, on how many reactions and processes are involved.

To consider an easy example, look at a portion of a possible network in Fig. 5. In this graph the molecules $B_{1}$ and $B_{2}$ are connected with the molecule A by means of two edges labelled with $A\otimes B_{1}$ and $A\otimes B_{2}$, respectively. Then, two edges depart from A to arrive in $C_{1}$ and $C_{2}$. The edges $A\longrightarrow C_{1}$ and $A\longrightarrow C_{2}$ are labelled with $A\odot B_{1}$ and $A\odot B_{2}$, respectively. Now consider the two-steps path $B_{1}{\mathop {\longrightarrow }\limits ^{A\otimes B_{1}}}A{\mathop {\longrightarrow }\limits ^{A\odot B_{1}}}C_{1}$. The first step links the molecule $B_{1}$ with the molecule A by means of the ‘action’ $A\otimes B_{1}$. Roughly speaking, the first step merges A and $B_{1}$ in the same context, while the second step $A{\mathop {\longrightarrow }\limits ^{A\odot B_{1}}}C_{1}$ produces the interaction $A\odot B_{1}$ delivering the molecule $C_{1}$. The path $B_{2}{\mathop {\longrightarrow }\limits ^{A\otimes B_{2}}}A{\mathop {\longrightarrow }\limits ^{A\odot B_{2}}}C_{2}$ works similarly. Though graphically allowed, the path $B_{1}{\mathop {\longrightarrow }\limits ^{A\otimes B_{1}}}A{\mathop {\longrightarrow }\limits ^{A\odot B_{2}}}C_{2}$ is not empirically allowed since the second step requires $B_{2}$ in the context to be carried out. Analogously, though graphically allowed, the path $B_{2}{\mathop {\longrightarrow }\limits ^{A\otimes B_{2}}}A{\mathop {\longrightarrow }\limits ^{A\odot B_{1}}}C_{1}$ is not empirically allowed since the second step requires $B_{1}$ in the context to be carried out.

Fig. 5

A node with 2 incoming and 2 outgoing edges

As a real case, let us consider the melanoma network and focus on the MAPK and PI3K/AKT pathways³.

We consider here only the first two reactions occurring in both pathways, since they are sufficient to exemplify our discussion.

The MAPK pathway is a series of cellular reactions that communicates a signal from a receptor on the surface of the cell to the DNA in its nucleus. The signal starts when a signaling molecule binds to the receptor on the cell surface and ends when the DNA in the nucleus expresses a protein and produces some change in the cell, such as cell division. Any defect in the MAPK pathway leads to that uncontrolled growth and, therefore, to melanoma. This pathway starts from SCF, which is a transmembrane growth factor and ends in MAPK (mitogen-activated protein kinase). We consider just the first two reactions:

• The first concerns the bonding interaction involving SCF and c - KIT (tyrosine kinase receptor):

  $$\begin{aligned} (\mathsf {SCF}\otimes \mathsf{c\,-\,Kit}) \rightarrow (\mathsf {SCF}\odot \mathsf{c\,-\,Kit}). \end{aligned}$$

• The second involves two ATP molecules, one binding at the locus 568 ($\mathsf {ATP}_{\mathsf {568}}$) and one at the locus 570 ($\mathsf {ATP}_{\mathsf {570}}$):

  $$\begin{aligned}&(\mathsf {SCF}\odot \mathsf{c\,-\,Kit}) \otimes \mathsf{ATP}_{568} \otimes \mathsf{ATP} _{570}\rightarrow \mathsf {SCF}\odot ( \mathsf{c\,-\,Kit}\\&\qquad \odot \mathsf {P}_{\mathsf {568}} \odot \mathsf {P}_{\mathsf {570}}) \otimes \mathsf {ADP} \otimes \mathsf {ADP} \end{aligned}$$

  where $\mathsf {P}_{\mathsf {568}}$, $\mathsf {P}_{\mathsf {570}}$ and ADP are the phosphate binding at the loci 568 and 570 and the adenosine diphosphate, respectively.

The PI3K/AKT pathway is a series of cellular reactions starting again from SCF and arriving at MITF (microphthalmia-associated transcription factor), a protein involved in the regulation of many types of cells including melanocytes, via PI3K (phosphoinositide 3-kinases). This family of enzymes is notoriously involved in cell growth, proliferation, differentiation, motility, survival, and intracellular trafficking, and, thus, in cancer. As in the previous case, we focus attention on the first two pathway reactions.

• The first concerns the same pathway considered above:

  $$\begin{aligned} (\mathsf {SCF}\otimes \mathsf{c\,-\,Kit}) \rightarrow \mathsf {SCF}\odot \mathsf{c\,-\,Kit} \end{aligned}$$

• The second involves only one ATP molecule binding at the locus 721 ($\mathsf {ATP}_{\mathsf {721}}$)

  $$\begin{aligned} (\mathsf {SCF}\odot \mathsf{c\,-\,Kit}) \otimes \mathsf {ATP}_{721} \rightarrow \mathsf {SCF} \odot ( \mathsf{c\,-\,Kit} \odot \mathsf {P}_{\mathsf {721}}) \otimes \mathsf {ADP} \end{aligned}$$

  where $\mathsf {P}_{\mathsf {721}}$ is the phosphate binding at the locus 721.

In terms of our graph-like representation, two different edges emerge from $\mathsf {SCF}\odot \mathsf{c\,-\,Kit}$: one concerning the MAPK pathway, while the other the PI3K/AKT pathway. Here again, context-sensitiveness crucially comes into play insofar as the choice between the two pathways entirely depends on the biochemical environment in which the reaction is expected to be produced. In other words, if there are two ATPs binding at the two correct loci (568, 570), then the MAPK pathway will be selected. If there is only one ATP binding at the correct locus (721), then the PI3K/AKT pathway is the one that will be triggered. That is, we can have these two alternatives:

(21)

(22)

In the situation described above we have 2 incoming and 2 outgoing edges from the node A, which become the point in which two different alternatives (that is, two different molecular processes, or molecular pathways) take place. Of course, we can easily generalize this frame to the case in which we have n incoming/outgoing edges from the node (the hub) A. In this case we would have n different alternatives (processes, pathways):

1.:

If ${\mathbf {S}}_{1}$, then

2.:

If ${\mathbf {S}}_{2}$, then

$\vdots$

n.:

If ${\mathbf {S}}_{n}$, then

Here, the type A plays the role of a hub with at least n incident edges—the ones connecting each one of the $B_{i}$s to A so as to deliver aggregate-types $A\otimes B_{i}$—, and at least n emerging edges forming the compound-types $A\odot B_{i}$. Each one of these n biochemical transitions is regulated by a corresponding (possibly empty) side condition.

5 Conclusive Remarks

Our aim in this paper is far from promoting the idea that logical theorizing should constrain the conceptual analysis of scientific issues. Rather, the point emerging from our discussion is that logic is a powerful tool that could, and should, be used whenever it may offer some alternative or complementary intellectual insights into a specific scientific topic.

The general idea of the Zsyntax project is that, modulo a suitable discretization, any biochemical process can be decomposed into a finite sequence of elementary transitions; these transitions can be written, and then analyzed, as inferential steps; processes can thus be described as derivations leading from a set of premises—the initial biochemical context triggering the reaction—to a final conclusion representing the biochemical aggregate produced by the process itself. The question whether a certain aggregate A can be actually obtained by making elements in $\varGamma$ react, is then reducible to the problem of the derivability of A from $\varGamma$.

The pathway-as-deduction paradigm has two main advantages over other discrete, merely descriptive, modelizations, in primis those based on Petri Nets. First of all, such approach makes the non-classical nature of biochemical transitions clearly emerge. All this brings many interesting new philosophical questions about the logical nature of context-sensitiveness, the relation between context-sensitiveness and non-monotonicity, and, more in general, about the specific logic governing molecular mechanisms.

Furthermore, using logic as a formal representation language allows us to properly address the problem of how extra-logical information should be treated in a way to permeate the standard logical apparatus and interact with the tautological background information. In this paper, the empirical information is accommodated via specific inference rules introducing the bonding operator ‘$\odot$’. Another possibility would be to directly introduce a cluster of new axioms as is the normal practice in formal theories of mathematics and physics. Which kind of strategy should be preferred over the other is a matter deserving further investigation.

Appendix: Zsyntax and SMBL: A Comparison

There are several formal languages trying to grasp the complexity of molecular biology, and some of them have been already the focus of a comparison with Zsyntax (see Boniolo et al. 2010). Here we wish to propose a comparison with the System Biology Markup Language (SMBL) (Hucka et al. 2003), that is a language allowing for the formal representation of the specific information involved in the model-based study of biological systems: reactants, concentrations, side conditions, reactions transforming molecular aggregates. In order to have a very first grasp on how the SMBL grammar deals with information of this sort, one can think of a state transition system made by a set of arrows formally connecting different states. Arrows are labelled with a package of parametrised conditions ${\mathscr {C}}$ to be met in order to produce $S_2$ from $S_1$. In a nutshell, a transition $S_1{\mathop {\longmapsto }\limits ^{{\mathscr {C}}}}S_2$ can be read in this way: if $S_1$ happens under conditions ${\mathscr {C}}$, then $S_2$ is delivered from $S_1$ (after a certain amount of time).

The SMBL formal grammar is general and basic enough to admit for a sound interpretation in terms of almost any kind of computational model for system biology. That is, biochemical models can be seen as possible interpretations for the SMBL language, interpretations in which the SMBL patterns of transition are satisfied. Let ${\mathscr {M}}$ and ${\mathscr {N}}$ be two computational models, S and $S'$ two states expressed in the SMBL language and $S{\mathop {\longmapsto }\limits ^{{\mathscr {C}}}}S'$ an SMBL transition. S constitutes a possible input for both ${\mathscr {M}}$ and ${\mathscr {N}}$ to the extent that ${\mathscr {M}}$ and ${\mathscr {N}}$ interpret S as a possible input: $S^{\mathscr {M}}$ is an input for ${\mathscr {M}}$ and $S^{\mathscr {N}}$ an input for ${\mathscr {N}}$. Usually, $S^{\mathscr {M}}$ and $S^{\mathscr {N}}$ are sets of differential equations. After due computations, ${\mathscr {M}}$ and ${\mathscr {N}}$ return their outputs $S_1^{\mathscr {M}}$ and $S_2^{\mathscr {N}}$, respectively. Now, $S_1^{\mathscr {M}}$ and $S_2^{\mathscr {N}}$ can be reported to the SMBL ground level and easily confronted by directly considering $S_1$, $S_2$ and $S'$.

Like SMBL, Zsyntax is designed as a formal language interpretable in the model-theoretic way just seen. However, Zsyntax proves something more than a mere formal language: it is a logic in which reactants are formulas and reactions are proofs. This is a remarkable qualitative leap for several reasons. First of all, it paves the way to a model-independent mathematical study of Zsyntax’s structural properties. Actually, proof theory is the branch of mathematical logic which specifically investigates the combinatorial properties of formal proofs without resorting to possible interpretations in other mathematical realms. As is well-known, via the Curry-Howard correspondence, logical proofs can be interpreted as computations in the typed $\lambda$-calculus. In a proofs-as-reactions setting, this very fact means that Zsyntax constitutes a computational model for itself, not only a formal grammar. Second, being a resource-sensitive logic, Zsyntax allows for the internal, logical treatment of both qualitative and quantitative (conveniently discretised) constraints that regulate biochemical state transitions. Last point, as shown in Boniolo et al. (2013), proofs in Zsyntax can be represented as graphs called proof-nets. This allows the user to fill the gap between intuitive diagrammatic representations and software oriented, much less user friendly, sequential notations.