Introduction

There is no doubt, as the philosopher C. S Peirce wrote, that (Peirce 1896): “Mathematics is the most abstract of all the sciences”. Then, if we were able to watch in a film the lives of famous mathematicians and statisticians like William T. Tutte (Younger 2012), John W. Tukey (McCullagh 2003), William S. Gosset (Boland 1984), Frances Chick Wood (Cole 2017), Harald Cramér (Blom 1987), William J. Youden (Eisenhart and Rosenblatt 1972), William R. M. H. Threlfall (O’Connor and Robertson 2000j), Floyd Burton Jones (O’Connor and Robertson 2000b), Itsván Fenyő (Paganoni 1988), Elliot W. Montroll (Weiss 1994), and Gordon T. Whyburn (Floyd and Jones 1971), and see that they spent their youth studying not mathematics, but chemistry, we possibly will cry: “What is a mathematician doing in a chemistry class?” All these remarkable mathematicians completed their B.Sc., and some their M.Sc. and even their Ph.D., in chemistry. But, also others like John Warner Backus (Bjørner 2008), George Edward Pelham Box (O’Connor and Robertson 2000c), Pao-Lu Hsu (Anderson et al. 1979), Kazimierz Kuratowski (Krasinkiewicz 1981), Gottfried Köthe (Weidmann 1990), Einar Hille (Dunford 1981), Rzsa Péter (O’Connor and Robertson 20000i), Hermann Amandus Schwarz (O’Connor and Robertson 2000d) and John von Neumann (Glimm et al. 2006; Bhattacharya 2021; Macrae 2019) started their university studies in chemistry, and some of them spent up to two years, before swapping to mathematics. Other great mathematicians have declared that they had fallen in love with chemistry and named this subject as their first preference before deciding to study mathematics.

All the surprise mainly comes from the fact that chemistry has always being seen as a practical science. Its own name derives from “alchemy”, which makes reference to a “set of practices” to transform basic elements and metals into other substances. The philosopher Immanuel Kant declared that (see McNulty 2014): “chemistry can be nothing more than a systematic art or experimental doctrine, but never a proper science, because its principles are merely empirical, and allow of no a priori presentation in intuition.” Nowadays, in spite of the growing importance of theoretical chemistry—including all its subdisciplines, such as quantum chemistry, mathematical chemistry, cheminformatics, chemometrics, etc.—chemistry is still a practical science. As remarked by the great theorist and Nobel Prize for Chemistry Roald Hoffmann (Hoffmann 2008): “Theoreticians are a minority in chemistry, which remains an experimental science.”

It seem at first sight that there could be nothing too antagonistic to each other than chemistry and mathematics. But the reality is that some of these great minds have studied chemistry and then have revolutionized fields like cryptography, statistics, topology, analysis, geometry, algebra, software development and others. Therefore, I argue here that there should be some motivational concepts and examples, some way of thinking in chemistry, which are relevant for the creativity of a mathematician. A chemistry student is confronted with the problem of deciphering the molecular structure encoded by nature in their chemicals, not too different as a code-breaker deciphers the information contained in a coded message. The repetitive analysis of the quantities of elements and compounds in samples of very different nature inspire statistically-oriented minds in the classes of analytical chemistry. The many structural possibilities of molecules in the three-dimensional space where they adopt so many topological shapes cannot escape the attention of geometers- and topologists-to-be. More importantly, the retroanalytic way of thinking of chemists, in which a molecular structure should be constructed from its building blocks, appeals more to the way in which mathematicians prove theorems than to the way in which others, like physicists, think. In this paper I describe some historic facts about the life of these mathematicians and statisticians. I speculate how they could be influenced in their further mathematical developments by what they learned in their chemistry days. My hope is that, mathematically-oriented minds, recognize that they can become professional mathematicians and statisticians even if they are currently sat in a chemistry class.

Methodology

The methodology followed in this work is the following. I first searched for the words “chemistry” and “chemist” at the MacTutor History of Mathematics Archive (O’Connor and Robertson 2000g). A list of mathematicians who have had any connection with chemistry was then collected. Every single mathematician in the list was checked for her implication with this matter and classified as: (i) those who completed a degree in chemistry or have worked as a chemist, (ii) those who studied chemistry for more than one year and then swapped to mathematics, and (iii) those who have stated some attraction by chemistry before studying mathematics. Then, I investigated the historic details provided by MacTutor about the claimed links and performed a bibliographic search for primary information corroborating and/or widening such information. The most relevant documented connections are the ones presented here. Therefore the list analyzed in this paper is not exhaustive.

The code-breakers

The first two actors in this play are William Thomas Tutte (1917–2002) (Younger 2012) and John Wilder Tukey (1915–2000) (McCullagh 2003). Apart from being contemporary, a priori, both mathematicians appear to be very distant in their fields of research. While Bill Tutte is well known for his many and important contributions in graph theory, Tukey is better known for his important contributions in statistics. To be more precise, in the period 1940–1949 Tutte published one fifth of all papers published in graph theory (Hobbs and Oxley 2004). His thesis published in 1948 with the title An Algebraic Theory of Graphs, was devoted to graphs and contains the first major contributions in the study of matroids. Accordingly, A. M. Hobbs and J. G. Oxley (Hobbs and Oxley 2004) state that Tutte “advanced graph theory from a subject with one text (D. König’s) toward its present extremely active state, and he developed Whitney’s definitions of a matroid into a substantial theory.” All in all, Tutte published 160 papers and 6 books [see electronic information at Younger (2012)] among which there are the famous Connectivity in Graphs (Tutte 1966a) first published in 1966, Introduction to the Theory of Matroids (Tutte 1966b) and Graph Theory as I have Known it (Tutte 1998) in 1998. Some of the mathematical concepts named after him are: Hannai-Tutte theorem, Tutte 12-cage, Tutte embedding, Tutte graph, Tutte homotopy theorem, Tutte matrix, Tutte polynomial, Tutte-Berge formula, Tutte-Coxeter graph, Tutte-Gothendieck invariant, Tutte’s 1-factor theorem, Tutte’s fragment, Tutte linking theorem, Tutte’s planarity criterion, Tutte’s triangle lemma, Tutte’s wheel theorem, all of them in graph theory.

On the other side of the coin we find Tukey (McCullagh 2003), who published his thesis in topology with the title On Denumerability in Topology. His further career was marked by his many contributions to exploratory data analysis, projection pursuit, and the invention of the Fast Fourier Transform (FFT) as well as of the box plot. His name is associated to: Tukey’s range test, Tukey \({\lambda }\) distribution, Tuckey-Duckworth test, Siegel-Tuckey test, Tuckey’s trimean, Tuckey’s lemma, Tuckey median, and several others in statistics. A complete list of his papers is found at (Beebe 2020).

The first mathematical paper published by Bill Tutte was entitled The dissection of rectangles into squares (Brooks et al. 1940), which appeared in 1940 together with R. L. Brooks, C. A. B. Smith and A. H. Stone. The paper deals with the problem of dividing a rectangle into a finite number of non-overlapping squares, no two of which are equal. It uses some graph theoretic concepts in the form of directed networks and connects with the electrical theory of networks and Kirchhoff’s law, which are nowadays active field of research in algebraic graph theory. Curiously, one of the authors of this paper, Arthur Harold Stone, published the paper Generalized “sandwich” theorems (Stone and Tukey 1942) with John Tukey in 1942. Therefore, Tutte and Tukey are separated only by one coauthor in the collaboration network of mathematicians. However, this is not the most interesting of their points of coincidence as they both: (i) studied Chemistry, and (ii) worked as code-breakers during the II World War (IIWW).

Tutte obtained his undergraduate degree in Chemistry with first-class honors in Cambridge University in 1938 (Younger 2012; Hobbs and Oxley 2004). Tuckey obtained a B.Sc. in Chemistry in 1936 at Brown, followed by a M. Sc. in Chemistry in 1937 at the same University (McCullagh 2003). It is well-known that Tutte was chosen to work at Bletchley Park (Younger 2012; Hobbs and Oxley 2004), where he arrived in May 1941 as a member of the Research Section. This section has been widely known through the legendary work made by Alan Turing with the German coding machine Enigma. However, the Germans also had the Lorenz cipher, codenamed “FISH” by the British (Tutte 2000). “Working from scratch, Tutte performed, with colleagues, a similar feat against Lorenz by deducing from signal traffic how it worked and how it was built–without ever having seen the machine itself, still less got his hands on a plan or drawing of it ” (van der Vat 2002). His work has been described as “the greatest intellectual feat of the whole war” (cited by Younger (2012)). Although the wartime information about the activities of Tukey is scarce, there are suggestions that he was also a code-breaker during and after WWII. For instance, W. O. Baker (cited by Brillinger (2002)) has affirmed that: “John was indeed active in the analysis of the Enigma system and then of course was part of our force in the fifties which did the really historic work on the Soviet codes as well. So he was very effective in that whole operation.”

There is a third point of coincidence in the careers of Tutte and Tukey which I would like to remark. It is their relation with a physical chemistry technique known as “spectroscopy” (Pavia et al. 2014). Spectroscopy, as any student of chemistry learns, refers to the study of the quantized interaction of electromagnetic radiations with matter. The techniques are then classified according to the region of the electromagnetic spectrum which is used for this interaction with atoms or molecules, e.g., visible, ultraviolet, infrared, X-rays, microwaves, etc. Bill Tutte started to do research in physical chemistry with Gordon Brims Black McIvor Sutherland (1907–1980), FRS 1949 (Sheppard 1982), on infrared spectroscopy. Gordon Sutherland is well-known for his major contributions to the “transformation of infrared spectroscopy from a research technique practiced in few laboratories into a powerful and widely used method for analysis and for the determination of molecular structure” (Sheppard 1982). This is one of the most powerful uses of spectroscopy in chemistry. It is a “machine” to decode information coded in the form of molecular structures. Tutte and Sutherland published a short letter in Nature entitled Absorption of polymolecular films in the infra-red (Sutherland and Tutte 1939). A year later, Bill Tutte collaborated with another spectroscopist at Cambridge, William Charles Price (1909–1993) (Dixon et al. 1997), elected FRS in 1959, this time on ultraviolet spectroscopy. This second collaboration was published in the article The absorption spectra of ethylene, deutero-ethylene and some alkyl-substituted ethylenes in the vacuum ultraviolet (Price and Tutte 1940). Bill Price was “a superb experimentalist, a formidable theorist and an extraordinary innovator” (Dixon et al. 1997) who was capable of building his own instruments, making his own measurements and developing his own theories to explain his results.

The many contributions of John Tukey to the analysis of spectra were reviewed by Brillinger in (2002). According to Brillinger the contributions of Tukey to spectroscopy cover the areas of methods, their properties, terminology, popularization, philosophy, applications and education. It seems that most of Tukey’s work on spectrum analysis remained unpublished until 1959 when he made his approach accessible to a wide audience. The impact of the Fast Fourier Transform developed by Cooley and Tukey in (1965) on spectroscopy can be categorized as a revolution, which nowadays is known as “Fourier-transform spectroscopy” (Griffiths and de Haseth 2008). In his collected works published in 1984 Tukey recognizes the importance of spectral analysis in his work by saying that (Jones 1986): “It is now clear to me that spectrum analysis, with its challenging combination of amplified difficulties and forcible attention to reality, has done more than any other area to develop my overall views of data analysis.”

How the knowledge of Tutte and Tukey on spectroscopy which they have learned during their studies could have influenced their work as code breakers? We possibly will never know, but I would like to speculate about it on the basis of the similarities of breaking information codes and the way in which spectroscopy is used in organic chemistry to “decipher” molecular structures.

On coding and decoding

An encrypted message is written by an encoder with the goal that it is interpreted by an appropriate receiver but not by possible interceptors. The discipline of encoding and decoding secret messages is cryptography, from kryptos, meaning hidden or secret in Greek, and graphia meaning writing in the same language. The forward process consists of encrypting a plaintext into a ciphertext or encrypted message to be sent to a receiver. The backward process, called decrypting or decoding the message, consists in turning the ciphertext into a readable plaintext, for which the receiver needs a code or key which allow her to decode the encrypted information. More formally, a cryptosystem is a five-tuple \((\mathscr {P},\mathscr {C},\mathscr {K},\mathscr {E},\mathscr {D})\) fulfilling the following conditions (Stinson 20005):

  1. 1.

    \(\mathscr {P}\) is a finite set of possible plaintexts;

  2. 2.

    \(\mathscr {C}\) is a finite set of possible ciphertexts;

  3. 3.

    \(\mathscr {K}\) is a finite set of possible keys;

  4. 4.

    For each \(K\in \mathscr {K}\) there is an encryption rule \(e_{K}\in \mathscr {E}\) and a corresponding decryption rule \(d_{K}\in \mathscr {D}\). Each \(e_{K}:\mathscr {P}\rightarrow \mathscr {C}\) and \(d_{K}:\mathscr {C}\rightarrow \mathscr {P}\) are functions such that \(d_{K}\left( e_{K}\left( x\right) \right) =x\) for every plaintext \(x\in \mathscr {P}\).

An interceptor of that message, who does not have the code or key to decipher it, needs to find a way to crack or break the code in order to know the content of the original message.

An example of encryption system is the famous Enigma machine used by the Germans during WWII to transmit coded messages [see Chapter 3 in Singh (1999)]. It uses a form of substitution encryption, but to make the codes more secure, the Enigma machine gives a mechanized way of performing one alphabetic substitution cipher after another. The machines used by German army also have a plugboard allowing for even more configuration possibilities, up to a total of 158,962,555,217,826,360,000 ones. Then, such codes are in principle unbreakable. However, as it used to be with most of systems of any kind, the structure of the system determines its function. As the molecular biologist Francis Crick once put it (Crick 1991): “If you want to know function, study structure”. One of these structural features, which can be seen as a weak point, is the fact that in the Enigma code a letter could never be encoded as itself. That is, an “A” will never appear as an “A” in the codes. Then, the codebreakers could guess a word or phrase that would probably appear in the message, such as a weather report, or the “Heil Hitler” at the end of the messages. By comparing a given phrase to the letters in the code, having in mind the impossibility that a letter could be encoded as itself, they could begin cracking the code with a process of elimination approach. The process can be made automatically, as Alan Turing and Gordon Welchman did with a machine called the Bombe. It was able to crack Enigma messages in less than 20 min by determining the settings of the rotors and the plugboard of the German machine. What is most important here, from my point of view, is this intuition based on the hidden principles of structure-function relations, that allowed code-breakers to start disentangling the information encoded in German messages.

The difficulties that Bill Tutte had to confront in deciphering the messages encoded by the Lorenz machine were even greater (Tutte 2000). This machine was used to encrypt communications between Hitler and his generals. It operates under the same principles than the Enigma machine but it was far more complicated. The process for code-breaking of Lorenz also started when John Tiltman and Bill Tutte discovered a weakness in the way in which this cipher was used. Thus, here again the intuition based on structure-function principles plays an important role. As it has been put forward by Singh (1999): “breaking the Lorenz cipher required a mixture of searching, matching, statistical analysis and careful judgment.”

Breaking molecular codes

Let us suppose that an organic chemistry teacher motivates her students by telling them the following story. We have received a mysterious parcel containing a white to very pale yellow crystalline powder, which is almost odorless. Our task is to decipher what is the molecular structure of this chemical substance, she said. In full analogy with cryptoanalysis we can consider that this problem consists on deciphering a cryptosystem \((\mathscr {P},\mathscr {C},\mathscr {K},\mathscr {E},\mathscr {D})\), where \(\mathscr {P}\) is the finite set of all molecular structures that can be formed with the chemical elements of the periodic table, \(\mathscr {C}\) is a finite set of possible physical and chemical properties that of this substance can display as a consequence of its molecular structure. There is at least one key \(K\in \mathscr {K}\) which is the one Nature has used to encrypt the chemical structure in the form of physical and chemical properties: \(e_{K}\in \mathscr {E}\), such that \(e_{K}:\mathscr {P}\rightarrow \mathscr {C}\). Then, our task is to interpret those physical and chemical properties to decipher the molecular structure: \(d_{K}:\mathscr {C}\rightarrow \mathscr {P}\) in a unique way.

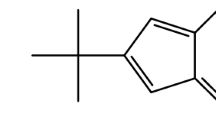
The first task in deciphering the molecular structure of a given substance is analogous to the frequency analysis for deciphering a monoalphabetic cipher. It is the determination of the chemical elements composing the substance, both qualitatively and quantitatively. In this case, Albert Szent-Gyorgyi (Grzybowski and Pietrzak 2013)—who was awarded the Nobel Prize for Medicine in 1937–determined experimentally in 1928 that the same substance contained in our parcel is formed only by three chemical elements, i.e., \(\mathscr {P}=\left\{ \text {C,H,O}\right\}\). He also determined the “frequency” with which these elements appeared in the corresponding substance: C(40.7%), H(4.7%) and O(54.6) (Szent-Györgyi 1928). Using the molecular weight, also determined by Szent-Gyorgyi, for this substance, \(178\pm 2\) g/mol, he arrives at the global molecular formula: C6H8O6. This information is equivalent to knowing the letters and their frequency in the corresponding ciphertext, but of course, the arrangement of these letters is what determines all the information in the message. With this global molecular formula and molecular weight (176.12 g/mol) we can build many different isomers, i.e., molecules with the same global formula but different molecular structures, such as the ones illustrated in Fig. 1. In this small sample of isomers we have acyclic structures (a and d), monocyclic ones (b, e and f), bicyclic (c), structures with a pentagon (b) and with an hexagon (e and f), acidic groups (a, e and f), alcohol groups (b, c, d, e), etc.

Fig. 1
figure 1

Examples of isomers with the global molecular formula C6H8O6 and molecular weight 176.12 g/mol

Full size image

Using a brute force strategy for determining which of all possible structures correspond to the one in question is in general a bad strategy. The reason is the same as for not using such strategy for deciphering substitution cipher codes: the combinatorial explosion of possible structures. Thus, chemists follow a rational strategy principled in the structure-function relations between a molecule and its properties. It combines the analysis of physical properties and chemical reactions to decipher the molecular structural code. We can said here that chemists follows a strategy or an algorithm for deciphering the code, in an exact analogy of what code breakers should do to decipher their codes. As put forward by chemist Henry Eyring (1901–1981): “The ingenuity and effective logic that enable chemists to determine complex molecular structures from the number of isomers, the reactivity of the molecule and of its fragments, the freezing point, the empirical formula, the molecular weight, etc., is one of the outstanding triumphs of the human mind” (Eyring 1963).

The students in the class of organic chemistry will then learn such “effective logic” to decode chemical structures (Hoffmann 2017). At this point the student can record the IR spectrum of the powder, obtaining the plot illustrated in Fig. 2. Her knowledge of IR spectroscopy allows her to determine that the strong bands at 3526, 3410, 3315, and 3216 correspond to stretching vibrations of OH groups typical of alcohols. Therefore, the structures (a) and (f) are immediately discarded because they contain acidic but not alcoholic OH. The strong band at 1764 corresponds to the stretching of C=O, particularly when it appears in a lactone structure like in (b) and (c). The very strong band at 1675 corresponds to C=C stretching when this group is in a ring (Panicker et al. 2006), which left only the structure (b) as the candidate to be the structure corresponding to the white powder. This structure is the one of Ascorbic Acid or vitamin C.

Fig. 2
figure 2

Infrared (IR) spectrum of a white powder under investigation in a chemistry lab. according to (Panicker et al. 2006)

Full size image

In a similar way as a code breaker who has cracked a code can infer the structure of the machine that has coded it, the chemistry student can ask fundamental questions about the coding-decoding process of this molecule. How and why Nature encoded the molecular structure of ascorbic acid in this way? Who is the receiver of this message? This certainly will introduce her into deeper knowledge in the frontiers of chemistry, biochemistry and molecular biology (Davies et al. 2007). What I think is undoubtful is the fact that a mathematician-to-be studying chemistry will find the determination of molecular structures as a challenging code breaking game. At the end of the day, the code breaker here is playing the decoding game not against an enemy of the same intellectual capacity as herself, but against the powerful Nature.

It could be thought that the process of decoding Nature’s encoded structures by a chemist is a relatively easy task. Nothing could be farther from the reality. To illustrate the complexities arising by the many (chemically meaningful) combinatorial possibilities in which a set of atoms can be grouped in a molecule, let me give the example of strychnine (for historic facts described here see Seeman and Tantillo (2020). Strychnine is an alkaloid known since XIX century. It has been known as a potent lethal weapon against small vertebrates such as birds and rodents, but which can also produce death through asphyxia in humans. The efforts for decoding the structure of strychnine started at the end of the XIX century with the works of the Swiss-born organic chemist Julius Tafel and ended up in 1947 with the structure determined by Robert Robinson. Although it was not until 1954 that the structure was obtained synthetically in a lab by R. B. Woodward, definitively confirming its molecular structure. More than 50 years of efforts and angry battles between different schools of chemistry. Up to 1950 the determination of the structure of strychnine saw the publication of 245 scientific papers, and involved luminaries like Herman Leuchs, father of the Leuchs reaction and the Leuchs anhydride, Vladimir Prelog, who was Nobel Prize in Chemistry in 1975, Robert Robinson, Nobel Prize in Chemistry in 1947, Heinrich Wieland, Nobel Prize in Chemistry in 1927, and R.B. Woodward, Nobel Prize in Chemistry in 1965. In Fig. 3 I illustrate some of the structures proposed between 1910 and 1947 by two of the main players in this career, Robinson and Woodward. The reader is left free to compare the efforts and time consumed to decipher the code of strychnine to those employed to decipher the codes of human encrypted messages.

Fig. 3
figure 3

Several of the proposals of Robinson and Woodward for the structure of strychnine in chronological order

Full size image

The statisticians

The statisticians William Sealy Gosset (1876–1937) (Boland 1984), Frances Chick Wood (1883–1919) (Cole 2017), Harald Cramèr (1893–1985) (Blom 1987) and William John Youden (1900–1971) (Eisenhart and Rosenblatt 1972) studied Chemistry as their major field. Additionally, George Edward Pelham Box (1919–2013) (O’Connor and Robertson 2000c) and Pao Lu Hsu (1910–1970) (Anderson et al. 1979) studied two years for a degree in Chemistry and then swapped to mathematical statistics. Box made his change as a consequence of the lack of reproducibility of his experiments with poison gas on animals at the British Army Engineers, and Hsu who has started his studies of chemistry at Yangjing University decided to change subject as well as university, and so he went to Tsing Hua University to read for a degree in mathematics. Box is mainly known for his results in quality control, time-series analysis, design of experiments and Bayesian inference. His name is associated with the Box-Jenkins method, Box-Cox transformation, Box-Cox distribution, Box-Pierce test, Box-Behnken design and the Liung-Box test. Hsu is known for his work in probability theory and statistics, where his name is for instance related to the Hsu–Robbins–Erdős theorem.

William S. Gosset, who is better known by his pseudonym “student”, “will be remembered primarily for his contributions to the development of modern statistics” (Boland 1984) [see also McMullen (1939) and Pearson (1939)]. He is better known for his invention of the so called (Student’s) t-distribution proposed in his paper The probable error of a mean (Student 1908). This paper has been qualified as (Zabell 2008): “truly remarkable for its richness. It simultaneously heralded the advent of small-sample distributional studies in statistics, used simulation in a serious way to investigate such distributions, and investigated the robustness of its results against modest departures from normality.” In total Gosset published 22 papers, 14 of them in Biometrika (Boland 1984). Wood, nee Chick, made important contributions to medical statistics, including topics such as “Real Wages in London”, “Index correlations”, “Mortality from Cancer”, “Cancer and Diabetes Death-rates”, among others which included the analysis of the cost of food during the outbreak of the First World War or a paper about the fertility of English middle classes (Cole 2017). She published in Journal of the Royal Statistical Society; Proceedings of the Royal Society of Medicine; Journal of Hygiene, among others. Cramèr was mathematician, statistician and actuary, specializing in mathematical statistics and probabilistic number theory. He has been called “one of the giants of statistical theory” (Zabell 1986). Cramér is well-known for the Cramér-Rao inequality, the Cramér-Wood theorem, the Cramér’s theorem on large deviations as well as for his books Mathematical Methods of Statistics (Cramér 1999) and Random Variables and Probability Distributions (Cramér 2004). He is also well known for his contributions to Insurance Mathematics. Finally, Youden (Eisenhart and Rosenblatt 1972) was a statistician known for his formulation of new techniques in statistical analysis and in design of experiments. Some examples of his works are the development of the “Youden square” which is an incomplete block design, introduced the concept of restricted randomization, and “Youden’s J statistic” devised as a simple measure summarizing the performance of a binary diagnostic test. He published in journals like Biometrics; Technometrics, among others (Hamada 2022).

When “student” published his remarkable 1908 paper he was not a statistician but a chemist. He had obtained a First-Class Degree in Chemistry in 1899 at Winchester College and New College, Oxford, U.K. (Boland 1984; Pearson 1939). At the time of his seminal paper he was employee of Arthur Guinness, Son & Co., Ltd. in Dublin, Ireland. For this reason it has been considered that publishing such paper was “a singular accomplishment, especially so given the limited formal background in mathematics and statistics that Student had” (Zabell 2008). On the other hand, “Chick” Wood started her academic life with a B.Sc. with Honours in Chemistry from the University College London in 1904 (Cole 2017). She then spent three years to research work in chemistry, first with Sir William Ramsay, a Scottish chemist who received the Nobel Prize in Chemistry in 1904 for his discovery of the noble gases, and then with Sir Arthur Harden, an English chemist who won the Nobel Prize in Chemistry in 1929 together with Hans von Euler-Chelpin for their investigations into the fermentation of sugar and fermentative enzymes. In this period “Chick” Wood published papers on experimental chemistry signing as Frances Chick (Chick and Wilsmore 1908, 1910; Chick 1912), before dedicating entirely to medical statistics. When Cramér started his career in 1912 at Stockholms Högskola, his main interests were both chemistry and mathematics (Blom 1987). However, he started his contributions on experimental biochemistry. In the years 1913–1914 Cramér was a research assistant under the famous chemist Hans von Euler-Chelpin (Nobel Prize for Chemistry in 1929) and they published five papers on experimental biochemistry: 2 in Zeitschrift für physiologische Chemie (now Biological Chemistry) and 3 in Biochemische Zeitschrift (now European Journal of Biochemistry) (see Blom (1987) for references). Then, in 1917 he complete his Ph. D. dissertation in mathematics (Cramér 1917), and continues his career as a mathematician. Youden entered Columbia University in September 1922 where he obtained first his Master’s Degree in 1923 and then his doctorate in 1924, both in chemistry (Eisenhart and Rosenblatt 1972; Hamada 2022). His Ph.D. thesis has the title: A new method for the gravimetric determination of zirconium, which covers an important and classical area of analytical chemistry.

Quantitative analysis: a matter of doses

Analytical chemistry is a branch of chemistry which deals with the separation, identification and quantification of matter (Skoog et al. 2013). The example illustrated in the previous section about the identification of the chemical structure of vitamin C corresponds to the area of qualitative research. However, the thesis of Youden (portrayed in the previous subsection) belongs to the area of quantitative analysis, which determines the numerical amount or concentration of a given chemical previously identified. The importance of quantification in analytical chemistry can be resumed in the quote of Paracelsus, a Swiss physician, alchemist, theologian and philosopher who lived between 1493–1494 and 1541, who is credited as the “father of toxicology” (Borzelleca 2000), when he said that “All things are poisons, for there is nothing without poisonous qualities. It is only the dose which makes a thing poison.”

Drinking a beverage containing methanol–known to produce decreased level of consciousness, poor or no coordination, vomiting, abdominal pain, and may produce blindness, kidney failure and death–, arsenic, hydrogen sulfide, furfural, 2,3-pentanedione, dimethyl sulfide, and many other chemicals known for their toxicity, seems to be a very bad idea. However, if we know that the beverage is formed by Buiatti (2009): 90–94% of water, followed by ethanol (ethylic alcohol) in about 3–5% v/v, that the concentration of methanol is only 0.5\(-\)3.0 mg/l, that all sulfur compounds are present in concentrations below 10 mg/l, and that arsenic is present at tiny concentrations below 0.05 mg/l, we can decide to drink it. Indeed, this beverage is beer, which reveals the importance of concentrations of chemicals in a given product to be healthy or not as it was remarked by Paracelsus.

Chemicals present in beer are derived from raw materials used in its fabrication, either passing unchanged through the brewing process or produced during the own process (Buiatti 2009). Beer is fabricated by using water, malts and its adjuncts, hops and yeast. Malt and hops are responsible for characteristic acidic, bitter, astringent, winey, malty, peppery, fruity, grainy, spicy, vinous, mouldy, woody, metallic flavors that can be detected in a beer, among many others that only experts can detect (Hough et al. 1982). However, hops and barley are agricultural products, which are subjects to many variables, some of them controllable, like the species of hops and barley used, or the region where they are grown, and others uncontrollable like the meteorological conditions of a particular season.

It is evident then that the quality control of these raw materials represents a major challenge for brewery industry. This was the major challenge encountered by Guinness company at the end of the XIX century when they expanded their production having to spend millions of imperial pounds in hops. At this point the traditional method of choosing hops by directly looking and smelling at it was unpractical and need to be replaced by the analysis of small samples of every lot. Thomas B. Case, Guinness’s first scientific brewer, started experiments to check the quality of hops from USA and from Kent in England [see Ziliak (2008) for historic events described in this paragraph]. The procedure consisted in analyzing the percentages of soft and hard resin in samples of 50 grams from the different lots. Case and his team found that the average of soft resin in 11 samples of Kent hops was 8.1%. Another team analyzed 14 samples from the same lot detecting 8.4%, which indicates a difference of 0.3 percentage points. The same analysis for the American hops produced differences of 0.7% for soft resin and 1.0% for the hard one. The question arising was: Are these differences “significant”? At the time of these experiments the answer was: “We could not... support the conclusion that there are no differences between pockets of the same lot.” This was due to the fact that there was not a statistical theory to make inferences from small samples like the ones analyzed at Guinness. In 1899 Guinness has hired a recently graduated chemist who has being also awarded a First in the Mathematical Moderations examination in 1897. The name of this fellow is William Sealy Gosset, who revolutionized the statistical analysis of small samples and other areas of statistics. Nowadays, a branch of analytical chemistry known as “chemometrics”, which deals with “the application of principles of measurement science and multivariate mathematics and statistics to efficiently extract maximum useful information from data” is used for the analysis of beers (Siebert 2001). No doubts that “student” is its father.

Similar situations can be confronted by any practitioner of quantitative methods of chemical analysis. Youden, according to Hamada (Hamada 2022), becomes frustrated for the impossibility of making comparisons with the existing “analyses” of the highly variable biological experimental data while working at the Boyce Thompson Institute for Plant Research (BTI) in Yonkers, NY. The seed of an applied statistician in Youden was already in his PhD thesis where, in 1924, he showed his knowledge about measurement and how to develop precise measurement methods. After his thesis he started to prepare himself as a statistician, first by studying Student’s 1908 paper, then by studying Fisher’s (1925) Statistical Methods for Research Workers and later attending in 1931, Hotelling’s mathematical statistics course taught at Columbia University in Manhattan, NY. In his 1931 paper with I. D. Dobroscky he already uses an experimental plan “that eliminates a source of error and further eliminates another source by differentiating the measurements” (Youden and Dobroscky 1931). As (Hamada 2022) has put it forward “Youden was an applied statistician. He was not a mathematical (theoretical) statistician. He invented a number of designs, but was not a combinatorial designer.” Among the scientists he had a reputation of “a statistician we can talk to” (Zelen 1971).

The topologists

One of the mathematicians which I have presented before, John Wilder Tukey (McCullagh 2003), also contributed to topology across his career and his name is associated to many terms in this field: Galois-Tuckey connections, Tuckey equivalence, Tuckey reducibility, the Tuckey theory of analytic ideals, Tuckey ordering and the Tuckey lemma, which already appeared in his Ph.D. thesis. He has said about topology that it “exists to provide methodology for large chunks of the rest of mathematics.” We have seen before that Tukey obtained his B.Sc. and M.Sc. in Chemistry. Similarly, the renowned topologists William Richard Maximilian Hugo Threlfall (1888–1949) (O’Connor and Robertson 2000j), Floyd Burton Jones (1910–1999) (O’Connor and Robertson 2000b), and Gordon Thomas Whyburn (1904–1969) (Floyd and Jones 1971) obtained their degrees in Chemistry. An interesting case was that of Kazimierz Kuratowski (1896–1980) (Krasinkiewicz 1981; O’Connor and Robertson 2000f), who is well-known for his contributions to the characterization of planar graphs (Kuratowski’s theorem), Kuratowski’s closure axioms, Knaster-Kuratowski fan, the development of homotopy in continuous functions, among other contributions in set theory and topology. Kuratowski studied engineering for a year at the University of Glasgow where he studied chemistry at the Technical College during the summer (O’Connor and Robertson 2000f). After the I World War he could not return to Scotland from his holidays in Poland, and then he swapped his studies to mathematics. In a similar vein I include here Gottfied Maria Hugo Köthe (1905–1989) (Weidmann 1990) who made important contributions to the study of topological vectors spaces, abstract algebra and functional analysis. He published the book: Topological vector spaces (Köthe and Köthe 1983). He studied Chemistry during two years at the University of Graz and then started studies in mathematics and philosophy due mainly to his fascination with epistemology.

Threlfall was well known for his contributions in algebraic topology. He is famous for his books Gruppenbilder published in 1932 and reviewed by Coxeter in (1934), Lehrbuch der Topologiewritten with his former student Herbert Seifert and published in 1934, reviewed by Whitehead (1934) and Variationsrechnung im grossen (Morsesche Theorie) also with Seifert, published in 1938 and also reviewed by Whitehead (1939). On the other hand, Floyd Burton Jones (O’Connor and Robertson 2000b) is known for his contributions to metrization of Moore space (after Robert Lee Moore, an American mathematician specialized in general topology) published in (Jones 1937), as well as for the concept of aposyndesis and its development as a theory published in (Jones 1941). Jones published in total 67 papers mainly in Proc. Amer. Math. Soc.; Bull. Amer. Math. Soc.; and Amer. J. Math. Whyburn’s work was mainly in the area of topology showing a great unity in the topics of his researches (Floyd and Jones 1971). He published a total of 149 scientific papers, mainly on the areas of: (i) Cyclic elements and the structure of continua; (ii) Regular convergence and monotone maps; (iii) Open maps; and (iv) Compact maps and quotient maps. His results were mainly published in Bull. Amer. Math. Soc.; Fund. Math; Trans. Amer. Math. Soc.; Amer. J. Math.

As advanced before these three topologists obtained their degrees in Chemistry. Threlfall graduated with a degree in chemistry in 1910 and then went to the University of Gottingen to study mathematics in the year 1911–12 (O’Connor and Robertson 2000j). Jones obtained his B. A. in Chemistry at the University of Texas, Austin, (O’Connor and Robertson 2000b) and Whyburn started his scientific career with an A. B. in chemistry in 1925 and then with a M.Sc. in Chemistry in 1926. This last, in spite of the insistence of Moore for him to move from chemistry to mathematics (Floyd and Jones 1971). This move finally took place naturally after his Master, as he was already doing high quality research in mathematics. A very curious fact is that after publishing 19 papers in pure mathematics, Jones published, together with J. R. Bailey, the paper The behavior of 2-phenyl semicarbazones upon oxidation, in the top chemistry journal Journal of the American Chemical Society (Whyburn and Bailey 1928). This paper is entirely dedicated to experimental organic chemistry, which is apparently very far from topology. Bailey was an organic chemist who studied under such eminent German chemists as Friedrich Thiele, developer of many laboratory techniques to isolate organic compounds, Adolf von Baeyer, Nobel Prize in Chemistry of 1905 for his contributions to the synthesis of organic dyes and hydroaromatic compounds, and Wilhelm Ostwald, Nobel Prize in Chemistry in 1909 for his work on catalysis, chemical equilibrium and reaction velocities, and in London under William Ramsay, which has been already mentioned here.

Organic molecules topologies

From the very initial courses of organic chemistry a student learns about the non-flat structures of many organic molecules, whose structures are projected in stereochemical forms in the three-dimensional space (Robinson 2000). But, until relatively recently, most of the organic molecules with which a chemist was confronted could be “deformed” into a plane (see Flapan 2000). This is the case of a tetrahedron, which although it is a three-dimensional figure, can easily draw in the plane without the intersection of any line. It is easy to associate a graph \(G=\left( V,E\right)\) to every molecule, such that every atom is represented by a node \(v\in V\) of the graph and every covalent bond corresponds with an edge \(\left\{ v,w\right\} \in E\) of the graph. This representation possibly starts with the pioneering works of mathematicians Arthur Cayley (1821–1895) and James Sylvester (1814–1897) (Rouvray 1989; Griffith 1964). In a short note published in Nature (Sylvester 1878a), Sylvester describes his 1878’s paper in the American Journal of Mathematics (Sylvester 1878b), by expressing that “Every invariant and covariant thus becomes expressible by a graph precisely identical with the Kekuléan diagram or chemicograph”. Hermann Weyl (1885–1955) recognized the importance of Sylvester work in the Appendix D of his essay Philosphy of Mathematics and Natural Science (Weyl 1949) when he stated that “We can see today that only such radical departure as that of quantum mechanics could reveal the significance of the picture that Sylvester had stumbled upon as a purely formal, though very appealing, mathematical analogy”. Although Weyl advices us not to “take too literally such preliminary combinatorial schemes”, we should recognize that it is only this graph-molecule correspondence what allow us to say that a molecule is planar if its graph can be drawn in the plane in such a way that pairs of edges intersect only at vertices, if at all. If the molecule has no such representation, it is called nonplanar. It was Kazimierz Kuratowski who proved in 1930 in the paper Sur le problème des courbes gauches en topologie (Kuratowski 1930), the mathematical conditions for a graph to be planar. The theorem basically states that a graph is planar if and only if it contains no subdivision of \(K_{5}\) (complete graph of 5 nodes) or \(K_{3,3}\) (complete bipartite graph with 3 nodes in each partition). A subdivision of an edge in a graph is a substitution of the edge by a path. A graph H is a subdivision of G if H can be obtained from G by a finite sequence of subdivisions.

I can imagine that many chemistry students with a topology-oriented way of thinking could have had in mind molecules that escape from planar-land. But is was not until 1981 when the groups of H. Simons (Simmons and Maggio 1981) and L. A. Paquette (Paquette and Vazeux 1981) synthesized independently the molecule illustrated in Fig. 4 which is homeomorphic to \(K_{5}\). To see it I have drawn the molecule in the right panel of Fig. 4 by coloring the 5 nodes of \(K_{5}\) in red. Then, the reader can see that there is a subdivided edge connecting every pair of red nodes, where each subdivision contains two gray nodes. Therefore, the Simmons-Paquette molecule is topologically nonplanar according to the Kuratowski theorem as it is homeomorphic to \(K_{5}\).

Fig. 4
figure 4

Structure of the Simmons-Paquette molecule (left), a graph-theoretic representation (center) and its representation as a subdivision of the graph \(K_{5}\)

Full size image

What about \(K_{3,3}\)? It took more time, but in 1995 Chao-Tsen Chen et al. synthesized the “Kuratowski Cyclophane” (Chen et al. 1996) which is illustrated in Fig. 5a.

Fig. 5
figure 5

a “Kuratowski Cyclophane” obtained by Chao-Tsen Chen et al. in (1996). b Graph representation of the “Kuratowski Cyclophane” as a subdivision of the \(K_{3,3}\) graph. The nodes marked in red and blue correspond to the benzene rings with the same colors in panel (a)

Full size image

To see it as \(K_{3,3}\) just think about every blue hexagon as one of the three vertices in one of the two partitions, and the three red ones in the other partition. Then, notice that every blue is connected to every red, and vice versa. Now, chemists and topologists can be equally happy to say that there are nonplanar molecules out there waiting for interesting applications (see Fig. 5b).

Once chemists have identified the structure of a molecule they need to describe it. This description includes information about the order in which given numbers of specific atoms are joined, the type of bonds which connect these atoms and some information about the spatial arrangement formed by groups of atoms. But, in 1961 the chemists H. L. Frisch and E. Wasserman (Frisch and Wasserman 1961) called the attention of the chemical community about the fact that such information may not be enough for describing molecular structures. In some cases, “topology” also plays a role. This is, according to their own example, the case of cycloalkanes (also known as cycloparaffins), which every chemistry student finds in the first course of organic chemistry. In this case the typical cyclic chain of \(C_{n}H_{2n}\) atoms in the form of a circle can alternate with a “knotted” one, when \(n\ge 50\). Then, the two compounds are “topological isomers” or “topoisomers”. By the end of 1970s and beginning of 1980s, trefoil knots were discovered in both single- and double-stranded DNA [see Forgan et al. (2011) and references therein]. By mid 1980s highly complex knotted DNA architectures, including composite knots, had been reported, enriching the field coined as “Biochemical Topology”.

In 1989 Christiane O. Dietrich-Buchecker and Jean-Pierre Sauvage (Dietrich-Buchecker and Sauvage 1989) synthesized in the lab a trefoil knot whose structure is illustrated in Fig. 6. Further synthetic procedures allowed to obtain other symmetric knotted systems like “Solomon Link” and “Borromean Rings” (Forgan et al. 2011). In 2020, a Nature paper announced the synthesis of three topoisomers of the same molecular framework. They correspond to the unknotted macrocycle (\(0_{1}\)), a trefoil (\(3_{1}\)) knot, and a three-twist (\(5_{2}\)) knot (Leigh et al. 2020). What else a topology-oriented mind needs to trigger its interest? Maybe some carbon “fuel”.

Fig. 6
figure 6

a The molecular trefoil knot synthesized by Dietrich-Buchecker and Sauvage (Dietrich-Buchecker and Sauvage 1989) and b its representation. Representation of the \(5_{2}\) knot, a topoisomer synthesized by Leigh et al. in (2020)

Full size image

The many “shapes” of carbon

In any introductory course of Inorganic Chemistry, a chemistry student learns about the concept of allotrope, which are the different structural modifications of a chemical element. In old courses and textbooks of inorganic chemistry it is mentioned that carbon has two allotropes: diamond and graphite (see Tiwari et al. 2016). The main structural difference between diamond and graphite is that the first forms a three dimensional structure in which every carbon has four nearest neighbors, while graphite is formed by a system of hexagonal layers one on top of the other. In the first, carbon is bonded through single C-C bonds, and in the second through alternate single and double C=C bonds.

A student with a topology-oriented mind could imagine other topological arrangements of carbon atoms which would be potential allotropes of this element. This was what Eiji Osawa did in 1970, when he published (in Japanese) the work: “Superaromaticity” in Kagaku (Kyoto) 1970, 25, 854–863. There, he imagined a truncated icosahedron of 60 atoms of carbons. The structure is formed by twenty hexagons and twelve pentagons with symmetry \(I_{h}\), exactly as the form of a soccer ball. This molecule existed only in Osawa’s imagination until 1985 when Harry Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl, and R. E. Smalley, published the paper C60: buckminsterfullerene (Kroto et al. 1985) announcing the discovery of the exact molecule that Osawa had imagined 15 years before. Unfortunately, the authors of the Nature paper were unaware of Osawa’s paper until 1986 (Boyd and Slanina 2001; Curl et al. 2001). A less imaginative approach was to consider the individual layers of graphite as simple molecules, which was theorized for decades, but prepared only in 2004 and coined “graphene” (Geim 2009). It was observed by the first time supported on metal surfaces in 1962, and finally isolated and characterized in 2004 by Andre Geim, Novoselov et al. (2004) (see central figure in Fig. 7).

Continuing with the topologically-oriented minds I would like to mention that in 1991 A. L. Mackay and H. Terrones (Mackay and Terrones 1991) proposed the structures of triply periodic minimal surfaces (TPMS) as possible carbon allotropes. The proposal of Mackay and Terrones consisted in taking the TPMS studied by Karl Herman Amandus Schwarz (1843–1921) in 1890 and “decorate” them with graphite mesh in which some hexagons are strategically replaced by octagons to avoid tensions in the structure. They considered two structures proposed by Schwarz and denoted them as P- and D-surfaces. In 1992 Thomas Lenosky et al. (1992) studied the hypothetical carbon allotropes with TPMS structures and proposed that these structures were named “schwarzite” “partly in anticipation of their likely color but mainly to honor the mathematician H. A. Schwarz”. The letter of Mackay and Terrones in Nature ends with the sentence (Mackay and Terrones 1991): “we find that a variety of ordered graphite foams look quite possible. The question is how to synthesize them.” The synthesis of schwarzites was a very elusive task. In several experiments it was observed that there were local regions with negative Gaussian curvature in amorphous carbon, but not the long-range ordering required to assign them the periodic nets that describe TPMSs. We had to wait until 2018 in which Braun et al. (2018) were able to obtain in the lab carbon materials with nonpositive Gaussian curvature that resemble TPMSs (see right figure in Fig. 7). We now have carbon allotropes of positive (fullerene), zero (graphene) and negative (swartzite) curvature.

Fig. 7
figure 7

Examples of carbon allotropes with positive (fullerene), zero (graphene) and negative (schwarzites) curvature

Full size image

But carbon is a box of surprises! Apart from diamond, graphite, fullerene, single and multi-layer graphene and schwarzites, it can also appears in many different topological structures, such as single-walled carbon nanotubes, toroidal forms or nanorings, nanocorns, nanohorns, peapods, nanoribbons, among others. We can characterize these structures by some of their topological invariants, such as the genus and the Euler characteristic (after mathematician Leonhard Euler, 1707–1783), as it is shown in Fig. 8, resumed by (Gupta and Saxena 2014).

Fig. 8
figure 8

Topological characteristics of a few carbon allotropes. Gently provided by Gupta and Saxena (2014)

Full size image

Carbon can also form triple bonds, C\(\equiv\)C. Thus, E. Estrada and Y. Simón-Manso (Estrada and Simón-Manso 2012) theorized about belt-shaped carbon allotropes alternating single, double and triple bonds, which form Möbius bands. They were coined “Escherines” in honor to the artist M. C. Escher (see Fig. 9). These structures remain constrained to the world of human imagination yet, but they can jump to the real-world at any time. Thus, carbon allotropes offer a fascinating world for introducing topological and geometric concepts not only in chemistry but also in mathematics.

Fig. 9
figure 9

Map of the electrostatic potential surface on \(C_{60}\) Möbius Escheryne (Estrada and Simón-Manso 2012)

Full size image

In search of beauty

The search for beauty has been in the own essence of doing mathematics. Godfrey Harold Hardy wrote that (Hardy 1992) “The mathematician’s patterns, like those of the painter’s or the poet’s, must be beautiful”. In a more general context Henri Poincaré (Poincaré 1890) claimed that “Le savant digne de ce nom, le géomètre surtout, éprouve en face de son oeuvre la même impression que l’artiste; sa jouissance est aussi grande et de même nature”, which is frequently translated as (Johnson and Steinerberger 2019) “A scientist worthy of the name, above all a mathematician, experiences in his work the same impression as an artist; his pleasure is as great and of the same nature”. In the same lines Bertrand Russell (Russell 2013) emphasized that “The pure mathematician, like the musician, is a free creator of his world of ordered beauty.” A chemistry student also confronts beauty in many different ways. As Nobel prize winner Roald Hoffmann has affirmed (Hoffmann 2003): “The human beings who are drawn to chemistry, in both its analytical and synthetic parts, construct compounds and meaning. And imbue the substances, and the little pictograms we draw of them, with intimations of beauty. Why? Because building a pleasurable rationale for hard labor is a psychological necessity. And because we naturally seek beauty, as we seek good. At least that matches Kant.”

Then, I would like to speculate that many of the following great mathematicians of all times, who were also captivated by chemistry at some point of their lives, were searchers of the “world of ordered beauty”. At the end of the day, as Samuel G. B. Johnson and Stefan Steinerberger (Johnson and Steinerberger 2019) pointed out, “It is not a surprising claim that the search for beauty, both in theorems and in proofs, is one of the great pleasures of engaging with mathematics.” I will present a brief list of these mathematicians who have loved chemistry at some point of their careers in an alphabetic order. The list is not exhaustive, but it serves to give an empirical proof of the role that chemistry may have played in their mathematical careers.

Emil Artin (1898–1962) was an Austrian mathematician considered as one of the leading mathematicians of the twentieth century. He significantly contributed to algebraic number theory, in particular to class field theory and the construction of L-functions. He was the recipient of the Ackermann–Teubner Memorial Award in 1932. Chemistry was also the subject which Artin did show more talent for, and which attracted him the most (Brauer 1967). He studied mathematics and chemistry at the University of Leipzig (Zassenhaus 1964). He continued to have love for chemistry along his life. Sir Michael Atiyah (1929–2019) a British-Lebanese mathematician specializing in geometry and known, among other things, for the Atiyah-Singer index and the Atiyah-Segal completion theorem. He was awarded the Fields Medal in 1966 and the Abel Prize in 2004. Atiyah has said that when he was 15, he was very much interested in chemistry and took a whole year course in this field (Minio 1984). He was disappointed by the amount of facts needed to memorize in inorganic chemistry, but reckon that organic chemistry was more interesting as it has more structure (cited in O’Connor and Robertson (2000h)). John Warner Backus (1924–2007) is renowned for the development of FORTRAN. He started to study chemistry at the University of Virginia but changed to mathematics due to the fact that he enjoyed the theory of chemistry but disliked the lab work (Bjørner 2008). Itsván Fenyő (1917–1987) (Paganoni 1988) was an Hungarian mathematician making significant contributions to diverse areas of mathematics, such as analysis, algebra and integral equations. He was Editor of prestigious mathematics journals like Aequationes Mathematicae and of Zeitschrift für Analysis und ihre Anwendungen and was the author of several books. In 1942 he obtained the Diploma in Chemistry. Three years later he changed his field to mathematics with his thesis On the theory of mean values (in Hungarian). In 1951 he wrote the book Mathematics for chemists (in Hungarian) with György Alexits (a Hungarian mathematician), then translated to German as Mathematik für Chemiker in 1962, and to French as Les méthodes mathématiques en chimie in 1969. Alfréd Haar (1885–1933) (Szökefalvi-Nagy 1985; O’Connor and Robertson 2000a), was a Hungarian mathematician whose thesis was supervised by David Hilbert and that contributed to orthogonal systems of functions, singular integrals, analytic functions, differential equations, set theory, function approximation and calculus of variations. His name is attached to the Haar measure, Haar wavelet, and Haar transform. Haar also felt that it was chemistry his preferred subject at the Gymnasium, although he also did outstanding work in mathematics. Paul Richard Halmos (1916–2006) was a Hungarian-Jewish-born American mathematician. He is well-known for his fundamental contributions to mathematical logic, probability theory, statistics, operator theory, ergodic theory, and functional analysis (in particular, Hilbert spaces). At the age of fifteen he entered the University of Illinois to study chemical engineering (Albers 1982). However, after the first year he became disappointed due to the experimental work in chemistry, so he changed to mathematics and philosophy. Carl Einar Hille (1894–1980) (Dunford 1981) was an American mathematician who made important contributions to functional analysis, semigroup theory and the study of ordinary differential equations. He authored or co-authored 12 books on semigroup theory, functional analysis, differential equations and analytic function theory. He studied chemistry for 2 years where he was taught by von Euler-Chelpin, who has been mentioned before in this paper. They published Uber die Primare Umwandlumg der Hexosen bei der alkoholischen Garung, Z. Gârungsphysiologie 3 (1913), 235–240. Hille then swapped to mathematics, graduating in 1913 with his first degree in mathematics in 1913 and the equivalent of a Master’s degree in the following year. Elliot Waters Montroll (1916–1983) (Weiss 1994) was an American mathematician known for his contributions to continuous-time random walk analysis and traffic flow analysis. He published papers on a variety of topics which cover apart from several areas of statistical mechanics, crystalline solids, Bessel functions, traffic dynamics, social dynamics, and sociotechnical systems to mention just a few. Montroll received a B.S. degree in Chemistry in 1937. In 1939–1940 he carried out research in the Chemistry Department of Columbia University. He obtained his Ph.D. in Mathematics in 1939 from the University of Pittsburgh. However, after completing his Ph.D. Montroll spent three years of postdoctoral studies with three chemistry luminaries: Joseph Edward Mayer who developed the cluster expansion method and Mayer-McMillan solution theory, Lars Onsager (Nobel Prize in Chemistry, 1968) and John Gamble Kirkwood (American Chemical Society Award in Pure Chemistry and Langmuir Award both in 1936). John Forbes Nash Jr. (1928–2015) (O’Connor and Robertson 2000e), an American mathematician who contributed significantly to game theory, differential geometry, and the study of partial differential equations. He was awarded the John von Neumann Theory Prize in 1978, the Nobel Prize in Economic Sciences in 1994 and the Abel Prize in 2015. Chemistry was the favorite topic of Nash when he entered at Bluefield College in 1941 where he took mathematics and sciences courses. He liked so much chemistry that he conducted his own chemistry experiments. Rózsa Péter (1905–1977) (O’Connor and Robertson 20000i) was a Hungarian mathematician and logician, who is known as the ”founding mother of recursion theory”. She was the author of the books Playing with Infinity: Mathematical Explorations and Excursions, Dover Publications, 1971, which has been translated into at least 14 languages, and Recursive Functions in Computer Theory, Halsted Press New York, NY, USA, 1982. Péter started to study chemistry at the Pázmány Péter University (renamed Loránd Eötvös University in 1950) in Budapest. Then she changed to mathematics under the influence of the lectures of Lipót Fejér. Jean-Pierre Serre (1926–), a French mathematician who has made contributions to algebraic topology, algebraic geometry, and algebraic number theory. He was awarded the Fields Medal in 1954 and the Abel Prize in 2003. Serre enjoyed very much chemistry although he never took interest in physics. At 15–16 he was engulfed into chemistry books that his father, a pharmacist, had (Chong and Leong 1986). Karl Hermann Amandus Schwarz (1843–1921) (O’Connor and Robertson 2000) was a German mathematician, known for his contributions in complex analysis. His name appears in the additive Schwarz method, Schwarzian derivative, Schwarz minimal surface, Schwarz integral formula, Schwarz alternating method, Schwarz-Christoffel mapping, Schwarz triangle, and the Cauchy-Schwarz inequality. Schwarz started his studies at the Gewerbeinstitut, later called the Technical University of Berlin, not in mathematics but in chemistry. Then, after the influence of Ernst Eduard Kummer (January 29, 1810–May 14, 1893) and Karl Theodor Wilhelm Weierstrass (October 31, 1815–February 19, 1897) he swapped to mathematics and obtained his Ph.D. under the supervision of Weierstrass in1864. John von Neumann (Glimm et al. 2006; Bhattacharya 2021; Macrae 2019)(1903–1957) was a Hungarian-American mathematician, known for his many contributions in a wide variety of areas. These include, for instance, contributions to mathematical logic, measure theory, functional analysis, ergodic theory, group theory, operator algebras, matrix theory, geometry, and numerical analysis, but he is also known for his contributions to physics, particularly to quantum mechanics, quantum statistical mechanics, nuclear physics among others. The polymath character of von Neumann is very much manifested by the fact that he also made important contributions to computer sciences, statistics and economics. von Neumann studied chemistry for two years at the University of Berlin, from 1921 to 1923. Then, he moved to Zürich where he received his diploma in chemical engineering from the Technische Hochschule in 1926. An anecdote described in (Bhattacharya 2021) tells that when people asked him if he had come to Berlin to study math, he answered: “No, I already know mathematics. I’ve come here to learn chemistry.”

Conclusions

“The complexities of modern science and modern society have created a need for scientific generalists, for men trained in many fields of science.” This is a paradigm of science in the XXI century, where the advent of such fields like the study of complex systems requires multidisciplinary approaches. But the previous phrase was not written in the XXI century. It is the starting sentence in The education of a scientific generalist” published in Science in 1949 (Bode et al. 1949). The authors of this paper include John Wiley Tukey, who has been portrayed in this paper, as well as the eminent statistician Frederick Mosteller (1916–2006), the engineer, inventor and scientist Hendrik Bode (1905–1982) and engineer, physiologist and biostatistician Charles Winsor (1895–1951). What is extraordinary of the proposals in this paper is that of proposing to use “the methods of description and model-construction which, in the individual sciences, have made the partial syntheses we call organic chemistry, sensory psychology, and cultural anthropology” as a remedy for these complexities in education and in science. They claimed that using such approaches “eventually, one can learn science, and not sciences.”

The specific mention of organic chemistry as a necessary training for a scientific generalist is not only well ahead of its time, but even ahead of modern times. The authors ask “What is the logical framework of organic chemistry? Or equivalently, what are the characteristic ways in which a good organic chemist thinks and works?” I want to briefly explore an answer to this question in the context of the current work. Particularly, I would like to explore: What should be in common in the ways of thinking of an organic chemist and of a mathematician? To start with, I would remark that an organic chemist hardly starts her work by mixing up chemicals to see what they can produce. Namely, she has “in mind” a molecule that she wants to synthesize, a “synthetic target”. Then, she retrosynthetically thinks on how to obtain such a molecule from some known or imagined precursors. This process could give rise to a sequence of molecules, some of which exist and some need to be prepared by the chemist. In other words, as put forward by Evan Hepler-Smith, organic chemist “thinks backwards” (Hepler-Smith 2018). In his Nobel prize speech Elias James Corey defined retrosynthetic analysis as (Corey 1991) “a problem-solving technique for transforming the structure of a synthetic target molecule to a sequence of progressively simpler structures along a pathway which ultimately leads to simple or commercially available starting materials for a chemical synthesis.” The process of analyzing retrosynthetically the possible routes for synthesizing a molecule involves the gedankenexperiments (thought experiments), known by chemists as “paper chemistry”, where they discuss possibilities or ideas or hypotheses used for the preparation of the synthesis of a given target. As Seeman (2018) has pointed out, chemists are involved in such paper chemistry “perhaps on a chalk board or white board and on the back of an envelope or dinner placemat or autograph book”, so much that “apparently is not recognized by historians and philosophers of science for its ubiquity.” Mathematicians work in a similar way. They start from a hypothesis that they want to prove and try “retroanalytically” to connect it with other mathematical facts, some of which are known and others that they need to prove. Here we have considered the analogies between code-breaking in cryptography and structure determination in chemistry. A chemist cannot be completely sure that the structure she has proposed for a given molecule is the correct one until such a molecule has been synthesized (with the corresponding rethrosynthetic analysis performed) and the two structures coincide. This is the equivalent in mathematics of the verification process to check for the correctness of the proof of a given theorem.

Another coincident way of thinking between an organic chemist and a mathematician is about the importance that patterns play in their research. Chemist searches for patterns in the physical properties of the molecule under study, in its chemical reactivity, in the way that groups and motifs can be glued together, etc. Mathematics has been defined as the science of patterns. Thus, mathematicians search for “numerical patterns, patterns of shape, patterns of motion, patterns of behavior, voting patterns in a population, patterns of repeating chance events, and so on” (Byers 2010). Once a pattern is identified either in chemistry or in mathematics, the researcher can proceed to the clarification of the systematic rule which is behind that pattern. This is evident in the analogy used here between code-breaking and structure elucidation. This attachment to patterns makes both chemists and mathematicians very prone to the use of pictures. An organic chemist hardly can say anything about the chemical reactivity (or any physical or chemical property) of a molecule from its exact quantum-mechanical Hamiltonian. However, she will construct a complete narrative about the physical and chemical properties of a molecular structure drawn in a piece of paper, even if such a molecule is completely imagined. The power of pictures in mathematics is discussed in the book Mathematics and the Unexpected by Ivar Ekeland (1990) where its value is recognized as fundamental in the early stages of the development of mathematical ideas. This also introduces a very important analogy among chemists and mathematicians. Namely, that they use a proper language in their respective fields. While physicists use the mathematical language in their investigations, chemists use the sophisticated language of chemical formulas and specific symbols to represent charges, rearrangements, partial equilibria, etc. These “invented” languages mainly appear only in Chemistry and in Mathematics, making them unique intellectual activities.

There are a few other important connections between the way of thinking of (organic) chemists and mathematicians which could have played a role in the development of the mathematical way of thinking of some of the remarkable mathematicians portrayed here. I will leave it to others for exploring more deeply such connections with the mind not only in the past but also on the education of future generations as it was the preoccupation in: The education of a scientific generalist (Bode et al. 1949).