Abstract
Group 3 as Sc–Y–La, rather than Sc–Y–Lu, dominates the literature. The history of this situation, including involvement by the IUPAC, is summarised. I step back from the minutiae of physical, chemical, and electronic properties and explore considerations of regularity and symmetry, natural kinds, and quantum mechanics, finding these to be inconclusive. Continuing the theme, a series of ten interlocking arguments, in the context of a chemistry-based periodic table, are presented in support of lanthanum in Group 3. In so doing, I seek to demonstrate a new way of thinking about this matter. The last of my ten arguments is recast as a twenty-word categorical philosophical (viewpoint-based) statement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Scope
My focus is intended to be philosophical or systematic rather than descriptive or theoretical. Along the way some more detailed ancillary arguments will be encountered where I feel these are required to provide context, are novel, or provide useful insights.
Arguments in support of lutetium in Group 3 have been summarised by Scerri and Parsons (2018); Scerri (2020a, pp. 392–403); and Scerri (2020b). Landau and Lifshitz (1958, pp. 256–257) argued for group 3 membership of Lu on the basis of its complete 4f subshell. Scerri (2015, pers. comm., 9 December) referred to this as “one of the oldest categorical statements in favor of Sc Y Lu Lr”. Please refer to the Appendix to this paper for a commentary.
I mention some recent arguments, in passing.
Stewart (2018a, p. 117) observed that an argument for lutetium in Group 3 was that the pth element in the f-block series, with the exception of Gd, has p (for place) f-electrons. In contrast, Wulfsberg (2006, p. 3) opined that:
…valence electron configurations of atoms and ions are also important in predicting the periodicity of chemical properties. Since ions are more important than isolated gaseous atoms for nearly all atoms, and important ions have no anomalous electron configurations, there is little reason to worry students with anomalous electron configurations of atoms: we prefer to teach ‘characteristic’ electron configurations without anomalies in the occupancies of d- and s-orbitals in the transition elements or d-, s-, and f- orbitals in the inner transition elements.
Thus, with lanthanum in Group 3, the number of f-electrons in the trivalent cations of the f-block elements corresponds perfectly with their position in that block. The series starts with Ce3+ as [Xe]4f1 and concludes with Yb3+ [Xe]4f13 and Lu3+ [Xe]4f14.
Tsimmerman and Boyce (2019) argued for lutetium in Group 3 on the basis of the regularity of spin multiplicity, which is one of the three components of an element’s spectrographic term symbol. Unfortunately this argument introduces an anomaly in the overall regularity of term symbols.
Alvarez (2020) supports lutetium on the basis of trends in atomic size, coordination number, and relative abundance of metal–oxygen bonds. However, the trends involved apply regardless of whether lutetium is under Y or at the end of the f-block, after Yb.
Other than to provide necessary context, I will not further revisit lutetium in Group 3 arguments.
Contents
PART A: History, philosophy, audience | PART B: The domain of chemistry |
Historical background Modern background The role of the IUPAC Physical, chemical, and electronic properties: Inconclusive(?) A philosophical approach Natural kinds Regularity and symmetry Quantum mechanics Audience: Chemical, pedagogic, and designer periodic tables | I The periodic law II Predominant differentiating electrons III Immediate neighbours of Group 3 IV Horizontal triads V Isodiagonality VI Monocations of Sc-La, Lu VII Nature of the rare earths: Sc, Y and the Ln VIII The lanthanoid or f-block contraction IX f-block integrity X Most important electronic orbitals |
PART C: Bringing the threads together | PART D: End matter |
A new Group 3 philosophy Conclusion Pictorial representation | Notes Acknowledgements Appendix: Landau and Lifshitz (1958), a redux References |
PART A: History, philosophy, audience
Historical background
Lanthanum was discovered in 1839. Mendeleev published his first periodic table in 1869. Lanthanum subsequently came to be associated with Group 3, along with scandium and yttrium (Thyssen and Binnemans 2011, p. 36).
Lutetium was not discovered until 1907. Like lanthanum, it was regarded as one of the rare earth metals, these being a grouping of 14–16 (depending on the author) metals that also came to be associated with Group 3.
In 1925, Goldschmidt proposed the name “lanthanide” for the elements cerium to lutetium, in reference to the similarity of their properties to lanthanum.
Early spectroscopic work on lanthanum and the lanthanoids determined the ground state electron configuration of lanthanum was [Xe]d1s2 and seemed to indicate that the following lanthanoids (cerium to lutetium) had, with few exceptions, an electronic configuration of the form [Xe]f = 1–14, d1s2. So cerium, as the first lanthanoid was [Ce]f1d1s2; ytterbium, as the penultimate lanthanoid, was thought to be [Xe]f13d1s2; and lutetium, as the last lanthanoid, [Xe]f14d1s2.
Thus, lanthanum, like scandium and yttrium, had a d- differentiating electron whereas lutetium had an f- differentiating electron. Here the differentiating electron is the electron that distinguishes an element from its predecessor. For example, the differentiating electron of Z = 21 scandium [Ar]3d14s2 is a d-electron since the configuration of Z = 20 calcium is [Ar]4s2.1 It thereby seemed that the position of lanthanum under yttrium, and lutetium as the last of the lanthanoids, was settled.2
Meggers and Scribner (1937) subsequently determined that most of the lanthanoids were in fact f = 1–14, s2. Only cerium, gadolinium, and lutetium also had a d-electron. And it turned out that ytterbium was f14s2 i.e. the 4f subshell was completed over the course of 13 rather than 14 elements, a little bit like the 3d subshell of the first row of the transition metals being filled over the course of nine rather than ten elements.
Lanthanum and lutetium thereby each had a d- differentiating electron and, ostensibly, an equal claim to the periodic table position under yttrium, in Group 3.
The views of the spectroscopists were not helpful. Frye (1949, p. 4) wrote: “Lanthanum, the first member of the series, has no 4f-electrons and is not considered a rare earth by some spectroscopists.” And from Collier’s Encyclopedia (1958):
Lanthanum, 57, is excluded by spectroscopists because it has no electron in the fourth shell and, therefore, has a markedly different spectrum from that shown by the other members of the group. Lutetium, 71, is sometimes excluded from the rare earth group because its fourth shell is filled completely. Elements 57 and 71 are, however, usually included by chemists because the chemical behaviour of these elements makes them typical rare earths.
In this context; the fact that nothing had changed with regard to the chemistry of lutetium; and that the physicists were content to leave the periodic table to the chemists, lanthanum kept its position under yttrium, and lutetium stayed at the end of the lanthanoids, never mind that the 4f subshell closed at ytterbium rather than lutetium.
A few tables of the 1920s and 30s showed lutetium under yttrium for reasons of regularity (Janet’s left step table, Fig. 9) or because lutetium occurred in the “yttrium” separation group (along with scandium and yttrium) rather than the “cerium” group (which included lanthanum). But this never took off.3
In terms of chemical separation behaviour, that scandium, yttrium and lutetium occurred in the so-called yttrium group, and that lanthanum occurred in the “cerium” group did not imply anything particularly significant; it is simply a reflection of the increasing basicity of these elements as atomic radius increases. Taking the alkaline earth metals as another example, magnesium (less basic) belongs in the “soluble group” and calcium, strontium and barium (more basic) occur in the “ammonium carbonate group”. Moving lutetium under yttrium because they occur in the same chemical separation group failed to consider separation group patterns elsewhere in the periodic table.
Further, the separation group behaviour of yttrium can be ambiguous, and scandium, yttrium, and lanthanum appear to show complexation behaviour different to that of lutetium. As observed by Vickery (1960, p. 37):
In separating yttrium from the heavy lanthanoids, advantage is always taken of the phenomenon by which yttrium sometimes assumes characteristics similar to those of the light lanthanoids, and sometimes follows the heavy lanthanoids in behaviour.
Over a decade later Vickery (1973, p. 344) observed that:
Polymerization of the yttrium ion has been shown now to account for its apparently nomadic behaviour in earlier classical separation techniques. Evidence is also available for the existence of lanthanum hydroxy-polymers in solution. There is, indeed, to be seen an interesting sequence through…Group III in this respect. Hydroxyl bridged polymerization has been shown for aluminium, scandium, yttrium, and lanthanum ions, but does not appear to exist with the series Ce3+ → Lu3+. On the other hand, gallium, indium and thallium do appear to complex in this fashion. On a thermodynamic basis, ionic hydration—or hydroxo complex formation—may depend upon free energy rather than enthalpy and plots of such free energy link the pre-lanthanon triad more closely to aluminium, on the one hand, and gallium, etc., on the other, than to the lanthanoid group of elements.
The chemists who kept lanthanum under yttrium were on the mark, chemically speaking.
In 1982, Jensen published an article in the Journal of Chemical Education re-examining the composition of Group 3 and asserting that lutetium should be under yttrium, rather than lanthanum. While this sparked a mini-revival of interest in the composition of Group 3, his arguments did not gain traction.
Modern background
The IUPAC (2015) recently established a task group to address the question of precisely which elements should be placed in Group 3 of the periodic table. The question has been debated from time to time with no resolution. The remit of the task group is to deliver a recommendation in favour of the composition of Group 3 of the periodic table as consisting either of the elements:
-
1.
Scandium, yttrium, lutetium and lawrencium, or
-
2.
Scandium, yttrium, lanthanum and actinium.4
The impetus for the task group was that students and instructors are typically puzzled by the fact that published periodic tables vary in the way Group 3 of the periodic table is displayed. A survey reported by the task force, of 193 chemistry books published during the 1970s to the 2010s, found that 130 books (67%) had Group 3 as Sc–Y–La–Ac; 33 (17%) as Sc–Y-*-**; and 30 (16%) as Sc–Y–Lu–Lr. The project further notes the question is of considerable importance for chemists and physicists, but does not elaborate.
The role of the IUPAC
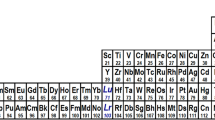
The periodic table appearing on the IUPAC web site (Fig. 1) depicts the first two elements of Group 3 as being scandium and yttrium. Below the box for yttrium is found one box for the lanthanoids and below that one box for the actinoids. The lanthanoids and actinoids then appear as a 15-element wide “f-block” positioned below the main body of the table. If this table is presented in a 32-column form it is not clear which elements are supposed to appear below yttrium.
The “IUPAC Periodic Table” is neither a recommended nor approved periodic table. This is not made very clear in the preface to their Red Book (Connelly et al. 2005):
That on the inside front cover is the current IUPAC-agreed version.
That is to say, the subject table (Fig. 1) is agreed within IUPAC only (Leigh 2009).
Nor does IUPAC prescribe which elements, for example hydrogen and helium, belong in which group. All they have done is approve collective names for like elements e.g. chalcogens (oxygen, selenium, selenium, tellurium, polonium) and noble gases (helium, neon, argon, krypton, xenon, radon) (Connelly et al. 2005, p. 61). For example, if helium is placed over beryllium then helium still belongs to the noble gases.
Why then would IUPAC be interested in prescribing which element goes under yttrium when, depending on the circumstances, either lanthanum or lutetium could be suitable? For example, in electronic structure terms, lanthanum has the advantage of incumbency, since the 5d1 electron appears for the first time in its structure whereas it appears for the third time in lutetium, having already made a brief appearance in gadolinium (Trifonov 1970, pp. 201–202). On the other hand, lutetium may be a better choice if crystallography is the focus, since the crystalline structures of scandium, yttrium, and lutetium are all hexagonal close packed whereas that of lanthanum is double hexagonal close packed. As another example of the flexibility of group assignments, Group 14 in the Earth Scientist’s periodic table is composed of carbon, silicon, titanium, zirconium, and hafnium rather than the standard set of carbon, silicon, germanium, tin, and lead (Railsback 2018).
The current confusion for students and teachers as to why the IUPAC table has a 15-element wide f-block, whereas other authors show lanthanum or lutetium under yttrium and an associated 14-element wide f-block, arises from a lack of IUPAC guidance along the lines of the previous paragraph, rather than because it has not formed a view as to the composition of Group 3.
Such guidance could read, for example, as follows:
Draft IUPAC Red Book guidance
ELEMENTS IN THE PERIODIC TABLE
The periodic table on the insider cover is the form agreed and used within the IUPAC, rather than being IUPAC recommended or approved. In this instance, the lanthanoids are shown as a 15-element wide series in light of their chemical similarities.
Different forms of the periodic table may be more or less appropriate in particular contexts. For example, a 14-element wide lanthanoid series may be more appropriate to better bring out the concept of an f-block. Such a series could start with, for example, lanthanum or cerium depending on the context.
IUPAC does not recommend or approve any particular format of periodic table or system, nor does it mandate the composition of Groups.
That said, let us consider the composition of Group 3.
Physical, chemical, and electronic properties: Inconclusive(?)
As long ago as 1929 Hevesy (cited in Trifonov 1970, p. 188) observed that:
If scandium, yttrium, lanthanum and actinium are the only rare-earth elements, the series would have revealed the same gradual change in properties as the calcium, strontium, barium and radium series, and hence it would not have been of any special interest.
The question of the composition of Group 3 has been debated from time to time on the basis of physical (including spectroscopic), chemical, and electronic properties and trends, without resolution.
Scerri (2020a, p. 381) opined, and I agree, that the matter cannot be resolved using this rubric, since the two options are effectively indistinguishable. Figures 2–7 compare the two options across six properties. Sometimes there is no difference; sometimes Group 3 looks better as –La–Ac; sometimes it looks better as –Lu–Lr.6 Dozens of these charts can be compiled noting lawrencium would present a challenge since many predicted values would have to used. The end result is that it is not possible to practically distinguish between the two options of Sc–Y–La–Ac and Sc–Y–Lu–Lr.7
Figure 2 shows that a Z plot of the density values for Sc, Y, La, Lu, Ac and Lr follows a smooth trendline.
Figure 3 shows that a Z plot of first ionization energy values follows a smooth trendline.
Figure 4 shows that a Z plot of the 6-coordinate ionic radii for the subject elements bifurcates after Y into an –La–Ac tranche (R2 = 0.99) and a –Lu–Lr tranche (0.61). The trendline for –La–Ac is smoother.8
Figure 5 shows a Z plot of 3rd ionisation energy values bifurcating after Y into a –Lu–Lr tranche (R2 = 0.83) and a –La–Ac tranche (0.98). The trendline for –La–Ac is smoother.
Figure 6 shows that a Z plot of melting points bifurcates after Y into an –Lu–Lr (R2 = 0.72) tranche and a –La–Ac (0.71) tranche. While the fit values for the two options are comparable, –Lu–Lr is preferred since Y and La show a greater departure from trend.9
Figure 7 has a Z plot of electron affinity values bifurcating after Y into an –La–Ac tranche (R2 = 0.85) and a –Lu–Lr tranche (0.99).10 The trendline supports Lu–Lr.
The trendlines, by themselves, are inconclusive: two show no difference; two support –La–Ac; two support –Lu–Lr.
A philosophical approach
A further option is to step back from the minutiae of physical, chemical, and electronic properties and trends and take a philosophical approach. Such an approach seeks to understand if there is a fundamental structure or theory of physics underlying the organisation of the periodic table. If so, this may provide a perspective on Group 3.
Regularity and symmetry; natural kinds (“carving Nature at its joints”)11; and quantum mechanics have been inconclusively explored to this end.
Natural kinds
A natural kind is a part of the furniture of reality that reflects divisions in the world (“Nature carved at its joints”) that can be considered to exist independently of human classification practices. Examples of natural kinds include electrons, iron, and cats; non-examples are tables and sewing machines (Martinich and Stroll 2007, p. 113). Another conception is that a kind is natural if it corresponds to a grouping or ordering that does not depend on humans (Hjørland et al. 2011).
The periodic table is considered by many authors to be a perfect illustration of how things in the world are divided into natural kinds. For instance, knowing that something is hydrogen gas allows us to infer that it will spontaneously react with chlorine and fluorine at room temperatures, thus forming potentially hazardous acid anhydrides.
In this vein, it could be argued that the placement of elements into Groups is not a matter of convention (Scerri 2020a, p. 388). If periodic relationships are objective rather than subjective this would seem to imply there is one optimal periodic classification regardless of whether or not it had been discovered. There ought therefore be a fundamental truth as to the composition of Group 3.
An emerging view of natural kinds is that they cannot exist as mind-independent reality. Natural kinds are instead held to be useful and evolving scientific facts and concepts, rather than representing the unchanging structure of truth and reality. So, for instance, phlogiston was a natural kind in eighteenth-century chemistry, even though today we do not consider it as such. This changeability is characteristic of natural kinds and we should not, it has been argued, consider stable categories as more natural than others.
Scerri now contends that:
The realization that classification in general, and the specification of natural kinds, is not a purely ontological question forces us to confront the fact that seeking an objectively optimal periodic table is rather futile. We should accept that a degree of convention must be used in selecting a periodic table that can be presented as perhaps the best possible table that combines objective factors as well as interest dependence.
He goes on to recommend lutetium in Group 3 on the basis that it avoids a split d-block in the 32-column form and that it shows a periodic table with blocks having column widths consistent with the requirements of quantum mechanics (Fig. 8; Scerri 2020b, p. 4).
While Fig. 8 still splits the first row of the s-block, and goes as far as locating helium, an s-block element, in the p-block, several arguments have been put forward for this arrangement (for example, Kurushkin 2020). Equally, a referee for the article you are now reading observed that helium over beryllium requires a lot humour.
Regularity and symmetry
Scerri (2008, p. 57) has argued for lutetium under yttrium (and helium over beryllium), since the periodic table can then be arranged, from a philosophical point of view,12 so that it shows the greatest degree of regularity and symmetry. Such a table may better reflect the regularity of the periodic law. He cites as an example, the left-step or Janet periodic table (Fig. 9). Such a table facilitates a regular array of vertical triads (Fig. 10), in which the middle element of the triad has an atomic number that is the average of those of the first and third elements. Scerri does not support lanthanum under yttrium since, in a 32-column table, and on the basis of regularity and symmetry, this once again results in awkward split d-block (Fig. 11).13
His argument remains inconclusive as there is no basis to regard regularity or symmetry as fundamental requirements (Scerri 2004, p. 149; 2019, p. 385). Stewart (2018b, p. 75) observed that, “Triads are a consequence of the structure of the system and cannot at the same time be its cause.” Scerri (2020a, pp. 387, 401) acknowledges that we should be aware of arguments based on regularity or symmetry. Jensen (2019), whose 1982 article in the Journal of Chemical Education kicked off the debate on the composition of Group 3, recently attacked the relevance of [vertical] triads.
Curiously, as discussed later in this article, increasing regularity in the shape of the periodic table increases the number of irregularities amongst various other properties and relationships across the table.14 Indeed, as Imyanitov (2016, pp. 153–154) observed:
If one seeks for the maximum chemical utility…[one] should opt for the more ‘unruly’ tables. If one seeks maximum elegance and orderliness above all…[one] should favor the more regular representations.
The obsession of the Greeks with the concept of symmetry retarded progress in astronomy for at least 1500 years (Yang 1996, p. 271). They perpetuated the idea of the Harmony of the Spheres and the Dogma of the Circles. According to these works, the heavenly bodies must observe the most symmetrical rules, and the circle and the sphere are the most symmetrical forms. But the heavenly bodies do not make simple circular motions. So they tried to fit their motions with circular ones superposed on circular ones. When that did not work either, they tried circular ones on circular ones on circular ones, and so on.
The first time I saw a 32-column table with a split d-block (Fig. 11) I thought it must have been “wrong” since it appeared so awkward; I later came to realise that I’d subconsciously adopted the Western cultural obsession with symmetry.15 Jensen earlier referred to the abuse of (Platonic) symmetry considerations in the construction and interpretation of periodic tables in general, including to the extent of triumphing over the inconvenient facts of chemistry (Jensen 1986, passim; 2003, pp. 953–954).
An emerging field of thought is the importance of symmetry breaking,16 rather than pure symmetry:
…symmetries matter, largely because we like to see them broken sometimes: the laws, particles and forces of physics all have their roots in symmetry-breaking. They create what David Gross of the Kavli Institute for Theoretical Physics at the University of California, Santa Barbara, calls the “texture of the world”. These considerations have led Florian Goertz at the Max Planck Institute for Particle and Astroparticle Physics in Heidelberg to propose the existence of a new particle that is single-handedly capable of cleaning up five of the stickiest problems in physics. “Complete symmetry is boring,” says Goertz. “If symmetry is slightly broken, interesting things can happen.” (Brooks 2018, p. 30)17
As Eugen Schwarz (2019, pers. comm., 8 Dec) stated, “The real, rich pattern of elements’ chemistry does not fit into a clear-cut rectangular grid.” This view is consistent with that of Dias (2004, p. 375), who asserted that:
A periodic table is defined as a partially ordered [italics added] set forming a two-dimensional array which complies with the triad principle where any central element has some metric property that is the arithmetic mean of two flanking [i.e. horizontal] member elements.18,19
In this vein, Mendeleev used horizontal triads when he predicted the properties of the then undiscovered elements scandium, gallium, and germanium. He discussed his technique using the horizontal triad arsenic-selenium-bromine to estimate the atomic weight of selenium (Scerri 2008, pp. 585–589).
A high degree of orderliness, and explanatory power, can nevertheless be found in Rossotti’s (1998) split d-block periodic table template (Fig. 12).
Rossotti shows where each subshell starts; how the lanthanoids and actinoids are interpositioned between Groups 2 and 4 and, in this instance, the electron configuration make-up of gadolinium and its predecessor, europium. Here, the lanthanoids run from cerium to lutetium; and the actinoids from thorium to lawrencium.20
The split d-block is thus integrated into the overall design of the table.
Quantum mechanics21
In quantum mechanics, the aufbau principle (German Aufbauprinzip, “building-up principle”) uses a simple numerical rule to describe the sequence in which orbitals are filled. This is known as the Madelung rule, after physicist Erwin Madelung, who (among others) formalized it in the 1930s. The sequence is straightforward for the first three rows of the periodic table (in which elements have only s- and p-orbitals). The 3p orbitals fill from aluminium to argon. But things get complicated in the fourth row. The 4s orbital fills next, for potassium and calcium. But then the transition elements appear. The additional electron in the next element, scandium, doesn’t go into 4p, but into 3d. Hence, transition metals are also known as d-block elements. The Madelung rule accommodates these non-intuitive steps, such that electron occupancy of 4s precedes that of 3d, and 4p is occupied before 5s. But the Madelung rule has not yet been derived from quantum mechanics or other fundamental physical principles.
Worse, there are about 20 elements whose electron structures do not follow the Madelung rule. Some philosophers of science have argued that this points to a failure of quantum mechanics to explain the periodic table (Scerri 2019, p. 558).
In 1969, on the 100th anniversary of the periodic table, physicist Per-Olov Löwdin declared this derivation to be one of chemistry’s major theoretical challenges. It still is, fifty years on although the jury remains undecided as to whether a deep dive into quantum mechanics might reveal a fundamental explanation of the Madelung rule, or a new way of thinking about it (Scerri 2019, p. 559).
Scerri and Parsons (2018, pp. 146, 150–151) attempted to resolve the Group 3 question by relying, in part, on an argument incorporating aspects of quantum mechanics. Unfortunately, their argument did not do the job they had initially hoped for (Eric Scerri, pers. comm., 14 Feb 2020).
More recently, Labarca and Gonzalez (2019) argued that quantum mechanics is inconclusive(!) when it comes to the Group 3 question. They may have been echoing Christie and Christie (2000, p. 42) who argued that, “chemistry rests much more strongly on its…foundations of the 19th century and earlier, and much less on the insights of modern quantum physics.”
Audience: chemical, pedagogic, and designer periodic tables
…there’s no reason to think one table can capture the whole picture. ‘This notion of periodicity was so important for chemistry when the periodic table was first put forward and in the subsequent decades to make sense of this chaos of elements,’…But today it should be more of a rule of thumb rather than a law of nature…there’s room for more than one periodic table: ‘Chemistry is about compromise.’ (Lemonick 2019)
No categorical argument addressing the composition of Group has been presented to date. As Poliakoff (2011) said:
In the end, I think that one should remember that Mendeleev devised the PT for a textbook to help rationalize the mass of facts in inorganic chemistry…For me, the PT remains a tool to help reduce the complexity, not a metaphysical truth that has a correct form yet to be discovered.
Rather than seeking a definitive answer to the Group 3 question we can give a contextual response. Scerri suggested there is a continuum-like series of periodic tables, with those of a more chemistry-orientated bent towards one end of the series and those relying more on philosophy- or physics-informed aspects at the other (Scerri 2020a, p. 402–403). At the chemistry end of the series, for example, can be found Rayner-Canham’s “unruly” inorganic chemist’s periodic table, which focuses on best representing the chemical relationships among the elements (Fig. 13). At the other end can be found the left step or Janet periodic table, which Scerri refers to as the Platonic form (Fig. 9). Scerri further described the chemistry-based tables as being less symmetric whereas those at the other end of the continuum were more symmetric and abstract (Scerri 2012a, p. 334).
The inorganic chemist’s periodic table, designed by Rayner-Canham and Overton (2003). Shadings denote (n) and (n +10) relationships (grey); diagonal relationships (green); knight’s move relationships (tan); aluminium-iron link (red); lanthanoid-actinoid relationships (grey), combination elements (violet); psuedoelements (blue) (Colour version online)
Cao et al. (2019) introduced a classification of periodic tables as chemical, pedagogic, or designer. The notion of a chemical table is analogous to Scerri’s idea of a chemistry-end to his continuum of periodic tables. A pedagogic table is one that has been simplified for teaching purposes. A designer table focuses on other matters including aesthetic considerations and the external shape of a periodic table. It corresponds more with Scerri’s idea of a philosophical or physics-based end to his continuum.
The basic idea is that the particular context will determine the periodic table that represents better practice for that purpose, at the time in question. I have used the term “better practice” rather than “best practice” to further emphasise the time- and place-limited nature of the latter.
The notion of a continuum of periodic tables or systems is powerful since it preserves the utility of different periodic representations and enrichens an appreciation of the vast array of the quantitative and qualitative properties of the elements, and the relationships between them. There is no categorical table or system that could “best” capture this situation since what may be better for one or more purposes will be a poor cousin for others. That is the nature of chemistry, significant parts of which are qualitative rather than quantitative. A better chemist is able to hold these different perspectives in their head, and recognise they all have value depending on the context, rather than insisting there is one correct answer. As noted, it is a question of the right tool for the job rather than one size fits all.22
PART B: The domain of chemistry
…it helps to remember that, when all is said and done, the periodic table remains primarily in the domain of chemistry, although the relationship between chemistry and the underlying explanation from physics remains as the underlying theme… (Scerri 2020a, p. ix).23
If the context is chemistry, as one would expect for the IUPAC, the composition of Group 3 can largely be addressed from a perspective external to Group 3 rather than on the individual physical, chemical, or electronic properties of lanthanum or lutetium.
A related consideration is that the internal structure and external shape of a chemical periodic table is determined by chemical facts rather than considerations of regularity, beauty or symmetry (Cao et al. 2019, p. 26, passim). Here, the use of multiple considerations to triangulate a solution is consistent with the role of classification science, as well as the premise that “Classes are usually defined by more than two attributes…” (Jones 2010, p. 169). In other words, in the absence of a categorical solution we are obliged to use quantitative or qualitative arguments to establish a solution.24
My arguments are presented as an interlocking progression of concepts and relationships.
I | The periodic law |
II | Predominant differentiating electrons |
III | Immediate neighbours of Group 3 |
IV | Horizontal triads |
V | Isodiagonality |
VI | Monocations of Sc–La, Lu |
VII | Nature of the rare earths: Sc, Y and the Ln |
VIII | The lanthanoid or f-block contraction |
IX | f-block integrity |
X | Most important electronic orbitals |
I start with the periodic law25 and how its application can be used to discern a periodic table with a block-like structure. The relationship of Group 3 with its neighbours (immediate, horizontal, and diagonal) is examined. At this point I briefly note some reactions of the monocations of scandium, yttrium, lanthanum, and lutetium. Extending my perspective, I survey how the Group 3 question impacts the presentation of the rare earths namely scandium, yttrium, and the lanthanoids. The nature of the f-block is considered having regard to the f- electron induced lanthanoid contraction, and double periodicity.
I conclude with a discussion of the most important electronic orbitals in a chemical sense and how these address the Group 3 question in a philosophical context.
I. Periodic law
The periodic law implies, ceteris paribus, that since lanthanum represents the first recurrence of comparable periodicity after yttrium it should be the one to go under yttrium rather than lutetium.26 Another way of expressing this is that lanthanum represents the first occurrence of a 5d electron, gadolinium the second, and lutetium the third, and that there is no case for skipping lanthanum in favour of lutetium. In terms of condensed phase configurations, lanthanum represents the first occurrence of a 5d electron and lutetium the thirteenth. There is no prima facie case for skipping lanthanum in favour of lutetium.
II. Differentiating electrons
“…for the purpose of selecting an optimal periodic table we prefer to consider block membership as a global property in which we focus on the predominant differentiating electron.” (Scerri and Parsons 2018, p. 151).
Arguments concerning the composition of Group 3 are sometime based on spectroscopic gas phase electron configurations.
In this context, as noted, the differentiating electron is the electron that distinguishes an element from its predecessor. Differentiating electrons are relevant from a chemistry perspective since they enable the periodic table to be parsed into four major blocks according to the predominant differentiating electron in each block, and each block shows distinctive physical and chemical properties (Stewart 2018a, p. 118).27
From this perspective a 32-column table with an intact d-block is quantitatively less homogenous than a split d-block table. By this I mean a periodic table with Sc–Y–Lu–Lr, and helium over neon, has 13 differentiating electron discrepancies whereas a table with Sc–Y–La–Ac, and helium over neon, has 12 (Table 1).28
For example, manganese [Ar] 3d54s2 is located in the d-block yet has an s- differentiating electron since the previous element chromium is [Ar] 3d54s1. If lanthanum [Xe]5d16s2 is placed in Group 3, which is in the d-block, there is no discrepancy since the previous element is barium [Xe]5 s2 whereas lanthanum becomes a discrepancy if it is placed in the f-block since it has a d- differentiating electron.
Two related considerations dealing with outer electrons and the term symbols of the elements mitigate against Group 3 as Sc–Y–Lu–Lr. Placing lanthanum and actinium in the f-block would be the only case where a pair of elements that belong in the same column are placed such that they have no outer electrons in common with that block (and at its start, at that). Spectroscopically,29 an Sc–Y–La–Ac table has one less term symbol discrepancy than is the case with an Sc–Y–Lu–Lr table (Table 2).30 Thus, in a –Lu–Lr table the term symbols for lanthanum, cerium, and actinium to neptunium, and lawrencium are anomalous whereas in an –La–Ac table this is only the case for cerium, thorium to neptunium, lutetium and lawrencium.
The presence of an anomalous electron in an incomplete subshell does not always result in an anomalous spectroscopic term symbol. For example, in Group 9, the incomplete subshell configurations of cobalt, rhodium and iridium are 3d7, 4d85s1, and 5d7. Despite the anomalous configuration of rhodium, all three elements have an 4F9/2 term symbol.
III. Immediate neighbours
Chemically similar groups should be close together, either as vertical groups or horizontal triads, with links between related elements clearly visible. (Scerri 2004, p. 138)
While the two basic options for the composition of Group 3 cannot be distinguished on individual physical, chemical, or electronic grounds they can be distinguished according to their external environment i.e. their immediate neighbours. In a split d-block table Group 3 is adjacent to Groups 1–2 (Fig. 11). In a “no-split” table Group 3 is adjacent to Groups 4–11 (Fig. 14).
The chemical behaviour of Group 3 generally resembles that of Groups 1–2 rather than that of Groups 4–11. While Groups 1–3 feature a predominately ionic chemistry, Groups 4–5, for example, exhibit predominately covalent behaviour (Greenwood and Earnshaw 1998, pp. 948, 958).31,32
“For chemists…the most important feature of an element is its pattern of chemical behaviour, in particular, its tendency toward covalent bond formation (or its preference for cation formation).” |
Rayner-Canham G and Overton T In Descriptive Inorganic Chemistry (2010, p. 29) |
Further, Group 4 is the first group in which the really characteristic transition metal properties of coloured compounds, multiple oxidation states, and paramagnetism are commonly seen (courtesy of the chemistry of Ti3+). It is additionally pertinent to note that the impact of the lanthanoid contraction (discussed elsewhere in this article), and as mainly caused by the filling of the 4f-subshell from cerium to lutetium, is “never more pronounced” than in Group 4 (Greenwood and Earnshaw 1998, pp. 957–958). Finally, Group 4 is the first to show the characteristic phenomena of variable valance, combined with a trend of “compounds of higher valence number…[becoming] increasingly more stable in any family with increasing atomic number.” The contrary trend is observed in the p-block (Fernelius 1986, p. 265).
It follows that Group 3 is better placed next to Groups 1–2, with the result that elements of like chemistry are more closely grouped together.
Showing Group 3 split from Groups 4–12 is consistent with Moeller (1973, p. 3) who observed that:
There is…a closer configurational similarity between the lanthanoid ions and the Group Ia–IIIa cations than between the lanthanoid ions and the d- transition metal ions. The presence of shielded 4f electrons in the lanthanoid ions does not materially alter the noble-gas core that they present to incoming chemical groups.
King (1995, p. 289) picks up the theme:
…lanthanoid chemistry is predominately the chemistry of highly electropositive metals in the +3 oxidation state, just as the chemistry of the alkali metals and alkaline earth metals is the chemistry of the highly electropositive metals in the +1 and +2 states, respectively. For this reason, the chemistry of the lanthanoids is conveniently discussed in the same book as the chemistry of the alkali and alkaline earth metals.
The resulting split d-block has two highly uneven portions and the external shape of the table becomes irregular but these are not fundamental considerations from a chemical perspective. An analogous uneven distribution occurs with Groups 1–2, and 12–18, which become spatially separated by Groups 3–11, although this is not as extreme. Here, Groups 1–2 and 12–18, from a chemical point of view, effectively form a joint “sp-” block of elements (Cao et al. 2019, p. 5). In structural terms, the larger and more energetic s- and p-block orbitals provide the framework for the periodic table, which is internally perturbed by the smaller d- and f-orbitals (Allen and Knight 2003).
In contrast, a 32-column table with an intact d-block (in which scandium and yttrium are above lutetium and lawrencium) has as its fundamental premise the beauty of its outer shape, symmetry, and regularity, as informed by collocating elements in each electronic block. This approach appears to be consistent with another passage by Scerri (2020a, p. 403):
The left-step table (LST), I suggest, embodies the elements entirely as basic substances since it relegates the chemical and physical properties of elements such as helium and places greater importance on more fundamental aspects. From a philosophical point of view, I believe the LST may provide an optimal periodic system in showing the greatest degree of regularity, while also adhering to the deepest available principles relating to the elements as basic substances.33
IV. The +2 +3 +4 pattern
Mendeleev based his work on the compounds of the elements and their proportions of combination. He wrote that, “the forms of oxides and…atomic weights…give us the means to erect an unarbitrary system as complete as possible” (1879, p. 303). Mendeleev focused on the oxides as oxygen generally brought out the maximum oxidation states (MOS) among the elements, and it was here that a certain periodicity could be discerned.
In the modern periodic table, with lanthanum in Group 3, there is a unique, recurring MOS sequence of +2, +3, and +4, up to at least Z = 100 (Fm). This happens for the sets of consecutive elements or horizontal triads (P = period) shown in Table 3. Whether or not the triad sequence will extend to the copernicium-nihonium-flerovium triad is unclear.
The recurring sequence does not work for lutetium in Group 3. Whereas scandium, yttrium, lanthanum, and actinium are the middle elements of such recurring triads, lutetium and lawrencium are not. Thus, ytterbium is +3, lutetium is +3, and hafnium is +4; as is the pattern for nobelium +3, lawrencium +3, and rutherfordium +4.
The significance of horizontal triads was noted earlier under Regularity and symmetry, per Dias (2004, p. 375). See also the introductory extract from Scerri (2004, p. 138), at the start of argument III.
A table with lanthanum in Group 3 is thus more regular in this particular context of MOS horizontal triads than is the case for lutetium in Group 3. Mendeleev may have been pleased given, as noted, he used horizontal triads when predicting the properties of the then undiscovered elements scandium, gallium, and germanium.
V. Isodiagonality
Rayner-Canham (2011) has written extensively on isodiagonality, this referring to diagonal relationships in the periodic table seen between elements including lithium and magnesium; beryllium and aluminium; and boron and silicon. Such relationships were recognized by both Mendeleev and Newlands. They are, in some ways:
…a general attribute of the properties of the chemical elements. For example, the metal-nonmetal divide forms an almost diagonal demarcation (Edwards and Sienko 1983, pp. 691–692). Similarly, the elements often considered to be semimetals fall on a roughly diagonal border between the metals and nonmetals (Rayner-Canham 2011, p. 122).
Mingos (1998) counts diagonal relationships as one of the three patterns that characterise the periodic table, along with vertical and horizontal trends.
With lanthanum in Group 3 (Fig. 15) an isodiagonal relationship can be seen along calcium-yttrium-cerium. All three elements are strongly basic. Similarities between calcium and the lanthanoids (including cerium) are well known. Yttrium is a member of the rare earths, as are the lanthanoids. All three elements exhibit predominantly ionic chemistry. In atomic number terms the three elements form a perfect triad: 20 (Ca) +58 (Ce) = 78; 78/2 = 39 (Y). To the extent that vertical triads have any relevance, scandium-yttrium-lanthanum form such a triad: 21 (Sc) +57 (La) = 78/2 = 39 (Y). Yttrium thus occupies the central position of a unique triple triad.34 In turn, each of Sc–Y–La are middle members of +2 +3 +4 MOS triads.
With lutetium in Group 3 (Fig. 16), isodiagonality is lost and replaced with the diagonal sequence Ca–Y–Hf. Calcium and yttrium are strongly basic; hafnium is amphoteric. Calcium and yttrium exhibit a predominately ionic chemistry, whereas hafnium exhibits a predominately covalent chemistry (Talbot and Talbot 2018, p. 336).
A table with lanthanum in Group 3 is thus more regular in this particular context.
VI. Monocations of scandium, yttrium, and lutetium
This argument deals with periodic trends in chemical reactivity, as observed in the reactions of Sc+, Y+, La+ and Lu+ with H2, D2, HD, CH4, and C2H6 (Elkind et al. 1989; Sunderlin and Armentrout (1989). It is more detailed and ancillary in nature. I have included it here as it appears to have been overlooked in the composition of Group 3 literature.
The first ionization energy of the elements, as a first order approximation, is a useful indicator of periodic trends. That is why the monocations of these metals, while not being representative of their general (trivalent) chemistry, can nevertheless shed some light on their interrelationships. Hydrogen represents one of the two elements, the combining power of which Mendeleev based his periodic table of elements on, the other element being oxygen.
Under the experimental conditions set out in the article, the Lu+ system was found to be rather different from the other three systems in several respects, including electron configuration, reactivity onset, thermodynamic behaviour, and interactivity mechanism. Meanwhile, scandium, yttrium, and lanthanum showed properties consistent with periodic trends. The different behaviour of lutetium has been attributed to an indirect effect of its 4f14 subshell.
VII. Rare earth metals
This is a curious, somewhat subtle, consistency-based argument.
The context here is the statement that the “The horizontal, vertical, and diagonal trends that characterise the periodic table are based on an increasing sequence of atomic numbers” (Scerri and Parsons 2018. p. 146).
The rare earth series (scandium, yttrium and the lanthanoids; Connelly et al. 2005, p. 51) appear listed in order of their atomic numbers in a 32-column periodic table with Group 3 as Sc–Y–La–Ac. If Group 3 is shown as Sc–Y–Lu–Lr, the minority of the rare earths appear in order of their atomic number whereas the majority appear in a backwards order. Thus, in the first instance they appear as…

…whereas in the second instance, as follows:

In the mentioned fundamental context of an increasing sequence of Z, and compared to the 18 groups and two series (the lanthanoids and actinoids) that make up the periodic table, the second option is cognitively dissonant, awkward, or highly anomalous at best.
Even for secondary groupings such as the platinum group metals, the post-transition metals, and the metalloids, all their individual members or the majority appear in order of increasing atomic number.
In making this argument I am observing the architectural maxim that form follows function. That is to say, if the periodic table is to present the elements in order of Z so to should the members of its categories or sets of elements. Thus:
Whether it be the sweeping eagle in…flight, or the open apple-blossom, the toiling work-horse, the blithe swan, the branching oak, the winding stream at its base, the drifting clouds, over all the coursing sun, form ever follows function, and this is the law. Where function does not change, form does not change. The granite rocks, the ever-brooding hills, remain for ages; the lightning lives, comes into shape, and dies, in a twinkling.
It is the pervading law of all things organic and inorganic, of all things physical and metaphysical, of all things human and all things superhuman, of all true manifestations of the head, of the heart, of the soul, that the life is recognizable in its expression, that form ever follows function. This is the law. (Sullivan 1896).
The architecture of the periodic table is then harmonized in this philosophical functional sense.
VIII. The lanthanoid or f-block contraction
The lanthanoid contraction is the greater-than-expected decrease in ionic radii of the elements in the lanthanoid series from Z = 58, cerium to Z = 71, lutetium, which results in smaller than otherwise expected ionic radii for the subsequent elements starting with Z = 72, hafnium.
The main cause of the contraction is poor shielding of the outer 5s and 5p electrons from the nuclear charge, by f-electrons, starting at Ce3+ [Xe]4f1 and finishing in Lu3+ [Xe]4f14 (Greenwood and Earnshaw 1998, p. 1232, 1234). A similar phenomenon occurs with the actinoids (Cotton 2006, pp. 10–12). Among the lanthanoids, relativistic effects were found to contribute from 9 to 23% of the contraction in their trihalides (Clavaguéra et al. 2006). The lanthanoid contraction, per se, does not start with lanthanum since in the electron configuration of its trivalent cation [Xe]3+ no f- electron is present. In the corresponding contractions across the series of transition metals, there are important contributions from the inner d-electrons and outer s- and p-electrons (Lloyd 1986).
A key distinction is made here between the direct contraction associated with the progressive occupation of the 4f subshell from Ce3+ to Lu3+, and the indirect knock-on consequences starting at hafnium where 4f electrons are no longer being added. (Cotton 2006, pp. 10–12; Mingos 1998, p. 375)
In a lanthanum table, the cause of the contraction naturally spans the f-block as cerium to lanthanum. Cause and form harmonised.
In a lutetium table the cause of the contraction does not start until the second element of the f-block; and the contraction then finishes after the end of the f-block, in the d-block (1st element, period 6). Cause and form are disaggregated.
A table with lanthanum in Group 3 is thus more regular in this particular context.35
IX. f-block integrity
Shchukarev (1974, p. 118), a well-regarded Russian chemist, supported –La–Ac on the grounds that the 4f subshell does not start filling until cerium and that (effectively) the filling sequence—which runs from cerium to lutetium—is periodic, with two periods. Thus, after the occurrence of a half-full 4f subshell at europium and gadolinium, the filling sequence repeats with the occurrence of a full subshell at ytterbium and lutetium (Rokhlin 2003, pp. 4–5). A similar, but weaker, periodicity (Wiberg 2001, pp. 1643–1645) is seen in the actinoids, with a half-full 5f subshell at americium and curium, and a full subshell at nobelium and lawrencium.
Placing lutetium and lawrencium under yttrium obscures the start of the filling of the f-block (it would appear to start at lanthanum) and visually truncates its double periodicity (it would be cut off at ytterbium whereas it would actually end in the d-block). In Shchukarev’s words, the “correctness of placing of imitators before gadolinium and curium as well as lutetium and lawrencium, would be lost. The exceptional uniqueness of gadolinium and curium, akin to that of manganese and zinc, would also be unclear.”
Here is what a lanthanum table looks like:

Shchukarev’s imitators are Eu2+ and Yb2+ which like to attain the Gd3+ and Lu3+ cores. Then there is Ce4+, which likes to attain the core of its lanthanoid progenitor namely La3+; and Tb4+ attaining the same configuration as Gd3+.
Europium, the most reactive of the lanthanoids, is associated with the place of a halogen, and gadolinium is associated with place of a noble gas, although to a much lesser degree. See the Rare-earth metal long term air exposure test (Hamric 2007). Terbium to lutetium are much less reactive, and the Group 17/18 analogy is not seen here.
The f-block contraction starts with Ce3+ and culminates in Lu3+.
The lutetium option is less regular:

The half-filled and filled f- subshell regularity is lost; the correspondence of europium and gadolinium to Group 17 and 18 metals is lost; the f-block contraction starts with Ce3+ and awkwardly finishes in the d-block.
Shchukarev’s approach is consistent with the observation of a progressively delayed start of filling of the f- subshell as one goes down the periodic table i.e. at cerium for 4f; and at protactinium for 5f although some 5f involvement may be possible for thorium (Edelstein and Kot 1993, p. 86); and at E123–125(?) for 5g (Dognon and Pyykkö 2017).
X. Most important electronic orbitals
The gas phase electronic configurations of neutral isolated atoms in a vacuum have traditionally been used to underpin the four-block structure of the periodic table.
That said, how many chemists ever work with isolated atoms(?):
Sure, a few gas phase spectroscopists do, but nearly all general chemistry experiments are done in water solution. Nearly all industrial chemistry is done in condensed phases. Nearly all organic chemistry is done in solution. (Millikan 1982)
Let us turn to the most important electronic orbitals in a chemical sense (Table 4).
In their condensed states most of the lanthanoids:
…are composed of a lattice of LnIII ions with a 4fn configuration and 3 electrons in the 5d/6s conduction band. Metallic europium and ytterbium, however, are composed predominately of the larger LnII ions with 4fn+1 configurations and only 2 electrons in the conduction band. (Johansson and Rosengren 1975, p. 1367; Greenwood and Earnshaw 1998, pp. 232, 1234)
Similar arrangements are seen in the actinoids (Haire 2007, p. 65; Moore and van der Laan 2009, p. 269; passim; Lawson 2016, p. 87).
Per the broad contours of Table 4, and using Group 13 (B-Al-Ga-In-Tl) as an example, an expected decrease in ionization energy from boron to aluminium is not followed by a decrease to gallium i.e. p(d), due to the scandide contraction; and the decrease between gallium and indium is reversed in thallium i.e. p(f), due to the lanthanoid contraction (Greenwood and Earnshaw 1998, p. 222).
In a similar fashion, the knock-on impact of the period 6 f-block contraction (cerium to lutetium) is such that the following period 6 d(f) metals tend to have sizes and properties similar to their period 5 counterparts.
In a lanthanum table then, the number of f-electrons, for the elements in their condensed states, is congruent with the place of each f-block element in 12 of 14 cases; in a lutetium table the situation is reversed, with congruency seen in only 2 of 14 places.
More specifically, the filling of the 4f sub-orbital is the raison d’etre of the lanthanoid metals (cerium to lutetium). While 4f electrons rarely participate in bonding interactions they contribute to the lanthanoid contraction running from cerium to lutetium, and the uniform and characteristic +3 oxidation state among the metals concerned (Mingos 1998, p. 375; Cotton 2006, p. 12).
While gas phase electron configurations appear to indicate that lanthanum [Xe]5d16s2 and lutetium [Xe]4f145d16s2 have equal claims to the position under yttrium, lanthanum is not subject to the lanthanoid contraction (as is the case with yttrium) whereas lutetium is, having incurred a 16.5% reduction in ionic radius. Lutetium is subsequently the least basic of the lanthanoids.
On this basis, including that the most important sub-orbital is 4d for lanthanum and 4fd for lutetium, placing lanthanum under yttrium is more congruent in a chemical periodic table.
Finally, argument X can be expressed in the form of a 20-word philosophical statement, featuring two key principles:
1. The primary ordering criterion is Z. |
2. The secondary such criterion is the most important electronic orbital in a chemical sense. |
PART C: Bringing the threads together
A new Group 3 philosophy
Group 3 is the least studied of the groups and series of the periodic table, in terms of its composition and location.
Rather than obsessing over the minutiae of the individual properties of lanthanum and lutetium, I advocate taking more of a helicopter view. This means examining the group in the context of its surrounds; the congruity of the f-block; patterns seen elsewhere in the periodic table; the periodic law; and global considerations.
This approach is systematic in that each one of the ten arguments set out in this article are interlocking, consistent with the facts and parts of the periodic table as an integrated, complex structure (Scerri 2012b, pp. 282–283). Figure 17 sets out these mutually reinforcing arguments in pictorial form.
Conclusion
From a Platonic symmetry perspective and perhaps that of physics, and on some grounds of regularity but not others, it can be argued that lutetium is better placed under yttrium. But not from a chemical or IUPAC perspective.
Confusion as to the status of the “IUPAC periodic table” can be addressed by updating the guidance in the IUPAC Red Book.
The composition of Group 3 can be pragmatically resolved on the basis of the context within which the applicable table is being used, rather than an inconclusive comparison of the physical, chemical, or electronic properties of lanthanum and Lu. This is done without the need for an indiscriminate bombardment of arguments.
Given the periodic table remains primarily in the domain of chemistry, consideration of the select ten arguments set out in this article support Group 3—in a chemistry-based periodic table—as Sc–Y–La–Ac. The arguments are interlocking, consistent with the nature of the periodic table as an integrated, complex structure whereas lutetium in Group 3 unravels this rich tapestry of chemical relationships. Further, lanthanum in Group 3 is the predominant form appearing in the chemistry literature.
Argument X provides a categorical philosophical (viewpoint-based) confirmation of this approach.
It is ironic that, akin to a game of whack-a-mole, attempts to improve regularity in the appearance of the periodic table increases the number of irregularities amongst various other properties and relationships across the table, and cognitive dissonance with respect to chemical relationships between or within groups or series of elements. While Nature does not care about aesthetics, the composition of Group 3 as Sc–Y–La–Ac appears to be more consistent with the texture of the world.
That said, since periodic tables or systems form a continuum-like series of representations, different approaches to the Group 3 question (even that used within the IUAPC) will continue to have their uses. And please remember to explain the relevant context to your students.
PART D: End matter
Notes
-
1
Sometimes the differentiating electron (d/e) is not immediately apparent. For example Z = 40 Zr is 4d2s2 and Z = 41 Nb is 4d45s1. Here the d/e seems to be d2s−1. In such cases the d/e is taken to be the newly added d-electron, rather than the s-electron that was already there (so to speak).
-
2
See, for example, the 1934 (35-column) periodic table by Romanoff, or White’s 18-column table of the same year: https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=290; https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=465.
-
3
Zmaczynski's fan-shaped system (1937), is a hybrid example with Lu–Ac under Y: https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=286.
-
4
These two are not the only options for Group 3. For example, Group 3 can be represented as bifurcating after Y into an La-Ac branch, and an Lu-Lr branch. See the Appendix to this article, Fig. 19.
-
5
The current IUPAC table includes a logo under the s-block which has forced the f-block one column to the right, so that the start of the f-block is aligned with Group 4 rather than Group 3. This version of the IUPAC table restores the f-block to its original position.
-
6
Data points for lawrencium, other than for first ionization energy, are predictions.
-
7
For example, since yttrium is commonly found in nature together with the heavier lanthanoids including lutetium it is sometimes argued that this supports Group 3 as Sc-Y-Lu-Ac (Thyssen and Binnemans 2011, p. 80). In fact yttrium is unique among the rare earth elements in that, depending on the circumstances, it can behave like a light lanthanoid e.g. Pr, Nd, Sm, or a heavy lanthanoid e.g. Dy, Tm, Lu (Marsh 1947, p. 1084; Jowsey et al. 1958, p. 64; Bünzli and McGill 2011, pp. 19, 26; Gupta and Krishnamurthy 2005, p. 165). In terms of the stoichiometry of binary compounds, yttrium is reported to be more like lanthanum than lutetium (Restrepo (2018, pp. 94–95). In a similar vein, lanthanum has a sufficiently distinct nature compared to the cerium to lutetium series (Liu et al. 2019).
-
8
To this end, a comparison of ionic data by Atkins et al. (2006, p. 34) concludes that Sc-Y-La is preferred over Sc-Y-Lu. Their comparison is expressed as a problem and answer, in the context that ionic radii generally increase down a group (pp. 89–90):
-
Problem 1.14
-
At various times the following two sequences have been proposed for the elements to be included in Group 3: (a) Sc, Y, La, Ac; (b) Sc, Y, Lu, Lr. Because ionic radii strongly influence the chemical properties of the metallic elements, it might be thought that ionic radii could be employed as one criterion for the periodic arrangement of the elements. Use this criterion to describe which of the sequences is preferred.
-
Answer
-
The common ionic state for the Group 3 elements is +3, so the electron configurations for the elements in each sequence are:
-
Sequence (a) Sc3+: [Ar] Y3+: [Kr] La3+: [Xe] Ac3+: [Rn]
-
Sequence (b) Sc3+: [Ar] Y3+: [Kr] Lu3+: [Xe]4f 14 Lr3+: [Rn]5f14
-
The electron configurations in sequence (a) are all rare gas configurations so the ionic radii should increase slowly as the principal quantum number, n, increases. In sequence (b), Lu3+ and Lr3+ also have filled f-subshells. Since f-electrons shield the nuclear charge so poorly, Z* is expected to be much larger for Lu3+ and Lr3+, thereby reducing the ionic radius. Thus, sequence (a) is preferred based on ionic radii. The measured ionic radii bear this conclusion out. For six coordinate radii, the values found are 0.885 Å for Sc3+, 1.040 Å for Y3+, 1.172 Å for La3+, and 1.001 Å for Lu3+.
-
-
9
Lundin and Wilson (2000) divide the rare-earths into five groups:
-
1.
those with low MP and high BP: La, Ce, Pr, Nd
-
2.
low BP: Sm, Eu, Yb, Tm
-
3.
high MP and high BP: Gd, Tb, Y, Lu
-
4.
high MP, mid to low BP and a high vapour pressure at the melting point: Dy, Ho, Er and Sc
-
5.
Pm which really belongs in Group 1 but is highly radioactive and for that reason has no significant commercial use.
For the lanthanoids, that looks like this:

Or in double periodicity form, where Group 3 = Sc-Y-La-Ac:

Or where Group 3 = Sc-Y-Lu-Lr:

-
1.
-
10
Wulfsberg (2018, p. 362) provides the clearest explanation of electron affinity that I have seen:
The energy change involved in adding an electron to an atom to form an anion is known as the electron affinity of that element (EA). Due to an unfortunate tradition regarding the signs of electron affinities, they are better regarded as the energies required to remove the electron of a gaseous anion of −1 charge to produce a gaseous atom of that element. Hence we list them in Table 6.8 (p. 366) as ionization energies of the −1 ions; they could also be called zeroth ionization energies: \( {\text{Cl}}^{-} \,\left( {\text{g}} \right) \to {\text{Cl}}\,\left( {\text{g}} \right) + {\text{e}}^{-} \Delta {\text{H}} = {\text{EA}} = {\text{IE}}\,\left( 0 \right) = + 348.8\,{\text{kJ}}\,{\text{mol}}^{{{-}1}} \)
-
11
Plato, Phaedrus 265d–266a.
-
12
See also Scerri (2020b).
-
13
Hamilton (1965) shows a periodic table extract (Groups 1 to 11, plus footnoted lanthanoids and actinoids, showing Ce, Pr…Lu; and Th, Pa…Lw) with a split d-block (the gap is between Groups 3 and 4) and says that—without any fuss—this is “the periodic table as it is usually presented”. Reger et al. (2010, p. 295) write that “perhaps” the correct shape of the 32-column periodic table should feature a split d-block given the electron configurations of La and Ac, but that “we avoid these structures by splitting the f-block from the rest of the periodic table. This also has the advantage of being able to print a legible periodic table on a single piece of paper.” (They show La below Y in the rest of their book.)
In a similar vein, Scerri (2020b, p. 5) notes that with respect to the 32-column form, “After any new insights are gained, one can well return to the 18-column format with deepened knowledge.”
The split-d table dates from as early as 1934 (Romanoff). It was the table of choice for van Spronsen (1969) in his history of the first hundred years of the periodic system of chemical elements.
-
14
A simple example is to rearrange the line of elements shown on the cover of Bent’s (2006) monograph, into the conventional 18-column layout with the two Group 3 options, as follows:
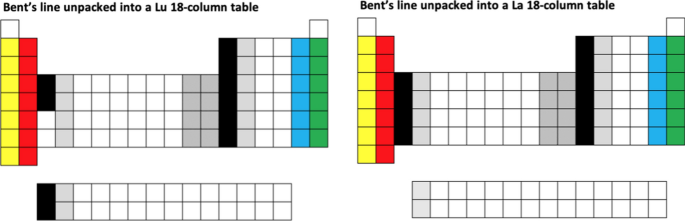
-
15
In a related manner, notions of beauty and ugliness show some variation across time, and between cultures and people (Shiraev and Levy 2013, p. 102). For example:
-
Mountains are seen as sublime expressions of nature; only two hundred years ago they were regarded as loathsome things to be avoided at all costs (Bayley 2015).
-
Two years before it was finished, the great Paris “intellos” of the day lined up in opposition to the Eiffel Tower, writing letters to the papers denouncing it as an ugly and hateful column of bolted tin; of course, it is now one of the world’s most beloved monuments (Bayley 2015).
-
Foreigners in Japan were known to refer to a good deal of ikebana (flower arrangement) as unattractive (Shiraev and Levy 2013, p. 102).
The ACS Division of Inorganic Chemistry had been using a split-d table as its e-mail header, without any concerns being raised, as far as I know, on ugliness or disorderliness. It looks engaging to my subjective eye—ordered, yet with intriguing flourishes:
Scerri (2020b, p. 11) reports that the logo was withdrawn due to the controversy associated with the Group 3 question.
-
-
16
Yang (1996), p. 286:
Through the work of many physicists, the concept of broken symmetry was introduced into elementary particle physics in the 1960s and 1970s. The idea was, in the simplest language, to keep the mathematical forms symmetrical, but the physical consequence unsymmetrical. The standard model, for which Glashow, Salam, and Weinberg shared the Nobel prize in 1979, was based on gauge theory with broken symmetry. It has been extremely successful.
-
17
“Physical chemistry is fundamentally asymmetric. How could it not be when the proton weighs so much more than the electron?” (Philip Stewart, pers. comm. 30 Dec 2019). A recent article along these lines appeared in New Scientist:
Evidence of new physics could have been under our noses all along
Many of these remaining problems boil down to one. Crudely phrased, some things are exceptionally small while related things are exceptionally big. This is known as the hierarchy problem, and once you spot it, you start seeing it everywhere.
Take the four fundamental forces of nature. The weakest two are gravity, and the weak nuclear force, which only operates on the tiniest of scales and is responsible for certain types of radioactive decay. The weak force is weak, but compared with it, gravity is some 25 orders of magnitude weaker—a bizarre state of affairs that, as yet, has no good explanation.
The asymmetry reappears elsewhere. Dark energy, the mysterious force that is causing the universe’s expansion to accelerate, is 120 orders of magnitude weaker than we would expect. Dark matter, which is the dominant form of matter in the universe, interacts very weakly with regular matter. Neutrinos, the lightest particles in the standard model, are thousands of times lighter than anything else.
These disparities are profoundly vexing to physicists, who prefer to see related parameters in a theory take broadly consistent values. This preference for “naturalness” drives much theoretical speculation—some would say to a fault. “Nature doesn’t care about our aesthetics,” says [Nathaniel] Craig [a theoretical physicist at the University of California, Santa Barbara].
* * *
Ten years on, nothing has changed. We were fixated on supersymmetry for too long, says Isabel Garcia at the University of California, Santa Barbara, searching under the convenient street light to the detriment of the field. But the story of the LHC is far from over. The collider has recorded only 3% of the data we expect it to collect in its lifetime, and an upgrade to higher energies in 2020 will further raise its chances of seeing something surprising.
But the LHC’s failure to break any new ground has emboldened a new generation to question the hunches that motivated previous searches. “This optimism is most widespread amongst the youth,” says Matthew McCullough, a theoretical physicist at CERN. “We’ve shaken off the cobwebs of the theories handed down by our PhD advisers.” (Eure 2019)
It remains to be seen if the YAPs (young asymmetrical pups) can teach the OSDs (old symmetrical dogs) some new tricks.
-
18
Klein (1995, pp. 341–342) elaborates the concept of a periodic table as a partially ordered set:
Even in elementary chemistry texts many “rules of thumb” are given which in effect make partial orderings of various chemico-physical properties (melting points, boiling points, electronegativities, solubilities, reactivities, etc.). For example, the ionization potentials of elements arranged in a suitable typical periodic chart generally decrease in proceeding down columns and in proceeding right-to-left across rows, so that while some pairs of elements have ionization potentials ordered by this rule, others pairs don’t…Indeed, the periodic chart can be viewed as what we might call a multi-poset, where there are ordering links along both vertical and horizontal directions but orderings are to be in different directions (interchanging upward vs. downward and/or leftward vs. rightward) for various properties.
-
19
Even so I consider that (a) asymmetry cannot be appreciated or understood without understanding (b) symmetry, and how and why things go from (b) to (a). See also Hegstrom and Kondepudi (1990), and Rosen (1996).
-
20
According to Philip Stewart (pers. comm. 12 February 2020) Rossotti, “did not attach any great importance to the form of table, which was taken ‘off the shelf’.” Indeed, the back inside cover of her book features an IUPAC style table. That said, the clarity of the La periodic table template used throughout her book, speaks for itself.
-
21
Scerri (2019), pp. 557–559.
-
22
The left-step table, or its 18-column form, is an excellent fundamental model based closely on the aufbau principle.
That said, I advocate wariness in asserting this—or any other table—is the one model that applies in all situations, rather than acknowledging that one or more variations may be more useful in some situations. As the physical chemist Henry Bent (2006), who was an aficionado of the left-step table, repeatedly observed there is no “best” periodic table (pp. 108, 127, 151, 140, 170, 175, 183, 191). Using more than one table is a step to perfection (p. 119). Use whichever table is best suited for the task at hand (pp. 151, 158).
Restrepo reiterated this idea (Starr 2019) with an example of trying to capture what a sculpture looks like with just one view of its shadow. The IUPAC table represents one of these shadows, taken from a chemistry perspective, where He sits over Ne, and Group 3 is shown as Sc-Y-[La to Lu]. Most chemistry text-book authors then drill down into the electronic filling sequence, and present the table as Sc-Y-La, because it is not until Ce and Th where f- electrons first make their presence felt. The split-d block issue does not become visible due to the dominance of the 18-column form of the table.
-
23
Scerri now contentiously generalises however, that “The periodic table has now become as much the property of physicists, geologists, astronomers and others as it is of its chemical originators.” (2020b, p. 7).
I suggest the periodic table, in the first instance, remains the organising icon of chemistry. Rather than becoming a shared commodity, the periodic table concept has been borrowed, adapted, tailored and presented in various different guises—including the 15-element wide f-block version—by the physicists, geologists, astronomers and others.
As Scerri (2020b) rightly says:
“It becomes increasingly clear that there may not be any such thing as one optimal table in a purely objective sense. The question seems to depend on what criteria are considered and, most importantly perhaps, on whether one favours chemical or physical criteria or general didactic considerations.” (p. 12)
To this commendable end, he goes on:
“We should accept that a degree of convention must be used in selecting a periodic table that can be presented as perhaps the best possible table that combines objective factors as well as interest dependence.” (p. 14)
Quite so, having regard to the priorities of each interest group.
-
24
Jones adds (2010, pp. 169–171):
Though classification is an essential feature of all branches of science, there are always hard cases at the boundaries. The boundary of a class is rarely sharp…Scientists should not lose sleep over the hard cases. As long as a classification system is beneficial to economy of description, to structuring knowledge and to our understanding, and hard cases constitute a small minority, then keep it. If the system becomes less than useful, then scrap it and replace it with a system based on different shared characteristics.
-
25
The periodic law can be expressed in the following form, “If the elements are arranged in order of increasing atomic number, approximate chemical similarities occur after various regular intervals.”
-
26
While the periodic law may seem more like a rule than a law, it is said to be exact in the same philosophical sense as are the laws of physics (Vihalemm 2003).
-
27
Historically, the division into blocks was based on chemical properties (electrons had not been discovered; electron configurations were unknown). Four types of spectral lines of elements were primarily discovered empirically, and only after the development of the atomic model in 1913–1925 did it become clear that these four types corresponded to different electronic subshells (Imyanitov 2016, pp. 159–160).
-
28
I have constructed a differentiating electron scale of periodic tables, as follows:
Table
Details
#
Notes
0
Madelung rule (1928)
0
Idealised form
11
La–Ac w/HeBe
11
Physics-based optimal block solution
12a
LSPT
12
Elegant 32-column version showing theoretical tetrahedral symmetry
12b
Lu–Lr w/HeBe
12
18-column version of LSPT
12c
La–Ac w/HeNe
12
The chemistry literature standard
13a
Lu–Lr w/HeNe
13
A compromise (?) between 12c. and 14a
13b
Volumetric (1949)
13
La–Ac, He–Ne, and Groups 11–12 as s-block members, here: https://www.meta-synthesis.com/webbook/35_pt/pt_database_SqSp.php?PT_id=921 †
14a
IUPAC, current
14
Further along the chemistry end of the scale
14b
Metallurgist’s (1994)
14
La–Ac w/HeNe, H-F, and Al–Sc, here: https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=18 †
15
Remy’s (1956)
15
La–Ac w/H-F, Th–Pa–U as d-block elements, and Np+ as transuranic elements, analogous to Pm + , here: https://www.meta-synthesis.com/webbook/35_pt/pt_database.php?PT_id=976 †
17
Rayner-Canham (2003)
17
aka the Inorganic Chemist’s Periodic Table (Fig. 13)
21
Pauling (1980)
21
La–Ac w/HeNe; Sc–La as s-block;* Th–Pu as d-block and as f-block; Ku (104) as f-block
-
29
In this context, Jensen (1982) argues for Sc-Y-Lu on the basis of commonalities in the excited state spectra of Sc, Y and Lu. He says the atomic spectra for Sc, Y, and Lu differ from that of La. Specifically, for La, “excited energy levels have been observed which can be attributed to an electron in an f-orbit” (Hamilton 1965, p. 637) whereas this is not the case for Sc, Y, or Lu thereby indicating, “that the 4f wave function in La differs from the 4f wave function in Sc and Y or the 5f wave function in Lu; this causes the various line strengths to be different.” (Hamilton 1965, p. 637).
That said, an analogous situation occurs in Group 2, when comparing Be and Mg with the heavier alkaline earths (Ca, Sr and Ba). Here, the empty d-bands in the latter lie close enough to influence spectroscopic properties and enter into supervalent hybridisation in CaF2, SrF2, SrCl2 and BaX2, such that Ca, Sr and Ba have been called “incipient transition metals” (Myers 1997, pp. 201–202). Rayner-Canham (2020, p. 153) observes that, “A new term entering the vocabulary of inorganic chemistry is that of honorary d elements or honorary transition metals. These terms have been devised to describe organometallic compounds of Group 1 or Group 2 elements that, it is claimed, are using their inner d-orbitals in bonding. Such compounds have been identified by computational studies and/or by synthesis under extremely low temperatures. As such, they are excluded by the earlier definition from study here.”
I would regard La as an “incipient inner transition metal” with a similar presence of f-bands. However, just as Ca, Sr, and Ba are not d-block elements and precede the d-block, so I argue that La (and Ac by default) are placed quite well in the positions immediately preceding the f-block. Thus, the incipient block metals, based on d- subshell involvement in the heavier alkaline earths, f-band presence in La-Ac, and p-hybridisation in Be-Mg and Group 12, occur in the following locations:
-
30
Tsimmerman and Boyce (2019) argue for Sc-Y-Lu-Lr since this results in each block of the periodic table starting with a group or column of elements that have a spin multiplicity of 2, and ending with a group or column in which each elements has a spin multiplicity of 1. This is not the case with an La-Ac table since the f-block starts with Ce and Th having multiplicity values of 1 and 3 respectively, and the end of block finishes with Lu-Lr, each having M values of 2.
The reason for the difference in M values is that in the Lu-Lr table the f-block is presumed to start before the appearance of the first f-electron. In this option the first two elements, La and Ac, each have just one d-electron in an unfilled subshell. And the last two elements Yb and No have no incomplete subshells. The M values reflect this.
Whereas in the La-Ac table the f-block is presumed to start with the delayed appearance of the first f-electron. While Th has a 5d2 configuration, its crystalline structure is influenced by the presence of some f-character, and an f-electron may rarely be available for chemistry in the form of Th3+ [Rn]5f 1.
This results in the first two elements, Ce and Th each having two electrons in unfilled subshells, and the last two elements Lu and Lr each having one electron in one unfilled subshell. The M values reflect this.
The delayed start in the La-Ac table does not upset the chemistry of the lanthanoids and actinoids since the +3 oxidation state is common to all of them. And f-electrons are not available for chemistry in the last two f-block members Lu Lr, as is the case with the last three d-block members Zn, Cd and Hg.
Unfortunately, the Lu-Lr table introduces more discrepancies or irregularities, as set out elsewhere in this article, dealing with e.g. chemical behaviour; differentiating electrons (after which the blocks are named); outer electrons in common with the rest of the block; term symbols; and the periodic law.
-
31
Downs and Adams (1973, pp. 1245–1248) and Porterfield (1993, pp. 122–123) usefully delineate between the metal halides MXn, as follows:
Formed by
Description
Ionic
Most metals from Groups 1–3; Ln and An in lower oxidation states (+2, +3) and TM fluorides
Electrostatic lattice model; ordered 3-D lattices with high CN for all atoms; lattice energies very well reproduced by Madelung-constant expression
Partly ionic
TM in low charge states (+1 to +3) and Group 13–14 metals
Electrostatic model or band theory; halide in unsymmetrical environment in lattice, usually chain or layer structures, low CN frequent, lattice energies from Madelung constant deviate from experimental by 5–20%
Covalent
Nonmetals and all MXn, where n is > 3
Shared-electron bonds (valence-bond or MO models); symmetry of molecules predictable by VSEPR; very weak bonding in solid lattice due to van der Waals forces
The former authors add:
Notwithstanding the substantial differences between the individual halogens, chlorides, bromides and iodides are sufficiently similar to permit a collective classification, although it must be appreciated that there are no clear lines of demarcation between the different classes. Rather there is uniform gradation from halides which are for all practical purposes ionic, through those of intermediate character, to those which are essentially molecular…most binary halides other than those of transition metals in oxidation states >+3 are most profitably discussed in terms of the simple ionic model and of deviations from this model.
More simply, this table (Schweitzer and Pesterfield 2010) shows the solubility (aq) of a range of compounds from Groups 1–5:
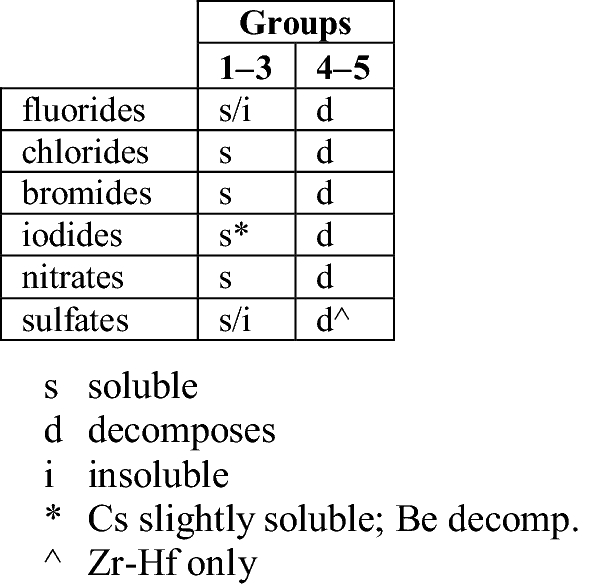
-
32
Williams (1981, pp. 362–363) writes:
2. THE CHEMICAL CLASSIFICATION OF ELEMENTS
“The classification of elements in the Periodic Table is now known to be a reflection of restrictions imposed by quantization of energy states of electrons in atoms. However, without recourse to other than empiricism in the study of chemistry the same classification had been observed for over 100 years. In fact it has long been a standard educational practice to separate elements into Groups IA, IIA, and IIIA; transition metals; Groups IB, IIB and IIIB; and the non-metals of Groups IVB to VIIB of the Periodic Table to simplify discussion of their chemistry. Although the distinctive properties in aqueous solution of each of the four classes does not provide sharp divisions it is very useful to treat separately three types of metal: Groups IA, IIA and IIIA metals are associated with equilibrium ionic-model chemistry; transition metals with one-electron redox chemistry and, across each such series, increasingly covalent chemistry concommitant with increasing Lewis-acid strengths of ions, usually at equilibrium with their surroundings; and Groups (IB), IIB and IIIB metal ions with a compromise ion chemistry involving strong Lewis-acid properties while maintaining fast equilibration but little redox activity…Finally, there is the further chemistry of non-metals…”
The upshot is that, according to Phillips, and in the specific context of simple chemistry, a split d block is very useful.
-
33
Scerri distinguishes here between simple and basic substances. For example, carbon exists as a simple substance in the form of its allotropes such as graphite and diamond. Carbon as a basic substance is the atomic form of carbon found in its compounds such as CO2. The focus is on the atomic number of carbon rather than the differing physical, chemical, and electronic properties of its allotropes. Mendeleev took a similar approach when he designed his periodic table. He wrote that it was atomic weight that served as the departure point for the discovery of the periodic law and that a law expressed a relationship between variables. Atomic weight was the first variable, and chemical and physical properties were the second (Jensen 2002, pp. 45, 116).
-
34
Not forgetting the trifurcate form of the Y symbol for yttrium.
-
35
The lanthanoids are characterised by, inter alia, their magnetic properties:
Molar magnetic susceptibility (MMS) is a measure of how much a material will become magnetised in an applied magnetic field. It is the ratio of magnetisation M (magnetic moment per unit volume) to the applied magnetising field of intensity H. This allows a simple classification into two categories of most materials’ responses to an applied magnetic field: an alignment with the magnetic field, χ > 0, called paramagnetism, or an alignment against the field, χ < 0, called diamagnetism.
Values are from Haynes (2016); Kanellakopulos et al. (Cm; 1975); and Brodsky (Cm-Cf; 1978).
The average value for each block is:

MMS reduces going down all groups of the d-block. The average reduction going from 4d to 5d is 50%.
In Group 3 there is a reduction of 48% on going from Y to La. If Lu is instead placed under Y the reduction is 2%.
-
36
For a similar approach to understanding the periodic table as a network of (eight in this case) interconnected ideas see Rodgers (2014).
Change history
12 October 2020
A Correction to this paper has been published: https://doi.org/10.1007/s10698-020-09390-4
References
Allen, L.C., Knight, E.T.: The Löwdin challenge: origin of the n + l, n (Madelung) rule for filling the orbital configurations of the periodic table. Int. J. Quantum Chem. 90, 80–88 (2003)
Alvarez, S.: The transition from 4f to 5d elements from the structural point of view. Cryst. Eng. Comm (2020)
Atkins, P., Overton, T., Rourke, J., Weller, M., Armstrong, F.: Shriver & Atkins inorganic chemistry, 4th edn. Oxford University Press, Oxford (2006)
Bayley, S.: So you think you’re ugly? Don’t worry—perceptions change. The Guardian, Australian edition. https://www.theguardian.com/commentisfree/2015/nov/23/ugly-perceptions-change-beauty-art (2015), accessed 6 Jan 2020
Bent, H.: New ideas in chemistry: fresh energy for the periodic law. AuthorHouse, Bloomington, IN (2006)
Bonnelle, C., Spector, N.: Rare-earths and actinoids in high energy spectroscopy. Springer, Dordrecht (2015)
Brodsky, M.B.: Magnetic properties of the actinide elements and their metallic compounds. Rep. Prog. Phys. 41, 1547 (1978)
Brooks, M.: This one particle could solve five mega-mysteries of physics. New Scientist, 3191 (2018)
Bünzli, J., McGill, I.: Rare-earth elements. In: Elvers, B. (ed.) Ullmann’s Encyclopaedia of Industrial Chemistry, 7th edn. Wiley-VCH, Wiesbaden (2011)
Cao, C., Hu, H., Li, J., Schwarz, W.H.E.: Physical origin of chemical periodicities in the system of elements. Pure Appl. Chem. 91, 1969–1999 (2019)
Clavaguéra, C., Dognon, J.-P., Pyykkö, P.: Calculated lanthanide contractions for molecular trihalides and fully hydrated ions: the contributions from relativity and 4f-shell hybridization. Chem. Phys. Lett. 429, 1–3 (2006)
Christie, M., Christie, J.R.: “Laws” and “Theories” in chemistry do not obey the rules. In: Bushan, N., Rosenfeld, S. (eds.) Mind and Molecules: New Philosophical Perspectives on Chemistry, pp. 34–50. Oxford University Press, Oxford (2000)
Connelly, N.G., Hartshorn, R.M., Damhus, T., Hutton, A.T.: Nomenclature of inorganic chemistry: IUPAC recommendations. RSC Publishing, Cambridge (2005)
Cotton, S.: Lanthanide and actinide chemistry. Wiley, Chichester (2006)
Dias, J.R.: The periodic table set as a unifying concept in going from benzenoid hydrocarbons to fullerene carbons. In: Rouvray, D.H., King. R.B. (eds): The periodic table: into the 21st century, Institute of Physics Publishing, Philadelphia, 371–396 (2004)
Dognon, J.-P., Pyykkö, P.: Chemistry of the 5g elements: relativistic calculations on hexafluorides. Angew. Chem. Int. Ed. 56, 10132–10134 (2017)
Downs, A.J., Adams, C.J.: Chlorine, bromine, iodine, and astatine. In: Bailar, J.C., et al. (eds.) Comprehensive Inorganic Chemistry, pp. 1107–1595. Pergamon Press, Oxford (1973)
Edelstein, N.M., Kot, W.K.: Spectroscopic and magnetic studies of tetravalent Pa and trivalent Th compounds. J. Alloys Compd. 193, 82–87 (1993)
Edwards, P.P., Sienko, M.J.: On the occurrence of metallic character in the periodic table of the elements. J. Chem. Educ. 60, 691 (1983)
Elkind, J.L., Sunderlin, L.S., Armentrout, P.B.: Periodic trends in chemical reactivity: reactions of Sc+, Y+, La+, and Lu+ with H2, D2 and HD. J. Phys. Chem. 93, 3151–3158 (1989)
Eure, J.: Evidence of new physics could have been under our noses all along. New Scientist, 3217, 16 Feb (2019)
Fernelius, W.C.: Some reflections on the periodic table and its use. J. Chem. Educ. 63, 263–266 (1986)
Frye, H.G.: A scheme of analysis for the ceric rare earths. University of the Pacific, Thesis (1949). https://scholarlycommons.pacific.edu/uop_etds/1093
Greenwood, N.N., Earnshaw, A.: Chemistry of the elements, 2nd edn, p. 223. Butterworth-Heinemann, Oxford (1998)
Gupta, C.K., Krishnamurthy, N.: Extractive Metallurgy of Rare Earths. CRC Press, Boca Raton (2005)
Haire, R.G.: Insights into the bonding and electronic nature of heavy element materials. J. Alloys Compd. 444–445, 63–71 (2007)
Hamilton, D.C.: Position of lanthanum in the periodic table. Am. J. Phys. 33, 637–640 (1965)
Hamric, D.: Rare-earth metal long term air exposure test. Metallium, Inc. https://www.elementsales.com/re_exp/index.htm (2007) (viewed 7 March 2020)
Haynes, W.M. (ed.): CRC Handbook of Chemistry and Physics, 97th edn. CRC Press, Boca Raton (2016)
Hegstrom, R.A., Kondepudi, D.K.: The handedness of the universe. Sci. Am. 62, 108–115 (1990)
Hevesy, G.: Redkie zemeli s tochki zreniya stroeniya atoma. (Rare earths from the point of view of structure of atom.) NKhTI, Lenningrad (1929) cited in Trifonov 1970
Hjørland, B., Scerri, E., Dupré, J.: Forum: the philosophy of classification. Knowl. Organ. 38, 9–24 (2011)
Imyanitov, N.S.: Spiral as the fundamental graphic representation of the Periodic Law. Blocks of elements as the autonomic parts of the Periodic System. Found. Chem. 18, 153–173 (2016)
IUPAC: The constitution of Group 3 of the periodic table. https://iupac.org/projects/project-details/?project_nr=2015-039-2-200, (2015), viewed 6 March 2020
Jensen, W.B.: The positions of lanthanum (actinium) and lutetium (lawrencium) in the periodic table. J. Chem. Ed. 59, 634–636 (1982)
Jensen, W.B.: Classification, symmetry and the periodic table. Comput. Math Appl. 12, 487–510 (1986)
Jensen, W.B. (ed.): Mendeleev on the Periodic Law: Selected Writings, 1869–1905. Dover, Mineola (2002)
Jensen, W.B.: The place of zinc, cadmium, and mercury in the periodic table. J. Chem. Ed. 80, 952–961 (2003)
Jensen, W.B.: Trouble with triads. Program and abstracts, 258th ACS National Meeting San Diego, CA August 25–29. American Chemical Society. 13 (2019)
Johansson, B., Abuja, R., Eriksson, O., Wills, J.M.: Anomalous fcc crystal structure of thorium metal. Phys. Rev. Lett. 75, 280–283 (1995)
Johansson, B., Rosengren, A.: Interpolation scheme for the cohesive energies for the lanthanoids and actinoids. Phys. Rev. B 11, 1367–1373 (1975)
Jones, B.W.: Pluto: Sentinel of the Outer Solar System. Cambridge University Press, Cambridge (2010)
Jowsey, J., Rowland, R.E., Marshall, J.H.: The comparative deposition of yttrium, cerium, and thallium in bone tissue of dogs. In: Argonne National Laboratory, Radiological Physics Division Semiannual Report, July to December 1957. Illinois, 63–75 (1958)
Kanellakopulos, B., Blaise, A., Fournier, J.M., Müller, W.: The magnetic susceptibility of americium and curium metal. Solid State Commun. 17(6), 713–715 (1975)
King, R.B.: Inorganic Chemistry of Main Group Elements. Wiley-VCH, New York (1995)
Klein, D.J.: Similarity and dissimilarity in posets. J. Math. Chem. 18, 321–348 (1995)
Kurushkin, M.: Viatscheslaw Romanoff: unknown genius of the periodic system. Pure Appl. Chem. 91(12), 1921–1928 (2019)
Kurushkin, M.: Helium’s placement in the Periodic Table from a crystal structure viewpoint. IUCrJ 7(4), 577–578 (2020)
Labarca, M., Gonzalez, J.C.M.: On the membership of group 3 of the periodic table: a new approach. Theoria 34, 297–310 (2019)
Landau, L.D., Lifshitz, E.M.: Quantum Mechanics: Non-relativistic Theory, 2nd ed. Pergamon Press, Oxford, pp. 252–257 (1958)
Lawson, A.C.: 5f-electron localisation in the actinoid metals: thorides, actinoids and the Mott transition. Philos. Mag. Lett. 96(3), 85–89 (2016)
Leach M.D.: 1922 Bohr’s system. The Internet database of periodic tables. https://www.metasynthesis.com/webbook/35_pt/pt_database.php?PT_id=285. Accessed 11 Sept 2020
Leigh, J.: Periodic tables and IUPAC. Chem. Int. 31, 4–6 (2009)
Lemonick, S.: The periodic table is an icon. But chemists still can’t agree on how to arrange it. Chemical & Engineering News. 97 (2019). The two internal quotes are by Philip Ball
Liu, R., Mao, G., Zhang, N.: Research of chemical elements and chemical bonds from the view of complex network. Found. Chem. 21, 193–206 (2019)
Lloyd, D.R.: On the lanthanide and “Scandide”1 contractions. J. Chem Ed. 63(6), 502–503 (1986)
Lundin, R., Wilson, J.R.: Rare Earth Metals—overview of the physical and chemical characteristics of the rare earths includes details on their applications as alloying elements in metals and in zinc alloy coatings. Adv. Mater. Process. 158(1), 52–56 (2000)
Martinich, A.P., Stroll, A.: Much ado about nonexistence: fiction and reference. Rowan & Littlefield, Lanham, MA (2007)
Marsh, J.K.: The relation of yttrium to the lanthanons: A study of molecular volumes. J. Chem. Soc. 1084–1086 (1947)
Mendeleev, D.I.: The periodic law of the chemical elements. Chem. News J. Phys. Sci. 40, 1048, 303–304
Meggers, W.F., Scribner, B.F.: The arc and arc spectra of ytterbium. J. Res. Nat. Bur. Stand. 19, 651–664 (1937)
Millikan, R.C.: Why teach the electron configuration of the elements as we do? J. Chem. Educ. 59, 757 (1982)
Mingos, D.M.P.: Essential Trends in Inorganic Chemistry. Oxford University Press, Oxford (1998)
Moeller, T.: The Chemistry of the Lanthanoids. Pergamon Texts in Inorganic Chemistry, vol. 26. Pergamon Press, Oxford (1973)
Moore, K.T., van der Laan, G.: Nature of the 5f states in actinoid metals. Rev. Mod. Phys. 81, 235–298 (2009)
Myers, H.P.: Introductory Solid State Physics, 2nd edn. CRC Press, Boca Raton (1997)
Pauling, L.: General chemistry, 3rd edn. Dover Publications, New York (1980)
Poliakoff, M.: In Bradley, D.: Periodic debate: Complete not finished. ChemViews Magazine, 9 June, https://www.chemistryviews.org/details/webinar/1077259/Periodic_Debate.html?page=24 (2011) viewed 4 Jan 2020
Porterfield, W.W.: Inorganic Chemistry: A Unified Approach, pp. 122–123. Academic Press, San Diego (1993)
Railsback, L.B.: The earth scientist’s periodic table of the elements and their ions: A new periodic table founded on non-traditional concepts. In: Scerri, E., Restrepo, G. (eds.) Mendeleev to Oganesson: A multidisciplinary perspective on the periodic table, pp. 140–151. Oxford University Press, New York (2018)
Rayner-Canham, G.: Isodiagonality in the periodic table. Found. Chem. 13(2), 121–129 (2011)
Rayner-Canham, G.: The Periodic Table: Past, Present, Future. World Scientific, Singapore (2020)
Rayner-Canham, G., Overton, T.: Descriptive inorganic chemistry, 3rd edn. W. H. Freeman and Company, New York (2003)
Reger, D.L., Goode, S.R., Ball, D.W.: Chemistry Principles and Practice, 3rd edn. Brooks/Cole Cengage Leaning, Australia (2010)
Restrepo, G.: The periodic system: A mathematical approach. In: Scerri & Restrepo (2018)
Rodgers, G.E.: A visually attractive “Interconnected network of ideas” for organizing the teaching and learning of descriptive inorganic chemistry. J. Chem. Educ. 91(2), 216–224 (2014)
Rokhlin, L.L.: Magnesium Alloys Containing Rare Earth Metals: Structure and Properties. Taylor & Francis, London (2003)
Romanoff, V.: Le système périodique de Mendéléef par représentation graphique. Rev. Sci. 72, 661 (1934). cited in Kurushkin (2019)
Rosen, J.: Symmetry in Science: An Introduction to the General Theory. Springer, New York (1996)
Rossotti, H.: Diverse Atoms: Profiles of the Chemical Elements. Oxford University Press, Oxford (1998)
Scerri, E.: The best representation for the periodic table: The role of the n + l rule and the concept of an element as a basic substance. In: Rouvray, D.H., King, R.B. (eds.) The periodic table: into the 21st century, pp. 143–160. Institute of Physics Publishing, Philadelphia (2004)
Scerri, E.: The role of triads. J. Chem. Educ. 85, 585–589 (2008)
Scerri, E.: The periodic table. In: Woody, A.I., Hendry, R.F., Needham, P. (eds.) Philosophy of Chemistry, Handbook of the Philosophy of Science, vol. 6. Elsevier, Amsterdam (2012a)
Scerri, E.: A critique of Weisberg’s view on the periodic table and some speculations on the nature of classifications. Found. Chem. 14(3), 275–284 (2012b)
Scerri, E.: Can quantum ideas explain chemistry’s greatest icon? Nature. https://www.nature.com/articles/d41586-019-00286-8?proof=trueMay.#ref-CR6 (2019). Viewed 8 March 2020
Scerri, E.: The Periodic Table: Its Story and Significance, 2nd edn. Oxford University Press, New York (2020a)
Scerri, E.: Recent attempts to change the periodic table. Philos. Trans. R. Soc. A. 378, 20190300 (2020b)
Scerri, E.R., Parsons, W.: What elements belong in Group 3 of the periodic table? In: Scerri, E., Restrepo, G. (eds.) Mendeleev to Oganesson: A multidisciplinary perspective on the periodic table, pp. 140–151. Oxford University Press, New York (2018)
Scerri, E., Restrepo, G. (eds.): Mendeleev to Oganesson: A Multidisciplinary Perspective on the Periodic Table. Oxford University Press, New York (2018)
Schweitzer, G.K., Pesterfield, L.L.: The Aqueous Chemistry of the Elements. Oxford University Press, Oxford (2010)
Shchukarev, S.A.: Neorganicheskaya khimiya, vol. 2. Vysshaya Shkola, Moscow (in Russian) (1974)
Shiraev, E.B., Levy, D.A.: Cross-cultural psychology: Critical thinking and contemporary applications, 5th edn. Routledge, London (2013)
Silberberg M.S.: Chemistry: The Molecular Nature of Matter and Change, 4th ed. McGraw-Hill, Boston, p. 303 (2006)
Starr, M.: Mathematicians have proposed a new structure to the periodic table. ScienceAlert, 18 June, https://www.sciencealert.com/the-periodic-table-could-be-organised-more-like-a-network-than-a-matrix (2019) viewed 25 December 2019
Stewart, P.J.: Amateurs and professionals in chemistry. In: Scerri, E., Restrepo, G. (eds.) Mendeleev to Oganesson: A Multidisciplinary Perspective on the Periodic Table, pp. 66–79. Oxford University Press, New York (2018a)
Stewart, P.J.: Tetrahedral and spherical representations of the periodic system. Found. Chem. 20, 111–120 (2018b)
Sullivan, L.H.: The tall office building artistically considered. Lippincott’s Magazine. March 403–409 (1896)
Sunderlin, L.S., Armentrout, P.B.: Periodic trends in chemical reactivity: reactions of Sc+, Y+, La+, and Lu+ with methane and ethane. J. Phys. Chem. 93, 3151–3158 (1989)
Talbot, D.E.J., Talbot, J.D.R.: Corrosion Science and Technology, 3rd edn. CRC Press, Boca Raton (2018)
Thyssen, P., Binnemans, K.: 2011, Accommodation of the rare earths in the periodic table: A historical analysis. In: Gschneider Jr., K.A. (ed.) Handbook on the Physics and Chemistry of the Rare Earths, vol. 41, pp. 1–94. Elsevier, Amsterdam (2011)
Trifonov, D.N.: Rare-earth elements and their position in the periodic system. Translated from the 1966 Russian edition, Academy of Sciences of the USSR Institute of the History of Natural Sciences and Technology, Moscow. Published for the Atomic Energy Commission and the National Science Foundation, Washington, by the Indian National Scientific Documentation Centre (1970)
Tsimmerman, V., Boyce, C.: Using Hund’s Rule and spin multiplicity to assess competing versions of Group 3 and f-block constituency. Chem. Ed. 24, 1–10 (2019)
Van Spronsen, J.W.: The Periodic System of Chemical Elements: A History of the First Hundred Years. Elsevier, Amsterdam (1969)
Vickery, R.C.: The Chemistry of Yttrium and Scandium. Pergamon Press, New York (1960)
Vickery, R.C.: Scandium, yttrium, and lanthanum. In: Bailar Jr., J.C., Emeléuse, H.J., Nyholm, R., Trotman-Dickenson, A.F. (eds.) Comprehensive Inorganic Chemistry, vol. 3, pp. 329–354. Pergamon Press, Oxford (1973)
Vihalemm, R.: Are laws of Nature and scientific theories peculiar in chemistry? Scrutinizing Mendeleev’s discovery. Found. Chem. 5, 7–22 (2003)
Wiberg, N.: Inorganic Chemistry. Academic Press, San Diego (2001)
Williams, R.J.P.: The Bakerian Lecture, 1981 Natural selection of the chemical elements. Proc. R. Soc. Lond. B. 213, 361–397 (1981)
Wulfsberg, G.P.: Periodic table: Trends in the properties of the elements. In: Encyclopedia of Inorganic Chemistry, 2nd ed. John Wiley & Sons, New York (2006)
Wulfsberg, G.P.: Foundations of Inorganic Chemistry. University Science Books, CA (2018)
Yang, C.N.: Symmetry and physics. Proc. Am. Philos. Soc. 140, 267–288 (1996)
Acknowledgements
I thank:
• Eric Scerri, Philip Stewart, Jess Tauber, Valery Tsimmerman, and Conal Boyce, and other members of the Periodic table mailing list for many years of stimulating and robust discussion on the nature of the periodic table;
• Geoff Rayner-Canham for sparking my interest in periodic patterns;
• Simon Cotton for early guidance on the nature of the lanthanoids;
• Tina Overton for help with the electron configurations of the lanthanoids;
• Peter Nelson for considered views on the Group 3 question;
• members of Wikipedia’s WikiProject Elements for their indefatigable stress-testing of an early draft of this article;
• Bill Jensen for reopening the subject matter in 1983, and for providing me with a copy of his presentation on triads (2019); and
• Eugen Schwarz for earlier discussions, and for bringing Millikan (1982) to my attention.
I further thank Eric Scerri for the insights he kindly shared with me, and his thought leadership on this question in other media and forums.
I gratefully acknowledge the chemistry- and philosophy-based insights of referees.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Mention of electron configurations in this article are those of the free atoms, unless otherwise specified.
The original online version of this article was revised: Two references were corrected, 5 g in last paragraph of section “IX. f-block integrity” was corrected to 5g and the name “Ligshitz” was corrected throughout the article.
Appendix: Landau and Lifshitz (1958), a redux
Appendix: Landau and Lifshitz (1958), a redux
A puzzling layout
The authors discuss aspects of the periodic system of DI Mendeleev. The electron configurations of hydrogen and helium are briefly noted. This is followed by three tables setting out the electron configurations of the sp-, d- and f-elements. I joined up their note and three tables to produce the subject periodic table (Fig. 18). Curium was the last known element at their time of writing; transcurium elements are shown in parentheses.
Landau and Lifshitz (1958)
Some extracts from their discussion follow:
“The elucidation of the nature of the periodic variation of properties, observed in the series of elements when they are placed in order of increasing atomic number, requires an examination of the peculiarities in the successive completion of the electron shells of atoms. (p. 252)
Many properties of atoms (including the chemical properties of elements…depend principally on the outer regions of the electron envelopes.
The elements containing complete d and f shells (or not containing these shells at all) are called elements of the principal groups; those in which the filling up of these states is actually in progress are called elements of the intermediate groups. These groups of elements are conveniently considered separately. (p. 254)
We see that the occupation of different states occurs very regularly in the series of elements of the principal groups: first the s states and then the p states are occupied for each principal quantum number n. The electron configurations of the ions of these elements are also regular (until electrons from the d and f shells are removed in the ionisation): each ion has the configuration corresponding to the preceding atom. Thus, the Mg+ ion has the configuration of the sodium atom, and the Mg++ ion that of neon. (p. 255)
Let us now turn to the elements of the intermediate groups. The filling up of the 3d, 4d, and 5d shells takes place in groups of elements called respectively the iron group, the palladium group and the platinum group. Table 4 gives those electron configurations and terms of the atoms in these groups that are known from experimental spectroscopic data. As is seen from this table, the d shells are filled up with considerably less regularity than the s and p shells in the atoms of elements of the principal groups. Here a characteristic feature is the “competition” between the s and d states.
This lack of regularity is observed in the terms of ions also: the electron configurations of the ions do not usually agree with those of the preceding atoms. For instance, the V+ ion has the configuration 3d4 (and not 3d24s2 like titanium); the Fe+ ion has 3d64s1 (instead of 3d54s2 as in manganese).
A similar situation occurs in the filling up of the 4f shell; this takes place in the series of elements known as the rare earths.† The filling up of the 4f shell also occurs in a slightly irregular manner characterised by the “competition” between 4f, 5d and 6s states.
†In books on chemistry, lutetium is also usually placed with the rare-earth elements. This, however, is incorrect, since the 4f shell is complete in lutetium; it must therefore be placed in the platinum group.
The last group of intermediate elements begins with actinium. In this group the 6d and 5f shells are filled, similarly to what happens in the group of rare-earth elements. (pp. 256–257)”
Observations
The table that arises from merging their three sub-tables is 16- rather than 18-elements wide. It may be the squarest useful table I have seen (16w x 15h).
Landau and Lifshitz are sometimes cited as providing the earliest argument for placing lutetium in group 3.
Looking at their tables of electron configurations, and their categorisation of principle and intermediate elements, I suggest this is a misinterpretation of their position. A more plausible interpretation is that they supported lanthanum and lutetium in group 3, an option which other authors have featured from time to time. The earliest example I know is that of Bohr (1922), which features bifurcations at Na, Mg, and Y but no group numbers, per se.
A more recent example is that of Silberberg (2006) (Fig. 19).
I recall some early discussion about placing lawrencium 7s27p1 under thallium 6s26p1. This was discounted since the position under thallium was already occupied by nihonium. It works fine however within Landau and Lifshitz’s paradigm.
The puzzle
The authors exclude lanthanum from the rare earths since the 4f subshell has not started filling. Yet actinium and thorium are included by them with what we now call the actinoids even though these two metals have no f electrons (p. 258).
No explanation is provided for this puzzling lack of consistency with their categories. In this light I have moved actinium and thorium out of the actinoids and into the d-block.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vernon, R.E. The location and composition of Group 3 of the periodic table. Found Chem 23, 155–197 (2021). https://doi.org/10.1007/s10698-020-09384-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10698-020-09384-2