Abstract
A statistical mechanical treatment is given of thermal contact between two systems. Reciprocal temperature (1/T) emerges from this as the relative change in the number of microscopic states a macroscopic system at equilibrium ranges over, at constant volume and chemical composition, with change in internal energy. The significance of this is discussed in detail with reference to a monatomic gas and an Einstein solid.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
One of the aims of statistical mechanics is to provide an understanding of the thermodynamic quantity, entropy (S). In this it has had considerable success. Entropy is now generally accepted as being a measure of the number of microscopic statesFootnote 1 a system ranges over when it is in a particular macroscopic state, and as being given by
where Ω is the number of microscopic states and k is Boltzmann’s constant (see, e.g., Bent 1965).
So much for entropy. But what about temperature (T)? In many presentations of statistical mechanics, temperature appears out of the mathematics without any obvious statistical-mechanical interpretation. For example, in derivations of Boltzmann’s distribution law employing Lagrange’s method of undetermined multipliers (Tolman 1938, Schrödinger 1946, and many modern texts), temperature emerges as the reciprocal of one of these multipliers \((\upbeta)\):
While it can easily be shown that \(1/{\upbeta}\) has all the properties of temperature, it is difficult to explain what this quantity is in statistical-mechanical terms. The same applies to the divisor Θ introduced by Gibbs (1902). As thus presented, statistical mechanics merely succeeds in solving the mystery of what entropy is by creating a mystery of what temperature is.
My aim in this paper is to present statistical mechanics in a way that brings out the statistical-mechanical significance of temperature. The method is the same as the one I used to provide a deeper understanding of entropy (Nelson 1994).
Method
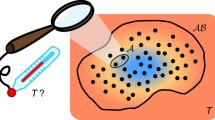
Consider the system shown in Fig. 1. This comprises two subsystems, A and B, which are thermally insulated from each other and from their surroundings. Each subsystem has rigid and impermeable walls, so that its volume and overall chemical composition are fixed. A small device C enables thermal contact to be made between the two, without any other interaction taking place. Our interest is in what happens when contact is made for a short period of time, and a small quantity of energy flows from one subsystem to another. By a ‘short period of time’, I mean a period short enough for the resulting changes \((\updelta)\) in the properties of A and B to be treated to a good approximation as infinitesimals, but not so short for these changes to be confused with fluctuations.
Thermodynamic treatment
Suppose that, before contact is made, each subsystem is in an equilibrium state, with temperature TX, internal energy UX, and entropy SX (X = A or B). Suppose further that, after contact has been made, each subsystem settles again into an equilibrium state. Let the heat absorbed by subsystem A during contact be qA and by B be qB, where qB = ‒qA.
Consider first the temperature. If TA > TB, heat flows from A to B when contact is made. If TA < TB, heat flows from B to A. If TA = TB, no heat flows. In terms of temperature, therefore, the condition for A and B to be in equilibrium when they are brought into contact is TA = TB.
This condition can also be expressed in terms of entropy. In this form, a direct link can be made with statistical mechanics.
Consider the total entropy
The change in this quantity when thermal contact is made between A and B is given byFootnote 2
From the thermodynamic definition of entropy,Footnote 3 Equation 4 can be written:Footnote 4
Now if TA < TB, qA is positive, (1/ΤΑ ‒ 1/TB) is positive, and so \(\updelta\)St is positive. If TA > TB, qA is negative, (1/ΤΑ ‒ 1/TB) is negative, and so \(\updelta\)St is again positive. If TA = TB, (1/ΤΑ ‒ 1/TB) is zero, so \(\updelta\)St is zero.Footnote 5 Hence for spontaneous changes
In terms of entropy, therefore, the condition for A and B to be in equilibrium when they are brought into contact is \(\updelta\)St = 0.
At constant volume and composition, \(q_{\text{x}} = {\updelta}U_{\text{x}}\). Thus, Eq. 5 can also be written
Statistical mechanical treatment
To derive the thermodynamic properties of an isolated system from statistical mechanics, it is necessary to assume that such a system is not perfectly isolated, but is subject to small perturbations that cause it to spend time in all possible microscopic states, consistent with the macroscopic state, having an energy E within a small range (e) of its mean value (Ē = U) (Denbigh and Denbigh 1985: Sect. 2.3 and App. 2.2). The value of e is not critical.Footnote 6
Suppose, therefore, that, before contact is made between the two systems in Fig. 1, the microscopic motion of system A ranges over ΩA distinct states and that of B over ΩB. Consider the quantity
Since systems A and B are independent, this represents the number of states the system as a whole ranges over before thermal contact is made. This is because any of the motions of one block can take place at the same time as any of the motions of the other block. After contact has been made, this number changes by the amount
This can be written as
or
where \({\updelta}_{\text{r}}\) is the relative change in the quantity indicated.
Equation 11 can also be written in the more familiar form,
However, this obscures the interpretation of entropy and temperature, as we shall see.
Now when A and B are brought into contact, the distribution of the total internal energy (Ut) between them (UA, UB) changes in the direction of the equilibrium distribution (UAeq, UBeq). According to the basic postulates of statistical mechanics (Tolman 1938), the latter distribution occurs when the combined system spends an equal proportion of time in all of the microscopic states it can assume when its energy is Ut.
Thus, the number of states the combined system ranges over after contact is in general greater than the number before contact; that is, \({\updelta}\Omega_{\text{t}}\,{\ge}\,0\). Hence in Eq. 11, the condition for spontaneous change is
with the condition for equilibrium being \({\updelta}_{\text{r}}{\Omega}_{\text{t}} = 0\).
Equation 13 corresponds to the entropy condition, Eq. 6. Comparison of the two equations suggests that
where k is a constant whose value is to be determined. This equation is at constant volume and composition. Integration gives
To obtain the statistical mechanical analog of temperature, we rewrite Eq. 11 as
where
Combining Eqs. 14 and 16 gives
Comparison with Eq. 7 suggests that
This again is at constant volume and composition.
That \(\upbeta\) has the properties of 1/T follows from Eq. 16. Thus the condition for equilibrium between A and B (\({\updelta}_{\text{r}}{\Omega}_{\text{t}} = 0\)) is realized when \({\upbeta}_{\text{A}} = {\upbeta}_{\text{B}}\); and when \({\upbeta}_{\text{A}} \neq {\upbeta}_{\text{B}}\), energy flows from the system with the lower value of \({\upbeta}\) to the system with the higher value (e.g. if \({\upbeta}_{\text{A}} > {\upbeta}_{\text{B}}\), then \({\updelta}_{\text{r}}{\Omega}_{\text{t}} > 0\) if \({\updelta}\)UA > 0).
Interpretation
Entropy
I have discussed the interpretation of entropy previously (Nelson 1994). In brief, the change in entropy of a system corresponds to the relative change in the number of microscopic states a system ranges over (Eq. 14). Correspondence is with the relative, not the absolute, change because, when a system is brought into thermal contact with another system, it is the relative change that determines the direction of energy flow (Eq. 13).
Temperature
From Eqs. 17 and 19, reciprocal temperature (1/T) corresponds to the relative change in the number of microscopic states of a system with change in internal energy. This correspondence arises as follows.
From Eqs. 11 and 13, the condition for A and B to be in equilibrium when they are brought into contact is that, when a small quantity of energy is taken from one and added to the other, the relative increase in the number of microscopic states that one of them ranges over should be equal to the relative decrease in the number the other ranges over. Since the gain in energy of one system is equal to the loss in energy of the other, this condition is realized when the relative change in number of states with change in energy (\({\updelta}_{\text{r}}{\Omega}/{\updelta}U\)) is equal for the two systems (Eqs. 16 and 17). When this quantity is different for the two systems, energy flows from the system with the lower value to the system with the higher one, thereby increasing the number of states that the system as a whole ranges over (Eq. 13). Thus the lower value is associated with the hotter system and the higher value with the colder one. Hence the reciprocal temperature or degree of coldness of a system can be identified as the relative change in the number of microscopic states of the body, at constant volume and composition, with change in energy (Eqs. 17 and 19).
That temperature is related to the relative change in number of microscopic states, not the absolute change, is to be expected. When a hot body is brought into contact with a cold body, heat flows from the hot one to the cold one irrespective of how big or small either body may be. The direction of flow must necessarily therefore be determined by a relative quantity, not an absolute one.
That temperature is a differential quantity is, however, unexpected. We are used to thinking of temperature as a simple quantity, measured by, for example, the length of mercury in a capillary, or the volume of a gas at constant pressure. As we shall see from the examples below, temperature can be related to simple properties of systems, but what these properties are differs from one system to another.
Examples
To illustrate the above identification of temperature, I consider two examples.
Ideal monatomic gas
Consider first the case of an ideal monatomic gas. Let the energy of the gas be sufficiently high that the proportion of microscopic states in which two or more atoms share the same motion is negligibly small. Then according to the quantum theory, the number of microscopic states of the gas having an internal energy within a range (u) of a particular value (U) is given to a good approximation by
where N is the number of atoms, a is a constant, and U0 is the energy of the gas when all the atoms are stationary (Denbigh 1981: Sect. 12.10). Equations 17 and 20 give
Hence from Eq. 19
where \(\stackrel{-}{\varepsilon }\) is the average kinetic energy of each atom. This is a familiar result from the kinetic theory (Present 1958: Chap. 2).
Equation 22 is sometimes used to identify temperature. However, the connection it makes between temperature and average kinetic energy arises from the particular form of Eq. 20, and is not a general property of temperature (see next example). Use of this relation to identify T is therefore misleading.
From Eq. 22, the molar heat capacity of a monatomic gas at constant volume (\({\updelta}U_{\text{m}}/{\updelta}T\)) is given by (3/2)Lk, where L is the Avogadro constant. Comparison of this with the experimental value (3/2)R identifies k as R/L.
Einstein solid
As a second example, consider a crystalline solid comprising Nat identical atoms. Einstein treated this as 3Nat (N) simple harmonic oscillators, each with an energy (n + ½)hν, where ν is the classical frequency and n = 0, 1, 2 …. The energy of the solid is then
where U0 is the zero-point energy (½Nhν) and m is the number of quanta.
Now if N is large, the number of indistinguishable ways of distributing m quanta among N oscillators is (Callen 1985: Sect. 15–2):
Hence from Eq. 17, Footnote 7
Thus,
This is different from Eq. 22.
Note that elimination of m between Eqs. 23 and 26 gives
Differentiation of this gives the molar heat capacity at high temperatures as 3Lk or 3R.Footnote 8
Conclusion
In statistical mechanics, reciprocal temperature (1/T) corresponds to the relative change in the number of microscopic states a macroscopic system at equilibrium ranges over, at constant volume and chemical composition, with change in internal energy.
Notes
Also called ‘micro-states’, ‘quantum states’, ‘configuration states’, or ‘complexions’.
In this and subsequent equations, the conditions are those specified in the initial description of the system, viz. constant volume and composition.
For a full discussion of this definition, see my paper ‘Understanding entropy’ (submitted).
If qX is very small, the change in TX is negligible.
In this case, qA is also zero. However, it can be made finite by effecting the change to the system, not by closing C, but by using a cold body to remove a quantity of heat from one subsystem and a hot body to add an equivalent amount to the other.
I have evaluated \({\updelta}_{\text{r}}\Omega/{\updelta}U\) as \({\updelta}({\text{ln}}\,\Omega)/{\updelta}U\) and used Stirling’s approximation (ln x! ≈ x ln x ‒ x for x >> 1).
Using N = 3Nat and ex ≈ 1 + x (x << 1).
References
Bent, H.A.: The Second Law. Oxford University Press, New York (1965)
Callen, H.B.: Thermodynamics and an Introduction to Thermostatistics, 2nd edn. Wiley, New York (1985)
Denbigh, K.G.: Principles of Chemical Equilibrium, 4th edn. Cambridge University Press, Cambridge (1981)
Denbigh, K.G., Denbigh, J.S.: Entropy in Relation to Incomplete Knowledge. Cambridge University Press, Cambridge (1985)
Gibbs, J.W.: Elementary Principles in Statistical Mechanics. Scribner’s Sons, New York (1902)
Nelson, P.G.: Statistical mechanical interpretation of entropy. J. Chem. Educ. 71, 103–104 (1994)
Present, R.D.: Kinetic Theory of Gases. McGraw-Hill, New York (1958)
Schrödinger, E.: Statistical Thermodynamics. Cambridge University Press, Cambridge (1946)
Tolman, R.C.: The Principles of Statistical Mechanics. Oxford University Press, Oxford (1938)
Acknowledgements
I am grateful to a reviewer for suggesting many improvements to my exposition.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nelson, P.G. Statistical mechanical interpretation of temperature. Found Chem 21, 325–331 (2019). https://doi.org/10.1007/s10698-019-09337-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10698-019-09337-4