1 Introduction

With the development of container transportation, the task of efficiently managing scarce storage space resources in container terminals has become an important role for marine transport hubs. Containers arrive at the storage area randomly and are stacked on the ground in the arrangement of a yard block as shown in Fig. 1. Yard cranes (YCs) must first handle the containers located at the top tier, and the containers already stacked are rehandled to access the target container buried beneath them. Thus, inefficient handling can result in excessive operational delays, which can lead to bottlenecks in container flows. Therefore, to improve the productivity of container terminals, effective methods for determining the most efficient storage location of the arriving containers must be employed (Zhang et al. 2003).

Fig. 1
figure 1

Yard block configuration

Full size image

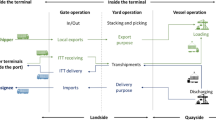
Container terminals handle various types of incoming containers, which can be classified as import or export containers depending on the vehicles that carry them. Import containers are discharged from vessels and loaded onto external trucks (ETs), whereas export containers are transported to the terminal by ETs and are loaded onto vessels. All of these containers are temporarily stored in the yard, and the goal of the storage strategy is to minimize the amount of time the vehicles that are to be loaded stay in the terminal. For this reason, the way the containers are stored depends on the characteristics of the vehicles that are to be loaded, such as the vehicles’ capacities and their arrival times. For example, ETs have small carrying capacities and large uncertainties in arrival times depending on the traffic conditions. Therefore, import containers are stacked at higher tiers, as the estimated retrieval times are shorter. In contrast, vessels carry large quantities of containers, and their arrival times are expected via berth plans. Thus, export containers are stored through decisions at two different levels: planning and operational (Chen and Lu 2012; Jiang and Jin 2017; Zhou et al. 2020; He et al. 2020a, b; Feng et al. 2021). At the planning level, containers are assigned to sub-blocks based on the container group, which is defined as a group of containers having the same departing vessel, port of destination (POD), size, and type (Kim et al. 2004; Zhen 2013, 2014; Jiang and Jin 2017; He et al. 2020a). At the operational level, containers are stacked within the range of a single yard bay in consideration of the loading operation (Kim et al. 2000; Zhang et al. 2010, 2014a, b). In the loading operation, planners schedule the loading sequence with two objectives: minimizing the handling effort of quay cranes (QCs) and YCs, and ensuring the stability of the vessel (Kim et al. 2000). Therefore, the storage configuration of export containers must be in a good shape to generate an efficient loading sequence. In this study, we focus on the container stacking problem (CSP) for export containers at the operational level in order to aid planners in constructing optimal load sequences.

The CSP for export containers is a real-time decision problem because incomplete and imperfect information is involved (Steenken et al. 2004; Borgman et al. 2010; He et al. 2020b). First, as most studies assume, the time at which the containers arrive at the yard cannot be accurately predicted because the arrival times are dynamically updated depending on the traffic conditions. Therefore, it is difficult to achieve the optimal results. Second, information on the weight of the containers to be loaded onto the vessel is uncertain. Many studies assume that container weight falls within one of three classes: heavy (H), medium (M), and light (L) (Kim et al. 2000; Zhang et al. 2010, 2014a). Some extended studies have converted the uncertainty of the weight information into probabilities (Kang et al. 2006; Zhang et al. 2014b). In practice, the estimated weight class can be identified as a different weight class when the container arrives at the terminal. Because of this, terminal operators use their experience as the basis for classifying container weights into different classes for each vessel. Third, the stowage instructions are not known one to two weeks in advance. Container ships are berthed at multiple ports along the shipping line, and stowage instructions vary depending on the loading operations performed at the previous port. For example, as shown in Fig. 2, heavier containers are required in section A and lighter containers are required in section B. This requires a stacking strategy that responds flexibly to this uncertain environment. Lastly, the YC workload at the time of container arrival is unknown in advance (Jiang and Jin 2017). Therefore, containers are dynamically allocated to multiple bays depending on the YC's workload at the time of arrival, resulting in different container weight distributions in each bay.

Fig. 2
figure 2

Example of a set of stowage instructions

Full size image

In this study, we propose a stacking strategy based on an online algorithm in which decisions are made with incomplete knowledge of the future (Karp 1992). Unlike an offline algorithm that yields optimal solutions with extensive computations, an online algorithm facilitates operations in dynamic environments that do not have ample time to compute before performing tasks. Because containers cannot be held after they arrive and the order in which they arrive cannot be controlled, an online algorithm that allocates storage locations when containers arrive at the block is appropriate (Murty et al. 2005).

A number of studies have employed online algorithms for the CSP (Dekker et al. 2006; Borgman et al. 2010; Park et al. 2011; Chen and Lu 2012; Ambrosino et al. 2013; Güven and Eliiyi 2014, 2019; He et al. 2020b), but they do not take into account many practical considerations such as uncertainty of the weight, type and arrival timing of containers, uncertainty about the stowage instruction of the vessel, and the dynamic nature of YC workload according to other interconnected operations. Therefore, this study proposes a data-driven dynamic stacking strategy (DSS) based on an online algorithm.

The data-driven DSS consists of two modules. The first is the Gaussian mixture model (GMM) generation module, which clusters the container weight into several weight classes. The second is the DSS module based on the online algorithm to determine the storage location of an arriving container in real time. This module adjusts itself to dynamically respond to the environment.

The remainder of this paper is organized as follows. In Sect. 2, relevant literature on the CSP is reviewed. A detailed description of the proposed method is provided in Sect. 3. In Sect. 4, computational experiments are conducted and interpreted. Finally, the conclusions are drawn in Sect. 5.

2 Literature review

In this section, we review previous studies related to the CSP in container terminals. Many researchers have studied on the related problem, and we refer to Vis and De Koster (2003), Steenken et al. (2004), Stahlbock and Voß (2008), and Carlo et al. (2014) which conducted comprehensive reviews of numerous studies on the efficient operation of container terminals. The solutions to the CSP have been classified into two types: one for import containers and one for export containers. For import containers, De Castillo and Daganzo (1993) proposed two stacking strategies: a non-segregation strategy that includes all stacks of the same size from all vessels, and a segregation strategy in which containers from different vessels are segregated. Kim and Kim (1999) implemented a segregation strategy for import containers that estimated the expected total number of rehandles. They presented a mathematical model for the relationship between the height of the stack and the number of rehandles. They also considered the uncertainty in the arrival times of import containers for constant, periodic, and dynamic arrival rates. Kim and Kim (2002) proposed a cost model that determines the optimal storage space and number of transfer cranes for import containers. The cost model included the costs of space, transfer cranes, and ETs, and they illustrated the effectiveness of their deterministic and stochastic models using numerical examples. Ting et al. (2010) proposed a category stacking strategy (also called a clustering stacking strategy) for import containers by analyzing historical data. They presented a pick-up booking system that categorizes the containers into several groups according to the pick-up priority predicted by historical data. Sauri and Martin (2011) extended the work of De Castillo and Daganzo (1993) and developed a segregation strategy that generates the fewest number of rehandles by mixing containers from different vessels. In addition, they considered the different probabilities of the time that elapsed before each container left the terminal as a function of the time each container arrived. Ambrosino et al. (2013) modeled import containers being loaded onto a train by comparing train loading policies (sequential, non-sequential, and partially sequential) for different stacking strategies (random, based on container weight, and based on container weight and commercial priority) in a container terminal. Maldonado et al. (2019) proposed three different stacking strategies based on the prediction (nominal, numerical, and nominal and numerical) of expected dwell times using the random forest method. They assessed their proposed method by applying it to two strategies (horizontal and vertical) in two scenarios (average and stressed).

Because the storage periods for import containers vary depending on the arrival time of ETs and trains, the CSP for import containers has been studied in a way that enables the arrival times to be predicted probabilistically. In contrast, the CSP for export containers considers vessel characteristics. Kim et al. (2000) proposed a dynamic programming (DP) model to determine the storage locations of export containers based on their weights. They assumed that heavier containers should be loaded onto the lower tiers of a vessel to guarantee its stability. Therefore, heavier containers are stacked at the higher tiers of the yard block to reduce the expected number of rehandles. Furthermore, they developed a decision tree to support real-time decisions. Duinkerken et al. (2001) evaluated the performance of the remaining stack capacity (RSC) strategy, which considers the stack height and container category using various stacking strategies (random, levelling, and closest position). Dekker et al. (2006) proposed a category stacking strategy that allows online optimization to facilitate loading operations. They used a simulation method to compare random stacking with category stacking based on the number of rehandles. Kang et al. (2006) presented a stacking strategy for export containers with uncertain weight information using a simulated annealing approach to minimize the number of rehandles. Furthermore, they proposed an advanced stacking strategy that overcomes the uncertainty in container weight through machine learning techniques. Park et al. (2011) proposed stacking strategies to dynamically determine the stacking location as the operational environment changes. The proposed strategies, which were based on an online algorithm, were generated by evaluating the weights of the decision criteria during the evaluation period. Simulations were conducted for a variety of stacking strategies, which were demonstrated to be effective in reducing QC delays. Chen and Lu (2012) proposed a hybrid sequence stacking algorithm (HSSA) based on an online algorithm to make decisions in real time. They observed that the HSSA outperformed the random and vertical stacking strategies in terms of the number of rehandles. Zhang et al. (2010) analyzed the error of a key model transformation in Kim et al. (2000) and presented the correct form. Zhang et al. (2014a), which was an extension of the studies by Kim et al. (2000) and Zhang et al. (2010), proposed two conservative models by reinterpreting the punishment coefficient for stacking light containers on top of stacks loaded with heavy containers. The proposed models outperformed the previous optimized models in terms of static and dynamic indicators. Zhang et al. (2014b) considered adjusting the proportion of unarrived containers in each weight class to a non-constant proportion in the constant proportion DP model proposed by Kim et al. (2000) and Zhang et al. (2010). In numerical experiments, they demonstrated that the proposed models with the adjusted weight class proportions for the remaining containers improved the stacking quality. Hu et al. (2014) proposed a branch-and-bound method based on the least-cost priority queue (LCBB) to obtain an optimal solution in which the number of rehandles is minimized, using the HSSA proposed by Chen and Lu (2012) to calculate the upper bound for the LCBB. Güven and Eliiyi (2014) studied two stacking strategies (random stacking and category stacking) for export containers. They considered container weight as another category attribute, and grouped containers with a weight of less than three tons into the same category. Güven and Eliiyi (2019) extended Güven and Eliiyi (2014) and expanded the stacking strategies to include all types of containers (export, transit, import, and empty containers). They compared three stacking strategies (random stacking, attribute-based stacking, and weight-relaxed stacking) through simulations. He et al. (2020b) studied stacking strategies that consider the uncertainty in the arrival sequence of vessels, assuming that the weight information and arrival order of the containers are known. Based on the three stacking rules (least reshuffle rule, lowest stack rule, and nearest stack rule), five heuristic algorithms were proposed according to a set of rules.

The contributions of our study in the context of the aforementioned studies are summarized as follows. First, this is the first study that applies predictive analytics for container weight classification to prescribe optimal decisions for the CSP. Most previous studies have simplified the problem by assuming three classes (light, medium, and heavy), and certain studies (Kang et al. 2006; Zhang et al. 2014b) have considered the weight uncertainty for each class. However, in practice, these assumptions are not practical because the weight is classified according to the size of the vessel and the range of weights of the containers to be loaded. Therefore, this study analyzes the historical data for container weight, and estimates the classification model for container weight class as a GMM using a machine learning technique. Second, we propose a dynamic stacking strategy that considers multiple bays. To the best of our knowledge, most studies have focused on the CSP for a single bay, and the stacking strategy was applied homogeneously to each bay. However, in a real-world environment, the proportion of containers in each weight class assigned to each bay is not constant. Hence, the remaining containers must respond dynamically to the containers that are already stacked. Therefore, this study presents a stacking strategy that responds to the configurations of multiple bays. Third, we develop a category stacking strategy to present practical alternatives that reflect real-world considerations. In most studies on the CSP for export containers (the exceptions being Dekker et al. 2006; Güven and Eliiyi 2019), the problem is defined as minimizing the expected number of rehandles based on the weight class. However, heavier containers are normally loaded onto lower tiers, depending on the configuration of the stowage and the precise weight of the containers. The category stacking that clusters containers with similar weights into the same stack can facilitate stowage planning by providing containers of various weights on the top tier in the yard.

3 Problem description

This study aims to optimize real-time decisions regarding the precise storage location of export containers for a given storage area while the containers are arriving. The storage area consists of multiple stacks in a bay, as shown in Fig. 3. In this study, the decision on the storage location refers to the selection of one stack in the storage area. In practice, the storage areas of export containers are not shared with those of import containers (Kim and Kim 1999; He et al. 2020b; Hu et al. 2021). Furthermore, each storage area designates areas for containers belonging to the same container group (Kim et al. 2004; Zhen 2013, 2014; Jiang and Jin 2017; He et al. 2020a). For these reasons, different stacking decisions are made depending on the container group. Therefore, we focus on stacking decisions that apply to the containers in a single container group.

Fig. 3
figure 3

Yard bay configuration

Full size image

The goal is to assign an arriving container to a stack in a way that conforms to the category stacking strategy. Category stacking for export containers aims to cluster containers with similar weights in the same stack. However, it is difficult to achieve this outcome due to the randomness of the arriving containers. The following two aspects need to be considered to improve the stacking quality according to the category stacking strategy: (1) how to define the similarity in container weights and (2) how to define the specific location assignment rules for each storage area. For aspect (1), researchers have manually classified container weights into several weight classes with approximate weight ranges. For aspect (2), the location assignment rules have been executed in the same way for all storage areas. However, predictive analytics for container weight classification and container assignment rules specific to dynamic storage areas can enhance the stacking strategy. In this respect, we propose a data-driven DSS that outperforms existing stacking strategies.

The proposed container stacking system is divided into two modules, as shown in Fig. 4. Module 1 is executed in advance, and module 2 is triggered by a container arriving at the port. In module 1, GMM-based predictive models, which cluster the container weights into several weight classes for each container group, are generated. Next, once a container has arrived, the pre-selected storage area is given, and the weight class for the container is predicted by the GMM generated in module 1. In module 2, the precise storage location (i.e., stack) for the container is selected using the proposed dynamic stacking strategy for the given storage area. The proposed stacking strategy is intended to dynamically adjust itself depending on the stack configuration in the storage area. A detailed description of the modules is provided in the following subsections.

Fig. 4
figure 4

Overview of the proposed container stacking system

Full size image

3.1 Module 1: generation of GMM

In module 1, we aggregate the historical data for the container weights over the entire voyage for each container group, and then generate the GMM specific to each container group for the container weight classification. The GMM is a model that represents a population as a linear superposition of subpopulations, and it assumes that each subpopulation follows a Gaussian distribution. Because the class label (i.e., subpopulation) of the data point is unknown, the GMM is an unsupervised learning method (Figueiredo and Jain 2002). In addition, the GMM is a soft clustering method that uses probabilistic inference to explain how much a given data point is associated with a certain cluster (i.e., subpopulation). Due to these characteristics, the GMM has been widely employed in unsupervised classification applications in which data tend to follow multimodal and complex distributions. In this study, the container weight class was defined for each cluster of the GMM. Furthermore, the probable weight class was predicted for new container input. For the detailed description, the following notations are introduced:

Notation

\(G\)

Set of container groups, indexed by \(g\)

\({K}_{g}\)

Set of clusters (i.e., weight class) for container group \(g\), indexed by \(k\)

\(x\left(i\right)\)

Container weight of container \(i\)

\(g\left(i\right)\)

Container group of container \(i\)

\(k\left(i\right)\)

Probable weight class of container \(i\)

\({\mu }_{k}^{g}\)

Mean of cluster \(k\) for container group \(g\)

\({\Sigma }_{k}^{g}\)

Covariance of cluster \(k\) for container group \(g\)

\({\pi }_{k}^{g}\)

Mixture weight of cluster \(k\) for container group \(g\); \(0\le {\pi }_{k}^{g}\le 1\) and \(\sum_{k\in {K}_{g}}{\pi }_{k}^{g}=1\)

\({z}_{k}^{g}\)

Latent indicator variable; defined as 1 if the observation data belongs to cluster \(k\) and 0 otherwise; \(\sum_{k\in {K}_{g}}{z}_{k}^{g}=1\), \(p\left({z}_{k}^{g}=1\right)={\pi }_{k}^{g}\)

\(p\left(x|g\right)\)

Marginal probability distribution of container weight \(x\) for container group \(g\)

\(\gamma \left({z}_{k}^{g}|g\right)\)

Posterior probability (i.e., “responsibility”) that container weight \(x\) is observed from cluster \(k\) for container group \(g\); \(\gamma \left({z}_{k}^{g}|g\right)=p\left({z}_{k}^{g}=1|x,g\right)\)

The GMM is parameterized by the mean \({\mu }_{k}^{g}\), covariance \({\Sigma }_{k}^{g}\), and mixture weight \({\pi }_{k}^{g}\). The assignment of the unknown class label \({z}_{k}^{g}\) is considered a latent variable instead of a parameter. It enables the joint distribution \(p\left(x,{z}_{k}^{g}\right)\) to marginalize the variable \({z}_{k}^{g}\) out to define the cost function independently of \({z}_{k}^{g}\). The resulting standard form of the GMM is written as

$$p\left( {x{|}g} \right) = \mathop \sum \limits_{{k \in K_{g} }} p\left( {z_{k}^{g} } \right)p\left( {x{|}z_{k}^{g} } \right) = \mathop \sum \limits_{{k \in K_{g} }} \pi_{k}^{g} N\left( {x{|}\mu_{k}^{g} , \Sigma_{k}^{g} } \right).$$
(1)

To estimate the three parameters of the GMM, the objective function is to maximize the marginal likelihood of the data (\(p\left(x|g\right)\)). Because there is no analytical solution, a numerical method was employed for the maximum likelihood estimation. The most widely used method is expectation maximization (EM). The EM algorithm estimates the model parameters through iterations of the expectation step (E step) and maximization step (M step). Given the initialized model parameters and the log-likelihood estimate, the E step uses the model parameters to evaluate the responsibility \(\gamma \left({z}_{k}|g\right)\) via

$$\gamma \left( {z_{k}^{g} {|}g} \right) = C_{g} \times \pi_{k}^{g} N\left( {x{|}\mu_{k}^{g} , \Sigma_{k}^{g} } \right),$$
(2)

where \({C}_{g}=1/\sum_{k\in {K}_{g}}{\pi }_{k}^{g}N\left(x|{\mu }_{k}^{g}, {\Sigma }_{k}^{g}\right)\). Then the M step re-estimates the model parameters using this responsibility value. These iterations lead to the convergence of the model parameters, and the resulting trained GMM provides the probable weight class of the new container input via

$$k\left( i \right) = \mathop {{\text{argmax}}}\limits_{{k \in K_{g} }} \gamma \left( {z_{k}^{g} {|}g} \right)$$
(3)

3.2 Module 2: dynamic stacking strategy

In module 2, we executed the DSS as an online algorithm to determine the storage location of an arriving container in real time. The overall framework of the proposed DSS is shown in Fig. 5. The algorithm inputs include the GMM-based prediction results for the weight class as well as the yard stack configuration of the pre-selected storage area for the arriving container. The storage location for the container is determined after the weight class-to-stack assignment. Both methods accommodate the GMM-based prediction results for the weight class obtained from module 1. Furthermore, the weight class-to-stack assignment method adapts the adjustment mechanism according to the dynamic change in the stack configuration, which leads to the generation of the stacking strategy that is specific to the storage area.

Fig. 5
figure 5

Framework of the proposed dynamic stacking strategy

Full size image

For the weight class-to-stack assignment, conventional approaches of category stacking apply the assignment method homogeneously for all storage areas, and they remain consistent during the period in which containers are arriving. However, in real-world environments, the stack configuration cannot be the same for all storage areas, and thus the stacking strategy must be adjusted according to the different stack configurations. Taking into account the limitations of conventional methods, we propose an improved approach to accommodate the dynamic change in the stack configuration of the storage areas. For the detailed description, the following notations are introduced:

Notation

 

\({A}_{g}\)

Set of storage areas for container group \(g\), indexed by \(a\)

\({S}_{a}\)

Set of stacks in storage area \(a\), indexed by \(s\)

\({K}_{as}\)

Set of weight classes designated for stack \(s\) in storage area \(a\), indexed by \(k\)

\({R}_{k}^{g}\)

Range of cumulative mixture weight values for weight class \(k\)

\({R}_{as}\)

Range of cumulative mixture weight values for stack \(s\) in storage area \(a\)

\(a\left(i\right)\)

Pre-selected storage area for container \(i\)

\(s\left(i|a\right)\)

Stack to be selected for container \(i\) given storage area \(a\)

\({t}_{as}\)

Remaining slot capacity (in number of containers) of stack \(s\) in storage area \(a\)

\({f}_{as}^{k}\)

Contribution of weight class \(k\) to \({R}_{as}\) for \(k\in {K}_{as}^{g}\)

\({X}_{as}^{g}\)

List of container weights for stack \(s\) in storage area \(a\) of container group \(g\)

First, we describe the procedure for the weight class-to-stack assignment. This assignment satisfies a many-to-many relationship. Regarding the GMM-based prediction results for the weight class, we focus on the mixture weight \({\pi }_{k}^{g}\), which represents the estimated size of the weight class \(k\). Given that the indices of the GMM are sorted in ascending order according to weight, the cumulative range of \({\pi }_{k}^{g}\) for each weight class can be represented by

$$R_{k}^{g} = \left\{ {r : \mathop \sum \limits_{{\begin{array}{*{20}c} {k^{\prime} \in K_{g} } \\ {k^{\prime} < k } \\ \end{array} }} \pi_{{k^{\prime}}}^{g} < r \le \mathop \sum \limits_{{\begin{array}{*{20}c} {k^{\prime} \in K_{g} } \\ {k^{\prime} \le k } \\ \end{array} }} \pi_{{k^{\prime}}}^{g} , r \in {\mathbb{R}}} \right\}.$$
(4)

Likewise, given that the indices of the stacks are sorted, the cumulative range of \({\pi }_{k}^{g}\) for each stack can be represented by

$$R_{as} = \left\{ {r :\mathop \sum \limits_{{\begin{array}{*{20}c} {s^{\prime} \in S_{a} } \\ {s^{\prime} < s } \\ \end{array} }} C_{a} \times t_{{as^{\prime}}} < r \le \mathop \sum \limits_{{\begin{array}{*{20}c} {s^{\prime} \in S_{a} } \\ {s^{\prime} \le s } \\ \end{array} }} C_{a} \times t_{{as^{\prime}}} , r \in {\mathbb{R}}} \right\},{ }$$
(5)

where \({C}_{a}=1/\sum_{s\in {S}_{a}}{t}_{as}\). Equation (5) calculates the coverage range for each stack based on the number of remaining slots, \({t}_{as}\). For example, if the storage area consists of four empty stacks, the cumulative ranges \({R}_{as}\) are set to (0, 0.25], (0.25, 0.5], (0.5, 0.75], and (0.75, 1]. Then,

$$K_{as}^{g} = \left\{ {k: R_{k}^{g} \cap R_{as} \ne \emptyset , k \in K_{g} } \right\}$$
(6)

defines the weight class-to-stack assignment \({K}_{as}^{g}\) such that the membership of the weight classes in a stack is determined by whether the elements of \({R}_{k}^{g}\) lie in the specified \({R}_{as}\). The variable \({K}_{as}^{g}\) is continuously adjusted because dynamic container placements change \({t}_{as}\), which impact \({R}_{as}\).

Figures 6 and 7 provide an example of the adjustment mechanism in the weight class-to-stack assignment procedure. It is supposed that two storage areas are assigned containers that belong to the same container group. The number of weight classes is set to four for the container group, and the number of stacks is set to four for both storage areas. The mixture weights \({\pi }_{k}^{g}\) are set to 0.25 for all weight classes. Figure 6 shows the initialized \({K}_{as}^{g}\) in which there are no differences between the storage areas.

Fig. 6
figure 6

Illustration of an initialized weight class-to-stack assignment (\({{\varvec{\pi}}}_{{\varvec{k}}}^{{\varvec{g}}}=0.25\;{\mathbf{for}\;\mathbf{k}}=1,2,3,4\))

Full size image
Fig. 7
figure 7

Illustration of an adjusted weight class-to-stack assignment (\({{\varvec{\pi}}}_{{\varvec{k}}}^{{\varvec{g}}}=0.25\;{\mathbf{for}\;\mathbf{k}}=1,2,3,4\))

Full size image

In contrast, Fig. 7 shows the adjusted \({K}_{as}^{g}\) after a total of 22 containers are stacked. The adjustment varies depending on the storage area. We now elaborate the steps to derive \({K}_{as}^{g}\) for storage area “A” using Eqs. (4)-(6). First, \({R}_{k}^{g}\) is always (0, 0.25], (0.25, 0.5], (0.5, 0.75], and (0.75, 1] for the weight classes. Second, \({R}_{as}\) is initialized as (0, 0.25], (0.25, 0.5], (0.5, 0.75], and (0.75, 1] for the empty storage area. After three, three, one, and three containers are stacked in each stack, \({R}_{as}\) is updated as (0, 0.2], (0.2, 0.4], (0.4, 0.8], and (0.8, 1] for the stacks. Therefore, it is necessary to check whether there is an overlap between \({R}_{k}^{g}\) and \({R}_{as}\). For weight class 1, the infimum and supremum of \({R}_{k}^{g}\) lie in \({R}_{as}\) for stacks 1 and 2, respectively. Accordingly, \({K}_{as}^{g}\) of weight class 1 includes stacks 1 and 2. In this way, the \({K}_{as}^{g}\) of the weight classes are dynamically updated when the stack configuration is changed, establishing the stacking strategy specific to the storage area.

Next, we describe the procedure for the storage location assignment for a container, given the weight class-to-stack assignment. Regarding the GMM-based prediction results for the weight class, we focus on the responsibility value \(\gamma \left({z}_{k}^{g}|g\right)\), which represents the probability that a container belongs to a certain weight class. If a single weight class is assigned to each stack (e.g., the weight class-to-stack assignment is 1–1, 2–2, 3–3, 4–4), as shown in Fig. 6, an effective strategy is to select a stack with the largest \(\gamma \left({z}_{k}^{g}|g\right)\) for the corresponding weight class \(k\). However, because multiple weight classes can be assigned to each stack, as shown in Fig. 7, a more sophisticated strategy that considers the contributions of multiple weight classes should be employed. In this context,

$$f_{as}^{k} = {\text{min}}\left\{ {\sup R_{k}^{g} ,\sup R_{as} } \right\} - {\text{max}}\left\{ {\inf R_{k}^{g} ,\inf R_{as} } \right\}$$
(7)

defines the contribution of weight class \(k\) to \({R}_{as}\). Then,

$$s\left( {i{|}a} \right) = \mathop {{\text{argmax}}}\limits_{{s \in S_{a} }} \mathop \sum \limits_{{k \in K_{as}^{g\left( i \right)} }} C_{as} \times f_{as}^{k} \times \gamma \left( {z_{k} {|}g\left( i \right)} \right),$$
(8)

where \({C}_{as}=1/\sum_{k\in {K}_{as}^{g\left(i\right)}}{f}_{as}^{k}\), indicates the proposed strategy that ensures the selection of a stack with the largest weighted average of \(\gamma \left({z}_{k}^{g}|g\right)\) according to the normalized \({f}_{as}^{k}\).

Figure 8 provides an example of the storage location assignment procedure, extending the example for storage area “A” in Fig. 7. In this example, \({f}_{as}^{k}\) of stack 1 is derived as \({f}_{A1}^{1}=\mathrm{min}\left\{\mathrm{0.25,0.2}\right\}-\mathrm{max}\left\{\mathrm{0,0}\right\}=0.2-0=0.2\) for weight class 1. Similarly, the resulting \({f}_{as}^{k}\) of stack 2 for weight classes 1 and 2 are \({f}_{A2}^{1}=0.25-0.2=0.05\) and \({f}_{A2}^{2}=0.4-0.25=0.15\), respectively. Then the weighted averages of \(\gamma \left({z}_{k}^{g}|g\right)\) are derived as \({f}_{A1}^{1}/{f}_{A1}^{1}\times \gamma \left({z}_{1}^{g}|g\right)\) for stack 1 and \({f}_{A2}^{1}/\left({f}_{A2}^{1}+{f}_{A2}^{2}\right)\times \gamma \left({z}_{1}^{g}|g\right)+{f}_{A2}^{2}/\left({f}_{A2}^{1}+{f}_{A2}^{2}\right)\times \gamma \left({z}_{2}^{g}|g\right)\) for stack 2. Thus, for a new container input, the stack that yields the largest weighted average of \(\gamma \left({z}_{k}^{g}|g\right)\) is selected among all the stacks in the given storage area.

Fig. 8
figure 8

Illustration of the storage location assignment procedure (\({{\varvec{\pi}}}_{{\varvec{k}}}^{{\varvec{g}}}=0.25\;{\mathbf{for}\;\mathbf{k}}=1,2,3,4\))

Full size image

The overall procedure of the DSS is described by Algorithm 1.

figure a

4 Numerical experiments

We conducted numerical experiments to validate the data-driven DSS (also called a GMM-DSS), which features the GMM-based weight clustering and dynamic adjustment mechanism for storage location assignment. We illustrate the improvements achieved by our proposed method through the experiments comparing with the stacking strategies that do not employ GMMs and/or dynamic adjustment mechanisms. First, the input data in the numerical experiment are described. Second, as a result of module 1, the generated GMM to define the weight class for each test instance is reported. Third, the impacts of the unit number of stacks on the algorithm performance are analyzed. Finally, an analysis comparing the stacking performances of the container stacking strategies is presented. This analysis shows how the wealth of data can be applied in the CSP to provide valuable decision support. All the algorithms were coded in Python and executed on a PC with an i5-6600H 3.3 GHz Intel Core processor and 8.0 GB of RAM.

4.1 Input data

The input data used in the numerical experiments were collected for 10 months in 2018 from a typical container terminal in Busan, Republic of Korea. The original data included detailed container information, such as the time of arrival and departure, departing vessel, POD, size, type, and weight of each container. Because the stacking decisions are made according to the container group, the original data were classified into container groups with the same attributes (e.g., departing vessel, POD, size, and type). In addition, only 20-foot containers were used in this study. Subsequently, a dataset of 12 container groups was used for the analysis. Table 1 reports the details of the selected 12 instances.

Table 1 Test instances for numerical experiments
Full size table

Next, we present the input data distributions over the entire voyage to check the justification for converting the container weights. This analysis comes from our assumption that the probability distribution of the container weights can be made available from the historical data due to the repeated tendencies over the voyage. It is rarely studied in literature to handle the information on container weights. Only a few studies, such as Kang et al. (2006) and Zhang et al. (2014b), utilized the true probability distribution or portion of the weight groups assuming such information is given or estimated by analysis of historical data in advance.

Figure 9 shows the distribution of the container weights over the entire voyage for instances 4 and 7. The x-axis indicates the range of container weight uniformly divided by 10 classes, and the y-axis indicates the number of containers for each voyage which is normalized to a value between 0 and 1. In this case, the distribution of container weights was similar over the entire voyage of the same instance. This is reasonable because the composition of the export cargo tends to be similar for each voyage. Due to the extensive data, GMM-based predictions for weight classes can be a powerful tool for effective category stacking in yards.

Fig. 9
figure 9

Distribution of container weights over the entire voyage (Instances 4 and 7)

Full size image

For container groups of a general type, the terminal had 19 blocks consisting of 50 bays each, as well as 10 stacks and six tiers. The storage area for the same container group was reserved in a unit of stacks. Because the unit number of stacks is usually set to 10 stacks (i.e., one bay) or five stacks, we conducted the experiments for both cases where the experimental results are presented in Sect. 4.5. The total number of storage areas was set to the minimum value required for the corresponding container group. Considering the buffer storage space for rehandling operations that exists in practice, the maximum allowable tier for containers was limited to the fifth tier.

4.2 Design of experiments

For each instance in this study, we divided a training dataset for generating the GMM in module 1 and a test dataset for simulation. The test dataset is constructed by randomly selecting a voyage and collecting a corresponding list of loaded containers from the historical data of the test ship-lanes (test instances). The training dataset is the remainder of historical data except for the test dataset. The results of GMM-based clustering with the training dataset are provided in Sect. 4.3, followed by sensitivity and comparative analysis results.

In simulation experiments, two kinds of randomness are considered: the container arrival sequence and assignment to a storage area. The detailed list of the to-be-stacked containers is unknown in advance and even unpredictable in practice. Further, a pre-selected storage area is given because the designation of the storage area for an arriving container is dynamically assigned depending on the workload of the YC. Therefore, the container arrival sequence was made by randomly selecting a container list in the test dataset, and a storage area was randomly assigned to a container in the simulations.

The stacking performance was evaluated based on category stacking, which aims to cluster containers with similar weights into the same stack. Therefore, we introduced an evaluation function

$$E\left( g \right) = \frac{{\mathop \sum \nolimits_{{a \in A_{g} }} \mathop \sum \nolimits_{{s \in S_{a} }} SD\left( {X_{as}^{g} } \right)}}{{\mathop \sum \nolimits_{{a \in A_{g} }} \left| {S_{a} } \right|}},$$
(9)

where the standard deviation of the container weights in the stack was measured. The evaluation function \(E\left(g\right)\) indirectly minimizes the makespan during future loading operations for a given category stacking strategy.

4.3 GMM-based clustering for container weights

Using 12 test instances, we employed the GMM method to cluster the container weights into \(K\) clusters. For the training data, a set of preliminary experiments was conducted to investigate the appropriate value of \(K\) for each test instance, varying \(K\) from 1 to 5 in steps of 1. The value of \(K\) was assigned the smallest value based on the Bayesian information criterion (BIC). Figure 10 shows the resulting GMM for the two test instances. The histogram in Fig. 10 indicates that the container weights exhibited a multi-peak distribution, and in both instances, it can be seen that five clusters are most appropriate. Figure 10 shows that GMM obtained via statistical modeling reasonably represents a distribution that is difficult to express as a single normal distribution. The results of module 1 for all the instances are presented in Appendix A.

Fig. 10
figure 10

Histogram and GMM-based density curve of the container weights (Instances 7 and 11)

Full size image

4.4 Sensitivity analysis of the unit number of stacks

This section validates the performance of GMM-DSS according to the unit number of stacks. The unit number of stacks within a storage area is usually set to 10 stacks for export containers, but it varies from terminal to terminal. For the sensitivity analysis of the unit number of stacks, \(\left|{S}_{a}\right|\) was set to 5, 10, 15, and 20. The GMM was generated using the training dataset, and then GMM-DSS was implemented using the test dataset. Table 2 reports the change in the average of \(E\left(g\right)\) according to the variation in the unit number of stacks \(\left|{S}_{a}\right|\). In the case of instance 1, it was excluded from experiments on more than 15 stacks as the number of tested containers was less than 50. In most instances, it is observed that \(E\left(g\right)\) decreases as the unit number of stacks increases. These results imply that as the number of unit stacks increases, the weight distribution of containers may have been relatively stable and homogeneous over storage areas since the containers are less scattered into multiple storage areas. Meanwhile, Instances 3, 5, and 6 yield the minimum \(E\left(g\right)\) when the unit number of stacks is equivalent to 10 and 15, although the differences of \(E\left(g\right)\) in instances are not significant. The GMM-DSS works reliably to comply with the category stacking strategy, including the case of 10 stacks widely used in container terminals. Thus it is believed to be worth being introduced into the terminal operating system.

Table 2 Impact of the unit number of stacks on average \({\varvec{E}}\left({\varvec{g}}\right)\)
Full size table

4.5 Comparative analysis of container stacking strategies

For comparison purposes, we implemented four alternative stacking strategies: a GMM-based static stacking strategy (GMM-SS), current practice, hybrid sequence stacking strategy (HSSS), and a random stacking strategy (RSS). For the GMM-SS, the weight classes and storage locations of the containers were determined by our GMM-based dynamic stacking strategy (GMM-DSS), while the dynamic adjustment mechanism in the weight class-to-stack assignment was ignored. For the current practice, the weight classes were defined by dividing the container weights into weight classes by ‘number of stacks in a bay,’ where each weight class has equal size of weight range according to the historical data. In addition, the storage locations of the containers were determined in such a way that the stack and weight classes were allocated on a one-to-one basis. For the HSSS proposed by Chen and Lu (2012), the weight classes were defined by dividing the container weights weight classes by ‘(number of stacks in a bay)\(+\)(number of tiers in a stack)\(-3.\)’ Then, HSSS induces heavier containers to be stacked in the left upper locations and lighter containers to be stacked in the right lower locations. In the RSS, the containers were stacked in a way that filled the stack sequentially according to the arrival order without considering the container weights. All five strategies, including our proposed method, were executed in seconds; thus, they are suitable for an online algorithm.

We conducted a simulation to compare the proposed method to the four alternative strategies for two different cases where the unit of storage area is five stacks or 10 stacks. The resulting performance for the stacking strategies is presented in Tables 3 and 4 for the cases in terms of the average \(E\left(g\right)\) for 100 repetitions. For both cases, the proposed GMM-DSS method obtained the minimum \(E\left(g\right)\) on average for all test instances. Specifically, for the case of five stacks in Table 3, the GMM-DSS performed better than the GMM-SS by 6.0%. This is the result of the dynamic adjustment mechanism in the weight class-to-stack assignment. In addition, the performance of the GMM-DSS was better than the current practice, HSSS, and RSS by 33.1, 41.6 and 44.1%, respectively. This result implies that the proposed method was more effective as the data-driven approach as well as the dynamic adjustment mechanism was incorporated into the stacking strategy. For the case of 10 stacks in Table 4, the results show that proposed method is superior to the other methods as in the case of five stacks. The performance of the GMM-DSS was better than the GMM-SS, current practice, HSSS, and RSS by 8.1, 43.6, 52.8, and 59.6%, respectively. Moreover, Fig. 11 demonstrates the robust performance of our proposed method for the experimental repetitions. The current practice performed better on average than the HSSS and RSS, and the proposed GMM-DSS and GMM-SS are dominant over the current practice. Therefore, we can conclude that the proposed GMM-DSS method is worth introducing in practice because it has the most reliable and best performance.

Table 3 Experimental results for the test instances (the unit of storage area = five stacks)
Full size table
Table 4 Experimental results for the test instances (the unit of storage area = 10 stacks)
Full size table
Fig. 11
figure 11

Box plots of experimental results for \(E\left(g\right)\) after 100 repetitions (the unit of storage area = 10 stacks, Instances 10 and 12)

Full size image

4.6 Comparative analysis according to variability

This section validates the algorithm performances according to variability in container weights. The proposed GMM-DSS utilizes the information on container weights from historical data and creates a GMM to approximate the distribution of container weights; thus it should be verified whether the GMM-DSS and GMM-SS can yield robust performance under a certain degree of variability. To this end, container weights \(x\left(i\right){^{\prime}}\) for the test were randomly generated as follows: \({x\left(i\right)}^{^{\prime}}=\mathrm{min}\left(\mathrm{max}\left(x\left(i\right)+500\times \sigma \times N\left(0, 1\right),LB\left(i\right)\right),UB\left(i\right)\right)\)(kg), where \(x\left(i\right)\) is a randomly selected sample data from the training dataset, \(\sigma\) is related to the variability, \(N\left(0, 1\right)\) is the random generator from a standard normal distribution, and \(LB\left(i\right)\) and \(UB\left(i\right)\) are the lower bound and upper bound on weights of container \(i\) introduced to avoid extreme values. \(\sigma\) was set to 0, 1, 2, 3, and 4. Figure 12 shows the performance of five stacking algorithms for the experimental repetitions under variability on container weights. For all the cases of σ, the proposed GMM-DSS and GMM-SS dominantly outperform the other algorithms in terms of \(E\left(g\right)\). GMM-DSS slightly outperforms GMM-SS. Furthermore, although performance degrades as variability increases, there is no significant difference in the change compared to other algorithms. Thus, it can be concluded that the proposed algorithms are robust to variabilities by taking advantage of predictive analytics.

Fig. 12
figure 12

Results according to variability on \(E\left(g\right)\) (the unit of storage area = 10 stacks, Instances 5 and 9)

Full size image

5 Conclusion

The goal of this paper is to introduce the wealth of data generated by the container terminal into the methodology of determining the storage location of the arriving containers. We presented a two module-based DSS to manage the CSP in container terminals. In our study, the CSP was solved by a category stacking strategy to facilitate stowage planning. In contrast to previous studies, the proposed method applies predictive analytics for container weight classification using historical data, and container assignment to a specific storage area is executed dynamically to outperform the existing stacking strategies. To the best of our knowledge, these two main features have not been introduced in the literature before. Specifically, in module 1, we generated a container group-specific GMM for container weight classification. In module 2, we implemented the DSS as an online algorithm to determine the storage location of an arriving container in real time. We conducted numerical experiments to validate the effectiveness of the proposed method using real-life data from a typical container terminal in Busan, Republic of Korea. For the generality of terminal environments, two different cases for the reservation unit in a storage area are considered in the experiments. The experimental results showed that the proposed method outperforms four other alternative stacking strategies (i.e., the GMM-SS, current practice, HSSS, and RSS). Therefore, our proposed method performs robustly and can further improve yard operations and terminal competitiveness.

The experimental results are encouraging in that it implies that the improvements in the stacking performance are related to the category stacking. The proposed method is expected to achieve greater improvements in practice when data-driven inferences can be derived from more historical data. In future research, our method could be extended to transshipment containers by considering the detailed characteristics of those operations. In addition, novel stacking strategies, such as the flexible space-sharing strategy and related operations such as stowage planning, could be integrated into our method to generate greater effectiveness in terminal operations.