Anticipating technical car sequencing rules in the master production scheduling of mixed-model assembly lines

Abstract

In this paper, we propose a new linear programming-based approach that enables the consideration of technical car sequencing rules in the master production scheduling of mixed-model assembly lines at a much higher level of detail than previous approaches. To this end, we investigate certain interdependencies of car sequencing rules, which have largely been neglected, both in practice and in the research literature. We illustrate the existence and impact of these interdependencies and show that they induce additional implicit constraints, which can be represented by linear inequalities and incorporated into linear optimization models for master production scheduling. In a numerical study, we evaluate the approach and show, that it can significantly reduce sequencing violations compared to existing approaches.

1 Introduction

The concept of assembly lines was originally invented by Henry Ford to efficiently produce a uniform product in a high volume. However, currently, the age of mass customization, often a multitude of product variants is concurrently manufactured on the same assembly line. In the automotive industry, this approach is driven to the extreme, allowing customers to configure billions of model variants by selecting and combining optional equipment (short options) (Holweg and Pil 2001). At the assembly line, complex options require more assembly time than simple standard options, such as the installation of an electric sunroof (Herlyn 2012), increasing the risk of work overloads, which at this level can only be coped with by the deployment of an expensive additional workforce.

Many authors have addressed the challenge of finding good production sequences, alternating work-intensive models with less work-intensive models to avoid overloads (Boysen et al. 2009b). One approach, commonly known as car sequencing and widely used in industrial practice, requires that among every N_o subsequent models in a production sequence, only H_o may contain a certain complex option o (Dörmer 2012; Boysen et al. 2009b). In addition, Solnon et al. (2008) distinguished between hard and soft sequencing rules. Hard rules are caused by technical capacity limits and must be strictly followed, as violations lead to a production line standstill such that the facility can complete its work and thus lead to loss of output. Soft rules are caused by personnel resources and can be violated for a short period if more personnel are assigned to the corresponding facilities. In this study, we concentrate on the hard restrictions, which typically affect only a small subset of all available equipment options (often no more than five or six of them).

Other approaches in addition to car sequencing aim to explicitly minimize the work overload of a production sequence (mixed-model sequencing) or optimize part logistics by leveling material supply (level scheduling). For more details on these approaches, we refer to Bautista and Cano (2008), Boysen et al. (2009b), Dörmer (2012), and Golle et al. (2014).

Clearly, the achievable quality of the production sequence heavily depends on the set of model variants, which are to be sequenced, that is, which are assigned to a certain shift or a certain day by the preceding planning step, the master production scheduling. In this planning step, the major goal is to fulfill production deadlines while keeping inventory costs low. Previous studies have attempted to anticipate and incorporate the requirements of the sequencing step (Boysen et al. 2009a) or even integrate the two planning steps (Doermer et al. 2013). While the former approaches pursue rather simple strategies, such as ensuring certain ratios of equipment options in the production program, the full integration leads to very complex optimization problems, which are difficult to solve for practically relevant problem dimensions.

In this paper, we propose an approach of the first type, which enables the consideration of sequencing requirements at a much higher level of detail compared to previous approaches. Consequently, we focus on the car sequencing approach and investigate the interdependencies of car sequencing rules, which have largely been neglected, both in practice and in previous studies. We illustrate the existence and impact of these interdependencies and show that they can be represented by linear inequalities, which can be incorporated into linear optimization models for master production scheduling. Although assembly lines, in reality, may have numerous manufacturing constraints, in practice, special attention is usually attributed to the few hard restrictions, as their violation cannot easily be mitigated. Examples of affected options are roof systems (sunroof, panoramic roof, cabriolet) and all-wheel drive. In a numerical study, we evaluate our approach and show that it can significantly reduce the resulting violations of hard restrictions in the sequencing step.

The remainder of this paper is structured as follows. In the next section, we review previous studies that investigate master production scheduling with anticipated or integrated sequencing. In Sect. 3, the problem setting is explained, and basic models for master production scheduling and sequencing are presented. We discuss the basic model for master production scheduling and provide a simple extension. Subsequently, we show by means of an illustrative example that interdependencies between car sequencing rules exist and can prevent the existence of a feasible car sequence. In Sect. 4, we derive linear inequalities, generalize these findings, and derive a general approach to consider interdependencies in master production scheduling using additional linear constraints. In Sect. 5, we evaluate novel approaches in a numerical study.

2 Literature review

Despite its high relevance, only relatively few studies on master production scheduling problems and their interplay with a succeeding sequencing problem have been conducted. One of the first model-based approaches for master production scheduling was proposed by Hindi and Ploszajski (1994). They focus on the selection of orders from an order bank, considering the desired number of orders and the maximum acceptable level of options. For each option k, there is a fixed upper bound ${b}_{k}$, which allows the planner to consider the sequencing rules.

Bolat (2003) points out that the model of Hindi and Ploszajski “greedily choose[s] the easy jobs and leave[s] the difficult ones for later periods” To avoid “cherry picking,” Bolat’s model considers the upper and lower capacity limits for each station. The lower limit prevents the selection of only “simple” orders with a few options, whereas the upper limit represents the sequencing rules. The goal of the model is to select a fixed number of orders for the next period and minimize the total cost caused by deviation from the due dates.

Ding and Tolani (2003) developed a model to schedule the production of n models in a planning horizon of m time periods to achieve level production. The authors assume that the demands of various models are known. They calculated the ideal daily total production as well as the ideal average daily production for each model i and minimized the square deviation. In this model, the sequencing rules for the model options are not considered.

Boysen (2005) and Boysen et al. (2007, 2009a) develop a basic mixed-integer programming model for master scheduling (MS-B) that, like Bolat's model, minimizes total costs by deviation from the due date. As an extension, they consider T planning periods and assume that costs for the deviation of an order from its due date increase linearly in terms of time, causing inventory costs for early production and penalty costs for late delivery. In addition, Boysen et al. (2009a) developed linear constraints to anticipate the sequencing objectives in the master scheduling for each of the three sequencing approaches, thereby allowing for better coupling of master scheduling and sequencing. We will discuss this approach in the case of car sequencing in detail below. Fliedner and Boysen (2008) presented an approach to solve the car sequencing problem via Branch and Bound, also incorporating the coupling approach.

According to Bolat's model, Volling (2009), and Volling and Spengler (2011) investigate the link between master production scheduling and order promising. They proposed mixed-integer linear model formulations for both planning steps. In master scheduling, a resource-related and period-related capacity is introduced as the quotient of the available working time and cycle time. To include sequencing constraints, they defined fixed upper and lower bounds on resource utilization.

Doermer et al. (2013) presented an approach in which master production scheduling (MPS) and sequencing were integrated. Orders from an order bank are assigned not only to a period but also to a cycle within a period. The mixed-model conditions of the sequencing were considered by restrictions. Doermer et al. indicated that this optimization problem can be solved optimally within a reasonable time for small-sized problem instances. To solve real-life instances, an adapted assignment heuristic was presented.

We will show below, that even if the ratios imposed by sequencing rules are considered in the master scheduling step as proposed by Bolat (2003), Boysen (2005), and Volling (2009), it is not guaranteed that a feasible sequence exists in the car sequencing step. This phenomenon is caused by the interplay of the car sequencing rules, which leads to additional implicit constraints on car models featuring combinations of options. This issue is addressed only in the approach of Boysen et al. (2009a) by introducing an additional parameter, which enforces an over-fulfillment of the rule ratios. In the remainder of this paper, we will show that these implicit constraints can be made explicit and added to the master scheduling formulation in the form of linear inequalities, significantly decreasing the number of rule violations in the car sequencing step.

3 Problem setting, basic modeling, and an illustrative example

Most automotive OEMs pursue a build-to-order production strategy accompanied by an order-driven planning process (ODP) to match the supply of resources and given capacities with highly variable product demand (Meyr 2004; Volling and Spengler 2011). In this study, we took a short-term planning perspective, that is, we assumed that production capacities and shift plans are given as a result of a mid-term aggregate production planning step (Sillekens et al. 2011). In the following section, we briefly describe and formalize the parts of the ODP process, which are relevant for our investigation.

3.1 Master production scheduling

We present two approaches for the basic modeling of master production scheduling. The basic model (MPS) from existing studies, and an approach with a small modification to improve the anticipation of sequencing rules (MPS+).

3.1.1 Basic model (MPS)

Within the ODP, first, delivery dates for individual customer requests are determined in a real-time order promising (OP) process, considering lead times, sales quotas, and available capacities, and communicated to the customer. If the customer accepts the offer, a production order associated with a production due date is added to the order bank. The main purpose of MPS in the automotive context is to assign individual customer orders to production periods, such that the capacity constraints are met and the violation of due dates and the incurring of inventory costs are prevented.

In this study, we formalize the MPS along the lines of Boysen et al. (2009a). A complete list of all the symbols used in this study is given in Appendix 1. We divide the planning horizon into T production shifts to which N $\left( {i = 1, \ldots ,N} \right)$ production orders are to be assigned, which are associated with due dates $L_{i}$ and characterized by a subset of a set O of equipment options. Deviating from the formulation in Boysen et al. (2009a), we use an additional period T + 1 to capture orders, which cannot be assigned within the planning horizon because of the violation of constraints. The system capacity for each period is limited by P cycles. The cost coefficients $c_{it}$ account for inventory holding costs in the case of early and penalty costs in the case of late production with respect to the due date $L_{i}$ of an order $i$. We elaborate on the details of the calculation of these coefficients in Sect. 5.

According to Boysen et al. (2009a) and using the notation given in Table 1, we can model the MPS planning task as the following binary linear programming problem:

$$Minimize\; z_{1} = \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{t = 1}^{T + 1} c_{it} \cdot x_{it}$$

(1)

Table 1 Notation for the master production scheduling model (MPS)

subject to

$$\mathop \sum \limits_{t = 1}^{T + 1} x_{it} = 1\quad \forall \,i = 1, \ldots ,N$$

(2)

$$\mathop \sum \limits_{i = 1}^{N} x_{it} \le P\quad \forall \,t = 1, \ldots ,T$$

(3)

$$x_{it} \in \left\{ {0{ },{ }1} \right\}\quad \forall \,i = 1, \ldots ,N{ };\;t = 1, \ldots ,T + 1$$

(4)

The objective function (1) minimizes the total deviation and inventory holding costs. Constraint set (2) ensures that each order is assigned to exactly one planning period. For each period, the sum of the assigned orders may not exceed the number of available production cycles, P (3).

As mentioned above, Boysen et al. (2009a) proposed an extension of their formulation to anticipate the sequencing rules by controlling the demand for option occurrences by adding the following set of constraints:

$$\mathop \sum \limits_{i = 1}^{N} d_{io} \cdot x_{it} \le \lambda \cdot \frac{{H_{o} }}{{N_{o} }} \cdot P\quad \forall \,o \in O{ };\;t = 1, \ldots ,T$$

(5)

In this constraint set, the number of option occurrences per planning period is limited by the quotient of $H_{o}$ and $N_{o}$ times the available production cycles P controlled by a weighting factor $\lambda$. Boysen et al. (2009a) indicated that the weighting factor $\lambda$ determines whether the resulting car sequencing problem can be solved without violations, and proposed an approach to set $\lambda$ appropriately by lower-bound computations (Fliedner and Boysen 2008). However, there is no exact approach to determine $\lambda$. Furthermore, $\lambda$ is a constant value that applies to all options in the same manner. This means that all options are equally weighted to improve the results of the car sequencing problem. In addition, $\lambda$ directly influences the utilization of the station at which option o is installed. As $\lambda$ decreases, the utilization of this station also decreases. However, the goal of a decision-maker should be to utilize all resources to their maximum capacity ($\lambda = 1)$ without violating sequencing rules.

3.1.2 A model variant with improved anticipation (MPS+)

Another major issue of Inequality (5) is that the maximum installation rate on the right-hand side depends on the production capacity instead of the actual number of orders assigned to a period. Assuming the logistic problems of an option o led to the fact that this option could not be installed for a while, the percentage of this option in the order pool is now higher than the installation rate. Consider the following example: Assume an order pool with 100 orders and two periods with production capacities $P = 50$. Owing to the logistic problems of an option o, the percentage of orders in the order pool featuring this option is assumed to be 60%, that is, 60 orders. A sequencing rule of 1:2 is imposed on this option, which implies a maximal installation rate of 50%. The optimization model will schedule as many orders as possible while respecting Inequality (5), because the unscheduled orders (in period $T + 1$) cause the highest deviation costs. Owing to (5), a maximum of 25 orders with option o can be scheduled per period. This results in 50 orders for period one, and 25 of them with option o. According to (5), only 25 of the remaining 35 orders with option o can be scheduled in period two. Thus, 40 orders are scheduled in period two, among which 25 with option o and 15 without option o. Ten orders with option o remain in the order pool. The actual installation rate of option o in period two is therefore ${\raise0.7ex\hbox{${25}$} \!\mathord{\left/ {\vphantom {{25} {40}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${40}$}} = 62.5\%$, which inevitably leads to violations of the sequencing rule.

Thus, to better anticipate the sequencing rules in each period, it is necessary to consider the installation rate as a function of the total sum of orders in each period. Therefore, we suggest replacing the production capacity $P$ with the number of scheduled orders:

$$\mathop \sum \limits_{i = 1}^{N} d_{io} \cdot x_{it} \le \lambda \cdot \frac{{H_{o} }}{{N_{o} }} \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \quad \forall \,o \in O{ };\;{ }t = 1, \ldots ,T$$

(6)

In our example, the new Inequality (6) results in period one still scheduling 50 orders and 25 of them with option o, and in period two, 30 orders and 15 of them with option x. In both periods, the installation rate of option o is 50% and can therefore, be sequenced without violations. This leaves 20 orders with option o in the order pool that cannot be scheduled.

We refer to model (1)–(5) originally suggested by Boysen et al. (2009a) as the MPS approach and to our modified model (1)–(4) plus (6) as the MPS+ approach. A comparison and discussion of these two approaches are provided in the numerical studies.

3.2 Car sequencing

After the orders for individual car models are assigned to production shifts, a production sequence must be determined, which prevents work overload at the stations of the assembly line. Because each car model is characterized by an individual combination of equipment options, the workload at the workstations usually varies from model to model. Typically, work overload occurs when several models with high workloads at a specific station (e.g., caused by the installation of a sunroof) directly follow each other in the production sequence. Work overload can require costly counter-actions, such as line stoppages (Boysen et al. 2009a; Wild 1972).

In this paper, we focus on the car sequencing approach, which is still of major relevance in the automotive industry (cf., e.g., Fliedner and Boysen 2008). A set of sequencing rules of type $H_{o} :N_{o}$ is imposed, ensuring that in the production sequence, out of $N_{o}$ successive models, only $H_{o}$ may contain option o.

To formalize the approach, we use a formulation as an optimization model, which is based on Boysen et al. (2009b). In this formulation, the planning horizon is divided into $T^{S}$ production cycles (with $t = 1, \ldots ,T^{S}$), where $T^{S}$ coincides with the number of orders that are assigned to the shift for which the production sequence is to be generated. In the traditional statement of the car sequencing model, violations of car sequencing rules are allowed; however, their number is minimized in the objective function. We list the notations used in the following model formulation in Table 2.

$$Minimize z_{2} = \mathop \sum \limits_{m \in M} \mathop \sum \limits_{t = 1}^{{T^{S} }} z_{ot}$$

(7)

$$\mathop \sum \limits_{m \in M} x_{mt} = 1\quad \forall \,t = 1, \ldots ,T^{S}$$

(8)

$$\mathop \sum \limits_{t = 1}^{{T^{S} }} x_{mt} = d_{m} \quad \forall \,m \in M$$

(9)

$$\mathop \sum \limits_{m \in M} \mathop \sum \limits_{{t^{{\prime }} = t}}^{{min\left\{ {t + N_{o} - 1;T^{S} } \right\}}} a_{mo} *x_{{mt^{{\prime }} }} - \left( {1 - \mathop \sum \limits_{m \in M} a_{mo} *x_{mt} } \right)*BI \le H_{o} + BI*z_{ot} \quad \forall \,o \in O; \forall \,t = 1, \ldots ,T^{S}$$

(10)

$$x_{mt} \in \left\{ {0,1} \right\}\quad \forall \,m \in M;\;t = 1, \ldots ,T + 1$$

(11)

$$z_{ot} \in \left\{ {0,1} \right\}\quad \forall o \in O;\;t = 1, \ldots ,T + 1$$

(12)

Objective function (7) minimizes the number of total sequencing rule violations. Constraint sets (8) and (9) ensure that each model is assigned to exactly one cycle and that, for each individual model $m \in M$, a demand $d_{m}$ is met. Sequencing rules of type $H_{o} : N_{o}$ are considered in the constraint set (10). The binary coefficient $a_{mo}$ indicates whether model m contains option o.

Table 2 Notation for the car sequencing model

3.3 An illustrative example of the interdependency of car sequencing rules

In this section, we demonstrate using an example that even if we limit option occurrences in the master production schedule according to the car sequencing rules, we cannot guarantee the existence of a feasible sequence in the car sequencing problem. Assume a set of orders consisting of models with up to two options, A and B. The sequencing rule for option A is defined as $1:2 = 50\%$ and for option B as $1:5 = 20\%$. Figure 1 shows the sequence in which orders with options A and B are ideally scheduled according to the sequencing rules. Row one displays the cycle number, rows two and three indicate whether the car model in this cycle contains options A and/or B, respectively, and line four shows the resulting model sequence. We have four possible combinations of the two options in the resulting sequence: option A only, option B only, both options AB or none of the two. The resulting sequence is characterized by an installation rate of 50%, 20%, and 10% for options A, B, and AB, respectively. We call this sequence ideal because the option-specific ratios $H_{o} :N_{o}$ prescribed by the sequencing rules are exactly matched by the resulting production sequence. In the remainder of this paper, we will denote the installation rates of options and combinations of options by $\sigma_{o \ldots o^{\prime}}$.

Fig. 1

Ideal sequence of two options, A and B

A sequence can always be completed by repetition when the state from cycle one reoccurs. As shown in Fig. 1, the sequence could therefore be cut off after cycle ten.

Assuming the production schedule contains 15% AB and we want to sequence as many models with option B as possible, to improve the installation rate of AB, in Fig. 2, a model that features only option B is replaced by a model featuring the combination AB in cycle six. Thus, no model with option A can be scheduled in cycles five and seven without violating the sequencing rule for option A.

Fig. 2

Sequence of two options A and B with 15% AB

As a result, the upper bound $H_{o} :N_{o}$ is met by option B, but no more than 45% of the models with option A can be sequenced. Consequently, no feasible model sequences exist for any production programs with a share of 15% of models featuring options A and B and more than 45% of models including option A. However, such production programs can easily be generated by the master production scheduling, even if the option occurrences are considered by upper bounds $H_{o} :N_{o}$.

This example illustrates that a fixed share of models featuring a combination of both options can impose implicit limits on the maximum installation rates of the two individual options, which fall below the levels induced by the sequencing rules. Hence, even if the rule-specific ratios are met by the master production schedule, a feasible car sequence may not exist. To ensure that a sequence can be generated from the production plan without violating the sequencing rules, master production scheduling must consider these implicit limits.

4 Linear inequalities for implicit constraints imposed by two options

We now derive linear inequalities, which represent the implicit limits imposed on the installation rates of options and combinations of options based on the interdependencies of the sequencing rules.

We consider a production program consisting only of models featuring up to two options, A and B, with car sequencing rules $H_{o} :N_{o}$. In this section, we consider the case $H_{o} = 1$, because this constellation is most prevalent in car sequencing rules in both theory and practice (Solnon et al. 2008). In Sect. 4.4, we generalize our findings. We denote the minimal distance between two models featuring the same option o as the ratio of $N_{o}$ and $H_{o}$:

$$q_{o} = \frac{{N_{o} }}{{{ }H_{o} { }}}$$

(13)

First, we formalize the construction of an ideal production sequence. Accordingly, we assume that both options A and B are scheduled starting at cycle one and each $q_{A} /q_{B}$ cycle. As in cycle one, all $u_{AB}$ cycle orders contain A and B with

$$u_{AB} { } = LCM\left( {q_{A} ,{ }q_{B} } \right),$$

(14)

where LCM denotes the least common multiple.

In Fig. 3, the vertical lines in the first and second row indicate that the model scheduled in this cycle features options A and B, respectively. If both options are scheduled in the same cycle, the dotted line between them indicates this. The resulting sequence in Fig. 3 is called the ideal sequence, because options A and B can be scheduled without a loss with respect to their car sequencing rules.

Fig. 3

Ideal sequence of two options with the average distances $q_{A}$ and $q_{B}$

If $u_{AB}$ equals $q_{B}$, then $q_{B}$ is a multiple of $q_{A}$ (cf. Fig. 4). Assuming that we start with options A and B in cycle one. Then, we can schedule both options every $q_{B}$ cycle, and the ideal sequence does not contain any model that features option B only. Assuming the model in cycle one features either option A or option B. Here, the ideal sequence does not contain any model that features both options. By combining these two subsequences, any proportion of the combination of options A and B can be sequenced. The loss of one of the two options always occurs when changing from one subsequence to another.

Fig. 4

Sequence of two options with $q_{B}$ equals $u_{AB}$

In an infinite sequence with few changes between the subsequences, this special case leads to a negligible loss. To exclude the special case of $u_{AB}$ = $q_{B}$ for further research, we assume

$$1 < q_{A} < q_{B} < u_{AB}$$

(15)

Under this assumption, we now show that deviations from the ideal installation rate $\sigma_{AB}$ of the combination of options A and B can implicitly reduce the maximum individual installation rates $\sigma_{A}$ and $\sigma_{B}$ of options A and B to levels below the ratios $H_{A} /N_{A}$ and $H_{B} /N_{B}$, respectively.

Typically, when we deviate from the ideal installation rate $\sigma_{AB}$, we can either prefer the installation of option A or the installation of option B. Therefore, we first investigate the two extreme cases, in which we always prefer the same type of option. Subsequently, we consolidate the obtained results and derive general dynamic limits representing the implicit interdependencies induced by the sequencing rules in the form of linear inequalities.

4.1 Prefer option B over option A

We start with the case in which the more demanding option B is preferred, that is, we attempt to design a sequence that contains as many models featuring option B as possible, given a fixed share of AB-type models. As demonstrated in the illustrative example above, under these assumptions, the maximal installation rate of option A depends on the share of AB-type models in the production program. We derive the maximal installation rate of A for three distinctive installation rates of AB, which is then used in developing a representation as a piece-wise linear function. We start with the case in which none of the produced models features both options A and B.

Proposition 1

Under the assumption that option B is preferred and that $\sigma_{AB} = 0$, the installation rate of A is limited by

$$\sigma_{A} \le \frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} *q_{A} { }}}{ }.$$

(16)

where

$$\alpha_{A,B} = \mathop {\min }\limits_{{t_{A} ,t_{B} \in \left\{ {1..T^{S} } \right\}}} \left\{ {t_{B} q_{B} {|}t_{B} q_{B} = 1 + t_{A} q_{A} } \right\}.$$

(17)

Hence, $\alpha_{A,B}$ represents the minimum number of cycles until options A and B would have to be sequenced in the same cycle, assuming that A is sequenced from cycle two every $q_{A}$ cycle and B is sequenced from cycle one every $q_{B}$ cycle.

Proof

According to its sequencing rule, starting in cycle 1, we can schedule option B at maximum every $q_{B}$ cycle, resulting in an upper bound on the installation rate of B, which is independent of the installation rates of A and the combination AB:

$$\sigma_{B} \le \frac{1}{{{ }q_{B} { }}}{ }$$

(18)

To determine the maximum installation rate of option A, our goal is to install option A in as many cycles as possible while avoiding those cycles in which option B is already scheduled ($\sigma_{AB} = 0$). The resulting sequence is illustrated in Fig. 5. Because option B is scheduled in cycle one, we can only start scheduling option A in cycle two. Thus, we can schedule option A every $q_{A}$ cycle until it falls again together with option B. This is the case after $\alpha_{A,B}$ cycles.

Fig. 5

Subsequence $\alpha_{A,B}$

This subsequence can be repeated until the maximum number of cycles $T^{S}$ is reached, resulting in a loss of one cycle per $\alpha_{A,B}$ cycles for option A. Thus, in a subsequence of $\alpha_{A,B} - 1$ cycles, we sequence option A every $q_{A}$ cycle, such that the number of assigned options is $\frac{{\alpha_{A,B} - 1}}{{q_{A} }}$. If we divide this by the number of cycles in the subsequence, we obtain the maximum installation rate of A:

$$\sigma_{A} \le \frac{{ \frac{{\alpha_{A,B} - 1}}{{q_{A} }} }}{{\alpha_{A,B} { }}} = \frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} *q_{A} { }}}$$

(19)

□

As the installation rate of combinations AB increases from zero, we can shift the schedule of option A by one cycle to the left in an increasing number of subsequences, as shown in Fig. 5 until we reach the ideal sequence (Fig. 3). In the ideal sequence, we have $\sigma_{AB} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {u_{AB} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${u_{AB} }$}}$ and $\sigma_{A} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {q_{A} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${q_{A} }$}}$.

The installation rate of AB can increase to a maximum of the installation rate of B because the sequencing rule for B also applies to AB.

Proposition 2

Under the assumption that option B is preferred and that $\sigma_{AB} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {q_{B} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${q_{B} }$}}$, the installation rate of A is limited by

$$\sigma_{A} \le \bigg\lfloor\frac{{q_{B}}}{{q_{A}}}\bigg\rfloor*\frac{1}{{q_{B}}}.$$

(20)

Proof

In this scenario, as shown in Fig. 6, a subsequence is $q_{B}$ cycles long. As seen in this subsequence, option A can be scheduled at most $\bigg\lfloor\frac{{q_{B} }}{{q_{A}}}\bigg\rfloor$ times, which leads to a maximal installation rate of

$$\sigma_{A} \le \frac{{\bigg\lfloor\frac{{q_{B} }}{{q_{A}}}\bigg\rfloor}}{{q_{B}}} = \bigg\lfloor\frac{{q_{B} }}{{q_{A}}}\bigg\rfloor*\frac{1}{{q_{B}}}.$$

(21)

Fig. 6

Subsequence for the maximum installation rate of AB (prefer B)

□

Because the subsequences discussed in Propositions 1 and 2 and the ideal sequence can be arbitrarily combined, linear relationships are applied between the three extreme scenarios. The linear interdependencies between the maximal installation rate of option A and the installation rate of combination AB is shown in Fig. 7.

Fig. 7

Maximum installation rate of option A as a function of the installation rate of the combination AB (prefer B)

The findings of this subsection are summarized in the following proposition.

Proposition 3

Under the assumption that option B is preferred, the installation rate of option A is constrained by the following linear inequalities:

$$\sigma_{A} \le \frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} *q_{A} }} + m_{A,AB,1} *\sigma_{AB} \quad {\text{if}}\;{ }0 \le \sigma_{AB} < \frac{1}{{u_{AB} }} \;{\text{and}}$$

(22)

$$\sigma_{A} \le \left( { - m_{A,AB,2} *\frac{1}{{u_{AB} }} + \frac{1}{{q_{A} }}} \right) + m_{A,AB,2} *\sigma_{AB} \quad {\text{if}}\;\frac{1}{{u_{AB} }} \le \sigma_{AB} \le \frac{1}{{q_{B} }}.$$

(23)

with gradients

$$m_{A,AB,1} = \frac{{u_{AB} }}{{\alpha_{A,B} *q_{A} }} \quad {\text{and}}\quad m_{A,AB,2} = \frac{{u_{AB} \left( {\frac{{q_{B} }}{{q_{A} }} - \bigg\lfloor\frac{{q_{B} }}{{q_{A}}}\bigg\rfloor} \right)}}{{q_{B} - u_{AB} }}.$$

Proof

From the results of Propositions 1 and 2 and Fig. 7 it is easy to see that the gradients $m_{A,AB,1}$ and $m_{A,AB,2}$ can be calculated as follows:

$$m_{A,AB,1} = \frac{{\frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} *q_{A} }} - \frac{1}{{q_{A} }}}}{{0 - \frac{1}{{u_{AB} }}{ }}} = \frac{{u_{AB} }}{{\alpha_{A,B} *q_{A} }}$$

(24)

$$m_{A,AB,2} = \frac{{\frac{1}{{q_{A} }} - \frac{{\bigg\lfloor\frac{{q_{B} }}{q_{A} }\bigg\rfloor}}{{q_{B} }}}}{\frac{1}{u_{AB} } - \frac{1}{{q_{B} }}} = \frac{{\frac{{q_{B} }}{{q_{A} }} - \bigg\lfloor\frac{{q_{B} }}{{q_{A} }}}\bigg\rfloor}{{\frac{{q_{B} - u_{AB} }}{u_{AB} }}}$$

(25)

□

4.2 Prefer option A over option B

We proceed with the case in which the less demanding option A is preferred, that is, we attempt to design a sequence that contains as many models featuring option A as possible, given a fixed share of AB-type models. Similarly, we derive a set of linear inequalities, which limit the installation rates of options A and B depending on the installation rate of the combination AB. As mentioned above, we derive limits for a set of distinct values for $\sigma_{AB}$, which can then be combined linearly. We start with the case where $\sigma_{AB} = 0$.

Proposition 4

Under the assumption that option A is preferred and that $\sigma_{AB} = 0$, the installation rate of B is limited by

$$\sigma_{B} \le \frac{{\alpha_{B,A} - 1}}{{\alpha_{B,A} *q_{B} { }}}{ }.$$

(26)

where

$$\alpha_{B,A} = \mathop {\min }\limits_{{t_{A} ,t_{B} \in \left\{ {1..T^{S} } \right\}}} \left\{ {t_{A} q_{A} {|}t_{A} q_{A} = 1 + t_{B} q_{B} } \right\}.$$

(27)

Proof

The proof is analogous to the proof of Proposition 1.

□

Similarly, we can increase the installation rate for AB from zero up to one order per ${u}_{AB}$ cycle by shifting the schedule of option B by one cycle to the left in an increasing number of subsequences underlying Proposition 4, until the ideal sequence is reached.

Assuming that option A is installed in every $q_{A}$-th cycle, the installation rate of AB can be further increased until the scenario in Fig. 8 is reached. Every model featuring option B also includes option A; however, compared to the ideal sequence, the scheduling of option B is delayed for a couple of cycles, resulting in a reduced installation rate $\sigma_{B}$. At this point, option B can be installed in every $\left( {\bigg\lfloor\frac{{q_{B} }}{{q_{A} }}\bigg\rfloor + 1} \right)*q_{A}$ cycle. Hence, the installation rate of both B and AB is the reciprocal of this value.

Fig. 8

Subsequence for the maximum installation rate of AB (Prefer A)

A further increase in the installation rate of AB can only be achieved at the cost of a reduced installation rate of A, resulting in fewer A and more B being installed until the subsequences in Fig. 6 are reached. Figure 9 shows the installation rates of options A and B depending on the installation rate of AB, and Proposition 5 summarizes these findings in the form of linear inequalities.

Fig. 9

Option A and B as a function of AB (Prefer A)

Proposition 5

Under the assumption that option A is preferred over option B, the installation rates of options A and B are limited in the following way based on the installation rate of AB.

If $0 \le \sigma_{AB} \le \frac{1}{{u_{AB} }}$:

$$\sigma_{A} \le \frac{1}{{q_{A} }}$$

(28)

$$\sigma_{B} \le \frac{{\alpha_{B,A} - 1}}{{\alpha_{B,A} \cdot q_{B} }} + m_{B,AB,1} \cdot \sigma_{AB}$$

(29)

If $\frac{1}{u_{AB} } < \sigma_{AB} \le \frac{1}{{\left( {\bigg\lfloor\frac{q_{B} }{q_{A} }\bigg\rfloor + 1} \right) \cdot q_{A}}}$:

$$\sigma_{A} \le \frac{1}{{q_{A} }}$$

(30)

$$\sigma_{B} \le \left( { - m_{B,AB,2} \cdot \frac{1}{{u_{AB} }} + \frac{1}{{q_{B} }}} \right) + m_{B,AB,2} \cdot \sigma_{AB}$$

(31)

If $\frac{1}{{\left( {\bigg\lfloor\frac{{q_{B}}}{{q_{A}}}\bigg\rfloor + 1} \right) \cdot q_{A}}} < \sigma_{AB} \le \frac{1}{{q_{B}}}$:

$$\sigma_{A} \le \left( { - m_{A,AB,3} \cdot \frac{1}{q_{B}} + \bigg\lfloor\frac{q_{B}}{q_{A}}\bigg\rfloor \cdot \frac{1}{q_{B}}} \right) + m_{A,AB,3} \cdot \sigma_{AB}$$

(32)

$$\sigma_{B} \le \left( { - 1 \cdot \frac{1}{{q_{B} }} + \frac{1}{{q_{B} }}} \right) + 1 \cdot \sigma_{AB} = \sigma_{AB}$$

(33)

with gradients

$$m_{A,AB,3} = \frac{{\frac{1}{q_{A} } - \bigg\lfloor\frac{{q_{B} }}{q_{A}}\bigg\rfloor \cdot \frac{1}{q_{B}}}}{{\frac{1}{{\left( {\bigg\lfloor\frac{{q_{B}}}{{q_{A}}}\bigg\rfloor + 1} \right) \cdot q_{A} }} - \frac{1}{q_{B}} }}$$

(34)

$$m_{B,AB,1} = \frac{{\frac{{\alpha_{B,A} - 1}}{{\alpha_{B,A} \cdot q_{B} }} - \frac{1}{{q_{B} }}}}{{0 - \frac{1}{{u_{AB} }}}} = \frac{{u_{AB} }}{{\alpha_{B,A} \cdot q_{B} }}$$

(35)

$$m_{B,AB,2} = \frac{{\frac{1}{q_{B} } - \frac{1}{{\left( {\bigg\lfloor\frac{q_{B} }{q_{A} }\bigg\rfloor + 1} \right) \cdot q_{A} }}}}{{\frac{1}{{u_{AB} }} - \frac{1}{{\left( {\bigg\lfloor\frac{{q_{B} }}{{q_{A} }}\bigg\rfloor + 1} \right) \cdot q_{A}}}}}$$

(36)

$$m_{B,AB,3} = \frac{{\frac{1}{{\left( {\bigg\lfloor\frac{q_{B}}{q_{A}}\bigg\rfloor + 1} \right) \cdot q_{A} }} - \frac{1}{q_{B} }}}{{\frac{1}{{\left( {\bigg\lfloor\frac{q_{B}}{{q_{A} }}\bigg\rfloor + 1} \right) \cdot q_{A} }} - \frac{1}{q_{B}}}} = 1$$

(37)

Proof

The inequalities and gradients can be directly concluded from Fig. 9.

□

4.3 Prefer no attribute

Clearly, in master production scheduling, we do not know a priori whether and to what extent we prefer the installation of one of the equipment options. Next, we utilize the findings from the preceding subsections to derive generally valid inequalities, which represent the interdependencies of the installation rates. These findings are summarized in Fig. 10. The shaded region represents the solution space in a general case. We cast our results into the following two propositions.

Fig. 10

Attribute A and B as a function of AB (Prefer no attribute)

Proposition 6

If we have for the installation rate $\sigma_{AB}$ of the combination AB that $0 \le \sigma_{AB} \le \frac{1}{{u_{AB} }}$, then the installation rates of options A and B are limited by the following inequalities:

$$\sigma_{A} \le \frac{1}{{q_{A} }}$$

(38)

$$\sigma_{A} \le \left( { - m_{A,B,1} \cdot \frac{1}{{q_{B} }} + \frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} *q_{A} }}} \right) + m_{A,B,1} \cdot \sigma_{B} + m_{A,AB,1} \cdot \sigma_{AB}$$

(39)

$$\sigma_{B} \le \frac{1}{{q_{B} }}$$

(40)

with

$$m_{A,B,1} = - \frac{{m_{A,AB,1} }}{{m_{B,AB,1} }}$$

(41)

Proof

We start by investigating the case where no combination AB is installed at all, that is, $\sigma_{AB} = 0$. As shown in Fig. 10, we can install either option A at a rate of $\frac{1}{{q_{A} }}$ and option B at a rate of $\frac{{\alpha_{B,A} - 1}}{{\alpha_{B,A} \cdot q_{B} }}$ (preferring option A) or A at a rate of $\frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} \cdot q_{A} }}$ and B at a rate of $\frac{1}{{q_{B} }}$ (preferring option B), or we can trade off A against B (combining the corresponding subsequences). Figure 11 shows the installation rate of A as a function of the installation rate of B in this situation. From this diagram, we can directly derive the gradient $m_{A,B,1}$ of the trade-off.

$$m_{A,B,1} = \frac{{\frac{1}{{q_{A} }} - \frac{{\alpha_{A,B} - 1}}{{\alpha_{A,B} \cdot q_{A} }}}}{{\frac{{\alpha_{B,A} - 1}}{{\alpha_{B,A} \cdot q_{B} }} - \frac{1}{{q_{B} }}{ }}} = - \frac{{\alpha_{B,A} \cdot q_{B} }}{{\alpha_{A,B} \cdot q_{A} }} = - \frac{{m_{A,AB,1} }}{{m_{B,AB,1} }}$$

(42)

Fig. 11

The installation rate of A $\left( {\sigma_{A} } \right)$ as a function of the installation rate of B $\left( {\sigma_{B} } \right)$ given that $\sigma_{AB} \le \frac{1}{{u_{AB} }}$ or $\sigma_{AB} \ge \frac{1}{{u_{AB} }}$

When $\sigma_{AB}$ increases from zero, the linear trade-off function moves upward until the ideal sequence is reached with $\sigma_{AB} = \frac{1}{{u_{AB} }}$, $\sigma_{A} = \frac{1}{{q_{A} }},$ and $\sigma_{B} = \frac{1}{{q_{B} }}$. From Proposition 3 (Eq. (22)), we can conclude that the gradient used to move the trade-off function is $m_{A,AB,1}$ and obtain Inequality (42).

□

Proposition 7

If we have for the installation rate $\sigma_{AB}$ of the combination AB that $\frac{1}{{u_{AB} }} \le \sigma_{AB} \le \frac{1}{{q_{B} }}$, then the installation rates of options A and B are limited by the following inequalities:

$$\sigma_{A} \le \left( {\frac{1}{{q_{A} }} - m_{A,B,2} \cdot \frac{1}{{q_{B} }} - m_{A,AB,2} \cdot \frac{1}{{u_{AB} }}} \right) + m_{A,B,2} \cdot \sigma_{B} + m_{A,AB,2} \cdot \sigma_{AB}$$

(43)

$$\sigma_{A} \le \left( {\frac{{q_{B} }}{{q_{A} }} \cdot \frac{1}{{q_{B} }} - m_{A,AB,3} \cdot \frac{1}{{q_{B} }}} \right) + m_{A,AB,3} \cdot \sigma_{AB}$$

(44)

with

$$m_{A,B,2} = - \frac{{m_{A,AB,2} }}{{m_{B,AB,2} { }}}$$

(45)

and inequalities (38) and (40)

Proof

When the installation rate of AB exceeds $\frac{1}{{u_{AB} }}$, a choice between A and B must be made. The trade-off function limiting the installation rate of A in dependency of B moves downwards until AB is sequenced once per $q_{B}$ cycle, as shown in Fig. 11. From Proposition 3 and Inequality (23), the gradient used to move the function is $m_{A,AB,2}$ yielding Inequality (43).

In addition, we can conclude from Proposition 5 and Inequality (32) that the upper bound on $\sigma_{A}$ moves downwards with the gradient $m_{A,AB,3}$ as soon as $\sigma_{AB}$ is greater than $\frac{1}{{\left( {\bigg\lfloor\frac{q_{B}}{q_{A}}\bigg\rfloor + 1} \right) \cdot q_{A} }}$ yielding Inequality (44).

□

We can summarize the following: in case no preferences are given the implicit limits on the installation rates caused by the interdependencies of the sequencing rules are described by the inequalities (38)–(40) and (43)–(44).

4.4 Generalization

In the previous sections, we devised implicit constraints when considering two options with $H_{O} = 1$. In practice, it is necessary to consider more than two options, and options with $H_{O} > 1$. Therefore, we generalize the inequalities and present the modifications of the basic MPS model.

While possible, in principle, the derivation of implicit constraints becomes increasingly complicated for more than two options. In this study, we do not pursue this direction further; however, it was left for future research. Instead, in cases of more than two options, we generate implicit constraints for all possible pairs of options and add them to the basic MPS model (Sect. 4.5). The more pairs and interdependencies are included, the better the sequencing can be anticipated. For instance, for three options (A, B, and C), restrictions for three pairs can be generated (A-B with AB, A-C with AC, and B-C with BC). The restrictions for A-B with AB means the proportion of AB is set in each period such that A and B are scheduled as often as possible (ideally $\sigma_{AB} = \frac{1}{{u_{AB} }}$, see Fig. 10). We also call these restrictions Level-2 restrictions because the number of options in the considered combination is exactly two. We can define Level-3 restrictions as well, for example, for A-C with ABC. These determine the proportion of the car model ABC, such that, in this example, A and C can be optimally scheduled.

For each pair of two options A and B, five parameters need to be determined to construct the additional constraints for the MPS model; $q_{A}$, $q_{B}$, $u_{AB}$, $\alpha_{A,B} ,$ and $\alpha_{B,A}$. $q_{A}$ and $q_{B}$ describe the minimum distance between two orders (Eq. (13)) and can easily be determined by

$$q_{A} = \frac{{N_{A} }}{{{ }H_{A} { }}}$$

(46)

$$q_{B} = \frac{{N_{B} }}{{{ }H_{B} { }}}$$

(47)

For level-2 restrictions, the parameter $u_{AB}$ defines the ideal distance between two orders containing options A and B (Eq. (14)) and with

$$u_{AB} { } = \frac{{LCM\left( {N_{A} ,{ }N_{B} } \right)}}{{H_{A} \cdot H_{B} }}$$

(48)

where LCM denotes the least common multiple. Analogously, for level-3 restrictions, the ideal distance between orders containing A, B, and C is given by:

$$u_{AB} { } = \frac{{LCM\left( {N_{A} ,{ }N_{B} , N_{C} } \right)}}{{H_{A} \cdot H_{B} \cdot H_{C} }}$$

(49)

The parameter $\alpha_{A,B}$, inserted in Inequality (16), determines the maximum installation rate $\sigma_{A}$ for option A if the installation rate $\sigma_{AB}$ for AB is zero and option B is preferred (analogous to parameter $\alpha_{B,A}$). For options o with $H_{o} = 1$, the value of the parameter can easily be determined using Eq. (17).

For the case of $H_{o} > 1$ for at least one of the considered options, the determination of $\alpha_{A,B}$ and $\alpha_{B,A}$ is more challenging, because $H_{o}$ options can be sequenced arbitrarily in $N_{o}$ cycles, thus providing more flexibility. We address this problem by devising and solving a specially tailored sequencing problem to directly determine the maximum installation rates $\sigma_{A}$ and $\sigma_{B}$ and then use Inequality (16) to deduce values for $\alpha_{A,B}$ and $\alpha_{B,A}$. The procedure is described in detail in Appendix 2.

4.5 Modifications to the MPS model

After determining all parameters, we can incorporate the inequalities derived in Propositions 6 and 7 into the MPS model formulation (1)–(4). We start by transforming Inequalities (38) and (40) by replacing the installation rate $\sigma_{o}$ for a certain option o with the quotient of the number of orders containing this option and the total number of orders:which results after multiplying with the denominator of the left-hand term in the following set of linear constraints for all options and periods:

$$\frac{{\mathop \sum \nolimits_{i = 1}^{N} d_{io} \cdot x_{it} }}{{\mathop \sum \nolimits_{i = 1}^{N} x_{it} }} \le \frac{1}{{q_{o} }},$$

$$\mathop \sum \limits_{i = 1}^{N} d_{io} \cdot x_{it} \le \lambda \cdot \frac{1}{{q_{o} }} \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \quad \forall \,o \in O;\;t = 1, \ldots ,T$$

(50)

Constraint set (50) replaces constraint set (5) in the basic MPS model. Note that we introduced a parameter $\lambda$ to control the utilization rate (Sect. 3.1) in our numerical experiments. The default value of $\lambda$ should be 1.

The following constraint sets (51)–(53) are derived similarly from Inequalities (39) and (43)–(44), respectively, and are added as additional constraints to the basic MPS model. The parameters $m_{ \cdot , \cdot , \cdot }$ are defined in the related propositions.

$$\begin{aligned} \mathop \sum \limits_{i = 1}^{N} d_{io} \cdot x_{it} & \le \left( { - m_{{o,o^{{\prime }} ,1}} \cdot \frac{1}{{q_{{o^{{\prime }} }} }} + \frac{{\alpha_{{o,o^{{\prime }} }} - 1}}{{\alpha_{{o,o^{{\prime }} }} *q_{o} }}} \right) \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \\ & \quad + m_{{o,o^{{\prime }} ,1}} \cdot \mathop \sum \limits_{i = 1}^{N} \left( {d_{{io^{{\prime }} }} \cdot x_{it} } \right) \\ & \quad + m_{{o,oo^{{\prime }} ,1}} \cdot \mathop \sum \limits_{i = 1}^{N} \left( {d_{io} \cdot d_{{io^{{\prime }} }} \cdot x_{it} } \right) \\ & \quad - \left( {1 - \lambda } \right) \cdot \frac{1}{{q_{o} }} \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \quad \forall \,o,o^{{\prime }} \in O:q_{o} < q_{{o^{{\prime }} }} ;\;\forall \,t = 1, \ldots ,T \\ \end{aligned}$$

(51)

$$\begin{aligned} \mathop \sum \limits_{i = 1}^{N} d_{io} \cdot x_{it} & \le \left( {\frac{1}{{q_{o} }} - m_{{o,o^{{\prime }} ,2}} \cdot \frac{1}{{q_{o^{\prime}} }} - m_{{o,oo^{{\prime }} ,2}} \cdot \frac{1}{{u_{{oo^{{\prime }} }} }}} \right) \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \\ & \quad + m_{{o,o^{{\prime }} ,2}} \cdot \mathop \sum \limits_{i = 1}^{N} \left( {d_{{io^{{\prime }} }} \cdot x_{it} } \right) \\ & \quad + m_{{o,oo^{{\prime }} ,2}} \cdot \mathop \sum \limits_{i = 1}^{N} \left( {d_{io} \cdot d_{{io^{{\prime }} }} \cdot x_{it} } \right) \\ & \quad - \left( {1 - \lambda } \right) \cdot \frac{1}{{q_{o} }} \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \quad \forall \,o,o^{{\prime }} \in O:q_{o} < q_{{o^{{\prime }} }} ;\;\forall \,t = 1, \ldots ,T \\ \end{aligned}$$

(52)

$$\begin{aligned} \mathop \sum \limits_{i = 1}^{N} d_{io} \cdot x_{it} & \le \left( {\frac{{q_{{o^{{\prime }} }} }}{{q_{o} }}*\frac{1}{{q_{o} }} - m_{{o,oo^{{\prime }} ,3}} *\frac{1}{{q_{{o^{{\prime }} }} }}} \right) \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \\ & \quad + m_{{o,oo^{{\prime }} ,3}} \cdot \mathop \sum \limits_{i = 1}^{N} \left( {d_{io} \cdot d_{{io^{{\prime }} }} \cdot x_{it} } \right) \\ & \quad - \left( {1 - \lambda } \right) \cdot \frac{1}{{q_{o} }} \cdot \mathop \sum \limits_{i = 1}^{N} x_{it} \quad \forall \,o,o^{{\prime }} \in O:q_{o} < q_{{o^{{\prime }} }} ;\;\forall \,t = 1, \ldots ,T \\ \end{aligned}$$

(53)

To add level-3 restrictions, the terms $\sum\nolimits_{i = 1}^{N} {\left( {d_{io} \cdot d_{{io^{{\prime }} }} \cdot x_{it} } \right)}$ are replaced by $\sum\nolimits_{i = 1}^{N} {\left( {d_{io} \cdot d_{{io^{{\prime }} }} \cdot d_{{io^{{\prime \prime }} }} \cdot x_{it} } \right)}$. Here, $o, o^{\prime}$ and o″ represent the three options considered.

Consequently, our enhanced MPS model (EMPS) consists of constraint sets (1)–(4) and the additional constraints (50)–(53).

5 Numerical study

In this section, we evaluate the effect of considering the implicit sequencing constraints in the master production scheduling step on the number of rule violations in the sequencing step. Accordingly, we compare our EMPS derived in Sect. 4.5 with the original MPS approach suggested by Boysen et al. (2009a) and our modified MPS+, both discussed in Sect. 3.1. We concentrate on hard sequencing rules, as these are critical to be fulfilled, and violations lead to losses in output.

We compared the three planning approaches based on the sequencing rule violations. After solving the master production scheduling model, each period is sequenced using the heuristic “very fast local search,” as described in Appendix 3. In Appendix 4, we show that the heuristic delivers near-optimal results. During the planning process, a production sequence is formed for each production shift. However, at the assembly line, an infinite sequence is manufactured, which must fulfill all the sequencing rules at the transitions from one shift to the next. Because we do not know the sequence of the following shift when sequencing and the cycle normally contains a so-called heavy order with many options, we evaluate the last orders as if in the first cycle of the following shift, only orders with all considered options would be sequenced. For example, suppose that we are sequencing 20 orders, in the sequencing step when calculating the sequencing rule violations, we considered five more orders with all considered options in cycles 21 to 25. This results in few options being sequenced in the last cycles or they are detected as rule violations. However, both behaviors are desired with respect to the transition of the two shifts.

In the following, we present and discuss three experiments. In Experiment 1, we compare the three approaches on specially generated ‘ideal’ benchmark instances, of which we know that perfect scheduling and sequencing without rule violations is possible. Hence, on these instances all rule violations that occur in the sequencing phase can be attributed to the planning quality of the MPS phase. Having shown that our new approaches can provide a significant advantage for realistic applications, we conduct a deeper analysis of the EMPS approach in Experiment 2. In particular, we want to understand why and under which circumstances the EMPS approach outperforms the other two approaches. For this purpose, we investigated a case with two options, each with a 100% utilization rate, that differ only in the number of orders containing both options (installation rate ${\sigma }_{AB}$). Because this installation rate is not considered in the approaches MPS and MPS+, we expect a substantial and coinciding number of sequencing rule violations for them, whereas according to our theoretical results, EMPS should cause no violations at all. Finally, in Experiment 3, we show the influence of lambda on the number of scheduled orders as well as on the number of violations, and we investigate the limitations of the EMPS approach by investigating the number of considered options.

For each experiment, we first describe the data generation before we present and discuss the numerical results. The instances of experiment one and three are available online at the Harvard repository (Krüger 2021a). The instances of Experiment two were easily reproducible based on these data.

All model instances were solved for a maximum of 10 min or to at least 99,9% optimality with IBM ILOG Cplex 12.4 on an Intel® Xeon® CPU E5-2667 v3 3.2 GHz PC.

5.1 Experiment 1: Effectiveness on ‘ideal’ benchmark instances

5.1.1 Data generation

In this experiment, we selected five instances of the car sequencing problem (90-1, 90-2, 90-3, 90-5 and 90-7) from the CSPLib (Smith n.d.), which can be sequenced without violations. These instances consist of 200 orders and five options with five different sequencing rules (1:2, 1:3, 1:5, 2:3, and 2:5). In the master sequencing step, we want to assign the order pool to $T = 10$ periods. Therefore, we increase the number of each car model by a factor of ten to reach $n = 2000$ orders in the pool. Therefore, the instances are constructed such that they can be sequenced without rule violations if the orders of the car sequencing instance are assigned once to each period. To avoid “cherry picking,” we set the due date $L_{i}$ and the order-specific due date deviation costs $c^{\prime}_{i}$ to 1.0 for each order i. Furthermore, we assume in line with Boysen (2005), that assigning an order in periods smaller than the due date causes inventory holding costs $\left( {l = 0.1} \right)$, which are less than the late delivery costs per period $\left( {s = 0.2} \right)$. Because all orders have the due date of one, orders cannot be produced early, and we can determine the order-specific and period-dependent scheduling costs of each order with the late delivery costs $s$.

$$c_{it} \cdot \left( {t - L_{i} } \right) \cdot s \cdot c_{i}^{{\prime }} ,\quad \forall i = 1, \ldots ,n; \;t = 1, \ldots ,T + 1$$

(54)

In this experiment, we set $\lambda = 1$ for all instances.

5.1.2 Numerical results

The results of the five benchmark instances are presented in Table 3. All instances were solved in less than 7 s, whereby the runtime of the MPS was approximately one-fourth of the runtime of the EMPS.

Table 3 Results of the five benchmark instances

The “Solution” column shows the optimal objective function value of the master production scheduling problem, that is., the due date deviation costs. All instances in each model incur the same deviation costs because all orders have the due date one and the same order-specific deviation costs. Furthermore, it can be seen in the column “Assigned orders” that, in almost all cases, the complete order pool has been assigned to production periods. This results in 200 orders meeting their due date in period one. In period two, 200 orders are one period late and cause deviation costs of $1*200*0.2 = 40$. In period three, another 200 orders are two periods late and cause costs of $2*200*0.2 = 80$ etc.

After sequencing each period for each instance using the sequencing heuristic described in Appendix 3, the resulting violations are shown for each instance in the column “Viol.”. Using the MPS+ approach, the number of violations is reduced on average by 55%, and using the EMPS approach on average by 74%. This corresponds to 3.6 violations per period for EMPS, compared to 13.7 violations per period for the MPS approach.

The improvement of the MPS+ approach is noteworthy because the production capacity is almost completely exhausted in each period, such that $\sum\nolimits_{i = 1}^{N} {x_{it} = P}$ applies. Hence, Inequalities 5 and 6 are identical. This improvement can be explained using Fig. 12, which shows the violations depending on the average utilization rates over five options for each period t, calculated as follows:

$$\frac{1}{5} \cdot \mathop \sum \limits_{o \in O} \left( {{{\frac{{\mathop \sum \nolimits_{i = 1}^{N} d_{{io^{{\prime }} }} \cdot x_{it} }}{{\mathop \sum \nolimits_{i = 1}^{N} x_{it} }}} \mathord{\left/ {\vphantom {{\frac{{\mathop \sum \nolimits_{i = 1}^{N} d_{{io^{{\prime }} }} \cdot x_{it} }}{{\mathop \sum \nolimits_{i = 1}^{N} x_{it} }}} {\frac{{H_{o} }}{{N_{o} }}}}} \right. \kern-\nulldelimiterspace} {\frac{{H_{o} }}{{N_{o} }}}}} \right)$$

(55)

Fig. 12

Violations depending on the utilization rates for the five benchmark instances

The utilization rate of an option is the quotient of the actual installation rate and the maximum installation rate of an option. The higher the utilization rate of an option, the more difficult it is for the sequencing step. A utilization rate of 100% means that $H_{o}$ orders with option $o$ must be sequenced in $N_{o}$ cycles. In term (55), the number of assigned orders with option $o$ is divided by the total number of orders in period $t$ and then divided by the maximum installation rate of option $o$. Thus, the mean value of the five option-specific utilization rates is calculated.

First, Fig. 12 shows that the MPS approach generates more periods with utilization rates of less than 80% and more than 90% compared to MPS+ and EMPS. Therefore, the MPS+ approach better distributes the orders containing options over all periods, thus avoiding utilization peaks. We can only speculate the reasons for this favorable behavior. One reason might be that Inequality 6 behaves differently in the course of the branch-and-bound solution process and thus guides the solution algorithm to more favorable solutions. Second, a higher utilization rate leads to more violations. Consequently, the MPS+ approach caused fewer violations than the MPS approach. By introducing $\lambda$ into the MPS approach (5), the maximum utilization per period is limited, and thus, the number of violations is reduced. However, the decision maker would like to have a high utilization of his system and still receive no violations of the sequencing rules. Therefore, in the next experiment, we examine an order pool with 100% utilization.

It is noteworthy that the models assign all orders in all instances, incur the same deviation costs, and our approach still causes significantly fewer sequence violations. This is achieved by the additional constraints of EMPS, which limit the solution space to those solutions that can be sequenced with fewer violations. As shown in Fig. 12, fewer than 15 violations are caused by EMPS in each period, and even for utilization rates of more than 90%, significantly fewer violations are caused than MPS and MPS+. The results also show that the EMPS approach currently cannot consider all interdependencies; owing to the construction of the test instances, there must be a solution in which all periods can be sequenced without sequence violations. We further detailed our investigation in the next experiment. In this study, we consider only two options to investigate the effectiveness of the EMPS approach and choose a 100% utilization rate for both options.

5.2 Experiment 2: Impact of combined and mutually exclusive options

5.2.1 Data generation

In this experiment, we generate five instances to investigate the impact of the fraction of orders featuring a combination of two options on the number of violations produced in the sequencing step. As before, we consider a planning horizon of ten periods ($T = 10$) and assume that each period has the same length such that the number of available cycles can be calculated by dividing the length by the cycle time. An 8-h shift with a one hour break $\left( {length = \left( {8 - 1} \right) \cdot 3600 = 25,200 \,{\text{s}}} \right)$ and a cycle time of 120 s resulted in $P = 210$ production cycles. Thus, the size of the order bank for ten periods was 2100 orders. We consider two options, A (1:2) and B (1:3), which are available in the order pool at 50% and 33.3% respectively (resulting in the utilization of the option stations of 100%). The five instances, which differ in the percentage of orders containing A and/or B, are listed in Table 4. In the instance AB-0, we choose two mutually exclusive options; therefore, the percentage of AB is zero. For example, consider two different roof systems. Option A is a panoramic roof that cannot be opened. Option B is a sliding roof that can be opened. Both options can be very complex to install and thus cause car sequencing rules. However, because a car can only have one of the two options installed, these two options are mutually exclusive; therefore, the installation rate of the combination AB of both options must be zero. Based on the percentage of AB, the percentages for A and B were calculated such that orders with A and AB together were 50% and orders with B and AB together were 33.3%. Orders “–” contain neither A nor B. In the other four instances, we increased the percentage of AB by 1/12 in each instance and calculated the percentages for A and B.

Table 4 Instance overview of Experiment 2

As in the preceding experiment, the order-specific due date deviation costs $c^{\prime}_{i}$, the due dates, and the parameter $\lambda$ are set to 1.

5.2.2 Numerical results

The results of the sensitivity analysis are presented in Table 5. The column “Solution” shows the deviation costs caused by the scheduling step, the column “Assigned orders” presents the number of orders assigned over ten periods and the column “Viol.” shows the resulting sequencing rule violations over ten periods.

Table 5 Results of the sensitivity analysis of the combination installation rate

Because the order pool induces maximal installation rates for options A and B, it is plausible that MPS and MPS+ assign all orders to periods for all five instances and thus cause the same deviation costs for all instances (considering that all orders have the due date, and thus 90% of them exceed their due date). This results in up to 360 violations using MPS and MPS+ approaches. Unlike in Experiment 1, we did not observe any advantage of MPS+ compared to MPS. This is because there were no utilization peaks that could be avoided. The experimental setup is such that a utilization of 100% already exists for both options in the order pool and each period. It follows that MPS+ results in sometimes more and sometimes fewer violations than MPS. This difference is only caused by the different distributions of the orders in which both options are installed (combination AB). This dependence can be observed in Figs. 13 and 14, which resemble Fig. 10. For each period of the five instances, the position of each bubble indicates the installation rates for options A, B, and combination AB. The installation rates of A and B consider all orders containing these options, that is, including orders with the combination AB. The size of each bubble indicates the number of violations in the respective periods. Each bubble in Fig. 13 has a corresponding bubble in Fig. 14 with the same installation rate of AB. We marked three pairs of bubbles, 1, 2 and 3, as examples. We also separated the bubbles of the five instances by color.

Fig. 13

Violations per period depending on the installation rates of option A and combination AB

Fig. 14

Violations per period depending on the installation rates of option B and combination AB

The two graphs show that MPS and MPS+ schedule 50% A and 33.3% option B in each period, that is, reach utilizations of 100% for both options in each period. The EMPS approach produced a considerable number of bubbles that were below the maximum installation rate. Only when the installation rate of AB reaches a value of 16.67% does the EMPS approach schedule 50% A and 33,3% B. These values correspond to the ideal distribution shown in Fig. 1. As shown in Sect. 3.3, for this distribution alone, a 100% utilization rate can be achieved for both options without violations.

The smaller or larger the installation rate of AB deviated from this ideal installation rate, the more violations are caused by MPS and MPS+. In Figs. 13 and 14, we added the dashed lines from Fig. 10 showing the decision limits of the EMPS approach that result in these two options. These limits are determined with $q_{A} = 2$, $q_{B} = 3$, $u_{AB} = 6$, $\alpha_{A,B} = 3$ and $\alpha_{B,A} = 4$. If the installation rate of AB is larger or smaller than 16.67% for EMPS, a tradeoff between options A and B occurs (corresponding to the grey-shaded area in Fig. 10). This tradeoff depends on the installation rate of AB, as shown in Fig. 11. The closer the installation rate for option A is to the maximum, the closer the corresponding bubble for option B must be to the dashed limit or below to avoid violations.

The additional constraints of the EMPS approach ensure that the orders are assigned to periods such that this tradeoff is considered, and all instances can be sequenced without violations. This is achieved by postponing some orders to later periods or not scheduling them at all. This leads to somewhat higher deviation costs in some cases.

In summary, for high utilization rates, the MPS+ approach is not superior to the MPS approach; however, the EMPS approach still achieves significant improvements in these cases. Therefore, the sequencing step is anticipated early, and it can be recognized that not all orders can be scheduled. In the industry, master production scheduling is performed in rolling-horizon frameworks. This means rescheduling is performed at regular intervals. Orders that cannot be scheduled in the current schedule are assigned to the period T + 1 in the model and must therefore be considered again in the next rescheduling. If the interval between the current and the new scheduling is smaller than the planning horizon of the master production scheduling, orders that have already been scheduled but not yet built must also be considered again. In addition, new orders are added from the order promising at defined regular intervals. When rescheduling in the rolling process, orders which have already received a production date, orders without a production date (T + 1), and new orders are all available. Orders without a production date have an earlier due date than new orders, reason why the model will prefer these orders to the new ones. If the same options cannot be assigned to a production date after several rolling planning steps, special costly measures are necessary. These should ensure that the number of affected options in the order pool is reduced such that all orders can be scheduled in future planning steps. Possible special measures could be a shift in which this equipment option is built as a priority, or an adjustment in the order promising step such that fewer orders with this option are added to the order pool.

Consequently, it would be possible for the decision maker to react already after the scheduling step. It is also plausible that more orders are scheduled as the percentage of AB in the order pool approaches the ideal percentage (1/u = 1/6). With this knowledge, the decision maker can also check which orders should ideally be added to the order pool in the order promising step. In addition, it can be seen that we have properly integrated the interdependence between the two options. All instances were sequenced without violations.

In the third experiment, we highlighted the limitations of the EMPS approach. Consequently, we varied the number of considered options between two and seven, and we also investigated whether values for $\lambda < 1$ led to an improvement in the sequencing step for the three models.

5.3 Experiment 3: Impact of the number of considered options

5.3.1 Data generation

In this experiment, we the impact of $\lambda$ and the number of options considered in the program planning. As before, we examined ten periods and 2100 orders. We generated order pools for the different scenarios listed in Table 6. For each scenario, ten different order pools were generated.

Table 6 MPS scenarios

When generating the order pool, for each order $i$ and each option $o,$ a random number $rnd$ between zero and one is used to decide whether this option is included (Eq. (56)).

$$d_{io} : = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {rnd \le H_{o} /N_{o} } \hfill & {\forall \,i \in I} \hfill \\ {0,} \hfill & {otherwise} \hfill & {\forall \,o \in O} \hfill \\ \end{array} } \right.$$

(56)

Similar to Boysen (2005), we assume that orders with many options cause higher deviation costs than those with few options. Accordingly, the base costs $c_{0}$ and costs for each option $o$ were determined randomly between one and two. With these costs and the due date $L_{i} = 1$ for each order i, we calculated the cost coefficients $c_{it}$ as follows:

$$\begin{array}{*{20}l} {({\text{a}})} \hfill & {c_{i}^{{\prime }} : = c_{0} + \sum\nolimits_{o = 1}^{O} {d_{io} \cdot c_{o} } } \hfill \\ {({\text{b}})} \hfill & {c_{it} : = \left\{ {\begin{array}{*{20}l} {\left( {L_{i} - t} \right) \cdot lcc_{i}^{{\prime }} ,} \hfill & {t \le L_{i} } \hfill \\ {\left( {t - L_{i} } \right) \cdot s \cdot c_{i}^{{\prime }} ,} \hfill & {otherwise} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} \;\forall \,i = 1, \ldots ,n; \;t = 1, \ldots ,T + 1$$

(57)

5.3.2 Numerical results

Figure 15 shows the average results of ten experiments for each value of $\lambda$ and indicates that with a decreasing value for $\lambda ,$ fewer orders are planned. This is because, for each option, the expected value of the proportion in the order pool corresponds to the quotient of $H_{o}$ and $N_{o}$ and thus a workload of 100%. The goal is to achieve 100% utilization of machines with zero violations. This requires $\lambda$ to be equal to 1. For $\lambda < 1$ the maximum utilization for each option is limited; thus, not all orders can be scheduled. The random distribution can cause the utilization of some options in the order pool to be over 100%, reason why not all 2100 orders are scheduled for $\lambda = 1$. In each model, $\lambda$ has the same influence on the number of scheduled orders. Figure 15 also shows that an increase in ${\uplambda }$ lead to a significant increase in violations for MPS+, whereas EMPS generates production programs for each $\lambda$ that can be sequenced with almost no violations. MPS causes many violations for all $\lambda$ values.

Fig. 15

Impact of the weighting factor $\lambda$

Two observations can be made. First, more orders are assigned using the MPS approach than MPS+ and EMPS. This observation is in line with the illustrative example in Sect. 3.1 in which options are limited only by an upper bound depending on the fixed production capacity and the sequencing rules in the MPS approach. In MPS+ and EMPS, this upper limit is determined by the number of orders assigned and the sequencing rules. Because the production capacity is not exhausted, fewer options and fewer orders can be scheduled. Second, as seen, MPS causes significantly more violations for all $\lambda$ values and the number of violations increases as $\lambda$ decreases, although a decrease in $\lambda$ should lead to improved sequencing (Sect. 3.1). For $\lambda < 1$, fewer orders with option $o$ are scheduled than those allowed by the installation rate. Because all orders have the due date of one, orders without option $o$ are assigned instead. Consequently, orders with option $o$ are moved backward, and orders without option $o$ are moved forward. With a high number of orders with option $o$ in the order pool, many orders with this option and only a few orders without this option are scheduled in the last period. Figure 16 shows that the MPS approach leads to significantly more violations in the last periods because the upper limit for option $o$ does not depend on the number of orders assigned in these periods. In MPS+, this limit is dynamic and depends on the number of scheduled orders. Thus, orders that cannot be sequenced are not scheduled in the last period. With an increase in $\lambda$, the number of violations also increases because the interdependencies between the two options are not considered in MPS+. Only the EMPS approach can regulate the percentage of orders containing both options such that sequencing can be performed almost without violations.

Fig. 16

Sequencing rule violations per period of MPS and MPS+

After investigating the impact of $\lambda$, we combine both graphs of Fig. 15 in Fig. 17 showing the violations depending on the assigned orders for the first three scenarios. This demonstrates that EMPS outperforms MPS and MPS+ in each case and leads to 98% to 100% fewer violations, which is an awesome result. Owing to Inequalities (5) and (6), the models schedule over ten experiments on average have a maximum of approximately 2075 (MPS+ and EMPS) and 2086 (MPS) of the existing 2100 orders. This is because the sequencing rules $H_{o} /N_{o}$ limit the options. If the percentage in the order pool is higher than $H_{o} /N_{o}$, some orders cannot be assigned.

Fig. 17

Violations depending on the assigned orders of the scenarios 1 to 3

The results demonstrate that the MPS+ approach considerably reduces the number of violations, whereas the EMPS approach can almost completely prevent violations in the sequencing step when considering two options. In practice, sequencing usually requires consideration of five, six, or even more difficult sequencing rules. Figure 18 shows that even for this number of sequencing rules, an improvement in the sequencing is achieved. For the three options, EMPS generates production programs, especially by considering level-3 restrictions (cf. Sect. 4.4), which are sequenced almost with no loss. As a result, we obtained up to 98% fewer violations. The more the options to be considered, the smaller the improvement by EMPS compared to MPS+. This shows that the EMPS approach has limitations. The limit seems to be seven options for which no improvement in the sequencing step could be achieved compared to MPS+. Nevertheless, MPS+ and EMPS resulted in fewer violations than MPS.

Fig. 18

Violations depending on the assigned orders of the scenarios 4 to 7

The limitation of EMPS is the interdependencies of car models, which contain multiple options. We derived the dependencies for the two options and considered them in the model. As shown, this can reduce the number of violations by 100%. For three options (A, B, and C), there are orders that contain all three options. For this combination, there exists an ideal ratio such that all options can be fully sequenced. We have integrated this in Experiment 3 with the level-3-restrictions (49). Looking at the investigation with five options (A, B, C, D, and E), there are some combinations (ABCD, ABCE, ABDE, ACDE, BCDE, and ABCDE) for which no dependencies are currently considered. Each of these combinations has an ideal ratio for 100% utilization of the workstations associated with the considered options. The deviation from this ideal ratio influences the maximum installation rates of the options, which currently cannot be considered. Our investigations into this direction resulted in highly nonlinear dependencies and were not further pursued in this study. However, we believe that this research direction might provide the potential to further reduce the number of violations. This experiment demonstrates the conflict between the assigned orders and the number of violations, which can be influenced by the parameter $\lambda$. Small values of $\lambda$ lead to a lower number of assigned orders (for a high utilization rate in the order pool), and $\lambda = 1$ leads to a high number of assigned orders, but also to a high number of violations. The decision-maker must therefore decide whether less output should be produced or whether to put in place cost-intensive measures to mitigate the violations (e.g., use of additional resources). Orders that are not built can also be rebuilt in special shifts, which also leads to high additional costs. Thus, a good anticipation of the sequencing rule is important for $\lambda = 1$, such that all orders can be assigned without additional costs.

6 Summary and outlook

This study considers the problem of selecting orders from an order bank to be produced on a mixed-model assembly line using a car sequencing approach. We described and discussed the basic master production scheduling approach and presented a simple extension as well as an enhanced approach with additional constraints. We showed that interdependencies between car sequencing rules resulted in the existence of additional implicit and dynamic sequencing constraints on models that feature more than one option. In the case of two options, we derived linear inequalities that fully represent these implicit constraints in the master production scheduling step and presented a generalized modification to the basic master production scheduling model. In numerical studies, we compare the standard basic approach with a simple extension and an enhanced approach. Compared to the basic approach, our simple extension approach caused fewer violations in the sequencing step for most instances. The two approaches cause nearly the same number of violations if the utilization rate approaches 100% for all options. The enhanced approach outperformed the basic approach in each of the experiments. Compared to our simple extension approach, we showed that for up to six options, the implicit constraints in the master production scheduling step can cause a significantly lower number of violations in the sequencing step. Especially for options that are mutually exclusive or conditional, an integration of interdependencies leads to a significant reduction in violations. Another advantage is the early anticipation of the sequencing step, such that it can be recognized that not all orders can be scheduled. Consequently, the decision-maker can react during the scheduling step.

For practical applications, the presented inequalities should be derived for hard sequencing rules, as these must be strictly met during the sequencing step as it may lead to a loss in the output if not met. In principle, additional soft sequencing rules can be considered in the enhanced master production scheduling approach through Inequality (6). We believe that this might reduce the number of violations of hard sequencing rules without influencing the violations of soft sequencing rules. Further research in this field may identify the potential of combining the two approaches for hard and soft sequencing rules.

Another use case of our findings should be order promising. Presently, to accept orders and allocate them to production weeks, order promising usually uses the same restrictions as the standard master production scheduling model. As shown, sequencing is insufficiently anticipated in this case. This can lead to order pools that cannot be completely allocated to periods with improved sequencing anticipation in the master production scheduling step. The assurance that orders can be sequenced already in the promising step can thus ensure the assignment to periods and thus lead to an overall reduction in deviation costs in the master production step, which would arise if orders had to be postponed to earlier or later periods. Further investigations are left for future studies.

Appendices

Appendix 1

See Table 7.

Table 7 List of all symbols

Appendix 2

Here, we present an approach to determine the parameters $\alpha_{A,B}$ and $\alpha_{B,A}$ in the case of $H_{o} > 1$ for at least one of the considered options. We address this problem by devising and solving a specially tailored sequencing problem to determine the maximum installation rates $\sigma_{A}$ and $\sigma_{B}$ directly, and then use Inequality (16) to deduce values for $\alpha_{A,B}$ and $\alpha_{B,A}$.

As in Proposition 1, we start with the assumption that option B is preferred and that the installation rate $\sigma_{AB} = 0,$ However, we presume that $H_{B} > 1$. Thus, the goal is to determine $\alpha_{A,B}$. First, we calculate the maximum number of possible occurrences of option B in T cycles as follows:

$$max_{{^{{\prime }} B}}^{T} = \frac{T}{{N_{B} }}*H_{B} + {\text{max}}\left( {0, T - \left( {\frac{T}{{N_{B} }}*N_{B} } \right) - \left( {N_{B} - H_{B} } \right)} \right)$$

(58)

The first term determines how often a subsequence of $N_{B}$ cycles fits into T. This is multiplied by $H_{B}$, because option B fits $H_{B}$ times into each of the subsequences. The second term checks how many cycles are left in addition to these subsequences and whether further options can be sequenced. To avoid side effects (i.e., rule violations) with the car sequence of the following shift, we do not sequence option B in the last $N_{B} - H_{B}$ cycles.

We can determine how often the non-preferred option A can be scheduled without causing violations while avoiding scheduling both options in the same cycle. Consequently, we solve the following specially tailored car sequencing model:

$$\max \quad \mathop \sum \limits_{t = 1}^{T} x_{tA}$$

(59)

$$x_{tA} + x_{tB} \le 1\quad \forall \,t = 1, \ldots ,T$$

(60)

$$\mathop \sum \limits_{t = 1}^{T} x_{tB} = max_{B}^{T}$$

(61)

$$\mathop \sum \limits_{{t^{{\prime }} = t}}^{{t + N_{o} - 1}} x_{{t^{{\prime }} o}} \le H_{o} \quad \forall \,t = 1, \ldots ,T\;\forall \,o \in \left\{ {A,B} \right\}$$

(62)

$$x_{to} = 0\quad \forall \,t \ge T - \left( {N_{o} - H_{o} + 1} \right)\;\forall \,o \in \left\{ {A,B} \right\}$$

(63)

In the objective function (59) the number of occurrences of the non-preferred option A is maximized. Inequality (60) ensures that only one option is sequenced per cycle (and not both) and inequality (61) prescribes the number of occurrences of the preferred option B. Inequalities (62) and (63) ensure that the car sequencing rules are followed and that no options are sequenced in the last $N_{o} - H_{o}$ cycles.

Let $x_{to}^{*}$ for $o \in \left\{ {A,B} \right\}$ be an optimal solution to model (59) to (63). Thus, the maximum installation rate $\sigma_{A}$ and parameter $\alpha_{A,B}$ can be determined as:

$$\sigma_{A} = \frac{{\mathop \sum \nolimits_{t = 1}^{T} x_{tA}^{*} }}{T}$$

(64)

$$\alpha_{A,B} = \frac{1}{{1 - \sigma_{A} *q_{A} }}$$

(65)

where Eq. (65) is derived from Inequality (16).

The parameter $\alpha_{B,A}$ can be determined analogously by preferring option A and maximizing the occurrences of option B.

Appendix 3

3.1 Greedy heuristic

Greedy heuristics are useful in obtaining good initial solutions. Greedily building a sequence means that the next car to sequence is iteratively chosen with respect to some given heuristic functions. First, an order that introduces the smallest number of new sequencing rule violations should be chosen. If more than one candidate minimizes the number of new violations, another heuristic function must be applied. The function we use is inspired by the DHU heuristic from Gottlieb et al. (2003), which is based on the dynamic utilization rate

$$dynUtilRate\left( {o,\pi_{j} } \right) = \frac{{N_{o} }}{{H_{o} }}*\frac{{r\left( {C,o} \right) - r\left( {\pi_{j} ,o} \right)}}{{\left| C \right| - \left| {\pi_{j} } \right|}}$$

(66)

defined for each option o, where $\pi_{j}$ represents the partial sequence built until position j, $C = \left\{ {c_{1} , \ldots ,c_{n} } \right\}$ is the set of cars to be produced, $\left| C \right|$ is the number of cardinality of set $C$ and $\left| {\pi_{j} } \right|$ is the length of a sequence $\pi_{j}$. $H_{o} :{ }N_{o}$ defined the sequencing rule (see Table 1). The number of cars that require an option o within a sequence $\pi_{j}$ (resp. within a set $S$ of cars) is denoted $r\left( {\pi_{j} ,o} \right)$ (resp. $r\left( {S,o} \right)$). In each iteration and after evaluating all options, we choose car $c_{i}$ that maximizes the heuristic

$$\mu_{DHU} \left( {c_{i} } \right) = \mathop \sum \limits_{o \in O} r\left( {c_{i} ,o} \right)*2^{k}$$

(67)

if o is the option with the $k^{th}$ smallest utilization rate. The function $r\left( {c_{i} ,o} \right)$ indicates whether car $c_{i}$ requires option $o$ $\left( {r\left( {c_{i} ,o} \right) = 1} \right)$ or not $\left( {r\left( {c_{i} ,o} \right) = 0} \right)$.

3.2 Local search

The idea of local search is to improve an initial sequence by locally exploring the “neighborhood” of orders, iteratively. For local search, we use the formulation of Estellon et al. (2008), which enabled them to win the ROADEF 2005 challenge. The broad lines of the heuristic are as follows:

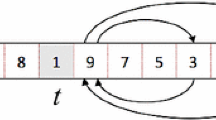
We use five basic transformations: swap, forward insertion, backward insertion, reflection, and random shuffle (see Fig. 

Fig. 19

The five VFLS transformation (Estellon et al. 2008)

19, for detailed information, see Estellon et al. 2008).

After choosing the transformation, we must define the positions $k$ and $l$, where to apply swap, insertion, and reflection transformations. Because we do not consider colors in this study, we use the following five variants: generic, similar, consecutive, violation, and denominator (see Table 8).

Table 8 The different VFLS variants for choosing positions

Through extensive experiments on RENAULT’s instances, Estellon et al. (2008) determined good proportions for transformations and variants. Because we examined sequencing rules and not colors, the number of swaps should dominate. The compositions in Table 9 were taken from Estellon et al. (2008).

Table 9 The composition for the optimization subroutine

Our C++ source code is provided in the Harvard repository (Krüger 2021b).

Appendix 4

4.1 Evaluation of the car sequencing heuristic

To prove the suitability of the heuristic for our investigations, we solved some self-created car sequencing instances with the optimization model (7)–(12) and the heuristic and compared them using car sequencing violations. Because high utilization of the options leads to difficult problems to solve (Miguel et al. 2021), we investigated nearly 90% and 100% utilization with four options. More options are also difficult to solve and are generally not solved using the optimization model within an acceptable time. For both utilization rates, we created and solved 20 instances with 100 orders. The results are shown in Tables 10 and 11 show that the average deviation from the optimal solution is less than one. Thus, the heuristic is well-suited for our investigations. The column “Solution” shows the resulting number of violations for this instance and the column “Best Solution” shows the best solution found within 60 min. In both investigations, some instances could not be solved to 100% optimality in 60 min. In addition, we showed the number of violations in the greedy heuristic and the very fast local search (VFLS) when applied for 5, 15, and 60 s. In the column “Delta between OM and VFLS-5 s” we calculate the difference between the solution of the optimization model and the solution of the VFLS after 5 s.

Table 10 Comparison of the optimization model and car sequencing heuristic for four options with the expected 100% utilization rate

Table 11 Comparison of the optimization model and car sequencing heuristic for four options with the expected 90% utilization rate

Appendix 5

5.1 Detailed overview of the results of Experiment 3

In experiment 3, eleven different values for $\lambda$ were examined for each of the seven scenarios, and ten experiments were performed for each $\lambda$. An overview of the variance of the results is presented in Tables 12, 13 and 14. MPS is the basic approach, MPS+ is the modified basic approach (Inequality (6) instead of (5)), and EMPS is our enhanced MPS model. Column “Objective” shows the average deviation costs for ten experiments and the column “Objective gap” shows the average solution gap of the solutions because we solved the models for a maximum of 10 min or to at least 99.9% optimality. For the “assigned orders” and the resulting “violations” in the sequencing step, we presented the average, minimum, and maximum values as well as the standard deviation of the ten experiments. A discussion of the results is provided in Sect. 5.3.

Table 12 Overview of the results from Experiment 3 for the EMPS

Table 13 Overview of the results from Experiment 3 for the MPS+

Table 14 Overview of the results from Experiment 3 for the MPS