1 Introduction

Smallholder farmers constitute about two thirds of the developing world’s rural population (Rapsomanikis 2015). Due to the limited access to markets and services, many of these farmers do not obtain sufficient earnings for a decent standard of living (Willoughby and Gore 2018). These findings are consistent with The World Bank (2018) data, which suggest that 65% of the poor working adults in 2016 depended on agriculture. In general, farmers’ average earnings are significantly lower than the returns earned downstream in the supply chain (Willoughby and Gore 2018). Therefore, downstream firms’ role is undeniable in improving the living conditions of smallholder farmers. This can be achieved through corporate social responsibility (CSR) practices. The United Nations Industrial Development Organization (UNIDO) views CSR practices as a way “through which a company achieves a balance of economic, environmental and social imperatives” (UNIDO 2018). In other words, CSR can help firms to incorporate social and environmental concerns in their operations without compromising their economic viability. In this paper, we focus on the integration of economic and social concerns for an agri-food firm. In particular, we study stakeholder engagement and social equity. These two key practices can be aimed at the social development of smallholder farmers, but they can also bring economic benefits to firms (through, for example, increased sales, operational cost savings, and improved productivity and quality) (UNIDO 2018). The objective of this paper is to study the impact of these two practices (i.e., achieving equity and stakeholder engagement in decision-making) on the economic and social objectives of a (supplier) farmer and a (buyer) agri-food firm in a dyadic supply chain setting.

Murphy (2012) defines equity as “distribution of welfare goods and life chances on the basis of fairness”. He argues that an equitable distribution means that everyone should have an equal opportunity to survive and fulfill their development potentials. This is often not the case for smallholder farmers as a result of their low earnings. Many socially responsible firms consider equity in their decisions regarding pricing and investment. This is due to its social importance and its causal ties to long-term change through efficiency growth, poverty reduction, and social cohesion (Jones 2009). In addition, the United Nations Development Programme (UNDP) assures that effective stakeholder engagement is fundamental in combating inequality and ensuring equity (UNDP 2017). Stakeholder engagement is based on the idea that stakeholders should be given the opportunity to comment and input into the development of decisions that affect them (Jeffery 2009). Thus, one form in which agri-food firms can implement stakeholder engagement is by involving the farmers in the aforementioned pricing and investment decisions.

In practice, some agri-food firms have implemented practices that incorporate equity and stakeholder engagement in their objectives. For example, global firms such as Nestlé and Starbucks are investing in funds to improve the productivity of their supplier farmers. They consider a more equitable profit sharing scheme when it comes to pricing decisions. This approach not only benefits the farmers, but it also leads to improved availability of supplies for the global firms promoting it (Tang et al. 2016). Furthermore, firms do not need to have a global presence to implement CSR practices. A clear example is Fractal Café—a small, local coffee retailer in Mexico City—which obtains similar benefits by engaging its suppliers in the pricing decisions. Typically, smallholder coffee farmers in Mexico have very little negotiation power with large agri-food firms. Fractal Café reaches out to the farmers and allows them to set the wholesale price on the basis of what the farmers consider equitable. By agreeing on the farmer’s proposed wholesale price, Fractal Café provides the farmer with a retail channel that generates sufficient funds. This enables the farmer to invest her funds in improving her production processes and, hence, her living conditions. This kind of stakeholder engagement mechanism also allows Fractal Café to access a continued supply of coffee.

Motivated by these practices, we consider a game-theoretical, dyadic setting, which involves a (supplier) farmer and a (buyer) agri-food firm. (In what follows, we refer to the supplier as “she” and to the buyer as “he”). Our base model represents the setting in which players are not concerned with social responsibility. Specifically, we consider a two-stage Stackelberg game where the agri-food firm has the upper hand (i.e., the leadership) in decision-making with respect to pricing and investment decisions, with the sole objective of maximizing profit. In the first stage, the players decide on how much to invest in improving the farmer’s production process. By decreasing the production cost, such an investment leads to further changes in the wholesale and retail prices, which are studied in the second stage. In order to account for the players’ social objectives (i.e., achieving an equitable profit distribution and stakeholder engagement), we then extend our base model. Our first extended model includes players’ equity concerns in decision-making through a utility-maximizing objective, where a player’s utility equals his or her profit less the disutility of deviating from what he or she considers equitable (Fehr and Schmidt 2001). In our second extended model, we incorporate stakeholder engagement in decision-making. Specifically, we consider a setting in which the agri-food firm engages the farmer in decision-making by granting her the leadership in setting the optimal investment and pricing decisions. This setting is representative of the aforementioned stakeholder engagement practices of Fractal Café. These stakeholder engagement settings become more common now as also smallholder farmers obtain access through more and better information because of (mobile) internet connectivity. In our study, we assume that supply and demand are deterministic, and there are no capacity restrictions. Later, we look at a case with capacity restrictions and the implications on the results. Finally, we look at the effects of introducing equity concerns in a two-part tariff contract. By analyzing these three models, we aim to address the following research questions:

  • How does incorporating social objectives in decision-making affect the players’ optimal pricing and investment decisions?

  • Do equity concerns have the power to reduce the advantage of the first mover in the decision-making process?

  • Under what conditions can socially responsible practices, such as equity concerns and stakeholder engagement, be economically beneficial for the supply chain as well as for the individual players?

  • What is the social cost of ignoring equity in decision-making?

Our main objective is to study how the dynamics of the selected decision-making processes are affected by the inclusion of socially responsible practices, namely equity and stakeholder engagement. Through the analysis of the base model, we find that it is optimal for the buyer to let the supplier make all the investment to lower the unit production cost. This investment results in a lower wholesale price and a higher demand, which enables both players to benefit from higher profits. The introduction of equity concerns shows that the only case in which both players can achieve equity is when the profit amount that the players want to distribute aligns with the actual supply chain profit. Regarding the investment decisions, the buyer still finds it optimal not to invest an amount in the supplier’s production processes. However, equity concerns may lead to a setting where the no-investment strategy is optimal for both parties. Together with the equity concerns, we introduce stakeholder engagement practices and find that the buyer settles for a lower profit margin than when he has a profit maximizing objective whenever the wholesale price is sufficiently low. In this case, as game leader, the supplier now finds it optimal not to invest in her own production processes, leaving the buyer to make all the investment, if any. In addition, we find that the effects of these socially responsible practices on the pricing and investment decisions can be overpowered by a restriction in the supplier’s production quantity, which is a common scenario for smallholder farmers. Finally, we find that a two-part tariff contract results in some cases with higher inequity. Only when the leader’s concern for advantageous inequity is high, both players receive an equitable outcome.

Our contribution to the operations management literature on socially responsible operations is fourfold: First, we model a dyad of supplier and buyer incorporating stakeholder engagement in combination with equity concerns. Based on the real-life cases described, we study the impact that this combination of supply chain structure and socially responsible practices has on the players’ investment and pricing decisions as well as on the profits, both per player and for the entire supply chain. Second, we extend previous models that study equity in pricing decisions by incorporating the levels of investment as decision variables for both players. Third, we relax a prior assumption on the equity parameters to capture the concept of social responsibility. With this, we allow a player to have a higher concern for receiving more than his equitable share of the profit (rather than only being concerned with receiving less). Fourth, we study the effects of equity concerns in a two-part tariff contract.

The remainder of this paper is organized as follows. In Sect. 2, we provide an overview of the related literature. Next, we present our base model in Sect. 3, followed by the impact of equity concerns in Sect. 4 and the impact of stakeholder engagement in Sect. 5. Then we extend our proposed models in Sect. 6 to include capacity constraints. In Sect. 7 we present a model based on a two-part tariff contract with equity concerns. We complement our analytical findings with a numerical study in Sect. 8. Finally, in Sect. 9, we present our conclusions and limitations.

2 Literature review

The relevant literature includes research related to quantitative measures of equity, supplier–buyer relationships with equity concerns, investment in suppliers’ production processes, stakeholder engagement in socially responsible firms, and power structures in pricing games. In what follows, we present a brief overview of the most related works and present our contributions to each research stream.

Adams (1965) provides one of the earliest definitions of equity, which dictates that a person experiences equity when his outputs are equal to his inputs. Based on this definition, it is a common approach to measure the degree of equity in a given relationship via a numerical scale in the marketing domain (see Jambulingam et al. 2011; Kim et al. 2017). In the field of operations management, equity is modeled both as an exogenous parameter and as an endogenous outcome. For example, similar to the aforementioned studies, McCoy and Lee (2014) define equity on a numerical scale using an exogenous parameter, where a higher value indicates a more equitable outcome allocation. On the other hand, Ye et al. (2017) introduce the objective of max-min fairness, which maximizes the minimum utility over all stakeholders in the system. Similar measures have been utilized in problems that are pertinent to facility location, transportation, health delivery and distribution of public services (Maimon 1986; Marsh and Schilling 1994; McCoy and Lee 2014; Demirbilek et al. 2019; Savas 1978). In our work, we adopt the economic model of Fehr and Schmidt (2001) to model inequity aversion in the decision-making process of a supplier and a buyer within a dyadic game-theoretical setup. They introduce inequity aversion through a disutility in the decision-makers’ utility functions when the outcome deviates from what they consider equitable (see Rabin 1993; Cooper and Stockman 2002; Falk et al. 2008). We contribute to this literature by relaxing the assumption by Fehr and Schmidt (2001) that a player’s concern for disadvantageous inequity must be higher than that for advantageous inequity. This allows us to consider a more general setting, where the assumption presented by Fehr and Schmidt (2001) holds for a subset of the parameter combinations. For example, our findings show that if the follower’s concern for advantageous equity is higher than his or her concern for disadvantageous equity, then the leader benefits from this by receiving a higher utility.

The second relevant stream is the body of research that investigates the impact of equity concerns on the interactions between a supplier and a buyer. For example, a number of empirical works in the marketing discipline shows that high levels of equity perceived by both parties promote successful supplier–buyer relationships. They do this by inducing mutual knowledge sharing, continuous commitment, and investment in the relationship (see Duffy et al. 2013; Gu and Wang 2011; Liu et al. 2012). Similarly, Katok and Pavlov (2013) experimentally show that inequality aversion is one of the most important factors that explain why supply chain contracts designed according to standard theory often fail to be accepted in practice. On the theoretical side, Cui et al. (2007) demonstrate that equity concerns alleviate the double-marginalization problem in a vertical supply chain that consists of a manufacturer and a retailer, and a simple wholesale price (that is higher than the marginal cost) coordinates the channel when the players exercise inequity aversion in their decision-making. In a follow-up work, Cui and Mallucci (2016) extend their earlier research to a two-stage setting where in the first stage the players determine the investment level to increase demand, and in the second stage they determine the optimal wholesale and retail prices. The authors derive analytically the optimal pricing and investment decisions for the standard economic model with no equity concerns, and the optimal pricing decisions for the model where the players exercise inequity aversion. Du et al. (2014) consider a similar setting and include the players’ preferences for reciprocity. They find that the buyer, as game follower, uses the retail price to reward or punish the supplier based on the retailer’s perception of the supplier’s intention. Caliskan-Demirag et al. (2010) extend the work by Cui et al. (2007) by introducing nonlinear demand functions and find that an exponential demand function facilitates the supply chain coordination when only the buyer exhibits fairness concerns. Ingene et al. (2019) study different linear and nonlinear pricing schemes where the buyer has inequity aversion, including wholesale price, quantity discount, and two-part tariff contracts. They show under which conditions each contract can coordinate the supply chain for the scenario where the supplier is the game leader. Ho et al. (2014) and Nie and Du (2017) study the interaction between distributional and peer-induced fairness in wholesale price and quantity discount contracts in supply chains with one supplier and two competing retailers. However, they provide contradictory results regarding which type of fairness is more dominant and the resulting profit for the retailers. Our model builds on to Cui et al. (2007). In addition to providing the analysis for the case where the supplier is the leader (similar to Cui et al. 2007; Cui and Mallucci 2016; Ingene et al. 2019), we also analyze the setting in which the buyer is the leader. The latter is a more realistic representation of the context presented in this paper, i.e., the case where smallholder farmer supplies to a big agri-food firm. By comparing both leadership scenarios, we provide insights into the social and economic impacts of stakeholder engagement in decision-making, where the big agri-food firm grants the farmer the leadership in decision making. Our results show that the interaction between investment decisions and equity concerns may diminish the leadership advantage in the game, and in some settings, it may reverse it.

We also consider the stream of research about investments in supplier development, specifically in the suppliers’ production processes. Several works study contracts that include capacity investments by the suppliers, motivated by different incentives from buyers (Van Mieghem 1999; Taylor and Plambeck 2007a, b). Bai and Sarkis (2016) study a series of cooperative and non-cooperative game theoretic models and find the optimal investment quantities for each setting. They conclude that a cooperative scheme can result in higher profits for all players and identify some conditions in which it is more profitable not to make an investment. Cui and Mallucci (2016) study a pricing game with equity concerns where they include the investment as a parameter to calculate each player’s equitable profit share. In contrast, our model introduces each player’s investment as a decision variable, which reduces the supplier’s unit production cost. We also provide the analytical solutions to the investment as well as the pricing decisions when both parties have equity concerns in their decision-making.

According to Greenwood (2007), stakeholder engagement encompasses “practices the organisation undertakes to involve stakeholders in a positive manner in organisational activities.” Prado-Lorenzo et al. (2009) emphasize that the economic objectives of firms must be reached under the consideration of other stakeholder’s needs and demands along social dimensions. Similarly, Eccles et al. (2014) identify stakeholder engagement as one of the four pillars that characterize sustainable organizations. They find empirical evidence that companies with a high level of sustainability focus on understanding the needs of their stakeholders take actions in managing their relationships, and they report on their quality. Liu et al. (2018) study the initiative of creating consortia of retailers to address the social challenge of improving the working conditions of supplier factories in developing countries. They highlight that including all stakeholders in the value chain in the process of decision-making makes the improvement efforts “more effective, efficient, sustainable or just.” We contribute to this stream of literature by studying how big (buyer) agri-food firms can help (supplier) smallholder farmers by granting them the leadership in decision-making. Motivated by the practices of Fractal Café, we examine the impact of this direct stakeholder engagement in pricing and investment decisions on improving equity in the supply chain. However, we find that granting the leadership in decision-making to farmers may have reverse effects than intended, leading to even lower (higher) profits and utilities for the farmer (agri-food firm).

In our model, we incorporate stakeholder engagement through different power structures, where we change which player acts as game leader. Choi (1991) studied Stackelberg leadership in pricing games and found that the game leader gets a higher share of the total supply chain profit. Cai et al. (2009) identified some conditions where the use of inconsistent pricing and price discounts allows the game follower to earn a higher profit than the leader. Similarly, Zhang et al. (2012) studied a pricing game with product substitutability. They found that the game leader does not always get the highest profit, although all players have an incentive to lead. In our paper, we study the effects of the interaction between power structure and equity concerns in both the investment and pricing decisions. We analyze two different contracts and identify the conditions under which the game leader does not enjoy an advantage.

3 Base model

We start by introducing the base model, where the buyer agri-food firm (indexed by B) has the upper hand in decision-making in his interactions with a supplier smallholder farmer (indexed by S) in a dyadic supply chain with no equity concerns. In other words, we have a Stackelberg game setting where the buyer leads and the supplier follows. The objective of each player is to maximize his or her own profit. We use a two-stage framework to model the problem. Specifically, in Stage 1, the optimal investment decisions are determined to lower the supplier’s production cost. These decisions then influence the optimal pricing decisions in Stage 2. The order of events is as follows. First, the buyer decides on his investment \(I_B\) and then the supplier decides her investment \(I_S\). Given these investments, the buyer now sets the retail price p and then the supplier sets the wholesale price w.

Let \(D(p)=a-bp\) represent the buyer’s demand as a function of the retail price p, where \(a>0\) denotes the potential market demand, and \(b>0\) denotes the price sensitivity of demand. The supplier’s unit production cost \(c_0\) can be reduced by an amount \(f(I_T)\) via a total investment of \(I_T\) in her production processes. Both the supplier and the buyer can contribute to the total investment via amounts \(I_S\) and \(I_B\), respectively. The total investment \(I_T = I_S+I_B\) leads to a reduced production cost of \(c=c_0-f(I_T)\), where \(f(I_T)=\sqrt{s\cdot I_T}\) with s representing the sensitivity of production cost reduction to total investment. This simple functional form is in line with Etro (2007), which states that investment is subject to diminishing marginal returns on the output produced. (Trivially, we impose the condition \(I_T \le I_{max} \equiv c_0^2/s\) to avoid a negative production cost.) In the absence of capacity constraints, the supplier’s and buyer’s profits, \(\Pi _i,\; i \in \{S,B\}\), are given by:

$$\begin{aligned} \Pi _S= & {} \pi _S-I_S , \;\;\;\text {and} \;\;\;\; \Pi _B=\pi _b-I_B,\nonumber \\ & \text {where,} \; \pi _S=\left( w-c\right) (a-bp) , \ \text {and} \ \pi _B=(p-w)(a-bp), \end{aligned}$$
(1)

and w represents the supplier’s wholesale price, and m denotes the buyer’s sales margin (i.e., \(m=p-w\)). Following the approach presented in Choi (1991), we set the buyer’s margin m as the buyer’s decision variable in order to be able to analyze the Stackelberg setting in which the buyer is the leader.

Then, we use backward induction to first consider the Stage 2 problem in order to derive the expressions for the optimal pricing decisions for a given set of investment levels, i.e \(w^{*}(I_S, I_B)\) and \(m^{*}(I_S, I_B)\). Next, we determine the optimal investment decisions, \(I^{*}_S\) and \(I^{*}_B\), in Stage 1. The following lemma characterizes the optimal solution to the base model. (We denote the optimal solution to the profit-maximizing base model with the superindex PR in the remaining of the paper.) To improve the exposition of the paper, all proofs are relegated to the “Appendix”.

Lemma 1

The optimal solution for the base model is given by:

$$\begin{aligned} w^{*PR}= & {} \frac{1}{4}\left( \frac{a}{b}+3\left( c_0-\sqrt{s\cdot min\left\{ \frac{s\left( a-bc_0\right) ^2}{\left( bs-16\right) ^2},\frac{c_0^2}{s}\right\} }\right) \right) ,\\ m^{*PR}= & {} \frac{1}{2}\left( \frac{a}{b}-c_0+\sqrt{s\cdot min\left\{ \frac{s\left( a-bc_0\right) ^2}{\left( bs-16\right) ^2},\frac{c_0^2}{s}\right\} }\right) ,\\ I^{*PR}_S= & {} min\left\{ \frac{s\left( a-bc_0\right) ^2}{\left( bs-16\right) ^2},\frac{c_0^2}{s}\right\} , \text {and }\ I^{*PR}_B=0. \end{aligned}$$

Lemma 1 shows that a reduction in the unit production cost is beneficial for both players. Not surprisingly, as the game leader, the buyer finds it optimal that the supplier makes all the investment to lower the unit production cost. Although an investment in the production processes results in additional costs for the supplier, it leads to a lower wholesale price. This enables the supplier to obtain higher profits due to higher demand by the buyer. This is also beneficial for the buyer, as he enjoys higher sales with a higher sales margin. Next, we extend our base model to study the impact of equity concerns on the optimal solution.

4 The impact of equity concerns

We now consider a setting where the (buyer) agri-food firm is concerned not only about the economic outcomes, but also about the social outcomes of his decisions in terms of equity. In order to demonstrate this, we use the inequity aversion model proposed by Fehr and Schmidt (2001). They assume that the objective of each player is to maximize their own utility, which equals their monetary payoff less the disutility of obtaining a profit amount that deviates from the amount they perceive as equitable. In this setting, the utility functions for the supplier (\(U_S\)) and the buyer (\(U_B\)), are given by:

$$\begin{aligned} U_S= & {} \Pi _S-\alpha _S\cdot max\{\gamma _S(\pi _S+\pi _B)-\pi _S,0\}-\beta _S\cdot max\{\pi _S-\gamma _S(\pi _S+\pi _B),0\}, \end{aligned}$$
(2)
$$\begin{aligned} U_B= & {} \Pi _B-\alpha _B\cdot max\{\gamma _B(\pi _S+\pi _B)-\pi _B,0\}-\beta _B\cdot max\{\pi _B-\gamma _B(\pi _S+\pi _B),0\}. \end{aligned}$$
(3)

Equations (2) and (3) show that given the exogenous parameter \(\gamma _i\), which denotes the proportion of the total supply chain profit that is considered equitable by player \(i\in \{S,B\}\), an equitable profit allocation occurs if \(\gamma _i\cdot (\pi _S+\pi _B)=\pi _i\). Otherwise, disadvantageous inequity occurs if player \(i\in \{S,B\}\) receives a lower profit than his equitable share of the total supply chain profit, i.e., \(\pi _i<\gamma _i\cdot (\pi _S+\pi _B)\). Advantageous inequity occurs if player \(i\in \{S,B\}\) receives a higher profit than his equitable share of the total supply chain profit, i.e., \(\pi _i>\gamma _i\cdot (\pi _S+\pi _B)\). The impact of disadvantageous and advantageous inequity on the players’ utility functions is captured via exogenous parameters \(\alpha _i\) and \(\beta _i\), respectively, where \(0\le \alpha _i<1,\ 0\le \beta _i<1\) for \(i\in \{S,B\}\). This formulation extends the model presented by Fehr and Schmidt (2001). While they define a player’s equitable profit share in relation to the other player’s profit outcome, we assume that the equitable profit is defined in relation to the total supply chain profit (similar to Khan 2018). We also relax the assumption that \(\alpha _i\ge \beta _i, i\in \{S,B\}\), as we consider that a player with high level of social responsibility could have a higher concern for advantageous inequity than for disadvantageous inequity. This allows us to consider a more general setting where the assumptions presented by Fehr and Schmidt (2001) hold for a subset of the parameter combinations.

We use backward induction in our analysis (similar to our solution approach for the base model presented in Sect. 3). In what follows, we first present the optimal pricing decisions as a function of the players’ investments under equity concerns (Stage 2).

4.1 Optimal pricing decisions (Stage 2)

4.1.1 Supplier’s problem

We start our analysis with the supplier’s (follower’s) problem, which is to maximize her utility \(U_S\) by optimizing the wholesale price w for any given retail margin m. Equation (2) shows that the supplier’s utility function \(U_S\) exhibits a piece-wise structure in the supplier’s wholesale price w. Hence, based on the retailer’s sales margin, the optimal wholesale price follows a different functional form. Theorem 1 fully characterizes the structure of the optimal wholesale price for any given retail margin (\(w^{*EQ}(m)\)). This constitutes the optimal solution at the subgame equilibrium, given that this solution does not yet consider the results from the investment decisions (Stage 1).

Theorem 1

The supplier’s utility \(U_S\) is concave in the wholesale price w, and for any given retail margin m, the optimal wholesale price \(w^{*EQ}(m)\) has the following structure:

$$\begin{aligned} w^{*EQ}(m)= {\left\{ \begin{array}{ll} w_2(m)\equiv \frac{1}{2}\left( \frac{a}{b}+c+\frac{m\left( \beta _S(1-2\gamma _S)-1\right) }{1+\beta _S(\gamma _S-1)}\right) ,&{} \hbox { if}\ \ m\le \bar{m}_2 \\ \bar{w}(m)\equiv \frac{c\left( \gamma _S-1\right) -\gamma _Sm}{\gamma _S-1},&{} \hbox { if}\ \ \bar{m}_2<m\le \bar{m}_1\\ w_1(m)\equiv \frac{1}{2}\left( \frac{a}{b}+c+\frac{m\left( 1+\alpha _S(1-2\gamma _S)\right) }{\alpha _S(\gamma _S-1)-1}\right) ,&{} \text {if }m >\bar{m}_1, \end{array}\right. } \end{aligned}$$
(4)

where \(\bar{m}_1 \equiv \frac{(-a+bc)\left( -1+\alpha _S(\gamma _S-1)\right) (\gamma _S-1)}{b\left( \gamma _S(\alpha _S-1)-(1+\alpha _S)\right) }\), and \(\bar{m}_2\equiv \frac{(-a+bc)\left( 1+\beta _S(\gamma _S-1)\right) (\gamma _S-1)}{b\left( 1+\beta _S(\gamma _S-1)+\gamma _S\right) } \le \bar{m}_1\).

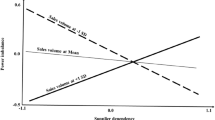
Theorem 1 shows that when the buyer’s sales margin is sufficiently small (i.e., \(m \le \bar{m}_2\)), the supplier will set her wholesale price to a value that is lower than the profit-maximizing wholesale price presented in the base case model; see Sect. 3. By sacrificing a portion of her profits, the supplier maximizes her utility and obtains advantageous inequity in this setting [i.e., \(w^{*EQ}(m) = w_2(m)\)]. However, as the retail margin grows, the supplier’s optimal wholesale price gradually decreases to a value that results in an equitable profit share for the supplier [i.e., \(w^{*EQ}(m) = \bar{w}(m)\)]. While an equitable profit share holds for intermediate retail margin (i.e., \(\bar{m}_2 < m \le \bar{m}_1\)), further growth in the retail margin raises the optimal wholesale price beyond the profit-maximizing wholesale price presented in the base case model. Consequently, a large retail margin (i.e., \(m > \bar{m}_1\)) forces the supplier to set her wholesale price such that she experiences disadvantageous inequity [i.e., \(w^{*EQ}(m) = w_1(m)\)]. Figure 1 depicts the behavior of \(w^{*EQ}(m)\) for a problem instance.

Fig. 1
figure 1

Supplier’s optimal wholesale price response function \(w^*(m)\) for a given set of investment levels \(I_S,I_B\) (where \(a=550,\ b=2.3,\ c_0=10,\ s=0.08,\ \alpha _S=0.7,\ \beta _S=0.5,\ \gamma _S=0.4,\ \alpha _B=0.4,\ \beta _B=0.6,\ \gamma _B=0.7,\ I_S=700,\ I_B=0\))

Full size image

Theorem 1 also shows that as the supplier’s concern for advantageous inequity (\(\beta _S\)) increases, her optimal wholesale price (\(w_2(m)\)) decreases. On the other hand, a greater concern for disadvantageous inequity (\(\alpha _S\)) forces the supplier to raise her wholesale price (\(w_1(m)\)). These findings are not surprising, as greater equity concerns would put more weight on the disutility terms in the utility-maximizing objective function. Therefore, a higher deviation between the profit-maximizing wholesale price and the utility-maximizing wholesale price becomes inevitable. These findings can be extended to the impact of \(\gamma _S\) (i.e., the proportion of the total supply chain profit that is considered equitable by the supplier) on the optimal wholesale price, as the impact of \(\gamma _S\) on the utility-maximizing objective function is similar to that of \(\alpha _S\) and \(\beta _S\).

4.1.2 Buyer’s problem

The supplier’s wholesale price response function, \(w^{*EQ}(m)\), takes a different form for different ranges of the buyer’s retail margin, m. Therefore, the buyer’s utility function \(U_B\) follows a piece-wise functional form in m when \(w^{*EQ}(m)\) is substituted into the buyer’s utility function, see Fig. 2.

Fig. 2
figure 2

Buyer’s utility \(U_B\) as function of the retail margin m for a given set of investment levels \(I_S,I_B\) (where \(a=872,\ b=2.4,\ c_0=13.4,\ s=0.3,\ \alpha _S=0.13,\ \beta _S=0.35,\ \gamma _S=0.62,\ \alpha _B=0.55,\ \beta _B=0.3,\ \gamma _B=0.5,\ I_S=1125,\ I_B=0\))

Full size image

As depicted in Fig. 2, \(U_B\) is not concave in m, and it may have multiple local optima. The set of candidate solutions can be characterized based on the parameter \(\gamma _T = \gamma _S+\gamma _B\), which can be interpreted as the proportion of the total supply chain profit, \(\pi _S+\pi _B\), that leads to an equitable profit distribution among players. In other words, if \(\gamma _T=1\), the sum of the individual profit amounts that players consider equitable, \(\gamma _T(\pi _S + \pi _B)\), is equal to the actual supply chain profit. On the other hand, if \(\gamma _T<1\) (\(\gamma _T>1\)), the sum of the individual profit amounts that players consider equitable is less (greater) than the actual supply chain profit. The following theorem characterizes the structure of the buyer’s optimal retail margin.

Theorem 2

The buyer’s utility function \(U_B\) is not concave in the retail margin m, and for any given \(\gamma _T\), the optimal retail margin \(m^{*EQ}\) has the following structure:

$$\begin{aligned} m^{*EQ}= {\left\{ \begin{array}{ll} m_1,&{} \text {if }\ \gamma _T<1, d_1>d_2 \;\&\; d_3>d_4, \\ m_2,&{} \text {if }\ \gamma _T<1, d_4>d_3, d_5>0 \;\&\; d_7>d_6, \\ m_4,&{} \text {if }\ \gamma _T<1, d_6>d_7, \\ \bar{m_2},&{} \text {if }\ \gamma _T=1 \;\&\; d_7>d_6, \\ m_4,&{} \text {if }\ \gamma _T=1 \;\&\; d_6>d_7, \\ m_3,&{} \text {if }\ \gamma _T>1, d_9>d_8,\\ m_4,&{} \text {if }\ \gamma _T>1, d_8>d_9,\\ \end{array}\right. } \end{aligned}$$
(5)

where

$$\begin{aligned} m_1\equiv & {} \frac{(1+\alpha _B)(-a+bc)(1+\beta _S(\gamma _S-1))^2}{b(\beta _S-1)((\beta _S-1)(-2+\alpha _B(\gamma _B-2))+2\beta _S\gamma _S(1+\alpha _B))},\\ m_2\equiv & {} \frac{(\beta _B-1)(-a+bc)(1+\beta _S(\gamma _S-1))^2}{b(\beta _S-1)((\beta _S-1)(2+\beta _B(\gamma _B-2))+2\beta _S\gamma _S(\beta _B-1))},\\ m_3\equiv & {} \frac{(1+\alpha _B)(-a+bc)(1+\alpha _S(1-\gamma _S))^2}{b(1+\alpha _S)((1+\alpha _S)(-2+\alpha _B(\gamma _B-2))+2\alpha _S\gamma _S(1+\alpha _B))},\\ m_4\equiv & {} \frac{(\beta _B-1)(-a+bc)(1+\alpha _S(1-\gamma _S))^2}{b(1+\alpha _S)((1+\alpha _S)(2+\beta _B(\gamma _B-2))+2\alpha _S\gamma _S(\beta _B-1))}.\\ \end{aligned}$$

For ease of exposition, the expressions for \(\{d_i\}_{1\le i\le 9}\) are given in the “Appendix”. Theorem 2 has implications for the players’ equity outcomes for different values of \(\gamma _T\). The following corollary summarizes the equity outcome of different candidate solutions of \(m^{*EQ}\) for the buyer and supplier.

Corollary 1

For any given \(\gamma _T\), the set of possible optimal solutions \((m^{*EQ}\) and \(w^{*EQ}(m^{*EQ}))\) and the resulting equity outcomes can be characterized as in Table 1.

Table 1 The candidate optimal solutions and the corresponding equity outcomes for players for any given \(\gamma _T\)
Full size table

Interestingly, Table 1 shows that when the sum of the individual profit amounts that players consider equitable is less than the actual supply chain profit, i.e., \(\gamma _T<1\), then the supplier always experiences inequity. While any equity outcome is possible for the buyer in this setting, the supplier never experiences equity. Another extreme setting occurs when the sum of the equitable profit amounts is greater than the actual supply chain profit, i.e., \(\gamma _T>1\). In this setting, the supplier suffers both in terms of profit and in terms of equity, as the only possible outcome for the supplier is disadvantageous inequity. In contrast, the buyer can experience any of the three possible equity outcomes. Table 1 shows that the only case in which both players can achieve equity is when \(\gamma _T=1\), as this represents the setting where the sum of the equitable profit amounts equals to the actual supply chain profit (i.e., the profit amount that the players want to distribute aligns with the actual supply chain profit). The intuition for these findings is as follows. Since the setting with \(\gamma _T<1\) allows for an excess profit amount (i.e., the actual profit amount minus the sum of profit amounts that are considered equitable by the players) to be distributed across players, at least one player obtains a profit amount that is greater than what he considers equitable, which leads to advantageous equity. The opposite holds when \(\gamma _T>1\). Although an equitable outcome is possible for the buyer (since he is the leader of the game), the follower always obtains a disadvantageous equity when players try to distribute a profit amount that deviates from the actual supply chain profit.

In the next section, we consider the Stage 1 problem.

4.2 Optimal investment decisions (Stage 1)

In Stage 1, we consider the optimal investment decisions using backward induction. Since the buyer is the leader of the game, we first analyze the supplier’s problem, which is to find the optimal investment amount for any given investment level by the buyer, \(I_S^{*EQ}(I_B)\). Then we move to the buyer’s problem, which is to find the optimal investment, \(I_B^{*EQ}\). The following theorem characterizes the structure of the optimal investment decisions.

Theorem 3

The supplier’s utility function \(U_S\) is either concave or convex decreasing in \(I_S\), depending on problem parameters. Hence, there exists a unique optimal solution \(I_S^{*EQ}(I_B)\) that maximizes the supplier’s utility. The buyer finds it optimal not to invest an amount, i.e., \(I^{*EQ}_B = 0\).

Theorem 3 shows that despite the equity concerns, the buyer still finds it optimal not to invest an amount in the supplier’s production processes (similar to the findings of the base model, see Sect. 4). This finding can be attributed to the leadership structure of the game. However, an interesting finding follows from Theorem 3: equity concerns may lead to a setting in which the supplier’s optimal investment amount is also zero. Consequently, in contrast to the base case scenario where the supplier (farmer) always finds it optimal to invest in her production processes, equity concerns may lead to a setting where the no investment strategy is optimal for both parties. In Sect. 6, we numerically quantify the impact of equity concerns on the optimal solution and the profit for both players compared to the base model, where the sole objective of the players is to maximize profits.

5 The impact of supplier engagement

In addition to bringing equity concerns into the decision-making, the agri-food firm can also try to empower the smallholder farmer through stakeholder engagement, similar to Fractal Café. In this section, we analyze the setting in which the agri-food firm engages the smallholder farmer in decision-making. This is, the smallholder farmer is granted the leadership in setting the wholesale price as well as the investment for improving the production processes. For this case, we follow the same approach as in Sect. 4. That is, we use backward induction to first study the optimal pricing decisions and then find the optimal investment levels in a setting where the supplier is the leader. We show that the results for this setting have a similar structure to the case where the buyer is the leader, see Sect. 4. The results can be summarized as follows (We use the superindex ST to denote the optimal solution of this model.).

Theorem 4

The buyer’s utility \(U_B\) is concave in the retail margin m, and for any given wholesale price w, the optimal retail margin \(m^{*ST}(w)\) has the following structure:

$$\begin{aligned} m^{*ST}(w)= {\left\{ \begin{array}{ll} m_2(w)\equiv \frac{1}{2}\left( \frac{a}{b}-w-\frac{\beta _B\gamma _B\left( w-c\right) }{1+\beta _B(\gamma _B-1)}\right) ,&{} \text {if }\ w\le \bar{w}_2 \\ \bar{m}(w)\equiv \frac{\gamma _B\left( w-c\right) }{1-\gamma _B},&{} \text {if }\bar{w}_2 < w\le \bar{w}_1 \\ m_1(w)\equiv \frac{1}{2}\left( \frac{a}{b}-w-\frac{\alpha _B\gamma _B\left( w-c\right) }{\alpha _B(\gamma _B-1)-1}\right) ,&{} \text {if }w > \bar{w}_1, \end{array}\right. } \end{aligned}$$
(6)

where \(\bar{w}_1\equiv \frac{a(1-\gamma _B)\left( \alpha _B(\gamma _B-1)-1\right) +bc\gamma _B\left( 2-\alpha _B(\gamma _B-1)\right) }{b\left( 1+\alpha _B(1-\gamma _B)+\gamma _B\right) }\), \(\bar{w}_2\equiv \frac{a(1-\gamma _B)\left( 1-\beta _B(\gamma _B-1)\right) +bc\gamma _B\left( 2-\beta _B(1-\gamma _B)\right) }{b\left( 1-\beta _B(1-\gamma _B)+\gamma _B\right) }\le \bar{w}_1\).

Thus, if the wholesale price is sufficiently low (i.e., \(\ w\le \bar{w}_2\)), then the buyer will experience advantageous inequity. The opposite holds when the wholesale price is sufficiently high (i.e., \(w > \bar{w}_1\)). The buyer experiences equity only when the wholesale price is neither too high nor too low (i.e., \(\bar{w}_2 < w\le \bar{w}_1\)). We find that when the agri-food firm grants the leadership in decision-making to the farmer, he will settle for a lower profit margin than when he has a profit maximizing objective [i.e., \(m^{*ST}(w) < m^{*PR}(w)\)] whenever the wholesale price is also sufficiently low (i.e., \(\ w\le \bar{w}_2\)), as this still leaves the buyer at an advantage. Below, we present the structure of the optimal wholesale price.

Theorem 5

The supplier’s utility \(U_S\) is not concave in the wholesale price w, and for any given \(\gamma _T\), the optimal wholesale price w has the following structure:

$$\begin{aligned} w^{*ST}= {\left\{ \begin{array}{ll} w_1,&{} \text {if }\ \gamma _T<1, d_{10}>d_{11}\; \&\; d_{12}>d_{13}, \\ w_2,&{} \text {if }\ \gamma _T<1, d_{13}>d_{12}, d_{14}>0\; \&\; d_{16}>d_{15}, \\ w_4,&{} \text {if }\ \gamma _T<1, d_{15}>d_{16}, \\ \bar{w_2},&{} \text {if }\ \gamma _T=1\; \&\; d_{16}>d_{15}, \\ w_4,&{} \text {if }\ \gamma _T=1\; \&\; d_{15}>d_{16}, \\ w_3,&{} \text {if }\ \gamma _T>1, d_{18}>d_{17},\\ w_4,&{} \text {if }\ \gamma _T>1, d_{17}>d_{18},\\ \end{array}\right. } \end{aligned}$$
(7)

where

$$\begin{aligned} w_1\equiv & {} \frac{-(1+\alpha _S)(1+\beta _B(\gamma _B-1))\left( a(1+\beta _B(\gamma _B-1))-bc\left( \beta _B(1+\gamma _B)-1\right) \right) +\alpha _S\gamma _Sbc(\beta _B-1)^2}{b(\beta _B-1)\left( 2(1+\alpha _S)(1+\beta _B(\gamma _B-1))+\alpha _S(\beta _B-1)\gamma _S\right) },\\ w_2\equiv & {} \frac{-(\beta _S-1)(1+\beta _B(\gamma _B-1))\left( a(1+\beta _B(\gamma _B-1))-bc(\beta _B(1+\gamma _B)-1)\right) +\beta _S\gamma _Sbc(\beta _B-1)^2}{b(\beta _B-1)\left( 2(\beta _S-1)(1+\beta _B(\gamma _B-1))+(\beta _B-1)\beta _S\gamma _S\right) },\\ w_3\equiv & {} \frac{-(1+\alpha _S)(-1+\alpha _B(\gamma _B-1))\left( -(1+\alpha _B)(a+bc)+\alpha _B\gamma _B(a-bc)\right) +\alpha _S\gamma _Sbc(1+\alpha _B)^2}{b(1+\alpha _B)\left( 2(1+\alpha _S)(-1+\alpha _B(\gamma _B-1))+(1+\alpha _B)\alpha _S\gamma _S\right) },\\ w_4\equiv & {} \frac{-(\beta _S-1)(-1+\alpha _B(\gamma _B-1))\left( -(1+\alpha _B)(a+bc)+\alpha _B\gamma _B(a-bc)\right) +\beta _S\gamma _Sbc(1+\alpha _B)^2}{b(1+\alpha _B)\left( 2(\beta _S-1)(-1+\alpha _B(\gamma _B-1))+(1+\alpha _B)\beta _S\gamma _S\right) }. \end{aligned}$$

For ease of exposition, the expressions for \(\{d_i\}_{10\le i\le 18}\) are given in the “Appendix”. The possible solution pairs depend on the value of \(\gamma _T\) as we show in Corollary 2. The results show that the candidate optimal solutions and the corresponding equity outcomes follow a similar structure to that of the equity model.

Corollary 2

For any given \(\gamma _T\), the set of possible optimal solutions \(w^{*ST}\) and \(m^{*ST}(w^{*ST})\) and the resulting equity outcomes can be characterized as in Table 2.

Table 2 The candidate optimal solutions and the corresponding equity outcomes for players for any given \(\gamma _T\)
Full size table

Table 3 summarizes the outcomes in terms of equity that the supplier experiences as a result of stakeholder engagement. These results show that, when \(\gamma _T>1\), she has the possibility to have an advantageous outcome. This is an improvement from the model without stakeholder engagement, where the supplier is always at a disadvantage. Similarly, when \(\gamma _T=1\), the supplier no longer has the possibility to end at a disadvantage. Although some of these results protect the supplier from a disadvantageous outcome, having an advantage over the buyer is also undesirable. A more detailed comparison of the outcomes from both models is presented in our numerical study in Sect. 8.

Table 3 Possible equity outcomes for the supplier for any given \(\gamma _T\) with the two proposed models
Full size table

Finally, we analyze the optimal investment decisions. We identify the same behavior of the utility functions as in the case where the buyer leads the game. Theorem 6 characterizes the optimal solutions.

Theorem 6

The buyer’s utility function \(U_B\) is either concave or convex decreasing in \(I_B\), depending on problem parameters. Hence, there exists a unique optimal solution \(I_B^{*ST}(I_S)\) that maximizes the buyer’s utility. The supplier finds it optimal not to invest an amount, i.e., \(I^{*ST}_S = 0\).

The supplier’s utility function decreases in her investment \(I_S\), so as game leader she finds it optimal not to make an investment. Similar to the result in Sect. 4.2, the buyer as game follower finds it optimal to make an investment only when needed, depending on the problem parameters.

6 The impact of production quantity constraints

Smallholder farmers are often faced with capacity restrictions that can result in their inability to satisfy the buyer’s demand in its totality. To understand the effects of such restrictions in the pricing and investment decisions, in this section we consider the case where the farmers have a restricted capacity. The farmer is only capable of producing a maximum quantity of \(\bar{q}\), which restricts the buyer’s purchased quantity, such that \(a-bp\le \bar{q}\). Given that our focus is on pricing decisions, we rewrite this restriction as \(p\ge \frac{a-\bar{q}}{b}\) or equivalently \(m\ge \frac{a-\bar{q}}{b}-w\). The implications of this restriction in each model are as follows.

Equity model. In this model, the optimal retail margin is found during the second step of the backward induction process, which means that it does not depend on the value of the wholesale price. Based on the properties of the behavior of \(U_B(m)\) found in the previous section for each of the intervals defined in m, the optimal retail price has the following form when the constraint in \(\bar{q}\) is tight:

$$\begin{aligned} m^{*EQ}= {\left\{ \begin{array}{ll} \underset{m\in \{m^{\bar{q}},m_4\}}{{{\,\mathrm{argmax}\,}}} U_B(m),&{} \text {if }\ \gamma _T<1 \\ \underset{m\in \{m^{\bar{q}},m_4\}}{{{\,\mathrm{argmax}\,}}} U_B(m),&{} \text {if }\ \gamma _T=1\\ \underset{m\in \{m^{\bar{q}},m_3,\hat{m}_3,m_4\}}{{{\,\mathrm{argmax}\,}}} U_B(m),&{} \text {if }\ \gamma _T>1, \end{array}\right. } \end{aligned}$$
(8)

Stakeholder engagement model. In this model, the optimal retail margin is found during the first step of the backward induction process. Hence, the solution is a function of the wholesale price selected by the supplier \((m^*(w))\). Furthermore, we observe that \(m^*\) is increasing in w. Then, we can conclude that, if the constraint in \(\bar{q}\) is tight, then the retail margin that yields this quantity, \(m^{\bar{q}}\), constitutes the new optimal solution.

In both models, when the supplier’s capacity is not enough to fulfill the buyer’s demand, the retail price is increased to compensate for the lower production quantity. This can be seen from the restriction \(p\ge \frac{a-\bar{q}}{b}\), where the quantity constraint imposes a lower threshold on the value of the retail price (and the retail margin, accordingly). Recall Fig. 2, which shows the different intervals in the value of the retail margin that correspond to each equity outcome for the buyer. From this plot we can see that the size of the quantity constraint will determine its effect on the model outcomes. If the gap in the production quantity is small, then the retail price increases as the only effect of the capacity restriction. However, a larger gap in the production quantity will result in a larger price increase, which can cause the optimal solution to move to a different interval of the function. This would translate into a change in the equitable outcome (equity, disadvantageous or advantageous inequity) for the players. Then, the effects of the socially responsible practices can be overpowered by a restriction in the production quantity.In the next section, we present our analysis of a two-part tariff contract with equity concerns.

7 Two-part tariff contract

In this section, we consider an alternative to the contracts proposed in the previous sections. We study a two-part tariff contract (Lewis 1941) in our original problem setting, where the buyer acts as Stackelberg leader and both players have equity concerns. To distinguish from the other models, we use the superindex TP. In this contract, the buyer proposes a retail margin m and a fixed payment F to be paid by the supplier. This setting is very common in a retail environment where the supplier pays a slotting fee F to have her product listed. The slotting fee is expected to cover part of the fixed costs such as the space needed on the shelf and promotional expenses (Hamilton 2003; Aydin and Hausman 2009; Pfeiffer 2016). If the supplier accepts the contract, then she will set her wholesale price w. In this setting, the player’s profits are given by:

$$\begin{aligned} \pi _B^{TP}=m(a-b(w+m))+F, \quad \text {and} \quad \pi _S^{TP}=(w-c)(a-b(w+m))-F \end{aligned}$$
(9)

Each player has the objective to maximize his or her own utility function:

$$\begin{aligned} U_B^{TP}= & {} \pi _B^{TP}-\alpha _B\cdot max\{\gamma _B(\pi _S^{TP}+\pi _B^{TP})-\pi _B^{TP},0\}-\beta _B\cdot max\{\pi _B^{TP}-\gamma _B(\pi _S^{TP}+\pi _B^{TP}),0\}, \end{aligned}$$
(10)
$$\begin{aligned} U_S^{TP}= & {} \pi _S^{TP}-\alpha _S\cdot max\{\gamma _S(\pi _S^{TP}+\pi _B^{TP})-\pi _S^{TP},0\}-\beta _S\cdot max\{\pi _S^{TP}-\gamma _S(\pi _S^{TP}+\pi _B^{TP}),0\}. \end{aligned}$$
(11)

As with the previous models, we solve this game using backward induction. We first find the solution to the supplier’s optimization problem.

Theorem 7

The supplier’s utility \(U_S^{TP}\) is concave in the wholesale price w, and for any given retail margin m, the optimal wholesale price \(w^{TP}(m)\) has the following structure:

$$\begin{aligned} w^{*TP}(m,F)= {\left\{ \begin{array}{ll} w_2^{TP}(m,F)\equiv \frac{1}{2}\left( \frac{a}{b}+c+\frac{m(-1+\beta _S(1-2\gamma _S))}{1+\beta _S(\gamma _S-1)}\right) ,&{} \hbox { if}\ \ m\le \bar{m}_2^{TP} \\ \bar{w}^{TP}(m,F)\equiv \frac{(a+bc)(\gamma _S-1)+bm(1-2\gamma _S)\sqrt{(a^2-2abc)(\gamma _S-1)^2-2abm(\gamma _S-1)+b(4F(\gamma _S-1)+b(c(1-\gamma _S)+m)^2)}}{2b(\gamma _S-1)},&{} \hbox { if}\ \ \bar{m}_2^{TP}<m\le \bar{m}_1^{TP}\\ w_1^{TP}(m,F)\equiv \frac{1}{2}\left( \frac{a}{b}+c+\frac{m\left( 1+\alpha _S(1-2\gamma _S)\right) }{\alpha _S(\gamma _S-1)-1}\right) ,&{} \text {if }m >\bar{m}_1^{TP}, \end{array}\right. } \end{aligned}$$
(12)

where

$$ \begin{aligned} \bar{m}_1^{TP}\equiv & {} -\frac{(a-bc)(1+\alpha _S(1-\gamma _S))^2+\sqrt{(1+\alpha _S(1-\gamma _S))^2(4(1+\alpha _S)^2bF-4(\alpha _S^2-1)bF\gamma _S+(a-bc)^2\gamma _S^2)}}{b(1+\alpha _S)(-1+\alpha _S(\gamma _S-1)-\gamma _S)}\\ \bar{m}_2^{TP}\equiv & {} -\frac{(a-bc)(1+\beta _S(\gamma _S-1))^2+\sqrt{(1+\beta _S(\gamma _S-1))^2(4(\beta _S-1)^2bF-4(\beta _S^2-1)bF\gamma _S+(a-bc)^2\gamma _S^2)}}{b(\beta _S-1)(1+\beta _S(\gamma _S-1)+\gamma _S)} \le \bar{m}_1^{TP} \end{aligned}$$

Theorem 7 shows that the expressions for \(w^{*TP}(m,F)\) are the same as those for \(w^{*EQ}(m)\) (Theorem 1) in the intervals \(m\le \bar{m}_2^{TP}\) and \(m > \bar{m}_1^{TP}\). Then, the wholesale price only depends on the value of the fixed fee F in the interval \(\bar{m}_2^{TP}<m\le \bar{m}_1^{TP}\). Now, we solve the buyer’s optimization problem.

Theorem 8

The buyer’s utility function \(U_B^{TP}\) is not concave in the retail margin m and the fixed fee F, and for any given \(\gamma _T\), the optimal strategy \((m^{*TP},F^{*TP})\) has the following structure:

$$\begin{aligned} (m^{*TP},F^{*TP})= {\left\{ \begin{array}{ll} (m_1^{TP},F_{max}),&{} \text {if }\ \gamma _T<1, d_{19}>d_{20}, d_{21}>d_{22}\;\&\; d_{23}>0, \\ (m_2^{TP},F_{max}),&{} \text {if }\ \gamma _T<1, d_{20}>d_{19}, 0>d_{24} \;\&\; d_{25}>0, \\ (m_4^{TP},F_{max}),&{} \text {if }\ \gamma _T<1, d_{22}>d_{21}, d_{23}>0, d_{24}>0 \;\&\; d_{26}>0, \\ (m_5^{TP},F_5^{TP}),&{} \text {if }\ \gamma _T<1, 0>d_{23}, 0>d_{25} \;\&\; 0>d_{26}, \\ (m_4^{TP},F_{max}),&{} \text {if }\ \gamma _T=1 \;\&\; d_{26}>0, \\ (m_5^{TP},F_5^{TP}),&{} \text {if }\ \gamma _T=1 \;\&\; 0>d_{26}, \\ (m_3^{TP},F_{max}),&{} \text {if }\ \gamma _T>1, d_{27}>0 \;\& \;d_{29}>d_{28},\\ (\hat{m_3}^{TP},F_{max}),&{} \text {if }\ \gamma _T>1, 0>d_{23} \;\&\; 0>d_{27},\\ (m_4^{TP},F_{max}),&{} \text {if }\ \gamma _T>1, d_{23}>0\; \&\; d_{28}>d_{29},\\ \end{array}\right. } \end{aligned}$$
(13)

where

$$\begin{aligned} m_1^{TP}= & {} \frac{(1+\alpha _B)(-a+bc)(1+\beta _S(\gamma _S-1))^2}{b(\beta _S-1)((\beta _S-1)(-2+\alpha _B(\gamma _B-2))+2\beta _S\gamma _S(1+\alpha _B))}\\ m_2^{TP}= & {} \frac{(1-\beta _B)(-a+bc)(1+\beta _S(\gamma _S-1))^2}{b(\beta _S-1)((\beta _S-1)(2+\beta _B(\gamma _B-2))+2\beta _S\gamma _S(\beta _B-1))}\\ m_3^{TP}= & {} -\frac{(1+\alpha _B)(a-bc)(1+\alpha _S(1-\gamma _S))^2}{b(1+\alpha _S) \left( (1+\alpha _S)\left( -2+\alpha _B(\gamma _B-2)\right) +2\alpha _S\gamma _S(\alpha _B+1)\right) }\\ m_4^{TP}= & {} -\frac{(\beta _B-1)(a-bc)(1+\alpha _S(1-\gamma _S))^2}{b(1+\alpha _S)((1+\alpha _S)(2+\beta _B(\gamma _B-2))+2\alpha _S\gamma _S(\beta _B-1))}\\ \hat{m_3}^{TP}= & {} \frac{(-a+bc)(-1+\alpha _S(\gamma _S-1))}{b(1+\alpha _S)}\\ F_{max}= & {} (w-c)(a-b(w+m))\\ F_5^{TP}= & {} -\frac{(a-bc)^2(\gamma _S-1)}{4b}-\frac{m(a-bc)}{2} \end{aligned}$$

For ease of exposition, the expressions for \(\{d_i\}_{10\le i\le 18}\) are given in the “Appendix”. Our analysis shows that, in the intervals \(m\le \bar{m}_2^{TP}\) and \(m>\bar{m}_1^{TP}\), the buyer’s utility function increases in F, which means that the buyer will find optimal to set the fixed fee as high as possible. The fixed fee must be set in a way such that the supplier will accept to participate in the contract. This means that she should at least earn her reservation profit, which would then be equal to the profit that the supplier would earn if she chooses not to participate in the contract (Feng and Lu 2013). In our problem setting, both players’ profits would be zero if the parties do not reach a contract agreement, so the game leader can set F equal to the follower’s total revenue (Ingene et al. 2019). Hence, in these intervals, \(F^*=F_{max}=(w-c)(a-b(w+m))\). In contrast, in the interval \(\bar{m}_2^{TP}<m\le \bar{m}_1^{TP}\), multiple solutions can maximize the buyer’s utility depending on the parameter values. This solution corresponds to a line where all points, for any \(m_5^{TP}>0\), represent optimal solutions to our maximization problem. From the expression of \(F_5^{TP}(m_5^{TP})\), we can see that \(F_5^{TP}\) decreases in \(m_5^{TP}\), the retail margin. This can be interpreted as a way to balance both quantities, as charging a high fixed fee corresponds to a low retail margin, and viceversa. We now show under which conditions the candidate solutions from this interval are the optimal solutions to the problem. Table 4 summarizes the outcomes for each player in terms of equity for each set of candidate solutions.

Table 4 Set of candidate solutions for each equity outcome for any given \(\gamma _T\) in the two-part tariff contract
Full size table

These results show that a two-part tariff contract with equity concerns can be used by the game leader to regain his or her advantage (compared to our proposed base model with equity concerns). A two-part tariff contract results in a higher utility and profit for the game leader through the fixed fee. This occurs because in most cases the leader finds it optimal to charge a fixed fee as high as the total profit of the follower. As a result, this contract also increases inequity, as the follower will receive zero profit in most cases.

The game leader only chooses not to charge a fixed fee when certain conditions on the parameter values are met. This is when \(d_8<0\), which occurs when the buyer’s concern for advantageous inequity \(\beta _B\) takes a high value. This result is intuitive, since the buyer as game leader restrains from charging a fixed fee that takes the entire supplier’s profit when the buyer is largely concerned with experiencing advantageous inequity. This solution corresponds to the only solution where the game follower experiences equity and the leader can either experience equity, or disadvantageous inequity. When this solution is optimal, different pairs of the retail margin and fixed fee can achieve the same utility for the buyer. In these cases, it might be useful for the buyer to have a second objective, such as maximizing profit, to choose among the possible pairs of values.

Based on these results, we can conclude that a two-part tariff contract is not convenient when the players are concerned with equity. This type of contract increases inequity and only increases the utility of the game leader.

8 Numerical study

In order to quantify the impact of equity considerations and stakeholder engagement on the players, we performed an extensive numerical study. Our results show that while the demand and production parameters \((a, b, c_0, s)\) have an impact on the optimal solution, the behavior of the solutions stay the same as equity parameters \((\alpha _i,\ \beta _i,\ \gamma _i,\ i\in \{S,B\})\) are varied. The parameters used for this study were based on Fractal Café’s demand and cost data. However, the price elasticity could not be approximated with the data available. We performed a sensitivity analysis to consider a wide range of scenarios for the missing parameters. In order to keep our study brief and focused, in the remainder of this section we only present our findings for the case where \(a=500\), \(b=1\), \(c_0=45\), \(s=0.05\), if otherwise is not noted.

8.1 Comparison of models

In order to get a general overview of the optimal utilities and profits generated by the three different models, we first calculated the optimal profit generated by the base model with the aforementioned demand and production parameters. Then, for the same demand and production parameters, we evaluated the optimal utilities obtained by the players when they include (1) equity concerns, and (2) stakeholder engagement in their decision-making. For this analysis, we varied \(\alpha _i, \beta _i,\) and \(\gamma _i,\ i\in \{S,B\}\), using three levels \(\{0.1,0.5,0.9\}\) for each. That is, six parameters at three levels each, yielding \(3^{6}=729\) problem instances. Table 5 shows the optimal investment, optimal utilities and profits at the utility maximizing solutions for the equity and stakeholder engagement models. We show the mean across the 729 instances, as well as the minimum and the maximum values (in parenthesis), and the profit maximizing solution of the base model.

Table 5 Statistics with various equity parameters when \(a=500\), \(b=1\), \(c_0=45\), \(s=0.05\) (mean (min;max))
Full size table

The first relevant observation from the results shown in Table 5 is that the investment made by the supplier is higher after introducing equity concerns in the profit maximizing model. This suggests that the equity concerns effectively constitute an incentive for investment. We can see that even the minimum value of the supplier’s profit is higher than that obtained with the base model, due to the fact that in every instance \(w^{*EQ}>w^{*PR}\), while \(w^{*PR}+m^{*PR}>w^{*EQ}+m^{*EQ}\). This means that the introduction of equity concerns results in a lower retail price, which also means a higher demand. As a consequence, the supplier is inclined to make a higher investment given that the equity concerns will allow her to set a higher wholesale price and, as a result, get a higher share of the benefits obtained from the investment. However, when the players also introduce stakeholder engagement practices, the investment is lower in average than when they only introduce equity concerns in their decision making. In most of the instances (97%), the buyer sets a lower margin with the stakeholder engagement model than with the equity model. Contrary to what occurred for the supplier using the equity model, the lower margin using the stakeholder engagement model means that the buyer will not get such a high benefit from the investment, thus he finds it optimal to invest a lower amount than the supplier invests when she acts as follower.

Also from Table 5, we observe that the supplier’s utility and profit are higher when using the equity model (where she acts as follower) than with the stakeholder engagement model (where she acts as leader). This can be observed for each one of the instances that we studied. If we replicate our experiment by only optimizing Stage 2 for each model (i.e., finding \(p^*\) and \(m^*\) with \(I_S\) and \(I_B\) as constant parameters), we observe the opposite behavior: a player obtains a higher utility and profit from the model with equity concerns where he acts as leader than when he acts as follower. Thus, we infer that the behavior observed in Table 5 can be attributed to the investment, as this modifies the initial problem conditions (i.e., different production cost) and this in turn modifies the maximum achievable profits and utilities for each player. As we mentioned before, the total investment tends to be higher when using the equity model, which means a higher profit and utility for the supplier (follower).

We identify that for some instances in which \(\gamma _T=1\), the results follow the behavior of the standard Stackelberg game, where the leader exercises his or her advantage and receives a higher profit and utility. Table 6 shows some instances that exemplify these results.

Table 6 Sample instances showing different behaviors for the optimal utilities and profits when \(\gamma _T=1\)
Full size table

Another relevant observation from Table 5 is that the total supply chain profit is higher when introducing equity concerns and stakeholder engagement than when only maximizing profit. This can be due to two different effects. The first effect is that the introduction of equity concerns effectively encourages the players to make an investment as we explained before. Then, this investment reduces the production cost and this can result in a higher total supply chain profit. The second effect is that the transfer of profit to the follower can result in a decrease of the game leader’s advantage.

Additionally, after introducing equity concerns and stakeholder engagement practices, we observe that the leader’s utility (and in some cases the profit) attains its maximum value from all the instances studied when the follower has a high sense of social responsibility (i.e., \(\beta >\alpha\)). This result again reflects the impact of the equity concerns on the outcome for each player. While they can reverse the game leader’s advantage, they can also benefit him or her when the follower is more concerned with getting an advantage than a disadvantage. In Table 7, we can observe for the equity model that the buyer’s utility is higher in average when \(\beta _S>\alpha _S\). This condition also yields the highest possible value of profit for the buyer, as well as for the supply chain profit. For the stakeholder engagement model, Table 8 shows that the supplier’s utility and profit are higher in average when \(\beta _B>\alpha _B\). Again, this condition yields the highest possible value for the total supply chain profit, as well as a higher average value than when \(\beta _B\le \alpha _B\).

Table 7 Statistics for equity model distinguishing \(\beta _S>\alpha _S\) and \(\beta _S\le \alpha _S\) (mean(min;max))
Full size table
Table 8 Statistics for stakeholder engagement model distinguishing \(\beta _B>\alpha _B\) and \(\beta _B\le \alpha _B\) (mean(min;max))
Full size table

8.2 Cost of ignoring equity

Now we look at cost of ignoring equity. We define the solution vectors \(x^{*y}=\left( w^{*y},m^{*y},I_S^{*y},I_B^{*y}\right)\), where \(y=\{ PR,EQ \}\). To assess the cost of ignoring equity, we implement both solution vectors in the model with equity concerns, where the buyer acts as game leader, and compare the outcomes. This comparison is shown through the changes in utility as \(\Delta U_S\%=\frac{U_S(x^{*PR})-U_S(x^{*EQ})}{U_S(x^{*EQ})}\) and \(\Delta U_B\%=\frac{U_B(x^{*PR})-U_B(x^{*EQ})}{U_B(x^{*EQ})}\). This measure captures the change in utility that results from using a profit-maximizing solution in a setting where the players are concerned with equity. Table 9 exhibits some selected results exemplifying the relevant results discussed in what follows.

Table 9 Resulting utilities for the equity model that reflect the cost of ignoring equity
Full size table

Table 9 shows that the buyer, as game leader, always receives a higher utility by including equity concerns in his decision making process \(\left( U_B(x^{*EQ})\right)\). From the instances that we studied, we identify that this increase in utility can go as high as 70%. It is also important to acknowledge that this increase in the buyer’s utility can come at a cost to the supplier’s utility. The highest values of \(\Delta U_B\%\) also correspond to the lowest values of \(\Delta U_S\%\). However, it is interesting how in some cases both players can experience an increase in their utility when introducing equity concerns. In these cases, the increase is smaller than when only the buyer experiences an increase.

Considering that our main premise is to promote social equity by increasing smallholder farmers’ (suppliers’) profits, the results from this and the previous section lead us to conclude that the suppliers are better off by acting as followers and including equity concerns in their decision making process.

8.3 Capacity constraints

To study the effects of introducing a constraint in the supplier’s production capacity, we consider again the base case studied in Sect. 8.1 (where \(a=500\), \(b=1\), \(c_0=45\), \(s=0.05\) and we varied \(\alpha _i, \beta _i,\) and \(\gamma _i,\ i\in \{S,B\}\) using three levels \(\{0.1,0.5,0.9\}\) for each). From the previous results, we observed that these instances yield a total demand \(D=a-bp\) within the range [119.3, 228.8]. Hence we imposed a capacity constraint of \(\bar{q}=160\), which would be binding for a fraction of the instances studied. According to the analytical results in Sect. 6, this results in the constraint \(p\ge 340\). Table 10 shows a summary of the results obtained after introducing the capacity constraint.

Table 10 Statistics varying equity parameters when \(a=500\), \(b=1\), \(c_0=45\), \(s=0.05\), \(\bar{q}=160\) (mean (min;max))
Full size table

If we compare the results to those in Table 5, where the capacity is not constrained, we can see that the constraint causes the profits and utilities of the follower in each model to decrease in average, whereas those of the leader increase. In general, if we look at each individual instance, the optimal solution is to produce the maximum possible amount \(\bar{q}\) when the constraint is binding. This means that the retail price is higher than that corresponding to the unconstrained optimal solution. This is achieved by increasing the wholesale price when the supplier is the leader, or by increasing the retail margin otherwise. Hence, we can see that the capacity constraint serves as a mechanism through which the game leader exercises his power by increasing his price. However, the introduction of constraints means that the total demand cannot be satisfied, and thus the resulting total supply chain profit will be lower.

9 Conclusions

In this paper we include equity concerns in the investment and pricing decision-making processes in agri-food supply chains to increase their levels of social responsibility. Using Stackelberg games, we model a supplier and buyer dyad with inequity aversion and show that equity concerns have an impact on the wholesale and retail prices, as well as on the investment levels. Our model is based on the works by Cui et al. (2007) and Cui and Mallucci (2016). We based our study on the business model of the socially responsible company Fractal Café and made several modelling changes to the referred models to capture the characteristics of the relationship the company has with their coffee supplier. We model the equitable profit as a share of the total profit and not as a fraction of the other player’s payoff. Also, we include the investment levels as decision variables in the model with equity concerns and relax the assumption in earlier work that \(\alpha _i\ge \beta _i, i\in \{S,B\}\) to capture the concept of social responsibility. Finally, we consider a variation of our model where the supplier acts as game leader.

One of the purposes of this study is to understand if equity concerns and stakeholder engagement impact the pricing and investment decisions in supplier–buyer relationships. For the investment decisions, we find that the structure of the game is stronger than the equity concerns, so the leader of the game will always find it optimal not to make an investment. Since some social responsibility policies rely on buyers making an investment at the supplier, our results suggest that such a policy may require a different strategic relationship between both players. Despite this, the follower will still find it optimal to invest in some cases. Overall, compared to the base model, the investment is higher when using the equity model and lower when using the stakeholder engagement model. Regarding the pricing decisions, we find that the game follower uses his or her price as a mechanism to move towards an equitable distribution. Given that he or she is restricted by the leader’s decision, he or she can only use his price decision to minimize his deviation from an equitable distribution. Thus, he or she will increase the price when facing a situation of disadvantage, and decrease it when experiencing an advantage.

The second objective of our study concerns the effects of socially responsible practices on the game leader’s advantage. We find that being the leader of the game gives a player the power to be at an advantage, but this will not always be the outcome due to the equity concerns. In other words, the game leader will not always choose to be at an advantage and get a higher utility than the follower. Both player’s equity concerns will impact the pricing decisions, and in some situations the follower can receive a higher utility than the leader. In contrast, we find that the leader retains his or her advantage when equity concerns are introduced in a two-part tariff contract. This results in some cases with higher inequity, given that the game leader charges a fixed fee that is as high as the follower’s profit. Only when the leader’s concern for advantageous inequity is high, both players receive an equitable outcome.

Our numerical study helped us fulfill the third objective of our work, which consisted of identifying under which conditions the players and the supply chain as a whole can derive an economic benefit from implementing socially responsible practices. The results suggest that, when \(\gamma _T\ne 1\), each player will obtain the highest profit when he or she has equity concerns but does not lead the Stackelberg game. Also, we identify that introducing equity concerns increases the total supply profit by increasing the investment and reducing the double marginalization. The results from the numerical study also provide us some insights regarding our final objective: the social cost of ignoring equity. We found that ignoring equity can result in a significant cost in the leader’s utility, but this also represents a gain in the follower’s utility. However, we also find that ignoring equity in some cases comes at a cost for both players, but this costs are not as high as in the aforementioned case, where there is a trade-off between both players’ utilities.

Finally, the introduction of production capacity constraints in the Equity and Stakeholder engagement models allowed us to show that the main findings still hold even when the smallholder farmer has capacity restrictions. In the cases where the constraint is binding, it is still optimal for the buyer to purchase the entire production and to compensate for the quantity gap with an increase in the retail price. However, in the Stakeholder engagement model where the supplier acts as the leader, this increase in retail price is a result of an increase in the wholesale price. The buyer only benefits from this retail price increase in the Equity model, where he acts as leader. Thus, when there are capacity constraints, the discussed effects of introducing equity concerns in decision making are reversed and the game leader again exercises his advantage.

Overall, it is interesting to see how the prices are used by both players to attempt to reach an equitable allocation, but the investment decisions are not affected by equity concerns. We could argue that, despite having equity concerns, the players’ are conservative in the sacrifices they are willing to make for the other player. In other words, a player can be willing to reduce his price and, in turn, reduce his advantage over the other player, but still he will not be willing to make an investment if he is in a position of power. Thus, considering our setting where a smallholder farmer does not obtain sufficient earnings for a decent standard of living from her interactions with an agri-food firm, we conclude that this situation can be reversed if both stakeholders engage in socially responsible practices in their decision-making in the form of equity concerns. Contrary to our initial belief based on Fractal Café’s case, the farmer will actually not benefit from stakeholder engagement practices.