Study on Bayesian Skew-Normal Linear Mixed Model and Its Application in Fire Insurance

Abstract

Fire insurance is a crucial component of property insurance, and its rating depends on the forecast of insurance loss claim data. Fire insurance loss claim data have complicated characteristics such as skewness and heavy tail. The traditional linear mixed model is commonly difficult to accurately describe the distribution of loss. Therefore, it is crucial to establish a scientific and reasonable distribution model of fire insurance loss claim data. In this study, the random effects and random errors in the linear mixed model are firstly assumed to obey the skew-normal distribution. Then, a skew-normal linear mixed model is established using the Bayesian MCMC method based on a set of U.S. property insurance loss claims data. Comparative analysis is conducted with the linear mixed model of logarithmic transformation. Afterward, a Bayesian skew-normal linear mixed model for Chinese fire insurance loss claims data is designed. The posterior distribution of claim data parameters and related parameter estimation are employed with the R language JAGS package to obtain the predicted and simulated loss claim values. Finally, the optimization model in this study is used to determine the insurance rate. The results demonstrate that the model established by the Bayesian MCMC method can overcome data skewness, and the fitting and correlation with the sample data are better than the log-normal linear mixed model. Hence, it can be concluded that the distribution model proposed in this paper is reasonable for describing insurance claims. This study innovates a new approach for calculating the insurance premium rate and expands the application of the Bayesian method in the fire insurance field.

1 Introduction

The impact of fire on the social environment and people’s lives should not be underestimated, and major fire accidents occur frequently in the world, resulting in severe casualties and property losses. Property insurance should be established for compensating economic losses in fire accidents. Therefore, it is imperative to determine insurance rates scientifically and reasonably and forecast fire insurance loss claim for insurance rate determination.

It is particularly complicated for setting insurance rates due to the heterogeneity of insurance portfolios and different insurance risks in the fire insurance field. Hence, a linear mixed model (LMM) is typically employed to handle this heterogeneity. Random effects and random errors are commonly assumed to follow a normal distribution in the typical linear mixed model framework Zhang and Davidian [1], Ghidey and Lesaffre [2], Frees and Young [3]. The typical distribution of fire insurance loss claims is characterized by asymmetry and a thick tail. some researchers have changed the distribution to eliminate the complicated characteristics of insurance. For example, the log-phase type (Log PH) distribution was introduced to fit the heavy-tail distribution of fire losses in Ahn and Kim [4] study. Huang and Meng [5] corrected the skewness and heavy tail problem of insurance loss using a Bayesian nonparametric regression model based on Gaussian distribution. Escobar and Pflug [6] determined the worst case of insurance distribution with the distance variance of the probability model. These methods can produce more appropriate empirical results. Nevertheless, data transformation may reduce the information provided by the original data’s potential generation mechanism, and only applies to a single individual and does not guarantee joint normality, presenting some limitations. Furthermore, the accuracy of a normal hypothesis is difficult to be verified, and accurate estimation of inter-subject variation cannot be guaranteed.

Consequently, the hypothesis method of skew distribution is gradually considered by many researchers. The linear mixed model could be expanded for a better understanding of asymmetric insurance loss claim data, and one plausible modification is to assume the random errors following a skewed distribution. Numerous researchers Azzalini and Capitanio [7], Capitanio and Azzalini [8]; Sahu and Dey [9]; Arellano-Valle and Bolfarine [10]; Huang et al. [11], Jung and Lee [12] have explored linear regression models with skewed distribution, systematically introduced the family of skew distribution, and established a method to obtain skew distribution by symmetric distribution.

Some researchers have applied a skew linear mixed model to medical research and the economic field Bandyopadhyay et al. [13], Huang and Chen [14], Leisen and Marin [15]. They fitted different experimental data and achieved more robust estimation results, while its application in insurance loss claims has caused little attention. In the fire insurance actuarial, the Bayesian method is mainly used for problems such as estimating loss distribution, adjusting rates, and corrections. De Simone and Piangerelli [16] applied Bayesian procedures to quantify the impact of COVID-19 epidemic cases in eight different countries and all regions of Italy on determining effective reproduction numbers. Meanwhile, a considerable number of researchers (Jara and Quintana [17]; Scollnik [18]; Bermúdez and Bermúdez [19]; Esmaeili and Klüppelberg [20]; Moreno and Jiménez et al. [21]) investigated the application of the Markov Chain Monte Carlo (MCMC) Bayesian method to estimate and fit insurance losses through different regression models. The corresponding studies mentioned above demonstrate the potential of the Bayesian method in insurance actuarial.

This paper aims to investigate the use of a skew linear mixed model in the prediction of fire insurance loss claims and propose a Bayesian skew-normal linear mixed model to describe the relationship between covariates and response variables flexibly. The random errors and random effects are assumed to obey skew-normal distribution in comparison to the traditional linear mixed model for eliminating the influence of the loss distribution’s skewed characteristics. The MCMC method makes Bayesian inference a viable alternative for this prediction model. Regarding parameter estimation, the Bayesian method and the MCMC method apply to the prior distribution and the posterior distribution, respectively. The parameter posterior means are Gibbs sampling using the JAGS package in R language. This approach can improve the flexibility of the Bayesian method.

Linear mixed models (LMM) are often used to analyze repeated measurement data because they are more flexible in modeling intra-subject correlations, which are usually present in such data. The most popular continuous response LMM assumes that both the random effects and the internal errors of the subjects are normally distributed, which may be an unrealistic assumption that conceals important features of changes within and between units (or groups). In this work, a skew normal linear mixed model (SNLMM) is proposed, which relaxes the normality assumption by using multivariate skew normal distribution, including normal distribution as a special case, and is suitable for the structure of repeated measurement data and clustering data analysis. The Bayesian skew-normal linear mixed model proposed in this study outperforms the log-linear mixed model and the regression model on two fire insurance real loss datasets, expanding the method’s application in the fire insurance business.

2 Data Sources

The correctness of the Bayesian skew-normal linear mixed model is verified on two different property insurance datasets. The first dataset is the U.S. employer liability insurance loss claims data from Klugman [22], which is originally sourced from the National Council on Compensation Insurance and contains a large sample and small categorical covariates. The second dataset consists of a significant number of continuous covariates by introducing mainland China property insurance claims data, sourced from the China Statistics Bureau and the China Insurance Regulatory Commission (CIRC) website (http://www.stats.gov.cn/tjsj/ndsj/).

Employer liability insurance, classified as property insurance, is mainly used to manage claims for permanent or partial incapacity of employees. A total of 121 risk categories are included in the longitudinal dataset, and 847 data are collected in seven observation years, including occupational categories, income, and compensation. The applicability of the model is verified by exploring the data characteristics of the pure premium (PP) (PP = claim amount/income) data features.

Property insurance in mainland China is majorly employed to handle fire losses claims. The property insurance loss claims data and the gross regional product (GRP) dataset of various regions for 2011–2020 in mainland China are cited in this study. The panel data contains 340 data items for 34 regional categories over 10 observation years and are adopted in the study owing to the strong regional characteristics of property insurance business size and claims. The model is applied for this dataset to investigate and estimate the association between property premium loss claims and GRP.

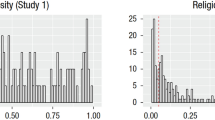
Figure 1 illustrates the histograms of frequency distributions of pure premiums of employer liability insurance and property insurance loss claims. As observed in Figure 1, both insurance datasets exhibit remarkable right skew and heavy tail characteristics. Thus, it is difficult for them to accurately apply to the traditional actuarial model. Fortunately, the application of the skewness distribution proposed in this study can better tackle this problem.

Figure 1

Frequency distribution histogram of two different datasets

3 Methodology

3.1 Bayesian Skew-Normal Linear Mixed Model

The skew-normal distribution is a further extension of the normal distribution. The Bayesian method is primarily applied to parameter estimation of the loss distribution. The traditional linear mixed model is generally insufficient to describe the insurance loss claim due to the complicated characteristics of skewness, heavy tail, and multimodality. As a result, the mature application of the Bayesian method and skewness distribution is required. Bayesian skew-normal linear mixed model (SNLMM) can better handle this type of panel data. Sahu et al. [9], Arellano-Valle and Genton [10], Arellano-Valle et al. [23], Bernardi and Petrella [26], Miljkovic and Grün [27], and other researchers have conducted correlation studies on the Bayesian skew-normal linear mixed model. In this section, the expression function studied by the previous researchers is introduced to define the Bayesian skew-normal linear mixed model (SNLMM).

3.1.1 Skew-Normal Linear Mixed Model

Firstly, multivariate skew-normal distribution is introduced to define the proposed SNLMM. According to the multivariate skew-normal distribution studied by Arellano-Valle and Genton [10], the density function of e-element skew-normal distribution of random variable X = (X₁,…,X_e) ^T at point x is defined as

$$f_{SN} (x|\mu ,\Sigma ,\alpha ) = 2\psi_{e} (x - \mu ;\Sigma )\Psi \left( {\alpha^{T} \sigma^{ - 1} (x - \mu )} \right)$$

(1)

where Σ denotes the positive definite covariance matrix, σ represents the diagonal matrix $\sum = \sigma \overline{\sum }\sigma$ formed by the standard deviation in Σ, and $\overline{\Sigma }$ indicates the correlation matrix. The density function of e-element normal distribution N_e (μ, Σ) at point x is expressed as ψ_e (x-μ; Σ), and the corresponding distribution function is expressed as Ψ_e (x-μ; Σ).

The most commonly used linear mixed model (LMM) was proposed by Laird and Ware [28] for a continuous response. Assuming that the loss data come from m different individual risks, there are k_i (i = 1,2,…,m) observations at different stages for each risk. Additionally, Y_i represents the k_i dimension vector of the continuous measurement of individual i. Then, the linear mixed model of Y_i is expressed as

$$Y_{i} = X_{i} \beta + Z_{i} b_{i} + \varepsilon_{i} ,i = 1,2, \ldots ,m$$

(2)

where X_i (k_i × p) indicates the explanatory variable matrix corresponding to the fixed effect vector β, and Z_i (k_i × q) denotes the explanatory variable matrix corresponding to the random effect vector b_i. The random effect b_i and the random error ε_i are independent of each other and obey the mean value of 0. The normal distribution of the covariance matrix is determined by Σ_b and σ_e²: b_i ~ N_q (0, Σ_b) and ε_i ~ N (0,σ_e²). Covariance matrixes Σ_b and σ_e² represent the variance between individuals and within individuals, respectively.

Generally, the parameter estimation of skew distribution is complicated. The skew-normal distribution linear mixing model proposed in this study extends the general linear mixed model, defined based on the linear model in Eq. (2). Assuming that the random effects and random errors obey the skew-normal distribution, the specific distribution is expressed as

$$b_{i} \mathop \sim \limits^{iid} SN_{q} \left( {0,\Sigma ,\alpha_{b} } \right),\varepsilon_{i} \mathop \sim \limits^{ind} SN_{ki} \left( {0,\Sigma_{i} ,\alpha_{ei} } \right),i = 1, \ldots ,m.$$

(3)

The assumptions of random effects and random errors are independent of each other, contributing to the following hierarchical structure.

$$Y_{i} |b_{i} ,\beta ,\Sigma_{i} ,\alpha_{ei} \mathop {\mathop \sim \limits^{ind} N_{{k_{i} }} \left( {X_{i} \beta + Z_{i} b_{i} ,\Sigma_{i} ,\alpha_{ei} } \right)}\limits^{{ \, {. }}}$$

(4)

$$b_{i} |\Sigma ,\alpha_{b} \mathop \sim \limits^{ind} SN_{q} \left( {0,\Sigma ,\alpha_{b} } \right),i = 1, \ldots ,m.$$

(5)

where α_ei and α_b are vectors, containing shape parameters α_ei1,…, α_eini and α_b1,…, α_bq, respectively. It is assumed that Σ_i = σ_e²I_ni and α_ei = α_e1_ni, i = 1,…, m, where 1 _g denotes the g-dimensional vector of ones. The standard diagonal matrix of matrix Σ_i is σ_i = σ_eI_ki, where σ_e a real number. According to the characteristics of skew normal distribution, the expectation and variance of response variable Y_i are obtained as follows.

$$E\left[ {Y_{i} |b_{i} ,\beta ,\sigma_{e}^{2} ,\delta_{ei} } \right] = X_{i} \beta + Z_{i} b_{i} + \sigma_{e} \delta_{ei} (2/\pi )^{1/2} 1_{{k_{i} }}$$

(6)

$${\text{Var}} \left[ {\left. {Y_{i} } \right|b_{i} ,\beta ,\sigma_{e}^{2} ,\delta_{ei} } \right] = \sigma_{e}^{2} \left( {I_{{k_{i} }} - \delta_{ei} \delta_{ei}^{T} (2/\pi )} \right).$$

(7)

where б_ei = (1 + α_ei^T·α_ei)^−1/2α_ei; the observation value y = (y₁^T,…, y_m^T)^T is conditionally distributed for a given random effect b = (b₁^T,…, b_m^T)^T; other parameters are shown as

$$f(\left. y \right|b,\beta ,\sigma_{e}^{2} ,\delta_{e} ) = \prod\limits_{i = 1}^{m} {2^{{k_{i} }} } \psi_{{k_{i} }} \left( {y_{i} - X_{i} \beta - Z_{i} b_{i} ;\sigma_{e}^{2} I_{{k_{i} }} } \right)\Psi \left( {\alpha_{e}^{T} \sigma_{e}^{ - 1} \left( {y_{i} - X_{i} \beta - Z_{i} b_{i} } \right)} \right).$$

(8)

The model mainly infers parameter vector θ = (β^T, σ_e^T, α^T)^T, α = (α_e, α_b^T)^T, α_b = (α_b1, …, α_bq)^T. This model is based on the distribution of response variable Y_i. Random effects and random errors are not limited to the normal distribution and can be used to evaluate asymmetric data.

3.1.2 Bayesian Estimation of SNLMM

The loss distribution is estimated using the Bayesian method by specifying the prior distribution of unknown parameters to determine the posterior distribution of parameters. The prior distribution of the fixed effect vector β is usually taken as multivariate Gaussian distribution N (β | μ_β, σ_β²), with density function given by

$$\pi \left( {\beta |\mu_{\beta } ,\sigma_{\beta }^{2} } \right) \propto \exp \left\{ { - \frac{1}{2}\left( {\beta - \mu_{\beta } } \right)\sigma_{\beta }^{ - 2} \left( {\beta - \mu_{\beta } } \right)} \right\}$$

(9)

The prior covariance structure of scale parameter σ_e² is the inverse Wishart distribution IG (σ_e² | τ_e, T_e) of matrix T_b, with density function given by

$$\pi \left( {\left. {\sigma_{e}^{2} } \right|\tau_{e} ,T_{e} } \right) = \frac{{\left( {T_{e} } \right)^{{\tau_{e} }} }}{{\Gamma \left( {\tau_{e} } \right)}}\left( {\frac{1}{{\sigma_{e}^{2} }}} \right)^{{\left( {\tau_{e} } \right) + 1}} \exp \left\{ { - \frac{{T_{e} }}{{\sigma_{e}^{2} }}} \right\}$$

(10)

The prior distribution of scale matrix Σ with random effect is τ_b degrees of freedom and the variable covariance structure is inverse Wishart distribution IW (Σ | T_b) of matrix T_b. The prior distribution of skewness parameters α_e and α_b is a normal distribution N (α_e | μ_e, γ_e²) I {α_e > 0} and a multivariate truncated Gaussian distribution N_q (α_b | μ_b, γ_b²) I {α_b > 0}, respectively, where γ_b² denotes a positive definite matrix, and I{A} represents the indicative value of dataset A, with density function given by

$$\pi \left( {{\alpha }_{e}}|{{\mu }_{e}},\gamma _{e}^{2} \right)\propto \exp \left\{ -\frac{1}{2\gamma _{e}^{2}}{{\left( {{\alpha }_{e}}-{{\mu }_{e}} \right)}^{2}} \right\}I\left\{ {{\alpha }_{e}}>0 \right\}$$

(11)

and

$$\pi \left( {{\alpha }_{b}}|{{\mu }_{b}},{{\gamma }_{b}} \right)\propto \exp \left\{ -\frac{1}{2}{{\left( {{\alpha }_{b}}-{{\mu }_{b}} \right)}^{T}}\gamma _{b}^{-1}\left( {{\alpha }_{b}}-{{\mu }_{b}} \right) \right\}I\left\{ {{\alpha }_{b}}>0 \right\}$$

(12)

Assuming that the prior distribution of the above parameters is independent of each other, according to the conditional distribution of the parameters, the posterior distribution of all relevant parameters can be obtained by

$$\pi (\theta ,b,\Sigma |y) \propto \prod\limits_{i = 1}^{m} S N_{{n_{i} }} \left( {y_{i} |X_{i} \beta + Z_{i} b_{i} ,\sigma_{e}^{2} I_{{n_{i} }} ,\alpha_{e} } \right) \times \prod\limits_{i = 1}^{m} S N_{q} \left( {b_{i} |0,\Sigma ,\alpha_{b} } \right)$$

$$\quad\quad\quad \times\, N\left( {\beta |\mu_{\beta } ,\sigma_{\beta }^{2} } \right) \times IG\left( {\sigma_{e}^{2} |\tau_{e} , {\text{T}}_{e} } \right)$$

$$\quad\quad\quad \times\, IW_{{\tau_{b} }} \left( {\Sigma |T_{b} } \right) \times N\left( {\alpha_{e} |\mu_{e} ,\gamma_{e}^{2} } \right)I\left\{ {\alpha_{e} > 0} \right\}$$

$$\quad\quad\quad \times\, N_{q} \left( {\alpha_{b} |\mu_{b} ,\gamma_{b}^{2} } \right)I\left\{ {\alpha_{b} > 0} \right\}$$

(13)

However, it is quite complicated a to obtain the marginal distribution of the amount of interest involved in Eq. (13) from an analytical perspective. The MCMC method is adopted in this study to perform Bayesian analysis, considering that the traditional Bayesian method is difficult to conduct on such models. In this study, the MCMC method is used to simulate the posterior distribution of each parameter, and Gibbs sampling is applied to the conditional posterior distribution of each parameter to simplify its sophisticated formula.

3.2 MCMC Simulation Analysis

The MCMC method involves the skew-normal distribution function, which is difficult to establish the model. The hierarchical structure studied by Arellano-Valle et al. [23] is employed in this paper to solve the complicated skew problem. The skew-normal linear mixed model is expressed in the equivalent form of simple normal distribution, making it convenient to use Gibbs sampling for posterior distribution. The complete layered structure of the model is expressed as

$$Y_{i} |b_{i} ,\beta ,\sigma_{e}^{2} ,\alpha_{e} ,w_{ei} \sim N_{{n_{i} }} \left( {X_{i} \beta + Z_{i} b_{i} + \alpha_{e} w_{ei} ,\sigma_{e}^{2} I_{{n_{i} }} } \right),i = 1, \ldots ,m.n$$

(14)

$$w_{ei} \sim N_{{n_{i} }} (0,I)I\left\{ {w_{ei} > 0} \right\}$$

(15)

$$b_{i} |\Sigma ,\alpha_{b} ,w_{bi} \sim N_{q} \left( {\alpha_{b} w_{bi} ,\Sigma } \right)$$

(16)

$$w_{bi} \sim N_{q} (0,I)I\left\{ {w_{bi} > 0} \right\}$$

(17)

$$\beta \sim N_{p} \left( {\mu_{\beta } ,\sigma_{\beta }^{2} } \right)$$

(18)

$$\sigma_{e}^{2} \sim IG\left( {\tau_{e} , {\text{T}}_{e} } \right)$$

(19)

$$\Sigma \sim IW_{{\tau_{b} }} \left( {T_{b} } \right)$$

(20)

$$\alpha_{e} \sim N\left( {\mu_{e} ,\gamma_{e}^{2} } \right)I\left\{ {\alpha_{e} > 0} \right\}$$

(21)

$$\alpha_{b} \sim N_{q} \left( {\mu_{b} ,\gamma_{b}^{2} } \right)I\left\{ {\alpha_{b} > 0} \right\}$$

(22)

The corresponding programming code can be easily obtained according to the layered expressions. According to Eqs. (14)–(22), the complete conditional distribution required to realize the Gibbs sampler can be directly derived and sampled. The algorithm starts from the initial value and cycle of all variables mentioned, which generates samples from the above conditional distribution until convergence. The method mentioned by Gelman and Rubin [24] is utilized to verify the conditions, such as running several parallel chains. Regarding unbalanced datasets, existing statistical software, such as MATLAB, can be used to easily calculate the above equations. For balanced datasets, the Gibbs sampler can be implemented by OpenBUGS or JAGS software. Besides, the R language jags programming is employed to perform Gibbs sampling in this study.

4 Case Study

In this section, the Bayesian skew-normal linear mixed model is established and compared with Frees et al. [3] model to verify the accuracy of SNLMM model based on the US employer liability insurance loss claim data Klugman [22]). Then, the SNLMM model is applied to China’s mainland property insurance statistics [29] (http://www.stats.gov.cn/tjsj/ndsj/) to explore the relationship between the relevant variables. Additionally, the premium claims are estimated to determine the premium rate based on variance analysis to determine the premium rate.

4.1 U.S. Employer Liability Insurance Claims Data

Pure premium (PP) is defined as the loss of income per dollar due to permanent, partial disability. Frees selected the logarithm of pure premium (LnPP) as the response variable Y; other explanatory variables were the observation year t and the occupation category w. Frees established a logarithmic normal linear mixed model, which used logarithmic transformation to explain heteroscedasticity. Figure 1 demonstrates that the pure premium claim data are panel data with right deviation and heavy tail. The correlation between the same set of data needs to be considered, and the logarithmic transformation exhibits data information loss and increase errors. In this study, the model is optimized by establishing a Bayesian skew-normal linear mixed model, so as to improve the reliability of data prediction.

4.1.1 Model Analysis

Frees conducted logarithmic transformation of pure premiums under the consideration of the right-deviation characteristics of data. After logarithmic transformation, the right-deviation of the data was offset. The distribution map of logarithmic pure premium data presented symmetry. The established logarithmic linear mixed Model I was

$$\log \left( {PP_{wt} } \right) =\upgamma _{1} + d_{1w} + d_{2w} Year_{t} + e_{wt}$$

$$w = 1, \ldots ,121;t = 1, \ldots ,7.$$

(23)

where w denotes the occupational category and t represents the observation year. Since the pure premium does not change with the observation year, the model only contains a constant term γ₁ as a fixed effect variable. The value of the observation year is (Year-4) /8. Additionally, the model is a general linear mixed model. The random effect d_w and the random error term e_wt are subject to the normal distribution with the mean value of zero, and the random effect d_w follows the binary normal distribution. Frees used t statistics and likelihood statistics to judge the adequacy of the model, which fitted the panel data model with the data to create a credibility predictor to solve the skew problem of the model.

Logarithmic transformation reduces the correlation of the same group of data. After the establishment of the linear mixed model, there are some defects in the internal structure, and the prediction data lacks certain authenticity. This study uses the proposed Bayesian skew-normal linear mixed model to analyze pure premium data. Normal distribution is a special case of skew normal distribution. Therefore, the skewed normal linear mixed model can process both skewed data and symmetric distribution data.

According to the evaluation results of the Bayesian model, DIC statistics Spiegelhalter et al. [29] and BIC criterion Yuan and Lu [30] are employed in this paper to analyze the accuracy of the three models. The expressions of DIC and BIC are

$$DIC = 2\overline{D\left( \theta \right)} - D\overline{\left( \theta \right)} = D\overline{\left( \theta \right)} + 2k$$

(24)

$$BIC = \ln (n)k - 2\ln (L)$$

(25)

where D (θ) is equal to the logarithmic likelihood function of negative twice, k denotes the number of effective parameters of the model, and L indicates the likelihood function. As suggested in the previous studies, smaller DIC and BIC were better in fitting and prediction effects of the model.

In this paper, the partial normal distribution is used to define the random effect d_w and the random error term e_wt to form a partial normal linear mixed model. This paper will compare and analyze the two models, and the response variables are pure premium logarithm. The first model is a general linear mixed model, and the random effects and random errors obey the normal distribution. The second model introduces skew normal distribution, assuming that both random errors and random effects obey skew normal distribution. Suppose that the random error term obeys the normal distribution, that is, the Frees model.

In order to facilitate the comparison of the same parameters of the two models, the same prior distribution is given. In each simulation,100 Monte Carlo data sets are simulated from Eq. (23) according to additional specification described below, and Eq. (23) is fit to each data set via the strategy in Proposition 1 (see Appendix) using the R software jointly with the R2WinBUGS package and the following prior specifications. The prior distribution of the fixed effect is regarded as a normal distribution γ₀ ~ N (0,10²). The prior distribution of the scale parameter of the error distribution is assumed to obey inverse gamma distribution σ_e² ~ IG (0.01,0.01). The prior distribution of the scale matrix of the random effect prior distribution d_w is inverse Wishart distribution ∑ ~ IW₂ (I₂). The skewness parameter is α_e ~ N (0,10²) I{α_e > 0}, α_w ~ N (0,10²) I{a_b > 0}. The prior distributions of parameters ω_e and ω_w are assumed as ω_e ~ N (0,1) I{ω_e > 0}, ω_d ~ N (0,1) I{ω_d > 0}. The prior distribution considered is close to the non-informative distribution, that is, the prior distribution with large variance is considered. The parameter estimates and standard deviations of various models are shown in Table 1.

Table 1 The Posterior Mean of Parameters with the Logarithm of Net Premium as the Response Variable

Σ11 is the variance of the random effect d_1w, Σ12 is the covariance of the random effects d_1w and d_2w, Σ22 is the variance of the random effect d_2w. The last two lines are negative twice the log-likelihood function value and DIC information for comparative analysis of the model.

It can be seen from Table 1 that when the random error term obeys the partial normal distribution, the DIC value of the model is obviously the smallest, indicating that the model has the best fitting effect on the pure premium logarithm. However, comparing the fitting values of the models with the actual values, it can be found that the fitting values of these models for the logarithm of pure premiums are not much different. See Figures 2 and 3, this is mainly because the logarithm of pure premiums presents an approximate symmetrical shape, so the superiority of skewed distribution is not fully reflected.

Figure 2

Scatter plot of pure premium and fitting value

Figure 3

Residual and compensation scatter plot

4.1.2 Model Optimization

Logarithmic transformation reduces the correlation of the same group of data. After the establishment of the linear mixed model, there are some defects in the internal structure, and the prediction data lacks certain authenticity. This study uses the proposed Bayesian skew-normal linear mixed model to analyze the pure premium observation data directly.

The skew-normal linear mixed model for the pure premium claim dataset is established directly in this study, and the explanatory variables mentioned above are the same as Model II. Therefore, the Bayesian skew-normal linear mixed Model III can be obtained as

$$PP_{tn} = \Upsilon_{o} + d_{on} + d_{1n} Year_{n} + e_{tn} .$$

(26)

In this model, the random effects and random errors are assumed to follow the skew-normal distribution, and the pure premium is considered the response variable.

The skew-normal linear mixed model does not need to transform the data and can directly calculate the pure premium data on the right. In this way, the explanatory ability of the model to the data is significantly improved, and the influence of the correlation of the same set of data caused by the transformation is avoided. For the convenience of comparison, the same meaning parameters give the same prior distribution.

The prior distribution of parameters is obtained based on the Bayesian method, and the hierarchical expression of the model is acquired using the equivalent form of the skew-normal linear mixed model. In this paper, the hierarchical expression operation code is programmed by JAGS in R language through Gibbs sampling of MCMC method, with 30,000 iterations. The first 10,000 iterations are abandoned until the sample converges. Then, the parameter posterior distribution sample value is obtained. Meanwhile, the lag value is set as 4 to avoid related problems in the generated Markov chain. The mean value and standard deviation of the estimated values of each parameter are obtained using the sample values of the posterior distribution, as listed in Table 2.

Table 2 A Posteriori Mean of Parameters with Pure Premium as Response Variable

Table 2 implies that the posterior distribution mean of the skewness parameter is close to 0.5, and the variance interval of the error parameter is relatively narrow. The dotted line in Figure 4 represents the median of the skewness parameter and error parameter. The median of skewness parameter is close to 0.5, and the median of error parameter is close to the mean, suggesting that the established skew-normal linear mixed model is more suitable for this dataset.

Figure 4

The posterior distribution frequency distribution curve of parameters. (a) The posterior distribution frequency curve of the skewness parameter α_d1. (b) The posterior distribution frequency curve of the error parameter σ_e²

4.1.3 Comparative Analysis

Since the response variables used in Tables 2 and 1 are completely different, one is the pure premium and the other is the logarithm of the pure premium, their DIC values cannot be directly compared, but the fitting values and model residuals of different models can be compared and analyzed.

Figure 5 is a scatter plot between the observed values of the residuals and pure premiums of the partial slash linear mixed model and their fitted values. It can be seen that the fitted value and the observed value of the model III with the pure premium as the response variable are closer to the diagonal, and the fitting effect is better than that of the Figure 2. It can be seen that the fitted values and observed values of the partial slash linear mixed model are closer to the diagonal, and the residual fluctuation range is smaller. The residuals are concentrated near the zero value, and the fitting effect is significantly better than the normal linear mixed model shown in Figures 3 and 4, which further indicates that the model has a better fitting effect on the pure premium data.

Figure 5

Scatter plot of observations and fitting values of net premiums

Figure 6 represents the scatter plot of residuals. From the graph, it can be seen that the residual fluctuation range is small and gathers near the zero value. The fitting effect is obviously better than the model I and model II shown in Figure 3, which further shows that the model III fitting of pure premium data greatly improves the model’s ability to interpret data.

Figure 6

Residual scatter plot

4.2 Mainland China Property Insurance Statistics

Property insurance business scale and loss claims have strong regional characteristics. In this study, the relationship between regional property insurance loss claims and regional economy GRP is mainly discussed. The data of the two over the years are fitted and analyzed. The claims for property insurance losses in the next 3 years are further predicted.

4.2.1 Variable Assumptions

Figure 7 illustrates the relationship between total property insurance losses with GDP and economic growth over the past decade. The total insurance loss claims and GDP increase with time; the total amount of insurance loss claims grows faster when GDP grows faster; the growth rate of total insurance loss claims decreases when GDP growth slows down, implying a linear relationship between the two parameters. In recent years, China has entered a transitional period, with a large GDP base and rapid growth of per capita GDP, while the growth rate has declined.

Figure 7

Comparison and growth of premium claim with GDP

Figure 8 exhibits the time series of claims for property insurance losses in the regions over the past decade with the observation year. Figure 8 reveals that the level of insurance loss claims increases with the increasing observation years for most regions, while there are significant differences in the level of insurance loss claims among regions with different economic levels.

Figure 8

Property insurance claims in different regions

According to the property insurance loss claim data in China Statistical Yearbook and China Fire Yearbook, these data variables are summarized in Table 3. As suggested in Table 3, the trend of insurance loss claims and regional economy with time is somewhat consistent, and their variances are relatively large.

Table 3 Summary Statistics of Insurance Claim Data and Regional Economy GRP, by Year

A preliminary analysis indicates that it is somewhat similar to the linear trend of regional economies GRP with time, though the level of claims for property insurance losses may depend on the complicated characteristics of different regions. Moreover, the dataset demonstrates the distribution characteristics of right deviation, thick tail, and asymmetry. In this study, regional property insurance loss claim is designated as response variable Y (billion). Random variables include observation year t, regional economy GRP (billion), observation area category n, explanatory variable n = 34, and t = 10 (2011,…, 2020). Different letters instead of region names are used to protect data sources and information security. Meanwhile, no more information about the region category is provided.

4.2.2 Model Establishment

The above analysis implies a certain linear trend between the amount of property insurance loss compensation and the observation year, as well as a correlation between the amount of property insurance loss compensation and the regional economy GRP. Furthermore, the residual error of the amount of property insurance loss compensation fitted from a single region does not exhibit a special trend. Then, the following skew-normal linear mixed model expression is obtained by

$$Y_{tn} = \beta_{o} + \beta_{1} GRP_{tn} + b_{on} + b_{1n} T_{n} + e_{tn}$$

(27)

$$n = 1, \ldots ,31;t = 1, \ldots ,10.$$

(28)

where, Y_tn represents the claim for property insurance loss with time t and regional category change n, and the constant term β₀ denotes the fixed effect variable. The random effects include the constant term b_on, the observation year b_1n and the regression coefficient β₁ of the observation region. It mainly manages the correlation between different observation years and the observation regions. The value of the observation year is (Year-5) /10, which is convenient for calculation and statistics. Three different distribution models of random effects and random errors are adopted in this study to make a comparative analysis.

Model 1: The random error term e_n = (e_1n,…, e_10n)^T and the random effect are assumed to obey the multivariate skew-normal distribution model;

Model 2: A model with the random error term e_n = (e_1n,…, e_10n)^T for a multivariate normal distribution, and the random effect for the multivariate skew-normal distribution model;

Model 3: The response variable is the logarithm of premium claims, random effects and random errors obey the Gaussian distribution model.

The prior distributions of the same parameters of the three models are assumed to be the same to perform comparative analysis. This study is based on a large variance. The prior distribution of the fixed effect is set to independent distribution γ₀ ~ N (0,10²), and the prior distribution of the scale parameter of the error distribution is set to σ_e² ~ IG (0.01,0.01). Hence, the mean value of the distribution is 2. The prior distribution of the scale matrix of the prior distribution d_n of random effects is considered inverse Wishart distribution ∑ ~ IW₂ (I₂); the skewness parameter is assumed to α_e ~ N (0,10²) I{α_e > 0}, α_b0 ~ N (0,10²) I{a_b0 > 0}, and α_b1 ~ N (0,10²) I{a_b1 > 0}. It is demonstrated that the results of the analysis are quite robust since all previous considerations are based on large variances.

4.2.3 Data Analysis

The 40,000 iterations were conducted after the previous 10,000 iterations were abandoned, so as to analyze the data. The lag value is set as 5 to avoid the related problems in the generation chain. The JAGS programming code in Model 1 is provided in the appendix, and the posterior estimation average of model parameters are presented in Table 4.

Table 4 A Posteriori Average of Three Model Parameters

The results of parameter estimation (posterior mean) are listed in Table 4. Following the analysis of the Table 4, BIC and DIC criteria suggest that model 1 is most suitable for data.

Figure 9 provides the Markov data chain and posterior distribution sample frequency histogram of some parameters in Model 1. As observed in Figure 9, the skewness parameter is closer to 0.5, and the error confidence interval is relatively narrow. It can be seen from the figure that there is no convergence problem in the chain generated by the parameters. Figure 10 exhibits the comparison curve between the estimated value and the real value of each region. The analysis results in Figure 10 reveal that the values of the two curves are very close, and the changing trends are consistent. Hence, Model 1 has a high fitting degree.

Figure 9

Sample chain of simulated data (left image) and histogram of posterior distribution of parameters (right image). a is Identified as σ_e² Sample chain, b is Identified as σ_e² posterior distribution histogram, c is Identified as β₀ Sample chain, d is Identified as β₀ posterior distribution histogram, e is Identified as D11 Sample chain, f is Identified as D11 posterior distribution histogram, g is Identified as α_b0 Sample chain, h is Identified as α_b0 posterior distribution histogram

Figure 10

Comparison of actual values and fitting values for each region

Figure 11 demonstrates the prediction values of regional property insurance loss claims in the following 3 years. The previous analysis implied that the insurance loss claims significantly varied in different regions, and the insurance loss claims generally changed little in small regions, otherwise changed dramatically. The development trend of insurance loss claims in Figure 9 meets this result analysis.

Figure 11

Forecast value of property insurance claims in regions in the next 3 years

In summary, the proposed Bayesian SNLMM model has superior performance in intra-sample fitting and sample prediction and provides a reasonable model to analyze the influence of covariates.

5 Discussions

An essential aspect of analyzing insurance loss claim data is that they tend to follow a skew distribution, because extreme events are not uncommon and exhibit a heavy tail. A Bayesian linear mixed model is proposed in this paper. Its random effects and random errors belong to skew-normal distribution. This model can identify non-normal and asymmetric behaviors that may occur in the random errors or effects. Firstly, the methods used and the Bayesian skew-normal linear mixed model are introduced. Secondly, the data fitting results of logarithmic linear mixed model and Bayesian skew-normal linear mixed model are compared based on the dataset of American Employers liability industrial insurance to empirically tests the superiority of the Bayesian skew-normal linear mixed model (Pure premium is the response variable). Finally, the Bayesian SNLMM model is applied to the property insurance loss dataset in mainland China to explore the relationship between insurance claims and the regional economy GRP and predict insurance loss claims.

The results of this study suggest that both the US employer liability insurance claim dataset and the Chinese mainland property insurance loss dataset have complicated characteristics of right deviation and heavy tail. As revealed by asymmetric pure premium panel data analysis, the Bayesian skew-normal linear mixed model has a more accurate fitting effect and higher data accuracy compared with the logarithmic linear mixed model. The research based on property insurance loss claim datasets demonstrates a certain linear relationship between regional economy and insurance claims, and the trend is consistent. It is assumed that the first model simulation is more advantageous among the three different linear mixed models. Then, the insurance loss claims in different regions in the next 3 years present a trend of first decreasing and then increasing. This flexibility that other linear models cannot achieve highlights the advantages of Bayesian methods over existing actuarial models.

In previous linear mixed model research, a robust reasoning method using heavy tail distribution is proposed. For example, Pinheiro and Vidakovic [31] used maximum likelihood to describe the robust Gaussian LMM model proposed by Laird and Ware [28]. They assumed that the distribution of errors had the same degree of freedom as the distribution of random effects, and the random effects were independent. Two different stochastic processes are difficult to be controlled by the same degree of freedom parameters. The method designed in this paper can solve this problem by allocating different parameters. Modeling by modifying the known distribution is a hot topic. Many alternative structures of Arellano-Valle et al. [23] are based on Genton [10]. In this study, the structure proposed by Arellano-Valle et al. [23] is selected mainly for simple calculation.

The fourth section analyzes the Frees data case. When the data is converted, some information may be lost. The fitting results between the models are not much different, and the superiority of the skewed distribution model is not fully reflected. When analyzing data directly, the fitting results and residual values of the SNLMM model are more accurate. Although the related density function is difficult to handle, the MCMC method can easily fit the model. This method can be implemented on computing by using simple and accessible software (such as R language, WinBUGS). Other skewed distribution variants currently available are not so easy to implement. The MCMC method and standard information standards are very effective in identifying correct normal asymmetric models, as shown in simulation studies. A relatively large advantage of this model is that it can give more flexible assumptions about the random effects and random errors of the model. However, when applying the SNLMM model to analyze the data, the prior distribution of the parameters considered is close to the non-informative distribution, that is, the prior distribution with large variance is considered, and the model is suitable for asymmetric longitudinal data.

To sum up, the same method can also be applied to other types of data, and these data have similar skewness characteristics. In other words, the Bayesian SNLMM model for objective Bayesian analysis of data, including parameter distribution and prior, is applicable to other disciplines, such as engineering and environmental science.

6 Conclusions

Forecasting fire insurance loss claims is a critical part of rate determination analysis. However, the insurance rates calculation is still in the exploring stage for fire insurance loss claim data, which usually has a characteristic of right skew and heavy tail and is difficult to be described by the traditional normal distribution linear mixed model.

In this paper, an asymmetric fire insurance loss claim prediction model is proposed by combining the Bayesian method with the skew-normal linear mixed model. Based on the traditional linear mixed model, it is assumed that the random effects and random errors obey the skew-normal distribution. Then, it can describe the complicated characteristics of skewness and the heavy tail of insurance loss claim data. Moreover, the Bayesian MCMC method is adopted to estimate the model parameters, and the posterior parameter mean estimation is obtained using Gibbs sampling, contributing to addressing complicated operational problems. These improvements have achieved better results compared to the normal linear mixed model in theory and practice.

Additionally, the proposed Bayesian SNLMM model has been validated on two property insurance loss claims datasets, including the latest insurance data statistics. Firstly, this model demonstrates better goodness of fitting for pure premium data, better data interpretation ability, and lower DIC compared with the log linear mixed model. Secondly, in the process of predicting the number of fire insurance claims, the accuracy of the model is high, and the influence of different data characteristics is small. Finally, the method estimates parameter samples by simple and easy-to-use software (such as R language, WinBUGS). The Bayesian skew-normal linear mixed model can describe the specific form of claim data in different categories by identifying skew patterns. This model has great flexibility and is suitable for modeling and analysis in various complicated situations.

In addition, the estimation model proposed in this paper also has shortcomings and needs further study. Firstly, the random model of different factors in MCMC simulation is explored to reduce the influence of variable weight structure and improve the accuracy. Secondly, when the model is applied to the prediction of fire insurance loss claim data, it is necessary to directly model and analyze the original longitudinal data to improve the accuracy of data prediction.

Appendix

To obtain the marginal distribution of Y_j, we drop the subscript j, corresponding to the j the group (or individual) to simplify notation. From Eqs. (5, 6) and the definition of skew-normal multivariate distribution in Eq. (3) with k = n and D = diag (δ), it follows that the marginal density of Y is obtained by computing the following integral:

$$f_{{\mathbf{Y}}} ({\mathbf{y}}|{{\varvec{\uptheta}}},\lambda ) = \int_{{{\mathbb{R}}^{q} }} f \left( {{\mathbf{y}}|{\mathbf{b}},{{\varvec{\upbeta}}},\sigma_{e}^{2} ,\delta_{e} } \right)f\left( {{\mathbf{b}}|{{\varvec{\upalpha}}},{{\varvec{\updelta}}}_{b} } \right)d{\mathbf{b}}$$

$$= \int_{{{\mathbb{R}}^{q} }} {2^{n + q} } \phi_{n} \left( {{\mathbf{y}}|{\mathbf{X\beta }} + {\mathbf{Zb}},\left( {\delta_{e}^{2} + \sigma_{e}^{2} } \right){\mathbf{I}}_{n} } \right)$$

$$\quad\quad\quad \times \phi_{q} \left( {{\mathbf{b}}|{\mathbf{0}},{{\varvec{\Delta}}}_{b}^{2} + {\mathbf{D}}} \right)\Phi_{q} \left( {{{\varvec{\Delta}}}_{b} \left( {{{\varvec{\Delta}}}_{b}^{2} + {\mathbf{D}}} \right)^{ - 1} {\mathbf{b}}|{\mathbf{0}},\left( {{\mathbf{I}}_{q} + {{\varvec{\Delta}}}_{b} {\mathbf{D}}^{ - 1} {{\varvec{\Delta}}}_{b} } \right)^{ - 1} } \right)$$

$$\quad\quad\quad \times \Phi_{n} \left( {\frac{{\delta_{e} }}{{\sqrt {\sigma_{e}^{2} \left( {\delta_{e}^{2} + \sigma_{e}^{2} } \right)} }}({\mathbf{y}} - {\mathbf{X\beta }} - {\mathbf{Zb}})|{\mathbf{0}},{\mathbf{I}}_{n} } \right)d{\mathbf{b}}$$

(A-1)

For which the following proposition will be used.

The values of standard information standards in the SNLMM model can be used to detect deviations from normal conditions, which will be seen in the simulation study. The specific algorithm is as follows.

Let $Y_{i} = {\mathbf{X}}_{i} {{\varvec{\upbeta}}} + {\mathbf{Z}}_{i} {\mathbf{b}}_{i} + \epsilon_{i}$,where $b_{i} \mathop \sim \limits^{iid} SN_{q} \left( {0,\Sigma ,\alpha_{b} } \right)$ and $\varepsilon_{i} \mathop \sim \limits^{ind} SN_{ki} \left( {0,\Sigma_{i} ,\alpha_{ei} } \right)$ are independent. Then, the marginal distribution of Y_i is given by

$$f_{{{\mathbf{Y}}_{i} }} \left( {{\mathbf{y}}_{i} |{{\varvec{\uptheta}}},{{\varvec{\uplambda}}}} \right) = 2^{{n_{i} + q}} \phi_{{n_{i} }} \left( {{\mathbf{y}}_{i} |{\mathbf{X}}_{i} {{\varvec{\upbeta}}},{{\varvec{\Sigma}}}_{i} } \right)\Phi_{{n_{i} + q}} \left( {{{\varvec{\upmu}}}_{2i} - {{\varvec{\Gamma}}}_{i} {{\varvec{\upmu}}}_{1i} |{\mathbf{0}},{\mathbf{R}}_{i} + {{\varvec{\Gamma}}}_{i} {{\varvec{\Lambda}}}_{i} {{\varvec{\Gamma}}}_{i}^{T} } \right)$$

where

$$\begin{gathered} {{\varvec{\Sigma}}}_{i} = \left( {\delta_{e}^{2} + \sigma_{e}^{2} } \right){\mathbf{I}}_{{n_{i} }} + {\mathbf{Z}}_{i} \left( {{{\varvec{\Delta}}}_{b}^{2} + {\mathbf{D}}} \right){\mathbf{Z}}_{i}^{T} ,\quad {{\varvec{\upmu}}}_{1i} = \frac{{{{\varvec{\Lambda}}}_{i} {\mathbf{Z}}_{i}^{T} \left( {{\mathbf{y}}_{i} - {\mathbf{X}}_{i} {{\varvec{\upbeta}}}} \right)}}{{\delta_{e}^{2} + \sigma_{e}^{2} }}, \hfill \\ {{\varvec{\upmu}}}_{2i} = \left( {\begin{array}{*{20}c} {\frac{{\delta_{e} }}{{\sqrt {\sigma_{e}^{2} \left( {\delta_{e}^{2} + \sigma_{e}^{2} } \right)} }}\left( {{\mathbf{y}}_{i} - {\mathbf{X\beta }}} \right)} \\ {{\mathbf{0}}_{q} } \\ \end{array} } \right),\quad {{\varvec{\Gamma}}}_{i} = \left( {\begin{array}{*{20}c} {\frac{{\delta_{e} }}{{\sqrt {\sigma_{e}^{2} \left( {\delta_{e}^{2} + \sigma_{e}^{2} } \right)} }}{\mathbf{Z}}_{i} } \\ { - {{\varvec{\Delta}}}_{b} \left( {{{\varvec{\Delta}}}_{b}^{2} + {\mathbf{D}}} \right)^{ - 1} } \\ \end{array} } \right), \hfill \\ {\mathbf{R}}_{i} = \left( {\begin{array}{*{20}c} {{\mathbf{I}}_{{n_{i} }} } & {\mathbf{0}} \\ {\mathbf{0}} & {\left( {{\mathbf{I}}_{q} + {{\varvec{\Delta}}}_{b} {\mathbf{D}}^{ - 1} {{\varvec{\Delta}}}_{b} } \right)^{ - 1} } \\ \end{array} } \right),{{\varvec{\Lambda}}}_{i} = \left( {\left( {{{\varvec{\Delta}}}_{b}^{2} + {\mathbf{D}}} \right)^{ - 1} + \frac{{{\mathbf{Z}}_{i}^{T} {\mathbf{Z}}}}{{\delta_{e}^{2} + \sigma_{e}^{2} }}} \right)^{ - 1} ,\quad i = 1, \ldots ,m.n. \hfill \\ \end{gathered}$$

Thus, denoting the log-likelihood function for θ and λ given the observed sample y = (y₁^T,…, y_m^T) ^T by $\ell ({{\varvec{\uptheta}}},{{\varvec{\uplambda}}}|{\mathbf{y}})$, it can be written as

$$\ell (\theta ,\lambda |y) \propto - \frac{1}{2}\sum\limits_{i = 1}^{m} {\log } \left| {\Sigma_{i} } \right| - \frac{1}{2}\sum\limits_{i = 1}^{m} {\left\{ {\left( {y_{i} - X_{i} \beta } \right)^{T} \sum {}_{i}^{ - 1} \left( {y_{i} - X_{i} \beta } \right)} \right\}}$$

$$+ \sum\limits_{i = 1}^{m} {\log } \Phi_{{n_{i} + q}} \left( {\mu_{2i} - \Gamma_{i} \mu_{1i} |0,R_{i} + \Gamma_{i} \Lambda_{i} \Gamma_{i}^{T} } \right).$$

The results are important because it allows to find values of standard information criteria which may be used to detect departures from normality, as shown in the simulation study. Besides, a closing form of this likelihood may be used to carry out classical inference with standard optimization techniques. For instance, in the R software, the mvtnorm package and the optim routine.