Probabilistic Study of the Resistance of a Simply-Supported Reinforced Concrete Slab According to Eurocode Parametric Fire

Abstract

We present the application of a simple probabilistic methodology to determine the reliability of a structural element exposed to fire when designed following Eurocode 1-1-2 (EC1). Eurocodes are being used extensively within the European Union in the design of many buildings and structures. Here, the methodology is applied to a simply-supported, reinforced concrete slab 180 mm thick, with a standard load bearing fire resistance of 90 min. The slab is subjected to a fire in an office compartment of 420 m² floor area and 4 m height. Temperature time curves are produced using the EC1 parametric fire curve, which assumes uniform temperature and a uniform burning condition for the fire. Heat transfer calculations identify the plausible worst case scenarios in terms of maximum rebar temperature. We found that a ventilation-controlled fire with opening factor 0.02 m^1/2 results in a maximum rebar temperature of 448°C after 102 min of fire exposure. Sensitivity analyses to the main parameters in the EC1 fire curves and in the EC1 heat transfer calculations are performed using a one-at-a-time (OAT) method. The failure probability is then calculated for a series of input parameters using the Monte Carlo method. The results show that this slab has a 0.3% probability of failure when the compartment is designed with all layers of safety in place (detection and sprinkler systems, safe access route, and fire fighting devices are available). Unavailability of sprinkler systems results in a 1% probability of failure. When both sprinkler system and detection are not available in the building, the probability of failure is 8%. This novel study conducts for the first time a probabilistic calculation using the EC1 parametric curve, helping engineers to identify the most critical design fires and the probabilistic resistance assumed in EC1.

1 Introduction

Performance based design for fire has been incorporated into legal frameworks around the world [1] and allows designers to employ a rational engineering approach to the provision of fire safety in the built environment [2].

The fundamental principles of performance based fire engineering for structures are outlined in multiple guidance codes [3, 4]. Performance based design codes lay down what safety standards need to be met by a designer, leaving scope for new materials, systems, and methods to be used in a building’s design, whereas prescriptive design codes simply describe how a building should be built. Performance-based design codes mainly discuss qualitatively, rather than quantitatively, the factors and input parameters that should be considered in the design process. Designers should define the input variables required for design using any number of sources. This can lead to a significant variability in the design fires used, and thus inconsistent levels of safety for buildings [5].

Epistemic and Aleatory uncertainties exist in any engineering problem. The former is connected to a lack of complete scientific knowledge, and limited data sources for the modelled scenario, while the latter is linked to the stochastic variability in population [6]. These uncertainties lead to the need for assumptions and simplifications to be made in analytical and numerical models, and within methodologies used by engineers for structural fire safety design [6, 7]. A sensitivity analysis can be used to characterise the significance of uncertainties in order to determine the impact of these on the results of any analysis.

Moving from a prescriptive approach to performance based design enables designers to apply knowledge of real structural behaviour during fire, while accounting for uncertainties allows designers to quantify the reliability of the proposed solution, as well as the overall level of risk associated with the design, and to more confidently inform any further decision-making based on the results [8,9,10].

Reliability-based structural fire engineering has progressed in recent years. Examples in the literature include the application of the Monte Carlo method and various variable reduction techniques to determine the probability of failure and/or the reliability of both protected and unprotected elements [11], to evaluate the behaviour of steel beams under fire, taking account of uncertainties in the fire load [12], to evaluate designs carried out according to EN 1992-1-2, and to study the influence of the input variables for a slab the ISO 834 standard fire [13]. A new set of fire resistance periods in the development of codes of practice DD9999 were developed in [14], and a risk based methodology was defined, while the fundamental design challenges in the context of time equivalence were addressed in [15]. Other examples could be mentioned, including identifying the most critical fire scenarios for the structural response of car parks to fires [16], and the failure probability of redundant cables in a cable tunnel fire [17]. An approach such as this, based on the Monte Carlo method, can compensate for the lack of certainty in modelling inputs in the case of real fires, as there is the opportunity to vary input parameters within a defined range.

This paper presents a method to identify the most important parameters that need to be considered in a fire safety engineering design. It presents a structured approach that could help to justify some of the assumptions and simplifications which are made in fire safety engineering by identifying parameters for which more information is needed for different applications, thus allowing engineers to exclude variations in some of the other parameters in Monte Carlo analysis; in turn reducing the number of runs needed in Monte Carlo analysis to obtain a converged answer.

2 Methodology

Several fire scenarios for a uniformly burning and fully developed fire were produced based on a range of values for input parameters such as fuel load, ventilation size, contribution of fire protection systems, boundary material properties etc. to select a “reference case” fire scenario. A set of temperature time curves were produced in accordance with the EC1 parametric fire method [18], which assumes a uniformly burning fire and is valid for compartments with floor areas up to 500 m² and 4 m height [18]. Heat transfer analyses were then carried out so as to identify the “reference case” scenario with the aim of sensitivity analyses. The analytical equation given in EC1 [18] to calculate the fire temperature is:

$$ T_{g} = \, 1325\left[ {1 - 0.324\exp \left( { - \,0.2t^{*} } \right) - 0.204\exp \left( { - \,1.7t^{*} } \right) - 0.472\exp \left( { - \,19t^{*} } \right)} \right] \, \left( {^{ \circ } {\text{C}}} \right) $$

(1)

$$ t^{*} = \, t \cdot \Gamma \left( h \right) $$

(2)

where t is the time (h), Γ is given as

$$ \Gamma = \left[ {O/b} \right]^{2} /\left( {0.04/1160} \right)^{2} $$

(3)

$$ O = A_{v} \left( {h_{eq} } \right)^{0.5} /A_{t} $$

(4)

where b is the thermal inertia of the enclosure boundary, O is the opening factor of the fire compartment (m^1/2), A_v is the total vertical opening on all walls (m²), H_eq is weighted average of window heights on the wall (m), and A_t is the total area of enclosure (walls, ceiling and floor, including openings) (m²).The maximum temperature T_max occurs at t ^* _max as:

$$ t_{\hbox{max} }^{*} = \, t_{\hbox{max} } \cdot \, \Gamma \, \left( h \right) $$

(5)

$$ t_{max} = \, max \, [(0.2 \cdot 10^{ - 3} \cdot q_{t,d} /O); \, t_{lim} ] \, \left( h \right) $$

(6)

$$ q_{t,d} = \, q_{f,d} \cdot A_{f} / \, A_{t} $$

(7)

where q_t,d is the design value of the fire load density related to the total surface area A_t of the enclosure (walls, ceiling and floor, including openings) (MJ/m²), and q_f,d is the design value of the fire load density related to the surface area A_f of the floor (MJ/m²).

The limiting temperature t_lim of 25 min is taken, assuming a medium fire growth rate [18]. After t ^* _max the cooling phase begins and the temperature–time curve during this phase is given by:

$$ T_{g} = \, T_{max} {-} \, 625 \, \left( {t^{*} - \, t_{\hbox{max} }^{*} \cdot \, x} \right) \, for \, t_{\hbox{max} }^{*} \le \, 0.5 $$

(8)

$$ T_{g} = \, T_{max} {-} \, 250 \, \left( {3 \, - \, t_{\hbox{max} }^{*} } \right) \cdot \, \left( {t* - \, t_{\hbox{max} }^{*} \, x} \right) \, for \, 0.5 \, \le \, t_{\hbox{max} }^{*} \, \le \, 2 $$

(9)

$$ T_{g} = \, T_{max} {-} \, 250 \, \left( {t^{*} - \, t_{\hbox{max} }^{*} \cdot \, x} \right) \, for \, 2 \, \le \, t_{\hbox{max} }^{*} $$

(10)

Once this fundamental part has been addressed, a detailed sensitivity analysis of the main parameters in the EC1 parametric curves and heat transfer model were performed for a wide range of values. The heat transfer was solved by means of a one-dimensional finite difference method for conductive heat transfer inside the material, and boundary conditions for both convective and radiant heating were taken into account [19, 20]. As such, a range of input variables in EC1 parametric fire and heat transfer model were investigated (Tables 1 and 2). A sensitivity analysis of the “reference case” scenario examined a large number of fire scenarios using a one-at-a-time method (OAT).

Table 1 Parameter Values for the Reference Case and Range of Input Variables Investigated Using the Eurocode 1 Parametric Approach

Table 2 Parameter Values for the Reference Case and Range of Input Variables Investigated in the Heat Transfer Model

OAT is a sensitivity analysis method, which simply varies one input at a time, keeping others at their baseline, and calculates the variation in the output. All input parameters are examined and results are compared to determine which of the input parameters have the highest impact on the final results. The OAT sensitivity analysis has been used in different examples, such as identifying the governing parameters of a solid ignition model and global level of confidence associated with the model predictions [21], and determining the most sensitive parameters in travelling fire methodology for structural design [19]. The OAT sensitivity analysis was useful in this study to determine which input data were important for further the Monte Carlo analysis and required more information, and which were unimportant, thus reducing the number of variables required to be considered as uncertain. In addition, it highlighted the range of possible fire scenarios for which the designed element is structurally safe.

A Monte Carlo analysis was then carried out to evaluate the reliability of the concrete slab, in terms of the failure probability P_f, given uncertainty in key model parameters. Monte Carlo analysis is a method that performs numerical experiments using a large number of randomly generated sample sets from the input space, containing all possible values of the input variables according to their probability distributions. It is suitable when it is impossible to compute an exact result with a deterministic approach and also to understand the impact of uncertainty in forecast modelling [22].

3 Case Study

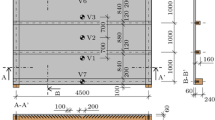
The methodology presented here was applied to a simply-supported reinforced concrete slab 180 mm thick with 44 mm axis-distance of the tension reinforcements to the soffit of the slab (fire exposed surface) and a concrete cover of 36 mm. The compartment was an open-plan office building, 30.25 m long by 14.25 m wide and 4 m high (Fig. 1). The simplified calculation method in Eurocode 2-1-2 [23] was used to measure the performance of the slab, as the simply-supported slab was subjected to a uniformly distributed load, and the design at ambient temperature was based on linear analysis. There are different methods to evaluate the failure modes of concrete structures for different levels of assessment in fires: maximum deflection (which is typically taken as a ratio of deflection), the maximum temperature of the tension reinforcement, the ultimate strain in the tension reinforcement, and the shear capacity [23]. The slab is exposed to fire from below, so the strength of the structural element may be assumed to be a function of the temperature of the rebar in the tension zone [2]. The critical temperature of the tension reinforcement in the slab was therefore selected as the limiting criteria.

Figure 1

Plan and elevation of the structure and slab cross section, dimensions in meter

The critical temperature of the reinforcement steel was calculated assuming a reduction factor of 0.6 for the load combination (e.g. permanent and variable loads) in the fire situation [23]. The effects of actions on structural element (e.g. internal force, moment) for the fire situation, may be deduced from those determined in normal temperature design using the reduction factor for the load combination in the fire situation [23]. A partial safety factor of 1.15 for reinforcement steel was selected in accordance with Eurocode 2-1-1 [24]. As such, failure in the selected structural member for the fire situation, occurred when reduction factor for the strength of reinforcement steel was 0.52. In accordance with clause 4.2 [23], for rebar (hot rolled) in concrete and for strain greater than 2% (which is the case for slabs and beams without a high reinforcement ratio), the critical temperature is 583°C. This temperature is normally considered as the limiting temperature above which steel loses strength such that the failure of a typical simply supported slab could occur under the load assumed to be applied during a fire [25]. The maximum temperature of the tension rebar was compared with the critical rebar temperature.

It was assumed that explosive spalling is unlikely to occur, as the XC1 class is considered with moisture content less than 3% and the concrete strength is below 55 MPa in accordance with EC2-1-2 [23].

A concrete density of 2300 kg/m³, thermal conductivity of 1.33 W/m K, specific heat of 900 J/kg K, convective heat transfer coefficient of 35 W/m² K for the exposed surface and 4 W/m² K for the unexposed surface of the concrete element, and an emissivity of 0.7 were assumed [18, 24]. In this illustrative example, the concrete properties were assumed to be constant. It is shown elsewhere that 1D heat transfer with constant effective properties results in a 7–15% higher in-depth concrete temperature than the case of temperature dependent concrete properties [19]. Therefore, we deemed the method in this paper to be appropriate, because it is simple but still accurate enough. To make the reference case scenario representative of habitual practice for this type of building, it was assumed that suppression and detection systems operated in the case of a fire, and safe access routes and fire fighting devices were fitted in the building. The design value of the fire load density q_f,d related to the surface area A_f of the floor in Annex E of EC1 is given by:

$$ q_{f, \, d} = \, q_{f, \, k} \cdot \, \delta_{q1} \cdot \, \delta_{q2} \cdot \, \delta_{n} \cdot m \, \left( {{\text{MJ/}}m^{2} } \right) $$

(11)

The product of (1) characteristic fire load density for an office building (q_f,k) equal to 511 MJ/m² (80% fractile), (2) different active firefighting measures (δ_n) assumed to be 0.66 (in Table 1), (3) fire activation risk due to the size of the compartment (δ_q1) equal to 1.53, (4) fire activation risk due to the type of occupancy (δ_q2) equal to 1, and (5) a combustion factor of m = 0.8, were assumed to be 0.8 in accordance with EC1 [18]. As such the design value of the fire load density, q_{f, d} is 410 MJ/m².

It should be noted that the Eurocodes are the required standards, providing a common approach for the design of buildings within the European Union and being used extensively in the design of buildings and slabs. On the other hand, each country is expected to issue a National Annex to the Eurocodes and choose those parameters which are left open in the Eurocode for national choice, known as Nationally Determined Parameters, to be used in the design of buildings in the country concerned [18]. For example there are national annexes of EC1 which do not use the factors in Eq. 11, which affects characteristic fire load density (q_f,k) [26]. A number of slabs around Europe have been designed without applying the Annex E of EC1, therefore, for comparison, these cases were also considered.

3.1 Design Fire

The fire duration and severity in a fully developed fire depends on the amount of ventilation and the nature, distribution, and quantity of fuel, which all have a significant effect on duration and severity [25].

In a modern building, a double or triple glazed system may not break as readily as single panels of ordinary glass. Characteristics, orientation and dimensions of the glazed external openings are architectural variables. Due to all the uncertainties associated with glass breakage and fall-out of glass [27], both fuel-controlled and ventilation-controlled design fires were examined. To cover all possibilities of ventilation, a series of parametric temperature–time curves were produced, in which the opening factor varied from 0.02 to 0.2 m^1/2, in accordance with the limitations imposed by EC1 [18]. The external walls were considered to be 100% glazed and ranges of the opening factor cover all possibilities of glass breakage. The thermal inertia of the concrete and glazing were assumed to be 1659 W s^1/2/m²K and 1312 W s^1/2/m²K respectively. The calculated average compartment temperatures for different opening factors are presented in Fig. 2. The results show that opening factors lying between 0.097 m^1/2 and 0.2 m^1/2 produced a relatively short fuel-controlled fire. The decrease in opening factor to below 0.097 m^1/2 resulted in a fire restricted by ventilation. Opening factors between 0.074 m^1/2 and 0.02 m^1/2, due to the façade glass breakage, resulted in a ventilation-controlled fire with peak gas temperatures between 750°C and 850°C.

Figure 2

Gas temperature in a compartment for different opening factors using the EC1 parametric approach and resulting rebar temperatures in the concrete slab. The reference case with the maximum rebar temperature is obtained from ventilation-controlled fires without using Annex E of EC1 and was used for sensitivity analysis

The calculated temperature fields were used as an input to a one dimensional heat transfer model to calculate the resulting temperature in the concrete slab at the location of the rebar. The rebar was assumed to have the same temperature as the adjacent concrete, as it has a much higher thermal diffusivity than concrete.

A comparison of the rebar temperatures in Fig. 2 clearly shows that the highest temperatures were caused by a ventilation-controlled fire, obtained from an opening factor of 0.02 m^1/2. The maximum rebar temperature was 408°C after 95 min of fire exposure. This scenario is named the “reference case” scenario and was used for further analysis.

Without considering the Annex E of EC1, Fig. 2 shows that the maximum rebar temperature obtained from an opening factor of 0.02 m^1/2 was 448°C after 102 min of fire exposure which is 9% higher than the case in accordance with Annex E of EC1.

4 Parametric Sensitivity Study Using OAT Method

As the most challenging scenario was the one with an opening factor of 0.097 m^1/2, it was examined as the “reference case” for all the sensitivity studies performed in this section. The OAT (one-at-a-time) method was used to observe how varying one input variable affects the output results, particularly the maximum rebar temperature (RMT) and time to reach the maximum rebar temperature (t_RMT). In OAT sensitivity analysis, the input parameters were incremented across the ranges investigated.

The parameter values for the reference case scenario and the ranges investigated are given in Tables 1 and 2. The study includes all the input variables in the EC1 parametric fire and the heat transfer models.

The following sections present the sensitivity analysis of the parameters in Tables 1 and 2.

4.1 Characteristic Fire Load Density

The amount of fuel in a building significantly alters the dynamics of a fire. The available guidance provides the characteristic ranges of the fire load, which should include temporary and permanent fire loads, and the fire loads from construction elements, linings, and finishes [18]. Some national annexes of EC1 provide different values of fire load density for an individual occupancy and recommend using the 80% or 90% fractile [26]. On the other hand, comparison of the office fire load density in EC1 with recent surveys shows that the fire load given in EC1 may be nonconservative compared to the data in survey. Results of the survey are approximately 40% higher [28] than EC1, and therefore, the 95% fractile is a reasonable fire load density for an office building [29].

The range of fire load density was therefore selected to cover everything from sparsely furnished (classroom, 347 MJ/m²) [18] to densely loaded (business office, 1315 MJ/m²) spaces [2].

Figure 3 shows the variations of the maximum rebar temperature and the corresponding time, relative to the reference case, with a characteristic fire load density ranging from 347 MJ/m² to 1315 MJ/m².

Figure 3

Maximum rebar temperature and corresponding times versus characteristic fuel load density with and without factors in Annex E of EC1

The results show that the critical rebar temperature (critical case) occurred when the characteristic fire load density was above 1140 MJ/m² after 140 min of fire exposure, using the Annex E of EC1. Without considering the Annex E of EC1, the critical case occurred for a characteristic fire load density of 912 MJ/m² after 120 min of fire exposure. It should be noted that, when Annex E of EC1 was used, the characteristic fire load density (q_{f, k}) of 1140 MJ/m² was multiplied by the product of factors in Eq. 11 equal to 0.8 (obtained in Sect. 3), and thus the design fire load density (q_{f, d}) was equal to 912 MJ/m² (using Eq. 11). Without using Annex E of EC1, the characteristic fire load density and the design fire load densities were both 912 MJ/m². This shows that using the factors in Annex E of EC1 (i.e. δ_q1, δ_q2, δ_n, m) could highly decrease the characteristic fire load density used to calculate the gas temperature. Figure 3 indicates that without using Annex E of EC1 the critical temperature was reached for a lower characteristic fire load density (in this case study 20% less than using Annex E of EC1). The fuel load densities which lead to the critical cases are representative value for densely loaded (i.e. library, business office) spaces.

4.2 Fire Fighting Measures Index

The presence of active fire protection systems influences the severity of the fire environment and fire duration in an enclosure. This index takes into account different active firefighting measures and ranges from 0.148 (full fire protection) to 3.37 (no active fire protections and intervention of fire fighters) in accordance with Annex E of EC1 [18]. Cases with and without the firefighting measures index were studied here and serve to illustrate the effect of this method on the resulting level of safety.

Figure 4 shows how rebar maximum temperatures and associated times vary with the firefighting measure index.

Figure 4

Maximum rebar temperature and corresponding time versus active fire fighting measures index in accordance to EC1

The results indicate that cases where the firefighting measures index has a value greater than 1.46 (i.e. the case when either sprinkler systems or detection and alarm systems are not installed [18]) resulted in a temperature greater than the rebar critical temperature (i.e. 583°C) after 150 min of fire exposure. Without using Annex E of EC1, the maximum rebar temperature was 408°C after 95 min of fire exposure. This demonstrates that using Annex E of EC1 prolongs the failure time of the structural element.

4.3 Axis Distance of Reinforcement

Axis distance of the reinforcement is a fundamental design variable in any concrete structure and is likely to be a fixed value early in the design of a building. Typical concrete covers a range from 20 mm to 60 mm [19]. It is worth understanding the impact of axis distances on peak rebar temperatures, as it could make a significant difference to the performance of the structure.

Figure 5 indicates that the peak rebar temperatures were lower than the rebar critical temperature for all axis distances. A concrete cover of 36 mm was used for the reference case; in addition, the range selected implicitly included the possible loss of 24 mm concrete cover due to spalling. For each rebar depth in Table 2, we also checked that the bending strengths with different lever arms were above the applied bending moment.

Figure 5

Maximum rebar temperature and corresponding time versus rebar axis distance. No critical case is found in this range of the parameters

4.4 Opening Factor

Figure 6 shows the variation of the maximum rebar temperature and the time taken to reach the maximum temperature with a ventilation size of 0.02 m^1/2 to 0.2 m^1/2. Figure 6 illustrates that the maximum rebar temperature value corresponds to opening factor 0.02 m^1/2. It is notable that the sharp gradient changes in the maximum rebar temperature were due to a change in fire environment, from fuel-controlled to ventilation-controlled. Therefore, the predicted structural element temperature from parametric fire is highly sensitive to small variation of the size of opening.

Figure 6

Maximum rebar temperature and corresponding time versus opening factor. No critical case is found in this range of the parameters

4.5 Concrete Density

Density varies greatly for concrete types, and guidance exists which provides typical ranges. The reference case density was taken as the density of normal weight concrete, equal to 2300 kg/m³ [23]. Figure 7 shows the maximum rebar temperature and the time to reach the maximum temperature against concrete densities from 1900 kg/m³ to 2300 kg/m³ [25]. Results show that concrete density affects the maximum rebar temperature. The results indicate that the lower the density, the higher the peak bay rebar temperatures and the shorter the time to reach the peak rebar temperature.

Figure 7

Maximum rebar temperature and corresponding time versus density of concrete. No critical case is found in this range of the parameters

4.6 Other Parameters

The results from the OAT sensitivity analysis for the rest of the parameters in Tables 1 and 2 are illustrated in Figs. 12, 13, 14, 15, 16, 17, 18 and 19 in “Appendix”. The results demonstrate the effects of varying the input parameters on the maximum rebar temperature and corresponding time. No critical scenario, where the slab reached the critical rebar temperature, was found in the investigated ranges of these parameters, and consequently, the range of values for which the designed slab is structurally safe (i.e. with no critical temperature) was determined. Variations in concrete thickness were not varied, and it is assumed that the effects of these variations are included in the variations in rebar depth. The results confirm that variation in the total area, sample thickness, time to reach maximum gas temperature t_lim, coefficients in O_lim and Γ_lim, and unexposed surface’s convective coefficient do not change the maximum rebar temperature from the reference case value.

OAT analysis allowed the identification of the input parameters which have little to no impact on maximum rebar temperature, and the mean values were used for 6 input variables in a further probabilistic analysis, thus reducing the number of simulations needed and their runtime.

5 Probabilistic Assessment of Structural Fire Safety

This section seeks to investigate the fire resistance and reliability of the reinforced slab probabilistically, using Monte Carlo simulations, accounting for the uncertainties in the fire and heat transfer models in the case of a fully developed fire.

The OAT sensitivity analysis (Sect. 4) identified the key input parameters which had the greatest effect on the maximum rebar temperature for the purpose of the Monte Carlo simulation. The parameter ranges found in the literature and their expected values are given in Tables 1 and 2. Probabilistic distributions were then defined for the selected parameters. A Gumbel distribution was assumed for the fire load density in accordance with EC1 [18], with a mean value of 411 MJ/m² and a variance of 0.3. Since little is known about the probability distribution of the other input parameters [30], for the purpose of this study a uniform distribution was conservatively assumed. Consequently, any value has the same probability of being selected over the set range. This assumption is conservative, since it is the shape of the tail of each distribution that is important; in this case, if the high end (or the low end if this is critical) is artificially ‘fattened’ then the likelihood of randomly sampling from the tail is increased.

In Monte Carlo simulation, a value was selected at random for each of the input variables based on the given distributions, and the maximum rebar temperature in the concrete slab was calculated as before. The results for the model were recorded and the process was repeated. The Monte Carlo analysis comprised 1500 individual runs. One way to select the number of trials in a Monte Carlo simulation is to run the model repeatedly until the mean value of the outputs converges [31]. In this case, convergence was satisfied based on a tolerance of 5% change in the mean and standard deviation in the output. It should be noted that the probabilities of failure were small, so less than 5% change in the mean value of the outputs did not significantly affect the probabilities of failure. Therefore, it was concluded that 1500 runs were enough.

The probability of failure P_f was calculated by evaluating the ratio between the number of simulations in which the structure failed and the number of times the simulation was performed, given by:

$$ P_{f} = n_{f} /n $$

(12)

where n_f is the number of failed simulations, and n is the total number of simulations.

The reliability of a system (R) was defined as the probability that it will perform successfully [32], which is given by:

$$ R = 1 - P_{f} $$

(13)

The effect of the different variables on the maximum rebar temperature was compared from the results of the OAT, which let us exclude some of the lower impact variables, and in turn reduce the number of runs needed to obtain a converged answer. The relationship between two variables can be ranked using the Spearman’s correlation coefficient [17], which shows the strength and direction of a monotonic relationship between paired data. In this study, all graphs from the OAT analysis showed a linear and monotonic relationship, with very strong strength between the input and output data.

Instead, the strength of relationship between maximum rebar temperature and different variables (i.e. sensitivity of the probability of failure to different input data) was obtained from the results of the OAT. The resulting percentage change in the maximum rebar temperature, against a 10% variation of each parameter from the corresponding reference case, was plotted in Fig. 8.

Figure 8

The resulting percentage change of the maximum rebar temperature to 10% variation of the reference case values of the most important input variables which were identified by the OAT sensitivity analysis

Figure 8 shows that conductivity, emissivity, and convective coefficient are the lower impact variables. These parameters were excluded from the Monte Carlo simulation. The calculated reliability was thus slightly increased, and the number of simulations needed to achieve convergence of solution decreased to 750, where the probability of failure varied by less than 3.5% in 100 iterations compare to 1500 trials (3.5% variation of probability of failure was too small). The simulation time also decreased to 2 h for 750 runs, compared with 3.30 h for 1500 runs, performed on a 2.1 GHz Intel Core i7 processor.

We found that the maximum rebar temperature is sensitive to the active fire fighting measure index. Analyses were therefore conducted for the system with specified values for this sensitive parameter, where the probability of failure was calculated for different set up of active fire protection measures.

To examine a number of scenarios with different chains of events, an event tree approach was used. An event tree is a logical model expressing the possible outcomes of an event. The construction of event trees start with specifying an event, and then various events following the initial event are modelled as branches of the tree. Each branch represents a specific risk scenario. The possible event sequence arising from the lack of active fire protections was structured, and the event tree is shown in Fig. 9. Each final scenario is an aggregation of events and was assigned a firefighting measures index in accordance with EC1. A reliability analysis was performed on sub-scenarios in the event tree by varying all other parameters using Monte Carlo simulation.

Figure 9

Event tree and possible scenarios for Monte Carlo sensitivity analysis. Each final scenario is an aggregation of events and was assigned a fire fighting measures index in accordance with EC1

For comparison, the Monte Carlo analysis was performed without considering the impact of active fire protection in the Annex E of EC1. This meant that the range for the firefighting measures index was dropped from the input variables in this specific analysis.

5.1 Results of the Monte Carlo Analysis and Discussion

Figure 10 shows the probability of reaching the failure criteria in a concrete slab when the active firefighting measures index ranges from 0.66 (i.e. sprinklers, automatic smoke detection and fire alarm, safe access routes, and fire fighting devices) to 3.35 (no active fire protection and no intervention of fire fighters), in accordance with [18].

Figure 10

Probability of failure for a range of active fire fighting measures of EC1 from a Monte Carlo simulation based on 750 trials

Figure 10 illustrates that, for the reference scenario where detection and sprinkler systems, safe access route, and fire fighting devices were available in the building, the probability of failure of slab was 0.3%, therefore the reliability, R, was 99.7%, using Eq. (10). Unavailability of sprinkler systems, which also covers the case of “no detection system”, resulted in a 1% probability of failure. The reliability of the structure for this case was then R = 99%. When both sprinkler system and detection and alarm systems were not available in the building, the probability of failure was 8%, which corresponds to 92% reliability. The higher the firefighting measure index, the higher the design fire load density and, consequently, the higher the probability of failure. The highest probability of failure corresponded to an extreme case when no active fire protection measures, and no fire fighting intervention were available, and therefore the randomly generated fuel load density was always multiplied by 3.37 in accordance with the methodology in EC1 [18], which is indicated in the event tree in Fig. 9. For this extreme case, the mean characteristic fuel load density of 411 MJ/m² (in Table 1) was multiplied by 3.37, and thus the mean value of 1385 MJ/m² was taken for the Monte Carlo analysis. As such a high probability of failure is expected.

Figure 10 also shows that, for the case without considering Annex E of EC1 where the fire fighting measures index was taken 1, the probability of failure of the slab was 0.6%, which implies a reliability of R = 99.4%.

For illustrative purposes all of the possible temperature curves in the compartment, from the Monte Carlo simulation using EC1 parametric fire, are demonstrated in Fig. 11. The red line in Fig. 11, is the converged result, and that the other lines are included to show how many scenarios are captured by the probabilistic approach. These gas temperatures were applied to calculate the probability of failure of the slab. In this case (Fig. 11), the sprinkler system was not unavailable, but detection systems, safe access routes and firefighting devices were available in the compartment.

Figure 11

Resulting gas temperatures in the compartment from the Monte Carlo simulation using EC1 parametric method. The red line is the converged result, and that the other lines are included to show how many scenarios are captured by the probabilistic approach. The sprinkler system is not available but there are detection system, safe access route and fire fighting devices available in the compartment. The probability of failure is 1% in this case

6 Conclusion

The work herein applies a simple, but powerful, structured methodology to: (1) identify the most important parameters that need to be considered during fire safety engineering, and (2) to determine the reliability of a structural element exposed to fire when designed following EC1. The methodology was applied to a simply-supported reinforced concrete slab 180 mm thick; with a standard load bearing fire resistance of 90 min; subjected to a fire in an office building compartment of 420 m² floor area and 4 m height. Design fires were constructed in accordance with the EC1 parametric fires. It was demonstrated that opening factors under 0.097 m^1/2 resulted in a ventilation-controlled fire with peak gas temperatures lying between 750°C and 850°C and maximum rebar temperatures between 300°C and 408°C. The maximum rebar temperature of 448°C was found after 102 min of fire exposure by a ventilation-controlled fire with opening factor 0.02 m^1/2, without using the Annex E of EC1. It was found that using the Annex E of EC1 decreased the maximum rebar temperature of the slab by 20%.

Analyses of the main input parameters in the EC1 curves and heat transfer model were performed, in order to assess the sensitivity of the main results to parameter uncertainty, and also to define the safe and critical design fires using an OAT method. The critical design fires were found when the characteristic fire load density was above 1140 MJ/m² (densely loaded spaces) and 912 MJ/m², for cases with and without using Annex E of EC1 respectively. It was concluded that using the factors in Annex E of EC1 (i.e. δ_q1, δ_q2, δ_n, m) could highly affect the characteristic fire load density used to calculate the gas temperature.

The safe ranges of design fire scenarios were identified for the firefighting measures indices lower than 1.46 (i.e. sprinkler and detection systems were not available, however safe access route and fire fighting devices were available) in the building. The axis distance of reinforcement-the most sensitive parameter- has a fixed value early in the design. The range selected for sensitivity analysis of axis distance of rebar implicitly included the possible loss of 24 mm concrete cover due to spalling, which does not have any impact on the resistance of the slab. The maximum gas temperature and corresponding rebar temperature from the parametric fire in EC1 is highly sensitive to small variation of the size of opening (i.e. ventilation), due to the change of fire environment from fuel–controlled to ventilated-controlled. The concrete density was found to have a large effect on the rebar maximum temperature. The study shows that OAT sensitivity analysis provides an insight into the range of fire parameters for which the design is structurally safe.

The OAT analysis determined that 8 out of 17 input parameters were the most sensitive in regard to changes in the maximum rebar temperature: axis distance of reinforcement, ventilation sizes, concrete density, coefficient in t_max, fuel load density, fire protection measures, specific heat, and floor area.

Such a structured approach could help to justify some of the assumptions and simplifications which are made in fire safety engineering, by identifying parameters for which more information is needed for different applications, thus allowing engineers to ignore some of the other parameters in Monte Carlo analysis, thus reducing the number of runs needed to have a converged answer. In this study, the number of simulations were decreased from 1500 to 750.

It was found that unavailability of fire protection measures, as indicated in the EC1 method, leads to an increased probability of failure (lower reliability of structure). It was found that probability of failure of the concrete slab was 0.3% (i.e. 99.7% structural element reliability) where detection and sprinkler systems, safe access route, and fire fighting devices were available in the building. Unavailability of either sprinkler systems or detection systems resulted in 1% probability of failure of the slab (i.e. 99% reliability), and unavailability of sprinkler and detection systems resulted in 8% probability of failure of the slab (i.e. 92% reliability). Probability of failure of the slab was equal to 0.6% (i.e. 99.4% reliability) without considering Annex E of EC1.

The methodology presented in this paper quantifies the reliability of a structural element in terms of collapse probabilities, using the Monte Carlo method. This methodology could be applied to define the reliability of a fire-affected structure. In that case, more performance criteria and detailed structural analysis should be used to assess the failure modes of structures. This study demonstrates that sensitivity and probabilistic analyses can provide a comprehensive understanding of the factors affecting the structural fire resistance and inform further fire development and detailed structural analysis.

This novel study which conducted for the first time the OAT analysis and the Monte Carlo simulation of a slab exposed to the EC1 parametric fire, was considered by the International Organization for Standardization (ISO) for inclusion in an ISO technical report [33].

Appendix: Results from OAT Sensitivity Analyses

The results from the OAT sensitivity analysis for the some of the parameters in Tables 1 and 2 are illustrated in Figs. 12, 13, 14, 15, 16, 17, 18 and 19. The results demonstrate the effects of varying the input parameters on the maximum rebar temperature and corresponding time.

Figure 12

Maximum rebar temperature and corresponding time versus the convective heat transfer Coefficient of exposed surface. No critical case is found in this range of the parameters

Figure 13

Maximum rebar temperature and corresponding time versus concrete thermal inertial characteristic. No critical case is found in this range of the parameters

Figure 14

Maximum rebar temperature and corresponding time versus coefficient in the time. No critical case is found in this range of the parameters

Figure 15

Maximum rebar temperature and corresponding time versus Coefficient in time factor function Γ. No critical case is found in this range of the parameters

Figure 16

Peak bay temperature and corresponds time versus coefficient in the time t_max. No critical case is found in this range of the parameters

Figure 17

Maximum rebar temperature and corresponding time versus the emissivity of concrete. No critical case is found in this range of the parameters

Figure 18

Maximum rebar temperature and corresponding time versus thermal conductivity of concrete. No critical case is found in this range of the parameters

Figure 19

Maximum rebar temperature and corresponding time versus specific heat of boundary of enclosure. No critical case is found in this range of the parameters