Extremal characteristics of conditional models

Abstract

Conditionally specified models are often used to describe complex multivariate data. Such models assume implicit structures on the extremes. So far, no methodology exists for calculating extremal characteristics of conditional models since the copula and marginals are not expressed in closed forms. We consider bivariate conditional models that specify the distribution of X and the distribution of Y conditional on X. We provide tools to quantify implicit assumptions on the extremes of this class of models. In particular, these tools allow us to approximate the distribution of the tail of Y and the coefficient of asymptotic independence $\eta$ in closed forms. We apply these methods to a widely used conditional model for wave height and wave period. Moreover, we introduce a new condition on the parameter space for the conditional extremes model of Heffernan and Tawn (Journal of the Royal Statistical Society: Series B (Methodology) 66(3), 497-547, 2004), and prove that the conditional extremes model does not capture $\eta$, when $\eta <1$.

1 Introduction

Extreme value theory is a topic of growing interest because of its many important applications in for example risk management (Embrechts et al. 1999) or ocean engineering (Castillo et al. 2005). For instance, in the design or assessment of offshore facilities it is crucial to understand the distribution of extreme sea states. Such extreme sea states are quantified in terms of extreme wave heights, wave periods possibly associated with resonant frequencies, and extreme wind speeds. In risk management, it is important to identify which stocks are likely to suffer extreme losses simultaneously, and to which extent this might happen. In general, we need to use well-estabilished extreme value methods to model such events. Traditionally, such multivariate extreme value methods are composed of marginal models and a dependence copula, each having parametric forms for the tails.

In other areas of statistics, however, it is common to use conditional models for multidimensional data. Intuitively, this is the most sensible approach. We observe X that partially explains Y. So, we define a model for X and a model for Y conditional on X. There exist many examples in the literature of models within this conditional framework with applications in extremes, e.g., the conditional extreme value model (Heffernan and Tawn 2004; Fougeres and Soulier 2012), the Weibull-log normal distribution (Haver and Winterstein 2009, henceforth the Haver-Winterstein distribution), and hierarchical models (Eastoe 2019). Although conditional models are easy to interpret, it can be rather difficult to study the extremes of both Y and (X, Y) within this class. Recently, Engelke and Hitz (2020) developed graphical models for extremes. However, we do not know of any literature that links existing conditional models directly to extremal dependence measures.

There are two extremal dependence measures that are key in identifying and measuring the degree of asymptotic dependence or asymptotic independence (Coles et al. 1999). Identifying the correct asymptotic dependence class is important since extrapolation of models from different classes is different. To define asymptotic dependence, we first define $\chi \in [0,1]$, with

$$\begin{aligned} \chi :=\lim _{p\uparrow 1}\chi (p) := \lim _{p\uparrow 1} \mathbb {P}\left\{ Y>F_Y^{-1}(p)\mid X>F_X^{-1}(p)\right\} , \end{aligned}$$

(1)

where $F_X$ and $F_Y$ denote the marginal distribution functions of X and Y. We say that these random variables are asymptotically dependent if $\chi >0$, i.e., when the joint probability that both random variables are large is of the same magnitude as when one is large. If the coefficient of asymptotic dependence $\chi =0$, we say that the variables are asymptotically independent. In this case, $\chi$ does not give us information on the level of asymptotic independence. So, we additionally define the coefficient of asymptotic independence $\eta \in (0,1]$ (Ledford and Tawn 1996). This coefficient describes the rate of decay to zero of the joint exceedance probability $\mathbb {P}\{X>F_X^{-1}(p),\ Y>F_{Y}^{-1}(p)\}$ as p tends to 1. More specifically, $\eta$ is defined to satisfy

$$\begin{aligned} \mathbb {P}\left\{ X>F_X^{-1}\left[ F_E(u)\right] ,\ Y>F_Y^{-1}\left[ F_E(u)\right] \right\} \sim \mathcal {L}\left( e^u\right) e^{-u/\eta } \end{aligned}$$

(2)

as $u\rightarrow \infty$, where $F_E(u) = 1 - \exp (-u)$ is the distribution function of a standard exponential, and where $\mathcal {L}$ is a slowly varying function. Here, we write $f(x)\sim g(x)$ as $x\rightarrow \infty$ when $f(x)/g(x)\rightarrow 1$ as $x\rightarrow \infty$. We rewrite definition (2) as

$$\begin{aligned} \eta := \lim _{p\uparrow 1} \eta (p) := \lim _{p\uparrow 1}\frac{\log (1-p)}{\log \left[ (1-p)\chi (p)\right] }. \end{aligned}$$

(3)

If the variables are asymptotically dependent, then $\eta =1$; if the variables are asymptotically independent, then $\eta \in (0,1)$ or $\eta =1$ and $\mathcal {L}(u)\rightarrow 0$ as $u\rightarrow \infty$.

Evaluating $\chi$ for a bivariate random variable (X, Y) is relatively straightforward. First, define for each $z\in \mathbb {R}$,

$$\overline{H}(z) := \lim _{p\uparrow 1}\mathbb {P}\left( \log \left( \frac{1-F_X(X)}{1-F_Y(Y)}\right)> z\ \Big |\ F_X(X)>p\right) .$$

Although this formulation looks complex, it is simply an analogue of the spectral measure (Engelke and Hitz 2020) in Fréchet margins but here it is expressed as a representation in exponential margins, see Sect. 4. We then apply the dominated convergence theorem to get

$$\chi = \int _0^{\infty } \overline{H}(-x) e^{-x}\,\mathrm {d}x.$$

In particular, $\chi >0$ if and only if $\lim _{z\rightarrow -\infty } \overline{H}(z)>0$.

Additionally calculating $\eta$ is straightforward for distributions when the joint distribution function is specified parametrically, e.g., a bivariate extreme value distribution (Ledford and Tawn 1996), or when the joint density function is specified parametrically (Nolde and Wadsworth 2021), e.g., a multivariate normal distribution. In this paper, we consider models specified within the conditional framework. For these cases, it is hard to calculate $\eta$ analytically, and numerical estimation can be difficult since convergence of $\eta (p)$ to $\eta$ can be exceptionally slow. We set up methodology to calculate $\eta$ in closed form within this framework and demonstrate the techniques on two widely used examples specified below. We support these limiting results using numerical integration.

First, we consider the model described in Haver and Winterstein (2009), used to explain the dependence between extreme significant wave height and their associated wave periods. Secondly, we investigate the model of Heffernan and Tawn (2004). This is a conditional model which describes the distribution of $Y\mid X$ for large X, where both X and Y are on standard margins. As the Heffernan-Tawn model focusses on normalising the distribution of $Y|X=x$ as $x\rightarrow \infty$ to give a non-degenerate limit, it asymptotically focusses on a different aspect of the joint distribution to the events which determine $\eta$, i.e., $\{X>x,\ Y>x\}$ as $x\rightarrow \infty$, when the variables are asymptotically independent. As a consequence, it seems reasonable to expect that the upper tail of $Y|X=x$ for large x does not give $\eta$. We will show by giving an example that there exist distributions that share the same Heffernan-Tawn normalization but do not share the same $\eta$. More theoretical examples, like $Y\mid X := X^{\beta } Z$ and $Y\mid X := \vert Z\vert ^{\vert X\vert }$ where Z is some random variable independent of X, can be found in the Ph.D. thesis of Tendijck (2023).

The layout of the article is as follows. In Sect. 2, we demonstrate novel techniques for calculating the coefficient of asymptotic independence $\eta$ and illustrate the techniques with some examples. In Sects. 3 and 4, we apply these techniques to the Haver-Winterstein model and the Heffernan-Tawn model, respectively. Proofs are found in the Appendix and Supplementary Material.

2 Methodology

2.1 Motivation

We aim to investigate the extremal properties of the bivariate distribution of (X, Y), for which the distribution of X and the distribution of $Y\mid X$ are specified. In particular, we aim to investigate the tail of the distribution of Y and joint extremes of X and Y via the coefficient of asymptotic independence $\eta$. Deriving such extremal quantities in closed form within this class is not trivial. In this section, we provide a set of tools, derived from the Laplace approximation, to calculate such properties for any conditional model.

First, we consider the tail of the distribution of Y. Because the distributions of X and $Y\mid X$ are specified, it is natural to write

$$1 - F_Y(y) := \mathbb {P}(Y>y) = \int _{-\infty }^{\infty } \mathbb {P}(Y>y\mid X=x)f_X(x)\,\mathrm {d}x,$$

where $f_X$ is the density of X. In general, this integral is analytically intractable. In Sect. 2.2, we present the tools with which we can derive the asymptotic properties of this integral as y tends to the upper end point of the distribution of Y.

To derive the coefficient of asymptotic independence, we additionally need the inverse distribution $F_Y^{-1}(p)$ for values of p close to 1, and

$$\mathbb {P}(X>F_X^{-1}(p),\ Y>F_Y^{-1}(p)) = \int _{F_X^{-1}(p)}^{\infty } \mathbb {P}(Y>F_Y^{-1}(p)\mid X = x) f_X(x)\,\mathrm {d}x.$$

This integral is also intractable in general; the tools from Sect. 2.2 can again be applied to derive the asymptotic decay to 0 as p tends to 1.

2.2 Extension to the Laplace approximation

Here we present our theory to calculate asymptotic rates of decay of integrals, that can be used to compute extremal properties, such as $\eta$, of conditional models. We first recall the Laplace approximation, a technique commonly used in Bayesian inference for approximating intractable integrals. This asymptotic approximation forms the basis of our main result. We then state that result, and illustrate key differences with the Laplace approximation by comparing examples.

Proposition 1

(Laplace approximation) Let $a<b$. Suppose $g:[a,b]\rightarrow \mathbb {R}$ is twice continuously differentiable and assume there exists a unique $x^*\in (a,b)$ such that $g(x^*) = \max _{x\in [a,b]}g(x)$ and $g''(x^*)<0$. Then

$$\int _a^b e^{n g(x) - n g(x^*)}\,\mathrm {d}x \cdot \sqrt{n(-g''(x^*))} \sim \sqrt{2\pi }$$

as $n\rightarrow \infty$.

The main disadvantage of the Laplace approximation is that it can only be used to approximate integrals where the integrands are of the form $f(x)^n$, where $f(x)=e^{g(x)}$ is a positive function. However, we are interested in calculating integrals with integrand $f_n(x) = e^{g_n(x)}$, for some sequence of functions $\{g_n\}_{n\in \mathbb {N}}$. Now we extend the Laplace approximation under the assumptions that: (i) the analogue $x_n^*$ of $x^*$ is allowed to depend on n; (ii) $x^*_n$ can be equal to either a or b; (iii) $g_n''(x^*_n)$ does not need to be negative.

Proposition 2

Let $I\subseteq \mathbb {R}$ be connected with non-zero Lebesgue mass, $k_0\ge 1$ an integer, and $g_n\in C^{k_0}(I)$ a sequence of real-valued (at least) $k_0$-times continuously differentiable functions defined on I. For $1\le i \le k_0$, we define $g_n^{(i)}$ as the ith derivative of $g_n$. We assume that for all $n\in \mathbb {N}$, there exists a unique $x_n^*\in I$ such that $g_n(x_n^*)>g_n(x)$ for all $x\in I\setminus \{x_n^*\}$. Moreover, we assume that $k_0$ is the smallest integer such that $g_n^{(k_0)}(x_n^*) < 0$ and $\lim _{n\rightarrow \infty } g_n^{(i)}(x_n^*)[-g_n^{(k_0)}(x_n^*)]^{-i/k_0}=0$ for all $1\le i<k_0$. Additionally, assume that there exists a $\delta >0$ for which there exists an $\varepsilon >0$ such that for all $\vert x \vert <\delta$

$$\lim _{n\rightarrow \infty } \frac{g_n^{(k_0)}\left\{ x_n^* + x\left[ -g_n^{(k_0)}(x_n^*)\right] ^{-\frac{1}{k_0}}\right\} }{g_n^{(k_0)}(x_n^*)} < 1+\varepsilon .$$

Then, for $n>N$, there exists a constant $C_1>0$ such that

$$\int _{I} e^{g_n(x) - g_n(x_n^*)}\,\mathrm {d}x \cdot \left[ -g_n^{(k_0)}(x_n^*)\right] ^{\frac{1}{k_0}} \ge C_1.$$

The proof of Proposition 2 can be found in Appendix 1. One disadvantage of our extension is that it only gives an asymptotic lower bound. In many practical applications, an upper bound can be found directly using inequalities like that in Eq. (8).

Functions for which Proposition 2 is applicable include functions $g_n$ with a single mode $x_n^*$ that are approximated well with a Taylor expansion of some order on a large enough neighbourhood of the mode. For example, for $g_n(x)=-|x|^p$ with $p\in \mathbb {R}$, the proposition is applicable if and only if $p\in \mathbb {Z}$. We specify further that the first set of assumptions ensures that the $k_0$th order Taylor approximation of $g_n$ around $x_n^*$ has at most two significant terms (the 0th and the $k_0$th term) by setting a limit on the size of the ith terms in this Taylor approximation, where $1\le i \le k_0-1$. The second set of assumptions defines if the Taylor approximation is good enough on a neighbourhood of $x_n^*$, see the second example in Sect. 2.3

2.3 Examples

We demonstrate the use of Proposition 2 in three cases. Firstly, let $g_n(x)=-n x^m$ for $n\in \mathbb {N}$, $m\in \mathbb {Z}_{\ge 1}$ and $I=[0,\infty )$. It is then valid to apply Proposition 2 with $x^*_n=0$ and $k_0=m$. Applying the proposition yields a constant $C_1>0$ such that for sufficiently large n,

$$n^{\frac{1}{m}}\int _{0}^{\infty } e^{-n x^m} \,\mathrm {d}x \ge C_1.$$

This lower bound is tight for each $m\ge 1$. We verify this by using the variable transformation $y = n x^{m}$ to give

$$n^{\frac{1}{m}}\int _{0}^{\infty } e^{-n x^m} \,\mathrm {d}x = \frac{1}{m} \int _{0}^{\infty } y^{\frac{1}{m}-1} e^{-y} \,\mathrm {d}y = \Gamma \left( \frac{1}{m}+1\right) .$$

After recognizing that the integral over $[0,\infty )$ is equal to half of the integral over $\mathbb {R}$, we see that Proposition 1 is applicable only when $m=2$. In this case, Proposition 1 additionally gives as $n\rightarrow \infty$

$$\int _{0}^{\infty } e^{-n x^2} \,\mathrm {d}x = \frac{1}{2}\int _{-\infty }^{\infty } e^{-n x^2} \,\mathrm {d}x \sim \frac{\sqrt{\pi }}{2\sqrt{n}}.$$

Secondly, let $g_n(x)=-x - n x^2$ and $I=[0,\infty )$. Now Proposition 1 is not applicable since no function g(x) exists for which $g_n(x)=n g(x)$ holds. Note that Proposition 2 is also not applicable with $k_0=1$, since $x_n^*$ has to be equal to 0 and for $x\ne 0$

$$\lim _{n\rightarrow \infty } \frac{g_n'\left( 0 + x\cdot n\right) }{g_n'(0)} = \lim _{n\rightarrow \infty } 1+2n^2 x =\infty ,$$

contradicting one of the assumptions. Proposition 2 is applicable with $k_0=2$, yielding a constant $C_2>0$ such that for sufficiently large n,

$$\sqrt{n}\int _{-\infty }^{\infty } e^{-x- n x^2} \,\mathrm {d}x \ge C_2.$$

Similar to our first example, this lower bound is tight since we can also directly calculate as $n\rightarrow \infty$

$$\sqrt{n}\int _{-\infty }^{\infty } e^{-x- n x^2} \,\mathrm {d}x = \sqrt{n}\int _{-\infty }^{\infty } e^{-n\left( x + \frac{1}{2n}\right) ^2 + \frac{1}{4n}} \,\mathrm {d}x \sim \sqrt{\pi }.$$

Finally, let $\alpha _n>0$, $\beta _n>0$ for $n\in \mathbb {N}$ and assume $\liminf \alpha _n > 0$. Define $g_n(x) = \alpha _n \log x - \beta _n x$. Using an argument similar to that in the second example, we see that Proposition 1 is not applicable. However Proposition 2 is applicable with $k_0=2$, yielding a constant $C_3>0$ such that for sufficiently large n,

$$\alpha _n^{-\alpha _n - \frac{1}{2}} \beta _n^{\alpha _n+1} e^{\alpha _n} \int _{0}^{\infty } x^{\alpha _n} e^{- \beta _n x} \,\mathrm {d}x \ge C_3.$$

This bound is also tight, which can be seen from recognizing the density of a gamma distribution in the expression above, and applying limit results for the gamma function.

3 Haver-Winterstein model

Haver and Winterstein (2009) introduce the Haver-Winterstein (HW) distribution for significant wave height $H_S$ and wave period $T_p$ in the North Sea. Their model is set up in the conditional framework: they specify a class of distributions for $H_S$ and a class of distributions for $T_p\mid H_S$. Variations of this approach have been widely applied in ocean engineering with over 150 citations, 25 of which correspond to 2021, see for example Drago et al. (2013). However we are not aware of any literature quantifying $\chi$ and $\eta$ in closed form for the HW distribution; we now show how to calculate these.

The marginal distribution of the HW is formulated as

$$\begin{aligned} f_{X}(x) = {\left\{ \begin{array}{ll} \frac{1}{\sqrt{2\pi } \alpha x} \exp \left\{ -\frac{(\log x - \theta )^2}{2\alpha ^2}\right\} ,\ &{} \text {for}\ 0<x\le u, \\ \frac{k}{\lambda ^{k}} x^{k-1} \exp \left\{ -\left( \frac{x}{\lambda }\right) ^{k}\right\} ,\ &{} \text {for}\ x>u. \end{array}\right. } \end{aligned}$$

(4)

where $u,\alpha ,k,\lambda >0$ and $\theta \in \mathbb {R}$. In particular, the parameters are constrained such that $f_X$ is continuous at u and integrates to 1. Secondly, they take $Y\mid X$ to be conditionally log-normal

$$\begin{aligned} f_{Y\mid X}(y\mid x) = \frac{1}{\sqrt{2\pi } \sigma (x) y} \exp \left\{ -\frac{(\log y - \mu (x))^2}{2\sigma (x)^2}\right\} ,\ \ \ \ \text {for}\ x,y>0, \end{aligned}$$

(5)

where $\mu (x):=\mu _0+\mu _1 x^{\mu _2}$ and $\sigma (x):=\left[ \sigma _0 + \sigma _1 \exp (-\sigma _2 x)\right] ^{1/2}$ with $\mu _0\in \mathbb {R},\ \mu _1,\mu _2,\sigma _0,\sigma _1,\sigma _2 > 0$.

Model parameter estimates (Haver and Winterstein 2009) from data observed in the northern North Sea are given in the Supplementary Material. For ease of presentation, we make two assumptions about the parameter space of the HW distribution that are consistent with parameter estimates $(\hat{\mu }_2,\hat{k})=(0.225,1.55)$ from Haver and Winterstein (2009). Specifically, we make the following restrictions: $0<\mu _2<0.5$ and $2\mu _2<k$. These assumptions reduce the number of cases to be considered significantly whilst including realistic domains for the parameters as considered by practioners.

We now show how to use Proposition 2 to calculate the extremal dependence measures $\chi$ and $\eta$ for the bivariate random vector (X, Y) distributed according to the HW distribution in the restricted parameter space. Calculation of $\eta$ is split into two steps. In the first step, we calculate the distribution function $F_Y$ of Y and in the second we evaluate the rate of decay of joint probabilities $\mathbb {P}\{X> F_X^{-1}[F_E(u)],Y>F_Y^{-1}[F_E(u)]\}$ as u tends to infinity.

We have

$$\begin{aligned} \mathbb {P}(Y> y) = \int _0^{\infty } \mathbb {P}(Y> y\mid X=x)f_X(x) \,\mathrm {d}x = \int _0^{\infty } \overline{\Phi }\left( \frac{\log y - \mu (x)}{\sigma (x)}\right) f_X(x)\,\mathrm {d}x, \end{aligned}$$

(6)

where $\overline{\Phi }$ is the survival function of a standard Gaussian. This integral is analytically intractable but we can calculate its limiting leading order behaviour in closed form. Proposition 2 gives a lower bound and an upper bound of the same order as the lower bound is then found directly. For ease of notation, we denote the integrand by

$$\begin{aligned} g_y(x) := \overline{\Phi }\left( \frac{\log y - \mu (x)}{\sigma (x)}\right) f_X(x) \end{aligned}$$

(7)

for $x>0$. In Fig. 1, we plot $g_y$ for various values of y. From the figure, we note that $g_y$ has two local maxima for suffiiciently large y. These are $x_y^*$, which converges to zero, and $x_y^{**}$, which diverges to infinity. This observation implies that we cannot apply Proposition 2 directly in this case. We therefore proceed as follows: (i) calculate $x_y^*$ and $x_y^{**}$; (ii) partition the interval of integration into intervals $I_1$ and $I_2$, where $x_y^*\in I_1$ and $x_y^{**}\in I_2$, such that the conditions of Proposition 2 hold for both intervals, and then apply the proposition on each interval; (iii) combine the two lower bounds found to get a lower bound for integral (6); (iv) derive a limiting upper bound for integral (6) of the same order as the lower bound.

Fig. 1

The function $\log g_y$ from Eq. (7) for $y=10,\ 20,\ 30,\ 40,\ 50,\ 100$ with parameters as reported in Haver and Winterstein (2009), see Supplementary Material

In the Supplementary Material, we derive that as $y\rightarrow \infty$

$$\begin{aligned} x_y^* \sim \left( \frac{\sigma _1 \sigma _2\cdot \log y}{2\mu _1\mu _2(\sigma _0+\sigma _1)}\right) ^{-\frac{1}{1-\mu _2}}\ \ \ \text {and}\ \ \ x_y^{**} \sim \left( \frac{ \lambda ^k\mu _1\mu _2\cdot \log y}{k \sigma _0}\right) ^{\frac{1}{k-\mu _2}}, \end{aligned}$$

where in the calculation of $x_y^*$ we use $0<\mu _2<0.5$. From Fig. 1, we recognize that $g_y(x_y^*) > g_y(x_y^{**})$ as $y\rightarrow \infty$. We show that this holds analytically in the Supplementary Material when $2\mu _2<k$. We now apply Proposition 2 and find that $k_0=2$ is appropriate. The proposition then gives a lower bound for integral (6) around $x_y^*$ as $y\rightarrow \infty$ of

$$\mathbb {P}(Y>y) \ge \exp \left\{ -\frac{\log ^2 y}{2(\sigma _0+\sigma _1)} + O(\log y)\right\} .$$

Finally, since $g_y(x_y^*)>g_y(x_y^{**})$, it is straightforward to show as $y\rightarrow \infty$ that

$$\mathbb {P}(Y>y) \le \exp \left\{ -\frac{\log ^2 y}{2(\sigma _0+\sigma _1)} + O(\log y)\right\}$$

using the inequality

$$\begin{aligned} \mathbb {P}(Y> y\mid X=x)f_X(x) \le g_y(x_y^*)\mathbbm {1}\{x\in [0,x_y^{**}]\} + f_X(x) \mathbbm {1}\{x>x_y^{**}\}. \end{aligned}$$

(8)

We now can calculate $\eta$ and show that $\chi =0$. To that end, we first need to calculate the inverse probability integral transform, transforming Y to standard exponential margins; i.e., we need $F_Y^{-1}[F_E(u)]$. Next, we need to evaluate the asymptotic behaviour of $\mathbb {P}\{Y>F_Y^{-1}[F_E(u)],X>F_X^{-1}[F_E(u)]\}$ as $u\rightarrow \infty$. To evaluate $F_Y^{-1}\circ F_E$, we first calculate for $y\rightarrow \infty$

$$\begin{aligned} F_E^{-1}(F_Y(y)) = -\log (1-F_Y(y))= \frac{\log ^2 y}{2(\sigma _0+\sigma _1)} + O(\log y). \end{aligned}$$

We invert this expression by solving $F_E^{-1}(F_Y(y))=u$ for $\log y$. This yields $\log y = \sqrt{2(\sigma _0+\sigma _1)u} + O(1)$ as $u\rightarrow \infty$. We can now write down an asymptotic expression for $\chi (u)$ as $u\rightarrow \infty$

$$\begin{aligned} \chi (u)&:=\mathbb {P}\left\{ F_E^{-1}\left[ F_Y(Y)\right]> u,\ F_E^{-1}\left[ F_X(X)\right]> u\right\} \\&= \mathbb {P}\left\{ \log Y>\sqrt{2(\sigma _0+\sigma _1)u} + O(1),\ (X/\lambda )^k > u\right\} \\&= \int _{\lambda u^{1/k}}^{\infty } \overline{\Phi }\left( \frac{\sqrt{2(\sigma _0+\sigma _1)u} + O(1) - \mu (x)}{\sigma (x)}\mid X=x\right) \cdot \frac{k x^{k-1}}{\lambda ^k} \exp \left\{ -\left( \frac{x}{\lambda }\right) ^k\right\} \,\mathrm {d}x. \end{aligned}$$

In the Supplementary Material, we show that Proposition 2 is applicable for this integral with $k_0=1$ and $x_u^*=\lambda u^{1/k}$. Moreover, we derive directly an upper bound of the same order, obtaining

$$\chi (u) =\exp \left\{ - \left( 2 +\frac{\sigma _1}{\sigma _0}\right) u + O\left( u^{1/2 + \mu _2/k}\right) \right\}$$

as $u\rightarrow \infty$. Hence, $\chi =0$ and

$$\begin{aligned} \eta = \left( 2 +\frac{\sigma _1}{\sigma _0}\right) ^{-1}. \end{aligned}$$

In particular, for the parameter estimates from Haver and Winterstein (2009), the value of $\eta \in (0,1/2)$ implies that the distribution exhibits negative asymptotic independence (Ledford and Tawn 1996). This contrasts with the positive correlation of the Haver-Winterstein distribution, which might lead practitioners to assume falsely that the positive correlation also exists in the extremes of the Haver-Winterstein model; this is far from the truth.

What we learn from our work is not necessarily that the Haver-Winterstein model should not be used - we can derive this conclusion in many simpler ways than with this paper. Instead, we can use this example to understand how a conditional model makes complex assumptions on the dependence structure: imposing a positive correlation overall but a highly negative correlation in the extremes.

4 Heffernan-Tawn model

In multivariate extreme value theory, the conditional extreme value model of Heffernan and Tawn (2004), henceforth denoted the HT model, is widely studied and applied to extrapolate multivariate data. The HT model has been cited over 600 times, and is applied e.g. in oceanography (Ross et al. 2020), finance (Hilal et al. 2011), and spatio-temporal extremes (Simpson and Wadsworth 2021). The HT model is a limit model and its form is motivated by derived limiting forms from numerous theoretical examples.

Let (X, Y) be a bivariate random variable with standard Laplace margins (Keef et al. 2013) and assume that its joint density exists. Next, assume there exist parameters $\alpha \in [-1,1]$, $\beta <1$ and a non-degenerate distribution function H such that for $x>0$, and for all $z\in \mathbb {R}$ the following limit

$$\begin{aligned} H(z) = \lim _{x\rightarrow \infty } \mathbb {P}\left( \frac{Y-\alpha x}{x^{\beta }} \le z \mid X=x\right) \end{aligned}$$

(9)

exists. This implies, according to l’Hopital’s rule, that

$$\begin{aligned} \lim _{u\rightarrow \infty } \mathbb {P}\left( \frac{Y-\alpha X}{X^{\beta }} \le z,\ X-u>x\mid X>u\right) = H(z) \exp (-x). \end{aligned}$$

(10)

The latter in turn has the interpretation that as u tends to infinity, $(Y-\alpha X)X^{-\beta }$ and $(X-u)$ are independent conditional on $X>u$, and are distributed as H and a standard exponential, respectively. As is common practice in extreme value theory, the limit results are assumed to hold above some high threshold. So here, the HT model assumes that the corresponding limiting family in (9) holds exactly at a finite level u and beyond.

Now, if we additionally assume that a $u>0$ exists such that for all $x>u$

$$\begin{aligned} \mathbb {P}(Y> y\mid X=x) = \overline{H}\left( \frac{y - \alpha x}{x^{\beta }}\right) \end{aligned}$$

(11)

holds for all $y\in \mathbb {R}$ where $\overline{H} = 1- H$ is some non-degenerate survival function. Then, we say that (X, Y) is modelled with the exact version of the HT model.

In this case study, we assume that (X, Y) is modelled with the exact version of the HT model with the additional assumption that $\alpha ,\beta \in [0,1)$. We consider two cases for H, corresponding to finite and infinite upper end points. If H has a finite upper end point $z^H$, calculations for $\eta$ are trivial. Indeed, when $X=x$, Y cannot be larger than $\alpha x + x^{\beta } z^H$. Thus, as $u\rightarrow \infty$, $Y> u$ implies $X> u/\alpha +o(u)$. So, as $u\rightarrow \infty$

$$\begin{aligned} \mathbb {P}(X>u,Y>u)&\sim \mathbb {P}\left\{ X>u,X>u/\alpha +O(u^{\beta })\right\} \\&\sim \mathbb {P}\left\{ X>u/\alpha +O(u^{\beta })\right\} \\&=\exp \left\{ -u/\alpha +O(u^{\beta })\right\} . \end{aligned}$$

Therefore, $\eta =\alpha$ when $\alpha >0$ and otherwise does not exist.

Now assume that H has an infinite upper end point. To make calculations tractable, we parameterise $\overline{H}$ as

$$\begin{aligned} \overline{H}\left( z\right) = \exp \left\{ - \gamma z^{\delta } + o\left( z^{\delta }\right) \right\} \mathbbm {1}\{z>0\} + \mathbbm {1}\{z\le 0\} \end{aligned}$$

(12)

for $\gamma >0$, $\delta \ge 1$. For simplicity, we do not consider potential negative arguments for $\overline{H}$ since the precise form of its lower tail is not relevant to the current work. Parameterisation (12) covers most non-trivial light-tailed cases for the upper tail including Gaussian, Weibull and exponential tails; see examples in Heffernan and Tawn (2004). It is also the tail model of the delta-Laplace (generalised Gaussian) distribution used in spatial conditional extremes model, e.g., Shooter et al. (2021). Moreover if the tail of $\overline{H}$ is heavier than that of the exponential, Y cannot possibly follow a standard Laplace distribution. This links to the restricton $\delta \ge 1$. For illustration, we set $o(z^{\delta })=0$ in Eq. (12). The resulting Weibull survival function is a suitable choice for $\overline{H}$, since it has an extreme value tail index of 0, but a varying tail thickness controlled by $\delta$.

Proposition 3

If (X, Y) follows distribution (11) with H as in (12) with $o(z^{\delta })=0$, then $\delta \ge (1-\beta )^{-1}$.

The proof of Proposition 3 is found in Appendix 1. Following similar arguments to those used in the proof of Proposition 3, we calculate $\chi$ and $\eta$ for any combination of the parameters $(\alpha ,\beta ,\delta ,\gamma )$ in their specified parameter space. We collect results in Table 1. In the Supplementary Material, we only give details of the $\eta$ calculations when $\alpha ,\beta \in (0,1)$, $\gamma >0$ and $\delta =(1-\beta )^{-1}$. For the other five cases in Table 1, we state results without proof. In particular, the argument underpinning the $\eta$ calculation when $\delta >(1-\beta )^{-1}$ is similar to the argument used when $\overline{H}$ has a finite upper end point. In this case, $\eta =\alpha$ when $\alpha >0$ and when $\alpha =0$, $\eta$ is not defined.

In Table 1, it is convenient to refer to $c=\max \{1,c_0\}\in [1,1/\alpha )$ where $c_0\in (0,1/\alpha )$ satisfies

$$\begin{aligned} \gamma (1-\alpha c_0)^{\delta -1}\left( \delta -1 +\alpha c_0\right) = c_0^{\delta }. \end{aligned}$$

(13)

Table 1 Values of $\eta$ for model (11) with $\overline{H}$ as in (12) for different ranges of parameter combinations, where $c=\max \{1,c_0\}\in [1,1/\alpha )$ for $c_0$ given in Eq. (13)

Fig. 2

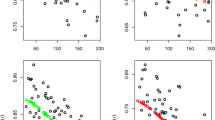
Visualisation of $c_0$ from Eq. (13) for $\gamma =1,\ 1.5,\ 2,\ 5$ and $\delta =(1-\beta )^{-1}$. The region corresponding to $c_0\in (0,1)$ is shown in red; the region corresponding to $c_0\in (1,1/\alpha )$ is shown in green

Fig. 3

The value of $\eta$ as a function of $\alpha$, $\beta$ and $\gamma$ with $\delta =(1-\beta )^{-1}$ from the HT model (11) and (12)

To give some intuition on the value of c, in Fig. 2 we sketch the region of the parameter space corresponding to $c=1$ (in red) for different values of $\gamma$. Finally in Fig. 3 we visualise $\eta$ for a set of different parameter combinations with $\delta =(1-\beta )^{-1}$.

We note the following interesting findings. The parameter $\eta$ is non-decreasing with increasing $\alpha$ and with increasing $\beta$. Parameter combinations $(\alpha ,\beta ,\gamma ,\delta )$ exist for which $\alpha ,\beta >0$ but $\eta <0.5$. Hence, there are cases for which Y increases with X but the extremes of (X, Y) are negatively associated as measured by $\eta$ (Ledford and Tawn 1996).

Finally we note that the Heffernan-Tawn model is not $\eta$ invariant, i.e., there exist models that asymptotically follow the same conditional Heffernan-Tawn representation but have different $\eta$. We illustrate this result below with an example, but first we comment on its implications. Our finding implies that if X and Y are asymptotically independent, then there do not exist asymptotically consistent Heffernan-Tawn model-based estimators for probabilities $\mathbb {P}(Y>X>v)$ and $\mathbb {P}(X>v,\ Y>v)$ where v is large. This in turn provides an interesting insight in the lack of self-consistency of the Heffernan-Tawn model with regard to the choice of conditioning variable, see Liu and Tawn (2014).

To illustrate our claim, we consider two bivariate random variables (X, Y) and $(X_{HT},Y_{HT})$. Let (X, Y) follow an inverted bivariate extreme value distribution with a logistic dependence structure (Ledford and Tawn 1996) on Laplace margins with parameter $\xi \in (0,1]$, such that

$$\begin{aligned} \mathbb {P}(X>x,\ Y>y) = \exp \left\{ -\left[ t_x^{1/\xi } + t_{y}^{1/\xi }\right] ^{\xi }\right\} , \end{aligned}$$

(14)

where $t_x := \log 2 - \log [2-\exp (x)]$ for $x<0$ and $t_x:=\log 2 + x$ for $x>0$, with $t_y$ similarly defined. It is straightforward to derive that in the limit, the Heffernan-Tawn model (11) is applicable to (X, Y) with $\overline{H}$ as in Eq. (12) and $o(z^{\delta })=0$. Specifically,

$$\lim _{x\rightarrow \infty }\mathbb {P}\left( Y X^{\xi - 1}> z \mid X=x\right) = \exp \left( - \xi z^{1/\xi }\right) .$$

Now let $(X_{HT},Y_{HT})$ be distributed following the exact version of the HT model associated with (X, Y). That is, for $X_{HT}<u$, we have $(X_{HT},Y_{HT})=(X,Y)$, and for $X_{HT}\ge u$, $X_{HT}-u$ is a standard exponential and $Y_{HT}\mid X_{HT}$ follows model (11) with $\overline{H}$ as in (12) with parameters $(\alpha ,\ \beta ,\ \gamma ,\ \delta )=(0,\ 1-\xi ,\ \xi ,\ 1/\xi )$ and $o(z^{\delta })=0$. In this case $\gamma < (1-\beta )/\beta$, and Table 1 implies that the coefficient of asymptotic independence $\eta _{HT}$ of $(X_{HT},Y_{HT})$ is equal to $1/(\xi +1)$. In contrast, it is straightforward to derive directly from definition (14) that $\eta$ of (X, Y) is equal to $2^{-\xi }$. Hence $\eta _{HT}\ne \eta$ when $\xi \in (0,1)$.

Finally we illustrate numerically the differences between $\eta$, $\eta _{HT}$ and their finite level counterparts $\eta (p)$ and $\eta _{HT}(p)$ for $p\in (0,1)$. For definiteness, we let (X, Y) follow distribution (14) with $\xi =0.35$. We simulate a sample $\{(x_i,y_i):\ i=1,\dots ,n\}$ of size $n=10,000$. First we empirically estimate $\eta (p)$ from Eq. (3) for $p\in (0,1)$ and calculate pointwise $95\%$ confidence intervals using the binomial distribution. Next we note that $\eta (p)=\eta$ for $p\in (0.5,1)$. Finally we calculate the corresponding $\eta _{HT}(p)$ for p near 1 using numerical integration.

Results are shown in Fig. 4. Left and right hand plots are the same except for the scale of the x-axis, illustrating the behaviour of $\eta _{HT}(p)$ for p near 1. Reassuringly, the true $\eta$ of the underlying model (red dashed) falls within the $95\%$ confidence interval for its empirical counterpart $\hat{\eta }(p)$ (blue). Further, $\eta _{HT}(p)$ (black dashed) converges to $\eta _{HT}$ (green dashed). We note that $\eta _{HT}(p)$ varies as a function of p and only seems to asymptote for $p>1-\exp (-50)/2 \approx 1 - 9.6\cdot 10^{-23}$. Finally, since $\eta _{HT}<\eta$, we would expect that $\eta _{HT}(p)$ would underestimate $\eta$, but it turns out this is only the case for $p>1-\exp (-7.5)/2\approx 0.9997$.

Fig. 4

Coefficients of asymptotic independence $\eta$ (red dashed) for distribution (14) with $\xi =0.35$, and the corresponding value for the exact limiting HT model $\eta _{HT}$ (green dashed), and its finite level counterpart $\eta _{HT}(p)$ (black dashed). Empirical estimates $\hat{\eta }(p)$ for a sample of size 10, 000 with pointwise confidence intervals are shown in blue. Left and right hand panels are the same except for the scale of the x-axis, set on the right to illustrate the behaviour of $\eta _{HT}(p)$ for p near 1

Appendix

1.1 Proofs

Proof of Proposition 2

We prove that for sufficiently large n, there exists a constant $C_1>0$ such that

$$\mathcal {I}_n := \int _{I} e^{g_n(x) - g_n(x_n^*)}\,\mathrm {d}x \cdot \left( -g_n^{(k_0)}(x_n^*)\right) ^{\frac{1}{k_0}} \ge C_1.$$

To bound $\mathcal {I}_n$ from below, we first simplify its expression by applying the variable transformation $y = t_n(x):= (x-x_n^*)\left( -g_n^{(k_0)}(x_n^*)\right) ^{1/k_0}$ and defining

$$h_n(y) := g_n\left( x_n^* + y \left( -g_n^{(k_0)}(x_n^*)\right) ^{-\frac{1}{k_0}}\right) , \ \ \text {for}\ y \in I_n' := \left\{ t_n(x):\ x\in I\right\} .$$

Then, the integral $\mathcal {I}_n$ becomes

$$\begin{aligned} \mathcal {I}_n = \int _{I_n'} e^{h_n(y)- h_n(0)}\,\mathrm {d}y. \end{aligned}$$

We note that for all $n\in \mathbb {N}$, we have $0\in I_n'$, $h_n\in C^{k_0}(I_n')$, and $h_n(0)>h_n(y)$ for all $y\in I_n'\setminus \{0\}$. Moreover, we have for $y\in I_n'$, $i=1,\dots ,k_0$,

$$h_n^{(i)}(y) = g^{(i)}_n\left( x_n^* + y\left( -g_n^{(k_0)}(x_n^*)\right) ^{-1/k}\right) \cdot \left( -g_n^{(k_0)}(x_n^*)\right) ^{-i/k_0}.$$

Hence, $h_n^{(k_0)}(0)=-1$ and $\lim _{n\rightarrow \infty } h_n^{(i)}(0)=0$ for all $1\le i<k_0$. Using Taylor’s theorem, there exists a function $\xi (y)$ taking on a value between 0 and y such that

$$\begin{aligned} h_n(y) - h_n(0)&= \sum _{i=1}^{k_0-1} \frac{y^i}{i!} h_n^{(i)}(0)+ \frac{y^{k_0}}{k_0!} h_n^{(k_0)}(\xi (y)). \end{aligned}$$

Let $\tilde{\varepsilon }>0$. Because $\lim _{n\rightarrow \infty } h_n^{(i)}(0)=0$ for all $i<k_0$, we can find an $N_0\in \mathbb {N}$ such that for all $n>N_0$, we have $\max _{i=1,\dots ,k_0-1}|h_n^{(i)}(0)|<\tilde{\varepsilon }$. Moreover, from the assumptions of the proposition, we can find a $\delta >0$ and associated $\varepsilon >0$ and $N_1\in \mathbb {N}$ such that for all $n>N_1$, $h_n^{(k_0)}(y)>-(1+\varepsilon )$ for $y\in (-\delta ,\delta )\cap I_n'$. For $n>\max \{N_0,N_1\}$,

$$\begin{aligned} h_n(y) - h_n(0)&> -|y| \tilde{\varepsilon } - \frac{|y|^2}{2!} \tilde{\varepsilon } - \cdots - \frac{|y|^{k_0-1}}{(k_0-1)!} \tilde{\varepsilon } - \frac{(1+\varepsilon )|y|^{k_0}}{k_0!} > -\tilde{\varepsilon } e^{\delta }- \frac{(1+\varepsilon )|y|^{k_0}}{k_0!} \end{aligned}$$

for $y \in (-\delta ,\delta )\cap I_n'$. Hence, we derive a lower bound

$$\mathcal {I}_n \ge e^{ -\tilde{\varepsilon } e^{\delta }} \int _{I_n' \cap (-\delta ,\delta )} e^{-\frac{(1+\varepsilon ) |y|^{k_0}}{ k_0!}}\,\mathrm {d}y =: C_1.$$

From the connectedness of I and $0\in I_n'$, we conclude that $I_n' \cap (-\delta ,\delta )$ has positive mass under the Lebesgue measure. Hence, $C_1\in (0,\infty )$. $\square$

Proof of Proposition 3

Let (X, Y) be a random vector such that X and Y both have standard Laplace margins. Moreover, assume that there exist $-1\le \alpha \le 1$, $0\le \beta <1$ and $u>0$ such that for $x>u$

$$\mathbb {P}(Y> y\mid X=x) = \overline{H}\left( \frac{y - \alpha x}{x^{\beta }}\right)$$

holds for all $y\in \mathbb {R}$ with

$$\overline{H}\left( z\right) = \exp (- \gamma z^{\delta })\mathbbm {1}\{z>0\} + \mathbbm {1}\{z\le 0\},$$

where $\gamma ,\delta >0$. Now, let Z be a random variable that is independent of X and have survival function $\overline{H}$. We derive that $\delta \ge (1-\beta )^{-1}$ must hold. Since Y is distributed as a standard Laplace, we have for $y>0$

$$\begin{aligned} \frac{\exp (-y)}{2}&= \mathbb {P}(\alpha X + X^{\beta } Z \ge y,\ X\ge u) + \mathbb {P}(Y \ge y,\ X< u) \\&\ge \mathbb {P}(\alpha X + X^{\beta } Z \ge y,\ X\ge u) \ge \mathbb {P}(X^{\beta } Z \ge y,\ X\ge u) \\&= \int _{u}^{\infty } \mathbb {P}\left( Z \ge \frac{y}{x^{\beta }}\right) f_X(x)\,\mathrm {d}x = \frac{1}{2}\int _{u}^{\infty } \exp \left( - \frac{\gamma y^{\delta }}{x^{\beta \delta }} - x\right) \,\mathrm {d}x =: \tilde{\mathcal {I}}_y. \\ \end{aligned}$$

We will show that $2\exp (y)\tilde{\mathcal {I}}_y > 1$ for sufficiently large y, if $\delta < (1-\beta )^{-1}$, which thus would contradict with the marginal distribution of Y. This result holds trivially for $\beta =0$. So, for now, we let $\beta >0$. We will prove this asymptotic inequality by applying Proposition 2, with $k_0=2$, to bound $\tilde{\mathcal {I}}_y$ from below.

First define $I:=[u,\infty )$ as the integration domain, and

$$g_y(x):= \exp \left( - \frac{\gamma y^{\delta }}{x^{\beta \delta }} - x\right) \mathbbm {1}\{x\in I\},\ \ \ \text {and}\ \ \ h_y(x):=\left( - \frac{\gamma y^{\delta }}{x^{\beta \delta }} - x\right) \mathbbm {1}\{x\in I\}.$$

Next we find the mode $x_y^*$ of $g_y(x)$. We assume that $x_y^*$ lies in the interior of I such that $h_y'(x_y^*)=0$, which implies that $\beta \delta \gamma y^{\delta } (x_y^*)^{-\beta \delta -1} = 1$. So, $x_y^* = \left( \beta \delta \gamma \right) ^{\frac{1}{\beta \delta +1}} y^{\frac{\delta }{\beta \delta +1}}$, which lies in the interior of I for sufficiently large y. We now compute

$$g_y(x_y^*) = \exp \left( - \frac{\gamma y^{\delta }}{(x_y^*)^{\beta \delta }} - x_y^*\right) = \exp \left( - A y^{\frac{\delta }{\beta \delta +1}}\right)$$

with $A:=\gamma \left( \beta \delta \gamma \right) ^{-\frac{\beta \delta }{\beta \delta +1}} + \left( \beta \delta \gamma \right) ^{\frac{1}{\beta \delta +1}}$. Secondly,

$$h_y''(x_y^*) = - \beta \delta (\beta \delta +1) (x_y^*)^{-\beta \delta -2} \gamma y^{\delta } = - (\beta \delta +1)\left( \beta \delta \gamma \right) ^{-\frac{1}{\beta \delta +1}} y^{-\frac{\delta }{\beta \delta +1}}.$$

Using these expressions, we can now check that the assumptions from Proposition 2 with $k_0=2$ are satisfied. First we note that $h_y'(x_y^*)(-h_y''(x_y^*))^{-1/2} = 0$. Next let $C>0$ and $|x|\le C$, then

$$\begin{aligned} \lim _{y\rightarrow \infty }&\frac{h_y''\left( x_y^*+\frac{x}{\sqrt{-h_y''(x_y^*)}}\right) }{h_y''(x_y^*)} \\&= \lim _{y\rightarrow \infty } \frac{ - \beta \delta (\beta \delta +1)\left( \left( \beta \delta \gamma \right) ^{\frac{1}{\beta \delta +1}} y^{\frac{\delta }{\beta \delta +1}}+\frac{x}{\sqrt{ (\beta \delta +1)\left( \beta \delta \gamma \right) ^{-\frac{1}{\beta \delta +1}} y^{-\frac{\delta }{\beta \delta +1}}}}\right) ^{-\beta \delta -2} \gamma y^{\delta }}{ - (\beta \delta +1)\left( \beta \delta \gamma \right) ^{-\frac{1}{\beta \delta +1}} y^{-\frac{\delta }{\beta \delta +1}}} \\&= \lim _{y\rightarrow \infty } \frac{\left( y^{\frac{\delta }{\beta \delta +1}}+\frac{x}{\sqrt{ (\beta \delta +1)\left( \beta \delta \gamma \right) ^{\frac{1}{\beta \delta +1}} y^{-\frac{\delta }{\beta \delta +1}}}}\right) ^{-\beta \delta -2} y^{\delta }}{ y^{-\frac{\delta }{\beta \delta +1}}} \\&= \lim _{y\rightarrow \infty } \left( 1+\frac{x}{\sqrt{ (\beta \delta +1)\left( \beta \delta \gamma \right) ^{\frac{1}{\beta \delta +1}} y^{\frac{\delta }{\beta \delta +1}}}}\right) ^{-\beta \delta -2} \\&= 1, \end{aligned}$$

which is sufficient to show that for each $\tilde{x}$, Proposition 2 is applicable with $k_0=2$ on interval $I_{\tilde{x}} := \left[ x_y^*-\frac{\tilde{x}}{\sqrt{-h_y''(x_y^*)}},x_y^*+\frac{\tilde{x}}{\sqrt{-h_y''(x_y^*)}}\right]$. Hence for each $\tilde{x}$, there exists a constant $C_1(\tilde{x})>0$ such that for sufficiently large y,

$$\begin{aligned} y^{-\frac{\delta /2}{\beta \delta +1}} \exp \left( A y^{\frac{\delta }{\beta \delta +1}}\right) \cdot \tilde{\mathcal {I}}_y&\ge y^{-\frac{\delta /2}{\beta \delta +1}} \exp \left( A y^{\frac{\delta }{\beta \delta +1}}\right) \cdot \int _{I_{\tilde{x}}} g_y(x)\,\mathrm {d}x \\&= \frac{C_1(\tilde{x}) \left( \beta \delta \gamma \right) ^{\frac{1}{2(\beta \delta +1)}} }{\sqrt{\beta \delta +1}}. \end{aligned}$$

Using the inequality $2\exp (y) \tilde{\mathcal {I}}_y \le 1$, we must have

$$\begin{aligned} y^{-\frac{\delta /2}{\beta \delta +1}} \exp \left( A y^{\frac{\delta }{\beta \delta +1}}\right) \cdot \frac{1}{2}\exp (-y) \ge \frac{C_1(\tilde{x}) \left( \beta \delta \gamma \right) ^{\frac{1}{2(\beta \delta +1)}} }{\sqrt{\beta \delta +1}} \end{aligned}$$

(15)

for sufficiently large y. Since $0\le \beta <1$, we note that if $\delta <(1-\beta )^{-1}$ then inequality (15) does not hold. So, we derive that $\delta \ge (1-\beta )^{-1}$. $\square$