Abstract
The paper surveys the experimental literature on centralized matching markets, covering school choice and college admissions models. In the school choice model, one side of the market (schools) is not strategic, and rules (priorities) guide the acceptance decisions. The model covers applications such as school choice programs, centralized university admissions in many countries, and the centralized assignment of teachers to schools. In the college admissions model, both sides of the market are strategic. It applies to college and university admissions in countries where universities can select students, and centralized labor markets such as the assignment of doctors to hospitals. The survey discusses, among other things, the comparison of various centralized mechanisms, the optimality of participants’ strategies, learning by applicants and their behavioral biases, as well as the role of communication, information, and advice. The main experimental findings considered in the survey concern truth-telling and strategic manipulations by the agents, as well as the stability and efficiency of the matching outcome.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For a long time, economists have focused on markets where prices coordinate demand and supply. However, in many markets, prices do not determine who receives what. Examples include matching markets such as entry-level labor markets, school choice, university admission, social housing allocation, and kidney exchange. Over the past decades, the study of matching markets has become an active area of research. These markets have in common that agents have preferences over other agents or over objects they can be matched to. For instance, workers have preferences over firms, or students have preferences over universities. Many of these markets are centralized where a clearinghouse collects the preferences from the agents and uses a mechanism to determine the matching which satisfies the designer’s objectives, like efficiency or fairness.
Economists have been involved in re-designing centralized matching markets, canonical examples being the National Resident Matching Program for young doctors in the US (Roth and Peranson 1999) and school choice in Boston (Abdulkadiroğlu et al. 2005). A growing interest in the topic as well as novel questions arising when analyzing existing matching procedures have fueled the rapid progress of research on the topic, and a considerable fraction of this research employs experiments.
This survey provides a comprehensive overview of the experimental literature on centralized matching that is based on the school choice and the college admissions model. It thereby complements the chapter on experiments in market design by Roth (2015).Footnote 1 The two models speak to a number of practical applications such as school choice programs, centralized university admissions, the allocation of public housing, and entry-level labor markets, among others. Almost all of the experiments are lab experiments. Field experiments on matching are faced with the difficulty that the preferences of participants are not known, but we report on two papers that find a way around this limitation (Guillen and Hakimov 2018; He and Magnac 2017). The goal of the survey is not only to summarize the main experimental findings but also to identify what appear to be robust results across studies. To do so, we provide statistics across studies if possible, and also compare the results of related studies. Finally, by grouping the articles into a set of topics, we structure the current state of research.
Experiments are useful tools in the domain of market design for a number of reasons:
-
1.
Experiments can be used to demonstrate problematic aspects of existing mechanisms, also vis-à-vis policymakers. For instance, the large number of participants misrepresenting their preferences in the mechanism that was employed in Boston to allocate school seats has been demonstrated with the help of experiments which helped to convince practitioners. Also, experiments have permitted researchers to identify the causes of market failure, which is often impossible with observational data alone.
-
2.
In many matching markets, the market participants are inexperienced. Thus, the equilibrium predictions that rely on fully rational players might not be in line with actual behavior. Understanding whether a new mechanism is behaviorally robust with the help of experiments is crucial. For example, one of the central themes of market design is whether participants have an incentive to reveal their preferences truthfully and whether they behave in line with this incentive. Experiments play a primary role in testing the theoretical predictions regarding preference reporting. The advantage of experiments is that preferences can be induced by the experimenter, e.g., by assigning monetary payoffs for being matched to different schools, and are therefore fully controlled for.
If the properties of the outcomes of a mechanism are analyzed under the assumption that participants state their preferences truthfully or that they play the equilibrium strategy, this can lead to wrong conclusions regarding the desirability of the mechanism. The efficiency of the allocation has to be calculated based on the true preferences of participants, which are hard to know from field data. Thus, experiments are a handy tool for the comparison of mechanisms, since they allow for testing whether subjects understand the incentive properties of the mechanisms and for comparing allocations based on the true preferences of participants.
-
3.
Experiments enable researchers to identify the factors that influence the agents’ strategies, such as the information available to them about the preferences of other market participants, the size of the market, and so on.
-
4.
Experiments can be used to test a new mechanism before the mechanism is implemented on a large scale with real consequences. By creating counterfactual situations, experimenters can use the lab as a testbed for new mechanisms.Footnote 2
While experiments play an important role for the study of centralized matching markets, market experiments are complex and have many degrees of freedom regarding their design. For example, school choice problems are characterized not only by the preferences of participants, but also by the size of the market, by whether schools have preferences or follow rules when ranking students, the amount of information provided about own and others’ preferences, and the capacities of schools. For this reason and because the literature is still relatively young, there are fewer replications than in other areas of experimental economics. Nevertheless, we believe that there is a lot to be learned from relating the existing work to each other. Thus, we compare experiments that share a number of similarities even if they differ with respect to some other features of the markets. Overall, we find a great level of consistency in the findings with clear patterns of behavior emerging. At the end of each subsection, we provide a short summary of the main findings.
Most of the results that we review concern individual behavior, namely the input of subjects into the mechanisms. The studies consider whether participants report truthfully in strategy-proof mechanisms and manipulate optimally in the ones where manipulations are part of an equilibrium. The rates of equilibrium reporting often have a direct effect on the properties of the resulting allocation. However, different subjects can have a different influence on the allocation with their preference reports. Moreover, subjects often have a weakly dominant strategy of reporting truthfully in strategy-proof mechanisms, and thus not every deviation from truthful reporting influences the resulting allocation. For this reason, some papers (typically papers that compare allocations reached by different mechanisms) study the stability and Pareto efficiency of the matching outcomes. Some papers emphasize efficiency, others stability, depending on the main interest and the mechanisms studied. For instance, if allocations reached under the student-proposing deferred acceptance (DA) mechanism are analyzed, the emphasis is on stability, as DA is predicted to produce stable allocations which do not have to be efficient. In the case of the top trading cycles mechanism (TTC), the emphasis is on efficiency, as TTC is predicted to produce Pareto-efficient allocations that are not necessarily stable.
2 Basic concepts of matching theory
In this section, we provide a brief introduction to the central concepts and results of matching theory regarding the school choice and college admissions models on which the experiments are based. For a thorough and detailed introduction of the theory, we refer the reader to the textbooks by Roth and Sotomayor (1990) for the college admissions model and by Haeringer (2017) for the school choice model.
2.1 School choice model
In the school-choice model, only students have preferences over schools and act strategically, while schools do not have preferences and are not strategic in their choice of students. Therefore, the school choice model is a one-sided matching model. This model can be appropriate for the allocation of seats in public schools, for example. Public schools typically do not have preferences over students but priorities which determine the rankings of agents. Unlike preferences, priorities are determined in advance by law or the mechanism designer and are not strategically reported to the mechanism. Examples are priorities for students who live in the neighborhood of a school, who have a sibling at the school, or based on grades. Importantly, in the school choice model, only the welfare of students is considered. The model also applies to centralized university admissions where students are accepted based on exam scores or school grades, and the allocation of public housing based on priorities, among others.
We call the two sets of agents ‘students’ and ‘schools.’ The students are denoted by i, and the schools are denoted by s. Each student i wants to find a seat at a school s. Thus, each student has a strict ordinal preference over the set of schools (which might include the option of being unassigned). Each school has a maximum quota of students it can accept, qs. A matching is a mapping that assigns each student i to a school s or leaves her unmatched, and it maps school s to student i if and only if student i is mapped to school s. The interpretation is that student i is only matched to school s if she chooses s and is chosen by s.Footnote 3 The total number of students mapped to school s is no higher than qs.
The matching game proceeds as follows: The designer asks all students to report a rank-order list over schools (i.e., to submit their ordinal preferences). The designer also collects information on schools’ priorities over students. The matching mechanism uses these reported preferences and priorities to produce a matching, and the agents are informed about the outcome.
Before turning to the matching mechanisms, we introduce some important properties of matching outcomes. A matching can satisfy elimination of justified envy. The envy of student i toward student j regarding school k is justified if student j is assigned to school k, student i ranks school k higher than her assigned school, and student i has a higher priority than student j at school k. A matching that eliminates justified envy is often referred to as a stable matching. Note that stability is a concept formally defined for the setup when both sides of the market are strategic, but we follow the convention in the literature and use the terms “elimination of justified envy” and “stability” interchangeably in the school choice context. A matching is Pareto efficient if there is no other matching which assigns every student a weakly better match and at least one student a strictly better match.
The mechanism designer is concerned not only with the properties of the allocation but also with the incentive properties of the mechanism. How complicated is it for agents to optimally submit their rank-order lists to the designer? One of the most desirable incentive properties is strategy-proofness. The mechanism is strategy-proof if truthful preference revelation is a (weakly) dominant strategy for strategic agents. Thus, if the mechanism is strategy-proof, an optimal application strategy is straightforward for the agents. They should report their true preferences to the designer in the form of a rank-order list which ensures them the best possible outcome (relative to alternative reports). Once again, in the school-choice model we consider only the incentives of students, since the priorities of schools are assumed to be known.
In the following, we describe the five most important matching mechanisms in the literature. Only one of the five mechanisms presented possesses all three desirable properties: strategy-proofness, elimination of justified envy, and Pareto efficiency. It is the Serial Dictatorship mechanism. However, it can only be used in markets where all agents on one side of the market have the same ordinal ranking of the agents on the other side. In the context of school choice, this implies that all schools rank all students in the same manner, i.e., all schools have the same priority order over students. The other four mechanisms can be used under any preferences but do not possess all three desirable properties. In fact, it has been shown that such a mechanism does not exist (Alcalde and Barberà 1994). The first three mechanisms described, namely DA, School-DA, and Boston, are the most frequently used procedures in school choice and college admissions. The fourth mechanism, TTC, is applied less frequently despite its efficiency.
For the description of the five mechanisms, we use the context of a school-choice problem. Students report their preferences over schools in the form of rank-order lists. The mechanism also receives the rank-order lists of schools (priorities), and the capacities of schools (the maximum number of students each school can admit). The preferences and priorities are strict, and if not, the ties are broken arbitrarily. According to these reports and the priorities, the mechanism produces a matching.
2.1.1 Student-proposing deferred acceptance mechanism (DA)
-
Step 1 Each student applies to the school that is ranked first in her preference list. Each school admits acceptable students up to its capacity, following its priority order. The remaining students are rejected.
-
Step k, k ≥ 2 Each student rejected in the previous step applies to the most-preferred acceptable school among those she has not yet applied to. Each school receiving applications considers the set of students it admitted in the previous step together with the set of new acceptable applicants. From this set, the school admits students up to its capacity, following its priority order. The remaining students are rejected.
-
End The algorithm stops when no student is rejected, or all schools have filled their capacity. Any remaining students are unassigned.
Note that the allocation is temporary at each step until the last step.
The student-proposing DA is strategy-proof for students. Moreover, DA eliminates justified envy, and the outcome Pareto dominates all other envy-free outcomes from the perspective of the students. However, DA is not Pareto efficient.
2.1.2 School-proposing deferred acceptance mechanism (school-DA)
The mechanism receives the rank-order lists of students (preferences), the rank-order lists of schools (priorities), and the capacities of schools (the maximum number of students each school can admit).
-
Step 1 Each school offers seats to students with the highest priority up to its capacity. Each student accepts the best acceptable offer she has received, according to her preference list. The other schools are rejected.
-
Step k, k ≥ 2 Each school rejected in the previous step makes offers to the students with the highest priority among those that have not rejected an offer from the school yet such that the number of accepted offers from previous steps and the number of new offers do not exceed capacity. Each student receiving at least one offer considers the school she accepted in the previous step together with the set of new offers from schools. From this set, the student accepts the school that is highest on her preference list. All other schools are rejected.
-
End The algorithm stops when no school is rejected, or all students have found a seat. Any remaining students are unassigned.
Note that the allocation is temporary at each step until the last step.
The school-proposing DA, or short School-DA, is not strategy-proof. The School-DA eliminates justified envy. However, the School-DA is not Pareto efficient.
2.1.3 Boston mechanism (BOS)
-
Step 1 Each student applies to the school that is ranked first in her preference list. Each school admits acceptable students up to its capacity, following its priority order. These assignments are final. The remaining students are rejected.
-
Step k, k ≥ 2 Each student who was rejected in the previous step applies to the most-preferred acceptable school among the schools to which the student has not yet applied. Each school admits acceptable students up to its remaining capacity, following its priority order. These assignments are final. The remaining students are rejected.
-
End The algorithm stops when no student is rejected, or all schools have filled the seats up to their capacity. All remaining students are unassigned.
Note that the allocation is final at each step of the mechanism.
BOS is not strategy-proof for the students. In Nash equilibrium, BOS eliminates justified (Ergin and Sönmez 2006). However, the equilibrium requires strategic play by the students. If all students report truthfully, BOS produces a Pareto efficient but possibly not a stable allocation (that is, it does not eliminate justified envy).
2.1.4 Top trading cycles (TTC)
-
Step 1 For each student, we point from this student to the school that is the most preferred by that student. If there is no such school, she points at herself, since she prefers to remain unmatched.
For each school, we point from the school to the student who has the highest priority for the school.
There must be at least one cycle of students and schools pointing at each other or a student pointing to herself.Footnote 4 Every student in a cycle is assigned to the school she is pointing to or to herself if pointing to herself,Footnote 5 and is removed. The remaining capacity of each school in the cycle is reduced by one and if it reaches zero, the school is removed.
-
Step k, k ≥ 2 For each student, we point from the student to the acceptable school that is the most preferred by that student among the schools that are still present. If there is no such school, she points at herself.
For each school, we point from the school to the student who has the highest priority for the school among the acceptable students who are still present.
There must be at least one cycle. Every student in a cycle is assigned to the school she is pointing to or to herself and is removed. The remaining capacity of each school in the cycle is reduced by one and if it reaches zero, the school is removed.
-
End The algorithm stops when all students or all schools have been assigned. Any remaining students are assigned to themselves.
Note that the allocation is final at each step of the mechanism.
TTC is strategy-proof for the students. TTC produces a Pareto efficient allocation but it does not eliminate justified envy (Abdulkadiroğlu and Sönmez 2003).
The next mechanism relies on all schools ranking the students in the same way.
2.1.5 Serial dictatorship mechanism (SD)
-
Step 1 The student at the top of the schools’ priorities is assigned to the school at the top of her preference list. The student is deleted from the priority list and the capacity of the respective school is reduced by one. If capacity reaches zero, the school is removed from all the preference lists.
-
Step k, k ≥ 2 The highest remaining acceptable student on the priority list of the schools is assigned to the acceptable school at the top of her preference list.
-
End The procedure terminates when the list of priorities is exhausted, or all schools have zero capacity.
Note that the allocation is final at each step of the mechanism.
SD is strategy-proof for the students, eliminates justified envy, and leads to the Pareto efficient allocation for students. If priorities in SD are determined randomly and not known ex-ante, the mechanism is called Random Serial Dictatorship (RSD).
One important common feature of strategy-proof mechanisms is that the dominant strategy of truthfully submitting the rank-order list is not necessarily unique. One source of the multiplicity of undominated strategies is the presence of guaranteed schools. A school is guaranteed for a participant if it ranks this participant among the top q students where q is the capacity of the school. For this student, the rankings of schools below the guaranteed school are irrelevant for the allocation. Thus, a dominant strategy only requires the truthful ranking of the schools up to the guaranteed school. In experiments where the subjects have a guaranteed school, the truthful submission of the ranking up to the guaranteed school is counted as a truthful submission.
Another important consideration is the multiplicity of equilibrium strategies and equilibrium outcomes. In BOS, equilibrium strategies always result in a stable allocation under complete information (Ergin and Sönmez 2006). In DA, equilibrium strategies result not only in a stable allocation but potentially in the Pareto dominant allocation. This is because some students can allow others to get a better school by not listing that school; at the same time, their assignment is unchanged (see Kesten 2010 for details). Only some markets have equilibrium allocations that Pareto dominate the student-optimal stable allocation.
Much of the experimental work that we review studies the mechanisms above or modifications of these mechanisms. Some articles investigate other mechanisms that we explain in the respective paragraphs.
2.2 College admissions model
The college admissions model refers to a two-sided market. Both sides of the market, namely students and colleges, are strategic players. The model covers applications such as college admissions where the preferences of the colleges determine the acceptance of students like in the US, and centralized labor markets, like the entry-level labor market for doctors in some countries. When studying two-sided markets, the incentives and welfare of both sides, students and colleges, are considered. Thus, in the college admissions model each college has a strict ordinal preference over the set of students (which includes only the list of acceptable students) and wants to accept at least one student. A matching is Pareto efficient if there is no other matching which assigns every agent (student or college) a weakly better match and at least one agent a strictly better match.
A matching is stable (1) if every agent prefers the assigned matching partner to remaining unmatched, i.e., the student is matched to a college that she prefers to being unmatched, and the college is matched only to acceptable students, and (2) if there is no college–student pair such that each prefers one another to their respective match. Stability is important because it precludes situations where students and colleges would like to avoid being matched through the clearinghouse.
The incentives of both colleges and students must be considered in the college admissions model. Note, however, that there is no stable mechanism that is strategy proof for both sides of the market (Roth 1982). Note that the mechanisms described above for school choice can be modified in a straightforward manner to be applicable in the college admissions model: the mechanism asks colleges to report preferences over students and uses these reported preferences instead of the schools’ priorities. This, however, can change the properties of the resulting matching. We discuss these differences at the beginning of Sect. 5, before reviewing the experiments on college admissions.
In the next two sections we survey experiments on the school choice and the college admission model. Appendix A briefly presents methodological aspects of the design of such experiments.
3 Experiments on one-sided matching: the school choice model
By far the largest part of the experimental literature on one-sided markets deals with the school choice model.Footnote 6 In school choice problems, the schools are assumed to be non-strategic, and welfare considerations only apply to the students. The following theoretical predictions have been studied experimentally:
-
1.
The DA and the TTC mechanism are strategy-proof while BOS and School-DA are not.Footnote 7
-
2.
The DA and School-DA mechanisms eliminate justified envy while TTC and BOS with truthful preference revelation do not.
-
3.
TTC is Pareto efficient as is BOS with truthful preference revelation but DA and School-DA are not.
-
4.
Under BOS, the Nash equilibrium outcomes with complete information eliminate justified envy but are not Pareto efficient.
3.1 Comparison of mechanisms
The literature starts with the seminal paper of Chen and Sönmez (2006). The experiment studies preference reporting under three alternative mechanisms, namely BOS, DA, and TTC, and compares the outcomes of these mechanisms from the perspective of efficiency and stability. BOS is used as a natural baseline, since it was actually used for school choice in Boston and New York. DA and TTC are the two leading mechanisms suggested by economists. The experiment was run in class and was paper-based. This allowed the authors to run fairly large markets, namely 36 participants competing for 36 seats in seven schools.
For the preference profiles, the authors used two alternative environments. The ‘designed’ environment was aimed at capturing realistic preferences. In order to do so, each student’s ranking of the schools was generated by a utility function which depended on the school’s quality, proximity, and a random factor. The utility derived from the quality of the school was common for all students. To determine the utility from proximity, the authors first determined a district school for each student. Each student received utility from the proximity of this school. In the second environment the preferences were randomly determined, and this environment was used as a robustness check. Based on the resulting rankings, fixed payoffs were assigned to each rank, such that there was no difference in the cardinality of preferences. As for priorities of schools, in both environments the highest priority was given to district students, and for all other students the priorities were determined by a lottery. This ‘designed’ environment was employed in many subsequent school choice experiments.
With the three matching mechanisms and two preference environments, the experiment by Chen and Sönmez (2006) follows a 3 × 2 design. The six treatments were run between subjects, meaning each subject participated in only one mechanism in one environment. The experiment involved incomplete information in that subjects in the experiment knew which school was their district school and could observe their own preferences but they had no information about the preferences of the other students. The experiments were one-shot, meaning each subject played the game just once.
The main result regarding individual behavior is in line with the theoretical predictions: in both the designed and random environments, the proportion of truthful preference revelations under BOS was significantly lower than the proportion of truthful preference revelations under either DA or TTC.Footnote 8 This is one of the main insights of the paper, which was replicated in almost all subsequent studies on school choice. Additionally, it turned out that despite the strategy-proofness of both mechanisms, the proportion of truthful reporting was significantly higher in DA than in TTC, especially in the designed environment. The finding is surprising, since both mechanisms are strategy-proof. However, subsequent papers show that it is not robust to other environments and settings.Footnote 9
The authors also identified a common tendency in the manipulated reports, the “district school bias.” It refers to the finding that the district school (or safe school) is ranked higher in the reported list than in the true preferences. In BOS, 75.1% and 59.6% of subjects displayed the district school bias in the designed and random environments, respectively. As for the analysis of allocations, recombinant estimation is used with 200 recombinations per subject (Mullin and Reiley 2006), following the original suggestion by Mullin and Reiley (2006) of at least 100 recombinations.Footnote 10 The results of the recombinant estimation show a significantly higher efficiency of allocations in DA mostly due to higher rates of truthful reporting. However, a subsequent analysis of their data by Calsamiglia et al. (2011) show that all mechanisms lead to similar efficiency levels when using larger number of recombinations (up to 100,000 per subject). Note that the experimental design with an assignment of identical cardinal utilities to the first rank, the second rank, etc., precludes efficiency gains in BOS due to the possibility to express preference intensities.
One controversial design feature of the experiment by Chen and Sönmez (2006) is the decision to provide no information about the preferences of other students. Note, however, that this is only relevant for BOS but should not matter for DA and TTC since both mechanisms have dominant strategies. While the participants of school choice procedures in practice most likely do not know the exact preferences of their peers, it seems unlikely that they do not know anything about others’ preferences. Often parents know which schools are more popular than others. Pais and Pintér (2008) investigate the effect of providing richer information for participants. However, they implemented a smaller market than Chen and Sönmez (2006), with five teachers competing for seats in three schools. In their 3x4 design, three mechanisms—namely BOS, DA, and TTC—were run under four different information conditions between subjects.Footnote 11
Pais and Pintér (2008) replicated the result of Chen and Sönmez (2006) that truthful preference revelation is higher in DA and TTC than in BOS in the same information condition as Chen and Sönmez (2006), namely their low information treatment, as well as in two other information environments with more information provided about the preferences of other participants. In the zero-information environment when students knew only their own preferences and did not know the priorities of schools, there was no difference between the mechanisms with respect to truth-telling. The main take-away from the experiment is that subjects reacted to the additional information about the preferences of others and the schools’ priorities by misrepresenting their preferences more frequently in all mechanisms. While the effect was strongest in BOS, it was also significant in DA and TTC. The findings for DA and TTC are not predicted by the theory and can be interpreted as suggesting that truthful revelation in the incomplete information environment represents an upper bound. The truth-telling rate in DA was just 66.7% (both with full and partial information), while it was 75% in TTC (partial information). Note that unlike in Chen and Sönmez (2006), TTC had, on average, a 12% higher rate of truthful reporting than DA in all treatments, with the difference being significant in three out of four environments.
The provision of information was also detrimental for the efficiency in BOS and DA but not in TTC. Regarding comparisons across mechanisms, TTC led to a significantly higher efficiency of allocations than DA and BOS in the partial and full information conditions. Moreover, the provision of information did not have an effect on the stability of allocations. As predicted, DA led to the highest rates of stable allocations but the difference is only significant in three out of four information conditions relative to TTC and two out of four information conditions relative to BOS. Despite its worse performance under complete information, DA still outperforms BOS in Pais and Pintér (2008) at least weakly from the perspective of truth-telling and stability.
In a later paper using exactly the same environment as Chen and Sönmez (2006) but with complete information, Chen et al. (2016) study the effect of students being informed about other students’ preferences, school priorities (including tie-breakers) and capacities. They find truth-telling to be highest in TTC, followed by DA and then BOS. Overall, information improves the performance of TTC and BOS while leaving DA unchanged. In line with the theory and with Pais and Pintér (2008), TTC is the best mechanism regarding efficiency, and DA outperforms the other two mechanisms with respect to stability.
Many Chinese provinces use a hybrid mechanism between DA and BOS—the so-called parallel mechanism (Chen and Kesten 2017)—which has been studied experimentally by Chen and Kesten (2019). The parallel mechanism uses choice-bands. The size of a choice-band determines the number of colleges a student can list per band. The algorithm is run for each choiceband separately, starting with the first choice-band. Within a choice-band all assignments are tentative while they are final once a student is either assigned to a school in the choice-band or has been rejected by all his choices in this choiceband. Then, the algorithm proceeds to the next choice and where another set of seats is allocated. Thus, both BOS and DA are nested in the parallel mechanism with choice-band sizes of 1 and infinity, respectively. The experiments are designed to test the theoretical predictions of Chen and Kesten (2017) with respect to the effects of the size of the choiceband on the amount of truth-telling, efficiency, and stability.
In a complete information environment with markets of either four or six schools, it is found that the parallel mechanism with two schools per choiceband induces truth-telling rates that are between those of BOS and DA, in line with the theory. With respect to efficiency, the results depend on the exact environments studied, and there is no clear ranking of the mechanisms, as predicted. Finally, the observed stability of the matchings again supports the theory, with DA leading to more stable matchings than the parallel mechanism and BOS. The parallel mechanism induces (weakly) more stable matchings than BOS, depending on the markets considered. Thus, one can interpret the findings of the intermediate performance of the parallel mechanism as a successful robustness check for the superior performance of DA relative to BOS with respect to truthful reporting and stability. An important difference to other papers is that the authors pay close attention to other equilibria of the game. For instance, in the four-school market, there is a Pareto-dominant outcome relative to the stable outcome. It can be reached in the equilibrium of both the parallel mechanism and DA, but not in BOS. The authors observe that the stable equilibrium is played more often than the Pareto-dominant equilibrium. However, the Pareto dominant-equilibrium is played more often at the end than at the beginning of the experiment. In a closely related paper, Chen et al. (2017) replicate the finding of Chen and Kesten (2019) for the setup of six colleges with identical priorities over students, a characteristic of Chinese college admissions that are solely based on the centralized entrance exam. Moreover, the authors show that their theoretical and experimental findings are in line with data from the Sichuan province of China where BOS was changed to the parallel mechanism: students started to list more colleges, and the prestigious colleges were ranked as a top choice more often.
The comparison of DA and BOS holds up in larger markets where the number of schools is kept constant but the number of students is 40 or 4000 (Chen et al. 2018). In these experiments, some students are played by robots that use the strategies of real subjects who participated in previous sessions. More details about the experiments of Chen et al. are presented in the next subsection.
Dur et al. (2018c) introduce another mechanism, the secure Boston mechanism (secure BOS), which can be understood as an intermediate mechanism between BOS and DA, just like the Chinese parallel mechanism. The authors note that BOS can be seen as a version of DA that is run on the modified priorities of schools according to the preference reports of students, such that the students who rank a school first move to the top of the priority list of that school. The secure BOS mechanism also modifies the original priorities of schools but keeps the most-preferred students of each school up to its capacity at the top of the priority list, independent of how students rank the school. The secure BOS runs DA on the modified priority lists. The secure BOS is not strategy-proof but it is less manipulable than BOS. The intuition is that the students still have seats in their district schools guaranteed for them, even if they do not rank them first. The authors compare BOS and secure BOS in the lab, in a setup where experimental subjects play against computerized players. Subjects knew the top choices submitted by the computer players. In line with the theoretical predictions, secure BOS led to fewer manipulations than BOS. However, the rates of truthful reporting were rather low with 28.4% and 17.1%, respectively. Secure BOS led to fewer instances of justified envy than BOS.
The experiments of this subsection demonstrate that the concerns regarding the manipulability and the inferior outcomes of BOS find support in the lab. TTC and DA appear to be superior mechanisms although the absolute levels of truth-telling and the decrease in truth-telling the more information is provided have raised concerns of whether the properties of DA and TTC are transparent enough for the participants. Evidence regarding this question comes from an experiment by Guillen and Hakimov (2017). The authors use TTC in a setup where students play against computers in a matching market of four schools and four students. In every market three students are played by computers, and one student is represented by an experimental subject. Each subject had to make two decisions. In the first decision subjects knew the preferences of the computer players and they were told that the computer players submitted their rankings truthfully. In the second decision, subjects were provided with different partial information on the possibly non-truthful strategies of computer players depending on the treatment.Footnote 12 The two decision problems were presented on the same screen, so participants made both decisions simultaneously. While a great majority (85% of subjects) reported truthfully in the first situation, the rate of truth-telling was dramatically lower in the second decision. Only 31% of subjects were truthful in both decisions. Thus, the experiment demonstrates that subjects do not perceive truth-telling as a dominant strategy but are influenced by the behavior of others. This lends support to the concern that understanding the incentives of TTC and possibly other strategy-proof mechanisms is not straightforward for the participants.
A recent paper by Guillen and Veszteg (2019) tests whether the observed truthful reporting in DA and TTC in experiments can be attributed to participants understanding that it is a dominant strategy. They run one-shot incomplete information experiments with each participant playing against three computer players. There are four schools, with one seat each, and four students, competing for these seats. They run four treatments between subjects. The first two treatments are DA and TTC. The other two are reverse versions of DA and TTC. In the reversed versions of the mechanisms, the applications are considered from the bottom to the top of the list. Thus, it is a weakly dominant strategy to submit the preferences in the reverse order, listing the best school at the bottom of the list and so on. The authors find much higher rates of rational behavior in DA and TCC relative to the reverse version of the mechanisms, which suggest that some of the subjects play the dominant strategy of truthful reporting as a default strategy, without understanding the incentive property of the mechanisms. The paper emphasizes the importance of extensive training and explanations of the mechanisms before implementing them in practice.
While lower truth-telling rates under BOS relative to DA were found in almost all studies, it is possible that the strategies played in BOS are in line with the equilibrium prediction. This is crucial given the theoretical results of Abdulkadiroğlu et al. (2011), showing that the equilibrium of BOS can dominate DA from an ex-ante efficiency perspective, since it allows the students to express their cardinal utilities through the strategies played in BOS. Featherstone and Niederle (2016) run experiments comparing DA and BOS in two different environments. All results are presented for the last five rounds of each environment. In the environment with correlated preferences where BOS has a unique equilibrium in non-truthful strategies, only 42.9% of the reports were consistent with the unique pure-strategy Bayes–Nash equilibrium in BOS. Moreover, 40% of reports were truthful under BOS, which is significantly lower than 80% of truthful reporting under DA. However, in the environment with uncorrelated preferences, BOS admits truth-telling by all students in the ordinal Bayes-Nash equilibrium. The results show that in this environment the truth-telling rate under BOS is 58%, which is not statistically different from 66% of truthful reports under DA, resulting in a higher efficiency of BOS. The authors interpret this result as a proof of concept that non-strategy-proof mechanisms with a truthful ordinal Bayes-Nash equilibrium might succeed in practice. As for DA, the truth-telling rates were 66% in the uncorrelated environments and 80% in the correlated environment.
Figure 1 presents the proportions of truth-telling across experiments. We include all papers from this section that compare at least two of the three main mechanisms, namely BOS, DA, and TTC. It also includes Calsamiglia et al. (2010) which is discussed in Sect. 3.5.
Rates of truthful reporting by mechanisms. Notes: All studies are run with full information unless otherwise indicated. For experiments with repeated play, the average over all rounds is reported. While ‘des’ stands for the designed markets, ‘random’ denotes markets with randomly generated preference profiles. The correlation of preferences is varied (aligned or uncorrelated), as is the number of schools. Calsamiglia et al. (2010) is discussed in detail in Sect. 4.5
3.1.1 Summary
Most studies find that the truth-telling rates under BOS are lower than under strategy-proof mechanisms. The comparison of truth-telling rates under DA and TTC is inconclusive. Moreover, most manipulations in BOS do not represent equilibrium play. DA mostly outperforms the other mechanisms in terms of stability while the comparison of mechanisms with respect to efficiency is inconclusive and depends on the environment. In spite of the relative success of the strategy-proof mechanisms DA and TTC, the sensitivity of the rates of truthful reporting to the information provided and to the market environment raises concerns regarding the successful implementation of these mechanisms in practice. One possible explanation of the relatively low truth-telling rates under the strategy-proof mechanisms DA and TTC is the absence of experience. The next subsection reports evidence on learning in BOS and DA.Footnote 13
3.2 Learning and effect of market size
This subsection focuses on the dynamics of the subjects’ reports in experiments where they play DA or BOS repeatedly. Most of the papers mentioned in this subsection do not focus on learning but they employ multiple rounds of matching markets such that the data can be used to study learning.
The baseline treatments of Ding and Schotter (2019) include repeated play of BOS and DA for 20 rounds. The market consisted of five students competing for three schools. The participants knew their own preferences and the priority schools of all students but not the preferences of other students. The group was randomly re-matched and the ties in priorities were broken randomly in every round. The authors found a significant increase in truthful reporting in DA, from 65 to 77%, over 20 rounds. There was no significant change in the efficiency of the allocations, with a slight decrease of efficiency with experience. Note that efficiency may be in conflict with stability, which is why an increase in truthful reporting does not necessarily translate into higher efficiency. There was no increase in truth-telling in BOS, which can be expected since truth-telling is not a Nash equilibrium strategy. However, experience did not increase the efficiency of the allocation reached in BOS either.
In the baseline treatment of Chen and Kesten (2019), subjects played DA and BOS for 20 rounds, in either a four-school environment or a six-school environment. The experiments were run under complete information, where both the preferences of other players and the priorities of schools were known to participants. In the four-school environment, there was no significant learning under DA but the truth-telling rates were relatively high at around 75% on average. Note, however, that in this environment, there was a Pareto dominant allocation relative to the student optimal stable matching, and it could be reached by two out of four players manipulating their preference reports. Indeed, the authors observe that the Pareto dominant allocations are more often reached toward the end of the experiment. This could explain the absence of earning to choose the truthful strategy. As for the six-school environment, truth-telling under DA was lower at 47% on average, and there was a significant negative effect of experience on truth-telling. Note again that in the complete information environment, many strategies can be equilibrium strategies. Chen and Kesten (2019) show that despite the decrease in truth-telling, almost all strategies in DA were best-responses, and they resulted in 79% of allocations being equilibrium allocations. As for BOS, the truth-telling rates were lower than under DA in both environments (46% and 23%, respectively, in the four-school and the six-school environment), and experience had a slightly negative effect that was significant only in the four-school environment.
In the baseline of Zhu (2015), subjects played DA for 15 rounds under complete information about preferences and priorities. The experiments were run in two environments. Each environment had three students and three schools with one seat each. In the first environment, there were no conflicts between top choices (uncorrelated preferences), and in the second environment preferences were correlated. Results show significant learning in both environments, with truthful reporting rates reaching around 75% in the final rounds of the experiment. Finally, in the baseline of Bó and Hakimov (2020a) subjects played DA for 20 rounds. The preferences were generated anew every round, following a procedure inspired by the designed markets of Chen and Sönmez (2006). There were eight students and eight schools with one seat each in every round. The authors found a significant increase in truthful reporting when comparing the first 10 to the last 10 rounds of the experiments. Experience had a positive effect on truth-telling rates which increased from 38% in the first five rounds of the experiment to 56% in the last five rounds.
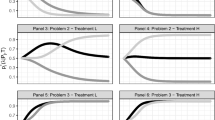
Figure 2 presents the average rates of truthful reporting in all studies using repeated DA, and the dynamics of truthful reporting by rounds. Summing up, the majority of studies find some evidence in favor of learning to report truthfully. There is an increase in truthful reporting in all but two studies, namely Chen and Kesten (2019) in the six-school environment and Chen et al. (2018) in environments with 40 human players. However, the levels of truth-telling vary between the studies.
One might conjecture that the longer the list to submit, that is, the more schools to choose from, the lower the truth-telling rates are. This conjecture is supported by Chen and Kesten (2019) when comparing the four-school environment to the six-school environment.Footnote 14 It is also in line with the levels of truthful behavior between the studies. For instance, all of the studies with high rates of truth-telling in Fig. 2 have three or four schools to be ranked, while Bó and Hakimov (2020a) with eight schools, Chen et al. (2017) with six schools, and Chen and Kesten (2019) with six schools display the lowest average truth-telling rates.
Figure 3 presents the regression of truth-telling on the number of schools that can be ranked for nine studies with at least 15 rounds of play. We chose 15 rounds, since this is the minimum length of matching experiments with repeated play, as can be taken from Fig. 2. The coefficient for the length of the list is significant and negative. Nevertheless, due to many differences between the studies, this evidence is merely suggestive and might be worth testing systematically. Also, it is an open question as to why this relationship seems to hold, e.g., whether it is due to random choices by some subjects, implying that the longer the rank-order lists, the lower the probability of randomly picking the truthful strategy.
The effect of market size on behavior and on the properties of the allocation under DA and BOS are studied in the experiments of Chen et al. (2018). The authors keep the length of the rank-order list fixed (four schools) but increase the size of the match by increasing the number of students and the number of seats in each school. One environment replicates the four-school environment of Chen and Kesten (2019). The other two environments increase the number of students to 40 and 4000, alongside increasing the number of seats in each school to 10 or 1000. Note that the number of students is increased by creating 10 or 1000 students for each preference type of students in the four-school environment of Chen and Kesten (2019). To make the large-scale experiment possible, the authors run some treatments where students interact with robots. Robots either play the empirical strategies of other subjects or they report truthfully, depending on the treatment. The results show that in all environments the truth-telling rates under DA are higher than under BOS, while the proportion of students exhibiting justified envy is lower under DA than under BOS. No difference between mechanisms was found regarding efficiency. The theory predicts that the scale should not influence the subjects’ strategies under BOS and DA. It is found that the increase in the scale from four to 40 students has a weakly significant and positive effect on truth-telling under DA and a significant negative effect on truth-telling under BOS. The increase from 40 to 4000 students has a positive effect on truth-telling under DA and a negative effect on truth-telling under BOS but these effects are not statistically significant. There is a small negative effect of the increase in market size from four to 40 on efficiency under both mechanisms but no effect on stability. Finally, strategies of subjects are not significantly different whether they are playing against human subjects or robots whose strategies are drawn from empirical human strategies, keeping the size of the market fixed at 40.
3.2.1 Summary
The majority of studies find a positive effect of repeated play on truthful reporting under DA. The number of schools, i.e., the length of the rank-order list, can partially explain the variation in truth-telling: the longer the list, the lower the truth-telling rates. If the size of the market grows by increasing the number of school seats and students while keeping the number of schools fixed, this has a weakly significant positive effect on truthful reporting under DA. Thus, the overall effect of market size is unclear: an increase in market size while keeping the number of schools fixed if at all has a positive effect on truth-telling under DA but an increase in the number of schools has the opposite effect. This raises the question of how these two effects interact, since real-life markets tend to be much larger than typical experimental markets along both dimensions.
The commonly observed misreporting in strategy-proof mechanisms begs the question of whether advice and communication between players can improve outcomes. This is discussed in the next subsection.
3.3 Nudging, chatting, and advice
An important aspect of market design is how the rules of the market are explained to the participants and what information they receive about the strategic properties of the mechanism. Experimental economists usually refrain from pointing out the optimal choice or the Nash equilibrium to participants but this maxim does not necessarily hold for experiments in market design. The reason is that explanations and advice are part of the design of markets, and experiments can be useful for testing the effectiveness of providing such advice. For example, some studies explore systematically how participants can be taught to state their true preferences under a strategy-proof mechanism.
The first experimental paper on advice given to subjects in matching markets is the paper by Guillen and Hing (2014). The subjects played against three computer players under the TTC mechanism. In the baseline, they submitted their preferences in a one-shot game. In the other three treatments, the subjects received advice from a third party before submitting their preferences. This advice was either correct (report truthfully), wrong (think about realistic schools), or both pieces of advice were given at the same time. The advice was framed as advice from a third party in order to avoid experimenter demand effects and possible concerns regarding deception. Subjects were told that the information was found in a newspaper, or on parental forums, or was spread by word of mouth. The information given to the subjects was not deceptive, since the wrong advice was indeed taken from the Boston school board forum of parents. In all three treatments with advice, the effect on truthful reporting was detrimental. While the percentage of truthful reports was above 70% in the baseline without advice, it was only 50% in the case of correct advice, 28% in the case of wrong advice, and 42% in the case of both types of advice. The differences to the baseline treatment without advice are significant in the treatments with wrong advice and with both pieces of information, while only marginally significant in the case of correct advice. The most puzzling result of the paper is the negative effect of correct advice on truth-telling. Possibly, the subjects became suspicious due to the source of the advice that was indicated to them. Moreover, the detrimental effect of two contradicting pieces of information on truth-telling points to the possibility that participants find advice in favor of manipulations more convincing than advice to report truthfully. The study highlights the importance of understanding how correct advice should be given to participants when they also receive wrong advice from their peers.
Another study on the effect of advice in TTC was conducted by Guillen and Hakimov (2018) in a field setting. The topics of semester projects were allocated among students in a microeconomics course. In order to identify the preferred topic of each student among three possible topics, the authors first asked the students to choose their most-preferred one. Later, the instructor announced that the distribution of choices was not satisfactory and an allocation procedure had to be used. In the baseline treatment, the students received the usual experimental instructions about TTC with an explanation of the mechanism. In the second treatment, they were additionally given advice to report truthfully. In the third treatment they only saw the advice without learning the details of the mechanism. Contrary to Guillen and Hing (2014), the advice to report truthfully significantly increased the rate of truthful reporting from 81 to 94%. Interestingly, the disclosure of the mechanism reduced the rate of truth-telling among a subsample of subjects. Because the advice was given in a natural setting by the instructor of the course, it may have come across as more natural and credible. However, a positive effect of advice has also been observed in a lab experiment. Braun et al. (2014) explained to their subjects the strategy-proofness of DA (and made available a verbal explanation of the proof), which led to more truthful reporting than in the treatment without advice. Thus, the source and the framing of the advice seem to matter.
Koutout et al. (2018) replicate the designed environment of Chen and Sönmez (2006) in the baseline under BOS and DA, and introduce strategic advice for both mechanisms in the main treatments. In DA with advice to report truthfully, the proportion of subjects reporting truthfully is 19 percentage points higher than in the baseline without the advice, and this difference is statistically significant. In BOS the advice included the statement that the truthful strategy was risky; instead, one of the following two strategies was suggested: the risky strategy of ranking the true top choice first and ranking the district school second, or the safe strategy of ranking the district school first. The advice led to a significant increase in the proportion of subjects who played the advised strategy and a significant decrease in the proportion of subjects who submitted their preferences truthfully. Note that under DA advice decreased the number of blocking pairs but slightly decreased the average payoff due to the conflict between stability and efficiency. Under BOS advice led to an increase in the number of blocking pairs and a decrease in efficiency.
In real markets, advice is often given by peers. Parents in school choice programs consult with other parents participating in the mechanism or with parents whose child had participated in the program in previous years. Ding and Schotter (2017) studied how the possibility to chat before submitting one’s preferences to the system influences the reports and the market allocation in DA and BOS. Each subject took two decisions in the experiment. The first decision was taken individually and the second was taken after chatting with other subjects. Either the participants chatted with other participants (three or five) with the same preferences, or with other participants who had different preferences. The main result is that with both chatting protocols, chatting increased the likelihood of subjects changing their reports which led to, on average, higher payoffs of subjects who chatted relative to those who did not chat both in DA and BOS. However, chatting had no significant effect on truth-telling under both mechanisms. Finally, there was no difference between truth-telling rates under BOS and DA in both phases.
In a companion paper, Ding and Schotter (2019) investigate the effect of intergenerational advice by mimicking the communication between parents about their strategies with previous cohorts of parents. In the experiment subjects played either DA or BOS. The other dimension of treatment variation was the source of learning: subjects either played the same mechanism repeatedly for 20 rounds, or received advice from the previous generation of players but played the mechanism only once. In this intergenerational advice treatment, right after learning about their allocation the subjects were asked to give advice to the next group of participants. To incentivize them to give payoff-maximizing advice, subjects earned 50% of the payment of the subject to whom they gave the advice. Contrary to the increase in truth-telling rates when DA is played repeatedly, intergenerational advice led to a significant decrease in truthful reporting from 72% in the first five rounds to 44% in the last five rounds. In BOS, in contrast, the advice increased truthful reporting. In both DA and BOS, advice strongly increases the probability of the advised strategy being chosen. Based on a structural estimation, the authors find that any advice, even the advice to choose a dominated action, increases the probability of playing the advised strategy. Returning to the question of how convincing a certain piece of advice is, the advice to play the most frequent non-truthful strategy, namely exchanging the top and the second most-preferred choices in the reported lists, is followed most often. Based on a simulated model of how subjects follow the advice, the authors estimate that advice increases the probability of playing the strategy from 32 to 74%, i.e., by 42 percentage points, while correct advice increases the probability of truthful reporting from 54 to 88%, i.e., by 34 percentage points. Note that in the experiment each subject received only one piece of advice, and these numbers are based on a between-subjects comparison.
Rees-Jones and Skowronek (2018) conducted a large experiment with medical students immediately after their participation in the medical residency match (NRMP) that relies on the DA mechanism. Unlike the other papers which implement advice in experiments, the authors investigate the effect of advice by surveying participants about the advice received in the NRMP. After participants submitted their rank-order lists in the experiments, they were asked whether they had received advice from the medical school, the NRMP, or other students, and if so, which kind of advice was given. The NRMP website turned out to be the most reliable source regarding the content of advice, as 75% of students who reported receiving advice from NRMP report the correct advice. Other sources often provided mixed—correct and wrong—advice. Although these estimates do not separate the causal effect of advice from selection effects related to who seeks advice, the positive effect of receiving correct advice from NRMP on truthful reporting is in line with the field evidence of Guillen and Hakimov (2018).
3.3.1 Summary
In all but one study the correct advice increased the rates of truthful reporting. However, there is evidence that the subjects are more likely to follow the wrong advice, namely to manipulate their preference reports, than the correct advice to state their preferences truthfully. Thus, two challenges emerge regarding the provision of advice in practice. First, it is essential to make sure that the advice coming from officials (the clearinghouse, schools, or hospitals) is correct, since it has a significant effect on choices. Second, it is necessary to deliver such advice effectively in order to make sure that it is more convincing than the advice of peers that can be wrong. The latter is a challenging empirical question that invites further research.
3.4 Determinants of reporting strategies: biases, risk aversion, and cognitive ability
The papers presented in the previous subsections demonstrate that a substantial share of subjects misreport their preferences under DA, despite experimental treatments aimed at limiting the submission of dominated strategies. In this subsection, we try to take a closer look at the types of strategies subjects used, and we survey possible determinants of truth-telling and manipulations that have been investigated in the literature.
Chen and Sönmez (2006) identified three types of biases that subjects display: a district school bias, a small school bias, and a similar preferences bias. The district school bias refers to a participant putting her district school higher up on the reported list than its position in the true preference order. Under BOS, the district school bias can be part of an equilibrium strategy. Participants with a small school bias move smaller schools down to a lower position than in the true preference order. Participants with a similar preferences bias put schools with the highest payoffs into lower positions. This manipulation is interpreted as subjects assuming that other subjects have the same or similar preferences. Note that in their experiments, the participants did not know the preferences of others, nor the degree of the correlation of preferences.
In the experiments of Chen and Sönmez (2006), almost two-thirds of subjects misreported their preferences in line with the district school bias under BOS.Footnote 15 Note that in the majority of cases the biases cannot be uniquely identified, which explains why the following proportions do not add up to 100%. As for the strategy-proof mechanisms, the district school bias was consistent with 29.8% and 31.5% of the misreported lists in the designed and the random environment under DA, and with 58.4% and 56.2% of the misreported lists in the designed and the random environment under TTC. The respective numbers for the small school bias are 84.9% and 59.5% for DA, and 91.8% and 46.4% for TTC. The numbers for the similar preferences bias are 84.9% and 62.6% in DA, and 80.6% and 75.6% in TTC.
Pais and Pintér (2008) study the district school and the small school bias. In their allocation problems, the small school bias and the similar preferences bias coincide, since the small schools are the most competitive. In the full information environment under DA, the district school bias was found in 17.8% of reported lists and, in addition, 8.9% of the lists were consistent with both the district school bias and the small school bias. Overall, the district school bias can explain 80.2% of misreported lists. In the full information environments under TTC, 8.9% of lists were consistent with the district school bias, which explains 67% of all misreported lists.
Despite the high percentage of reports under strategy-proof mechanisms that are explained by the small school bias and the similar preferences bias, a number of studies concentrate on the district school bias. One reason is that it is in line with the typical strategic advice given to participants for BOS in school choice procedures. Another reason is that many studies employ markets where all schools have the same number of seats such that there are no small and big schools.
Unlike previous studies, Guillen and Hakimov (2017) found that only around 10% of manipulations in TTC are in line with the district school bias. One reason for the relatively small percentage of district-school bias manipulations might be that the district school was always at the bottom of the true preference list. The switch of the top two choices was the most common misrepresentation, which seems to be in line with the similar preferences bias of Chen and Sönmez (2006). However, the experiment by Guillen and Hakimov reveals that the cause of these misreports must be a different one. In Chen and Sönmez (2006), subjects did not know the preferences of other subjects, and thus the authors attributed the switch of the two top choices to the similar preferences bias, since they assumed that these switches were driven by the belief that participants might have similar preferences. In the case of Guillen and Hakimov (2017), the participants knew the other subjects’ preferences and there was no conflict of top choices. Thus, the switch of the two top choices cannot be easily rationalized.
Further evidence of such irrational choices comes from the experiment by Ding and Schotter (2017) in which three out of five players have their district school as their second most-preferred school. First, they find that 57% of these players submitted preferences in line with the district school bias in the second phase of the experiment, which explains 96% of their misreports. Again, note that these submissions are also in line with the similar preferences bias, as the players have the same most-preferred school. Second, the other two player types vary their reports in a manner that allows us to distinguish between the similarity of preferences bias and an irrational choice that cannot be rationalized by beliefs about other students’ preferences. Both types had no priority at their second choice and reported it first on their list 60% and 52% of times, respectively. For the type who reported the second choice first in 60% of the cases, the true second choice was not popular among other players, while for the type who misreported in 52% of the cases, it was the most-preferred choice of the other players. This is again evidence that the switch of the two top choices cannot be rationalized by the similarity of preferences bias. Note that these manipulations are also not in line with the district school bias.
More evidence of switching the first and the second preference comes from Klijn et al. (2013). They study the effect of preference intensities and risk aversion on application strategies under DA and BOS. Three participants competed for three seats in three schools. The payment for receiving the first choice and the last choice was fixed, while the value of the middle option changed between the treatments by being either closer to the top choice, in the middle between the top and the last choice, or closer to the last choice. The safe school (the analogue of the district school) was always the least preferred by the subjects. In DA, 53% of reports were truthful, and this proportion did not vary significantly between treatments with different preference-intensities. Between 6 and 14% of reports under DA were in line with the district school bias while the majority of misrepresentations were switches of the first and second choices. Since all three participants had different most-preferred schools, once again these strategies are only consistent with irrational choices and not with the similarity of preferences bias. The frequency of this switching strategy was 34% but varied between conditions: it was 19% when the relative value of the second choice was the lowest and 43% when it was the highest. Thus, the higher the value of the second choice, the more frequent the irrational switching choices were and the less truthful reporting was observed. A similar tendency of switching first and second preferences was observed in BOS, where this strategy can be in line with equilibrium. Moreover, the authors found a positive correlation between risk aversion (the switching point in the Holt and Laury task) and the propensity to submit the truthful strategy in DA. Note, however, that the effect was mostly driven by extremely risk-averse subjects who switched to the less risky option in the Holt and Laury task with a 90% or higher probability of winning. The effect of risk aversion on the propensity to misreport in TTC was also studied by Guillen and Hakimov (2017), and no correlation of misreporting in TTC with the measure of risk aversion was found. Basteck and Mantovani (2018) show a positive correlation of risk tolerance with payoffs in BOS.
To investigate the reasons for biased choices, several studies include some measure of the cognitive ability of the subjects. Guillen and Hakimov (2017) use the CRT and Wonderlic tests to measure cognitive ability. They find that subjects who performed well in these tests were more likely to report the preferences truthfully under TTC. Basteck and Mantovani (2018) study whether students with lower cognitive ability are disadvantaged in BOS. The authors classify subjects as being of low or high ability based on their performance in a Raven matrices test as compared to the median performance in this test. In order to make the preference profiles uncorrelated with ability, they assigned preference profiles to students such that half of the students with each preference profile were of low ability and half were of high ability. Under BOS, low-ability subjects are more likely to report truthfully than their high-ability peers, while under DA they are less likely to do so. This led to higher earnings of high-ability subjects relative to low-ability subjects in both mechanisms but the difference is significantly higher in BOS, which confirms the concern that BOS disadvantages students of low cognitive ability. These findings are complemented by the empirical work of Dur et al. (2018b) which quantifies the costs of sincere reports under BOS and shows that they are substantial.
In a follow-up paper, Basteck and Mantovani (2018b) investigate whether information about the popularity of schools (in particular, the number of students who ranked the school first in their reported preferences) helps to level the playing field and close the gap between high- and low-ability subjects under BOS. The authors use two different school choice problems. In the treatment with information, the proportion of low-ability subjects best-responding to the average play of others is higher than in the treatment without information in both problems. As for high-ability subjects, there is a significant increase in the proportion of best responses in the treatment with information relative to no information in only one of the two problems. Despite a significant reduction in the best responses gap between high- and low-ability subjects in the treatment with information, there is no significant difference in the payoff gaps between treatments. The authors explain this finding by a higher propensity of high-ability subjects to play the best response in high-stakes situations of the information treatment, and the fact that the remaining strategic mistakes of low-ability subjects are particularly costly.
Hakimov and Bó (2020) used an incentivized quiz for DA where subjects were paid a fixed amount if they were able to correctly determine the allocation of a school choice problem. The authors found no correlation between truthful reporting and the ability to find the correct allocation when controlling for other factors such as the preference profiles and priorities. Instead, the main determinant of truthful reporting was the priority of the student: the higher the average priority, the more likely she was to report truthfully. This observation is in line with the district school bias, since high priority students can be sure to get into their most-preferred schools. It is also in line with the field observations of Hassidim et al. (2020) who consider admissions to psychology programs in Israel where applicants are ranked by the programs mostly based on their school grades. They observe that applicants with bad grades are more likely to submit dominated rank-order lists to the DA mechanism than applicants with good grades. However, this result from the field can be driven by differences in the priority and cognitive ability of students. Moreover, Schmelzer (2018) found that subjects with very low and very high levels of contingent reasoning, as measured by choices in the two-person beauty contest game, are more likely to report truthfully in RSD and TTC than subjects with intermediate levels of contingent reasoning.
Finally, Rees-Jones and Skowronek (2018) conducted a large experiment with 1714 medical students immediately after their participation in the medical residency match. While participating in the match, students received significant training and advice regarding the mechanism (a modified version of DA that preserves incentives to truthfully rank the residencies (Roth and Peranson 1999). In the experiment, students were told that they would be allocated to hypothetical residency programs using the same mechanism as the NRMP, and they had access to a detailed explanation of the mechanism. The preferences of students were generated such that all students had the same preferences over the five residency programs. The preferences of residency programs were correlated with hypothetical test scores which were known to the students. However, the preferences were not uniquely defined by the test scores, and the students were aware that every student could be assigned to every program with some positive probability. It turns out that 23% of students did not report their rank-order lists truthfully. This finding shows that preference misreports in DA can be observed for a highly relevant group of participants in a lab experiment. The authors also investigate some variables that influence misreporting. Similar to other studies, it is found that students with a lower performance in cognitive tests and students with lower perceived chances of being accepted to the best residency programs (students that were assigned low test scores in the experiment) are more likely to misreport their lists. The authors also asked participants whether they trusted NRMP to run the mechanism correctly, and 97% of participants indicated that they did trust the system. However, when asked whether the medical residency programs ranked students fairly, only 42% of participants agreed, which shows a significant negative correlation with truthful reporting.
3.4.1 Summary
In spite of correlations of subjects’ misreports with various measures of ability, clear evidence on the reasons for these misreports is still missing.Footnote 16 In many studies, the modal manipulation is the switch of the two top choices, which is present even when it cannot be rationalized by the district school bias (safety motive) or by the similarity of preferences bias (motive to avoid competition). Most biases were documented in one-shot experiments. It would be interesting to look at the biases in repeated environments to see which of them are more persistent than others. Experiments with repeated play could also allow for a cleaner identification of possible biases and their drivers. We summarize recent theoretical developments that could explain deviations from truthful reporting in incentive-compatible matching mechanisms in Sect. 5.
3.5 Constrained rank-order lists
In many practical settings, the number of items that can be ranked on the preference list is smaller than the number of options available. The effects of such constraints have been studied by Calsamiglia et al. (2010) for BOS, DA, and TTC. They used the designed and random markets of Chen and Sönmez (2006). In the designed treatment small schools and district schools are more preferred while preferences are uncorrelated in the random markets. There are 36 students that have to be assigned to seven schools. In the constrained treatment, only lists of up to three schools can be submitted while the lists can contain up to seven schools in the unconstrained environment. In case a student is not accepted by any of the three listed schools, she remains unassigned and receives a payoff of zero from the match. A 3 × 2 design was employed in a one-shot environment with incomplete information about the preferences of other applicants. As predicted, since DA and TTC are no longer strategy-proof for many students when the lists are constrained, it is found that subjects rank their safe district school higher and small schools lower in the constrained than in the unconstrained version of the two mechanisms. The district-school bias leads to fewer students not being assigned to their district school in all three mechanisms. Furthermore, efficiency is significantly lowered by the constraint in all three mechanisms. Regarding stability, DA performs better than BOS and TTC both under the constrained and the unconstrained version of the mechanism but the constraint in DA significantly increases the number of blocking pairs. The authors conclude that “removing the constraint will come at a small cost but will clearly improve the performance of the school choice mechanisms.”
Note that in an equilibrium of DA under constrained lists, subjects have to rank a safe school among the schools ranked in the list. This is closely related to the “insurance strategy” in BOS and the Chinese parallel mechanism discussed in Chen and Kesten (2019). In BOS, participants should often list a safe school as the top choice while in the parallel mechanism, it is enough to put it within the choice-band. Thus, other choices within the band can be used for more preferred schools relative to the one which would be the outcome of BOS equilibrium. In this sense, the parallel mechanism provides insurance for applicants. Note that this strategy resembles the equilibrium strategy in constrained DA where participants should put the safe option last on the list while using the other choices to apply to better schools. In Chen and Kesten (2019) by the last period, 53% of participants in the Chinese parallel mechanism adopt the insurance strategy. In Calsamiglia et al. (2010), this number is not reported but they observe almost universal deviations from the naïve truth-telling of participants who should manipulate the constrained list to include a safe school. This suggests that “insurance” strategies are likely to be used.Footnote 17
One rationale for constraining the length of the rank-order lists is the cost of dealing with many applications that can lead to congestion. He and Magnac (2017) use a field experiment to study how the costs of university programs incurred by inspecting student applications under DA can be reduced by restricting the number of choices that can be put on the rank-order list. They run a field experiment with 129 students applying for seven master’s programs at Toulouse School of Economics. They compare constrained and unconstrained DA with a version of DA that includes a Pigouvian tax on each application that is supposed to internalize the cost imposed on the selection committees of the programs. The tax was implemented by requiring a motivation letter from the students for each application from the fourth application on. The students knew that either DA, DA with motivation letters, or constrained DA with only four programs would be implemented. Each student could submit a rank-order list for each of the mechanisms. The authors treat the submissions under unconstrained DA as the true preferences. This allows them to simulate the effect of the tax and the constrained lists on stability. While both DA with a Pigouvian tax and constrained DA significantly lower the number of applications to each of the programs, the constraint on the list leads to high distortions of stability and to some students being unassigned. Simulations and counterfactual analyses suggest that the small application cost is the best regime: while lowering the screening costs of the programs due to fewer applications, stability is unaffected.
3.5.1 Summary
There is robust evidence of a detrimental effect of a constraint on rank-order lists in DA on stability. However, once the constraint is implemented as a small tax, the detrimental effect disappears. This may be due to the effect that risk-averse participants overspend on the tax instead of dropping the good schools from their reported list. Thus, the participants possibly report more options than the student-optimal stable match requires, while in the case of constrained lists risk aversion might drive them to not list the student-optimal stable match in favor of safer schools. This differential effect of a constrained list versus a Pigouvian tax on reporting behavior is highly relevant in practice, given the prevalence of application costs, and might be of interest for further studies.
3.6 Affirmative action
In many school choice and university admissions procedures, affirmative action policies or quotas for certain groups of students play an important role. Also, lotteries are used to admit students when seats are scarce in order to provide equal access ex ante. The goal can be to increase the enrolment of minority students, to foster diversity in schools, or to satisfy fairness criteria. Experiments have been employed to understand the effects of different ways to implement affirmative action policies in matching markets.
Two alternative approaches to affirmative action are majority quotas and minority reserves. Majority quotas specify the maximum share (or number) of seats in each school that can be allocated to majority students. Minority reserves specify the share (or number) of students for each school such that in case the number of minority students in the school is lower than this number, any minority student is preferred to any majority student. Before turning to the experiments, we summarize the main theoretical findings guiding the experiments. Kojima (2012) and Matsubae (2011) show that the introduction of majority quotas can result in undesirable effects for both majority and minority students under DA and TTC. The reason is that a majority student who is rejected by her preferred school due to the quota and who gets a seat at her second most-preferred school may thereby take the seat of a minority student at this school, making the minority student worse off. Hafalir et al. (2013) analyze minority reserves and demonstrate that the reserves do not affect the strategy-proofness of DA and TCC, and are an improvement relative to majority quotas. Unlike majority quotas, minority reserves are flexible. This means that when the demand from minority students is lower than the number of seats reserved for minority students, these seats can be filled by majority students. This feature of minority reserves is crucial for preserving good properties of DA and TCC such as strategy-proofness.
Two possibilities of implementing quotas have been studied experimentally by Braun et al. (2014). The first relies on the existing procedure for university seats in medicine in Germany where quotas for certain groups of students are filled sequentially. The second procedure is a modified version of DA that is strategy-proof (Westkamp 2013) and that is similar in spirit to the minority reserves described by Hafalir et al. (2013). In the sequential procedure, first the 20% of applicants with the best grades submit a rank-order list of universities for seats reserved for the top-grade students. Then, the same students have a chance to participate in the allocation of general seats by submitting a potentially different preference list. Since the quotas are filled sequentially, the German procedure creates incentives for strategic behavior by the students who are eligible for the top-grade quota. Intuitively, the students with the best grades have two chances of being admitted: through the top-grade quota, or later when the remaining seats are distributed among all students. Sometimes a student is better off when she is not matched to a university right away through the quota for best-grade students, since she can be matched to a better university which rejected her in this quota but accepts her under the general quota later on. Thus, in equilibrium the students need to truncate their list for the top-grade quota that is administered first. Thus, the strategic incentives are due to the sequential process of filling the quotas. The experiment employed four markets that differ with respect to the correlation of preferences. Participants played each market three times in different roles, amounting to 12 rounds overall. The results show that many students fail to optimally truncate their preference list for the first quota, even when the truncation is a dominant strategy, and achieve worse outcomes than in the modified DA that is strategy-proof.
The theoretical results of Hafalir et al. (2013) were tested in the lab by Klijn et al. (2016) who compare DA and TTC, each with and without minority quotas. The results show that the mechanism with reserves favors minority students, since they are less likely to form a blocking pair and have higher payoffs than in the mechanism without reserves. No effect on truth-telling rates was observed, except for an increase in truth-telling by some minority students in the case of DA with reserves when compared to DA. Overall, DA performed better than TTC regarding both stability and efficiency.
Kawagoe et al. (2018) employ experiments to compare majority quotas and minority reserves for DA. They used two environments. As predicted, in the first environment DA with minority reserves led to higher efficiency than DA with a majority quota, with no significant difference in the second environment. Both mechanisms are strategy-proof but led to approximately 60% of truthful preference reporting with significant differences between mechanisms and environments. The authors document a systematic pattern of deviations from the dominant strategy, namely the skipping-down strategy. Under the skipping-down strategy, subjects rank higher in their reported rank-order list of schools for which they have higher priority. The authors show that this strategy might be in line with the equilibrium under DA with majority quotas but not with minority reserves.
Lotteries have been proposed to desegregate schools in the UK (School Admissions Code 2006) and they are also employed in Berlin for this purpose. Basteck et al. (2018) study the existing school choice procedure that combines lotteries with the BOS mechanism and compare it to DA with an equivalent lottery quota under both mechanisms. A certain proportion of seats at each oversubscribed school is allocated based on lottery draws while all other seats are allocated based on the priority of students. Thus, the policy reserves seats for applicants with the highest lottery numbers, independent of their priority at the school (which is based on school grades in Berlin). The BOS and DA mechanisms with a lottery quota are compared to BOS and DA without a lottery. In line with the theoretical predictions, truth-telling is higher in DA than in BOS and strictly increases with the lottery quota in both mechanisms. Schools are less segregated with a lottery quota but students of intermediate priority are less likely to receive seats at their preferred schools.
3.6.1 Summary
The experimental evidence mostly confirms the theoretical predictions concerning the effects of quotas and reserves. Majority quotas as well as the sequential implementation of quotas can backfire by harming those students who are supposed to benefit, and can destroy the incentives to report truthfully. On the other hand, lotteries can strengthen truth-telling both theoretically and empirically and lead to more mixed schools.
3.7 Information acquisition
The matching literature typically starts with the assumption that students know their own preferences. However, it is evident that in practice forming preferences over a set of schools can be a time-consuming and complex task. Chen and He (2017) compare students’ incentives to invest in learning their own preferences and the preferences of others under BOS and DA. They show that in theory students have incentives to find out both their own preferences and the preferences of other students under BOS. In contrast under DA, due to its strategy-proofness only one’s own preferences matter for the optimal strategy. Furthermore, the willingness-to-pay to find out about one’s own cardinal preferences is predicted to be higher for BOS than for DA. The authors test these predictions in a lab experiment. The results show that the subjects’ WTP for information on their own preferences is higher under BOS than under DA, as predicted. However, the WTP is significantly higher than what the theory predicts for DA. Regarding the WTP for information on the preferences of others, again subjects’ WTP is higher under BOS than under DA but it is significantly higher than predicted under both mechanisms. The welfare of the different information regimes is also studied. There are no significant differences regarding the efficiency of the allocations under the two mechanisms in the uninformed case. The free provision of information about the students’ own preferences leads to significantly higher efficiency under both mechanisms, while providing information about the preferences of others for free has no effect on the efficiency in either mechanism. Under regimes with information provision about own or others’ preferences, however, the allocations reached under BOS are closer to the efficient one than the allocations under DA.Footnote 18
3.8 Preferences over mechanisms
It is possible that people have preferences over matching procedures themselves and not just over outcomes. If this is the case, such preferences should be taken into consideration by the policymakers when choosing among mechanisms. However, almost all existing studies on matching procedures implement a between-subjects design regarding the allocation mechanism. The main reason is probably that some of the mechanisms are not straightforward to understand, and the instructions for only one mechanism are already quite involved. However, there are two experimental papers (Schmelzer 2016, 2018) that investigate subjects’ preferences over mechanisms. Schmelzer (2016) studies DA with different tie-breaking rules for priorities. Motivated by recent policy debates, two common ways of dealing with ties due to coarse priorities are tested in the lab. The author elicits the preferences of subjects over DA with single and multiple tie-breaking by ensuring that the ex-ante outcomes (before the lottery) are the same by design. The subjects have to make two decisions, namely submit the preference lists under single and under multiple tie-breaking. Under single tie-breaking, all schools use the same lottery to rank students, while under multiple tie-breaking each school runs its own lottery. Without providing information about the allocation reached under each tie-breaking regime, the subjects can pay 10 cents (€) to express their preference over the tie-breaking regime. One of the subjects is randomly chosen to determine the regime that will be applied. Though the majority of subjects are indifferent, among those who are not most express a preference for multiple tie-breaking.
In a second paper on choice between mechanisms (Schmelzer 2018), TTC is compared to RSD in a house allocation problem. The hypothesis was that subjects might prefer RSD because of its simplicity relative to TTC. RSD is straightforward to explain, and thus it is possible to run it together with TTC in a within-subjects design without risking confusing the subjects. Around 40% of subjects are willing to pay a small amount to vote for one of the mechanisms, and the number of votes for each of the mechanisms is not significantly different.
3.8.1 Summary
The elicitation of preferences over mechanisms has demonstrated that many subjects are indifferent between the mechanisms. This might be driven by the fact that the mechanisms that were compared are similar from a theoretical perspective. It seems important to find ways to elicit preferences over more distinct mechanisms, like BOS, DA, and TTC. However, this is challenging since the preference over mechanisms has to be disentangled from the motive to reach the best possible assignment.
3.9 Timing of the publication of centralized exam scores
A seemingly small institutional detail such as the timing of information about the results from the university entrance exam can have implications for the matching outcome. Lien et al. (2016) run experiments inspired by a policy change in China regarding this issue. The universities accept students based on the exam scores. The experiment tests the hypothesis that not knowing the result of the exam when submitting one’s preferences can lead to an ex-ante fair and efficient outcome. Ex-ante [ex-post] fairness means that there is no justified envy with respect to the expected [realized] exam scores while efficiency accounts for the preference intensities (cardinal utilities). This hypothesis relies on the idea that people have an unbiased prior about their ability while the exam score is a noisy signal of it. Therefore, the noisy exam score can lead to a matching that is not stable with respect to ability under DA. The same holds under BOS if students know their realized exam score. However, if they do not know the score of the exam, they can only base their choice on their expected exam score which, by assumption, is a better measure of ability. In the experiments, students are informed of their true ability, that is, the average of their score distribution. It emerges that BOS where students do not know their exam score leads to the most efficient but least ex-post fair outcome, while there is no support for the prediction that it is ex-ante fair. Overall, it turns out that despite small markets (three students and three schools), the equilibrium strategies are often not played when students do not know their exam score.
Pan (2019) questions the assumption by Lien et al. (2016) that people have an unbiased expectation of their ability before the exam score is published. She shows that biased self-assessments further weaken the ex-ante fairness of the matching under BOS. She runs experiments in a similar setup but instead of exogenously given priorities, the priorities in the mechanism were determined by a real-effort task. The theoretical prediction that BOS should lead to a higher percentage of ex-ante stable matchings under the regime of publishing the grades after the submission of preferences finds no support in the data, and DA outperforms BOS in all publishing regimes.Footnote 19 This is another piece of evidence for the strategic complexity of BOS. Despite the fact that in theory BOS can improve on DA with respect to efficiency, the prediction typically fails in experiments due to the low percentage of equilibrium outcomes reached under BOS (see, for instance, Featherstone and Niederle 2016).
3.9.1 Summary
In situations where the benefits of a particular mechanism are based on the assumption of participants holding correct beliefs about their ability, the predictions often fail to find support in experiments. This is not surprising given the robust experimental evidence on biased self-assessments. This subsection underscores the importance of empirical evidence when recommending policies instead of basing the recommendations on the predicted equilibrium outcome alone. Here, theoretical and empirical results lead to opposite recommendations, which is rare in the matching literature.
3.10 Dynamic mechanisms
While most research has focused on direct mechanisms where students have to report their rank-order list before the algorithm is run, dynamic or iterative mechanisms can be an alternative. Motivated by the high rates of misreporting observed in lab experiments and in field studies with strategy-proof mechanisms (see Hassidim et al. 2020; Chen and Pereyra 2020; Rees-Jones 2018), a number of papers test dynamic mechanisms. Unlike direct mechanisms, these mechanisms allow for multiple interactions between the participants and the designer. This allows for learning and for the correction of mistakes during the allocation process. Due to their dynamic nature, these mechanisms might provide feedback to the participants about intermediate allocations. However, the exact implementation of the mechanisms differs largely between studies, and seemingly small details influence the strategic properties of the mechanisms as well as their observed outcomes.
The first two studies reported on in this subsection by Klijn et al. (2019) and Bó and Hakimov (2020a) consider the iterative DA mechanism. Instead of submitting rank-order lists before the algorithms starts as in static DA, under iterative DA the proposing side makes one proposal at a time. If a proposal is tentatively accepted, the proposer cannot make any other proposals. If it is rejected, the proposer is asked to make another proposal. Following the literature, we use the terms “iterative” and “dynamic” interchangeably to refer to this modification of DA. Klijn et al. (2019) compare the student- and school-proposing DA to their iterative counterparts.Footnote 20 The experiment implements a one-sided matching setup where the schools were played by the computer and always behaved truthfully (either by proposing in the order of priorities or by choosing among proposals according to their priorities). The authors used four different environments with complete information. Each environment had four students and four schools, with one seat each. Subjects played the same environment for six rounds in a row before switching to the next environment. Klijn et al. show that the strategy-proofness of the static student-proposing DA is lost in the dynamic version of the mechanism. In the school-proposing DA, the set of equilibrium outcomes for the static and dynamic versions coincide but a wide range of behavior is supported in equilibrium in the dynamic version. The results of the experiment show that subjects switch the ranking of schools relative to their true preferences weakly more often in static mechanisms than in the dynamic versions. The overall truth-telling rate in dynamic DA was 55%, while it was 47% in static DA, and the difference is not statistically significant. Moreover, there is no significant increase in the number of stable allocations under the iterative student-proposing DA relative to its static version. In the school-proposing DA (where offers were made by the computer in the order of priorities), however, in two out of four environments the dynamic version led to a significantly higher proportion of stable outcomes. Finally, the overall frequencies of stable matchings were 64% in the static student-proposing DA, 77% in the dynamic student-proposing DA, 69% in the static school-proposing DA, and 90% in the dynamic school-proposing DA.
In a closely related paper by Bó and Hakimov (2020a), the authors also compare static and iterative versions of student-proposing DA. Unlike Klijn et al. (2019), they implemented incomplete information about the priorities, i.e., participants only knew their grades for each university, but not the grades of other students. They knew, however, the distribution of the grades. Subjects played a mechanism for 20 rounds, facing a new set of preferences and priorities in each round. Eight students competed for seats at eight colleges with one seat each. In contrast to Klijn et al. (2019), they find that under iterative DA stable allocations are reached significantly more often than under static DA. The difference is driven by a significantly higher proportion of subjects behaving truthfully in the iterative mechanism.
The results of both Bó and Hakimov (2020a) and Klijn et al. (2019) indicate a failure of the theoretical prediction of more truthful behavior under static mechanisms.Footnote 21 Bó and Hakimov (2020a) investigate different possible explanations for the observed difference between static and dynamic DA and conclude that the advantage of dynamic DA is the feedback it provides after every step (rejection from the previously applied university) and the possibility to re-strategize given this feedback. This allows subjects to realize that the strategy of skipping the most-preferred schools is not successful and makes them abandon this strategy in favor of truthful behavior.Footnote 22
Additionally, Bó and Hakimov (2020a) conducted a treatment under iterative DA where the tentative cut-off grades of students are posted after each step of iterative DA. These grades reflect the minimum grade necessary to be accepted by a particular university at each step. The cut-off grades can only improve between the steps of the iterative DA, since only those applicants who were not tentatively accepted can reapply. The provision of these cutoffs leads to a significant increase in truthful behavior relative to the iterative version without the provision of cutoffs but this increase does not translate into a significantly higher proportion of stable allocations.
The effect of intermediate information in the allocation process is also explored by other studies. Stephenson (2016) tests the effect of continuous feedback on allocations depending on the lists submitted by the participants. The subjects first submitted a report, were then able to revise it multiple times, and immediately received feedback about the allocation they would have reached given the current reports of all students. The treatments vary with respect to the mechanism used, namely BOS, DA, and TTC, and the frequency of the feedback, either after all participants submit their reports (discrete feedback), or already after tentative reports (continuous feedback). In all three mechanisms, the continuous feedback improved the rationality of the lists submitted and moved the allocations significantly closer to those predicted by the theory. A stable outcome was reached in 83% of markets under discrete feedback, and in almost 99% of markets under continuous feedback, which are the highest rates of stability observed in the experimental literature.
Gong and Liang (2017) study the college admission mechanism of the Chinese province of Inner-Mongolia. It is a dynamic mechanism where students are given real-time feedback about the current allocation and are allowed to revise their choices. The mechanism is based on DA but unlike in the iterative DA that was tested by Bó and Hakimov (2020a) and by Klijn et al. (2019), subjects can revise their applications at any time. In this respect, the mechanism is similar to the continuous feedback explored by Stephenson (2016). However, participants can only submit one choice at a time as opposed to a full rank-order list in Stephenson (2016). Additionally, the students are split into groups according to their grades. Each group has its own deadline for the final submission after which the allocations are finalized. The authors compare the dynamic mechanism to standard DA and BOS. In the environment with highly correlated preferences, the dynamic mechanism leads to significantly less stability and lower efficiency than in DA, while students misreport at a similar rate. In the low correlation environment, the dynamic mechanism is as stable and efficient as DA but has lower rates of misreporting.
Dur et al. (2018a) investigate a modification of BOS where rank-order lists are submitted sequentially, and late movers can observe the submissions of previous students. This is motivated by the mechanism used in the Wake County Public School System. The equilibrium of BOS with sequential submission under complete information can lead to improvements in efficiency compared to standard BOS. In experiments with four students and four schools with one seat each, the authors compare the standard versions of BOS and DA to mechanisms where the preferences are submitted sequentially. The order of moves is predetermined in the experiment. The theoretical predictions hold: while there was no difference in efficiency between both versions of DA and standard BOS, BOS with sequential submissions reached the highest level of efficiency and the difference to the other mechanisms was significant. In DA, on average, 77% of students reported truthfully, and the rates were not different in the standard DA and the DA with sequential submissions.
A dynamic mechanism is also considered by Li (2017) who compares RSD in a standard and in a sequential version. In the standard version, subjects are asked to submit their full rank-order lists over all options. In the sequential version of RSD subjects have to pick their preferred choice from a set of options. The sequential version of RSD is obviously strategy-proof, a property of the incentive structure introduced by Li (2017). A truthful strategy is obviously dominant if, for any deviating strategy, starting from any earliest deviation from the truthful strategy, the best possible outcome from the deviating strategy is no better than the worst possible outcome from the truthful strategy. A mechanism is obviously strategy-proof if it has an equilibrium in obviously dominant strategies. Thus, in the sequential version of RSD it does not require contingent reasoning by the players to realize that truthful behavior is a dominant strategy, while it is required in the standard version of RSD (Li 2017). The experimental results show that higher rates of truthful behavior are observed in the dynamic version of RSD than in the static version, which can be explained by obvious strategy-proofness.
3.10.1 Summary
The experimental evidence weakly favors dynamic mechanisms over their direct counterparts, the only exception being the study by Gong and Liang (2017) where the evidence is mixed. Note, however, that the meaning of the term “dynamic” varies across studies. Very broadly, dynamic mechanisms can be categorized into three groups: (1) Subjects take decisions step-by-step, submitting one choice at a time, as in iterative DA studied by Klijn et al. (2019) and Bó and Hakimov (2020a) or in sequential RSD studied by Li (2017). (2) Subjects are allowed to revise their strategies (rank-order lists or just one choice) multiple times as in the experiments by Stephenson (2016) and Gong and Liang (2017). (3) Subjects report rank-order lists one after another in a standard direct mechanism, learning about the strategies of players who chose before them, as in Dur et al. (2018).
While all these modifications seem to lead to improvements in the quality of the allocations relative to static mechanisms, the size of these improvements varies between studies and modifications. More research is needed to understand whether the benefits are robust and what their channels are.
4 Experiments on two-sided matching: the college admissions model
The section covers experiments on the college admissions model. With respect to matching mechanisms, the experimental literature focuses mainly on DA. Two versions are considered, namely static and dynamic DA. The following theoretical predictions hold:
-
1.
In DA, it is a weakly dominant strategy for the proposers to state their preferences truthfully unless colleges with multiple seats are proposing.Footnote 23 It is a weakly dominant strategy of receivers to report their first preference truthfully.
-
2.
The Nash equilibria of the game induced by DA lead to matchings that are stable with respect to the stated preferences.
-
3.
DA leads to the proposer-optimal stable matching.
Experiments are employed to test these theoretical properties, with a strong focus on the stability of market outcomes. A second focus is on the question of which of the stable matchings is selected if there is more than one and thus on the distribution of welfare. While the theory makes a clear prediction that the proposer-optimal matching should be reached, the experimental evidence does not univocally support this. The information available and—in dynamic two-sided markets— the exact market rules play an important role.
Table 1 in “Appendix 2” presents an overview of the studies summarized in Sects 4.1 and 4.2, and displays the connection between the market rules and the experimental findings. We start out with experiments implementing the static DA mechanism where participants in the role of students and universities submit their rank-order lists, and the central clearinghouse played by the computer determines the matching. We then move on to dynamic implementations of DA where there are no submissions of rank-order lists but offers, acceptances, and rejections are made by the market participants one at a time, following the protocol of the static DA mechanism.Footnote 24
4.1 Static DA
The earliest experiment on the marriage market studies the strategic misrepresentation of preferences by the participants under the student-proposing DA (Harrison and McCabe 1996). Markets with three or four students and three or four universities were played for 25 periods with complete information about the preferences of all market participants. Both the role of universities and of students were taken on by the experimental subjects but the treatments varied the number of players that were computerized and programmed to always report the true preferences. At least one market participant was played by the computer in every market, and all markets with eight players (four universities and four students) were run with all students computerized. In the six-player markets, there were two stable matchings, while in the eight-player markets there were four stable matchings. Thus, the receiving side had incentives to misrepresent their preference reports in order to secure a more favorable stable matching.
In the six-player environments with three students and three universities where only one or two players were not computerized, the best response (either telling the truth for the proposing side or manipulating for the receiving side) was frequently chosen by the participants. However, with fewer computerized players and with markets of four students and universities, the subjects were not able to secure themselves favorable outcomes by manipulating their preferences. The efficiency of the matching was lower in markets with more human players, and experience did not help to reduce the efficiency losses. The number of blocking pairs was also higher in the larger markets and the markets with more human players.
The authors computed the payoff distance of the realized outcome to the student-optimal stable matching. They state that in markets with three players on each side, matchings were realized that were closer to the outcome preferred by the universities than to that of the students. However, in the markets with four players on each side, the matchings were closer to the student-optimal outcomes. To figure out what drives these results, the strategies of the universities given the two different market sizes can be compared in the treatments with computerized students who tell the truth. This analysis suggests that the strategic complexity for the universities increases from markets of six to markets of eight players and prevents them from optimal manipulations in the larger markets.
Market participants need to have sufficient information to effectively manipulate their preference lists. To investigate this systematically in a two-sided matching market with a centralized clearinghouse, a within-subjects design was employed by Pais et al. (2011) where each participant played DA under three different information conditions: no information except one’s own preferences, partial information (standing for subjects knowing their own preferences, the capacities of schools as well as the preference lists over students by each school up to capacity, and the school that is top-listed by each student), as well as full information, always in this order. There were five students and three colleges, and two of the colleges offered two seats. The authors observe a considerable amount of preference manipulations by the colleges and the students with full information. In particular, under student-proposing DA with full information only 56% of the students and 27% of the colleges report truthfully.Footnote 25 Almost all manipulations by the colleges (93%) were due to moving up students that ranked the college highly in their preference order. The manipulations by the students were predominantly due to moving up a college by which the student was ranked highly (a bias analogous to the district school bias) and moving down small colleges with fewer seats (small school bias), or a combination of both (73%). Truth-telling rates were higher in the treatments with less information available to the players. The stability rates ranged from 31 to 82% depending on treatments. The proportion of stable matchings was 38% in the zero-information condition, 48% in the partial-information condition, and 2% in the full information condition. In the zero-information condition, all stable outcomes were student-optimal while with partial and full information the proportion of student and school optimal outcomes was approximately the same. This is in line with the theoretical predictions, as colleges have the possibility to manipulate reports optimally only if they have enough information about the preferences of other players.
Strategic manipulations by the receiving side are also the focus of Castillo and Dianat (2016) who investigate the use of truncation strategies under DA. Truncation strategies are exhaustive in the sense that any matching that can be achieved with a misrepresentation that is not a truncation of one’s preference list can also be achieved by a truncation (Roth and Rothblum 1999). When all agents can only truncate their list and no other misrepresentations are allowed, the optimal truncation strategy of an agent does not depend on the other agents’ strategies. Thus, the complex market game is reduced to a single-person decision problem. A complete information environment is used, and the proposing side is computerized by stating the true preferences. Two behavioral predictions are tested, namely that the profitability and the riskiness of the truncation strategy affect its frequency of being chosen. However, it turns out that the observed truncation strategy of the receivers is not sensitive to the payoff differences between the different matchings, contradicting the prediction. On the other hand, the hypothesized relationship between the riskiness and the likelihood of truncations finds support: Subjects whose best achievable matching partner is higher on their list are less likely to truncate their list above the best achievable partner, which would lead to no assignment. The lower the most-preferred achievable firm on the list is, the higher the probability that the subject will truncate the list optimally. A stable outcome is reached in 88% of the markets (but note that only truncations above the best achievable matching partner can lead to unstable matchings in the markets considered). Finally, it is found that outcomes are closer to the receiver-optimal stable matching than to the proposer-optimal stable matching.
A closely related paper by Featherstone and Mayefsky (2015) also focuses on the strategies of the receiving side in DA. They consider two environments: the first environment is characterized by multiple stable matchings, which implies that the receiving side has incentives to truncate the reported lists; in the second environment the stable matching is unique, which implies that the receiving side should report truthfully. In the experiments, the proposing side was played by computers, and truthful lists were always submitted. The results show that subjects do not differentiate between the two environments, and the rate of truthful reporting by the receiving side is not statistically different between the two environments. The difference increases in the last 10 rounds of the experiments but remains small (and only marginally significant). Surprisingly, a stable matching is never reached.
4.1.1 Summary
A couple of common findings emerge from the experiments on static DA. The receiving side tends to manipulate the rank-order lists but the success of the truncations and the rates are far from those predicted. Manipulations seem to be more successful when only a truncation of the rank-order list is allowed. Once the proposing side is played by human participants, the outcomes are even more distorted since both sides tend to deviate from equilibrium strategies. In the next subsection we will consider situations where the receiving side can react to the strategies of the proposing side.
4.2 Dynamic DA
Many matching markets are organized in a decentralized manner. However, even without a centralized clearinghouse, there can be rules that govern the process of offers and acceptances. If such rules are similar to the protocol of matching algorithms, the outcomes of decentralized markets can be described with the help of these algorithms. Thus, studying the dynamic version of DA is useful, since it captures decentralized markets following the protocol of DA. Another feature of the dynamic version of DA is that it may be less demanding in terms of information collection and preference formation. Participants do not have to submit their full rank-order list but are only asked to name their preferred choice among a set of options. This may be one of the motivations for why policymakers have opted for dynamic mechanisms in real markets in recent years. Finally, for the sake of lab experiments the study of dynamic versions of DA has the advantage that when the preferences are induced by the experimenter, a dynamic procedure makes reporting the truth seem less artificial than in a static DA mechanism.
The experiments of Haruvy and Ünver (2007) were designed to investigate the hypothesis that DA is a good predictor of behavior in repeated decentralized matching markets. Moreover, the study tests whether the amount of information of the side that receives offers affects the matching outcome. Workers and firms search for a matching partner by making and accepting offers bilaterally, without a clearinghouse as an intermediary. In the markets consisting of four firms and four workers, each firm can make an offer to one worker in every period. In the second part of a period, the workers decide whether they want to accept a contract offer or not. The market ends after a certain number of periods, where each of the periods is payoff-relevant. This feature of the game creates incentives for firms to skip offers that are rejected by the worker with a high probability. The final outcome, however, is still predicted to be stable, as contracts can be reneged upon in the next period and can also be repeated with the same worker. Three different markets requiring a different number of iterations to reach the stable matching were implemented in a within-subjects design. A 2x2 design was employed: all workers were either humans or computers programmed to state the truth, and low and high information conditions were implemented where market participants only had information about their own preferences, or about the preferences of all participants.
Haruvy and Ünver (2007) find that in all four conditions, the firm-optimal stable matching was reached in the majority of cases, confirming the hypothesis that DA can predict the outcome in certain decentralized settings. With non-strategic computerized workers, the firm-optimal stable matching was reached in 65% of the markets, while in 8% of the markets the worker-optimal stable allocation was reached. With participants playing the role of workers, the firm-optimal stable matching was still by far the modal outcome with 72% of allocations, and the worker-optimal stable matching was reached in 16% of the markets.
A systematic analysis of strategic behavior under dynamic DA was conducted by Echenique et al. (2016). Their version of the mechanism follows the description of the DA algorithm but offers, acceptances, and rejections are all executed by the subjects. In this respect the setup is comparable to Haruvy and Ünver (2007) but in contrast to their study only the final allocation is payoff-relevant in Echenique et al. (2016). They study different markets with eight subjects on each side and complete information, varying the number of stable matchings, and the cardinal representation of preferences. It is observed that proposers often skip entries of their preference list to avoid proposing to responders who do not rank them highly.Footnote 26 Most of the responders in the experiment behave straightforwardly by accepting the best offer at any stage. Note that due to the dynamic implementation, the choices of the responders are restricted by the proposers’ strategies. Across all markets, the average payoffs of proposers are closer to the average predicted payoff under the receiver-optimal stable matching than under the proposer-optimal stable matching, which is a consequence of the proposers’ skipping behavior. Finally, half of the markets lead to unstable outcomes, and only 29% of them are proposer-optimal.
As observed by Echenique et al. (2016), the skipping behavior of the proposers has interesting implications for patterns observed in the NRMP. In the NRMP, a high percentage of residents (proposers) receive their first choice (mostly above 50% in recent years) compared to their second choice (around 15%) and their third choice (below 10%). The authors argue that this is consistent with the decision heuristic that conflates the likelihood of matching with a certain partner and the preference for this partner.
An extensive form implementation of DA was also studied by Castillo and Dianat (2017). The main goal of their paper is to understand the impact of information of market participants about the preferences of others on their strategies and on the matching outcome. The paper is closely related to Pais et al. (2011) but runs DA in a dynamic setting, just like Echenique et al. (2016). Their main finding is that the distribution of information affects which outcome is selected but it does not affect the stability of the outcome. As in Echenique et al. (2016), if proposers have full information about the preferences of the receivers, proposers often skip preferred partners if they are not ranked highly by them. This explains the finding that the average distance to the responders’ preferred stable outcome is smallest in the treatment with full information. This relationship between the stable matching selected and the amount of information is the same as in Pais et al. (2011) for static DA but, in contrast to their findings, the stability of the outcome does not decrease in the amount of information available. This difference could be due to the dynamic implementation, giving participants flexibility to change their strategy in the process and thereby avoid instabilities. Additionally, the dynamic implementation allows receivers to observe that proposers manipulate in the receivers’ interest, which leaves less room for profitable manipulations by the receivers. In static DA, receivers do not expect this and manipulate their lists, thereby failing to best-respond to deviations from the predicted behavior of the proposers.
4.2.1 Summary
The step-by-step implementation of DA limits the analysis of the strategies of the receiving side: the biggest difference to static mechanisms is found for the receivers who often best-respond to the deviating strategies of the proposers. However, we cannot distinguish whether receivers report truthfully because truth-telling has become the best response or because they do not understand the incentives for skipping and would have been truthful anyway. The possibility to react to the proposer’s offer increases the proportion of stable allocations relative to the static mechanism in which both sides submit their strategies simultaneously. Both in static and dynamic DA, the more proposers know about the preferences of the other side of the market, the more they deviate from their optimal strategy, and thus the further away they move from the proposer-optimal toward the receiver-optimal stable matching. Note that similar findings exist for school choice problems where students react to priorities and tend to rank higher schools at which they have a higher priority.
5 Behavioral aspects of matching markets
The aim of this section is to demonstrate how school choice and college admission experiments connect to a broader behavioral and experimental literature. Most of the existing work tries to answer the question of how the frequently observed failure to choose a dominant strategy can be explained. We have already discussed the role of biases specific to matching markets, and the relationship between the propensity to violate dominant strategies and cognitive ability or risk aversion (see Sect. 3.4). In this section, we summarize recent work that connects the findings from matching experiments with behavioral theories.
5.1 Loss aversion
Two recent theoretical papers show that loss aversion can explain the observed dominated reports in DA (Dreyfuss et al. 2019; Meisner and von Wangenheim 2019). While the two papers take different modeling assumptions, they share the following intuition: if an agent only has a small chance of being accepted to the most-preferred school, she might be better off not listing this school in her list. This is because the submitted rank-order list of schools induces expectations over the distribution of final assignments, creating a reference point. If the agent is not accepted by the most-preferred school, she experiences a loss relative to the reference point. Under relatively strong loss aversion, it can be optimal not to list the most-preferred school at all.
Note that the comparative statics of the models predict that agents with lower chances of getting their top choice are more likely to misrepresent their preferences, which holds true, on average, for the experiments surveyed. Meisner and von Wangenheim (2019) also characterize the set of rationalizable strategies through loss aversion while Dreyfuss et al. (2019) show that their predictions are in line with the experimental data in Li (2017). There are no direct tests yet of the predictions of these models which could identify and test potential differences between them.
5.2 Complexity of finding the optimal strategy
Several papers address the question of the complexity of finding the dominant strategies. Li (2017) introduces the concept of obvious strategy-proofness (OSP). It is defined only for extensive-form games. A truthful strategy is obviously dominant if, for any deviating strategy, starting from any earliest deviation from the truthful strategy, the best possible outcome from the deviating strategy is no better than the worst possible outcome from the truthful strategy. A mechanism is obviously strategy-proof if it has an equilibrium in obviously dominant strategies. As discussed in Sect. 3.10, the concept explains the higher truth-telling rates in the sequential version of SD compared to direct SD. Unlike dominant strategies, obviously dominant strategies do not require foresight from the players. Pycia and Troyan (2019) go one step further, claiming that many OSP games are complicated, in the sense that they require perfect foresight from agents. They introduce the concept of strong obvious strategy-proofness that does not require foresight. In strong OSP, agents take an action only once, and this action is a direct selection of their final allocation. The truthful strategy in sequential SD also satisfies strong OSP. An empirical test of the predictions of OSP versus strong OSP has yet to be conducted.
Two recent papers take an opposite approach and consider the relaxation of implementation in dominant strategies while keeping the game simple. Börgers and Li (2019) consider games where equilibrium strategies depend only on the first-order beliefs of players and the assumption of rationality and call such strategies “strategically simple.” According to this concept, all games with dominant strategies are strategically simple. Thus, the results of Börgers and Li (2019) cannot be used to rationalize suboptimal behavior observed in DA. However, equilibrium strategies in BOS are not simple which might explain the experimental finding that the equilibrium is rarely reached in BOS. The other attempt to weaken strategy-proofness while keeping the game “simple” is by Bó and Hakimov (2020b) who consider mechanisms where equilibrium strategies are straightforward in the sense that the equilibrium consists of choosing the best object from a given menu, at each step of the mechanism. The equilibrium behavior has some similarities with OSP strategies for object allocation mechanisms. The authors argue that playing this equilibrium is often simpler than playing a dominant strategy in the direct mechanism. Their experimental results support this hypothesis for TTC. The argument is also in line with the experimental results of Klijn et al. (2019) on direct and sequential mechanisms.
5.3 Correlation neglect
When the clearinghouse restricts the number of options that can be listed in the submitted rank-order list, i.e., when the choice is constrained, the participants have to think strategically about which school to include in the list. It is essential to include a “safety school” in order to avoid being unassigned. A safety school is a school that would definitely accept the participant, i.e., where she has a high priority. Rees-Jones et al. (2020) show that correlation neglect can explain the failure of participants to include the safety school in the list. This is because participants fail to account for the correlation of preferences of schools and thus fail to understand that the rejection from a competitive school is informative about their chances at another highly competitive school.
5.4 Self-confidence
Pan (2019) shows that biased beliefs of students about their scores in entrance exams can hamper potential efficiency gains from BOS. The use of strategy-proof mechanisms limits this harm, since the reporting strategy is independent of expectations about exam scores. It is straightforward to speculate that self-confidence should affect the optimality of rank-order lists in constrained school choice (in addition to correlation neglect).Footnote 27
5.5 Social preferences
All experiments discussed so far assume that participants care only about their own payoffs. However, it is well documented in behavioral economics that payoffs of others may affect the decisions of agents. A recent paper by Haruvy (2019) studies the relevance of relative payoffs for two-sided matching. While a stable matching is robust to blocking by individual pairs, the matching can be blocked by a coalition of agents on the same side of the market who move the matching to another stable matching that is more favorable for them. The author predicts that this is more likely to happen when the payoffs are very unequal between the two sides, and when the increase in payoffs from switching to another stable matching is large.
In a lab experiment, Haruvy (2019) tests these hypotheses. In order to block a stable matching successfully, the agents of one side have to reject the proposed stable matching simultaneously in favor of an alternative matching. The treatments of the experiment vary the parameters of the game, such as the initial stable matching, the payoffs, and the preference profiles of both sides. Overall, the predictions regarding a coalition of agents blocking the stable matching find support. While proposers never block the proposer-optimal stable matching, a coalition of proposers often blocks the intermediate or receiver-optimal stable matching. The probability of a coalition blocking a matching depends on both the individual payoff difference between the matches and the aggregate payoff difference of all agents of the coalition. Thus, relative payoffs and inequality matter for stability.
5.6 Anticipated regret
Fernandez (2017) models the incentives of the receiving side in DA to truncate the submitted rank-order lists under incomplete information. He shows that if participants on the receiving side are averse to regret, they will avoid truncations of reported lists and instead report their preferences truthfully.
5.7 Summary
The strategies pursued in matching markets have only recently been investigated systematically from the point of view of existing behavioral theories. More research is needed to understand the relative importance of these behavioral factors, as well as to identify other behavioral aspects that are relevant for school choice and centralized college admissions.
6 Conclusions
The purpose and style of experiments on school choice and college admissions has changed over time. Many of the early experiments were tests of the theory. Horse races between different school choice mechanisms were conducted. Recently, many studies have dealt with systematic biases in behavior that matter in matching markets, such as bounded rationality, biased self-assessments, etc. Moreover, recent work also focuses on the question of how the exact implementation of a mechanism, e.g., static versus dynamic, with or without advice, affects market outcomes. Thus, the matching literature has started to establish behavioral regularities that can be of interest for policy makers involved in market design and behavioral theorists.
Matching experiments are not only of interest for researchers working in the area of matching markets but they also shed light on questions that are relevant for mechanism design in general. For example, the robust finding that people often do not play their dominant strategy under DA challenges the concept of implementation in dominant strategies. It is important to understand the causes of this behavioral regularity and the conditions under which dominant strategies are actually chosen. We believe that theories addressing the behavioral regularities will prove useful in systematizing these findings. At the same time, market design is needed to come up with mechanisms that are simpler in the sense that more people understand that truth-telling is optimal. While we cover some of the first behavioral theories that address this question, we believe this is only the start.
This survey showcases research that has predominantly been conducted over the past 20 years. We believe that the dialogue between experimentalists, theorists, and practitioners in the domain of matching markets has been a fruitful one. More recently, empirical work using data from the field has entered the scene, often confirming the external validity of experimental findings but also leading to novel results.
At the same time, we believe that there are many open questions that deserve closer scrutiny. A more rigorous consideration of certain established behavioral biases in the context of matching seems fruitful. For example, it could be investigated whether the district-school bias is due to an endowment effect. Also, self-deception and wishful thinking could play a role when making choices between programs. Moreover, the environment is changing constantly with new requirements and opportunities. For example, many clearinghouses have started to rely on more frequent interactions with the participants during the matching procedure through online systems. This opens up new possibilities, in particular with respect to the transparency of the matching procedure, but it also creates new challenges and questions.
Notes
We focus on experiments based on the school choice and the college admissions model which are not part of the survey chapter by Roth (2015). We cite all experimental papers on these topics that we are aware of to date. The handbook chapter mainly covers auctions and labor market clearinghouses (with a focus on unraveling and exploding offers), decentralized markets as well as course allocation.
It is worth noting that student subjects in experiments about college admissions are similar to the target population. While students often serve as a convenience sample, they are the relevant sample for these matching experiments, which increases their external validity.
This interpretation is true only for individually rational matchings, where no student is forced to attend a school which is worse than her outside option. In what follows only individually rational mechanisms are considered.
The existence of at least one cycle is guaranteed since there are finitely many agents. A cycle can consist of one student pointing to herself, one student and one school pointing to each other, four, six, or another equal number of students and schools pointing at each other such that the first member of a cycle points to the second, the second to the third …, and the last points to the first.
Being assigned to herself means that the student will remain unmatched.
A relatively large literature of matching experiments on one-sided matching concerns the house-allocation and course-allocation problems. A survey of these papers can be found in the working paper version, see Hakimov and Kübler (2019). For a survey of the course-allocation literature see Roth (2015). Another related literature studies object allocation without money in the context of booking systems, e.g., for appointments at public offices. Insights from matching can help in fighting undesirable properties of these systems, see a recent experiment by Hakimov et al. (2019).
Note that in this section we consider only the students as agents. We therefore say that DA is strategy-proof. It is not strategy-proof for schools but they are not considered as players in the one-sided matching setup. School-DA is not strategy-proof for either for the students or the schools.
Truthful preference revelation means that a full list is submitted which corresponds to the true ranking for BOS. For TTC and DA truthful preference revelation in the study required only reported choices from the first to the district school to be truthful for DA and TTC. This is because the district school is a guaranteed school, and all choices below it are irrelevant for the allocation under DA and TTC.
For instance, in the baseline treatment of Klijn et al. (2013), which is a replication of Chen and Sönmez (2006), the proportion of truthful preference revelation under TTC is higher than under DA. The main result of Chen and Sönmez (2006), however, that the proportion of truthful preference revelation under DA is higher than under BOS, was replicated in the designed and random environments of the baseline treatments of Klijn et al. (2013) and in the designed environment of the baseline treatment of Koutout et al. (2018).
Recombinant estimation is a technique from statistics that allows for a robust estimation of group-level outcomes in one-shot games. Assuming that the strategies of subjects are independent of the identity of the partners (due to the one-shot nature of the interaction), one can recombine players from different sessions, and calculate an allocation for each recombination. The recombination technique leads to a distribution of possible outcomes and thus to a more robust estimation of treatment differences.
In zero information, participants only know their own preferences and the capacities of schools. In low information, subjects also know each school’s favorite student. In partial information, they additionally know the favorite students at each school up to capacity. In full information, they know the full priority lists of schools and the preferences of all students.
Partial information on the strategies of the computer players included a statement that some players manipulate their reports in an unknown way in one treatment. In another treatment, the participants were given an exact report of one of the computer player’s non-truthful choices.
To the best of our knowledge, there are no studies in which subjects play TTC for multiple rounds.
This conjecture is also supported by Hakimov and Kesten (2018) who test TTC against another strategy-proof and Pareto efficient mechanism, equitable TTC. They use markets with three, four, and five schools. Truthful reporting is highest in the markets with three schools, and lowest in the market with five schools. There is no significant difference between rates of truthful reporting under the different mechanisms.
Hassidim et al. (2017) list the following potential explanations for the observed deviations: Failure to identify the dominant strategy; mistrust toward the designer; self-selection, meaning that participants do not list those schools high on the list to which they assign zero probability of being accepted; non-standard utility. In addition, some manipulations in experiments might be due to a demand effect. Subjects may believe that truth-telling is too simple and therefore cannot be optimal.
The findings of Calsamiglia et al. (2010) were replicated for DA by Bó and Hakimov (2020a) who compared standard DA to constrained DA as a robustness check, and find that constrained DA leads to stable matches significantly less often than unconstrained DA. These results are reported on in the appendix of their paper. Also, efficiency under constrained DA is significantly lower than under unconstrained DA. These relationships also hold for the iterative versions of DA where the constraint means a limit on the maximum number of steps of the iterative procedure.
The results are related to the evidence in Pais and Pintér (2008) who find that information about the preferences of others decreases truthful reporting in DA. If this was the case in the experiment by Chen and He (2017), subjects would not only pay for information that is irrelevant but even for information that makes them submit worse choices. Chen and He (2017) do not analyze their data with respect to this question, however.
Stability is defined here with respect to the abilities of students and not with respect to exam grades which are a noisy measure of ability.
The study uses a setup where schools only have one seat each. Therefore, the schools only make one proposal at a time.
Bó and Hakimov (2020a) observe a significantly higher rate of truth-telling in the dynamic mechanism while this is not significant in Klijn et al. (2019). This difference in the results may be due to the environments studied, namely markets with four schools in Klijn et al. versus eight schools in Bó and Hakimov. Additionally, the choice of the informational setup of the experiments (complete versus incomplete information about the priorities) might contribute to the difference.
There is no stable and strategy-proof mechanism for colleges (Roth and Sotomayor 1990).
In the working paper version (Hakimov and Kesten 2018), we also present research on unstructured interactions in two-sided matching markets, and the possible unraveling of such markets.
The authors also study BOS and TTC in a two-sided market and compare them to DA. The main result is that DA leads to the lowest proportion of stable matchings among the mechanisms. This finding is driven by low rates of truthful reporting by the proposing side, and suboptimal preference manipulations by the receiving side in DA.
This is consistent with the observations from school choice experiments in DA and dynamic DA where students move up on their list those schools that rank them highly.
A causal effect of self-confidence on matching markets has been shown in the context of unraveling. It is found that under-confidence leads to more early offers being accepted, and thus distorts market outcome away from efficiency (see Dargnies et al. 2019 for details).
References
Abdulkadiroğlu, A., Che, Y.-K., & Yasuda, Y. (2011). Resolving conflicting preferences in school choice: The ‘Boston mechanism’ reconsidered. American Economic Review, 101(1), 399–410.
Abdulkadiroğlu, A., Pathak, P. A., Roth, A. E., & Sönmez, T. (2005). The Boston public school match. American Economic Review, 95(2), 368–371.
Abdulkadiroğlu, A., & Sönmez, T. (2003). School choice: A mechanism design approach. American Economic Review, 93(3), 729–747.
Alcalde, J., & Barberà, S. (1994). Top dominance and the possibility of strategy-proof stable solutions to matching problems. Economic Theory, 4(3), 417–435.
Basteck, C., Klaus, B., & Kübler, D. (2018). How lotteries in school choice help to level the playing field. Working paper.
Basteck, C., & Mantovani, M. (2018a). Cognitive ability and games of school choice. Games and Economic Behavior, 109, 156–183.
Basteck, C., & Mantovani, M. (2018b). Aiding applicants: Leveling the playing field within the immediate acceptance mechanism. Working paper.
Bó, I., & Hakimov, R. (2020a). Iterative versus standard deferred acceptance: Experimental evidence. The Economic Journal, 130(626), 356–392.
Bó, I., & Hakimov, R. (2020b). Pick-an-object mechanisms. Working paper.
Börgers, T., & Li, J. (2019). Strategically simple mechanisms. Econometrica, 87(6), 2003–2035.
Braun, S., Dwenger, N., Kübler, D., & Westkamp, A. (2014). Implementing quotas in university admissions: An experimental analysis. Games and Economic Behavior, 85, 232–251.
Calsamiglia, C., Haeringer, G., & Klijn, F. (2010). Constrained school choice: An experimental study. American Economic Review, 100(4), 1860–1874.
Calsamiglia, C., Haeringer, G., & Klijn, F. (2011). A comment on “School choice: An experimental study. Journal of Economic Theory, 146(1), 392–396.
Castillo, M., & Dianat, A. (2016). Truncation strategies in two-sided matching markets: Theory and experiment. Games and Economic Behavior, 98, 180–196.
Castillo, M., & Dianat, A. (2017). Information effects in the dynamic Gale-Shapley mechanism: An experimental study. Working paper.
Chen, L., & Pereyra, J. S. (2020). Self-selection in school choice. Games and Economic Behavior, 117, 59–81.
Chen, Y., & He, Y. (2017). Information acquisition and provision in school choice: An experimental study. Working paper.
Chen, Y., Jiang, M., & Kesten, O. (2017). Chinese college admissions reforms: Experimental and empirical evaluations. Working paper.
Chen, Y., Jiang, M., Kesten, O., Robin, S., & Zhu, M. (2018). Matching in the large: An experimental study. Games and Economic Behavior, 110, 295–317.
Chen, Y., & Kesten, O. (2017). Chinese college admissions and school choice reforms: A theoretical analysis. Journal of Political Economy, 125(1), 99–139.
Chen, Y., & Kesten, O. (2019). Chinese college admissions and school choice reforms: An experimental study. Games and Economic Behavior, 115, 83–100.
Chen, Y., Liang, Y., & Sönmez, T. (2016). School choice under complete information: An experimental study. Journal of Mechanism and Institution Design, 1(1), 45–82.
Chen, Y., & Niederle, M. (forthcoming). Market design experiments: A survey of methods. In F. Echenique, N. Immorlica, & V. V. Vazirani (Eds.), Online and matching-based market design. New York, NY: Cambridge University Press.
Chen, Y., & Sönmez, T. (2006). School choice: An experimental study. Journal of Economic Theory, 127(1), 202–231.
Dargnies, M.-P., Hakimov, R., & Kübler, D. (2019). Self-confidence and unraveling in matching markets. Management Science, 65(12), 5449–5956.
Ding, T., & Schotter, A. (2017). Matching and chatting: An experimental study of the impact of network communication on school-matching mechanisms. Games and Economic Behavior, 103, 94–115.
Ding, T., & Schotter, A. (2019). Learning and mechanism design: An experimental test of school matching mechanisms with intergenerational advice. The Economic Journal, 129(623), 2779–2804.
Dreyfuss, B., Heffetz, O., & Rabin, M. (2019). Expectations-based loss aversion may help explain seemingly dominated choices in strategy-proof mechanisms. Working paper.
Dur, U., Hammond, R. G., & Kesten, O. (2018a). Sequential school choice: Theory and evidence from the field and lab. Working paper.
Dur, U., Hammond, R. G., & Morrill, T. (2018b). Identifying the harm of manipulable school-choice mechanisms. American Economic Journal: Economic Policy, 10(1), 187–213.
Dur, U., Hammond, R. G., & Morrill, T. (2018c). The secure Boston mechanism: Theory and experiments. Experimental Economics, pp. 1–36. https://doi.org/10.1007/s10683-018-9594-z.
Echenique, F., Wilson, A. J., & Yariv, L. (2016). Clearinghouses for two-sided matching: An experimental study. Quantitative Economics, 7, 449–482.
Ergin, H., & Sönmez, T. (2006). Games of school choice under the Boston mechanism. Journal of Public Economics, 90(1–2), 215–237.
Featherstone, C. R., & Mayefsky, E. (2015). Why do some clearinghouses yield stable outcomes? Experimental evidence on out-of-equilibrium truth-telling.. Working paper.
Featherstone, C. R., & Niederle, M. (2016). Boston versus deferred acceptance in an interim setting: An experimental investigation. Games and Economic Behavior, 100, 353–375.
Fernandez, M. A. (2017). Deferred acceptance and regret-free truth-telling: A characterization result.
Gong, B., & Liang, Y. (2017). A dynamic college admission mechanism in Inner Mongolia: Theory and experiment. Working paper.
Guillen, P., & Hakimov, R. (2017). Not quite the best response: truth-telling, strategy-proof matching, and the manipulation of others. Experimental Economics, 20(3), 670–686.
Guillen, P., & Hakimov, R. (2018). The Effectiveness of top-down advice in strategy-proof mechanisms: A field experiment. European Economic Review, 101, 505–511.
Guillen, P., & Hing, A. (2014). Lying through their teeth: Third party advice and truth telling in a strategy proof mechanism. European Economic Review, 70, 178–185.
Guillen, P., & Veszteg, R. (2019). Strategy-proofness in experimental matching markets.. Working paper.
Haeringer, G. (2017). Market design. Auctions and matching. Cambridge: MIT Press.
Hafalir, I. E., Yenmez, M. B., & Yildirim, M. A. (2013). Effective affirmative action in school choice. Theoretical Economics, 8(2), 325–363.
Hakimov, R., Heller, C. P., Kübler, D., & Kurino, M. (2019). How to avoid black markets for appointments with online booking systems. Working paper.
Hakimov, R., & Kesten, O. (2018). The equitable top trading cycles mechanism for school choice. International Economic Review, 59(4), 2219–2258.
Hakimov, R., & Kübler, D. (2019). Experiments on matching markets: A survey. No. SP II 2019-205, WZB Discussion Paper.
Harrison, G. W., & McCabe, K. A. (1996). Stability and preference distortion in resource matching: An experimental study of the marriage problem. In R. Mark Isaac (Ed.), Research in experimental economics, Vol. 6. Greenwich, CT: JAI Press, pp. 53–129.
Haruvy, E. (2019). On the importance of relative payoffs in two-sided matching. Journal of Institutional and Theoretical Economics, 175(1), 58–85.
Haruvy, E., & Ünver, M. U. (2007). Equilibrium selection and the role of information in repeated matching markets. Economics Letters, 94(2), 284–289.
Hassidim, A., Romm, A., & Shorrer, R. I. (2017). The mechanism is truthful, why aren’t you? American Economic Review: Papers & Proceedings, 107(5), 220–224.
Hassidim, A., Romm, A., & Shorrer, R. I. (2020). The limits of incentives in economic matching procedures. Management Science. https://doi.org/10.1287/mnsc.2020.3591.
He, Y., & Magnac, T. (2017). A Pigouvian approach to congestion in matching markets. Working paper.
Kawagoe, T., Matsubae, T., & Takizawa, H. (2018). The skipping-down strategy and stability in school choice problems with affirmative action: Theory and experiment. Games and Economic Behavior, 109, 212–239.
Kesten, O. (2010). School choice with consent. The Quarterly Journal of Economics, 125(3), 1297–1348.
Klijn, F., Pais, J., & Vorsatz, M. (2013). Preference intensities and risk aversion in school choice: A laboratory experiment. Experimental Economics, 16(1), 1–22.
Klijn, F., Pais, J., & Vorsatz, M. (2016). Affirmative action through minority reserves: An experimental study on school choice. Economics Letters, 139, 72–75.
Klijn, F., Pais, J., & Vorsatz, M. (2019). Static versus dynamic deferred acceptance in school choice: A laboratory experiment. Games and Economic Behavior, 113C, 147–163.
Kojima, F. (2012). School choice: Impossibilities for affirmative action. Games and Economic Behavior, 75(2), 685–693.
Koutout, K., Van der Linden, M., Dustan, A., & Wooders, M. (2018). Mechanism performance under strategy advice and sub-optimal play: A school-choice experiment. Working paper.
Li, S. (2017). Obviously strategy-proof mechanisms. American Economic Review, 107(11), 3257–3287.
Lien, J. W., Zheng, J., & Zhong, X. (2016). Preferences submission timing in school choice matching: Testing fairness and efficiency in the laboratory. Experimental Economics, 19, 116–150.
Matsubae, T. (2011). Do the minority students benefit from affirmative action policy in school choice markets? Reconsidered. Working paper.
Meisner, V., & von Wangenheim, J. (2019). School choice and loss aversion. Working paper.
Mullin, C. H., & Reiley, D. H. (2006). Recombinant estimation for normal-form games with applications to auctions and bargaining. Games and Economic Behavior, 54, 159–182.
Pais, J., & Pintér, A. (2008). School choice and information: An experimental study on matching mechanisms. Games and Economic Behavior, 64(1), 303–328.
Pais, J., Pintér, A., & Veszteg, R. F. (2011). College admissions and the role of information: An experimental study. International Economic Review, 52(3), 713–737.
Pan, S. (2019). The instability of matching with overconfident agents: Laboratory and field investigations. Games and Economic Behavior, 113, 396–415.
Pycia, M., & Troyan, P. (2019). A theory of simplicity in games and mechanism design.
Rees-Jones, A. (2018). Suboptimal behavior in strategy-proof mechanisms: Evidence from the residency match. Games and Economic Behavior, 108, 317–330.
Rees-Jones, A., Shorrer, R., & Tergiman, C. J. (2020). Correlation neglect in student-to-school matching. Working paper.
Rees-Jones, A., & Skowronek, S. (2018). An experimental investigation of preference misrepresentation in the residency match. Proceedings of the National Academy of Sciences, 115(45), 11471–11476.
Roth, A. E. (1982). The economics of matching: Stability and incentives. Mathematics of Operations Research, 7(4), 617–628.
Roth, A. E. (2015). Experiments in market design. In J. H. Kagel, & A. E. Roth (Eds.), Handbook of experimental economics (Vol. 2, pp. 290–346).
Roth, A. E., & Peranson, E. (1999). The redesign of the matching market for American physicians: Some engineering aspects of economic design. American Economic Review, 89(4), 748–780.
Roth, A. E., & Rothblum, U. G. (1999). Truncation strategies in matching markets—In search of advice for participants. Econometrica, 67(1), 21–43.
Roth, A. E., & Sotomayor, M. A. (1990). Two-sided matching: A study in game-theoretic modeling and analysis. Econometric Society Monograph Series. Cambridge: Cambridge University Press.
Schmelzer, A. (2016). Single versus multiple randomization in matching mechanisms. Working paper.
Schmelzer, A. (2018). Strategy-proofness of stochastic assignment mechanisms. Journal of Mechanism and Institution Design. https://doi.org/10.2139/ssrn.2997888.
Stephenson, D. G. (2016). Continuous feedback in school choice mechanisms.. Working paper.
Westkamp, A. (2013). An analysis of the German university admissions system. Economic Theory, 53, 561–589.
Zhu, M. (2015). Experience transmission: Truth-telling adoption in matching. Working paper.
Acknowledgements
Open access funding provided by University of Lausanne. The survey has benefited from frequent interactions with members of the Matching-in-Practice network. We would also like to thank Christian Basteck, Puja Bhattacharya, Inácio Bó, Yan Chen, Marie-Pierre Dargnies, Tingting Ding, Federico Echenique, Bob Hammond, Toshiji Kawagoe, Bettina Klaus, Martin van der Linden, Marco Mantovani, Joana Pais, Alex Rees-Jones, Assaf Romm, Andy Schotter, Utku Ünver, Roel van Veldhuizen, and Leeat Yariv for helpful comments on earlier drafts of the paper as well as Jennifer Rontganger for copy editing. We are grateful to two reviewers and the editor Marie Claire Villeval for constructive comments. Dorothea Kübler thanks Al Roth and Stanford University for their hospitality. Financial support from the DFG through CRC TRR 190 is gratefully acknowledged. Rustamdjan Hakimov acknowledges financial support from the Swiss National Science Foundation Project #100018_189152.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Design of matching experiments
Experiments on matching markets have a number of typical features in comparison to other lab experiments. First of all, matching experiments often focus on market outcomes, with less attention being paid to individual behavior. One important design issue is to achieve a sufficient number of independent observations in spite of larger matching groups due to market interactions. The experimental markets that are typically much smaller than real markets need to be designed in such a way that they capture the relevant features of larger markets. Finally, the procedures that are tested are usually more complicated than the games typically studied in the lab. This means that the instructions are longer, and often include several examples and quizzes. In this section we summarize the main methodological aspects of matching experiments and the trade-offs encountered when designing such experiments. For more detailed coverage of methodological aspects of market design experiments see a recent survey of Chen and Niederle (forthcoming).
1.1 Treatments
The majority of matching experiments tests the difference between matching mechanisms. Thus, one of the main treatment dimensions is the mechanism, and such treatments are almost exclusively run between subjects. The reason for this is the complexity of explaining the mechanisms to the subjects. The instructions typically include not only a description of the mechanism, but also examples of how the mechanism determines the allocation. Often, instructions do not use neutral language but a context-specific framing such as ‘workers and firms’ or ‘students and schools.’ The main purpose of such a framing is to contribute to a better understanding of the mechanisms.
1.2 Incentives
In all matching experiments subjects receive a monetary payoff corresponding to their matching outcome. In school choice, their payoff depends on which school they are matched to, for instance. By comparing the induced preferences to the rank-order lists submitted, researchers can measure the degree of truthful reporting. In repeated experiments, typically only one randomly determined round is payoff-relevant.
1.3 Markets
A crucial and one of the most challenging tasks when designing a matching experiment is to choose the appropriate markets, i.e., the preferences of subjects and the priorities. Once the market is chosen, the equilibrium allocation can be calculated. There are several decisions to make:
-
Size of market There are two dimensions to the size of markets:- the number of participants, and the number of schools and school seats. In all experiments so far on school choice and college admissions, the markets are balanced such that each subject can receive a seat. While smaller markets are easier to implement and yield more independent observations, larger markets are often more realistic. Some measures of interest, like the proportion of truth-telling subjects, may depend on the size of the market. As discussed in Sect. 4.2, markets with a greater number of schools tend to lead to a higher proportion of non-truthful reports.
-
Correlation of preferences/correlation of priorities Imagine the simplest case when all schools have one seat, all students have a different favorite school, and the respective schools also value the most those applicants that rank them highest. This is the simplest market, as there are no overdemanded objects, and thus all mechanisms that have been tested will lead to the same allocation: everyone receiving the best choice. This is different from a market where everyone likes the same object. The correlations of preferences and of priorities thus not only determine the underlying equilibrium allocation but are crucial for the perceived complexity of the decisions. While in many matching experiments, the markets are chosen to demonstrate a specific characteristic of a mechanism, the most common approach in school choice experiments is to generate markets that capture market characteristics observed in reality. Here, Chen and Sönmez (2006) were pioneers by introducing a procedure to design environments which mimic the preferences of students, and priorities of schools (see details in Sect. 4.1). The choice of particular markets can also be driven by the intention to demonstrate a specific treatment difference. For instance, when comparing the effect of a constrained rank-order list on the outcome of DA, it is crucial to make sure that the constraint is binding. That is, in the equilibrium outcome of DA, some students receive a school with a lower rank in their true preferences than the length of the constrained list.
1.4 One-shot versus repetition
Most participants in school choice and college admissions are inexperienced, since they participate in such markets only once in their lifetime. Therefore, one-shot experiments were originally perceived to be a good approximation of behavior in real markets. The other reason for running one-shot experiments was computational complexity. Many early experiments were run with paper and pencil, with payoffs being calculated afterwards. Nowadays, most matching mechanisms are programmed in zTree and oTree. Thus, running a computerized matching experiment with repeated interactions is not a problem anymore. One rationale for running multiple rounds of matching mechanisms is that experienced behavior might be a better approximation of the performance of the mechanisms, since it is likely that participants in real markets devote a lot of time and effort to studying the mechanism and getting advice from others.
1.5 Computerized agents
Some questions addressed in matching markets through experiments can benefit from a simplification of the decision environment to individual decision-making. This is often done when the focus of the study is whether the agents choose particular strategies, or whether they understand equilibrium strategies. In the case of substituting human subjects by robots, it is essential to explain the strategies played by the robots. Most often, they are programmed to maximize their payoffs. Alternatively, they can simulate real agents from other sessions. The choice depends on the research question. Note that the inclusion of computerized agents simplifies the decision of subjects in the experiments but makes it harder to claim external validity, especially with respect to matching outcomes.
1.6 Restricting the set of strategies
Some studies restrict the set of agents’ strategies by requiring the submission of full rank-order lists of preferences. Once the agents have a dominant strategy of truthful reporting, the submission of truncated lists is a dominated strategy. Note, however, that truncations can be optimal, for instance, if an agent is on the receiving side of DA. Some papers restrict the set of possible deviations from truthful strategies. Any restriction biases the results and should only be used when it does not bias the treatment comparison.
1.7 Outcomes of interest
There are two dimensions of outcomes.
-
Individual behavior The analysis of individual strategies often boils down to the comparison of rank-order lists submitted to the induced preferences of subjects. This is because a lot of attention in market design is devoted to developing strategically simple revelation mechanisms that are strategy proof. It is important to keep in mind, however, that the set of undominated strategies may include other strategies than reporting the full list truthfully, especially under complete information about preferences and priorities. Thus, undominated strategies have to be defined for each participant and each market separately. Some studies also consider equilibrium strategies, which is typically a richer set of strategies.
-
Properties of allocations Not every individual deviation from the predicted strategy is relevant for the allocation. This depends on the exact deviation, the market, and the strategies of others. The difference between the realized and the predicted market outcome can be used to measure the relevance of the observed deviations. Often attention in market experiments is given to the comparison of market allocations with respect to efficiency and stability. However, such measures are relative to the design of the markets which determines the scope of efficiency and stability differences.
Appendix 2: Additional tables
See Table 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hakimov, R., Kübler, D. Experiments on centralized school choice and college admissions: a survey. Exp Econ 24, 434–488 (2021). https://doi.org/10.1007/s10683-020-09667-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-020-09667-7