Abstract
It is well known that habitat boundaries affect ecological dynamics, but their influence on evolutionary dynamics is less well understood. Here, we study the effects of different kinds of boundaries on evolutionary branching in clonal populations along environmental gradients by systematically analyzing individual-based stochastic models in small- and large-range systems, as well as their large-population-size limits through deterministic approximations. Specifically, we examine four prototypical kinds of boundaries: impermeable boundaries at which individuals stop (“stopping”), or from which they continue back into the interior as if bouncing back mechanically (“reflecting”), or that let them abort the dispersal attempt, return to their original position and try a different direction (“reprising”), and semipermeable boundaries that can be crossed without hindrance, but do not allow the crossing individual to return (“absorbing”).We find that boundary conditions shape branching patterns only in small-range systems, where stopping boundaries generate disruptive selection for a wide range of parameters, whereas absorbing boundaries always generate stabilizing selection. Reflecting and reprising boundaries generate disruptive selection at low individual mobilities, and stabilizing selection at high mobilities. To further analyze these findings, we introduce a simple approximation of the invasion fitness in a mobile population, which predicts the observed outcome. The effect of stochasticity on evolutionary outcomes is small even in small populations: stochasticity causes random branch extinctions at steeper slopes and higher mobilities. In large-range systems, frequency-dependent interactions alone induce evolutionary branching for almost all parameters and independent of boundary conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
All natural habitats have boundaries, which influence ecosystem dynamics (Fagan et al. 1999; Strayer et al. 2003). Species diversity is known often to be higher at habitat boundaries than in a habitat’s more homogeneous interior regions (Kunin 1998; Schilthuizen 2000). Although such patterns have been recognized for some time, theoretical investigations often concentrate on model systems that deliberately attempt to exclude habitat edges, or minimize their effect. In turn, studies focusing on edge effects are mostly concerned with their influence on ecological dynamics (Matlack 1994; Strayer et al. 2003; Ries et al. 2004; Babak and He 2009). To date, little work seems to have been devoted to investigating the evolutionary consequences of habitat boundaries.
Biodiversity affects ecosystem structure and function, and thus ecosystem services (Sala et al. 2000; Foley et al. 2005). A general consensus is emerging that biodiversity often has a positive effect on sustainability (Millennium Ecosystem Assessment 2005; Mertz et al. 2007). A major component of biodiversity is species diversity which is generated through processes of extinction and speciation (Etienne and Apol 2009; Rabosky 2009; Sugden et al. 2009). Here, we investigate how habitat boundaries influence speciation. We are interested not in the well-established allopatric speciation scenarios (Mayr 1963), but in scenarios in which the emerging species share the habitat and its boundaries, i.e., scenarios of parapatric speciation.
Speciation in parapatry may be common (Gavrilets et al. 2000; Doebeli and Dieckmann 2003; Coyne and Orr 2004; Gavrilets 2004; Leimar et al. 2008; Ispolatov and Doebeli 2009), but the resulting biogeographic patterns are empirically not easily distinguishable from patterns resulting through divergence in allopatry and secondary contact (Endler 1977; Futuyma and Mayer 1980; Barton and Hewitt 1985; Doebeli and Dieckmann 2003). A thorough theoretical understanding of the ecological determinants of parapatric speciation is therefore required to correctly identify the past processes underlying extant biogeographic patterns (Doebeli and Dieckmann 2003; Dieckmann et al. 2004).
Parapatric speciation may occur as a coincidental by-product of divergent evolution (Darwin 1859; Fisher 1930) or genetic drift, if the gene flow between the involved demes is low enough (Wright 1943; Endler 1977). Parapatric speciation may also occur as an adaptive response to hybrid inferiority (Dobzhansky 1940). Of particular interest to us are scenarios in which hybrid inferiority is not caused by extrinsic factors (such as at an ecotone, a boundary between different habitats), but instead is the result of frequency-dependent interactions within the ancestral population (Rosenzweig 1978; Slatkin 1979a, b; Seger 1987; Dieckmann et al. 2004). In such scenarios of adaptive speciation, ecological differentiation through evolutionary branching in an ecological trait (Metz et al. 1996; Geritz et al. 1998; Dieckmann and Doebeli 1999; Doebeli and Dieckmann 2004; Doebeli 2011) is one prerequisite for speciation in sexual populations, while the other is the evolution of assortative mating (Fisher 1930; Dobzhansky 1940; Udovic 1980; Dieckmann and Doebeli 1999; Kirkpatrick 2000; Turelli et al. 2001; Matessi et al. 2002; Nosil et al. 2003, 2009; Doebeli 2005, 2011). We can isolate the ecological aspects of adaptive speciation by considering clonal populations, in which ecological differentiation is not hindered by recombination.
While adaptive speciation can occur in homogeneous environments if interactions are directly frequency-dependent (that is, explicitly depend on the interacting phenotypes; Taylor 1989; Christiansen 1991; Abrams et al. 1993; Dieckmann and Doebeli 1999; Dieckmann et al. 2004), it can occur under more general conditions in heterogeneous environments, where divergent evolution may induce a correlation between phenotype and location. One consequence of such a correlation is that localized interactions, even if they do not explicitly depend on phenotype, are effectively limited to certain phenotypes, namely, to those phenotypes that are likely to be encountered within an individual’s interaction range. In heterogeneous environments, effectively frequency-dependent selection may therefore be generated through any kind of localized interaction if the distribution of phenotypes is not uniform.
A simple and frequently discussed example of a heterogeneous environment is a linear environmental gradient, which implies that the ecological trait conferring optimal adaptation to the local environment changes linearly along a spatial direction (Roughgarden 1972). If mobility is not too high, density-dependent resource competition can stabilize phenotypic branches even if the strength of competition between individuals does not explicitly depend on their phenotypes (Doebeli and Dieckmann 2003).
Polechová and Barton (2005) have argued that such speciation under the condition of gradient-induced frequency-dependent selection was an artifact of habitat boundaries. Specifically, they showed that habitat boundaries alone can generate disruptive selection. This raises the general question of the effects of habitat boundaries on the process of adaptive speciation along environmental gradients. Here, we focus on ecological differentiation as one aspect of adaptive speciation, and analyze the influence that various kinds of boundaries can be expected to exert on evolutionary branching in an ecological trait.
The overall fitness of mobile individuals depends on the fitness they experience at the various locations visited during their lifetime. The direct effect of a boundary as understood here is to make certain locations (namely, those beyond the boundary) unreachable by dispersal. Therefore, the presence of boundaries may in principle alter the overall fitness of mobile individuals in the boundaries’ proximity, and evidently, individuals relatively close to a boundary are affected by its presence more than those farther away. If there exists, in addition, some correlation between phenotype and location, phenotypes more commonly found in the proximity of a boundary therefore experience a stronger fitness effect from the boundary than phenotypes more commonly found farther away. Hence, the mere presence of boundaries may generate selection for or against certain phenotypes (even if we do not consider that its phenotype may also directly affect an individual’s movement towards or its response to a boundary). This selection may be stabilizing or disruptive. We will show how these alternative impacts depend on how exactly dispersal dynamics are altered near the boundaries.
In this study, we reveal a specific consequence of spatio-phenotypic correlations by examining their impact on boundary effects. As highlighted above, such spatio-phenotypic correlations have two different fundamental, evolutionarily relevant, consequences: gradient-induced frequency-dependent selection, and boundary-induced selection. We disentangle these effects by systematically comparing the branching patterns obtained with a stochastic eco-evolutionary model and its deterministic large-population-size approximation for four different, commonly used boundary conditions, and for two different system ranges: a large-range system where the influence of boundary-induced selection is negligible, and a small-range system where boundary-induced selection can be expected to strongly influence the outcome.
Methods
We begin with some qualitative reasoning about boundary-induced selection along a one-dimensional environmental gradient. We then describe the four boundary conditions applied in the models and their effect on dispersal, and introduce the reproductive ratio as a fitness proxy. We finally turn to a detailed description of the models studied here, which we prepend with an overview of their basic structure, and with a discussion of the dimensionless parameters that determine model dynamics.
Boundaries affect fitness
We consider an individual that is optimally adapted at its location along the gradient. After a dispersal step, it will find itself in an environment to which it is not optimally adapted—thus, dispersal incurs a fitness penalty, which is greater on steeper gradients and for larger dispersal distances. Therefore, survival becomes more difficult on steeper gradients, as was already pointed out by Kirkpatrick and Barton (1997). In the absence of boundaries, this does not imply a fitness advantage or disadvantage for specific phenotypes, because—if their dispersal patterns are identical—all phenotypes will suffer the same penalty. Different fitness penalties for different phenotypes may arise, however, when boundaries exist, since these influence dispersal in characteristic ways.
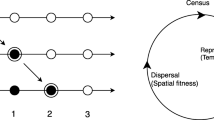
For stopping and absorbing boundaries, qualitative reasoning already allows us to understand the basic trends. Stopping boundaries interrupt dispersal steps, so the fitness loss for individuals adapted to locations near the boundary is smaller than the fitness loss for individuals adapted to locations more in the middle of the range (Fig. 1a). Effectively, stopping boundaries therefore produce a fitness advantage for extreme phenotypes—in other words, stopping boundaries generate disruptive selection. Conversely, absorbing boundaries always generate a fitness disadvantage for phenotypes adapted to locations closer to the boundaries, because of the increased probability of dying through dispersal (Fig. 1d). Reflecting and reprising boundaries tend to reposition individuals towards the interior (Fig. 1b, c), which may at higher mobilities be advantageous to individuals adapted near the middle. To develop a quantitative understanding, however, we must first formalize our description of how these boundary types influence dispersal.
Schematic illustration of fitness losses incurred by dispersal steps. a With stopping boundaries, individuals in the middle of the spatial range on average make larger dispersal steps than individuals near the boundaries, and consequently suffer a larger fitness loss (\(\Delta u > \Delta u^{{\prime }}\)). Since individuals are usually located where they are adapted, intermediate phenotypes are thus at a disadvantage as compared to extreme phenotypes—stopping boundaries hence generate disruptive selection (unless mobility is excessively large; Fig. 3a). b, c With reflecting and reprising boundaries, individuals near the boundaries suffer smaller fitness losses at lower mobilities, but higher fitness losses at higher mobilities than individuals in the middle (Fig. 3b, c). d With absorbing boundaries, individuals near the boundaries are lost more frequently than individuals in the middle of the spatial range. Extreme phenotypes are thus at a disadvantage—absorbing boundaries hence generate stabilizing selection (Fig. 3d)
Dispersal kernels
We incorporate the effect of a given boundary condition into the dispersal kernel d, assuming that the distribution of jump distances in the absence of boundaries would be described by a normalized Gaussian, i.e., \(d(x,x^{{\prime }} ) = N_{m} (x^{{\prime }} - x) = \exp ( - (x - x^{{\prime }} )^{2} /(2m^{2} ))/(\sqrt {2\pi } m)\), in which m is the scaled mobility, x the starting location, and \(x^{{\prime }}\) the target location along a one-dimensional environmental gradient. If boundaries are considered, this expression is possibly augmented by a term that describes, for all locations within the range, the probability that an individual that would have left the range in the absence of boundaries, ends up precisely there. In other words, we construct dispersal kernels by specifying how the probability mass of the “tails” cut off by the boundaries (shown in Gray in Fig. 2a) is redistributed, considering a certain boundary behavior.
Boundaries affect dispersal. a Boundaries at a = 0 and b = 1 cut off the tails of the Gaussian dispersal kernel (shown for location x = 0.3 and mobility m = 0.4). b Probability P to jump into a boundary from a location x ∊ [0, 1], shown for different mobilities from m = 0.02 (lowermost line) to m = 0.98 (uppermost line). The filled circle in b indicates the setting (x, m) shown in a
After introducing boundaries at a and b (to keep expressions generic; we will set a = 0 and b = L in our actual calculations), only locations \(x^{{\prime }} \in [a,b]\) are valid (Fig. 2a). Generally, the expected effect of boundaries is stronger if mobility is higher, because the rate at which individuals jump into the boundaries, and so experience their effect, increases with mobility (Fig. 2b). The boundary effect is therefore expected to depend on mobility.
We consider four dispersal kernels, which differ with respect to how individuals crossing the boundaries are handled. We implement stopping, reflecting, reprising, and absorbing boundaries. Of these, stopping, reflecting, and reprising boundaries implement the common assumption that the boundary is impermeable, that is, a barrier to movement.
Stopping boundaries
Stopping boundaries describe the situation that individuals are forced to, or decide to, abort their dispersal step at the boundary, if it would lead across. Consequently, the probability mass contained in the cut-off tails of the unperturbed kernel (see Fig. 2a) is assigned to the respective end points of the habitat, a or b. The associated dispersal kernel is therefore
in which the Dirac function δ, defined by \(\int_{ - \infty }^{\infty } {\delta (y - y_{0} )f(y)\,{\text{d}}y} = f(y_{0} )\), is used to assign the probabilities of jumps outside the valid range, obtained by integrating the unperturbed kernel from the boundary to infinity, to a and b, respectively. These integrals can be expressed via the so-called error function \(\text{erf}\), as shown in the second line.
This is also a computationally simple way to implement impermeable boundaries, and the one chosen in Doebeli and Dieckmann (2003) for movement in direction of the gradient. Population densities at stopping boundaries tend to be higher than in the interior.
Reflecting boundaries
Reflecting boundaries describe the situation that individuals complete their dispersal step by changing direction, as if bouncing off a wall, if it would lead across. Consequently, the cut-off tails of the unperturbed kernel (see Fig. 2a) are mirrored back into the interior, mirrored again at the other boundary etc., leading to an infinite number of additive terms, which, however, quickly decrease in magnitude. The associated dispersal kernel is therefore
In practice—for reasonable mobilities—this infinite series can be truncated after only a few terms. This boundary condition has a certain appeal because it preserves the length of the dispersal step, and mostly prevents crowding at the boundary.
Reprising boundaries
Reprising boundaries describe the situation that individuals realize the futility of their attempt to move to a point beyond the boundary, return to their location, and try another direction at random until they succeed in completing a dispersal step. Consequently, the probability mass in the tails is equally distributed over all accessible target locations, which amounts to simply renormalizing the unperturbed kernel in [a, b] as
The relative probabilities for jumps to valid locations remain the same as with the unperturbed kernel. Reprising boundaries are easily implemented by the computational rule: “Given a source location x, draw target locations \(x^{{\prime }} \sim\;N_{m} (x^{{\prime }} - x)\) until \(x^{{\prime }} \in [a,b]\)”, but applying this method in an individual-based model is relatively costly, as it may require generating and testing many random numbers until a new location is accepted. Like the reflecting boundary condition, this boundary condition preserves the length of the dispersal step, and also prevents crowding of the boundary. At lower mobilities, however, it can lead to reduced population densities near the boundary.
Absorbing boundaries
In contrast to the impermeable boundaries introduced above, absorbing boundaries describe a situation where individuals can cross the boundary and do so without hesitation, but are then lost and never return or interact with individuals within the region under consideration. Consequently, if a dispersal step would lead across the boundary, the individual is simply removed from the population. The associated dispersal kernel is the unperturbed kernel,
but defined only for locations in [a, b]. This dispersal kernel is thus not normalized in [a, b], which reflects the fact that it does not preserve the total abundance. At higher dispersal rates, there is consequently a risk of extinction resulting from the added density-independent mortality due to dispersal beyond boundaries. This happens almost certainly if the expected dispersal distance per generation is higher than the expected distance from the boundaries. We therefore estimate the threshold mobility in a well-mixed population as
For m > m*, rapid dispersal-induced extinction due to loss through the boundaries is very likely. Even when, at smaller mobilities, the population persists, population densities at absorbing boundaries are always smaller than in the interior.
Demographic models
To assess the robustness of our results with respect to demographic assumptions, we consider two different demographic models. The first model (fecundity-regulated model) is based on the well-known discrete-time logistic equation, assumes non-overlapping generations, synchronized seasonal reproduction, and dispersal only at birth. Fecundities depend on location and local competition. The second model (mortality-regulated model) follows previous studies of evolutionary branching on environmental gradients (e.g., Doebeli and Dieckmann 2003; Doebeli 2005; Leimar et al. 2008; Ispolatov and Doebeli 2009) and assumes overlapping generations, dispersal also outside of birth events, and density-dependent mortalities with constant fecundities. In both models, reproduction creates offspring (possibly mutated) at the location of the parent, from where they immediately disperse. Dispersal is equal across all individuals and independent of location.
For both demographic models, we investigate individual-based stochastic versions and their deterministic approximations. Their differences are summarized in Table 1.
Environmental gradient
In all models, individuals are, in addition to their location, characterized by a quantitative ecological character u (“phenotype”), which describes adaptation to the local environment. Following Roughgarden (1972), we assume a linear environmental gradient by considering a linear map from location to the specific phenotype locally optimally adapted to the available environmental resources. Phenotypes deviating from the locally optimal phenotype experience a diminished carrying capacity, which reduces their fecundity in a way described in detail in the model descriptions below. Thus, a certain range of phenotypes around the optimal phenotype is supported at any location, depending on how quickly the carrying capacity decreases with phenotypic distance from the optimal type. We call this characteristic range the resource width.
Parameters and dimensional analysis
We utilize several scales naturally present in the considered models to define dimensionless quantities, and thus reduce the number of effective parameters in the models described below. We apply the general convention to denote a dimensional, unscaled quantity by a symbol with a “hat”, e.g., \(\hat{a}\), and the corresponding scaled, dimensionless quantity by the same symbol without the hat, e.g., a.
A natural time scale is provided by the cyclic reproduction schedule of the population. All other quantities are defined with respect to this generation time.
There are three relevant length scales in the system: its spatial extent \(\hat{L}\), or “range”, the expected dispersal distance of offspring individuals \(\hat{m}\) (in the absence of boundaries), and the average distance \(\hat{\sigma }\) over which competitive interactions manifest. We use the latter to scale the two former, thus setting the scaled interaction distance to 1, and introducing the scaled mobility \(m = \hat{m}/\hat{\sigma }\). Without loss of generality, we then fix the system boundaries at x = 0 and \(x = L = \hat{L}/\hat{\sigma }\).
The linear environmental gradient is characterized by specifying by how many units of phenotype the locally optimal phenotype changes per unit of space; it is described by a certain slope \(\hat{s}\). Since we assume the phenotypic resource width \(\hat{r}\) to be constant with respect to location and time, it can serve as a unit of phenotype (thus setting the scaled resource width to 1). We can therefore fully characterize the gradient by a single dimensionless quantity, the scaled slope \(s = \hat{s}\hat{\sigma }/\hat{r}\).
The dynamical behavior of the models therefore depends essentially on three dimensionless parameters: the scaled slope s of the gradient, the scaled mobility m of the individuals, and the scaled system range L.
Deterministic fecundity-regulated model
We specify the deterministic model first, because it has the same essential structure as the full stochastic model, but is otherwise simpler.
Individuals are characterized by their one-dimensional location x ∊ [0, L] along the gradient and their phenotype u ∊ (− ∞, ∞). Individuals sequentially disperse, reproduce, and die in synchrony. On this basis, we study the deterministic approximation for the population density n(u, x, t) as a function of location, phenotype, and generation. The density in the next generation is given by
with an individual fecundity following the well-known discrete-time logistic-growth model with a low-density growth rate b,
in which the effective competition
with the competition kernel \(c(x^{{\prime \prime }} ,x^{{\prime }} ) = \exp ( - (x^{{\prime \prime }} - x^{{\prime }} )^{2} /2)\) describing the competitive impact of all other individuals on the focal individual. The effective carrying capacity
in Eq. 6b accounts for local adaptation to a linear environmental gradient of slope s and also for the lack of competitors beyond the boundaries. The subscript (…)+ in Eq. 6b indicates that only positive values are taken (the fecundity cannot be smaller than 0). The inner integral in Eq. 6a describes mutation with a Gaussian mutation kernel \(h(u^{{\prime }} ,u) = \exp ( - (u^{{\prime }} - u)^{2} /(2\mu^{2} ))/(\sqrt {2\pi } \mu )\), while the outer integral describes offspring dispersal according to a dispersal kernel \(d(x,x^{{\prime }} )\) (see Dispersal kernels).
We assume a cline-like initial density, that is, individuals are distributed uniformly along the gradient and locally optimally adapted. Given a gradient slope s, individual mobility m, and system range L, we numerically obtain solutions by iterating Eqs. 6 on a fine grid until the initial density has converged to a stationary density.
While the range of possible phenotypes is infinite, in practice only phenotypes sufficiently close to the range [0, sL] can be supported by the gradient, because \(K(u^{{\prime }} ,x^{{\prime }} )\) quickly converges to zero for phenotypes farther outside this range. This makes the \(u^{{\prime }}\)-integration in Eqs. 6a,c numerically feasible. All parameter values are given in Table 2.
Approximation of invasion fitness in a mobile population
We analyze the selective effects of boundary conditions in the model introduced above quantitatively by calculating a phenotype’s invasion fitness, that is, its long-term reproductive ratio when the phenotype is rare and the monomorphic resident background population is at equilibrium (Metz et al. 1992; Metz 2008), neglecting further mutation after the appearance of the mutant. This calculation is feasible because the generational structure (Eq. 6a) allows us to write down the dynamics of the spatial density distribution n(u, x, t) of a rare variant phenotype u at time t as
in which d is a dispersal kernel and \(f(u,x^{{\prime }} )\) the fecundity an individual of phenotype u at location \(x^{{\prime }}\), which also depends on the stationary resident density. Note that the integration is taken over source locations. Denoting the total abundance of the rare phenotype u at a time t by Nt(u) and introducing the probability density pu,t = n(u, x, t)/Nt(u), Eq. 7 yields
where we have also reversed the order of integration. We thus see that the current reproductive ratio of a rare variant phenotype in an equilibrated resident population is given by its expected average number of offspring after dispersal. The spatial distribution described by pu,t(x) is itself a target of selection; however, after an initial transient period, it will be unimodal with a peak at \(\bar{x} = u/s\), that is, at the location where phenotype u enjoys its maximal reproductive success (Eq. 6b). When pu,t(x) stabilizes, so does the reproductive ratio in Eq. 7, which then describes the long-term reproductive ratio R(u) of u, as required by the definition of invasion fitness. Although we generally do not know the exact shape of pu,t(x), and thus of pu(x) = limt→∞ pu,t(x), we can make use of the fact that it has a strong peak at \(\hat{x} = u/s\), to expand the outer integral in Eq. 8 via a moment expansion (Gillespie 1981), which yields
The piecewise-defined fecundity in Eq. 6b is not very integration-friendly; we note, however, that \(1 + b(1 - N_{\text{eff}} /K_{\text{eff}} ) = c_{1} \exp ( - c_{2} (u - xs)^{2} /2) + \mathcal{O}((u/s - x)^{3} )\) with constants c1 and c2 suitably composed of the constants in Eq. 6b (shown by expansion with respect to (u/s − x) around 0), and therefore approximate f(u, x) ≈ c1 exp (− c2(u − xs)2/2), which conveniently also captures the property of decreasing toward 0, but not below, with increasing distance from the optimal location.
Since mutants will typically be very similar to the residents, they will experience \(N_{\text{eff}} /K_{\text{eff}} \approx 1\). For this case, we find c1 ≈ 1 and c2 ≈ b. For the deterministic model specified below, the relative success of equally lucky mutants is therefore approximately determined by
where the integrand is composed of two factors, of which the first describes local adaptation and the second dispersal from the optimal location. Somewhat loosely, this invasion fitness of a phenotype can be understood as the average fitness of the offspring of locally very well adapted individuals, taking into account offspring dispersal into habitats of lesser quality.
We quantify the aforementioned considerations for all types of boundary conditions by calculating the reproductive ratio in Eq. 10, which depends on mobility and boundary conditions via the dispersal kernel (Eqs. 1–4). The results of these calculations confirm the expectations from our qualitative reasoning above: selection induced by stopping boundaries is disruptive unless mobilities are unrealistically high (Fig. 3a), while selection induced by absorbing boundaries is always stabilizing (Fig. 3d). For reflecting and reprising boundaries, there is a clear transition from a disruptive to a stabilizing regime at intermediate mobilities (Fig. 3b, c).
Predicted reproductive ratio as a function of phenotype (Eq. 10; based on the deterministic fecundity-regulated model) in the small-range system (L = 3), with a stopping, b reflecting, c reprising, and d absorbing boundaries, shown for different mobilities from m = 0.1 (uppermost line) to m = 4.9 (lowermost line) and for a scaled slope of s = 1. In a, the transition from disruptive (at lower mobilities) to stabilizing boundary-induced selection (at higher mobilities) occurs at m ≈ 3.5. In d, boundary-induced selection is stabilizing for all mobilities (although rapid dispersal-induced extinction (Eq. 6) is almost certain for higher mobilities, e.g., above about m = 1.5 when L = 3). In c and d, there are transitions from a disruptive to a stabilizing regime at intermediate mobilities, like in a, but there transitions occur already at lower mobilities of m ≈ 2.5 and m ≈ 1.5, respectively
Stochastic fecundity-regulated model
The stochastic model has the same structure as the deterministic model, but we keep track of a finite number of individuals with phenotypes ui at locations xi, i = 1…nt. In each generation, the number of offspring of each individual i is drawn from a Poisson distribution with a mean given by its fecundity \(f_{i} = (1 + b(1 - N_{{{\text{eff,}}i}} /K_{\text{eff}} (u_{i} ,x_{i} ))_{ + }\) as in Eq. 6b, only that the effective competition is now obtained as the sum \(N_{{{\text{eff,}}i}} = \sum\nolimits_{j = 1}^{{n_{t} }} {c(x_{j} ,x_{i} )}\), taken over the whole population (this implies self-competition, which describes resource utilization by the focal individual). Offspring individuals have phenotypes drawn from a Gaussian distribution centered on the parental phenotype, \(u_{k} \sim\;h(u_{i} ,u_{k} )\), and disperse from the parent location according to the dispersal kernel, \(x_{k} \sim\;d(x_{i} ,x_{k} )\). The offspring generation of size nt+1 so constructed replaces the parent generation. See Deterministic model for a description of the functions \(K_{\text{eff}}\), c, h, and Dispersal kernels for d.
As in the discrete model, the population is initially cline-like with individuals placed at random locations drawn from a uniform distribution and the locally optimal phenotype. All parameter values are given in Table 2.
Deterministic mortality-regulated model
In the second demographic model, individuals are also characterized by their one-dimensional location x ∊ [0, L] along the gradient and their phenotype u ∊ (− ∞, ∞). Individuals disperse, possibly die according to a density-dependent mortality, and possibly reproduce. On this basis, we study the deterministic approximation for the population density n(u, x, t) as a function of location, phenotype, and time. The density in the next time step is given by
in which b is the low-density birth rate, q the probability per time step to reproduce (we can define 1/q as a “generation”) and
is the individual survival probability over one time step. Dispersal kernel d, mutation kernel h, effective competition \(N_{\text{eff}}\) and carrying capacity \(K_{\text{eff}}\) are introduced above. Dispersal occurs with an adjusted mobility \(m^{{\prime }} = \sqrt {qm^{2} }\), so that m remains the mobility per generation as before.
Stochastic mortality-regulated model
The stochastic model has the same structure as the deterministic model, but we keep track of a finite number of individuals with phenotypes ui at locations xi, i = 1…nt. Each time step, each individual i survives with a probability \(s_{i} = 1/(1 + qN_{{{\text{eff,}}i}} /K_{\text{eff}} (u_{i} ,x_{i} ))\) as in Eq. 11b, only that the effective competition is now obtained as a sum taken over the whole population. Surviving individuals then reproduce with a fixed probability q. Offspring individuals have phenotypes drawn from a Gaussian distribution centered on the parental phenotype and are inserted into the population at the parental location. All individuals then disperse according to the dispersal kernel with an adjusted mobility \(m^{{\prime }}\) (see Deterministic mortality-regulated model above).
This model is closely related to the model studied by Doebeli and Dieckmann (2003). It differs by the discrete-time updating schedule, by omitting the ecologically neutral second spatial dimension, and by two minor modifications addressing issues that have been brought up on occasion: to address the issue that the Roughgarden fitness function (Roughgarden 1972) lets solitary individuals not incur any adverse effect of maladaptation, which is widely considered unrealistic, we include self-competition (Eq. 6c); to address the issue that individuals near system boundaries experience reduced competition due to the lack of competitors beyond the boundary, we introduce a correction factor in the expression for the effective carrying capacity (Eq. 6d).
Rationale for choice of parameters and initial conditions
To maximize conceptual simplicity, we have specified our models in scaled, dimensionless parameters (Table 2). Of these, the small system range has been chosen so that two branches located near the two boundaries can avoid competition with each other (three times the width of the interaction kernel). The carrying capacity has been chosen so as to have a similar number of individuals in the stochastic model as Doebeli and Dieckmann (2003). Our mutability has been chosen higher by a factor of 3, which reduces the waiting time to branching, but still avoids the “mutation catastrophe” scenario, where branches become blurry and unstable due to high mutation. The low-density growth rate has been chosen to be as high as possible without coming too close to the value of b = 2 where the discrete-time logistic growth equation is known to become unstable (although these troubles should be already averted by forcing the fecundity to be positive-semidefinite in Eq. 6b). The influence of the remaining three parameters is the focus of this study.
Our models follow the eco-evolutionary dynamics from an initial state to the evolutionarily stable state. For the initial state, we choose the so-called cline-like distribution, which is sometimes considered the natural equilibrium for evolution along an environmental gradient (Kirkpatrick and Barton 1997; Polechová and Barton 2005). The same results can be achieved by starting with monomorphic populations, at the cost of increased waiting times.
Branching analysis
A question of major importance in this study is whether, for any given set of parameters, evolutionary branching occurs; that is, whether a clear, evolutionarily stable bi-or multimodality can be seen in the distribution of phenotypes.
For the deterministic model, we look at the marginal phenotypic stationary density. Since there is no noise and the density is always symmetric around the center, it is easy to detect branches algorithmically. We convolve the histogram with the inverse of the mutation kernel (because the last step was a mutation step), remove densities smaller than 5% of the maximum, and require a separation > 0.1 (ten times the width of the mutation kernel) between remaining contiguous clusters. This is a relatively strong criterion and rejects many cases that already appear clearly bi- or multimodal to the human observer, but lack the deep density minimum between them.
For the stochastic model, we look at the histogram of phenotypes accumulated every 10 generations over a period of 500 generations to ascertain evolutionary stability. These histograms are similar in appearance to the marginal densities produced by the deterministic model, but unequal branch heights and noise spikes in general make automatic detection unfeasible. Histograms were therefore classified manually, requiring essentially the same separation and minima between peaks, but allowing for noise spikes. We were not quite sure about our judgement in less than 2% of the cases, which turn out to lie exactly along the borders of the branching regions reported here. We classify them here as “not branched”, but classifying them otherwise leaves the appearance of the branching regions virtually unchanged.
Results
For all models, outcomes depend significantly on the scaled slope s and the scaled mobility m. We investigate the parameter space (s, m) ∊ [0, 2] × [0, 5], which corresponds to the range of slopes and mobilities also studied by Doebeli and Dieckmann (2003). Calculations are done for 25 × 25 different combinations (s, m) chosen on a regular grid on [0, 2] × [0, 5]. For the discrete models, we analyze the stationary state; for the stochastic models, we evolve the system for 5000 generations and base our analysis on the average pattern of the last 500 generations (see Methods: Branching analysis). Other parameters are given in Table 2.
Boundary conditions shape branching patterns only in small-range systems
As a first step, we investigate the hypothesis that the effect of boundary conditions becomes less pronounced as the system range increases, and that it should therefore be possible to identify a system range where boundary-induced selection can be neglected. Figure 4 shows an illustrative example of stationary population densities in the fecundity-regulated models as a function of location and phenotype (for the deterministic models), and spatio-phenotypic distributions after 5000 generations (for the stochastic models) for all four boundary conditions and large and small system ranges. A ten-fold increase in system range suffices to achieve practically the same branching patterns irrespective of boundary condition. This is similarly true for all other combinations of slope and mobility. We conclude that the role of boundary-induced selection is negligible in the large-range system.
Boundary conditions shape branching patterns only in small-range systems. a–d, m–p Stationary spatio-phenotypic population densities obtained in the deterministic fecundity-regulated models (gray levels indicate the relative density: black = maximum) and e–l stationary spatio-phenotypic distributions of individuals obtained in the stochastic fecundity-regulated models (small squares indicate the locations of individuals) for a large-range system (L = 30; upper two rows) and a small-range-system (L = 3; lower two rows) and all four boundary conditions (columns). Parameters: s = 0.52, m = 0.9
Frequency-dependent interactions alone induce evolutionary branching
To identify the general conditions that promote evolutionary branching, we show in Fig. 5 the evolutionarily stable branching status (Methods: Branching analysis) over the entire slope–mobility range for all model versions, boundary conditions, and both the small-range and the large-range system. It turns out that in the absence of boundary-induced selection and other small-range effects, branching occurs nearly everywhere (Fig. 5a–h), with the sole exception of a small region at shallow slopes and low mobilities (labeled as 1 in Fig. 5; this region, as regions 2 and 3 introduced below, is not sharply delineated, but roughly indicates areas where certain effects become prominent, see Discussion).
Frequency-dependent interactions alone induce evolutionary branching for a wide range of conditions. In the same basic layout as in Fig. 4 shading indicates whether stationary branches emerge (colors) or not (light gray) in the fecundity-regulated models for given combinations of scaled slope and scaled mobility. Transparency before a white background indicates the corresponding population sizes (opaque = at nominal carrying capacity). Visibility of the background grid in the stochastic model versions indicates that the population went extinct. Boldface numbers indicate regions where in region 1, branching never occurs, in region 2, branching occurs in the large-range system, but not in the small-range system, and in region 3, branching may occur in the deterministic models, but not the stochastic models. (Color figure online)
Interestingly, branching in the large-range system occurs also in the region 2 at shallow slopes and higher mobilities, where branching is never observed in small-range systems. There is nearly no difference in branching patterns between deterministic and stochastic models, indicating that stochastic effects play a minor role even at the relatively small population sizes occurring here (< 600 individuals in the small-range system, < 6000 individuals in the large-range system). The exception is region 3, where branching is sometimes not observed in stochastic models when it does occur in the corresponding deterministic models (Fig. 5k, o).
We conclude that frequency-dependent interactions nearly always induce branching, unless small-range effects interfere.
Increased stochasticity suppresses branching
Branching patterns obtained from the mortality-regulated model (Fig. 6) are overall similar to the patterns obtained from the fecundity-regulated model (Fig. 5). However, the higher number of dispersal steps per generation (at the same mobility) increases overall mortality, resulting in significantly lower abundances on intermediate-to-steep gradients and thus favoring random branch extinction. Therefore, with the stochastic mortality-regulated models, branching is generally not observed in region 3 in small-range systems.
Increased stochasticity causes random branch extinction and so suppresses branching at steeper slopes and higher mobility. Population sizes predicted by the mortality-regulated model are lower than those predicted by the fecundity-regulated model at intermediate-to-steep slopes and intermediate-to-high mobilities (compare Fig. 5). The stochastic model shows no branching in region 3 even with stopping boundaries. Parameters as in Table 2, except b = 1 and K0 = 100
Robustness
Except for the stochasticity effects in small-range systems, the outcomes of all models investigated here are remarkably similar (compare Figs. 5 and 6). This highlights the robustness of our results.
Discussion
To investigate how boundaries influence evolutionary branching along an environmental gradient, we have constructed a class of models that allow disentangling the effects of boundary-induced selection from other effects. We discuss our main results below.
Boundary conditions shape branching patterns only in small-range systems
Our first result is that, while there is a marked effect of boundary conditions on evolutionary branching in small-range systems, the influence of boundary conditions disappears as system range increases. The small system range has been chosen so that the effect of competitive interactions across the whole range is negligible, which allows two branches to just barely evade competition with each other. Here, we have shown that a further increase of the range by a factor of 10 suffices to remove the influence of boundary conditions almost completely (Fig. 4), which provides the basis for investigating evolutionary branching in the absence of boundary-induced selection.
Frequency-dependent interactions alone induce evolutionary branching
Our main result is that in the absence of boundary-induced selection, that is, in large-range systems, evolutionary branching is the default outcome for nearly all parameter combinations (Figs. 5a–h and 6a–h). The sole exception is a small region at shallow slopes and small mobilities (region 1 in Figs. 5 and 6), where phenotypic clusters form along the gradient like pearls on a string, as they can achieve the spatial separation, but not enough phenotypic separation to be considered separate. This changes as mobilities increase, because increased mobilities increase the spatial extent, and therefore overlap, of these clusters and so force competition, which removes intermediates and leaves a few remaining, clearly separated clusters.
Branching at shallow slopes and higher mobilities does not occur in small-range systems, because there is simply not enough heterogeneity to sustain two separate branches (region 2 in Figs. 5 and 6). While at small mobilities a strongly platykurtic peak in the phenotype histogram hints at the presence of two or more clusters, at higher mobilities with increased competition, only one remains and the peak loses its platykurtic shape (compare also Sasaki and Dieckmann 2011). At intermediate and higher slopes, there is enough heterogeneity to sustain separated branches, and consequently this is also the region where branching is observed in small-range systems. Sufficient separation generally occurs at slightly lower slopes in the mortality-regulated model, which is due to the increased selection via dispersal-induced mortality (which at steeper slopes has the opposite effect, see Increased stochasticity suppresses branching below). At higher mobilities, dispersive overlap again suppresses branches and only one branch remains.
The disappearance of branching at higher mobilities is a general small-range effect, but not sufficient to explain all observed patterns, specifically, the differences among the boundary conditions. In contrast to what the small-range effect predicts, branching is observed also at high mobilities with stopping boundaries. Conversely, branching is noticeably suppressed already for intermediate mobilities with absorbing boundaries. This leads us to the notion of boundary-induced selection.
Boundary-induced selection
The results for the small-range system (Figs. 5i–p and 6i–p) show that boundary conditions influence selection. These results show good agreement with the predictions concerning boundary-induced selection resulting from the invasion fitness approximation (Fig. 3): stopping boundaries generate disruptive selection for a wide range of mobilities and slopes (Figs. 5i, m and 6i, m), while absorbing boundaries generate stabilizing or no selection everywhere (Fig. 5l, p and 6l, p). Reflecting and reprising boundaries generate disruptive selection at lower and stabilizing selection at higher mobilities (Figs. 5j, k, n, o and 6j, k, n, o).
Our calculation of the reproductive ratio as shown in Fig. 3 serves to illustrate the main mechanism behind the phenomenon of boundary-induced selection, but should still be understood as a mostly qualitative argument. In mobile populations, individuals are found not only at locations where they are optimally adapted. The overall success of a phenotype is mostly dependent on the success of the relatively well-adapted individuals expressing this phenotype, rather than on the success of the poorly-adapted ones (or, to put it more succinctly: evolution is driven by the winners, not the losers), but the extent to which poorly-adapted individuals also contribute to the overall evolutionary success of a phenotype is a priori not clear. This suggests an interesting target for future theoretical research.
Increased stochasticity suppresses branching
In the small-range system, branching is sometimes not observed in the stochastic models, although it is observed in the deterministic models (region 3 in Fig. 5k, o). This always occurs at high slopes and higher mobility. Population sizes there are very low, because only at the optimal location can substantial reproduction be achieved, and dispersal from there offers no advantage. As branches consist of so few individuals, they are prone to random extinctions, which destroy the multimodality predicted by the deterministic model. In the fecundity-regulated models, this happens only for reprising boundaries, while in the mortality-regulated models it is also observed for stopping and reflecting boundaries (Fig. 6i, j, m, n; Doebeli and Dieckmann 2003), where increased mortalities reduce abundances and make random branch extinctions more likely. This disappearance of branches at higher slopes and intermediate to high mobilities gives rise to the notion that intermediate slopes are most favorable to evolutionary branching (Doebeli and Dieckmann 2003; Doebeli 2005; Leimar et al. 2008; Ispolatov and Doebeli 2009), with random branch extinction at higher slopes and lack of heterogeneity and boundary-induced selection at lower slopes shaping the observed branching regions.
In the stochastic models, there is even a risk of complete extinction. This manifests mostly for absorbing boundaries at higher mobilities, where significant population loss through the boundaries occurs (Figs. 5l and 6l; Eq. 5), but may also occur for the other models, when none of the few remaining individuals happens to produce offspring (Figs. 5f–h and 6e–k).
Except for the aforementioned effects, the branching patterns predicted by stochastic and deterministic models are remarkably similar. Insofar minor differences in the onset of branching are even visible, they can probably be attributed to uncertainties in the branching analysis (Methods: Branching analysis).
Spatial patterns
Mimicking current practices of taxonomic classification, we have focused our analysis of branching patterns on the marginal phenotype distribution, and so far not considered the spatial configurations in which phenotypic clusters appear. Processes of spatial redistribution and diversification patterns interact and do not play out at very different and “independent” spatial scales, but spatial patterns emerge together with the phenotypic patterns.
In our small-range systems (which are so small that individuals located near either boundary barely escape competition with individuals near the other) branches are generally located near the boundaries. In our large-range systems (which may approximate many real-world systems better) branching is generally more pronounced near the boundaries, while the bulk region may often show only spatially anchored polymorphisms, but no branching in our stricter sense. This is probably due to the absence of competing clusters beyond the boundaries (the correction factor Eq. 6d only accounts for the competitive effect of the cline-like equilibrium distribution), which creates an advantage for individuals adapted there, which then exert strong competitive pressure in their neighborhood, removing individuals adapted there and so on, propagating a weakening boundary effect inward further and further.
Suggestions for empirical tests
Designing empirical or experimental tests of the branching patterns predicted here will require mapping some key ingredients of our models.
We have specified our models in terms of populations densities, dispersal patterns, and phenotypes. While population densities and their relation to environmental carrying capacity are widely understood, dispersal patterns must be explained though individual traits and extrinsic constraints, which allows the assignment of mobilities and the identification of boundary conditions, respectively. The phenotypes of interest are those that confer adaptation to the extrinsic environment. We elaborate on these points below. Firstly, there must be identifiable system boundaries of a kind that relates to the types discussed here. Passive dispersal as common, for example, in plants and sessile maritime organisms, can probably often be linked to absorbing boundaries (when they delineate a habitable region, but do not hinder dispersal as such) or stopping boundaries (when they hinder dispersal so that dispersers collect at the boundary). Active dispersal as common in animals can be linked to one of the impermeable boundary types if organisms possess behavioral traits that allow them to recognize or avoid the limits of their habitable region. In the absence of such traits, absorbing boundaries may again approximate the situation. Dispersal must be unconditional (i.e., not evaluate local conditions unrelated to habitat boundaries) and not evolve together with the ecological trait with respect to which branching is studied, although our models could be extended to these cases with moderate effort (Heinz et al. 2009; Payne et al. 2011).
Secondly, there must be a quantifiable gradient in an environmental character to which a quantitative trait confers adaptation. Environmental gradients are common, and only approximate linearity is probably good enough for comparison with our results (see Haller et al. 2013 for more complex scenarios). Also taking into account the requirement of relatively small spatial habitat ranges as compared to dispersal and interaction distances, temperature gradients across elevations may be one of the most obvious candidates in terrestrial systems, while in aquatic systems the benthic zone offers also, e.g., gradients in light intensity as interesting candidate gradients.
Thirdly, we have presented results for asexual reproduction, although the extension to sexual reproduction is straight-forward (Doebeli and Dieckmann 2003).
Together this would suggest that likely candidates for empirical tests could be found among terrestrial plants and maybe insects with habitats on mountain slopes, as well as in the sea among benthos dwellers. In the laboratory, bacterial systems would probably make good candidates for branching experiments.
The main phenomenon predicted by our models is that habitat boundaries on environmental gradients should generally be “speciation-prone” even in the absence of other ecological effects, in the sense that there should be different morphs (if not complete sister species) found at habitat boundaries than in the interior. The practical challenge will be to disentangle this predicted effect from other ecological effects (e.g., species richness due to richer environments at boundaries, as is often the case).
Conclusions
Boundaries influence selection. Boundary-induced selection is mostly disruptive for stopping boundaries and stabilizing or absent for absorbing boundaries. For reflecting and reprising boundaries, it is slightly disruptive at low mobilities, and stabilizing at high mobilities. Boundary-induced selection influences evolutionary branching and may, when disruptive, mask the effects of frequency-dependent selection. All this is, however, only relevant for small-range systems. For large-range systems, evolutionary branching occurs without being promoted by boundary effects for a wide range of parameters and all types of boundary conditions, clearly highlighting the potential of frequency-dependent interactions to generate evolutionary branches through disruptive selection whenever environmental heterogeneity can support them.
Finally, we highlight that boundaries, whether spatial or phenotypic, are a ubiquitous feature of natural systems. Evolutionary branching at realistic slopes and mobilities has now been found in several studies with different boundary conditions (Doebeli and Dieckmann 2003; Leimar et al. 2008; Ispolatov and Doebeli 2009) using very different methods: Doebeli and Dieckmann (2003) investigated an individual-based model, Leimar et al. (2008) analyzed the stability of homogeneous solutions to a partial differential equation against perturbations, and Ispolatov and Doebeli (2009) numerically studied a partial differential equation, examining non-abrupt boundaries. Together with these studies, our results confirm that, while boundary conditions have significant effects in small-range systems, evolutionary branching can occur for all salient types of boundaries.
References
Abrams PA, Matsuda H, Harada Y (1993) Evolutionarily unstable fitness maxima and stable fitness minima of continuous traits. Evol Ecol 7:465–487
Babak P, He F (2009) A neutral model of edge effects. Theor Popul Biol 75:76–83
Barton NH, Hewitt GM (1985) Analysis of hybrid zones. Annu Rev Ecol Syst 16:113–148
Christiansen FB (1991) On conditions for evolutionary stability for a continuously varying character. Am Nat 138:37–50
Coyne JA, Orr HA (2004) Speciation. Sinauer Associates, Sunderland, MA
Darwin C (1859) On the origin of species. John Murray, London
Dieckmann U, Doebeli M (1999) On the origin of species by sympatric speciation. Nature 400:354–357
Dieckmann U, Doebeli M, Metz JAJ, Tautz D (eds) (2004) Adaptive speciation. Cambridge University Press, Cambridge
Dobzhansky T (1940) Speciation as a stage in evolutionary divergence. Am Nat 74:312–321
Doebeli M (2005) Adaptive speciation when assortative mating is based on female preference for male marker traits. J Evol Biol 18:1587–1600
Doebeli M (2011) Adaptive diversification. Princeton University Press, Princeton
Doebeli M, Dieckmann U (2003) Speciation along environmental gradients. Nature 421:259–264
Doebeli M, Dieckmann U (2004) Adaptive dynamics of speciation: spatial structure. In: Dieckmann et al. (eds) Adaptive speciation, pp 140–167
Endler JA (1977) Geographic variation, speciation, and clines. Princeton University Press, Princeton
Etienne RS, Apol ME (2009) Estimating speciation and extinction rates from diversity data and the fossil record. Evolution 63:244–255
Fagan WF, Cantrell RS, Cosner C (1999) How habitat edges change species interactions. Am Nat 153:165–182
Fisher RA (1930) The genetical theory of natural selection. Oxford University Press, Oxford
Foley JA, DeFries R, Asner GP et al (2005) Global consequences of land use. Science 309:570–574
Futuyma DJ, Mayer GC (1980) Non-allopatric speciation in animals. Syst Zool 29:254–271
Gavrilets S (2004) Fitness landscapes and the origin of species. Princeton University Press, Princeton
Gavrilets S, Li H, Vose MD (2000) Patterns of parapatric speciation. Evolution 54:1126–1134
Geritz SAH, Kisdi É, Meszéna G, Metz JAJ (1998) Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol Ecol 12:35–57
Gillespie DT (1981) Moment expansion representation of probability density functions. Am J Phys 49:552–555
Haller BC, Mazzucco R, Dieckmann U (2013) Evolutionary branching in complex landscapes. Am Nat 182:E127–E141
Heinz SK, Mazzucco R, Dieckmann U (2009) Speciation and the evolution of dispersal along environmental gradients. Evol Ecol 23:53–70
Ispolatov J, Doebeli M (2009) Diversification along environmental gradients in spatially structured populations. Evol Ecol Res 11:295–304
Kirkpatrick M (2000) Reinforcement and divergence under assortative mating. Proc R Soc Lond B 26:1649–1655
Kirkpatrick M, Barton NH (1997) Evolution of a species’ range. Am Nat 150:1–23
Kunin WE (1998) Biodiversity at the edge: a test of the importance of spatial mass effects in the Rothamsted Park Grass experiments. Proc Natl Acad Sci USA 95:207–212
Leimar O, Doebeli M, Dieckmann U (2008) Evolution of phenotypic clusters through competition and local adaptation along an environmental gradient. Evolution 62:807–822
Matessi C, Gimelfarb A, Gavrilets S (2002) Long-term buildup of reproductive isolation promoted by disruptive selection: how far does it go? Selection 2:41–64
Matlack GR (1994) Vegetation dynamics of the forest edge–trends in space and successional time. J Ecol 82:113–123
Mayr E (1963) Animal species and evolution. Harvard University Press, Cambridge, MA
Mertz O, Ravnborg HM, Lövei GL, Nielsen I, Konijnendijk CC (2007) Ecosystem services and biodiversity in developing countries. Biodivers Conserv 16:2729–2737
Metz JAJ (2008) Fitness. In: Fath BD, Jørgensen SE (eds) Encyclopedia of ecology: evolutionary ecology. Elsevier, New York, pp 1599–1612
Metz JAJ, Nisbet RM, Geritz SAH (1992) How should we define ‘fitness’ for general ecological scenarios? Trends Ecol Evol 7:198–202
Metz JAJ, Geritz SAH, Jacobs FJA, van Heerwarden JS (1996) Adaptive dynamics: a geometrical study of the consequences of nearly faithful reproduction. In: van Strien SJ, Verdun Luynel SM (eds) Stochastic and spatial structures of dynamical systems. North Holland, Amsterdam, pp 183–231
Millennium Ecosystem Assessment (2005) Ecosystems and human well-being: synthesis. Island Press, Washington, DC
Nosil PB, Crespi J, Sandoval CP (2003) Reproductive isolation driven by the combined effects of ecological adaptation and reinforcement. Proc R Soc Lond B 270:1911–1918
Nosil P, Harmon LJ, Seehausen O (2009) Ecological explanations for (incomplete) speciation. Trends Ecol Evol 24:145–156
Payne JL, Mazzucco R, Dieckmann U (2011) The evolution of conditional dispersal and reproductive isolation along environmental gradients. J Theor Biol 273:147–155
Polechová J, Barton NH (2005) Speciation through competition: a critical review. Evolution 59:1194–1210
Rabosky DL (2009) Ecological limits and diversification rate: alternative paradigms to explain the variation in species richness among clades and regions. Ecol Lett 12:735–743
Ries L, Fletcher RJ, Battin J, Sisk TD (2004) Ecological responses to habitat edges: mechanisms, models, and variability explained. Annu Rev Ecol Evol Syst 35:491–522
Rosenzweig ML (1978) Competitive speciation. Biol J Linn Soc 10:275–289
Roughgarden J (1972) Evolution of niche width. Am Nat 106:683–718
Sala OE, Chapin FS, Armesto JJ et al (2000) Global biodiversity scenarios for the year 2100. Science 287:1770–1774
Sasaki A, Dieckmann U (2011) Oligomorphic dynamics for analyzing the quantitative genetics of adaptive speciation. J Math Biol 63:601–635
Schilthuizen M (2000) Ecotone: speciation-prone. Trends Ecol Evol 15:130–131
Seger J (1987) Intraspecific resource competition as a cause of sympatric speciation. In: Greenwood PJ, Harvey PH, Slatkin M (eds) Evolution: essays in honor of John Maynard Smith. Cambridge University Press, Cambridge, pp 43–53
Slatkin M (1979a) Frequency- and density-dependent selection on a quantitative character. Genetics 93:755–771
Slatkin M (1979b) The evolutionary response to frequency- and density-dependent interactions. Am Nat 114:384–398
Strayer DL, Power ME, Fagan WF, Pickett STA, Belnap JA (2003) Classification of ecological boundaries. Bioscience 53:723–729
Sugden A, Ash C, Hanson B, Zahn L (2009) Happy birthday, Mr. Darwin. Science 323:727
Taylor PD (1989) Evolutionary stability in one-parameter models under weak selection. Theor Popul Biol 36:125–143
Turelli M, Barton NH, Coyne JA (2001) Theory and speciation. Trends Ecol Evol 16:330–343
Udovic D (1980) Frequency-dependent selection, and the evolution of reproductive isolation. Am Nat 116:621–641
Wright S (1943) Isolation by distance. Genetics 28:114–138
Acknowledgements
RM acknowledges open access funding provided by University of Veterinary Medicine Vienna. RM and UD acknowledge financial support by the Vienna Science and Technology Fund. MD acknowledges financial support from NSERC, Canada. UD acknowledges additional financial support by the Austrian Science Fund, the Austrian Ministry of Science and Research, the European Science foundation, and the European Commission. The authors declare no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mazzucco, R., Doebeli, M. & Dieckmann, U. The influence of habitat boundaries on evolutionary branching along environmental gradients. Evol Ecol 32, 563–585 (2018). https://doi.org/10.1007/s10682-018-9956-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10682-018-9956-1