Parameterising a public good: how experiments on predation can be used to predict cheat frequencies

Abstract

Chemical defence is superficially easy to understand as a means for individuals to protect themselves from enemies. The evolution of chemical defence is however potentially complex because such defences may cause the generation of a public good, protecting members of the population as a whole as well as individuals that deploy toxins defensively. If a public good of protection exists, it may be exploited and degraded by “cheats” that do not invest in defence. This can in turn lead to complex frequency (and density) dependent effects in toxin evolution. To investigate this we used ecologically relevant predators (Great tits, Parus major) and examined how individual and public benefits vary depending on the frequency of non-defended “cheating” prey and their spatial distribution. We found that the public benefit, of reduced attack probability, increased with increasing frequency of defended individuals. In contrast the individual benefit of chemical defence, measured as increased chance of rejection during an attack before injury, did not vary with the frequency of defended forms. Hence the selective dynamics of these two levels of benefits responded differently to the frequency of defended forms. Surprisingly, given the strong associations of chemical defences and grouping in animals, large aggregations did not help individuals in the group regardless of their defence status. The explanation for the result, may be that in our experiment birds did not have information about other potential aggregations (i.e. set up was sequential) and thus their giving up density was lower compared to the situations where set ups were simultaneous. We use behavioural data of our predators to construct a simple model of toxin evolution which can make quantitative predictions about the frequencies to which defence cheats evolve. We use this model to discuss how toxin evolution can be investigated in the wild and in laboratory settings.

Introduction

Almost all organisms are vulnerable to attack by enemies. A consequence is that natural selection has favoured individuals that invest in cost effective defences. Some kinds of defence are localised within taxa, for example camouflage is seen in animals (Stevens and Merilaita 2011; Stevens 2013) but not (often) in plants (Schaefer and Ruxton 2011). In contrast chemical defences that poison and repel enemies are found across the tree of life in microbes, plants and animals. Chemical defences are not only common, but they are also highly diverse, varying between taxa, species and even individuals within populations (Jones et al. 1986). There are many different ways in which chemicals can be acquired for defence, including different forms of biosynthesis, dietary sequestration and symbiont exploitation (Bowers 1990, 1992b; Waterfield et al. 2009; Kusari et al. 2012; Moore et al. 2014). There are also many methods of deployment, including stings, secretions and toxicity (Whitman et al. 1990; Eisner et al. 2005).

Despite this almost bewildering diversity however there are several biological fundamentals which mean that it may be possible to draw some generally applicable conclusions about the evolution of chemical defence. First, defensive chemicals are often costly to obtain and maintain (Bowers 1992a; Strauss et al. 2002; Ruxton et al. 2004; Lindstedt et al. 2010; Karban 2011; Reudler et al. 2015). Biosynthesis has obvious metabolic costs, but even dietary acquisition of toxins in animals can impose costs including movement of toxins across the gut, the prevention of auto-toxicity (where the consumer is poisoned by the toxin it has ingested), and the maintenance of storage organs (Bowers 1992a). Using a symbiont, as when plants rely on fungal endophytes (Kusari et al. 2012), may be a good way of cheaply subcontracting costs of chemical defence synthesis, but the endophyte itself will require resources from the host plant.

A second fundamental characteristic is, perhaps obviously, that individuals usually benefit from deployment of their own chemical defences. Victims repel and often injure their enemies when they use toxins and venoms, so that their probability of surviving an encounter increases (Eisner et al. 2005). In some situations however, individuals may be killed before the toxin acts aversively on the enemy, such as when a caterpillar with internally stored toxins is eaten whole. Such late-acting toxins are hard to explain unless there is a large enough benefit for nearby relatives (Fisher 1958) or if prey toxicity is the fortuitous by-product of other metabolic functions and not primarily targeted to fight enemies.

This brings us to the third and perhaps least well considered fundamental of chemical defences, that they often generate a “public good of protection”. When chemical defences disable and subdue enemies, they confer a benefit on other potential victims because they reduce the activity of the enemy (Speed et al. 2012). In generating an early version of kin selection theory, Fisher reasoned that close family could often be the beneficiaries (Fisher 1958), but more recently it has become apparent that any individual whether related or not to a victim can benefit when predators are “taken out of action” by chemical defences (Mappes et al. 1999a; Speed et al. 2006; Svennungsen and Holen 2007a; Sherratt et al. 2009). Hence chemical defence can generate “public good of protection”, which extends to other individuals in a population, and perhaps between species too (Turner and Speed 1999). This public good is primarily a by-product from individual defence (e.g. a prey animal defends itself against immediate attack from a predator), but it may nonetheless influence the decisions that individual prey make about how much to invest in costly defences. If many prey have defended themselves and disabled many predators for example, then the per capita risk will be diminished, and potential victims may then reduce investment in chemical defence. Furthermore, if there are many chemically defended prey in a habitat, then it might pay for some individuals to cease defence investment altogether and instead allocate resources to reproduction. Daly et al. (2012a) for example showed that frequency of nondefended prey increased with group size in caterpillars of the large white butterfly (Pieris brassicae). Such non-defended individuals might be considered parasitic cheats if their presence in a population of defended prey has a consequence of raising the attack rates as indicated in several recent experiments (Gamberale-Stille and Guilford 2004; Skelhorn and Rowe 2007; Jones et al. 2013). These cheats are often known as “automimics” (Speed et al. 2006). Note that automimicry can be taxonomically very widespread, for example it is likely in aquatic systems in which microbes produce a localised diffusible toxin which repels predators before contact, and nondefended “cheats” can be present (Sherratt et al. 2009; Driscoll and Pepper 2010).

Several important experiments suggest that automimicry may be common in prey populations, including bacteria protecting themselves against protists and amoebae (Jousset et al. 2009) and in vascular plants (see discussion in Till-Bottraud and Gouyon 1992; Speed et al. 2012). For the public good explanation of automimicry to apply, it is key to demonstrate experimentally both individual and public benefits from chemical defence. This has been investigated most thoroughly with lab models of bird-insect systems, in which the predator is usually a young, naïve domestic chicken (Gallus gallus) and the prey are artificial crumbs (Gamberale-Stille and Guilford 2004; Skelhorn and Rowe 2006b; Skelhorn and Rowe 2007). In this context both individual benefits (raised survival) and public benefits (reduced predation frequency) have been demonstrated from chemical defence but it is important to note that the “survival rate” of taste-rejected prey is not easy to estimate when chick crumbs take the place of insect prey. There are fewer examinations with wild predators, though Carroll and Sherratt (2013) recently demonstrated reduced damage to individual prey. In our own investigations with free living adult birds (Jones et al. 2013) and mealworms as prey we found strong public benefits of reduced attack rates as chemical defence (a distasteful bitrex treatment) became more common, but we did not observe individual survival, in which defended prey are released before ingestion. Rather birds either ate the prey at the foraging site, or flew away from our feeding stations before deciding to eat or reject prey, making it difficult to determine whether, or the extent to which, individual prey benefitted from their chemical defence. The size of individual benefits conferred by wild predators is important to evaluate experimentally by observing prey survival and predator behaviour for a range of frequencies of automimics.

There is also a growing theoretical literature describing defence cheating in which a number of mathematical treatments show that cheats can invade populations of defended prey and reach intermediate frequencies which are evolutionarily stable (Till-Bottraud and Gouyon 1992; Broom et al. 2005; Speed et al. 2006; Ruxton and Speed 2006; Svennungsen and Holen 2007a; Svennungsen et al. 2011). There is though presently not a strong linkage between experimental and theoretical treatments of the public good of protection conferred by chemical defence. Experiments on automimicry tend not to be used to parameterise models and models generally do not make quantitative predictions about levels of cheating in natural populations (though see exceptions in Till-Bottraud and Gouyon 1992; Daly et al. 2012a). Some of the theory papers are (rightly) mathematically complex, and this complexity may obscure the simplicity of the underlying concepts that underpin defence cheating. We intend in this paper therefore to present a simple nontechnical explanation, which we hope bridges empirical and theoretical approaches to toxin evolution.

We can then identify two gaps in current knowledge. First, how do wild predators cause prey to contribute to individual and common benefits of prey protection? Second, how can experiments be linked with theoretical treatments of defence evolution? To attempt to fill these gaps, we first evaluate survival of nondefended aggregated and non-aggregated prey using wild-caught adult birds as predators (Great tits, Parus major) and insect larvae as prey. Subsequently we use data from the experiment to show how a simple, parameterised quantitative model can be used to predict rates of automimetic cheating for a range of assumptions about costs of defences and season lengths. We use this combination of data and theory to discuss the evolutionary ecology of chemical defence and propose alternative ways that it could be investigated by merging theoretical models and empirical work.

Experiment: quantifying individual and public goods from chemical defence

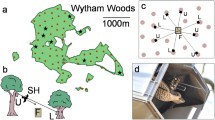
The rationale for merging theoretical models and empirical work is that there are currently no published datasets using wild predators with insect prey from which a simple model of automimicry can be parameterised. Published work uses young domesticated chickens (Gamberale-Stille and Guilford 2004; Skelhorn and Rowe 2007) whose feeding behaviour is rather different from most passerine birds. For example, chicks learn to find food items by pecking and tasting everything from non-organic objects to organic items. Instead passerine young learn from their parents “where to find food” and later the individual learning fine-tunes their food preferences (Langen 1996). Hence here we present great tits (Parus major) with mealworm prey that are either edible or unpalatable (soaked in quinine), and we gradually varied the frequency of distasteful prey (Mappes et al. 1999b). We extended the approach of Jones et al. (2013) by adding in variation in the degree of aggregation of the mealworms in this experiment.

Methods

Bird capture and housing

Fifty wild Great Tits (Parus major) were trapped at feeding sites at Konnevesi Research Station and Hytola, Finland from 13/11/13 to 11/12/13. Birds were kept in individually illuminated, ventilated plywood cages (64 × 46 × 77 cm) indoors with a 11.5:12.5 L:D cycle. Sunflower seeds, fat balls and fresh water were provided ad libitum except 2 h prior to experimental trials whereby birds were food deprived to ensure motivation to forage during experiments.

Prey design

Prey were mealworm larva (Tenebrio molitor) that were 15–20 mm in length, killed in 70 % ethanol for 1 min, and dried off. Palatable prey were rinsed with water and left to dry. Unpalatable prey were rinsed with water and then immersed in saturated quinine solution (chloroquinine diphosphate salt) for 5 min and left to dry. Quinine is bitter tasting and in high doses causes emesis in birds (Alcock 1970). These prey simulate those that have their toxins on the surface of their bodies as well as inside, such as hairy caterpillars that have histamine/irritating substances on their skin and hairs [e.g. many Arctiinae (Erebid) moth caterpillars] and many insect prey secrete toxins when attacked.

Experimental design

A total of 16 prey per trial were used with the relative frequency of cheats (palatable prey) varying from 0 to 1 in 0.25 increments. These various prey populations were then placed in either a “spatial” set-up of 4 small aggregations of 4 prey, or an “aggregated” set-up, one large aggregation of all 16 prey items. Prey communities were placed in corners of the cage behind black metal occluders (11 × 15 cm, bent at 12 cm to act as a base) so predators had to search behind each occluder for the prey and thus, they did not have information how many aggregations or prey items were available. Mealworms either “spatial” or “aggregated”, were placed randomly in a circular fashion in each petri dish behind the occluder.

Experiments were run in illuminated, ventilated plywood cages (50 × 50 × 57 cm) containing a perch and fresh water. They were observed through a one-way plastic front in a dark room to minimise observer effect. Before each experimental trial could begin, birds were required to consume a single sunflower seed behind each occluder to familiarise them with the experimental arena and foraging from the petri dishes. Petri dishes with the prey community set-up were then placed behind the relevant occluders and birds were allowed to forage for 15 min after their initial attack. The location and type of prey and any rejection behaviour were noted. Birds were utilised for one trial only, with 5 replicates for each treatment combination, had not previously experienced quinine and were released after experimental trials were run.

We recorded the outcome of interactions with predators, scoring mealworms as “dead” or “killed” if either (1) they were ingested or (2) they were severed into two or more fragments by the birds’ bills.

Statistics

We used generalized linear models (Lme4 in R) for a binary dependent variable (attacked vs not, killed vs. not). We consider first how the relative frequency and the spatial distribution of defended prey changes per capita probability of prey attack and the net probability of death. Second, we examine the likelihood of “death” once an attack has taken place. Unless stated otherwise, we report results from simplified models in which non significant interaction (relative frequency*spatial distribution) terms were removed (and AIC values fell as a result).

Results

As defended prey increased in relative frequency from zero (and frequency of edible prey therefore decreased) so the birds attacked a smaller proportion of all individual prey present (Fig. 1a, Z = 7.155, df = 799, p < 0.001). This is a demonstration of the “public good” of protection, since all remaining individuals benefit from attacks on defended individuals. The birds attacked more in the aggregated than the dispersed arrangement (Z = 2.299, df = 799, p = 0.022) and in the full model there was no evidence of an interaction between dispersion and prey frequency (Z = −0.127, df = 799, p = 0.900). Similarly the proportion of all prey killed decreased as defended prey frequency increased (Fig. 1b, Z = 8.740, df = 799, p < 0.001), and a higher proportion were killed in the aggregated than the dispersed distributions (Z = 2.402, df = 799, p = 0.0163); again no interaction in the full model (Z = –0.406, df = 799, p = 0.684). Since each bird had a single exposure to their experimental condition, they could assess defended prey frequency and adjust attack probability rapidly.

Fig. 1

Proportion of prey a attacked and b killed at different frequencies of defended prey (0–1) in the prey population that was arranged in a spatial (blue) or aggregated (red) pattern. (Color figure online)

We looked next at likelihood of survival in relation to edibility status (edible or defended) given that an attack had begun. Here we included bird ID as a random factor and examined the trials with mixed prey populations (taking edible prey frequencies 25, 50, 75 %). There was a significantly higher likelihood by this measure that an edible prey would be killed (as defined above) than a defended prey (Z = −4.897, df = 140, p < 0.001). The mean likelihood of death given attack for edible prey was 0.89 (SD = 0.31), whereas the mean likelihood for defended prey was only 0.38 (SD = 0.48). There was no effect of edible prey frequency on these behaviours (Z = 1.465, df = 799, p = 1.143). Dispersion also had no effect on probability of death given attack (Z = 1.518, df = 799, p = 0.129).

To examine whether the birds could to any extent discriminate mimics from models we used the method employed by Jones et al. (2013), in which we determine the difference between the observed proportion of prey attacked that are defended with that expected by their frequency in the set of prey presented. We then used a one-tailed t test, to determine if the mean difference across birds was different from zero. Birds could not discriminate mimics and models when the frequencies were toward the extremes (model frequency = 75 %, t = −1.586, df = 9, p = 0.147; model frequency = 25 %, t = 0.3458, df = 9, p = 0.7374), however there was a near-significant discrimination when the model frequency was 50 % (t = −2.2361, df = 9, p value = 0.052), in which the models were attacked less frequently than the mimics (supplementary material presents the mean values, and shows that even with some discrimination, models suffer from mimicry as mimic frequency increases).

A simple parameterised model of defence evolution

We now construct a simple model of toxin evolution to which we apply parameters from the experiment. Since there was no interaction between aggregation and automimic frequency on attack behaviours we have pooled the data, and ignore frequency dependent discrimination for simplicity here. We aim specifically to generate a clear, simple model here; more complex approaches are of course possible.

We can describe the general likelihood that a prey survives a time interval, T_i, simply as

$${\text{S}}_{\text{T = i}} = 1 - {\text{p}}_{ 1} {\text{p}}_{ 2} {\text{p}}_{ 3}^{\text{f}}$$

(1)

where p₁ is the probability that a predator notices a prey in this interval; p₂ is the probability that it attacks it given detection, and p ^f₃ the probability that it kills it given attack (i.e. S_T=i = 1 − probability that it will be killed in a time interval, where the superscript f refers to the defence presence or absence of defence). This assumes, for simplicity, stationary levels of prey and predator numbers within a generation, and stable levels of learning. Our data show very rapid learning about frequencies by predators, which is consistent with this latter assumption.

The probability that a prey survives t time intervals, for example a season before reproduction, is now

$${\text{S}}_{{{\text{T = i}} \ldots {\text{t}}}} = (1 - {\text{p}}_{ 1} {\text{p}}_{ 2} {\text{p}}_{ 3}^{\text{f}} )^{\text{t}}$$

(2)

We can estimate p₂ using the logistic regression equation from the analyses (Fig. 1)

$${\text{p}}_{2} = 1 - {1 \mathord{\left/ {\vphantom {1 {\left( {1 + \exp ( - (1.807 - 1.951*{\text{F}}_{\text{mi}} ))} \right)}}} \right. \kern-0pt} {\left( {1 + \exp ( - (1.807 - 1.951*{\text{F}}_{\text{mi}} ))} \right)}}$$

(3)

where F_mi = frequency of edible prey in the population. Hence attack probability decreases according to a decelerated function based on the data and shown in Fig. 2.

Fig. 2

Proportion of prey attacked as defended prey frequency increases estimated utilising functional form logistic regression

We now add a hypothetical fecundity penalty (F) incurred by investment in toxicity (see examples of toxin costs in Hetz and Slobodchikoff 1988; Ruxton et al. 2004; Higginson et al. 2011; Lindstedt et al. 2011). For the defended prey, this is F_o where F_o < 1 it indicates that fecundity is reduced from its initial value of 1 because resources are allocated away from reproduction and toward chemical defence. A value of F_o = 0.5 for example means that the prey depletes its fecundity by half to invest in chemical defence. The equivalent for the edible prey, F_i is always set to 1, because there is no investment in toxicity. Fitness is defined in as the product of fecundity and survival, ${\text{F}} . {\text{S}}_{{{\text{T}} = 1 \ldots {\text{t}}}}.$

Note that the value of p ^f₃ differs for edible prey and defended prey, we term this p₃′ for chemically defended prey (=0.38 in our experiment) and p₃′′ for edible prey (=0.89). We can now specify the survival of defended prey (using p₃′ and p₃′′) as So_T=1…t and hence their fitness as ${\text{F}}_{\text{o}} . {\text{So}}_{{{\text{T}} = 1 \ldots {\text{t}}}}$ and the corresponding value for edible prey as ${\text{F}}_{\text{i}} . {\text{Si}}_{{{\text{T}} = 1 \ldots {\text{t}}}}.$

Results

General outcomes of the model

We use this model to ask how toxicity would evolve in scenarios of different costs (variable values of F_o) and different season lengths (t). We keep p₁ at 10⁻³, a 1 in a thousand chance of a prey being spotted per time interval. We assume that the prey population is small enough that it does not affect demand from predators, i.e. it does not satiate them when prey are edible.

We can illustrate three outcomes for the case of t = 1000, in which costs of toxicity vary, and we initially consider how a mutant “defended prey” would fare if it entered a population of otherwise undefended “edible prey” (assuming asexual clonal reproduction for simplicity). We use these conditions to explain how and when stable dimorphisms can be predicted.

In the first case (Fig. 3a), toxicity has no costs and the defended prey always has higher fitness than the edible prey, because it survives attacks more often. Note though that as defended prey frequency rises (and edible prey frequencies therefore decline), so the fitness of both forms increase. This illustrates a growing “public” benefit from rising frequencies of defended prey which emerges because predators reduce attacks on all prey as defended individuals become more common. Note the fitness of edible prey increases faster than that of defended prey as chemical defence expands in the prey population. Edible prey lack protection once an attack has taken place, so they have more to gain, in survival terms, if the attack probability declines. Since defended prey’s fitness is always higher than the edible prey’s fitness we would expect a new “defended mutant” to rise to fixation in the prey population. In the second case (Fig. 3b) costs of toxicity are excessive (F_o = 0.5) and a new defended mutant should never increase from rarity.

Fig. 3

Illustrative effects of fitness of defended (red) and edible prey (green) as defended prey increases in frequency for three levels of cost. a F_o = 1, no costs. Defended prey is always more fit because it survives encounters more frequently. b F_o = 0.5, costs high enough that defended prey is less fit at any frequency. c F_o = 0.85, intermediate case, defended prey is the fittest form when rare, but not when common t = 1000. (Color figure online)

In the third case, F_o = 0.85 and the defended mutant prey is more fit than the edible prey when new and rare, but as it increases the fitness difference between prey types begins to close because of a higher rate of gain again for the edible prey from decreased attack probability (Fig. 3c). A point is reached where defended and undefended prey have equal fitness (red and green curves intersect). This is a stable equilibrium point. If for example defended prey frequency exceeded this equilibrium frequency, they would be less fit than edible prey and their frequency would shrink back to the equilibrium point. If in contrast they undershot the equilibrium frequency, they would be more fit and increase toward the equilibrium value. In the Supplementary Material we show that we can convert these fitness measures into a simple evolutionary simulation in which defended prey evolve to the specified equilibrium and return to it if frequencies are disturbed. Note also stability of defence dimorphisms has been examined in depth (Broom et al. 2005; Svennungsen and Holen 2007b) and we refer readers to mathematical treatments there.

A biological explanation for stable dimorphisms is that the individual benefit from costly toxins (of surviving an attack) declines as this phenotype becomes more common in the population, because prey are increasingly protected by the “public good” of reduced attack probabilities. Hence toxicity becomes less cost effective for individuals as its frequency rises. At the equilibrium point the net benefits of toxicity (increased survival from attack at a price of reduced fecundity) exactly match those of no toxicity (heightened survival from the public benefit of reduced attack probability, but with increased cost of death given attack).

Predicting equilibrium frequencies

We can now use our parameterised defended prey to predict the equilibrium frequencies of defended prey if costs of toxicity and season length varied as shown in Fig. 4. Looking first at the blue symbols (t = 1000 intervals) defended prey do not invade the population while the residual fecundity after paying for toxins is low (0.5–0.73), and as costs decrease (left to right) toxicity evolves to intermediate frequencies of increasing value until a point is reached at which toxicity is sufficiently cheap that it always rises to fixation. Considering increased season lengths we now see toxicity evolving more often and to higher equilibrium levels at high cost conditions. As the number of potential attacks increases with season duration so the value of the individual benefit of toxin caused survival increases. Note that these estimates are for infinite populations, and lack the influence of drift. So in cases where the benefits of toxicity are only slightly higher than nontoxicity at any frequency, we may expect much larger variations in toxin frequencies in natural populations. In our estimates in Fig. 4, this applies to conditions with long season lengths and high marginal costs of toxins (especially black symbols on the left side of the graph).

Fig. 4

Equilibrium frequencies of defended prey for variation in costs (x axis) and season length (symbols). Blue, t = 1000 intervals; red, t = 2000, green, t = 3000, black, t = 4000 intervals. Note that x axis origin indicates the highest cost of toxicity, costs decrease moving to the right. (Color figure online)

Discussion

It is easy to envisage that new defensive toxins might spread through prey populations in a straightforward manner, since the toxin can be beneficial to each individual that has it. This simple scenario however omits the wider effects that toxins can have, benefiting other potential victims by delaying and disabling enemies such as predators and thereby contributing to a “common good of protection”. Such a “common good” would disincentivise defence investment by individuals (Daly et al. 2012a). Furthermore it is possible that individuals do not gain a benefit of increased survival from their toxins, but rather close kin may be beneficiaries. The case for kin over individual selection for prey defences has been strengthened by a field study that failed to show individual benefits to chemical defence (Jones et al. 2013) in prey subject to predation by free-living birds. In our present experiment we use wild-caught birds as predators and insect larvae as prey hence we can gain some handle on how toxicity benefits individuals and other prey in more ecologically relevant conditions. This enables us to resolve the issue of individual benefits from defence. We discuss these results first. Subsequently we explore the application of experimental data to simple models of toxin evolution. We discuss ways that we might be able to predict the presence or absence and the frequency of “automimic” defence cheats.

Individual and common benefits from toxin investment

We demonstrated both a common good from toxin presence (lower attack probabilities on individuals) and strong survival benefits to defended individuals (higher likelihood of survival). The addition of the chemical defence substantially increased the probability of prey survival when an attack took place (by more than 65 %), irrespective of the frequency of nondefended cheats in the population (Lindström et al. 1997). The demonstration of individual survival contrasts with our fieldwork experiments in which individual survival benefits were not observed, probably because birds made decisions to ingest or reject prey hidden in trees and shrubs, away from the foraging site (Jones et al. 2013). A lack of effect of defence frequency on survival from attack contrasts with results from chick experiments (Gamberale-Stille and Guilford 2004; Skelhorn and Rowe 2007) where taste-rejection of prey was affected by the relative frequency as defended prey increased.

Chemical defence is sometimes associated with defensive aggregations because grouping leads to more rapid toxicosis in predators, and hence a higher, localised common good (Sillen-Tullberg and Leimar 1988; Curley et al. 2015). Hence we expected higher survival in aggregated than dispersed prey distributions. In contrast we found that aggregation tended to decrease survival probability (Fig. 1). One explanation is that our prey lacked aposematic colouration, and hence did not evoke the kind of phobic reactions that are associated with aposematic aggregation (Gamberale and Tullberg 1996; but see Alatalo and Mappes 1996; Riipi et al. 2001).

Overall then we can reproduce the general results of a field experiment (Jones et al. 2013) in the lab with ecologically relevant predators, these do show additionally however that individual survival is increased by chemical defence, making the results with ecologically appropriate predators consistent with those gained from studies with chicks. This experiment serves (importantly in our view) to verify publications using chickens as model predators (Gamberale-Stille and Guilford 2004; Skelhorn and Rowe 2007), as wild caught birds responded rapidly to variation in model frequency and showed taste-rejection behaviours similar to chicks. However our experiments used insect prey with experimentally added chemical defences (here “Chloroquinine”), so an important next step is to evaluate the effects of automimicry with real prey using their own chemical defences, for example including secretory chemical defences.

Though our data support the hypothesis that defensive toxins evolve to benefit individuals, we note that kin selection can none the less apply to toxin evolution if prey are localised in family groups. This may often be the case in chemically defended insect larvae, so that the optimal investment made by a prey is determined by both individual and kin selection. Kin selection has been arguably overlooked in studies of chemical defence evolution, since Fisher introduced the idea (Fisher 1958). Perhaps the most compelling example in the literature is the colonial grain aphid (Sitobion avenae) which uses cornicle secretions against enemies such as the parasitoid wasp (Aphidius rhopalosiphi). Wu et al. (2010) demonstrated that the secretion had no benefit for individuals, since aphids that used the defensive secretion were no more likely to survive the current attack, and were in fact less likely to survive a second attack in the same experimental trial. Smearing of the wasp with “aphid wax” however benefitted other group members because the wasp was diverted from attack behaviour by grooming behaviours to clean the wax off. A kin selection explanation predicts greater investment in defence if the family group size increases and indeed after statistically controlling for group size. Wu et al. (2010) found higher rates of smearing-secretion as the number of clone mates in the group increased.

Aphids are an obvious (and excellent) case study for the study of kin selection in prey defence, because colonies are often clonal. More challenging, but no less interesting, are examples of aggregations of sexually reproducing prey. Here there can be a complex balance of direct individual benefit from defence versus indirect benefits from the defence protecting close kin. Though we used quinine as a way to generate controlled levels of toxicity, many species reserve their costly toxins until attack takes place, and then secrete toxins as a last resort of defence (Skelhorn and Rowe 2006a; Daly et al. 2012b). Hence an interesting (but challenging) extension of our modelling would be to include secretory defences and kin selection, as in for example in the large white butterfly (Pieris brassicae, Higginson et al. 2011; Daly et al. 2012a).

We note that our experimental work is complimentary to a wider literature on private and public goods in microbial systems (see examples and reviews in Driscoll et al. 2013, 2016).

Evolution of toxicity in our model

In the second part of our work we took parameters from our lab experiments, and predicted the stable evolutionary levels of toxin frequencies within prey populations. The model used is by design very simple, we hope that it serves to explain in a nontechnical manner how defence cheating evolves and is stable (Fig. 3). More rigorous analyses of automimicry are (rightly) mathematically complex (Broom et al. 2005; Svennungsen and Holen 2007a). Perhaps the simplicity of the underlying mechanism that makes toxin cheating stable is not sufficiently obvious to empirically focused researchers from these technical treatments. We hope that the simple treatment here is effective in this respect.

Using parameters from our experiments it is possible to make predictions about the evolution of toxicity, albeit without kin selection. We can predict the course of new, rare, defended mutants judging whether they are likely to invade, to reach fixation, or to remain at a stable level. We can see (Fig. 4) that our model predicts toxin conferring mutants do not invade when there are high costs of toxicity combined with short season lengths (or relatively short juvenile periods, of 1000 time intervals, e.g. blue line, residual fecundity on x axis = 0.7). Conversely the same defensive mutant (residual fecundity value = 0.7) would rise to fixation with long season lengths (or juvenile periods, black line). Between these extremes we have stable dimorphisms, with toxin frequency rising with season length and falling with costs (right to left on x axis).

Can we predict frequencies of cheating in natural populations?

An interesting point which emerges from our simple model is how few parameters might be necessary to enable a quantitative prediction of the equilibrium frequency of defended prey forms. Our model needs data on: (1) the frequency of attacks per unit time, which can be decomposed into probability of detection per unit time (p₁), probability of attack given detection (p₂ in Eq. 1); (2) frequency of survival from attack (p₃) (3) costs of defence (F_o) and (4) duration to reproduction (t, assuming a semelparous life history), and number of offspring. The important question is then (in our view), can each of these be measured so that the frequency of cheats can be predicted for a given population?

Some of these parameters are relatively tractable for some systems. Using laboratory methods like those reported here we can for example ascertain probability of surviving an attack. In our study there is conveniently no effect of frequency of defended prey on this parameter; but this is not necessarily the case (Gamberale-Stille and Guilford 2004; Skelhorn and Rowe 2007), and a parameterised function will have to be generated to account for variation in this parameter. Costs of chemical defence for a number of systems can be measured (see reviews in Bowers 1992a; Ruxton et al. 2004), these are most helpful for our purposes when they are expressed as reduced fecundity or survivorship (an additional term to the model above would be needed). Costs measured as reduced growth and reduced population growth would require a more complex model.

However estimating probability of attack per unit time in the wild is probably more challenging. Estimating frequencies each of detection and attack given detection in the field are very difficult, because prey can be detected (and subsequently ignored) from considerable distances by predators. This is (in our view) almost impossible to estimate. More tractably, experimental prey could be set out in the field and with the use of sufficiently sensitive camera traps, the rate of attack per unit time can be measured. This is not likely to be a trivial task because each prey would require its own camera trap, limiting the number of prey that can be assessed. In addition since attack probability (likely) changes with the frequency of defended prey, experimenters would need to present a range of frequencies of defended prey. They would also need to carefully assess the density of the naturally occurring prey species in the locality.

Given the many challenges of testing quantitative predictions of the model in natural systems, an alternative (and promising) approach to testing the validity of the model presented here (and indeed of more complex alternatives (Broom et al. 2005; Svennungsen and Holen 2007a) is to use an experimental evolution approach, in which for example, artificial prey evolve toxin traits across generations in which costs of defence and duration of the juvenile period are specified by the experimenter. Lab housed, or free living predators provide selection between prey generations. The key benefit of this approach is to test whether predator behaviour can drive toxin evolution in a manner predicted by a simple model.

Conclusions

On the face of it, the evolution of defensive prey toxicity is straightforward, since mutations that confer defence often benefit the individuals that carry them. In fact toxin evolution is more complex because it incorporates the generation of a “common good” protecting members of the population, in some cases specifically protecting close kin. We have shown here that with ecologically relevant predators there can be both individual and common benefits from defence evolution. We show how the data can be used to inform a simple model of toxin evolution, and this can make predictions about when toxin conferring mutations can invade populations, and what their equilibrium frequencies are. Evaluating the quantitative predictions of this (and of more sophisticated) models with natural populations is possible but certainly challenging. We advocate as a “middle way” the use of experimental evolution methods to test the model quantitatively and thereby to test whether predators drive toxin evolution in the way that the model assumes.