Introduction

Feeding the ever increasing world population will be one of the major challenges for the next decades especially as arable land expansion is limited. During the green revolution, higher agricultural yields were achieved by intensification of agriculture, including high application rates of fertilizer (Foley et al. 2011; Gregory and George 2011). Additionally, high yielding maize varieties were developed that could respond to intensive nitrogen (N) fertilization with increased yield but without lodging (Borlaug 1971; Peng et al. 1999). Despite selection under high input conditions, new maize hybrids showed higher yield under low N conditions, and larger grain yield response per unit of N applied, relative to old hybrids (Ciampitti and Vyn 2012; York et al. 2015). Nevertheless, fertilizer recovery of cereal production systems is still less than 50% (e.g. Raun and Johnson 1999) resulting in environmental pollution from leaching of nitrate or nitrous oxide emission (Galloway et al. 2003, 2004; Smith et al. 1997). These nitrogen losses and the unaffordability of fertilizers in developing countries (Chen et al. 2010), make fertilizer use reduction even more important. Therefore, one of the major aims for coming decades is a second green revolution increasing fertilizer recovery and yield while at once lower inputs (Lynch 2007). However, to date it is unclear whether direct selection under low N conditions may be more efficient to improve N-use efficiency for grain yield (Presterl et al. 2003) than an indirect selection in a high N environment. Direct selection for crops with increased N-use efficiency under low N would be a breeding strategy to reduce fertilizer application rates without losses in yield. N-use efficiency in a breeding context is defined as the ability of a genotype to produce superior yields under low soil N compared to other genotypes (Graham 1984; Sattelmacher et al. 1994) or as the ability to convert fertilizer more efficiently into yield under optimal N availability (Clark et al. 1990).

Roots are the interface between the plant and soil, and root system architecture (RSA) determines access to soil resources, which influences plant performance and yield (Coque and Gallais 2006). For example, a greater nutrient use efficiency under limiting N was connected to deeper rooting, longer root length, root growth and root density (Ju et al. 2015; Mu et al. 2015). Furthermore, root growth angles, determining the spatial expansion of a root system, allow for foraging of different soil strata (Lynch 2011) and affect the extent of inter-root competition within an individual plant and a whole plant stand (Rubio et al. 2001). While more shallow rooting angles were often positively connected to lodging resistance, for example in wheat (Crook and Ennos 1994; Pinthus 1967), steeper angle are hypothesized to be advantageous under low N availability and drought (Lynch 2013).

Is there one specific root ideotype enabling efficient nitrogen uptake from soil in a wide range of environmental conditions? Breeding success suggests that this is the case: A higher N-use efficiency of modern varieties is characterized by a higher yield in a high N as well as in a low N environment (York et al. 2015). Under low N supply, the N-use efficiency seems to be associated with higher N uptake and a higher leaf N per unit leaf area (McCullough et al. 1994). Recent maize hybrids are characterized by more shallow nodal root growth angles, fewer nodal roots, less branching and longer crown lateral roots compared to their ancestors (York et al. 2015). The need for sustainable intensification of agriculture demands for an even more pronounced selection of high performance under low N conditions. This raises the question, if specific root system architecture traits can be identified, which convey an advantage under low input conditions. For example, long lateral roots instead of a higher number of lateral roots improved N capture (Zhan and Lynch 2015) specifically under low N conditions. Would such traits show a strong genotype-by-nitrogen fertilization interaction or would a constitutive one-size fits all root ideotype be a better solution? Important questions in this context are: (1) if the genetic variability across different environments is sufficiently large to select for a one-size fits all ideotype across fertilization levels or (2) if there is a larger genotype-by-nitrogen interaction variance to identify specific adaptions to low N. Nitrate is very mobile in soil and leaches into deeper soil layers, especially during wet springs when the crops are not yet taking up large amounts of N (Zihlmann et al. 2006). Starting from the six-leaf stage, the risk of nitrate leaching is increasingly reduced as the crop develops rapidly and N-uptake exceeds N-mineralization (Zihlmann et al. 2002). Around flowering, under Swiss climatic conditions, usually no mineral N is left in the root zone (Zihlmann et al. 2002) and RSA and its responses to N availability will determine the efficiency to capture the N throughout the soil profile. It is well established that there is considerable natural variation in RSA and most root traits are quantitatively inherited. For example, the length of different root types is controlled by at least 40 genomic regions (Hund et al. 2011). An important requirement for a successful selection is a high heritability of the targeted root trait (Walter et al. 2015), indicating sufficiently large genotypic variation.

Prominent examples of a successful selection of root traits are shallow rooting in phosphorus-poor soils (Lynch 2011) and aluminum tolerance in acidic, tropical soils (Kochian et al. 2005) or the “DEEPER ROOTING 1” (DRO1) gene controlling the root growth angle in rice (Uga et al. 2013). A higher expression of DRO1 increases the steepness of the rooting angle resulting in deeper rooting and drought resistance (Uga et al. 2013). However, the heritability of root traits is not intensively studied and little information is available about the heritability of root traits in the field. Most studies were performed under greenhouse conditions (Hund et al. 2004; Kumar et al. 2012; Ruta et al. 2010; Tuberosa et al. 2002). In a field study, Guingo et al. (1998) found heritabilities in a 2 years field experiment for the number of roots on different internodes (h2 = 0.56–0.62), the rooting angle (h2 = 0.32), the root diameter (h2 = 0.60), the length of internodes (h2 = 0.67) and the diameter of internodes (h2 = 0.52) for maize. However, to date there is little information about heritability of root traits obtained from multi-year, multi-environment experiments. Such information is urgently needed for a robust estimate of the variance components affecting RSA traits (RSAT) and their response to low nitrogen fertilization. Furthermore, only limited number of studies were performed at a field scale (e.g. Schjørring and Nielsen 1987; Weaver 1926) allowing to transfer findings from the lab to the field (e.g. Gahoonia and Nielsen 2004) and even less studies tried to test whether responses are conserved across environments (e.g. Fitter and Stickland 1992; Trachsel et al. 2013). Most studies have measured/counted root traits such as the axial root growth angle, branching density or the number of whorls (Trachsel et al. 2011). One method that is based on visual rating and became popular during the last years is the “shovelomics” approach, a method to visually score RSAT of the root crown of adult maize plants (Trachsel et al. 2011). Rating is a relatively fast method, but is susceptible to the researcher’s bias and habits. In contrast, measuring and counting are more accurate but more time consuming and it is difficult to achieve a throughput great enough for a breeding application. In recent years, image-based phenotyping approaches have been developed to overcome the limitations of the subjectivity of ratings and the slowness of counting (Bucksch et al. 2014; Colombi et al. 2015; Grift et al. 2011; York and Lynch 2015; Zhong et al. 2009). The work presented here is based on one of these methods. It is an adaptation of the shovelomics approach coupled with the automated analyzing software REST (Colombi et al. 2015) based on the “box-counting” algorithm described by Grift et al. (2011). In this study, root crowns were imaged under controlled light conditions and images were automatically processed without user interference.

The objective of this study was to quantify the effect of environmental factors as well as high and low N fertilization on RSAT of maize in the field, and to evaluate if there is genetic variation available for selection under low-input conditions. More specifically we aimed to (1) quantify the effect of year and soil environment on RSAT of maize (2) evaluate if there is a common response of RSAT to the level of N application (3) estimate the heritability of RSAT across environments and identify traits which may be utilized for genome mapping, and (4) identify genotype-by-nitrogen treatment interactions and discuss their potential application to adapt crops to low input of N. To achieve this we used a diverse set of 36 test cross hybrids across three different locations and over 2 years.

Material and methods

Plant material

The plant material consisted of the EURoot core maize panel of dent inbred lines defined by the EURoot consortium (www.euroot.eu). The EURoot panel is part of the larger DROPs (Drought-tolerant yielding Plants project) (www.dropsproject.eu) core panel consisting of 100 genotypes with a short window of flowering time. The DROPs panel and consists of temperate maize germplasm from the United States and Europe. The EURoot subset was selected to include the parental genotypes of the European NAM panel (Claude Welcker, personal communication) (B73, UH250, Mo17, EC169, F98902, FV353) and further genotypes, differing with regard to root architecture in aeroponics (Xavier Draye, personal communication).

All genotypes were crosses with the flint line UH007 as common tester to produce test hybrids. The test hybrids consisted of 35 dent mother components (in brackets EURoot-ID): B73 (1), UH250 (2), Mo17 (3), EC169 (4), F98902 (5), FV353 (6), MS153 (7), F7028 (8), EZ47 (9), EZ37 (10), RootABA1−(11), RootABA1+(12), EZ11A (13), LH38 (14), Pa405 (15), Oh33 (16), OH43 (17), FC1890 (18), F912 (19), W64A (20), B84 (21), MS71 (22), LAN496 (23), B100 (24), N6 (25), N25 (26), A310 (27), EP52 (28), F894 (29), PB40R (30), PHK76 (31), A347 (32), PH207 (33), F1808 (34), B89 (35) and B97 (36). In the test site Alma 2013, the hybrids B84, EZ47 and UH250 were excluded because of low seed availability.

Experimental sites

The experiment was carried out on three different sites over two seasons (2013/2014) with a high and a low N regime. One site was located in Alma, Limpopo, South Africa (24°33′00.12 S, 28°07′25.84 E, 1235 m a.s.l.), characterized by a dry and hot climate. Weather data were recorded by a local weather station in a 30 min. interval over the complete experimental period. The average temperature was 22.2 °C in 2013 and 22.3 °C in 2014 between sowing and harvest and 33 (2013) or 30 (2014) days reached a daily average temperature above or equal to 30 °C whereas the temperature remained below or equal to 12 °C only on three days in 2013 (Supplemental material 1). To compensate for the low precipitation level (2013: 0.04 mm day−1, 2014: 0.085 mm day−1), irrigation was provided from a centre pivot irrigation system as needed. The second and third site were located in Switzerland, the second in Delley (46° 54′ 48.03″ N, 6° 58′ 4.04″ E) and the third in Avenches (46° 52′ 48.01″ N, 7° 2′ 26.02″ E). The two Swiss sites were close to each other and climate data are consistent across these two sites. Weather data were collected on a daily basis. At the Swiss sites, the average temperature was 15.5 °C in 2013 and 15.4 °C in 2014 between sowing and harvest. Fourteen (2013) or seven (2014) days reached a daily average temperature above or equal to 30 °C (Supplemental material 1) whereas the temperature remained below or equal to 12 °C on 118 (2013) or 122 (2014) days. Precipitation was sufficient to ensure enough available water through the whole experiment period without additional irrigation (2.7 mm day−1 (2013) and 2.05 mm day−1 (2014)). To check whether the two Swiss sites differ in their water availability the gravimetric water content was measured in 2013 during the root sampling period shortly after flowering. The water content in Avenches (on average 1.11 gwater gsoil−1 in the depth 0–90 cm from soil level) was much higher than in Delley (on average 0.15 gwater gsoil−1 in the depth 0–90 cm from soil level) and after 90 cm the ground water reserves were already reached in Avenches.

The site in Alma was characterized by a loamy sand (Typic Ustipsamment according to USDA Soil Taxonomy), Delley by a sandy loam and Avenches by a loamy clay with a very high organic matter content. The fertilization strategies were adopted according to best-praxis protocols for each location. This was particularly necessary, as N leaching was expected to be more prominent in a sandy soil than in a clay soil. Other nutrients, irrigation and pesticides were applied as needed. Alma 2013: Prior to sowing, both fertilizer treatments received 46 kg N ha−1 in the form of urea as total N content in the soil was low (9 mg kgsoil−1 before planting). Due to the heavy leaching in the sandy soil, urea applications in the high N treatment were split in bi-weekly doses over the whole vegetative growth phase. Total amount of applied N was for low N 46 kg N ha−1 and for high N 192 kg N ha−1. Alma 2014: Before planting the high N treatment received 46 kg N ha−1 and the low N treatment 23 kg N ha−1 in the form of urea. The following urea applications in the high N treatment were split over the whole vegetative growth phase. One additional application of 10 kg ha−1 in the low N treatment was done due to a high stress level. Total amount of applied N was 33 kg N ha−1 for the low N and 207 kg N ha−1 for the high N treatment. Avenches 2013: The high N treatment was fertilized at the two leaf stage with 150 kg N ha−1 in the form of ammonium nitrate and urea solution (39% N, Lonza Sol N, ½ Urea, ¼ NH4, ¼ NO3). The low N treatment received no N because sufficient N supply from mineralization was expected. Total amount of applied N was 0 kg N ha−1 for the low N and 150 kg N ha−1 for the high N treatment. In 2014, by mistake, both the high N and low N plots were fertilized prior to sowing with 130 kg N ha−1 in the form of urea granulate (46% N). Since the low N plots were fertilized, they were not further included into the experiment. Delley 2013 and 2014: The first N application for high N plots was supplied with ammonium nitrate granulate (24% N, ½ NH4, ½ NO3) at a rate of 80 kg N ha−1 one week after sowing. An additional 70 kg N ha−1 was added to the high N plots four weeks after sowing as urea granulate (46% N). No N was applied in the low N plots because sufficient N supply from mineralization was expected. The total amount of applied N was 0 kg ha−1 for the low N and 150 kg ha−1 for the high N treatment. In 2013, total N at flowering was determined in Switzerland to confirm the assumption of higher N availability in Avenches due to higher mineralization rates. In Delley, total N was around 678 mg kgsoil−1 in the low N plots and around 588 mg kgsoil−1 jn the high N plots whereas in Avenches the total N content was much higher with 3643 mg kgsoil−1 in the low N plots and 3376 mg kgsoil−1 jn the high N plots.

Experimental design

The experimental designs at all sites consisted of a split plot design with two N-levels (high and low) as whole-plot factor and genotypes as split-plot factor. More specifically, the experimental design in Alma was a split-plot alpha (0,1) lattice design with four replications, while on the Swiss sites a split-plot 2D design with three replications was realized (Supplemental material 2). All designs were generated using the R library DiGGer (Coombes 2009; R Core Team 2015).

In Alma, the split-plots were arranged in three rows by twelve columns. The replications surrounded by border plants were independently distributed in an irrigation pivot. To control for spatial variability six incomplete blocks were arranged within the whole-plots. In 2013, each plot consisted of three rows of twenty individuals planted with jab planters with a planting distance of 15 cm and a row spacing of 75 cm. However, due to imprecise planting, incomplete germination, and lodging the intended stand density of 8.9 plants m−2 varied between 5.5 and 9.5 plants m−2 among the plots. In 2014, density was adjusted to 7.9 plants m−2 and jab planted along rope marked with planting positions every 16.9 cm in order to increase precision. At Avenches and Delley, a split-plot design with blocking in one dimension with three replications and two N levels as whole-plot factor and genotype as split plot factor was realized. A buffer row was planted between the high and low N treatment to avoid neighboring effects. The split-plots were arranged in six rows by six columns. A single plot consisted of two rows with 4.5 m length and a planting density of 7.4 plants m−2. Plant spacing was accordingly 16.9 cm; row spacing was 80 cm.

Soil sampling

In Avenches and Delley nine soil samples for each split-plot were taken at 30, 60 and 90 cm (N = 2 Sites × 3 Replications × 2 Treatments × 3 Sampling locations × 3 Depths) resulting in 54 samples per site on 06.08.13 and 13.08.13, respectively. Soil cores were taken starting from the right edge of the first split-plot, to the middle and finally to the left edge. For the following split-plot the reversed orientation was used.

Samples of the same split-plot were mixed, grouping them by soil depth resulting in 36 mixed samples to analyze (N = 2 Sites × 3 Replications × 2 Treatments × 3 Depth levels = 36 Samples in total; 18 Samples per site).

pH measurement

The pH of the above soils samples was measured as follows: 50 ml of CaCl2 solution (0.01 M) were added to 20 g of moist soil into 100 ml vials. Vials were then shaken for 30 min and afterwards the pH was determined (N = 36).

Gravimetric water content

Gravimetric water content (GWC) was determined by weighting moist and dry soil. Approximately 10 g of moist soil [1 replicate per soil sample (N = 36)] were weighted and then dried in an oven at 105 °C for 12 h. Afterwards, dry weight was recorded and GWC was calculated as follows:

$$GWC = \frac{moist\,soil\,(g) - dry soil\,(g)}{{dry\,soil\,(g)}}$$
(1)

Total organic carbon and total nitrogen content

10 g of moist soil of each sample were dried at 50 °C for 12 h. Afterwards, samples were milled (Retsch MM200, Verder Group, The Netherlands) and 50 mg of dry soil was weighed into tin capsules for total organic carbon (TOC) and total nitrogen (TN) determination (PrimacsSNC, Software: HTAccessTM V3, Skalar Analytical B.V., Breda, The Netherlands). Standards from the DOK-Trial and empty capsules were added (Gunst et al. 2007).

Root and shoot sampling

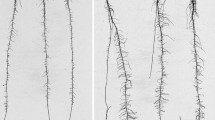
Root and plant sampling was done after flowering in all years and environments. Three representative, non-adjacent plants were sampled in the middle row of each three row plot in Alma and randomly one or two plants per row in the two row plots in Delley and Avenches (in total three plants per plot). Root stocks and shoots were sampled each morning following the order of incomplete blocks. Shoots were collected by cutting the stalks exactly 25 cm above the soil surface to enable automated image processing with the software REST (Colombi et al. 2015). Afterwards, the remaining stalk and root crown were split lengthwise with a knife either along or across the row’s orientation as illustrated by Colombi et al. (2015). After cutting the stalk, the root stock was dug out in a cylinder of around thirty centimeter diameter and depth using a spade. The excavated root crowns were shaken briefly to remove a large fraction of the soil adhering to the root crown. One half of the root stock was collected for analysis, the other half remained in the field. In Switzerland the collected roots were soaked in soap water before washing to facilitate the soil removal. Afterwards, the root crowns were washed under low pressure using a water hose and nozzle, then kept in water until RSAT analysis. For RSAT evaluation root stocks were imaged in a self-made imaging tent and analyzed using the software REST (Colombi et al. 2015). The software and manual can be downloaded at https://sourceforge.net (rest4roots). In Supplemental material 3 a subset of parameters are listed that were measured with the REST software and presented in the manuscript.

Root traits measured by the REST software and their meaning

The root traits measured with the REST software can be classified into two major categories: traits describing the spatial extension of the root crown and its size (light grey highlighted) and traits describing the inner structure of the root (white highlighted) (Supplemental material 3).

To correct for outstanding roots distorting the structure of the root stock, the outermost 2.5% of root pixels at the right and left side each and 5% of outer most pixels at the bottom were excluded from the analysis. Therefore, the blue box in Fig. 1a,  b represents the area covering 90% of the root stock. Accordingly, the 95% interquantile depth (depth) corresponds to the depth of the blue box.

Fig. 1
figure 1

a Segmented binary image with the arc where the outermost angle is determined (dashed red line) the root opening angle (RoA) and the 90% of region of interest covering 90% of all roots in the region of interest (blue box). b area of the convex hull (AcH) and its maximum width (mW). c Biplot of the principal component analysis of root traits. The component 1 describes the relation of large and small root stocks whereas the component 2 describes the relation of a highly versus a scarcely branched root system. Other traits are: tpSL total projected structure length, NoG number of gaps, mFD mean fractal dimension, mSW medium structure width, Ff fill factor, mGS median gap size. d Median gap size (mGS) displaying the size of the gaps within the root system with a color code, e medium structure width (mSW) displaying the distance from the structure to the background. The numbers in the biplot indicate the Euroot ID. (Color figure online)

Full size image

The REST software reports a range of different parameters and some of them are describing the same trait only differently expressed (Colombi et al. 2015). Accordingly, in the following only a portion of the root traits are discussed in detail to avoid the description of traits that complement each other (Supplemental material 3). For example, the horizontal expansion of the root stock can be described with the root opening angle (RoA) and the maximum width (mW) of the root stock. The RoA is widely used as trait to describe the expansion of the root stock, but using the REST software, the RoA is strongly depended on the dimensions of the excavated root stock as the angle is always measured between a point at a certain depth below the surface and the most distant horizontal pixel within the area covering 90% of the root stock. To minimize this bias, we decided to use the mW as variable to describe the extension of the root stock as this trait is a more reliable measure of the expansion than the angle.

The area of convex hull (AcH) is the smallest convex set of pixels that contains about 90% of the root stock. Further traits describing the outer dimensions were the total projected structure length (tpSL), calculated as the sum of the weighted length of root-derived structures and the number of background patches within the AcH and median fractal dimensions (mFD) derived from a box-count algorithm. The fill factor (Ff) was determined by dividing the number of root pixels within the AcH (white pixels) by the total number of pixels within the AcH (sum of black and white pixels) of the root stock. The median gap size (mGS) represents the size of all the background gaps within the AcH (Fig. 1d). A higher mGS results in a less dense root stock with bigger gaps between root patches and is a representation of the root stock complexity whereas the medium structure width (mSW) is the negative to the mGS and provides information about the diameters of the root clusters. The mSW is a measure of the distances of every root derived pixel to the closest background pixel and follows the principal of a heat map (Fig. 1e). The red regions are most distant from a background pixel whereas the blue regions are closer to the background (Fig. 1e). The number of gaps (NoG) is the total number of gaps enclosed by root derived pixels (for more details, see Colombi et al. (2015) or consult the REST user manual).

Shoot traits

Shoot traits were recorded from the same plants as those investigated for RSAT. As measurement for leaf greenness, SPAD values (SPAD-502, Konica Minolta, Tokyo, Japan) were recorded by taking three random measurement points on the second leaf above the ear. In Alma, shoots were stored in a cold room at 4 °C to avoid water loss after the shoots were cut from the rootstocks in the field. Plants were divided into leaf, husk, and stalk and fresh weights of those were assessed with a scale (Mettler-Toledo BBK422, Mettler-Toledo (Albstadt) GmbH, Albstadt, German) or with precision spring scales (Medio-Line 40,600 and 41,002, Pesola AG, Switzerland) on a five gram scale. Additionally, fresh weight (Sum of leaves + stalk + husk) [g] and biomass (Sum of leaves + stalk) [g] were calculated. Plant height [cm] was only investigated in Alma whereas early vigor, stay green (= late senescence) and lodging resistance rating were only done on the Swiss sites. Rating was done for the whole aboveground plant and rating ranged from 1–9 where 1 was no senescence or lodging and 9 all plants senescence or lodging. In Alma, kernel yield (kernel yield at a moisture content of ~ 24%) and in Switzerland silage yield (whole plant biomass yield harvested at a dry matter content of ~ 32%) was investigated at the end of the vegetation period.

Statistics

All statistics were computed in R version 3.1.3 (R Core Team 2015) and linear mixed models fitted by REML as implemented in the ASReml-R package (Butler 2015). Two linear mixed-effects models were fitted. First best linear unbiased estimators (BLUEs) were calculated for each site within each year. These data were subsequently used for a combined analysis across sites. All sites-by-year combinations were analyzed as a split-plot design with N treatment as main-block factor and genotype as split-plot factor:

$$Y_{ijk} = \mu + G_{i} + N_{j} + GN_{ij} + B_{k} + e1_{jk} + e2_{ijk} ,$$
(2)

where Yijk is the plot-mean trait value of the ith genotype (i = 1…ns), ns = (33 for Alma in 2013, 36 for the others) within the jth N treatment (j = high, low) and the kth replicate (k = 1…nr, nr = 3 for Swiss sites, 4 for Alma); G is the genotype main effect, N is the N treatment main effect, B is the replicate effect, e1 is the whole plot error and e2 small plot error.

Depending on the site, the models were extended by additional terms to control for spatial variability. In Switzerland, a first-order autoregressive covariance (ar1 x ar1) model was used to adjust for local variability in the field. In Alma, the incomplete blocks within main-plots were included in the model and an additional random term NBXkjs is indexing the effect of the sth incomplete block within each main-plot.

The subsequent model was fitted using the BLUEs of genotypes within each N treatment and site-year combinations (in total five environments). As Avenches was accidentally completely fertilized in 2014, the experimental design lacked orthogonality with regard to sites and years. Accordingly, the ANOVA was computed by defining the combination of site and year as individual environments.

$$Y_{ijk} = \mu + E_{k} + N_{j} + G_{i} + GE_{ik} + GN_{ij} + EN_{kj} + \varepsilon_{ijk} ,$$
(3)

where Yijk is the plot-mean trait value of the ith genotype (i = 1…ns), ns = (33 for Alma in 2013, 36 for the others) within the kth environment, consisting of each site-by-year combination missing out Avenches 2014 (k = 1…5) within the jth N treatment (j = high, low); E is the environment main effect; N is the N treatment main effect; G is the genotype main effect; EN is the interaction effect between environment and N treatment; GE is the interaction effect between genotype and environment; GN the interaction effect between genotype and N level and the residual. The model (ANOVA model, all factors set as fixed) in equation three was fitted as full fixed effects model and as mixed model with the genotype effects and their interactions set as random; the latter to report variance components and to calculate best-linear unbiased predictors (BLUPs). As some shoot traits were only investigated on Swiss sites or in Alma, a separated analysis of variance (ANOVA) was performed to get an impression about the impact of the different environmental factors on these traits.

Wald statistic tests were used to identify significant effects of fixed effects. For each variance component including the factor genotype [G, GE, GN and GEN (ε)], its proportion of the total phenotypic variance was calculated by diving it by the sum of the variances of the four components (Fig. 2). Best linear unbiased estimators were used to investigate the phenotypic diversity in the set (Piepho et al. 2008). Tukey’s honestly significant differences (Tukey HSD) were used as post-hoc test and calculated as:

$$TukeyHSD = q*\sqrt {\frac{MSE}{n},}$$
(4)
Fig. 2
figure 2

Proportion on total variance of the genotype, genotype-by-environment interaction, genotype-by-treatment interaction or genotype-by-environment-by-treatment interaction variance of traits measured across all sites (a) or of traits measured in Switzerland (b) or South Africa (c) only. See Fig. 1 for trait abbreviations

Full size image

where q is the critical values according to the chosen significance level and degrees of freedom, MSE is the mean square error calculated from the average standard error of the difference (avsed) supplied by the predict function of ASReml-R and n is the number of treatment levels.

Heritability estimations

Variance components were used to estimate the heritability of selected traits at the hybrid level. To check for the stability of trait inheritance under stress, estimations were done separately for high N and low N using the following linear mixed model:

$$Y_{ik} = \mu + E_{k} + G_{i} + \varepsilon_{ik} ,$$
(5)

where Yik is the plot-mean trait value of the ith (i = 1…ns), ns = (33, 36, 36) genotype within the kth environment (site x year) (k = 1…5); E is the main environment effect, G is the main genotype effect, and the residual. The environment was set as fixed factor while the genotype was set as random factor.

Heritability within each nitrogen treatment was calculated based on the mean values of each genotypes within each environment according to Falconer and Mackay (1996) as:

$$H^{2} = \frac{{\sigma_{g}^{2} }}{{\sigma_{g}^{2} + \frac{{\sigma_{e}^{2} }}{e}}},$$
(6)

where \(\sigma_{g}^{2}\) and \(\sigma_{e}^{2}\) are the genotypic and residual variance respectively obtained from the linear mixed model fitting (Eq. 5) and e as the number of tested environments.

We evaluated sources of variance affecting genotype ranking depending on environment, N treatment and their interaction. For root traits, a considerable genotype-by-environment-by-treatment interaction variance was observed (62% on average; Fig. 2a). Despite the large residual variation, the genotypic variance accounted for a considerable proportion of 23% across all root-based traits (Fig. 2a) while the genotype-by-environment interaction variance was only of minor importance (12%) and the genotype-by-treatment interaction variance was marginal (0.6%) (Fig. 2a). As we aimed to identify specific adaptation to low nitrogen application we did not treat the genotype-by-treatment interaction as nuisance factor. Instead, heritability was calculated within each, high and low nitrogen fertilization level, respectively.

Additive main effects and multiplicative interaction (AMMI) model

To characterize the patterns of genotype-by-environment interaction AMMI Analysis using the software “GenStat” was performed. In this analysis, each site-by-year-by-nitrogen level combination was defined as different environment using the BLUEs derived from model 2. Some traits were only measured in Alma or on the Swiss sites and were subjected to a separate AMMI analysis.

$$Y_{ijk} = \mu + G_{i} + E_{k} + \mathop \sum \limits_{x = 1}^{X} b_{ix} z_{kx} + \varepsilon_{ik} ,$$
(7)

where Yijk is the plot-mean trait value of the ith (i = 1, 2,…, 32, 33 (34.0.36)) genotype within the kth environment (site × year × N) (k = 1,2,…1,1, lacking Avenches 2014 at low N); E is the environment describing the combination of the experimental site, the year and the N treatment and the genotype-by-environment interaction is explained by multiplicative terms (x = 1…X). These terms consist of the product of a genotype sensitivity bix and a hypothetical environment characterization zkx given by the X dimensions of a principal component analysis (PCA). The scores were derived from a PCA on the genotype-by-environment interaction (Gauch 1988). All factors were set as fixed.

Multiple Regression

A multiple regression analysis was performed for the Swiss sites using the lm() function of R. Root characteristics related to the density and size of the root system were correlated with each of the above-ground trait (Biomass, SPAD values, vigor, lodging, stay green, and silage yield). The adjusted R2 was used as decision criterion, if the more complex model contributed significantly to the explanation in the variation of a shoot trait. Only models, for which the adjusted R2 was significant and improved by more than 0.05 compared the next simpler model, were considered.

Results

Sites differed with regard to productivity

Main effects, environment (site-by-year), N treatment and genotype, were significant for almost all traits (Table 1). The site had the strongest influence on most traits with the Swiss site Avenches and the South African site Alma being the most and least productive sites, respectively (Fig. 3). Shoot fresh weight in Avenches was four times greater than in Alma (Fig. 3a, Supplemental material 3b). The year was generally less influential with the exception of a strong effect on shoot fresh weight, which was greater in 2014 (Fig. 3a). On all three sites a reduction in shoot fresh weight under low N could be observed; especially in Alma with a halving of these values. Although the site in Alma was located in a climatic strongly differing region, it did not show a strongly increased number of hot days compared to the Swiss sites (Supplemental material 1). The silage yield (Switzerland) and kernel yield (South Africa) were comparable in both years, hypothesizing a comparable dry weight production (Fig. 3 e,  f). For the roots, with decreasing productivity (Avenches → Delley → Alma) a decreasing mW and a denser root stock characterized by an increasing Ff could be observed (Figs. 2, 3, Supplemental material 4b). This indicates an allometric relationship between shoot performance and many of the observed root traits. However, the density (indicated by the Ff; Fig. 3c) decreased in response to increased site productivity, which indicates a distinct response rather than pure allometry.

Table 1 Analysis of variance (ANOVA) across all environments or separated by the site in South Africa (Alma) and the two Swiss sites (Avenches and Delley) and heritability estimations (h2) under high or low N conditions
Full size table
Fig. 3
figure 3

Boxplots showing the variation in shoot fresh weight (a), leaf greenness (SPAD) (b), fill factor (c), maximal width (d), silage (e) and kernel yield (f) of the different environments (site + year + N fertilization level)

Full size image

We observed mild N-deficiency at the Swiss sites and strong N-deficiency at Alma, as judged by leaf greenness (SPAD values). The SPAD values were generally lower in Alma than at the Swiss sites and were generally reduced under low N fertilization (Fig. 3b, Supplemental material 4b). SPAD values and yield decreased under low N fertilization at all sites, but only the plants in Alma suffered from a severe N stress with a SPAD value around 38, reduced fresh weight of 50%, and a significant correlation between both traits (data not shown).

Root stocks may be characterized based on their size and structure

Using a PCA, we determined those traits that described the studied genotypes best without generating too much redundant information. In a first step, pairs of traits with a very high correlation (r > 0.95) were identified and only one trait was retained: The root angle opening (RoA) was closely correlated with the maximum width of the root stock (mW) (r = 0.96) and with the interquantile width (iQtW) (r = 0.96) of the root stock. We chose the mW to describe the vertical expansion of the root stock omitting iQtW and RoA.

To explore the relationship among the various root traits reported by the REST software, we used the first two principal components of a PCA (Fig. 1c) explaining 49% and 25% of the variation, respectively. The first component showed high loadings for the size-related tpSL (0.39), the area (0.41) and the NoG (0.37). This can be interpreted as distinguishing large root stocks with a denser inner structure from small, relatively sparse root stocks. Component 2 has high positive loadings for the mW (0.48) and AcH (0.37) and high negative loadings for the Ff (− 0.31) and mSW (− 0.32). Accordingly this component distinguishes wide, sparse root stocks from narrow, dense root stocks.

Based on the vectors representing the coefficients of the different root, three groups of closely related traits (angles of vectors close to 0 or 180°) could be distinguished: (1) general root size represented by the tpSL, area and NoG; (2) outer structure represented by the depth, mW and area and (3) inner structure represented by the mGS, mFD, mSW and Ff.

Root stocks in the most productive site were larger but less dense compared to the least productive site

Root stock size and density differed among sites. Avenches showed a larger mW of 14.37 cm compared to Alma with 10.78 cm but a lower average Ff of 0.442 compared to Alma with 0.633 under high N (Fig. 3c + c, Supplemental material 4b). Furthermore, the extension of the part of the root stock measured (smaller tpSL, area) and the shoot fresh weight were reduced with decreasing site productivity (Supplemental material 4b). Interestingly, the density decreased in response to low N, thus, responded opposite to the site productivity and followed the shoot response again.

Most root traits were highly heritable both under high and low N conditions

The heritability was generally high and comparable between low N and high N conditions for most traits (Table 1) as already indicated by the low genotype-by-treatment interaction variance (Fig. 2). Only for rooting depth, heritability was comparably low (h2high = 0.44; h2low = 0.32). Anyway, this trait has to be treated with caution, as the penetration of the shovel blade confounds it. Highest heritability for root traits was observed for mW (h2high = 0.80; h2low = 0.77) and the Ff (h2high = 0.74; h2low = 0.71) (Table 1a). These two traits, representing the outer and inner structure of the root stock, respectively, were not correlated with each other (Supplemental material 5a). Other traits related to the outer structure showed similar high heritability: AcH (h2high = 0.61; h2low = 0.49), area (h2high = 0.65; h2low = 0.70) or tpSL (h2high = 0.60; h2low = 0.61). The same was the case for traits of the inner structure: mSW (h2high = 0.51; h2low = 0.64), mGS (h2high = 0.45; h2low = 0.66) or NoG (h2high = 0.66; h2low = 0.67) (Table 1a). The heritability values of shoot traits were in a comparable range as the ones of the root traits: shoot fresh weight (h2high = 0.75; h2low = 0.66) and plant height (h2high = 0.69; h2low = 0.56). Shoot traits observed on an average per plot tended to have a higher heritability: staygreen (h2high = 0.78; h2low = 0.77), silage yield (h2high = 0.85; h2low = 0.76), dry matter content (h2high = 0.94; h2low = 0.94) and early vigor (h2high = 0.70; h2low = 0.67) (Table 1B + C). It has to be noted, that the EUROOT panel was selected to represent both, the genetic diversity within the dent pool of temperate maize and the diversity of root system architecture. Therefore, the presented heritabilities may mark the upper threshold of what can be expected. It is likely that the heritability is markedly lower within an elite germplasm.

Low genotype-by-nitrogen interaction reveals little genotypic N-responsiveness

The only root traits showing significant genotype-by-nitrogen interaction were the mW and the area (Table 1a). As the mW was significantly correlated to the area (r = 0.60) (Supplemental material 5a), only changes in mW are discussed. The average mW decreased by 0.3 to 13.0% under low N across all environments (Fig. 3d, Supplemental material 4c). One half of the genotypes showed a decreased mW by ≥ 8.8% (= more steep rooting) and the other genotypes remained shallow rooting under low N (Supplemental material 3e). The genotypes B97, PB40R and A310 were characterized by a more stable mW (change ≤ 7.3%) while the genotypes LAN496, FV353, PH207 and LH38 showed a stronger responsiveness to the N regime (change ≥ 9.6%) (Supplemental material 4e); these genotypes match the 10% genotypes with the strongest/weakest response in mW to low N availability. The genotype-by-nitrogen interaction variance was comparably low explaining on average only 0.6% of the total phenotypic variation (Fig. 2) and indicates a limited differential genotypic response to low N levels. Although some traits showed a somehow stronger interaction, the dominant factor, affecting the ranking of genotypes, was the genotype itself (23%), the environment given by year and site (12%) and error (62%). The large impact of the environment is illustrated with genotype LH38 (Fig. 4a). The genotype LH38 was chosen for visualization based on its strong response to the N fertilization regime (Supplemental material 4f). Although LH38 showed a strong responsiveness to N, the site had an equally strong or even stronger impact on the root system architecture (Fig. 4a).

Fig. 4
figure 4

a Representative images of root crowns of the genotype LH38 grown both under high or low N and on the three different sites. b Representative images illustrating the diversity in root system expansion (maximum width) and density (fill factor) of different genotypes

Full size image

The agronomic traits only investigated at the Swiss sites (silage yield and staygreen) or in Alma (plant height) revealed a significant genotype-by-nitrogen interaction (Table 1b + c, Fig. 2b + c, Supplemental material 6). For most genotypes yield under low N and high N was significantly correlated (Supplemental material 6).

We evaluated the genotype-by-nitrogen interaction of silage yield at Delley in more detail. Silage-yield was the only trait with a highly significant genotype-by-treatment interaction, which was mainly related to a different response at Delley. Figure 5 shows 10 genotypes differing with regard to their average performance and their response. The focus was on genotypes with consistent high yield under low and high N, on genotypes characterized by a consistent low yield and genotypes with a strong responsiveness. Based on the interaction plot, four different genotypes are worth a discussion: The genotypes F1808, F894 and EZ11A showed high general performance (mean across low N and high N), but F1808 was less sensitive to changes, which makes it more suitable for low N than F894 and EZ11A. In contrast, FV353 showed high yield under low input but did not respond well to increased N fertilization (Fig. 5). Thus, FV353 can be considered as specifically adapted to low N.

Fig. 5
figure 5

Interaction plot between silage yield and N treatment of a subset of genotypes characterized by a high or low yield in general and/or a strong or weak responsiveness to the N level

Full size image

AMMI analysis revealed consistent, environment-independent genotype-by-nitrogen interaction for silage yield but not for root traits

To evaluate the genotype-by-nitrogen interaction in more detail, we evaluated the traits showing significant genotype-by-nitrogen interaction by means of an AMMI analysis (Eq. 7). For the analysis, each N level within each environment (site + year) was coded as a different environment leading to a total of 11 N-site-year (NSY)—combinations (excluding the low N treatment in Avenches 2014).

There was no strong genotype-by-NSY interaction neither for the area nor for the mW. Most variability was explained by genotypic differences leading to a low genotype-by-NSY interaction. Genotypes differed in their response to the experimental sites and years to a much higher extent than to the N level (Fig. 6). Only for the mW in Alma, some indication is given for a genotype-by-nitrogen interaction as the high respective low N environments tend to correlate more with each other than within year (Fig. 6B).

Fig. 6
figure 6

AMMI analysis of the area of root derived pixels (a), maximal width (b), silage yield (c) or plant height (d). PCA consisted of either all 11 different environments (a, b) for root traits or a subset of the Swiss environments Delley (DEL) and Avenches (AVEN) for silage yield (c) and of Alma, South Africa (SA) for plant height (d)

Full size image

The AMMI analysis of shoot traits was performed separately for the Swiss sites and Alma as different sets of traits were measured. In contrast to the root traits, a relatively larger genotype-by-nitrogen interaction was observed (Table 1). Accordingly, a much clearer differential response of the genotypes to the N level could be detected in the biplot of the AMMI analysis. The first component influencing silage yield explained ~ 49% of the variation and distinguished genotypes with specific site adaptation (Delley or Avenches). The second component explained ~ 18% of the variation (Fig. 6c) and separated genotypes with specific nitrogen response in Delley. However, compared to the overall performance (combination of genotype plus genotype-by-NSY), the interaction had only a small effect on genotype ranking (Supplemental material 6). In Alma, the nitrogen effect was generally larger. The second principal component explaining 33% of the variability separated genotypes with a relatively better performance (higher plant height) under high or low nitrogen (Fig. 6D). The genotype-by-NSY interaction was of minor importance whereas the sampling year and treatment seemed to interact; the two years in the high N treatments were correlated whereas the two years under low N were independent.

The extension of the root stock and the branching density correlate with shoot performance

To correlate root and shoot traits, the sites in Switzerland and in Alma need to be considered separately as different traits were recorded on these sites except for SPAD and biomass. The mW was significantly correlated with SPAD (r = −0.38) across all sites (Supplemental material 5a), on the Swiss sites with lodging (r = −0.28) (Supplemental material 5b) and in Alma with kernel yield (r = 0.22) (Supplemental material 5c). Interestingly, the depth reached by the excavated root stocks, was more narrowly correlated to silage (r = 0.30) and kernel yield (r = 0.28) than the vertical expansion mW (r = −0.9 to 0.22; Supplemental material 5). Though not significant, also the correlations, with shoot fresh weight were larger for root depth (r = 0.21–0.18) than for mW (r = 0.11–0.05). Furthermore, a high branching density, described by a low mSW and NoG, correlated negatively with SPAD (r = −0.31 for NoG), lodging (r = −0.42 for mSW) and positively with silage yield (r = 0.31 for mSW) and kernel yield (r = 0.46 for NoG) (Supplemental material 5a). To check whether a combination of an expanded and dense root stock would be even better for plant performance, multiple regression analysis including the mW, Ff, NoG and mSW was performed. However, no strong correlation with shoot performance could be observed; e.g. between SPAD and mW + NoG (r = −0.31).

Discussion

The aim of this study was to identify root traits that could help to improve breeding strategies aiming the reduction of application rates of N fertilization without major losses in crop yield. We identified adaptations in RSA as response to N availability in maize, but the genotype-specific response pattern was not driven by one or two dominant components but rather by a wide range of different factors making it difficult to identify N-specific effects. Besides the nitrogen availability, the soil physical properties (overall site productivity) and the climatic conditions had a major effect on the structure of the root system and shoot performance. Based on these characteristics, the best growing environment for the tested maize hybrids was in Avenches and the least productive site was Alma. Along this gradient, the best differentiation of low-N response was in the order of low productivity to high productivity (i.e. Alma to Avenches).

While a severe N-deficiency was only achieved at low N in Alma, the mild N-deficiency in Delley led to a reduction in silage yield. The significantly lower shoot fresh weight in Alma compared to the Swiss sites could be a result of the poor sandy soil with regard to nutrient and water holding capacity in general or to the subtropical climate with a stronger disease pressure. In a similar set of flint-dent hybrids, Frey et al. (2016) used the number of hot days above 32 °C to separate between heat-stress and temperate environments and showed that yield in hot environments was reduced by about 50%. We did not observe strongly increased numbers of hot days at Alma compared to the Swiss sites (Supplemental material 1) and conclude that rather increased disease pressure and lower nutrient availability caused the lower yield. Indeed, the SPAD values at Alma were generally lower indicating severe N stress for the low N treatment. Severe N stress was defined by Piekielek et al. (1995) at a threshold SPAD value of 52. Piekielek et al. (1995) reported a similar shoot fresh weight reduction by 60% at similar SPAD values as observed for low N at Alma. By contrast, the generally high SPAD values measured on the Swiss sites and the missing correlation between SPAD and yield loss indicate that the plants were not exposed to a strong N stress resulting in a strong reduction in yield (Piekielek et al. 1995; Scharf et al. 2006; Zhang et al. 2008). However, correlation between N deficiency, chlorophyll content and yield loss cannot be generalized but needs to be defined for each site individually (Zhang et al. 2008) as a diverse set of (non-) biological factors influences N availability in the soil. Although the SPAD values did not indicate a severe N deficiency, the silage yield under low N in Delley was reduced.

The field site had not only an impact on shoot performance, but also shaped the RSA. The reduced mW under low N, which was closely correlated with a reduced RoA, could be an indication for a deeper rooting under low N. However, there is certainly a relationship between the RoA and plant size, which needs to be taken into account when interpreting the results of the RoA. Otherwise, the increased mW under high N conditions and on sites with a higher productivity could be a response to the higher N availability in the soil top layer resulting in a stronger expansion of the root system in a horizontal orientation. Conversely, The steeper angle under low N may support a stronger vertical root growth to deeper soil layers (Hund 2010; Trachsel et al. 2013; Uga et al. 2013) and can be advantageous under drought (Uga et al. 2013). Yet, based on the correlation with shoot traits it is difficult to judge where a selection to one or the other extreme would lead. A more narrow root stock is generally assumed to lead to deeper rooting, a hypothesis which we could not evaluate with the shovelomics method. The method covers only the uppermost part of the root stock. Thus, no exact prediction can be made about the rooting depth. It may be considered, that other traits leading to increased rooting depth and N uptake by means of reduced respiratory costs are involved. Such traits are, for example, reduced cortical cell numbers or a high proportion of root cortical aerenchyma (Saengwilai et al. 2014; Zhu et al. 2010). Thus, including additional, complementary traits into the root analysis pipeline would be of great benefit.

A further characteristic in response to low N is an altered root branching. The less dense root stock under low N is in agreement with findings for maize reporting a less branched root stock but with longer laterals as advantageous under N limitation (Zhan and Lynch 2015). On the other hand, a low-N efficient maize hybrid at the seedling stage was characterized by a more intense rooting but decreased nitrogen metabolism (Han et al. 2015) and a differential placement of roots in nutrient-rich zones may be an important adaptation strategy (in ‘t Zandt et al. 2015). However, the value of such information derived at the seedling stage will have to be evaluated under field conditions.

Towards this end, the method of shovelomics may be complemented with soil coring using fast methods to evaluate root distribution in soil. An attractive system is the core break method in combination with a fluorescence imaging system to automate root counting (Wasson et al. 2016).

Our major reason to evaluate a relatively large set of 36 genotypes in several environments was to estimate heritability, i.e. the proportion of the variation among genotypes compared to the overall phenotypic variation. Usually heritability is assessed by testing varieties in a large number of years and environments. However, due to the difficulties to access roots, such multi-year, multi-environment studies are rarely found for root traits. If reported at all, heritability is most frequently estimated based on single experiments in the field (0.45 ≤ h2 ≥ 0.81) (Colombi et al. 2015) or under controlled conditions (0.27 ≤ h2 ≥ 0.88) (Grieder et al. 2014; Hund et al. 2004; Kumar et al. 2012; Ruta et al. 2009). Though valuable, such estimates of repeatability in single test site may overestimate the heritability because the genotype-by-replication interaction variance is expected to be low. The reason for this is that all variances are estimated based on replications within the same field or platform rather than differences among environments. In comparison, Cai et al. (2012) reported lower heritability (between 0 and 0.55) for root traits evaluated on two field sites and Trachsel et al. (2011) observed heritabilities for brace and crown root traits investigated by the shovelomics method between 0.3 and 0.67 across three different environments. Here we present heritability across contrasting environments in different years, which give a much more reliable estimate, not only of heritability but also of the genotypic means. The data may be used for platform cross-comparison. Six of the eleven reported root traits showed slightly higher heritability at low N. This is surprising, as low N application usually leads to increasing environmental error due a pronounced effect of soil inhomogeneity (Gallais and Hirel 2004). One possible explanation for the comparable heritability could be the correction for spatial variability in the linear model.

The large heritability across sites indicates a large potential to alter root traits constitutively while the low genotype-by-nitrogen interaction indicates limited genetic variation for specific responses to low nitrogen (Fig. 3). Thus, traits may be selected that are advantageous in a wide range of environments, such as the proposed steep, cheap and deep ideotype to optimize water and N acquisition (Lynch 2013). Uga et al. (2013) identified a gene responsible for steep rooting angles resulting in a deeper root stock and increased drought resistance of rice. Depending on the environment, this trait might be also efficient to improve nitrogen-use efficiency.

Given the large effort to excavate roots, wash and measure them (approximately 300 man-hours for 900 plants), an indirect selection for root traits based on shoot traits would be desirable and was already successful performed in the past. For example, for rooting depth it could be shown that an indirect selection via leaf area would be half as efficient as direct selection for root traits (Grieder et al. 2014). Although the correlations between root and shoot traits were low, some root traits describing the expansion and density of the root stock were positive correlated with shoot parameters in low and high N environments. The root trait showing the strongest response to low N was the mW. However, in this study the mW was not correlated with yield, stay green or early vigor eliminating the opportunity to select for mW by selection of a closely correlated shoot trait. Moreover, the aboveground traits stay green and silage yield, assessed by breeders, showed not only highest heritability but also a clearer N-response. Thus, we were better able to identify genotypes responsive to low N based on aboveground traits than directly observing root traits. Today, many aboveground traits may be assessed in high throughput (Liebisch et al. 2015). This enables to evaluate very large sets of genotypes for specific response to low-N conditions. We propose the screening of plant features related to nitrogen responsiveness, such as height, leaf area index, vegetation indices and stay green using remote sensing techniques. After such screenings, in-depth observation of the root system of genotypes with contrasting response to low-N may shed light on the specific adaptations of root system traits to low N.

The majority of inbred lines used in this study were derived from public breeding programs in Europe and the United States. These lines had been already selected for yield under high input conditions. This selection process might have caused a large degree of unresponsiveness to low-N conditions. Extending the evaluation to old, exotic varieties may be a strategy to identify new allelic variation lost from breeding elite material programs due to selection. Furthermore, a more direct test of the utility of root phenotypes would be a comparison of a set of lines which had equivalent vigor under high N but differential vigor under low N. Understanding the integration of root traits and how it relates to yield in a particular environment would be an important way towards targeted selection of efficient root systems (York et al. 2013).

Conclusion

The tested EURoot core maize panel covered a large proportion of the genetic variability of the dent heterotic group. Based on silage yield, height or stay green we could differentiate genotypes with regard of their response to nitrogen. The sites with a generally lower productivity (Alma and Delley), were better suited for such a differentiation than the highly productive site Avenches. Across the three different environments, we did not find promising root adaptations explaining the differences in nitrogen responsiveness. We conclude that the assessed root traits do not enable an efficient selection for low N adaptation in the studied population of environments. This is remarkable as the set was selected to cover the genetic diversity of the temperate dent genepool. Yet the characteristic of the root stocks were generally highly heritable, i.e. showed a high proportion of genetic variability across years, sites and nitrogen treatments. Moreover, root structure (represented by the Ff) and root stock dimensions (represented by the mW) were independent from each other and, thus can be independently selected.