Abstract
Increased modern farming of superior types of the oil palm, Elaeis guineensis Jacq., which has naturally efficient oil biosynthesis, has made it the world’s foremost edible oil crop. Breeding improvement is, however, circumscribed by time and costs associated with the tree’s long reproductive cycle, large size and 10–15 years of field testing. Marker-assisted breeding has considerable potential for improving this crop. Towards this, quantitative trait loci (QTL) linked to oil yield component traits were mapped in a high-yield population. In total, 164 QTLs associated with 21 oil yield component traits were discovered, with cumulative QTL effects increasing in tandem with the number of QTL markers and matching the QT+ alleles for each trait. The QTLs confirmed all traits to be polygenic, with many genes of individual small effects on independent loci, but epistatic interactions are not ruled out. Furthermore, several QTLs maybe pleiotropic as suggested by QTL clustering of inter-related traits on almost all linkage groups. Certain regions of the chromosomes seem richer in the genes affecting a particular yield component trait and likely encompass pleiotropic, epistatic and heterotic effects. A large proportion of the identified additive effects from QTLs may actually arise from genic interactions between loci. Comparisons with previous mapping studies show that most of the QTLs were for similar traits and shared similar marker intervals on the same linkage groups. Practical applications for such QTLs in marker-assisted breeding will require seeking them out in different genetic backgrounds and environments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Increasing yield is the most important target for most oil palm breeders and growers. Oil yield is a complex character measured by at least 21 components traits of the fruit bunches, their fruits and the oil bearing mesocarp of each fruit. The mapping and identification of quantitative trait locus (QTL) for these component traits will increase our knowledge of their genetic control for more efficient selection in breeding programmes. Knowledge of their positions and effects could help in linking the phenotype to the genotype in developing tools and methodologies for marker-assisted breeding. However, despite advances in the genetic mapping of the oil palm, only a handful of papers have reported mapping for oil yield and its component traits (Billotte et al. 2010; Jeennor and Volkaert 2014; Mayes et al. 1997; Rance et al. 2001). We aimed to map the QTLs associated with oil yield component traits in a high-yield oil palm cross created at FGV R&D and coded DA41. The genetic linkage map of this cross (Seng et al. 2011) provided the base information for the QTL mapping. Molecular markers at reasonable density on all the chromosomes in the linkage map allowed for identification of loci co-segregating with yield-related traits. The approach was to establish the statistical relationships between the inheritance of the traits and their molecular markers, which map positions were already known, to locate the QTLs. It involved determining the allelic configurations at each QTL, their specific effects (positive or negative) on the trait and computation of the cumulative effects of all the QTL+ alleles for each trait.
Materials and methods
Mapping population
The mapping population is a high-yielding dura × pisifera cross, coded DA41, which was planted at FGV’s main research station in Jerantut, Malaysia. The female parent (coded ARK86D) is a dura from selfing and sib-mating in small populations over seven generations from a few founder palms of Deli, Sumatra origin. The male parent (coded ML161P) is a pisifera descended through sib-mating, also in a very small population over four generations, beginning from selections at Yangambi in the Congo. Both parents are extensively used in FGV’s breeding programme, are extant and have unambiguous pedigree as well as productivity and growth data of themselves and their progenies. Of particular interest is the high oil content of the fruit bunches of this cross, 35.4 % in an early trial and 32.3–35.4 % in three subsequent trials (FGV, unpublished data). Current commercial palms have a bunch oil content of ~26 %. The high oil content of DA41 derives from more mesocarp and more oil in the mesocarp. Fruit bunch production was average in the trials but the higher oil content meant 8–21 % higher oil yield than the trial average in the four trials mentioned above. In one trial, the cross was represented by 562 palms, of which 120, complete with growth and productivity records, were selected for the mapping work.
Genetic linkage maps (Seng et al. 2011) were built with RFLP, AFLP and SSR markers. The 294 segregating markers (258 SSRs, 30 AFLPs and 6 PCR–RFLPs) contributed 805 marker loci (490 SSRs, 307 AFLPs and 8 PCR-RFLPs) used for linkage analysis and map construction, of each parent separately and an integrated map. The linkage map of the female parent comprised 317 marker loci and that of the male parent 331 loci, both in 16 linkage groups each. The number of markers per group ranged from 8 to 47 in the former and 12 to 40 in the latter. The integrated map was 2247.5 cM long and included 479 markers and 168 anchor points.
Phenotypic data analysis
The oil yield component traits of the progenies were measured following established methods in oil palm breeding. The regular harvesting and weighing of all fruit bunches from each palm over a period, or yield recording, measures the fruit crop production of the palm. From the harvest occasional bunches are sampled to measure the oil content through a procedure known as bunch analysis. Bunch analysis involves a series of sub-samplings and solvent extraction for oil content and provides measurements of different features or traits of the fruit bunch (Table 1), their aggregation providing an estimate of its oil and kernel content. The product of crop production, measured by yield recording, and the oil content, determined by bunch analysis, gives the estimated oil yield of the palm.
The measurements of each trait conformed to a normal distribution, from tests of skewness and kurtosis, as required by the mapping software. Simple correlations were also computed to ascertain the relatedness of the traits to each other (Table S1). The correlations provide insight into the traits, and possibly their QTLs, as well as the characteristics of DA41 compared to other crosses. Notably, for the work, significant genetic variation was found between the progenies for all the oil yield component traits.
Quantitative trait loci (QTL) analyses
The QTL mapping and analyses used MAPRF7 software, developed and described by Ritter et al. (1990) and Ritter and Salamini (1996). All marker intervals in both parental linkage maps were used to identify the genomic regions linked to the yield traits. Each phenotype value and marker genotype association was subjected to a t test and interval analysis using SAS software (SAS Institute Inc., USA). To minimize false positives, an exclusion threshold of P < 0.01 was set for declaring a significant link between a QTL and a marker locus. Analysis of variance of the phenotypic means was performed at each single-marker locus, depending on the number of marker genotypic classes that were distinguishable at each marker locus (Ritter et al. 1990), using the generalized linear model (GLM) procedure of the SAS software.
The QTLs were mapped using least square interval mapping with PROC NLIN computational analysis. The program computes non-linear regressions for a specified QTL model in a marker interval, extending the approach of Knapp and Bridges (1990) and Knapp et al. (1990) together with multiple linear regressions on specified intervals (or fragments as referred to in MAPRF7). The procedures were applied to the map intervals defined by two consecutive markers in the genetic linkage maps. This analysis estimates the effect of a possible given QTL and its location in a particular interval. The proportion of the total phenotypic variance (PV) accounted for by the sum of the individual QTLs was estimated by the coefficient of determination (R2), calculated using multiple regression analysis on the corresponding intervals.
Cumulative effects of quantitative trait allele (QTA) analysis
MAPRF7–MAS (Ritter unpublished) was used to further analyse the QTL markers, in particular, their configurations as QTAs and their corresponding effects on their respective traits. Favourable or unfavourable effects are shown by positive and negative values respectively. This procedure involved two steps: step 1—identifying the potential QTAs nearest the QTL peak, in the interval between two marker alleles, based on QTL interval and marker position information; step 2—calculating the effect of the QTA, which can be positive or negative, associated with the particular trait.
In addition to computing the effect of individual QTLs, the cumulative effects of quantitative trait plus (QT+) alleles for each trait were also computed. A QT+ allele refers to an allele that increases the (value of) trait, relative to the population mean for that trait, while a QT− is the opposite. Positive and negative, in this sense do not refer to an allele being favourable or unfavourable for breeding, as in some traits a decrease is desired. The QTA effect of each of the potential markers was determined as mentioned above followed by enumeration of the number of QTL markers matching the QTA effects and binning according to their numbers.
Results
QTL analysis: linkage of markers to oil yield component traits
The number and distribution of QTLs for each trait, over all linkage groups (LGs), and the proportion of the phenotypic variance or PV ascribable to them (Total R2) are shown in Table 2. In total, 164 QTLs were identified for the 21 oil yield component traits, ranging from 2 to 15 QTLs for each trait. QTLs are named after the trait they influence, the prefixes “q” and “Q” denoting from male and female parent respectively, and are consecutively numbered “a, b, c, and so forth”. The QTLs had an average confidence region of 15.4 cM, with no marker interval exceeding 50 cM.
Three QTLs were detected for the trait FIWP and two each for FIB and OB Fourteen traits had a moderate number (5–10 each), while four (KB, KF, MKW and MSW) had >10 QTLs each. Of the 164 QTLs, 101 were in the female parent (ARK86D), and the remaining 63 in the male parent (ML161P). The distribution of QTLs by LGs also varied, with LG7, LG9 and LG15 having the highest numbers, viz, 22, 27 and 17, respectively, while the least (two QTLs) mapped to LG6. The number of QTLs on the other LGs ranged from 5 to 12. The cumulative proportion of variance accounted for by all the QTLs for a particular trait ranged from 4.9 to 50.3 % (Table 2).
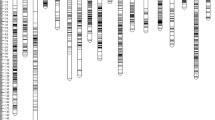
The QTLs, shown at their candidate loci peak positions on the 16 LGs of the integrated map, are shown in Fig. 1a–d. This map probably represents the genome distribution of the QTLs for these traits. In several instances, some traits shared the same QTL positions on a particular LG, e.g., in LG1 (33.3 cM), qKB_l, qKF_j and qFFB_e showed co-localization, and in LG7 (99 cM), the putative location of qMSW_l, qMKW_l, qKB_n, qWPF_g, qSF_i and qKF_l were very closely linked. These shared or close locations mirror the observed close correlations between the corresponding traits.
a Integrated linkage map of cross DA41 (ARK86D × ML161P) with markers and QTLs (Linkage Groups 1–4). Markers descending from P1 and P2 are shown in normal and italic font, respectively. Common fragments are underscored. Microsatellite (SSR) and Amplified fragment length polymorphism (AFLP) markers are shown in black, while the QTLs are shown in red and coded as in Table S2. b Integrated linkage map of cross DA41 (ARK86D × ML161P) with markers and QTLs (Linkage Groups 5–8). Formats and colour codes are as explained in a. c Integrated linkage map of cross DA41 (ARK86D × ML161P) with markers and QTLs (Linkage Groups 9–12). Formats and colour codes are as explained in a. d Integrated linkage map of cross DA41 (ARK86D × ML161P) with markers and QTLs (Linkage Groups 13–16). Formats and colour codes are as explained in a. (Color figure online)
Two QTLs locations were found each sharing the effects from male and female parents for a number of traits. In LG12, three correlated traits, QMFW_f QMPW_e, qMSW_h, the first two from the male and the third from the female parent, were found at position 100.5 cM. Similarly, in LG13, at position 100.3 cM, four different QTLs were detected from both parents for the traits qMFW_h, qMPW_g, QKB_i, QSF_e.
Table S2, with an example in Table 3 below, shows for each trait: the QT alleles effect (at P < 5 %), the contributing parent, the location of the QTL (interval) in the parental maps, the interval length in the integrated map and the distance of the QTL from the left marker of the interval. The variance (R2) explained by individual QTLs was as high as 19.38 % (WPF). For all traits, the total R2 was lower than the summed contribution of individual QTLs, possibly due to interactions between the alleles of the different QTLs. In general, the percentage of PV explained by the QTLs for each trait ranged from low to medium.
QTLs for fruit bunch production traits
Three component traits are measured: ABW, BNO and FFB, the abbreviations explained in Table 1. Twenty-two QTLs were identified on nine LGs, namely LG1, 5, 7, 8, 9, 10, 13, 14 and 15. Three QTLs were identified on LG1: −qFFB_d, +qFFB_e and −qBNO_d where the prefix (+ or −) refers to the direction of the effect of the QTL. Only one QTL was identified in each of the following LGs: LG5 (+qFFB_f), LG7 (−qABW_e) and LG15 (+QFFB_c). Three QTLs, associated with BNO, were mapped to LG8, of which two (−QBNO_a and +QBNO_b) were from the female parent and a positive third +qBNO_e from the male parent. Two QTLs (−QABW_a and +QBNO_b) were detected in the same marker interval from mEgCIR3282 to mEgCIR0800 on LG8; these QTLs were from the female parent. On LG9, three negative QTLs were identified: two (−QBNO_c and −QFFB_a) were on the same interval (sEg00040–sMo00066), while −QABW_b was near marker sEg00037. Two QTLs (−QFFB_b and +QABW_c) were co-localized on LG10. Two QTLs associated with ABW (+QABW_d and −qABW_f) were on LG13; the first from the female and the second from the male parent and of opposite effects. Three QTLs were located on the mid-stretch of LG14 (−qFFB_g, −qFFB_h and −qBNO_g); all three were negative, while the positive +qBNO_h was towards the lower end of the same LG.
QTLs for fruit oil yield component traits
Fruit kernel traits: KB, KF and MKW
Thirty-eight QTLs relating to kernel measurements (KB, KF and MKW) were detected on all LGs except on LG8, 12, 13 and 15. Twenty-three QTLs were mapped in the female parent (ARK86D) and 15 in the male parent (ML161P). The QTLs accounted for 39–48 % of the PV of the three traits. Six of the QTLs (−QMKW_d, +QKF_f, +QKB_f, −QMKW_c, +QKF_g and +QKB_g) each accounted for >10 % of the PV. The QTLs were mostly clustered, especially those for KB and KF, in the same eight marker intervals. The additive effects of these similar QTLs were also consistent in direction, i.e., either positive or negative. For example, −QKB_b and −QKF_b were on the marker interval mEgCIR0795_1—EACT/MCAG_372_1, and both had negative additive effects (−0.59 and −0.89, respectively). The only marker interval with all three kernel-related measurements (+qKB_m, +qKF_j and +qMKW_i) was mEgCIR3878_1—EAAT/MCAT_219_1 were on LG7. All three had positive values here, indicating that the alleles increased kernel weight. Interestingly, two shell-related QTLs (+qMSW_g and +qSF_g) and one for mesocarp (−qWPF_i) were detected in the same marker interval and would contribute to the high correlation between kernel, shell and mesocarp traits.
Fruit shell traits: MSW and SF
Twenty shell-related QTLs were identified on ten different LGs: LG1, 2, 3, 7, 9, 12, 13, 14, 15, and 16. Equal numbers mapped to both parental maps and accounted for 50 % of PV for MSW and 39 % for SF. Three QTLs (+QMSW_a, −QMSW_c and +QSF_c) individually explained >10 % of the PV of the two traits. Four marker intervals were detected for both the shell QTLs, namely, +QMSW_a & +QSF_a, −QMSW_b & +QSF_c, −QMSW_c & −SF_d and +qMSW_g & +qSF_g. Interestingly, kernel and mesocarp QTLs were also clustered at these QTLs. For example, at marker interval sEg00087_1—sEg00038_1 (LG9), six QTLs, viz. +QDPF_b, −QFB_d, −QMKW_d, −QMSW_c, −QSF_d and +QWPF_g) were found clustered, while the same number for the three traits measurements (−QDPF_a, −QFB_b, −QMKW_c, −QMSW_b, +QSF_c and −QWPF_f) clustered at mEgCIR3782_1—DHP3_1 (LG9). For the trait MSW, only four QTLs were from the female parent while seven were from the male parent, but for SF, five were from the female and three from the male parent. Interestingly, several QTLs for shell overlapped the QTLs for kernel and mesocarp.
Fruit mesocarp traits: DPF, MPW and WPF
Twenty-three QTLs relating to mesocarp were identified on 10 LGs: LG1, 2, 5, 7, 9, 10, 11, 12, 13 and 15. Sixteen of these QTLs were in the female ARK86D map and seven in the male ML161P map and together accounted for 19.46 % of the PV for DPF, 27.26 % for MPW and 33.94 % for WPF. However, only two QTLs (−QDPF_a and −QWPF_f) individually accounted for >10 % of the PV of the trait. Five QTLs were detected for DPF, all with positive effects, except for −QDPF_a, and nine QTLs on seven LGs for MPW, all showing negative effects except two (+QMPW_a and +QMPW_d). Notably, none clustered with the QTLs for the other two mesocarp-related traits. However, eight MPW QTLs clustered with the MFW QTLs in the same marker intervals, which is not surprising as MPW is the largest component in MFW. No similar marker loci were detected between MPW and WPF or DPF, the latter two being ratio traits. For DPF and WPF, four QTLs were located on two similar marker intervals, namely, −QDPF_a & −QWPF_f and +QDPF_b & +QWPF_g. Five LGs contained QTLs for WPF, often co-localized with shell or kernel QTLs or both.
Fruit oil content traits: OB, ODP and OWP
Only 14 oil content QTLs were identified on nine LGs: LG2, 3, 5, 7, 10, 12, 14, 15 and 16. Except for two in the male parent (ML161P), the rest were all in the female parent (ARK86D). These QTLs accounted for 8.11 % of the PV for OB, 11.99 % for ODP and 15.07 % for OWP. None of them accounted for >10 % of the PV of the trait, with only +QOWP_e close at 9.38 %. This is not unexpected given the low genetic variance for these traits in an advanced cross such as DA41. Only two QTLs related to OB, and both negative, were detected while five were detected for ODP, but again, all negative. One of these QTLs (−qODP_a) co-localized with +qFIWP_a and +qWPF_a on LG2. Similarly, +qFIWP_c and −qODP_d co-localized in the marker interval sMg00234_1—19/1 on LG16. Seven OWP-related QTLs that were dispersed on LG7, 14 and 15 co-localized at seven marker intervals with WWP or WFI or both but with opposite (additive) effects.
Quantitative trait allele (QTA) analysis: cumulative effects
Potential QTAs nearest the QTL peaks and their specific effects on associated traits are shown in Table S3 and for discussion the 11 QTLs detected for MSW in Table 4. The marker alleles (in bold) were identified as potential QT alleles nearest the QTL peaks between the stated intervals. Next, the positive/negative effect or contribution of the QTA to its associated trait was determined. For example, marker sEg00087_1 was identified as a QTA in the interval sEg00087_1—sEg00038_1 in QTL QMSW_c. The mean value for this trait (MSW) in the 63 progenies in which the marker was present (Nv1) was 0.67 (designated V1-mean), while in the remaining 55 palms (Nv0), without the marker, the mean was 0.81 (V0-mean), The difference (i.e., V1−V0) of −0.14 suggests that the QT allele has a negative effect on the trait, i.e., the presence of this marker will mean a thinner shell.
The frequency distributions of the numbers of palms and the cumulative number of QT+ alleles for each of the 21 traits were computed (Fig. 2) and the cumulative effects of the QT+ alleles. As an illustration (Fig. 3), 12 QTL markers were found associated with MKW (g). Following identification of potential markers close to the QTLs (based on the QTL interval and marker position information), the QT allele effect of each of the potential markers was determined. The number of QTL markers matching the QT allele effects were then computed and bins set and sorted according to the total number of QTL markers. In DA41, the MKW was 0.44–1.21 g, with a mean of 0.73 g. Figure 3 shows the cumulative QTL effects, as percentage change from the mean, for increasing numbers of QTL markers. Clearly, while a small number of QT alleles caused MKW to fall below the population mean, this decrease was reversed with increasing numbers of alleles. The coefficient of determination (R2) was 0.50, with a slope of 7.24 and an intercept at −41.03 %. The results from similar analyses for all the other traits are summarized in Table 5, and the graphs of the cumulative QTL effects, depicted as percentage changes from the mean for each trait, are presented in Fig S1.
For most traits, the estimated mean trait values exceeded the population mean when more than half of the QT+ alleles for the trait were accumulated. To reiterate, a QT+ allele means a QTL that increases the (value of) trait, relative to the population mean for that trait. Positive and negative, in this sense do not refer to an allele being favourable or unfavourable for breeding, as in some traits a decrease is desired. For example, for FB, when a palm showed <3 matching QT+ alleles, its FB value was <68.42 (mean value), but with >4 markers, the value increased by 0.3–4.5 % above the mean, i.e., to 68.62–71.49.
Comparative QTL analysis
The QTLs detected here cannot be directly compared to those of Rance et al. (2001), as there are no common markers between the maps. Likewise, with the 16 QTLs detected by Jeennor and Volkaert (2014) for several oil yield related traits in a 69 (tenera) palm-population, as common markers were quite limited. However, alignment of linkage groups and QTL comparisons with Billotte et al. (2010) are possible, for similar oil yield component traits, as there are more shared markers. Furthermore, two of the four parents, in their populations, share the same Yangambi and Deli ancestry as the parents of cross DA41. Of the 76 vegetative and oil yield components QTLs in their study, 43 were associated with the latter. They were dispersed over 13 LG and were associated with three groups of trait measurements—fruit bunch production, fruit bunch components and oil unsaturation. However, even for common traits, care must be exercised in comparisons as some traits were measured differently. For example, Billotte et al. (2010) measure fruit bunch yield at two periods, from 3 to 5 years and from 6 to 9 years after planting, whereas in our study the yields are from 5 consecutive years from first bearing.
For convenience of further discussion, the LG from this study are prefixed TY while those of Billotte et al. (2010) prefixed as NB_2010. Thus TY_LG:1 had 6 common markers with NB_2010_LG:16. In the former, five bunch production QTLs (PO6_9_3, PO3_5_2C, BWT6_9_C, BWT3_5_2 and FFB3_5_2) and three fruit bunch component QTLs (%PF_1C, Fwt_2C and %KF_1C) were detected in the first 43 cM, marker interval mEgCIR3745 to mEgCIR0782, and these are highlighted in blue in NB_2010_LG:16 in Fig. 4a. The other QTLs detected in this region in TY_LG:1 were associated with three bunch production traits (FFB-2 and BNO) and eight fruit component traits (MSW, WWP, MKW, KB-2, KF-2, and DPF). The common QTLs in both maps are associated with FFB production and are located near marker mEgCIR3750. In this region, two similar fruit component QTLs, namely, %KF, KF and %PF, DPF, were detected in the interval mEgCIR3745—mEgCIR2436. Linkage group, TY_LG:3 shared six common markers with NB_2010_LG:6 of which only one QTL (Bwt6_9_C) was reported by Billotte et al. (2010) in the region flanked by markers mEgCIR3543 and mEgCIR0219, which is the same region as in the present study. On the other hand, Jeennor and Volkaert (2014) reported QTLs for two traits (Oil-to-fruit and FB) in this region, flanked by a gene-based marker and mEgCIR0219, as shown in Fig. 4b.
a Comparative mapping from this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:1 and NB_2010_LG:16 are aligned using common QTL markers (shown in green). Distances (in cM) between the markers in both maps are given to the left. Red denotes QTLs detected in this study, and blue denotes QTLs detected in Billotte et al. (2010). The vertical solid blue segments in the TY map represent marker intervals and QTL regions similar to those of the latter. b Comparative mapping from this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:3 and NB_2010_LG:6 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. c Comparative mapping, this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:5 and NB_2010_LG:4 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. d Comparative mapping, this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:7 and NB_2010_LG:9 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. e Comparative mapping, this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:8 and NB_2010_LG:2 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. f Comparative mapping, this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:9 and NB_2010_LG:1 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. g Comparative mapping, this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:11 and NB_2010_LG:15 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. h Comparative mapping, this study (TY) and from Billotte et al. (2010) (NB_2010). The homologous chromosome arms TY_LG:14 and NB_2010_LG:8 are aligned using common QTL markers. Colour coding same as explained for Fig. 4a. (Color figure online)
Nine markers in TY_LG:5 were common with those beyond section 100 cM in NB_2010_LG:16. The latter detected five QTLs (aBWT_1, aBWT_3, IER_3C, BWT3_5 and Bn3_5_1C) in the interval between markers mEgCIR3535 (137.7 cM) and mEgCIR3557 (247.3 cM), as shown in Fig. 4c. Their study included a bunch production trait (BWT) and nine fruit component traits (KB-2, KF-2, WPF-2, OB, DPF and WFI). The only common QTL in both studies is one for bunch weight (aBwt–BWT). Nine markers were common in TY_LG:7 and NB_2010_LG:9, as shown in Fig. 4d. Billotte et al. (2010) identified one QTL (PO6_9_3) in the region flanked by markers mEgCIR3878 and mEgCIR2332, whereas in the present study, six QTLs (MSW, MKW, KB, WPF, SF and KF) were found in the same region. TY_LG:8 shared seven common markers with NB_2010_LG:2 (Fig. 4e). Again, while the latter reported only one QTL (Bwt6_9_C) in the region of marker mEgCIR0408, four (MFW, WWP, WFI and BWT) were found in the similar flanking region in our study with one common QTL, associated with bunch weight, detected by both.
TY_LG:9 had ten markers in common with NB_2010_LG:1 (Fig. 4f). Six bunch production QTLs (FFB6_9, BWT6_9, BWT3_5, PO_5, FFB3_5 and Bn3_5) were detected in the interval between mEgCIR3819 (52.6 cM) and mEgCIR0874 (102.9 cM)—highlighted in blue in NB_2010_LG:1 in the figure. Five of these were associated with fruit and bunch components (MPW, MFW, KB, KF and FB). Similarly, while six bunch component QTLs (%PF_1C, IER_1C, Fwt_-C, %KF_1C, %POP_1C and aBwt_1) were reported in NB_2010_LG:1, between markers mEgCIR0280 (107.6 cM) and mEgCIR0802 (153.3 cM), seven were detected in the same region in TY_LG:9 (MSW, MKW, DPF, SF, WPF, KB and KF). In this region, there are two, possibly identical, QTLs (%KF–KF and %PF–WPF/DPF) on both maps based on common marker locations.
The linkage groupTY_LG:11 shared 16 markers with NB_2010_LG:15 (Fig. 4g). In the latter, three QTLs (%PF_1C, FFB3_5_3 and Bn3_5_3) were mapped between mEgCIR1492 (0 cM) and mEgCIR3727 (43.3 cM). Another QTL associated with bunch number (Bn6_9_C) was mapped between mEgCIR3737 and mEgCIR2860 in NB_2010_LG:15 (Fig. 4g). Four QTLs (MKW, MFW-2 and MPW) were mapped into these two regions in our study but none were common with (Billotte et al. 2010). Linkage group TY_LG:14 had 9 markers in common with NB_2010_LG:8 but no common QTLs (Fig. 4h).
Discussion
Linkage to quantitative traits (QTLs)
Most of the economic traits in the oil palm, including the all-important oil yield, are inherited quantitatively. As oil yield is a complex trait, genetic dissection of its component traits through QTL mapping would contribute to its better understanding. Similar work as ours, for some of these component traits, has been reported (Rance et al. 2001; Billotte et al. 2010; Jeennor and Volkaert 2014).
Interval mapping narrows down the likely location of a QTL between adjacent linked markers on a linkage map (Collard et al. 2005). Increased marker density and smaller intervals (usually ~10 cM) would more likely give closer linkages and facilitate QTL detection. A third important factor is the size of the mapping population. For equivalent genetic variances, a larger population improves the accuracy of QTL assignment and identifies more QTLs of small effects (Vales et al. 2005; Raghavan and Collard 2012). Smaller populations can mean reducing the statistical power to detect QTLs with an attendant risk of false positives, especially for QTLs with weak effects, although this also depends on the trait heritability and the particular QTL effects (Beavis 1998). An alternative approach, when population size is limiting, is multi-parent QTL analysis, as demonstrated by Billotte et al. (2010) to detect common QTLs in four linked oil palm crosses, each of a small size.
As QTL detection is more efficient for more heritable traits, high heritability may itself provide clues about the accuracy of the detected QTLs. Theoretically, the heritability of a trait is the proportion of the PV accounted for in aggregate by all the true QTLs associated with that trait, each QTL accounting for a different proportion of the variance. As a rough guide, in this study, if the proportion of PV accounted for by a particular QTL is <10 %, it is considered a minor effect QTL whereas if >10 % it is as a major QTL. In this study, all the 164 yield related QTLs in this study were minor QTLs (Table S2), the large number and small effects not surprising as the traits examined are complex with a notable number of them of very low heritability compounded by the small size and relatively narrow genetic variance of the study population. Complex traits in small advanced populations are however the working materials of oil palm breeding programmes. A parallel may be drawn with a barley QTL study (Wang et al. 2014) for grain yield and component traits, such as spike number, kernel number, kernel weight and thousand-kernel weight. Most of the QTLs detected affected only a small amount of the total PV, and their effects were very dependent on the growth environment.
Rance et al. (2001) detected six QTLs, for nine of the 21 traits reported here, by interval mapping in 83 palms of a F2 self-cross, but their linkage map comprised fewer markers (153 RFLPs). Billotte et al. (2010) reported of 76 QTLs in four connected families, each of small size, when consensus mapped with 251 SSR markers. Of the 76 QTLs, 43 were associated with oil yield components. The larger population, which increases the probability of detecting small effect QTLs, from combing the four crosses, may be the reason for the more QTLs than Rance et al. (2001). The large population size of cross DA41 in this study allowed the mapping of even more QTLs, 101 from the dura parent ARK86D and 63 from the pisifera parent ML161P. Although Deli dura genotypes, such as ARK, are reported to exhibit generally lower polymorphisms for breeding traits, the dura parent contributed more QTLs to DA41. The Yangambi family ML, developed over a few breeding cycles involving close matings, may be even more homozygous for the traits examined.
As FFB production in the oil palm is the product of the BNO and ABW, finding common marker-associated QTL effects for these three traits is not surprising. Twenty-two QTLs were located on five LGs (LG1, 8, 9, 10 and 14) in clusters. The traits BNO and ABW are strongly negatively correlated with BNO highly positively correlated with FFB (Ooi et al. 1973; Van Der Vossen 1974; Okwuagwu et al. 2008). The QTLs for BNO and ABW in this study were on the same three marker intervals in the DA41 map. Given the relationship between BNO and FFB, any QTL effect observed on BNO is also likely to be detected for FFB, unless a compensating effect by the QTLs associated with ABW masks the effect.
BWT has generally been reported to have low heritability (Hardon et al. 1985), making it difficult to elucidate its genetic control. The total variation explained by the QTLs in this study was higher for BNO (26.4 %) and FFB (27.1 %) than for ABW (19.7 %). Rance et al. (2001) located a putative QTL on LG13 that explained 5.5 % of the variance in FFB and 19.7 % for BNO, while a QTL detected for ABW on LG4 explained 19.7 % of the variance for that trait. The QTLs detected by Jeennor and Volkaert (2014) accounted for approximately 12 % and 54 % of the variation for FFB and ABW, respectively, but no significant QTLs were detected for BNO.
Turning to bunch and fruit characteristics Jacquemard et al. (1982) and Hardon et al. (1985) reported that some components, such as MF, SF and KF ratios, have relatively high heritability. Durand-Gasselin et al. (2006) suggested that some traits, such as vertical growth, mesocarp-to-fruit, oil-to-mesocarp and bunch number are inherited more from specific parents and, hence, in which the traits can be selected for in breeding programmes. Rance et al. (2001) detected potential QTLs for MF, KF and SF in an F1 population with values significant at the genome-wide threshold level. Their single QTL marker for each of the three traits accounted for 12.3, 8.5 and 44 %, respectively, of the total variance for that trait. The larger proportion of the PV accounted for by the QTLs in our study may be due to their higher number. For example, for two mesocarp-related traits the QTLs accounted for 19.5 % (DPF) and 33.9 % (WPF) of the total variance. Three kernel-related measurements had an average of 12 QTLs each, and they accounted for 40.8 % of total variance in KB, 39.1 % in KF and 48 % in MKW. Additionally, two shell-related measurements (MSW and SF) had an average of 10 QTLs each, accounting for 50.3 and 39.2 %, respectively, of the total trait variance.
Comparing across traits, QTLs for kernel-related traits accounted for the highest proportion of the trait phenotypic variance, ranging from 39 to 48 %. This is useful, as kernel yield is also valuable and contributes to profitability for the oil palm grower. Furthermore, in the oil palm, kernel development only occurs following successful fruit set and thus also contributes to BWT and OB. Their importance notwithstanding, the relationships, at the molecular level, between kernel-related traits and yield components are still poorly understood.
Rance et al. (2001) reported a putative QTL for OB at the linkage threshold of 21.5 %. However, in our study, though two QTLs were detected for OB, they accounted for only 8.1 % of the variation, while five accounted for 12.0 % of the variation in ODP, and seven for 15.1 % in OWP. This may be due to strong selection for oil content traits in the breeding of DA41 as evidenced by its very high mean OB of 35.4 % in one trial and 32.3–35.4 % in three subsequent trials (FGV, unpublished data). These values, close to the theoretical maximum, and the observed narrow range between individual palms imply very small genetic variation, for these traits in particular. Most of the QTLs for the oil-related traits were from the female parent, with only two from the male parent. This may be due to limited additive variation for the trait in the latter, as suggested by its good general combining ability across a range of female parents and by its consistent transmission of high bunch oil content (Chin et al. 2005).
The cumulative QTL effects and the number of QTL markers matching the QT+ alleles increased for all traits. This portends well for the QTLs as potential markers for applications in molecular assisted breeding. The results also provide information on the magnitude and direction of the QTL effects and the parental source of desirable QTL alleles. However, one limitation of the present type of study is the inability to estimate epistasis because interactions between different QTLs may not merely be the sum of effects of the individual QTLs.
As QTLs for complex traits are often associated with those of their component traits, QTL clustering was common in this study, and such clustering was present on almost all LGs. Some highly correlated traits controlled by cluster QTLs (Fig. 1) suggest that the co-located QTLs reflect either a set of closely linked loci or a single pleiotropic locus. A good example is the clustering of fruit component QTLs in LG9 (−QMSW_c, −QMKW_d, +QWPF_g, −QSF_d, and +QDPF_b). It has been suggested that if the same allelic phases are involved in the clustered QTLs then, these co-localized QTLs are most likely a result of pleiotropism. In rice, for example, a QTL coded Ghd8 was identified as a major QTL with pleiotropic effects on grain yield, heading date and plant height (Yan et al. 2011). Similarly, in maize, marker npi280 on the long arm of chromosome 6 accounted for 19 % of 100-g weight, 35 % of the PV in ear length and 35 % of the PV in yield (Veldboom and Lee 1994). In contrast, where the allelic phases are different in the clustered QTLs, they may correspond to closely linked loci/genes. For example, in oil palm, the alleles influencing shell or kernel traits are likely to also affect mesocarp-related traits and vice versa. From our study and earlier work, seven chromosomal regions (on LG1, 2, 5, 7, 9, 13 and 15) appear to harbour most of the QTLs underlying fruit characteristics relating to kernel, mesocarp, shell and oil content. Similarly, the clusters of QTLs on LG8, 9 and 10 were associated with fruit bunch production traits. These regions are the more important target regions for markers for oil yield component traits.
Several plant studies have reported QTL clusters with multiple effects on yield and yield-related traits (Coque and Gallais 2006; Laperche et al. 2006; Sun et al. 2012). In rice (Oryza sativa), three yield-related traits [spikelet fertility, 1000 grain weight (TGW), and number of spikelets per panicle (SPP)] were identified in one yield-enhancing QTL cluster, to the tune of 4.6 g grain per plant (Liu et al. 2013). In pea, Burstin et al. (2007) reported that most of the QTLs for seed traits mapped into a cluster possibly corresponding to genes controlling vegetative and flowering development as well as having pleiotropic effects on plant morphology, i.e., the source capacity contributing to final seed protein content and seed yield. In wheat (Triticum aestivum), the dwarfism gene Rht-B1 is associated with numerous QTLs, including those related to root development and grain yield (Laperche et al. 2006). In barley (Hordeum vulgare L.), a dwarf gene (uzu1) with pleiotropic effects has been recognized that influences spike morphology, including grain density, spike length and awn length (Chen et al. 2012). Using meta-analysis in Brassica napus, Shi et al. (2009) reported that 82.5 % consensus QTLs were clustered and integrated into 111 pleiotropic unique QTLs, 47 of which were associated with seed yield.
The existence of pleiotropic effect genes for quantitative traits is well founded in classical genetics and is the basis for indirect selection of secondary traits (yield components) with higher heritability to improve yield, the primary trait but of lower heritability (Austin and Lee 1996; Gupta et al. 2006; Messmer et al. 2009). Obviously, the success of such an approach will also depend on the associations between the secondary and primary traits. High genetic correlations between the secondary and primary traits and high heritability of the former may provide more gain in the primary trait, in less time and effort.
Epistasis has been demonstrated in the expression of traits involving more than one loci (Yan et al. 2006; Ma et al. 2007; Li et al. 2011); thus, it is reasonable to assume that the effects are operative in complex quantitative traits such as oil yield. It would not be surprising if the additive effects QTLs, found in this study, are also involved in digenic interactions with background loci. Several reports also suggest that epistatic interactions play an important role in heterosis, especially in rice (Hua et al. 2003; Li et al. 1997; Luo et al. 2001; Yu et al. 1997). Heterosis is also exploited in oil palm breeding, where the commercially planted thin-shell tenera hybrid is from crossing thick-shelled duras with shell-less pisiferas, both from genetically distinct populations. Gascon and de Berchoux (1964) and Durand-Gasselin et al. (2000) have suggested that the hybrid vigour in their “inter-origin” oil palm crosses is likely from combined dominance, additive and epistatic effects.
Comparative mapping using, for example, meta-QTL analysis (Goffinet and Gerber 2000), Join Map (Stam 1993; Stam and Van Ooijen 1995) or cosine projection (Ritter et al. 1990; Ritter and Salamini 1996) can integrate the QTL results from several maps of different populations, even if they are of different genetic backgrounds. These approaches allow the extrapolation of QTL results to other progenies to estimate the number of real and stable QTLs when common markers can be shared as anchor points between different maps. Comparative mapping, using shared markers and similar traits, with the results of Billotte et al. (2010) showed that most of the QTLs were the same and shared similar marker intervals on the LGs. However, as only a few oil palm maps have been published and even fewer of these maps have identified oil yield-related QTLs, such comparative mapping is very limited. This limitation is unfortunate, as additional information would facilitate the narrowing of confidence intervals for each QTL and aid in identifying genuine QTLs against spurious ones in overlapping genomic regions. In other crops, comparative mapping has been used to detect real QTLs for traits such as Fusarium head blight resistance (Häberle et al. 2009) and plant height in wheat (Griffiths et al. 2012), late blight resistance and plant maturity traits in potato (Danan et al. 2011) and yield in maize (Truntzler et al. 2010; Li et al. 2011).
Conclusions
QTL mapping in oil palms will facilitate the study of quantitatively inherited traits such as oil yield and its component traits and in identifying QTL markers associated with these traits. However, obtaining robust QTL data sets is a challenge, as extensive and costly phenotyping is required; the measurement of oil yield components in the oil palm being difficult, tedious and laborious. Bunch and fruit components are derivatives from multi-stage sub-sampling and only relatively few fruit bunches and fruits are taken for measuring the components, including oil content, due to costs. The multi-stage and limited sampling amplify measurement errors and biases. Furthermore, oil yield is the total expression of the genotype, from the time the fruits are formed until harvest, in each fruit bunch, and over many fruit bunches in the economic life-time of the palm. In practice, the oil yield components are determined only during certain stages of ontogeny of the genotype so it is their expression only during that portion of the growing period that is being viewed.
Lastly, for obvious reasons, a reasonable linkage between the marker and the causal quantitative trait expression is a pre-requisite for the marker to be useful, given the complex genetic architecture and varying heritability as well as environmental influences on oil yield components. These caveats notwithstanding, knowledge of the positions and effects of QTLs would be useful to link the phenotype to genotype for developing appropriate tools and methodologies for marker–assisted breeding. This knowledge will also provide a better understanding of the biological basis of various traits, for example, which genes are involved and their effects.
References
Austin DF, Lee M (1996) Comparative mapping in F2:3 and F6:7 generations of quantitative trait loci for grain yield and yield components in maize. Theor Appl Genet 92:817–826. doi:10.1007/BF00221893
Beavis WD (1998) QTL analyses: power, precision, and accuracy. In: Paterson AH (ed) Molecular dissection of complex traits. CRC Press, New York, pp 145–162
Billotte N, Jourjon MF, Marseillac N, Berger A, Flori A, Asmady H, Adon B, Singh R, Nouy B, Potier F, Cheah SC, Rohde W, Ritter E, Courtois B, Charrier A, Mangin B (2010) QTL detection by multi-parent linkage mapping in oil palm (Elaeis guineensis Jacq.). Theor Appl Genet 120:1673–1687. doi:10.1007/s00122-010-1284-y
Burstin J, Marget P, Huart M, Moessner A, Mangin B, Duchene C, Desprez B, Munier-Jolain N, Duc G (2007) Developmental genes have pleiotropic effects on plant morphology and source capacity, eventually impacting on seed protein content and productivity in pea. Plant Physiol 144:768–781. doi:10.1104/pp.107.096966
Chen GD, Li HB, Zheng Z, Wei YM, Zheng YL, McIntyre CL, Zhou MX, Liu CJ (2012) Characterization of a QTL affecting spike morphology on the long arm of chromosome 3H in barley (Hordeum vulgare L.) based on near isogenic lines and a NIL-derived population. Theor Appl Genet 125:1385–1392. doi:10.1007/s00122-012-1918-3
Chin CW, Ng WJ, Junaidah J, Suhaimi S, Mohd Nasruddin M (2005) Developing high oil yield DxP: the Felda experience. Proceedings of the 2005 National Seminar on Advances in Breeding and Clonal Technologies for Super Yielding Planting Material
Collard BCY, Jahufer MZZ, Brouwer JB, Pang ECK (2005) An introduction to markers, quantitative trait loci (QTL) mapping and marker-assisted selection for crop improvement: the basic concepts. Euphytica 142:169–196. doi:10.1007/s10681-005-1681-5
Coque M, Gallais A (2006) Genomic regions involved in response to grain yield selection at high and low nitrogen fertilization in maize. Theor Appl Genet 112:1205–1220. doi:10.1007/s00122-006-0222-5
Danan S, Veyrieras JB, Lefebvre V (2011) Construction of a potato consensus map and QTL meta-analysis offer new insights into the genetic architecture of late blight resistance and plant maturity traits. BMC Plant Biol 11:16. doi:10.1186/1471-2229-11-16
Durand-Gasselin T, Kouame KR, Cochard B, Adon B, Amblard P (2000) Diffusion variétale du palmier à huile (Elaeis guineensis Jacq.). Oil Corps Gras Lipides 7:203–206. doi:10.1051/ocl.2000.0207
Durand-Gasselin T, Hayun S, Jacquemard JC, Indra S, Adjé I, Flori A, Nouy B (2006) Palm oil yield potential of oil palm (Elaeis guineensis) seeds developed in a network by CIRAD and its partners. Presented at the International Seminar on Yield Potential in Oil Palm II, Phuket, Thailand. 27–28 Nov 2006
Gascon JP, de Berchoux C (1964) Caractéristiques de la production d’Elaeis guineensis (Jacq.) de diverses origines et leurs croisements. Application a la sélection du palmier a huile. Oléagineux 19:75–84
Goffinet B, Gerber S (2000) Quantitative trait loci: a meta-analysis. Genetics 155:463–473
Griffiths S, Simmonds J, Leverington M, Wang Y, Fish L, Sayers L, Alibert L, Orford S, Wingen L, Snape J (2012) Meta-QTL analysis of the genetic control of crop height in elite European winter wheat germplasm. Mol Breed 29:159–171. doi:10.1007/s11032-010-9534-x
Gupta PK, Rustgi S, Kumar N (2006) Genetic and molecular basis of grain size and grain number and its relevance to grain productivity in higher plants. Genome 49:565–571. doi:10.1139/g06-063
Häberle J, Holzapfel J, Schweizer G, Hartl L (2009) A major QTL for resistance against fusarium head blight in European winter wheat. Theor Appl Genet 119:325–332. doi:10.1007/s00122-009-1041-2
Hardon JJ, Rao V, Rajanaidu N (1985) A review of oil palm breeding. In: Russell GE (ed) Progress in plant breeding. Butterworths, London, pp 139–163
Hua J, Xing Y, Wu W, Xu C, Sun X, Yu S, Zhang Q (2003) Single-locus heterotic effects and dominance by dominance interactions can adequately explain the genetic basis of heterosis in a neliterice hybrid. Proc Natl Acad Sci USA 100:2574–2579. doi:10.1073/pnas.0437907100
Jacquemard JC, Meunier J, Bonnot F (1982) Genetic study of the reproduction of an Elaeis guineensis oil palm cross. In: Pushparajah E, Chew PS (eds) The oil palm in agriculture in the eighties, vol 1. Incorpated Society of Planters, Kuala Lumpur, pp 19–32
Jeennor S, Volkaert H (2014) Mapping of quantitative trait loci (QTLs) for oil yield using SSRs and gene-based markers in African oil palm (Elaeis guineensis Jacq.). Tree Genet Genomes 10:1–14. doi:10.1007/s11295-013-0655-3
Knapp SJ, Bridges WC (1990) Programs for mapping quantitative trait loci using flanking molecular markers and nonlinear models. J Hered 81:234–235
Knapp SJ, Bridges WC, Birkes D (1990) Mapping quantitative trait loci using molecular marker linkage maps. Theor Appl Genet 79:583–592. doi:10.1007/BF00226869
Laperche A, Devienne-Barret F, Maury O, Le Gouis J, Ney B (2006) A simplified conceptual model of carbon/nitrogen functioning for QTL analysis of winter wheat adaptation to nitrogen deficiency. Theor Appl Genet 113:1131–1146. doi:10.1007/s00122-006-0373-4
Li Z, Pinson SR, Park WD, Paterson AH, Stansel JW (1997) Epistasis for three grain yield components in rice (Oryza sativa L.). Genetics 145:453–465
Li JZ, Zhang ZW, Li YL, Wang QL, Zhou YG (2011) QTL consistency and meta-analysis for grain yield components in three generations in maize. Theor Appl Genet 122:771–782. doi:10.1007/s00122-010-1485-4
Liu T, Yu T, Xing Y (2013) Identification and validation of a yield-enhancing QTL cluster in rice (Oryza sativa L.). Euphytica 192:145–153. doi:10.1007/s10681-013-0929-8
Luo LJ, Li ZK, Mei HW, Shu QY, Tabien R, Zhong DB, Ying CS, Stansel JW, Khush GS, Paterson AH (2001) Overdominant epistatic loci are the primary genetic basis of inbreeding depression and heterosis in rice II. Grain yield components. Genetics 158:1755–1771
Ma XQ, Tang JH, Teng WT, Yan JB, Meng YJ, Li JS (2007) Epistatic interaction is an important genetic basis of grain yield and its components in maize. Mol Breeding 20:41–51. doi:10.1007/s11032-006-9071-9
Mayes S, Jack PL, Corley RH, Marshall DF (1997) Construction of a RFLP genetic linkage map for oil palm (Elaeis guineensis Jacq.). Genome 40:116–122. doi:10.1139/g97-016
Messmer R, Fracheboud Y, Bänziger M, Vargas M, Stamp P, Ribaut JM (2009) Drought stress and tropical maize: QTL-by-environment interactions and stability of QTLs across environments for yield components and secondary traits. Theor Appl Genet 119:913–930. doi:10.1007/s00122-009-1099-x
Okwuagwu CO, Okoye MN, Okolo EC, Ataga CD, Uguru MI (2008) Genetic variability of fresh fruit bunch yield in Deli/dura x tenera breeding populations of oil palm (Elaeis guineensis Jacq.) in Nigeria. J Trop Agric 46:52–57
Ooi SC, Hardon JJ, Phang S (1973) Variability in the Deli dura breeding population of the oil palm (Elaeis guineensis Jacq.). I. Components of bunch yield. Malays Agric J 49:112–121
Raghavan C, Collard BCY (2012) Effect of small mapping population sizes on reliability of quantitative trait locus (QTL) mapping. Afr J Biotechnol 4:10661–10674. doi:10.5897/AJB11.2032
Rance KA, Mayes S, Price Z, Jack PL, Corley RHV (2001) Quantitative trait loci for yield components in oil palm (Elaeis guineensis Jacq.). Theor Appl Genet 103:1302–1310
Ritter E, Salamini F (1996) The calculation of recombination frequencies in crosses of allogamous plant species with applications to linkage mapping. Genet Res 67:55–65. doi:10.1017/S0016672300033474
Ritter E, Gebhardt C, Salamini F (1990) Estimation of recombination frequencies and construction of RFLP linkage maps in plants from crosses between heterozygous parents. Genetics 125:645–654
Seng TY, Mohamed Saad SH, Chin CW, Ting NC, Harminder Singh RS, Qamaruz Zaman F, Tan SG, Syed Alwee SS (2011) Genetic linkage map of a high yielding FELDA deli × yangambi oil palm cross. PLoS ONE 6:e26593. doi:10.1371/journal.pone.0026593
Shi J, Li R, Qiu D, Jiang C, Long Y, Morgan C, Bancroft I, Zhao J, Meng J (2009) Unraveling the complex trait of crop yield with quantitative trait loci mapping in Brassica napus. Genetics 182:851–861. doi:10.1534/genetics.109.101642
Stam P (1993) Construction of integrated genetic linkage maps by means of a new computer package: joinMap. Plant J 3:739–744. doi:10.1046/j.1365-313X.1993.03050739.x
Stam P, Van Ooijen JW (1995) JoinMap™ version 2.0: software for the calculation of genetic linkage maps. Centre for Plant Breeding and Reproduction Research-Agriculture Research Department (CPRO-DLO), Wageningen
Sun F, Liu P, Ye J, Lo LC, Cao S, Li L, Yue GH, Wang CM (2012) An approach for jatropha improvement using pleiotropic QTLs regulating plant growth and seed yield. Biotechnol Biofuels 5:42. doi:10.1186/1754-6834-5-42
Truntzler M, Barrière Y, Sawkins MC, Lespinasse D, Betran J, Charcosset A, Moreau L (2010) Meta-analysis of QTL involved in silage quality of maize and comparison with the position of candidate genes. Theor Appl Genet 121:1465–1482. doi:10.1007/s00122-010-1402-x
Vales MI, Schön CC, Capettini F, Chen XM, Corey AE, Mather DE, Mundt CC, Richardson KL, Sandoval-Islas JS, Utz HF, Hayes PM (2005) Effect of population size on the estimation of QTL: a test using resistance to barley stripe rust. Theor Appl Genet 111:1260–1270. doi:10.1007/s00122-005-0043-y
Van Der Vossen H (1974) Towards more efficient selection for oil yield in the oil palm (Elaeis guineensis Jacq.). Dissertation. University of Wageningen, the Netherlands, p 107
Veldboom LR, Lee M (1994) Molecular-marker-facilitated studies of morphological traits in maize. II: determination of QTLs for grain yield and yield components. Theor Appl Genet 89:451–458. doi:10.1007/BF00225380
Wang J, Yang J, Jia Q, Zhu J, Shang Y, Hua W, Zhou M (2014) A new QTL for plant height in barley (Hordeum vulgare L.) showing no negative effects on grain yield. PLoS One 9:e90144. doi:10.1371/journal.pone.0090144
Yan J, Tang H, Huang Y, Zheng Y, Li J (2006) Quantitative trait loci mapping and epistatic analysis for grain yield and yield components using molecular markers with an elite maize hybrid. Euphytica 149:121–131. doi:10.1007/s10681-005-9060-9
Yan WH, Wang P, Chen HX, Zhou HJ, Li QP, Wang CR, Ding ZH, Zhang YS, Yu SB, Xing YZ, Zhang QF (2011) A Major QTL, Ghd8, plays pleiotropic roles in regulating grain productivity, plant Height, and heading date in Rice. Mol Plant 4:319–330. doi:10.1093/mp/ssq070
Yu SB, Li JX, Xu CG, Tan YF, Gao YJ, Li XH, Zhang Q, Saghai Maroof MA (1997) Importance of epistasis as the genetic basis of heterosis in an elite rice hybrid. Proc Natl Acad Sci USA 94:9226–9231. doi:10.1073/pnas.94.17.9226
Acknowledgments
The authors wish to thank their respective organizations for their support and permission to publish this paper.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
10681_2016_1771_MOESM1_ESM.docx
Fig S1. Graphs of number of palms in cross DA41 with increasing cumulative number of positive QT alleles for each trait tested. Supplementary material 1 (DOCX 4697 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Seng, TY., Ritter, E., Mohamed Saad, S.H. et al. QTLs for oil yield components in an elite oil palm (Elaeis guineensis) cross. Euphytica 212, 399–425 (2016). https://doi.org/10.1007/s10681-016-1771-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10681-016-1771-6