Bridge Principles and Epistemic Norms

Abstract

Is logic normative for belief? A standard approach to answering this question has been to investigate bridge principles relating claims of logical consequence to norms for belief. Although the question is naturally an epistemic one, bridge principles have typically been investigated in isolation from epistemic debates over the correct norms for belief. In this paper we tackle the question of whether logic is normative for belief by proposing a Kripkean model theory accounting for the interaction between logical, doxastic, epistemic and deontic notions and using this model theory to show which bridge principles are implied by epistemic norms that we have independent reason to accept, for example, the knowledge norm and the truth norm. We propose a preliminary theory of the interaction between logical, doxastic, epistemic and deontic notions that has among its commitments bridge principles expressing how logic is normative for belief. We also show how our framework suggests that logic is exceptionally normative.

1 Introduction

Suppose that Donald believes the following claims:

• (1) Iran is a nuclear threat;

• (2) If a nation is a nuclear threat, then it has the ability to produce nuclear weapons. Yet, Donald disbelieves (3):

• (3) Iran has the ability to produce nuclear weapons.

Prima facie, Donald ought not to have this combination of doxastic attitudes, and is irrational for doing so. The following is one diagnosis of what is wrong with Donald:

• 1. (3) is a logical consequence of (1) and (2); and

• 2. If (3) is a logical consequence of (1) and (2), then Donald ought not disbelieve (3) if he believes both (1) and (2).

This diagnosis suggests that logic is normative for belief and other doxastic and epistemic attitudes. Put another way, there are true conditionals from claims about logical consequence (or known logical consequence) to norms concerning what doxastic and epistemic attitudes to have. For instance, the following general principle yields the previously mentioned diagnosis:

$\textsc {Wo}$ $-$::

If q is a logical consequence of $p^1$,$\ldots$, $p^n$, then one ought not to (disbelieve q, if one believes $p^1$ and $\ldots$ and one believes $p^n$).

Wo− is a “bridge principle” combining three kinds of expressions: deontic operators (‘ought’), doxastic operators (‘believes’ and ‘disbelieves’) and logical operators (‘is a logical consequence’). MacFarlane (2004) has offered a useful taxonomy of principles, like Wo−, that link claims of logical consequence to epistemic norms governing doxastic attitudes, and addressed the question of which of those bridge principles, if any, are true. Following MacFarlane, we propose to address the question of whether logic is normative by examining which bridge principles are true. However, unlike others who have addressed this question, we will begin from epistemic norms that we have good reason to endorse, and use these to infer which bridge principles are true, given those epistemic norms. To do this, we build a model able to represent both the bridge principles and the epistemic norms. We then use our model to infer bridge principles from the epistemic norms. As we note, this model also has further potential uses, as it allows one to represent and examine the relationships between distinct phenomena involving combinations of logical, doxastic, epistemic and deontic operators.

Our method is somewhat different to the method that has more often been employed to examine which bridge principles are true. MacFarlane (2004)—and others—compare candidate bridge principles based on how well they meet various intuitive desiderata, such as how well they deal with the Preface Paradox, or whether they are too demanding (or not demanding enough).¹ One difficulty with this methodology is that it relies on background intuitions about epistemic matters that pull in opposite directions. For example, MacFarlane lists as desiderata both that logic not make “excessive demands” of agents by requiring them to clutter their minds with the logical consequences of their beliefs, and “strictness”—the idea that there is something wrong with someone who does not believe the logical consequences of her beliefs. This incompatibility suggests that these desiderata reflect competing background epistemic commitments. It is thus not possible to use this methodology to decide on correct bridge principles without also resolving the tension between these background epistemic commitments. By contrast, our approach for adjudicating between bridge principles primarily consists in determining whether they are consequences of general epistemic norms which form a stable package. Here, we begin from a package of stable and, we think, plausible epistemic norms, but it is worth noting that it would be possible to employ the same approach using an alternative package of norms.

Whether, and how, logic is normative for belief is, we think, a primarily epistemic question. It is thus natural to begin from our epistemic theories in answering it. With this in mind, we do this by constructing a model in which the relationships between epistemic norms and bridge principles can be examined.²

As MacFarlane highlighted, ascertaining which are the true bridge principles promises to be important for ascertaining which logic is the true one. Accordingly, a further distinctive aspect of our investigation is that it will strive for some logical neutrality in the investigation of which bridge principles follow from which epistemic norms, so as not to bias our results in favour of any particular logical theory. We do so by officially conducting our inquiry in a language without boolean connectives. Instead, our language will be equipped with conditional logical, epistemic, doxastic and deontic operators. This neutrality promises to have important implications for  both the normativity of logic and the plurality of logic. We offer a simple example of how the framework may come to be relevant to inquiry into such issues in Sect. 4.2.³

We have two related aims in this paper. The first is to propose and defend a theory of the interaction between logical, doxastic, epistemic and deontic operators. The second is to show how the bridge principles in the MacFarlanian taxonomy and specific epistemic norms relate to each other.⁴ Our focus will be on what we will call ‘purely epistemic norms,’ i.e., norms formulated solely in terms of boolean connectives, deontic operators, and doxastic or epistemic operators.⁵

MacFarlane’s choice of the expression ‘bridge principle’ to describe principles like Wo− is suggestive. ‘Bridge principles’ are formulas that involve expressions from different kinds of formal theories, and are familiar from discussions of how best to combine theories formulated in terms of different kinds of expressions into a single, unified theory.⁶ Bridge principles, in the combination of logics’ sense, are of interest because they yield predictions about the interaction of the expressions of the different theories being combined that go beyond those theories’ original predictions. Since all MacFarlanian bridge principles are formulated in terms of logical, doxastic, epistemic and deontic expressions, they are bridge principles also in the combination of logics’ sense. MacFarlanian bridge principles thus make it possible to unify logical, epistemic, doxastic and deontic theories, thus yielding predictions about how their respective expressions interact.

There is more than one way of combining logics governing different expressions. We will do so via a Kripkean model theory. This makes it possible to determine the principles that govern these expressions in terms of how we conceive of their interaction, formulated in terms of constraints on accessibility relations between worlds. Principles combining logical, epistemic, doxastic and deontic expressions are thus interpreted in terms of conditions on the accessibility relations associated with those expressions (for example, reflexivity, symmetry, etc.). In this setting, the truth of particular bridge principles or epistemic norms implies that the accessibility relations between worlds associated with the logical, epistemic, doxastic and deontic expressions satisfy particular constraints. Likewise, particular constraints satisfied by the accessibility relations imply the truth of particular bridge principles or epistemic norms. Accordingly, one’s views on particular principles combining logical, epistemic, doxastic and deontic expressions may be used to inform one’s views on the conditions on accessibility relations that are associated with those expressions, and vice-versa.

Despite its obvious relevance for inquiry into the normativity of logic, the broader question of how best to combine theories of logical, doxastic, epistemic and deontic operators has, for the most part, been neglected in the literature. A notable exception is (Tajer, 2020). Notwithstanding, there are a number of important differences between our approach and Tajer’s. Arguably, the most relevant of these concerns the epistemic norms appealed to when investigating the question. While we use wide-scope epistemic norms, Tajer uses narrow-scope norms. This difference means that we arrive at different conclusions about the normativity of logic. We say more about this issue in Sects. 7.3 and 8. Another difference between our approach and Tajer’s is that our investigation puts a greater emphasis on model-theoretic tools, given how we take epistemic norms to encode hypotheses about accessibility relations between worlds. Accordingly, we investigate the conditions on accessibility relations which are encoded by epistemic norms (we further distinguish our approach from Tajer’s in Sect. 7.3).

More specifically, our focus will be on the following epistemic norms. Call these the ‘basic norms’:

Basic Norms:

Knowledge norm::

It is obligatory to be such that (one knows that p if one believes that p).

Truth norm::

It is obligatory to be such that (p if one believes that p).

Immodesty norm::

It is obligatory to be such that (one believes that p if p is obligatory).

The following are two particularly interesting results shown in the paper:

• 1. Bridge principle Wo− is a consequence of the truth norm (and of the knowledge norm);

• 2. The following bridge principle is a consequence of the immodesty norm:

Wo+::

If q is a logical consequence of $p^1,\ldots ,p^n$, then one ought to (believe q if one believes $p^1$, $\ldots$, $p^n$).

These results are interesting insofar as both Wo− and Wo+ have been thought to be subject to important objections. For example, some (including MacFarlane) have thought that Wo− does not account for the Preface Paradox correctly, and that it fails to account for the putative irrationality of failing to believe the obvious logical consequences of one’s beliefs (as MacFarlane calls it, “Logical Obtuseness”). Wo+ has been thought to impose excessive demands on agents, and inappropriately require them to clutter their minds with a vast number of useless beliefs. However, we show that both of these bridge principles are entailed by some fairly plausible epistemic norms: the knowledge norm, the truth norm and the immodesty norm. As we argue in Sect. 3, rejecting Wo+ or Wo− requires rejecting these epistemic norms.⁷

The plan for the paper is as follows. The specific reading of the deontic operators that we are interested in is singled out in Sect. 2. Section 3 introduces the basic epistemic norms we begin from. The formal language $\mathfrak {L}$ used in the formulation of the theses discussed throughout the paper is presented in Sect. 4. Section 5 introduces the Kripkean model theory in which the results presented in the paper are proven. In Sect. 6 we present and motivate what we call the ‘minimal principles’ governing the logical, doxastic, epistemic and deontic operators. Among these are the theses that logical necessity is factive and that knowledge implies belief.

Section 7 presents the key results concerning which MacFarlanian bridge principles are implied by which minimal principles and basic norms. In particular, in Sect. 7.4 we bring together the various elements already discussed to give an account of how logic bears on an agent’s epistemic obligations, via a theory of how the logical, epistemic, doxastic, and deontic operators interact. This theory has among its commitments all the minimal principles, all the basic norms, as well as several bridge principles—among which are principles of Wo+ and Wo−. Finally, in Sect. 8 we reconsider how our framework and results bear on the question whether logic is normative for belief. We argue that our results and framework suggest, but do not entail, that logic is exceptionally normative relative to at least some sciences.

2 Norms: Epistemic, Evaluative and Owned

Epistemic norms, as we understand them here, express distinctively epistemic obligations and permissions. That is, they have epistemic force and are thus distinct from moral, prudential, or aesthetic norms.⁸

Specifically, the adopted reading of ‘ought’ is the following. Let a world x be an epistemically ideal world for an agent A relative to a world y if and only if, at x, A’s epistemic and doxastic states are epistemically best from the standpoint of y. Then, $\ulcorner$ought $\varphi \urcorner$ is true at y relative to A if and only if $\varphi$ is true at every world x that is epistemically ideal for A from the standpoint of y. The readings of the other deontic expressions of interest (e.g., ‘permissible’ and ‘forbidden’) are also formulated in terms of epistemically best worlds. They are presented in Sects. 4–5.

Strictly speaking, ‘ought’ stands for a relation between an agent and a proposition, for it concerns the states that are epistemically best for a given agent.⁹ It is thus similar to Broome’s (2013, Sect. 2.3) “owned ought”.¹⁰ On this reading the knowledge norm states that, for every proposition p and world x that is epistemically best for agent A from the standpoint of the actual world, A believes p at x only if A knows that p at x.

Our focus is on an evaluative understanding of epistemic norms.¹¹ Evaluative norms provide objective standards by which a state of the world can be evaluated as epistemically best. They do not provide rules by which agents can be guided towards an epistemically best state. Nor do they concern whether agents are to be credited or criticised for being in a particular state. Our epistemic norms are also understood propositionally rather than doxastically—they specify the attitudes the agent ought to have in order to be epistemically best, but not how she could come to have those attitudes in an epistemically acceptable way given her situation.¹² Epistemic norms are thus distinct from both guiding rules aimed at improving epistemic attitudes and considerations that contribute to the appraisal of agents as praiseworthy or blameworthy.¹³

We have chosen to focus on evaluative norms since there is reason to think that these are “theoretically prior”. Evaluative epistemic norms play a useful role in the other normative projects of guiding agents towards better states and of appraising agents. For example, it would be very difficult to determine norms that guide agents towards epistemically ideal states without first having in mind a conception of which states are epistemically ideal. Evaluative norms can help in guidance because they tell us what agents are to be guided towards. By telling you how to get to Larissa I presuppose that ideally you should get to Larissa, not London.¹⁴

Similarly, only in light of a set of primary evaluative norms can we begin to think about what kind of epistemic appraisal an agent deserves. It would be difficult to determine whether agents are to be praised, blamed, or excused without first knowing whether they have done well or badly relative to some epistemic ideal.¹⁵ Whereas evaluative epistemic norms focus on whether the agent has the epistemic attitudes she ought to have, when appraising an agent’s epistemic conduct we focus on considerations such as whether she was misled, deceived, did as well as she could given her circumstances, or lacked the relevant capacity.¹⁶ But, prima facie, agents should not always be praised (or escape blame) for having the epistemic attitudes they ought to have, nor should they always be blamed for failing to have the attitudes that they ought to have.¹⁷

Since they are not concerned with guidance, evaluative epistemic norms are independent of the agent’s abilities. Evaluative situation-independent standards are useful in various arenas—in ice skating a figure skater can be evaluated on an attempt to perform a triple axel by reference only to the moves required for doing it. These are the same regardless of whether the skater is able, given her present situation and capacities, to execute it. Considerations such as that the skater is not currently wearing her skates, is out of shape, or has a false belief about how many rotations a triple axel requires, do not affect what a triple axel requires. Similarly, evaluative epistemic norms provide standards for assessing states of the world and agents independently of whether the agents have the capacities to meet those standards.¹⁸ As Christensen (2004, p. 162) puts it, epistemic standards, “need not grade on effort”. We need not consider the agent’s capacities when evaluating whether a state of the world is epistemically ideal.¹⁹

3 Basic Norms

Two of the three Basic Norms from which we begin find widespread support in epistemology. For example, if Williamson (2000, p. 47) is correct that “mere believing is a kind of botched knowing”, then believing without knowing is a less than ideal epistemic state. But, in epistemically ideal worlds, beliefs are not botched. A plausible idea is thus that knowledge is the most valuable of the possible epistemic states. So, an agent’s belief state is epistemically best when it is a state of knowledge.

Not only might we think that knowledge is intrinsically valuable, but we also might think it provides the normative standard for action and assertion. For example, knowledge removes the risk of being wrong.²⁰ If knowledge is the most epistemically valuable belief state, then the knowledge norm is true—agents ought to be such that they believe p only if they know p. That is, in all epistemically ideal worlds, agents believe only what they know. Since knowledge implies truth, the truth norm is a consequence of the knowledge norm. The knowledge and truth norms are both endorsed by Hattiangadi (2010), Smithies (2012), Sutton (2005, 2007) and Williamson (2000). Meanwhile, the truth norm alone has even broader appeal. It is endorsed, in some form, by externalists and internalists alike (Gibbard, 2005; Gibbons, 2013; Littlejohn, 2012; Shah, 2003; Wedgwood, 2002; Whiting, 2012; Velleman, 2000).

A common objection to the knowledge and truth norms is that they are excessively demanding. This objection can seem compelling when we consider agents in unfortunate epistemic situations—agents who have systematically misleading evidence, who are brains in vats, or who are otherwise doomed to arrive at false beliefs despite managing their beliefs in what would seem to be epistemically acceptable ways. It is impossible for such agents to acquire knowledge, since knowledge is factive. Still, it can seem counterintuitive to say that these agents are failing to meet epistemic norms. After all, they seem to be doing everything right.

However, these agents are non-ideal, and here we are concerned with the epistemic norms that express how it would be epistemically ideal for agents to be. Brains in vats are not epistemically ideal. They are connected to their environment in suboptimal ways, and so fail to have knowledge. While they are not at fault for this - they are merely unlucky - we can distinguish norm conformity from other positive epistemic evaluations, such as blamelessness. Doing so permits us to conclude that agents who do everything right, but fail to know, may deserve a positive evaluation of blamelessness (or praiseworthiness) despite failing to meet the knowledge norm. For example, if they have employed good epistemic habits (Hawthorne & Srinivasan, 2013), been reasonable (Lasonen-Aarnio, 2010), or done what someone who was disposed to meet the knowledge norm would do (Srinivasan, 2015a; Williamson, Forthcoming).

We have not been able to find discussion of a norm quite like the immodesty norm in the literature.²¹ This norm says that ideal agents believe whatever is invariantly true across all ideal worlds. To put it differently, it says that being ideal is incompatible with having doxastic attitudes that fail to rule out that you are not ideal. One way to get a better understanding of the immodesty norm is by noting that epistemically ideal agents have beliefs that have appropriate epistemic bases, and are not defeated. For example, if, for all an epistemically ideal agent believes, she is being deceived or malfunctioning, then that this is left open by the agent as a live possibility provides an undercutting defeater for the reasons she would otherwise have for believing any other proposition. She cannot, then, be ideal because epistemically ideal agents do not have reasons that are undercut in this way.

Take the epistemically non-ideal circumstances to be circumstances in which the agent is, in one way or another, “tricked” by her environment—as she would be in a sceptical scenario—as well as circumstances in which, internally, she is not functioning correctly. Thus, the epistemically non-ideal circumstances include not only circumstances in which the agent is, e.g., a brain in a vat, but also circumstances in which she is having a perception as of being in front of a red wall although lighting conditions are misleading, as well as circumstances in which she is having a perception as of being in front of a red wall although her color vision is malfunctioning. According to the immodesty norm, when the agent is neither being deceived by her environment nor malfunctioning, she also believes that she is neither being deceived by her environment nor malfunctioning. This is because it is true in all epistemically ideal worlds that the agent is neither being deceived nor malfunctioning.

Epistemically ideal agents are thus immodest. They believe they are the “epistemically lucky” ones, the ones that are neither being deceived nor malfunctioning, and, indeed, they are.²² As should be clear, when circumstances are epistemically ideal, the agent’s belief that she is epistemically lucky will be true. So, the immodesty norm does not require that epistemically ideal agents believe what is false. This is, of course, consistent with non-ideal agents not believing that they are epistemically lucky.²³

For instance, suppose that Eliza’s perceptual apparatus is functioning appropriately, that lighting conditions are optimal, that no illusions are taking place, and so on. In other words, suppose that circumstances are epistemically ideal. Suppose, furthermore, that Eliza is currently having a perception as of being in front of a red wall. Her evidential bases are faultless. In such a circumstance, she should believe that she is in front of a red wall.

Now, assume that, for all Eliza believes, John has been playing with the lights, so that lighting conditions are not ideal. For this reason, she refrains from believing that she is in front of a red wall. “For all I believe, John is tricking me”, she thinks to herself, “so I don’t believe that this wall is red”. Now, in fact, John is not playing tricks on Eliza, and in fact there is no good reason for her to entertain that possibility. After all, circumstances are epistemically ideal. But she leaves open the possibility that she is being tricked by John nonetheless. Her beliefs do not rule this out. By entertaining the “sceptical hypothesis’ that John is tricking her, Eliza’s beliefs are not ideal, because entertaining this epistemic possibility undercuts her appropriately based beliefs. So, if one’s beliefs do not rule out the possibility that one is not epistemically ideal, then one cannot, in fact, be epistemically ideal. The immodesty norm rules out such cases.

As with the truth norm and the knowledge norm, there is debate to be had about the immodesty norm, its prospects, and how it fits with other norms already in the literature. Indeed, we hope that this first appearance of the norm will motivate further discussion on it. Here, we have aimed to show only that it is interesting, and that its consequences are worth exploring. As will be seen, some of its consequences are surprising with regard to the normativity of logic.

This concludes the presentation of the basic epistemic norms on which our results will be based. Although we have chosen to use these norms, in principle one could employ the same methods using different epistemic norms, which might lead to different results. In Sects. 4–5 we present the formal language and model-theoretic framework that we will use to inquire into which bridge principles are consequences of which basic norms.

4 The Language

Our first step is to delineate the formal object language that we will use. Our language contains none of the customary logical constants of first-order logic. No boolean connectives, quantifiers or identity.

One reason that led us to adopt such a language is that bridge principles concern primarily how logical, epistemic, doxastic and deontic operators interact. They do not, at least in the first instance, concern the customary logical constants. So, questions concerning what principles govern the logical constants would appear to be distracting. By leaving these expressions out we avoid the need to incur commitments concerning which principles govern them.

A related reason is that by formulating our results in a language without the customary logical constants it is possible to achieve a higher degree of neutrality with respect to which logic of the boolean connectives, quantifiers and identity is the correct logic. This promises to make our findings neutral ground for some debates between some proponents of different logics—even if our findings turn out not to constitute neutral ground with respect to all such debates. We will further clarify the sense in which classical logic is being presupposed, and the sense in which it isn’t, later in this section.

4.1 Language $\mathfrak {L}$

The following are the primitive expressions and formulae of the formal language $\mathfrak {L}$ in which we will be operating.

Primitive expressions of ${\varvec{\mathfrak {L}}}$:

• 1. Propositional variables: $\ulcorner p^i\urcorner$, for each i in the positive integers;

• 2. Conditional operators:

  • Actuality operator: ‘@’;

  • Logical operators: $\text {`}\Box _{L}\text {'}$, $\text {`}\Diamond _{L}\text {'}$, $\text {`}\blacksquare _{L}\text {'}$, and $\text {`}\blacklozenge _{L}\text {'}$;

  • Epistemic operators: $\text {`}\Box _{K}\text {'}$, $\text {`}\Diamond _{K}\text {'}$, $\text {`}\blacksquare _{K}\text {'}$, and $\text {`}\blacklozenge _{K}\text {'}$;

  • Doxastic operators: $\text {`}\Box _{B}\text {'}$, $\text {`}\Diamond _{B}\text {'}$, $\text {`}\blacksquare _{B}\text {'}$, and $\text {`}\blacklozenge _{B}\text {'}$;

  • Deontic operators: $\text {`}\Box _{O}\text {'}$, $\text {`}\Diamond _{O}\text {'}$, $\text {`}\blacksquare _{O}\text {'}$, and $\text {`}\blacklozenge _{O}\text {'}$.

Formulae of ${\varvec{\mathfrak {L}}}$:

• 1. Every propositional variable is a formula;

• 2. For any operator $\#$, formulae $\varphi$, $\psi ^1$, $\ldots$, $\psi ^n$, and natural number n: $\ulcorner \#(\varphi |\psi ^1,\ldots ,\psi ^n)\urcorner$ is also a formula.

We use $\ulcorner \#(\varphi )\urcorner$ to abbreviate $\ulcorner \#(\varphi |)\urcorner$, for all operators $\#$ and formulae $\varphi$ of $\mathfrak {L}$. Also, we will informally be using ‘p’, ‘q’, ‘r’, with as well as without superscripts, rather than the official propositional variables ‘$p^1$’, ‘$p^2$’ and ‘$p^3$’. Where $\overline{p}$ abbreviates $p^1,\ldots ,p^n$, the intended reading of the language’s operators is as follows, for every $X\in \{L,K,B,O\}$:²⁴

• 1. $\ulcorner @(q|\overline{p})\urcorner$: actually, q given that $\overline{p}$;

• 2. $\ulcorner \Box _{X}(q|\overline{p})\urcorner$: it is logically necessary that/ x knows that/ x believes that/ x ought to be such that q given that $\overline{p}$;

• 3. $\ulcorner \Diamond _{X}(q|\overline{p})\urcorner$: it is logically possible that/ for all x knows/ for all x believes/ x is permitted to be such that q given that $\overline{p}$;

• 4. $\ulcorner \blacksquare _{X}(q|\overline{p})\urcorner$: it is logically impossible that/ x’s knowledge state rules out/ x’s belief state rules out/ x is forbidden to be such that q given that $\overline{p}$;

• 5. $\ulcorner \blacklozenge _{X}(q|\overline{p})\urcorner$: it is logically possible that/ for all x knows/ for all x believes/ x is permitted to be such that q isn’t the case given that $\overline{p}$.

A few clarifications about language $\mathfrak {L}$ are in order. Firstly, $\mathfrak {L}$ contains logical operators rather than logical predicates.²⁵ Syntactically, logical operators take as arguments a (finite) sequence of formulae and a formula. By contrast, logical predicates—predicates standing for, e.g., logical consequence and logical consistency—take as arguments sequences of names of formulae. Semantically (as will be seen in Sect. 5) $\mathcal {L}$’s logical operators stand for functions from pairs of a sequence of propositions and a proposition to propositions, whereas logical predicates stand for relations between formulae. Since the objects of the epistemic, doxastic and deontic operators are propositions, there is a mismatch between their objects and the relata of logical consequence. This mismatch is the main reason why $\mathfrak {L}$ contains a logical necessity operator rather than a logical consequence predicate.²⁶ The elimination of this mismatch thus simplifies the shape of principles involving logical as well as deontic, doxastic and epistemic expressions. Furthermore, the choice of a logical operator rather than a logical predicate makes it possible to articulate such principles in terms of a basic Kripkean model theory for multi-modal languages. Otherwise, further complications would be needed in order to distinguish between the values, in a model, of names of sentences and those of sentences themselves.

Secondly, $\mathfrak {L}$ contains a large stock of primitive logical, epistemic, doxastic and deontic operators when compared to more standard languages containing expressions of these kinds. Whereas it is common to take one of ‘necessity’ and ‘possibility’ as a primitive, defining the remaining operators in terms of the chosen primitive, $\mathfrak {L}$ contains 4 primitive operators of each one of these kinds. Owing to the absence of boolean connectives from $\mathfrak {L}$, none of these operators is definable in terms of the others.

Thirdly, $\mathfrak {L}$’s operators are conditional operators taking as arguments not formulae but pairs of a formula and a sequence of formulae. This makes it possible to formulate correlates of the MacFarlanian bridge principles and of the basic norms via formulae containing no occurrences of boolean connectives, which allows us to be neutral on the status of substantive principles concerning the logic of the boolean connectives.

Fourthly, $\mathfrak {L}$ contains no correlate of the natural language expression ‘has a reason’. Consequently, the bridge principles in the MacFarlanian taxonomy formulated in terms of ‘has a reason’ are not formalisable in $\mathfrak {L}$. So, our theory of the interaction between logical, epistemic, doxastic and deontic operators will be silent on their status. The reason for leaving out the ‘has a reason’ operator is that there currently is no standard model-theoretic treatment of this expression. Defending any of the existing treatments, or proposing a novel one, would take us much beyond the scope of this paper.

Fifthly, the presence of the actuality operator makes it possible to find correlates in $\mathfrak {L}$ of MacFarlane’s bridge principles—originally formulated in terms of the material conditional—without appealing to the boolean connectives. In Sect. 4.2 we explain how to obtain, in $\mathfrak {L}$, “neutral” correlates of formulae involving boolean connectives and the logical, epistemic, doxastic and deontic operators. Further details are given in the Appendix, Sect. A.1.

4.2 Neutral Value

Let $\mathfrak {L}^{\text {bool}}$ be a language containing the operators of $\mathfrak {L}$, together with the boolean connectives. It is possible to obtain, in our language $\mathfrak {L}$, the neutral values of some formulae of $\mathfrak {L}^{\text {bool}}$ as they are used by proponents of classical logic. Here, the neutral value of a formula $\varphi$ of $\mathfrak {L}^{\text {bool}}$ is a formula in which no boolean connectives occur and which is equivalent to $\varphi$ in the context of the classical logician’s theory of the behaviour of the boolean connectives. The neutral value of $\varphi$ is thus the result of “factoring out” from $\varphi$ those commitments of classical logicians which are independent from their theory of the boolean connectives.

For instance, classical logicians take $\Box _{L}(p\rightarrow p)$ (‘it is logically necessary that $p\rightarrow p$’) to be equivalent to $\Box _{L}(p|p)$ (‘it is logically necessary that p given that p’), there being no occurrence of boolean connectives in this last principle. Accordingly, a commitment to $\Box _{L}(p\rightarrow p)$ may be factorised into (i) a commitment to $\Box _{L}(p|p)$, a formula which is $\Box _{L}(p\rightarrow p)$’s neutral value, and (ii) a commitment to principles of a general theory of the behaviour of the boolean connectives—e.g., to $\Box _{L}(\Box _{L}(p\rightarrow p)|\Box _{L}(p|p))$ and $\Box _{L}(\Box _{L}(p|p)|\Box _{L}(p\rightarrow p))$.

By appealing to the neutral value of a formula we will be able to formulate our discussion as if we are using boolean connectives—and in the way that classical logicians use them—while in fact our object language possesses no boolean connectives, so that we may remain neutral on their logic. Formulating the discussion in terms of neutral value will thus have the benefit of making it easier to follow, given the familiarity of boolean connectives.

In the Appendix (Sect. A.1) we characterise the sublanguage $\mathfrak {L}^{\text {nv+}}$ of $\mathfrak {L}^{\text {bool}}$ for which we will offer neutral values, and specify in more detail the neutral value function, $[\cdot ]^{\text {nv}}$, that maps each formula of $\mathfrak {L}^{\text {nv+}}$ to its neutral value. Here we offer nothing but a gloss on the neutral value function. If $\varphi$ is a formula of $\mathfrak {L}$ (and so formulated solely in terms of our conditional operators), then

$[\varphi ]^{\text {nv}}=\varphi.$ Furthermore, for each operator $\#$, and where $\xi$ is not a negated formula, we have that:

$[\#((\psi ^{1}{\wedge }{\ldots }{\wedge }\psi ^{n}){\rightarrow }(\chi ^{1}{\rightarrow }({\ldots }{\rightarrow }(\chi ^{m}{\rightarrow }\xi ))))]^{\text {nv}}=\#([\xi ]^{\text {nv}}\;|\;[\psi ^{1}]^{\text {nv}},{\ldots },[\psi ^{n}]^{\text {nv}},[\chi ^{1}]^{\text {nv}},{\ldots },[\chi ^{m}]^{\text {nv}})$ Thus, the neutral value function “treats” conjunction as the comma and puts as further antecedents the antecedents of the nested sequence of conditionals $(\chi ^{1}\rightarrow (\ldots (\rightarrow (\chi ^{m}\rightarrow \xi ))))$. For instance,²⁷

$$\begin{aligned} {\begin{matrix} [\Box _{B}((p\wedge q)\rightarrow (r\rightarrow q)]^{\text {nv}}&= \Box _{B}(q|p,q,r). \end{matrix}} \end{aligned}$$

(1)

If $\xi :=\theta$ is a negated formula, then,

$[\#((\psi ^{1}{\wedge }{\ldots }{\wedge }\psi ^{n}){\rightarrow }(\chi ^{1}{\rightarrow }({\ldots }{\rightarrow }(\chi ^{m}{\rightarrow }{\lnot }\theta ))))]^{\text {nv}}=\#^{c}([\theta ]^{\text {nv}}\;|\;[\psi ^{1}]^{\text {nv}},{\ldots },[\psi ^{n}]^{\text {nv}},[\chi ^{1}]^{\text {nv}},{\ldots },[\chi ^{m}]^{\text {nv}})$, where $\#^{c}$ is $\#$’s solid version if $\#$ isn’t solid, and is $\#$’s nonsolid version if $\#$ is solid. For instance,²⁸

$$\begin{aligned} {\begin{matrix} [\Diamond _{O}(p\rightarrow \lnot q)]^{\text {nv}}=\blacklozenge _{O}(q|p). \end{matrix}} \end{aligned}$$

(2)

Formulae with a conditional as their main connective are not in the domain of the neutral value function. Yet, neutral values for some of those formulae may be found by appealing to the actuality operator in the following manner:²⁹

$[(\varphi ^1\wedge \ldots \wedge \varphi ^n)\rightarrow (\psi ^{1}\rightarrow (\ldots \rightarrow (\psi ^{m}\rightarrow \xi ))))]^{\text {nv}}=[@((\varphi ^1\wedge \ldots \wedge \varphi ^n)\rightarrow (\psi ^{1}\rightarrow (\ldots \rightarrow (\psi ^{m}\rightarrow \xi ))))]^{\text {nv}}$

For instance,³⁰

$$\begin{aligned} {\begin{matrix} [(p\wedge q)\rightarrow p]^{\text {nv}}=[@((p\wedge q)\rightarrow p)]^{\text {nv}}=@(p|p,q). \end{matrix}} \end{aligned}$$

(3)

Classical theorists and those who disagree with them on the logic of the boolean connectives may nonetheless agree on the truth of the neutral values of some formulae. For instance, while classical logicians and ${\mathsf {K}}_3$ers disagree about whether $\Box _{L}(p\rightarrow p)$ is true, they do agree that $\Box _{L}(p|p)$ ($\Box _{L}(p\rightarrow p)$’s neutral value) is true.³¹ In this sense $\Box _{L}(p|p)$ captures, for $\mathsf {K}_3$ers, the “kernel of truth” of $\Box _{L}(p\rightarrow p)$ as this formula is used by classical logicians. Their disagreement with respect to $\Box _{L}(p\rightarrow p)$ may be seen as stemming from a disagreement on how a theory of the conditional is to be built on top of a principle on which they agree, specifically, $\Box _{L}(p|p)$.³²

The possibility of such agreements promises to be of relevance to debates on the normativity of logic involving proponents of different logical theories. When theorists have disagreeing views on the logic of the boolean connectives, their disagreements may give rise to disagreements on the status of particular bridge principles, as well as on which bridge principles are consequences of which epistemic norms. Still, it may happen that these further disagreements are spurious in the sense that, once their idiosyncratic views on the boolean connectives are filtered out, the theorists come to agree on at least some of the issues involving the normativity of logic with respect to which they previously seemed to disagree.³³

Considering the neutral values of bridge principles and epistemic norms can thus help in ascertaining whether classical and nonclassical logicians are involved in spurious disagreements of the sort just described. To give a simple example, consider the following bridge principle:

• (4) $\Box _{L}(p|p)\rightarrow \Box _{O}(\Box _{B}p\rightarrow \Box _{B}p)$.

A $\mathsf {K}_3$er and a classical logician may disagree on the truth of (4) owing to nothing but divergent views on the conditional. For instance, it may be that while the classical logician accepts (4), the $\mathsf {K}_{3}$er does not. For the $\mathsf {K}_{3}$er may think that $\Box _{B}p$ is truth-valueless for some values of ‘p’, and so that $\Box _{O}(\Box _{B}p\rightarrow \Box _{B}p)$ is truth-valueless for some values of ‘p’. In such a case she will think that (4) itself lacks a truth-value, given how she takes $\Box _{L}(p|p)$ to be true. Accordingly, our $\mathsf {K}_{3}$er will reject (4). She will also reject Wo+, given how (4) is among its instances. But it should be clear that the disagreement between the classical logician and the $\mathsf {K}_{3}$er is not really about the way in which logic is normative, but rather about what it takes for sentences involving the conditional to be true.

Appealing to the notion of neutral value thus allows us to move past such spurious disagreements between the classical logician and the $\mathsf {K}_{3}$er. For they may nonetheless both agree on the truth of $[(4)]^{\text {nv}}$, since in $[(4)]^{\text {nv}}$ their divergent views with respect to the logic of the conditional are filtered out. Indeed, it may be that they agree on the truth of $[\textsc {Wo+}]^{\text {nv}}$ in its full generality. In such a case their disagreement with respect to Wo+ would not emerge due to contrasting views on the normativity of logic, but rather due to their divergent commitments on the logic of the boolean connectives.

The notion of neutral value thus promises to be of relevance to issues at the intersection of debates on the normativity of logic and the plurality of logics. Indeed, to continue with our example, it is not unreasonable to think that considerations similar to the ones we have adduced involving the $\mathsf {K}_{3}$ers’ views on the conditional could be deployed to make a case that they should reject all MacFarlanian bridge principles. Those committed to the view that logic is normative might then regard this fact as offering some reason for rejecting the logic $\mathsf {K}_{3}$. Yet, by resorting to the notion of neutral value it is possible to ascertain some of the ways in which their thought would be misguided. For $\mathsf {K}_{3}$ers may reject the truth of MacFarlanian bridge principles while accepting the truth of their neutral values, and so while taking logic to be normative for thought. MacFarlanian bridge principles would be rejected by $\mathsf {K}_{3}$ers owing not to their views on the normativity of logic, but rather to their views on the conditional. Consideration of the notion of neutral value would be helpful in not prejudging the discussion against proponents of $\mathsf {K}_{3}$.

While this is nothing but a toy example, it shows that the fact that our investigation and findings do not involve object-language presuppositions with respect to the logic of the boolean connectives does promise to make them useful in addressing issues at the intersection of debates on the normativity of logic and the plurality of logics. Also, note that our theory does presuppose that the conditional operators of our language $\mathfrak {L}$ are governed by a number of principles, even if it does not exhibit object-language presuppositions with respect to the logic of the boolean connectives.

A related issue that is important to clarify concerns the status of our model theory, yet to be presented, and its relationship to our object-language. Our model theory is formulated in a classical metatheory. So, we do assume, in the metalanguage, a classical logic of the boolean connectives (as they are used in the metalanguage). Notwithstanding, we expect our metatheory to yield an object-level theory of the conditional operators of $\mathfrak {L}$ over which there can be agreement among at least some proponents of different logics of the boolean connectives (like the agreement of classical logicians and $\mathsf {K}_{3}$rs with respect to $[\Box _{L}(p\rightarrow p)]^{\text {nv}}$, despite their disagreement with respect to $\Box _{L}(p\rightarrow p)$), even if there won’t be universal agreement with respect to it. For while our metatheory is classical, adherence to the object-level theory that results from it does not require adherence to the metatheory – in the same way that a classical metatheory for intuitionistic logic does not require adherence to classical logic by intuitionistic logicians. To further clarify the issue, the role of the meta-theory is to specify the object language commitments involving $\mathfrak {L}$’s conditional operators. It is not to “endow those operators with meanings”. We presuppose that they are already meaningful and not unfamiliar, even if their use is by all means not as common as that of their nonconditional counterparts.

Overall, we intend our results to be available as neutral ground for different parties involved in disputes over questions such as which logic of the boolean connectives is the correct logic, even if we expect them not to be available as neutral ground for all parties involved in such disputes, since they may disagree with our object level theory of $\mathfrak {L}$’s conditional operators.

We are now able to obtain the neutral value of both MacFarlane’s bridge principles and of the basic norms. For simplicity, we will here focus solely on the MacFarlanian bridge principles Wo+ and Wo−, as these are the ones which have attracted most attention in the literature (where $\bigwedge _{i\le n}(\Box _{B}p^i)$ abbreviates $\Box _{B}p^1\wedge \ldots \wedge \Box _{B}p^n)$, and $\overline{\Box _{B}p}$ abbreviates the sequence $\Box _{B}p^1,\ldots ,\Box _{B}p^n$):³⁴

Bridge principles Wo+ and Wo−:

Wo+::

$\Box _{L}(q|\overline{p})\rightarrow \Box _{O}(\bigwedge _{i\le n}(\Box _{B}p^i)\rightarrow \Box _{B}q)$$[\textsc {Wo+}]^{\text {nv}}=@(\Box _{O}(\Box _{B}q|\overline{\Box _{B}p})|\Box _{L}(q|\overline{p}))$.

Wo−::

$\Box _{L}(q|\overline{p})\rightarrow \Box _{O}(\bigwedge _{i\le n}(\Box _{B}p^i)\rightarrow \lnot \blacksquare _{B}q)$. $[\textsc {Wo}-]^{\text {nv}}=@(\blacksquare _{O}(\blacksquare _{B}q|\overline{\Box _{B}p})|\Box _{L}(q|\overline{p}))$.

As for the basic norms and their neutral values, these are formulated as follows:

Basic Norms:

Knowledge norm::

$\Box _{O}(\Box _{B}p\rightarrow \Box _{K}p)$$[\textsc {Knowledge norm}]^{\text {nv}} = \Box _{O}(\Box _{K}p|\Box _{B}p)$

Truth norm::

$\Box _{O}(\Box _{B}p\rightarrow p).$$[\textsc {Truth norm}]^{\text {nv}} = \Box _{O}(p|\Box _{B}p).$

Immodesty norm::

$\Box _{O}(\Box _{O}p\rightarrow \Box _{B}p).$$[\textsc {Immodesty norm}]^{\text {nv}} = \Box _{O}(\Box _{B}p|\Box _{O}p).$

For ease of readability and familiarity, we will for the most part refer to the formulae of $\mathfrak {L}$ indirectly, via the formulae of which they are neutral values. We now turn to the model theory for $\mathfrak {L}$.

5 Model Theory

5.1 Frames and Operator Frames

Frames provide the basic resources for representing the interpretations of the different conditional operators of $\mathfrak {L}$. Formulae are interpreted as sets representing collections of worlds—which themselves represent propositions. Each conditional operator is interpreted as a function mapping each pair of a sequence of propositions and a proposition to a proposition. As expected, the interpretation of $\mathfrak {L}$’s conditional operators is constrained by the different accessibility relations between worlds. Frames are defined as follows:

Definition 1

(Frames) A frame is a sequence $\langle \mathcal {W},\mathcal {A},\mathcal {R}_{L},\mathcal {R}_{K},\mathcal {R}_{B},\mathcal {R}_{O}\rangle$ such that:

• 1. $\mathcal {W}$ is a nonempty set—$\mathcal {W}$ represents the set of worlds;

• 2. $\mathcal {A}\in \mathcal {W}$—$\mathcal {A}$ represents the actual world;

• 3. $\mathcal {R}_{L},\mathcal {R}_{K},\mathcal {R}_{B},\mathcal {R}_{O}\subseteq \mathcal {W}\times \mathcal {W}$—$\mathcal {R}_{L},$ $\mathcal {R}_{K},$ $\mathcal {R}_{B}$ and $\mathcal {R}_{O}$ are, respectively, logical, epistemic, doxastic and deontic accessibility relations between worlds;

• 4. $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$—the actual world is logically possible relative to itself.

The accessibility relations of frames capture the fact that what is logically necessary, known, believed and epistemically obligatory may depend on which world one is in. The only condition on the accessibility relations that will be imposed from the outset is that the actual world be logically possible relative to itself.

Our model-theory makes use of operator frames—structures more complex than frames. Operator frames are defined in terms of the notion of a (model-theoretic correlate of) a conditional operator:³⁵

Definition 2

(Conditional operators) A conditional operator of a nonempty set $\mathcal {W}$ is a function from $\bigcup _{n\in \mathbb {N}}((\wp (\mathcal {W}))^{n})\times \wp (\mathcal {W})$ to $\wp (\mathcal {W})$.

Each conditional operator thus represents a function mapping each pair of a finite sequence of propositions and a proposition to a proposition. Conditional operators will be the interpretation of $\mathfrak {L}$’s operators.

Operator frames consist of frames together with a specification of the particular conditional operators that constitute the interpretation of $\mathfrak {L}$’s operators, since their interpretation is partially but not completely determined by a frame’s accessibility relations.

Definition 3

(Operator frames) An operator frame is a pair $\mathcal {F}=\langle \mathcal {S},\mathcal {O}\rangle$, where $\mathcal {S}$ is a frame and $\mathcal {O}$ is a function assigning to each operator of $\mathfrak {L}$ a conditional operator of $\mathcal {W}$ such that, for every world w logically accessible to the actual world, every finite sequence $Y=\langle y^{1},\ldots ,y^{n}\rangle$ of propositions, every proposition z and every $X\in \{L,K,B,O\}$:³⁶

• If $\#$ is $\ulcorner @\urcorner$, then $\mathcal {O}(\#)(Y,z)$ is a proposition true at w (i.e., $w\in \mathcal {O}(\#)(Y,z)$) iff, if all members of Y are true at the actual world, then z is true at the actual world (i.e., $\mathcal {A}\in y$, for all members y of Y, only if $\mathcal {A}\in z$);

• If $\#$ is $\ulcorner \Box _X\urcorner$, then $\mathcal {O}(\#)(Y,z)$ is true at w iff, for every world v such that v is $\mathcal {R}_{X}$-accessible from w (i.e., $w\mathcal {R}_{X}v$), if all members of Y are true at v, then z is true at v;

• If $\#$ is $\ulcorner \blacksquare _X\urcorner$, then $\mathcal {O}(\#)(Y,z)$ is true at w iff, for every world v such that v is $\mathcal {R}_{X}$-accessible from w, if all members of Y are true at v, then z fails to be true at v;

• If $\#$ is $\ulcorner \Diamond _X\urcorner$, then $\mathcal {O}(\#)(Y,z)$ is true at w iff there is some world v such that v is $\mathcal {R}_{X}$-accessible from w and z is true at v if all members of Y are true at v;

• If $\#$ is $\ulcorner \blacklozenge _X\urcorner$, then $\mathcal {O}(\#)(Y,z)$ is true at w iff there is some world v such that v is $\mathcal {R}_{X}$-accessible from w and z isn’t true at v if all members of Y are true at v.

Only at worlds logically possible relative to the actual world is it guaranteed that the truth of the proposition that is the value of $\mathcal {O}(\#)$ for a sequence $\langle Y,z\rangle$ depends on the truth of $y^{1},\ldots ,y^{n}$ and z in a standard way. Whether this is so also at worlds logically impossible relative to the actual world depends on the specific operator frame in question. So, the only difference between operator frames based on precisely the same frame concerns the behaviour of operators at worlds logically impossible relative to the actual world. Thus, operator frames complement the representation of reality afforded by frames by distinguishing the conditional operators that represent the semantic values of the operators of $\mathfrak {L}$.

One of our results (Theorem 2) will make use of a particular class of operator frames, defined as follows:

Definition 4

An operator frame is focused just in case $\forall x,y((\mathcal {A}\mathcal {R}_{L}x\; \& \;x\mathcal {R}_{L}y)\Rightarrow \mathcal {A}\mathcal {R}_{L}y)$.

Thus, focused operator frames are operator frames in which a world is linked to the actual world by a chain of logical accessibility only if that world is itself logically accessible to the actual world.

5.2 Models, Truth and Consequence

We now turn to the definition of models for the language $\mathfrak {L}$.

Definition 5

(Models) A model $\mathcal {M}$ for $\mathfrak {L}$ is a pair $\mathcal {M}=\langle \mathcal {F},\mathcal {V}\rangle$, where $\mathcal {F}$ is an operator frame and $\mathcal {V}$ is a valuation function which assigns to each propositional variable of $\mathfrak {L}$ a a subset of worlds (i.e., $\mathcal {V}(p)\subseteq \mathcal {W}$, for every propositional variable p of $\mathfrak {L}$).

Thus, each model for $\mathfrak {L}$ consists of a particular interpretation of the propositional variables of the language. Each model for $\mathfrak {L}$ furthermore determines an interpretation for each formula of the language:

Definition 6

(Interpretation in a model) For each model $\mathcal {M}$, the interpretation $\llbracket \varphi \rrbracket$ in $\mathcal {M}$ of a formula $\varphi$ is determined as follows:

• 1. Atomic formulae: $\llbracket \varphi \rrbracket =\mathcal {V}(\varphi )$, if $\varphi$ is an atomic formula;

• 2. Complex formulae: $\llbracket \#(\varphi |\psi ^1,\ldots ,\psi ^n)\rrbracket =\mathcal {O}(\#)(\langle \langle \llbracket \psi ^1\rrbracket ,\ldots ,\llbracket \psi ^n\rrbracket \rangle ,\llbracket \varphi \rrbracket \rangle )$, for every conditional operator $\#$ of $\mathfrak {L}$, all formulae $\varphi$, $\psi ^1,\ldots ,\psi ^n$, and every $n\in \mathbb {N}$.

Truth in a model and world is then defined as follows:

Definition 7

(Truth in a model relative to a world) A formula $\varphi$ of $\mathfrak {L}$ is true in a model $\mathcal {M}$ relative to a world $w\in \mathcal {W}$, $\mathcal {M},w\vDash \varphi$, iff $w\in \llbracket \varphi \rrbracket$.

This section’s final definitions are those of truth in a model, truth in an operator frame and consequence:

Definition 8

(Truth in a model)

• 1. A formula $\varphi$ is true in a model, $\mathcal {M}\vDash \varphi$, if and only if $\mathcal {M},\mathcal {A}\vDash \varphi$.

• 2. A set of formulae $\Gamma$ is true in a model, $\mathcal {M}\vDash \Gamma$, if and only if $\mathcal {M}\vDash \gamma$ for all $\gamma \in \Gamma$.

Definition 9

(Truth in an operator frame) A formula $\varphi$ is true in an operator frame $\mathcal {F}$, $\mathcal {F}\vDash \varphi$, if and only if $\mathcal {M}\vDash \varphi$ for all models based on operator frame $\mathcal {F}$.

Definition 10

(Consequence)

• 1. $\varphi$ is a consequence of $\Gamma$ in an operator frame $\mathcal {F}$, $\Gamma \vDash _{\mathcal {F}}\varphi$, iff, if $\mathcal {F}\vDash \Gamma$, then $\mathcal {F}\vDash \varphi$;

• 2. $\varphi$ is a consequence of $\Gamma$, $\Gamma \vDash \varphi$, iff, $\Gamma \vDash _{\mathcal {F}}\varphi$ for all operator frames $\mathcal {F}$.

Each operator frame encodes a certain hypothesis about the different accessibility relations between worlds, and about the behaviour of operators at non-logically possible worlds. Thus, truth at an operator frame is best understood as representing truth, at the actual world, given certain hypotheses about the structure of accessibility relations, and the behaviour of conditional operators at worlds logically impossible relative to the actual world. Accordingly, with (model-theoretic) consequence, as we’ve defined it, we aim to represent actual truth-preservation independently of the particular structure of the logical, epistemic, doxastic and deontic accessibility relations, their interaction, and of the behaviour of operators at logically impossible worlds. In particular, we do not intend it to represent logical consequence, nor logical necessity.³⁷

Our model-theoretic definitions of truth and of consequence presuppose that the formulae of the language are interpreted as implicitly universally quantified. For the truth of a formula in an operator frame boils down to the truth of the result of prefixing the formula with universal quantifiers binding all of its free propositional variables. Thus, we are treating principles containing free variables as being of a general character—independent of the particular values that the variables in them take.

One important idea behind our model-theoretic framework is that there may be worlds which are logically impossible relative to the actual world and yet linked to the actual world via chains of accessibility relations. For this reason, worlds which are logically impossible relative to the actual world may nonetheless be relevant for the evaluation of the truth, at the actual world, of some of the formulae in the language. Relatedly, some worlds which are logically impossible relative to the actual world may be logically possible relative to other, nonactual, worlds. Thus, what is logically possible may itself be a “contingent” matter.³⁸

One of our aims is to investigate the way in which the logical, epistemic, doxastic and deontic operators interact by considering the operator frames which are determined by the truth of distinguished principles governing those operators. These principles may informally be understood as encoding specific hypotheses about the structure of the logical, epistemic, doxastic and deontic accessiblity relations, and their interaction. Since this is one of our aims, our model-theory allows for close to maximal variation with respect to the structure of the logical, epistemic, doxastic and deontic accessibility relations, and their interaction. The one requirement which we impose is that the actual world be logically possible relative to itself. For, if it weren’t, then the conditional operators might behave in unruly ways even at the actual world. In such a case, the truth at the actual world of the principles to be investigated, such as the basic norms and the MacFarlanian bridge principles, would impose no particular conditions on the accessibility relations between worlds.

We now turn to the presentation of some plausible principles governing the conditional operators of our language, and to the investigation of the specific hypotheses concerning the structure of the logical, epistemic, doxastic and deontic accessibility relations encoded by them.

6 Minimal Principles

The following are plausible, logically necessary principles governing our operators:

Minimal principles:

T$_{L}$::

$[\Box _{L}(\Box _{L}p\rightarrow p)]^{\text {nv}}$—Logical necessity is factive in all logically possible worlds;

4$_{L}$::

$[\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$—Logical necessities are logically necessary in all logically possible worlds;

B$_{L}$::

$[\Box _{L}(p\rightarrow \Box _{L}\Diamond _{L} p)]^{\text {nv}}$—Truths are (logically) necessarily logically possible in all logically possible worlds;

T$_{K}$::

$[\Box _{L}(\Box _{K}p\rightarrow p)]^{\text {nv}}$— Knowledge is factive in all logically possible worlds;

KB::

$[\Box _{L}(\Box _{K}p\rightarrow \Box _{B}p)]^{\text {nv}}$—Knowledge implies belief in all logically possible worlds;

D$_{O}$::

$[\Box _{L}(\Box _{O}p\rightarrow \Diamond _{O}p)]^{\text {nv}}$—Obligations are permitted in all logically possible worlds;

LO::

$[\Box _{L}(\Diamond _{O}p\rightarrow \Diamond _{L}p)]^{\text {nv}}$—Permission implies logical possibility in all logically possible worlds.

Now, consider the following conditions on the accessibility relations of frames:

• Logical reflexivity@: $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow x\mathcal {R}_{L}x)$;

• Epistemic reflexivity@: $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow x\mathcal {R}_{K}x)$;

• Doxastic-epistemic inclusion@: $\forall x, y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow x\mathcal {R}_{K}y))$;

• Deontic seriality@: $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow \exists y(x\mathcal {R}_{O}y))$;

• Logical-deontic inclusion@: $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{O}y\Rightarrow x\mathcal {R}_{L}y))$;

• Logical symmetry@: $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{L}y\Rightarrow y\mathcal {R}_{L}x))$;

• Logical transitivity@: $\forall x,y,z\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow ((x\mathcal {R}_{L}y\; \& \;y\mathcal {R}_{L}z)\Rightarrow x\mathcal {R}_{L}z))$.

We have the following correspondences between frame truth and frame conditions:

Theorem 1

For all operator frames $\mathcal {F}$:

• 1. $\mathcal {F}\vDash {\textsc {T}}_{L}$ iff $\mathcal {F}$ satisfies logical reflexivity@;

• 2. $\mathcal {F}\vDash {\textsc {4}}_{L}$ iff $\mathcal {F}$ satisfies logical transitivity@;

• 3. $\mathcal {F}\vDash {\textsc {T}}_{K}$ iff $\mathcal {F}$ satisfies epistemic reflexivity@;

• 4. $\mathcal {F}\vDash {\textsc {KB}}$ iff $\mathcal {F}$ satisfies doxastic-epistemic inclusion@;

• 5. $\mathcal {F}\vDash {\textsc {D}}_{O}$ iff $\mathcal {F}$ satisfies deontic seriality@;

• 6. $\mathcal {F}\vDash {\textsc {LO}}$ iff $\mathcal {F}$ satisfies logical-deontic inclusion@.

In Theorem 1 are presented the so-called frame correspondents of principles $\textsc {T}_{L}$, $\textsc {T}_{K}$, $\textsc {KB}$, $\textsc {D}_{O}$, $\textsc {L}_{O}$, and $\textsc {4}_{L}$, these being the hypotheses concerning the structure of accessibility relations encoded by those principles.

Our next result concerns the relationship between principle $\textsc {B}_{L}$ and logical symmetry@. As it turns out, logical symmetry@ fails to be the frame correspondent of $\textsc {B}_{L}$.³⁹ Still, if only focused frames are considered, then logical symmetry@ does turnout to be $\textsc {B}_{L}$’s frame correspondent:

Theorem 2

$\mathcal {F}\vDash {\textsc {B}}_{L}$ iff $\mathcal {F}$ satisfies logical symmetry@, for all focused operator frames $\mathcal {F}$.

The following is a corollary of Theorems 1 and 2, and the fact that a frame satisfies logical transitivity@ only if it is focused.

Corollary 1 If $\mathcal {F}\vDash {\textsc {4}}_{L}$, then $\mathcal {F}\vDash {\textsc {B}}_{L}$ iff $\mathcal {F}$ satisfies logical symmetry@, for all operator frames $\mathcal {F}$.

How plausible are the minimal principles? Very plausible, presumably. Arguably, these principles are encapsulated in the usual understanding of the operators, and appear to be implicit in their standard logics. These observations afford some reasons for thinking that they hold of logical necessity (though a full defence of this claim lies outside our paper’s scope). For example, principles T$_{L}$, 4$_{L}$ and B$_{L}$ are relatively uncontroversial principles about logical necessity. According to T$_{L}$, logical necessity is factive; 4$_{L}$ states that if p is logically necessary, then it is not logically contingent, nor logically impossible, that p is logically necessary; and, according to B$_{L}$, if p is true, then it is logically necessary that it is logically possible that p is true.

Principles T$_{K}$ and KB are closely related to commitments of the standard logics for knowledge and belief. They are also independently plausible. Presumably, it is logically necessary that knowledge is factive, and it is logically necessary that knowledge implies belief. Principle D$_{O}$ is closely related to the “ought implies permission” axiom of Standard Deontic Logic (SDL).⁴⁰

According to principle LO, every epistemically ideal world is logically possible. To our knowledge this principle has not been discussed in the literature. Still, it is suggested by SDL’s rule of necessitation. For, according to this rule, if $\varphi$ is a logical truth of SDL, then that $\varphi$ is obligatory is also a logical truth of SDL—and so, presumably, a plain truth. So, presumably, whatever is a logical truth is epistemically obligatory. Arguably, this principle—whatever is a logical truth is epistemically obligatory—is logically necessary, in which case we obtain principle $\textsc {LO}$.

It is worth clarifying the role of the minimal principles in our investigation. They afford legitimate hypotheses, to be conjoined with the basic norms, with regard to the aim of deriving MacFarlanian principles Wo+ and Wo−. Even if none of Wo+ and Wo− is derivable from just the basic norms, they turn out to be derivable from the basic norms together with the minimal principles. Insofar as the minimal principles constitute intuitively plausible hypotheses on the behaviour of our language’s conditional operators, deriving Wo+ and Wo− from nothing but the basic norms and the minimal principles reveals the extent to which the MacFarlanian bridge principles may be seen as outright consequences of general epistemic norms. In addition, negative results showing that Wo− or Wo+ are not derivable from some basic norms even in conjunction with all the minimal principles suggest that those bridge principles encode substantive assumptions about the structure of epistemic normativity which go beyond the ones encoded by the basic norms in question. Minimal principles also play a role in our investigation of whether logic is autonomously normative, as we further discuss in Sect. 8.

7 Results

The principal aim of this section is to present the main results of our framework in relation to the normativity of logic. In Sect. 7.1 we show what the frame correspondents of the basic norms are. By considering the hypotheses about the structure of accessibility relations encoded by the basic norms, our correspondence results will make it possible to extract consequences about the relationship between bridge principles, basic norms and minimal principles. In Sect. 7.2 we prove our main results by appealing to the frame correspondents of the minimal principles and the basic norms. In Sect. 7.3 we discuss Tajer’s alternative routes for deriving Wo− and Wo+ from purely epistemic norms. Finally, in Sect. 7.4 we show what MacFarlanian bridge principles are consequences of the full theory resulting from collecting together the minimal principles and the basic norms.

We will make use of the following conventions. By ‘minimal’ and ‘basic norms’ we will mean the collections consisting of, respectively, the minimal principles, and the neutral values of the basic norms. Furthermore, given formulae $\varphi ^{1},\ldots ,\varphi ^{n}$ of $\mathfrak {L}$, by $\ulcorner \textsc {minimal}-\{\varphi ^{1},\ldots ,\varphi ^{n}\}\urcorner$ we mean the collection of principles in minimal which are distinct from all of $\varphi ^{1}$, $\ldots$, $\varphi ^{n}$, and by $\ulcorner \textsc {basic norms}-\{\varphi ^{1},\ldots ,\varphi ^{n}\}\urcorner$ we mean the collection of basic norms which are distinct from all of $\varphi ^{1}$, $\ldots$, $\varphi ^{n}$. For instance, ${\textsc {minimal}}-\{{\textsc {LO}},{\textsc {T}}_{K}\}$ consists of the collection of those principles in minimal which are distinct from both LO and ${\textsc {T}}_{K}$.

7.1 Frame Correspondents of the Basic Norms

Consider the following conditions on the accessibility relations on frames:

• Truth norm condition: $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}x)$;

• Knowledge norm condition: $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{K}y\Rightarrow x\mathcal {R}_{B}y))$;

• Immodesty norm condition: $\forall x, y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow x\mathcal {R}_{O}y))$.

These conditions are the natural candidates for being the frame correspondents of the neutral values of their respective norms. Indeed, once the class of frames is restricted to those frames in which $\textsc {LO}$ is true, the basic norms do have as correspondents their respective conditions.⁴¹

Theorem 3

$\mathcal {F}\vDash [{\textsc {truth norm}}]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the truth norm condition, for all operator frames $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

Theorem 4

$\mathcal {F}\vDash [{\textsc {knowledge norm}}]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the knowledge norm condition, for all operator frames $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

Theorem 5

$\mathcal {F}\vDash [{\textsc {immodesty norm}}]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the immodesty norm condition, for all operator frames $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

The final result of Sect. 7.1 maps the relationships between the different basic norms:

Theorem 6

• 1. The $[{\textsc {truth norm}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with the $[{\textsc {immodesty norm}}]^{\text {nv}}$;

• 2. The $[{\textsc {immodesty norm}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with the $[{\textsc {knowledge norm}}]^{\text {nv}}$;

• 3. The $[{\textsc {knowledge norm}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with ${\textsc {basic norms}}-\{[{\textsc {knowledge norm}}]^{\text {nv}}\}$;

• 4. The $[{\textsc {truth norm}}]^{\text {nv}}$ is a consequence of ${\textsc {T}}_{K}$, ${\textsc {LO}}$ and the $[{\textsc {knowledge norm}}]^{\text {nv}}$.

Of particular significance is the observation that the $[\textsc {immodesty norm}]^{\text {nv}}$ and the $[\textsc {knowledge norm}]^{\text {nv}}$ are independent, as are the $[\textsc {immodesty norm}]^{\text {nv}}$ and the $[\textsc {truth norm}]^{\text {nv}}$.

7.2 Bridge Principles and Basic Norms

What follows are the substantial results of the framework with respect to the relationship between the basic norms and bridge principles $[\textsc {Wo}$-$]^{\text {nv}}$ and $[\textsc {Wo+}]^{\text {nv}}$. Given the importance of the results, we prove them in the main text. In the appendix further results concerning the neutral values of the remaining bridge principles singled out in (MacFarlane, 2004) are presented.

7.2.1 Wo−

We begin with a preliminary result:

Theorem 7

$[{\textsc {Wo}}-]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ and the $[{\textsc {immodesty norm}}]^{\text {nv}}$.

Proof of Theorem 7

The following model $\mathcal {M}$ witnesses the fact that $[\textsc {Wo}$-$]^{\text {nv}}$ fails to be a consequence of minimal and the $[\textsc {immodesty norm}]^{\text {nv}}$:

Model $\mathcal {M}$ (Fig. 1) has two worlds, the actual world $\mathcal {A}$, and w. Arrows represent the accessibility relations. For instance, world w is both epistemically and doxastically possible relative to the actual world. It is neither logically nor deontically possible relative to the actual world. The placement of a propositional letter inside a world represents the fact that the proposition assigned to that propositional letter contains the world in question, and so that the propositional letter is true at that world. For instance, since p occurs in both $\mathcal {A}$ and w, p is true at both the actual world and w; q is true at $\mathcal {A}$ but not at w.

Fig. 1

Witness to ${\textsc {minimal}},{\textsc {immodesty norm}}\not \vDash [\textsc {Wo}$-$]^{\text {nv}}$

Checking that the $[\textsc {immodesty norm}]^{\text {nv}}$ and all the minimal principles are true in the operator frame $\mathcal {F}$ on which $\mathcal {M}$ is based is a routine exercise, owing to Theorems 1 and 5 and Corollary 1. But $[\textsc {Wo}$-$]^{\text {nv}}$ fails to be true in $\mathcal {M}$, and so in $\mathcal {F}$. For p is true at w whereas q isn’t (Fig. 1). So, p is true at every world doxastically possible relative to the actual world, and q fails to be true at every world doxastically possible relative to the actual world. So, $\Box _{B}p$ and $\blacksquare _{B}q$ are both true at the actual world, as the actual world is logically possible relative to itself. So, $[\Box _{O}(\Box _{B}p\rightarrow \lnot \blacksquare _{B}q)]^{\text {nv}}$ is false at the actual world, since the actual world is deontically and logically possible relative to itself. Yet, the actual world is the only world logically possible relative to itself, and q is true at the actual world. Hence, $[\Box _{L}(q|p)]^{\text {nv}}$ is true at the actual world. Therefore, $[\textsc {Wo}$-$]^{\text {nv}}$ is false at the actual world, and so on the operator frame on which $\mathcal {M}$ is based.

Our first positive result shows that the assumption of the truth of the basic norms does yield positive predictions vis-à-vis the normativity of logic.⁴²

Theorem 8

$[{\textsc {Wo}-}]^{\text {nv}}$ is a consequence of ${\textsc {LO}}$ and the $[{\textsc {truth norm}}]^{\text {nv}}$.

Proof of Theorem 8

Suppose that $\Box _{L}(q|\overline{p})$ is true at the actual world. Suppose also that x is an arbitrary world deontically possible relative to the actual world at which $\Box _{B}p^i$ is true, for all members $p^i$ of $\overline{p}$. So, x is doxastically possible relative to itself, by the $[\textsc {truth norm}]^{\text {nv}}$ and Theorem 3. Furthermore, x is logically possible relative to the actual world, by LO and Theorem 1. So, all the $p^i$s are true at x. So, q is true at x. Hence, $\blacksquare _{B}q$ is false at x, since x is logically possible relative to the actual world. So, $\Box _{B}p^i$ is true at x, for all members $p^i$ of $\overline{p}$ only if $\blacksquare _{B}q$ is false at x. Therefore, $[\Box _{O}(\bigwedge \Box _{B}p^i\rightarrow \lnot \blacksquare _{B}q)]^{\text {nv}}$ is true at the actual world, since the actual world is logically possible relative to itself. So, $[\textsc {Wo}$-$]^{\text {nv}}$ is true at the actual world.

Theorem 8 thus reveals that if epistemically best beliefs must be true—as advocated by, among others, proponents of Knowledge First epistemology—then Wo− is true. Relatedly, a straightforward corollary of Theorems 6 and 8 is that $[\textsc {Wo}$-$]^{\text {nv}}$ is a consequence of ${\textsc{LO}}$ and the $[{\textsc {knowledge norm}}]^{\text {nv}}$.

7.2.2 Wo+

Our next result is a reveals the limitations of the $[\textsc {knowledge norm}]^{\text {nv}}$:

Theorem 9

$[{\textsc {Wo+}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with the $[{\textsc {knowledge norm}}]^{\text {nv}}$.

Proof of Theorem 9

Consider the following model $\mathcal {M}$:

Checking that the $[\textsc {knowledge norm}]^{\text {nv}}$ and all minimal principles and are true in the operator frame $\mathcal {F}$ on which $\mathcal {M}$ (Fig. 2) is based is a routine exercise. To see why $[\textsc {Wo+}]^{\text {nv}}$ fails to be true in $\mathcal {M}$, note that $\Box _{B}q$ is false at the actual world, since w is doxastically possible relative to the actual world, q is false at w, and the actual world is logically possible relative to itself. Also, p is true at both the actual world and w, these are the only worlds doxastically possible relative to the actual world, and the actual world is logically possible relative to itself. So, $\Box _{B}p$ is true at the actual world. Moreover, the actual world is deontically possible relative to itself. So, there is a possible world deontically possible relative to the actual world such that $\Box _{B}p$ is true at it, but $\Box _{B}q$ isn’t. Furthermore, the actual world is logically possible relative to itself. So, $[\Box _{O}(\Box _{B}p\rightarrow \Box _{B}q)]^{\text {nv}}$ isn’t true at the actual world. Furthermore, $\Box _{L}(q|p)$ is true at the actual world, since the actual world is the only world logically possible relative to the actual world and q is true at the actual world. Therefore, $[\textsc {Wo+}]^{\text {nv}}$ fails to be true at the actual world.

Fig. 2

Witness to $\textsc {minimal},[\textsc {knowledge norm}]^{\text {nv}}\not \vDash [\textsc {Wo+}]^{\text {nv}}$

Next comes the second main positive result of our framework.⁴³

Theorem 10

$[{\textsc {Wo+}}]^{\text {nv}}$ is a consequence of the $[{\textsc {immodesty norm}}]^{\text {nv}}$, ${\textsc {LO}}$ and ${\textsc {4}}_{L}$.

Proof of Theorem 10

Let $\mathcal {F}$ be an arbitrary operator frame such that LO, $4_L$ and the $[\textsc {immodesty norm}]^{\text {nv}}$ are all true at $\mathcal {F}$. Suppose that $\Box _{L}(q|\overline{p})$ is true at the actual world, x is an arbitrary world deontically possible relative to the actual world, and $\Box _{B}p^i$ is true at x, for every member $p^i$ of $\overline{p}$. Since x is deontically possible relative to the actual world, and the actual world is logically possible relative to itself, it follows from LO that x is logically possible relative to the actual world, by Theorem 1. Now, let y be any world doxastically possible relative to x. Then, every member $p^i$ of $\overline{p}$ is true at y, since x is logically possible relative to the actual world. Furthermore, y is deontically possible relative to x, by Theorem 5, since LO and the $[\textsc {immodesty norm}]^{\text {nv}}$ are all true at operator frame $\mathcal {F}$. So, y is logically possible relative to x, by Theorem 1, since LO is true at $\mathcal {F}$. Hence, y is logically possible relative to the actual world, by Theorem 1, since $\textsc {4}_{L}$ is true at $\mathcal {F}$.

Since y is logically possible relative to the actual world, all the $p^{i}$s are true at y only if q is true at y, as $\Box _{L}(q|\overline{p})$ is true at the actual world and the actual world is logically possible relative to itself. So, q is true at y. So, $\Box _{B}q$ is true at x, since y was an arbitrary world doxastically possible relative to x, and x is logically possible relative to the actual world. Moreover, x was an arbitrary world deontically possible relative to the actual world. So, $[\Box _{O}(\bigwedge (\Box _{B}p^{i})\rightarrow \Box _{B}q)]^{\text {nv}}$ is true at the actual world, since the actual world is logically possible relative to itself. Hence, $[\textsc {Wo+}]^{\text {nv}}$ is true at the actual world.

The status of Wo+ has been disputed. The principle is fairly strong as it implies, for instance, logical omniscience—an agent ought to believe everything that is logically necessary. So, Theorem 10 is quite substantive. It reveals that if epistemically ideal agents’ belief states rule out that conditions fail to be ideal—as presumably required by anti-sceptic views such as Knowledge First epistemology—, then Wo+ is true.

Essentially, the result is available owing to the fact that any frame in which LO, $\textsc {4}_{L}$ and the $[{\textsc {immodesty norm}}]^{\text {nv}}$ are all true is a frame in which, for all worlds x and y, x is deontically possible relative to the actual world and y is doxastically possible relative to x only if y is logically possible relative to the actual world. Thus, if a frame has worlds related as follows,

and if $[\textsc {immodesty}]^{\text {nv}}$, LO, and $\textsc {4}_L$ are satisfied by $\mathcal {F}$, then $\mathcal {F}$ must be complemented as follows:

7.3 Alternatives Routes to Wo− and Wo+

The following principles afford alternative routes for basing MacFarlanian bridge principles in purely epistemic norms:⁴⁴

${T}_{\rightarrow }$::

$p\rightarrow \Box _{O}\Box _{B}p$ – If p, then it is epistemically obligatory to believe p.

${F}_{\rightarrow }$::

$p\rightarrow \blacksquare _{O}\blacksquare _{B}p$ – If p, then it is epistemically forbidden to disbelieve p.

We begin by presenting a result concerning the frame correspondents of both $[\textsc {T}_{\rightarrow }]^{\text {nv}}$ and $[\textsc {F}_{\rightarrow }]^{\text {nv}}$. Consider the following conditions on frames.

• $\textsc {T}_{\rightarrow }$ condition: $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow \mathcal {A}=y))$.

• $\textsc {F}_{\rightarrow }$ condition: $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}\mathcal {A})$.

Then, the following result offers a characterisation of the frame correspondents of $[\textsc {T}_{\rightarrow }]^{\text {nv}}$ and $[\textsc {F}_{\rightarrow }]^{\text {nv}}$:⁴⁵

Theorem 11

• 1. $\mathcal {F}\vDash [{\textsc {F}}_{\rightarrow }]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the ${\textsc {F}}_{\rightarrow }$ condition, for every operator frame $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

• 2. $\mathcal {F}\vDash [{\textsc {T}}_{\rightarrow }]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the ${\textsc {T}}_{\rightarrow }$ condition, for every operator frame $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

Here we offer a proof only of part 2 of Theorem 11. The proof of Theorem 11.1 is found in the appendix.

Proof of Theorem 11.2

Suppose that $\textsc {LO}$ is true for all values of p. We start by establishing the left-to-right direction of the theorem. Suppose that and $[\text {T}_{\rightarrow }]^{\text {nv}}$ is true for all values of p. Furthermore, let x be an arbitrary world deontically possible relative to the actual world and y be an arbitrary world doxastically possible relative to x. Let p stand for the set whose only element is the actual world. Then, clearly, p is true at the actual world. So, it is also true at the actual world that $\Box _{O}\Box _{B}p$, since $\textsc {LO}$ is assumed to be true for all values of p. So, $\Box _{B}p$ is true at x, as x is deontically possible relative to the actual world and the actual world is logically possible relative to itself. Since $\textsc {LO}$ is true at the actual world, x is also logically possible relative to the actual world, by Theorem 1. So, p is true at y, as y is doxastically possible relative to x, $\Box _{B}p$ is true at x and x is logically possible relative to the actual world. So, y must be identical to the actual world, since the actual world is the only world at which p is true. Therefore, $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow y=\mathcal {A}))$.

As to the theorem’s right-to-left direction, suppose that $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow y=\mathcal {A}))$, x is an arbitrary world deontically possible relative to the actual world, y is an arbitrary world doxastically possible relative to x, and p is true at the actual world, for an arbitrary proposition p. Then, y just is the actual world. So, p is true at y. Furthermore, x is logically possible relative to the actual world, by $\textsc {LO}$ and Theorem 1. So, $\Box _{B}p$ is true at x, as y was an arbitrary world doxastically possible relative to x and x is logically possible relative to the actual world. Hence, $\Box _{O}\Box _{B}p$ is true at the actual world, since x was assumed to be an arbitrary world deontically possible relative to the actual world, and x is logically possible relative to the actual world. So, $[\text {T}_{\rightarrow }]^{\text {nv}}$ is true at the actual world.

The alternative routes for Wo− and Wo+ are encapsulated in the following theorems.

Theorem 12

$[{\textsc {Wo}-}]^{\text {nv}}$ is a consequence of $[{\textsc {F}}_{\rightarrow }]^{\text {nv}}$ and ${\textsc {LO}}$.

Theorem 13

$[{\textsc {Wo+}}]^{\text {nv}}$ is a consequence of $[{\textsc {T}}_{\rightarrow }]^{\text {nv}}$ and ${\textsc {LO}}$.

Results close to Theorems 12 and 13 are proven in (Tajer, 2020), and the discussion in Sect. 8 will make reference to them. There, we argue that $\text {T}_{\rightarrow }$ and $\text {F}_{\rightarrow }$ are both seemingly implausible on the present evaluative understanding of epistemic obligation. Given this understanding of epistemic obligation, Theorems 12 and 13 fail to legitimise conclusions with respect to the way in which logic is normative for belief. It was for this reason that we did not include $\text {T}_{\rightarrow }$ and $\text {F}_{\rightarrow }$ in the basic norms. Still, Theorems 12 and 13 give us the opportunity to further clarify some of the ways in which our approach to inquiry into the normativity of logic differs from Tajer’s.

By contrast to our result, in Tajer’s framework ${\textsc {Wo+}}$ doesn’t follow simply from ${\textsc {T}}_{\rightarrow }$ even given standard deontic logic’s rule of necessitation—Tajer’s version of LO. The assumption of ${\textsc {F}}_{\rightarrow }$ is also required. Arguably, the reason for the mismatch between the results available in ours and Tajer’s respective frameworks concerns a difference with respect to the generality with which we and Tajer, respectively, interpret the principles by us investigated. By contrast with our interpretation, Tajer adopts a restricted and schematic reading of the different epistemic norms and bridge principles which he investigates. Only the result of replacing the propositional variables by formulae of standard propositional logic are instances of those schemas.

Tajer’s schematic reading of epistemic norms is guided by the view that the epistemic norms ${\textsc {T}}_{\rightarrow }$ and ${\textsc {F}}_{\rightarrow }$ are implausible when understood unrestrictedly, given how they give rise to Moorean anomalies.⁴⁶ We agree with Tajer that ${\textsc {T}}_{\rightarrow }$ and ${\textsc {F}}_{\rightarrow }$ are implausible when understood unrestrictedly. Yet, Tajer’s alternative reading removes close to all generality from epistemic norms and bridge principles. Essentially, according to it a bridge principle fails to follow from an epistemic norm if there is some way of interpreting the atomic propositional letters that makes true all instances of the epistemic norm formulated in terms of boolean formulae built out of atomic propositional letters, while making false some boolean instance of the bridge principle. By contrast, according to our “universalist” reading of bridge principles and epistemic norms a bridge principle fails to follow from an epistemic norm just in case the bridge principle is false on some way of interpreting the atomic propositional letters, even though the epistemic norm is true no matter how its atomic propositional letters are interpreted.⁴⁷

To give a parallel, Tajer’s interpretation would lead to the result that identity ($a=b$) does not follow from set-indiscernibility ($a\in S\leftrightarrow b\in S$) in a language in which the only set term is ‘S’, since ‘a’ and ‘b’ can be interpreted as, respectively, Joe Biden and Vladimir Putin, and ‘S’ can be interpreted as $\{\text {Biden},\text {Putin}\}$, which would make true ‘$a\in S\leftrightarrow b\in S$’, while making false ‘$a=b$’. But this counts as a counterexample only if one disregards the intended reading of set-indiscernibility as an implicitly universally quantified claim ($\forall S(a\in S\leftrightarrow b\in S)$). Given this reading, one must also consider the interpretation of ‘S’ as $\{\text {Biden}\}$. But on this interpretation ‘$a\in S\leftrightarrow b\in S$’ come out as false, since $\text {Biden}\in \{\text {Biden}\}$ and yet $\text {Putin}\not \in \{\text {Biden}\}$. The purported counterexample to the entailment from set-indiscernibility to identity turns out not to be a counterexample at all.⁴⁸ Indeed, and for the reason just given, on our interpretation, identity would follow from set-indiscernibility.

The effect of Tajer’s restriction is a weaker theory. For instance, on Tajer’s framework the following model $\mathcal {M}$ would be a counterexample to the claim that Wo+ follows solely from $\text {T}_{\rightarrow }$.

Here, a world is logically possible just in case it has a rectangular shape. So, the actual world is the only world which is logically possible. World w is thus a logically impossible world. In this model all the formulae of classical propositional logic which are true at the actual world are also true at w. This guarantees that any suitable instance of $\text {T}_{\rightarrow }$ is true at the actual world. Furthermore, exactly one more formula is true at w, specifically, the formula $\lnot p$. Then, $\Box _{B}p$ and $\Box _{B}\lnot p$ are both true at the actual world, since w is the only world doxastically possible relative to the actual world. But $\Box _{B}(p\wedge \lnot p)$ is false at the actual world, as $p\wedge \lnot p$ is not true at w. Since the actual world is deontically possible relative to itself, $\Box _{O}((\Box _{B}p\wedge \Box _{B}\lnot p)\rightarrow \Box _{B}(p\wedge \lnot p))$ is false at the actual world. But $\Box _{L}(p\wedge \lnot p|p,\lnot p)$ is true at the actual world (assuming classical logic, as Tajer does). So, the model is a counterexample to the claim that Wo+ is a consequence of $\text {T}_{\rightarrow }$ on its own.

From our standpoint, $\mathcal {M}$ fails to constitute a genuine counterexample to the claim that Wo+ is a consequence of $\text {T}_{\rightarrow }$ (given the truth of LO). For, if we are completely general, then $\text {T}_{\rightarrow }$ is true also when p is that proposition which is true at the actual world, and only at it. In such a case, world w of model $\mathcal {M}$ must be the actual world itself, otherwise $\Box _{O}\Box _{B}p$ would be false at the actual world while p was true at it. But the actual world is logically possible, and so it cannot be that p and $\lnot p$ are both true at it.

This discrepancy between ours and Tajer’s results is not problematic per se. Our results complement Tajer’s insofar as we are considering unrestricted readings of $\textsc {T}_{\rightarrow }$ and $\textsc {F}_{\rightarrow }$, whereas Tajer is only concerned with particular restricted readings. But the discrepancy does mean that one of our most important results, that $[{\textsc {Wo+}}]^{\text {nv}}$ is a consequence of the $[{\textsc {immodesty norm}}]^{\text {nv}}$ (given LO and $\textsc {4}_{L}$) is unavailable in Tajer’s framework, owing precisely to the fact that Tajer finds countermodels where we find none. Consider the following model $\mathcal {M}$:

In this model u, w and the actual world are all logically possible worlds, whereas v is a logically impossible world. Furthermore, all formulae of classical propositional logic which are true at u are also true at v. The effect of this feature of the model is that all instances of the immodesty norm which result from replacing p by some formula in the language of classical propositional logic are true at the actual world. Moreover, $\lnot p$ is also true at v, this being the only formula not true at u which is true at v. So, $\Box _{B}p$ and $\Box _{B}\lnot p$ are both true at w. Yet, $\Box _{B}(p\wedge \lnot p)$ is false at w. So, $\Box _{O}((\Box _{B}p\wedge \Box _{B}\lnot p)\rightarrow \Box _{B}(p\wedge \lnot p))$ is false at w. But $\Box _{L}(p\wedge \lnot p|p,\lnot p)$ is true at the actual world, assuming classical logic, as Tajer does. So, the model constitutes a (putative) counterexample to the claim that Wo+ is a consequence of the immodesty norm. But the model does not constitute a counterexample to the claim that Wo+ is a consequence of the immodesty norm (together with LO and $\textsc {4}_{L}$) given a completely general interpretation of the immodesty norm. In such a case v must itself be deontically possible relative to w (given Theorem 1), and so a logically possible world. So, it cannot be that p and $\lnot p$ are both true at v.

So, arguably, Tajer’s restricted reading of the bridge principles and epistemic norms leads one to miss out on important connections between these—such as the connection between the immodesty norm and Wo+. In Sect. 7.4 we consider the result of combining the minimal principles and the basic norms.

7.4 Putting it All Together

Together, the principles in minimal and in the basic norms give rise to the combined theory:

Combined theory::

The combined theory consists in the joint consequences of minimal and the basic norms.

The combined theory affords a substantive theory of the interaction between the logical, epistemic, doxastic and deontic operators. It yields predictions with respect to different domains. For example, how logical necessity and obligation interact, how logical necessity and belief interact, how logical necessity and knowledge interact, how logical necessity and epistemic obligation interact, and so on. Since we are interested in whether logic is normative for belief, we focus on the interaction between all the operators in the language.

The results of Sect. 7.2 reveal that among the commitments of the combined theory are principles $[\textsc {Wo}$-$]^{\text {nv}}$ and $[\textsc {Wo+}]^{\text {nv}}$. More generally, in the appendix we prove the following result (in the appendix are also given the formulations and neutral values of the extra bridge principles referred to in Theorem 14) :

Theorem 14

The MacFarlanian bridge principles $[{\textsc {Wo+}}]^{\text {nv}}$, $[{\textsc {Wo+k}}]^{\text {nv}}$, $[{\textsc {Wo}-}]^{\text {nv}}$, $[{\textsc {Wo-k}}]^{\text {nv}}$, $[{\textsc {Wp+}}]^{\text {nv}}$, $[{\textsc {Wp+k}}]^{\text {nv}}$, $[{\textsc {Wp-}}]^{\text {nv}}$, $[{\textsc {Wp-k}}]^{\text {nv}}$, $[{\textsc {Bo+}}]^{\text {nv}}$, $[{\textsc {Bo+k}}]^{\text {nv}}$, $[{\textsc {Bo-}}]^{\text {nv}}$ and $[{\textsc {Bo-k}}]^{\text {nv}}$ are all commitments of the combined theory. No other MacFarlanian bridge principle is a commitment of the combined theory.

Observe that the combined theory does not rule out the truth of the (neutral values of) the remaining MacFarlanian bridge principles. It is just that it is not committed to them. Note also that the combined theory will have a number of other predictions. To give a simple example, consider the following bridge principle not in the MacFarlanian taxonomy:

LWo+::

$\Box _{L}(q|\overline{p})\rightarrow \Box _{O}\Box _{B}\Box _{L}(q|\overline{p})$—If q is logically necessary given that $\overline{p}$, then it is obligatory to believe that (q is logically necessary given that $\overline{p}$).

As it turns out, $[\textsc {LWo+}]^{\text {nv}}$ is among the commitments of the combined theory. This reveals some of the combined theory’s predictive power. Relatedy, Steinberger (2019c) has characterised an interesting family of “internal” bridge principles in which the deontic operator takes “super wide scope” (as he puts it) over the whole conditional rather than just wide scope over the conditional’s conditional consequent.⁴⁹ Our theory will also deliver predictions concerning the status of these Steinbergerian bridge principles.⁵⁰

This concludes the presentation of the main results of our framework vis-à-vis the relationship between the MacFarlanian bridge principles and the basic norms. In Sect. 8 we consider how these results may shed light on the question in what way logic is normative for belief.

8 Is Logic Normative?

There are a number of ways of fleshing out the idea that logic is normative. Here, we focus on two of these: (i) the view that logic is autonomously normative; and (ii) the view that logic is exceptionally normative.⁵¹

A domain D of inquiry is autonomously normative when its truths have as consequences, on their own, normative demands. Domain D is derivatively normative when D’s truths have as consequences normative demands only when combined with true assumptions from other (presumably normative) domains. A domain will be neither autonomous nor derivatively normative if it fails to have as consequences normative demands both on its own and when combined with true assumptions from other domains.⁵²

To give an example, ethics is arguably autonomously normative. Some of its truths (assuming that there are ethical truths) seem to themselves consist of normative demands, and so to have normative consequences on their own. By contrast, physics is, either derivatively normative, or neither autonomously nor derivatively normative. Prima facie, no truth of physics consists in a normative demand, and the truths of physics do not have as consequences, on their own, normative demands.

Since our specific concern is with the normativity of logic for belief, in what follows we are interested in whether the truths of logic have as consequences, on their own, normative requirements for belief. Given the central role that MacFarlanian bridge principles have played in investigation into the normativity of logic, we will focus on the question whether MacFarlanian bridge principles are consequences of the truths of logic on their own.⁵³ For if the truths of logic had as consequences, on their own, some MacFarlanian bridge principles, that would strongly suggest that logic is autonomously normative for belief.

The view that logic is normative might also be understood as the view that it is exceptionally normative, in these sense that it is normative in a manner distinct from the manner in which the sciences are normative (we are here following (Labukt, 2021); see, e.g., pp. 1025–1027). The view that logic is exceptionally normative can be associated with Frege (1979) (even if Frege doesn’t directly address this issue). Anti-exceptionalists about logic’s epistemology and methodology have argued that logical theories are in principle revisable in the same way that the sciences are, and that rational choice of a logical theory is to be done using the same methodology as rational choice of other scientific theories.⁵⁴ If logic were unexceptionally normative, a claim defended by Labukt (2021) and Russell (2020), then this would constitute another way in which it would be on a par with the other sciences.

The following result is arguably of relevance to the issue whether logic is autonomously normative:⁵⁵

Theorem 15

No neutral value of any MacFarlanian bridge principle is a consequence of minimal.

It is reasonable to count the minimal principles as auxiliary assumptions since these consist of logically necessary facts concerning the relationship between the logical, epistemic, doxastic and deontic operators. Still, no neutral value of any MacFarlanian bridge principle is a consequence of the minimal principles. The chief relevance of Theorem 15 to the question whether logic is autonomously normative is as a limitative result. Minimal, which consists of minimal principles about the logical, epistemic, doxastic and deontic operators, and their interaction, does not have as a consequence any one of the MacFarlanian bridge principles. To be sure, this does not deliver the result that logic is not autonomous. For there may be other principles which hold of logical necessity and from which the MacFarlanian bridge principles follow.⁵⁶

Other results of ours are also relevant to the issue. Recall that it was an open possibility that logic was neither autonomously nor derivatively normative. But we have shown that $[\textsc {Wo}$-$]^{\text {nv}}$ and $[\textsc {Wo+}]^{\text {nv}}$ are consequences of the minimal principles together with the basic norms. Thus, assuming the truth of the basic norms, these results reveal that logic is at least derivatively normative.⁵⁷

Turning to the question whether logic is exceptionally normative, in what follows we will be interested on a particular of way of narrowing down this view. Where S is a place-holder for a scientific field, let $\ulcorner \Box _{S}\varphi \urcorner$ formalise $\ulcorner \varphi$ is a truth of science $S\urcorner$. Also, let the S-correlate of a MacFarlanian bridge principle $\varphi$ be a principle obtained by substituting $\ulcorner \Box _{S}((p^{1}\wedge \ldots \wedge p^{n})\rightarrow q)\urcorner$ for ‘$\Box _{L}(q|p^{1},\ldots ,p^{n})$’ in $\varphi$. For instance, for each science S, S Wo− is $\textsc {Wo}$ $-$’s S-correlate:

S Wo−::

$\Box _{S}(\bigwedge _{i}(p^{i})\rightarrow q)\rightarrow \Box _{O}(\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \lnot \blacksquare _{B}q)$—If it is a truth of science S that (q, if $p^{1}$ and $\ldots$ and $p^{n}$), then one epistemically ought to (not disbelieve that q, if one believes each one of $p^{1}$, $\ldots$, $p^{n}$).

Say that a MacFarlanian bridge principle $\varphi$ is normatively exceptional just in case it is true for all values of its propositional values, even though there is some science S—such as physics or psychology—such that $\varphi$’s S-correlate is false for some values of its propositional values. Our specific interest will be in the question whether there is some normatively exceptional MacFarlanian bridge principle. For a positive answer to this question would presumably imply that logic is normatively exceptional. For instance, showing that Wo− is true and yet there is some science S such that S Wo− is false would presumably suffice for establishing logic’s exceptional normativity.

Labukt and Russell argue against the normative exceptionality of, respectively, Wo+ and Wo−. Their arguments are usefully seen as applications of the following general strategy. Given true bridge principles connecting logical facts with claims about what to believe, the strategy consists in finding one or more true epistemic norms having as their consequences both those bridge principles and their S-correlates, for all sciences S. For then, the truth of the epistemic norms establishes the truth of all of the bridge principles’ S-correlates, thus revealing that those bridge principles’ normative unexceptionality.

Accordingly, Labukt and Russell argue against the normative exceptionality of, respectively, Wo+ and Wo− in the following manner. As Labukt notes, for all sciences S, $S\textsc {Wo+}$ is a consequence of $\text {T}_{\rightarrow }$. So, Labukt concludes that Wo+ isn’t normatively exceptional, on the assumption that $\text {T}_{\rightarrow }$ is true. Similarly, as Russell notes, for all sciences S, S Wo− is a consequence of $\text {F}_{\rightarrow }$. So, Russell concludes that Wo− isn’t normatively exceptional, since $\text {F}_{\rightarrow }$ is true.

As should be clear, arguments based on the strategy we’ve just described are successful only given the truth of the proposed general epistemic norms which have as consequences both the relevant bridge principles and their S-correlates, for all sciences S. So, one way to undermine arguments based on this strategy is to show that the proposed general epistemic norms are implausible. We argue that Russell and Labukt’s arguments are problematic precisely because they rely on implausible epistemic norms.

In order to do so, it will be helpful to spell out our model-theoretic treatment of ‘$\Box _{S}$’, the $\ulcorner \text {truth in S}\urcorner$ operator. This operator will function as all other conditional operators. We add an extra accessibility relation $\mathcal {R}_{S}$ to our frames and assign to ‘$\Box _{S}$’ a conditional operator on propositions satisfying our framework’s typical clause for a necessity operator.⁵⁸ The following principle presumably governs $\ulcorner$truth of $S\urcorner$, for every science S:⁵⁹

$\textsc {T}_{S}$::

$\Box _{L}(\Box _{S}p\rightarrow p)$—It is logically necessary that (p, if p is a truth of science S).

Preliminarily, we show that $[S\textsc {Wo}$-$]^{\text {nv}}$ is not a consequence of the basic norms even when these are conjoined with the minimal principles and $[\textsc {T}_{S}]^{\text {nv}}$. Here’s a countermodel:

Fig. 3

Witness to $\textsc {combined theory}, [\textsc {T}_{S}]^{\text {nv}}\not \vDash [\textsc {Wo}$-$_{X}]^{\text {nv}}$

A quick inspection shows that $[\textsc {T}_{S}]^{\text {nv}}$, the principles in $\textsc {minimal}$ and the $\textsc {basic norms}$ are all true at the model’s frame. Furthermore, $\Box _{S}p$ is true at the actual world, given how the actual world is the only world S-possible relative to the actual world. But p fails to be true at w, and so $\blacksquare _{B}p$ is true at w, since w is the only world doxastically possible relative to w. So, there is some world deontically possible relative to the actual world at which $\blacksquare _{B}p$ is true. Hence, $[\Box _{O}\lnot \Box _{B}p]^{\text {nv}}$ is false at the actual world. Therefore, $[\Box _{S}p\rightarrow \Box _{O}\lnot \Box _{B}p]^{\text {nv}}$ is itself false at the actual world. The countermodel in Fig. 3 further reveals that $[S\textsc {Wo+}]^{\text {nv}}$ is not a consequence of $\textsc {minimal}$, $\textsc {basic norms}$ and $[\textsc {T}_{S}]^{\text {nv}}$. So, pending further principles governing $\ulcorner \Box _S\urcorner$, our basic norms fail to support the view that Wo+ and Wo− are normatively unexceptional.

Of course, this result does not show that Labukt’s and Russell’s arguments for the normatively unexceptional character of, respectively, $\textsc {Wo+}$ and $\textsc {Wo}$ $-$ are unsuccessful. For they defend the truth of $\textsc {Wo+}$ and $\textsc {Wo}$ $-$ not on the basis of the basic norms, but instead on the basis of $\text {T}_{\rightarrow }$ and $\text {F}_{\rightarrow }$. So, the question becomes: how plausible are $\text {T}_{\rightarrow }$ and $\text {F}_{\rightarrow }$?

These norms are implausible. According to the evaluative reading of epistemic obligation which we have singled out in Sect. 2, what one ought to believe is what one does believe whenever one is as one epistemically ought to be. So, as a counterexample to $\text {T}_{\rightarrow }$, suppose that Jill is cognitively biased (that is, suppose that Jill is cognitively biased at the actual world). Then, it follows from $\text {T}_{\rightarrow }$ that Jill ought to believe that she is cognitively biased. That is, it follows from $\text {T}_{\rightarrow }$ that whenever Jill is as she epistemically ought to be (i.e., whenever Jill is in an epistemically ideal world), she believes that she is cognitively biased. Yet, whenever Jill is as she epistemically ought to be, she is not cognitively biased. So, it follows from $\text {T}_{\rightarrow }$ that, whenever Jill is as she epistemically ought to be, she believes a falsehood—in particular, she believes that she is not as she epistemically ought to be. First, observe that this consequence of $\text {T}_{\rightarrow }$ clearly conflicts with the truth norm. Moreover, it just seems implausible. Why think that whenever an agent is as she epistemically ought to be, she believes that she is not?

The counterexample to $\text {F}_{\rightarrow }$ is similar. Given that Jill is cognitively biased, it follows from $\text {F}_{\rightarrow }$ that whenever she is as she epistemically ought to be, she fails to disbelieve that she is cognitively biased. First, observe that this consequence of $\text {F}_{\rightarrow }$ conflicts with immodesty. For whenever Jill is as she epistemically ought to be, she epistemically ought to be cognitively unbiased. So, whenever Jill is as she epistemically ought to be, Jill disbelieves that she is biased, by $\textsc {immodesty}$. Furthermore, this consequence of $\text {F}_{\rightarrow }$ just seems implausible. For it is never the case that Jill is as she epistemically ought to be and yet is cognitively biased. So, why think, then, that it is never the case that Jill as she epistemically ought to be and yet disbelieves that she is cognitively biased?

So, Labukt’s and Russell’s arguments against the exceptional normativity of Wo+ and Wo− are unsuccessful. For those arguments are based on implausible epistemic norms. Of course, this does not show that Wo+ and Wo− are normatively exceptional. For all we have shown, there may be other general epistemic norms which are true and have as consequences $S\textsc {Wo+}$ and S Wo−, for all sciences S.

There is one aspect of the relation between logic and epistemic obligation that we want to highlight, for it gives an indication of a potential source of the normative exceptionality of logic—if logic does turn out to be exceptionally normative. Recall that our results showing that $[\textsc {Wo}$-$]^{\text {nv}}$ and $[\textsc {Wo+}]^{\text {nv}}$ are consequences of the basic norms both presupposed the truth of $\textsc {LO}$. For instance, if LO were false, then an agent might do everything that is required to comply with the $[\textsc {truth norm}]^{\text {nv}}$ at an ideal world x while disbelieving a logically necessary truth p, owing in part to the fact that x, a world doxastically accessible to her, is a world in which p isn’t true. Principle LO, according to which every ideal world is logically possible, rules out such a possibility.

So, consider the following analogue of LO, for each science S:

$S\textsc {O}$::

$[\Box _{L}(\Box _{S}p\rightarrow \Box _{O}p)]^{\text {nv}}$ – It is logically necessary that (p is epistemically obligatory, if p is a truth of science S).

As it turns out, the following result can be shown in a manner similar to the proof of Theorem 8:

Theorem 16

$[{S\textsc {Wo}-}]^{\text {nv}}$ is a consequence of ${\textsc {LO}}$, $S{\textsc {O}}$ and the $[{\textsc {truth norm}}]^{\text {nv}}$.

Now, one thought is that, ultimately, logic is exceptionally normative because $\textsc {LO}$ is true whereas some other sciences S are such that $S\textsc {O}$ (and, indeed, $[\Box _{S}p\rightarrow \Box _{O}p]$), turns out to be false. Logic is exceptionally normative because every epistemically ideal world is logically possible, even though the (actual) truths of some science may fail at some epistemically ideal world.⁶⁰

For instance, consider our previous example involving cognitive biases. Even though Jill actually has some cognitive biases that invariably lead her to possess false beliefs, she will not possess those biases in at least some epistemically ideal worlds. Thus, this particular truth of psychology—that Jill is cognitively biased in this particular way—will fail to be true at some (indeed, all) epistemically ideal worlds. So, some truths of psychology—true, that is, at the actual world—are arguably false at some epistemically ideal worlds. Accordingly, $S\textsc {O}$ will be false when the science S in question is psychology.⁶¹

For all that we have said, it is not unreasonable to think that every mathematical truth holds at every epistemically ideal world, so that logic is not normative in a manner distinct from the way mathematics is normative. Still, the case of a paradigmatic science such as physics is not so clear. Does every physical truth—true, that is, at the actual world—hold at every epistemically ideal world? If so, then presumably psychology does not have a physical basis, in the specific sense that logically possible worlds that are physically indiscernible–i.e., in which the physical truths are exactly the same—may nonetheless be psychologically discernible.⁶² For Jill is cognitively biased at the actual world, but fails to be cognitively biased at every epistemically ideal world. This seems an unwelcome consequence of the view that every truth of physics holds at every epistemically ideal world, though we leave a fuller treatment of this issue for another occasion.⁶³

We again point out that we do not take the considerations which we have here presented to show that logic is exceptionally normative. What we have shown is that Labukt’s and Russell’s arguments for the normative unexceptionality of Wo+ and Wo− are premised on what appear to be false assumptions. We have also singled out a principle, principle LO, which, if logic does turn out to be normatively exceptional, promises to afford some insight as to why it is. While LO is arguably true, $S\textsc {O}$ appears to be false for some sciences S.

We leave further discussion on logic’s normative status for another occasion. There is certainly much more to be said about the issue, and we hope our remarks raise a number of interesting questions.

9 Conclusion

We have examined whether logic is normative for belief through inquiry into the interaction between logical, epistemic, doxastic and deontic operators. To do this, we formulated a model-theoretic framework with which to inquire into the best way of combining these operators, and showed how it can be used to determine particular bridge principles. Furthermore, we carried our investigation in a language without boolean connectives, with the aim of making our results available for research at the intersection of logical normativity and logical plurality/logical rivalry.

Beginning from epistemic norms—the basic norms—that we found independently plausible, and minimal principles governing the logical, epistemic, doxastic and deontic operators, we arrived at a substantive theory of how these operators interact. Among the commitments of this theory are the widely discussed MacFarlanian bridge principles Wo+ and Wo−.

We then inquired into whether our framework and results gave us reason to think that logic is autonomously normative for belief, and whether it is exceptionally normative for belief. We showed that our results offer some insight into the first question, and suggest that the answer to the second question is that logic is exceptionally normative—though we also noted that the evidence was far from conclusive.

Additionally, the framework devised here enables clarification of further issues relating to interactions between epistemic norms. For example, potential applications include theorising about the true epistemic norms, as well as conflicts between norms. The model-theoretic framework also makes it possible to assess arguments for or against particular logical theories based on the normativity of logic, such as arguments to the effect that the law of explosion conflicts with the normativity of logic.⁶⁴

Appendix A

We will start by offering a rigorous characterisation of the notion of neutral value. Then, we offer proofs of the results stated in the main text, except for those already proven there.

1.1 A.1 Neutral Value

We begin by defining the neutral value function for the following fragment of $\mathfrak {L}^{\text {bool}}$:

Definition 11

(Language $\mathfrak {L}^{\text {nv}}$) The set of formulae of $\mathfrak {L}^{\text {nv}}$ consists of the smallest set such that:

• 1. If $\varphi$ is a formula of $\mathfrak {L}$, then $\varphi$ is a formula of $\mathfrak {L}^{\text {nv}}$;

• 2. $\#((\psi ^{1}\wedge \ldots \wedge \psi ^{n})\rightarrow (\varphi ^{1}\rightarrow (\ldots \rightarrow (\varphi ^{m}\rightarrow \xi ))))$ is a formula of $\mathfrak {L}^{\text {nv}}$, if $\varphi ^{1}$, $\ldots$, $\varphi ^{m}$, $\xi$, $\psi ^{1}$, $\ldots$, $\psi ^{n}$ are formulae of $\mathfrak {L}^{\text {nv}}$, and $\#$ is an operator of $\mathfrak {L}$;

• 3. $\#((\psi ^{1}\wedge \ldots \wedge \psi ^{n})\rightarrow (\varphi ^{1}\rightarrow (\ldots \rightarrow (\varphi ^{m}\rightarrow \lnot \xi ))))$ is a formula of $\mathfrak {L}^{\text {nv}}$, if $\varphi ^{1}$, $\ldots$, $\varphi ^{m}$, $\xi$, $\psi ^{1}$, $\ldots$, $\psi ^{n}$ are formulae of $\mathfrak {L}^{\text {nv}}$, and $\#$ is a logical, epistemic, doxastic or deontic operator of $\mathfrak {L}$.

The neutral value function $[\cdot ]^{\text {nv}}$ mapping each formula $\varphi$ of $\mathfrak {L}^{\text {nv}}$ to $\varphi$’s neutral value is defined as follows:

Definition 12

(Neutral value) Where $\#$ is any operator, and $\#^{c}$ is $\#$’s solid version if $\#$ isn’t solid, and $\#^{c}$ is $\#$’s nonsolid version if $\#$ is solid:

• 1. $[\varphi ]^{\text {nv}}=\varphi$, if $\varphi$ is a formula of $\mathfrak {L}$;

• 2. $[\varphi ]^{\text {nv}}=\#([\xi ]^{\text {nv}}|[\psi ^{1}]^{\text {nv}},\ldots ,[\psi ^{n}]^{\text {nv}},[\chi ^{1}]^{\text {nv}},\ldots ,[\chi ^{m}]^{\text {nv}})$, if $\varphi$ is the formula $\#((\psi ^{1}\wedge \ldots \wedge \psi ^{n})\rightarrow (\chi ^{1}\rightarrow (\ldots \rightarrow (\chi ^{m}\rightarrow \xi ))))$ of $\mathfrak {L}^{\text {nv}}$ and $\#$ is an operator of $\mathfrak {L}$;

• 3. $[\varphi ]^{\text {nv}}=\#^{c}([\xi ]^{\text {nv}}|[\psi ^{1}]^{\text {nv}},\ldots ,[\psi ^{n}]^{\text {nv}},[\chi ^{1}]^{\text {nv}},\ldots ,[\chi ^{m}]^{\text {nv}})$, if $\varphi$ is the formula $\#((\psi ^{1}\wedge \ldots \wedge \psi ^{n})\rightarrow (\chi ^{1}\rightarrow (\ldots \rightarrow (\chi ^{m}\rightarrow \lnot \xi ))))$ of $\mathfrak {L}^{\text {nv}}$ and $\#$ is a logical, epistemic, doxastic or deontic operator of $\mathfrak {L}$.

We will now extend $[\cdot ]^{\text {nv}}$ to a larger fragment of $\mathfrak {L}$. Let $\mathfrak {L}^{\text {nv+}}$ be the following language:

Definition 13

(Formulae of $\mathfrak {L}^{\text {nv+}}$) The set of formulae of $\mathfrak {L}^{\text {nv+}}$ consists of the smallest set that contains the formulae of $\mathfrak {L}^{\text {nv}}$ and such that $(\psi ^1\wedge \ldots \wedge \psi ^n)\rightarrow (\chi ^{1}\rightarrow (\ldots \rightarrow (\psi ^{m}\rightarrow \xi )))$ are all formulae of $\mathfrak {L}^{\text {nv+}}$ whenever $\psi ^1$, $\ldots$, $\psi ^n$ and $\chi ^{1}$, $\ldots$, $\chi ^{m}$, $\xi$ are all formulae of $\mathfrak {L}^{\text {nv}}$.

Then, the neutral value function is extended to $\mathfrak {L}^{\text {nv+}}$ in the following manner:

Definition 14

(Extension of the neutral value function) For every formula $\varphi$ of $\mathfrak {L}^{\text {nv+}}$:

$$\begin{aligned} {[}\varphi ]^{\text {nv+}}={\left\{ \begin{array}{ll}^{\text {nv}} &{} \text {if }\varphi \text { is a formula of }\mathfrak {L}^{\text {nv}}\\ {[}@(\varphi )]^{\text {nv}} &{} \text {otherwise }\end{array}\right. } \end{aligned}$$

The rationale for extending the neutral value function to $\mathfrak {L}^{\text {nv+}}$ in the manner specified in Definition 14 is that the schema $\ulcorner @p\leftrightarrow p\urcorner$ is commonly taken to govern the actuality operator. Thus, provided that classical logicians accept $\ulcorner @p\leftrightarrow p\urcorner$, they will be committed to the truth of p just in case they are committed to the truth of @p. For instance, since classical logicians are committed to the truth of $p\rightarrow p$, they are also committed to the truth of $@(p\rightarrow p)$. But this formula does have a neutral value. Specifically, $[@(p\rightarrow p)]^{\text {nv}}=@(p|p)$.

Since no confusion is likely to arise, in the main text we use ‘$[\cdot ]^{\text {nv}}$’ to refer both to the original neutral value function $[\cdot ]^{\text {nv}}$ as well as to its extension $[\cdot ]^{\text {nv+}}$ to the language $\mathfrak {L}^{\text {nv+}}$. We now turn to the proof of the paper’s relevant results.

1.2 A.2 Proofs

Theorem 1

For all operator frames $\mathcal {F}$:

• 1. $\mathcal {F}\vDash {\textsc {T}}_{L}$ iff $\mathcal {F}$ satisfies logical reflexivity@;

• 2. $\mathcal {F}\vDash {\textsc {4}}_{L}$ iff $\mathcal {F}$ satisfies logical transitivity@;

• 3. $\mathcal {F}\vDash {\textsc {T}}_{K}$ iff $\mathcal {F}$ satisfies epistemic reflexivity@;

• 4. $\mathcal {F}\vDash {\textsc {KB}}$ iff $\mathcal {F}$ satisfies doxastic-epistemic inclusion@;

• 5. $\mathcal {F}\vDash {\textsc {D}}_{O}$ iff $\mathcal {F}$ satisfies deontic seriality@;

• 6. $\mathcal {F}\vDash {\textsc {LO}}$ iff $\mathcal {F}$ satisfies logical-deontic inclusion@.

Proof of Theorem 1

• 1. ($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow p)]^{\text {nv}}$, for an arbitrary operator frame $\mathcal {F}$, and that $\mathcal {A}\mathcal {R}_{L}w$, for an arbitrary world $w\in \mathcal {W}$. Let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{x\in \mathcal {W}:w\mathcal {R}_{L}x\}$. Then, $\mathcal {M},w\vDash \Box _{L}p\Rightarrow \mathcal {M},w\vDash p$, owing to the fact that $\mathcal {A}\mathcal {R}_{L}w$. Furthermore, $\mathcal {M},w\vDash \Box _{L}p$, again owing to the fact that $\mathcal {A}\mathcal {R}_{L}w$. So, $\mathcal {M},w\vDash p$. Hence, $w\in \mathcal {V}(p)$, and so $w\mathcal {R}_{L}w$. Therefore, $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow x\mathcal {R}_{L}x)$. ($\Leftarrow$) Suppose that $\mathcal {F}$ is an operator frame such that $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow x\mathcal {R}_{L}x)$. Let $\mathcal {M}$ be an arbitrary model based on $\mathcal {M}$ such that $\mathcal {A}\mathcal {R}_{L}w$ and $\mathcal {M},w\vDash \Box _{L}p$, for an arbitrary $w\in \mathcal {W}$. Since $\mathcal {A}\mathcal {R}_{L}w$, we have that $w\mathcal {R}_{L}w$ and, for every u such that $w\mathcal {R}_{L}u$, $\mathcal {M},u\vDash p$. So, $\mathcal {M},w\vDash p$. So, for every w such that $\mathcal {A}\mathcal {R}_{L}w$, $\mathcal {M},w\vDash \Box _{L}p\Rightarrow \mathcal {M},w\vDash p$. But $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. So, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(\Box _{L}p\rightarrow p)]^{\text {nv}}$. Hence, $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow p)]^{\text {nv}}$.

• 2. ($\Rightarrow$) We begin by showing that $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$ only if $\mathcal {F}$ is focused, for every operator frame $\mathcal {F}$. So, suppose that $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$ for an arbitrary operator frame $\mathcal {F}$. Let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{x:\mathcal {A}\mathcal {R}_{L}x\}$. Then, $\mathcal {M},\mathcal {A}\vDash \Box _{L}p$, since $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. Moreover, $\mathcal {M},\mathcal {A}\vDash \Box _{L}p\Rightarrow \mathcal {M},\mathcal {A}\vDash \Box _{L}\Box _{L}p$, as $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. So, $\mathcal {M},\mathcal {A}\vDash \Box _{L}\Box _{L}p$. Now, suppose that $\mathcal {A}\mathcal {R}_{L}x$ and $x\mathcal {R}_{L}y$, for arbitrary $x,y\in \mathcal {W}$, Then, $\mathcal {M},x\vDash \Box _{L}p$, as $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$ and $\mathcal {A}\mathcal {R}_{L}x$. So, $\mathcal {M},y\vDash p$, as $\mathcal {A}\mathcal {R}_{L}x$ and $x\mathcal {R}_{L}y$. Hence, $\mathcal {A}\mathcal {R}_{L}y$. Therefore, $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$ only if $\mathcal {F}$ is a focused operator frame. Now, suppose that $\mathcal {F}$ is an arbitrary operator frame such that $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$, $\mathcal {A}\mathcal {R}_{L}x$, $x\mathcal {R}_{L}y$ and $y\mathcal {R}_{L}z$. Then, $\mathcal {A}\mathcal {R}_{L}y$, as $\mathcal {F}$ is focused. Now, let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{u:x\mathcal {R}_{L}u\}$. Then, $\mathcal {M},x\vDash \Box _{L}p\Rightarrow \mathcal {M},x\vDash \Box _{L}\Box _{L}p$, as $\mathcal {A}\mathcal {R}_{L}x$ and $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$, and $\mathcal {M},x\vDash \Box _{L}p$, since $\mathcal {A}\mathcal {R}_{L}x$. So, $\mathcal {M},x\vDash \Box _{L}\Box _{L}p$. So, $\mathcal {M},y\vDash \Box _{L}p$, as $x\mathcal {R}_{L}y$ and $\mathcal {A}\mathcal {R}_{L}x$. So, $\mathcal {M},z\vDash p$, since $y\mathcal {R}_{L}z$ and $\mathcal {A}\mathcal {R}_{L}y$. So, $x\mathcal {R}_{L}z$. Hence, $\forall x, y, z\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow ((x\mathcal {R}_{L}y\; \& \;y\mathcal {R}_{L}z)\Rightarrow x\mathcal {R}_{L}z))$. ($\Leftarrow$) Suppose that $\mathcal {F}$ is an arbitrary operator frame such that $\forall x, y, z\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow ((x\mathcal {R}_{L}y\; \& \;y\mathcal {R}_{L}z)\Rightarrow x\mathcal {R}_{L}z))$. Suppose that an arbitrary model $\mathcal {M}$ based on $\mathcal {F}$ is such that $\mathcal {M},x\vDash \Box _{L}p$, for an arbitrary x such that $\mathcal {A}\mathcal {R}_{L}x$. Suppose also that y and z are arbitrary elements of $\mathcal {W}$ such that $x\mathcal {R}_{L}y$ and $y\mathcal {R}_{L}z$. Then, $\mathcal {A}\mathcal {R}_{L}y$, since $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. It also follows that $x\mathcal {R}_{L}z$. So, $\mathcal {M},z\vDash p$. Hence, $\mathcal {M},y\vDash \Box _{L}p$. So, $\mathcal {M},x\vDash \Box _{L}\Box _{L}p$. Therefore, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$. So, $\mathcal {F}\vDash [\Box _{L}(\Box _{L}p\rightarrow \Box _{L}\Box _{L}p)]^{\text {nv}}$.

• 3. ($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\Box _{L}(\Box _{K}p\rightarrow p)]^{\text {nv}}$. Suppose that $\mathcal {A}\mathcal {R}_{L}x$, for an otherwise arbitrary $x\in \mathcal {W}$. Let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{w:x\mathcal {R}_{K}w\}$. Then, $\mathcal {M},x\vDash \Box _{K}p$. So, $\mathcal {M},x\vDash p$. Hence, $x\mathcal {R}_{K}x$. So, $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow x\mathcal {R}_{K}x)$. ($\Leftarrow$) Suppose that $\mathcal {F}$ is an arbitrary operator frame such that $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow x\mathcal {R}_{K}x)$. Suppose that $\mathcal {A}\mathcal {R}_{L}x$, for an arbitrary $x\in \mathcal {W}$ and $\mathcal {M},x\vDash \Box _{K}p$. So, $x\mathcal {R}_{K}x$. Therefore, $\mathcal {M},x\vDash p$, since $\mathcal {A}\mathcal {R}_{L}x$. So, $\mathcal {M},x\vDash \Box _{K}p\Rightarrow \mathcal {M},x\vDash p$. Hence, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(\Box _{K}p\rightarrow p)]^{\text {nv}}$. Therefore, $\mathcal {F}\vDash [\Box _{L}(\Box _{K}p\rightarrow p)]^{\text {nv}}$.

• 4. ($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\Box _{L}(\Box _{K}p\rightarrow \Box _{B}p)]^{\text {nv}}$, for an arbitrary operator frame $\mathcal {F}$, $\mathcal {A}\mathcal {R}_{L}x$, and $x\mathcal {R}_{B}y$, for arbitrary $x,y\in \mathcal {W}$. Let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{w:x\mathcal {R}_{K}w\}$. Then, $\mathcal {M},x\vDash \Box _{K}p$. So, $\mathcal {M},x\vDash \Box _{B}p$. Hence, $\mathcal {M},y\vDash p$. So, $x\mathcal {R}_{K}y$. Therefore, $\forall x, y\in \mathcal {W}((\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow x\mathcal {R}_{K}y))$. ($\Leftarrow$) Suppose that $\forall x, y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{B}y\Rightarrow x\mathcal {R}_{K}y))$, for an arbitrary operator frame $\mathcal {F}$, $\mathcal {M}$ is an arbitrary model based on $\mathcal {F}$, x is an arbitrary element of $\mathcal {W}$ such that $\mathcal {A}\mathcal {R}_{L}x$, $\mathcal {M},x\vDash \Box _{K}p$, and $x\mathcal {R}_{B}y$ for an arbitrary $y\in \mathcal {W}$. Since $x\mathcal {R}_{B}y$, we have that $x\mathcal {R}_{K}y$. Hence, $\mathcal {M},y\vDash p$. So, $\mathcal {M},x\vDash \Box _{B} p$. Therefore, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(\Box _{K}p\rightarrow \Box _{B}p)]^{\text {nv}}$. Hence, $\mathcal {F}\vDash [\Box _{L}(\Box _{K}p\rightarrow \Box _{B}p)]^{\text {nv}}$.

• 5. ($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\Box _{L}(\Box _{O}p\rightarrow \Diamond _{O}p)]^{\text {nv}}$, for an arbitrary operator frame $\mathcal {F}$, $\mathcal {A}\mathcal {R}_{L}x$, for an otherwise arbitrary $x\in \mathcal {W}$, and $\mathcal {M}$ is a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{w:x\mathcal {R}_{O}x\}$. Then $\mathcal {M},x\vDash \Box _{O}p$. So, $\mathcal {M},x\vDash \Diamond _{O}p$. Hence, there is some y such that $x\mathcal {R}_{O}y$. So, $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow \exists y(x\mathcal {R}_{O}y))$. ($\Leftarrow$) Suppose that $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow \exists y(x\mathcal {R}_{O}y))$, for some arbitrary operator frame $\mathcal {F}$, $\mathcal {M}$ is an arbitrary model based on $\mathcal {F}$ such that $\mathcal {A}\mathcal {R}_{L}x$, and $\mathcal {M},x\vDash \Box _{O}p$. So, there is some $y\in \mathcal {W}$ such that $x\mathcal {R}_{O}y$. Hence, $\mathcal {M},y\vDash p$. So, $\mathcal {M},x\vDash \Diamond _{O} p$. So, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(\Box _{O}p\rightarrow \Diamond _{O}p)]^{\text {nv}}$. Therefore, $\mathcal {F}\vDash [\Box _{L}(\Box _{O}p\rightarrow \Diamond _{O}p)]^{\text {nv}}$.

• 6. ($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\Box _{L}(\Diamond _{O}p\rightarrow \Diamond _{L}p)]^{\text {nv}}$, $\mathcal {A}\mathcal {R}_{L}x$, $x\mathcal {R}_{O}y$, for arbitrary $x,y\in \mathcal {W}$, and $\mathcal {M}$ is a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{y\}$. Then, $\mathcal {M},y\vDash p$. So, $\mathcal {M},x\vDash \Diamond _{O}p$. So, $\mathcal {M},x\vDash \Diamond _{L}p$. So, there is some z such that $x\mathcal {R}_{L}z$ and $\mathcal {M},z\vDash p$. Hence, $x\mathcal {R}_{L}y$, as $y=z$. So, $\forall x, y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{O}y\Rightarrow x\mathcal {R}_{L}y))$. ($\Leftarrow$) Suppose that $\forall x, y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{O}y\Rightarrow x\mathcal {R}_{L}y))$ for an otherwise arbitrary frame $\mathcal {F}$, $\mathcal {A}\mathcal {R}_{L}x$ and $\mathcal {M},x\vDash \Diamond _{O}p$. Then, there is some y such that $x\mathcal {R}_{O}y$. So, $x\mathcal {R}_{L}y$. Therefore, $\mathcal {M},x\vDash \Diamond _{L}p$. So, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(\Diamond _{O}p\rightarrow \Diamond _{L}p)]^{\text {nv}}$. Hence, $\mathcal {F}\vDash [\Box _{L}(\Diamond _{O}p\rightarrow \Diamond _{L}p)]^{\text {nv}}$.

Theorem 2

$\mathcal {F}\vDash {\textsc {B}}_{L}$ iff $\mathcal {F}$ satisfies logical symmetry@, for all focused operator frames $\mathcal {F}$.

Proof of Theorem 2

Let $\mathcal {F}$ be an arbitrary focused operator frame.

($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\Box _{L}(p\rightarrow \Box _{L}\Diamond _{L}p)]^{\text {nv}}$. Suppose that $\mathcal {A}\mathcal {R}_{L}x$ and $x\mathcal {R}_{L}y$, for arbitrary worlds $x,y\in \mathcal {W}$. Then, $\mathcal {A}\mathcal {R}_{L}y$, as $\mathcal {F}$ is focused. Let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{x\}$. Then, $\mathcal {M},x\vDash p$. So, $\mathcal {M},x\vDash \Box _{L}\Diamond _{L}p$. So, $\mathcal {M},y\vDash \Diamond _{L} p$. Hence, there is some z such that $y\mathcal {R}_{L}z$ and $\mathcal {M},z\vDash p$. But then, $z=x$. So, $y\mathcal {R}_{L}x$. Therefore, $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{L}y\Rightarrow y\mathcal {R}_{L}x))$;

($\Leftarrow$) Suppose $\mathcal {F}$ is a focused frame such that $\forall x, y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{L}x\Rightarrow (x\mathcal {R}_{L}y\Rightarrow y\mathcal {R}_{L}x))$, $\mathcal {M},x\vDash p$, for an arbitrary $x\in \mathcal {W}$ such that $\mathcal {A}\mathcal {R}_{L}x$, and $x\mathcal {R}_{L}y$, for an arbitrary $y\in \mathcal {W}$. Then, $y\mathcal {R}_{L}x$, and $\mathcal {A}\mathcal {R}_{L}y$, as $\mathcal {F}$ is focused. So, $\mathcal {M},y\vDash \Diamond _{L}p$. So, $\mathcal {M},x\vDash \Box _{L}\Diamond _{L}p$. Hence, $\mathcal {M},\mathcal {A}\vDash [\Box _{L}(p\rightarrow \Box _{L}\Diamond _{L}p)]^{\text {nv}}$. Therefore, $\mathcal {F}\vDash \textsc {B}_{L}$.

Theorem 3

$\mathcal {F}\vDash [{\textsc {truth norm}}]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the truth norm condition, for all operator frames $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

Proof of Theorem 3

Suppose that $\mathcal {F}\vDash \textsc {LO}$, for an arbitrary operator frame $\mathcal {F}$.

($\Rightarrow$) Suppose $\mathcal {F}\vDash [\textsc {truth norm}]^{\text {nv}}$ and $\mathcal {A}\mathcal {R}_{O}x$, for an arbitrary $x\in \mathcal {W}$. Then, $A\mathcal {R}_{L}x$ by Theorem 1, since $\mathcal {F}\vDash \textsc {LO}$. Let $\mathcal {M}$ be an arbitrary model such that $\mathcal {V}(p)=\{w:x\mathcal {R}_{B}w\}$. Then, $\mathcal {M},x\vDash \Box _{B}p$, as $\mathcal {A}\mathcal {R}_{L} x$. So, $\mathcal {M},x\vDash p$, since $\mathcal {F}\vDash [\textsc {truth norm}]^{\text {nv}}$ and $\mathcal {A}\mathcal {R}_{\mathcal {L}}\mathcal {A}$. Hence, $x\mathcal {R}_{B}x$. Therefore, $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}x)$.

($\Leftarrow$) Suppose that $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}x)$, $\mathcal {A}\mathcal {R}_{O}x$, and $\mathcal {M},x\vDash \Box _{B}p$, for an arbitrary model $\mathcal {M}$ based on $\mathcal {F}$ and arbitrary $x\in \mathcal {W}$. So, $x\mathcal {R}_{B}x$. From Theorem 1 and $\mathcal {F}\vDash \textsc {LO}$ it follows that $\mathcal {A}\mathcal {R}_{L}x$. Hence, $\mathcal {M},x\vDash p$, since $\mathcal {M},x\vDash \Box _{B}p$. Therefore, $\mathcal {M},\mathcal {A}\vDash [\Box _{O}(\Box _{B}p\rightarrow p)]^{\text {nv}}$, since $\mathcal {A}\mathcal {R}_{L}x$. Hence, $\mathcal {F}\vDash [\Box _{O}(\Box _{B}p\rightarrow p)]^{\text {nv}}$.

Theorem 4

$\mathcal {F}\vDash [{\textsc {knowledge norm}}]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the knowledge norm condition, for all operator frames $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

Proof of Theorem 4

Suppose that $\mathcal {F}\vDash \textsc {LO}$, for an arbitrary operator frame $\mathcal {F}$.

($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\textsc {knowledge norm}]^{\text {nv}}$, $\mathcal {A}\mathcal {R}_{O}x$, and $x\mathcal {R}_{K}y$, for arbitrary $x,y\in \mathcal {W}$. So, $\mathcal {A}\mathcal {R}_{L}x$, by Theorem 1, since $\mathcal {F}\vDash \textsc {LO}$. Let $\mathcal {M}$ be an arbitrary model such that $\mathcal {V}(p)=\{w:x\mathcal {R}_{B}w\}$. $\mathcal {M},x\vDash \Box _{B}p\Rightarrow \mathcal {M},x\vDash \Box _{K}p$, since $\mathcal {F}\vDash [\textsc {knowledge norm}]^{\text {nv}}$, $\mathcal {A}\mathcal {R}_{O}x$ and $\mathcal {A}\mathcal {R}_{L}A$. Also, $\mathcal {M},x\vDash \Box _{B}p$, since $\mathcal {A}\mathcal {R}_{L}x$. Hence, $\mathcal {M},x\vDash \Box _{K}p$. So, $\mathcal {M},y\vDash p$, as $\mathcal {A}\mathcal {R}_{L}x$. So, $x\mathcal {R}_{B}y$. Therefore, $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{K}y\Rightarrow x\mathcal {R}_{B}y))$.

($\Leftarrow$) Suppose that $\forall x,y\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow (x\mathcal {R}_{K}y\Rightarrow x\mathcal {R}_{B}y))$, $\mathcal {A}\mathcal {R}_{O}x$, $\mathcal {M},x\vDash \Box _{B}p$ and $x\mathcal {R}_{K}y$, for arbitrary $x,y\in \mathcal {W}$ and an arbitrary model $\mathcal {M}$. $x\mathcal {R}_{B}y$, since $\mathcal {A}\mathcal {R}_{O}x$ and $x\mathcal {R}_{K}y$. Furthermore, $\mathcal {A}\mathcal {R}_{L}x$, since $\mathcal {A}\mathcal {R}_{O}x$, by $\mathcal {F}\vDash \textsc {LO}$ and Theorem 1. So, $\mathcal {M},y\vDash p$, since $\mathcal {A}\mathcal {R}_{L}x$. Therefore, $\mathcal {M},x\vDash \Box _{K}p$, since $\mathcal {A}\mathcal {R}_{L}x$. Hence, $\mathcal {M},x\vDash \Box _{B}p\Rightarrow \mathcal {M},x\vDash \Box _{K}p$. So, $\mathcal {M},\mathcal {A}\vDash [\Box _{O}(\Box _{B}p\rightarrow \Box _{K}p)]^{\text {nv}}$, as $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. Hence, $\mathcal {F}\vDash [\Box _{O}(\Box _{B}p\rightarrow \Box _{K}p)]^{\text {nv}}$.

We omit the proof of Theorem 5, as it follows closely that of Theorem 4.

Theorem 6

• 1. The $[{\textsc {truth norm}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with the $[{\textsc {immodesty norm}}]^{\text {nv}}$;

• 2. The $[{\textsc {immodesty norm}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with the $[{\textsc {knowledge norm}}]^{\text {nv}}$;

• 3. The $[{\textsc {knowledge norm}}]^{\text {nv}}$ is not a consequence of ${\textsc {minimal}}$ together with ${\textsc {basic norms}}-\{[{\textsc {knowledge norm}}]^{\text {nv}}\}$;

• 4. The $[{\textsc {truth norm}}]^{\text {nv}}$ is a consequence of ${\textsc {T}}_{K}$, ${\textsc {LO}}$ and the $[{\textsc {knowledge norm}}]^{\text {nv}}$.

Proof of Theorem 6

• 1. Consider the following operator frame $\mathcal {F}$:

  

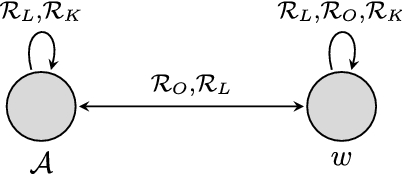
  It is a routine exercise to check that $\mathcal {F}$ satisfies the frame correspondents of all the minimal principles. So, $\mathcal {F}\vDash {\textsc {minimal}}$, by Theorem 1 and Corollary 1. Similarly, $\mathcal {F}$ satisfies the immodesty norm condition, and so $\mathcal {F}\vDash [{\textsc {immodesty norm}}]^{\text {nv}}$, by Theorem 5. But $\mathcal {A}\mathcal {R}_{O}w$ and yet it is not the case that $w\mathcal {R}_{B}w$. Hence, $\mathcal {F}$ does not satisfy the truth norm condition. So, $\mathcal {F}\not \vDash [{\textsc {truth norm}}]^{\text {nv}}$, by Theorem 3.

• 2. Consider the following operator frame $\mathcal {F}$:

  

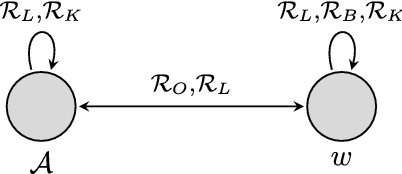
  It is a routine exercise to check that $\mathcal {F}$ satisfies the frame correspondents of all the minimal principles. So, $\mathcal {F}\vDash {\textsc {minimal}}$, by Theorem 1 and Corollary 1. Similarly, $\mathcal {F}$ satisfies the knowledge norm condition, and so $\mathcal {F}\vDash [{\textsc {knowledge norm}}]^{\text {nv}}$, by Theorem 4. But $\mathcal {A}\mathcal {R}_{O}w$, $w\mathcal {R}_{B}w$, and yet $\lnot w\mathcal {R}_{O}w$. Hence, $\mathcal {F}$ does not satisfy the immodesty norm condition. So, $\mathcal {F}\not \vDash [{\textsc {immodesty norm}}]^{\text {nv}}$, by Theorem 3.

• 3. Consider the following operator frame $\mathcal {F}$:

  

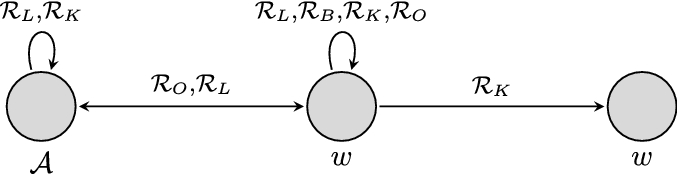
  It is a routine exercise to check that $\mathcal {F}$ satisfies the frame correspondents of all the minimal principles. So, $\mathcal {F}\vDash {\textsc {minimal}}$, by Theorem 1 and Corollary 1. Similarly, $\mathcal {F}$ satisfies the truth norm and the immodesty norm conditions, and so $\mathcal {F}\vDash [{\textsc {truth norm}}]^{\text {nv}}$ and $\mathcal {F}\vDash [{\textsc {immodesty norm}}]^{\text {nv}}$, by Theorems 3 and 5. But $\mathcal {A}\mathcal {R}_{O}w$, $w\mathcal {R}_{K}u$, and yet $\lnot w\mathcal {R}_{B}u$. Hence, $\mathcal {F}$ does not satisfy the knowledge norm condition. So, $\mathcal {F}\not \vDash [{\textsc {knowledge norm}}]^{\text {nv}}$, by Theorem 4.

• 4. Suppose $\mathcal {F}\vDash \textsc {T}_{K}$, $\mathcal {F}\vDash \textsc {LO}$, and $\mathcal {F}\vDash [\textsc {knowledge norm}]^{\text {nv}}$, and $\mathcal {A}\mathcal {R}_{O}x$, for an arbitrary $x\in \mathcal {W}$. Then, $\mathcal {A}\mathcal {R}_{L}x$ by Theorem 1 and the fact that $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$ (since $\mathcal {F}\vDash \textsc {LO}$). So, $x\mathcal {R}_{K}x$, by Theorem 1 and the assumption that $\mathcal {F}\vDash \textsc {T}_{K}$. So, $x\mathcal {R}_{B}x$, by Theorem 4 and the assumption that $\mathcal {F}\vDash [\textsc {knowledge norm}]^{\text {nv}}$. So, $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}x)$. So, $\mathcal {F}\vDash [\textsc {truth norm}]^{\text {nv}}$, by Theorem 3.

Theorem 11

• 1. $\mathcal {F}\vDash [{\textsc {F}}_{\rightarrow }]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the ${\textsc {F}}_{\rightarrow }$ condition, for every operator frame $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

• 2. $\mathcal {F}\vDash [{\textsc {T}}_{\rightarrow }]^{\text {nv}}$ if and only if $\mathcal {F}$ satisfies the ${\textsc {T}}_{\rightarrow }$ condition, for every operator frame $\mathcal {F}$ such that $\mathcal {F}\vDash {\textsc {LO}}$.

Proof of Theorem 11.1

• 1. Suppose that $\mathcal {F}$ is an arbitrary operator frame such that $\mathcal {F}\vDash \textsc {LO}$. ($\Rightarrow$) Suppose that $\mathcal {F}\vDash [\text {F}_{\rightarrow }]^{\text {nv}}$, and $\mathcal {A}\mathcal {R}_{O}x$ for an arbitrary $x\in \mathcal {W}$. Then, $\mathcal {A}\mathcal {R}_{L}x$, by Theorem 1. Let $\mathcal {M}$ be a model based on $\mathcal {F}$ such that $\mathcal {V}(p)=\{\mathcal {A}\}$. Then, $\mathcal {M},\mathcal {A}\vDash p$. So, $\mathcal {M},\mathcal {A}\vDash \blacksquare _{O}\blacksquare _{B}p$. So, $\mathcal {M},x\not \vDash \blacksquare _{B}p$, since $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$ and $\mathcal {A}\mathcal {R}_{O}x$. Then, there is some y such that $x\mathcal {R}_{B}y$ and $\mathcal {M},y\vDash p$, since $\mathcal {A}\mathcal {R}_{L}x$. So, $y\in \{\mathcal {A}\}$. Hence, $y=\mathcal {A}$. Therefore, $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}\mathcal {A})$. ($\Leftarrow$) Suppose that $\forall x\in \mathcal {W}(\mathcal {A}\mathcal {R}_{O}x\Rightarrow x\mathcal {R}_{B}\mathcal {A})$. Suppose that $\mathcal {M},\mathcal {A}\vDash p$ and $\mathcal {A}\mathcal {R}_{O}x$ for an arbitrary model $\mathcal {M}$ based on $\mathcal {F}$ and an arbitrary $x\in \mathcal {W}$. Then $x\mathcal {R}_{B}\mathcal {A}$. So, there is some y such that $x\mathcal {R}_{B}\mathcal {A}$ and $\mathcal {M},y\vDash p$. Therefore, $\mathcal {M},x\not \vDash \blacksquare _{B}p$, as $\mathcal {F}\vDash \textsc {LO}$, and so $\mathcal {A}\mathcal {R}_{L}x$, by Theorem 1. So, $\mathcal {M},\mathcal {A}\vDash \blacksquare _{O}\blacksquare _{B}p$, since x was an arbitrary world such that $\mathcal {A}\mathcal {R}_{O}x$ and $\mathcal {A}\mathcal {R}_{L}x$. So, $\mathcal {F}\vDash [\text {F}_{\rightarrow }]^{\text {nv}}$.

Theorem 12

$[{\textsc {Wo}-}]^{\text {nv}}$ is a consequence of $[{\textsc {F}}_{\rightarrow }]^{\text {nv}}$ and ${\textsc {LO}}$.

Proof of Theorem 12

Suppose $\mathcal {F}\vDash \textsc {LO}$, and $\mathcal {F}\vDash [\textsc {F}_{\rightarrow }]^{\text {nv}}$, $\mathcal {M},\mathcal {A}\vDash \Box _{L}(q|\overline{p})$ for an arbitrary model $\mathcal {M}$ based on $\mathcal {F}$, and x is an arbitrary world such that $\mathcal {A}\mathcal {R}_{O}x$ and $\mathcal {M},x\vDash \Box _{B}p^i$, for all members $p^i$ of $\overline{p}$. So, $\mathcal {A}\mathcal {R}_{L}x$, by LO and Theorem 1. Furthermore, $x\mathcal {R}_{B}\mathcal {A}$, by Theorem 11, as $\mathcal {F}\vDash [{\textsc {F}}_{\rightarrow }]^{\text {nv}}$. So, $\mathcal {M},\mathcal {A}\vDash p^{i}$, for all $p^{i}$ of $\overline{p}$. So, $\mathcal {M},\mathcal {A}\vDash q$. So, $\exists y\in \mathcal {W}(x\mathcal {R}_{B}y\; \& \;\mathcal {M},y\vDash q)$. So, $\mathcal {M},x\not \vDash \blacksquare _{B}q$. So, $\mathcal {M},\mathcal {A}\vDash [\Box _{O}(\bigwedge _{i\le n}\Box _{B}p^i\rightarrow \lnot \blacksquare _{B}q)]^{\text {nv}}$. So, $\mathcal {F}\vDash [\textsc {Wo}$-$]^{\text {nv}}$.

Theorem 13

$[{\textsc {Wo+}}]^{\text {nv}}$ is a consequence of $[{\textsc {T}}_{\rightarrow }]^{\text {nv}}$ and ${\textsc {LO}}$.

Proof of Theorem 13

Suppose that $\Box _{L}(q|\overline{p})$ is true at the actual world. Suppose furthermore that x is an arbitrary world deontically possible relative to the actual world such that $\Box _{B}p^i$ is true at x, for all members $p^i$ of $\overline{p}$. So, x is logically possible relative to the actual world, by LO and Theorem 1. Suppose that y is an arbitrary world doxastically possible relative to x. Then, all the $p^i$s are true at y. But y is just the actual world, by Theorem 11 and $[{\textsc {T}}_{\rightarrow }]^{\text {nv}}$. Since the actual world is logically possible relative to itself, and all the $p^i$s are true at the actual world, we have that q is true at the actual world, since $\Box _{L}(q|\overline{p})$ is true at the actual world. So, q is true at y. Hence, $\Box _{B}q$ is true at x, since y was assumed to be an arbitrary world doxastically possible relative to x. So, $[\Box _{O}(\bigwedge \Box _{B}p^i\rightarrow \Box _{B}q)]^{\text {nv}}$ is true at the actual world, since the actual world is logically possible relative to itself and x was assumed to be an arbitrary world deontically possible relative to the actual world. So, $[\textsc {Wo+}]^{\text {nv}}$ is true at the actual world.

As announced, we will now prove a number of results which culminate in a proof of Theorem 14. We start by briefly noting the neutral values of the remaining MacFarlanian bridge principles of interest:

• $[{\textsc {Bo+}}]^{\text {nv}}= [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{O}\Box _{B}p^{i})\rightarrow \Box _{O}\Box _{B}q)]^{\text {nv}} = @(\Box _{O}\Box _{B}q|\Box _{L}(q|\overline{p}), \overline{\Box _{O}\Box _{B}p})$

• $[{\textsc {Bo-}}]^{\text {nv}}= [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{O}\Box _{B}p^{i})\rightarrow \Box _{O}\lnot \blacksquare _{B}q)]^{\text {nv}} = @(\blacksquare _{O}\blacksquare _{B}q|\Box _{L}(q|\overline{p}), \overline{\Box _{O}\Box _{B}p})$

• $[{\textsc {Bp+}}]^{\text {nv}} = [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Diamond _{O}\Box _{B}p^{i})\rightarrow \Diamond _{O}\Box _{B}q)]^{\text {nv}} = @(\Diamond _{O}\Box _{B}q|\Box _{L}(q|\overline{p}), \overline{\Diamond _{O}\Box _{B}p})$

• $[{\textsc {Bp-}}]^{\text {nv}} = [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Diamond _{O}\Box _{B}p^{i})\rightarrow \Diamond _{O}\lnot \blacksquare _{B}q)]^{\text {nv}} = @(\blacklozenge _{O}\blacksquare _{B}q|\Box _{L}(q|\overline{p}), \overline{\Diamond _{O}\Box _{B}p})$

• $[{\textsc {Wp+}}]^{\text {nv}} = [\Box _{L}(q|\overline{p})\rightarrow \Diamond _{O}(\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \Diamond _{B}q)]^{\text {nv}} = @(\Diamond _{O}(\Diamond _{B}q|\overline{\Box _{B}p})|\Box _{L}(q|\overline{p}) )$

• $[{\textsc {Wp-}}]^{\text {nv}} = [\Box _{L}(q|\overline{p})\rightarrow \Diamond _{O}(\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \lnot \blacksquare _{B}q)]^{\text {nv}} = @(\blacklozenge _{O}(\blacklozenge _{B}q|\overline{\Box _{B}p})|\Box _{L}(q|\overline{p}) )$

• $[{\textsc {Co+}}]^{\text {nv}}= [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \Box _{O}\Box _{B}q)]^{\text {nv}} = @(\Box _{O}\Box _{B}q|\Box _{L}(q|\overline{p}), \overline{\Box _{B}p})$

• $[{\textsc {Co-}}]^{\text {nv}}= [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \Box _{O}\lnot \blacksquare _{B}q)]^{\text {nv}} = @(\blacksquare _{O}\blacksquare _{B}q|\Box _{L}(q|\overline{p}), \overline{\Box _{B}p})$

• $[{\textsc {Cp+}}]^{\text {nv}} = [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \Diamond _{O}\Box _{B}q)]^{\text {nv}} = @(\Diamond _{O}\Box _{B}q|\Box _{L}(q|\overline{p}), \overline{\Box _{B}p})$

• $[{\textsc {Cp-}}]^{\text {nv}} = [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{B}p^{i})\rightarrow \Diamond _{O}\lnot \blacksquare _{B}q)]^{\text {nv}} = @(\blacklozenge _{O}\blacksquare _{B}q|\Box _{L}(q|\overline{p}), \overline{\Box _{B}p})$

We now turn to the proof of the relevant theorems.

Theorem 17

The neutral value of the $\textsc {k}$-variant of each MacFarlanian bridge principle is, when defined, a consequence of the neutral value of that bridge principle together with $\textsc {T}_K$.

Proof of Theorem 17

It suffices to show that $\mathcal {F}\vDash \textsc {T}_K$ and $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow \varphi ]^{\text {nv}}$ only if $\mathcal {F}\vDash [\Box _{K}\Box _{L}(q|\overline{p})\rightarrow \varphi ]^{\text {nv}}$, for every operator frame $\mathcal {F}$. So, suppose that $\mathcal {F}\vDash \textsc {T}_K$ and $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow \varphi ]^{\text {nv}}$. Then, $\mathcal {A}\mathcal {R}_{K}\mathcal {A}$, as $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$, by Theorem 1 and the assumption that $\mathcal {F}\vDash \textsc {T}_K$. Moreover, suppose that $\mathcal {M},\mathcal {A}\vDash \Box _{K}\Box _{L}(q|\overline{p})$, for an arbitrary model $\mathcal {M}$ based on $\mathcal {F}$. Then, $\mathcal {M},\mathcal {A}\vDash \Box _{L}(q|\overline{p})$. But $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow \varphi ]^{\text {nv}}$, by assumption. So, $\mathcal {M},\mathcal {A}\vDash [\Box _{K}\Box _{L}(q|\overline{p})\rightarrow \varphi ]^{\text {nv}}$. Hence, $\mathcal {F}\vDash [\Box _{K}\Box _{L}(q|\overline{p})\rightarrow \varphi ]^{\text {nv}}$.

Theorem 18

• 1. $[{\textsc {Bo-}}]^{\text {nv}}$ is a consequence of $[{\textsc {Wo}-}]^{\text {nv}}$;

• 2. $[{\textsc {Wp-}}]^{\text {nv}}$ is a consequence of $[{\textsc {Wo}-}]^{\text {nv}}$ together with ${\textsc {D}}_O$.

Proof of Theorem 18

• 1. Suppose that $\mathcal {F}\vDash [\textsc {Wo}$-$]^{\text {nv}}$. Suppose that $\mathcal {M}$ is an arbitrary model based on $\mathcal {F}$ such that $\mathcal {M},\mathcal {A}\vDash \Box _{L}(q|\overline{p})$, $\mathcal {M},\mathcal {A}\vDash \Box _{O}\Box _{B}p^{i}$, for all members $p^{i}$ of $\overline{p}$, and $\mathcal {A}\mathcal {R}_{O}x$, for an arbitrary $x\in \mathcal {W}$. Then, $\mathcal {M},x\vDash \Box _{B}p^i$, for all members $p^i$ of $\overline{p}$, since $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. Moreover, $\mathcal {M},x\vDash \Box _{B}p^i$ for all members $p^i$ of $\overline{p}$ only if $\mathcal {M},x\not \vDash \blacksquare _{B}q$, as $\mathcal {F}\vDash [\textsc {Wo}$-$]^{\text {nv}}$. So, $\mathcal {M},x\not \vDash \blacksquare _{B}q$. Hence, $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i\le n}(\Box _{O}\Box _{B}p^{i})\rightarrow \Box _{O}\lnot \blacksquare _{B}q)]^{\text {nv}}$.

• 2. Suppose that $\mathcal {F}\vDash [\textsc {Wo}$-$]^{\text {nv}}$. Also, suppose that $\mathcal {M}$ is an arbitrary model based on $\mathcal {F}$ and that $\mathcal {M},\mathcal {A}\vDash \Box _{L}(q|\overline{p})$. Then, $\mathcal {M},\mathcal {A}\vDash [\Box _{O}(\bigwedge _{i\le n}(\Box _{B}p^i)\rightarrow \lnot \blacksquare _{B}q)]^{\text {nv}}$. So, for every $x\in \mathcal {W}$ such that $\mathcal {A}\mathcal {R}_{O}x$, $\mathcal {M},x\vDash \Box _{B}p^i$, for all members $p^i$ of $\overline{p}$, only if $\mathcal {M},x\not \vDash \blacksquare _{B}q$. By Theorem 1 and the assumption that $\mathcal {F}\vDash \textsc {D}_O$, there is some x such that $\mathcal {A}\mathcal {R}_{O}x$. So, there is some x such that $\mathcal {A}\mathcal {R}_{O}x$ and $\mathcal {M},x\vDash \Box _{B}q$ if $\mathcal {M},x\vDash \Box _{B}p^i$, for all members $p^i$ of $\overline{p}$. Hence, $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow \Diamond _{O}(\bigwedge (\Box _{B}p^i)\rightarrow \lnot \blacksquare _{B}q)]^{\text {nv}}$.

Theorem 19

• 1. $[{\textsc {Bo+}}]^{\text {nv}}$ is a consequence of $[{\textsc {Wo+}}]^{\text {nv}}$;

• 2. $[{\textsc {Wp+}}]^{\text {nv}}$ is a consequence of $[{\textsc {Wo+}}]^{\text {nv}}$ together with ${\textsc {D}}_{O}$.

Proof of Theorem 19

• 1. Suppose that $\mathcal {F}\vDash [{\textsc {Wo+}}]^{\text {nv}}$, for an otherwise arbitrary operator frame $\mathcal {F}$, and $\mathcal {M}$ is an arbitrary model based on $\mathcal {F}$ such that $\mathcal {M},\mathcal {A}\vDash \Box _{L}(q|\overline{p})$ and $\mathcal {M},\mathcal {A}\vDash (\Box _{O}\Box _{B}p^{i})$, for each $p^{i}$ in $\overline{p}$. Finally, suppose that $\mathcal {A}\mathcal {R}_{O}x$, for an arbitrary $x\in \mathcal {W}$. Since $\mathcal {F}\vDash [{\textsc {Wo+}}]^{\text {nv}}$, we have that $\mathcal {M},x\vDash \Box _{B}q$ if $\mathcal {M},x\vDash \Box _{B}p^i$, for every member $p^i$ of $\overline{p}$, since $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. But $\mathcal {M},x\vDash \Box _{B}p^i$, for every member $p^i$ of $\overline{p}$, since $\mathcal {M},\mathcal {A}\vDash \Box _{O}(\Box _{B}p^{i})$, for each member $p^{i}$ of $\overline{p}$. Hence, $\mathcal {M},x\vDash \Box _{B}q$. So, $\mathcal {M},\mathcal {A}\vDash \Box _{O}\Box _{B}q$, as x was assumed to be an arbitrary world deontically possible relative to $\mathcal {A}$. So, $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow (\bigwedge _{i}(\Box _{O}\Box _{B}p^{i})\rightarrow \Box _{O}\Box _{B}q)]^{\text {nv}}$.

• 2. Suppose that $\mathcal {F}\vDash [{\textsc {Wo+}}]^{\text {nv}}$, for an otherwise arbitrary operator frame $\mathcal {F}$, and that $\mathcal {F}\vDash \textsc {D}_{O}$. Suppose furthermore that $\mathcal {M},\mathcal {A}\vDash \Box _{L}(q|\overline{p})$, for an arbitrary model $\mathcal {M}$ based on $\mathcal {F}$. So, there is some $x\in \mathcal {W}$ such that $\mathcal {A}\mathcal {R}_{O}x$, by Theorem 1, since $\mathcal {F}\vDash \textsc {D}_O$ and $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. Since $\mathcal {F}\vDash [{\textsc {Wo+}}]^{\text {nv}}$, we have that $\mathcal {M},\mathcal {A}\vDash [\Box _{O}(\bigwedge _{i}(\Box _{B}p^{i})\rightarrow \Box _{B}q)]^{\text {nv}}$, and thus, that $\mathcal {M},x\vDash \Box _{B}q$ if $\mathcal {M},x\vDash \Box _{B}p^i$, for every member $p^i$ of $\overline{p}$. Hence, $\mathcal {M},\mathcal {A}\vDash [\Diamond _{O}(\bigwedge _{i}(\Box _{B}p^{i})\rightarrow \Box _{B}q)]^{\text {nv}}$. Therefore, $\mathcal {F}\vDash [\Box _{L}(q|\overline{p})\rightarrow \Diamond _{O}(\bigwedge _{i}(\Box _{B}p^{i})\rightarrow \Box _{B}q)]^{\text {nv}}$.

Theorem 20

None of $[{\textsc {Co+}}]^{\text {nv}}$, $[{\textsc {Co-}}]^{\text {nv}}$, $[{\textsc {Cp+}}]^{\text {nv}}$, $[{\textsc {Cp-}}]^{\text {nv}}$, $[{\textsc {Bp+}}]^{\text {nv}}$, $[{\textsc {Bp-}}]^{\text {nv}}$, and none of their k-variants, is a joint consequence of the minimal principles and the basic norms.

Proof of Theorem 20

In light of Theorems 1, 4, 6, 17 and Corollary 1, it suffices to show that, for each one of $[{\textsc {Co+k}}]^{\text {nv}}$, $[{\textsc {Co-k}}]^{\text {nv}}$, $[{\textsc {Cp+k}}]^{\text {nv}}$, $[{\textsc {Cp-k}}]^{\text {nv}}$, $[{\textsc {Bp+k}}]^{\text {nv}}$, $[{\textsc {Bp-k}}]^{\text {nv}}$, there is a model $\mathcal {M}$ based on an operator frame $\mathcal {F}$ such that the principle is false at $\mathcal {M}$ even though $\mathcal {F}$ satisfies all of logical reflexivity@, epistemic reflexivity@, doxastic seriality@, logical-deontic inclusion@, logical symmetry@, logical transitivity@, the knowledge norm condition and the immodesty norm condition. So, consider the following model $\mathcal {M}$:

It is a routine exercise to check that $\mathcal {M}$ is based on a frame that satisfies all of logical reflexivity@, epistemic reflexivity@, doxastic seriality@, logical-deontic inclusion@, logical symmetry@, logical transitivity@, the knowledge norm condition and the immodesty norm condition. Moreover, it is clear that $\mathcal {M},\mathcal {A}\vDash \Box _{L}(p|p)$, $\mathcal {M},\mathcal {A}\vDash \Box _{K}\Box _{L}(p|p)$ and that $\mathcal {M},\mathcal {A}\vDash \Box _{B}p$.

• In order to show that $\mathcal {M},\mathcal {A}\not \vDash [\textsc {Co+k}]^{\text {nv}}$ it suffices to show that $\mathcal {M},\mathcal {A}\not \vDash \Box _{O}\Box _{B}p$. But this is a straightforward result, since $\mathcal {A}\mathcal {R}_{O}w$, $w\mathcal {R}_{B}w$, $\mathcal {M},w\not \vDash p$ and $\mathcal {A}\mathcal {R}_{L}w$;

• In order to show that $\mathcal {M},\mathcal {A}\not \vDash [\textsc {Co-k}]^{\text {nv}}$ it suffices to show that $\mathcal {M},\mathcal {A}\not \vDash [\Box _{O}\lnot \blacksquare _{B}p]^{\text {nv}}$. Since w is the only world doxastically accessible to w and $\mathcal {M},w\not \vDash p$ it follows that $\mathcal {M},w\vDash \blacksquare _{B}p$. So, there is some world w such that $\mathcal {A}\mathcal {R}_{O}w$ and $\mathcal {M},w\vDash \blacksquare _{B}p$; Hence, $\mathcal {M},\mathcal {A}\not \vDash [\Box _{O}\lnot \blacksquare _{B}p]^{\text {nv}}$.

• In order to show that $\mathcal {M},\mathcal {A}\not \vDash [\textsc {Cp+k}]^{\text {nv}}$ it suffices to show that $\mathcal {M},\mathcal {A}\not \vDash \Diamond _{O}\Box _{B}p$. As already seen, $\mathcal {M},w\not \vDash \Box _{B}p$. But w is the only x such that $\mathcal {A}\mathcal {R}_{O}x$. So, $\mathcal {M},\mathcal {A}\not \vDash \Diamond _{O}\Box _{B}p$;

• In order to show that $\mathcal {M}\not \vDash [\textsc {Cp-k}]^{\text {nv}}$ it suffices to show that $\mathcal {M},\mathcal {A}\not \vDash [\Diamond _{O}\lnot \blacksquare _{B}p]^{\text {nv}}$. As already seen, $\mathcal {M},w\vDash \blacksquare _{B}p$. But w is the only world x such that $\mathcal {A}\mathcal {R}_{O}x$. So, $\mathcal {M},\mathcal {A}\not \vDash [\Diamond _{O}\lnot \blacksquare _{B}p]^{\text {nv}}$.

Counterexamples to $[{\textsc {Bp+}}]^{\text {nv}}$ and $[{\textsc {Bp-}}]^{\text {nv}}$ require considering a different model $\mathcal {N}$:

It is a routine exercise to check that $\mathcal {N}$ is based on a frame that satisfies all of logical reflexivity@, epistemic reflexivity@, doxastic seriality@, logical-deontic inclusion@, logical symmetry@, logical transitivity@, the knowledge norm condition and the immodesty norm condition. Moreover, it is clear that $\mathcal {N},\mathcal {A}\vDash \Box _{L}(r|p,q)$, $\mathcal {N},w\vDash \Box _{L}(r|p,q)$, and $\mathcal {N},u\vDash \Box _{L}(r|p,q)$. So, $\mathcal {N},\mathcal {A}\vDash \Box _{K}\Box _{L}(r|p,q)$. Observe also that $\mathcal {N},w\vDash \Box _{B}p$, since w is the only world x such that $w\mathcal {R}_{B}x$, and $\mathcal {A}\mathcal {R}_{L}w$. So, $\mathcal {N},\mathcal {A}\vDash \Diamond _{O}\Box _{B}p$, since $\mathcal {A}\mathcal {R}_{O}w$ and $\mathcal {A}\mathcal {R}_{L}\mathcal {A}$. Finally, observe that, by symmetrical reasoning, we have that $\mathcal {N},\mathcal {A}\vDash \Diamond _{O}\Box _{B}q$.

Now, w is the only world x such that $w\mathcal {R}_{B}x$, $\mathcal {M},w\not \vDash r$, and $\mathcal {A}\mathcal {R}_{L}w$. So, $\mathcal {M},w\not \vDash \Box _{B}r$ and $\mathcal {M},w\vDash \blacksquare _{B}r$. By symmetrical reasoning, we have that $\mathcal {M},u\not \vDash \Box _{B}r$ and $\mathcal {M},u\vDash \blacksquare _{B}r$. So, $\mathcal {M},\mathcal {A}\not \vDash \Diamond \Box _{B}r$, and $\mathcal {M},\mathcal {A}\not \vDash [\Diamond \lnot \blacksquare _{B}r]^{\text {nv}}$. Therefore, $\mathcal {M},\mathcal {A}\not \vDash [\Box _{L}(r|p,q)\rightarrow ((\Diamond _{O}\Box _{B}p\wedge \Diamond _{O}\Box _{B}q)\rightarrow \Diamond _{O}\Box _{B}r)]^{\text {nv}}$ and $\mathcal {M},\mathcal {A}\not \vDash [\Box _{L}(r|p,q)\rightarrow ((\Diamond _{O}\Box _{B}p\wedge \Diamond _{O}\Box _{B}q)\rightarrow \Diamond _{O}\lnot \blacksquare _{B}r)]^{\text {nv}}$.

We now prove Theorem 14, here restated:

Theorem 14

The MacFarlanian bridge principles $[{\textsc {Wo+}}]^{\text {nv}}$, $[{\textsc {Wo+k}}]^{\text {nv}}$, $[{\textsc {Wo}-}]^{\text {nv}}$, $[{\textsc {Wo-k}}]^{\text {nv}}$, $[{\textsc {Wp+}}]^{\text {nv}}$, $[{\textsc {Wp+k}}]^{\text {nv}}$, $[{\textsc {Wp-}}]^{\text {nv}}$, $[{\textsc {Wp-k}}]^{\text {nv}}$, $[{\textsc {Bo+}}]^{\text {nv}}$, $[{\textsc {Bo+k}}]^{\text {nv}}$, $[{\textsc {Bo-}}]^{\text {nv}}$ and $[{\textsc {Bo-k}}]^{\text {nv}}$ are all commitments of the combined theory. No other MacFarlanian bridge principle is a commitment of the combined theory.

Proof of Theorem 14

Theorem 14 is a straightforward corollary of Theorems 8, 10, 17, 18, 19, and 20.

We conclude with the proof of Theorem 15, here restated:

Theorem 15

No neutral value of any MacFarlanian bridge principle is a consequence of minimal.

Proof of Theorem 15

Theorems 7 and 9 reveal that neither $[\textsc {Wo}$-$]^{\text {nv}}$ nor $[\textsc {Wo+}]^{\text {nv}}$ are among the consequences of minimal. More generally, the countermodels used in the proofs of Theorems 7 and 9 are also countermodels to respectively, bridge principles $[\textsc {Wp-}]^{\text {nv}}$ and $[\textsc {Bo-}]^{\text {nv}}$, and bridge principles $[\textsc {Wp+}]^{\text {nv}}$ and $[\textsc {Bo+}]^{\text {nv}}$. So, the following result is an easy corollary of these facts together with Theorems 14 and 17.