Abstract
We present a framework for epistemic logic, modeling the logical aspects of System 1 (“fast”) and System 2 (“slow”) cognitive processes, as per dual process theories of reasoning. The framework combines non-normal worlds semantics with the techniques of Dynamic Epistemic Logic. It models non-logically-omniscient, but moderately rational agents: their System 1 makes fast sense of incoming information by integrating it on the basis of their background knowledge and beliefs. Their System 2 allows them to slowly, step-wise unpack some of the logical consequences of such knowledge and beliefs, by paying a cognitive cost . The framework is applied to three instances of limited rationality, widely discussed in cognitive psychology: Stereotypical Thinking, the Framing Effect, and the Anchoring Effect.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Econs, Logons, and Humans
2017 Nobel laureate in economics Richard Thaler dubbed “Econs” and “Humans” two different species studied, respectively, by mainstream economists and by behavioral and cognitive scientists (Thaler and Sunstein 2008). Econs are the agents of classical economic theory: fully consistent and endowed with well-ordered preferences as per Bernoulli’s expected utility theory. Of course, the terminology implies that Humans, unlike Econs, are the real thing. The discrepancies between the two kinds of agents have sparked a well-known “rationality debate” (Cohen 1981; Kahneman and Tversky 1983; Cherniak 1986; Evans and Over 1996; Gigerenzer 1996; Kahneman and Tversky 1996; Stein 1996; Stanovich and West 2000; Stenning and van Lambalgen 2008). As 2002 Nobel laureate in economics Daniel Kahneman has it:
[Assume] rationality is logical coherence—reasonable or not. Econs are rational by this definition, but there is overwhelming evidence that Humans cannot be. [...] The definition of rationality as coherence is impossibly restrictive; it demands adherence to rules of logic that a finite mind is not able to implement. Reasonable people cannot be rational by that definition, but they should not be branded as irrational for that reason. (Kahneman 2011, p. 411)
Now just as mainstream economics has forgotten Humans to focus on Econs, so has mainstream logic forgotten them to focus on Logons. We name this way the ideal agents studied in ‘static’ epistemic logic with possible worlds semantics (Hintikka 1962) and in AGM belief revision theory (Alchourrón et al. 1985). These agents are logically omniscient: perfectly consistent, closed under classical logical consequence in their beliefs, and free from framing effects in their belief revision policies (Hintikka 1975; Fagin and Halpern 1987; Moses 1988; Parikh 2008; Halpern and Pucella 2011). In fact, Econs may just be Logons engaged in rational choice. The focus on Logons has opened a rift between logic and cognition, similar to the one between the latter and economics. Experiments like the Wason Selection Task (Wason 1968) or the Suppression Task (Byrne 1983) have had in deductive reasoning roles similar to the Framing Effect and Anchoring Bias (Tversky and Kahneman 1974, 1985): they have exhibited widespread, persistent fallacies leading various cognitive scientists to conclude that logic is utterly peripheral to Humans’ reasoning (Cosmides 1989).
We think that such a conclusion has been distorted by the interpreters’ understanding of “logic” as normal, static modal logic. The goal of this paper is to present a system of epistemic logic that does more justice to Humans by modeling the logical aspects of a distinction, which has played a key role in the rationality debate: the one between System 1 and System 2 or, in Kahneman’s more colorful terminology, fast and slow thinking. We briefly present this distinction, and explain the sense in which we claim to logically model it, in the following Section. The Section after that recaps the logical foundation of this paper, namely the worlds semantics of normal modal-epistemic logics and its development into Dynamic Epistemic Logic (DEL). These will serve as the background for our model of the two Systems’ logic, in Sect. 4. In Sect. 5, the framework is put to work in the modeling of three kinds of phenomena: Stereotypical Thinking, the Framing Effect, and the Anchoring Effect. We close with a philosophical coda in Sect. 6, where we wonder whether our model is normative. We answer that it is, but its rational “ought”, unlike the “ought” of normal, static epistemic logic, implies “can”.
2 Dual Process Theories of Reasoning
The talk of System 1 and System 2, introduced by Stanovich and West in their dual process view, had a key role in countering the picture of agents as Econs in economics.Footnote 1 It may have a key role in countering the picture of agents as Logons in static epistemic logic. Systematic errors in reasoning and choice are not to be taken as corruption of rationality. Rather, they are grounded in the ordinary workings of the machinery of cognition—specifically, in a combination of mistakes due to System 1—which, however, conforms to logic most of the time: (Bago and De Neys 2017)—and System 2—which can run out of cognitive resources, or be lazy when it should take over from System 1.
Dual process theories characterize the operations of System 1 as fast, automatic, and associative, governed by habit, biases, and evolutionary heuristics. They typically have no cognitive cost. System 1’s task is to make sense of the continuously incoming new information, integrating it with our background beliefs and building a coherent picture starting from minimal clues (Paul is French: does he like red wine?). In Kahneman’s words:
The main function of System 1 is to maintain and update a model of your personal world, which represents what is normal in it. [...] System 1 excels at constructing the best possible story that incorporates ideas currently activated, but it does not (cannot) allow for information it does not have. (Kahneman 2011, p. 71 and p. 85)
The operations of System 2 are slower, stepwise, rule-based, deliberately controlled, and have cognitive costs (What is \(19 \times 26 =\) ?). System 2 exploits the workings of System 1 to generate its own outputs, following an orderly application of steps:
I describe System 1 as effortlessly originating impressions and feelings that are the main sources of the explicit beliefs and deliberate choices of System 2. The automatic operations of System 1 generate surprisingly complex patterns of ideas, but only the slower System 2 can construct thoughts in an orderly series of steps. (Kahneman 2011, p. 21)
When System 2 takes over, it engages in reasoning processes, of which deductive reasoning is a key example, based on the available information. Its slow, step-wise and rule-adhering workings generate our—now explicit—knowledge and beliefs. To unpack information, System 2 breaks larger tasks into parts:
We normally avoid mental overload by dividing our tasks into multiple easy steps, committing intermediate results to long-term memory or to paper rather than to an easily overloaded working memory. We cover long distances by taking our time and conduct our mental lives by the law of least effort. (Kahneman 2011, p. 38)
Given that the process is effortful, and our resources are bounded, it must eventually halt, whether it succeeds or not. This is in accordance with our experience of occasionally failing in demanding tasks due to cognitive overload.
As clarified in (Evans 2018), one should not take System 1 as merely descriptively representing what people, as a matter of fact, do most of the time, and System 2 as embedding the normative standards of rationality. On the contrary, System 2 can occasionally fail to do its job in correcting the mistaken outputs of System 1, which, on the other hand, can display good logical intuitions and get things right on most occasions: see Bago and De Neys (2017).
Dual process theories have been mostly neglected by formal modelers in logic (relevant exceptions are Stenning and van Lambalgen 2008; Balbiani et al. 2016). We aim to contribute to filling the gap by modeling the logical aspects of System 1 and System 2 reasoning activities: those that are connected to logical inferences—a most classical topic of logical investigation—and the formation and revision of beliefs—a core topic of doxastic-epistemic logic and belief revision theory.Footnote 2
3 Background: Dynamic Epistemic Logic
3.1 Epistemic Logic
Possible-worlds semantics has been used in epistemic logic since Hintikka (1962). Epistemic logic is here conceived as a propositional logic, supplemented with two modal operators K and B where \(K \phi \) reads “the agent knows that \(\phi \)” and \(B \phi \), “the agent believes that \(\phi \)”. In knowing or believing something, one obtains a way of determining which among a range of possibilities is the way things actually are, i.e., the actual world. In this representation, possible worlds represent the alternative ways things could be. The semantic interpretations are then given in terms of these possible worlds: an agent knows(/believes) that \(\phi \) if and only if, in all possible worlds compatible with what the agent knows(/believes), it is the case that \(\phi \). More concretely, the modeler captures the compatibility among the agent’s epistemic or doxastic alternatives via binary relations on a set of possible worlds, that represent the agent’s epistemic or doxastic accessibility. The set of worlds and the accessibility relations, augmented by a valuation function to indicate which propositional atoms are true at each world, provide us with the formal model in which every sentence of the new language is interpreted recursively with respect to a world. As standard, a formula is said to be valid in a model whenever it is true at each world of the model. Algebraic properties of the accessibility relations are associated with the validity of certain formulas that capture epistemologically desirable properties of knowledge and belief. Requiring that a model satisfies these properties leads to the definitions of epistemic and doxastic models as in the received view (e.g., Fagin et al. 1995; van Ditmarsch et al. 2007).
The standard epistemic logical system is static: it doesn’t represent the constant changes in our knowledge and beliefs triggered by both our internal mental processes (e.g., performing inferences) and our external interactions (e.g., the integration of information provided by an interlocutor). To capture such processes, we have to move to a dynamic setting.
3.2 Tools of Dynamic Epistemic Logic
Dynamic Epistemic Logic (DEL) (Baltag et al. 1998; Baltag and Moss 2004; van Ditmarsch et al. 2007; van Benthem 2011) is the name for a class of logical systems enriching the language of static epistemic logic by modal operators that encode actions capable of altering an agent’s epistemic or doxastic state. Such actions are understood as triggering model transformations: they take us from a model representing one’s epistemic/doxastic state to a new model representing the updated epistemic/doxastic state. Given action \(\alpha \), a formula of the form \([\alpha ] \phi \), where \([\alpha ]\) is a dynamic operator, is then evaluated in a model by examining what the truth value of \(\phi \) is at the model obtained by transforming the original model when carrying out the action encoded by \(\alpha \).
While the first logical systems within DEL were designed to model epistemic updates, more sophisticated theories have been developed to represent a variety of informational changes including epistemic updates, doxastic changes, preference change, etc. The tools that we need to represent an agent’s beliefs are called plausibility models (Grove 1988; van Benthem 2007; Baltag and Smets 2008b). Such models allow the study of nuanced epistemic and doxastic attitudes and facilitate the introduction of a repertoire of epistemic and doxastic actions. They will be the background for our representation of fast and slow thinking, and we provide the definition here:
Definition 3.1
(Plausibility model) A plausibility model M is a structure \(\langle W, \ge , V \rangle \) where:
-
W is a non-empty set of possible worlds.
-
\(\ge \) is a locally well-preordered (plausibility) relation on W, such that \(w \ge u\) reads “w is considered no more plausible than u”.
-
V is a valuation such that each propositional atom from a given set \(\Phi \) is assigned to the set of worlds where it is true.
Between any two possible worlds entertained by the agent as ways things could be, there is a (relative) plausibility ordering. The ordering is a local well-preordering, which means that \(\ge \) is reflexive, transitive, locally connected, and converse wellfounded, i.e., there is no infinite ascending \(\ge \)-chain, thus a set of most plausible worlds can always be retrieved (Baltag and Renne 2016). A pair (M, w) consisting of a model M and a designated world w of the model, taken as the actual world from the perspective of the modeler, is called a pointed model.Footnote 3
Plausibility models allow us to characterize a variety of epistemic and doxastic attitudes (Baltag and Smets 2011, 2013) including, besides the strong concept of Knowledge mentioned above in the context of static epistemic logic (i.e., knowledge as truth in all possible worlds), also weaker epistemic attitudes. In Baltag and Smets (2008b), one such weaker attitude is coined “safe belief” or “ (in)defeasible knowledge” referring to the epistemic concept described in Lehrer and Paxson (1969), Lehrer (2000), Stalnaker (2006). If we explain defeasible knowledge in terms of the extra ingredients one needs to add to belief, the most straighforward way is to refer to a ‘stability’-account (Rott 2004): defeasible knowledge is justified true belief stable when new true information is received.Footnote 4 We follow in this paper the literature of DEL in Baltag and Smets (2008b) and represent Defeasible knowledge by a modal operator \(\Box \). The truth conditions for \(\Box \phi \), when evaluated at a world in a plausibility model, ask for \(\phi \) to hold at all worlds that are at least as plausible as the point of evaluation. The truth conditions for \(B \phi \) require that \(\phi \) holds at the set of most plausible worlds of the model, denoted by min(W).Footnote 5
The cognitive workings of System 1 and System 2 are aligned with this more graded outlook of different attitudes. Our attitude towards a piece of information uncovered by one of the two systems is oftentimes not as strong as the strong concept of infallible knowledge requires, nor as weak as plain belief.
As for the dynamic operators in this plausibility setting, Baltag and Smets (2008b), van Benthem (2007, 2011) introduce a number of different ones, transforming a given plausibility model into a new one. Three specific operators can be matched to three different policies of integrating external information, depending on the level of trust one has over the information source (van Benthem 2011). A radical upgrade with \(\psi \), denoted by \([\psi \Uparrow ]\), stands for a communicative action whereby the source is mostly, but not entirely, trusted; the updated model triggered by \([\psi \Uparrow ]\) is one where the \(\psi \)-satisfying worlds are prioritized in terms of plausibility over the non-\(\psi \) ones, leaving the ordering intact in the two zones. The ways the two cognitive systems shape our epistemic/doxastic state will be expressed precisely as model-changing actions on plausibility models.
3.3 The Problem of Logical Omniscience
The described DEL models use only possible worlds, which are closed under logical consequence: if a world makes \(\phi \) true, it makes true any logical consequence of \(\phi \). Since the interpretations for formulas involving propositional attitudes quantify over sets of possible worlds, the corresponding agents know or believe everything that follows from what they already know or believe. In logic and Artificial Intelligence (AI), this situation is labeled as the problem of logical omniscience (Fagin et al. 1995, Chapter 9): such agents will not be susceptible to the logical errors that might have been generated by System 1, and they are not subjected to the cognitive limitations of System 2.
To deal with the problem of logical omniscience, the logic and AI literature contains a number of different proposals (Halpern and Pucella 2011). We will focus on one in particular. Starting with Hintikka (1975), a number of authors (Rantala 1982; Wansing 1990; Priest 2001; Kiourti 2010; Berto 2012; Nolan 2013; Jago 2014; Rasmussen and Bjerring 2018) have suggested to supplement the usual possible-worlds models with non-normal or impossible worlds: worlds that represent logical impossibilities, i.e., that are not closed under logical consequence. If these worlds are epistemically accessible by the agent, the closure properties of knowledge and belief that generate the problem are invalidated. But a naive impossible worlds approach faces an issue of ‘bounded rationality’: how should one constrain the accessible worlds, so as to model a moderately rational, though not omniscient, agent, which manages to unpack some, though not all, of the logical consequences of its beliefs or knowledge? The model we present below answers the question by combining non-normal worlds semantics with DEL techniques.Footnote 6
4 Modeling Fast and Slow Thinking
In this section we introduce a new logical system, define its syntax and semantics in order to use them to represent and model agents capable of fast and slow thinking. Overall our logic-technical aims are to:
-
Enrich the standard possible worlds semantics of epistemic logic with non-normal worlds to encode the beliefs of a Human, logically competent but not omniscient, agent.
-
Use tools from DEL to model how incoming information is automatically incorporated by System 1 into the currently held beliefs.
-
Use tools from DEL to capture the agent’s stepwise deductive reasoning via System 2.
-
Allow for the interaction of the two systems.
-
Account for how the two systems differ in terms of cognitive resource consumption.
4.1 Language
Besides operators for (defeasible) knowledge, \(\Box \), and belief, B, our language has dynamic operators to express (1) System 1’s fast upgrades in the arrangement of our beliefs—policies of automatic integration of new information—and (2) System 2’s cognitively costly choices and applications of logical inference rules.
Definition 4.1
(Language) Given a set P of propositional atoms and a set of inference rules R available to the agent, the language \({\mathcal {L}}\) is inductively defined from:
where
-
\(p \in P\)
-
\(\Box \phi \) reads “the agent defeasibly knows that \(\phi \)”.
-
\(B \phi \) reads “the agent believes that \(\phi \)”.
-
\([\alpha ]\) is schematic for a model-changing action performed in thought. These can be of the two aforementioned kinds:
-
(1)
\([\psi \Uparrow ]\), where \(\psi \) is a propositional formula, denotes a fast upgrade with \(\psi \): given incoming information \(\psi \), the agent automatically makes plausible sense of the situation in the light of its background knowledge and beliefs. Then \([\psi \Uparrow ] \phi \) reads “after upgrading with \(\psi \), \(\phi \) is true”.
-
(2)
\(\langle R_k \rangle \), where \(R_k \in R\), that is, an inference rule available to the agent.Footnote 7 The agent can deliberately choose one of them, apply it to some available information and, as we shall see, pay some cognitive cost for it. Then \(\langle R_k \rangle \phi \) reads “after some application of inference rule \(R_k\), \(\phi \) is true”.Footnote 8
-
(1)
4.2 Semantics
We supplement the possible worlds apparatus with non-normal or impossible worlds, but we don’t aim at a modeling of thought where anything goes. In particular, we adopt the principle of Minimal Rationality, put forward by Cherniak (1986) as a realistic alternative to the notions of perfect rationality. According to Minimal Rationality, the agent undertakes some, but not necessarily all, of those actions that are apparently appropriate. This, in turn, translates to the ability of the agent to eliminate inconsistencies: the agent eliminates some, but not necessarily all, of the inconsistencies arising in her belief set. As a result, our agent is fallible and entertains inconsistencies, for example due to inputs of System 1; this fallibility is witnessed by the impossible worlds of the model. On the other hand, the agent should be endowed with the ability to eliminate some of them. To start with, we introduce a Minimal Consistency (MC) requirement on our model: none of the impossible worlds accessible to an agent will at least represent a blatant contradiction of the form \(\phi \), \(\lnot \phi \). An implicit contradiction arising in her belief set can be eliminated, e.g. because the agent resorts to System 2, but only provided that certain conditions are met.
We further impose a plausibility ordering on worlds, encoding the agent’s background beliefs: the more plausible a world looks given the agent’s experience, biases, etc., the better it is ranked (the ordering is qualitative, mirroring belief entrenchment). Plausibility is instrumental in modeling, as we will see, the changes induced by both (1) the fast incorporation of external information by System 1, (2) the slow reasoning processes of System 2.
We need ways to represent which cognitive resources are explicitly depleted during System 2 reasoning (time, memory, etc.), what each reasoning step costs, and what the agent can afford with respect to them. Each step corresponds to an application of an inference rule. Yet not all inference rules require equal cognitive effort, as indicated by experimental evidence. For example, Johnson-Laird et al. (1992), Rips (1994), Stenning and van Lambalgen (2008) claim that the asymmetry in performance observed when a subject uses Modus Ponens and Modus Tollens is suggestive of an increased difficulty to apply the latter. Similarly, Rijmen and De Boeck (2001) also provide experimental evidence to support the claim that different costs should be assigned to different basic rules. Cherniak (1986) also argues for a “well-ordering of inferences” in terms of their difficulty. Concrete assignments of the different cognitive costs and capacity rely on empirical research that sheds light on the units that best describe resources, the values corresponding to each inference rule, etc. We adopt a simple numerical approach to the values of resources because this seems convenient in terms of capturing the availability and cost of time, and it is also supported by psychologists’ research on memory (Miller 1956; Cowan 2001).Footnote 9
Definition 4.2
(Dual-process plausibility model) Fix R, the set of inference rules available to the agent, and Res, a finite set of resources, such as memory, time etc. Let \(r {:}{=} |Res|\), i.e., the number of resources. A dual-process plausibility model is a tuple \(M= \langle W^P, W^I, ord, V, C, cp \rangle \) where:
-
\(W^P, W^I\) are countable non-empty sets of possible and impossible worlds respectively.
-
\(ord: W \rightarrow \Omega \) is a function from \(W{:}{=} (W^P \cup W^I)\) to the class of ordinals \(\Omega \), assigning one to each world. Intuitively: the smaller the ordinal is, the more plausible the world.
-
\(V: W \rightarrow {\mathcal {P}}({\mathcal {L}})\) is a function assigning to each world in W a set of sentences in \({\mathcal {L}}\). The function assigns to each \(w \in W^P\) the set of atomic formulas true at w. It assigns to each \(w \in W^I\) all formulas, atomic or composite, true at w.Footnote 10 Thus, V maps logically complex formulas to truth values directly at impossible worlds, in a non-recursive fashion: this allows such worlds to break any (non-trivial, i.e., different from ‘If \(\phi \), then \(\phi \)’) logical principle (they can, e.g., be such that \(\phi \) is true at them while \(\phi \vee \psi \) isn’t, or they can make both \(\phi \) and \(\psi \) true without making true their conjunction.) However, according to our (MC), we stipulate that \(\{ \phi , \lnot \phi \} \not \subseteq V(w)\) for all \( w \in W^I\).
-
\(C: R \rightarrow {\mathbb {N}}^r\) is a function such that every inference rule \(R_k \in R\) is assigned a particular cognitive cost for each resource.
-
\( cp \) denotes the agent’s cognitive capacity, i.e., \( cp \in {\mathbb {N}}^r\), intuitively standing for what the agent is able to afford with regard to each resource.
We will work with pointed plausibility models (M, w), where M is a dual-process plausibility model and w a designated-base world in it. The ord extracts a plausibility ordering in the usual sense, i.e., a binary relation on W: \( w \ge u\) if and only if \(ord(w) \ge ord(u)\). The ranking of worlds is reflected in the ordering of ordinals. The intended reading is “w is no more plausible than u”. The ordering satisfies reflexivity, transitivity, connectedness, and converse wellfoundedness.
Fast and slow thinking will be reflected in the interpretation of the sentences involving the operators for upgrades and inference rule application. We thus have to define how the model changes through these actions.
4.3 Model Transformations, Fast and Slow
4.3.1 The Fast Updater
Each transformation is governed by its corresponding system: thus, System 1’s actions of integrating new information will be affected by the agent’s stereotypes, biases, experience, etc., as these are hardwired in the initial plausibility ordering. Based on this, the system incorporates new information by prioritizing the worlds satisfying it. That is, an upgrade with \(\psi \) changes the plausibility ordering as follows: \(\psi \)-worlds become more plausible than non-\(\psi \) ones (i.e., those that do not satisfy \(\psi \)) keeping the previous ordering intact within the two zones. Moreover, as fast thinking, this activity requires no effort; therefore the relevant components of the model should be unaffected by the upgrade.
Definition 4.3
(Plausibility model transformation by a System 1 upgrade) Given a model \(M=\langle W^P, W^I, ord, V, C, cp \rangle \), its transformation by \(\psi \Uparrow \) is a model \(M^{\psi \Uparrow } = \langle W^P, W^I, ord^{\psi \Uparrow }, V, C, cp \rangle \) where \(ord^{\psi \Uparrow }\) can be any function from the setFootnote 11\(\{f: W \rightarrow \Omega \mid {\text { for any }} w, u \in W: f(w) \ge f(u)\) if and only if \(w \ge ^{\psi \Uparrow } u\}\).
The characterization via ordinals does not interfere with radical upgrades. We will not be interested in the assigned number per se, but in the action-induced re-arrangement (i.e., plausibility of worlds relative to other worlds). Thus, all functions from \(\{f: W \rightarrow \Omega \mid {\text { for any }} w, u \in W: f(w) \ge f(u)\) if and only if \(w \ge ^{\psi \Uparrow } u\}\) work for our purposes.
4.3.2 The Slow Controller
We account for the step-wise, deliberate and cognitively costly workings of System 2 via our rule-application operators. To define the transformation induced by these operators, we will employ the notion of \(R_k\)-accessibility. For a pointed plausibility model \((M', w)\) to be \(R_k\)-accessible from a given pointed plausibility model (M, w), the set \(P_{\ge } (w) {:}{=} \{ u \in W \mid w \ge u \}\) of worlds at least as plausible as w is replaced by a choice of worlds reachable by an application of \(R_k\) from the elements of \(P_{\ge } (w)\), while the remaining ordering is adapted accordingly. We focus on the more or equally plausible worlds, as these would be prioritized whenever one applies an inference rule. By specifying the effect of each rule separately, it is possible to trace back a sequence of slow reasoning, unravel it and verify its order-sensitivity. In addition, the agent’s cognitive capacity should be reduced by the cost of applying this particular inference step.
To capture the change induced by applications of inference rules, we first have to encode their effect on the structure of our models. The effect of applying a rule is an expansion of the agent’s factual information. We first introduce the following, assuming that propositional formulas are assessed as usual in possible worlds:
Definition 4.4
(Propositional truths) Let M be a model, \(w \in W\) a world of the model and \({\mathcal {L}}_P\) the standard propositional language. If \(w \in W^P\), its set of propositional truths is \(V^* (w)= \{ \phi \in {\mathcal {L}}_P \mid M, w \models \phi \}\). If \(w \in W^I\), \(V^*(w) = \{ \phi \in {\mathcal {L}}_P \mid \phi \in V(w)\}\).
\(V^*\) is in fact determined by V. Next, we fix a particular instance of the inference rule \(R_k\). This has a set of (propositional) premises, denoted by \(pr(R_k)\), and a conclusion, denoted by \(con(R_k)\). Then we impose the condition of Succession:
For every \(w \in W\), if:
-
1.
\(pr(R_k) \subseteq V^*(w)\)
-
2.
\(\lnot con(R_k) \not \in V^*(w)\)
-
3.
\(con(R_k) \ne \lnot \phi \) for all \(\phi \in V^*(w)\)
then there is \(u \in W\) such that \(V^*(u)=V^*(w) \cup \{ con(R_k) \}\).
We use \(V^*(w) \vdash _{R_k} V^*(u)\) to say that for some instance of \(R_k\), u expands w in terms of this condition. If \(pr(R_k) \subseteq V^*(w)\) for no instance of \(R_k\), we take the only \(R_k\)-expansion of w to be itself. This is because, in that case, an application of \(R_k\) would trigger no further expansion on w. If \(pr(R_k) \subseteq V^*(w)\) for an instance of \(R_k\), but condition 2 or 3 is violated, then there is simply no \(R_k\)-expansion with regard to this instance. This is because, in that case, the application of \(R_k\) would uncover an inconsistency in the composition of w.Footnote 12 Notice that by conjoining successive rules, such as \(R_1, \ldots , R_n\), the notation can be generalized to \(\vdash _{R_1, \ldots , R_n}\).
Definition 4.5
(Rule-specific radius) Given an inference rule \(R_k \in R\), the \(R_k\)-radius of a world \(w \in W\) is \(w^{R_k} = \{ u \mid V^*(w) \vdash _{R_k} V^* (u) \}\).
A member of \(w^{R_k}\) is therefore an \(R_k\)-expansion of w. Note that \(w^{R_k} = \{w\}\) for \(w \in W^P\) due to the deductive closure of possible worlds, while the \(R_k\)-radius of impossible worlds can contain different \(R_k\)-expansions. Under the conditions, \(\vdash _{R_k}\) is such that \(V^*(u)\) preserves \(V^*(w)\) and extends it just by a conclusion of \(R_k\). This is how we obtain a monotonicity feature: \(R_k\)-expansions (as per the name) enrich the state from which they originate, in terms of \(R_k\); inferences are not defeated as reasoning steps are taken, to the extent that MC is respected. Granting a sort of monotonicity that is restricted by MC is in line with the workings of System 2 and the criterion of informational economy (Board 2004), adapted to our framework: belief change in light of new information should be no greater than is necessary to incorporate that new information. As a result, applications of rules should refine the state of the agent, not only by allowing her to know or believe more, but also by eliminating inconsistencies when spotted. However, in light of an application of a rule \(R_k\), an expansion should involve just the conclusion of some instance of \(R_k\).
Not all instances of a rule are equally informative. Compare an application of Conjunction Introduction that allows the agent to conclude that \(\phi \wedge \psi \), from \(\phi \) and \(\psi \), and an application that generates \(\phi \wedge \phi \) from \(\phi \). In Rips (1994), rules are classified into self-constraining and self-promoting. Self-constraining rules, such as Modus Ponens, generate a limited number of new sentences from their premises. Self-promoting rules, such as Conjunction Introduction, generate an infinite number of conclusions from their premises. It is natural to aim at reducing the space \(W^I\) from the (possibly infinite) worlds corresponding to non-informative applications of self-promoting rules. This is not to say that the conclusions of these applications should not be available to the agent. In principle, the setting should allow for applications leading to the agent knowing/believing such conclusions. In order to do justice to both points, the modeler might simply assume that a world’s expansion corresponding to a non-informative instance is the world itself. However, we abstain from imposing this as a strict condition on the general class of our models, in order to allow for the modeling of a variety of types of agents that may require different readings of informativeness, thus different compositions of a world’s radius.
Definition 4.6
(Choice function) Let \({\mathcal {C}}: {\mathcal {P}}({\mathcal {P}}(W)) \rightarrow {\mathcal {P}}({\mathcal {P}}(W))\) be a choice function that takes a set \({\mathcal {W}} = \{ W_1, \ldots , W_n \}\) of sets of worlds as input and returns the set \({\mathcal {C}} ({\mathcal {W}})\) of sets of worlds which results from all the ways in which exactly one element can be picked from each non-empty \(W_i \in {\mathcal {W}}\). A member of \({\mathcal {C}}({\mathcal {W}})\) is called a choice of \({\mathcal {W}}\).
A choice function on a set consisting of the radii of worlds will capture how System 2 can deliberate and choose its next step of slow thinking. Given the aforementioned remark on informative and non-informative instances, the several choices that the function yields correspond to the different effects of applying a particular rule.
Now we can explain the effect of System 2’s applications of an inference rule \(R_k\): if a world u was considered at least as plausible as w before an application of the rule \(R_k\), but does not survive such application, then the agent can rule u out as a doxastic or epistemic possibility. This world must have been an impossible world: a possible world will always survive applications of inference rules, as its radius amounts to itself. What was taken as an epistemic possibility has been spotted as impossible by a slow computation of System 2. Once we rule out such worlds, we preserve the previous ordering to the extent that it is unaffected by the application of the inference rule, again in agreement with informational economy. That is, there might be parts of the model still independent of this particular application of deductive reasoning, remaining influenced by System 1 alone.
To make this precise, we use the ordinal function and the notion of rule-specific radius. Let \(M= \langle W^P, W^I, ord, V, C, cp \rangle \) a plausibility model. We spell out the transformation in steps:
- Step 1:
-
Let (M, w) be a pointed model. Then, given an inference rule \(R_k\), let \(P^{R_k} (w) {:}{=} c\) where c is some choice in \({\mathcal {C}}(\{v^{R_k} \mid v \in P_{\ge }(w)\})\). In words, a choice of \(R_k\)-expansions of the worlds initially considered at least as plausible as w.
- Step 2:
-
Based on the argument used above, if \(u \in P_{\ge }(w)\) but \(u \not \in P^{R_k} (w)\), then u must be excluded from the new model. So in any case, the \(R_k\)-accessible pointed model \((M',w)\) should be such that its set of worlds is \(W^{R_k}=W \setminus \{ u \in P_{\ge }(w) \mid u \not \in P^{R_k} (w) \}\). The elimination in fact affects \(W^I\).
- Step 3:
-
We now develop the new ordering \(ord^{R_k}\) following the application of the inference rule. Let \(u \in W^{R_k}\):
-
1.
If \(u \not \in P_{\ge }(w) \cup P^{R_k} (w)\), then \(ord^{R_k}(u) = ord(u)\), i.e., the assigned ranking remains the same, for worlds that were less plausible than w and are not contained in the choice.
-
2.
Next consider \(u \in P^{R_k}(w)\). This means that there is at least one \(v \in P_{\ge }(w)\) such that \(u \in v^{R_k}\) for the particular choice c that gave rise to \(P^{R_k}(w)\). Denote the set of such v’s by T. Then \(ord^{R_k}(u)=ord(z)\) for \(z \in min (T)\). Therefore, if a world is in \(P^{R_k}(w)\), then it takes the position of the most plausible of the worlds from which it originated.Footnote 13
-
1.
- Step 4:
-
Finally, for worlds \(u,v \in W^{R_k}\): \(u \ge ^{R_k} v\) if and only if \(ord^{R_k} (u) \ge ord^{R_k} (v)\), therefore again all the required properties are preserved.
- Step 5:
-
The other components of the model remain unchanged, except from V which is restricted to the worlds in \(W^{R_k}\) and \( cp ^{R_k} {:}{=} cp -C(R_k)\). Reducing the value of cognitive capacity models slow thinking as resource-consuming.Footnote 14
Here’s an example to get a feel of how this model transformation works:
Example 1
Let s stand for “the odds of survival one month after surgery are 90%”, m for “mortality within one month of surgery is 10%”, r for “the surgery is safe”. Suppose Jill entertains the worlds depicted in the model M below, where \(W^P = \{w_1\}\) and \(W^I=\{w_2, w_0\}\). Let \(ord(w_2)=2, ord(w_1)=1, ord(w_0)=0\). For the possible world \(w_1\), we list only the propositional atoms it satisfies, since all the rest can be computed recursively. For the impossible worlds, we write down all the propositional formulas satisfied there (and only those) to illustrate Succession and the definitions involved in the model transformation. All worlds validate \(s \rightarrow r\), s, r and \(s \rightarrow m\), but m does not hold in the most plausible world \(w_0\): the most plausible world is such to represent that Jill has not inferred that m follows from sFootnote 15 although she has inferred r from s. Finally, given that we focus on the resources of time and memory, we take the cost of applying Modus Ponens to be \(C(MP)= (3,2)\), and the capacity of the agent to be \( cp =(15,9)\).
We then unravel step-by-step the model transformations due to applications of MP (once we give our semantic clauses, we will see how these transformations affect the development of Jill’s epistemic and doxastic state). In search of all the ways the pointed model \((M, w_1)\) can change following an application of the rule MP, we follow the procedure sketched above:
-
Step 1 First, we compute \(\{ v^{MP} \mid v \in P_{\ge } (w_1)\}\). It amounts to \(\{ \{w_1\} ,\{w_0, w_2\} \}\).
As a resut, \({\mathcal {C}} (\{ \{w_1\}, \{w_0, w_2\} \})= \{ \{w_1, w_0\}, \{w_1, w_2\} \}\).
So \(P^{MP} (w_1)= \{w_1, w_0\}\) or \( P^{MP} (w_1)= \{w_1, w_2\}\).
-
1.
In case \(P^{MP} (w_1)= \{w_1, w_0\}\):
Step 2 \(W^{MP}=W\)
Step 3 Since \(w_2 \not \in P^{MP} (w_1) \cup P_{\ge } (w_1)\), \(ord^{MP} (w_2)= ord(w_2)=2\). Next, \(w_1 \in P^{MP} (w_1)\) and \(w_1 \in w^{MP}_1\), so \(ord^{MP}(w_1)=ord(w_1)=1\). Finally, \(w_0 \in P^{MP} (w_1)\) and \(w_0 \in w^{MP}_0\), so \(ord^{MP}(w_0)=ord(w_0)=0\).
The MP-transformed model is in this case identified with the initial model because it was generated by an application of MP that yielded no new information.
-
2.
In case \(P^{MP}(w_1)= \{w_1, w_2\}\):
Step 2 \(W^{MP}=W \setminus \{ u \in \{w_1, w_0\} \mid u \not \in \{w_1, w_2\} \}= \{w_1, w_2 \}\).
Step 3 As above, \(ord^{MP} (w_1)= ord(w_1)=1\). Then, \(w_2 \in P^{MP} (w_1)\) and, checking from which world(s) it originated in the particular choice, we find \(w_2 \in w^{MP}_0\), so \(ord^{MP}(w_2)=ord(w_0)=0\).
The MP-transformed model is in this case different; the impossible world that did not satisfy m, despite satisfying both \(s \rightarrow m\) and s, was uncovered by Jill, precisely because she used an application of MP that generated new information. The effect of taking this slow inferential step is now reflected in the new model.
-
1.
-
Step 4 The new plausibility ordering is depicted in the figure.
-
Step 5 The new valuation is obviously restricted to the worlds that survive the application of MP. The cognitive capacity of both MP-accessible models is reduced by the cognitive cost of applying MP, therefore \( cp =(12,7)\) (Fig. 1).
The first figure depicts the model M, with an MP-dashed arrow from w to u denoting that u is an MP-expansion of w. The node of \(w_1\) is thicker to show that this world is in \(W^P\). Then, we obtain two potential transformations of the pointed model \((M, w_1)\), i.e., two MP-accessible pointed models, based on the two ways the set of \(w_1\)’s more (or equally) plausible worlds can change due to MP
4.4 Semantic Clauses
We have explained how the original model changes after fast upgrades and slow applications of inference rules. Now come the truth conditions:
Definition 4.7
(Semantics) The following inductively define when a formula \(\phi \) is true at w in M (notation: \(M, w \models \phi \)) and when \(\phi \) is false at w in M (notation:
\( M,w \)
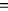 \( \phi \)).
\( \phi \)).
For \(w \in W^P\):
-
\(M,w \models p\) if and only if \(p \in V(w)\), where \(p \in \Phi \)
-
\(M,w \models \lnot \phi \) if and only if \(M,w \not \models \phi \)
-
\(M,w \models \phi \wedge \psi \) if and only if \(M,w \models \phi \) and \(M,w \models \psi \)
-
\(M,w \models \Box \phi \) if and only if \(M,w' \models \phi \) for all \(w'\) such that \(w \ge w'\)
-
\(M,w \models B \phi \) if and only if \(M, w' \models \phi \) for all \(w' \in min(W)\)
-
\(M, w \models [\psi \Uparrow ] \phi \) if and only if \(M^{\Uparrow \psi }, w \models \phi \)
-
\(M,w \models \langle R_k \rangle \phi \) if and only if \(M', w \models \phi \) for some \((M', w)\) which is \(R_k\)-accessible from (M, w)
-
\( M,w \)
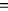 \( \phi \)
if and only if \(M,w \not \models \phi \)
\( \phi \)
if and only if \(M,w \not \models \phi \)
For \(w \in W^I\):
-
\(M,w \models \phi \) if and only if \( \phi \in V (w)\)
-
\( M,w \)
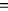 \( \phi \) if and only if \(\lnot \phi \in V(w)\)
\( \phi \) if and only if \(\lnot \phi \in V(w)\)
Logical validity is defined in terms of possible worlds only: a sentence is valid in a model if and only if it is true at every possible world.
In accordance to what the dual-process theories prescribe, our System 1 actions affect what is (defeasibly) known or believed without checking whether there is valid reasoning supporting the piece of information.Footnote 16 This fits manifestations of System 1 being in charge. For example, experiments on the belief bias (Evans 1989, 2003) demonstrate that subjects are reluctant to believe “unbelievable” (given their prior conceptions) statements even when they logically follow from a set of premises. They also tend to believe “believable” conclusions, even though the underlying reasoning is problematic, due to the influence of pre-existing impressions and biases. These are hardwired in the model’s plausibility ordering, while the fast upgrades integrate information based on them, thus forming the agent’s epistemic or doxastic state without engaging in the effortful task of assessing what is valid. This falls under the responsibility of System 2; if the agent comes to know or believe something new following an action of System 2, this must follow logically from what is already known or believed.
Now we can develop our initial example into:
Example 2
Recall the scenario of Example 1. It is now easy to see that, based on our semantics, \(\lnot \Box m\), \(\lnot B m \), \(\Box s\), Bs, \(\Box r\), Br are all valid; initially, Jill does not know, nor believes that m, despite knowing and believing that s. In addition, \(\langle MP \rangle \Box m\), \(\langle MP \rangle B m\), \(\langle MP \rangle \lnot \Box m\), \(\langle MP \rangle \lnot B m\) are all valid. That is, there is some application of MP that provides Jill with knowledge and belief of m (because she inferred it from \(s \rightarrow m\) and s) and another application of MP that does not provide her with any new information (because she merely used \(s \rightarrow r\) and s as premises, which only comes as a confirmation of her already held belief and knowledge of r).
The example shows how different applications of a rule, captured as different choices of expansions, may lead to different developments of the agent’s knowledge and beliefs. Notice that the reading of \(\langle R_k \rangle \phi \) is existential: it asks that there be some application of \(R_k\) leading to \(\phi \). Different choices allow both informative and uninformative applications by a competent agent with sufficient resources. One can have a dual \([R_k] \phi {:}{=} \lnot \langle R_k \rangle \lnot \phi \), read as “after all applications of \(R_k\), \(\phi \) is true”. This is satisfied whenever all \(R_k\)-accessible pointed models validate \(\phi \). Using the universal operator, the modeler may express the overall effect of a rule to the agent’s reasoning.
The previous example illustrated a simple case where slow thinking is affordable and the reasoning step of Modus Ponens is performed. In the next example, we model a failure to apply Conjunction Introduction (CI), following an application of Double Negation Elimination (DNE) and Modus Ponens. This is illustrative of a depletion of resources that would halt the reasoning processes of System 2 and make the agent fall back to System 1. It corresponds to a series of examples offered by (Kahneman 2011, ch. 2): whenever the mental effort that System 2 requires wears the agent out completely, then she retreats to default System 1 activity.
Example 3
-
Let model \(M= \langle W^P, W^I, ord, V, C, cp \rangle \) with \(R=\{ DNE, MP, CI \}\), \(Res=\{ time, memory \}\). Also take \(C(MP)=CI=(2,2), C(DNE)=(3,1)\) while \( cp =(5,10)\). In addition, suppose that for world \(w \in W^P\): \(M, w \models \Box \lnot \lnot \phi \wedge \Box (\phi \rightarrow \psi )\).
-
Then, \(M, u \models \lnot \lnot \phi \) and \(M, u \models \phi \rightarrow \psi \) for all u such that \(w \ge u\). Because of Succession, there is a model \(M'\) with \( cp '= cp - C(DNE)= (2,9)\) such that \(M', w \models \Box \phi \).
-
Following the same procedure for MP, we get a model \(M''\) with \( cp ''= cp ' - C(MP) = (2,9)- (2,2)= (0, 7)\) such that \(M'',w \models \Box \psi \).
-
But then there cannot be any CI-accessible pointed model as the step is not affordable (compare C(CI) and \( cp ''\)).
-
So finally, \(M'',w \not \models \langle CI \rangle \Box (\phi \wedge \psi )\), therefore \(M'', w \models \lnot \langle CI \rangle \Box (\phi \wedge \psi )\). But this means that \(M', w \models \langle MP \rangle \lnot \langle CI \rangle \Box (\phi \wedge \psi )\).
-
In turn \(M,w \models \langle DNE \rangle \langle MP \rangle \lnot \langle CI \rangle \Box (\phi \wedge \psi )\).
-
As a result, indeed \(M,w \not \models [DNE][MP] \langle CI \rangle \Box (\phi \wedge \psi )\).
Before moving on to applications of the model, we introduce the following two Theorems. These cast light on reasoning processes involving both inference rules used by System 2, provided that they are affordable, and fast upgrades by System 1. They can be generalized for more upgrades, applications of rules, and thus number of premises. Theorem 4.2 also exemplifies the order-sensitivity of a reasoning process that is orchestrated by both systems.
Theorem 4.1
(Reasoning from rules) If \(\psi \) logically follows from \(\{\phi _1, \ldots , \phi _k\}\) by applying the rules \(R_1, \ldots , R_n \in R\) and \(\langle \ddag \rangle ^{m_i} \Box \phi _i\) is valid for \(1 \le i \le k\), where each \(\langle \ddag \rangle ^{m_i}\) is a sequence of \(m_i\)-many inference rules available to the agent, then \(\langle \ddag \rangle ^{m_1} \ldots \langle \ddag \rangle ^{m_k} \langle R_1 \rangle \ldots \langle R_n \rangle \Box \psi \) is valid.
Proof
Let arbitrary model M and world \(w \in W^P\) of the model. Suppose \(M, w \models \langle \ddag \rangle ^{m_i} \Box \phi _i, {\text { for }} 1 \le i \le k\). For each \(\phi _i\), there is a model \(M^i\) such that \(M^i,w \models \Box \phi _i\) which has \(W^i = W \setminus \{ u \in P_{\ge }(w) \mid u \not \in P^{i} (w) \}\) where
-
\(P^{i} (w) = c\) where c is some choice in \({\mathcal {C}}(\{v^{i} \mid v \in P_{\ge }(w)\})\)
-
\(v^{i} = \{ u \mid V^*(v) \vdash _{\langle \ddag \rangle ^{m_i}} V^*(u) \}\)
-
\(V^*(v) \vdash _{\langle \ddag \rangle ^{m_i}} V^*(u)\) denotes that u is a \(R_{i1}, \ldots , R_{i{m_i}}\)-expansion of v for \(R_{i1}, \ldots , R_{im_{i}}\) composing the sequence \(\langle \ddag \rangle ^{m_i}\).
This means that for all \(u \in W^i\) such that \(w \ge u\), \(M^i, u \models \phi _i\). Due to Succession, there is some model \(M^*\) such that for all \(u \in P^* (w)\): \(M^*, u \models \phi _i\), for all \(1 \le i \le k\), where \(W^* = W \setminus \{ u \in P_{\ge }(w) \mid u \not \in P^{*} (w) \}\) with:
-
\(P^{*} (w) = c\) where c is some choice in \({\mathcal {C}}(\{v^{*} \mid v \in P_{\ge }(w)\})\)
-
\(v^{*} = \{ u \mid V^*(v) \vdash _{\langle \ddag \rangle ^{m_i} \ldots \langle \ddag \rangle ^{m_k} } V^*(u) \}\)
-
\(V^*(v) \vdash _{\langle \ddag \rangle ^{m_1} \ldots \langle \ddag \rangle ^{m_k} } V^*(u)\) denotes that u is a \(R_{11}, \ldots , R_{1m_{1}}, \ldots , R_{k1}, \ldots , R_{km_{k}}\)-expansion of v.
Next, from the fact that \(\psi \) logically follows from \(\{\phi _1, \ldots , \phi _k\}\) through applying \(R_1, \ldots , R_n \in R\), and Succession, we get that there is a model \(M^{\circledast }\) such that for all \(u \in P^{\circledast }(w)\): \(M^{\circledast }, u \models \psi \), which has \(W^\circledast = W \setminus \{ u \in P_{\ge }(w) \mid u \not \in P^{\circledast } (w) \}\) where
-
\(P^{\circledast } (w) = c\) where c is some choice in \({\mathcal {C}}(\{v^{\circledast } \mid v \in P_{\ge }(w)\})\)
-
\(v^{\circledast } = \{ u \mid V^*(v) \vdash _{\langle \ddag \rangle ^{m_i} \ldots \langle \ddag \rangle ^{m_k}, R_1, \ldots , R_n} V^*(u) \}\)
-
\(V^*(v) \vdash _{\langle \ddag \rangle ^{m_1} \ldots \langle \ddag \rangle ^{m_k}, R_1, \ldots , R_n } V^*(u)\) denotes that u is a \(R_{11}, \ldots , R_{1m_{1}}, \ldots , R_{k1}, \ldots , R_{km_{k}}, R_1, \ldots , R_n\)-expansion of v.
But then clearly \(M^{\circledast }, w \models \Box \psi \), and overall \(M , w \models \langle \ddag \rangle ^{m_1} \ldots \langle \ddag \rangle ^{m_k} \langle R_1 \rangle \ldots \langle R_n \rangle \Box \psi \). \(\square \)
Theorem 4.2
(Reasoning from upgrades and rules) If \(\chi \) logically follows from \(\{\phi _1, \phi _2\}\) by applying the rules \(R_1, \ldots , R_n \in R\) and \([\psi \Uparrow ] ( \Box \phi _1 \wedge \langle \ddag \rangle ^m \Box \phi _2)\) is valid, then \([\psi \Uparrow ] \langle \ddag \rangle ^m \langle R_1 \rangle \ldots \langle R_n \rangle \Box \chi \) is valid.
Proof
Let arbitrary model M and world \(w \in W^P\) of the model. Suppose \(M, w \models [\psi \Uparrow ] (\Box \phi _1 \wedge \langle \ddag \rangle ^m \Box \phi _2)\). This amounts to \(M^{\psi \Uparrow }, w \models (\Box \phi _1 \wedge \langle \ddag \rangle ^m \Box \phi _2)\), i.e., \(M^{\psi \Uparrow }, u \models \phi _1\) for all \(u \in P^{\psi \Uparrow }(w)\) [1] and there is a model \(M^*\) such that \(M^*,w \models \Box \phi _2\) which has \(W^* = W \setminus \{ u \in P^{\psi \Uparrow }(w) \mid u \not \in P^{*} (w) \}\) where
-
\(P^{*} (w) = c\) where c is some choice in \({\mathcal {C}}(\{v^{*} \mid v \in P^{\psi \Uparrow }(w)\})\)
-
\(v^{*} = \{ u \mid V^*(v) \vdash _{\langle \ddag \rangle ^{m} } V^*(u) \}\)
Then, \(M^*,u \models \phi _2\), for all \(u \in P^* (w)\). Due to Succession and [1], \(M^*,u \models \phi _1\), for all \(u \in P^*(w)\). Due to \(\chi \) following from \(\{\phi _1, \phi _2\}\) and Succession, there is a model \(M^{\circledast }\) such that \(M^{\circledast }, u \models \chi \), for all \(u \in P^{\circledast } (w)\) where
-
\(P^{\circledast } (w) = c\) where c is some choice in \({\mathcal {C}}(\{v^{\circledast } \mid v \in P^{\psi \Uparrow }(w)\})\)
-
\(v^{\circledast } = \{ u \mid V^*(v) \vdash _{\langle \ddag \rangle ^{m}, R_1, \ldots , R_n} V^*(u) \}\)
But then clearly \(M^{\circledast },w \models \Box \chi \), and overall \(M, w \models [\psi \Uparrow ] \langle \ddag \rangle ^m \langle R_1 \rangle \ldots \langle R_n \rangle \Box \chi \). \(\square \)
By making the semantic interpretations of propositional attitudes quantify over impossible worlds, it is guaranteed that some consequences of the agent’s knowledge or beliefs are not known or believed: logical omniscience is thus avoided. Unlike other approaches though, the problem is escaped in a balanced manner, committed to the idea that competent agents would come to know and believe consequences lying within affordable applications of rules.
In view of considerations coming in Sect. 6, notice that one can read our models as normative, but realistic: an agent ought to choose and apply slow thinking rules to the extent that she can do it, given the cognitive resources at hand, and until these are depleted. Before we get there, in the next Section, we put the framework to work.
5 Three Case Studies
Interaction between System 1 and System 2 (or, stereotypes gone wrong) System 1 provides its—sometimes incorrect—impressions to System 2. These impressions exemplify biases that are often attributed to our experience, the so-called familiarity heuristic. System 2 can then unpack their logical consequences. It is not uncommon for System 2 to eventually override System 1. To demonstrate this, we introduce and analyze a variant of the restaurant scenarioFootnote 17:
Jack (agent 1) and Jill (agent 2) have entered a restaurant. They are joined by John (agent 3) shortly after. Waiter A takes their order, which includes three dishes: Vegan, Meat and Fish. Waiter B is supposed to serve them. Waiter B is acquainted with Jack: he knows that Jack is a passionate animal rights activist, often arguing against the consumption of any animal product. He has not met Jill but he has the impression that she is pretty close to Jack and implicitly assumes that she shares his opinion and lifestyle. On the other hand, John is a frequent customer: almost every time he orders the same meat-based dish. As the meals are prepared, Waiter B has an intuitive, yet incomplete, idea on their distribution. System 1 is at work. Influenced by his stereotypes and experience, he thinks that Jack will definitely get the vegan dish, and John the meat. For someone carefully and consciously reading the story, this would mean that Jill ordered fish. Not for waiter B, though: due to Jill’s closeness to Jack, he has trouble inferring this conclusion. He is also willing to consider, albeit reluctantly, that John gets fish. Again he is subconsciously confused enough to take a stance on Jill’s option. Finally scenarios in which Jack orders meat or fish are ruled out by the waiter.
Denote by \(v_i\), \(m_i\), \(f_i\) (\(i=1,2,3\)) the atoms expressing which dish goes to which agent. Let R be the set of rules containing Conjunction Introduction (CI) and Modus Ponens (MP). The following figure depicts the plausibility modelFootnote 18 for waiter B, and according to our semantics, both \(B v_1 \) and \(B m_3 \) are valid.

“John got fish this time!”, says Waiter A. Waiter B overhears the comment and instantly incorporates this new piece of information.
The new model, following the upgrade with \(f_3\), is depicted below and is the outcome of combining the already held opinions of the waiter and incoming information. System 1 deals with what is believed, on the basis of incoming information and biases generated by familiarity, experience etc., and it does not investigate what follows logically.

As Waiter B prepares to serve our three agents and prompted by his curiousness, he takes a moment to figure out what Jill actually ordered, contrary to what he would have expected. In particular, he realizes that he should not let her relationship with Jack interfere with his beliefs, but instead infer what follows from what he already believes, i.e., that Jill got the meat-based dish after all! This is due to a conscious procedure of System 2.
Following an application of CI and MP, in that order, it is easy to verify that overall \( [f_3 \Uparrow ] \langle CI \rangle \langle MP \rangle B m_2\) (as well as \( [f_3 \Uparrow ] \langle MP \rangle B m_2\)) is valid. For example, the final pointed plausibility model based on \(w_1\) has worlds eliminated as epistemic possibilities by slow thinking: it exemplifies how System 2 took over System 1.

Framing effect Decision-making by Humans is heavily influenced by the mode of presentation of options (Kahneman 2011, Part 4). For instance, different responses are evoked whenever a question on the outcome of a surgery is presented in terms of survival or in terms of mortality. The statements “the odds of survival one month after surgery are 90%” and “mortality within one month of surgery is 10%” are equivalent: they have the same truth conditions. But under the first frame or mode of presentation, the situation seems somewhat more reassuring.
The framing effect poses a challenge for ‘static’ epistemic logic. Propositional attitudes towards logically equivalent statements are the same under possible worlds semantics, due to the closure properties of possible worlds. Also, according to the AGM approach to belief revision (Alchourrón et al. 1985), the beliefs of an agent are represented by a set of sentences in a formal language. This set is taken as closed under logical consequence. Therefore, if two sentences p and q are logically equivalent, then believing the one amounts to believing the other, and revising one’s beliefs after being informed that p gives the same outcome as revising them after being informed that q. This too disregards the influence of the mode of presentation on Humans, as opposed to Logons.
We will now show that framing can fit into our logical framework.Footnote 19 Let s and m denote the two statements discussed earlier (odds of survival/mortality rate). Let \(s \leftrightarrow m\) be valid in our dual-process semantics. Suppose that the initial plausibility model for our agent is as follows, i.e., \(\lnot B m\) and \(\lnot B s\):

Following an upgrade with m, based on something the agent heard at the patients’ waiting room, we obtain the model below. Therefore \([ m \Uparrow ] B m\). As a result of framing, the agent has upgraded with m and believed in it, without simultaneously believing in s.

Again, some slow reasoning performed by System 2 will help the agent overcome framing: by performing an inference using Modus Ponens (assuming, as we have done so far, that the agent believes that \(m \rightarrow s\)), the agent can come to believe that s too.

Anchoring effect The anchoring effect (Tversky and Kahneman 1974) is a cognitive bias that makes Humans rely heavily on the first piece of information they receive: this piece works as an “anchor”, and even if it is clearly arbitrary and irrelevant, it can over-influence the formation of subsequent beliefs. For example, suppose that an agent is interested in a new edition of a high-end smartphone but has not made up her mind on whether to purchase it. The agent considers three options:
-
\(r_1\): the new edition falls in the price range [1000–1100).
-
\(r_2\): the new edition falls in the price range [1100–1200).
-
\(r_3\): the new edition falls in the price range [1200–1300).
Suppose that the agent visits a store. She entertains the following options:
-
\(q_1\): the store’s offer is in the price range [1000–1100).
-
\(q_2\): the store’s offer is in the price range [1100–1200).
-
\(q_3\): the store’s offer is in the price range [1200–1300).
In the store, there is a tag indicating that the original price of the desired item is 1200, but the store offers it for 1100. As a result, the agent performs a fast System 1 upgrade with the formula \([(r_3 \wedge q_2) \Uparrow ]\). The value 1200 works as the anchor, because it is indicated by the store’s tag as the market price of the new phone. As a result the formula \([(r_3 \wedge q_2) \Uparrow ] B (r_3 \wedge q_2)\) is verified.
Next, the agent activates System 2, which performs a reasoning step that allows her to believe that she saves a certain amount of money, which makes the bargain good (denote “good bargain” by b; also note that whenever \(r_i \wedge q_i\), we consider the difference of prices negligible and thus not substantial enough to make the agent consider it a bargain). Therefore, we obtain a new validity: \([(r_3 \wedge q_2) \Uparrow ] \langle MP \rangle B b\). Based on that belief, she eventually acts accordingly and buys the smartphone. If there was no indication of an original market price of the smartphone or if the anchor was an initial value that the agent had set (i.e., deciding that only prices in the range [1000–1100) are acceptable/affordable), the evolution of the scenario would have been different and no purchase would have been made. Below, there is a depiction of the initial model, succeeded by the model following the anchoring upgrade, and one final model after the application of Modus Ponens.



6 Coda: “Ought Implies Can”
We conclude with a general philosophical issue: is our model merely descriptive of some of the cognitive workings of Humans, or rather normative? In the latter case, how so, since it aims to avoid the idealisation of agents as logically omniscient?
One may take the logical approach proposed above as roughly standing to ‘static’ (S5) epistemic logic and AGM belief revision theory as Kahneman and Tversky (1979)’s prospect theory of rational choice stands to expected utility theory. Just like prospect theory, our logic of fast and slow thinking is more complex than its mainstream counterpart: it adds operators and parameters to the standard framework for epistemic logic, in order to provide a more realistic account of reasoning by Humans. Complexity is generally taken as a theoretical cost, to be justified by a gain in explanatory and predictive power. Here we have an unavoidable trade-off. Any framework for epistemic logic needs to strike a balance between two desiderata. The pull towards simplicity and idealization leads in the direction of Logons. The pull towards modeling realistic Humans can easily lead to conceptually gerrymandered frameworks, or to logics that are too weak to be of serious interest. Take Human Jill, who knows that \(\phi \wedge \psi \). What epistemic facts follow? She may fail to unpack her knowledge, so she need not know that \(\psi \). She may also not know that \(\chi \), although \(\chi \) turns out to be logically equivalent to the conjunction of \(\phi \) and \(\psi \).
The trade-off between simplification and realism overlaps that between description and prescription. Prospect theory was justified as a descriptive theory of rational decision, in opposition to the normative status of classical expected utility theory. We have a more nuanced stance with respect to the logic proposed above. We aim at a normative logical theory; but, one whose rational “ought”, unlike the “ought” of static epistemic logic, implies “can”.
To unpack: the mainstream approach in both static (S5) epistemic logic and choice theory is most commonly defended on the basis of its normative status. It tells us how rational agents ought to reason and act. The experimental deviations don’t threaten the effectiveness of this normative model; they do not, according to its apologists, contradict the claims on human rationality. They are merely attributed to unsystematic performance errors, momentary failures that do not say much about the rational behavior agents are actually capable of achieving (Cohen 1981; Stein 1996). This view is at times defended by drawing analogies with other disciplines, such as the use of frictionless planes in physics. With respect to the idealized models, the observed fallibility of agents is merely a kind of negligible cognitive friction. Besides, such models are claimed to serve an evaluative purpose with respect to the performance of imperfect human agents. However Humans fail, their ultimate goal should be to approximate the standard predicted by the mainstream proposals: the closer, the better.
We find these arguments unsatisfactory. The internal coherence of Human subjects (Stanovich and West 2000; Stenning and van Lambalgen 2008) shows that the errors are not just random and unsystematic slips in one’s reasoning. Nor are the idealized models of other disciplines suitable for an accurate analogy. Once scientists manage to account for more realistic assumptions and complex elements, their new models are often considered more reliable. This is not in agreement with the “as good as it gets” campaign adopted by proponents of the traditional “ought”. Even when Humans are asked to approximate the predictions of mainstream models of reasoning, the indeterminacy involved in what counts as a good approximation weakens the effectiveness of such choices of normative standards (Pollock 2006).Footnote 20
Forcing one to commit to models that are either merely descriptive, or representing omniscient agents, may be a false dilemma. Whereas the mainstream logical “ought” fails to imply “can”, one may be interested in investigating an “ought” that does: “it seems simply perverse to judge that subjects are doing a bad job of reasoning because they are not using a strategy that requires a brain the size of a blimp” (Stich 1990, p. 26). Actually, even a blimp may not be enough: Logons know or believe the infinitely many logical consequences of what they know or believe. But Humans’ available resources are not infinite (Cherniak 1986), and “become infinite” is a strange thing to ask of a finite mind.
In our approach, factual evidence can contribute in picking the appropriate normative model. Limitations in terms of time, memory, computational power, etc., are important in adjusting the rationality standard expected from the agents. Empirical data should be utilized in constructing the right normative model, e.g., by filling in the right parameters for how different logical inference rules can be resource-consuming. So we put forth our logic above as a better normative model: one delivering a can-implying “ought”. A finite and fallible, but rational agent ought to reason to the extent that, ceteris paribus, its limited time, memory, and computational power resources allow. No more can be asked without violating that implication, but also no less: “Be rational until, ceteris paribus, you run out of cognitive steam”.Footnote 21
7 Conclusions and Further Work
To sum up, we have built a system of dynamic epistemic logic that avoids the problem of logical omniscience, which has plagued standard static logical systems. Most importantly, it does so by taking on board a popular line of research in psychology of reasoning: dual-process theories. Our system includes two different kinds of dynamic operators, one responsible for the fast and effortless integration of information and one accounting for the slow and costly steps of deductive reasoning. In order to accommodate the respective actions, tools from DEL (plausibility models, more nuanced propositional attitudes) were combined with non-normal worlds semantics. We demonstrated that this framework successfully captures desirable properties of reasoning processes composed by both systems. In particular, we showed that phenomena that have been studied multiple times in the literature of various disciplines can be now formally treated in logical terms. Our exposition was finally furnished with a philosophical discussion on the contribution of this attempt, and more specifically, on its normative nature.
The model deals only with a fragment of the activities undertaken by the two systems. Apart from adding probabilistic reasoning for a more elaborate modeling of System 2, other directions of further work can be envisaged. First, the policy of upgrading with incoming information need not be unique. More conservative System 1 actions can be modeled, sensitive to the reliability of the source (van Benthem 2011). Second, one may combine our work with the ideas of van Benthem (2008b) and Velázquez-Quesada (2009), who discern implicit acts of observation (“bare seeing”) and explicit acts of observation (“conscious realization”). This distinction can fit in our framework by introducing additional actions representative of the two systems: the former kind is effortless and corresponds to System 1’s fast processing of incoming information. The latter kind is resource-consuming and corresponds to System 2 activities. Third, one may model higher-order reasoning, accounting for how the agent thinks over its own reasoning processes, learns or forgets inference rules, that in turn affect her deductive inferences. So far, we have focused on how the agent expands her factual information without delving into the progress of metareasoning. It seems that, in order to enrich the picture of reasoning run by System 2, we need to impose additional constraints on the model’s structure and define suitable actions of rule-based and effortful higher-order reasoning .
Notes
There are concerns regarding the use of the term “system”, raised by Stanovich himself. Kahneman (2011), pp. 27–29, observes that Systems 1 and 2 are not systems in some standard sense. We stick to the terminology, thinking of it as a label for families of processes. Such fictions are convenient for formal modeling at a certain level of abstraction.
The official dual process doctrine has it that the two systems engage in a range of further activities: System 1 deals with face recognition, orientation, perception, etc. System 2 deals with probabilistic estimates, the weighing of options, etc. An expansion of the model proposed below in the direction of probabilistic reasoning may be especially interesting, as our setting can be combined with a probabilistic framework and as dual process theories have been developed in relation to the new Bayesian approaches in the psychology of reasoning (Elqayam 2018); this is left for further work.
Plausibility orderings make for a qualitative representation of belief entrenchment and dispositions to belief revision. However, the DEL framework can also be extended to a quantitative setting, representing degrees of belief and embedding probabilistic insights: see van Benthem (2003), Kooi (2003), Baltag and Smets (2008a), van Benthem et al. (2009). Such a framework makes for a plausible basis for the aforementioned promised extension of our logic of fast and slow thinking to a probabilistic setting.
One can further define conditional belief in terms of the two forms of knowledge we discussed, i.e., both the strong and weaker notion, see van Ditmarsch et al. (2015); Baltag and Renne (2016). This is instrumental in capturing so-called static belief change, as it expresses what we believe conditional to some other piece of information.
Jago (2009) already used insights from AI for a logic of rule-based agents, whose beliefs expand via transitions between states obtained whenever a logical inference rule is fired. Velázquez-Quesada (2011) discerns implicit and explicit information and constructs logical systems in DEL that capture how deductive inferences enrich the agent’s explicitly held information. Building on Duc (1997), Rasmussen (2015) and Rasmussen and Bjerring (2018) track the agent’s deductive reasoning via dynamic operators that stand for the agent’s applications of inference rules. The latter work also has a semantics using non-normal worlds, and is the closest antecedent of our proposal below.
One can, in principle, build dynamic models with rules representing various kinds of rule-based System 2 reasoning. For the purposes of this paper, however, we will take R as comprising just rules of elementary logic, such as Modus Ponens or Conjunction Introduction.
The idea of such operators comes from Rasmussen (2015), Rasmussen and Bjerring (2018), themselves drawing on Duc (1997). We should note here that, as clarified by recent literature (Bago and De Neys 2017; Ball and Thompson 2018), also System 1 is capable of detecting and appreciating simple logical forms. The key twofold difference between System 1 and System 2 in this respect is that the latter, but not the former, can choose which logical rules to apply, and must pay a cognitive cost for it. Thanks to an anonymous Referee for pressing us to clarify this point.
We will assume that worlds are unique valuation-wise: the valuation function can be taken as \(V{:}{=} V_p \cup V_i\), where \(V_p\) and \(V_i\), taking care of possible and impossible worlds respectively, are injective. This serves simplicity: we avoid a multiplicity of worlds unnecessary for our purposes.
To determine \(ord^{\psi \Uparrow }\), first consider the relation \(\ge \) that can be derived from it. As an auxiliary step take: \(\ge ^{\psi \Uparrow } = (\ge \cap (W \times [[\psi ]])) \cup (\ge \cap ( \overline{[[\psi ]]} \times W )) \cup ( \sim \cap (\overline{[[\psi ]]} \times [[\psi ]]))\), that is the familiar re-arrangement due to a radical upgrade as found in DEL.
Conditions 2 and 3 guarantee that there is no expansion that violates MC. In other words, “refining” a world that violates 2 or 3 amounts not to finding an expanded world in terms of \(R_k\), but to eliminating it altogether once the application of the rule takes place. Therefore, in these cases, there should be no \(R_k\)-expansion.
As emphasized before, in certain cases there are no \(R_k\)-expansions, so it might be that a world is eliminated without being replaced by one that preserves its propositional truths. This intuitively corresponds to those cases where the agent uncovers an inconsistency, realizing the explicit contradiction underlying it by means of reasoning, and therefore drops it. Thanks to an anonymous Referee whose comments helped in clarifying this.
Agents can, of course, use methods like note-taking, or resort to other external devices, for the offloading of cognitive resources such as memory. In terms of our quantitative assignments, this would entail an increase in capacity. This can be easily achieved by the introduction of actions that increase the value of \( cp \). It does not affect the crucial aspect hereby captured: the resource-consumption caused by System 2.
This is in fact just an example of framing as discussed in Kahneman (2011). More specifically, it has been shown that subjects are risk-averse when an option is presented in terms of gains and risk-seeking when presented in terms of losses.
But, recall the aforementioned capacity of System 1, of automatically appreciating simple logical forms of reasoning, in contrast to the tendency to endorse believed conclusions: see Bago and De Neys (2017). Our semantics does not prohibit System 1’s having logical cues: if there are any logical forms appreciated by it, they can be encoded in the plausibility model.
“You are in a restaurant with your parents, and you have ordered three dishes: Fish, Meat, and Vegetarian. Now a new waiter comes back from the kitchen with three dishes. What will happen?” (van Benthem 2008a).
Thicker borders of nodes are used to denote possible worlds. Here, we took CI arrows to be reflexive and wrote down only the conjunctions obtained between atoms to increase the readability of the figure. It need not be so, as applications of CI could have been informative for this given scenario.
We notice that Hintikka, who introduced standard epistemic and doxastic logics, did not presuppose a defense of his systems due to normativity: “Logical truths are not truths which logic forces on us; they are not necessary truths in the sense of being unavoidable. They are not truths we must know, but truths which we can know without making use of any factual information. [...] The fact that the so-called laws of logic are not ‘laws of thought’ in the sense of natural laws seems to be generally admitted nowadays. Yet the laws of logic are not laws of thought in the sense of commands, either, except perhaps laws of the sharpest possible thought. Given a number of premises, logic does not tell us what conclusions we ought to draw from them; it merely tells us what conclusions we may draw from them—if we wish and we are clever enough.”(Hintikka 1962, p. 37).
The ceteris paribus parameter matters. What amount of cognitive resources ought to be allocated to reasoning tasks is heavily context-dependent: one should not be asked to deploy cognitive resources to perform logical deductions when this would make it dangerous to thoughtlessly cross a busy street.
References
Alchourrón, C. E., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. The Journal of Symbolic Logic, 50(2), 510–530.
Bago, B., & De Neys, W. (2017). Fast logic? Examining the time course assumption of dual process theory. Cognition, 158, 90–109.
Balbiani, P., Fernández-Duque, D., & Lorini, E. (2016). A logical theory of belief dynamics for resource-bounded agents. In Proceedings of the 2016 international conference on autonomous agents & multiagent systems, AAMAS’16 (pp. 644–652). Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems.
Ball, L. J., & Thompson, V. A. (2018). Belief bias and reasoning. In L. Ball & V. Thompson (Eds.), The Routledge international handbook of thinking and reasoning (pp. 16–35). Abingdon: Routledge.
Baltag, A., & Moss, L. S. (2004). Logics for epistemic programs. Synthese, 139(2), 165–224.
Baltag, A., Moss, L. S., & Solecki, S. (1998). The logic of public announcements, common knowledge, and private suspicions. In Proceedings of the 7th conference on theoretical aspects of rationality and knowledge, TARK’98 (pp. 43–56). San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
Baltag, A., & Renne, B. (2016). Dynamic epistemic logic. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (winter 2016 ed.). Stanford: Metaphysics Research Lab, Stanford University.
Baltag, A., & Smets, S. (2008a). Probabilistic dynamic belief revision. Synthese, 165, 179–202.
Baltag, A., & Smets, S. (2008b). A qualitative theory of dynamic interactive belief revision. Logic and the Foundations of Game and Decision Theory, Texts in Logic and Games, 3, 9–58.
Baltag, A., & Smets, S. (2011). Keep changing your beliefs, aiming for the truth. Erkenntnis, 75(2), 255–270.
Baltag, A., & Smets, S. (2013). Protocols for belief merge: Reaching agreement via communication. Logic Journal of the IGPL, 21(3), 468–487.
Berto, F. (2012). Impossible worlds. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (winter 2016 ed.). http://plato.stanford.edu/archives/win2012/entries/impossible-worlds/. Accessed 1 May 2018.
Board, O. (2004). Dynamic interactive epistemology. Games and Economic Behaviour, 49, 49–80.
Byrne, R. (1983). Suppressing valid inferences with conditionals. Cognition, 31, 61–83.
Cherniak, C. (1986). Minimal rationality. Cambridge: Bradford Book, MIT Press.
Cohen, L. J. (1981). Can human irrationality be experimentally demonstrated? Behavioral and Brain Sciences, 4(3), 317–331.
Cosmides, L. (1989). The logic of social exchange. Cognition, 31, 187–276.
Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24(1), 87–114.
Duc, H. N. (1997). Reasoning about rational, but not logically omniscient, agents. Journal of Logic and Computation, 7(5), 633.
Elqayam, S. (2018). The new paradigm in psychology of reasoning. In L. Ball & V. Thompson (Eds.), The Routledge international handbook of thinking and reasoning (pp. 130–50). Abingdon: Routledge.
Evans, J. (2018). Dual process theories. In L. Ball & V. Thompson (Eds.), The Routledge international handbook of thinking and reasoning (pp. 151–64). Abingdon: Routledge.
Evans, J. S. B. T. (1989). Bias in human reasoning: Causes and consequences. Hillsdale, NJ, US: Lawrence Erlbaum Associates Inc.
Evans, J. S. B. T. (2003). In two minds: Dual-process accounts of reasoning. Trends in Cognitive Sciences, 7(10), 454–459.
Evans, J. S. B. T., & Over, D. E. (1996). Rationality and reasoning. Oxford, England: Psychology/Erlbaum (Uk) Taylor & Fr.
Fagin, R., & Halpern, J. Y. (1987). Belief, awareness, and limited reasoning. Artificial Intelligence, 34(1), 39–76.
Fagin, R., Halpern, J. Y., Moses, Y., & Vardi, M. Y. (1995). Reasoning about knowledge. Cambridge: MIT Press.
Floridi, L. (2005). Is information meaningful data? Philosophy and Phenomenological Research, 70(2), 351–70.
Gigerenzer, G. (1996). On narrow norms and vague heuristics: A reply to Kahneman and Tversky. Psychological Review, 103(3), 592–596.
Grove, A. (1988). Two modellings for theory change. Journal of Philosophical Logic, 17(2), 157–170.
Halpern, J. Y., & Pucella, R. (2011). Dealing with logical omniscience. Artificial Intelligence, 175(1), 220–235.
Hintikka, J. (1962). Knowledge and belief: An introduction to the logic of the two notions. Ithaca, NY: Cornell University Press.
Hintikka, J. (1975). Impossible possible worlds vindicated. Journal of Philosophical Logic, 4(4), 475–484.
Jago, M. (2009). Epistemic logic for rule-based agents. Journal of Logic, Language and Information, 18(1), 131–158.
Jago, M. (2014). The impossible: An essay on hyperintensionality. Oxford: Oxford University Press.
Johnson-Laird, P. N., Byrne, R. M., & Schaeken, W. (1992). Propositional reasoning by model. Psychological Review, 99(3), 418–439.
Kahneman, D. (1973). Attention and effort. Upper Saddle River: Prentice-Hall.
Kahneman, D. (2011). Thinking, fast and slow. New York: Farrar, Straus and Giroux.
Kahneman, D., & Beatty, J. (1967). Pupillary responses in a pitch-discrimination task. Perception & Psychophysics, 2(3), 101–105.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291.
Kahneman, D., & Tversky, A. (1983). Can irrationality be intelligently discussed? Behavioral and Brain Sciences, 6(3), 509–510.
Kahneman, D., & Tversky, A. (1996). On the reality of cognitive illusions. Psychological Review, 103(3), 582–591.
Kiourti, I. (2010). Real impossible worlds: The bounds of possibility. Ph.D. thesis, University of St Andrews.
Kooi, B. (2003). Probabilistic dynamic epistemic logic. Journal of Logic, Language and Information, 12, 381–408.
Lehrer, K. (2000). Theory of knowledge. Boulder: Westview Press.
Lehrer, K., & Paxson, T. (1969). Knowledge: Undefeated justified true belief. Journal of Philosophy, 66(8), 225–237.
Liu, F. (2008). Changing for the better: Preference dynamics and agent diversity. Ph.D. thesis, Institute for Logic, Language and Computation (ILLC), Universiteit van Amsterdam (UvA), Amsterdam, The Netherlands. ILLC dissertation series DS-2008-02.
Liu, F. (2011). Reasoning about preference dynamics. Berlin: Springer.
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81–97.
Moses, Y. (1988). Resource-bounded knowledge. In Proceedings of the 2nd conference on theoretical aspects of reasoning about knowledge, TARK’88 (pp. 261–275). San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
Nolan, D. (2013). Impossible worlds. Philosophy Compass, 8, 360–372.
Parikh, R. (2008). Sentences, belief and logical omniscience, or what does deduction tell us? The Review of Symbolic Logic, 1, 459–476.
Pollock, J. L. (2006). Thinking about acting: Logical foundations for rational decision making. Oxford: Oxford University Press.
Priest, G. (2001). An introduction to non-classical logic, 2nd ed. 2008. Cambridge: Cambridge University Press.
Rantala, V. (1982). Impossible worlds semantics and logical omniscience. Acta Philosophica Fennica, 35, 18–24.
Rasmussen, M. S. (2015). Dynamic epistemic logic and logical omniscience. Logic and Logical Philosophy, 24, 377–399.
Rasmussen, M. S., & Bjerring, J. (2018). A dynamic solution to the problem of logical omniscience. Journal of Philosophical Logic,. https://doi.org/10.1007/s10992-018-9473-2.
Rijmen, F., & De Boeck, P. (2001). Propositional reasoning: The differential contribution of “rules” to the difficulty of complex reasoning problems. Memory & Cognition, 29(1), 165–175.
Rips, L. J. (1994). The psychology of proof: Deductive reasoning in human thinking. Cambridge, MA, USA: MIT Press.
Rott, H. (2004). Stability, strength and sensitivity: Converting belief into knowledge. Erkenntnis, 61(2–3), 469–493.
Sears, C. R., & Pylyshyn, Z. (2000). Multiple object tracking and attentional processing. Canadian Journal of Experimental Psychology, 54, 1–14.
Stalnaker, R. (2006). On logics of knowledge and belief. Philosophical Studies, 128(1), 169–199.
Stanovich, K. E., & West, R. F. (2000). Individual differences in reasoning: Implications for the rationality debate? Behavioral and Brain Sciences, 23(5), 645–665.
Stein, E. (1996). Without good reason: The rationality debate in philosophy and cognitive science. Oxford: Clarendon Press.
Stenning, K., & van Lambalgen, M. (2008). Human reasoning and cognitive science. Boston, USA: MIT Press.
Stich, S. (1990). The fragmentation of reason: Preface to a pragmatic theory of cognitive evaluation. Cambridge: Bradford Books, MIT Press.
Thaler, R., & Sunstein, C. (2008). Nudge: Improving decisions about health, wealth, and happiness. New Haven: Yale University Press.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131.
Tversky, A., & Kahneman, D. (1985). The framing of decisions and the psychology of choice (pp. 107–129). Berlin: Springer.
van Benthem, J. (2003). Conditional probability meets update logic. Journal of Logic, Language and Information, 12, 409–421.
van Benthem, J. (2007). Dynamic logic for belief revision. Journal of Applied Non-Classical Logics, 17(2), 129–155.
van Benthem, J. (2008a). Logic and reasoning: Do the facts matter? Studia Logica: An International Journal for Symbolic Logic, 88(1), 67–84.
van Benthem, J. (2008b). Merging observation and access in dynamic logic. Journal of Logic Studies, 1, 1–17.
van Benthem, J. (2011). Logical dynamics of information and interaction. Cambridge: Cambridge University Press.
van Benthem, J., Gerbrandy, J., & Kooi, B. (2009). Dynamic update with probabilities. Studia Logica, 93, 67–96.
van Ditmarsch, H., Halpern, J., van der Hoek, W., & Kooi, B. (2015). Handbook of epistemic logic. London: College Publications. College.
van Ditmarsch, H., van der Hoek, W., & Kooi, B. (2007). Dynamic epistemic logic (1st ed.). Berlin: Springer.
Velázquez-Quesada, F. R. (2009). Inference and update. Synthese, 169(2), 283–300.
Velázquez-Quesada, F. R. (2011). Small steps in dynamics of information. Ph.D. thesis, Institute for Logic, Language and Computation (ILLC), Universiteit van Amsterdam (UvA), Amsterdam, The Netherlands. ILLC dissertation series DS-2011-02.
Wansing, H. (1990). A general possible worlds framework for reasoning about knowledge and belief. Studia Logica, 49(4), 523–539.
Wason, P. (1968). Reasoning about a rule. Quarterly Journal of Experimental Psychology, 20, 273–81.
Xu, Y., & Chun, M. M. (2009). Selecting and perceiving multiple visual objects. Trends in Cognitive Sciences, 13(4), 167–174.
Acknowledgements
Material relevant for this paper was presented at the Logic in the Wild workshop in Gent, at the Logic and Interactive Rationality seminar and at the Logic of Conceivability seminar in Amsterdam. We are grateful to the audiences as well as to two anonymous referees of this Journal for helpful comments and remarks. Anthia Solaki’s research is funded by the Netherlands Organisation for Scientific Research (NWO) ‘PhD in the Humanities’ programme, Grant No. 322-20-018. Franz Berto’s research is funded by the European Research Council (ERC CoG) ‘The Logic of Conceivability’ Project, Grant No. 681404.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Solaki, A., Berto, F. & Smets, S. The Logic of Fast and Slow Thinking. Erkenn 86, 733–762 (2021). https://doi.org/10.1007/s10670-019-00128-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-019-00128-z





