Alternatives to Histories? Employing a Local Notion of Modal Consistency in Branching Theories

Abstract

Branching theories are popular frameworks for modeling objective indeterminism in the form of a future of open possibilities. In such theories, the notion of a history plays a crucial role: it is both a basic ingredient in the axiomatic definition of the framework, and it is used as a parameter of truth in semantics for languages with a future tense. Furthermore, histories—complete possible courses of events—ground the notion of modal consistency: a set of events is modally consistent iff there is a history containing that set. We will explain these roles of histories and highlight some critical aspects having to do with the fact that histories are global and, in a relevant sense, “big” objects. The notion of modal consistency, on the other hand, has both local and global aspects. We ask in how far a local notion of modal consistency can serve as an alternative to the common uses of histories, and work out two recent approaches to alternatives to histories. Combining these approaches, we develop a novel semantics for branching time.

1 Introduction

The idea of an open future is deeply ingrained in many of our everyday concepts and practices. Hope, regret and arguably even the notion of an action presuppose the openness of the future, and betting and deciding make no real sense without open future possibilities. Even concepts having no practical import, such as many concepts of natural kinds, rely on the notion of future possibilities, since kinds of things are usually characterized via dispositions and potentialities.

Saying this may already be contentious, given a philosophical environment in which Lewis’s project of Humean supervenience is held in high esteem. It will be even more contentious to say the next thing: that the possibilities involved have to be interpreted objectively—as possibilities grounded in the way our world is like, independently of us—, and not as mere epistemic possibilities—grounded in the way we picture the world, be it in everyday talk or via scientific theories.

For present purposes it will be enough to acknowledge that the notion of an open future makes initial sense, and that it has its uses, whatever its ultimate metaphysical standing. It certainly is in need of elucidation.

Arguably, the best way to tackle the notion of an open future is via theories of branching histories—theories that take the everyday notion of “one present moment, many possibilities in the future” at face value and accordingly picture the world as a branching tree of possible courses of events, or via similar, technically more involved models. The hope is that formal branching theories can be both “proto-humanistic” and “proto-scientific” (Belnap 2007), thereby doing justice to the two “images of man” that Sellars (1963) introduced: the “manifest” image of everyday life and the “scientific” image that we create through our scientific practices.

Again, there is a big debate about the virtues of theories of branching histories, with respect to which we wish to remain officially neutral—in order to motivate our enterprise, it will be enough to grant that such theories make initial sense as attempts to spell out the notion of an open future, and to acknowledge that there are well developed, mathematically precise formal frameworks for branching histories.

There are two main strands of branching theories that have been discussed in metaphysics, semantics and philosophy of science to at least some extent: the Prior/Thomason theory of branching time (Prior 1967; Thomason 1970), and Belnap’s theory of branching space-times (BST; Belnap 1992). In both these theories, a crucial role is played by the notion of an (alternative) history: given a mathematical structure representing our world (with its thisworldly, but incompatible open futures of possibility), histories are singled out as maximally consistent substructures, in some modal sense of consistency.¹ Histories play at least two important roles in branching theories: (1) They are often used in the formulation of the axiomatic basis of a branching theory itself, e.g., in Belnap’s prior choice principle (see Sect. 2.2 below); (2) they play a crucial role in the semantics for the future tense that can be defined on the basis of such theories.

The present paper is concerned with developing some alternatives to the use of histories. This enterprise is motivated by the fact that even though histories are not possible worlds, they are still large structures with a global ring to them: given a branching structure, its histories normally extend as far, both spatially and temporally, as the structure itself. The technical employment of histories, however, often only uses local aspects of histories—in some non-technical sense of locality to be clarified—, and epistemic access to whole histories of our world is impossible. The paper thus continues a search for appropriate small structures for BST that was begun in papers by Placek (2011) and Müller (2010).

We start by introducing the two mentioned relevant formal branching theories, branching time and branching space-times, and their respective history definitions, in Sect. 2. The worries alluded to above will be spelled out in Sect. 3, where we look in more detail at the notion of modal consistency that stands behind the definition of a history in the two frameworks. We will try to explicate philosophical assumptions about modal consistency with a view to possible generalizations. Such generalizations are the topic of Sect. 4. We will work out two recent approaches: consistency in terms of possible continuations, as proposed by Placek (2011), and consistency in terms of sets of indeterministic transitions. Both approaches in our view provide promising local alternatives to the usual employment of histories, and their combination leads to a novel semantics for branching time.

2 Histories in Branching Theories

We start by discussing the case of branching time (Sect. 2.1) before considering the more complex case of branching space-times (Sect. 2.2). We will develop branching time in a way that makes the extension to branching space-times go smoothly.

2.1 Histories in Branching Time

The notion of an open future of possibilities brings together a temporal notion—the future—with a modal one—possibility. Interaction between time and modality is a common fact of everyday life; witness “no use crying over spilt milk”: before the spilling, we assume it was possible to prevent it, but now it isn’t any more, and we have to move on. Living, we think, means making use of some possibilities and letting others go by; and they don’t come back.

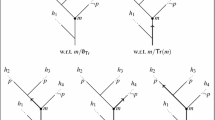
This picture—for what it’s worth—is well captured by the idea of the world (our world, the world we live in) as a branching tree of possibilities, such as the one pictured in Fig. 1.

Fig. 1

A branching tree of possibilities: rain or no rain at 4 o’clock

This image is explored in many works of fiction, such as the 1993 French movies Smoking/No Smoking, but it has also been worked out in terms of a logical theory called branching time (BT). Prior (1967, 122–127), following a suggestion by Kripke dating from 1958, gives a brief description of the main ideas; Thomason (1970) has the first fully worked-out system, which he uses in the context of supervaluationist semantics—an idea that is however independent of BT itself.

Technically, one defines the class of branching trees—BT-structures—as follows:

Definition 1 (BT-structure)

A BT-structure is a non-empty partial order of moments $\langle M,\leq\rangle$ (i.e., a nonempty set M with a transitive and antisymmetric relation ≤ ) such that

• (1) there is no backward branching, i.e., for all $m,m',m''\in M$ for which m′ < m and m′′ < m, we have either m′ ≤ m′′ or m′′ ≤ m′;

• (2) any elements m and m′ have a greatest common lower bound in M;

• (3) M has no maximal elements, i.e., for any $m\in M$, there is some $m'\in M$ s.t. m < m′.

The strict < order corresponding to ≤, used in clause (1), is defined, as usual, via

$$ m<m' \Leftrightarrow_{df} (m\leq m' \, \& \, m\neq m'). $$

Of the three mentioned conditions, (1) is standard, (2) and (3) are optional, but are included here for reasons of continuity with the case of branching space-times that is the subject of Sect. 2.2.

A further condition (4), which is especially useful if one wants to identify clock times across incompatible alternatives (e.g., rain or no rain at 4 o’clock, as in Fig. 1), already relies on the notion of a history, as does the use of BT-structures (also called BT-frames) in semantics.² Histories are taken to be complete possible courses of events: a history has to be (a) modally consistent in the sense of being possible as a whole (no event in a history excluding the occurrence of any other), and (b) maximally so. In BT the definition is as follows:

Definition 2 (History in BT)

Given a BT-structure $\langle M,\leq\rangle,$ a set $h\subseteq M$ is a history iff h is a maximal linear subset, or a maximal chain, in M, i.e., a subset h that is linearly ordered (for any $m,m'\in h,$ either m′ ≤ m or m < m′) and such that no proper superset $h'\,\supsetneq \,h$ has that feature.

Thus, modal consistency (a) is spelled out in terms of order-relatedness: a subset of M is modally consistent iff it is a chain, i.e., if any two of its members are order-related. This makes intuitive sense: in a branching tree of open future possibilities, you cannot consistently mix two incompatible futures after they have branched, so that consistency requires linearity. For example, events a and b in Fig. 1 are not order related, so there is no history containing them both. If there is only one history (which would be the case in a deterministic world), all of M is linearly ordered.

Maximality (b) is spelled out in the usual set-theoretic sense: histories are modally consistent and such that no proper superset is consistent. If you add even a single moment to a history, you will have added in a moment that is not order-related to all the others; the extended set then contains an incomparable and thus, inconsistent pair of moments.

In terms of histories, condition (2) of Definition 1 above says that all histories have a non-empty intersection, and that that intersection contains a greatest element. By (1), histories are downward closed, i.e., if $m\in h$ and m′ ≤ m, then $m'\in h.$

We can now also formulate the (optional) condition (4) mentioned above, which allows us to define clock times via a partition of M:

Optional Addendum to Definition 1

• (4) All histories in M are order-isomorphic, i.e., if h, h′ are histories in M, then there is a bijective mapping $f:h\rightarrow h'$ s.t. for all $m,m'\in h,$ we have m ≤ m′ iff f(m) ≤ f(m′). Often it is useful to require that all histories in M are order-isomorphic to the real numbers, ${\mathbb{R}};$ this further strengthens the parallel between BT and BST, as models of BST are required to be continuous. We will assume, in addition, that there is a function ${Time: M\rightarrow \mathbb{R}}$ that gives a clock time Time(m) for each moment $m\in M.$

This condition makes essential use of the history definition, showing that the notion of a history in BT can play an important role in the axiomatics. The condition also highlights the motivation for calling elements $m\in M$ “moments” and not “times”: many different (in fact, modally incompatible) moments can have the same clock time.

Above we also mentioned a second important use of histories: they function as parameters of truth in the semantics of the future tense. (Again, contentious issues are lurking, this time connected with the idea of a so-called Thin Red Line which makes possible an alternative semantics for the future tense; part of the debate is whether such a semantics still captures indeterminism. See Belnap et al. (2001, Ch. 6B, 8D), Øhrstrøm (2009) and Øhrstrøm and Hasle (2011) for discussion.)

From now on we will be using not just BT-structures, but also models built upon BT-structures: a BT-model ${\mathfrak{M}}=\langle M,\leq,v\rangle$ is a BT-structure $\langle M,\leq\rangle$ together with a valuation v that is invoked in the truth conditions for atomic sentences.³ In case condition (4) is fulfilled, we will be dealing with models ${\mathfrak{M}}=\langle {M,\leq, Time ,v}\rangle,$ where Time is a clock-time function as discussed above.

There is a problem about defining a future tense operator F based on such models, intimately related to the time-honored problem of future contingents (see, e.g., Øhrstrøm and Hasle 2011). Speaking from within the branching tree—at the moment of an utterance context, m _C —there are usually many histories passing through that moment, many possible futures. How do we decide whether a sentence referring to the future is true or not? An objective understanding of the openness of the future demands that none of the histories be singled out or marked as “the real future”, in contradistinction to all the others: we have to be egalitarians with respect to future possibilities if we want to retain objective indeterminism.⁴ This means that a context of utterance cannot supply a “true future of the utterance”—all possible futures have to be treated on a par. But how do we define truth conditions then? One option, which Prior (1967, 128–134) called “Peircean”, would be to quantify over all available histories universally. A sentence of the form Fϕ is then taken to be true at some m iff on all histories passing through m (in all possible futures of m) there is a future moment at which ϕ is true. This however leads to awkward results: truth thereby coincides with settled truth; “it will be” is given the sense of “it is now unpreventable that it will be”—which does not mesh well with common uses of the future tense in common discourse.⁵

The innovative idea behind the so-called Ockhamist semantics for the future tense in BT is to evaluate a sentence not just with respect to a model ${\mathfrak{M}}$ and a given moment m in a BT-structure, but also with respect to a given history h through that moment. (It is customary to write such a moment-history pair as “m/h”, indicating the presupposition that $m\in h.$) The past (“P”) and future tense (“F”) are then taken to move evaluation along that given history, backward (for the past) or forward (for the future), in accordance with the following semantic rules that resemble the tense logic for linear time:

• ${\mathfrak{M}},m/h \models P\phi$ iff there is some $m'\in h$ for which m′ < m and ${\mathfrak{M}},m'/h \models\phi;$

• ${\mathfrak{M}},m/h \models F\phi$ iff there is some $m'\in h$ for which m < m′ and ${\mathfrak{M}},m'/h \models\phi.$

While the history is superfluous in the clause for the past tense (given past linearity of BT-structures; see clause (1) of Definition 1), the history is really needed for definiteness of the clause for F.⁶

We will not embark on a more detailed discussion of Ockhamist semantics here. (See, e.g., Belnap (2002a), Øhrstrøm (2009) and Øhrstrøm and Hasle (2011) for a discussion of some controversial issues; MacFarlane (2013, Ch. 9) gives a detailed overview.) The main point for this paper is that in Ockhamist semantics (as well as in many of its rivals), histories are needed as parameters of truth in the semantic clauses of the language.

We will leave it at that for now: we have shown that histories—maximal modally consistent sets in a BT-structure, where consistency is spelled out as linearity—play an important role for the theory of branching time. The picture is similar, but also somewhat more intricate, in the case of branching space-times.

2.2 Histories in Branching Space-Times

While branching time allows one to capture some important aspects of the interaction between time and modality, it leaves out spatial relations among events. Indeed, a “moment” in a BT-structure, if interpreted realistically, has to be a “super-event” (Thomson 1977) spanning all of space simultaneously. This is an idea that does not mesh well with basic insights of relativity theory, according to which there is no fact of the matter as to whether distant (technically: space-like related) events are simultaneous or not. Furthermore, it is hard, in BT, to spell out how two things happening at the same moment can be either dependent (my coin’s landing heads, the coin making a sound when landing) or independent (my coin’s landing heads, your coin’s landing heads). More structure is needed; a plausible candidate for such additional structure is the space-time of relativity theory.

The big question is how to keep incorporating time (now: space-time) and modality in a single formal structure. A useful rewording of that question is: What is a history in BST, i.e., a maximal modally consistent set? Again this can be split up into two subquestions. We can safely assume that the maximality of a history can again be spelled out in set-theoretic terms, as in the case of BT. The difficult question that remains is: What does the notion of modal consistency come to?

Again, a clue from the single history case may be helpful: if there is just one history, the whole structure should be a single space-time. But how should that idea be captured formally? How can we characterize the unity of a space-time?

Belnap’s crucial insight in working out BST (Belnap 1992) was that one could keep the basic structure of a partial ordering of (not moments, but smaller, spatially local) possible point events in place and use a rather intuitive notion of modal consistency motivated by a consideration of perspective: intuitively, events e ₁ and e ₂ are modally compatible (can co-occur in one course of events) iff there is a perspective (given by a third event f) from which one can say that both events have occurred. Formally, two events e ₁ and e ₂ are modally compatible iff they have a common upper bound, i.e., iff there is some f for which e ₁ ≤ f and e ₂ ≤ f. Just like in branching time, the fixedness of the past in contrast to the openness of the future is the key to understanding modal consistency.

BST-structures are thus partial orderings $\langle W,\leq\rangle$ (fulfilling certain additional conditions to be spelled out below), and modally consistent subsets A of W are such that for any $e_1,e_2\in A$ there is $f\in A$ for which e ₁ ≤ f and e ₂ ≤ f. Such sets are called (upward) directed. In a directed set, for any two of its members the set itself incorporates a perspective from which these two members lie in the (causal) past.

Adding in the set-theoretic notion of maximality, the history definition of BST is thus the following:

Definition 3 (History in BST)

A history in a BST-structure $\langle W,\leq\rangle$ is a subset $h\subseteq W$ that is upward directed and maximally so, i.e., no proper superset of which is directed.

It remains to spell out what a BST-structure is. In that definition, histories play an important role in a number of places. We follow Belnap in calling a branching structure—in this case, a BST-structure—“our world”, or OW: it incorporates non-trivial, thisworldly modality.

Definition 4 (BST-structure)

A non-empty partial order $OW=\langle W,\leq\rangle$ is a BST-structure iff

• (1) OW has no maxima (i.e., for any $e\in W$ there is some $f\in W$ s.t. e < f);

• (2) each lower bounded chain (i.e., a linearly ordered subset $C\subseteq W$ for which there is some $e\in W$ s.t. for any $f\in C$, e ≤ f) has an infimum (a greatest lower bound) in W;

• (3) for each upper bounded chain $C\subseteq W$ and for each history $h\subseteq W,$ if $C\subseteq h,$ then C has a supremum-in-h.

• (4) (prior choice principle) if h ₁,h ₂ are histories and C is a lower bounded chain in h ₁ − h ₂ (i.e., a lower bounded chain wholly in h ₁ no element of which lies in h ₂), then there is some $e\in h_1\cap h_2$ s.t. e < C (i.e., for all $f\in C,$ e < f) and such that e is maximal in h ₁ ∩ h ₂.

In this definition, the notion of a history plays an essential role in clauses (3) and (4).⁷

This role of histories parallels the—less important—role that histories play in the definition of (specific types of) BT-structures. The parallel also holds for the second role of the history parameter in BT, viz., as a parameter of truth in semantic clauses. While we will not spell out a semantics for a language based on BST, it should be clear that the reasoning for the BT case applies as well: a context of utterance can specify a number of relevant parameters of truth—certainly the utterance event of the context, e _C , itself, and possibly also a rest frame grounding a notion of simultaneity—, but on pain of denying the objectivity of an open future, it cannot single out as “the real future” one of the histories through e _C rather than some other.

So we see that the notion of a history, both in BT and in BST, plays at least two important roles: as a building block for the definition of certain relevant structures, and as a parameter for semantic theory. We will now move on to a more detailed discussion of modal consistency, which will give rise to some worries about the mentioned uses of histories.

3 Modal Consistency

Above we have laid out how an intuitive notion of modal consistency is spelled out in order-theoretic terms in the two branching theories considered here, BT and BST. The respective history definitions lead to “big” histories in the sense that they span a complete possible temporal development within the branching tree of possibilities (in BT), or a whole space-time (in BST). That is, histories are “big” relative to the branching order in which they are defined. In what follows, we will assume that that branching order is meant to cover all of our (indeterministic) world, and so we will be speaking of histories as whole temporal courses of events from the big bang until after the death of the sun (in BT), or as whole space-times (in BST). Of course, a history cannot be bigger than the branching order in which it is defined—the important point is that it is global with respect to that ordering. There is however also a more “local”, generalized notion of modal consistency. We will motivate that notion here with a view towards technical considerations that will be the subject of Sect. 4.

3.1 Ways of Specifying Modal Consistency

It will be good to first discuss some assumptions about the notion of modal consistency that we are working with. For this we will not presuppose that we are working with a theory based on partial orders (such as BT and BST), but admit also more general resources. There appear to be three ways to spell out modal consistency.

• 1. First, modal consistency can be specified explicitly. When we map out possibilities in the form of stories, for example, we will normally describe the individual options directly, thereby (implictly) proclaiming them to be individually modally consistent. If I deliberate where to go next weekend, for example, I will map out individual options separately (to a very limited degree of detail of course), and there is no need for me to “carve up” any given larger structure containing all these possibilities into individual, consistent scenarios. Technically, option (1) amounts to treating histories as basic entities.

• 2. Second, it can be helpful to tackle the notion of modal consistency via its negation, modal inconsistency. The idea here is that if we have a full list of possible sources of modal inconsistency, we thereby have a guarantee that any scenario we specify that avoids the pitfalls, is thereby already modally consistent. One clear source of modal inconsistency is running together different “local” alternatives—in a sense to be specified. For example, it cannot be that the same thing has incompatible properties, like being red all over and being green all over, at the same time. Any scenario that describes things in such an inconsistent way is thereby itself inconsistent. A similar principle works against combinations of things that by their nature cannot be in one scenario together; not all things can coexist. It seems difficult, however, to spell this out in a perspicuous formal way in full generality.

  For a formally clear principle in the vicinity of these considerations, consider the following: if there are alternatives to a certain happening (such as my walking to the market today, when I could have stayed at home, or taken the bike), then a consistent scenario cannot contain more than one of them. If it runs together different concrete alternatives, we may call a scenario blatantly inconsistent, a clear sign of modal inconsistency. Furthermore, while a scenario may not be blatantly inconsistent the way it is described, we may know that filling in gaps in the description will lead to blatant inconsistency. As mentioned, the hope behind this second approach is that one may be able to list all ways in which inconsistencies can arise, and thereby derive a positive definition of modal consistency indirectly.

• 3. A third approach is to take the mentioned formal definitions of modal consistency and extend them by relaxing certain assumptions. It is hard to see what this should amount to in the case of BT, but there is a clear motivation for wanting to relax BST’s history definition specified in terms of directedness.

3.2 A First Reason for Relaxing BST’s History Definition

The definition of a history as a maximal directed set in BST has the following trivial consequence: if in a BST-structure $\langle W,\leq\rangle$ there is only a single history, then that history—which is equal to all of W—must itself be directed. This is a limitation of BST: even in the (deterministic) case of just a single history, that history is forced to be a directed set. It seems clear, however, that there are modally consistent scenarios that do not correspond to a directed set of space-time points. We can think of two classes of examples here. First, there are space-times that are not time-orientable, i.e., for which we cannot define a global ordering.⁸ Such an ordering is however needed in the definition of a directed set. Thus, for non-time-orientable space-times, the BST approach to modal consistency is inappropriate. Second, even if we limit attention to standard examples of time-orientable space-times, in describing a scenario we may restrict attention to a (small) region of space-time rather than all of space-time. We will then want to be able to say that there are, e.g., two different (modally incompatible) alternatives for the region in question, each of which is itself modally consistent. Using directedness as the criterion of consistency will not work in such a case unless the region is itself directed,⁹ or consistency of an alternative for the region is treated as a merely derivative concept. It seems therefore that the BST definition of modal consistency enforces too strict a global constraint here, and that a more local, relaxed definition of modal consistency should fare better.

One may even have the following worry: Given that we may want to depict a scenario in a chosen geometrical region of space-time, may not the BST definition of a history wrongly identify “additional” histories, i.e., mistake aspects of geometrical shape for modal branching? Here we have a somewhat comforting (though rather limited) result precluding the creation of spurious histories.

By Minkowski space-time we mean the following:

Definition 5 (ordered n-dimensional Minkowski space-time)

For n ≥ 2, the n-dimensional Minkowski space-time M ⁿ is the n-dimensional Euclidean space ${\mathbb{R}^n}$ (with its usual topology) together with the (causal) ordering ≤ defined by¹⁰

$$ \begin{aligned} &\quad\quad\quad\quad\langle x^1, \ldots ,x^n \rangle \leq \langle y^1,\ldots,y^n\rangle \quad \hbox{iff}\\ &x^1 \leq y^1 \quad\hbox{and} \quad (x^2-y^2)^2 + \cdots + (x^n-y^n)^2 \leq (x^1-y^1)^2. \end{aligned} $$

Elements $\langle x^1,\ldots,x^n\rangle$ and $\langle y^1,\ldots,y^n\rangle$ that are not order-related, are called space-like related.

Here is the mentioned theorem. While it falls short of fully characterizing all single history models of BST in Minkowski space-time, it illustrates a general point that motivates a generalization of the BST definition of modal consistency.

Theorem 1

Let the region $R\subseteq M^2$ be an open set in two-dimensional Minkowski space-time with ordering ≤. Let R be downward closed (i.e., if $x\in R$ and $y\in M^2$ s.t. y ≤ x, then $y\in R$) and such that each upper bounded chain in R has a supremum in R and each lower bounded chain in R has an infimum in R. Then $\langle R,\leq\rangle$ is a BST model iff R is directed.

Proof

The “$\Leftarrow$” direction is trivial: if R is directed, it is the unique maximal directed subset of R itself, so that R has just one history, trivializing the prior choice principle (PCP). The other axioms of BST are fulfilled by assumption (note that an open set in M ² cannot have a maximum). $\square$

In order to prove the “⇒” direction, we derive a contradiction from the assumption that there are (at least) two different histories in R. That way we have shown that R contains only a single (directed) history and thus, must itself be directed.

So, assume that there are two histories $h_1,\,h_2\subseteq R$ with $h_1\neq h_2,$ meaning that there must be $e\in h_1-h_2.$ This e constitutes a (trivial) chain, so by the PCP there must be some $s\in h_1\cap h_2$ s.t. s < e and s is maximal in $h_1\cap h_2.$ Now by density (which follows from the fact that R is an open set) we can find f for which s < f < e, and working in coordinates and using downward closedness of R we can indeed find such an f on the intersection of the rim of the backward light cone of e and the rim of the forward light cone of s. Clearly $f\in h_1,$ by downward closure of histories. Now let C be a chain whose proper supremum is f (for $f=\langle f_1,\,f_2\rangle,$ we can use ${C = \{ \langle f_1-1/n,\,f_2\rangle \mid n\in \mathbb{N}\}}$); by downward closure we have $C\subseteq h_1.$ Now we can show that $C\subseteq h_2$ as well: Assume otherwise, then there has to be some $c\in C$ such that $c\in h_1-h_2;$ the PCP gives us a choice point s′ < c maximal in $h_1\cap h_2,$ which must be different from s as C (and therefore c) lies below f, and by construction of C, $s \not\leq c.$ s and s′, both being maxima of $h_1\cap h_2,$ must be space-like related. By directedness of histories h ₁ and h ₂, there have to be upper bounds $t_i\in h_i$ with s, s′ ≤ t _i , i = 1,2. Now let x be the unique intersection of the forward light cones of s and s′; we have x ≤ t ₁ and x ≤ t ₂, and thus, by downward closure of histories, $x\in h_1\cap h_2.$ But s < x, contradicting maximality of s in $h_1\cap h_2.$

We have shown that $C\subseteq h_2$ as well. By assumption there is a supremum-in-h ₂, $f'\in h_2.$ We can show that f = f′, which proves our theorem, since then we have s < f with $f\in h_1\cap h_2,$ contradicting the maximality of s. So, assume f ≠ f′, so that $f'\in h_2-h_1;$ the PCP gives us a choice point r maximal in $h_1\cap h_2$ s.t. r < f′. Now as f′ is the supremum-in-h ₂ of C, there is some $c_2\in C$ for which r < c ₂. But $c_2\in C\subseteq h_1\cap h_2,$ contradicting the maximality of r. Thus, f = f′, and our theorem is proved. $\square$

This theorem may give us some comfort: its upshot is that if a region fulfills a number of reasonable constraints including clauses (1)–(3) of Definition 4, then the full set of BST axioms (and thus, the prior choice principle as the most characteristic BST axiom, clause (4)) is fulfilled if and only if the region is a directed set; the BST model then accordingly has only one history. Thus, the BST definition of modal consistency does not create spurious histories, in the following sense: there is no reasonable region (fulfilling the premises of the theorem) that fulfils the BST axioms in such a way that the region is split up into more than one history. This would be bad since we know that the full 2-dimensional Minkowski space-time does not contain modally incompatible events, and therefore no subregion can contain modally incompatible events either; so any region is modally consistent. BST accords with this assessment, at least for the regions for which the theorem applies.

The theorem however also reinforces the worry mentioned above: why shouldn’t it be possible to have a modally consistent (single history) scenario in a non-directed region of space-time (see note 9 above)? It seems that the BST demand of global directedness rules out too many intuitively sensible scenarios. Maybe the directedness requirement can be localized? This is in fact so, leading to the project of defining modal consistency via so-called continuations (Placek 2011); see Sect. 4.1 below.

3.3 A Semantical Reason for Generalizing Modal Consistency

So far we have motivated a generalization of BST’s definition of modal consistency by recourse to the role of histories in the BST axioms: it seems that that role leads to spurious geometrical constraints on BST models that should be relaxed. Above we also pointed out that the notion of a history, and thus the notion of modal consistency, plays another role in BT and BST: it is used as a semantic parameter of truth. If we want to evaluate a sentence about the future, we normally need to specify which of the equally possible futures we mean to refer to, for otherwise no assessment may be possible.

But do we really need to specify a full history, a full course of events from the beginning till the end of time? That seems a bit too much, really, and it can’t be what is going on when we assess sentences containing the future tense: we have to make do with much more limited information. And we can. In fact, MacFarlane’s project of spelling out a notion of relative truth via assessment sensitivity (MacFarlane 2003, 2013) gives a useful model for how we can often determine a truth value for sentences about the future of their context of utterance, given in addition a second, later context of assessment (see also Belnap (2002a) on “double time references”). In order to develop a more general picture that also applies to BST, however, we have to spell out modal consistency in terms of transitions—a notion that we need to introduce before we can go on.

In a model of BT or of BST, we can sensibly ask where or when histories branch. We will discuss the more general case of BST; given our assumptions about maxima in the intersection of any two histories in BT (which is meant to mimic BST’s prior choice postulate), transfer from BST to BT is immediate.

We need the following defined relations:

Definition 6 (Undividedness; splitting)

We call two histories h ₁ and h ₂ undivided at $e, h_1\equiv_e h_2,$ iff (a) $e\in h_1\cap h_2$ and (b) there is some e′ > e for which $e'\in h_1\cap h_2.$ Undividedness at some e means that two histories continue to overlap for at least a little while after e. On the other hand, if e is maximal in $h_1\cap h_2,$ so that e is a choice point for the two histories, we say that h ₁ and h ₂ split at $e, h_1 \perp_e h_2.$

It turns out, given the axiomatic basis of BST, that undividedness at e is an equivalence relation. This means that the set H _e of histories containing e is partitioned into equivalence classes via ≡ _e . The elements of this partition we can call the possibilities open at e—there are normally (far) fewer than there are histories through e, as histories can split (much) later. The selection of one of the possibilities open at some e corresponds to a basic transition.

Definition 7 (Basic transition)

Let $e\in W$ in a BST-structure $\langle W,\leq\rangle,$ and let ≡ _e be the relation of undividedness-at-e among histories of W; let H _e be the set of histories in W containing e. The partition of H _e via ≡ _e , the set of possibilities open at e, is denoted $\Uppi_e.$ For $H\in \Uppi_e,$ we call the pair $\langle e,\,H\rangle,$ also written $e\, \rightarrowtail \,H,$ a basic transition. If $\Uppi_e=\{H\}=\{H_e\}$ (i.e., the partition has just one element, corresponding to ≡ _e being the universal relation on H _e ), we call the transition $e\, \rightarrowtail \,H$ trivial, otherwise, indeterministic. We call e the initial and H the outcome of the transition $e\, \rightarrowtail \,H.$

The notion of a transition allows for a fresh look at modal consistency. Instead of asking whether a total scenario is modally consistent or not (which, as we have seen, is decided in BST via directedness), we can ask whether a set of transitions is consistent or not. From a global point of view, this is easy: given a BST-structure, a set of transitions is consistent iff there is a history in which all of the transitions occur together; a maximally consistent set of transitions then fully corresponds to a history (see Lemma 1 below). Formally, for $T=\{t_i=e_i\, \rightarrowtail \,H_i\mid i\in I\},$ with I an index set, we can define the set of histories allowed by T, H(T), to be

$$ H(T) := \cap_{i\in I} H_i. $$

T is consistent iff $H(T) \neq \emptyset,$ i.e., iff T allows at least one history to occur.¹¹

In order to develop a more local approach to transitions, it is useful to consider the transitions themselves as an ordered set, in accordance with the following definition:

Definition 8 (Transition ordering)

Given a BST-structure $OW = \langle W,\leq\rangle$ with the set TR(OW) of basic indeterministic transitions, and transitions $t_1=e_1\, \rightarrowtail \,H_1,$ $t_2=e_2\, \rightarrowtail \,H_2\in TR(OW),$ we say that t ₁ is below $t_2 \,(t_1 \prec t_2)$ iff (a) e ₁ < e ₂ and (b) $H_2\subseteq H_1.$ In the same vein, for $t_1=e_1\, \rightarrowtail \,H_1$ and $e\in W,$ we say that t ₁ is below $e \,(t_1\prec e)$ iff e ₁ < e and $H_e\subseteq H_1.$

This defines a partial ordering $\prec$ among all the transitions TR(OW) in a BST-structure OW (the ordering properties carry over from < and $\subseteq$). Note that different transitions with the same initial, which are modally incompatible, are incomparable according to $\prec$. Such a partial ordering can form a natural interface for specifying a BST-structure with much less information than the full BST partial ordering among events; this theme is developed in detail in Müller (2010).

The following Lemma shows that histories are maximally consistent in the transition sense of consistency, too.

Lemma 1 (Histories and maximally consistent sets of transitions)

Let $OW=\langle W,\leq\rangle$ be a BST structure without funny business (see Sect. 4.2 below) and TR(OW) its set of indeterministic (non-trivial) basic transitions. Let $T\subseteq TR(OW)$ be a set of transitions that is downward closed (i.e., if $t\in T$ and $t'\in TR(OW)$ s.t. $t'\prec t$ , then also $t'\in T$). Then T is maximally consistent (i.e., T is consistent but no proper superset is) iff there is a history h in OW s.t. H(T) = {h}. Thus, a maximally consistent set of transitions admits a singleton set containing just one specific history.

Proof

“⇒”: In case $H(T)=\emptyset, T$ is not consistent and thus, a fortiori, not maximally so. So, let T be such that there are histories $h_1,\,h_2\in H(T),$ $h_1\neq h_2.$ Then T is consistent. We have to show that it isn’t maximally consistent. So let $e\in h_1-h_2,$ by the prior choice principle there is some choice point s < e maximal in $h_1\cap h_2,$ and $\Uppi_s$ has at least two members; let H be the member of $\Uppi_s$ containing h ₁, we know that $h_2\not\in H.$ Let $t=s\, \rightarrowtail \,H;$ t is an indeterministic basic transition in TR(OW), and $t\not\in T$ as t excludes h ₂ ∈ H(T). Then the set T′ = T ∪ {t} is consistent ($H(T')\supseteq\{h_1\}$), so T isn’t maximally consistent.

“$\Leftarrow$”: If T is inconsistent, $H(T)=\emptyset$. So let T be consistent but not maximally so, i.e., there is some non-trivial $t=e\, \rightarrowtail \,H\in TR(OW)-T$ s.t. T ∪ {t} is consistent. As T is downward closed, t must be maximal in T ∪ {t}. By consistency, $H(T)\cap H\neq\emptyset,$ whence $H(T)\cap H_e\neq\emptyset,$ as $H\subseteq H_e.$ In fact we have $H\subseteq H(T),$ as t is maximal in the transition ordering. We even have that all of $H_e\subseteq H(T):$ we have $H_e=\cup\Uppi_e,$ and any local alternative $t'=e\, \rightarrowtail \,H'$ with the same initial e as t and some $H'\in \Uppi_e$ is also maximal w.r.t. T, and thus, T ∪ {t′} is consistent as well, securing $H'\subseteq H(T).$ ¹² But as t is non-trivial, there are at least two non-empty members of the partition $\Uppi_e$ of H _e , i.e., there are at least two histories $h_1,\,h_2\in H_e, h_1\neq h_2.$ As $H_e\subseteq H(T),$ the set H(T) thus cannot be a singleton. $\square$

While the definition of consistency for sets of transitions via histories is straightforward, it would however also be useful to have a more properly local characterization of consistency. One thing is clear: a consistent set must not contain two different transitions with the same initial—that would be blatantly inconsistent. Furthermore, any subset of a consistent set of transitions is also consistent. Spelling out further local conditions of consistency and inconsistency is an intricate issue, especially given the possibility of modal correlations (so-called modal funny business, mentioned in note 12). We will discuss these issues in Sect. 4.2 below.

Transitions are “where the action is”: at the initial of an indeterministic transition, there are different possibilities for the immediate future.¹³ One can characterize a scenario within a BST-structure fully by giving the transitions that occur in it. Here is the promise of sets of transitions for semantics: in evaluating a sentence as to its truth or falsity, it should normally not be necessary to specify a maximal consistent set of transitions corresponding to a history. Specifying some consistent set of transitions should be enough. In this way we can hope to combine insights of both Belnap’s idea of “double time references” and of MacFarlane’s theory of relative truth for future contingents. Small sets of transitions can play the relevant role in semantics because the carry enough information, and they have a good chance of being epistemically and computationally tractable.¹⁴

4 Alternatives to Histories

The two types of considerations for rethinking modal consistency mentioned above—relaxing the history definition of BST for more generality; focusing on sets of transitions for a more local view—can be identified as driving forces behind recent work by Placek (2011) and Müller (2010). We describe Placek’s generalization of modal consistency in terms of “snake-links” in Sect. 4.1 before considering the “sets of transitions”-approach in Sect. 4.2. We will draw some lessons for semantics, combining ideas from both approaches, in Sect. 4.3.

4.1 Continuations

In Sect. 3.2 we have seen that BST’s history definition enforces geometrical constraints on possible space-times that are not independently motivated. There is a rather natural generalization of BST’s notion of modal consistency in terms of directedness that properly generalizes the allowed range of space-times. Placek (2011) has developed the idea of “continuations” as a background for spelling out possibilities without the notion of possible worlds or histories. In that paper he also develops the generalized notion of modal consistency that we will discuss.

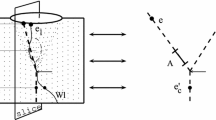
Recall the motivation for viewing directedness as a criterion for modal compatibility: if there is a perspective from which both events e ₁ and e ₂ have occurred, then e ₁ and e ₂ are modally compatible. One may ask why it is necessary that there be a global perspective on e ₁ and e ₂. It seems that a suitable multitude of local perspectives should also be enough to guarantee local consistency: e.g., if there is no f above both e ₁ and e ₂, but there is some f ₁ above e ₁ and some f ₂ below f ₁ such that there is some f ₃ above f ₂ and e ₂, that should also do. See Fig. 2 for the idea.¹⁵

Fig. 2

A snake-link between e ₁ and e ₂

Fig. 3

Illustrating the sets W ^C _e . c ₁, c ₂ and c ₃ are the choice events in e’s causal past indicated by the dashed lines (c ₄ and c ₅ are outside that region). The region W ^C _e is shaded grey; the boundary is not part of W ^C _e . Note that W ^C _e contains all events above c ₅, even though events in different continuations of c ₅ are incompatible

Based on the zig-zag nature of such links, Placek (2011) has called them “snake-links”.

Here is the official definition, including the important generalization of “being snake-linked in a region”:

Definition 9 (Snake-link (in a region))

Let 〈W,  ≤ 〉 be a partial order. Events e, f ∈ W are snake-linked (e≈ f) iff there is some $n\in\mathbb{N}$ and there are elements e ₀,…, e _n  ∈ W such that (a) e ₀ = e, e _n  = f and (b) for i = 1,…, n, we have either e _i−1 ≤ e _i or e _i  ≤ e _i−1.

e and f are snake-linked in a region $R\subseteq W$ (e≈ _R f) iff there is a snake-link e ₀ = e,…, e _n  = f such that all of e ₀,…, e _n  ∈ R.

In order to generalize the notion of modal consistency via snake-links, we need two additional defined concepts. Following Placek, we will use

$$ W_e:=\{x\in W\mid e<x\} $$

to denote the set of events above e. Being snake-linked in W _e is an equivalence relation on W _e (reflexivity and symmetry are obvious from the definition; for transitivity, observe that snake-links in W _e can be easily concatenated). Thus we have a natural partition P _e of W _e . If P _e has more than one member, we call e a choice event. Indeterministic transitions can now be specified via such a choice event e and one member of the partition P _e . We let CE(W) be the set of choice events in W. Now we define the sets

$$ W_e^C := \{x\in W\mid \forall c\in CE(W) (c<e\rightarrow c<x)\}, $$

which comprise all those events x that occur after any choice events in e’s causal past. These sets play a crucial role in generalizing the notion of modal consistency, so it is good to have a close look. Clearly, we have $W_e\subseteq W_e^C,$ by transitivity of <. Figure 3 pictures the set W ^C _e in a situation in which there are three choice events c ₁, c ₂ and c ₃ in e’s causal past.

Based on the sets W ^C _e , Placek’s definition of modal consistency (Placek 2011, Def. 6) is the following:

Definition 10 (Modal consistency, snake-link style)

Let $\langle W,\leq\rangle$ be a partial order. Elements e and f are modally compatible iff they are snake-linked in the region W ^C _e ∪ W ^C _f . A subset $A\subseteq W$ is modally consistent iff any two of its members are compatible.

In order to elucidate this definition, it is helpful to see that directed sets are modally consistent according to the new definition: in fact, if there is $f\in W$ such that e ₁ < f and e ₂ < f, then we have $f\in W_{e_1}\cap W_{e_2}\subseteq W_{e_1}^C\cup W_{e_2}^C,$ and e ₁, f, e ₂ is a snake-link. It is also easy to see that the new notion of modal consistency properly generalizes the notion of directedness: e.g., in the one-history case, now any convex subset of M ⁿ (and in fact many other subsets) counts as modally consistent. So we have reached our aim of generalizing the notion of modal consistency, and the generalized notion has a claim to both naturalness and to counting as local, as no global viewpoint for securing consistency is needed any more.

On the basis of the new definition, BST can be generalized in a relatively straightforward manner, replacing “history” by “maximally modally consistent set” in the new sense. The axioms of BST referring to histories can then either be retained, using the new sense of “history”, or “localized”, e.g., in the manner described by Placek (2011, Def. 8). We will have to leave the question of the exact interrelation between the old and the new framework for another occasion; see the mentioned paper for some pertinent remarks.

Placek (2011) also suggests that snake-link based continuations can play a useful role in semantics, replacing the history parameter in Ockhamist semantics by something more properly local, viz., by a pair e/A, where $A\neq\emptyset$ and the set A ∪ {e} is modally consistent. We will here develop a complementary approach, in which the history parameter is replaced by a set of transitions (Sect. 4.3). But first we need to work out more fully the notion of modal consistency in terms of sets of transitions.

4.2 Small Sets of Transitions

We will be working with a BST-structure $OW=\langle W,\leq\rangle$ in which the basic indeterministic transitions $t_i=e_i\, \rightarrowtail \,H_i$ are identified; we will not consider trivial transitions here. The set TR(OW) is the set of all basic indeterministic transitions in OW, ordered by $\prec$ (see Definition 8). In Sect. 3.3 above we mentioned a “top down” approach to modal consistency in terms of transitions: a set T of transitions is consistent iff all the transitions occur in one history, so that the intersection of the outcomes of all transitions$,H(T)=\cap_{i\in I} H_i,$ is non-empty—the transitions taken together allow at least one history to occur. When trying to develop a local perspective, this approach is not ideal, as it still works with sets of (global) histories. The transition ordering is helpful for the necessary local perspective.

A general idea for spelling out modal consistency of transitions in terms of the transition partial ordering is the following: A set that contains two transitions with the same initial is obviously (“blatantly”) inconsistent. In the end, all inconsistency should be due to blatant inconsistency. (This approach thus follows option (2) of Sect. 3.1). It is clear, however, that there can be inconsistency without blatant inconsistency; a set of transitions does not have to give the whole story, so to speak. To illustrate, consider OW such that T = TR(OW) = {t ₁, t ₂, t ₃, t ₄}, where $t_i=e_i\, \rightarrowtail \,H_i$ and e ₁ = e ₂, i.e., the transitions t ₁ and t ₂ have the same initial. (So, T is blatantly inconsistent.) Now suppose $t_1\prec t_3$ and $t_2\prec t_4.$ The set T′ = T − {t ₂} = {t ₁, t ₃, t ₄} is not blatantly inconsistent: no two of the transitions in it have the same initial. T′ is however inconsistent: the initial e ₃ of t ₃ occurs in the outcome H ₁ of e ₁, while the initial e ₄ of t ₄ occurs in the outcome H ₂ of e ₁ = e ₂, so that e ₃ and e ₄ cannot occur together in one history, and accordingly, we have $H(T')=\emptyset.$ In order to unmask the inconsistency of T′, we need to look at the downward closure of T′, defined as

$$ DC(A) = \{ t\in TR(OW)\mid \exists t'\in A\, t\preceq t'\}. $$

We call a set of transitions $A\subseteq TR(OW)$ prima facie consistent iff DC(A) is not blatantly inconsistent. It is easily seen that in our example of T′, we have DC(T′) = T, and as remarked, T is blatantly inconsistent. So T′ isn’t even prima facie consistent.

Why the cautious “prima facie”? In BT, the qualification is in fact unnecessary. However, as spelled out in detail in Müller et al. (2008), the spatial aspect of BST leads to complications here. Assume that A is prima facie modally consistent and contains two non-order-related transitions t ₁ and t ₂ with different initials that are space-like related. Can we be sure that A is really consistent—i.e., that $H(A)\neq\emptyset ?$ Even in the simplest case of A = {t ₁,t ₂}, this may be problematic, due to what is called “modal funny business” (Belnap 2002b). It could be that local possibilities t ₁ and t ₂ do not combine to form a global possibility (i.e, admit at least one history together); something like this may be what is behind distant quantum correlations (quantum non-locality). Whatever the empirical facts, it seems clear that given the possibility of such non-local effects, a purely local approach to consistency in terms of transitions is doomed; the non-local modal correlations convey additional information that is not present in the local transition ordering. Absent such funny business, however, prima facie consistency is sufficient for consistency.¹⁶ In the following, final section, we will revert to the framework of branching time, in which modal funny business cannot occur as there are no space-like-related moments (i.e., moments in one history that are not order-related): by the definition of a history in BT as a maximal linear chain, any two moments in one history have to be order-related.

4.3 Semantics in Terms of Sets of Transitions

We will now show how departing from the use of histories in semantics leads to a more local analysis of the future tense in branching time structures.¹⁷ The basic idea is to replace the semantic parameters of truth, which in standard Ockhamist semantics are a moment m together with a history h, by a moment m together with a set of transitions T. As in the standard case that requires m/h s.t. $m\in h,$ not any combination of m and T is allowed as a parameter: m and T have to be compatible. In terms of the set of histories allowed by T, H(T), the demand that m and T form a useable set of parameters of truth then is that T allows for m to occur: $H_m\cap H(T)\neq\emptyset$ (note that this enforces consistency of T). When we write “m/T”, we thereby indicate that that condition is met. We will presuppose a model based on a BT-structure $OW=\langle M,\leq\rangle$ with a set of basic transitions TR(OW); a model will have the form ${\mathfrak{M}}=\langle M,\leq,v\rangle.$ We will use the following defined notions in what follows:

• The set of transitions occurring before a moment m, TR(m), is

  $$ TR(m) := \{ m'\, \rightarrowtail \,H'\in TR(OW) \mid m'<m\,\&\,H_m \subseteq H'\}. $$

• Given a history h in OW, the set of transitions characterizing h, TR(h), is

  $$ TR(h) := \{ m'\, \rightarrowtail \,H'\in TR(OW)\mid h\in H'\}. $$

  According to Lemma 1, this guarantees H(TR(h)) = {h}.

Our idea for using sets of transitions in the semantics is the following: a set of transitions T admits a certain set of histories H(T). We can simply extend the Ockhamist semantics in terms of m/h by quantifying over all histories from H(T) where needed, without any changes to the model. Thus, the base case and the propositional cases remain unchanged. (In line with what was said above, we always assume that m/T is consistent in the sense that $H_m\cap H(T)\neq\emptyset.$)

• ${\mathfrak{M}},m/T \models p$ iff v(m, p) = 1.

• ${\mathfrak{M}},m/T \models \neg\phi$ iff ${\mathfrak{M}},m/T \not\models \phi.$

• ${\mathfrak{M}},m/T \models \phi \, \& \, \psi$ iff ${\mathfrak{M}},m/T \models \phi$ and ${\mathfrak{M}},m/T \models\psi$.

The T parameter is used, but not altered, in the clauses for the temporal operators:¹⁸

• ${\mathfrak{M}},m/T \models P\phi$ iff for all $h\in H_m\cap H(T)$ there is some $m'\in h$ for which m′ < m and ${\mathfrak{M}},m'/T \models\phi;$

• ${\mathfrak{M}},m/T \models F\phi$ iff for all $h\in H_m\cap H(T)$ there is some $m'\in h$ for which m < m′ and ${\mathfrak{M}},m' / T \models \phi.$

Note that the shifted index of evaluation used in both clauses, m′/T, again fulfills the requirement that $H_{m'}\cap H(T)\neq\emptyset,$ as $m'\in h$ for some $h\in H(T).$ Note also that in the case of the past tense P, the parameter T plays no role; given past linearity of BT structures, we could equivalently have written

• ${\mathfrak{M}},m/T \models P\phi$ iff there is some m′ < m for which ${\mathfrak{M}},m'/T \models\phi.$

It is only with respect to the future tense F that anything interesting happens. To see what, it is useful to look at two extreme cases. (a) If T = TR(h) for some history h, we are back to the standard m/h semantics: there is only one single history, viz., the $h\in H_m\cap H(T),$ and m′ stays on h. So our semantics is an extension of standard Ockhamism: we can get Ockhamism back if we want. (b) If T is maximally unspecific given m, so that $H_m\subseteq H(T)$ and accordingly, the clause for F quantifies over all histories in H _m , we get back the Peircean truth conditions for F, demanding a witness in each history through m. Note that this will always be the case if $T=\emptyset,$ and that our framework thus amounts to treating a Peircean index of evaluation, consisting of a moment m only, as the moment/set-of-transitions pair $m/\emptyset,$ which is another welcome sign of continuity with established semantic frameworks. The Peircean behavior in case (b) is the price to be paid for the fact that the given clause does not leave any cases undecided and does not have to rely on supervaluations or similar.

The most interesting cases are cases in between, in which the given T is neither too big to be accessible (recall that a history in a BT structure stretches all the way into the future—we are never in a position to point out a history uniquely), nor too small to tell us anything above the fact that m is occurring. Are there such cases? A context of utterance does not specify a history uniquely—that is, in a nutshell, the assertion problem confronting Ockhamist semantics. Belnap (2002a) and MacFarlane (2003, 2013) both argue that in many cases in which a sentence is uttered at some moment of context m _C , we assess the sentence at a later moment of assessment m _A , when the occurrence of the indeterministic event the sentence was about has been settled. Thus, e.g., if before a coin toss, I say, “it will land heads”, and in fact it lands heads, then from the perspective of that later moment, I can assess my earlier utterance as having been true.¹⁹ Belnap and MacFarlane propose different ways of making sense of that observation. Belnap uses a speech-act analysis according to which later on, the earlier assertion is either vindicated or impungned, which can have further normative consequences. MacFarlane, on the other hand, proposes a postsemantics employing two contexts, both a context of utterance and a context of assessment; relative to a certain context of assessment, a sentences uttered earlier then can come out as true or false. The current proposal easily handles MacFarlane’s approach, but it is more general, and it is also open towards a speech-act reading à la Belnap (we will however not comment on this in the following).

Let us fix a specific situation: at a moment m _C (for “moment of context of utterance”), Peter utters the sentence ϕ = “the coin will land heads”. At the later moment m _A (“moment of assessment”), he says, “what I said was true”. The right diagnosis seems to be that while the sentence is contingent relative to the context of utterance, and accordingly cannot be assigned a truth value there unless additional information or structure is given, it is no longer contingent relative to the context of assessment, so that assigning a truth value seems appropriate. We can give the following definition of relative contingency based on the m/T semantics:

Definition 11 (Relative contingency)

A sentence ϕ is contingent w.r.t. ${\mathfrak{M}},m/T$ iff there are histories $h_1,\,h_2\in H(T)$ s.t. ${\mathfrak{M}},m/TR(h_1)\models\phi$ and ${\mathfrak{M}},m/TR(h_2)\models\neg\phi.$

It follows immediately that no sentence is contingent w.r.t. T for which H(T) = {h}—that is the fact on which standard Ockhamist semantics rests. On the other hand, many sentences pertaining to the future are contingent given T = TR(m _C ) with m _C the moment of utterance. In our example case, we have contingency relative to ${\mathfrak{M}},m/TR(m_C),$ but not relative to ${\mathfrak{M}},m/TR(m_A),$ so that the sentence can indeed be assessed relative to the context of assessment.

There are two advantages of our transition semantics over assessment sensitive postsemantics for Ockhamism, as far as we can see: For one, the semantics is uniform; no additional parameters are introduced to handle assessment. Everything is dealt with in the uniform framework of m/T semantics. Second, while we are here limiting discussion to branching time, the m/T approach easily extends to BST. In fact in BST there is a second case of relative contingency: there can be no knowledge about contingent happenings space-like related to a context of utterance, so that there is contingency in the causal elsewhere (the region of space-time outside the past and future light-cone). In general, then, contingency can be resolved by expanding a given parameter T to some $T'\,\supsetneq\,T.$ The recipe to “wait and see” that is behind Belnap’s and MacFarlane’s approaches is a highly relevant special case of this, but not the only one imaginable, especially in the context of a more general information dynamics.

5 Conclusion

The guiding theme of the considerations in this paper is the following: useful possibilities have to be identified below the level of maximally consistent sets, or histories, in branching structures. This goes against the standard approach to modality in terms of “possible worlds”, which are likewise maximal. Branching structures supply some useful resources for localizing possibilities in terms of modal consistency. We have outlined two recent approaches for capturing that notion: Placek’s “continuations” program and the “small sets of transitions” approach. Combining ideas from both approaches, we have spelled out a novel semantics for a temporal logic based on branching-time in which the index of evaluation is not a moment/history pair, as in Ockhamism, but a pair consisting of a moment and a (compatible) set of transitions. That semantics extends both Ockhamism and assessment-sensitive postsemantics, and it promises to make branching-time based temporal logic more tractable.