Abstract
To analyse contingent propositions, this paper investigates how branching time structures can be combined with probability theory. In particular, it considers assigning infinitesimal probabilities—available in non-Archimedean probability theory—to individual histories. This allows us to introduce the concept of ‘remote possibility’ as a new modal notion between ‘impossibility’ and ‘appreciable possibility’. The proposal is illustrated by applying it to a future contingent and a historical counterfactual concerning an infinite sequence of coin tosses. The latter is a toy model that is used to illustrate the applicability of the proposal to more realistic physical models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper addresses the issue of how to evaluate contingency claims about the future or counterfactual possibility claims that involve events that are logically and physically possible yet so unlikely that we usually assign probability zero to them. So, if we only use standard probability values as our guide, we are forced to assign the same numerical value to possibilities that we must also assign to the impossible event (represented by the empty set). In doing so, we seem to lose some nuance in distinguishing contingent from impossible events.
On the one hand, it could be argued that this is a virtue: after all, the events are extremely unlikely, so perhaps they can be treated as ‘practically impossible’, i.e., impossible for all practical intents and purposes. On the other hand, it seems odd to be forced to give up the sharp distinction between possibility and impossibility even in purely theoretical contexts. In models that include an infinitely long possible future, for instance, this future will typically be assigned prior probability zero, even though this possibility could become actual. Moreover, there are situations in which every possible future has a priori zero probability, such as for infinite sequences of coin tosses. For these reasons, this paper investigates a new pair of modal notions that are intended to give us a choice in the matter of whether we want to include such unlikely events among the possibilities under consideration.
Let me first clarify which notion of possibility and probability appears in this paper. It has been remarked that the concept of probability encompasses a duality. This was pointed out at least as early as 1837 by Poisson (1837, Chapter I). Later, Hacking (1975) famously called probability a Janus-faced concept: one face looks inwards, towards rational degrees of belief (or credences), whereas the other face turns outwards, towards mind-independent chance processes in the external world. The probability functions from Kolmogorov ’s (1956) theory are intended to be applicable across this duality and can be interpreted as representing subjective credence as well as objective chance. Likewise, the probability functions from the alternative (non-Archimedean) probability theory that we will consider below can be interpreted as credences as well as chance functions.
In this paper, probability theory will be combined with branching time (BT) structures (Prior, 1967; Belnap et al., 2001), which are used in the tense-logical analysis of the problem of future contingents and of historical counterfactuals. BT structures only branch toward the future and are usually employed to represent ontological indeterminism—for instance by McCall (1994), whose model we discuss in Sect. 1.1. Yet, they may also represent merely epistemic uncertainty about the future. A congenial interpretation is that this paper deals with credences informed by a physical model of branching events.
The history of the development of BT structures is reviewed in Sects. 1.2–1.4, and the contemporary terminology and formalism can be found in Sect. 2. The main goal of this paper is to study how BT structures can be supplemented with probability assignments. Section 3 reviews the proposal of Müller (2011). This section also introduces an alternative probability theory that enables us to assign infinitesimal probabilities to individual histories in BT structures. Section 4 proposes the semantics for two new modal operators, called ‘appreciable possibility’ and ‘remote possibility’. The latter applies to remote contingencies that are infinitely less probable than the former. The term ‘appreciable’ comes from non-standard analysis, where it refers to a hyperreal number that is neither infinitesimal (or zero) nor infinite (see, e.g., Goldblatt, 1998, p. 50).
Throughout Sects. 1–4, the proposal is motivated and illustrated with the example of a future contingent and a historical counterfactual concerning an infinite sequence of coin tosses. This toy model may be considered as a stand-in for the temporal evolution of a physical system, demonstrating the applicability of the present proposal to a much wider class of physically relevant models. A proposed counterexample against infinitesimal probabilities is discussed in Sect. 5. Section 6 concludes the paper.
1.1 McCall ’s (1994) branching universe
McCall ’s (1994) branching model of the universeFootnote 1 is intended to represent ontological possibilities, rather than epistemically conceivable possibilities. McCall (1994, pp. 1–6) proposed to represent the past by one four-dimensional Minkowski diagram and possible futures by ‘branches’ each of which constitutes a different Minkowski diagram. Exactly one of the possible futures becomes actual, but which one this will turn out to be is not determined beforehand. So, the present is always the first branch point.
Inspired by the model’s potential for representing quantum probabilities as “branch proportionalities”, McCall (1994, Chapter 5) proposed a way to endow the model with probabilities connected to the branches. He presented this ‘branched’ definition of probability as an objective, de re interpretation of probability—an alternative to other common interpretations. Although the probabilities are objective, they change as time progresses, because some branches that were once possible have since been deleted. Moreover, branch probabilities allow the computation of inverse conditional probabilities, unlike propensities (which face problems like Humphreys’s paradox; Humphreys (1985).
On McCall ’s (1994) proposal, probability values are assigned to branch segments by a non-negative and finitely additive function, in such a way that the sum of the probabilities of all segments immediately above any branch point equals one. Probabilities of a branch are computed via the product of the probabilities of the segments that compose the branch. This approach works well when there are at most finitely many segments in any branch (associated with finite products of probability values) and when there are at most finitely many branch segments attached to a choice point (associated with finite sums of probability values).
McCall (1994, pp. 151–161) discussed how the proposal can be generalized to the infinite case: if there are branches that consist of a countable infinity of segments, infinite products can be introduced, and if there are countably infinitely many branch segments attached to a choice point, this is covered by countable additivity (which is indeed assumed in standard probability theory). McCall (1994) also discussed the possibility of having an uncountable infinity of branch segments connected to a branch point. Informed by the work of Skyrms (1980), McCall (1994, p. 160) suggested that infinitesimal probabilities can be introduced, which can be represented by hyperreal numbers in the sense of Robinson (1966). Finally, McCall (1994, p. 161) suggested that normalization can still be achieved by an uncountable sum of infinitesimal probabilities.
We will see in Sect. 3.4.2 that his claims can indeed be supported by a non-Archimedean probability theory. We build on his branching semantics for historical counterfactuals in Sect. 4.2.
1.2 Future contingents and historical counterfactuals
The problem of future contingents deals with the question of how to ascribe truth values to statements about future events, which are neither inevitable nor impossible (see Øhrstroøm & Hasle, 2011).
In classical times, this question came to the fore in Aristotle’s paradox of the sea battle. Later scholars have interpreted Aristotle’s position as denying that future contingents have a truth value before the relevant event has happened. In his Master Argument, Diodorus Cronus assumed the necessity of past events to infer the necessity of future events; Diodorus thereby denied the existence of future contingency and arrived at a deterministic view.
In medieval times, the problem recurred in a theological setting as an apparent incompatibility of human free will and divine omniscience, which includes foreknowledge of human actions. William of Ockham and other medieval scholars such as Richard of Lavenham rejected the view that past events are necessary, allowing for future contingency (and thus human free will). In the meantime, they held the view that future contingents do have a truth value before the relevant event has happened (allowing divine foreknowledge).
More recently, Arthur N. Prior reintroduced the problem of tense and time in the context of modern logic. Prior (1957) presented the first version of his tense logic, which is closely related to modal logic. In reaction to this book, Saul Kripke suggested the idea of branching time (BT) in a letter to Prior (see Ploug & Øhrstrøm, 2012). The BT formalism has since been developed by Belnap et al. (2001). The goal of this theory is to capture agency in a non-relativistic but indeterminist universe; we review it in Sect. 2. According to Belnap (2001, p. 179): “The fundamental idea is that possibility—real possibility, objective possibility—is in the world, not otherworldly.” So, on this view, invoking other (possible) worlds should not be needed to establish what is possible in the actual world. Instead, real possibilities are associated with multiple possible histories, all compatible with the actual world. Various semantical theories for future contingents take the BT formalism as their common starting point (see, e.g., Øhrstrøm & Hasle, 2011).
Another problem that the paper addresses pertains to historical counterfactuals: in this case, the classical question is how to ascribe truth values to statements about conditionals in the subjunctive mode with an antecedent that is false, but which was a historical possibility (see Placek & Müller, 2007). This paper focuses on the notion of possibility expressed by historical counterfactuals, in connection to the probability of the consequent relative to a (past) historical possibility: a real possibility at an instant prior to the current one, which is incompatible with the current actual moment. ‘Real possibilities’ are defined in Sect. 2.6; for now it suffices to know that they are partitions of histories at a particular moment. The paper does not analyse other types of conditionals and does not address the assertability of future contingents or counterfactual conditionals.
1.3 Aiming to combine branching time with probability
Probability seems to presuppose a notion of possibility: it can be considered as a function that gives weights to various possibilities. These possibilities or possible events can be represented equivalently by propositions or sets, because propositional algebras (used in modal logic) and (\(\sigma \)-)algebras of sets (used in probability theory) are both Boolean algebras.Footnote 2 Hence, one could expect a natural connection between probability theory and modal logic (including tense logic), semi-formally given by:

where
\(\mu \) is a standard probability function,
\(\phi \) is an arbitrary possible event,
 is the modal possibility operator, and
is the modal possibility operator, and
 is the modal necessity operator. The above implications indeed hold for finite sample spaces, but the right-to-left implication does not hold in general for the infinite case.Footnote 3 Well-known examples where it fails are uniform probability distributions over uncountably infinite sets of atomic possibilities.
is the modal necessity operator. The above implications indeed hold for finite sample spaces, but the right-to-left implication does not hold in general for the infinite case.Footnote 3 Well-known examples where it fails are uniform probability distributions over uncountably infinite sets of atomic possibilities.
The current paper investigates how BT structures (formally introduced in Sect. 2) can be combined with probability. I will consider an alternative to standard probability theory to avoid violating the natural connection between probability and modal notions in the case of tense logic. In addition, I hope that the new approach helps to shed new light on old issues related to future contingents and historical counterfactuals.
BT-based probabilities have also been investigated by Müller (2011), but the approach is limited to (i) associating probability spaces to ‘real possibilities’ in structures with finite branching and (ii) combining such probability spaces. This paper starts from a more global perspective by associating a probability space to the entire set of possibilities (histories) in a BT structure. Due to problems related to infinite sample spaces, classical probability theory is not suitable for the task at hand. If we use non-Archimedean probability (NAP) theory instead (see Sect. 3), which allows for the assignment of infinitesimal probability values, it turns out that (i) the conclusions are consistent with those of Müller (2011), and that (ii) the current approach allows us to analyse a more general class of problems of interest.
To preserve the natural link between probability theory and modal or tense logic, it is necessary to work in a probability theory that obeys the principle of ‘Regularity’ (see, e.g., Benci et al., 2018): such a theory will only assign probability zero to logically impossible events (represented by the empty set).
1.4 Remote possibilities and infinite coin toss sequences
Section 4 proposes a new definition for a modal operator that expresses ‘appreciable possibility’, which is contrasted with an operator for ‘remote possibility’. The first corresponds to a possibility that has a non-infinitesimal probability, whereas the second corresponds to a possibility that has a non-zero, infinitesimal probability. Here, I motivate this distinction and compare it to related proposals.
Lewis (1986, p. 176) insisted that “infinitesimal chance is still some chance”, when he argued for assigning infinitesimal probabilities rather than zero to possible outcomes. The non-Archimedean probability theory that I will apply in Sect. 3 achieves just that. In this paper, I similarly insist that a possibility that carries an infinitesimal probability (or ‘chance’, if interpreted as representing ontological uncertainty) is still some possibility—in particular, a remote possibility.
For a contrasting view, let’s start by considering Nover and Hájek ’s (2004) Pasadena game: it involves tossing a fair coin indefinitely until the first occurrence of heads, which leads to a pay-off of \((-1)^{n-1}2^n/n\). The absolute values of these terms constitute a harmonic series, but the signs alternate, so the value of the infinite sum for the expected value of the game depends on the order of the terms (by Riemann’s rearrangement theorem; see also Peterson, 2023, §7). Nover and Hájek (2004) argued that the temporal order does not suffice to settle the order of the terms and that therefore expected utility does not pick out a unique fair price to enter the game. In this context, Smith (2014, §6)Footnote 4 argued that “a rational agent is not required to value the game in one particular way”, because “normative theories of practical activities” “should not require arbitrary precision”, so “rationality does not require decision makers to factor in outcomes of arbitrarily low probability”. In particular, Smith’s Rationally Negligible Probabilities principle states that rational agents need not consider outcomes of a lottery (with at most countably infinitely many outcomes) that have a sufficiently small probability. In other words, probabilities below a certain threshold (which may depend on the agent, the lottery, and the decision problem) may be treated “as zero for purposes of making the decision at hand” (Smith 2014, §7). Instead, these minute probabilities can be truncated, i.e., replaced by zero. This is similar to the Lockean thesis (Foley, 2009), which also suggests that when agents assign a (context-dependent) sufficiently small degree of belief to a proposition, it is rational for them to disbelieve this proposition simpliciter. Truncation is in line with empirical evidence about human decision makers, as witnessed by experimental results in the fuzzy-trace literature (Reyna, 2004).
Observe that Smith, Foley, and Reyna were not considering infinitesimal probabilities, but some larger threshold. This raises a worry of arbitrariness: why this particular numerical value for the threshold? There may be contextual factors that determine what’s rational to neglect in a given situation, but observe that infinitesimal probabilities are by definition smaller than 1/n for any finite, positive n, so they can be neglected in any situation in which some non-infinitesimal threshold can be found at all.
At the same time, however, it seems that agents should be allowed to consider highly unlikely contingencies as possibilities (if they can and want to) or at least that we should not be forced to deny them as possibilities in a theoretical analysis. For instance, Levi (1989, pp. 367–368) proposed to call all propositions that an agent recognizes as such ‘serious possibilities’;Footnote 5 they depend on the agent’s information, that is the set of propositions of which the agent is (subjectively) certain. Levi’s motivation for this was that agents who are not logically omniscient may fail to recognize certain logical (im)possibilities as such, even on their own assumptions. Serious possibilities may include propositions that carry zero credence (or infinitesimal credence, on the non-Archimedean approach). Levi (1989, pp. 368–369) illustrated this with the following example: an agent who is certain that a fair coin will be tossed until it lands heads for the first time, should consider the event that the coin is tossed indefinitely (because it keeps landing tails) as a serious possibility, even though that event has prior probability zero.
Moreover, Levi (1989, p. 385) connected this to non-Archimedean probabilities: “To assign a proposition h positive infinitesimal probability is equivalent in the nonstandard representation to assigning h standard 0 probability but acknowledging it to be a serious possibility.” If we combine Levi’s observation that serious possibilities can include those that carry only infinitesimal probability with the earlier observation the latter do not depend on an arbitrary or context-dependent non-infinitesimal threshold, this suggests that remote possibility does represent a specific modal notion. So, I argue that possibilities that carry an infinitesimal probability indeed deserve to be distinguished from infinitely more probable ones that represent an appreciable possibility. For on overview of the terminology, see Fig. 1.
Overview of the terminology introduced in Sect. 1.4. Here, A represents an arbitrary set representing a proposition to which probability can be assigned, P represents a probability function (on a set algebra of the sample space \(\Omega \)) that may take infinitesimal values, and st(P) is that function with infinitesimals rounded off. Serious possibilities (in the sense of Levi) exclude the empty set, which represents logical impossibility, but may also exclude other possibilities not included in the sample space. Serious possibilities include appreciable as well as remote possibilities, which are central to this paper
Throughout the paper, various aspects of BT structures and their combination with probability theory are illustrated with a toy example: an infinite sequence of coin tosses. At each toss, the coin may land either heads ( \(\uparrow \)) or tails ( \(\downarrow \)). We assume that the coin is tossed for a countably infinite number of times, such that the instants at which it is tossed may be indexed with the elements of \({\mathbb {N}} = \{1,2,3,\ldots \}\). It is helpful to include the singleton \(\{n=0\}\) to indicate the last instant prior to the first toss and the notation \({\mathbb {N}}_0\) is used to refer to \({\mathbb {N}} \cup \{0\}\).
The paper focuses on \({\mathbb {N}}\) for clarity of presentation. However, it is important to observe that the approach is fully general and would apply just as well to a sequence of coin tosses that extends infinitely long into the past as well as into the future, such that the tosses may be indexed with the elements of \({\mathbb {Z}} = \{ \ldots ,-3,-2,-1,0,1,2,3,\ldots \}\) or even with a dense set, such as \({\mathbb {Q}}\) (if we allow supertasks).
Section 4 will analyse a future contingent concerning the toy example:
-
“The coin lands heads on each toss.”
The paper also discusses a corresponding historical counterfactual, where we assume that the first four tosses were heads, heads, tails, and heads ( \(\uparrow \uparrow \downarrow \uparrow \)):
-
“If the third toss had been heads, the coin could have landed heads on each toss.”
2 Branching time (BT) structures
This section introduces some concepts and notation that are common in the literature on BT structures. Readers who are familiar with this literature may skip it. This section is based on Belnap et al. (2001, Chapter 7) combined with the notation of Müller (2011).
2.1 Possible moments and ‘earlier-possibly later’ relation
The BT formalism represents the universe by a non-empty set of possible moments (or possible states of affairs that extend across all of space), M, endowed with a temporal relation, <. So, a BT structure consists of a pair \({{\textbf {M}}} = \langle M, < \rangle \), with < a relation on M that is:Footnote 6
where \(\le \) is defined by:
The relation symbol < can be read as ‘earlier–possibly later’. More specifically, \(m_1 < m_2\) means that moment \(m_1\) is in the past of moment \(m_2\) or, equivalently, that \(m_2\) is among the future possibilities of \(m_1\).
Since < is a partial order, there may be incomparable moments—indeed, this is the case of interest. The above stipulations rule out backward branching and postulate that there is a common past, so incomparable moments can only occur if there is branching towards future possibilities. If this is the case, \({{\textbf {M}}}\) has the shape of a tree.
Further assumptions:
-
As is usual in the literature, we assume that there is no maximal (final) moment:
$$\begin{aligned}\forall m \in M \exists m' \in M (m < m').\end{aligned}$$ -
It is often assumed that there is no minimal moment either:
$$\begin{aligned}\forall m \in M \exists m' \in M (m' < m).\end{aligned}$$However, in the toy example we do assume a minimal (first) moment, \(m_0\):
$$\begin{aligned}\exists m_0 \in M \forall m \in M \setminus \{ m_0 \} (m_0 < m).\end{aligned}$$Remark that if such an \(m_0\) exists, it is unique. This simplifying assumption is not essential to the method that is presented here, which is fully general in this respect.
-
For simplicity, we assume finite branching: each moment has a finite number of branches.
2.2 Possible histories
A history represents a maximal possible course of events—a possible way the world depicted by \(\langle M, < \rangle \) could develop. So, a history is a maximal subset of M such that all its moments are mutually comparable.Footnote 7
The set of all histories of M is called \({\mathcal {H}}{} \textit{ist}\). Consider a particular moment, m. Consider the set of possible histories which contain this moment, \(H_m\). Observe that the set of all possible histories in a BT structure with minimal element \(m_0\) can always be written as \(H_{m_0}\).
2.3 Instants
It can further be postulated that M can be partitioned into instants: the instants are subsets such that (i) for each history, there is exactly one moment in each instant, and (ii) for each pair of instants, the order relation of the pair of moments belonging to those instants on a given history agrees with the order relation of the pair of corresponding moments on any other history (Belnap, 2001, pp. 194–195).
In particular, we may define temporal instants as the equivalence classes of moments, \([m]_\sim \subset M\), that are cotemporal and hence incompatible (mutually inconsistent). We introduce two conditions for these equivalence classes (see, e.g., Placek, 2012, Appendix):
Call the set of all instants (i.e., the set of all equivalence classes \([m]_\sim \)) T and the linear ordering on this set \(<_T\). In general, T can be a dense set such as \({\mathbb {R}}\). We may now introduce a function, t, that expresses the instant at which a particular moment occurs: \(t(m) \in T\). Following Belnap and Müller (2010), we call the tuple \(\langle M,<, T, <_T, t \rangle \) a ‘branching time with date-times’ (BTDT) structure. Observe that
but not vice versa (the moments might be inconsistent and hence incomparable by <).
Since there is no maximal element in M, T is always an infinite set. In the trivial case, when each moment only has a single branch (i.e., linear time), M has the same cardinality as T, which is at least countably infinite. In general, however, M is uncountably infinite. Observe that even for finite branching and countably infinite T, M can easily become uncountably infinite. We encounter an example in the next section.
2.4 Example: BT structure of an infinite coin toss sequence
In the toy example, the set of instants is discrete and countably infinite; we choose \(T = {\mathbb {N}}_0\) and \(<_T \ = \ <_{{\mathbb {N}}_0}\). Each moment has exactly two branches, so the set of moments is uncountably infinite: \(M = \{ m_i \mid i \in 2^{{\mathbb {N}}_0} \}\). Each moment, \(m_i\), can be characterized as the outcome of all coin tosses up to a particular instant: an initial segment of \(\{ \uparrow , \downarrow \}^{\mathbb {N}}\). At an instant \(n \in {{\mathbb {N}}_0}\), there are \(2^n\) moments: \(\{ m_i \mid i \in \{ 2^n-1, \ldots , 2^{n+1}-2 \} \}\). A BT structure can be represented as a graph. For the toy example, this graph is an infinite complete binary tree: see Fig. 2.
In the toy example, each history can be regarded as an element of \( \{ \uparrow , \downarrow \}^{\mathbb {N}}.\) In Fig. 3, two particular histories in this BT structure are indicated: \(h_1 = \{ m_0,m_1,m_3,m_7, \ldots \}\) (\(= \uparrow \uparrow \uparrow \uparrow \ldots \)) and \(h_2 = \{ m_0,m_2,m_5,m_{12}, \ldots \}\) (\(= \downarrow \uparrow \downarrow \uparrow \ldots \)).
2.5 Prior–Thomason semantics for BT structures
The denotation of indexicals, such as ‘now’, depends on the context in which they are used. Hence, the semantics of indexical statements does not only depend on a model (in the sense of Tarski), but also on some further parameters. As explained by Belnap (2001, Chapters 6B and 8), BT semantics follows Kaplan ’s (1989) indexical semantics, which relativizes truth to a moment of evaluation, \(m \in M\). This moment of evaluation may be equal to the moment at which the statement is uttered: the moment of context, \(m_C \in M\). In general, however, this need not be the case. For instance, tense operators can shift the moment of evaluation m toward the past or future of \(m_C\).
Building on the work of Prior (1967) and Thomason (1970), BT semantics relativizes truth not only to a moment of evaluation, m, but to a pair of a moment of evaluation and a history of evaluation that includes this moment: m/h Belnap et al. (2001, pp. 224–225).
So, a BT model \({\mathcal {M}}\) is a BT structure \(\langle M, < \rangle \) together with a valuation \({\mathcal {V}}\) assigning extensions to atomic propositions at the point of evaluation, m/h (i.e., a moment m and a history h through it: \(m \in h\)).
Let us now define two modal operators that quantify over the possible futures of the moment of evaluation: they keep m fixed, and change h.
- POSS::
-
possibility \({\mathcal {M}}, m/h \models POSS\phi \ \ \text {iff} \ \ \exists h' \in {\mathcal {H}}{} \textit{ist}\) such that \(m \in h'\) and \({\mathcal {M}}, m/h' \models \phi \);
- SETT::
-
necessity or ‘settledness’ \({\mathcal {M}}, m/h \models SETT\phi \ \ \text {iff} \ \ \forall h' \in {\mathcal {H}}{} \textit{ist}\) if \(m \in h'\) then \({\mathcal {M}}, m/h' \models \phi \). Observe that: \(POSS = \lnot SETT \lnot \).
The semantics can be understood in terms of sets of possible histories, as we will see in Sect. 3.2. For now, observe that h is only mentioned at the left-hand side of these definitions, so only the moment of evaluation needs to be known, yet moment-history pairs are crucial in the right-hand side.
2.6 Real possibilities and choice points
For there to be real possibilities, as defined in this section, there have to be at least two incomparable moments in \({{\textbf {M}}}\). Since backward branching is prohibited by the postulates for BT structures, this means that there are at least two forward branches. Moreover, for there to be choice points, the overlap of an arbitrary pair of histories must have a maximal element.
Consider a particular moment, m. Define an equivalence relation on the set of all possible histories which contain m, \(H_m\), \(\equiv _m\) (‘are undivided at m’):
Real possibilities at m are the members of the partition \(\Pi _m\) of \(H_m\) induced by \(\equiv _m\). So, these possibilities form an exhaustive set of mutually exclusive alternatives.
Two histories ‘split’ at moment m, \(\bot _m\), if m is their last common moment: \(h_1 \bot _m h_2\) if and only if m is maximal in \(h_1 \cap h_2\). m is a ‘choice point’ if and only if \(\Pi _m\) has more than one member (i.e., if and only if there are at least two histories splitting at m). So, at a choice point m, its real possibilities coarse-grain the set of histories \(H_m\): within a member of the partition, all histories coincide beyond m; two histories that belong to different members of the partition differ immediately after m.
Example In the toy example, each moment has two branches. Hence, each moment is a choice point and the set of real possibilities has two members at any moment; one corresponds to possible histories in which the coin lands heads (\(\uparrow \)) at the very next instant, and one corresponds to possible histories in which the coin lands tails (\(\downarrow \)) at the very next instant.
3 Introducing probability in BT structures
The question we are concerned with in this paper is how we can combine BT structures with probability theory. We will consider two different forms of probability theory—namely, Kolmogorov’s standard probability theory and non-Archimedean probability (NAP) theory (Benci et al., 2013, 2018). NAP theory uses a field of hyperreal numbers, \(^*{\mathbb {R}}\), rather than the standard real numbers, \({\mathbb {R}}\), to play the role of probabilities. See Wenmackers (2019), for an introduction to hyperreal numbers. This allows us to assign infinitesimal probabilities to highly unlikely events. Since one of the axioms of NAP theory is Regularity, which guarantees that only the impossible event receives probability zero, the theory seems well suited to connect the modal notion of possibility with that of having non-zero probability.
Both types of probability theory require us to fix a ‘sample space’ or ‘universe’, \(\Omega \): a non-empty, possibly infinite set of atomic possible outcomes. A probability function, denoted by \(\mu \) for the standard function and by P for the NAP function, will assign probability values to members of the ‘event space’: a non-empty collection of subsets of \(\Omega \). In the case of NAP theory, the event space is always equal to the full power set of \(\Omega \), \({\mathcal {P}}(\Omega )\). In the case of Kolmogorov’s theory, the event space is written as \({\mathcal {A}}\) and may be a \(\sigma \)-algebra strictly smaller than \({\mathcal {P}}(\Omega )\) (in the case of infinite \(\Omega \)).
3.1 Various options to choose \(\Omega \)
Looking at a BT structure from the perspective of a probabilist, one can make the following initial observation. Instants are equivalence classes of mutually incompatible but cotemporal moments, \([m]_\sim \): these look similar to different partitions of one and the same sample space. See Fig. 4 for a schematic drawing: each partition \(\Omega _n\) corresponds to an instant \(t_n\), which is the equivalence class of cotemporal moments \([m_{2^n-1}]_\sim \). This suggests that (1) the probabilities assigned to the moments that belong to the same instant should sum to unity and that (2) we should assign the same probability to a moment as to the set of moments that branch from it at the very next instant (if there is such an instant). Branching diagrams indeed occur in the literature on probability to represent various possibilities even though they do not (necessarily) represent any temporal evolution. For instance, Kelly (1996) introduced the Baire space using ‘fans’ (equivalence classes of infinite data streams/possible histories) veering off (branching off) a common handle (observed data/past history). However, each instant contains different elements (moments), so the suggestion that they are ‘partitions of the same set’ cannot be taken literally.
It is fruitful to rephrase the initial observation in terms of partitions of histories that contain the cotemporal moments: in this case, we are indeed dealing with various partitions of the same set, \({\mathcal {H}}{} \textit{ist}\), and it is the case that the probabilities of subsets in each partition (all \(H_{m'}\) with \(m'\) in \([m]_\sim \) for some \(m \in M\)) sum to unity (for partitions that contain at most countably many members).
Let us now approach the problem in a more systematic way to ensure that the solution covers all aspects of interest. First, we make a list of probabilistic questions concerning BT structures one might be interested in. This will enable us to select the most appropriate sample space and event space.
-
Q1.a
What is the probability of a particular moment (state of affairs at that instant)? \(P(m)=?\) with \(m \in M\)
-
Q1.b
What is the probability of an arbitrary set of moments? \(P(X)=?\) with \(X \subseteq M\)
-
Q1.c
What is the conditional probability of a particular moment, given a prior moment? \(P(m \mid m')=?\) with \(m,m' \in M\) such that \(m' < m\)
-
Q2.a
What is the probability of a particular history? \(P(h)=?\) with \(h \in {\mathcal {H}}{} \textit{ist}\)
-
Q2.b
What is the probability of an arbitrary set of histories? \(P(Y)=?\) with \(Y \in {\mathcal {P}}({\mathcal {H}}{} \textit{ist})\)
-
Q3
What is the probability of a real possibility at a moment (i.e., a particular subset of histories)? \(P(Z)=?\) with \(Z \in \Pi _m\)
-
Q4
Can we introduce probability in a way that harmonizes with the modal operators? I.e., such that, relative to a moment of evaluation, m:
-
at m, the probability of \(\phi > 0 \ \ \text {iff} \ \ POSS \phi \) is true;
-
at m, the probability of \(\phi = 1 \ \ \text {iff} \ \ SETT \phi \) is true.
-
Q1 suggests using M as the sample space. Since there is no maximal moment, M is always infinite and so will \(\Omega \) be; the event space of Kolmogorov’s theory, \({\mathcal {A}}\), may be smaller than \({\mathcal {P}}(\Omega )\), thereby not necessarily containing all arbitrary sets of moments. Hence, Q1.b requires the use of NAP theory, where the event space is guaranteed to be equal to \({\mathcal {P}}(\Omega )\).
Q2 suggests using \({\mathcal {H}}{} \textit{ist}\) as the sample space. If there are uncountably many moments in M with at least two branches (which may happen even when the set of instants is countable), \({\mathcal {H}}{} \textit{ist}\) is an uncountably infinite set. For similar reasons as before, Q2.b requires the use of NAP theory, thereby guaranteeing the event space to be equal to \({\mathcal {P}}(\Omega )\).
Q3 is dealt with by Müller (2011), where \(\Pi _m\) is used as the sample space. Observe that, under the assumption of finite branching: \(\Pi _m\) is a finite set for any \(m \in M\).
Q4 is obviously the tense logical version of the general connection sought between modal logic and probability theory (cf. Sect. 1.3). Q4 suggests that we need an event space that is a propositional (or sentential) algebra, ranging over propositions such as \(\phi \).
As we have seen, on the Prior–Thomason semantics, truth values depend on a moment of evaluation as well as a history of evaluation. What about probabilities? On the one hand, it seems natural to expect that probabilities depend on the moment of evaluation as well. After all, as we already discussed in relation to McCall ’s (1994) approach, in an indeterministic, branching model even objective probabilities may change with the passage of time. On the other hand, if probabilities measure subsets of histories (for instance sets that contain a given set of moments), then they need not depend on a history of evaluation.
3.2 Uniform choice of sample space: \(\Omega ={\mathcal {H}}{} \textit{ist}\)
It may now appear as though there is no uniform choice of \(\Omega \) that will allow us to answer questions Q1–4 simultaneously. However, starting from \(\Omega = {\mathcal {H}}{} \textit{ist}\) (the obvious choice in light of Q2), it does turn out that we can also deal with questions Q1, Q3, and Q4.
Regarding Q1 (which relates to the discussion at the beginning of Sect. 3.1), observe that “the probability of a moment, m” can be interpreted as “the probability of all histories leading to that moment m” (i.e., all histories in \(H_m = \{ h \in {\mathcal {H}}{} \textit{ist} \mid m \in h \}\)).
-
Q1.a can be rephrased as: \(P(m) {\mathop {=}\limits ^{\text {def}}} P(H_m)=?\) with \(m \in M\);
-
Q1.b can be rephrased as: \(P(X) {\mathop {=}\limits ^{\text {def}}} P(\cup _{m \in X} H_m) = ?\) with \(X \in {\mathcal {P}}(M)\);
-
Q1.c can be rephrased as: \(P(m \mid m') {\mathop {=}\limits ^{\text {def}}} P(H_m \mid H_m')=?\) with \(m,m' \in M\) such that \(m' < m\).
The conditional probability in Q1.c can be computed from the ratio formula using the absolute probabilities in Q1.a, provided that \(P(H_m')>0\). Q1.c only deals with the case where \(m' < m\). However, observe that:
-
\(P(m \mid m')\) is 1 if \(m \le m'\) (for then \(H_m \supseteq H_m'\));
-
\(P(m \mid m')\) is 0 if m and \(m'\) are incomparable (for then \(H_m \cap H_m' = \varnothing \)).
Regarding Q3, Müller (2011) investigated the combination of standard probability spaces of the form \(PR_m = \langle \Omega _m=\Pi _m, {\mathcal {A}}_m={\mathcal {P}}(\Omega _m), \mu _m \rangle \) for different moments, m. However, it seems like one could avoid this complication, by choosing \(\Omega \) large enough from the start. Indeed, all the \(\Omega _m\)’s are contained in \(\Omega = {\mathcal {H}}{} \textit{ist}\) and all the \({\mathcal {A}}_m\)’s are contained in \({\mathcal {P}}({\mathcal {H}}{} \textit{ist})\). However, unlike the \(\Omega _m\)’s and \({\mathcal {A}}_m\)’s, \(\Omega = {\mathcal {H}}{} \textit{ist}\) and \({\mathcal {P}}({\mathcal {H}}{} \textit{ist})\) are infinite sets, which becomes problematic in the context of standard probability theory (see next subsection). Probably, this is the very reason why Müller (2011) focused on the finite \(\Pi _m\)’s instead. Moreover, taken in isolation, Q.3 does not require the assignment of probabilities to all of \({\mathcal {P}}({\mathcal {H}}{} \textit{ist})\). In the next section, we will see that to answer Q3 for the toy example with an infinite coin toss sequence, it suffices to have probability assignments to \({\mathcal {A}} = {\mathcal {C}}(\Omega )\): the collection of cylindrical events of \(\Omega = {\mathcal {H}}{} \textit{ist}\).
Also regarding Q4, \(\Omega = {\mathcal {H}}{} \textit{ist}\) can still be used. First, the proposition \(\phi \) evaluated at m corresponds to its extension on the domain of the set of histories (cf. footnote 2): \(H_{\phi ,m} {\mathop {=}\limits ^{\text {def}}} \{h \mid m \in h \wedge m/h \models \phi \}\), which is a subset of \(H_{m}\). So, we interpret the probability of \(\phi \) evaluated at m as \(P(H_{\phi ,m} \mid H_m)\). Second, the semantics of \(POSS\phi \) evaluated at m is equivalent to saying that \(H_{\phi ,m}\) is non-empty. Third, the semantics of \(SETT\phi \) evaluated at m is equivalent to saying that \(H_{\phi ,m}\) equals \(H_{m}\).
Taking this together, we can rewrite Q4 as the requirement that, relative to a moment of evaluation m:
-
\(P(H_{\phi ,m} \mid H_m) > 0 \ \ \text {iff} \ \ H_{\phi ,m} \ne \varnothing \);
-
\(P(H_{\phi ,m} \mid H_m) = 1 \ \ \text {iff} \ \ H_{\phi ,m} = H_{m}\).
If there is a minimal moment \(m_0\) and we set \(m=m_0\), then \(H_{m}={\mathcal {H}}{} \textit{ist}\). Then, in order to have \(H_{\phi ,m_0}=H_{m_0}={\mathcal {H}}{} \textit{ist}\), \(\phi \) must be a tautology. In other words, Q4 is a requirement of ‘Regularity’: the probability function should only assign measure zero to the empty set (corresponding to a contradiction) and only measure one to the full sample space.
Example In the toy example, the uniform choice of \(\Omega = {\mathcal {H}}{} \textit{ist}\) amounts to \(\Omega = H_{m_0} = \{ \uparrow , \downarrow \}^{\mathbb {N}}\).
3.3 Choice of probability theory
Except for cases in which only a countable number of moments have more than one branch, \(\Omega = {\mathcal {H}}{} \textit{ist}\) is an uncountably infinite set. With standard probability theory, the choice of \(\Omega = {\mathcal {H}}{} \textit{ist}\) will force us to set \(\mu (\{ h \})=0\) for all \(h \in {\mathcal {H}}{} \textit{ist}\), which is problematic for Q1.c and Q4. Moreover, the standard probability measure \(\mu \) cannot be defined on all of \({\mathcal {P}}( \Omega )\),Footnote 8 which is problematic for Q1.b and Q2.b. Therefore, I suggest applying the framework of NAP theory, rather than standard probability theory.
As we have seen, Q4 can be regarded as a demand for ‘Regularity’ of the probability function, which is an axiom of NAP theory. Regularity will also ensure that the ratio formula for conditional probabilities is always defined, except when conditionalizing on the empty set (inconsistency), thereby enabling the handling of Q1.c.
3.4 Application to an infinite sequence of coin tosses
Now, we can combine a BT structure of an infinite sequence of coin tosses with its corresponding NAP function, which is described in Benci et al. (2013, Sect. 5.5).
3.4.1 Standard probability space
Using standard probability theory, we are looking for a probability space \( \langle \Omega , {\mathcal {A}}, \mu \rangle \) to describe an infinite sequence of tosses with a fair coin. A generic infinite sequence of coin tosses is written as \(\omega = (\omega _1, \ldots , \omega _n, \ldots )\) with \(\forall i \in {\mathbb {N}}, \omega _i \in \{ \uparrow , \downarrow \}\). Hence, the sample space is the Cantor space \(\Omega = \{ \uparrow , \downarrow \}^{\mathbb {N}}\).
The measure on this infinite product space is generated by a pre-measure on a special type of events: events in which exactly n positions of the infinite sequence are known to be heads (\(\uparrow \)) or tails (\(\downarrow \)) (for details, see, e.g., Benci et al., 2013, §5.5). Such events are represented by ‘cylindrical sets’. We define a cylindrical set of co-dimension n as follows:
with \(\forall k \in \{ 1, \ldots , n \} \left( i_k \in {\mathbb {N}} \wedge t_k \in \{ \uparrow , \downarrow \} \right) \). Assuming an equal probability of heads and tails for a single toss (fair coin), the probability of an event is halved for each known position in the sequence. Hence, the probability measure on a generic cylindrical set is:
Using Carathéodory’s theorem (see, e.g., Gruber, 2007, Chapter 3), this probability measure \(\mu \) can be extended uniquely to \({\mathcal {A}}\), the \(\sigma \)-algebra generated by these cylindrical sets. This completes the description of the three components of a standard probability space \( \langle \Omega , {\mathcal {A}}, \mu \rangle \) for an infinite sequence of tosses with a fair coin.
Some consequences Using the notation of BT structures, we have that:
-
a generic infinite sequence of coin tosses represents a generic history: \(\omega = h\);
-
\(\Omega = \{ \uparrow , \downarrow \}^{\mathbb {N}} = H_{m_0} = {\mathcal {H}}{} \textit{ist}\);
-
the \(H_m\)’s correspond to cylindrical events.
This approach has the following immediate consequences:
-
each \(H_m\) has a non-zero probability that can be computed using Eq. (1);
-
each individual history \(\{ h \}\) has probability zero;
-
likewise, each finite set of histories F has probability zero;
-
hence, the conditional probability \( \mu ( \{h\} \mid F )\) is undefined, for any finite set of histories F;
-
so, even upon learning that h is the actual history, one cannot update to \( \mu ( \{h\} \mid \{h\} ) = 1\);Footnote 9
-
nevertheless, the union of all histories has probability unity;
-
also the union of all but a finite number of histories has probability unity;
-
moreover, there are sets of histories with an undefined probability (non-measurable sets).
3.4.2 Non-Archimedean probability (NAP) space
We now look into an alternative description of the probabilities pertaining to an infinite sequence of tosses with a fair coin using NAP theory. For details, see Benci et al. (2013, 2018), and for historical context and a more introductory approach: Wenmackers (2019). The purpose of this section is not to introduce the general scope of the theory, but rather to show what it takes to apply it to an example, and then to apply it to the case of infinite coin toss sequences. This amounts to choosing an appropriate NAP space \(\langle \Omega , {\mathfrak {I}}_{\max }, P \rangle \).
In standard probability theory, the limit operation and the range of the probability function are fixed in advance; they are the standard limit of classical calculus and the unit interval of the standard reals, \([0,1]_{\mathbb {R}}\), respectively. In a non-Archimedean setting, however, one has to adjust the properties of the non-standard limit operation and the range depending on the details of the application—most notably on the cardinality of the sample space of interest. Because this approach is not well-known, the following sections explain it in detail. Readers who just want to know the gist of it, can skip to Sect. 4, which starts with a brief summary of the main result.
3.4.2.1. General recipe Along the way towards defining the NAP space \(\langle \Omega , {\mathfrak {I}}_{\max }, P \rangle \), we have to fix eleven ingredients:Footnote 10
-
(1)
sample space, \(\Omega \): a non-empty set of atomic events;
-
(2)
weight function, w: a strictly positive, real-valued, 1-place function on the elements of \(\Omega \); the specific value of w for a single atom is of no consequence, only the relative weight of pairs of atomic events matters (for example, to generate a uniform probability measure, w should assign the same weight to all singletons, but it does not matter which value is chosen);
-
(3)
additive measure, m: a positive, real-valued, 1-place function on the finite subsets of \(\Omega \), which determines the relative measure of any two finite events;
-
(4)
directed set on \(\Omega \), \(\Lambda \):Footnote 11 the generic choice is \(\Lambda = {\mathcal {P}}_{fin}\left( \Omega \right) {\setminus } \varnothing \), but by choosing a smaller \(\Lambda \), additional properties can be obtained for P; this step is crucial (see below for an example);
-
(5)
elementary relative probability, p: a positive, real-valued, 2-place function, which determines the probability of any event conditional on any event in \(\Lambda \): \(p(A,\lambda )=m(A \cap \lambda )/m(\lambda )\);
-
(6)
ideal on the partially ordered ring \({\mathfrak {F}}(\Lambda ,{\mathbb {R}})\), \({\mathfrak {I}}_0\):Footnote 12 informally, an ideal is a set of elements that are negligible in some sense; this informal characterization is made precise as the set of functions that are eventually zero (where ‘eventually’ has to be interpreted according to the partial order given by set inclusion, \(\supseteq \), on \(\Lambda \)):
$$\begin{aligned} {{\mathfrak {I}}_0} = {\{ \phi \in {\mathfrak {F}}(\Lambda ,{\mathbb {R}}) \mid \exists A_0 \in \Lambda \forall A \supseteq A_0: \phi (A) = 0\}}; \end{aligned}$$ -
(7)
maximal ideal, \({\mathfrak {I}}_{\max } \supset {\mathfrak {I}}_0\): using Krull’s theorem, which is based on Zorn’s lemma (see, e.g., Burton, 1970, p. 74), the ideal \({\mathfrak {I}}_0\) is extended to a maximal ideal;
-
(8)
equivalence relation on the ring \({\mathfrak {F}}(\Lambda ,{\mathbb {R}})\), \(\sim _{{\mathfrak {I}}_{\max }}\): two functions are defined to be equivalent if they differ by at most a negligible amount (where ‘negligible’ is to be understood as an element of the maximal ideal); formally,
$$\begin{aligned} \forall \phi , \psi \in {\mathfrak {F}}(\Lambda ,{\mathbb {R}}): \phi \sim _{{\mathfrak {I}}_{\max }} \psi \ \ \text {iff} \ \ \exists \varepsilon \in {\mathfrak {I}}_{\max }: \phi + \varepsilon = \psi ; \end{aligned}$$this equivalence relation leads to the following equivalence classes:
$$\begin{aligned} \forall \phi \in&{\mathfrak {F}}(\Lambda ,{\mathbb {R}}): \\ \left[ \phi \right] _{{\mathfrak {I}}_{\max }}&= \{\psi \in {\mathfrak {F}}(\Lambda ,{\mathbb {R}}) \mid \exists \varepsilon \in {\mathfrak {I}}_{\max }: \phi + \varepsilon = \psi \} \\&= \{\psi \in {\mathfrak {F}}(\Lambda ,{\mathbb {R}}) \mid \phi \sim _{{\mathfrak {I}}_{\max }} \psi \}; \end{aligned}$$ -
(9)
set of all equivalence classes, \({\mathfrak {R}}_{\Omega ,{\mathfrak {I}}_{\max }}\): the set \({\mathfrak {F}}(\Lambda ,{\mathbb {R}})\) modulo \({\mathfrak {I}}_{\max }\) forms an ordered, non-Archimedean field;
-
(10)
a non-Archimedean limit on \({\mathfrak {F}}(\Lambda ,{\mathbb {R}})\), \(\lim _{\lambda \uparrow \Omega }\): using the directed set, a type of limit is defined as the following algebra homomorphism:
$$\begin{aligned} \forall \phi \in {\mathfrak {F}}(\Lambda ,{\mathbb {R}}), \lim _{\lambda \uparrow \Omega }\phi {\mathop {=}\limits ^{\text {def}}} [\phi ]_{{\mathfrak {I}}_{\max }} \in {\mathfrak {R}}_\Omega ; \end{aligned}$$ -
(11)
absolute probability, P: \(\forall A \in {\mathcal {P}}\left( \Omega \right) , P(A) = \lim _{\lambda \uparrow \Omega }p(A \mid \cdot )\).
3.4.2.2. Applying the recipe to the toy model Let’s now specify the appropriate choices to be made in the general recipe above to apply it to an infinite sequence of coin tosses.
(1) As in Sect. 3.4.1, a generic infinite sequence of coin tosses is written as \(\omega = ( \omega _1, \ldots , \omega _n, \ldots )\) with \(\omega _i \in \{ \uparrow , \downarrow \}\) for all \(i \in {\mathbb {N}}\). Again, we have the sample space \(\Omega = \{ \uparrow , \downarrow \}^{\mathbb {N}}\).
(2–3) The fairness assumption implies that we have to assign the same probability to each individual history (or atomic event). Hence, \(w \equiv 1\). There is no further freedom in the construction of m: m counts the finite number of elements in finite sets of histories.
(4) We do have some freedom in the choice of a directed set on \(\Omega \), \(\Lambda \). Because of the fairness assumption, we expect the probability function to obey Laplace’s classical definition: as a fraction of the number of favourable cases over the number all cases. In other words, we want to construct the NAP space in a way such that:
To achieve this, we will have to choose \(\Lambda \) smaller than \({\mathcal {P}}_{fin}(\Omega ) \setminus \varnothing \). In particular, we start by focusing on cylindrical events that specify the initial n tosses: \(i_1=1, \ldots , i_n=n\). Such an event takes the form: \(C_{(1,\ldots ,n)}^{(\alpha _1,\ldots ,\alpha _n)}= \alpha \circledast \beta \), with \(\alpha \in \{ \uparrow , \downarrow \}^n\), \(\beta \in \{ \uparrow , \downarrow \}^{\mathbb {N}}\), and \(\circledast \) stands for the concatenation operation on sequences. Now, we define families of finite sets of such events, \(\lambda _{n,F}\), which are special subsets of \(\Omega \):
We define the collection of all these sets, \(\Lambda _{CT}\):
Observe that:
which establishes that \(\Lambda _{CT}\) forms a directed set.
(5) p is fully determined by m and \(\Lambda \).
(6–7) Now we define an ideal on \(\Lambda _{CT}\), which we extend to a maximal ideal, \({\mathfrak {I}}_{\max }\). Since this step relies on Zorn’s lemma, the maximal ideal is not unique.
(8–11) The ordered, non-Archimedean field \({\mathfrak {R}}_{\Omega ,{\mathfrak {I}}_{\max }}\) is now determined and so is the algebra homomorphism on \({\mathfrak {F}}(\Lambda ,{\mathbb {R}})\) which defines the limit, \(\lim _{\lambda \uparrow \Omega }\). This determines the absolute probability function, P and completes the construction of a NAP space \(\langle \{ \uparrow , \downarrow \}^{\mathbb {N}}, {\mathfrak {I}}_{\max }, P \rangle \) for an infinite sequence of fair coin tosses.
3.4.2.3. Some consequences In cases of uniform probability distributions, it is helpful to state the results in terms of a ‘numerosity’ function, \(\text {num}\). \(\text {num}\) can be regarded as a way of ‘counting’ infinite sets, which is different from cardinality. It is based on the part–whole principle (a strict subset has strictly smaller numerosity, but not necessarily smaller cardinality, than its superset) rather than one-to-one correspondence (equal numerosity implies the existence of a one-to-one mapping, but the reverse implication does not hold in general as it does for cardinality). Although \(\text {num}\) can be introduced axiomatically (Benci & Di Nasso, 2003, 2019), it can also be obtained by the non-Archimedean limit of a finite counting function (Benci et al., 2013).
Using the NAP space constructed above and \(\text {num}\), we get:
-
\(\forall h \in \Omega , P(\{h\})=\frac{1}{\text {num}(2^{\mathbb {N}})}\), which implies \(\forall m \in M \left( P(H_m)=\mu (H_m) \right) \);
-
\(\forall H \in {\mathcal {P}}(\Omega ), P(H)=\frac{\text {num}(H)}{\text {num}(2^{\mathbb {N}})}\);
-
\(\forall H_1 \in {\mathcal {P}}(\Omega ) \forall H_2 \in {\mathcal {P}}(\Omega ) \setminus \varnothing , P(H_1 \mid H_2) = \frac{\text {num}(H_1 \cap H_2)}{\text {num}(H_2)}\).
Moreover, the above choice of \({\mathfrak {I}}_{\max }\) ensures that (for the proof, see Benci et al., 2013, Sect. 5.5):
-
\(P( C_{(i_1,\ldots ,i_n)}^{(t_1,\ldots ,t_n)} ) = \frac{1}{2^n}\);
-
as a result, for each \(\mu \)-measurable event E, \(\mu (E)\) and P(E) differ at most by an infinitesimal.
Two other approaches As we reviewed in Sect. 1.1, McCall (1994) equipped a branching model with probabilities by assigning probabilities to branches (akin to transition probabilities in physics). Although the current construction starts from probabilities assigned to sets of histories, a probability of branch between moments \(m_1<m_2\) can be found as \(P(H_{m_2} \mid H_{m_1})\) (cf. our discussion of question Q1.c). As such, the current NAP model vindicates McCall ’s (1994) suggestion that hyperreal probabilities can be used on infinitary branching models.
A different way to introduce infinitesimal probabilities is to replace the standard infinite set M by a hyperfinite set and to apply Nelson ’s (1987) probability theory to it. This would require the development of hyperfinite versions of BT structures, which are currently not available. To model infinite coin toss sequences, for instance, a hyperfinite set \(\{1,\ldots ,N\}\) can be used to represent infinitely many instants, where N is an infinite hypernatural number (in a non-standard model of Peano arithmetic). The possible moments can be represented by another hyperfinite set, \(\{m_1,\ldots ,m_L\}\), where \(L=2^{N+1}-1\) is a larger infinite hypernatural number. In the case of a fair coin, each possible history has a probability of \(1/2^N\), which is a hyperreal infinitesimal. This illustrates the main advantage of the hyperfinite approach: hyperfinite sets are as simple to handle as standard finite sets. At the same time, it also shows a possible drawback: the approach is not compatible with using standard infinite sets, such as \({\mathbb {N}}\) to index the instants. It is left to the BT research community to decide whether exploring this option would be worthwhile.
4 Appreciable versus remote possibility
The main result of the construction in the previous section is that the same probability value \(P(\{h\})=\frac{1}{\text {num}(2^{\mathbb {N}})}\) can be assigned to any possible history, h. The denominator, \(\text {num}(2^{\mathbb {N}})\), is an infinite hyperreal number, so this probability is a non-zero infinitesimal. All sets of histories are measurable and for each \(\mu \)-measurable event E, \(\mu (E)\) and P(E) differ at most by an infinitesimal.
Let us now return to the future contingents and historical counterfactuals concerning an infinite sequence of coin tosses as introduced in Sect. 1.4. We evaluate whether the application of NAP theory to the corresponding BT structure can teach us anything about the type of modality expressed by future contingents or about the truth value of historical counterfactuals. I use this example to motivate the introduction of a new definition of a modal operator that expresses ‘appreciable possibility’, which is contrasted with an operator for ‘remote possibility’. The first is intended to correspond with a possibility that has a non-infinitesimal probability, whereas the second is intended to correspond with a possibility that has a non-zero, infinitesimal probability. The definitions do indeed establish this natural connection between modality and probability in cases like an infinite sequence of coin tosses.
4.1 Future contingents concerning an infinite sequence of coin tosses
Let us look at the future contingent: “The coin lands heads on each toss.” From the analysis with NAP theory, we have established that \(P(\{h\})=\frac{1}{\text {num}(2^{\mathbb {N}})}\) for any possible history, h. So, in particular: \(P({h_{\uparrow \uparrow \uparrow \uparrow \ldots }})=\frac{1}{\text {num}(2^{\mathbb {N}})}\). In other words, we assign a non-zero, infinitesimal probability to the coin landing heads on each toss. To assess whether this expresses a contingency, we have to determine the strength of ‘possible’. In particular, we can introduce two levels of possibility: ‘appreciable possibility’ ( ) and ‘remote possibility’ (
) and ‘remote possibility’ ( ), which we relate to non-Archimedean probability. To this end, the BT model has to be extended accordingly: from this point on, the model \({\mathcal {M}}\) is defined as a BT structure \(\langle M, < \rangle \) together with a NAP space \(\langle {\mathcal {H}}{} \textit{ist}, {\mathfrak {I}}_{\max }, P \rangle \) and a valuation \({\mathcal {V}}\) assigning extensions to atomic propositions at the point of evaluation, m/h. The semantics of the two new operators is defined in the following way:
), which we relate to non-Archimedean probability. To this end, the BT model has to be extended accordingly: from this point on, the model \({\mathcal {M}}\) is defined as a BT structure \(\langle M, < \rangle \) together with a NAP space \(\langle {\mathcal {H}}{} \textit{ist}, {\mathfrak {I}}_{\max }, P \rangle \) and a valuation \({\mathcal {V}}\) assigning extensions to atomic propositions at the point of evaluation, m/h. The semantics of the two new operators is defined in the following way:
- POSS:
-
possibility \({\mathcal {M}}, m/h \models POSS \phi \ \ \text {iff} \ \ P(H_{\phi ,m} \mid H_m) > 0\);
 :
:-
appreciable possibility
 ;
;  :
:-
remote possibility
 is a non-zero infinitesimal;
is a non-zero infinitesimal;
where \(H_{\phi ,m}\) represents \(\{h \mid m \in h \wedge m/h \models \phi \}\) (as before) and where st is the standard part function, which maps a hyperreal number to the unique closest real number (cf. Wenmackers, 2019). Any standard probability—where it is defined—is equal to the standard part of the non-Archimedean probability.
With standard, real-valued probability values alone, we cannot distinguish some (remote) possibilities from impossibility. We could use standard probability together with a check that \(H_{\phi ,m}\) is non-empty (cf. Easwaran, 2014). For measurable sets, this would be equivalent to using NAP theory. This also means that, at least for sets that are measurable on the standard approach, remote and appreciable possibility can be defined based on standard methods alone: these remote possibilities correspond exactly to Levi ’s (1989, p. 385) serious possibilities with zero (standard) probability.
Observe that  is true if and only if
is true if and only if  is true. So, on this proposal, future possibility encompasses appreciable and remote possibility, where the latter can be thought of as remote contingencies (hence the name) that are logically possible but carry only infinitesimal probability.
is true. So, on this proposal, future possibility encompasses appreciable and remote possibility, where the latter can be thought of as remote contingencies (hence the name) that are logically possible but carry only infinitesimal probability.
For the example of a future contingent, \(\phi \): “The coin lands heads on each toss.”, there are two options. First, if it is evaluated at an m such that the coin has already landed tails at least once, then \(P(H_{\phi ,m} \mid H_m)=0\),Footnote 13 so \(POSS \phi \) is false. Second, if it is evaluated at an m such that the coin has not yet landed tails (for instance, at \(m_0\)), then \(P(H_{\phi ,m} \mid H_m)\) is infinitesimal.Footnote 14 So, \(P(H_{\phi ,m} \mid H_m)>0\) but \(st\left( P(H_{\phi ,m} \mid H_m)\right) =0\): \(POSS \phi \) and  come out as true, while
come out as true, while  is false.
is false.
Of course, the outcome of the analysis depends on the future contingent under consideration. Consider, for instance, \(\lnot \phi \): “The coin does not land heads on each toss.” Its probability at any m is \(P(H_{\lnot \phi ,m} \mid H_m)=P(H_m {\setminus } H_{\phi ,m} \mid H_m)\). If it is evaluated at an m such that the coin has already landed tails at least once, then \(H_{\phi ,m}=\varnothing \), so \(P(H_{\lnot \phi ,m} \mid H_m)=P(H_m \mid H_m)=1\) and \(SETT\lnot \phi \) is true. If it is evaluated at \(m_0\) or any m prior to a tails outcome, \(P(H_{\lnot \phi ,m} \mid H_m)\) equals one minus an infinitesimal, so it is not yet settled that \(\lnot \phi \) (corresponding to the remote possibility of \(\phi \)).
This paper does not offer a definite position on whether ‘possible’ in natural language corresponds more closely to the operator POSS,  , or
, or  , but it seems that we do need all three operators to represent distinctions that are made in discourse, at least in technical contexts.
, but it seems that we do need all three operators to represent distinctions that are made in discourse, at least in technical contexts.  stresses the existence of a possibility, no matter how improbable (cf. Lewis, 1986, p. 176: “some chance”), whereas
stresses the existence of a possibility, no matter how improbable (cf. Lewis, 1986, p. 176: “some chance”), whereas  preselects possibilities that are infinitely more substantive in probability. One might even wonder whether the dominance of Kolmogorov’s approach to probability theory has made us less sensitive to the notion of possibility in the sense of
preselects possibilities that are infinitely more substantive in probability. One might even wonder whether the dominance of Kolmogorov’s approach to probability theory has made us less sensitive to the notion of possibility in the sense of  .
.
In the case at hand,  if \(\phi \) is true in an uncountable subset of \(H_{m}\) and
if \(\phi \) is true in an uncountable subset of \(H_{m}\) and  if \(\phi \) is true in at most a countable non-empty subset of \(H_{m}\). This is due to the assumed fairness of the coin: all individual histories carry the same infinitesimal probability, and we can focus on the cardinalities (or numerosities) of the sets. So, at any m, \(H_m\) is an uncountable set, so \(P(H_{\phi ,m} \mid H_m)\) is infinitesimal as long as \(H_{\phi ,m}\) is a countable subset of \(H_{m}\). In general, however, the semantics for
if \(\phi \) is true in at most a countable non-empty subset of \(H_{m}\). This is due to the assumed fairness of the coin: all individual histories carry the same infinitesimal probability, and we can focus on the cardinalities (or numerosities) of the sets. So, at any m, \(H_m\) is an uncountable set, so \(P(H_{\phi ,m} \mid H_m)\) is infinitesimal as long as \(H_{\phi ,m}\) is a countable subset of \(H_{m}\). In general, however, the semantics for  and
and  cannot be expressed without explicit consideration of the probability assignment.
cannot be expressed without explicit consideration of the probability assignment.
4.2 Historical counterfactuals concerning an infinite sequence of coin tosses
The goal of this section is to analyse the relation between possibility and (regular) probability of historical counterfactuals. To focus the discussion, we consider an example that applies to the toy model of a BT structure. Assume that the first four tosses are heads, heads, tails, and heads (i.e., all possible histories that contain \(m_C=m_{17}\) are elements of \(H_{\uparrow \uparrow \downarrow \uparrow }\)) and we consider this historical counterfactual: “If the third toss had been heads, the coin could have landed heads on each toss.”
As our starting point, we consider the semantics for counterfactuals on a branching model due to McCall (1994, Chapter 6), who presented it as a special case of the semantics of conditionals. First, he distinguished conditionals that are invariant under a change of the tense from those that are not. He observed that the former type of conditionals also tend to be invariant under an insertion of ‘it is (im)probable that’ (or other probabilistic expressions) before the consequent. According to McCall (1994, Chapter 6), only the first type of conditionals can be given a probability semantics.Footnote 15
Let us check this for our example historical counterfactual: from a perspective prior to the third toss, a conditional in the future tense expresses the same idea: “If the third toss will be heads, the coin may land heads on each toss.” From a (counterfactual) perspective on which the third toss was indeed heads, an antecedent in the past tense works as well: “Since the third toss landed heads, the coin may land heads on each toss.”Footnote 16 This shows that our example is invariant under changes of tense. It is also robust under to insertion of an expression of probability before the consequent: “If the third toss had been heads, it would have been improbable that the coin could have landed heads on each toss.”
Adapting McCall’s (1994, Chapter 6) proposal to our notation, he suggested that the probability of the conditional \(A \rightarrow C\) (with A the antecedent and C the consequent) evaluated a m should be represented by \(P(H_{C,m} \mid H_{A,m})\).Footnote 17 In the case of an indicative conditional, we can assume that the moment of evaluation is the moment of context, \(m=m_C\). Then, applying a regular probability function, we can conclude \(SETT (A \rightarrow C)\) at \(m_C\) iff \(P(H_{C,m_C} \mid H_{A,m_C})=1\) and \(SETT \lnot (A \rightarrow C)\) iff \(P(H_{C,m_C} \mid H_{A,m_C})=0\).
In the case of a historical counterfactual, the antecedent is a contingent proposition that is false at the moment of context, so \(H_{A,m_C}=\varnothing \), but there exists a prior moment m such that \(H_{A,m} \ne \varnothing \). Indeed, the subjunctive mode of the counterfactual indicates that evaluating its probability requires moving the moment of evaluation to some non-actual moment, \(m < m_C\). The idea here is akin to ‘rewinding the tape’ of actual history to a moment prior to A.Footnote 18 The question is how to determine m and whether the moment of evaluation is all that should be changed.
As a first attempt, we may consider the latest moment, \(m_L\), for which the actual history, represented by the set \(H_{m_C}\), overlapped with that of the antecedent, \(H_A\). In the terminology of Sect. 2.6, \(H_{m_C}\) and \(H_A\) split at choice point \(m_L\): \(H_{m_C} \bot _{m_L} H_A\). This proposal is simple and yields a unique outcome if the topology on \({{\textbf {M}}}\) indeed guarantees such a choice point exists, which is the case in our example. Moreover, it is congenial to the idea of closeness or similarity of possible worlds in the Stalnaker–Lewis semantics of counterfactuals (see, e.g., Starr, 2022). This proposal amounts to rewinding the tape of actual history to \(m_L\) and then evaluating the probability of C by conditionally positing A. If \(P(H_{C,m_L} \mid H_{A,m_L})>0\), the counterfactual is possible, and we can again distinguish between remote and appreciable possibility by considering the standard part. If the probability equals one, the counterfactual is settled. If \(P(H_{C,m_L} \mid H_{A,m_L})=0\), the counterfactual is not possible and its negation is settled.
Applying this proposal to our toy example, the moment of evaluation is \(m_L=m_3\), i.e., the moment at which only the first two tosses have happened and both are heads. The antecedent A corresponds to the cylindrical event \(H_A=C^\uparrow _3\), which indicates that the third toss results in heads, and the consequent C corresponds to the singleton event \(H_C=\{h_{\uparrow \uparrow \uparrow \uparrow \ldots }\}\). So, \(H_{A,m_3}=H_{m_7}=C^{\uparrow ,\uparrow ,\uparrow }_{1,2,3}\) with probability \(\frac{1}{2^3}\) and \(H_{C,m_3}=H_C\) with probability \(\frac{1}{num(2^{\mathbb {N}})}\). Hence, the probability of “If the third toss had been heads, the coin could have landed heads on each toss.” is \(P(H_{C,m_3} \mid H_{A,m_3})=\frac{ 2^3 }{ num(2^{\mathbb {N}}) }\), a non-zero infinitesimal. So, for our example, \(POSS (A \rightarrow C)\) and  come out as true, while
come out as true, while  is false.
is false.
Although this proposal may seem convincing in the toy example, it faces a problem in more realistic cases. As an example, McCall (1994, Chapter 6) considered a counterfactual of the form “If I had turned left, I would not be in this traffic jam.” In this example, the counterfactual history that maximizes the overlap with the actual history corresponds to turning left at the last possible moment (which might be very dangerous), rather than at an earlier intersection (obeying the traffic rules). So, \(m_L\) does not seem to select the most similar possible world after all and McCall (1994, Chapter 6) considered this ‘last-minute deviation objection’ to be fatal. To overcome the last-minute deviation objection, one may consider a past moment of evaluation prior to \(m_L\), but there seems to be no principled way of selecting this m.
Moreover, even in our toy example, there may be a more similar sets of histories after all, which agree with the actual world regarding the outcome of tosses that occurred after and independently of the counterfactual outcome. In general, this modified proposal (which is closer to the traditional Lewisian reading) amounts to evaluating the probability of a counterfactual \(A \rightarrow C\) in terms of \(P(H_{C,m_L} \cap H_X \mid H_{A,m_L} \cap H_X)\), where \(H_X\) selects histories that agree with \(H_m\) in terms of events that happened after \(m_L\) and that were independent of C.Footnote 19 For our example, \(H_X\) is the cylindrical event \(C^\uparrow _4\) and \(P(H_{C,m_3} \cap H_X \mid H_{A,m_3} \cap H_X )=\frac{ 2^4 }{ num(2^{\mathbb {N}}) }\). Since this is again a non-zero infinitesimal, this modification does not make a crucial difference in the subsequent possibility. For other examples, however, the verdicts on whether a conditional is (remotely) possible may differ.
5 A counterargument against infinitesimal probabilities?
Williamson (2007) has offered an argument against infinitesimal probabilities assigned to an infinite sequence of coin tosses. Consider a fair coin that is tossed at some point in time and forever again at equal time intervals. Williamson argues that the probability that all tosses starting from the first toss, result in heads equals half the probability that they do so starting from the second toss (by the assumption of a fair coin). He also argues that the former probability should equal half the latter probability since they represent isomorphic sequences. Even if we allow infinitesimal values, the two equalities can only hold simultaneous if the probabilities are zero. We can now reconsider this argument in the context of BT structures. Let’s index the individual tosses in the infinite sequence by \(T = {{\mathbb {N}}_0}\). This fixes the present instant (or at least the beginning of observations) at index \(t=0\). If we conditionalize on the initial segment of a history, say up to an instant \(t>0\), the conditional probability of any history that contains this initial segment is a factor \(2^{t+1}\) larger than the corresponding absolute probability. So, we retain Williamson’s first equality but not the second, which is indeed incompatible with infinitesimal probabilities.
Of course, the choice of 0 as the present moment is completely arbitrary. We are free to choose a later index \(t>0\) as the present moment; doing so will yield a different (larger) infinitesimal probability to any history starting from the present moment. In any case, this shows the model-dependence of absolute probabilities. It is a counterargument against infinitesimal probabilities only if one presupposes that such model-dependence does not exist. Indeed, classical probability theory does not violate translation symmetry in this case, but it does assign probability 0 to individual histories, which has its own drawbacks. (For instance, it makes the theory unsuitable to express any learning from conditionalizing on finite, initial segments.)
Recall that NAP theory also allows us to model an infinite sequence, in which the individual tosses are indexed by \(T = {\mathbb {Z}}\). In this case it may still be suggestive to consider the moment indexed by \(t=0\) as the present. (Formally, in this case there are infinitely many, mutually inconsistent moments in the instant \(t=0\).) If the outcome of all past tosses are known, one may conditionalize on this information, after which the probabilities come out exactly the same as in the model where time starts at \(t=0\).
6 Conclusion
This paper showed how branching time structures can be combined fruitfully with non-Archimedean probability theory. This approach vindicates McCall’s (1994, p. 161) suggestion that normalization at each instant can be achieved by an uncountable sum of hyperreal probabilities. As illustrated by the toy example of an infinite sequence of coin tosses, doing so allows us to assign an infinitesimal prior probability to each individual history. Based on this, I defined two new modal operators, called ‘appreciable possibility’ and ‘remote possibility’. The approach allows us to analyse future contingents and historical counterfactuals in a subtle way, and opens the path to further applications in the philosophy of time, modality and probability, and the foundations of physics.
Notes
I am grateful to a referee for pointing me to this reference.
Recall that, relative to a given universe, \(\Omega \), the following sentential and set-theoretic notions are equivalent, respectively: tautology and universe, contradiction and empty set, conjunction and intersection, disjunction and union, and negation and complement. The set-theoretic extensions of propositions can also be used to represent semantic entailment as is done in the algebraic logic tradition of Tarski and others (see, e.g., Beall et al., 2019, §3.1).
A complication may arise for finite sample spaces that are obtained by conditioning or partitioning starting from an infinite sample space. In such cases, it may happen that \(\mu (\phi )=0\) while
 is true for some
\(\phi \). Although we do not focus on this case here, resolving it can be achieved along the same lines as the proposal in this paper.
is true for some
\(\phi \). Although we do not focus on this case here, resolving it can be achieved along the same lines as the proposal in this paper.I am grateful to a reviewer for bringing this paper to my attention.
I am grateful to a reviewer for suggesting this connection.
From transitivity and irreflexivity, it follows that the relation < is also asymmetric:
$$\begin{aligned}\forall m_1,m_2 \in M \left( (m_1< m_2) \Rightarrow \lnot (m_2 < m_1) \right) .\end{aligned}$$Specifically, h is a ‘history’ if and only if all of the following hold:
-
\(h \subseteq M\),
-
h is linearly ordered:
$$\begin{aligned}\forall m,m' \in h (m < m' \vee m = m' \vee m > m'),\end{aligned}$$ -
h is maximal with respect to the above linear order.
Hence, in a history, any two distinct elements are comparable via <.
-
The existence of non-measurable subsets of any uncountable set is a consequence of the Axiom of Choice. An early example of subsets of the real numbers that are not Lebesegue-measurable was given by Vitali (1905). For this reason, Kolmogorov (1956) phrased his axiomatization of probability theory in terms of \(\sigma \)-algebras of measurable subsets, called events.
Although in realistic cases one cannot expect to learn which history is actual, the point here is that even an ideal observer with infinite memory in a toy scenario cannot achieve this update using standard probability theory.
Although the details are usually not spelled out in this way, also in applications of standard probability theory one has to define ingredients (1–3) and (5), after which the properties of classical calculus together with Carathéodory’s theorem lead straight to the absolute probability function, \(\mu \), in the final ingredient (11).
A family of finite, non-empty subsets of \(\Omega \), \(\Lambda \), is called a directed set if the following two conditions are satisfied: (1) if \(\lambda _1, \lambda _2 \in \Lambda \), then \(\exists \lambda _3 \in \Lambda \) such that \(\lambda _1 \cup \lambda _2 \subset \lambda _3\) and (2) the union of all the elements of \(\Lambda \) is equal to \(\Omega \).
Observe that if we fix a certain event \(A \in {\mathcal {P}}(\Omega )\), \(p(A \mid \cdot )\) is a one-place function and an element of the set \({\mathfrak {F}}(\Lambda ,{\mathbb {R}})\). (So, A may be infinite, but the conditioning set must be finite and an element of \(\Lambda \).) One can introduce addition, multiplication, and a partial order on functions, such that this set is effectively a partially ordered ring.
Observe that in this case \(P(H_{\phi ,m})=P(\varnothing )=0\), while \(P(H_m)>0\).
Observe that, in this case, \(P(H_{\phi ,m})\) is the infinitesimal probability of a single history, while \(P(H_m)\) is larger than an infinitesimal for all m.
Crucially, McCall ’s (1994) distinction does not align with Adams ’s (1970) distinction between indicative and subjunctive conditionals. In fact, an example of McCall’s second type is Adams’s indicative example: “If Oswald didn’t kill Kennedy, somebody else did.” We will not consider this case further.
The goal here is not to analyse this ‘since’-conditional, but merely to show that the historical counterfactual under consideration (with ‘if’) is of the kind that admits a probabilistic analysis (cf. McCall, 1994, p. 183).
The link between the assertability of conditionals and their corresponding conditional probability has been widely discussed in the context of Adams’s thesis (due to Adams, 1965), see, e.g., Egré and Rott (2021, §5.1). The assertability of counterfactuals falls outside the scope of the current paper, but remark that this issue has been discussed in a branching context by Wawer and Wroński (2015).
The metaphor is a nod to the thought experiment of “replaying life’s tape”, introduced by Gould (1989, p. 48) and discussed by Beatty (2006) and other philosophers of biology to address matters of contingency in biological evolution. McCall (1994, Chapter 6) speaks of “resurrecting” a past branched snapshot of the universe.
In the example, independence may be understood as statistical independence, but in other cases causal independence might be the relevant notion. In their analysis of truth values of historical counterfactuals in the context of branching space-times, Placek and Müller (2007, §6.1) indeed considered taking into account causally independent (construed as space-like separated) events.
References
Adams, E. (1965). The logic of conditionals. Inquiry, 8, 166–197.
Adams, E. (1970). Subjunctive and indicative conditionals. Foundations of Language, 6, 89–94.
Beall, J., Restall, G., & Sagi, Gil. (2019). Logical consequence. In E. N. Zalta, (Ed.), Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/spr2019/entries/logical-consequence/
Beatty, J. (2006). Replaying life’s tape. Journal of Philosophy, 103, 336–362. https://doi.org/10.5840/jphil2006103716
Belnap, N., & Müller, T. (2010). Branching with uncertain semantics. British Journal for the Philosophy of Science, 61, 681–696. https://doi.org/10.1093/bjps/axq001
Belnap, N., Perloff, M., & Xu, M. (2001). Facing the future: Agents and choices in our indeterminist world. Oxford University Press.
Benci, V., & Di Nasso, M. (2003). Numerosities of labelled sets: A new way of counting. Advances in Mathematics, 173, 50–67. https://doi.org/10.1016/S0001-8708(02)00012-9
Benci, V., & Di Nasso, M. (2019). How to measure the infinite: Mathematics with infinite and infinitesimal numbers. World Scientific.
Benci, V., Horsten, L., & Wenmackers, S. (2013). Non-Archimedean probability. Milan Journal of Mathematics, 81, 121–151. https://doi.org/10.1007/s00032-012-0191-x
Benci, V., Horsten, L., & Wenmackers, S. (2018). Infinitesimal probabilities. British Journal for the Philosophy of Science, 69, 509–552. https://doi.org/10.1093/bjps/axw013
Burton, D. M. (1970). A first course in rings and ideals. Addison-Wesley Publishing Company.
Easwaran, K. (2014). Regularity and hyperreal credences. Philosophical Review, 123, 1–41. https://doi.org/10.1215/00318108-2366479
Egré, P., & Rott, H. (2021). The logic of conditionals. In E. N. Zalta, (Ed.), Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/win2021/entries/logic-conditionals/
Foley, R. (2009). Beliefs, degrees of belief, and the Lockean thesis. Synthese Library. In H. Huber & C. Schmidt-Petri (Eds.), Degrees of belief (Vol. 342, pp. 37–47). Springer.
Goldblatt, R. (1998). Lectures on the hyperreals; An introduction to nonstandard analysis. Graduate texts in mathematics (Vol. 188). Springer.
Gould, S. J. (1989). Wonderful life: The Burgess Shale and the nature of history. Norton.
Gruber, P. M. (2007). Convex and discrete geometry. Grundlehren der mathematischen Wissenschaften (Vol. 336). Springer.
Hacking, I. (1975). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.
Humphreys, P. (1985). Why propensities cannot be probabilities. Philosophical Review, 94, 557–570.
Kaplan, D. (1989). Demonstratives: An essay on the semantics, logic, metaphysics, and epistemology of demonstratives and other indexicals. In J. Almog, J. Perry, & H. Wettstein (Eds.), Themes from Kaplan (pp. 481–563). Oxford University Press.
Kelly, K. T. (1996). The logic of reliable inquiry. Oxford University Press.
Kolmogorov, A. N. Grundbegriffe der Wahrscheinlichkeitrechnung. Ergebnisse der Mathematik. 1933. Translated by N. Morrison, Foundations of probability. Chelsea Publishing Company, 1956 (2nd ed.).
Levi, I. (1989). Possibility and probability. Erkenntnis, 31, 365–386. https://doi.org/10.1007/bf01236570
Lewis, D. K. (1986). Philosophical papers (Vol. 2). Oxford University Press.
McCall, S. (1994). A model of the universe: Space-time, probability, and decision. Clarendon Press.
Müller, T. (2011). Probabilities in branching structures. In D. Dieks, W. C. Gonzalez, S. Hartmann, T. Uebel, & M. Weber (Eds.), Explanation, prediction, and confirmation. The philosophy of science in a European perspective (Vol. 2, pp. 109–121). Springer.
Nelson, E. (1987). Radically elementary probability theory. Princeton University Press.
Nover, H., & Hájek, A. (2004). Vexing expectations. Mind, 113, 237–49. https://doi.org/10.1093/mind/113.450.237
Øhrstrøm, P., & Hasle, P. Future contingents. In N. Zalta (Ed.), Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/future-contingents
Peterson, M. (2023). The St. Petersburg paradox. In E. N. Zalta & U. Nodelman (Eds.), Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/fall2023/entries/paradox-stpetersburg/
Placek, T. (2012). On individuals in branching histories. Synthese, 188, 23–39. https://doi.org/10.1007/s11229-012-0082-2
Placek, T., & Müller, T. (2007). Counterfactuals and historical possibility. Synthese, 154, 173–197. https://doi.org/10.1007/s11229-005-0617-x
Ploug, T., & Øhrstrøm, P. (2012). Branching time, indeterminism and tense logic; Unveiling the Prior–Kripke letters. Synthese, 188, 367–379. https://doi.org/10.1007/s11229-011-9944-2
Poisson, S.-D. (1837). Recherches sur la probabilité des jugements en matiére criminelle et en matiére civile, précédées des régles gènérales du calcul des probabilités. Paris: Bachelier.
Prior, A. N. (1957). Time and modality. Oxford University Press.
Prior, A. N. (1967). Past, present, and future. Oxford University Press.
Reyna, V. F. (2004). How people make decisions that involve risk: A dual-processes approach. Current Directions in Psychological Science, 13, 60–66. https://doi.org/10.1111/j.0963-7214.2004.00275.x
Robinson, A. (1966). Non-standard analysis. North-Holland.
Skyrms, B. (1980). Causal necessity. Yale University Press.
Smith, N. J. J. (2014). Is evaluative compositionality a requirement of rationality? Mind, 123, 457–502. https://doi.org/10.1093/mind/fzu072
Starr, W. (2022). Counterfactuals. In E. N. Zalta & U. Nodelman (Eds.), Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/win2022/entries/counterfactuals/
Thomason, R. H. (1970). Indeterminist time and truth-value gaps. Theoria, 36, 264–281.
Vitali, G. (1905). Sul problema della misura dei Gruppi di punti di una retta: Nota. Tipografia Gamberini e Parmeggiani.
Wawer, J., & Wroński, L. (2015). Towards a new theory of historical counterfactuals. In A. Arazim & M. Dancak (Eds.), Logica Yearbook 2014 (pp. 293–310). College Publications.
Wenmackers, S. (2019). Infinitesimal probabilities. In J. Weisberg & R. Pettigrew (Eds.), Open handbook of formal epistemology (pp. 199–265). PhilPapers Foundation. https://philpapers.org/archive/WENIP.pdf
Williamson, T. (2007). How probable is an infinite sequence of heads? Analysis, 67, 173–180. https://doi.org/10.1093/analys/67.3.173
Acknowledgements
I am grateful to the anonymous referees for their constructive comments that greatly helped to improve this paper. I also want to thank Hannes Leitgeb and the other participants of the Bristol workshop on ‘Historical Counterfactuals’ held in August 2012 for their encouraging feedback on an early version of this paper. This project was supported by the Research Foundation Flanders (FWO Grant No. G066918N and G0C3322N).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wenmackers, S. Remote possibilities in branching time structures. Synthese 204, 62 (2024). https://doi.org/10.1007/s11229-024-04622-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-024-04622-y


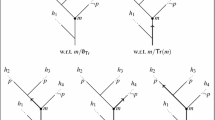





 :
: ;
; :
: is a non-zero infinitesimal;
is a non-zero infinitesimal; is true for some
is true for some