A comprehensive and policy-oriented model of the hydrogen vehicle fleet composition, applied to the UK market

Abstract

Road vehicles play an important role in the UK’s energy systems and are a critical component in reducing the reliance on fossil fuels and mitigating emissions. A dynamic model of light-duty vehicle fleet, based on predator-prey concepts, is presented. This model is designed to be comprehensive but captures the important features of the competition between types of vehicles on the car market. It allows to predict the evolution of the hydrogen based vehicle’s role in the UK’s vehicle fleet. The model allows to forecast effects of policies, hence to inform policy makers. In particular, it is shown that the transition happens only if the hydrogen supply can absorb at least 350,000 new vehicles per year. In addition to this, the model is used to predict the demand for hydrogen for the passenger vehicle fleet for various scenarios. A key finding of the policy-oriented model is that a successful transition to a clean fleet before 2050 is unlikely without policies designed to fully support the supply chain development. It also shows that the amount of hydrogen required to support a full hydrogen based vehicle fleet is currently not economically viable; the needed infrastructure requires yearly investment larger than £2.5 billions. In order to mitigate these costs, the policy focus should shift from hydrogen based vehicles to hybrid vehicles and range extenders in the transport energy system.

1 Introduction

The global energy consumption rate is increasing annually, even after the signature of the Paris Agreement. In particular, the demand for fossil fuels is still increasing, (International Energy Agency 2020b). The transportation sector is currently responsible for a quarter of energy demand, thus impacting the level of greenhouse gases and pollution produced, as shown in (International Energy Agency 2020a). It has remained stable for the last three decades, as demonstrated in (Acar and Dincer 2014; International Energy Agency 2020a). Consequently, governing bodies are putting into place policies to transition to a low carbon transport system. There is indeed a major shift in the public policies; almost twenty countries are planning on removing diesel and petrol cars from the roads (Meckling and Nahm 2019). In particular, the UK government has recently planned the "road to zero" policy. The UK’s objectives are simple but ambitious: the entire fleet should be composed of zero-emissions vehicles by 2050 (UK Department of Transport 2018). By 2030, no more conventional vehicles will be sold.

Such policies can drive the increasing demand and investments in alternative fuel vehicles (see works from (Bauer et al. 2020; Hackbarth and Madlener 2013; Ito et al. 2013; Tsai et al. 2023; Zhang and Fujimori 2020)), to replace the internal combustion engine vehicle (ICEVs) fleet with zero-emission vehicles. Two technologies for zero-emissions vehicles seem promising at this point: the celebrated electric vehicles, and hydrogen-based vehicles (HBVs). Using hydrogen in a fuel cell only produces water and heat as waste, eliminating emissions produced by internal combustion engine vehicles. For this reason, and to comply with the Road To Zero objectives, the UK government (see (UK Secretary of State for Business, Energy & Industrial Strategy 2021)) among many other countries and institutions, are planning to develop the hydrogen industry. In particular, the UK government is planning 5GW of production capacity for transport and industrial sector in the 2020 Green Industrial Revolution plan (UK Government 2020). The production and distribution of hydrogen is associated with an energy cost (Yu et al. 2021), and so, emphasis on producing hydrogen from renewable energy resources is critical for long-term green, sustainable transport network, as known for more than two decades (Abbasi and Abbasi 2011; Al-Mufachi and Shah 2022; Bolat and Thiel 2014; Fayaz et al. 2012; Momirlan and Veziroglu 2005; Tolga Balta et al. 2009). Hydrogen-technologies has the potential to become cheaper and more environmental friendly than battery technologies (Habib and Butler 2022). Noteworthy, hydrogen is not only a possible fuel, but can be used as well for developing energy storage systems (see (Dincer and Acar 2015; Kovač et al. 2021)), effectively mitigating some issues related to renewable energy resources. In particular, alternative technologies for transport are critical to investigate and develop, when a transition to a full battery-based vehicle fleet is known to be at risk with current mining and metal resources (Bongartz et al. 2021; Liu et al. 2022), with possibilities of metal shortage in the next few years.

Consequently, hydrogen has the potential to play a fundamental role in tomorrow’s energy system, as shown in many works such as (Capurso et al. 2022; Fayaz et al. 2012; Faye et al. 2022; Pudukudy et al. 2014; Sharma and Ghoshal 2015). The main obstacle hindering vehicle manufacturers and consumers from embracing hydrogen fuel cell vehicles are the high costs and high levels of complexity associated with the hydrogen supply chain infrastructure, i.e., in terms of the options available at each infrastructure node and recharge stations (Bolat and Thiel 2014; Dagdougui et al. 2012). Constructing new infrastructures is indeed extremely costly, and poor choice in the design of the support infrastructure can lead to failure in the transition, as several studies have suggested (Park et al. 2022; Ratnakar et al. 2021; Stephan and Sullivan 2004). The fact that the UK is still a net importer of hydrogen in 2022 highlights the importance of the matter (Al-Mufachi and Shah 2022). As a matter of fact, refuelling stations in London deliver hydrogen from electrolysis at around £0.20/kWh, making refuelling twice more expensive than petrol. To this date (early 2023), there is only fourteen hydrogen refuelling station in the UK. Indeed, one of the key challenges is to secure sufficient investments when there is no assurance of profitable demand, which is enslaved to the hydrogen based vehicle fleet. Moreover, it has been shown that a growth of the delivery infrastructure triggers a feedback mechanism (see (Bauer et al. 2020)), sustaining in return the growth of the hydrogen supply chain and of the hydrogen-based vehicles (Dagdougui et al. 2012; Haslam et al. 2012). It means that governing policies have a decisive role to play in encouraging the transition, as supported by several studies (Al-Mufachi and Shah 2022; Brand et al. 2020; Haslam et al. 2012). Strong policies are also put into place in EU, with the Hydrogen Strategy (European Commission 2020), and Japan (Ministry of Economy, Trade and Industry of Japan 2019).

To understand the current and future environmental impact of the UK road transportation system, models able to represent fleet evolution are needed. Such models are pivotal to develop policies through developing and evaluating scenarios and their consequences (Kloess and Müller 2011). To the author’s knowledge, models developed so far, do not encompass all the following properties: (i) the general growth of the fleet (Nazari et al. 2019; Tiwari et al. 2020; Wang 2011), (ii) the coexistence and the nonlinear interactions/feedback between the different types of advanced vehicles in the fleet composition (Comello et al. 2021; Park et al. 2011, 2022; Tiwari et al. 2020), (iii) the role of the supply chain in energy (Nazari et al. 2019; Stasinopoulos et al. 2021; Stephan and Sullivan 2004). Considering the fleet size is fundamental to design the infrastructure, but it is usually overlooked (see Moreno-Benito et al. 2017; Nazari et al. 2019; Stephan and Sullivan 2004) Additionally, predicting growth and decline allows to re-purpose the infrastructure (Samsatli and Samsatli 2019). Fleet composition is mostly tackled as a transitional process based on external factors (such as energy prices or the supply chain infrastructure, to name a few) as in (Park et al. 2022; Shafiei et al. 2017; Stephan and Sullivan 2004; Zhao and Melaina 2006). Other approaches are based on probabilistic models (Comello et al. 2021; Raugei et al. 2021; Tsai et al. 2023), rather than a competition process including feedback loop and the fleet composition (Musti and Kockelman 2011; Stasinopoulos et al. 2021). Bass models and logistic models, for instance, cannot represent fleet compositions when adoption of each type of vehicle is driven by different factors as seen in (Park et al. 2022). In (Stasinopoulos et al. 2021), the authors proposed a dynamic approach to evaluate fleet composition in order to estimate GHG emissions. The fleet model does not take into account sizing factors such as supply chains and energy availability. Policies are ill-represented, as scaling factors.

The UK intends to reduce its carbon account by at least 100% for the year 2020 than the 1990 baseline (UK Government 2019b). The UK government announced in 2017 that it will end the sale of all new conventional petrol and diesel cars and vans by 2040 (UK Government 2019a). It has recently been announced that this goal will be moved forward to 2030. This means drastic changes in the composition of vehicle fleet in the UK will happen, with associated changes and stress in the chain supply of fuel.

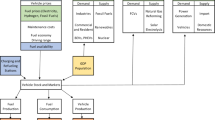
The main aim of this paper is to deliver a realistic model of the evolution of the conventional and zero-emission fleets that can be used to efficiently inform policy makers (see Fig. 1). It means that the model has to be comprehensible, informative and take into account the fleet composition, for policies to be crafted. Additionally, the model has to reflect reality and has to be able to predict the effects of policies. A dynamic systems based approached is chosen. The main reason is the flexibility of dynamical systems. They allow a holistic approach. Rather than focusing on individual, stochastic behavior such as in agent model (Köhler et al. 2009; Park et al. 2011; Spangher et al. 2019), system dynamics allows to study and understand the mechanisms of interactions between parts of the system. It allows to model feedback loops and nonlinearities, and how the current fleet composition influences directly its evolution and directly the parameters related to the growth rates of the each type of vehicles. In particular, it allows to model properly how small changes in the conditions can lead to large differences in the results. System dynamics models allow also to model directly stocks and flows, which is key in understanding the dynamics of fleet compositions. Finally, there exists already a zoology of models, such as (Maybury et al. 2022; Morrison 2012; Stasinopoulos et al. 2021).

Fig. 1

Dynamic model of the growth of vehicle fleets. Stocks are represented with the boxes, and fluxes are represented with the arrows

In the present work, the model is a modified Lotka-Volterra model (LVM). The LVM, also known as predator-prey model, is based on the growth model exploring interactions between two or more diverse competitors, (Wang and Wang 2016). This allows to inherently take into account non linear interactions in a tractable way. The non-linear approach allows to consider extreme fleet compositions without needing extra model parameters. Another main justification is that the LVM, upon light modification, shares similarities with Bass models in the structure of the self sustain growth. In particular, Lotka-Volterra models provide a comprehensive understanding of the landscape, rather than just focusing on individuals, contrary to agent based models. It makes such models appropriate for designing policies. The Lotka-Volterra equations have frequently been utilised in research areas modelling competing technologies (Zhang et al. 2014), despite being defined originally to analysis problems concerning population dynamics  (Gokmen et al. 2015). In particular, it has been used to study the impact of new technologies in competitive markets (see (Xia et al. 2022)) and for designing policies for regulating new markets in (Mitropoulou et al. 2022). In (Stasinopoulos et al. 2021), the dynamics system used shares similarities with an LVM, and (Liang and Meng 2021) used an LVM in the context of public transport, to model the competition between Bus and Metro. In this work, the LVM has been modified to reflect the effects of the supply chain in energy. The model is validated in the context of the United Kingdom’s market. The model delivers two main results. Firstly, it is able to reproduce the evolution of the vehicle fleet. It follows that the model captures some of the key principles that drive the vehicle fleet composition, and hence has some predictive properties that can be leveraged by stakeholders (Nikas et al. 2021). The influence on parameters of the model on the outcomes is also investigated. It follows that model-driven policies, based on the insight the model gives on the evolution on the fleet composition, are enabled. As stated earlier, it is fundamental to secure investments and hence sustain the growth of the fleet, hence triggering a reinforcement loop. Secondly, it allows to run predictive simulations with respect to different scenarios, and hence to determine the needs or efficiency of policies. In particular, to mitigate the cost of transition to a sustainable vehicle fleet, range extenders need to be considered (Dong et al. 2020).

The paper is organized as follows. The framework and model are discussed in Sect. 2. The resulting model is validated and its mathematical properties are investigated, in Sect. 3. Policies focused on the UK situation are discussed Sect. 4. Concluding remarks close the paper in Sect. 5. A list of acronyms and symbols used throughout the document is shown in Table 1.

Table 1 Acronyms, abbreviations and symbols used throughout the paper

2 A modified Lokta–Volettra model for vehicle fleet composition

Lack of historical data of hydrogen fuel cell vehicles can be a limitation in using forecasting models. Developing economic growth model driven by data from conventional vehicles may overcome this issue. Additionally, utilising dynamical systems to model the hydrogen supply chain opens up many possibilities in integrating various powerful mathematical tools such as sensitivity analysis and optimal control.

The product diffusion model (Wang and Wang 2016) is not able to fully explain the diffusion behaviour and mechanism in a mutually competitive market. Since, non fuel cell hybrids, electric vehicles and other ultra-low emissions vehicles are also expected to compete in the road transport market making the representation of mutual interaction necessary. For this reason the Lotka-Volterra model is considered. The model structure captures (i) opportunities of changing vehicles as in agent based models, (ii) growth rates and iii) the importance of the energy supply chain. It is hence expected to be robust and applicable even for extreme cases in fleet compositions. The model is presented Sect. 2.1. The classical predator-prey system was first considered by Lotka in 1920 modelling undamped oscillations for chemical reactions and then later by Volterra to predator-prey interactions (Evans and Findley 1999).

These equations will be modified for reflecting more accurately the market, using economic growth principles.

2.1 Lotka–Volterra model

The predator–prey interaction consists of a pair of nonlinear first-order autonomous ordinary differential equations. In the present study, the preys correspond to the population already in place, i.e., the conventional vehicles $N_{conv}$. The predators correspond to the new technology introduced on the market, i.e. the hydrogen-based vehicles $N_{zero}$.

The evolution of the number of preys is modelled by Eq. (1):

$$\begin{aligned} {\dot{N}_{conv}}= N_{conv}({\gamma }_{conv}- aN_{zero}) \end{aligned}$$

(1)

The number of preys, $N_{conv}$, increases with its own growth rate ${\gamma }_{conv}$, and decreases with the attacks of predators. This decrease depends on the number of predators $N_{zero}$, the attack rate $a$ of the predators and the number of available prey. The units of the rate of attack is $time^{-1} predator^{-1}$. It simply translates both the pressure on the population of preys and the effect on the growth rate, induced by the presence of the predators.

The number of predators evolves similarly:

$$\begin{aligned} {\dot{N}_{zero}}= N_{zero}(\epsilon N_{conv}- {\gamma }_{zero}) \end{aligned}$$

(2)

In Eq. (2), preys are replaced by predators in the system with an efficiency $\epsilon$. The units of the efficiency is $time^{-1} prey^{-1}$. It simply translates that the growth rate is mostly driven by the available food supply (the preys, or the market size). However, predators compete for the market; a negative sign is associated with the growth rate ${\gamma }_{zero}$.

The Lotka–Volterra model model (LVM) is the coupling of Eqs. (1) and (2):

$$\begin{aligned} \left\{ \begin{array}{ccc} {\dot{N}_{conv}}&{}=&{} N_{conv}({\gamma }_{conv}- aN_{zero})\\ {\dot{N}_{zero}}&{}=&{} N_{zero}(\epsilon N_{conv}- {\gamma }_{zero}) \end{array} \right. \end{aligned}$$

(3)

The LVM results in periodic growth and decay for both the predator and prey in response to the growth and decay of the other, see Fig. 2. The LVM models and predicts populations dynamics, including extreme cases when populations evolves from small to large. The growth rates are not only intrinsic to the type of vehicles, but reflects non-linear interactions between fleets. In that sense, it allows to take into account feedback and phenomenon hard to capture in Bass models (Stasinopoulos et al. 2021) or agent-based models (Spangher et al. 2019).

Fig. 2

Prey-predator system, with ${\gamma }_{conv}=2/3$, $a=4/3$, $\epsilon ={\gamma }_{zero}=1$. Initial conditions are $(N_{conv},N_{zero})=(r,0.5r)$, for various r. a Phase plot. bTime series. Solid lines correspond to preys, dashed lines to predators

An oscillatory behavior is not expected nor realistic for the evolution of conventional and hydrogen-based vehicles fleets. In the next section, the Lotka–Volterra model is modified to encompass more realistic dynamics.

2.2 Modified Lokta–Volettra model

The growth of the conventional vehicle fleet has been historically modelled as linear (Hugosson et al. 2016; Leibling 2008; Wei and Cheah 2015). This would mean that the fleet is expected to grow without a cap.

This is intuitively incorrect, and some recent models actively take that into account, using probabilistic approach in (Nazari et al. 2019), or dynamic systems approach with a negative feedback related to the retirement of vehicles in (Stasinopoulos et al. 2021). The fleet growth is expected to eventually decline due to several factors: (i) the availability of fuel (ii) the maturity of the market and (iii) the introduction of more desirable and sustainable alternatives.

To develop previous approaches, we propose that the linear transient growth can be interpreted as a first order model. The seemingly linear growth can be the sign of a non-mature market. Based on this remark,

a first order equation, based on the available energy, is introduced, to map the growth of conventional vehicles.

The total mass of fuel consumed per year, $m$, depends on the number of vehicles ${N_v}$ times the mass of fuel consumed per vehicle, $m_i$:

$$\begin{aligned} m={N_v}\times m_i \end{aligned}$$

(4)

Note that this equation can be applied to any fleet. For conventional IC vehicle, the total mass $m$ would be the mass of petrol used per year, while for hydrogen vehicle, it would be the mass of hydrogen being used per year.

Differentiating Eq. (4) leads to the rate of total mass consumed per year:

$$\begin{aligned} {\dot{m}}={\dot{{N_v}}} \times m_i+ {N_v}\times \dot{m}_i \end{aligned}$$

(5)

Rearranging:

$$\begin{aligned} \begin{array}{ccl} {\dot{{N_v}}} &{}=&{} -\dfrac{\dot{m}_i}{m_i}{N_v}+ \dfrac{{\dot{m}}}{m_i}\\ &{}=&{} -\gamma {N_v}+ \mu \end{array} \end{aligned}$$

(6)

where we note $\gamma := \dfrac{\dot{m}_i}{m_i}$ (per years, or in $years^{-1}$) and $\mu := \dfrac{{\dot{m}}}{m_i}$ (in vehicles per year, or Mveh/year). The quantity $\mu$ is the mass of fuel used annually divided by the mass of fuel consumed by a car. It corresponds to the maximum number of new vehicles that can be sustained, on a yearly basis, by the supply chain of fuel.

The amount of fuel consumed, annually, by a car is positive and can be approximated by a constant (it holds as long as there is no breakthrough in technology). The quantity $\gamma$ is the mass of fuel used annually by a car divided by the mass of fuel consumed by a car. This is an inverse time scale, which corresponds to the time needed by the fleet to absorb all the resources. In other words, it is the rate at which the system evolves. It corresponds to a growth rate. The rate, $\gamma$ is actually positive. It has a powerful implication: the actual rate is driven by the resources $\mu$; without resources, the number of vehicles tend to zero. The presence of the source term mitigates this dynamics: the available fuel, which acts as an available resource, drives up the number of vehicles.

One can assume that the individual car consumption, ${\dot{m_i}}$, is constant, and that the fuel consumption, per year, will reach either an optimal or maximal value.

Taking the limit, the number of vehicle will then reach a plateau as well:

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } {N_v}= \dfrac{{\dot{m}}}{{\dot{m_i}}} \end{aligned}$$

(7)

This value depends exclusively on the total fuel resources available for consumption per year ${\dot{m}}$, divided by the individual car consumption $\dot{m}_i$. It means that $\lim \limits _{t\rightarrow \infty } {N_v}$ is the number of cars that can, ultimately, be supported by the system, i.e., by the supply chain of fuel. It is a fundamental difference with a linear growth model, that diverges. Note that this analysis can be carried on for battery electric vehicles, by doing to following: (i) convert the mass of fuel into equivalent energy available, in kWh; (ii) identify the fraction of the full electric capacity that can be redirected to electric vehicle, in kWh. The rest of the methodology will remain unchanged.

The growth model from Eq. (6) does not allow to represent competition between conventional and hydrogen fleets. However, it enlights on how to modify the LVM equations from Eqs. (1) and (2) to take into account the realistic development of the fleet.

The growth rates are, in these equations, respectively ${\gamma }_{conv}$ and ${\gamma }_{zero}$ for the preys and the predators.

Considering the previous remarks, we propose to modify the standard Lotka-Volterra model for representing the competition between conventional and non-conventional vehicles.

The growth rate for conventional fleet ${\gamma }_{conv}$ is replaced, in Eq. (6), with the coupling term from Eq. (3):

$$\begin{aligned} {\gamma }_{conv}\leftarrow -{\gamma }_{conv}- aN_{zero}. \end{aligned}$$

(8)

Similarly, for the hydrogen fleet:

$$\begin{aligned} {\gamma }_{zero}\leftarrow \epsilon N_{conv}- {\gamma }_{zero}. \end{aligned}$$

(9)

Consequently, we propose that the number of cars that can be supported by the infrastructures in conventional fuel and hydrogen can be described by the following model:

(10)

where $\mu _{conv}$ and $\mu _{zero}$ correspond to the resources for conventional and hydrogen vehicles. The attack $a$ and efficiency $\epsilon$ rates translate how the policies influence the number of vehicles. In particular, when $a=\epsilon$, it means that no new cars is introduced due to external factors (i.e., policies), but that a fraction of the vehicles is simply transitioning from one fleet to the other. In the rest of the manuscript, for simplicity, the model from Eq. (10) will be referred as Lotka-Volterra model (LVM). The architecture of the model is illustrated Fig. 1.

3 Results and discussions of the proposed fleet composition model

In this section, we will first validate the model proposed in Sect. 2. Validating the model helps to determine if it represents the real-world fleet composition dynamics accurately and reliably. This is pivotal for decision making.

The second part of this section will focus on analyzing the properties of the model. It allows to get insight not only about the model, but as well into the behavior of the real-world system. This includes understanding the system’s stability and sensitivity to changes in input and to parameters. We believe comprehensive models are crucial for designing and implementing model-based policies.

3.1 Validation of the proposed model

The models introduced in Sect. 2 have been implemented. They are being solved using a standard Runge-Kutta 4 scheme. To validate the model, we aim at representing the UK market.

The first order growth model developed in Sect. 2 was simulated in Fig. 3. The parameters used are $\gamma = 0.01\,year^{-1}$ and $\mu = 0.65\,Mveh.year^{-1}$. These parameters were identified using a standard fit procedure, against the UK’s road vehicles data from (Leibling 2008). This data set provide the conventional vehicle fleet size evolution between 1960 and 2006, with predictions up to 2016.

Fig. 3

UK fleet size simulated with the growth model. a Comparison with data from (Leibling 2008). b long-term prediction

The point-wise error between a data point $x_{data}$ and a point produced by the model $x_{model}$ is defined as:

$$\begin{aligned} e(x_{data},x_{model}):=\left| \dfrac{x_{data}-x_{model}}{x_{data}}\right| . \end{aligned}$$

(11)

The growth of conventional vehicles is compared to the growth model, Fig. 3. The average point-wise error is $<e>=0.5\% \pm 0.3\%$. There is a strong agreement; it indicates that the model developed captures the UK’s growth.

The model is able to reasonably predict the UK’s growth for conventional vehicles. The main feature of the model is that it saturates with a total fleet of $\mu /\gamma = 65Mveh$, and around 48.5 Mveh in 2100. Assuming a population of 81 M in 2100¹, it means around 600 cars per thousand people. Not only the model matches the Gompertz saturation curve, but it also reproduces the numbers in (Dargay et al. 2007), which aligns with a saturation of two cars per household, or around 700–800 cars per thousand people (Rota et al. 2016).

There is no appropriate data, to the authors knowledge, to validate the LVM model on the hydrogen vehicle fleet. Instead, the LVM model is simulated based on the electric vehicle market, Fig. 4. The parameters used are $\gamma _{elec}= 0.001\,year^{-1}$ $a_{elec} = \epsilon _{elec}= 0.001\,year^{-1}$ and $\mu = 0.016\,Mveh.year^{-1}$. These parameters were identified using a standard fit procedure, against the UK’s road vehicles data from SMMT.

Fig. 4

UK EV fleet size simulated with the LVM model. a Comparison with data from SMMT 2022. b long term prediction

The average point-wise error is $<e>=2.6\% \pm 1.7\%$. There is a strong agreement; this indicates that the model developed captures the UK’s growth and can be used to model the evolution of the hydrogen vehicle fleet.

3.2 Analysis of the model

In this section, we investigate the mathematical properties of the model Eq. (10).

Significance of the model parameters

The significance of the parameters is fundamental when designing a model.

The growth rate parameters ${\gamma }_{zero},{\gamma }_{conv}$ are related to the first order settling time. It describes the dynamics of the organic growth of the fleet, driven by the available resources $\mu _{conv},\mu _{zero}$. The efficiency and attack rates $\epsilon ,a$ are mathematically related to the interactions between the fleets. Practically, it translates the incentive of switching from one type of vehicle to another type of vehicle similarly to the model from (Stasinopoulos et al. 2021).

Mathematical properties

We believe that investigating the properties of the model is key for decision-makers. It allows to gain a clear understanding of the behavior of the real-world system that the model aims at representing. It is fundamental, in particular, to determine how changes in the parameters of the system affect its behavior, which allows to develop data and model informed policies.

An important property is the global growth of the model. Without it, the model is not able to represent the raw evolution of the vehicle fleet. From Eq. (10):

$$\begin{aligned} {\dot{N}_{conv}}+ {\dot{N}_{zero}}= \begin{array}{l}{ N_{conv}N_{zero}(\epsilon -a) -( {\gamma }_{conv}N_{conv}+{\gamma }_{zero}N_{zero})}\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad { + \mu _{zero}+\mu _{conv}}.\end{array} \end{aligned}$$

(12)

For developing the intuition, let’s temporary assume that $a=\epsilon$ and ${\gamma }_{zero}={\gamma }_{conv}= \gamma$. Noting $N=N_{conv}+N_{zero}$ and $\mu = \mu _{zero}+ \mu _{conv}$, then Eq. (12) becomes:

$$\begin{aligned} {\dot{N}} = \mu - \gamma N \end{aligned}$$

(13)

The LVM collapses to the first-order model growth for the fleet of vehicles² (see Eq. (6)), and the total number of vehicles should be, as in Eq. (7):

$$\begin{aligned} N_{\infty } = \dfrac{\mu }{\gamma } \end{aligned}$$

(14)

Interestingly, the final fleet total is independent from the attack and efficiency rates. This means the proposed Lotka-Volterra model captures the following properties:

• the growth then saturation of the total fleet of vehicles;

• the competition between the type of vehicles;

• the dynamics of the fleet associated to each type of vehicle. A growth then saturation of the fleet, a transitional growth then decrease of the fleet, or simply a decline of the fleet are possible, depending on the set of parameters.

In the same spirit as Eq. (7), the model Eq. (10) reaches asymptotic values for $N_{conv}$ and $N_{zero}$. Putting the derivatives to zero and rearranging lead to:

$$\begin{aligned} {N_{conv}}_{\infty }=\, {} \dfrac{ {c}_{zero}+ {c}_{conv}+ \sigma - \sqrt{\Delta } }{2 \epsilon {\gamma }_{conv}}, \end{aligned}$$

(15)

$$\begin{aligned} {N_{zero}}_{\infty }=\, {} \dfrac{ {c}_{zero}+ {c}_{conv}- \sigma + \sqrt{\Delta } }{2 a {\gamma }_{zero}}, \end{aligned}$$

(16)

where

$$\begin{aligned} {c}_{zero}:=\, {} a \mu _{zero}\end{aligned}$$

(17a)

$$\begin{aligned} {c}_{conv}:=\, {} \epsilon \mu _{conv}\end{aligned}$$

(17b)

$$\begin{aligned} \sigma:=\, {} {\gamma }_{zero}{\gamma }_{conv}\end{aligned}$$

(17c)

$$\begin{aligned} \Delta:=\, {} {c}_{zero}^2 + 2 {c}_{conv}{c}_{zero}+ 2 \sigma {c}_{zero}\nonumber \\ {} + {c}_{conv}^2 + \sigma ^2 - 2 {c}_{conv}\sigma . \end{aligned}$$

(17d)

The quantities ${c}_{zero}$ and ${c}_{conv}$ can mainly be related to the supply chains for conventional and hydrogen fuels. It is expected that ${c}_{conv}> {c}_{zero}$. The asymptotic solution reveals important interactions between the conventional fleet and the hydrogen fleet.

Similarly to the first order model, the quantities $\mu _{zero}/{\gamma }_{zero}$ and $\mu _{conv}/{\gamma }_{conv}$ play a role in the asymptotic value. It captures the fact that policies, in particular when affecting the infrastructure and supply chains, influence the evolution of the fleet composition (Bauer et al. 2020). However, there are several other terms that can change the equilibrium point. The behavior of the asymptotic solution is related to the sign of the argument $\Delta$. If $\Delta$ is positive, then the asymptotic solution is a constant. If it is negative, then the solution will oscillate, as in Fig. 2.

Rearranging positive and negative terms of the argument leads to:

$$\begin{aligned} {c}_{zero}^2 + 2 {c}_{conv}{c}_{zero}+ 2 {c}_{zero}\sigma + {c}_{conv}^2 + \sigma ^2 > 2 {c}_{conv}\sigma \end{aligned}$$

(18)

The sign, in Eq. (18), is determined by the right hand side: the efficiency $\epsilon$, the growth rates, and the support received by the conventional vehicle chain supply $\mu _{conv}$. Intuitively, as long as there is enough drive for conventional vehicles, such as cheap fuel and massive availability, there will be burst of growth for this fleet, and the entire system will be destabilized.

The sensibility can also be studied, by calculating the gradient of the asymptotic solutions with respect to the parameters. The sensibility allows to predict how varying parameters affect the outcome of the system. The sensitivity has been plotted Fig. 5. Practically, it indicates how model-based policies can influence the evolution of the fleet.

Differentiation of the asymptotic value leads to Eq. (19) for the hydrogen fleet, and to Eq. (20) for the conventional fleet.

$$\begin{aligned} \dfrac{\partial {N_{zero}}_{\infty }}{\partial \mu _{zero}}= & {} \dfrac{{c}_{zero}+ {c}_{conv}+ \sigma + \sqrt{\Delta }}{2 {\gamma }_{zero}\sqrt{\Delta }} \end{aligned}$$

(19a)

$$\begin{aligned} \dfrac{\partial {N_{zero}}_{\infty }}{\partial \mu _{conv}}= & {} \epsilon \dfrac{{c}_{zero}+ {c}_{conv}- \sigma + \sqrt{\Delta }}{2 a {\gamma }_{zero}\sqrt{\Delta }} \end{aligned}$$

(19b)

$$\begin{aligned} \dfrac{\partial {N_{zero}}_{\infty }}{\partial \epsilon }= & {} \mu _{conv}\dfrac{{c}_{zero}+ {c}_{conv}- \sigma + \sqrt{\Delta }}{2 a {\gamma }_{zero}\sqrt{\Delta }} \end{aligned}$$

(19c)

$$\begin{aligned} \dfrac{\partial {N_{zero}}_{\infty }}{\partial a}= & {} -\dfrac{ \begin{array}{c} { {c}_{conv}{c}_{zero}+ \sigma {c}_{zero}+ {c}_{conv}^2 + \sigma ^2}\\ { - 2 \sigma {c}_{conv}+({c}_{conv}- \sigma ) \sqrt{\Delta }} \end{array}}{2 a^2 {\gamma }_{zero}\sqrt{\Delta } } \end{aligned}$$

(19d)

$$\begin{aligned} \dfrac{\partial {N_{zero}}_{\infty }}{\partial {\gamma }_{zero}}= & {} -\dfrac{ \begin{array}{c} { {c}_{zero}^2 + 2 {c}_{conv}{c}_{zero}+ \sigma {c}_{zero}+ {c}_{conv}^2 } \\ { - \sigma {c}_{conv}+ ( {c}_{zero}+ {c}_{conv}) \sqrt{\Delta } } \end{array}}{ 2 a {\gamma }_{zero}^2 \sqrt{\Delta } } \end{aligned}$$

(19e)

$$\begin{aligned} \dfrac{\partial {N_{zero}}_{\infty }}{\partial {\gamma }_{conv}}= & {} \dfrac{({c}_{zero}- {c}_{conv}+ \sigma - \sqrt{\Delta }) }{ 2 a \sqrt{\Delta } } \end{aligned}$$

(19f)

$$\begin{aligned} \dfrac{\partial {N_{conv}}_{\infty }}{\partial \mu _{zero}}= & {} a \dfrac{- {c}_{zero}- {c}_{conv}- \sigma + \sqrt{\Delta }}{2 \epsilon {\gamma }_{conv}\sqrt{\Delta }} \end{aligned}$$

(20a)

$$\begin{aligned} \dfrac{\partial {N_{conv}}_{\infty }}{\partial \mu _{conv}}= & {} \dfrac{- {c}_{zero}- {c}_{conv}+ \sigma + \sqrt{\Delta }}{2 {\gamma }_{conv}\sqrt{\Delta }} \end{aligned}$$

(20b)

$$\begin{aligned} \dfrac{\partial {N_{conv}}_{\infty }}{\partial \epsilon }= & {} \dfrac{ \begin{array}{c} {{c}_{zero}^2 + {c}_{conv}{c}_{zero}+ 2 \sigma {c}_{zero}} \\{- \sigma {c}_{conv}+ \sigma ^2 -( {c}_{zero}+ \sigma ) \sqrt{\Delta }} \end{array}}{ 2 \epsilon ^2 {\gamma }_{conv}\sqrt{\Delta }} \end{aligned}$$

(20c)

$$\begin{aligned} \dfrac{\partial {N_{conv}}_{\infty }}{\partial a}= & {} \mu _{zero}\dfrac{ - {c}_{zero}- {c}_{conv}- \sigma + \sqrt{\Delta } }{2 \epsilon {\gamma }_{conv}\sqrt{\Delta } } \end{aligned}$$

(20d)

$$\begin{aligned} \dfrac{\partial {N_{conv}}_{\infty }}{\partial {\gamma }_{zero}}= & {} \dfrac{ - {c}_{zero}+ {c}_{conv}- \sigma + \sqrt{\Delta } }{ 2 \epsilon \sqrt{\Delta } } \end{aligned}$$

(20e)

$$\begin{aligned} \dfrac{\partial {N_{conv}}_{\infty }}{\partial {\gamma }_{conv}}= & {} \dfrac{ \begin{array}{c} {{c}_{zero}^2 + 2 {c}_{conv}{c}_{zero}+ \sigma {c}_{zero}+ {c}_{conv}^2} \\{ - \sigma {c}_{conv}- ({c}_{zero}+ {c}_{conv}) \sqrt{\Delta } } \end{array}}{ 2 \epsilon {\gamma }_{conv}^2 \sqrt{\Delta } } \end{aligned}$$

(20f)

Naturally, the gradients $\dfrac{\partial {N_{zero}}_{\infty }}{\partial \epsilon }$ and $\dfrac{\partial {N_{conv}}_{\infty }}{\partial a}$ are respectively positive and negative.

Looking at the terms ${c}_{zero}= a \mu _{zero}$ and ${c}_{conv}=\epsilon \mu _{conv}$ develop the intuition concerning the effect of the availability of resources (i.e., the supply chains) on the fleet. In Eqs. (19a) and (19b), both terms are positive. It means the supply chains drive the augmentation in the final number of hydrogen vehicles. On the other hand, in Eqs. (20a) and (20b), both terms are negative. It means the chain supplies tend to impact negatively the number of conventional vehicle. It is reflected in the first two bars in Fig. 5a and b. It is counter-intuitive to see that the supply chain for conventional vehicle feeds more the growth of the hydrogen vehicle. But it is intrinsic to a predator-prey model: more preys mean a favorable ground (a larger market) for the predators. In general, more available resources means more possibilities from the consumer, and, ultimately, more chances for the long-term dominant competitor to enforce its position. It is reinforced by studying Eq. (19f). The gradient would be positive if ${c}_{zero}>{c}_{conv}$. A large supply chain in hydrogen triggers nonlinear effects: even the growth of conventional vehicles making the final position of the hydrogen fleet stronger. It is also shown, in Eqs. (20a) to (20f) that the hydrogen supply chain is a key parameter to reduce the number of conventional vehicles, as it appears to reduce all the gradients for the conventional fleet.

One final intuition can be developed concerning the importance of the attack rate $a$. A larger attack rate seems detrimental to the final value of the hydrogen fleet. It is unintuitive to see from Eq. (19d) unless we remember that ${c}_{conv}>{c}_{zero}$, but it is illustrated Fig. 5a. However, the effect is evident when looking at the sign of $a$ in Eq. (20a). A larger attack rate reduces the population of vehicles that hydrogen vehicles can predate on. Practically, it captures the intuition that strong policies toward zero emissions vehicles can actually drive people away from car ownership. It has been observed in highly-educated segment of the population in Norway (Fevang et al. 2021).

Fig. 5

Gradients of the asymptotic values (signed pseudo log10). a For the hydrogen fleet. b For the conventional fleet. Value used can be found in Table 2

Table 2 Parameters used for calculating the gradients of Fig. 5

4 Case study: UK market and policies

This section compares the simulation results in terms of vehicle fleet composition for different transition scenarios. A cost analysis of the hydrogen supply chain, based on the most likely scenario, follows. This section concludes on policy recommendations.

4.1 Scenarios and dynamics of fleet evolution

In 2017, the UK government announced that it will end the sale of all new conventional petrol and diesel cars and vans by 2040 (UK Government 2019a). The calendar has recently been accelerated to 2030. Further announcements by the government stated that all new vehicles and vans by 2035 will be zero emissions (UK Department of Transport 2018).

Three scenario have been designed, corresponding to policies for transitioning to hydrogen transport system. Parameters are found in Table 4. The growth rates are kept at ${\gamma }_{zero}={\gamma }_{conv}=0.01year^{-1}$, following the global results of Fig. 3. It means saturation of the fleet takes around 100 years. It will not be shown as the final values are described in Eqs. (19) and (20). To facilitate the analysis, it is assumed that $a=\epsilon$. Practically, it means that the overall growth of the fleet is only driven by the resources $\mu _{conv}$ and $\mu _{zero}$ (see Eq. (12)), and that individuals are incentivized to change cars, not to have more extra cars. The values of $a$ and $\epsilon$ reflect the level of incentivization to change vehicles. The first scenario (named Low) translates a business-as-usual policy. The available resources are kept low, and the policies for changing vehicles are not incentivized. For the second scenario (named Moderate), the parameters have been fitted to match the road-to-zero policy (UK Department of Transport 2018). The third scenario (named Aggressive) consider reaching the road-to-zero objectives by 2030.

Simulations results are plotted Fig. 6. Total growth of fleets are compatible with the expected trends, as seen Fig. 3, and both the Low and Moderate scenarios produce values similar to the ones reported in (Brand et al. 2020), as illustrated in Table 3.

Table 3 Comparison of scenario outputs for the share of zero-emissions vehicles in the fleet composition in 2050

As expected, if the hydrogen resources are low and if the incentives are low, the growth of the hydrogen fleet is slow, see Fig. 6a. This phenomenon has been reported to be the case in Korea as well in (Park et al. 2022). In particular, the scenario considered in (Park et al. 2022) corresponds to a supply chain of ${\gamma }_{zero}\approx 0.056MVeh/year$. In their work, the hydrogen vehicle fleet is expected to raise to around 2.5 M vehicle by 2040. It is very similar to the present results considering the low scenario, see Fig. 6a. Most of the fleet remain conventional. The third scenario (Fig. 6c), with an aggressive policies toward transionning from ICEVs to HBVs (translated by a high attach $a$ and efficency $\epsilon$ rates) exhibits a sharp decline in the conventional fleet, with barely conventional vehicles by 2035. The available resources in hydrogen does not yet match the conventional fuel ones, and it will take probably decades, even with strong policies, to fully transition. It is encompassed in the Moderate scenario, with $\mu _{zero}\approx \dfrac{1}{2} \mu _{conv}$. It takes around 20 years for the HBV fleet to reach initial ICEV fleet, and the conventional fleet seems to finally disappear only around 2050.

4.2 Consequences on the hydrogen supply chain

Identifying valid parameters based on the model allows to design and prepare the policies and investments. For instance, accordingly to the Moderate scenario, it means that around 0.35 Mveh new hydrogen vehicle have to be absorbed each year in the UK market.

Table 4 Values of parameters used in this study

Fig. 6

Evolution of fleets. a Low scenario. b Moderate scenario. c Aggressive scenario. Values can be found in Table 4

The model, simulated in Sect. 3, allows to predict the impact of introducing HBVs as a competitor to conventional vehicles. In the different scenarios, introducing hydrogen fuel cell vehicles into the road transport market on internal combustion engine vehicles means that hydrogen recharge stations (HRSs) have to be deployed to generate and meet the demand.

Two archetypical types of stations, one small and one large, are considered for the hydrogen production. Details are found in Table 5.

The parameters selected for the refuelling stations are given in Table 6. An assumption is that HRSs operate at $100\%$ efficiency. The parameters concerning the capacities of vehicles can be found in Table 6. It was assumed that the vehicle would be refuelled once a week when calculating the amount of fuel consumed per year per vehicle. Two kind of HBVs are considered, battery powered EVs with a fuel-cell range extender (HFCREs) and hydrogen fuel cell vehicles (noted as HFCs).

Table 5 Production capacities of small (hydrogen solar-powered electrolysis) and large (steam methane reforming) refuelling stations

Table 6 Storage capacity parameters selected for the growth model

The moderate scenario from Sect. 4.1 is considered. Around 0.35 Mveh hydrogen vehicles have to be absorbed each year by the hydrogen supply chain. Four transition scenarios are investigated in the following:

• S1: Fleet based on HFCs, supply chain based on small RS

A small station can power up to 40 HFCs per year. This means that around 8750 small HRSs have to be deployed each year, for a total of 262,500 deployed by 2050.

• S2: Fleet based on HFCREs, supply chain based on small RS

A small station can power up to 133 HFCREs per year. It means that around 2625 small HRSs have to be deployed each year, for a total of 78,750 deployed by 2050.

• S3: Fleet based on HFCs, supply chain based on large RS

A large station can power up to 400 HFCs vehicles per year. It means that around 1750 large HRSs have to be deployed each year, for a total of 20,010 deployed by 2050.

• S4: Fleet based on HFCREs, supply chain based on large RS

A large station can power up to 667 HFCREs vehicles per year. It means that around 525 large HRSs have to be deployed each year, for a total of 15,750 deployed by 2050.

A typical filling station delivers around 5 M kg/year of fuel³. It is 14 times more fuel than the corresponding hydrogen produced by a large HRS. Consequently, the amount of HRSs that has to be deployed is equivalent to 1429 fuel filling stations. This number can be positively compared to the actual 8000 filling stations in the UK. Discrepancies can be explained mostly by the assumption that HRSs operate at 100% capacity. Filling station are used at high capacity mostly during rush hours, roughly 25% of the time. At full capacity, around 2000 filling stations would be needed, a much closer figure to the 1429 filling station equivalent. Additionally, the efficiency of electric motor is higher than the efficiency of IC engines. It validates furthermore the proposed model and scenario.

4.3 Policy recommendations for UK’s transition to zero-emissions vehicles

4.3.1 Preliminary comments

The modified LVM proposed allows different penetration strategies and scenarios to be considered over time from a restrictive role to a holistic viewpoint. This is important when determining the role that hydrogen will play. However, the future private vehicle fleet will consist of more vehicle types, rather than simply HBVs and conventional ones. For further research, the two-state model can be extended to encompass other vehicles types to assess the interactions between multiple vehicles types, to outline the role that each will play. This will help assess whether hydrogen will assume a significant role as a HFCVs or constitute a role in the range-extender market. The role of HFCREs will also be interesting seeing as it demands a less exhaustive infrastructure, but a greater challenge for vehicle manufacturers.

It is important to note that hydrogen production may well result in environmental consequences. As the number of plants being built increases, the corresponding environmental impact will also increase. Stress on the grid is likely to increase dramatically as well. Notably, steam-methane reforming-based stations will have greater consequences for the environment than a solar-based electrolysis station. It is important that balance is achieved by determining the proportion of each type of station and the overall proportion of role hydrogen will play in the future’s road transportation network.

From an environmental and economic perspective, it is critical to increase the energy efficiencies and ratios of any process leading to a reduction in sources consumed, emissions, wastes and energy consumption (Spath and Mann 2000).

4.3.2 Cost of the transition

The results of the model indicate, as expected, that two factors are necessary for achieving the road-to-zero objectives.

The first one is the need for a growing hydrogen supply chain. The cost to build a small HRS is around £1million, and the cost for a larger HRS is around £5millions (Campíñez-Romero et al. 2018). It is to be noted that prices have not massively decreased, as capital cost reported in (Gallardo et al. 2022) is similar, and in (Rezaei et al. 2022), it is actually around 4 times higher. The price per kg of fuel varies little with the size of the plant, as shown in (Campíñez-Romero et al. 2018) and (Gallardo et al. 2022). It means that, at short-term, it is more likely that small-scale refuelling stations will be built, probably directly on filling station sites. For the long-term scenario, larger HRSs might be deployed to provide the hydrogen fuel, but it is not expected before a significant part of the fleet composition is based on hydrogen-based vehicles. Overall associated infrastructure costs would be around £2.5billions per year in the most conservative scenario. Such changes can only be driven by policy making, as the investments are between £2.6billion (S2 and S4) and £8.7billions (S1). These significant investments, if carried on by filling stations, will rely on businesses with usually thin margins. Strong public policies, including subsidies, will have to be dedicated to this transition (Nocera and Cavallaro 2016).

An integrated approach as part of a national strategy, is needed. Public bodies need to manage the general transition, while letting private investors and energy providers leading and deciding local investments. A reduction in costs, according to (Gallardo et al. 2022), is expected after deployement at scale. On the long term, some studies suggest an hydrogen powered vehicle fleet could be more economically efficient than a battery based one, (Habib and Butler 2022).

The second main factor is the exchange rate between ICEVs and HBVs. Strong incentive are needed for the population to transition from ICEVs to zero-emissions vehicles . Costs of alternative fuels vehicles are significantly higher than the costs for conventional ones. For allowing these vehicles to penetrate the mass market—a crucial assumption behind the proposed model—public policies are need to push both the research, development of car manufacturers and pushing for an attractive retail price of hydrogen-based vehicles (Engström et al. 2019). To minimize the cost of the infrastructure, it also means that policies should lean toward the development of a HFCRE fleet, rather than a HFC fleet.

Different studies in the literature have considered the hydrogen infrastructure deployment issue in the UK by assessing either one part of the HSC or a snapshot of the entire supply chain. This paper used a modified LVM to provide a holistic view of the UK’s private vehicle fleet by comparing three penetration strategies for both HFCVs and HFCREs. To capture the transition to a hydrogen-based infrastructure, three demand scenarios were considered derived from both current policies based on decarbonising the private vehicle fleet, and hydrogen-based projects being implemented. The annual hydrogen demand was calculated using the HFCV stock.

Current planning by the government has focused on implementing a pre-commercialised infrastructure before expanding on this across important driving routes across the country⁴. As a result, initial smaller HRSs can potentially face closure when the need for larger more centralised ones arises. Other studies have indicated that that initially a decentralised infrastructure will be built, and once the uptake of hydrogen has met 15-30% of the market share, then the strategy of a centralised infrastructure becomes more important (Seo et al. 2020). In contrast to the UK, the French government has aligned the development of the hydrogen infrastructure to the demand from different ‘niche applications’ to ensure growth of the infrastructure is matched by the growth of hydrogen fuel cell vehicles  (French Government 2019). One major component of designing a new infrastructure is to ascertain the demand and plan accordingly to avoid under-estimation and overzealous estimations, both resulting in excess costs and consumption of resources. Infrastructure planning should also encompass economies of scale from the outset, outlining a more robust and fit for purpose infrastructure ensuring that hydrogen fuel cell vehicles plays an important role and not simply a ‘niche-market’ role. Other studies have also cited the importance of economies of scale allowing hydrogen to penetrate the private vehicle market more successfully (Tlili et al. 2020). Economies of cost will play a huge role, both, in reducing costs associated with the infrastructure and pushing HFCVs towards a front runner to replace conventional vehicles.

5 Conclusions

In this paper, a dynamic model based on the Lotka–Volterra model and growth model was formulated and used to simulate the hydrogen demand based on literature. A first-order model was developed, and maps the growth of conventional vehicles. The growth model developed covers a period of 100 years and the number of vehicles is similar to those of RAC Foundation from 1971 to current projections. This suggests that the first order model developed can be used to represent the growth of conventional vehicle fleet. Since, the growth of the passenger vehicle fleet in the UK is expected to follow the same trajectory, the model can further be used to predict the number of alternative vehicles replacing the development of conventional ones. Then, a two state model was developed. It is able to project what might happen if hydrogen-based vehicles are introduced.

The original contributions presented in this work include the application of Lotka–Volterra model to UK’s road transportation. The main results are the prediction of the final composition of the fleet, and a sensitivity analysis on the parameters that influence it. It allows to identify the key parameters that policy makers can use to hasten the transition of the market and the decarbonification of the UK’s vehicle fleet. In particular, the supply chain in hydrogen is identified as the most important parameter. The cost associated to the deployment of the needed supply chain indicates that strong policies are mandatory for a successful transition.

A limitation of the work is that the simulation included assumed HRSs operation at 100% efficiency and in reality this is unlikely to be the case. Additionally, the increase in capacity has been assumed constant overtime.

This work is preliminary, and further development of the model and scenarios is being conducted. The primary benefit of utilising the Lotka–Volterra model alongside the growth model is a reduction in computing power and complexity in the modelling. Furthermore this reduced the number of parameters in comparison to other models in literature, providing a simpler means of analysing the introduction of hydrogen for passenger vehicles.

The modified LVM proposed allows different penetration strategies and scenarios to be considered over time from a restrictive role to a holistic viewpoint. This is important when determining the role that hydrogen will play. However, the future private vehicle fleet will consist of more vehicle types, rather than simply hydrogen-based vehicles and conventional ones. For further research, the two-state model can be extended to encompass other vehicles types to assess the interactions between multiple vehicles types, to outline the role that each will play. This will help assess whether hydrogen will assume a significant role as a hydrogen fuel cell vehicles  or constitute a role in the range-extender market. The role of HFCREs will also be interesting seeing as it demands a less exhaustive infrastructure, but a greater challenge for vehicle manufacturers. To improve the accuracy of the model, the parameters such as attack rates and growth rates can be empirically measured or calibrated using 4D-var method or similar data-driven filters (Fisher and Andersson 2001), and the effect of policies can be measured as well. It will allow to (i) use time dependent parameters, and (ii) identify near optimal policies, for instance using optimal control or model predictive control theories (Chu et al. 2012).