1 Introduction

According to the recently published EU Farm to Fork Strategy, farmers’ safety, health and working conditions will play a key role in building a sustainable and fair farming system, where it is especially crucial to reduce the socioeconomic impacts affecting the food and agricultural sector as well as ensuring that the European Pillar of Social Rights principles are adhered to. The European Working Conditions Survey (EWCS) reported that around 57% of farm workers experience backache, 55% upper limb pain and 46% lower limb pain, with agriculture and forestry being the most harmful occupations, with a high rate of injuries and threatening the sustainability of the sectors. (Eurofound, 2017). To integrate aspects of social sustainability of farming systems into the European Union’s (EU) Common Agricultural Policy (CAP) reform, the incorporation of social dimensions into farm performance measurement will be a real challenge. Initially, assessment of productive technologies was essentially based on economic and environmental aspectsFootnote 1 (Berre et al., 2013; Chung et al., 1997; Coelli et al., 2007; Färe et al., 1989; Førsund, 2009; Hailu & Veeman, 2001; Hoang & Coelli, 2011). Only recently, this line of research has been extended to include social factors into production technology analyses and the literature is still scarce, especially for agricultural technologies (Ait Sidhoum, 2018; Chambers & Serra, 2018; Skevas et al., 2021).

While several studies have explored the impact of the social dimension on business corporations (Berman et al., 1999; Garcia-Castro et al., 2010; Lima Crisóstomo et al., 2011; Margolis et al., 2009; Nollet et al., 2016; Saeidi et al., 2015), the literature is much scarcer on the potential benefits of socially sustainable practices on agricultural production activities. In order to incorporate the social aspects in production models, it is necessary first to define the relevant social indicators. The most often used social input indicator is related to human labor issues (Zhou et al., 2018). In this study, I have focused on working conditions to reflect the contribution of the social dimension to farm performance. In this analysis, four dimensions have been identified as components of working conditions: skill discretion; decision autonomy; psychological demand and health risk. A growing literature has documented that sustainable agriculture movements are considering workplace conditions as an important issue (Dumont & Baret, 2017). According to Gray (2013), in order to promote the social dimension of sustainability, improving workers’ conditions should be considered as important as preserving water resources or improving animal welfare.

It is being increasingly recognized that a holistic perspective of the firm performance measurement is required when targeting sustainable development. While a number of studies have already addressed the incorporation of environmental aspects when dealing with firms’ production processes (Kumbhakar & Malikov, 2018), few alternatives exist in the literature on the proper modeling of social netputs in production processes. These social factors can take a number of forms, such as labor burden reduction, improvement of farmers’ well-being, and labor conditions. Some activities, such as working conditions and farmers training, may have no direct impact on a firm's outputs, but they can improve the effectiveness of other operations (e.g., labor) that have a direct impact on its outputs. Moreover, information on the level of the social activities and their role on production processes may support the decision-making of managers in making informed choices and inform policy-makers in planning and implementing sustainable management practices. The consideration of social factors is especially crucial to reduce the socioeconomic impacts affecting the food and agricultural sectors. However, assigning a value to nonmarketable goods is not an easy process. Computing shadow prices is one methodological option for valuing non-traded goods. The literature contains a number of studies using parametric and nonparametric approaches to compute shadow prices of environmental externalities associated with production activities (Chambers et al., 2014; Fare et al., 1993; Lansink & Carpentier, 2001; Li & Ma, 2015). However, the role of social aspects on production activities has been under‐investigated so far. This study adds to the current body of knowledge evaluating the contribution of working conditions to agricultural efficiency under uncertainty by computing shadow prices of the working conditions. Measuring shadow prices of farmers’ working conditions is necessary for at least two reasons: (1) Shadow pricing may provide a direct management insight for achieving viability of the sector since they capture the quality of labor conditions in terms of its contribution to the production process. (2) The advantage of calculating shadow prices of non-marketed inputs is that they make their comparison with productive inputs possible, and therefore, making it easier for policymakers to design policies that would enhance sustainability and the economic viability of the sector.

The concept of pricing a non-marketed activity is not new. Previous works used the idea of shadow prices to quantify non-marketed goods (e.g., pollution). As the sustainability issues of production processes have become of great importance, the concept of shadow prices has been applied to other non-marketed activities such as Corporate Social Responsibility (CSR) (Aparicio et al., 2020; Puggioni & Stefanou, 2019). For agriculture, as previously mentioned, a number of studies employed parametric and nonparametric techniques to measure shadow prices of bad outputs. However, due to data challenges, few research has been conducted to quantify social activities of the agricultural sector. This work taps into this gap by measuring a price of working conditions that captures their contribution to agricultural performance.Footnote 2 According to a recent report from the EU on a new vision known as EU Farm to Fork Strategy, safety and working conditions in the agricultural sector will play an important role in the development of a sustainable food system. In this context, this paper provides the foundations for the measurement of the relative importance of working conditions in the farming sector.

In addition to the contributions mentioned above, this study also engages in other important methodological issues. First, this work addresses the gap in the current literature on data envelopment analysis by incorporating social aspects, namely working conditions to the productive efficiency of crop farms in the Spanish region of Catalonia. Second, only a few studies have accounted for the stochastic environment of the agricultural technology, and this paper aims to extend the classical deterministic DEA models by allowing for the stochastic environment of agriculture through a state-contingent approach. The rest of this article is structured as follows. In Sect. 2, I present related literature reviews. Section 3 is devoted to the methodology used in this study and describes the data. In Sect. 4, I present the results and discuss them. The last section is devoted to the conclusion.

2 Literature review

In addition to the traditional agricultural inputs (e.g., land, labor and capital), agricultural systems may require other inputs related to social performance, such as work-related issues. There is an increasing body of research exploring the socio-economic determinants of technical efficiency scores in a second stage analysis (Berre et al., 2017; Bozoǧlu & Ceyhan, 2007; García-Cornejo et al., 2020; Latruffe et al., 2004; Oladeebo & Fajuyigbe, 2007; Pérez Urdiales et al., 2016). Nevertheless, this approach has been criticized as the sample bias in the first stage affects the second step analysis, leading to inaccurate estimates of the determinants (Johnson & Kuosmanen, 2012). In this context, researchers and practitioners have been calling for the need to incorporate social aspects into models of production (Tajbakhsh & Hassini, 2018; Zhou et al., 2018). While the productivity and efficiency literature has numerous empirical applications that directly address environmental and economic measures, there is a scarcity of literature that integrates social aspects. The present study contributes to fill the research gap by considering working conditions as an input along with conventional agricultural inputs.

Improved working conditions, and similar choices by the farmers may have various impacts on crop yields. The literature on the impacts of workplace‐related factors on agricultural production efficiency is very scarce. Outside the agricultural efficiency literature, Ødegaard and Roos (2014) rely on the Malmquist productivity index and through bootstrapped DEA framework, they have investigated the effects of labor quality, measured using answers that relate to workers’ health, on the efficiency of Swedish companies. Their findings suggest an overall increase in efficiency, around half of the effect could be associated with an improvement in labor quality attributes. Veltri et al. (2016) propose a combined SFA-DEA approach to evaluate the performance of Italian banks through efficiency analysis. Their idea is to get an estimate of managerial ability from the first stage SFA model and to introduce it in the second stage DEA model as an input. They find differences in results with or without the introduction of managerial ability as a new input, which provide evidence of the contribution of work-related factors to efficiency and productivity. Chambers and Serra (2018) is another recent paper that extended the conventional efficiency measures that allow for corporate social responsibility activities of a sample of global firms using Data Envelopment Analysis. To allow for the work-related issues, the authors consider the average training hours per employee and per year as an input that positively affect firm performance. Skevas et al. (2021) also propose a framework of production performance that allows for socially responsible activities. The authors estimate a socially responsible input inefficiency of a sample of dairy farms. The socially responsible input is represented by the non-cash benefits (e.g., health insurance, pension contributions, food, accommodation, transportation, etc.) provided to workers. However, these two papers deal exclusively with efficiency estimation and not with shadow prices computation. Within the agricultural efficiency literature, the list of studies dealing with social-related issues is much shorter. There is actually only one study that integrates the working conditions of farmers in the production process (Ait Sidhoum, 2018). This companion paper seeks to quantify social outputs of agricultural activities; however, it does not account for the contribution of work-related issues to production efficiency.

Although the overall sustainability includes environmental, economic, and social dimensions, the latter has been given less attention compared to the other two pillars (Brent & Labuschagne, 2006; Lehtonen, 2004; White & Lee, 2009). While the literature has widely explored a broad spectrum of environmental indicators, there are few studies that have considered the social dimension of sustainability, in part due to its subjectivity, making its quantification very difficult. This may be reinforced by the fact that there is no scientific evidence on the framework used for measuring social sustainability, largely because there is still significant debate over the causes and effects of social impact, as well as the design and the selection of suitable social indicators (Dubois & Mahieu, 2002; Dyllick & Hockerts, 2002; Hutchins et al., 2019; van Haaster et al., 2017).

With the aim of promoting sustainability, the European Union identified appropriate metrics for sustainable agriculture (European Commission, 2008; Regulation, 2005, 2006). More specifically, the economic indicators that have been identified are linked to productivity growth, income distribution and investments, while environmental metrics are related to natural resources, land use and water quality and threats to biodiversity and wildlife habitat. While the social indicators are related to farmers’ quality of life and rural communities. In this regard, Van Calker et al. (2007) considered that social sustainability at farm level is based on labor conditions and societal sustainability indicators. Similarly, Lebacq et al. (2013) grouped the social sustainability indicators under two key categories: a private social dimension that corresponds to the well-being of farmers such as working conditions and education, and a second social dimension which can be described as a public dimension as it is linked to general expectations of the society. Our approach reflects the limited empirical data available and only focuses on the internal social dimension (related to farmers). More specifically, this paper provides a farm-efficiency model that incorporates farmers’ working conditions and shows the contribution of these work-related factors to productive efficiency.

Because of the unpredictable nature of agricultural activities, uncertainty in production should be taken into consideration when assessing farms’ efficiency. O’Donnell et al. (2010) have shown that efficiency evaluation can be significantly biased when the agricultural stochastic conditions are ignored. In the same spirit, in this paper, the state-contingent approach which identifies the relevant states of nature is employed to account for uncertainty (Chambers & Quiggin, 1998, 2000). This technique is used to account for uncertainty in production models by differentiating the outcomes according to the state of nature in which they are obtained. Our reading of the efficiency and productivity literature reveals very few applications of the state-contingent framework, and those studies which have been done have generally been limited to the estimation of very specific technologies that are concerned only by economic and environmental issues (e.g., Chambers et al., 2014; Chavas, 2008a, b; Nauges et al., 2011; Serra et al., 2014). However, the contribution of conventional inputs and social inputs, such as working conditions to production efficiency under uncertainty, has not been investigated so far.

The present study aims to derive the economic value of working conditions and assess their roles in agricultural production efficiency. To meet this objective, a DEAFootnote 3 framework is employed to measure farm-level efficiency scores and compute the shadow prices of working conditions. The contributions of this paper are threefold: First, this work addresses the gap in the current literature on data envelopment analysis by incorporating social aspects, namely working conditions to the productive efficiency of crop farms in the Spanish region of Catalonia. The second contribution is to derive the economic value of working conditions through the computation of shadow prices and compare them with other conventional inputs shadow prices to evaluate their relative importance. Third, only a few studies have accounted for the stochastic environment of the agricultural technology, and this paper aims to extend the classical deterministic DEA models by allowing for the stochastic environment of agriculture through a state-contingent approach.

3 Materials and methods

This study investigates farm efficiency while considering working conditions as a non-conventional input to reflect the social dimension of farm performance. The methodological roadmap is shown in Fig. 1.

Fig. 1 
figure 1

Methodological flowchart

Full size image

Here, I analyze a technology where the production process is subject to adverse weather conditions, pests, diseases, and other sources. The risk of agricultural production has to do with uncertainty in terms of potential output level and, sometimes also the level of inputs to be allocated, at the moment when production decisions are made.In a state-contingent framework, the stochasticity is represented by using a state-space \((S, \Omega )\), where the symbol \(S\) represents the states’ number, called the states of nature. Random variables are represented by the real vector space \({\mathbb{R}}^{\Omega }\). The stochastic production technology is represented as follow:

$$\Psi :\{ \left( {\tilde{y},x} \right):x\,\,{\text{can}}\,\,{\text{produce}}\,\,\mathop y\limits^{\sim } \}$$
(1)

where a vector of non-random input variables \(x\in {\mathbb{R}}_{+}^{N}\) can produce the state-contingent outputsFootnote 4\(\tilde{y }\in {\mathbb{R}}_{+}^{\Omega }\), where \(\tilde{y }=\{{y}_{s}:s\in \Omega \}\), being \({y}_{s}\) the ex-post value, the realizations of the random outputs are then \({y}_{1s},\dots ,\) \({y}_{Ms}\). It is important to note that “nature” makes the final decision on the ex-post outcomes, and not the decision-maker (Chambers et al., 2011).

To illustrate the procedure of estimating the best-practice frontier, I assume a single output technology \(\left(\tilde{y }\right)\), which denotes crop production. Land \(({x}_{1})\), labor \(({x}_{2})\), machinery \(({x}_{3})\) and I am also considering the use of energy, pesticides and fertilizers (EPF)\(({x}_{4})\) within conventional agricultural inputs. Although the efficiency literature has largely focused on assessing the relationship between traditional inputs and outputs in agricultural productions, the discussion over the appropriate framework which should be used to include social issues in the production technology has just been launched (Chambers & Serra, 2018). In this paper, working conditions \(({x}_{5})\) are considered as an input along with traditional inputs.

A state-contingent input-oriented DDF is used to fit the primal formulation to the stochastic production technology \((\Psi )\). The input-oriented DDF projects the input vector, in a pre-assigned direction, onto the technology frontier. Let \(g\in {\mathbb{R}}_{+}^{N}\) be the directional vector in which inputs can be scaled; the state-contingent directional distance function of the stochastic production technology \((\Psi )\) can be represented as (Chambers et al., 1998):

$$\overrightarrow {D} \left( {x_{n} ,\tilde{y}_{m} ,g} \right) = {\text{Max}}\{ \beta :x_{n} - \beta g \in \Psi \}$$
(2)

The \(\beta\) is non-negative and scaled to reach the efficient frontier \(({x}_{n}-\beta g \in\Psi )\) where \(\beta =\overrightarrow{D}\left({x}_{n},{\tilde{y }}_{m},g\right)\). A higher \(\beta\) means lower efficiency such that the agricultural holding is further away from the best practice frontier. If \(\beta\) equals zero, the farm is efficient and located at the production frontier.

\(\overrightarrow{D}\left(x,\tilde{y },g\right)\) inherits its properties from the production possibility frontier and satisfies the following properties: (1) \(\overrightarrow{D}\left(x,\tilde{y },g\right)\ge 0\) if and only if \(\left(x,\tilde{y },\right)\in\Psi\) assuming \(\left(x,\tilde{y },\right)\) are freely disposable; (2) non-decreasing in \(x\); (3) non-increasing in \(\tilde{y }\); (4) concavity in \(x\) and (5) verifies the translation property: \(\overrightarrow{D}\left(x-\gamma g,\tilde{y },g\right)=\overrightarrow{D}\left(x,\tilde{y },g\right)+\gamma , \gamma \in {\mathbb{R}}_{+}\). In the empirical application, a directional vector \(g=x\) is specifiedFootnote 5; thus, the derived distances from the DDF indicate the maximum contraction of inputs while keeping the outputs constant. The directional distance function is estimated using DEA framework, solving the model (3) for each observation in the sample (Chambers et al., 1998):

$${\overrightarrow{D}}_{I}\left({x}_{n},{\tilde{y }}_{m},g\right)=\underset{\lambda }{\mathrm{Max}} \left\{\beta \right\}$$
(3)
$$st. \left\{\begin{array}{c} \sum_{i}{\lambda }^{i}{x}_{n}^{i}\le {x}_{n}-\beta {g}_{x}, n=1,\dots ,N,\\ \sum_{i}{\lambda }^{i}{\tilde{y }}_{m}^{i}\ge {\tilde{y }}_{m}, m=1,\dots ,M,\\ \lambda \in {\mathbb{R}}_{+}\end{array}\right\}$$

where \(i=1,\dots , I\) denotes the observation number. \({\lambda }^{i}\) represents the intensity variable that weights all firms to define the benchmark for the production technology. \((1-\beta )\) is the efficiency measure.

The dual specification of the model in (3) is then used to derive a single shadow price for non-efficient units, while for the estimation of shadow prices for the efficient units, I follow the approach proposed by Chambers and Färe (2008) who have used a directional derivative feature to address this issue.

Because \(\overrightarrow{D}\left(x,\tilde{y },g\right)\) is concave in \(x\), its directional derivative can be represented as follows:

$$\vec{D}^{{\prime }} \left( {x,\tilde{y},g;x^{0} } \right) = ~\mathop {\lim }\limits_{{\gamma \to 0^{ + } }} \left\{ {\frac{{\vec{D}\left( {x + \gamma x^{0} ,\tilde{y},g} \right) - \vec{D}\left( {x,\tilde{y},g} \right)}}{\gamma }} \right\}$$
(4)

\(\vec{D}^{'} \left( {x,\tilde{y},g;x^{0} } \right)~\) can also be defined as a superlinear of \(\overrightarrow{D}\left(x,\tilde{y },g\right)\) in \(x\), which is denoted as \(\partial \overrightarrow{D}\left(x,\tilde{y },g\right)\) and can be formalized as:

$$\vec{D}^{\prime} \left( {x,\tilde{y},g;x^{0} } \right) = ~{\text{Inf}}~\{ v^{{\prime }} x^{0} :v \in ~\partial \vec{D}\left( {x,\tilde{y},g} \right),$$
(5)

where \(\partial \overrightarrow{D}\left(x,\tilde{y },g\right)=\{v\in {\mathbb{R}}^{N}: \overrightarrow{D}\left(x,\tilde{y },g\right)+v\mathrm{^{\prime}}({x}^{0}-x)\ge \overrightarrow{D}\left({x}^{0},\tilde{y },g\right) \forall {x}^{0}\in {\mathbb{R}}^{N}\}\)

Chambers and Färe (2008) show how shadow prices can be computed from the directional derivatives and super-differentials as well as how these shadow prices are associated with the concept of willingness to pay (WTP) and willingness to accept (WTA) for efficient firms. The WTP for a small unit improvement in \({x}_{n}\) can be expressed as:

$$\frac{{W_{n} }}{{W^{\prime} g}} = {\text{inf~}}\{ v_{n} :v \in ~\partial \vec{D}\left( {x^{*} ,\tilde{y},g} \right)$$
(6)

where \({x}^{*}\) denotes the efficient level of input quantities. Alternatively, the WTA a small unit increase in the input vector \(({x}_{n})\) can be represented by:

$$- \frac{{W_{n} }}{{W^{\prime} g}} = {\text{sup~}}\{ v_{n} :v \in ~\partial \vec{D}\left( {x^{*} ,\tilde{y},g} \right)$$
(7)

Shadow prices can be obtained directly from the solution to the dual problem in model (3). Shadow pricing is a way of assigning a monetary value to inputs in terms of their contribution to farm performance. The dual formulation of \({\overrightarrow{D}}_{I}\left({x}_{n},{\tilde{y }}_{m},g\right)\) in (3) can be derived as follows (Chambers et al., 2014):

$$\begin{array}{*{20}l} {\vec{E}_{I} \left( {x_{n} ,\tilde{y}_{m} ,g} \right) = \mathop {{\text{min}}}\limits_{{w \in \mathbb{R}^{N} ,p \in \mathbb{R}^{\Omega } }} \{ w_{n}^{\prime } x_{n} - p_{m}^{\prime } \tilde{y}_{m} \} } \\ {{\text{st}}{\text{.}}} \\ {w_{n}^{\prime } g \ge 1} \\ {w_{n}^{\prime } x_{n}^{i} - p_{m}^{\prime } \tilde{y}_{m}^{i} \ge 0,{\mkern 1mu} {\mkern 1mu} {\text{for}}{\mkern 1mu} {\mkern 1mu} {\text{all}}{\mkern 1mu} {\mkern 1mu} i,{\mkern 1mu} {\mkern 1mu} i = 1, \ldots ,I} \\ \end{array}$$
(8)

where \({w}_{n}\) and \({p}_{m}\) denote the shadow values associated with inputs \(({x}_{n})\) and state-contingent outputs \({(\tilde{y }}_{m})\), respectively. The shadow prices \({w}_{n}\) and \({p}_{m}\) are computed to solve the dual linear programming model in (8). These dual valuesFootnote 6 differ for each firm and are considered as an internal value estimation for inputs and outputs, consistently with cost minimization, these virtual prices represent the implicit values of the netputs to the efficiency of production, that can be particularly useful to investigate non-marketed inputs such as working conditions.

As shown by Chambers and Färe (2008), when the technology is smoothly differentiable, the dual problem in (8) has a single solution and can be formalized as:

$$\begin{array}{*{20}l} {\left\{ {\left( {w_{n}^{*} ,p_{m}^{*} } \right)} \right\} = {\text{arg}}{\mkern 1mu} {\mkern 1mu} {\text{min}}\{ w_{n}^{\prime } x_{n} - p_{m}^{\prime } \tilde{y}_{m} \} } \\ {{\text{st}}{\text{.}}} \\ {w_{n}^{\prime } g \ge 1} \\ {w_{n}^{\prime } x_{n}^{i} - p_{m}^{\prime } \tilde{y}_{m}^{i} \ge 0,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\text{for}}{\mkern 1mu} {\mkern 1mu} {\text{all}}{\mkern 1mu} {\mkern 1mu} i,{\mkern 1mu} {\mkern 1mu} i = 1, \ldots ,I} \\ \end{array}$$
(9)

In contrast, if the technology is not smooth, the resulting production frontier displays kinks, which are associated with the extreme efficient units. The lack of differentiability of the frontier yields to multiple solutions that are delimited by a lower (WTP) and an upper (WTA) bound within which shadow values are placed. Based on the directional derivative approach and the DEA framework, Chambers and Färe (2008) define the WTP for an extra unit increase in input:

$$\begin{gathered} w_{n} ,i,{\text{WTP}}^{*} = {\text{min}}\left\{ {w_{{n,i}} } \right\} \hfill \\ {\text{st}}. \hfill \\ w_{n} ^{\prime } x_{n} - p_{m} ^{\prime } \tilde{y}_{m} = 0 \hfill \\ w_{n} ^{\prime } g \ge 1 \hfill \\ w_{n} ^{\prime } x_{n}^{i} - p_{m} ^{\prime } \tilde{y}_{m}^{i} \ge 0,\,\,{\text{for}}\,\,{\text{all}}\,\,i,\,\,i = 1, \ldots ,I \hfill \\ \end{gathered}$$
(10)

while the WTA a small reduction in the input vector \(({x}_{n}^{i})\) is given by:

$$\begin{gathered} w_{{n,i,{\text{WTA}}}}^{*} = {\text{max}}\left\{ {w_{{n,i}} } \right\} \hfill \\ {\text{st}}{\text{.}} \hfill \\ w_{n} ^{{\prime }} x_{n} - p_{m} ^{{\prime }} \tilde{y}_{m} = 0 \hfill \\ w_{n} ^{{\prime }} g \ge 1 \hfill \\ w_{n} ^{{\prime }} x_{n}^{i} - p_{m} ^{{\prime }} \tilde{y}_{m}^{i} \ge 0,\,\,{\text{for}}\,\,{\text{all}}\,\,i,\,\,i = 1, \ldots ,I \hfill \\ \end{gathered}$$
(11)

Under duality theory and consistent with the concept of cost minimization, relative shadow prices are calculated from the dual formulation of the input distance function. The absolute shadow prices of productive inputs can be computed by assuming that the calculated shadow price of the output is representative of its market price. Following Färe et al. (1993), the output market price is used as our normalizing price, since intended outputs have an observable market price (while the working conditions do not), then absolute shadow prices are derived as follow:

$${W}_{n}^{^{\prime}}={p}_{m}^{o}\cdot \frac{\partial D\left(x,y,g\right)/\partial {x}_{n}^{^{\prime}}}{\partial D\left(x,y,g\right)/\partial {y}_{m}},$$
(12)

where \({p}_{m}^{o}\) is the observed (market) price of the output. Using the observed price of output to calculate absolute shadow prices of inputs is in line with other studies in the efficiency literature (Singbo et al., 2015; Skevas & Serra, 2017). In our empirical application, we use the expected price (under the normal state of nature) of each crop type (cereals, protein and oilseeds crops). Absolute shadow prices have the advantage of being linked to real market conditions, as opposed to relative shadow values.

3.1 Data

The data have been collected through a survey aimed at analyzing the efficiency of crop farms in Catalonia. Crops consist of cereals, protein, and oilseeds crops (COP). A farm is considered only if more than 80% of overall farm revenues are generated from COP crops. A total of 180 farms were surveyed.Footnote 7 The survey was specifically designed to implement an empirical representation of state-contingent technologies. To this end, the first part of the questionnaire was conducted before the starting of the growing season in October 2015 to gather predicted yields for three different states of nature. Specifically, farmers were asked to predict the yields they expect under bad, normal, and ideal states of nature.

Measuring ex-ante production is challenging because it is difficult to obtain objective responses from farmers on what represents a bad, normal or ideal growing season. Experts from the largest Catalan farmers’ association—Unió de Pagesos (UdP)—that was responsible for carrying out the survey, recommended collecting output data for bad, normal and ideal states of nature as the most appropriate and pragmatic method for gathering ex-ante output data.Footnote 8 According to UdP, yields under normal conditions can be used as a reference for farmers (e.g., the average yield over a ten-year period), then, identification of yield data for the bad and the ideal state of nature should be relatively easy for producers.

The collected data include information about planned use of inputs from each farm. These included details on cropland use (\({x}_{1}\) in hectares), labor use (\({x}_{2}\) in hours), machinery (\({x}_{3}\) in physical units) and EPF inputs (\({x}_{4}\) in euros), and working conditions (\({x}_{5}\) in scores). A total of 180 farms were chosen for the study purpose. Descriptive statistics are provided in Table 1.

Table 1 Descriptive statistics
Full size table

Data to assess the contribution of the working conditions to the production process were also elicited. Although some studies have focused on developing work conditions metrics, these usually depend on the particular sector of interest. Our working conditions indicators are based upon the work by Karasek et al. (1998), Pickett et al. (2008) and White and Cessna (1989). The items are, however, adapted to fit the specific context of research. A total of 22 items were introduced in our questionnaire to measure the working conditions.

To extract the relevant information from working conditions statements and further maximize the discriminatory power of data envelopment analysis, I used principal component analysis (PCA) as a descriptive technique on the working conditions items rated on a 4-point Likert scale, with increasing scores representing greater levels of working conditions. PCA reveals that four components (skill discretion, health risk, psychological demands and decision autonomy) provide a good description of the working conditions structure. The component skill discretion reflects the degree to which the job involves the need for a broad range of skills, development of individual skills and abilities, the absence of routinization and creativity. Decision autonomy represents the farmer's freedom to make decisions about his own job without constraint or coercion. The psychological demands component represents the psycho-social aspects of workload. While the health risk component sums up the damaging physical health effects of the workplace among farmers. Only the working conditions statements with high factor loadings were retained and considered for further study (Table 2). The working condition variable is quantified as the total points score of the four factors.

Table 2 Working conditions items that have been considered in this study
Full size table

4 Results and discussion

4.1 Efficiency scores

\(\overrightarrow{D}\left(x,\tilde{y },g\right)\) was calculated for each state of nature. Summary statistics on the average efficiency scores and the frequency distribution of ex-ante information as derived from the primal approach of the technology are presented in Table 3. The findings show that mean efficiency ratings in our sample fluctuate from 0.64 to 0.72 in bad and normal growing conditions. This indicates that our sample farms produce 36% and 28% less output than is technically possible under the bad and normal setting. Seventeen farms were found to be fully efficient (on the frontier) in the bad crop year, thirteen under normal growing conditions, and seventeen in the ideal state of nature. The analysis of individual farms shows some differences among units; for instance, larger farms are found to be more efficient, a result that is consistent with previous studies (Hallam & Machado, 1996; Skevas & Lansink, 2014), while we were unable to find any common pattern related with their working conditions levels.

Table 3 Frequency distribution of state-contingent efficiency scores
Full size table

Nonparametric kernel density distributions for the ex-ante efficiency scores are presented in Fig. 2. The three density distributions display a bimodal shape of our state-contingent data. Similarly, for the three distributions, the bimodal shape seems to indicate the existence of a specific group operating quite far from its output potential level (major-mode) who is clearly separated from another smaller group that has a high concentration of farms around 1. Under bad growing conditions, the major mode shows a concentration of farms around 0.55, while for the normal and ideal state, the group with considerable inefficiency is characterized by a high concentration of farms around 0.65. Furthermore, the two groups are discriminated by an anti-mode or a minimum, which may suggest the existence of an efficiency trap between the best performers and the inefficient ones. According to the Simar and Zelenyuk test, the efficiency ratings of bad state and normal/ ideal state of nature come from different statistical distributions (Table 5). While when comparing normal and ideal states, the result (similar statistical distributions) of the test is consistent with the plots shown in Fig. 1.

Fig. 2
figure 2

Kernel distributions of the efficiency ratings for each state of nature

Full size image

4.2 Shadow prices

Shadow values are computed as a means by which non-traded working conditions are assigned a monetary value for their contribution to technical efficiency. The virtual prices are estimated using Eq. 3. Although Eq. 3 is differentiable for inefficient farms, I use multiple shadow prices solutions (Chambers & Färe, 2008) for efficient farms. Calculated shadow prices (Table 4) present the needed increase in agricultural output while maintaining the efficiency level constant when inputs are changed.Footnote 9 Our results also provide differences between shadow prices across states of nature,Footnote 10 implying that the marginal productivity of inputs differs across the three different states of nature. The findings show that there exist substantial variations in the average shadow price of the inputs used. For the inefficient farms, capital machinery shows the higher average shadow value per farm that fluctuates from 137.49 euros to 160.93 euros in bad and good crop growing conditions (e.g., an additional unit of capital machinery (one machine) requires an increase in the crop value of 137.49 euros to keep the efficiency level constant under the bad state of nature). Our results also showed that our sample of crop farms presents shadow values of land on the order of 206 euros under the ideal state, which differs from the shadow prices levels (83–134 euros) under bad and normal states, implying that when the switch from bad to the good state of nature occurs, the productivity of an additional unit of land (hectare) increases by around 123 euros. Working conditions shadow prices for inefficient farms take a value of 27.15 euros per score point under bad conditions to about 25 euros in the normal and ideal states of nature. Therefore, an additional unit of working conditions is expected to increase the desirable outputs. Working conditions are the third most relevant input after capital machinery and land, a result that is consistent with the fact that farmers' well-being at work is likely to enhance agricultural productivity.

Table 4 Average shadow prices (Normalized values in euros)
Full size table
Table 5 Simar and Zelenyuk (2006) test for comparing efficiency scores and working conditions shadow prices between the three states of nature
Full size table

Interestingly, results show that for an additional euro of EPF, farmers’ return was less than 1 euro for the three alternative states of nature. This result implies that pesticides, chemical fertilizers and energy use are the less productive inputs for our sample farms. This suggests the possibility that farmers could improve their efficiency by reducing the use of environmentally detrimental inputs. This can be interpreted as an indication that farmers are allocatively inefficient with respect to the use of polluting inputs. These results are consistent with the widespread view that farmers overuse fertilizers and pesticides (Ait Sidhoum et al., 2020; Skevas et al., 2013; Zhang et al., 2015).

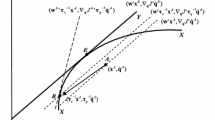
The estimation of the dual representation of the input distance functions in (10) and (11) allows us to generate multiple shadow value solutions in terms of WTP and WTA for efficient farms. Results are reported in Table 4. On average, the WTA for all inputs values in the ‘ideal’ state is relatively larger than the average input values in the ‘bad’ state, implying that these inputs are especially productive when growth conditions improve from bad to ideal. From a visual point of view, Fig. 3 summarizes this for the working conditions input in terms of the upper price limit for each efficient observation for each state of nature. Relative to inefficient farms, shadow prices of working conditions for the efficient units progress to be the second most valuable input after machinery, while land input downshifts to the third position. This result for land input is not expected but might reflect land quality differences among farms.

Fig. 3
figure 3

Farmers’ WTA for their working conditions input for each state (efficient units)

Full size image

4.3 Working conditions issues and sustainability in agriculture: from theory to practice

Based on the findings of this research, several theoretical and practical implications should be discussed. In terms of theoretical aspects, this work is among the first that empirically examines how working conditions contribute to farm technical performance. In view of the importance of working conditions in agricultural production, the incorporation of social performance indicators into production models would increase our understanding of how social aspects contribute to sustainable farming systems. However, the multi-dimensional nature of the social dimension makes it especially challenging from a methodological point of view. In light of this, it is crucial to develop harmonized methods and indicators for monitoring social indicators (Diazabakana et al., 2014). Furthermore, Lunner Kolstrup et al. (2013) note that farmers’ well-being and working conditions will be significantly affected by the fluctuating weather and the stochastic environment of agriculture and recommend the adoption of measures that mitigate the impact of these production risks. This study empirically measures the relative importance of working conditions in the farming sector under production uncertainty. The paper findings provide evidence on differences between shadow prices across states of nature. These differences in shadow prices between the different states show the importance of taking into account the stochastic environment of agriculture when calculating farms’ performance and shadow prices. These results confirm relevant previous research on the development of farm performance measures under uncertainty (Chambers et al., 2014; Mallawaarachchi et al., 2017; Nauges et al., 2011; Skevas & Serra, 2017).

In practice, this study makes a number of significant contributions to workplace sustainability practice. First, the option of developing better working conditions in the agricultural sector is a key organizational investment that spreads positive and green signals among co-workers and outside the farm and develops a strong connection with key stakeholders in order to gain their support and enhance the reputation of the agricultural sector among the general public. For instance, organic farming has been suggested as a production system that could provide better workplace conditions and hence contribute to the sustainability and viability of the sector without causing environmental damage. However, it is worth mentioning that in some agroecological systems, the farm managers prioritize the economic benefits over the social ones (Shreck et al., 2006). The estimates for working conditions shadow prices reveal that working conditions are the third most relevant input after capital machinery and land. This finding is consistent with the notion that work-related aspects are important factors when adopting more sustainable practices (Delecourt et al., 2019). In practice, transitions toward sustainable farming systems may require policy intervention to support farmers in adopting smarter and innovative solutions (e.g., precision and smart farming) that increase the attractiveness of the farming profession. While rural depopulation is an increasing source of worry for the European Commission (Schuh, 2019), as well as national agricultural authorities (Rodríguez-Soler et al., 2020), smart and sustainable technologies have the potential to improve safety, reduce the workload, and hence, prevent rural depopulation (Jones et al., 2020).

5 Conclusion

The consideration of social issues in a production system is important to achieve a sustainable business. Our article integrates farmers’ working conditions into the production process as an input and compares its importance relative to other inputs. The use of the state-contingent approach to allow for the stochastic conditions of agricultural production entails an improvement compared to the previous literature. Specifically, it estimated shadow prices of farmers’ working conditions under production uncertainty. The application focuses on the Catalan arable crop sector through a sample of 180 farms in 2015, where information on inputs and ex-ante state-contingent outputs have been collected through a survey.

This empirical analysis suggests several interesting results. First, on average, relatively poor performance scores have been obtained in terms of technical efficiency, suggesting that inputs use could be significantly reduced while leaving output levels unchanged. Additionally, farms appear to be operating at a lower production frontier as crop growing conditions worsen. This finding is compatible with the argument that farm performance improves with the improvement of conditions during the growing season (Ait Sidhoum et al., 2020; Serra et al., 2014). Although the empirical findings are consistent with the earlier literature, the interpretation of these results is limited to a particular geographical location. Second, significant differences in inputs shadow values across states of nature show the importance of considering production uncertainty when assessing farms performance. Finally, shadow prices suggest that working conditions represents the third most valuable input after capital machinery and land for the non-efficient farms and the second most valuable input after capital machinery for the efficient farms, which makes it significantly above the shadow values of EPF and labor for the inefficient farms and also considerably above the shadow prices of EPF, labor and land for the efficient farms.

In terms of policy recommendations, three main recommendations emanate from the analysis. First, policy-makers need to design agricultural policies that take into account the stochastic nature of agricultural production. In the future, climate change will have a significant impact on farmers’ safety and health (Applebaum et al., 2016). Successful adaptation by the farming sector requires appropriate farm performance measurement that allows for the stochastic environment of agriculture. Second, given the findings of the relative importance of working conditions in farm efficiency, this latter could be potentially improved by providing more freedomFootnote 11 for the workers to decide how to do their own work and providing more opportunities to make decisions (Langfred & Moye, 2004). For instance, Dumont & Baret (2017) suggested that the capacity to innovate and to participate in the decision-making process (e.g., adoption of new technology) can be important factors in determining farm performance. Third, the adoption of digital and smart farming technologies will be the key concern in the future; however, without sufficient training, the use of modern technologies alone will not enhance farmers well-being, working conditions and their overall performance in general. Finally, this study also shows evidence of differences in labor conditions between the efficient and non-efficient farms. This finding clearly indicates the need to improve the quality of workplace conditions for farmers who are lagging behind in terms of efficiency. The literature suggests that poor working conditions come from the absence/poor safe workplace practices. Therefore, with the aim of promoting sustainability practices, public policies should encourage these farmers to establish internal management systems and guide them in the implementation of quality management programs aimed specifically at improving working conditions and environmental practices (Gereffi et al., 2005; Nadvi, 2008).

To conclude, it is worth mentioning that there are different avenues for further follow-up research. This study confines the analysis to a consideration of working conditions to reflect the social dimension of farm performance. However, several indicators can be found in the existing literature for measuring social performance, such as investment in workers’ health (Ødegaard & Roos, 2014), qualitative control (Kuo & Lin, 2012), education and training (Chambers & Serra, 2018) and human rights (Ioannou & Serafeim, 2012). Therefore, a potential avenue for future research would be to consider other indicators which could better represent the social dimension of sustainability. A second future avenue for research is to investigate the differential effects of the different components of working conditions on farm performance. Finally, it would be interesting to extend the socio-economic approach to more recent approaches that allow modeling polluting-generating technologies (e.g., pesticides pollution). Farmers’ working conditions may be strongly linked to environmental protection and climate change mitigation practices. Better farmers’ working conditions (e.g., the use of precision equipment) may affect how pesticides and mineral fertilizers are applied, this implies that environmental pollution could be reduced by promoting innovative and sustainable solutions. Therefore, future research could explore the relative importance of working conditions in terms of their contribution to environmental pollution control by building on the methods proposed by Murty et al. (2012) or Murty and Russell (2018).