Abstract
Fine-resolution spatio-temporal maps of near-surface urban air temperature (Ta) provide crucial data inputs for sustainable urban decision-making, personal heat exposure, and climate-relevant epidemiological studies. The recent availability of IoT weather station data allows for high-resolution urban Ta mapping using approaches such as interpolation techniques or machine learning (ML). This study is aimed at executing these approaches and traditional numerical modeling within a practical and operational framework and evaluate their practicality and efficiency in cases where data availability, computational constraints, or specialized expertise pose challenges. We employ Netatmo crowd-sourced weather station data and three geospatial mapping approaches: (1) Ordinary Kriging, (2) statistical ML model (using predictors primarily derived from Earth Observation Data), and (3) weather research and forecasting model (WRF) to predict/map daily Ta at nearly 1-km spatial resolution in Warsaw (Poland) for June–September and compare the predictions against observations from 5 meteorological reference stations. The results reveal that ML can serve as a viable alternative approach to traditional kriging and numerical simulation, characterized by reduced complexity and higher computational speeds within the domain of urban meteorological studies (overall RMSE = 1.06 °C and R2 = 0.94, compared to ground-based meteorological stations). The results have implications for identifying the urban regions vulnerable to overheating and evidence-based urban management in response to climate change. Due to the open-sourced nature of the applied predictors and input parsimony, the ML method can be easily replicated for other EU cities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the 1950s, most climate regions have experienced an increase in minimum and maximum near-surface air temperatures, and warming trends will likely continue in the near future due to projected global warming [1, 2]. This impact is amplified in densely populated regions where the Urban Heat Island (UHI) effect is observed [3, 4]. The UHI results in higher vulnerability in urban areas to extreme heat events [5, 6], which increases the risk of occupational accidents [7], difficulty with energy distribution [8], and urban transport network disruptions [9]. Moreover, exposure to urban heat is an acknowledged hazard to individuals’ mental and physical health [10, 11], sleep quality [12], and indoor comfort [13], which can lead to death in extreme cases [14].
The urban-scale air temperature (Ta) can be influenced, even at fine spatial resolutions, by various factors such as building materials, heights, depths, surface imperviousness, albedo, vegetation cover within populated regions, and proximity to water bodies [15,16,17]. Mapping the spatio-temporal variation of the urban near-surface air temperature (Ta) can help minimize the impacts above through urban policy-making and management [18] and inform citizens when and where temperature hotspots will happen [19], climate-air pollution studies [20], epidemiological studies on exposure to overheating [21, 22], operational snowpack estimation [23], etc.
Several approaches can be used for mapping Ta, such as measurements (meteorological stations and remote sensing), weather numerical models, and statistical techniques. Meteorological stations provide high-quality measurements; however, they are not densely distributed, and in most cases, they are located outside of urban areas to minimize urban effects on measurements [24]. These measurements can be accomplished by remotely sensing Land Surface Temperature (LST). For example, the Temperature-Vegetation Index (TVX) method approximates Ta using the negative correlation between LST and the Normalized Difference Vegetation Index (NDVI). This is established on the assumption that the surface temperature over an infinitely thick vegetation canopy is approximately equal to Ta while an unvegetated surface can be highly warmer than the surrounding air temperatures [25, 26]. However, this method is only valid in regions with varying densities of vegetation cover and areas with gradual variations in temperature, which is not the case in urban areas [27,28,29].
Climate and Numerical Weather Prediction (NWP) models simulate the planet’s atmospheric processes, aiding in long-term climate projections and short-term weather forecasts. Regional NWP models focus on smaller geographical areas, delivering higher-resolution predictions for localized weather patterns and events. With the aid of the NWP and Energy Balance approaches, Ta can be estimated based on the laws of thermodynamics and physical parametrization of Earth-atmosphere energy transfers [30, 31]. The least sophisticated surface parametrizations implemented into NWP models are slab or bulk urban parameterizations (urban canopy models) [32], which treat the urban geometry as a flat surface with prescribed surface roughness and albedo. However, to reach a higher accuracy, these surface parametrizations need high-resolution information on morphology of the urban canopy and physical characteristics of the surfaces, which is not the readily available information, especially at a high spatial resolution [33].
The third group is statistical methods, which allow for Ta estimates at locations without available measurements, like numerical weather models. This is achieved by training a statistical model that provides a function between measured Ta values and a set of relevant auxiliary data (or predictors) available for the whole study region, such as LST. Zhang and Du [34] and Taheri-Shahraiyni and Sodoudi [35] provided relatively comprehensive reviews on the wide variety of statistical methods ranging from geostatistical interpolation to advanced data-driven Machine Learning (ML), that have been recently used in the field. Handling the spatial and temporal data gaps in predictors, overfitting, the uncertainty of predictors, and the lack of open-source data resources can challenge model training and prediction. Vastly, the statistical methods’ accuracy and efficiency depend on the size of the initial training dataset, study location/area, applied regression approach, model (hyper)parameterization, and predictor selection. The main goal of previous studies is to improve the accuracy of the predictions compared to available observational data. Considering the complexity and nature of the problem, Zhang and Du [34] argue that applying popular ML approaches, such as gradient boosting or random forest regression models suffices for reaching desirable accuracies in the prediction of urban Ta. The field of urban Ta should focus more on other aspects of statistical urban temperate prediction/modeling [34].
Here, we address another aspect, which is less considered in the literature: comparing different approaches for spatio-temporal urban Ta mapping of a study site. Speed, flexibility, and easy input/tuning data access define the suitable approach. In this study, (1) we selected three methods, including meteorological modelling (Weather Research and Forecasting [WRF] mesoscale model), interpolation (Ordinary Kriging [OK]), and ML (Extreme Gradient Boosting [XGBoost]) for predicting Ta at ≈ 1 km2 during warm months (Jun-Sep) in the city of Warsaw, Poland. (2) We compare the estimates against five meteorological stations scattered across Warsaw to reference their predictive power. (3) We provide spatio-temporal variability of Ta to identify urban areas vulnerable to heat stress in Warsaw. This manuscript’s primary objective was not to compare the WRF numerical simulation approach and ML regarding accuracy. In other words, our intention was not to establish a conclusive judgment on the superiority of the numerical simulation or the ML methodology. Incorporating more complex land cover schemes or urban parameterizations might enhance the capacity of WRF. However, this level of refinement might not be practical for operational situations or when fast and accurate results are necessary. Different parametrizations or forcing data might or might not lead to improved outcomes, which could be the subject of a separate study. Similar principles apply to the ML approach. Results could vary with different sets of predictors or other ML models, but delving into these intricacies would require a distinct study beyond the scope of this manuscript. Our core goal was to evaluate different approaches regarding pragmatism and effectiveness in cases where data availability, computational constraints, or specialized expertise pose challenges. However, the user or the project’s objectives determine the necessary degree of precision.
2 Methodology
2.1 Study Area
Warsaw, the capital of Poland, with a total area of 517.24 km2 (bounded approximately to longitudes between 20.85° E and 21.3° E and latitudes between 52.1° N and 52.4° N), hosts ca. 1.8 million residents (Fig. 1). With an average elevation of 100 m, Warsaw is a city in the middle of the Masovian Plain, where the highest and lowest points of the city have approximately 46 m difference in height. Warsaw’s climate is oceanic (mild summers and cool but not cold winters), denoted by Cfb in the Köppen climate classification, generally a temperate climate zone [36]. The city of Warsaw was selected as this study is part of a research project entitled “Embodying Climate Change: Trans-Disciplinary Research on Urban Overheating” (EmCliC—https://www.emclic.com/, accessed in January 2023), focused on characterizing the elderly people adaptive abilities in response to rising temperatures in Warsaw.
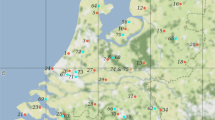
Netatmo stations and administrative boundary of Warsaw, Poland. The spatial distribution of 85 stations available in the warm months of 2021 (Gregorian calendar days 150–270) used in this study for kriging and Machine Learning prediction of 2-m air temperature (Ta); colours show the average recorded air temperature measurement by each station in warm months of 2021 (June–September)
2.2 WRF: Weather Research and Forecast Model
The meteorological modelled data were generated with the Weather Research and Forecast model (WRF) version 4.1.5, using initial and boundary conditions from the 6-hourly 0.25° × 0.25° National Centers for Environmental Prediction (NCEP) Final (FNL) operational global analysis and forecast data [37]. WRF (https://www.mmm.ucar.edu/weather-research-and-forecasting-model, accessed in January 2023) [38] is a three-dimensional, non-hydrostatic mesoscale numerical model designed to serve both operational forecasting and atmospheric research needs.
WRF has several options for urban canopy models. The problem with using an urban canopy model is the data needed (unavailable here) and their uncertainty. For this study simulation, WRF was configured in a system with three one-way nested domains (Supplementary Fig. 1). Specifically, the largest domain (domain 1) had a grid size of 9 km, the middle (domain 2) was 3 km, and the smallest (domain 3) was 1 km. All three domains consist of a 100 × 100 grid-cell configuration. We used the terrain following the vertical coordinate system for these domains with an upper boundary at 103 hPa. To parameterize physical processes that cannot be calculated explicitly by the model, we used the NCAR Convection-Permitting suite (CONUS). The former suite comprises the following schemes: Thompson microphysics scheme [39], Mellor-Yamada-Janjic planetary boundary layer scheme and Monin-Obukhov Janjić surface layer scheme [40], Noah land surface model [41, 42], rapid radiative transfer model for global applications (RRTMG) shortwave and longwave radiations schemes [43], and Tiedtke cumulus scheme [41, 44]. CONUS was developed and tested over several years until its release in 2016 [45, 46].
For domains one and two, land use originates from NOAH-modified 20 category IGBP-MODIS (https://ral.ucar.edu/solutions/products/wrf-noah-noah-mp-modeling-system, accessed in January 2023). The land use information for domain 3 is from Broxton et al. [47]. This means 21 land categories in our WRF simulation, being that the most represented in our domain 3 are the “urban and built-up land,” “croplands,” “forested categories,” and “water” surfaces. The fraction of the WRF grid occupied by “urban and built-up land” is considered impervious, and surface fluxes and temperature are calculated for the vegetated areas and the urban built-up areas. There are no explicit 3D structures considered as street canyons. The Noah land surface model [41] in its bulk urban parameterization uses the following parameter values to represent zero-order effects of urban surfaces [48]: (1) roughness length of 0.8 m to represent turbulence generated by roughness elements and drag due to buildings; (2) surface albedo of 0.15 to represent shortwave radiation trapping in urban canyons; (3) volumetric heat capacity of 3.0 J m−3 K−1 for urban surfaces (walls, roofs, and roads), assumed as concrete or asphalt; (4) soil thermal conductivity of 3.24 W m−1 K−1 to represent the large heat storage in urban buildings and roads; and (5) reduced surface moisture availability over urban areas relative to vegetated areas to decrease evaporation. Terrain height is from the Global Multi-resolution Terrain Elevation Data 2010—GMTED 2010 [49]. Regarding the treatment of urban geometry, we used WRF in the slab/bulk mode. The WRF simulation was executed continuously for the calendar year 2021.
2.3 Crowd-Sourced Station Data
We use crowd-sourced Ta data from the Netatmo Internet of Things (IoT) weather station network as the primary input to develop interpolation and ML models. Crowd-sourced data, such as that collected from the Netatmo IoT network, offers distinct advantages for our research. The extensive coverage of Ta measurements across Warsaw through Netatmo’s network aligns with our objective of predicting Ta variability at a fine scale (≈ 1 km2). The diverse urban settings covered by Netatmo’s IoT network ensure our analysis encompasses various land use types, crucial for identifying heat-stressed areas. The accessible free nature of Netatmo data further simplifies its integration into our chosen prediction methods.
Although the conditions at which the crowd-sourced weather stations operate do not follow the technical standards and requirements for measuring equipment/sensors part of the reference weather station networks, the spatial density (number of stations per area) of crowd-sourced weather stations makes them promising indicators of Ta spatial variability [50]. The potential of crowd-sourced data for mapping air temperature at fine spatio-temporal resolutions has been suggested by, e.g., Venter et al. [51] or Zumwald et al. [19]. Accordingly, in this paper, we apply the term Ta to air temperature measured by crowd-sourced weather stations, despite their lack of accuracy.
We retrieved all publicly available Netatmo (https://www.Netatmo.com/en-gb/weather, accessed in January 2023) weather station data (outdoor module) until December 13th, 2021, through the Netatmo Weather API (https://dev.Netatmo.com/apidocumentation/weather, accessed in January 2023) inside the longitudes between 20.86° E and 21.24° E and latitudes between 52.1° N and 52.37° N (Supplementary Fig. 2). We used the “patatmo” (https://nobodyinperson.gitlab.io/python3-patatmo/index.html, accessed in January 2023) Python module to access the Netatmo Weather API. Data are available at the 10-min temporal resolution, and we retrieved hourly averages. Given that citizens operate the Netatmo weather stations, there is a possibility that the measured data can be erroneous due to device malfunction, exposure to sunlight/warm surfaces, and malposition of the sensors. We performed a Quality Assessment (QA) on the data (Fig. 2) following the procedure proposed by Napoly et al. [52] and programmed in the “CrowdQC” package for the statistical software R [53].
Air temperature data recorded by Netatmo weather stations, before and after the statistically based quality control. Blue and red lines show the measured 2-m air temperature data retrieved from Babice and Okecie (Warsaw, Poland) reference meteorological stations, respectively. In short, (1) stations with similar coordinates were removed, and (2) the data of an individual station in a particular month were removed if the calculated Pearson correlation coefficient between the station data and the median of crowd-sourced data (in that month) was less than 0.9. We ignored the height correction step as it has a negligible effect on a city like Warsaw with relatively flat topography
We delimited the stations to the exact administrative boundaries of Warsaw (https://www.openstreetmap.org, accessed in January 2023). The downloaded weather station data are primarily related to recent years, particularly 2021 (Supplementary Fig. 2). To acquire more robust results in the interpolation and ML parts, we limited the crowd-sourced weather station dataset to 2021, with the highest number of stations available. Additionally, we did not include the data of cold months in 2021 for two reasons: (1) our final aim was to map the urban areas vulnerable to overheating, and (2) that would add more complexity to ML training which could reduce the predictive performance of the final trained models. Following QA and delimiting steps, 85 station records were available for the warm months of 2021 (between 30-05-2021 and 27-09-2021—Gregorian calendar days 150—270 in 2021). The data measured from these 85 Netatmo stations where the input to interpolation and ML model development parts (Fig. 1).
2.4 Interpolation: Ordinary Kriging
As the most straightforward approach for air temperature distribution modelling, we used Ordinary Kriging (OK) for predictions of Ta. The choices of Kriging with residuals and Regression-Kriging (combination of interpolation and regression techniques) were also available; however, we here used OK as it was the most straightforward approach, computationally reasonable, and needs less auxiliary parametrization and predictors, which adds to the complexity of semi-variogram fitting per se [35]. The main goal was to compare an approach as simple as possible that does not need additional input data or assumptions compared to ML or meteorological simulation, solely dependent on the air temperature weather station data. However, one assumption was that kriging outperforms simpler interpolation techniques, e.g., Inverse Distance Weighting. We used the “SciKit GStat” Python module [54] for OK calculations. Assuming time as the third coordinate dimension, we treated each day separately and used 3D OK to make predictions. We assumed that Ta is stationary relative to the time coordinate dimensions to reduce the calibrating parameters. Further technical details on the applied 3D OK approach are provided in the Supplementary Information Appendix: Interpolation: Ordinary Kriging.
2.5 Developing Predictive Machine Learning (ML) Models
We used the XGBoost (https://xgboost.readthedocs.io/en/latest/index.html, accessed in January 2023—Chen and Guestrin [55]) gradient boosting algorithm to establish a data-driven relation (model) between crowd-sourced measured Ta and a set of auxiliary predictor data, to estimate Ta. We first prepared a collection of predictor data that we assume are primarily relevant to Ta. We trained ML models based on these predictor data and their relevance to crowd-sourced air temperature data. The trained models were then used to make predictions of Ta in Warsaw.
2.5.1 Predictor Data
LST is assumed to be one of the predictors. The rest of the predictors discussed below are chosen as they are widely used in the literature [27, 34, 51], freely available, and allow for the transferability of the method to other geographical regions. However, in our predictor (feature) selection step, we tried to consider the typical accuracy levels observed in previous studies to avoid the addition of unnecessary predictors (see the Supplementary Information Appendix: Comparison with the literature). We stopped the addition of predictors as we reached the desirable accuracy. The auxiliary predictor data used here were primarily derived from Earth Observation satellite data and can be divided into two categories: spatial and spatio-temporal predictors (Table 1).
Spatial predictors included Landsat 8 LST (30-m spatial resolution, resampled from native thermal data at 100 m resolution), and Sentinel-2 band nine (B9) water vapor product (60 m spatial resolution) to account for the water vapor absorption effect within the Thermal Infrared bands. These datasets are not “purely spatial” but we chose to average out the temporal dimension as part of the processing; we calculated the average of layers from the USGS Landsat 8 Level 2, Collection 2, Tier 1 (Band 10) [56, 57] and Sentinel-2 MSI: Multi-Spectral Instrument, Level-2A [58] satellite images captured in summers between 2016 and 2022. We performed these calculations in Google Earth Engine (GEE) platform. We used images’ averages as these two satellites pass over Warsaw every 16 days, and in most cases, the captured satellite images are cloud contaminated.
Other auxiliary purely spatial predictor data included coordinates (i.e., longitude and latitude in degrees) of the weather stations and their distance to water (in meters) of the region of interest. The maximum water extent layer from the Global Surface Water dataset (at 30-m spatial resolution) [59] available on the GEE platform was used to calculate the Netatmo stations’ distance to the nearest grid cell identified as water.
Unlike Landsat and Sentinel-2, LST data available from the MODIS (Moderate Resolution Imaging Spectroradiometer) instruments onboard the Terra and Aqua satellites [60] exhibit in total ca. four overpasses per day (2 times per day and two days per night) and provide a spatial resolution of approximately 1 km2. MODIS LST data were chosen among the freely available, remotely sensed LST products by a trade-off between spatial and temporal resolution. For example, the SEVIRI instrument (Spinning Enhanced Visible and Infrared Imager) onboard the MSG (Meteosat Second Generation) geostationary satellites are available every 15 min. However, the 3-km spatial resolution does not allow mesoscale urban Ta mapping. We downloaded daytime and nighttime LST MODIS MOD/MYD11A1 version 6 products through Earth Data EOSDIS (NASA, https://earthdata.nasa.gov/) portal. Cloudy pixels and pixels with an average error higher than 2K were automatically removed based on the metadata available for each image. The newer V6.1 of these products was also available; however, we did not utilize them because of temporal gaps in those datasets (at the time of writing this paper).
MODIS Terra vegetative indices, including NDVI (Normalized Difference Vegetation Index) and EVI (Enhance Vegetation Index) MOD13Q1 V6 data [61], generated every 16 days at the 250-m spatial resolution, were also used as spatio-temporal predictors. We attributed the Netatmo weather station data to Terra vegetation indices based on the date bins. For example, Netatmo weather station data between 11-06-2021 and 26-06-2021 were attributed to the MOD13Q1 vegetation indices product available for 26-06-2021.
Additionally, 2-m air temperature (°K), 2-m dewpoint temperature (°K), and total terrestrial evapotranspiration (meter of water equivalent) gridded data—derived from hourly ERA5-land reanalysis at 0.1° spatial resolution (9 km2) [62]—were used as other spatio-temporal predictors to improve the predictive performance of the trained ML model. We additionally used the Gregorian calendar day of the measurement by Netatmo weather stations as a predictor.
We decided not to use land cover and/or surface imperviousness as predictors in our analysis. Firstly, we operated under the assumption that the LST and vegetation (NDVI and EVI) data could serve as a suitable proxy for capturing the effects of land cover and surface imperviousness. Given this assumption, we believed including explicit land cover and imperviousness variables might introduce collinearity issues among our predictors. Secondly, our research design specifically focused on investigating the impact of land cover on the predicted/observed air temperatures (will be discussed later).
2.5.2 T a Model Training and Cross-Validation
We used the Python package “XGBoost” to implement gradient boosted trees ML approach [55, 63]. We chose a tree-based ML method as they are computationally efficient, highly flexible in capturing non-linear trends [64], and have already been shown to be robust for urban Ta prediction [27, 65]. Tree-based models are also highly efficient in treating collinearity and outliers [63]. MAE (Mean Absolute Error), RMSE, R2 (coefficient of determination), and maximum error (Predication minus Observation) evaluation metrics were also calculated for the final trained models using a tenfold cross-validation scheme (see Supplementary Information Appendix: Ta Model training and cross-validation).
2.6 Models’ Deployment and Spatio-temporal Prediction
The four final cross-validated models were then deployed to new predictor data to estimate urban-scale Ta (at nearly 1-km2 spatial resolution) across Warsaw four times per day at MODIS Aqua and Terra satellite passing times. To do so, we first created a base point layer delimited to the administrative boundaries of Warsaw at 0.008° spatial resolution (total of 1067 grid-cells) in the WGS 1984 spatial coordinates. Then we extracted the predictors’ values when the LST data of the MODIS instrument was available. For each point, we made predictions of Ta for Gregorian calendar days between 30-05-2021 and 27-09-2021 in 2021. The daily semi-variograms calculated from 3D OK were similarly applied to the generated base point layer (i.e., the coordinates of the points) for the Netatmo weather station data of 2021 to make comparable predictions.
2.7 Validation Against Meteorological Stations
The WRF model, OK, and ML outputs were finally compared against the observations of 5 meteorological (one synoptic and four climatic) stations spread across Warsaw during the summer of 2021. Data were collected from the Institute of Meteorology and Water Management of the Poland National Research Institute (https://danepubliczne.imgw.pl/, retrieved in January 2023). Hourly data are only archived by one station (Okecie), and the rest of the stations only release daily/diurnal statistics and Ta at hours: 6:00, 12:00, and 18:00. Normally, Aqua and Terra satellites pass Warsaw at ≈ 1:00/11:25 and ≈ 9:50/20:24 UTC (Fig. 3). These overpass times do not necessarily overlap with the times when usually daily minimum and maximum air temperatures are recorded for Warsaw. Thus, our comparison analysis between different approaches was limited to Ta data recorded at 12:00 UTC, as this is very close to the daytime overpass of the Aqua satellite (in Warsaw). We calculated the RMSE and R2 between the outputs of the three approaches and the reference meteorological stations’ observations. As meteorological observations are at synoptic scales, we analyzed the difference among the weather station data (Supplementary Fig. 3) to ensure that it is appropriate to use meteorological stations to test the three approaches for 1-km2 spatial resolution temperature mapping. The average and standard deviation of each day Ta range (min–max difference) among five stations were 1.73 °C and 0.75 °C, respectively.
Diurnal 2-m air temperature (Ta) variability and approximate MODIS Aqua and Terra satellites’ overpass times in Warsaw. Ta is retrieved from the synoptic meteorological station (Okecie) in Warsaw. Satellite overpassing times are calculated by averaging the Land Surface Temperature (LST) day/night view times in Warsaw from 2021-05-30 to 2021-09-27. The time zone on the x-axis is UTC
The reanalysis data are generated based on the output of complicated atmospheric numerical models that assimilate observational data from various data resources. It is possible that meteorological stations’ observations have been used by ERA5 land reanalysis for model parametrization and assimilation. One may claim that the application of ERA5 Ta as a predictor in the training of a ML model and later comparison of the resultant predictions against observations results in a ML model biased towards the site-observed temperature data, leading to uncertain assessment of the predictive power of the ML approach compared to other methods [34]. To address this, we trained our ML model based on the daytime MODIS Aqua LST data, this time excluding the ERA5 Ta as a predictor. Therefore, such model predictions are unseen to ERA5 reanalysis Ta, which fairly assesses different approaches’ predictive performance. On the other hand, statistical accuracy metrics were not the only parameters we considered in our comparative analysis. Other parameters, such as running time, computational cost, and flexibility/efficiency in the realism of the spatial patterns were important.
3 Results
3.1 WRF, 3D Ordinary Kriging, and Machine Learning Predictions
The spatial distribution of Ta during the 2021 warm months (Jun-Sep) is mapped in Fig. 4a by averaging the hourly predictions of the WRF model. The predictions vary between 18.06 °C and 20.55 °C. The distribution follows the land use fields read by WRF, in which the highest temperatures are predicted in grids with high to 100% urban built-up. In contrast, the lowest is predicted in grids with higher than 60% cropland use (southeast and north in the domain) and/or forest (north and east). We note that the default land use for WRF that we used is a composite between 2001 and 2010.
The kriging results illustrating the spatial variations of Ta in Warsaw at ≈ 1-km2 resolution are presented in Fig. 4b. The average kriging predictions for all 120 days (warm months in 2021) are used to generate the map in Fig. 4b. According to the kriging predictions, Ta varies spatially between 18.34 °C and 21.17 °C across Warsaw in the warm months of 2021. The OK approach predicts higher Ta in northern areas, and the average air temperatures estimated in the east and south are lower than WRF predictions, especially near the Warsaw airport. The Ta map generated by the OK approach does not show any variability in response to the presence of the Vistula River.
Supplementary Table 1 illustrates the results of hyperparameters optimization and tenfold cross-validation for the four trained models corresponding to each overpass of the MODIS Aqua and Terra satellites. On average, the RMSE error for all four models (including ERA5 Ta) varied between 0.68 and 0.88 °C (with an average of 0.78 °C), while R2 ranged between 0.96 and 0.98. The respective Normalized RMSE (normalized to the range of input training datasets) for models trained on Aqua Day/Night and Terra Day/Night over passes was 3.42%, 3.27%, 3.80%, and 2.87%. The maximum absolute errors were also between 2.73 and 3.4 °C. The validation (predictions against measurements) and residuals (the differences between observed and predicted data values) plots are also represented in Fig. 5 and Supplementary Fig. 7 to visualize the quality and the predictive power of the four models. Additionally, we calculated the importance of predictors for predicting Ta at different MODIS overpassing times (Fig. 6) and their relative importance in each trained model (Supplementary Table 9). On average, ERA5 land reanalysis Ta, ERA5 land reanalysis dew temperature, and Gregorian calendar day were the essential predictors with a respective average importance of 40.63%, 14.40%, and 12.12%. In the absence of ERA5 Ta, the RMSE and R2 were reduced by 9.2% (relative to 0.86 °C) and 1% (relative to 0.96), respectively (see Supplementary Information Appendix).
Machine Learning (ML) models’ validation plots, adopting a tenfold cross-validation scheme. 2-m air temperature (Ta) predictions of the four trained ML models (trained based on input data at different MODIS Aqua/Terra overpass times) are validated against the air temperature measurements from the Netatmo weather stations. Red lines represent the y = x line. RMSE: Root Mean Squared Error. R2: coefficient of determination
Predictor (feature) importance order for predicting 2-m air temperature (Ta) using XGBoost ML algorithm. The results are reported for all trained models, based on input data at different MODIS Aqua/Terra overpass times. In addition, the green color presents predictor importance for the ML model trained based on input data at the Aqua daytime overpass, excluding ERA5 land reanalysis Ta as a predictor
3.2 Model Predictions Against Meteorological Stations’ Observations
The time series of predictions made by the ML model and the other two approaches, as well as observations are illustrated in Fig. 7. ML learning predictions are only available for days that daytime MODIS Aqua LST is available, resulting in temporal gaps in the time series of predictions made by the ML approach. Therefore, the RMSE and R2 values shown on each panel are calculated based on the dates that predictions are available from all three models. The number of these days was 43, 53, 54, 45, and 49 days for Babice, Okecie, Bielany, Filtry, and Obserwatorium II, respectively. Overall, for all five stations, respective RMSE and R2 values of 1.23 °C and 0.93 were calculated for the ML approach and 1.7 °C and 0.85 for the WRF meteorological model. The predictions from the OK approach showed the lowest performance compared to observations, and the overall RMSE and R2 of the five stations were 3.00 °C and 0.58, respectively. The comparison of the models’ predictions against observations assuming ERA5 Ta as one of the predictors is additionally in Supplementary Fig. 8. The addition of ERA5 Ta further increased the performance of the ML model, where the overall calculated RMSE and R2 between the predictions and measurements were 1.06 °C and 0.94, respectively.
Comparing three approaches for predictions of 2-m air temperature (Ta) against Ta data recorded by five meteorological reference stations across Warsaw at 12 pm, between 2021-05-30 and 2021-09-27. Machine Learning (ML) models are trained based on input data (different MODIS Aqua daytime overpass), excluding ERA5 land reanalysis Ta as a predictor. The geographical location of the meteorological stations is represented on the right-bottom corner map. RMSE: Root Mean Squared Error. R2: coefficient of determination. As the outputs of the ML approach include some gaps due to cloud contamination, RMSE, and R2 values are calculated based on the days for which predictions of all three approaches were available
4 Discussion
4.1 Comparison of the Three Approaches’ Performance
The spatial distribution of Ta estimated using the three approaches at some sample times with high LST data availability (low cloud cover) is presented in Fig. 8. According to our results, with or without using ERA Ta as a predictor, the predictions of the ML (XGBoost) approach showed a lower error than the other two approaches, compared to the Ta records of five meteorological stations spread across Warsaw (Fig. 7, Supplementary Fig. 8). Most of the time required for making predictions by the ML learning approach was relevant to input training data preparation. The XGBoost algorithm was very efficient in model training, and all models (for each MODIS overpassing time) were trained in less than 400s. The predictions made by the ML approach are fairly scattered around the y = x line. However, a negligible overestimation of the predictions can be observed at the higher temperature, especially for daytime predictions (Fig. 5). Excluding ERA Ta as a predictor, a total bias (mean of observations from the five stations minus the mean of corresponding predictions) of − 0.60 °C was calculated for the ML approach, representing the overall overestimation of the air temperatures during daytime. Overestimation of the Ta predictions based on ML and MODIS LST remote sensing is also reported by Venter et al. [24], who pointed out that the satellite-based UHI (Urban Heat Island) is overestimated by sixfold, relative to the UHI calculated based on station measurements over 342 European urban clusters.
The calculated bias was reduced to − 0.29 °C when the ERA Ta was added to the input dataset for training a predictive ML learning based on MODIS Aqua daytime LST measurements. According to our results, removing the most important predictor impacts the error from observations. The predictive model still effectively explains the variability in observations. Removing the ERA Ta as a predictor from the model training reduced the RMSE and R2 values only by 13.82% and 1.06%, respectively. Predictions made for the nighttime are more accurate than daytime predictions. The difference in daytime and nighttime accuracies may be relevant to MODIS LST estimations as LST data are closer to the surrounding air temperatures during the nighttime [15, 66]. Especially in built-up urban environments and during the daytime, the relationship between air temperature and LST can be very complex due to various affecting parameters such as clouds, sky-view factor, sensor view angle, and solar insolation intensity [67,68,69]. The correlation between the Surface Urban Heat Island (SUHI) and the Canopy-Layer Urban Heat Island (CLUHI) is recognized to be weak in the daytime. At nighttime, this can be reversed, and air temperature and remotely sensed LST can be more similar due to reduced solar shading and stability of the atmospheric boundary layer [70,71,72].
Regarding accuracy, WRF meteorological model predictions were the second and OK interpolation showed the worst performance. The overall calculated bias of the kriging technique relative to the five stations was 1.81°C, while this value was − 0.7 °C for the WRF meteorological model. In terms of model preparation and speed of calculations, however, WRF was the worst based on our computational resources—12 cores and model size of 17 × 17 horizontal grids at the first domain, 35 × 35 horizontal grids at the second domain, and 27 × 33 grids horizontal at the third domain (domain with the Warsaw results) and 59 vertical levels (Supplementary Fig. 1); it took around four days to predict Ta for one year at an hourly resolution in Warsaw. The required run time for fitting the semi-variograms for each day was in between, lasting an overall two hours for semi-variogram model calculation, although finding the optimal parameters (e.g., a suitable number of lags or maximum lag distance) required for semi-variogram fitting was a tedious task. By a trade-off between speed and accuracy in our analysis, the ML approach was the most efficient for predicting mesoscale Ta in Warsaw.
4.2 Air Temperature Variability in Warsaw
We used the ML approach for the final mapping of the Ta in Warsaw. The spatial variation of Ta in Warsaw at ≈ 1-km2 spatial resolution is visualized in Fig. 9 as an output of the trained ML models. The maps are created by averaging the ML model predictions for each MODIS Aqua/Terra overpassing time. We used the trained models (based on 2021 warm months data [Gregorian calendar days 150–270]) for making predictions in 2019 and 2020 as well as 2021 and calculated the average of predictions. The number of predictions participating in each map’s pixels is shown in Supplementary Fig. 9. We made the predictions for the previous years to have at least 50 participating predictions in our analysis and increase the reliability of the mapped Ta variability. The cooling effect of the Vistula River passing the middle of Warsaw is observable for daytime predictions. The results also suggest the impact of land cover on the spatial distribution of the Ta. Although Warsaw is topographically flat and no effects of elevation can be assumed for the urban Ta variation, the role of large vegetation coverage located in the eastern and southern regions of the city (Supplementary Fig. 10) is noticeable in the spatial distribution of Ta in Warsaw during warm months of the three studies years. In addition to shading, vegetation can cool the air through latent heat exchange and transpiration [15, 67].
The urban-built material and structures absorb the radiation during the day and release it at night, leading to higher nighttime temperatures [15]. This effect can also be seen for the nighttime predictions (Fig. 9) when the Ta difference between the built environment and the surrounding areas covered by vegetation is more noticeable. The relation between the Ta predictions made for each MODIS overpassing time and the building height is represented in Supplementary Fig. 15 (see Supplementary Information Appendix: Ta variability against land cover and building height). The impact of built environment structures and buildings on increasing nighttime Ta predictions is also evident. We further used warm month Ta averages predicted by ML models (including ERA Ta as a predictor) to analyze the variability of Ta within each land cover type in Warsaw (Supplementary Fig. 16). Overall, the lowest standard errors were calculated (Supplementary Tables 10 to 13) for urban fabrics and lands forests (SE ≈ 0.04 °C and SE ≈ 0.05 °C, respectively). In contrast, lands without current use and water bodies generally showed the highest standard errors (SE was calculated as the standard deviation divided by the square root of the number of samples).
4.3 Methodological Limitations
Cloud contamination is the main drawback of applying satellite remote sensing products for mapping Ta. Removing the cloud-contaminated pixels results in predictions biased toward clear-sky weather conditions, which can be misleading, especially for UHI quantification studies [51]. It was not possible to predict Ta for many days and locations. Although some studies have attempted to use statistical methods to fill the remotely sensed spatio-temporal gaps in LST [73, 74], applying LST for the gap-less prediction of Ta at high resolutions remains a challenge [34]. Additionally, here we could make predictions four times per day at nearly 1 km2 spatial resolution. The release of more accurate remotely sensed LST products such as ECOSTRESS (https://ecostress.jpl.nasa.gov/, accessed in January 2023) or GOES-R (https://www.goes-r.gov/, accessed in January 2023 https://www.goes-r.gov/) at higher spatial and temporal resolution could be promising for improving the quality of Ta spatio-temporal mapping [15, 34]. Additionally, the following can be listed as the limitations of the methodology used in this study:
-
We used only five stations that were geographically closer to the Warsaw center and/or its airport; the reference stations may be located near the stations used for ML and kriging and results in the ill-assessment of the three approaches’ performance. It is necessary to have an independent Ta dataset with a higher number of adequately scattered stations over the study region.
-
We used only the WRF meteorological model. In the future, it might be meaningful to compare other mesoscale urban energy-balance and climate/meteorological models with outputs of ML or kriging.
-
It is important to acknowledge that the discrepancies observed in the model estimations could potentially stem from the inherent characteristics of the initial datasets employed as inputs for each model. Regarding the ML approach, the decision to exclude NCEP data for training/prediction was driven by practical considerations, as all five reference stations were located on the same 0.25-degree grid. However, utilizing ERA5 outputs for the WRF simulations was a viable option. We evaluated the correlation and similarity between ERA5 and NCEP (the dataset used for WRF) covering the period from 2018 to 2021 (Supplementary Fig. 17). During the summer of 2021, when we compare the estimates derived from the different approaches, the two reanalysis datasets exhibit similarities (mean bias = 0.04 °C and Pearson correlation coefficient = 0.63). Since NCEP is utilized as a boundary for WRF simulations, we believe that substituting ERA5 as the boundary for WRF runs would not substantially alter the outcomes.
-
Particularly for evaluating the predictive performance of the urban meteorological models, an additional observational dataset is required, which is not used by the Global Circulation Models for assimilation.
-
In addition to device and network malfunctioning, the crowd-sourced weather stations used in this analysis may be subject to misplacement, e.g., being in indoor conditions or the proximity of hot surfaces. Note that the variations in the number of Netatmo station data may not accurately depict the actual station count. The metadata retrieved through the Getpublicdata() API method only includes IDs and locations for stations available at the time of the request. Consequently, this can impact the derivation of archive observations from stations that are not operational at the moment of the request.
-
There are not yet standards for quality control of crowd-sourced data of Ta measurement, even though the statistical method [52] we used here for quality control of the Netatmo station data has been used successfully in similar studies. For comparability of the results, still standard guidelines are required for the quality assessment of the crowd-sourced weather station data.
-
When it comes to interpolating into areas that are not adequately represented in the observational data, such as rivers and parks in the context of our study, the ability of statistical methods (OK and ML) to extrapolate might be limited when attempting to generate accurate maps. Varentsov et al. [72] found the main difficulty of the kriging methods without model input was water and plateau areas, where observational data are lacking.
5 Conclusions
Mesoscale (1 − 5 km2) mapping of the spatio-temporal variability in urban Ta has been challenging because of standard Ta measurements’ irregular/sparse spatial availability. In this study, we used the crowd-sourced, Netatmo weather station data to benchmark the performance of three popular approaches for spatio-temporal mapping of the urban Ta against observations of five meteorological reference stations in Warsaw. OK (Ordinary Kriging), as representative of approaches independent of external data and knowledge, ML (XGBoost), as representative of advance statistical predictive methods, and WRF meteorological model as representative of urban fine-resolution weather models were employed to predict the spatio-temporal variability of Ta during the warm months in 2021. In comparison with reference meteorological measurements, here, ML approach outputs (RMSE = 1.06 °C, R2 = 0.94) outperformed OK (RMSE = 3 °C, R2 = 0.58) and WRF meteorological model (RMSE = 1.7 °C, R2 = 0.85), considering speed, interpretability of outputs, accuracy, and methodological limits. So, we selected the ML approach as a parsimonious model to predict Ta in Warsaw. The output from the ML approach was used to map sub-daily (four times per day) variability in Ta for Warsaw at nearly 1 km2 spatial (0.008°) resolution. According to our results, Ta and 2-m dew temperature predicted by ERA5 land reanalysis were the most important predictor for the prediction of Ta using the ML approach. LST and Gregorian calendar day followed these predictors. Accordingly, we suggest including the Gregorian calendar day as a predictor in similar studies. The methodology provided here has implications for urban management and devising sustainable adoption plans in response to overheating at urban scales.
Availability of Data and Materials
Data required to replicate the results provided in this paper are available at https://doi.org/10.6084/m9.figshare.19786921. The codes are available in the Supplementary Information Appendix.
References
Perkins, S., Alexander, L. & Nairn, J. (2012). Increasing frequency, intensity and duration of observed global heatwaves and warm spells. Geophysical Research Letters, 39.
Stocker, T. (2014). Climate change 2013: the physical science basis: Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge university press.
Grimmond, C.S.B., Ward, H.C. & Kotthaus, S. (2015). How is urbanization altering local and regional climate?. Seto, K. C., Solecki, W. D. and Griffith, C. A. (eds.) The Routledge Handbook of Urbanization and Global Environmental Change., Routledge.
Kim, H. H. (1992). Urban heat island. International Journal of Remote Sensing, 13, 2319–2336.
Lai, D., Liu, W., Gan, T., Liu, K., & Chen, Q. (2019). A review of mitigating strategies to improve the thermal environment and thermal comfort in urban outdoor spaces. Science of the Total Environment, 661, 337–353.
Yenneti, K., Ding, L., Prasad, D., Ulpiani, G., Paolini, R., Haddad, S., & Santamouris, M. (2020). Urban overheating and cooling potential in Australia: An evidence-based review. Climate, 8, 126.
Rameezdeen, R., & Elmualim, A. (2017). The impact of heat waves on occurrence and severity of construction accidents. International journal of environmental research public health, 14, 70.
Choobineh, M., Tabares-Velasco, P. C., & Mohagheghi, S. (2016). Optimal energy management of a distribution network during the course of a heat wave. Electric Power Systems Research, 130, 230–240.
Chapman, L., Azevedo, J. A., & Prieto-Lopez, T. (2013). Urban heat & critical infrastructure networks: A viewpoint. Urban Climate, 3, 7–12.
Campbell, S., Remenyi, T. A., White, C. J., & Johnston, F. H. (2018). Heatwave and health impact research: A global review. Health & Place, 53, 210–218.
Amengual, A., Homar, V., Romero, R., Brooks, H. E., Ramis, C., Gordaliza, M., & Alonso, S. (2014). Projections of heat waves with high impact on human health in Europe. Global Planetary Change, 119, 71–84.
Hendel, M., Azos-Diaz, K., & Tremeac, B. (2017). Behavioral adaptation to heat-related health risks in cities. Energy Buildings, 152, 823–829.
Santamouris, M., Paolini, R., Haddad, S., Synnefa, A., Garshasbi, S., Hatvani-Kovacs, G., Gobakis, K., Yenneti, K., Vasilakopoulou, K. & Feng, J. (2020). Heat mitigation technologies can improve sustainability in cities. An holistic experimental and numerical impact assessment of urban overheating and related heat mitigation strategies on energy consumption, indoor comfort, vulnerability and heat-related mortality and morbidity in cities. Energy Buildings, 217, 110002.
Tan, J., Zheng, Y., Song, G., Kalkstein, L. S., Kalkstein, A. J., & Tang, X. (2007). Heat wave impacts on mortality in Shanghai, 1998 and 2003. International journal of biometeorology, 51, 193–200.
Hulley, G., Shivers, S., Wetherley, E., & Cudd, R. (2019). New ECOSTRESS and MODIS land surface temperature data reveal fine-scale heat vulnerability in cities: A case study for Los Angeles County, California. Remote Sensing, 11, 2136.
Saaroni, H., Ziv, B., & Climatology (2010). Estimating the urban heat island contribution to urban and rural air temperature differences over complex terrain: Application to an arid city. Journal of Applied Meteorology, 49, 2159–2166.
Oke, T. R. (1988). The urban energy balance. Progress in Physical Geography, 12, 471–508.
Ryan, D. (2015). From commitment to action: A literature review on climate policy implementation at city level. Climatic Change, 131, 519–529.
Zumwald, M., Knüsel, B., Bresch, D. N., & Knutti, R. (2021). Mapping urban temperature using crowd-sensing data and machine learning. Urban Climate, 35, 100739.
Chen, K., Wolf, K., Breitner, S., Gasparrini, A., Stafoggia, M., Samoli, E., Andersen, Z. J., Bero-Bedada, G., Bellander, T., & Hennig, F. (2018). Two-way effect modifications of air pollution and air temperature on total natural and cardiovascular mortality in eight European urban areas. Environment International, 116, 186–196.
Kuras, E. R., Richardson, M. B., Calkins, M. M., Ebi, K. L., Hess, J. J., Kintziger, K. W., Jagger, M. A., Middel, A., Scott, A. A., & Spector, J. T. (2017). Opportunities and challenges for personal heat exposure research. Environmental Health Perspectives, 125, 085001.
Nazarian, N., & Lee, J. K. (2021). Personal assessment of urban heat exposure: A systematic review. Environmental Research Letters, 16, 033005.
Shamir, E., & Georgakakos, K. P. (2014). MODIS Land Surface Temperature as an index of surface air temperature for operational snowpack estimation. Remote Sensing of Environment, 152, 83–98.
Venter, Z. S., Chakraborty, T. & Lee, X. (2021). Crowdsourced air temperatures contrast satellite measures of the urban heat island and its mechanisms. Science Advances, 7, eabb9569.
Prihodko, L., & Goward, S. N. (1997). Estimation of air temperature from remotely sensed surface observations. Remote Sensing of Environment, 60, 335–346.
Stisen, S., Sandholt, I., Nørgaard, A., Fensholt, R., & Eklundh, L. (2007). Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sensing of Environment, 110, 262–274.
dos Santos, R. (2020). Estimating spatio-temporal air temperature in London (UK) using machine learning and earth observation satellite data. International Journal of Applied Earth Observation Geoinformation, 88, 102066.
Vancutsem, C., Ceccato, P., Dinku, T., & Connor, S. (2010). Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sensing of Environment, 114, 449–465.
Ho, H. C., Knudby, A., Sirovyak, P., Xu, Y., Hodul, M., & Henderson, S. B. (2014). Mapping maximum urban air temperature on hot summer days. Remote Sensing of Environment, 154, 38–45.
Sun, Y., Wang, J., Zhang, R., Gillies, R., Xue, Y., & Bo, Y. (2005). Air temperature retrieval from remote sensing data based on thermodynamics. Theoretical Applied Climatology, 80, 37–48.
Grimmond, C., Blackett, M., Best, M., Barlow, J., Baik, J., Belcher, S., Bohnenstengel, S., Calmet, I., Chen, F., & Dandou, A. (2010). The international urban energy balance models comparison project: First results from phase 1. Journal of Applied Meteorology Climatology, 49, 1268–1292.
Garuma, G. F. (2018). Review of urban surface parameterizations for numerical climate models. Urban Climate, 24, 830–851.
Hamdi, R., Kusaka, H., Doan, Q.-V., Cai, P., He, H., Luo, G., Kuang, W., Caluwaerts, S., Duchêne, F. & Van Schaeybroek, B. (2020). The state-of-the-art of urban climate change modeling and observations. Earth Systems and Environment, 1–16.
Zhang, Z., & Du, Q. (2022). Hourly mapping of surface air temperature by blending geostationary datasets from the two-satellite system of GOES-R series. ISPRS Journal of Photogrammetry Remote Sensing, 183, 111–128.
Taheri-Shahraiyni, H., & Sodoudi, S. (2017). High-resolution air temperature mapping in urban areas: A review on different modelling techniques. Thermal Science, 21, 2267–2286.
Kottek, M., Grieser, J., Beck, C., Rudolf, B. & Rubel, F. (2006). World map of the Köppen-Geiger climate classification updated.
National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce. (2015). NCEP GDAS/FNL 0.25 degree global tropospheric analyses and forecast grids (updated daily) [Dataset]. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. https://doi.org/10.5065/D65Q4T4Z. Accessed 11 Nov 2023.
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Liu, Z., Berner, J., Wang, W., Powers, J. G., Duda, M. G., & Barker, D. M. (2019). A description of the advanced research WRF model version 4. National Center for Atmospheric Research: Boulder, CO, USA, 145, 145.
Thompson, G., Field, P. R., Rasmussen, R. M., & Hall, W. D. (2008). Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Monthly Weather Review, 136, 5095–5115.
Janjić, Z. I. (1994). The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Monthly Weather Review, 122, 927–945.
Tiedtke, M. (1989). A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Monthly weather review, 117, 1779–1800.
Chen, F., Janjić, Z., & Mitchell, K. (1997). Impact of atmospheric surface-layer parameterizations in the new land-surface scheme of the NCEP mesoscale Eta model. Boundary-Layer Meteorology, 85, 391–421.
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A. & Collins, W. D. (2008). Radiative forcing by long‐lived greenhouse gases: calculations with the AER radiative transfer models. Journal of Geophysical Research: Atmospheres, 113.
Zhang, C., Wang, Y., & Hamilton, K. (2011). Improved representation of boundary layer clouds over the southeast Pacific in ARW-WRF using a modified Tiedtke cumulus parameterization scheme. Monthly Weather Review, 139, 3489–3513.
Romine, G. S., Schwartz, C. S., Snyder, C., Anderson, J. L., & Weisman, M. L. (2013). Model bias in a continuously cycled assimilation system and its influence on convection-permitting forecasts. J Monthly Weather Review, 141, 1263–1284.
Powers, J. G., Klemp, J. B., Skamarock, W. C., Davis, C. A., Dudhia, J., Gill, D. O., Coen, J. L., Gochis, D. J., Ahmadov, R., & Peckham, S. E. (2017). The weather research and forecasting model: Overview, system efforts, and future directions. Bulletin of the American Meteorological Society, 98, 1717–1737.
Broxton, P. D., Zeng, X., Sulla-Menashe, D., Troch, P. A., & Climatology,. (2014). A global land cover climatology using MODIS data. Journal of Applied Meteorology, 53, 1593–1605.
Chen, F., Kusaka, H., Bornstein, R., Ching, J., Grimmond, C. S. B., Grossman-Clarke, S., Loridan, T., Manning, K. W., Martilli, A., & Miao, S. (2011). The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. International Journal of Climatology, 31, 273–288.
Danielson, J. J., & Gesch, D. B. (2011). Global multi-resolution terrain elevation data 2010 (GMTED2010). US Department of the Interior, US Geological Survey Washington, DC, USA.
Chapman, L., Bell, C., & Bell, S. (2017). Can the crowdsourcing data paradigm take atmospheric science to a new level? A case study of the urban heat island of London quantified using Netatmo weather stations. International Journal of Climatology, 37, 3597–3605.
Venter, Z. S., Brousse, O., Esau, I., & Meier, F. (2020). Hyperlocal mapping of urban air temperature using remote sensing and crowdsourced weather data. Remote Sensing of Environment, 242, 111791.
Napoly, A., Grassmann, T., Meier, F. & Fenner, D. (2018). Development and application of a statistically-based quality control for crowdsourced air temperature data. Frontiers in Earth Science, 118.
Grassmann, T., Napoly, A., Meier, F. & Fenner, D. (2018). Quality control for crowdsourced data from CWS.
Mälicke, M., Möller, E., Helge Schneider, D. & Sebastian, M. (2021). mmaelicke/scikit-gstat: a scipy flavoured geostatistical variogram analysis toolbox (Version v0.6.0). Zenodo, 1-43.
Chen, T. & Guestrin, C. 2016, Xgboost: a scalable tree boosting system, Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, pp. 785–794.
Cook, M., Schott, J. R., Mandel, J., & Raqueno, N. (2014). Development of an operational calibration methodology for the Landsat thermal data archive and initial testing of the atmospheric compensation component of a Land Surface Temperature (LST) product from the archive. Remote Sensing, 6, 11244–11266.
Vermote, E., Justice, C., Claverie, M., & Franch, B. (2016). Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sensing of Environment, 185, 46–56.
European Space Agency (ESA) (2015). Sentinel-2 User Handbook, 64.
Pekel, J.-F., Cottam, A., Gorelick, N., & Belward, A. S. (2016). High-resolution mapping of global surface water and its long-term changes. Nature Communications, 540, 418–422.
Wan, Z., Hook, S. & Hulley, G. (2015). MYD11A1 MODIS/Aqua Land Surface Temperature/Emissivity Daily L3 Global 1km SIN Grid V006 . NASA EOSDIS Land Processes DAAC. https://doi.org/10.5067/MODIS/MYD11A1.006. Accessed 23 Feb 2022.
Didan, K. (2015). MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006 . NASA EOSDIS Land Processes DAAC. https://doi.org/10.5067/MODIS/MOD13Q1.006. Accessed 23 Feb 2022.
Muñoz Sabater, J. (2019). ERA5-Land hourly data from 1981 to present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS).
Friedman, J.H. (2001). Greedy function approximation: a gradient boosting machine. Annals of Statistics, 1189–1232.
Breiman, L. (2001). Random forests. Machine learning, 45, 5–32.
Ma, X., Fang, C., & Ji, J. (2020). Prediction of outdoor air temperature and humidity using Xgboost, IOP Conference Series: Earth and Environmental Science, IOP Publishing, 012013.
Sun, H., Chen, Y., & Zhan, W. (2015). Comparing surface-and canopy-layer urban heat islands over Beijing using MODIS data. International Journal of Remote Sensing, 36, 5448–5465.
Hulley, G., & Ghent, D. (2019). Taking the temperature of the Earth: Steps towards integrated understanding of variability and change. Elsevier.
Good, E. J. (2016). An in situ-based analysis of the relationship between land surface “skin” and screen-level air temperatures. Journal of Geophysical Research: Atmospheres, 121, 8801–8819.
Sheng, L., Tang, X., You, H., Gu, Q., & Hu, H. (2017). Comparison of the urban heat island intensity quantified by using air temperature and Landsat land surface temperature in Hangzhou, China. Ecological Indicators, 72, 738–746.
Arnfield, A. J. (2003). Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. International Journal of Climatology: A Journal of the Royal Meteorological Society, 23, 1–26.
Voogt, J. A., & Oke, T. R. (2003). Thermal remote sensing of urban climates. Remote Sensing of Environment, 86, 370–384.
Varentsov, M., Esau, I., & Wolf, T. (2020). High-resolution temperature mapping by geostatistical kriging with external drift from large-eddy simulations. Monthly Weather Review, 148, 1029–1048.
Zhou, B., Erell, E., Hough, I., Shtein, A., Just, A. C., Novack, V., Rosenblatt, J., & Kloog, I. (2020). Estimation of hourly near surface air temperature across Israel using an ensemble model. Remote Sensing, 12, 1741.
Hough, I., Just, A. C., Zhou, B., Dorman, M., Lepeule, J., & Kloog, I. (2020). A multi-resolution air temperature model for France from MODIS and Landsat thermal data. Environmental Research Letters, 183, 109244.
Funding
Open access funding provided by NILU - Norwegian Institute For Air Research. Research for this project was funded from the EEA grants 2014–2021 under the Basic Research Programme operated by the Polish National Science Centre in cooperation with the Research Council of Norway (grant no. 2019/35/J/HS6/03992).
Author information
Authors and Affiliations
Contributions
Conceptualization: A.H., N.C. Methodology: A.H., N.C., G.S.S, and P.S. Funding acquisition: N.C. Supervision: N.C. and P.S. Data acquisition: A.H. and G.S.S. Data Analysis and programming: A.H. and G.S.S Investigation: A.H., N.C., G.S.S., and P.S. Visualization: A.H. Validation: A.H., N.C., G.S.S., and P.S. Writing — original draft: A.H., G.S.S Writing — review and editing: A.H., N.C., G.S.S, and P.S.
Corresponding author
Ethics declarations
Ethics Approval
Not applicable.
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hassani, A., Santos, G.S., Schneider, P. et al. Interpolation, Satellite-Based Machine Learning, or Meteorological Simulation? A Comparison Analysis for Spatio-temporal Mapping of Mesoscale Urban Air Temperature. Environ Model Assess 29, 291–306 (2024). https://doi.org/10.1007/s10666-023-09943-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10666-023-09943-9