1 Introduction

Steve Davis was a leader in fluid-mechanics research, making significant contributions to our understanding of hydrodynamic stability, interfacial thin-film flows and solidification [1, 2]. This short, pedagogical review about the formation of ripples on the surface of icicles touches on all those aspects of continuum mechanics, and I am pleased to offer it in Steve’s memory.

Two principles espoused by Steve made particular impact on me. The first was the frozen-temperature approximation that Steve made and exploited in many of his studies of morphological instability of solidifying binary alloys. It recognises that instability is driven principally by constitutional supercooling and the enhancement of solute diffusion of rejected impurities away from an advancing phase boundary, so that perturbations to the temperature field can be ignored. This simplifying approximation makes the driving mechanism for instability transparent and renders the calculation of instability analytically tractable, which allows significant additional progress to be made, as Steve exemplified with many studies of the nonlinear evolution of morphological instabilities.

The second principle was that, although non-dimensionalisation is a powerful way to identify key physical interactions and make mathematical solutions more applicable given a wide range of different material and controlling parameters, presenting mathematical answers in dimensional terms can be crucial to general understanding and for conveying important ideas to applied scientists. The prime example, for me, came again from the study of morphological instability during binary solidification. The compact, universal, analytical result, obtained using the frozen-temperature approximation, is that instabilities occur once the dimensionless Morphological number exceeds a certain function of the ratio of a diffusion length and a capillary length associated with the surface energy of the solid–liquid phase boundary. The trouble with this statement is that both sides of the inequality depend separately on the concentration of the alloy and the rate of solidification. Only when one unpacks the statement in terms of these controlling parameters does one appreciate that, although the phase boundary becomes unstable as the rate of solidification exceeds a critical value (the well-known result), it becomes stable again at larger solidification rates (compare Figs. 3.4 and 3.6 of Davis [2], for example). A single inequality in dimensionless variables hides a double inequality in control variables.

My aim in this paper is to emulate these principles while reviewing and developing theories for the formation and evolution of ripples on icicles, illustrated in Fig. 1, using and justifying simplifying approximations that allow for transparent analytical solutions, introducing dimensionless variables and parameters only when their use is unambiguous, and expressing results in dimensional form when they relate to experimental observations.

Fig. 1
figure 1

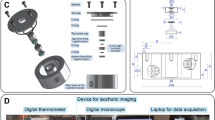
Full view (a) and close up (b) of a natural icicle hanging from a roof in Toronto, showing centimetre-scale ripples. (c) Image of a lab-grown icicle made from distilled water with 80 ppm NaCl impurity from the Icicle Atlas Run 120206, Frame 417 [3]. (d) Image of a lab-grown icicle with 519 ppm sodium fluorescein dye as the impurity. The dye glows green in the liquid phase but appears orange when trapped in inclusions within the ice. The partial wetting of the surface is evident. (e) The lower region of a lab-grown icicle with 130 ppm sodium fluorescein dye. The tip region is completely wetted by a thin liquid film. (All images courtesy of Stephen Morris.) (Color figure online)

Full size image

Icicles are a common phenomenon in cold climates, formed particularly when radiation from the sun or heat from the interior of a building melts the snow on a roof while the air is sufficiently cold to refreeze the dripping meltwater. In addition to their overall, carrot-like shape [4], scientists have been intrigued by the concentric ripples that form along their sides (Fig. 1). In particular, it seems from observations of natural icicles and those formed in controlled laboratory experiments [5,6,7] that the wavelength of the ripples is quite insensitive to environmental conditions or the rate of supply of water, varying only between about 8–12 mm. Additionally, it has been observed by time lapse that the phase of the ripples migrates slowly upwards as the icicle grows. These are the two primary observations that this paper seeks to address.

It has also been shown in laboratory experiments that ripples do not form on icicles grown from pure water but do form once some level of impurity is added to the water [7, 8]. Demmenie et al. [8] suggest that, because of the associated contact angle of water on ice, this may be related to their observation that pure water tends to form rivulets along the icicle rather than a continuous, essentially uniform film. However, extensive laboratory studies had already shown that rivulets are the most common form of water flow on rippled icicles at any impurity concentration (see Fig. 1d), though continuous films of water are more prevalent at higher impurity concentrations [9], particularly coating the lower portions of icicles (see Fig. 1e), which may be where ripples are born.

It is an open question how rivulets interact with the evolving morphology of icicles and, to my knowledge, no one has considered them in any theoretical study of icicle ripples. Given that this paper is, in large part, a review of existing theoretical studies and a springboard for future studies, I will for the most part ignore the rivulets and assume that the film of water is continuous and uniform, which may in any case be appropriate for the lower portions of the icicle, as mentioned above. For simplicity, I will also confine my analysis to two dimensions, focusing on physical processes acting across and along the film. The analyses in this paper are therefore more directly relevant to ice formed from water flowing down a vertical plane, and it is with such experiments that quantitative comparisons will be made. However, the physical interactions that form the main focus of my discussions apply equally to conical icicles.

Although Chen and Morris [7] have found significant influence of impurity concentration on the growth and migration of ripples, Ladan [10] found that the freezing-point depression caused by impurities had very little influence on his linear-stability results. The role of impurities is unclear, and they may have more influence on the nonlinear development of ripples than on their genesis. I will discuss this a little in Sect. 7 but will not consider impurities in any of the modelling presented here.

Some authors have focused on the hydrodynamics of the water film (e.g. Camporeale et al. [11]), considering the effect of the phase boundary on the roll waves that can form on the free surface of the film. Ogawa and Furukawa [12] and Ueno [13] start in a similar way, invoking the Orr–Sommerfeld equations to describe perturbations of the flow, but then effectively take the limit of small Reynolds number \(Re = Uh/\nu \) (where U is a characteristic speed of the longitudinal flow, h is the thickness of the film and \(\nu \) is its kinematic viscosity), at which such hydrodynamic instabilities do not occur. Indeed, the relevant dimensionless parameter determining the influence of inertia in a thin-film flow is the reduced Reynolds number (h/L)Re, where L is a characteristic longitudinal length scale, such as the wavelength of the ripples. Typical estimates for icicles are that \(U\approx 1\) cm s\(^{-1}\), \(h\approx 10^{-2}\) cm, \(\nu \approx 10^{-2}\) cm\(^2\) s\(^{-1}\) and \(L\approx 1\) cm, which gives a Reynolds number of about unity but a reduced Reynolds number of only about \(10^{-2}\). I shall therefore ignore inertia throughout and simply use lubrication theory to describe the thin-film flow.

Without hydrodynamic instability, it is widely anticipated and featured in theoretical models that the primary driving mechanism for ripple-forming instabilities on icicles is the point effect of diffusion: heat is diffused more efficiently from protrusions of the icicle into the ambient environment, which promotes their growth (see [14], for example). This is the driving mechanism for the Mullins–Sekerka, morphological instability of a solid growing into a supercooled melt and, with impurity concentration playing the role of heat, for morphological instability of an alloy solidifying from a binary melt [15]. The growth rate of instabilities resulting from the point effect of diffusion grows linearly with wavenumber, which leads to an ultra-violet catastrophe: the shorter the wavelength of an incipient ripple, the faster it grows. This catastrophe is averted during solidification from melts by the Gibbs–Thomson effect resulting from surface energy of the solid–liquid phase boundary, in consequence of which the melting temperature of protrusions is less than that of planar interfaces. This stabilises short-wavelength perturbations and results in the fastest growing wavelengths being of the order of microns given typical conditions, which is much smaller than the wavelengths of ripples seen on icicles. Morphological instabilities in binary systems caused by constitutional supercooling following rejection of impurities have wavelengths that are typically ten times smaller even than those caused thermally during solidification of a supercooled melt. This has led previous authors to neglect Gibbs–Thomson undercooling entirely. We shall see here, however, that it can play a significant role in wavelength selection for a variety of reasons.

From their analytical studies, Ogawa and Furukawa [12] and Ueno [13] both concluded that the heat advected by the film of water surrounding icicles would stabilise short wavelengths and result in wavelengths of the fastest growing ripples of around a centimetre, as observed. However, I find instead that the advection of heat by the flowing film is destabilising, as shown in Sect. 4. A significant new finding is that the phase shift between corrugations to the ice–film interface and the film–air interface, which Ueno [13] identifies but subsequently ignores in part, reduces the growth rate of short-wavelength perturbations sufficiently to explain wavelength selection at millimetric length scales that are independent of environmental conditions and quite insensitive to the flow rate of the film, as well as the observed upwards migration of ripples. However, in Sect. 4, I find that wavelength selection by this mechanism is lost at high flow rates once the point effect of diffusion ceases to influence the phase boundary and morphological instability is driven instead by perturbations to the advected heat flux caused by the surface-tension-driven Laplace pressure. I begin in Sect. 2 by developing a simple, heuristic model of ripple formation on icicles, involving just the point effect of diffusion and surface tension of the interface between the liquid film coating an icicle and the surrounding air. This proves sufficient to predict ripples of finite wavelength, of millimetric scale, that migrate upwards. In Sect. 3, I show that Gibbs–Thomson undercooling has little influence on the predicted wavelengths but does serve to stabilise completely ripples with wavelengths shorter than about 2 mm. In Sects. 4 and 5, I consider the role of advective heat transport in the film using detailed, thin-film analyses of the flow and associated heat transfer. The results of Sect. 4, in which I develop an asymptotic solution in the limit of small reduced Péclet number p are shown to reduce to the results of the heuristic model in the limit \(p\rightarrow 0\). For larger values of p, I show in Sect. 5 that the point effect of diffusion becomes ineffective at large flow rates but a new balance involving advective heat transport and Gibbs–Thomson undercooling serves to select a finite wavelength of instability that is still of order millimetres. In Sect. 6, I compare and contrast previous linear stability analyses of ripple formation in the light of the new calculations presented in this paper. While these results reproduce key qualitative observations, with appropriate magnitudes, they slightly under-predict the observed wavelengths and leave several questions unanswered, some of which are discussed in Sect. 7.

2 A heuristic model

There are several physical processes involved in the formation and evolution of the morphology of icicles, and very many dimensionless physical parameters to consider. Analytical progress is often made by exploiting the fact that some dimensionless parameters are small but care must be taken not to discard consideration of important physical processes, and we shall see that numerical factors (of 2\(\pi \) for example) can be significant when deciding whether certain parameters are large or small. One approach is to start from what might be considered as a full system of equations and to reduce those asymptotically by taking particular limits of the governing parameters. In this paper, I take a more synthetic approach, starting in this section with what seems to be the minimal model capable of describing the main observations: the formation of ripples with millimetric length scales that migrate upwards.

Fig. 2
figure 2

Schematic diagram of the surface of an icicle coated by a film of water. The dashed lines show the unperturbed positions of the ice–film and film–air interfaces. a At long wavelengths, the film is almost uniform in thickness and the air interface is almost in phase with the ice interface. b At shorter wavelengths, the air interface is flatter and its phase is shifted upwards with respect to the ice interface. The flow is illustrated in (a), while the undisturbed temperature field is shown in (b)

Full size image

2.1 Fluid flow

Consider a vertical, two-dimensional icicle covered with a continuous film of water that flows under gravity, as shown in Fig. 2. Let the positions of the ice–film and film–air interfaces be at \(y = \eta _1 \textrm{e}^{i\alpha x + \sigma t}\) and \(y = h + \eta _2 \textrm{e}^{i\alpha x + \sigma t}\) respectively, where x is vertically downwards and y is horizontal, measured from the undisturbed location of the ice–water interface. These represent normal-mode perturbations to a uniform film of thickness h with wavenumber \(\alpha \) and growth rate \(\sigma \). The perturbation amplitudes \(\eta _1\) and \(\eta _2\) may be complex and therefore allow for a phase shift between the two interfaces. To avoid clutter, I will often write perturbation quantities such as \( \eta _1 \textrm{e}^{i\alpha x + \sigma t}\) simply as \(\eta _1\), with the exponential structure of the normal mode left implicit. Given that the film is very thin, we use the lubrication approximation that \(\alpha h \ll 1\). A well known result in fluid mechanics, found in many introductory texts (e.g. Worster [16]), is that the volume flux per unit width q in a two-dimensional, free-surface film on a rigid boundary is proportional to the cube of its thickness H, given by

$$\begin{aligned} q = {1\over 3\mu }\left( \rho g - {\partial p\over \partial x}\right) H^3, \end{aligned}$$
(1)

where p is the dynamic pressure in the film, \(\rho \) is its density, \(\mu \) its dynamic viscosity and g the acceleration due to gravity. A detailed analysis leading to this result is given in Sect. 4.

For the film coating an icicle, the dynamic pressure is given solely by the Laplace pressure resulting from surface tension \(\gamma \) of the film–air interface, with \(p = \gamma \times \hbox {curvature} \approx -\gamma \eta _{2xx}\) relative to the ambient pressure of the air, where the approximation is made by linearising for small displacements \(\eta _2\). Therefore,

$$\begin{aligned} q = {1\over 3\mu }(\rho g - i\gamma \alpha ^3 \eta _2)(h + \eta _2 - \eta _1)^3, \end{aligned}$$
(2)

which can be linearised to give

$$\begin{aligned} q \sim {g\over 3\nu }h^3 + {g\over \nu }h^2(\eta _2 - \eta _1) - i{\gamma \alpha ^3 h^3\over 3\mu }\eta _2, \end{aligned}$$
(3)

where \(\nu = \mu /\rho \) is the kinematic viscosity of water.

The flow rate (about 1 cm s\(^{-1}\)) is much faster than the lateral growth rate (about \(10^{-4}\) cm s\(^{-1}\)), so on the time scales of interest, relating to the growth of ripples, the flow can be considered steady. In addition, for common, dripping icicles, the water supply rate is much greater than the rate at which water is converted to ice, so the volumetric dripping flux is very close to the supply rate and q can be taken to be independent of x. In accordance with most experiments, we also take q to be constant in time. Therefore, at leading order, Eq. (3) shows that

$$\begin{aligned} h = \left( {3\nu q\over g}\right) ^{1/3}, \end{aligned}$$
(4)

while the first-order contributions to the flux must be zero, which gives

$$\begin{aligned} \eta _2 = {\eta _1 \over 1 - i\Gamma \alpha ^3h }, \end{aligned}$$
(5)

where \(\Gamma \) is the square of the gravity-capillary length \(l_\textrm{gc} = (\gamma /3\rho g)^{1/2}\).

This result, determined by Ueno [13] after working through the Orr–Sommerfeld equation, is illustrated in Fig. 2. We see from the expression for \(\eta _2\) and in Fig. 2 that at small wave numbers (long wavelengths) the film–air interface is almost in phase with the ice–film interface and has a similar amplitude, while at large wave numbers (short wavelengths) the film–air interface is shifted upstream and its amplitude is smaller. The phase shift tends to \(\pi /2\) as \(\alpha \rightarrow \infty \). This primary result is sufficient to explain the main qualitative experimental observations, as described below.

2.2 Thermodynamics

We can estimate the film thickness h from expression (4). The kinematic viscosity of water \(\nu \approx 2\times 10^{-2}\) cm\(^2\) s\(^{-1}\), and the acceleration due to gravity \(g\approx 980\) cm s\(^{-2}\), while the maximum fluid flux per unit width reported by Ueno [13] is about 100 ml/h/cm \(\approx 3\times 10^{-2}\) cm\(^2\) s\(^{-1}\). These parameter estimates give \(h\approx 10^{-2}\) cm = 100 \(\mu \)m. In the unperturbed state, we assume that the ice–film interface is at the freezing temperature \(T_\textrm{m}\) and that the temperature decays to \(T_\infty \) across a boundary layer in the air. For the sake of estimation, we assume that the decay is exponential, with a characteristic decay length \(\delta \), and that the temperature varies linearly across the water film. The unperturbed temperature field is shown schematically in Fig. 2b. Note that the liquid film is supercooled.

In a quiescent environment, the thermal boundary layer in the air is quasi-steady, determined by a balance between conduction and advection and between thermal buoyancy and viscous dissipation. Its width can be estimated as \(\delta ~\sim Ra^{-1/4} z\), where z is the vertical distance from the tip and \(Ra = \alpha _T g \Delta T z^3 / \kappa _\textrm{a} \nu _\textrm{a}\) is a local Rayleigh number, where \(\alpha _T\), \(\kappa _\textrm{a}\) and \(\nu _\textrm{a}\) are the thermal expansion coefficient, thermal diffusivity and kinematic viscosity of air, respectively. Given the parameter values in Table 1 and taking \(z\approx 10\) cm, this gives an estimate of \(\delta \approx 3\) mm. We shall see, however, that the main results of this paper are insensitive to the value of \(\delta \).

While the interfaces are unperturbed, the balance of heat flux across the film–air interface requires that

$$\begin{aligned} k_\textrm{w}{T_\textrm{m} - T_\textrm{a} \over h} = k_\textrm{a} {T_\textrm{a} - T_\infty \over \delta }, \end{aligned}$$
(6)

where \(T_\textrm{a}\) is the temperature of the film–air interface, while \(k_\textrm{w}\) and \(k_\textrm{a}\) are the thermal conductivities of water and air respectively. This relationship can be rearranged to show that

$$\begin{aligned} T_\textrm{m} - T_\textrm{a} = {\epsilon \over 1+\epsilon }(T_\textrm{m} - T_\infty ), \end{aligned}$$
(7)

where

$$\begin{aligned} \epsilon = {k_\textrm{a}\over k_\textrm{w}}{h\over \delta }. \end{aligned}$$
(8)

The ratio of conductivities is about 1/25, while \(h/\delta \approx 1/30\). Therefore, \(\epsilon \) is about \(10^{-3} \ll 1\) and \(T_\textrm{a}\approx T_\textrm{m}\) to a very good approximation. For now, we simply assume that this remains true once the film is perturbed: the film–air interface is essentially at the freezing temperature, and the film simply carries the heat flux from the air to the freezing front. Formally, in what follows, we let \(\epsilon \rightarrow 0\).

Therefore, the Stefan condition governing the growth of the icicle is well approximated by

$$\begin{aligned} \rho _\textrm{s} L (V + \sigma \eta _1) = -k_\textrm{a}{\partial T\over \partial y}\bigg \vert _{h+\eta _2+}, \end{aligned}$$
(9)

where \(\rho _\textrm{s}\) is the density of ice, L is the latent heat of fusion, and V is the unperturbed freezing rate normal to the surface of the icicle. We shall see that it is the phase shift in this equation (the growth of the phase boundary at \(\eta _1\) is determined by the heat flux at \(h+\eta _2\)) that gives rise to the main observations.

The effective Stefan number for this problem \(\rho _\textrm{s} L /\rho _\textrm{a} c_\textrm{pa}\Delta T \), where \(\rho _\textrm{a}\) and \(c_\textrm{pa}\) are the density and specific heat capacity of air respectively, is very large (approximately \(10^4\)). Therefore diffusive transport relaxes to a steady state much faster than the time scale on which solidification proceeds, and we can consider the system depicted in Fig. 2 to be stationary when calculating the thermal field and associated heat fluxes. For simplicity, we also ignore advective heat transport of temperature perturbations in the air, which therefore satisfy Laplace’s equation in \(y>h+\eta _2\), giving

$$\begin{aligned} T = T_\infty + (T_\textrm{m} - T_\infty )\textrm{e}^{-(y - h)/\delta } + \theta _\textrm{a} \textrm{e}^{-\alpha (y - h)} \textrm{e}^{i\alpha x + \sigma t}, \end{aligned}$$
(10)

where \(\theta _\textrm{a}\) is a constant to be determined.

At leading order, the Stefan condition (9) gives

$$\begin{aligned} \rho _\textrm{s} L V = k_\textrm{a}{\Delta T \over \delta }, \end{aligned}$$
(11)

where \(\Delta T = T_\textrm{m} - T_\infty \). This expression determines the lateral growth rate V of the icicle.

At first order, the Stefan condition gives

$$\begin{aligned} \rho _\textrm{s} L \sigma \eta _1 = -k_\textrm{a}\left( {\Delta T\over \delta ^2}\eta _2 - \alpha \theta _\textrm{a}\right) , \end{aligned}$$
(12)

while the temperature at the film–air interface is supposed for now to be fixed at \(T_\textrm{m}\), which requires the perturbation fields to satisfy

$$\begin{aligned} 0 = -{\Delta T\over \delta }\eta _2 + \theta _\textrm{a}. \end{aligned}$$
(13)

We can eliminate \(\theta _\textrm{a}\) between these two equations and use the expression for \(\eta _2\) in terms of \(\eta _1\) given in Eq. (5) above to derive, finally, that the growth rate of disturbances of wave number \(\alpha \) is given by

$$\begin{aligned} {\delta \over V} \sigma = {-1 + {\alpha \delta } \over 1 - i\Gamma \alpha ^3 h } = {(-1 + \alpha \delta )(1 + i\Gamma \alpha ^3 h)\over 1 + \Gamma ^2\alpha ^6 h^2}. \end{aligned}$$
(14)

The amplification rate of perturbations is given by the real part, \(\sigma _\textrm{R}\), of \(\sigma \) given by

$$\begin{aligned} {\delta \over V}\sigma _\textrm{R} = (-1 + \alpha \delta )\left[ 1 + \Gamma ^2\alpha ^6 h^2\right] ^{-1}. \end{aligned}$$
(15)

This dispersion relation is plotted as the dashed curve in Fig. 3a using parameters from Table 1. These parameters are used for all the examples presented in this paper unless otherwise stated. The small, negative growth rates near \(\alpha =0\) arise in consequence of the neglect of advection of the perturbation temperature field in the air: the entrainment velocity that confines the thermal boundary layer in the air and determines the boundary-layer thickness \(\delta \) will also act on the perturbation field. Its effect would be a small modification to the growth rate near \(\alpha =0\) to bring the growth rate equal to zero there. In practical terms, both the wavelength of ripples \(2\pi /\alpha \) and the width \(\delta \) of the thermal boundary layer in the air are about a centimetre, which gives \(\alpha \delta \approx 2\pi \). It is, therefore, a reasonable approximation to take \(\alpha \delta \) to be large compared with unity, in which case Eq. (15) can be approximated by

$$\begin{aligned} {h \over V}\sigma _\textrm{R} = {\alpha h\over 1 + \Gamma ^2\alpha ^6 h^2}. \end{aligned}$$
(16)

This approximation, shown as the solid curve in Fig. 3a, is equivalent to taking a linear approximation for the unperturbed temperature field in the air (cf Ueno [13]), and is used for the remainder of this paper.

Fig. 3
figure 3

(a) The dispersion relation calculated using the heuristic model with water supply rate \(q=3\times 10^{-2}\) cm\(^2\) s\(^{-1}\). The dashed curve (Eq. (15)) includes the nonlinearity of the base-state temperature field in the air, while the solid curve (Eq. (16)) represents the approximation used throughout this paper that the base-state temperature field in the air is linear. (b) The wavelength of ripples predicted from linear stability theory (18) (solid curve) and data from Ueno et al. [6]

Full size image
Table 1 Physical parameter values used for illustration in this paper
Full size table

The wave number \(\alpha _\textrm{m}\) corresponding to the largest growth rate can be found straightforwardly by setting the derivative of Eq. (16) with respect to \(\alpha \) equal to zero to find

$$\begin{aligned} \Gamma \alpha _\textrm{m}^3 h = \left( {1\over 5}\right) ^{1/2}, \end{aligned}$$
(17)

which corresponds to a wavelength

$$\begin{aligned} \lambda _\textrm{m} = {2\pi \over \alpha _\textrm{m}} = 2{\pi (5)^{1/6} (l_\textrm{gc}^2 h)^{1/3} = 2}\pi \left( {125\over 81}\right) ^{1/18}\left( {\gamma ^3\nu q\over \rho ^3 g^4}\right) ^{1/9}, \end{aligned}$$
(18)

having made use of Eq. (4) for h and the definition of \(\Gamma \) in terms of physical parameters.

This is the primary result of this paper. We have found wavelength selection without Gibbs–Thomsom and without the advective heat transport focused on by previous authors. We have also found that the wavelength increases only very slowly with volume flux per unit width (proportional to \(q^{1/9}\)) and that it decreases with the strength of gravity. For flows down a plane inclined at an angle \(\phi \) to the horizontal, the effective gravity is \(g\sin \phi \) and we see that the wavelength decreases with \(\phi \) (cf. experimental results shown in Ueno et al. [6]), in proportion to \((\sin \phi )^{-4/9}\). It is interesting to note that, while the growth rate depends on the thermodynamic parameters, such as the degree of supercooling \(\Delta T\) and the width of the thermal boundary layer \(\delta \), the wavelength of the most unstable ripples in this leading-order theory depends only on the flow parameters, including the surface tension of the water–air interface, as shown in (18), and not at all on the thermal boundary layer in the air.

This result is shown in Fig. 3b, where it is compared with the data presented in Ueno et al. [6] for solidification from a thin film flowing down a planar, vertical surface. We see that, although it reproduces the observation that the wavelength increases only very little with volume flux, the prediction of this heuristic model under predicts the observations by a factor of almost 2.

In this heuristic model, ripples are formed from a morphological instability that relies on the point effect of diffusion. This is the same mechanism that drives the Mullins–Sekerka instability. However, whereas Gibbs–Thompson undercooling caused by surface energy of the phase boundary stabilises short wavelengths of the Mullins–Sekerka instability, here there is no stabilisation (the growth rates remain positive) but the growth of perturbations is weakened at large wavenumber for two reasons: surface tension in the film–air interface tends to flatten the interface more strongly at large wave numbers, which reduces the point effect of diffusion; the pressure gradients in the film caused by surface tension acting at the curved film–air interface drive a phase shift between the phase boundary and the film–air interface that tends to drive migration more than growth as the phase shift increases towards \(\pi /2\) as the wave number increases. This weakening is sufficient to provide a maximum growth rate at millimetric wavelengths proportional to the cube root of the square of the gravity-capillary length times the thickness of the water film that coats the icicle, \(\lambda _\textrm{m}\sim (l_\textrm{gc}^2h)^{1/3}\). These length scales are very much longer than the micron-sized wavelengths characteristic of the Mullins–Sekerka instability but of similar magnitude to those observed.

2.3 Migration of ripples

A further deduction can be made from our heuristic model, which is that ripples migrate upwards in consequence of the physical interactions described above. The phase speed of ripples in the x direction (downwards) is

$$\begin{aligned} c = -{\sigma _I\over \alpha }, \end{aligned}$$

where \(\sigma _I\) is the imaginary part of \(\sigma \). To the same approximation used above (\(\alpha \delta \gg 1\)), Eq. (14) gives the rate of translation for the fastest growing mode to be

$$\begin{aligned} c_\textrm{m} = -{\sigma _I(\alpha _\textrm{m})\over \alpha _\textrm{m}} = -{\sqrt{5}\over 6}V, \end{aligned}$$

which predicts that ripples migrate upstream with an angle of propagation \(\tan ^{-1}(\sqrt{5}/6) \approx 20^\circ \) to the horizontal. This is somewhat shallower than the values of roughly \(30^\circ \) measured by Ueno et al. [6] on a planar, vertical ice sheet and much shallower than the values of up to \(60^\circ \) measured by Ladan and Morris [17] on conical icicles.

3 The effect of surface energy

As has been noted above and by several previous authors, the competition between the point effect of diffusion and Gibbs–Thompson undercooling inherent in the Mullins–Sekerka instability predicts wavelengths of morphological instability that are far shorter than observed. This has resulted in the near neglect of surface energy in previous studies. However, we have seen that the phase shift between the ice–film interface and the film–air interface weakens the growth of ripples significantly at large wave numbers, so even a weak undercooling related to surface energy might be significant.

We can include the Gibbs–Thompson undercooling straightforwardly in the heuristic model of the previous section, noting that the equilibrium temperature at a phase boundary of curvature \({{\mathcal {K}}}\) is given by

$$\begin{aligned} T_\textrm{e} = T_\textrm{m} - {\gamma _\textrm{sl} T_\textrm{m}\over \rho _\textrm{s} L}{{{\mathcal {K}}}}. \end{aligned}$$
(19)

The unperturbed ice has uniform temperature \(T_\textrm{m}\), while the perturbed temperature field in the ice is

$$\begin{aligned} T = T_\textrm{m} - \Delta T\, l_\textrm{c} \alpha ^2\eta _1 \textrm{e}^{\alpha y} \textrm{e}^{i\alpha x + \sigma t}, \end{aligned}$$
(20)

where \(l_\textrm{c}\equiv \gamma _\textrm{sl} T_\textrm{m}/ \rho _\textrm{s} L \Delta T\) is the capillary length for the solid–liquid phase boundary (equal to half the critical nucleation radius at an undercooling of \(\Delta T\)). Equation (13) for the temperature at the film–air interface is therefore modified to

$$\begin{aligned} \theta _\textrm{a} = {\Delta T\over \delta }\eta _2 - \Delta T l_\textrm{c}\alpha ^2 \eta _1, \end{aligned}$$
(21)

while the Stefan condition (9) becomes

$$\begin{aligned} \rho _\textrm{s} L (V + \sigma \eta _1) = -k_\textrm{a}{\partial T\over \partial y}\bigg \vert _{h + \eta _2+} + k_i{\partial T\over \partial y}\bigg \vert _{\eta _1-}, \end{aligned}$$
(22)

where \(k_i\) is the thermal conductivity of ice. Putting this together, we find that the growth rate is given by

$$\begin{aligned} {h \over V}\sigma _\textrm{R} = {\alpha h \over 1 + \Gamma ^2\alpha ^6 h^2} -l_\textrm{c}\delta h\alpha ^3\left( 1 + {k_i\over k_\textrm{a}}\right) , \end{aligned}$$
(23)

using the same approximation \(\alpha \delta \gg 1\) used above. This reproduces the earlier result (15) if \(l_\textrm{c} = 0\). If instead we set \(\Gamma = 0\), we obtain the balance between the point effect of diffusion and Gibbs–Thomson undercooling of the ice–water phase boundary represented in the classical Mullins–Sekerka instability, shown by the dashed curve in Fig. 4. However, given that \({k_i / k_\textrm{a}} \approx 10^2\), the wavelength of the most unstable mode with \(\Gamma =0\) is \(\lambda _\textrm{m} = 2\pi \sqrt{3 l_\textrm{c}\delta \, k_i/k_\textrm{a}} \approx 600\;\mu \)m. This is an order of magnitude larger than typical wavelengths of the Mullins–Sekerka instability for ice growing into an extended region of supercooled water.

Fig. 4
figure 4

The dashed curve shows the dispersion relation resulting from a simple competition between the point effect of diffusion into surrounding air and Gibbs–Thomson undercooling of the ice–water phase boundary with water supply rate \(q=3\times 10^{-2}\) cm\(^2\) s\(^{-1}\). It is obtained by setting \(\Gamma = 0\) in Eq. (23). The solid curve (Eq. (23)) includes additionally the phase shift induced by the water–air surface tension. These curves are calculated with \(\Delta T = 10^\circ \)C

Full size image

The full expression (23) is plotted as the solid curve in Fig. 4. We see that the phase shift induced by surface tension of the film–air interface decreases the most unstable wavenumber (increases the most unstable wavelength) significantly. Gibbs–Thomson undercooling does have a significant influence in the sense that we see a cutoff in unstable wavenumber at about \(\alpha /2\pi =4\) but it has negligible influence on the most unstable wavelength shown in Fig. 3.

4 Advection of heat by the water film

Up till now, we have considered the film of water coating the icicle to be sufficiently thin that the temperature field within it remains linear and the heat flux conducted from the ice–film interface into the film is equal to the heat flux conducted out of the film at the film–air interface. In this section, we will find that, although it is very thin, the film carries a significant heat flux, which creates a mismatch between these conductive fluxes. To do this, we need to determine the structure of the velocity and temperature fields within the film.

Still using the thin-film, lubrication approximation, the vertical velocity u in the film satisfies the parallel-flow equation

$$\begin{aligned} \mu {\partial ^2 u \over \partial y^2} = - \rho g + {\partial p\over \partial x} \equiv -(\rho g - i\gamma \alpha ^3 \eta _2), \end{aligned}$$
(24)

in which we have used the linearised curvature to determine the Laplace pressure due to surface tension of the film–air interface. This equation is readily integrated, using the no-slip condition at \(y=\eta _1\) and the no-stress condition at \(y=h+\eta _2\), to find

$$\begin{aligned} u = {g\over 2\nu }\left( 1 - i{\gamma \over \rho g}\alpha ^3\eta _2\right) (y - \eta _1)\left[ 2(h + \eta _2 - \eta _1) - (y - \eta _1)\right] . \end{aligned}$$
(25)

The volume flux q per unit width of the flow is found by integrating this expression from \(y=\eta _1\) to \(y=h+\eta _2\), which gives Eq. (2).

Writing \(u = u_0 + u_1\), where \(u_1\ll u_0\), we can linearise Eq. (25) with respect to \(\eta \) to find the leading-order, undisturbed flow

$$\begin{aligned} u_0 = {g\over 2\nu }y(2h - y) \end{aligned}$$
(26)

and the first-order, linear perturbation

$$\begin{aligned} u_1 = -{g\over \nu } (h - y)\eta _1 + {g\over \nu } y (\eta _2 - \eta _1) - i{\gamma \over 2\mu }\alpha ^3 y(2h - y)\eta _2. \end{aligned}$$
(27)

We can then use relation (5) between \(\eta _2\) and \(\eta _1\) to show that

$$\begin{aligned} u_1 = -{g\over \nu } (h - y)\eta _1 + i{\gamma \over 6\mu }\alpha ^3 (3y^2 - 4hy)\eta _2,\end{aligned}$$
(28)

while the continuity equation \(\nabla \cdot \textbf{u} = 0\) shows that the cross-film velocity

$$\begin{aligned} v = -\int {\partial u\over \partial x} \; \text {d}y = -i\alpha \int u_1 \;\text {d}y \equiv v_1 = i\alpha u_0(y)\eta _1 - \Gamma \alpha ^4 y u_0(y)\eta _2, \end{aligned}$$
(29)

given that \(v_1 = 0\) at the ice interface. The first term arises in consequence of the deflection of the flow by the perturbed ice interface, giving a transverse flow that is \(\pi \over 2\) out of phase with the ice interface, while the second term represents the transverse flow driven towards the ice interface by the Laplace pressure in phase with the air interface. We will see shortly that the former drives a heat flux that is balanced by advection of heat along the film by the mean flow, while the latter compresses the isotherms, enhancing the heat flux away from the ice interface and thereby enhancing instability.

The advection–diffusion equation describing conservation of heat in a thin film is

$$\begin{aligned} \kappa {\partial ^2 T\over \partial y^2} = u{\partial T\over \partial x} + v{\partial T\over \partial y}, \end{aligned}$$
(30)

where \(\kappa \) is the thermal diffusivity of the liquid film. Ignoring Gibbs–Thomson undercooling for the moment, the temperature field in the film satisfies

$$\begin{aligned} T = T_\textrm{m} \quad \hbox {at}\quad y = \eta _1, \end{aligned}$$
(31)

given that the temperature of the phase boundary is equal to the freezing temperature, while

$$\begin{aligned} \left[ T \right] _-^+ = 0 \quad \hbox {at}\quad y = h+\eta _2, \qquad \hbox {and} \qquad k_\textrm{w}{\partial T\over \partial y}\bigg \vert _{h+\eta _2-} = k_\textrm{a}{\partial T\over \partial y}\bigg \vert _{h+\eta _2+}, \end{aligned}$$
(32)

representing continuity of temperature and heat flux at the film–air interface.

The undisturbed state is linear in the film with

$$\begin{aligned} T = T_0(y) \equiv T_\textrm{m} - {\epsilon \over 1+\epsilon }\Delta T{y\over h}, \end{aligned}$$
(33)

while we take the undisturbed temperature field in the air to be

$$\begin{aligned} T = T_\infty + {\Delta T\over 1+\epsilon }\textrm{e}^{-(y - h)/\delta } \end{aligned}$$
(34)

as before. We now take \(\epsilon \ll 1\), being careful only to neglect \(\epsilon \) when it is added to order-unity constants, such as in the denominator of the second terms in (33) and (34), and write

$$\begin{aligned} T = T_\textrm{m} - \epsilon \Delta T{y\over h} + \theta (y) \textrm{e}^{i\alpha x + \sigma t} \end{aligned}$$
(35)

in the film and

$$\begin{aligned} T = T_\infty + \Delta T\textrm{e}^{-(y - h)/\delta } + \theta _\textrm{a}\textrm{e}^{-\alpha (y-h)} \textrm{e}^{i\alpha x + \sigma t} \end{aligned}$$
(36)

in the air, where we have again assumed that the temperature perturbation in the air simply satisfies Laplace’s equation.

The boundary conditions on the perturbed temperature field in the film can be determined from Eq. (31), which gives

$$\begin{aligned} \theta (0) = \epsilon \Delta T{\eta _1\over h}, \end{aligned}$$
(37)

and Eqs. (32), which give

$$\begin{aligned} \begin{aligned} \theta (h) -\epsilon \Delta T{\eta _2\over h}&= \theta _\textrm{a} -\Delta T{\eta _2\over \delta }, \\ h\theta '(h)&= \epsilon \Delta T{\eta _2\over \delta } - \epsilon \alpha \delta \theta _\textrm{a}. \end{aligned} \end{aligned}$$
(38)

We can eliminate \(\theta _\textrm{a}\) between these last two equations to give the mixed boundary condition

$$\begin{aligned} h\theta '(h) = -\epsilon \alpha \delta \theta (h) - \epsilon \Delta T \alpha \eta _2, \end{aligned}$$
(39)

having used the approximations \(\epsilon \delta /h = k_\textrm{a}/k_\textrm{w} \ll 1\) and \(\alpha \delta \gg 1\) as before.

4.1 Scaled equations

From the advection–diffusion equation (30), we can deduce the perturbation equation

$$\begin{aligned} \kappa \theta '' = i\alpha u_0\theta + v_1T_0'(y). \end{aligned}$$
(40)

We now scale \(\theta \) with \(\epsilon \Delta T\) and scale y, \(\eta _1\) and \(\eta _2\) with h to obtain the dimensionless equation

$$\begin{aligned} \theta '' = ip f(y)(\theta - \eta _1 - i{{{\mathcal {G}}}}y\eta _2), \end{aligned}$$
(41)

in which the dimensionless unperturbed flow \(f(y) = {3\over 2}y(2-y)\) has a mean of unity, the reduced Péclet number \(p=\alpha h P\), where \(P = q/\kappa \) is the Péclet number, and \({{{\mathcal {G}}}} =\Gamma \alpha ^3\,h\) is the significant dimensionless grouping that arose in the heuristic model. This equation is subject to the dimensionless boundary conditions

$$\begin{aligned} \theta (0) = \eta _1 \end{aligned}$$
(42)

from (37) and

$$\begin{aligned} \theta '(1) = -\alpha h \eta _2 \end{aligned}$$
(43)

from (39), having used again the approximation that \(\epsilon \delta /h = k_\textrm{a}/k_\textrm{w} \ll 1\).

4.2 Solutions for small reduced Péclet number

We can start to understand the role of advective heat transport in the water film by considering the limit \(p\ll 1\). This is the same limit explored by Ueno [13]. Ueno developed a formal solution to an equation similar to (41) in terms of convolutions of hypergeometric functions and then used a low-order Taylor expansion to evaluate the integrals approximately for \(p\ll 1\). Here, we develop a series solution in \(p\ll 1\) iteratively, directly from the differential equation. At leading order as \(p\rightarrow 0\), the solution to (41) with boundary conditions (42) and (43) is linear, given by

$$\begin{aligned} \theta = \eta _1 - \alpha h \eta _2 y. \end{aligned}$$
(44)

At the next iteration, we use this leading-order solution in the right-hand side of (41) and integrate the equation across the layer to find that

$$\begin{aligned} \theta '(1) - \theta '(0) = -{5i\over 8}p\left[ \alpha h + i{{{\mathcal {G}}}} \right] \eta _2, \end{aligned}$$
(45)

Note that the factor \(5\over 8\) comes from the integral of yf(y) across the film. Note also that we haven’t needed to find the perturbed temperature field within the film explicitly, which we will explore further in the next section.

The Stefan equation

$$\begin{aligned} \rho _\textrm{s} L \sigma \eta _1 = -k_\textrm{w}{\partial \theta \over \partial y}\bigg \vert _{\eta _1+} \end{aligned}$$
(46)

can be expressed in terms of scaled variables as

$$\begin{aligned} {h\sigma \over V}\eta _1 = -\theta '(0) = -\theta '(1) - {5i\over 8}p\left[ \alpha h + i{{{\mathcal {G}}}} \right] \eta _2, \end{aligned}$$
(47)

using (45), which gives the dispersion relation

$$\begin{aligned} {h\over V}\sigma = {\alpha h + {5\over 8}p{{{\mathcal {G}}}} - {5i\over 8}p\alpha h \over 1 - i{{{\mathcal {G}}}}}, \end{aligned}$$
(48)

with real part

$$\begin{aligned} {h\over V} \sigma _\textrm{R} = {\alpha h + {5\over 8}p{{{\mathcal {G}}}}(1 + \alpha h)\over 1 + {{{\mathcal {G}}}}^2}. \end{aligned}$$
(49)

This has terms of similar structure to those obtained by Ueno [13] (his equation 48). However, Ueno used different boundary conditions, allowing an arbitrary temperature of the ice–film interface while fixing the temperature of the film–air interface, and determined that advection of heat is stabilising. In contrast, Eq. (49), derived using boundary conditions that the ice–film temperature is equal to the freezing temperature and allowing continuity of temperature at the ice–film interface without fixing it, shows advection to be destabilising. This is a significant point of departure and so requires scrutiny. We will do this in the next section and further in Sect. 6 but for now simply explore the predictions of the dispersion relation (49).

4.3 Effect of advection on the most unstable wavelength

We can approximate (49) by

$$\begin{aligned} {h\over V} \sigma _\textrm{R} = {\alpha h + {5\over 8}p{{{\mathcal {G}}}}\over 1 + {{{\mathcal {G}}}}^2} \end{aligned}$$
(50)

in the thin-film limit \(\alpha h \ll 1\). We can then set its derivative with respect to \(\alpha \) to zero, recalling that \(\mathcal{G} = \Gamma \alpha ^3\,h\) and \(p = \alpha h P\) are functions of \(\alpha \), to find that the maximum growth rate occurs at wavenumber \(\alpha _\textrm{m}\) determined from

$$\begin{aligned} 5P{{{\mathcal {G}}}}^3 + 20{{{\mathcal {G}}}}^2 - 10P{{{\mathcal {G}}}} - 4 = 0. \end{aligned}$$
(51)

It is cumbersome to find the root \({{{\mathcal {G}}}}_\textrm{m}(P)\) of this equation analytically but it is straightforward to show that \({{{\mathcal {G}}}}_\textrm{m}\rightarrow 1/\sqrt{5}\) as \(P\rightarrow 0\), while \({{{\mathcal {G}}}}_\textrm{m}\rightarrow \sqrt{2}\) as \(P \rightarrow \infty \). Given also that the wavelength corresponding to the maximum growth rate

$$\begin{aligned} {\lambda }_\textrm{m} = {2\pi }\left[ \mathcal{G}_\textrm{m}\left( {q\over \kappa }\right) \right] {^{-1/3}}\left( {{\gamma ^3\nu q}\over 9\rho ^3 g^4 }\right) ^{1/9}{, } \end{aligned}$$
(52)

which is equivalent to (18) when \({{{\mathcal {G}}}}_\textrm{m} = 1/\sqrt{5}\), only depends on \(\mathcal{G}_\textrm{m}^{1/3}\), we see that flow with small reduced Péclet number has little influence on the wavelength of ripples, multiplying the key result obtained from the heuristic model by at most a factor of \((10)^{1/6}\approx 1.47\) as the Péclet number varies. This contrasts strongly with the result given by Ueno, using different boundary conditions, who finds an expression similar to (50) but with a minus sign in front of the second term in the numerator, which leads to \({{{\mathcal {G}}}}_\textrm{m}(P) \propto P^{-1}\) as \(P \rightarrow \infty \). We see from Fig. 5 that, according to the result presented in Eq. (52), the variation of the wavelength with the input flux is even weaker than predicted by the heuristic model, but with values about 30% smaller, putting these predictions even further away from the experimental results.

Fig. 5
figure 5

The wavelength \(\lambda \) of the most unstable ripples determined to first order in p plotted as a function of volume flux q per unit span. The dashed curves show asymptotic results for \(\lambda \) at small and large values of q, both of which are proportional to \(q^{1/9}\)

Full size image

5 Advection-dominated heat transfer

The results of the previous section give an indication of the effects of advective transport of heat in the film. However, they are only relevant when the reduced Péclet number p is small, when the thermal field across the film is quasi-linear. To get a better understanding of the role of advection, it is helpful to determine how the thermal field is modified at higher flow rates, when the reduced Péclet number is not small. Equation (41) is linear and was solved formally by Ueno [13] as convolutions of hypergeometric functions. It could also be solved in closed form using similar hypergeometric functions, expressed as parabolic cylinder functions. However, a more transparent, approximate solution can be obtained by replacing the base-state velocity field \(u_0\) with its mean value, which is equivalent to putting \(f(y)\equiv 1\), to yield

$$\begin{aligned} \theta '' - ip\theta = -ip\eta _1 + p{{{\mathcal {G}}}}\eta _2 y. \end{aligned}$$
(53)

This is a reasonable approximation to make given that \(u_0(y)\) is one-signed. The resulting hyperbolic functions have a similar mathematical structure to the corresponding parabolic cylinder functions but are more familiar and so are more readily interpreted physically. This second-order, linear differential equation is subject to boundary conditions

$$\begin{aligned} \theta (0) = \eta _1, \qquad \theta '(1) = -\alpha h \eta _2. \end{aligned}$$
(54)

Equations (53) and (54) are readily solved to find

$$\begin{aligned} \theta (y) = \eta _1 + i{{{\mathcal {G}}}}y\eta _2 - {(\alpha h + i{{{\mathcal {G}}}}) \over \sqrt{ip}} {\sinh \left( \sqrt{i p} y\right) \over \cosh \sqrt{ip}}\eta _2. \end{aligned}$$
(55)

The dimensionless Stefan condition (47) then gives

$$\begin{aligned} {h\over V}\sigma \eta _1 = -\theta '(0) = \left[ (\alpha h + i\mathcal{G})\hbox {sech}\sqrt{ip} - i{{{\mathcal {G}}}}\right] \eta _2, \end{aligned}$$
(56)

which gives the dispersion relation

$$\begin{aligned} {h\over V}\sigma = {(\alpha h + i{{{\mathcal {G}}}})\hbox {sech}\sqrt{ip} - i{{{\mathcal {G}}}} \over 1 - i{{{\mathcal {G}}}}}. \end{aligned}$$
(57)

When \(p\ll 1\), sech\(\sqrt{ip} \sim 1 - {1\over 2}ip\) and

$$\begin{aligned} {h\over V}\sigma \sim {\alpha h + {1\over 2}p{{{\mathcal {G}}}} - {i\over 2} p \alpha h \over 1 - i{{{\mathcal {G}}}}}, \end{aligned}$$
(58)

so the real part of the growth rate \(\sigma _\textrm{R}\) is given by

$$\begin{aligned} {h\over V}\sigma _\textrm{R} \sim {\alpha h + {1\over 2}p{{{\mathcal {G}}}}( 1 + \alpha h) \over 1 + {{{\mathcal {G}}}}^2}. \end{aligned}$$
(59)

These are essentially the same results as those obtained in the previous section, simply with the factor of \(5\over 8\) replaced by \(1\over 2\), which gives confidence to the mathematical structure of these expressions and the physics they describe at small, non-zero, reduced Péclet number. The former result is the more accurate as it arises from an iterated expansion of the full equations rather than a series expansion of the solution to the approximated equations.

Fig. 6
figure 6

The solid curves show the dispersion relations calculated using the approximate model leading to the real part of (57) for three values of the Péclet number \(Pe=0.25, 1, 4\), while the dashed curves show the corresponding asymptotic results (59) valid for small reduced Péclet number \(p = \alpha h Pe\). The corresponding values of p at the local maxima are approximately 0.01, 0.08 and 0.5

Full size image

The asymptotic results (49) and (59) are valid in the limit of small reduced Péclet number, \(p = \alpha h Pe \ll 1\). However, using the parameters from Fig. 3 at the critical wavenumber, p is greater than unity once q is greater than about \(10^{-2}\) cm\(^2\)s\(^{-1}\), so we should consider the full dispersion relation (57). The analytical expression for the real part of (57) is cumbersome and not particularly illuminating but the expression can be used in Mathematica™(for example) to produce the plots of the growth rate shown in Fig. 6 for different film fluxes, expressed in terms of the Péclet number Pe. We see that the asymptotic result (59) is very close to the full solution when \(Pe = 0.25\) (the solid and dashed curves are almost indistinguishable), and the local maximum is reasonably well captured up to \(Pe = 4\), when the reduced Péclet number p at the wavenumber corresponding to the maximum growth rate is approximately 0.5. We also see the near independence of the wavenumber corresponding to maximum growth rate illustrated in Fig. 5.

At higher values of the Péclet number, there is no local maximum of the dispersion relation and so no wavelength selection. Given that \(\textrm{sech}\, z \rightarrow 0\) as \(|z|\rightarrow \infty \), it is straightforward to see from (57) that at large Péclet number

$$\begin{aligned} {h\over V}\sigma \sim {-i{{{\mathcal {G}}}} \over 1 - i{{{\mathcal {G}}}}}, \end{aligned}$$
(60)

which tends to unity as \({{{\mathcal {G}}}} = \Gamma \alpha ^3 h \rightarrow \infty \), so as \(\alpha \rightarrow \infty \). Stabilisation of small wavelengths is, however, still provided by Gibbs–Thomson undercooling. Its dominant effect is to provide a stabilising heat flux into the ice, which modifies the dispersion relation (60) to give

$$\begin{aligned} {h\over V}\sigma _\textrm{R} \sim {{{{\mathcal {G}}}}^2\over 1 + {{{\mathcal {G}}}}^2} - {l_\textrm{c}\delta \over l_\textrm{gc}^2}{k_i\over k_\textrm{a}}{{{\mathcal {G}}}}, \end{aligned}$$
(61)

as shown in the Appendix. Note that this gives the same additional term relating to Gibbs–Thomson undercooling as was given by Eq. (23) in the limit \(k_i / k_\textrm{a} \gg 1\). This modified dispersion relation gives a maximum growth rate when

$$\begin{aligned} 2{{{\mathcal {G}}}}_\textrm{m} = {l_\textrm{c}\delta \over l_\textrm{gc}^2}{k_i\over k_\textrm{a}}\left( 1 + \mathcal{G}_\textrm{m}^2\right) ^2, \end{aligned}$$
(62)

which has the approximate solution

$$\begin{aligned} {{{\mathcal {G}}}}_\textrm{m} \approx \left( 2 {l_\textrm{gc}^2 \over l_\textrm{c}\delta }{ k_\textrm{a} \over k_i}\right) ^{1/3}, \end{aligned}$$
(63)

with corresponding wavelength

$$\begin{aligned} \lambda _\textrm{m} \approx 2\pi \left( {1\over 2}{k_i\over k_\textrm{a}}\delta \, l_\textrm{c} l_\textrm{gc}^4 h^3 \right) ^{1/9}. \end{aligned}$$
(64)

We see from this expression that the predicted wavelength corresponding to maximum growth rate is still proportional to \(q^{1/9}\) and also that the role of the capillary length associated with the solid–liquid phase boundary is much diminished relative to the classical Mullins–Sekerka result, the wavelength being proportional to \(l_\textrm{c}^{1/9}\) rather than \(l_\textrm{c}^{1/2}\). The wavelength predicted by (64) is about 2 mm at \(q = 3\times 10^{-2}\) cm\(^2\) s\(^{-1}\). This prediction, made for very large Péclet number, is smaller than that at modest Péclet number (about 4 mm, see Fig. 5), which is itself smaller than that made by the heuristic model of Sect. 2, equivalent to zero Péclet number, (about 5.5 mm, see Fig. 3b). The point is that Gibbs–Thomson undercooling is required to stabilise short wavelengths when there is strong, destabilising advection and that it results in wavelengths on millimetre scales rather than the micron scales anticipated by previous authors.

5.1 Structure of the thermal field

The effects of advection of heat by the film flow can be understood by examining the eigenfunctions of the temperature field, shown in Fig. 7. These are contour plots of the real part of \((\theta (y)-\eta _1)\text {e}^{i\alpha x}/\eta _2\) (top row) and of \((\theta (y)-\eta _1)\text {e}^{i\alpha x}/\eta _1\) (bottom row). Thus the temperature contour at \(y=0\) corresponds to the freezing temperature in each panel. The top row is centred on protrusions of the film–air interface, while the bottom row is centred on protrusions of the ice–film interface.

In the top, left panel, at small reduced Péclet number \(p\approx 0.08\), we see that the temperature perturbation is in phase with the film–air interface and is colder where there are protrusions into the air (\(x = 0\)). This is the point effect of diffusion, which is the primary driving mechanism for morphological instability. In the bottom, left panel, we see that the phase shift upstream of the film–air interface relative to the ice–film interface weakens the thermal flux away from the ice–film interface, which tends to stabilise the perturbation. We also see that the magnitude of the temperature gradient is larger slightly upstream of the protrusion of the ice-film interface, which causes the growth rate to be larger there and results in upstream migration of the ensuing ripples.

In the top, middle panel, at intermediate reduced Péclet number \(p\approx 2\), we see that advection carries the temperature perturbation downstream and gives a maximum growth rate just downstream of protrusions of the film-air interface, which would tend to make ripples migrate downstream. However, the phase shift of the film–air interface relative to the ice–film interface more than compensates for this and the migration remains upstream, as shown by the bottom, middle panel.

The top, right panel shows that at very high flow rates corresponding to a high reduced Péclet number \(p\approx 40\), the temperature perturbation is almost everywhere \(\pi /2\) out of phase with the perturbation of the film–air interface, which would cause downstream migration with essentially no growth. However, as shown in the bottom, right panel, the phase shift of the film–air interface relative to the ice–film interface converts that migration into almost pure growth, with only very weak downstream migration remaining.

Fig. 7
figure 7

Eigenfunctions of the temperature perturbation relative to the temperature of the ice–film interface \(Re[(\theta (y)-\eta _1)\text {e}^{i\alpha x}\) at flow rates with Péclet numbers 1, 10, 100, which correspond to reduced Péclet numbers p approximately equal to 0.078, 1.7, 36 respectively, given the parameter values in Table 1 and wavenumber \(\alpha /2\pi = 3\) cm\(^{-1}\), which corresponds approximately to the maxima shown in Fig. 6. The top row shows the eigenfunctions relative to the film–air interface, while the bottom row shows them relative to the ice–film interface. The contour values given for the lowermost, non-zero contour in each of the lower panels show that the strength of the negative temperature gradient and hence the growth rate of instability increase as the flow rate increases

Full size image

At very large reduced Péclet number, Eq. (55) shows that the temperature perturbation has a linear contribution plus a complementary function

$$\begin{aligned} \theta _\textrm{c}(y) = -{(\alpha h + i{{{\mathcal {G}}}}) \over \sqrt{ip}} {\sinh \left( \sqrt{i p} y\right) \over \cosh \sqrt{ip}}\eta _2. \end{aligned}$$
(65)

whose character is illustrated in Fig. 8. We see that it is an exponentially decaying oscillation, characteristic of oscillatorally forced solutions of diffusion equations, such as Stokes layers, in consequence of temperature perturbations advected from upstream protrusions of the film–air interface. This complementary function has negligible influence on the phase boundary, contributing little to the heat flux there, which is dominated by the particular integral

$$\begin{aligned} \theta _p(y) = \eta _1 + i{{{\mathcal {G}}}}y\eta _2. \end{aligned}$$
(66)

The first term of this expression simply keeps the ice–film interface at the freezing temperature to first order in the perturbations. The second term is a consequence of the Laplace pressure associated with surface tension of the film–air interface. This tends to weaken the flow from trough to crest of the film–air interface. Therefore, conservation of heat in this advection-dominated flow requires that the temperature perturbation is strongest between trough and crest (travelling downstream) and weakest between crest as trough, as shown in the top, right panel of Fig. 7. It is this advection-dominated heat transfer that leads to the dispersion relation (60).

6 Discussion

The analysis of the preceding sections sheds light on some previous, related studies [10, 12, 18], which I compare and contrast here. Ueno’s analysis [18] is essentially repeated in Ueno [13] and Ueno et al. [6], the latter making some direct comparisons between the modelling assumptions of Ogawa and Furukawa [12] and those of Ueno [18].

Fig. 8
figure 8

The real part of the complementary function \(\theta _\textrm{c}(y)\) for the perturbation to the temperature field at reduced Péclet number \(p=100\), showing oscillatory character decaying away exponentially from the film–air interface \(y=1\)

Full size image

All of these studies formally consider hydrodynamic perturbations to the film flow via the perturbed Navier–Stokes equations leading to the Orr–Sommerfeld equation for the stream function. Ueno [13] makes explicit that the reduced Reynolds number \(\alpha h Re\) is small and neglects inertial contributions to the Orr–Sommerfeld equation. Ogawa and Furukawa [12] make series expansions in powers of \(\alpha h\) of all their perturbed quantities, and make an approximation for the stream function by keeping only its leading-order (zeroth-order) terms. So, without stating it as such, they also neglect inertia. Ladan [10] retains the inertial contributions to the Orr–Sommerfeld equation but it can be noted that he takes a Reynolds number of 0.36 and wavenumbers up to \(\alpha h = 0.2\), so considers reduced Reynolds numbers only up to \(\alpha h Re = 0.072\). Numerically speaking, therefore, inertia is negligible in his study too. In this paper, I have ignored inertia from the outset by using the thin-film equations rather than the Navier–Stokes equations to describe the film flow.

That all these studies are similar with respect to their modelling of the film flow is evidenced by the similarity between Fig. 5c (curve labelled ‘\(\alpha \ne 0\)’) of Ueno et al. [6], in which they compute solutions using their hydrodynamic boundary conditions but the thermodynamic boundary conditions used by Ogawa and Furukawa [12], which are the same as those used in this paper, Fig. 2.2 of Ladan [10], and Fig. 6 of this paper (curve labelled ‘\(Pe = 4\)’), which are computed for similar parameter values.

Although Ogawa and Furukawa [12] initially include surface tension between the water film and the surrounding air in their general set of equations and determine an associated phase shift between the film–air interface and the ice–film interface in their appendix (Eq. A28), they subsequently ignore it on the grounds that the product of the film thickness and the amplitude of perturbations to the interfaces is second-order in small quantities. This sounds physically reasonable but is formally incorrect because, though small by some measure, the film thickness is a finite quantity, whereas in linear stability theory perturbations are infinitesimal. The linearisation should be just in the infinitesimal perturbation quantities. The finite-amplitude perturbations that are witnessed experimentally and in nature are significantly larger than the film thickness but such consideration falls well outside the linear theory considered in all these works. Ueno [18] appropriately highlights the phase shift between the interfaces, and we have seen in this paper (Sect. 2) that it is sufficient to provide wavelength selection without advection of the thermal field by the film. Unfortunately, Ueno missed this point by ignoring \(\mathcal{G}^2\) in the denominator of his equivalent of Eq. (49). The most significant difference between these various studies lies in the thermal boundary conditions employed. Ogawa and Furukawa [12], Ladan [10] and the analysis presented here take the ice–film interface to be at the freezing temperature \(T_\textrm{m}\) and impose continuity of temperature and of heat flux across the film–air interface. These physical boundary conditions are used consistently for the base state and the perturbations. Given the very slow lateral growth rates of icicles, any kinetic undercooling of the phase boundary will be truly negligible, so imposing \(T=T_\textrm{m}\) is extremely robust, as are the conditions that temperature and heat flux are continuous at the film–air interface. Contrasting these studies, while Ueno uses these same physical boundary conditions for the base state, he arbitrarily keeps the temperature of the film–air interface fixed even as that interface is perturbed. In consequence, he finds that the temperature of the phase boundary must be allowed to deviate from \(T_\textrm{m}\) and is left arbitrary. To be clear, the temperature offset \(\Delta T_\textrm{sl}\) included in Ueno et al. [6], Eq. 12, for example)], is not prescribed or determined by any physical process but is an allowance necessitated by imposing the unphysical, mathematical boundary condition that the temperature of the disturbed water–air surface is held fixed.

The previous studies solved the thermal advection–diffusion equation either by series expansion (Ogawa and Furukawa [12] and Ueno [18] to second order in \(\alpha h\); Ladan [10] to 100 terms) or by numerical integration [6]. The low-order series expansions cannot capture behaviour at large Péclet numbers, while the high-order expansion (calculated numerically) and the numerical integrations were done at particular, modest Péclet numbers, typical of the laboratory experiments that have been done. An advantage of finding closed-form solutions to the thermal advection–diffusion equation, albeit approximated by assuming a uniform flow in place of the actual parabolic flow (Sect. 5), is that asymptotic solutions for large flow rates and large wave numbers can easily be discerned, which gives further insight into the physical interactions involved.

The system solved by Ogawa and Furukawa [12] is approximated by the solution found in this paper but with \({{{\mathcal {G}}}} = 0\), given that they ultimately ignore the role of surface tension. From Eq. (57), we see that their approximate dispersion relation would be

$$\begin{aligned} {h\over V}\sigma = \alpha h \, \hbox {sech}\sqrt{ip}. \end{aligned}$$
(67)

This has the asymptotic approximation for \(p\ll 1\)

$$\begin{aligned} {{h\over V}}{\sigma \sim \alpha h \left( 1 - {1\over 2}ip - {5\over 24} p^2\right) , } \end{aligned}$$
(68)

from which Ogawa and Furukawa [12] concluded that ripples would migrate downstream (the imaginary part of \(\sigma \) is negative) and ripples are stabilzed by advection at O(\(p^2\)). These results are represented physically by the top row of Fig. 7 given that Ogawa and Furukawa [12] do not include the phase shift between the interfaces.

We can see further from Eq. (67) that the model of Ogawa and Furukawa [12] would predict that the growth rate tends to zero at large Péclet numbers, though it oscillates between stability and instability as \(\alpha \) increases. That ultimate stabilisation can be understood from the top, right panel of Fig. 7, which shows that, at large values of the Péclet number, the temperature perturbation is \(\pi /2\) out of phase with the perturbation of the film–air interface, which causes downward migration of the ripples and no growth. Ogawa and Furukawa [12] conclude that ‘the water flow makes the temperature distribution more uniform, which inhibits the Laplace instability [point effect of diffusion]’. This is a reasonable conclusion reflected by the complementary function shown in Fig. 8 but misses the contribution of the Laplace pressure arising from surface tension that provides an advection-driven instability mechanism.

Though it cannot be interpreted physically, the mathematical boundary conditions imposed by Ueno [18] applied to the approximate Eq. (53) leads to the solution

$$\begin{aligned} \theta (y) = \eta _1 + i{{{\mathcal {G}}}}\eta _2 y - {(\alpha h + i{{{\mathcal {G}}}}) \over \sqrt{ip}} \eta _2\, \hbox {sinh}\left[ \sqrt{i p} (1-y)\right] \end{aligned}$$
(69)

and the dispersion relation

$$\begin{aligned} {h\over V}\sigma = {(\alpha h + i{{{\mathcal {G}}}})\hbox {cosh}\sqrt{ip} - i{{{\mathcal {G}}}} \over 1 - i{{{\mathcal {G}}}}}. \end{aligned}$$
(70)

It is readily shown that this has a similar low-order expansion in powers of p as the solution given by Ueno, in particular suggesting stabilisation at O(p). However, we also see that, when \({{{\mathcal {G}}}}\) is large, the growth rate is proportional to \(1 - \hbox {cosh}\,\sqrt{ip}\), whose real part oscillates with exponentially growing amplitude as either the Péclet number or the wavenumber increases. Such exponential growth, which cannot be overcome by the Gibbs–Thomson effect, is perhaps further indicative of the unphysical nature of this solution.

7 Conclusions

In this paper, we have revisited the interactions between heat transfer, fluid flow, liquid–vapour surface tension and solid–liquid surface energy during the formation of an icicle in cold, ambient air from a water film flowing over its surface. The main focus of this study was the formation of ripples seen on the surfaces of most icicles, using two-dimensional, linear stability analyses to gain understanding of what processes determine the wavelength of the ripples, which are observed to be about a centimetre.

There are four length scales associated with this system: a diffusion length \(\delta \) of a few millimetres, characterising the thermal boundary layer in the air surrounding the icicle; the capillary length \(l_\textrm{c}\) of about a nanometre, associated with Gibbs–Thompson undercooling of a curved ice–water phase boundary, which is characteristic of the critical nucleation radius for an ice crystal to grow in a supercooled melt; the thickness of the liquid film h coating the icicle, which is about 100 \(\mu \)m; and the gravity-capillary length \(l_\textrm{gc}\) of about a millimetre, which is proportional to the height to which water will rise in a capillary tube of similar diameter.

Focusing on the ice–water interface, analogy has often been drawn with the Mullins–Sekerka morphological instability for a solid growing into an supercooled melt. This instability has a characteristic wavelength proportional to the geometric mean of the diffusion length and the capillary length, which is a few microns, though it should be noted that the constant of proportionality is \(2\pi \sqrt{3}\approx 10\), which gives a wavelength of a few tens of microns. In Sect. 3, we noted that, although the icicle grows from a film of water, the controlling thermal gradient is in the air, so the classical Mullins–Sekerka result is modified by a factor of the square root of the ratio of thermal conductivities \(\sqrt{k_i/k_\textrm{a}}\approx 10\), where \(k_i\) and \(k_\textrm{a}\) are the conductivities of ice and air respectively, giving characteristic wavelengths of a few hundred microns, which is in range to influence the other mechanisms explored in this paper.

In Sect. 2, we developed a very simple, heuristic model of the flow and thermodynamics of the water film, relating the latent heat associated with freezing at the ice–film interface directly to heat transfer into the air. We saw that the phase shift between the film–air interface and the ice–film interface, which increases with the wavenumber of the ripples, stabilises the morphological instability driven by the point effect of diffusion into the air and results in a wavelength of maximum growth rate proportional to \((l_\textrm{c}^2 h)^{1/3}\), with typical values being a few millimetres. Given that the film thickness \(h\propto q^{1/3}\), where q is the volume flux per unit width of the film, this prediction is that the wavelength, proportional to \(q^{1/9}\), is quite insensitive to the water supply rate, in accordance with experimental observations. In contrast with Mullins–Sekerka instabilities, in which wavelengths are selected by the competition between diffusion and surface energy of the solid, here they are selected by a competition between diffusion and a phase shift caused by the surface tension of water in air.

In contrast with the conclusions drawn by Ogawa and Furukawa [12] and by Ueno [13], we found in Sect. 4 and confirmed with a separate analysis in Sect. 5 that advection of heat by the film of water is destabilising. But to first order in small reduced Péclet number \(p = \alpha h Pe\), where \(\alpha \) is the wavenumber of the ripples, the Péclet number \(Pe = q/\kappa \), and \(\kappa \) is the thermal diffusivity of water, advection of heat modifies the result that wavelengths are proportional to \((l_\textrm{c}^2 h)^{1/3} \propto q^{1/9}\) only by a factor of order unity. This can be contrasted with the results of Ueno’s analysis using arbitrary boundary conditions that, at small reduced Péclet number, the wavelength is predicted to be proportional to \((Pe \, l_\textrm{c}^2 h)^{1/3} \propto q^{4/9}\) and with the predictions of Ogawa and Furukawa [12], who neglect the influence of surface tension and predict that the wavelength is proportional to \(q^{4/3}\). The results of this paper suggest that, at small reduced Péclet number, wavelength selection remains dominated by the competition between diffusion and the phase shift.

We saw further in Sect. 5 that at higher water-supply rates, when the reduced Péclet number p is of order unity, the point effect of diffusion ceases to have significant influence on the phase boundary, leading only to a decaying oscillation of the temperature field from the air interface into the film that is concentrated near the interface with the air. Heat transfer controlling the evolution of perturbations to the ice surface becomes dominated by advection, and we saw that the phase shift becomes insufficient to suppress the growth of short wavelengths. A completely new balance was found involving three mechanisms: advective heat transfer; the phase shift caused by surface tension; and Gibbs–Thomson undercooling caused by surface energy of the phase boundary. This led to the selection of wavelengths proportional to \([(k_i/ k_\textrm{a})\delta \, l_\textrm{c} l_\textrm{gc}^4 h^3]^{1/9}\), involving all four of the length scales identified above. This scale is still proportional to \(q^{1/9}\) and has typical values of a few millimetres but a little less than those predicted at low flow rates.

Linear stability analyses can shed significant light on the interactions between competing physical mechanisms, as described above. However, they do not necessarily give an accurate indication of observed wavelengths, which are necessarily of finite amplitude. Perhaps a particular concern with regard to icicles is that linear stability analyses, such as described in this paper, consider infinitesimal disturbances with amplitudes therefore much less than the thickness of the coating film of water, whereas observed ripples have amplitudes significantly larger than the water film. An additional concern is that this study, in common with many others, has focused on flow and heat transfer associated with the water film, even though lateral growth of icicles is ultimately determined by heat transfer to the cold, surrounding air. This is acknowledged only by setting a scale for the thermal boundary layer in the air adjacent to the icicle, while no perturbations to that boundary layer have been considered. In their analysis of the melting of an inverted ice cylinder, Neufeld et al. [19] found that convection by the thermal boundary layer accounted for only a third of the heat transfer causing melting, a further third each being supplied by long-wave radiation from the surroundings and the latent heat of condensation of water vapour from the surroundings onto the cold ice surface. These processes may also be significant for the growth of icicles and the formation and scale of ripples on their surfaces.

Some final thoughts return to the observation that ripples do not form on icicles grown from pure water. A possible reason for this is that if the water forms rivulets rather than a continuous film then heat transfer from dry patches of the ice surface to the air would allow the icicle to cool below the freezing temperature, and the extraction of latent heat from the freezing front to the cold ice would be stabilising. A possible further role of impurities could be to cause constitutional supercooling, which would enhance morphological instability. While such constitutionally driven instabilities seem unlikely themselves to explain the observed ripples, it may be that the consequent surface roughness or perhaps even the formation of a mushy zone within the water film would decrease its effective Péclet number and thereby influence the wavelength of ripples.

The evidence to date [10] is that depression of the freezing point caused by impurities has little influence on the predictions of linear stability theory, though impurities do have have significant effects on the formation and evolution of ripples that have been found experimentally. It is hard to speculate but a possible nonlinear amplifying mechanism is the alteration of the thermal conductivity of the icicle caused by inclusions of concentrated impurity (liquid brine) seen in experiments [17], though it seems likely that the volume fraction of inclusions is too small to affect conductivity significantly. Perhaps an important goal in trying to understand the role of impurities theoretically is to model how, when and why inclusions form.

Another, completely different speculation is that perhaps the icicle grows laterally from a wetting film (note the glistening of the icicle in Fig. 1d) rather than a draining film, whose thickness is determined by intermolecular interactions rather than by a gravity–viscous balance, with excess water forming the rivulets that are seen experimentally. Changing the water supply rate might then simply add to the rivulets, leaving the dynamics and thermodynamics of the film insensitive to it. Conversely, the thickness of pre-melted or surface-melted films on ice are known to be strongly dependent on impurity concentration [20], which might relate to the significant dependence on impurity concentration of the growth rates and migration rates of ripples [10].

In this article, I have aimed to provide a simple, transparent mathematical framework that makes clear the interactions between certain physical mechanisms implicated in the development of ripples on the surface of icicles. There are many questions unanswered and pertinent mechanisms still to explore, and I hope that the analysis presented here will provide a suitable framework for future developments.