1 Introduction

When a vessel, partially filled with fluid, is constrained to move in some prescribed motion, the fluid within can experience complex motions. As the fluid sloshes back and forth in the vessel it interacts with the vessel walls, generating forces and moments on the vessel. If the vessel is free to move under the forces generated by the fluid motion (perhaps in some constrained manner) then this coupled motion could be stabilizing or destabilizing to the overall system. A simple everyday example of this instability is when we spill coffee while walking to our seat [1]. The destabilizing aspect of coupled sloshing can have disastrous effects, such as capsizing King crab boats [2], so being able to identify and mitigate against such effects is important. For example, the coffee spilling problem could be mitigated against using a ‘carry cradle’ which reduces the amplitude of the feedback response [3]. In the current paper we consider a simple model which mitigates against destabilization via the use of porous baffles.

Rigid impermeable baffles were first used to minimise sloshing in fuel tanks within the space industry [4, 5], mainly by simply blocking the fluid flow. They were also investigated for use in Tuned Liquid Dampers (TLDs), which are vessels partially filled with fluid, constrained to one-dimensional motions, with a spring acting as a restoring force of the system. Such dampers are typically used as stabilizers in highrise buildings to damp out oscillations induced by earthquakes or strong winds [6]. As well as just blocking the flow, baffles can also stabilize the system by altering the natural frequency of the system, such that forcing terms potentially act out of phase with the forcing frequency, causing flow velocities and accelerations to be less severe. Turner et al. [7] investigated such a scenario for multiple surface piercing impermeable baffles, which essentially split the vessel into multiple compartments. They found the frequency of the modes in the system were altered by the baffles and that potential internal resonances existed. Alemi Ardakani & Turner [8] devised an effective and efficient numerical scheme to model this system in the limit of shallow-water fluids, and investigated the effect on the system when considering a nonlinear spring.

Porous baffles have been well studied in the context of TLDs and ship fuel tanks, for example, because in these cases the baffles provide an important damping mechanism to the fluid in the system [9, 10]. Even the simplest scenario of forced sloshing in a rectangular vessel has been well studied via experimental and numerical simulations, using submerged or surface piercing baffles, set in various configurations such as vertical, horizontal or slanted baffles [11,12,13,14,15,16,17,18,19,20]. Whilst there are a varying array of results on such systems, the key messages are that the width of the baffles are not hugely significant, but the position and composition of the baffles are key to the amount of damping observed in the system [21, 22]. The construction of the porous baffle (e.g. randomly drilled porous metal blocks or regular perforated plates etc.) also has a significant effect on how best to model the transmission of the fluid through the baffle. Differing approaches to modelling the transmission conditions [23] include using Darcy’s law [24,25,26,27] or using a pressure drop condition [28, 29], which has also been applied to other water wave problems [30, 31].

The originality of the current paper is, we examine the effect of porous, surface piercing, baffles in a dynamically coupled rectangular TLD system with a linear restoring force. The novel difference here compared to the forced problems considered above, is that the motion of the vessel, which we assume is able to move in a single space dimension, is not known a priori and needs to be solved for. In order to gain a physical understanding of the significance of the baffle, we consider an idealised system consisting of an inviscid, incompressible, irrotational fluid in a rectangular vessel, where the vessel motion is modelled by a forced pendulum equation. Such an approximation is suitable over relatively short time periods, where viscosity doesn’t have time to act significantly. The current formulation could be amended to incorporate viscosity by including artificial dissipation [32, 33] or by adding additional terms to the free-surface boundary conditions [34]. The fluid transmission across the baffle is modelled using Darcy’s law, such that the velocity of the fluid at the baffle is directly proportional to the pressure difference across the baffle itself. Unlike for the zero baffle and impermeable baffle dynamical problems considered previously [7, 35], the porous baffle makes the system non-conservative and hence energy is extracted from the system. The main goal of this paper is to show that for a single baffle system an analytic characteristic equation can be derived for the natural frequencies of the system, to identify the parameters for which the system decays the fastest and to quantify how this maximum decay rate varies in terms of these parameters.

The current paper is laid out as follows. In §2 we formulate the governing nonlinear equations, and seek normal mode solutions after linearising about a quiescent state. For the single baffle problem an explicit analytical characteristic equation is derived, which is solved numerically. Results of the characteristic equation for a single baffle are presented in §3.1 including both complex frequency values, and free-surface elevations, while multiple baffle cases are considered in §3.2. Concluding remarks are given in §4.

2 Formulation

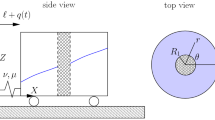
We consider the two-dimensional coupled sloshing system as detailed in Fig. 1. Here (X, Y) is a fixed coordinate system, while (x, y) are Cartesian coordinates fixed to the moving vessel. The coordinate systems are related via,

$$\begin{aligned} X=x+q(t),~~~~~~Y=y+y_0, \end{aligned}$$

where q(t) is the time dependent extension of the spring attached to the vessel and the wall at \(X=0\), and \(y_0\) is a constant.

Fig. 1
figure 1

Schematic diagram of a two-dimensional fluid-filled vessel with rectangular cross-section, and a porous baffle at \(x=x_1\). The vessel is restricted to move in x-direction and is connected to \(X=0\) via a linear spring of stiffness \(\nu \). The function q(t) denotes the extension of the spring from its equilibrium position

Full size image

We derive the system of equations for a single baffle for simplicity, but the approach can be extended to incorporate any number of baffles. We consider the vessel divided into two regions by a porous baffle at \(x=x_1\), labeled region 1 and region 2 from left to right, with \(x\in [0,x_1]\) for region 1 and \(x\in [x_1,x_2]\) in region 2. The lengths of each region are \(L_1\) and \(L_2\) respectively, hence \(x_1=L_1\) and \(x_2=L_1+L_2\), and the fluid occupies the region

$$\begin{aligned} x_{j-1}\le x\le x_j~~~~\textrm{and}~~~~0\le y\le h_j(x,t), \end{aligned}$$

for \(j=1,2\), with \(x_0=0\). Our ultimate goal in this work is to linearise about a quiescent state, hence the fluid velocities in the system are assumed to be low enough such that the fluid can be modelled as inviscid, incompressible and irrotational, without any wave breaking episodes. In this scenario the velocity components relative to the moving frame in each region \((\widehat{u}_j,\widehat{v}_j)\) can be derived in terms of a velocity potential \(\phi _j(x,y)\) such that

$$\begin{aligned} \widehat{u}_j=\frac{\partial \phi _{j}}{\partial x}-\dot{q}(t),~~~~\widehat{v}_j=\frac{\partial \phi _{j}}{\partial y}. \end{aligned}$$
(2.1)

Mass continuity then states that the velocity potentials satisfy Laplace’s equation

$$\begin{aligned} \frac{\partial ^2\phi _{j}}{\partial x^2}+\frac{\partial ^2\phi _{j}}{\partial y^2}=0, \end{aligned}$$
(2.2)

in each region.

The fluid pressure in each region is found via the unsteady Bernoulli equation which states

$$\begin{aligned} \frac{p_j}{\rho }+\frac{\partial \phi _j}{\partial t}+\frac{1}{2}\left[ \left( \frac{\partial \phi _j}{\partial x}\right) ^2+\left( \frac{\partial \phi _j}{\partial y}\right) ^2\right] -\dot{q}\frac{\partial \phi _j}{\partial x}+gy+\frac{1}{2}\dot{q}^2=0, \end{aligned}$$

where \(\rho \) is the constant density of the fluid, the dot indicates differentiation with respect to t and the Bernoulli constant has been absorbed into a linear time-dependent term of \(\phi _j\). Evaluating this on the free-surface (\(y=h_j(x,t)\)) gives the dynamic boundary condition \((p_j=0)\) as

$$\begin{aligned} \frac{\partial \phi _j}{\partial t}+\frac{1}{2}\left[ \left( \frac{\partial \phi _j}{\partial x}\right) ^2+\left( \frac{\partial \phi _j}{\partial y}\right) ^2\right] -\dot{q}\frac{\partial \phi _j}{\partial x}+gh_j+\frac{1}{2}\dot{q}^2=0, \end{aligned}$$
(2.3)

while the corresponding kinematic boundary condition is

$$\begin{aligned} \frac{\partial h_j}{\partial t}+\left( \frac{\partial \phi _j}{\partial x}-\dot{q}\right) \frac{\partial h_j}{\partial x}=\frac{\partial \phi _j}{\partial y}, \end{aligned}$$
(2.4)

for \(j=1,2\). Zero penetration boundary conditions are applied on the bottom and side walls of the vessel, thus

$$\begin{aligned} \left. \frac{\partial \phi _j}{\partial y}\right| _{y=0}=0,~~~~\textrm{and}~~~~\left. \frac{\partial \phi _1}{\partial x}\right| _{x=0}=\left. \frac{\partial \phi _2}{\partial x}\right| _{x=x_2}=\dot{q}, \end{aligned}$$
(2.5)

in the moving frame. We assume that the effects of the front and back walls of the vessel are negligible, such that our two-dimensional assumption is valid. Such an assumption has been proved to be valid such as in the work of [36] who showed the two-dimensional approximation agreed very well with experimental results.

The baffle at \(x=x_1\) is porous and as such, fluid is able to transmit between the regions. We do not physically model the fluid flow through the baffle, and instead use a transition condition to link the fluid velocities in the bulk fluid at the baffle to the pressure drop across the baffle. In this paper our main goal is to consider linear solutions to the governing equations in §2.1 about a fluid at rest. Hence our interest is in small magnitude fluid motions. Given this assumption, and the fact that the baffle is coherent, we apply a transmission condition based upon Darcy’s law [24, 37], namely that the velocity is continuous across the baffle with

$$\begin{aligned} \left. \frac{\partial \phi _1}{\partial x}\right| _{x=x_1}=\left. \frac{\partial \phi _2}{\partial x}\right| _{x=x_1}=\dot{q}-\frac{\beta }{\rho }\left( p_2(x_1,y,t)-p_1(x_1,y,t)\right) . \end{aligned}$$
(2.6)

At larger fluid velocities where nonlinear effects are more important the transmission condition can modelled via a Darcy-Forchheimer model [38] which includes a quadratic velocity term. At very large velocities this quadratic term dominates the transmission condition and a model as in [29] becomes applicable to leading order.

In (2.6) \(\beta \) is a complex coefficient which describes the porosity of the baffle, and has the dimensions of \(\textrm{sm}^{-1}\). The complex form of \(\beta =\beta _r+\textrm{i}\beta _i\) \((\beta _r,\beta _i>0)\) is such that the real part represents the resistance effect of the baffle against the flow, while the imaginary part represents the inertial effect of the fluid in the baffle [25, 27, 39, 40]. Experimental results for perforated plates show that \(\beta _i\approx 0.1\beta _r\) [41] and hence is typically small, so we will mostly consider \(\beta _i=0\), but we do consider cases with \(\beta _i\ne 0\) to show the effect of this quantity. The case \(|\beta |=0\) indicates that the baffle is impermeable (as considered in [7]), while \(|\beta |\rightarrow \infty \) indicates the baffle has no effect on the fluid motion, hence its presence can be neglected, and the vessel reduces to a single region vessel (as considered in [35]). In this work we consider our porosity parameter \(\beta \) to be a constant and we do not consider how its value relates to the physical construction of the baffle. In more complex scenarios such as in [29], the transmission rate of the baffle can be related to more physical parameters such as the solidity ratio. However, as we are not quantitatively fitting our results to experiments we do not go to this extent here.

The equation for the vessel motion, which couples to the fluid motion, is given via the forced linear pendulum equation

$$\begin{aligned} m_v\ddot{q}+\nu q=-\frac{\textrm{d}}{\textrm{d}t}\left[ \int _0^{L_1}\int _0^{h_1}\rho \frac{\partial \phi _1}{\partial x}\,\textrm{d}y \textrm{d}x+\int _{L_1}^{L_1+L_2}\int _0^{h_2}\rho \frac{\partial \phi _2}{\partial x}\,\textrm{d}y \textrm{d}x\right] , \end{aligned}$$
(2.7)

where \(\nu \) is the linear stiffness of the spring connected to the vessel. Here we assume a linear spring only, for simplicity, as we will be seeking modal solutions in §2.2.

Equations (2.2)–(2.7) denote the nonlinear system of equations which govern the coupled sloshing problem for the fluid and vessel motions.

2.1 Linearised equations

We wish to determine the modal solutions of the linearised system about a quiescent state. These would be the natural frequencies that the system would want to oscillate at if initialized appropriately. In a quiescent state we assume the fluid has equilibrated such that \(h_1=h_2=H\), and that the pressure in each region is hydrostatic \(p_j=\rho g (H-y)\). Therefore we introduce the perturbed quantities, denoted with a bar, such that

$$\begin{aligned} q(t)= & {} \epsilon \overline{q}(t),\\ h_j(x,t)= & {} H+\epsilon \overline{h}_j(x,t),\\ \phi _j(x,y,t)= & {} \epsilon \overline{\phi }_j(x,y,t),\\ p_j(x,y,t)= & {} \rho g (H-y)+\epsilon \overline{p}_j(x,y,t), \end{aligned}$$

where \(0<\epsilon \ll 1\) indicates the size of the perturbation and is small enough for linearisation. Substituting these expressions into (2.2)-(2.7) and retaining terms of \(O(\epsilon )\) only, leads to the following set of linear equations

$$\begin{aligned} \overline{\phi }_{jxx}+\overline{\phi }_{jyy}= & {} 0,~~~0<y<H,~~x_{j-1}<x<x_j, \end{aligned}$$
(2.8)
$$\begin{aligned} \overline{\phi }_{jy}(x,0,t)= & {} 0, \end{aligned}$$
(2.9)
$$\begin{aligned} \overline{\phi }_{1x}(0,y,t)=\overline{\phi }_{2x}(x_2,y,t)= & {} \dot{\overline{q}}, \end{aligned}$$
(2.10)
$$\begin{aligned} \overline{\phi }_{1x}(x_1,y,t)=\overline{\phi }_{2x}(x_1,y,t)= & {} \dot{\overline{q}}-\frac{\beta }{\rho }(\overline{p}_2(x_1,y,t)-\overline{p}_1(x_1,y,t)), \end{aligned}$$
(2.11)
$$\begin{aligned} \overline{\phi }_{jt}+g\overline{h}_j= & {} 0~~~\textrm{on}~~~y=H, \end{aligned}$$
(2.12)
$$\begin{aligned} \overline{h}_{jt}= & {} \overline{\phi }_{jy}~~~\textrm{on}~~~y=H, \end{aligned}$$
(2.13)

with the pressure perturbation given by

$$\begin{aligned} \frac{\overline{p}_j}{\rho }+\overline{\phi }_{jt}=0, \end{aligned}$$
(2.14)

and the vessel equation becoming

$$\begin{aligned} m_v\ddot{\overline{q}}+\nu \overline{q}=-\frac{\textrm{d}}{\textrm{d}t}\left[ \int _0^{L_1}\int _0^{H}\rho \frac{\partial \overline{\phi }_1}{\partial x}\,\textrm{d}y \textrm{d}x+\int _{L_1}^{L_1+L_2}\int _0^{H}\rho \frac{\partial \overline{\phi }_2}{\partial x}\,\textrm{d}y \textrm{d}x\right] . \end{aligned}$$
(2.15)

Here, and in the remainder of the paper, the subscripts x, y, t denote partial derivatives.

The governing set of linear equations can be manipulated into a problem dependent solely on the velocity potential \(\overline{\phi }_j\) and the spring extension \(\overline{q}\) by combining the free-surface conditions (2.12) and (2.13) to eliminate \(\overline{h}_j\)

$$\begin{aligned} \overline{\phi }_{jtt}+g\overline{\phi }_{jy}=0~~~\textrm{on}~~~y=H, \end{aligned}$$
(2.16)

and by using the pressure perturbation (2.14) to write the boundary conditions on the porous baffle as

$$\begin{aligned} \overline{\phi }_{1x}(x_1,y,t)=\overline{\phi }_{2x}(x_1,y,t)=\dot{\overline{q}}+\beta \left[ \overline{\phi }_{2t}(x_1,y,t)-\overline{\phi }_{1t}(x_1,y,t)\right] . \end{aligned}$$
(2.17)

The resulting linear equations can be solved by seeking normal mode solutions.

2.2 Normal modes

We seek modal solutions of the linear system of equations (2.8)-(2.10) and (2.15)-(2.17) so as to identify the natural frequencies of the system, which in a physical system, comprise the components of all solutions via superposition. To identify the modal solutions we write

$$\begin{aligned} \overline{\phi }_j(x,y,t)=\widehat{\phi }_j(x,y)e^{\textrm{i}\omega t}, ~~~~~\overline{q}(t)=\widehat{q}e^{\textrm{i}\omega t}. \end{aligned}$$
(2.18)

Unlike for the impermeable baffle problem considered in [7], the form of the solution in (2.18) consists of a superposition of both \(\sin \omega t\) and \(\cos \omega t\) terms, and also allows for the consideration of \(\omega \) being complex.

Substituting (2.18) into the governing linear equations leads to the following boundary value problem for the hatted variables

$$\begin{aligned} \widehat{\phi }_{jxx}+\widehat{\phi }_{jyy}= & {} 0,~~~0<y<H,~~x_{j-1}<x<x_j, \end{aligned}$$
(2.19)
$$\begin{aligned} \widehat{\phi }_{jy}(x,0)= & {} 0, \end{aligned}$$
(2.20)
$$\begin{aligned} \widehat{\phi }_{1x}(0,y)=\widehat{\phi }_{2x}(x_2,y)= & {} \textrm{i}\omega \widehat{q}, \end{aligned}$$
(2.21)
$$\begin{aligned} \widehat{\phi }_{1x}(x_1,y)=\widehat{\phi }_{2x}(x_1,y)= & {} \textrm{i}\omega \widehat{q}+\textrm{i}\beta \omega \left( \widehat{\phi }_2(x_1,y)-\widehat{\phi }_1(x_1,y)\right) , \end{aligned}$$
(2.22)
$$\begin{aligned} \omega ^2\widehat{\phi }_j(x,H)= & {} g\widehat{\phi }_{jy}(x,H), \end{aligned}$$
(2.23)

with vessel equation

$$\begin{aligned} \left[ \nu -m_v\omega ^2\right] \widehat{q}=\textrm{i}\omega \left[ \int _0^{L_1}\int _0^{H}\rho \frac{\partial \widehat{\phi }_1}{\partial x}\,\textrm{d}y \textrm{d}x+\int _{L_1}^{L_1+L_2}\int _0^{H}\rho \frac{\partial \widehat{\phi }_2}{\partial x}\,\textrm{d}y \textrm{d}x\right] . \end{aligned}$$
(2.24)

The homogeneous nature of the free-surface and bottom boundary conditions means the problem lends itself to seeking a solution for \(\widehat{\phi }_j\) in each region as a superposition of vertical eigenmodes. Properties of these vertical eigenmodes have been explored in [42], and for the coupled, single region, sloshing problem in [35]. Hence we quote here the relevant results for this paper, and refer the reader to these works for full details. Therefore the separable solution to (2.19) which satisfies (2.20) and (2.23) can be written as

$$\begin{aligned} \widehat{\phi }_j(x,y)=\sum _{n=0}^\infty A_{jn}(x)\psi _n(y), \end{aligned}$$
(2.25)

where the vertical eigenmodes \(\psi _n(y)\) have the form

$$\begin{aligned} \psi _0(y)=\frac{1}{N_0}\cosh k_0y,~~~\textrm{and}~~~\psi _n(y)=\frac{1}{N_n}\cos k_ny~~~\textrm{for}~~~n\ge 1. \end{aligned}$$

The constants \(N_0\) and \(N_n\) are normalization constants given by

$$\begin{aligned} N_0=\sqrt{\frac{1}{2}\left( 1+\frac{\sinh 2k_0H}{2k_0H}\right) },~~~~~~N_n=\sqrt{\frac{1}{2}\left( 1+\frac{\sin 2k_nH}{2k_nH}\right) }, \end{aligned}$$

while the eigenvalues \(k_0\) and \(k_n\) satisfy

$$\begin{aligned} k_0H\tanh k_0H-\frac{\omega ^2H}{g}= & {} 0, \end{aligned}$$
(2.26)
$$\begin{aligned} k_nH\tan k_nH+\frac{\omega ^2H}{g}= & {} 0~~~\textrm{for}~~~n\ge 1, \end{aligned}$$
(2.27)

which derive from the characteristic equation

$$\begin{aligned} \frac{\omega ^2H}{g}\cos \left( H\sqrt{\lambda }\right) +\left( H\sqrt{\lambda }\right) \sin \left( H\sqrt{\lambda }\right) =0, \end{aligned}$$

where \(\lambda \) is the eigenvalue.

In [42] and [35], where these eigenmodes are discussed, the frequency \(\omega \) is real. Hence the first eigenvalue of the system is negative, \(\lambda _0=-k_0^2\) (\(\sqrt{\lambda _0}\) being purely imaginary), and is associated with the ‘wave mode’, while the rest are positive, \(\lambda _n=k_n^2\) \(n\ge 1\), and are associated with the ‘evanescent modes’. In the case when \(\omega \) is complex, all the eigenvalues \(\lambda _n\) move off the real axis and become complex, and hence it may seem that the distinction between the wave mode and the evanescent modes becomes less obvious. However, in this case there is a single mode with \(\textrm{Re}(\lambda _0=-k_0^2)<0\), while the other modes have \(\textrm{Re}(\lambda _n=k_n^2)>0\) and so we still find a wave mode plus evanescent modes structure even when \(\omega \) is complex. Hence we still use these terms when describing the modes of the system.

The forms of the functions \(A_{jn}(x)\) are found by satisfying Laplace’s equation, which after satisfying the rigid wall boundary conditions (2.21) in the respective region, can be written as

$$\begin{aligned} A_{10}(x)= & {} B_{10}\cos k_0x+\frac{\textrm{i}\omega \widehat{q}c_0}{k_0}\sin k_0x, \end{aligned}$$
(2.28)
$$\begin{aligned} A_{1n}(x)= & {} B_{1n}\cosh k_nx+\frac{\textrm{i}\omega \widehat{q}c_n}{k_n}\sinh k_nx~~~\textrm{for}~~~n\ge 1, \end{aligned}$$
(2.29)
$$\begin{aligned} A_{20}(x)= & {} B_{20}\cos k_0(x-x_2)+\frac{\textrm{i}\omega \widehat{q}c_0}{k_0}\sin k_0(x-x_2), \end{aligned}$$
(2.30)
$$\begin{aligned} A_{2n}(x)= & {} B_{2n}\cosh k_n(x-x_2)+\frac{\textrm{i}\omega \widehat{q}c_n}{k_n}\sinh k_n(x-x_2)~~~\textrm{for}~~~n\ge 1, \end{aligned}$$
(2.31)

where \(B_{jn}\) for \(j=1,2\) and \(n\ge 0\) are constants to be determined. The constants \(c_0\) and \(c_n\) come from expanding the unit function in terms of the vertical eigenfunctions, and are given by

$$\begin{aligned} c_0=\frac{1}{N_0}\frac{\sinh k_0H}{k_0H},~~~~~~~~c_n=\frac{1}{N_n}\frac{\sin k_nH}{k_nH}. \end{aligned}$$
(2.32)

Satisfying the conditions (2.22) at the porous baffle \(x=x_1=L_1\) reduces to the 4 equations

$$\begin{aligned}{} & {} k_0\sin k_0L_1 B_{10}+k_0\sin k_0L_2 B_{20}=-\textrm{i}\omega c_0(\cos k_0L_2-\cos k_0L_1)\widehat{q}, \end{aligned}$$
(2.33)
$$\begin{aligned}{} & {} \left( k_0\sin k_0L_1-\textrm{i}\omega \beta \cos k_0L_1\right) B_{10}+\textrm{i}\beta \omega \cos k_0L_2 B_{20}\nonumber \\{} & {} ~~~~~~~~~~~~~~~~~=\omega c_0\left[ \textrm{i}(\cos k_0L_1-1)-\frac{\beta \omega }{k_0}(\sin k_0L_1+\sin k_0L_2)\right] \widehat{q}, \end{aligned}$$
(2.34)
$$\begin{aligned}{} & {} k_n\sinh k_nL_1 B_{1n}+k_n\sinh k_nL_2 B_{2n}=\textrm{i}\omega c_n(\cosh k_nL_2-\cosh k_nL_1)\widehat{q}, \end{aligned}$$
(2.35)
$$\begin{aligned}{} & {} \left( k_n\sinh k_nL_1+\textrm{i}\omega \beta \cosh k_nL_1\right) B_{1n}-\textrm{i}\beta \omega \cosh k_nL_2 B_{2n}\nonumber \\ {}{} & {} ~~~~~~~~~~~~~~~=\omega c_n\left[ \textrm{i}(1-\cosh k_nL_1)+\frac{\beta \omega }{k_n}(\sinh k_nL_1+\sinh k_nL_2)\right] \widehat{q}, \end{aligned}$$
(2.36)

for \(n\ge 1\). The second pair of equations (2.35) and (2.36) for \(\textbf{b}=(B_{1n},B_{2n})^T\) can be written in matrix form \(\textbf{A}\textbf{b}=\textbf{q}\), where

$$\begin{aligned} \textbf{q}= & {} \omega c_n\left[ \begin{array}{c} \textrm{i}(\cosh k_nL_2-\cosh k_nL_1) \\ \textrm{i}(1-\cosh k_nL_1)+\frac{\beta \omega }{k_n}(\sinh k_nL_1+\sinh k_nL_2) \end{array}\right] \widehat{q},\\ \textbf{A}= & {} \left[ \begin{array}{cc} k_n\sinh k_nL_1 &{} k_n\sinh k_nL_2 \\ k_n\sinh k_nL_1+\textrm{i}\omega \beta \cosh k_nL_1 &{} -\textrm{i}\omega \beta \cosh k_nL_2 \end{array} \right] . \end{aligned}$$

This system of equations has a unique solution if \(\det (\textbf{A})\ne 0\) where

$$\begin{aligned} \det (\textbf{A})=-k_n^2\sinh k_nL_1\sinh k_nL_2\Delta _n,~~~\Delta _n=1+\frac{\textrm{i}\omega \beta }{k_n}\left[ \coth k_nL_1+\coth k_nL_2\right] . \end{aligned}$$

This expression is zero if \(k_n=0\), which we can discard as a translation of the system, or \(\sinh k_nL_1=\sinh k_nL_2=0\), or if \(\Delta _n=0\). The \(\sinh k_nL_1=\sinh k_nL_2=0\) case corresponds to \(k_n\) being purely imaginary, which in fact corresponds to this mode being associated with the wave mode for \(\omega \) real, and hence is just a reordering of the eigenvalues. The third case leads to the trivial solution for \(B_{jn}\). Therefore we can consider the case \(\det (\textbf{A})\ne 0\) and deal with the above cases later. Assuming \(\det (\textbf{A})\ne 0\), inverting the coefficient matrix \(\textbf{A}\), and solving gives

$$\begin{aligned} B_{jn}= & {} \frac{(-1)^j}{k_n^2|\Delta _n|^2}\left[ -\omega ^2\beta c_n\frac{\tanh \frac{1}{2}k_nL_1+\tanh \frac{1}{2}k_nL_2}{\sinh k_nL_j}\right. \nonumber \\ {}{} & {} \left. +\textrm{i}\left( \omega c_nk_n\tanh \frac{1}{2}k_nL_j+\frac{\omega ^3\beta ^2c_n}{k_n}\tanh \frac{1}{2}k_n(L_1+L_2)\left( \coth k_nL_1+\coth k_nL_2\right) ^2\right) \right] \widehat{q},\nonumber \\ \end{aligned}$$
(2.37)

for \(j=1,2\) and \(n\ge 1\).

Next we consider the first pair of equations (2.33) and (2.34), which too can be written in matrix form \(\mathbf{\widehat{A}}{} \mathbf{\widehat{b}}=\mathbf{\widehat{q}}\), for the parameters \(\mathbf{\widehat{b}}=(B_{10},B_{20})^T\) with

$$\begin{aligned} \mathbf{\widehat{q}}= & {} \omega c_0\left[ \begin{array}{c} -\textrm{i}(\cos k_0L_2-\cos k_0L_1) \\ \textrm{i}(\cos k_0L_1-1)-\frac{\beta \omega }{k_0}(\sin k_0L_1+\sin k_0L_2) \end{array}\right] \widehat{q},\nonumber \\ \mathbf{\widehat{A}}= & {} \left[ \begin{array}{cc} k_0\sin k_0L_1 &{} k_0\sin k_0L_2 \\ k_0\sin k_0L_1-\textrm{i}\omega \beta \cos k_0L_1 &{} \textrm{i}\beta \omega \cos k_0L_2 \end{array} \right] . \end{aligned}$$
(2.38)

Again we have a unique solution if \(\det (\mathbf{\widehat{A}})\ne 0\) where

$$\begin{aligned} \det (\mathbf{\widehat{A}})=-k_0^2\sin k_0L_1\sin k_0L_2\Delta _0,~~~\Delta _0=1-\frac{\textrm{i}\omega \beta }{k_0}\left[ \cot k_0L_1+\cot k_0L_2\right] . \end{aligned}$$

In this case \(\det (\mathbf{\widehat{A}})=0\) if \(\sin k_0L_1=\sin k_0L_2=0\) simultaneously (again neglecting \(k_0=0\)), which occurs if

$$\begin{aligned} k_0L_1=m\pi ~~~\textrm{and}~~~k_0L_2=m'\pi , \end{aligned}$$

for \(m,m'\in \mathbb {N}\), and thus means the lengths of the two compartments must satisfy \(mL_2=m'L_1\). These solutions correspond to symmetric free-sloshing modes with \(k_0\in \mathbb {R}\). Also \(\det (\mathbf{\widehat{A}})\) could be zero if \(\Delta _0=0\), i.e. \(\omega =-\textrm{i}k_0/(\beta (\cot k_0L_1+\cot k_0L_2))\), but this again leads to the trivial solution. See Appendix A for more on these solutions.

Making the observation that \(\det (\mathbf{\widehat{A}})\) could be zero, then (2.33) and (2.34) essentially become two equations which couple the three unknowns \(B_{10}\), \(B_{20}\) and \(\widehat{q}\). A third equation linking these constants comes from the vessel equation (2.24). Substituting in the normal mode forms (2.18) and evaluating the integrals by using the fact that the vertical eigenmodes satisfy

$$\begin{aligned} \int _0^H\psi _0(y)\,\textrm{d}y=Hc_0~~~\textrm{and}~~~\int _0^H\psi _n(y)\,\textrm{d}y=Hc_n, \end{aligned}$$

leads to the vessel equation

$$\begin{aligned} \textrm{i}\omega \rho Hc_0(\cos k_0L_1-1)B_{10}+\textrm{i}\omega \rho Hc_0(1-\cos k_0L_2)B_{20}+\Theta \widehat{q}=0, \end{aligned}$$
(2.39)

where

$$\begin{aligned} \Theta =-\frac{\omega ^2\rho H c_0^2}{k_0}(\sin k_0L_1+\sin k_0L_2)+\widehat{\Theta }_{0}+\beta ^2\widehat{\Theta }_{1}-\beta \textrm{i}\widehat{\Theta }_{2}, \end{aligned}$$
(2.40)

and

$$\begin{aligned} \widehat{\Theta }_{0}= & {} \nu -m_v\omega ^2-2\omega ^2\rho H\sum _{n=1}^\infty \frac{c_n^2}{k_n|\widehat{\Delta }_n|^2}\left( \tanh \frac{1}{2}k_nL_1+\tanh \frac{1}{2}k_nL_2\right) ,\\ \widehat{\Theta }_{1}= & {} -2\omega ^4\rho H\sum _{n=1}^\infty \frac{c_n^2}{k_n^3|\widehat{\Delta }_n|^2}\tanh \frac{1}{2}k_n(L_1+L_2)\left( \coth k_nL_1+\coth k_nL_2\right) ^2,\\ \widehat{\Theta }_{2}= & {} -\omega ^3\rho H\sum _{n=1}^\infty \frac{c_n^2}{k_n^2|\widehat{\Delta }_n|^2}\left[ \tanh \frac{1}{2}k_nL_1+\tanh \frac{1}{2}k_nL_2\right] ^2. \end{aligned}$$

The three equations (2.33), (2.34) and (2.39) define 3 equations for the 3 unknowns \(B_{10}\), \(B_{20}\) and \(\widehat{q}\), which by seeking a non-trivial solution, yields an eigenvalue problem for \(\omega \).

2.3 The characteristic equation

The characteristic equation for the unknown frequency \(\omega \) is found by identifying non-trivial solutions to (2.33), (2.34) and (2.39). The equations can be written as the matrix problem

$$\begin{aligned} \textbf{T}{} \textbf{z}=\textbf{0}, \end{aligned}$$
(2.41)

where,

$$\begin{aligned} \textbf{T}= & {} \left[ \begin{array}{ccc} k_0\sin k_0L_1 &{} k_0\sin k_0L_2 &{} \textrm{i}\omega c_0(\cos k_0L_2-\cos k_0L_1) \\ k_0\sin k_0L_1-\textrm{i}\omega \beta \cos k_0L_1 &{} \textrm{i}\omega \beta \cos k_0L_2 &{} -\omega c_0\zeta \\ \textrm{i}\omega \rho Hc_0(\cos k_0L_1-1) &{}\textrm{i}\omega \rho Hc_0(1-\cos k_0L_2) &{} \Theta \end{array}\right] ,\\ \textbf{z}= & {} \left[ \begin{array}{ccc} B_{10}&B_{20}&\widehat{q}\end{array}\right] ^T, \end{aligned}$$

and

$$\begin{aligned} \zeta =\textrm{i}(\cos k_0L_1-1)-\frac{\omega \beta }{k_0}(\sin k_0L_1+\sin k_0L_2). \end{aligned}$$

Non-trivial solutions occur when the determinant of the coefficient matrix is zero, which leads to the characteristic equation

$$\begin{aligned} D(\omega )= & {} 2k_0\omega ^2H\rho c_0^2\sin k_0L_1\sin k_0L_2\left[ \tan \frac{1}{2}k_0L_1+\tan \frac{1}{2}k_0L_2\right] \\ {}{} & {} -2\textrm{i}\beta \omega ^3 H\rho c_0^2\left[ 1-\cos k_0(L_1+L_2)\right] \\ {}{} & {} -(\widehat{\Theta }_{0}+\beta ^2\widehat{\Theta }_{1}-\textrm{i}\beta \widehat{\Theta }_{2})\left[ k_0^2\sin k_0L_1\sin k_0L_2-\textrm{i}\omega \beta k_0\sin k_0(L_1+L_2)\right] , \end{aligned}$$

which is solved for the unknown frequencies \(\omega \). There are an infinite number of natural frequencies, and once each is calculated, the corresponding eigenvector \((B_{10},B_{20},\widehat{q})^T\) gives the ratios of the unknown amplitudes. In appendix A we show that the symmetric free-sloshing modes, when \(\sin k_0L_1=\sin k_0L_2=0\), occur when the vessel is at rest (\(\widehat{q}\equiv 0\)). Here the constants satisfy \(B_{10}=B_{20}\) and are arbitrary, being fixed by the initial conditions. In the case of non-symmetric sloshing modes when \(\det (\mathbf{\widehat{A}})\ne 0\) then we can solve for \(B_{10}\) and \(B_{20}\) as a function of \(\widehat{q}\) as

$$\begin{aligned} B_{j0}= & {} \frac{(-1)^j}{k_0^2|\Delta _0|^2}\left[ \omega ^2\beta c_0\frac{\tan \frac{1}{2}k_0L_1+\tan \frac{1}{2}k_0L_2}{\sin k_0L_j}\right. \nonumber \\ {}{} & {} \left. +\textrm{i}\left( \omega c_0k_0\tan \frac{1}{2}k_0L_j+\frac{\omega ^3\beta ^2c_0}{k_0}\tan \frac{1}{2}k_0(L_1+L_2)\left( \cot k_0L_1+\cot k_0L_2\right) ^2\right) \right] \widehat{q},\nonumber \\ \end{aligned}$$
(2.42)

where \(\widehat{q}\) is dependent on the initial conditions. Hence, as in (2.37), the value of \(B_{j0}\) couples to the vessel motion.

2.4 Non-dimensionalisation

The characteristic equation () contains many physical parameters, but the number of these parameters can be reduced by considering the non-dimensional form of the system. We non-dimensionalise the system of equations based on the non-dimensionalisation first set out by [43]. Here we define the non-dimensional quantities as

$$\begin{aligned} R= & {} \frac{m_v}{m_f},~~~~G=\frac{\nu (L_1+L_2)^2}{4gH m_f},~~~~s=\frac{\omega (L_1+L_2)}{2\sqrt{gH}},~~~~\gamma =2\sqrt{gH}\beta ,\\ \alpha _n= & {} k_n(L_1+L_2),~~~~\mu _1=\frac{L_1}{L_1+L_2}=\mu ,~~~~\mu _2=\frac{L_2}{L_1+L_2}=1-\mu ,\\ C_{jk}= & {} \frac{B_{jk}}{2\sqrt{gH}(L_1+L_2)},~~~~Q=\frac{\widehat{q}}{L_1+L_2}, \end{aligned}$$

where we define the fluid mass as \(m_f=\rho H(L_1+L_2)\). Then the characteristic equation becomes

$$\begin{aligned} D(s)= & {} 2\alpha _0 s^2 c_0^2\sin \alpha _0\mu \sin \alpha _0(1-\mu )\left[ \tan \frac{1}{2}\alpha _0\mu +\tan \frac{1}{2}\alpha _0(1-\mu )\right] -2\textrm{i}\gamma s^3 c_0^2\left[ 1-\cos \alpha _0\right] \nonumber \\{} & {} -(\Theta _0+\gamma ^2\Theta _{1}-\textrm{i}\gamma \Theta _{2})\left[ \alpha _0^2\sin \alpha _0\mu \sin \alpha _0(1-\mu )-\textrm{i}s\gamma \alpha _0\sin \alpha _0\right] , \end{aligned}$$
(2.43)

where we define

$$\begin{aligned} \begin{array}{cl} \Theta _{0}&{}=G-Rs^2-2s^2\displaystyle \sum _{n=1}^\infty \dfrac{c_n^2}{\alpha _n|\Delta _n|^2}\left( \tanh \dfrac{1}{2}\alpha _n\mu +\tanh \dfrac{1}{2}\alpha _n(1-\mu )\right) ,\\ \Theta _{1}&{}=-2s^4\displaystyle \sum _{n=1}^\infty \dfrac{c_n^2}{\alpha ^3|\Delta _n|^2}\tanh \dfrac{1}{2}\alpha _n\left( \coth \alpha _n\mu +\coth \alpha _n(1-\mu )\right) ^2,\\ \Theta _{2}&{}=-s^3\displaystyle \sum _{n=1}^\infty \dfrac{c_n^2}{\alpha _n|\Delta _n|^2}\left( \tanh \dfrac{1}{2}\alpha _n\mu +\tanh \dfrac{1}{2}\alpha _n(1-\mu )\right) ^2, \end{array} \end{aligned}$$
(2.44)

and

$$\begin{aligned} |\Delta _n|^2=1+\frac{\gamma ^2s^2}{\alpha _n^2}\left[ \coth \alpha _n\mu +\coth \alpha _n(1-\mu )\right] ^2. \end{aligned}$$

The eigenvalues \(\alpha _n\) for \(n\ge 0\) are found from (2.26) and (2.27) which in non-dimensional form are

$$\begin{aligned} \alpha _0\tanh \alpha _0\delta -4\delta s^2=0, ~~~\textrm{and}~~~ \alpha _n\tan \alpha _n\delta +4\delta s^2=0, \end{aligned}$$
(2.45)

where \(\delta =H/(L_1+L_2)\) is the non-dimensional fluid depth parameter.

For cases when \(\det (\mathbf{\widehat{A}})\ne 0\) the non-dimensional forms of the amplitude parameters (2.42) and (2.37) become

$$\begin{aligned} C_{j0}= & {} \frac{(-1)^j}{\alpha _0^2|\Delta _0|^2}\left[ s^2\gamma c_0\frac{\tan \frac{1}{2}\alpha _0\mu +\tan \frac{1}{2}\alpha _0(1-\mu )}{\sin \alpha _0\mu _j}\right. \nonumber \\{} & {} \left. +\textrm{i}\left( s c_0\alpha _0\tan \frac{1}{2}\alpha _0\mu _j+\frac{s^3\gamma ^2c_0}{\alpha _0}\tan \frac{1}{2}\alpha _0\left( \cot \alpha _0\mu +\cot \alpha _0(1-\mu )\right) ^2\right) \right] Q, \end{aligned}$$
(2.46)
$$\begin{aligned} C_{jn}= & {} \frac{(-1)^j}{\alpha _n^2|\Delta _n|^2}\left[ -s^2\gamma c_n\frac{\tanh \frac{1}{2}\alpha _n\mu +\tanh \frac{1}{2}\alpha _n(1-\mu )}{\sinh \alpha _n\mu _j}\right. \nonumber \\ {}{} & {} \left. +\textrm{i}\left( s c_n\alpha _n\tanh \frac{1}{2}\alpha _n\mu _j+\frac{s^3\gamma ^2c_n}{\alpha _n}\tanh \frac{1}{2}\alpha _n\left( \coth \alpha _n\mu +\coth \alpha _n(1-\mu )\right) ^2\right) \right] Q,~~~~~~ \end{aligned}$$
(2.47)

respectively, for \(j=1,2\), where

$$\begin{aligned} |\Delta _0|^2=1+\frac{\gamma ^2 s^2}{\alpha _0^2}\left[ \cot \alpha _0\mu +\cot \alpha _0(1-\mu )\right] ^2. \end{aligned}$$

The characteristic equation (2.43) can be shown to reduce to the equation presented in [35] when \(|\gamma |\rightarrow \infty \) and to the two compartment relation in [7] when \(|\gamma |=0\). We show this explicitly in appendix B where we calculate the first two terms of the asymptotic solutions for s in the limits \(\gamma \rightarrow 0\) and \(\gamma \rightarrow \infty \) with \(\gamma \in \mathbb {R}\).

2.5 Shallow-water limit

In the shallow-water limit the depth parameter \(\delta \ll 1\), with all other parameters held fixed. The eigenvalues related to the vertical eigenfunctions satisfy (2.45), the first of which describes the wave mode. In the limit \(\delta \rightarrow 0\) then

$$\begin{aligned} 4\delta ^2s^2=\alpha _0^2\delta ^2-\frac{1}{3}\alpha _0^4\delta ^4+O(\delta ^6), \end{aligned}$$

which at leading order gives

$$\begin{aligned} s=\frac{1}{2}\alpha _0. \end{aligned}$$

For the evanescent modes, we observe that each solution must lie in the range \((n-1)\pi<\textrm{Re}(\alpha _n\delta )<n\pi \), thus it can be shown that

$$\begin{aligned} \alpha _n\delta = n\pi -\frac{\alpha _0^2\delta ^2}{n\pi }+O(\delta ^4). \end{aligned}$$

Substituting these approximations into the coefficients \(c_0\) and \(c_n\) we find that the leading order terms satisfy

$$\begin{aligned} c_0=1+O(\delta ^4),~~~~\textrm{and}~~~~c_n=O(\delta ^2). \end{aligned}$$

Hence in the shallow-water limit the evanescent modes are \(O(\delta ^2)\) smaller in magnitude to the wave mode, and at leading order the characteristic equation can be written solely in terms of the frequency s as

$$\begin{aligned} D^\textrm{SW}(s)= & {} 4 s^2 \sin 2\mu s \sin 2(1-\mu )s\left[ s\tan \mu s+s\tan (1-\mu )s-G+Rs^2\right] \nonumber \\ {}{} & {} -2\textrm{i}\gamma s^2\sin 2s\left[ s\tan s-G+Rs^2\right] . \end{aligned}$$
(2.48)

In this limit the form of the characteristic equation is the sum of the two compartment shallow-water equation from [7] and the one compartment shallow-water equation from the work of [35] with an \(\textrm{i}\gamma \) prefactor. Hence it is clear that this equation gives the correct characteristic equations in the limits \(|\gamma |=0\) and \(|\gamma |\rightarrow \infty \), and there is a linear transition between the two cases as \(\gamma \) varies.

3 Results

3.1 Single baffle system

In this section we consider numerical solutions to the non-dimensional form of the characteristic equation for both finite, (2.43), and shallow depth, (2.48), fluids. In both cases the unknown complex frequency s is found via Newton iterations with the \(m^\textrm{th}\) update for s given by

$$\begin{aligned} s^{m+1}=s^m-\frac{D(s^m)}{D'(s^m)}, \end{aligned}$$

where the dash denotes differentiation with respect to s. For the initial guesses for \(s^0\) we use either results from the \(|\gamma |=0\) or \(|\gamma |\rightarrow \infty \) limits, as here \(s\in \mathbb {R}\) and we can identify \(s^0\) visually by plotting D(s) and manually looking for the roots. Iterations are continues until \(|s^{m+1}-s^m|<10^{-8}\). From these results we use parameter continuation techniques on \(\gamma \) to find values of s at finite values of \(\gamma \), both real and complex. The complex eigenvalues \(\alpha _n\) are identified by solving (2.45) iteratively via Newton iterations, and noting that \((n-1)\pi<\textrm{Re}(\alpha _n\delta )<n\pi \) so as to make sure we capture all the solutions. The infinite sums in (2.44) are truncated at 40 evanescent modes, which give converged results for all parameter sets considered. The initial guesses for \(\alpha _n\) are found by solving the vertical eigenvalue problem given in [35] directly by expanding the solution as a series of Chebyshev polynomials. This is discussed in detail in [35].

Initially we focus on two vessel configurations, a symmetric configuration with \(\mu =0.5\) and an asymmetric configuration with \(\mu =0.3\), with \(\gamma \in \mathbb {R}\).

Fig. 2
figure 2

Plots of \(s_r(\gamma )\) and \(s_i(\gamma )\) from (2.43) for \((G,R,\delta )=(1,0.5,0.5)\) and (a,b) \(\mu =0.5\) and (c,d) \(\mu =0.3\). The dashed lines represent modes which are symmetric modes in a stationary vessel (\(Q=0\)) in the limit \(\gamma \rightarrow \infty \). The circles at \(\gamma =0\) signify symmetric sloshing modes in this limit

Full size image

In Fig. 2 we consider the variation of the real and imaginary parts of \(s=s_r+\textrm{i}s_i\) as a function of \(\gamma \) for parameters \((G,R,\delta )=(1,0.5,0.5)\) and (a,b) \(\mu =0.5\) and (c,d) \(\mu =0.3\). In this figure the solid lines represent modes which are anti-symmetric sloshing modes (which couple to a moving vessel) in the \(\gamma \rightarrow \infty \) limit, while the dashed lines represent symmetric modes (i.e. which exist in a stationary vessel), in the \(\gamma \rightarrow \infty \) limit. The circles at \(\gamma =0\) show the frequencies of the symmetric sloshing modes in the \(\gamma =0\) limit. For the \(\mu =0.5\) configuration in panels (a,b), we observe that the symmetric modes remain symmetric modes as the wall porosity parameter \(\gamma \) is varied, with a fixed \(s_r\) value and \(s_i=0\). This means that these modes remain neutral modes, and the vessel remains stationary, i.e. \(Q=0\) as \(\gamma \) varies. In these cases the free-surface profile is similar to that given in Fig. 11 of Appendix A, where the fluid generates an equal and opposite force on the vessel walls and the baffle, resulting in no net force on the vessel.

The solid lines, representing the anti-symmetric modes, couple to the vessel motion, hence \(Q\ne 0\). Here we see that for \(\gamma \gtrsim 5\) these modes appear to have a constant value of \(s_r\) equal to the \(\gamma \rightarrow \infty \) limit result, but in panel (b) we see these modes have \(s_i>0\), meaning these modes are exponentially decaying modes. For \(\gamma \in [0,5]\) the frequency (real part of the complex frequency) of these modes rapidly varies from the \(\gamma \rightarrow \infty \) result to the \(\gamma =0\) result. In this region the corresponding decay rate \(s_i\) reaches its maximum value for each of these modes, hence the maximal damping of the system occurs when \(s_r\) varies the greatest. A similar conclusion was found for the lowest sloshing mode only in the model of [44]. The ordering of the decay rates is not directly related to the value of \(s_r\), i.e. larger \(s_r\) values do not necessary decay faster/slower than modes with smaller \(s_r\) values. In particular in Fig. 2, we observe that it is the mode labeled 2 which decays fastest in this system. When this mode intersects with \(s_r=0\) there is a bifurcation into two unstable modes with \(s_r=0\) and \(s_i\ne 0\). The reason for this is due to two modes with \(s_r=S(\gamma )\) and \(s_r=-S(\gamma )\) interacting at \(s_r=0\). When \(s_r=0\) for these two modes, they become unstable modes in a stationary vessel, and hence are not of significance in this study, as our main interest is in modes which are coupled to the vessel motion. One thing we do observe in this figure is that the lowest frequency mode as \(\gamma \rightarrow \infty \) remains the lowest frequency mode as \(\gamma \rightarrow 0\) (except for a tiny range of \(\gamma \) values where the mode labeled 2 goes to zero).

When we consider the \(\mu =0.3\) non-symmetric vessel configuration in panels (c,d) we observe that the symmetric sloshing modes (in either the \(\gamma =0\) or \(\gamma \rightarrow \infty \) limits) are no longer neutral for all values of \(\gamma \), and now decay except in these two limits. Also the value of \(s_r\) now varies as \(\gamma \) varies, i.e. they no longer have constant frequency. The overall behaviour of the mode frequencies, \(s_r\), is similar to the \(\mu =0.5\) case, with the variations in both the real and imaginary parts of s occurring mainly for \(0\le \gamma \le 5\), and with similar magnitude decay rates. We again observe a mode (labeled 2) which as \(\gamma \rightarrow 0\) we find \(s_r=0\) for small \(\gamma \). The difference in this case is this mode is a symmetric mode, in a stationary vessel, in the \(\gamma \rightarrow \infty \) limit, not an anti-symmetric mode. We now also observe modes which switch type in the two extremes of \(\gamma \), such as that labeled 3 in panel (c). This mode is an anti-symmetric mode as \(\gamma \rightarrow \infty \), but as \(\gamma \) is reduced it becomes a symmetric mode at \(\gamma =0\).

Fig. 3
figure 3

Plots of \(s_r(\gamma )\) and \(s_i(\gamma )\) from (2.43) for \((G,R,\delta )=(1,0.5,0.1)\) and (a,b) \(\mu =0.5\) and (c,d) \(\mu =0.3\). The dashed lines represent modes which are symmetric modes in a stationary vessel (\(Q=0\)) in the limit \(\gamma \rightarrow \infty \). The circles at \(\gamma =0\) signify symmetric sloshing modes in this limit

Full size image

As \(\delta \) is reduced to \(\delta =0.1\) (again with \((G,R)=(1,0.5)\)) in Fig. 3, i.e. as we move closer to the shallow-water limit, we find that the higher frequency modes, \(s_r\), become more distinct, i.e. more spread out, as do the decay rates, \(s_i\), of the modes. As a general observation, it appears that the maximum decay rates increase in magnitude as \(\delta \) is increased. This is particularly apparent in the \(\mu =0.3\) configuration. It is however, still the case that the majority of the variation in s is restricted to the region \(\gamma \lesssim 5\).

Fig. 4
figure 4

Plot of \(s_r(\gamma )\) and \(s_i(\gamma )\) for two modes from Fig. 3 with \((G,R,\delta ,\mu )=(1,0.5,0.1,0.3)\). The solid lines give the numerical solutions of (2.43) while the dashed lines give the asymptotic results calculated in Appendix B

Full size image

In appendix B we calculate the asymptotic form of s in the limits \(\gamma \rightarrow 0\) and \(\gamma \rightarrow \infty \) with \(\gamma \in \mathbb {R}\). In Fig. 4 these approximations (dashed lines) are compared to the full numerical result (solid lines), and we observe excellent agreement in both these limits, despite both \(s_r\) and \(s_i\) each containing only one term in their expansions. However, this level of approximation is not able to capture the maximum decay rate of the modes accurately, although it does allow for predictions of the system’s decay in the two extreme limits, along with an approximate maximum growth rate where the two approximations intersect. This would be of particular interest if the baffle porosity were time dependent, with sloshing waves generated with \(\gamma =0\) and then the baffle porosity was varied. The initial rate of decay of the system could then be accurately predicted by the asymptotic results, especially if the variation was slow.

Fig. 5
figure 5

Plots of \(s_r(\gamma _r)\) and \(s_i(\gamma _r)\) from (2.43) for \((G,R,\delta )=(1,0.5,0.5)\) and \(\mu =0.5\). Here \(\gamma =\gamma _r(1+0.1\textrm{i})\). The solid lines are the values of \(s_r\) and \(s_i\) for the complex value of \(\gamma \), while the dashed lines are the corresponding result with \(\gamma =\gamma _r\), as given in Fig. 2(a,b)

Full size image

In Fig. 5 we consider the form of \(s=s_r+\textrm{i}s_i\) when \(\mu =0.5\) (with \((G,R,\delta )=(1,0.5,0.5)\)) when \(\gamma =\gamma _r(1+0.1\textrm{i})\). Here the imaginary part of \(\gamma \) represents the inertial effect of the fluid in the baffle, and is typically smaller than the real part [41]. The results with \(\gamma \in \mathbb {C}\), given by the solid lines, are compared to the equivalent results with \(\gamma =\gamma _r\in \mathbb {R}\) from Fig. 2(a,b). What this figure shows is the inclusion of inertial effects typically increases the decay rate, \(s_i\), of the system for the higher frequency modes, but makes a relatively modest modification to the lowest frequency mode. The larger peaks in \(s_i\) in Fig. 5(b) are accompanied by sharper changes in the corresponding \(s_r\) value in Fig. 5(a). The other obvious change in this case compared to Fig. 2 is that the \(s_r\) value for mode 2 now does not go to zero, where it interacted with a second mode, and instead \(s_r\rightarrow \infty \) as \(\gamma _r\rightarrow 0\).

Fig. 6
figure 6

Plots of \(s_r(\gamma )\) and \(s_i(\gamma )\) in the shallow-water limit from (2.48) for \((G,R)=(1,0.5)\) and (a,b) \(\mu =0.5\) and (c,d) \(\mu =0.3\). The dashed lines represent modes which are symmetric modes in a stationary vessel (\(Q=0\)) in the limit \(\gamma \rightarrow \infty \). The circles at \(\gamma =0\) signify symmetric sloshing modes in this limit

Full size image

In the shallow-water limit, the characteristic equation simplifies to (2.48) and the solutions to this equation, plotted in Fig. 6, are found to agree well with those in Fig. 3, at least for the smaller frequency results. The main benefit of the shallow-water approximation is that the values of s can be calculated more easily (i.e. without calculating the intermediary eigenvalues \(\alpha _n\)). Also, in systems where the lower frequency modes dominate, and the higher frequency modes can be neglected, then the shallow-water approximation is beneficial due to the speed of computation.

A typical initial condition for an experimental setup for the system in Fig. 1, such as extending the spring and releasing the vessel from a stationary position, would consist of a superposition of these individual modes. However, unlike for the impermeable baffle problem, where all modes are undamped and so persist for all times, the higher frequency modes are typically damped out fastest, and so in this experimental setup we would expect the lowest frequency mode (as it is the least damped) to be the most significant. Also, following [36] the coefficient of the lowest frequency mode tends to have the largest amplitude in the eigenmode expansion for most initial conditions. Thus we focus our attention in the remainder of the paper on the lowest frequency mode in the shallow-water limit.

Fig. 7
figure 7

Plot of the non-dimensional free-surface elevation \(h_j(x,t)\) and horizontal velocity component \(u_j(x,t)=\phi _x(x,t)\) for \(j=1,2\) in the shallow-water limit for \((G,R,\delta ,\mu ,\epsilon )=(1,0.5,0.05,0.3,0.01)\) at times \(t/(2s_r)=0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4},\pi \) numbered 1-5 respectively. In (a,b) \(\gamma =0.8\), (c,d) \(\gamma =1.5\), while in (e,f) \(\gamma =5\)

Full size image

In figure 7 we consider the time evolution of the non-dimensional free-surface profiles \(h_j(x,t)\) and horizontal velocity \(u_j(x,t)\) for the lowest frequency mode in the shallow-water limit for \((G,R,\delta )=(1,0.5,0.05)\) with (a,b) \(\gamma =0.8\), (c,d) \(\gamma =1.5\) and (e,f) \(\gamma =5\). The form of the free-surface profile can be found from (2.12) which when non-dimensionalised is given by

$$\begin{aligned} h_j(x,t)=\delta -\left[ 2\textrm{i}\epsilon s A_{j0}(x)e^{2\textrm{i}st}+\mathrm{c.c}\right] , \end{aligned}$$
(3.49)

while the non-dimensional horizontal velocity in the fixed reference frame is given by

$$\begin{aligned} u_j(x,t)=\frac{\partial \phi _j}{\partial x}=\epsilon \frac{\partial A_{j0}}{\partial x}(x)e^{2\textrm{i}st}+\mathrm{c.c}, \end{aligned}$$
(3.50)

where c.c denotes the complex conjugate. Here \(j=1,2\) denotes the two separate regions of the vessel. The wave mode is the driving mode in the system, and hence plotting h(x, t) and u(x, t) without the evanescent modes provides excellent notion for the fluid motion. The evanescent modes provide a perturbation to this result, typically reducing the fluid height, h(x, t), at the side walls and baffle, and increasing it in the interior of the fluid. This was demonstrated for the zero-baffle problem in [35].

In panels (a,b) the baffle has a low porosity value and so there is a delay in the fluid flowing between each region, resulting in the average fluid depth in each region being significantly different at each time value, e.g. result 3 at \(t=\pi s_r\). There is also a very clear reduction in the horizontal fluid velocity at the baffle, where the fluid motion is restricted as it passes through it. In panels (c,d) the baffle porosity is larger, and the difference in the fluid heights at the baffle is reduced, while in panels (e,f) the baffle is even more porous and the difference in the fluid levels in each region is reduced further. In fact, in this case the free-surface elevations are almost continuous across the baffle. The horizontal velocity value at the baffle is also much less reduced in this final case, meaning the speed of the fluid is altered less by the presence of the baffle, and hence the lower decay rate of the coupled system.

Fig. 8
figure 8

Plot of the non-dimensional free-surface elevation \(h_j(x,t)\) and horizontal velocity component \(u_j(x,t)=\phi _x(x,t)\) for \(j=1,2\) in the shallow-water limit for \((G,R,\delta ,\mu ,\epsilon )=(1,0.5,0.05,0.3,0.01)\) at times \(t/(2s_r)=0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4},\pi \) numbered 1-5 respectively. The solid lines are the results for the complex value of \(\gamma =0.8(1+0.2\textrm{i})\), while the dashed lines are the corresponding result with \(\gamma =0.8\), as given in Fig. 7(a,b)

Full size image

In Fig. 8 we make a comparison of plots of h(x, t) and u(x, t) for \(\gamma =0.8(1+0.2\textrm{i})\) (solid lines) and \(\gamma =0.8\) (dashed lines). Here we have increased the size of \(\gamma _i\) compared to the real part to \(20\%\), in order to exaggerate the changes to h(x, t) and u(x, t), but as we saw in Fig. 5, the effect on the lowest frequency mode when \(s_i\ne 0\) is small. In fact, it is hard to make any meaningful observation in Fig. 8, because as \(\gamma \) changes, both \(s_r\) and \(s_i\) change, hence the results in this figure include a small phase change as well as a change in decay rate. Discerning the difference between these two features is difficult in this figure.

Fig. 9
figure 9

Plots of the decay rate \(s_i(\gamma ,\mu )\) for (a) \((R,G)=(0.5,1)\), (b) \((R,G)=(0.5,7)\), (c) \((R,G)=(5,1)\) and (d) \((R,G)=(5,7)\). The black contours signify the values \(\frac{1}{4}s_i^\textrm{max}\), \(\frac{1}{2}s_i^\textrm{max}\) and \(\frac{3}{4}s_i^\textrm{max}\) in each case

Full size image

Thus far we have fixed the non-dimensional parameters R and G, but in Fig. 9 we examine how the decay rate of the system, \(s_i\), varies for different (G, R) combinations for \(\gamma \in \mathbb {R}\). The results show that the maximum decay rate always occurs for \(\mu =0.5\) (i.e. for equally sized regions), with the value of \(\gamma \in [0,1.5]\), i.e. close to the rigid baffle limit. For \((G,R)=(7,0.5)\) in panel (b) the rate of damping is significantly increased, which is due to the spring being stiff in this case but with a heavy fluid mass in the vessel. In this case the horizontal velocities in the fluid are larger than in (a) (weak spring, heavy fluid), and hence the fluid is slowed more dramatically by the baffle. In panel (c) we have a light fluid (heavy vessel) and a weak spring, hence damping rates are low (due to low fluid velocities in the system). Also, the largest decay rates for this configuration are concentrated in a narrow band of small porosity values. While in panel (d) where we have a light fluid and a strong spring, we have a much larger region of the \((\gamma ,\mu )\)-plane where the decay rate of this mode is \(\ge \frac{1}{4}s_i^\textrm{max}\). Hence in a physical system with these parameters there is a larger margin for error in the construction of the baffle to have a porosity value needed to achieve a quick decay of the system. This could be useful if a rapid decay of any forced oscillations is required, and the porosity of the wall is not able to be altered via some mechanical means.

3.2 Multiple baffle system

Thus far we have focused on the single baffle problem, but the theory presented in §2 can easily be extended to multiple baffles, potentially each with a different porosity value. In the final part of this paper we consider the case of multiple, identical baffles, which are equally spaced in the vessel. Hence we only introduce one further parameter, M, which is the number of baffles. The case \(M=1\) we have extensively covered.

The challenge in this case is, despite the simple characteristic equation for the \(M=1\) case in (2.48), this expression very easily becomes complex and unwieldy as M increases. Hence we consider two simplifications, we only consider the limit of shallow-water fluids, and we consider direct numerical solutions to the governing boundary condition equations, rather than forming the characteristic equation analytically and then solving this numerically. To this end, we can write the non-dimensional shallow-water velocity potential in each vessel region from (2.25) as

$$\begin{aligned} \phi _j(x)=\widehat{A}_j(x)=\widehat{B}_j\cos (2s(x-x_{j-1}))+\widehat{C}_j \sin (2s(x-x_{j-1})), \end{aligned}$$

where

$$\begin{aligned} x_j=\frac{j}{M+1}~~~~\textrm{for}~~~~j=0,....,M+1, \end{aligned}$$

are the dimensionless positions of the vessel side walls and baffles. Here there is no longer a dependence on y as we are in the shallow-water limit, and the hats denote these constants are dimensionless. This solution satisfies all required equations except for the side-wall, and baffle boundary conditions, which fix the constants \(\widehat{B}_j\) and \(\widehat{C}_j\). For the M baffle problem the boundary conditions to be satisfied are

$$\begin{aligned} \widehat{A}_{1x}(x_0)= & {} \textrm{i}sQ,\\ \widehat{A}_{1x}(x_1)=\widehat{A}_{2x}(x_1)= & {} \textrm{i}sQ+\textrm{i}\gamma s(\widehat{A}_2(x_1)-\widehat{A}_1(x_1)),\\ \widehat{A}_{2x}(x_2)=\widehat{A}_{3x}(x_2)= & {} \textrm{i}sQ+\textrm{i}\gamma s(\widehat{A}_3(x_2)-\widehat{A}_2(x_2)),\\ \vdots= & {} \vdots \\ \widehat{A}_{(M+1)x}(x_{M+1})= & {} \textrm{i}sQ, \end{aligned}$$

which leads to \(2M+2\) equations for the \(2M+3\) unknowns (\(\widehat{B}_j\), \(\widehat{C}_j\) and Q). These equations together with the vessel equation (2.24), which in this notation becomes

$$\begin{aligned} \textrm{i}s\sum _{j=1}^{M+1}\left[ \widehat{A}_j(x_j)-\widehat{A}_j(x_{j-1})\right] +\left[ G-Rs^2\right] Q=0, \end{aligned}$$

can be written as the \(2M+3\) matrix system \(\textbf{B}{} \textbf{z}=\textbf{0}\) where \(\textbf{z}=(\widehat{B}_1,\widehat{C}_1,....,\widehat{B}_{M+1},\widehat{C}_{M+1},Q)^T\).

The characteristic equation would then be found from solving \(\det (\textbf{B})(s)=0\), such that there is a non-trivial solution to the above system. Here, rather than formulate this determinant analytically, we calculate s directly via Newton iterations, using the Jacobi formula to determine the derivative of the determinant with respect to s.

Fig. 10
figure 10

Plot of (a) \(s_r(\gamma )\) and (b) \(s_i(\gamma )\) in the shallow-water limit with \((G,R)=(1,0.5)\), for multiple, equally spaced porous baffles. The arrows indicate an increase in the value of M with \(M=1,2,4,9,14\) and 19 presented

Full size image

In Fig. 10 we consider results for \(s=s_r+\textrm{i}s_i\) for \((G,R)=(1,0.5)\) and values of \(M=1,2,4,9,14\) and 19 with \(\gamma \in \mathbb {R}\). The case \(M=1\) corresponds to the \(\mu =0.5\) case presented in Fig. 6 and shows a peak decay rate of the system located close to \(\gamma =0\). As the number of baffles is increased what we find is that the maximum decay rate, \(s_i^\textrm{max}\), increases to a maximum value at \(s_i^\textrm{max} \approx 0.031\) for \(M=19\), which is similar to the maximum decay rate when \(M=9\), i.e. the increase in decay rate slows for large M. The reason for this slow down in increasing \(s_i^\textrm{max}\) is due to what can be seen in panel (a), where as M increases, the maximum frequency of the multi-baffled vessel at \(\gamma =0\) changes only by a small amount, hence the difference \(s_r(\infty )-s_r(0)\) becomes almost constant, which in turn drives the maximum value of \(s_i\). The significant conclusion of the result in Fig. 10 is that placing more equally spaced, porous baffles into a system initially increases the decay rate, but only up to about \(M=9\) baffles in this example, after which the increased decay rate return is minimal. However, what is notable is that the range of \(\gamma \) values over which there is significant decay is greatly increased. This means that rapid decay can be achieved in a system with baffles with larger \(\gamma \) (which might be easier and cheaper to manufacture) rather than having to acquire baffles with small \(\gamma \), which might be more expensive to manufacture.

4 Conclusions

In this paper we studied the coupled vessel plus contained fluid, motion for rectilinear vessel motions and two-dimensional fluid motions, in the presence of porous, surface piercing baffles. The fluid was assumed to be inviscid, incompressible and irrotational, such that it can be written in terms of a velocity potential in each connected region. By linking each region together via a porous wall transmission condition given by Darcy’s law, and seeking normal mode solutions about a quiescent state, we derived an explicit characteristic equation in the single baffle case. The characteristic equation correctly reduced to the two compartment impermeable baffle case of [7] and the single compartment case of [35] in the limits \(|\gamma |\rightarrow 0\) and \(|\gamma |\rightarrow \infty \) respectively, where \(\gamma \) is the non-dimensional baffle porosity parameter.

The presented results for both finite-depth and shallow-water fluids showed that the modes which couple to the vessel motion (i.e. not symmetric free-modes in a stationary vessel) decay exponentially in time, i.e. they have a complex non-dimensional frequency \(s=s_r+\textrm{i}s_i\) with \(s_i\ge 0\). There was no obvious connection between the mode’s decay rate, \(s_i\), and its frequency, \(s_r\), but the maximum decay rate for each mode occurred in a region of \(\gamma \) values where \(s_r\) sharply varied from its \(|\gamma |=0\) value to its \(|\gamma |=\infty \) value. The lowest frequency mode typically had the smallest maximum decay rate (except in the special vessel configurations with neutral modes), and hence this mode is expected to be most significant in real systems which contain a superposition of these modes, at moderate times.

For a vessel configuration with M equally spaced identical baffles we were able to show that the maximum decay rate for the lowest frequency mode increased as M was increased towards some limiting value for large M. It was also found that the range of baffle porosity values \(\gamma \) over which the decay rate was, say, \(\ge \frac{3}{4}s_i^\textrm{max}\) increased with M. This means that in a physical system in order to achieve rapid damping, a large number of baffles should be installed. This could however, be expensive, and so a smaller number of baffles could be used if the wall porosity is tuned such that the mode frequency generated by some external mechanism lies close to a value where the lowest frequency mode decays fastest.

Future work of potential interest is to incorporate baffles which have a time dependent porosity, such as a wall with movable slats. If the time-scale of the wall porosity change is faster than the period of the fluid oscillations, then modes could be manipulated to some maximal decay rate, meaning any induced oscillations could be quickly removed. This could be particularly significant in Tuned Liquid Dampers in highrise buildings [45]. This is considered in future work.