Numerical validation of analytical formulas for channel flows over liquid-infused surfaces

Abstract

This paper provides numerical validation of some new explicit, asymptotically exact, analytical formulas describing channel flows over liquid-infused surfaces, an important class of surfaces of current interest in surface engineering. The new asymptotic formulas, reproduced here, were derived in a recent companion paper by the authors. The numerical validation is done by presenting a novel computational method for calculating longitudinal flow in a periodic channel involving finite-length closed liquid-filled grooves with a flat two-fluid interface, a challenging problem given the two-fluid nature of the flow. The formulas are asymptotically exact for wide channels where the grooves on the lower wall of the channel are well separated; the numerical method devised here, however, is subject to no such restrictions. Significantly, it is shown here that the asymptotic formulas remain good global approximants for the flow over a wide range of flow geometries, including those well outside the asymptotic parameter range for which they were derived. It is found that the formulas are more reliable for liquid-infused surfaces than for superhydrophobic surfaces.

1 Introduction

In a recent paper [1] the authors used a three-stage asymptotic analysis to derive explicit analytical formulas describing, to leading order in the asymptotic approximations, the longitudinal channel flow over a liquid-infused surface (LIS). Such surfaces are the subject of much recent interest to the surface engineering community owing to their diverse uses in applications: a recent review [2] surveys many of these. In the scenario considered, the fluid is taken to flow along the direction of alignment of a series of parallel grooves etched into the lower wall of a channel. The upper wall of the channel is taken to be a no-slip surface. The flow is driven along the channel by an imposed pressure gradient. The grooves in the lower wall are much longer than they are wide, and they can be open or closed. Closed grooves, which might also be referred to as “trenches”, have upstream and downstream ends and the fluid in them experiences a reverse pressure gradient causing it to engage in a recirculating flow in the grooves [3]. Given the complexities of such a two-phase flow scenario, the possibility of finding any analytical formula describing it is unexpected. This renders the formula found in [1] of some theoretical significance and it is important to assess its usefulness. That is the purpose of this paper.

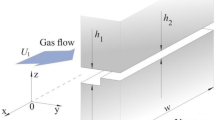
Figure 1 shows a typical two-fluid scenario as an $(x^*, y^*)$ cross-section at a typical $Z^*$ station in a Cartesian $(x^*, y^*, Z^*)$ coordinate system where the flow of both fluids is assumed to be in the “axial”, or streamwise, $Z^*$ direction. The main outcome of Rodriguez-Broadbent et al. [1] is now summarized. They show that, away from the upstream and downstream ends of well-separated circular grooves protruding by angle $\theta _2$ down into the lower channel wall, and where the interface protrudes by angle $\theta _1$ into the upper fluid, the coupled leading order axial velocity fields in the two-fluid phases are given by the explicit formulas

$$\begin{aligned} {\tilde{w}}^*_1(x^*,y^*) = \frac{\partial p_1^*}{\partial Z^*}\frac{H^2}{\mu _1}\tilde{w}_1\left( \frac{x^*}{H},\frac{y^*}{H}\right) ,{} & {} {\tilde{w}}^*_2(x^*,y^*) = \frac{\partial p_1^*}{\partial Z^*}\frac{H^2}{\mu _2} \tilde{w}_2\left( \frac{x^*}{H},\frac{y^*}{H}\right) , \end{aligned}$$

(1)

with

$$\begin{aligned} {\tilde{w}}_1(x,y)\sim&\, \frac{1}{2}y^2 + \frac{\delta \alpha }{2+\Delta \delta ^2\alpha \pi }\left( W_b\left( \frac{x}{\delta \alpha },\frac{y}{\delta \alpha }\right) + \delta \alpha \Delta \frac{y}{x^2+y^2} \right. \nonumber \\&+\left. \frac{\Delta \delta \pi }{2}\frac{\sinh (\pi y/\alpha )}{\cos (\pi x/\alpha )-\cosh (\pi y/\alpha )}\right) , \end{aligned}$$

(2)

$$\begin{aligned} \tilde{w}_2(x,y)\sim&\,\frac{\delta \alpha }{2+\Delta \delta ^2\alpha \pi }W_g\left( \frac{x}{\delta \alpha },\frac{y}{\delta \alpha }\right) , \end{aligned}$$

(3)

where $\alpha =L/H$, $\delta =a/L$, $\sigma =\mu _2/\mu _1$, and

(4)

Here denotes the principal part integral and explicit formulas for $\rho _b(k)$ and $\rho _g(k)$ are given in Appendix A. When a relevant capillary number is small [1] the interface protrusion angle $\theta _1$ will vary only slowly in the streamwise direction, i.e. $\theta _1=\theta _1(Z^*)$, and the formulas above give the leading order cross-plane flows at that $Z^*$ location.

Fig. 1

Cross-section of the boundary value problem relevant for channel flow over a liquid-infused surface as considered in [1] under a “slender groove” assumption. The fluid interface protrudes into fluid 1 by angle $\theta _1$ and the circular grooves protrude down into the solid substrate by angle $\theta _2$.

The formulas reported above are derived under the asymptotic assumptions that $\alpha =L/H\ll 1$ and $\delta = a/L \ll 1$. This means that the upper channel wall is not too close to the lower liquid-infused surface, and that the grooves etched on the lower wall are not too close together. The present paper carries out a numerical study to assess the scope and value of these formulas, the only restriction being that the interface is flat, i.e. $\theta _1=0$ (this requirement is necessitated by the nature of the numerical method devised here). All other geometrical features of the flow, such as $\alpha , \delta$, and $\theta _2$ are, however, variable which means that the numerical method can test the accuracy of results given by the asymptotic formulas as these parameters are varied. Remarkably, it is found here that the formulas provide excellent approximations for the flows over liquid-infused surfaces even well outside their expected range of validity, that is, when $\alpha$ and $\delta$ are not necessarily small. While this is only tested here for $\theta _1=0$ we conjecture it remains true for other values of $\theta _1$ that are sufficiently small.

While many previous authors have studied similar problems using a range of methods, the authors are not aware of any previous analytical results that have been derived without making heuristic assumptions. Such assumptions are often made to simplify the challenging coupled two-fluid problem. Schönecker et al. [4, 5] make the assumption that the interfacial shear stress is constant and offer strategies for approximating this constant value. Nizkaya et al. [6] use a so-called gas cushion model to study unbounded flow over periodic arrays of fluid-filled grooves with flat interfaces. Crowdy [7] studied rectangular fluid-filled grooves, with flat and weakly curved interfaces, using perturbation methods relevant for small and large viscosity contrasts but without making any heuristic assumptions.

There are many numerical studies of this two-fluid scenario. Ng et al. [8] used Fourier series in a numerical study of channel flow over closed grooves filled with a second fluid. They study both longitudinal and transverse flow scenarios for arbitrary viscosity contrast but only for flat interfaces. Moreover for the longitudinal flow they do not incorporate any longitudinal (axial) variation. Ge et al. [9] used finite element methods to resolve transverse flows over LISs incorporating interface curvature and the situation where the interface invades the grooves. Their interest is in studying the phenomenon of shear-induced failure whereby the subphase fluid can be dragged out of the grooves. Liu et al. [10] have investigated shear-driven failure for longitudinal channel flows over liquid-infused surfaces by making certain heuristic assumptions regarding the interface conditions. They consider the longitudinal evolution of the two-phase interface in order to characterize the failure mechanism and build on an earlier theoretical study by Wexler et al. [3]. Game et al. [11] used domain decomposition techniques to study longitudinal flow along unidirectional surfaces where the dynamical effects of a subphase fluid are also resolved but where they assume there is no axial variation of the geometry. Later, Game et al. [12] carried out an asymptotic expansion relevant at small capillary numbers to describe the slow axial evolution of the protrusion angle of the menisci in a model of longitudinal flow over a superhydrophobic surface but now ignoring the effects of the subphase fluid; the formulas in [1] extend this approach to the case of two fluids interacting across an interface. Ji et al. [13] use dual series and reciprocity relations to solve for two-phase flow with flat interfaces with a focus on quantifying the slip properties of these surfaces.

In this paper, the aim is to validate the analytical result given by [1] by presenting a new method for calculating longitudinal flows in a periodic channel involving closed liquid-filled grooves whose interfaces are flat. The method uses tools already employed in a study of superhydrophobic surfaces [14] but several features are different. In particular, while use is made of a conformal mapping from a triply connected preimage region described in Miyoshi et al. [14], the problems considered here involve two fluids, and their coupling across an interface is required. This is achieved here by making use of new mathematical tools known as “generalized Schwarz integrals” as constructed recently by Miyoshi and Crowdy [15]. A second conformal mapping from a simply connected disc to the groove region is also used to weld the flows together at the interface.

The structure of this paper is as follows. Section 2 explains the problem formulation and defines boundary value problem associated with the two-fluid setting. Section 3 introduces a complex analysis formulation and the relevant conformal mappings on which the method is based. The main findings are presented in Sect. 4 which gives numerical comparisons with the analytical predictions of formulas (2). Although it is not the primary aim of this work, Sect. 5 shows numerical results for velocity profiles on the interface and calculates useful quantities such as the effective slip lengths associated with the flows. Section 6 explains how the method is easily adaptable to account for other groove shapes and includes some illustrative calculations for triangular and rectangular grooves. Finally, Sect. 7 discusses the results and describes the future work.

Fig. 2

Periodic channel flow involving a liquid-infused surface on the lower wall and a no-slip upper wall. The grooves are filled (or “infused”) with a fluid that is generally of different viscosity to the upper working fluid. A single period window of a typical domain in the cross-plane with a flat interface $\theta _1=0$ is also shown

2 Problem setting

The geometry of the channel is shown in Fig. 2. Let $D_{1}^*$ denote the region in a single period window containing a “working fluid” with viscosity $\mu _1$, with $D_{2}^*$ denoting the groove region containing a fluid with viscosity $\mu _2$ and separated from fluid 1 by an interface. The lower wall of the channel outside a 2L-periodic arrangement of grooves is at $y^*=0$ and the upper no-slip wall of the channel above this surface is at $y^*=H$. The grooves are taken to have a circular profile protruding downwards into the surface with angle $\theta _2$. The width of each interface in the $x^*$ direction is 2a, $0<a<L$. For this study, the interfaces between the two fluids in the cross-sectional plane are taken to be flat, i.e. $\theta _1=0$: this is in order that the following conformal mapping formulation can be used. It should be noted, however, that in a real flow situation the interface will not remain flat for all $Z^*$: the present study should therefore be thought of as resolving the flow at a particular value of $Z^*$ in a geometry that changes with $Z^*$. The origin of the cross-sectional $(x^*,y^*)$ plane is at the centre of the interface in a principal period window. Steady flow of fluid 1 in the $Z^*$-direction along the channel is driven by an imposed constant pressure gradient. For closed grooves, this typically induces a counter, or “back”, pressure gradient in the groove-based fluid 2.

Fluid 1 satisfies the two-dimensional Stokes’ equations

$$\begin{aligned} \mu _1\nabla ^{*2} w^*_1(x^*,y^*) = \frac{\partial p_1^*}{\partial Z^*}, \quad (x^*,y^*)\in D_{1}^*, \end{aligned}$$

(5)

where $\nabla ^{*2}$ is a two-dimensional Laplacian $\partial _{x^*x^*}+\partial _{y^*y^*}$ with the condition $\partial w^*_1/\partial x^* = 0$ on $x^*=\pm L$ (resulting from the periodicity and symmetry) and a no-slip condition on the walls,

$$\begin{aligned}&{w}_1^*(x^*,H) = 0,~~ -L\le x^* \le L, \end{aligned}$$

(6)

$$\begin{aligned}&{w}_1^*(x^*,0) = 0,~~ a \le |x^*|\le L. \end{aligned}$$

(7)

When the grooves are closed an induced pressure gradient implies that fluid 2 also satisfies Stokes’ equations now in the form

$$\begin{aligned} \mu _2 \nabla ^{*2} w^*_2(x^*,y^*) = -{\mathcal {R}}\frac{\partial p_1^*}{\partial Z^*}, \quad (x^*,y^*)\in D_{2}^*,\quad {\mathcal {R}}>0. \end{aligned}$$

(8)

Fluid 2 satisfies a no-slip condition on the bottom wall of the groove. Fluid 1 and 2 interact across the interface. The interfacial conditions are continuity of the velocity and of viscous stress:

$$\begin{aligned} \left\{ \begin{aligned}&w^*_1 = w^*_2,\\&\mu _1 \frac{\partial w^*_1}{\partial y^*} = \mu _2 \frac{\partial w^*_2}{\partial y^*}, \end{aligned} \right. \end{aligned}$$

(9)

on $|x^*|<a$, $y^*=0$. The net volume flux across the groove cross-section must be zero due to mass conservation at steady state:

$$\begin{aligned} \int _{D_{2}^*}w_2^*(x^*,y^*) \textrm{d}x^*\textrm{d}y^* = 0. \end{aligned}$$

(10)

It is this latter condition that picks out the induced pressure gradient in the groove, i.e. it determines the parameter ${\mathcal {R}}$.

To non-dimensionalize the problem consider

$$\begin{aligned} (x^*,y^*) = H(x,y), \qquad w^*_n = \frac{\partial p_1^*}{\partial Z^*}\frac{H^2}{\mu _n} w_n,\quad n=1,2. \end{aligned}$$

(11)

The governing equations (5) and (8) reduce to

$$\begin{aligned} \nabla ^2 w_1 = 1,\quad (x,y)\in D_1, \end{aligned}$$

(12)

and

$$\begin{aligned} \nabla ^2 w_2(x,y) = - {\mathcal {R}},\quad (x,y) \in D_2, \end{aligned}$$

(13)

where $\nabla ^2$ denotes a two-dimensional Laplacian $\partial _{xx} + \partial _{yy}$ and the boundary conditions on the interface (9) become

$$\begin{aligned} \left\{ \begin{aligned}&\sigma w_1 = w_2,\\&\frac{\partial w_1}{\partial y} = \frac{\partial w_2}{\partial y}, \end{aligned} \right. \end{aligned}$$

(14)

on $-\delta \alpha \le x\le \delta \alpha$, $y=0$. Now $\lbrace D_j \mid j=1,2\rbrace$ denotes the non-dimensional counterparts to $\lbrace D_j^* \mid j=1,2\rbrace$. Let $C_-$ denote the no-slip lower circular-arc wall of the groove. The geometry is shown on the left of Fig. 3. Because of the periodicity and symmetries of the flow,

$$\begin{aligned} \frac{\partial w_1}{\partial x}(\pm \alpha ,y) = 0,\quad 0\le y \le 1. \end{aligned}$$

(15)

Also, from (6) and (7), $w_1(x,y)$ and $w_2(x,y)$ satisfy the no-slip conditions:

$$\begin{aligned}&w_1(x,1) = 0,\quad -\alpha \le x \le \alpha , \end{aligned}$$

(16)

$$\begin{aligned}&w_1(x,0) = 0,\quad \delta \alpha \le |x|\le \alpha , \end{aligned}$$

(17)

and $w_2(x,y)$ also satisfies

$$\begin{aligned} w_2(x,y) = 0,\quad (x,y) \in C_-. \end{aligned}$$

(18)

The velocities $w_1(x,y)$ and $w_2(x,y)$ can be split additively into basic Poiseuille profiles ${w}_{P,1}(x,y)$ and ${w}_{P,2}(x,y)$ and additional flows, ${\hat{w}}_1$ and ${\hat{w}}_2$, that are harmonic in regions $D_1$ and $D_2$, respectively:

$$\begin{aligned} \begin{aligned} w_1(x,y)&= w_{P,1}(x,y) + {\hat{w}}_1(x,y),\quad w_{P,1}(x,y)\equiv \frac{y(y-1)}{2}, \\ w_2(x,y)&= {\mathcal {R}} w_{P,2}(x,y) + {\hat{w}}_2(x,y), \end{aligned} \end{aligned}$$

(19)

where

$$\begin{aligned} w_{P,2}(x,y) \equiv \frac{1}{4}\left\{ \frac{\delta ^2\alpha ^2}{\sin ^2\theta _2} - x^2 - \left( y-\frac{\delta \alpha }{\tan \theta _2}\right) ^2 \right\} . \end{aligned}$$

(20)

Conditions (14) on the interface then become

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\sigma {\hat{w}}_1(x,0) = \frac{{\mathcal {R}}}{4}\left( \delta ^2\alpha ^2 - x^2\right) + {\hat{w}}_2(x,0), \quad \quad \quad (21{\textrm{a}})\\ &{}-\frac{1}{2} + \frac{\partial {\hat{w}}_1}{\partial y}(x,0) = \frac{{\mathcal {R}}\delta \alpha }{2 \tan \theta _2} + \frac{\partial {\hat{w}}_2}{\partial y}(x,0), \quad \quad \quad \quad (21{\textrm{b}}) \end{array}\right. \end{aligned}$$

for $-\delta \alpha \le x \le \delta \alpha$. Neither ${\hat{w}}_1(x,y)$ nor ${\hat{w}}_2(x,y)$ are known but, since they are harmonic, they can be obtained using complex analysis techniques and conformal mapping as will now be shown.

Fig. 3

Non-dimensional problem for the flow over a circular groove. The function ${\mathcal {Z}}(\zeta )$ is a conformal map from an upper half-disc outside of the inner circle $C_1$ to the period window. The function ${\mathcal {F}}(z)$ maps from $D_2$ to the upper half-disc

3 Complex analysis formulation

Consider the analytic functions (or “complex potentials”) $h_1(z)\equiv \chi _1+\textrm{i}{\hat{w}}_1$ and $h_2(z)\equiv \chi _2+\textrm{i}{\hat{w}}_2$, where $\chi _1$ and $\chi _2$ are the harmonic conjugates of ${\hat{w}}_1$ and ${\hat{w}}_2$, respectively. Use of the Cauchy–Riemann equations changes condition (21b) to

$$\begin{aligned} -\frac{1}{2} + \frac{\partial \chi _1}{\partial x}(x,0) = \frac{{\mathcal {R}}\delta \alpha }{2\tan \theta _2} + \frac{\partial \chi _2}{\partial x}(x,0). \end{aligned}$$

(22)

On integrating both sides of (22) from $-\delta \alpha$ to a general point x,

$$\begin{aligned} - \frac{1}{2}(x + \delta \alpha )+\chi _1(x,0) = \frac{{\mathcal {R}}\delta \alpha }{2 \tan \theta _2}(x+\delta \alpha ) + \chi _2(x,0), \end{aligned}$$

(23)

where the choice $\chi _1(-\delta \alpha ,0) =\chi _2(-\delta \alpha ,0)=0$ can be made without loss of generality. The two-fluid boundary conditions (21a) and (21b) are reduced to the following mixed interfacial conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\textrm{Im}[h_1(z)] = \frac{{\mathcal {R}}}{4\sigma }\left( \delta ^2\alpha ^2 - (\textrm{Re}[z])^2\right) + \frac{1}{\sigma }\textrm{Im}[h_2(z)], \quad \quad \quad \quad (24{\textrm{a}}) \\ &{}\textrm{Re}[h_1(z)] = \left( \frac{{\mathcal {R}}\delta \alpha }{2\tan \theta _2} + \frac{1}{2}\right) (\textrm{Re}[z]+\delta \alpha ) + \textrm{Re}[h_2(z)]. \quad \quad \quad (24{\textrm{b}}) \end{array}\right. \end{aligned}$$

The two unknown analytic functions $h_1(z)$ or $h_2(z)$ will be determined as functions of a convenient parametric variable $\zeta$ associated with a conformal mapping. Let $D_\zeta$ be a circular domain in a complex $\zeta$-plane interior to the unit circle denoted as $C_0$ but exterior to two inner circles $C_1$ and $C_2$. The radii of the circles are both q and the centres are $\zeta =d$, $\zeta =-d$, where d is purely imaginary. The circular domain $D_\zeta$ is illustrated in the upper right figure of Fig. 3. Now consider the following conformal map ${\mathcal {Z}}(\zeta )$ from $D_\zeta$ to the channel region $D_1$:

$$\begin{aligned} z = {\mathcal {Z}}(\zeta ) = \frac{\alpha }{\pi \textrm{i}}\log \frac{\omega (\zeta ,\Theta _1(\infty ))}{\omega (\zeta ,\Theta _2(\infty ))}, \end{aligned}$$

(25)

where

$$\begin{aligned} \Theta _1(\zeta ) \equiv d + \frac{q^2 \zeta }{1-\overline{d}\zeta },\qquad \Theta _2(\zeta ) \equiv -d +\frac{q^2 \zeta }{1+\overline{d}\zeta } = \overline{\Theta _1}(\zeta ). \end{aligned}$$

(26)

The overbar denotes the Schwarz conjugate of an analytic function, which is defined by $\overline{\Theta }_1(\zeta ) \equiv \overline{\Theta _1(\overline{\zeta })}$. The function $\omega (\cdot ,\cdot )$ is the so-called prime function that is naturally associated with the triply connected domain $D_\zeta$. The prime function $\omega (\zeta ,\gamma )$ has several important properties, the most important for present purposes is that it is analytic in $D_\zeta$ and has a simple zero when $\zeta =\gamma$: interested readers can refer to [16] for further background. The function ${\mathcal {Z}}(\zeta )$ maps the upper half-circle $C_0^+$ of the $\zeta$-plane to the portion $\{(x,y) \mid x \in [-\delta \alpha ,\delta \alpha ],\ y=0\}$, the negative real axis of the $\zeta$-plane to the portion $\{(x,y) \mid x \in [\delta \alpha ,\alpha ],\ y=0\}$, and the positive real axis of the $\zeta$-plane to the portion $\{(x,y)\mid x \in [-\alpha ,-\delta \alpha ],\ y=0\}$.

It is important to note that the same map (25) has been used to analyse flow in a periodic channel over superhydrophobic surfaces and with invaded grooves [14].

The objective now is to calculate $H_1(\zeta )\equiv h_1({\mathcal {Z}}(\zeta ))$ and $H_2(\zeta )\equiv h_2({\mathcal {Z}}(\zeta ))$. Because $\textrm{Im}[H_1(\zeta )]=0$ on the real axis of the $\zeta$-plane, i.e. $\overline{\zeta }=\zeta$, then

$$\begin{aligned} \overline{H_1(\zeta )} = \overline{H_1}(\zeta ) = H_1(\zeta ). \end{aligned}$$

(27)

By the Schwarz reflection principle, $H_1(\zeta )$ can be analytically continued to the lower half-unit disc exterior to circle $C_2$ defined by $D_\zeta ^-$.

The boundary condition (24a) is then reduced to

$$\begin{aligned} \textrm{Im}[H_1(\zeta )]=\left\{ \begin{aligned}&\frac{{\mathcal {R}}}{4\sigma }(\delta ^2\alpha ^2 - \textrm{Re}[{\mathcal {Z}}(\zeta )]^2) + \frac{1}{\sigma } \textrm{Im}[h_2({\mathcal {Z}}(\zeta ))] \qquad \textrm{on} \ C_0^+,\\&-\frac{{\mathcal {R}}}{4\sigma }(\delta ^2\alpha ^2 - \textrm{Re}[{\mathcal {Z}}(\zeta )]^2) - \frac{1}{\sigma }\textrm{Im}[h_2({\mathcal {Z}}(\zeta ))] \qquad \textrm{on} \ C_0^-,\\&0 \qquad \textrm{on} \ C_1,\ C_2. \end{aligned} \right. \end{aligned}$$

(28)

At first sight, this resembles a classical Schwarz problem for the analytic function $H_1(\zeta )$ in the domain $D_\zeta$. But the crucial point to note is that $h_2(z)$ is not known so the right-hand side does not constitute a given set of data for the imaginary part of $H_1(\zeta )$ on the boundary of $D_\zeta$.

One way to proceed is to assume that the imaginary part of $h_2(z)$ on $C_0^\pm$ is known. Then an integral form of the solution for $H_1(\zeta )$ is given by the following Schwarz integral formula [16, 17]:

$$\begin{aligned} H_1(\zeta )&= \frac{1}{2\pi }\int _{C_0}\textrm{Im}[H_1(\zeta ')][\textrm{d}\log \omega (\zeta ',\zeta ) + \textrm{d}\log \overline{\omega }(\overline{\zeta '},1/\zeta )] + c_1 {\mathcal {Z}}(\zeta ) + c_2, \end{aligned}$$

(29)

where $c_1,c_2\in {\mathbb {R}}$ and where the term ${\mathcal {Z}}(\zeta )$ has been added to account for the expected multi-valuedness of the real part of $H_1(\zeta )$ around $C_1$ and $C_2$. See [15] for more details.

Next, by using (27), condition (24b) is also reduced to the following (different) boundary value problem on $D_\zeta$:

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{Re}[H_1(\zeta )] = f(\zeta ),\quad \zeta \in C_0, \\&\textrm{Im}[H_1(\zeta )] = 0,\qquad \zeta \in \ C_1,\ C_2, \end{aligned} \right. \end{aligned}$$

(30)

where

$$\begin{aligned} f(\zeta ) \equiv \left( \frac{{\mathcal {R}}\delta \alpha }{2 \tan \theta _2} + \frac{1}{2}\right) (\textrm{Re}[{\mathcal {Z}}(\zeta )] +\delta \alpha ) + \textrm{Re}[h_2({\mathcal {Z}}(\zeta ))]. \end{aligned}$$

(31)

Assuming once again that the real part of $h_2(z)$ is known, this (now mixed) boundary value problem (30) can be solved uniquely by a so-called “generalized Schwarz integral” proposed recently in Miyoshi and Crowdy [15]:

$$\begin{aligned} H_1(\zeta ) = \frac{1}{\eta (\zeta )}\left( I(\zeta ) + \frac{{\hat{C}}}{\zeta -\gamma } + \textrm{i}{\hat{c}}_2 \right) + {\hat{c}}_1 {\mathcal {Z}}(\zeta ), \ {\hat{c}}_1,{\hat{c}}_2\in {\mathbb {R}}, \end{aligned}$$

(32)

where ${\hat{C}}\in {\mathbb {C}}$ and $I(\zeta )$ satisfies the more familiar Schwarz-type boundary value problem

$$\begin{aligned} \textrm{Re}[I(\zeta )] = \left\{ \begin{aligned}&\eta (\zeta ) f(\zeta )-\textrm{Re}\left[ \frac{{\hat{C}}}{\zeta -\gamma }\right] \quad \textrm{on} \ C_0,\\&-\textrm{Re}\left[ \frac{{\hat{C}}}{\zeta -\gamma }\right] \quad \zeta \in C_1, \ C_2, \end{aligned} \right. \end{aligned}$$

(33)

where

$$\begin{aligned} I(\zeta ) \equiv \eta (\zeta )H_1(\zeta ) - \frac{{\hat{C}}}{\zeta -\gamma }. \end{aligned}$$

(34)

The parameter $\gamma$ is a simple pole of the function $\eta (\zeta )$ which is a radial-slit map [16] defined by

$$\begin{aligned} \eta (\zeta ) \equiv c_\eta \frac{\omega (\zeta ,\beta )\omega (\zeta ,1/\overline{\beta })}{\omega (\zeta ,\gamma )\omega (\zeta ,1/\overline{\gamma })},\quad \beta ,\gamma \in D_\zeta . \end{aligned}$$

(35)

This mapping clearly also has a simple zero at $\beta$. The parameters $c_\eta$, $\beta$, and $\gamma$ should be chosen so that $\eta (\zeta )$ satisfies

$$\begin{aligned} \textrm{arg}[\eta (\zeta )] = \left\{ \begin{aligned}&0\ \textrm{or}\ \pi \qquad \textrm{on} \ C_0,\\&\pm \frac{\pi }{2} \qquad \textrm{on} \ C_1,\\&\pm \frac{\pi }{2} \qquad \textrm{on} \ C_2. \end{aligned} \right. \end{aligned}$$

(36)

The two integral expressions for $H_1(\zeta )$ in (29) and (32) must be consistent. This requires making the correct choice of $h_2(z)$ or, equivalently, by solving for the flow in the groove. The idea of the numerical construction is to obtain $h_2(z)$ by evaluating (29) and (32) at some collocation points $\{ \zeta _m \mid m= 1,2,\ldots ,{\mathcal {M}} \}$ on the interface and ensuring that they are self-consistent. The technique for solving this is explained in detail in Appendix B. It makes use of another conformal mapping between a simply connected preimage region to the groove region.

After calculating the flow on the interfaces, it is possible to calculate the slip length of the channel. The (dimensional) slip length $\lambda ^*$ is given by the integral of ${\hat{w}}_1$ on the interface as follows:

$$\begin{aligned} \lambda ^* = -\frac{H^2 \int _{-\delta \alpha }^{\delta \alpha } {\hat{w}}_1(x,0) \, \textrm{d}x}{L + H\int _{-\delta \alpha }^{\delta \alpha } {\hat{w}}_1(x,0) \, \textrm{d}x}. \end{aligned}$$

(37)

The derivation of the slip length is explained in detail in Appendix D.

4 Testing the accuracy of the analytical formulas derived in [1]

The formulas (2) are derived in [1] under the assumption that $\delta \rightarrow 0$ and $\alpha \rightarrow 0$ and they are valid for any angles $\theta _1$ and $\theta _2$ shown in Fig. 1. The numerical method just described has no such restriction on $\delta$ and $\alpha$ but is only valid for $\theta _1=0$. In this special case, the general formulas (2) become simpler. Using the notation $\tilde{\lambda }^*$ to denote the slip length formula emerging from the analytical solutions in [1], and $\tilde{{\mathcal {R}}}$ to denote the back-pressure in the groove, it can be shown that

$$\begin{aligned}&{\tilde{\lambda }}^*= \frac{\pi \alpha \delta ^2 H}{2}\Delta =\frac{\pi a^2}{2L}\Delta , \end{aligned}$$

(38)

$$\begin{aligned}&\tilde{{\mathcal {R}}} = \frac{{\mathcal {S}}}{\delta \alpha (2+\pi \alpha \delta ^2 \Delta )} , \end{aligned}$$

(39)

where $\Delta$ and ${\mathcal {S}}$ are given by

(40)

and, from the formulas given in Appendix A,

$$\begin{aligned}&\rho _{b,s}(k) \equiv -\frac{2\pi \textrm{i}e^{\pi k}}{\sinh \pi k }\cdot \frac{\sinh \theta _2 k}{{\mathcal {D}}(k) }, \end{aligned}$$

(41)

$$\begin{aligned}&\rho _{b,p}(k) \equiv \frac{\pi \textrm{i}e^{\pi k}}{\sinh \pi k }\cdot \frac{\cot \theta _2 \sinh \theta _2 k - k\cosh \theta _2 k }{{\mathcal {D}}(k)}, \end{aligned}$$

(42)

and

$$\begin{aligned} {\mathcal {S}} \equiv \frac{{\mathcal {Q}}_1}{{\mathcal {Q}}_0 + {\mathcal {Q}}_2}, \end{aligned}$$

(43)

where

(44)

(45)

(46)

with

$$\begin{aligned}&\rho _{g,s}(k) = \frac{2\pi \textrm{i}\sigma e^{-\theta _2 k} }{{\mathcal {D}}(k) }, \end{aligned}$$

(47)

$$\begin{aligned}&\rho _{g,p}(k) = \frac{\pi \textrm{i}e^{-\theta _2 k}}{\sinh \pi k}\frac{-k\cosh \pi k + e^{k\theta _2} \cot \theta _2 \sinh \theta _2 k (\cosh \pi k + \sigma \sinh \pi k)}{{\mathcal {D}}(k)}, \end{aligned}$$

(48)

where ${\mathcal {D}}(k)\equiv \sinh \theta _2 k \cosh \pi k + \sigma \sinh \pi k \cosh \theta _2 k$. The aim of this section is to test how good these formulas for ${\tilde{\lambda }}^*$ and $\tilde{{\mathcal {R}}}$ are at estimating the numerically computed values $\lambda ^*$ and ${{\mathcal {R}}}$.

Fig. 4

Relative errors of ${\tilde{\lambda }}^*$ and $\tilde{{\mathcal {R}}}$ compared with the full numerical solution for $\theta _2=\pi /2$ and varying values of $\sigma$ plotted for a range of values of $\delta$ and $1/\alpha$. The white region shows the relative error is less than $1\%$. The top left-hand corner of these plots are white since this is where good agreement is expected. The red region shows the relative error is more than $10\%$. For $\sigma$ values shown, the asymptotics work well when $\alpha \le 2$ and $0.1\le \delta \le 0.5$. The maximum relative errors of $\tilde{\lambda }^*$ and $\tilde{{\mathcal {R}}}$ for the case (i) are about $21\%$ and $41\%$, respectively

Fig. 5

Relative error in the local dimensional velocities given by the analytical predictions (2) compared with the full numerical solution for $\theta _2=\pi /2$ and $\sigma =0.2$ as $\alpha$ and $\delta$ are varied. It is confirmed that the relative error in a whole period window is less than 10$\%$ when $\alpha <1.0$ and $\delta <0.5$

In order to compare the results given by the analytical expressions (38) and (39) with the results of the numerical simulation, we first set $\theta _2=\pi /2$; this corresponds to semi-circular grooves. Figure 4 shows the relative errors of ${\tilde{\lambda }}^*$ and $\tilde{{\mathcal {R}}}$ compared with the full numerical solution for a range of values of $\delta$ and $\alpha$ (in fact, the parameter $1/\alpha$ is used) and for several values of $\sigma$. The white regions signify that the relative error is less than $1\%$. As expected, the approximations (38) and (39) are found to agree well with the numerical solution when $\delta$ and $\alpha$ are small, with larger values of $\sigma$ found to give better accuracy over a larger range. Physically, this means that the approximations work better as the viscosity contrast $\sigma$ increases.

Figure 5 gives a relative error of the local velocities predicted by the analytical formulas (2) for $\theta _2=\pi /2$ and $\sigma =0.2$. This error is defined by

$$\begin{aligned} w_j^\textrm{error}(x^*,y^*) = \frac{|{w}_j^*(x^*,y^*) - {\tilde{w}_j}^*(x^*,y^*)|}{w^*_{\textrm{av}}}, \qquad j=1,2, \end{aligned}$$

(49)

where

$$\begin{aligned} w^*_{\textrm{av}} \equiv \frac{1}{\textrm{Area}_{D^*_1}+\textrm{Area}_{D^*_2}}\left[ \int _{D_1^*} |w_1^*(x^*,y^*)|\textrm{d}x^*\textrm{d}y^* + \int _{D_2^*} |w_2^*(x^*,y^*) |\textrm{d}x^*\textrm{d}y^*\right] . \end{aligned}$$

(50)

This choice of average velocity in the denominator is made because the local velocity can vanish. As expected, agreement is found to be excellent when $\alpha$ and $\delta$ are small.

Fig. 6

Comparison of the normalized slip length $\lambda ^*/2L$ with the asymptotic formula for $\tilde{\lambda }^*/2L$ defined by (38) for different viscosity contrast $\sigma$. (i) $\theta _2=\pi /2$, and (ii) $\theta _2=\pi /3$. Accuracy is good across all $\sigma$ values but deteriorates when $\sigma$ is small

Figure 6 shows a comparison of the computed normalized slip length $\lambda ^*/2L$ with the result of the asymptotic formula for $\tilde{\lambda }^*/2L$ defined by (38) for different $\sigma$ and $\delta$ and for $1/\alpha =0.3, 0.5$, and 0.8. It shows that accuracy is good across all $\sigma$ values but deteriorates when $\sigma$ is small.

In summary, the evidence suggests that the analytical formulas (2) provide good approximants of the flows over liquid-infused surfaces in a wide range of channel geometries when $\theta _1=0$. While this has only been tested here for the case $\theta _1=0$, it is reasonable to conjecture that the formulas will continue to give good approximations for other choices of $\theta _1$, especially if they are sufficiently small.

5 Characterization of the solutions

Since the numerical method can be used, in principle, for any circular channel geometry with different $\alpha$, $\delta$, and $\sigma$ with $\theta _1=0$ it is now used to compute the flows, slip lengths, and back-pressures for a range of liquid-infused surfaces. In the following calculations the choices $L=1$ and $\dfrac{1}{\mu _1}\dfrac{\partial p^*_1}{\partial Z^*} =1$ are made.

Figures 7 and 8 show typical velocity contour plots of $w^*_1(x^*,y^*)$ and $w^*_2(x^*,y^*)$. Figure 7 features contours for $\delta =0.4$, $\alpha =1.25$, $L=1$, and $\theta _2=\pi /2$ and several values of $\sigma$. When $\sigma$ is large, the interface behaves like a “wall” because the fluid 2 is very viscous compared to fluid 1. In the upper-left panel of Fig. 7 the flow in fluid 1 is close to a Poiseuille flow in a channel; the deviation from this gets more noticeable as $\sigma$ decreases. In Fig. 8 the values of $\delta$, $\alpha$, and L are fixed to be 0.5, 2, and 1 and the viscosity contrast is fixed to be $\sigma =0.2$ while the groove shape is varied; this means several values of $\theta _2$ are taken. The colour scheme in these figures highlights the recirculating nature of the flow in the grooves with red and blue zones travelling in opposite directions.

Fig. 7

Dimensional velocity contour plots of $w^*_1(x^*,y^*)$ and $w^*_2(x^*,y^*)$ with different viscosity contrasts $\sigma$. The geometrical parameters $\delta =0.4$, $\alpha =1.25$, and $L=1$ are used in all figures. We have set $1/\mu _1\cdot \partial p^*_1/\partial Z^* = 1$

Fig. 8

Dimensional velocity contour plots of $w^*_1(x^*,y^*)$ and $w^*_2(x^*,y^*)$ for different angles $\theta _2$ and $\sigma =0.2$. The geometry parameters of the channel are fixed i.e. $\delta = 0.5$, $L=1$, and $\alpha =2$, while (i) $\theta _2=\pi /3$, (ii) $\theta _2=2\pi /5$, (iii) $\theta _2=2\pi /3$, and (iv) $\theta _2=4\pi /5$. We have set $1/\mu _1\cdot \partial p^*_1/\partial Z^* = 1$

Fig. 9

The velocity profile on the interface for (i) $\alpha =2$ and (ii) $\alpha =1.25$ when $\delta =0.25$, $\delta =0.5$, and $\delta =0.8$. We have set $L=1$. The angle $\theta _2$ is fixed to $\pi /2$. Note that the solution for $\sigma =0$ corresponds to the analytical solution for the bounded channel given by Philip [18]

Fig. 10

Normalized slip length with respect to $1/\alpha$ for different $\delta$. When $1/\alpha$ becomes large and $\sigma =0$, the normalized slip length converges to Philip’s result for semi-infinite shear flow over the surface (black dotted line)

Fig. 11

Slip length with respect to $\delta$ for fixed $\theta _2=\pi /2$ and different channel heights: (i) $\alpha =3.3333$, (ii) $\alpha =2$, (iii) $\alpha =1.25$. Black circles show results from Philip’s (1972) solution. When $\sigma =0$ the calculated slip length matches Philip’s slip length for the case of semi-infinite shear flow over the surface

When $\sigma \rightarrow 0$, the two-phase condition (14) for the dimensional velocity fields $w_1^*$ and $w_2^*$ implies that

$$\begin{aligned} \frac{\partial w_1^*}{\partial y^*} = \sigma \frac{\partial w_2^*}{\partial y^*}\rightarrow 0 \end{aligned}$$

(51)

which corresponds to a no-shear condition on fluid 1. This situation, modelling a superhydrophobic surface, was studied by Philip [18]; Crowdy found the analogous analytical solutions for flows in annular pipes [19]. Figure 9 shows some typical interfacial velocity profiles for $\text {(i)} \ \alpha =2$ and $\text {(ii)}\ \alpha =1.25$ and different viscosity contrasts $\sigma$ and for $\delta =0.25$, $\delta =0.5$, and $\delta = 0.8$. As expected the interface velocity increases as $\sigma \rightarrow 0$ since one expects a reduction in the hydrodynamic drag as $\sigma$ decreases. Moreover, the velocity as $\sigma \rightarrow 0$ agrees with that calculated by Philip [18] providing a corroboration of the accuracy of the numerical scheme.

From Philip’s analytical solutions [18] the corresponding slip lengths can be readily extracted. Figures 10 and 11 show the numerically computed slip length for a range of geometrical parameters, and confirms that they converge to Philip’s results as $\sigma \rightarrow 0$.

Fig. 12

(i), (ii), and (iii): Dimensional flows $w_1^*(x^*,y^*)$ and $w_2^*(x^*,y^*)$ over different groove shapes for $L=1$, $\alpha =1.25$, $\delta = 0.4$, $\sigma =0.2$, and $1/\mu _1\cdot \partial p^*_1/\partial Z^* = 1$. The areas of these grooves are chosen to be the same in each case. (Right-bottom) The interface velocities are also shown for a range of $\sigma$ values. It is seen, both from the flow contours and the closely similar interface velocity profiles, that precise details of the groove shape has only weak influence on the motion of the working fluid

6 Other groove shapes

The grooves in a liquid-infused surface need not be circular. The advantage of the method presented here is that it can be easily adapted to any groove geometry (although still with $\theta _1=0$). This is done by simply changing the form of an aforementioned conformal mapping to the groove region. For polygonal grooves, for example, instead of $\xi = {\mathcal {F}}(z)$ as specified in equation (B2), conformal maps from polygonal domains to semi-circular discs can be used; these are examples of Schwarz–Christoffel mappings. For simple shapes, these mappings are easy to find analytically. For more complicated shapes, a useful numerical package for finding such maps given by [20] can be used.

Figure 12 shows the velocity contour plots of (i) a circular groove, (ii) a rectangle groove, and (iii) a triangle groove. For the polygonal-shaped regions, a basis of 30 Fourier series coefficients were used. The area of all these grooves is taken to be identical. In this case, it is observed that the velocity on the interface is similar in all cases. The results indicate the important result that the shape of the grooves does not much affect the slip length of the flow. This has practical implications for the broad applicability of the analytical formulas of [1] whose accuracy was tested earlier: it means that they can provide good flow approximants even for non-circular grooves if one replaces the given groove geometry by an “equivalent circular groove” of the same width and area.

7 Discussion

This paper develops a new methodology for solving a two-fluid boundary value problem relevant to modelling pressure-driven channel flow over liquid-infused surfaces. This is done, following previous work by Miyoshi et al. [14], by considering conformal maps to the channel region from suitable triply connected circular domains. On changing the two-fluid boundary value problem to a mixed boundary value problem on those triply connected domains, the resulting problems can be solved by using “generalized Schwarz integrals” as devised recently in [15]. The slip lengths calculated here match those calculated by Philip when $\alpha \rightarrow 0$ providing a reassuring corroborative check on the formulation. As discussed in more detail in Miyoshi et al. [14], a significant advantage of using this preimage triply connected domain is that it “uniformizes” some of the singularities at points on the boundary where the conditions change type meaning that it naturally accounts for the singularities at such points. Other methods often require remeshing at such boundary point singularities.

A key finding is that the slip lengths and induced back-pressure found using the numerical scheme match well to those predicted by asymptotically exact analytical formulas found recently in [1], even well outside the formal range of validity of the derivation of those asymptotic formulas. This suggests those formulas provide useful theoretical tools giving good approximations to channel flows over liquid-infused surfaces over a broad range of operating conditions. This is particularly significant in view of the rarity of finding analytical descriptions of two-fluid flows. One important use of the formulas is that an ordinary differential equation approximating the evolution of $\theta _1(Z^*)$ can now be written down explicitly; such formulas help predict a phenomenon known as “shear-induced failure” of LISs [3]. Work in this direction is in progress.

Of course, the numerical method can be used with great accuracy for many flow configurations and is valuable in its own right. It has been used here to carry out a quantitative study of the slip properties of LISs in a range of configurations.

Appendices

Appendix A: Functions of k appearing in (4)

The functions of k appearing in formula (4) are

$$\begin{aligned} \rho _b(k)=\rho _{b,s}(k)-{\mathcal {S}}\rho _{b,p}(k), \rho _g(k)=\rho _{g,s}(k)-{\mathcal {S}}\rho _{g,p}(k), \end{aligned}$$

(A1)

where

$$\begin{aligned} \rho _{b,s}(k)=\,&\frac{2\pi \textrm{i}e^{k\pi }}{{\mathcal {D}}(k)\sinh \pi k}\left( {\sigma \cosh (\theta _1+\theta _2)k\sinh \theta _1k-\sinh (\theta _1+\theta _2)k\cosh \theta _1k}\right) , \end{aligned}$$

(A2)

$$\begin{aligned} \rho _{g,s}(k)=\,&\frac{2\pi \textrm{i}\sigma e^{-k\theta _2}}{{\mathcal {D}}(k)}, \end{aligned}$$

(A3)

$$\begin{aligned} \rho _{b,p}(k)=\,&\frac{\pi \textrm{i}e^{k\pi }}{{\mathcal {D}}(k)\sinh \pi k}\Bigg ((\cot \theta _1+\cot \theta _2)\sinh \theta _2k \end{aligned}$$

(A4)

$$\begin{aligned}&\qquad \qquad -\frac{\textrm{cosec}^2\theta _1}{k}\sinh \theta _1k\sinh (\theta _1+\theta _2)k\Bigg ), \end{aligned}$$

(A5)

$$\begin{aligned} \rho _{g,p}(k)=\,&\frac{\pi \textrm{i}e^{-k\theta _2}}{{\mathcal {D}}(k)\sinh \pi k}\bigg (-\cot \theta _1(\sinh \theta _1k\cosh (\pi -\theta _1)k \nonumber \\&+\sigma \cosh \theta _1k\sinh (\pi -\theta _1)k)\nonumber \\&+e^{k(\theta _1+\theta _2)}\cot \theta _2\sinh \theta _2k(\cosh (\pi -\theta _1)k+\sigma \sinh (\pi -\theta _1)k)\nonumber \\&+\sigma \frac{\textrm{cosec}^2\theta _1}{k}\sinh \theta _1k\sinh (\pi -\theta _1)k\bigg ),\nonumber \\ {\mathcal {S}}=\,&\frac{{\mathcal {Q}}_2(\theta _1,\theta _2,\sigma )}{{\mathcal {Q}}_0(\theta _1,\theta _2,\sigma )+{\mathcal {Q}}_1(\theta _1,\theta _2,\sigma )}, \end{aligned}$$

(A6)

and

$$\begin{aligned} {\mathcal {D}}(k) =&\, \sinh (\theta _1+\theta _2)k\cosh (\pi -\theta _1)k+\sigma \sinh (\pi -\theta _1)k\cosh (\theta _1+\theta _2)k, \end{aligned}$$

(A7)

with

(A8)

(A9)

(A10)

Note that these functions depend on the two angles $\theta _1$ and $\theta _2$. However, they will only be tested here in the case $\theta _1=0$.

Appendix B: Fourier series expression for the flow on the interface

For a suitable truncation parameter N, the following expansion of ${\hat{w}}_2(x,0)$ on $-\delta \alpha<x<\delta \alpha$ is defined:

$$\begin{aligned} {\hat{w}}_2(x,0) = \sum _{n=1}^{N} a_n \cos \left( \frac{(2n-1)\pi x}{2\delta \alpha }\right) ,\quad a_n \in {\mathbb {R}}. \end{aligned}$$

(B1)

The coefficients of this expansion are to be found. This is a parameterization of the imaginary part of the harmonic function $h_2(z)$ on the interface but to solve the boundary value problem (30), the real part of $h_2(z)$ is also needed. However, $h_2(z)$ has other constraints on it, in particular, its imaginary part must be zero on the semi-circular no-slip lower wall of the groove. To account for this, it is useful to introduce the following conformal map of the groove region:

$$\begin{aligned} \xi = {\mathcal {F}}(z) = -\frac{(\delta \alpha /z-1)^{1/2\phi }-\textrm{i}(\delta \alpha /z+1)^{1/2\phi }}{(\delta \alpha /z-1)^{1/2\phi }+\textrm{i}(\delta \alpha /z+1)^{1/2\phi }}, \end{aligned}$$

(B2)

where $\theta _2=\pi \phi$. This maps the groove region to the upper unit semi-circular disc in a complex $\xi$-plane: the interval $x\in [-\delta \alpha ,\delta \alpha ]$ is mapped to the upper semi-circle, and the lower boundary of the groove is mapped to the real diameter. The inverse of ${\mathcal {F}}(z)$ is

$$\begin{aligned} z = {\mathcal {G}}(\xi ) = \delta \alpha \frac{[\textrm{i}(\xi +1)]^{2\phi }-(\xi -1)^{2\phi }}{[\textrm{i}(\xi +1)]^{2\phi }+(\xi -1)^{2\phi }}. \end{aligned}$$

(B3)

Now define $H_2(\xi )\equiv h_2({\mathcal {G}}(\xi ))$ and define $D_\xi ^+$ as the upper semi-disc, $D_\xi ^-$ as the lower semi-disc. Let the semi-circular boundaries of the latter regions be $C_\xi ^+$ and $C_\xi ^-$, respectively. Because of the no-slip boundary condition on the lower groove wall $H_2(\xi )$ satisfies $\textrm{Im}[H_2(\xi )]=0$ on $\overline{\xi }=\xi$. By the Schwarz reflection principle,

$$\begin{aligned} H_2(\xi ) = \overline{H_2(\overline{\xi })},\quad \xi \in D_\xi ^-. \end{aligned}$$

(B4)

Considering (B1), the boundary condition for $H_2(\xi )$ in the $\xi$-plane is

$$\begin{aligned} \textrm{Im}[H_2(\xi )] \equiv \sum _{n=1}^{N} a_n r_n(\xi ), \quad r_n(\xi )\equiv \left\{ \begin{aligned}&+\cos \left( \frac{(2n-1)\pi {\mathcal {G}}(\xi )}{2\delta \alpha }\right) ,\quad \xi \in C_\xi ^+,\\&-\cos \left( \frac{(2n-1)\pi \overline{{\mathcal {G}}(\overline{\xi })}}{2\delta \alpha }\right) ,\quad \xi \in C_\xi ^-. \end{aligned}\right. \end{aligned}$$

(B5)

This boundary value problem can be solved by the Poisson integral formula for the unit disc:

$$\begin{aligned} H_2(\xi ) = a_{0,P} + \sum _{n=1}^{N}a_n P_n(\xi ),\quad P_n(\xi ) \equiv \frac{1}{2\pi }\oint _{C_\xi }\frac{\xi '+\xi }{\xi '-\xi }\frac{r_n(\xi ')}{\xi '}\textrm{d}\xi ', \end{aligned}$$

(B6)

where $C_\xi = C_\xi ^+\cup C_\xi ^-$ and $a_{0,P}\in {\mathbb {R}}$ is a constant which can be determined by the condition $\chi _2(-\delta \alpha )=\textrm{Re}[H_2(-1)]=0$.

This parameterization of $h_2(z)$ allows the formulation of a linear system for the coefficients $\lbrace a_n \rbrace$. First, the zero-flux condition (10) of $w_2(x,y)$ is written in terms of $a_n$ as follows:

$$\begin{aligned} \int _{D_2}w_2(x,y) \mathrm{{d}}x \, \mathrm{{d}}y&= {\mathcal {R}}\int _{D_2}w_{P,2}(x,y)\textrm{d}x \, \textrm{d}y + \sum _{n=1}^N a_n \int _{D_2}\textrm{Im}[P_n({\mathcal {F}}(z))]\textrm{d}x \, \textrm{d}y \nonumber \\&=s_0{\mathcal {R}} + \sum _{n=1}^{N} a_n s_n =0, \end{aligned}$$

(B7)

where

$$\begin{aligned} s_0 \equiv \int _{D_2}w_{P,2}(x,y)\textrm{d}x \, \textrm{d}y,\quad s_n \equiv \int _{D_2} \textrm{Im}[P_n({\mathcal {F}}(z))]\textrm{d}x \, \textrm{d}y. \end{aligned}$$

(B8)

The use of the reciprocal theorem again reduces $s_n$ to the simple form

$$\begin{aligned} s_0 = \frac{\delta ^4\alpha ^4}{8\sin ^2 \pi \phi }\left( \frac{\pi \phi }{\sin ^2 \pi \phi }-\frac{1}{\tan \pi \phi } \right) -\frac{\delta ^4\alpha ^4}{12\tan \pi \phi }, \end{aligned}$$

(B9)

and

$$\begin{aligned} s_{n} = \frac{1}{2}\int _{-\delta \alpha }^{\delta \alpha } x \textrm{Re}[P_n({\mathcal {F}}(z))]\textrm{d}x + \frac{2\delta ^2\alpha ^2(-1)^{n}}{(2n-1)\pi \tan \pi \phi },\quad n=1,\ldots ,N. \end{aligned}$$

(B10)

Appendix E gives a derivation. Thus ${\mathcal {R}}$ can be represented in terms of the coefficients $\lbrace a_n \rbrace$ as

$$\begin{aligned} {\mathcal {R}}= -\frac{1}{s_0}\sum _{n=1}^N a_n s_n. \end{aligned}$$

(B11)

Substituting this relation into (28) and (30), the data for each problem are now in terms of the coefficients $\lbrace a_n \rbrace$:

$$\begin{aligned} \textrm{Im}[H_1(\zeta )]=\left\{ \begin{aligned}&+\sum _{n=1}^N \frac{a_n}{\sigma } \left[ -\frac{s_n}{4s_0}(\delta ^2\alpha ^2 - \textrm{Re}[{\mathcal {Z}}(\zeta )]^2) + \textrm{Im}[P_n({\mathcal {F}}({\mathcal {Z}}(\zeta )))]\right] ,\quad \zeta \in C_0^+\\&-\sum _{n=1}^N \frac{a_n}{\sigma } \left[ -\frac{s_n}{4s_0}(\delta ^2\alpha ^2 - \textrm{Re}[{\mathcal {Z}}(\zeta )]^2) + \textrm{Im}[P_n({\mathcal {F}}({\mathcal {Z}}(\zeta )))]\right] ,\quad \zeta \in C_0^- \\&0 \qquad \textrm{on} \ C_1,\ C_2, \end{aligned} \right. \end{aligned}$$

(B12)

and

$$\begin{aligned} \left\{ \begin{aligned} \textrm{Re}[H_1(\zeta )]&= \sum _{n=1}^N a_n\left[ -\frac{s_n \delta \alpha }{2 s_0 \tan \pi \phi } (\textrm{Re}[{\mathcal {Z}}(\zeta )] +\delta \alpha )+\textrm{Re}[P_n({\mathcal {F}}({\mathcal {Z}}(\zeta )))]\right] \\&+ \frac{1}{2}(\textrm{Re}[{\mathcal {Z}}(\zeta )] +\delta \alpha ),\quad \zeta \in C_0, \\ \textrm{Im}[H_1(\zeta )]&= 0,\qquad \zeta \in \ C_1,\ C_2. \end{aligned} \right. \end{aligned}$$

(B13)

In order to derive the linear system for the coefficients $\lbrace a_n \rbrace$, it is convenient to define functions which satisfy the following boundary conditions:

$$\begin{aligned} \textrm{Im}[V_n(\zeta )]=\left\{ \begin{aligned}&-\frac{s_n}{4 s_0\sigma }(\delta ^2\alpha ^2 - \textrm{Re}[{\mathcal {Z}}(\zeta )]^2) + \frac{1}{\sigma }\textrm{Im}[P_n({\mathcal {F}}({\mathcal {Z}}(\zeta )))],\quad \zeta \in C_0^+,\\&+\frac{s_n}{4 s_0\sigma }(\delta ^2\alpha ^2 - \textrm{Re}[{\mathcal {Z}}(\zeta )]^2) - \frac{1}{\sigma }\textrm{Im}[P_n({\mathcal {F}}({\mathcal {Z}}(\zeta )))],\quad \zeta \in C_0^-, \\&0 \qquad \textrm{on} \ C_1,\ C_2, \end{aligned} \right. \end{aligned}$$

(B14)

$$\begin{aligned} \left\{ \begin{aligned} \textrm{Re}[T_n(\zeta )]&= -\frac{s_n\delta \alpha }{2 s_0 \tan \pi \phi } (\textrm{Re}[{\mathcal {Z}}(\zeta )] +\delta \alpha )+\textrm{Re}[P_n({\mathcal {F}}({\mathcal {Z}}(\zeta )))],\quad \zeta \in C_0,\\ \textrm{Im}[T_n(\zeta )]&= 0,\qquad \zeta \in \ C_1,\ C_2, \end{aligned} \right. \end{aligned}$$

(B15)

and

$$\begin{aligned} \left\{ \begin{aligned} \textrm{Re}[R(\zeta )]&= \frac{1}{2}(\textrm{Re}[{\mathcal {Z}}(\zeta )] + \delta \alpha ),\quad \zeta \in C_0,\\ \textrm{Im}[R(\zeta )]&= 0,\qquad \zeta \in \ C_1,\ C_2. \end{aligned} \right. \end{aligned}$$

(B16)

An over-determined linear system for the coefficients ${\underline{\varvec{a}}}=(a_1,a_2,\cdots ,a_{N})^\top$ now follows as

$$\begin{aligned} M_1 \underline{\varvec{a}} = M_2 \underline{\varvec{a}} + \underline{\varvec{r}}, \end{aligned}$$

(B17)

where

$$\begin{aligned} M_1 = \begin{pmatrix} V_1(\zeta _1) &{} V_2(\zeta _1) &{} \cdots &{} V_N(\zeta _1)\\ V_1(\zeta _2) &{} V_2(\zeta _2) &{} \ddots &{} V_N(\zeta _2)\\ \vdots &{} \ddots &{} \ddots &{} \vdots \\ V_1(\zeta _{\mathcal {M}}) &{} V_2(\zeta _{\mathcal {M}}) &{} \cdots &{} V_N(\zeta _{\mathcal {M}}) \end{pmatrix}, \end{aligned}$$

(B18)

and

$$\begin{aligned} M_2 = \begin{pmatrix} T_1(\zeta _1) &{} T_2(\zeta _1) &{} \cdots &{} T_N(\zeta _1)\\ T_1(\zeta _2) &{} T_2(\zeta _2) &{} \ddots &{} T_N(\zeta _2)\\ \vdots &{} \ddots &{} \ddots &{} \vdots \\ T_1(\zeta _{\mathcal {M}}) &{} T_2(\zeta _{\mathcal {M}}) &{} \cdots &{} T_N(\zeta _{\mathcal {M}}) \end{pmatrix}, \end{aligned}$$

(B19)

and $\underline{\varvec{r}}\equiv (R(\zeta _1),R(\zeta _2),\cdots ,R(\zeta _{\mathcal {M}}))^\top$ and where the collocation points are defined as $\lbrace \zeta _m \mid m=1,\ldots , {\mathcal {M}} \rbrace$ where ${\mathcal {M}}>N$. This system can be solved by the method of least-squares.

Once the components of these matrices are calculated, they can be used to calculate for the flow for a different viscosity contrast $\sigma$ in the same geometry. When the viscosity contrast $\sigma$ is changed to ${\hat{\sigma }}$, say, the matrices satisfy the linear transformations:

$$\begin{aligned} M_1 \rightarrow \frac{\sigma }{{\hat{\sigma }}} M_1,\quad M_{2} \rightarrow M_{2},\quad \underline{\varvec{r}}\rightarrow \underline{\varvec{r}}. \end{aligned}$$

(B20)

This reduces computational time since it is not necessary to reconstruct new matrices when $\sigma$ is changed.

Appendix C: Numerical calculation of the flow

Analytical formulas have been derived for the solution in terms of the prime function $\omega (.,.)$ associated with the triply connected domain $D_\zeta$. To calculate the flow, plot the velocity contours, and calculate effective slip lengths it is clearly necessary to be able to evaluate the prime function $\omega (.,.)$ and there are (at least) two ways to do this.

The most numerically efficient method is to make use of freely available MATLAB codes that compute $\omega (.,.)$ for any user-specified circular domain akin to $D_\zeta$ [16, 21]. These codes are based on a numerical algorithm described in detail in [22] and which extends an earlier algorithm proposed by Crowdy and Marshall [23].

For a triply connected domain, however, it is also known (see Chap. 14 of [16]) that the infinite product representation

$$\begin{aligned} \omega (z,\zeta ) = (z-\zeta )\prod _{\Theta \in \Theta ''}\frac{(\Theta (z)-\zeta )(\Theta (\zeta )-z)}{(\Theta (z)-z)(\Theta (\zeta )-\zeta )}, \end{aligned}$$

(C1)

is convergent; here each function $\Theta$ lies in the set of Möbius maps $\Theta ''$ which denotes all elements of the free Schottky group generated by the basic Möbius maps $\lbrace \Theta _j, \Theta _j^{-1}: j=1,2 \rbrace$ except for the identity and excluding all inverses [16, 22, 23]. For numerical purposes of evaluation it is necessary to truncate this product, and the natural way to do so is to include all Möbius maps up to a chosen level: see [16, 23] for more details. Use of this infinite product is feasible for most channel geometries, but maintaining a required degree of accuracy requires truncation at increasingly high levels as the radii of $C_1$ and $C_2$ get larger; then convergence of the product can become unacceptably slow. In such cases, use of the MATLAB code from [21] is preferred and advised.

The parameters d and q are determined uniquely, for a given channel geometry, by solving the two equations

$$\begin{aligned} {\mathcal {Z}}(-1) = \delta \alpha , \qquad {\mathcal {Z}}(d+q\textrm{i})= \textrm{i} \end{aligned}$$

(C2)

subject to the constraints $|d|+q<1$, $|d|>0$, and $q>0$. Equations (C2) are readily solved using any nonlinear solver such as Newton’s method.

Equally spaced collocation points on the interface are chosen in all numerical calculations. To be more precise, the collocation points $\zeta _m\in C_0$ are chosen so that

$$\begin{aligned} {\mathcal {Z}}(\zeta _m) = \delta \alpha \left( -1+\frac{m-1}{M-1}\right) ,\qquad m=1,\ldots , M. \end{aligned}$$

(C3)

The coordinates of $\zeta _m$ are obtained easily by the standard interpolation methods. Both the number of coefficients $a_n$ and the collocation points are set to be 100.

When $\delta$ is greater than 0.5, the inner circles $C_1$ and $C_2$ approach the unit circle. In this case, the appropriate radial-slit map is difficult to find, and even if it is found, the condition number of the radial-slit map defined by

$$\begin{aligned} {\textrm{cond}}\equiv \underset{m=0,1,2}{\hbox {max}} \bigg (\underset{{\zeta _{1}},{\zeta _{2}}\in {C_{m}}}{\hbox {max}} \bigg | \frac{\eta ({\zeta _{1}})}{\eta ({\zeta _{2}})} \bigg | \bigg ) \end{aligned}$$

(C4)

increases. In that case it is recommended that $\eta (\zeta )$ should be replaced by a product of radial-slit maps defined by

$$\begin{aligned} \eta (\zeta ) = {\hat{c}}_\eta \prod _{k=1}^K \frac{\omega (\zeta ,\beta _k)\omega (\zeta ,1/\overline{\beta _k})}{\omega (\zeta ,\gamma _k)\omega (\zeta ,1/\overline{\gamma _k})}, \quad K>1, \end{aligned}$$

(C5)

since the additional degrees of freedom lead to a reduction in the condition number and a more robust algorithm.

When the protrusion angle $\theta _2 \ge \pi /2$, it is recommended to use a Laurent series expansion in $\xi$ of the Poisson integral (B6) to reduce computation time. When $\theta _2<\pi /2$, it was observed that the number of coefficients in this Laurent series needed to retain accuracy becomes large and, in that case, the original Poisson integral (B6) is preferable.

To validate the accuracy of our numerical computation, the dimensional velocity $w_1^*(x^*,0)$ on the interface is compared with the velocity calculated by the asymptotics $\tilde{w}_1^*(x^*,0)$. Table 1 shows these values for $x^*=0,\ 0.025$, and 0.05, and the relative errors when $\delta =0.05$, $\alpha =1$, and $\sigma =0.3$. In this geometry, it is natural to consider that the flow in the period window should be approximated well by the asymptotics. Table 1 suggests that our numerical computation might be accurate for 7 digits when 100 Fourier coefficients are used. For the calculation of the Schwarz integral, 1500 equally spaced points are used.

We have also compared the flow for $\sigma =0$ against Philip’s solution for a bounded channel [18] when $\delta =0.8$, $\alpha =1.25$, and $L=1$. Table 2 shows the dimensional velocity when $x^*=0.2$ and 0.3, and the relative errors. Our numerical scheme also produces approximately $5.0\times 10^{-5}$ errors when 100 Fourier coefficients are used.

Table 1 Dimensional velocity $w_1^*(x^*,0)$ and $\tilde{w}_1^*(x^*,0)$ on the interface when $\delta =0.05$, $\alpha =1$, and $L=1$ when $\sigma = 0.3$. Both the number of coefficients for the Fourier expansions of ${\hat{w}}_2(x,0)$ and the collocation points are set to be 100. For the calculation of the Schwarz integral, 1500 equally spaced points are used

Table 2 Dimensional velocity $w_1^*(x^*,0)$ on the interface when $\delta =0.8$, $\alpha =1.25$, and $L=1$ when $\sigma = 0$. The results are compared against Philip’s solution for a bounded channel [18]. Both the number of coefficients for the Fourier expansions of ${\hat{w}}_2(x,0)$ and the collocation points are set to be 100. For the calculation of the Schwarz integral, 1500 equally spaced points are used

Appendix D: Calculation of the slip lengths

Once $w_1(x,y)$ has been determined, the effective slip lengths associated with the flow can be calculated. To do so, the approach proposed by Crowdy [7] is adapted where reciprocity arguments are used to determine the volume flux in the period window. The total flux $Q_F$ in the original period window $D_1^*$ is given by

$$\begin{aligned} Q_F&\equiv \int _{D_1^*} w_1^*(x^*,y^*)\textrm{d}x^*\textrm{d}y^*= \frac{\partial p_1^*}{\partial Z^*}\frac{H^4}{\mu _1} \int _{D_1}w_1(x,y)\textrm{d}x\textrm{d}y \nonumber \\&= \frac{\partial p_1^*}{\partial Z^*}\frac{H^4}{\mu _1}\int _{D_1}(w_{P,1}+{\hat{w}}_1)\textrm{d}x\textrm{d}y= \frac{\partial p_1^*}{\partial Z^*}\frac{1}{\mu _1}\left( -\frac{1}{6}H^3 L + H^4\int _{D_1}{\hat{w}}_1 \textrm{d}x\textrm{d}y\right) , \end{aligned}$$

(D1)

the second term is evaluated using Green’s second identity. By reciprocity,

$$\begin{aligned} \int _{D_1}(w_{P,1}\nabla ^2 {\hat{w}}_1-{\hat{w}}_1\nabla ^2 w_{P,1})\textrm{d}x\textrm{d}y = \oint _{\partial D_1}\left( w_{P,1}\frac{\partial {\hat{w}}_1}{\partial \varvec{n}} - {\hat{w}}_1 \frac{\partial w_{P,1}}{\partial \varvec{n}} \right) \textrm{d}s, \end{aligned}$$

(D2)

where $\varvec{n}$ is the normal vector pointing out the channel region and s is an element of arc lengths of the boundary of $D_1$. The symmetry at $x=\pm \alpha$ and the properties of $w_{P,1}(x,y)$ reduce this relation to

$$\begin{aligned} -\int _{D_1}{\hat{w}}_1\textrm{d}x\textrm{d}y = -\frac{1}{2}\int _{-\delta \alpha }^{\delta \alpha } {\hat{w}}_1(x,0)\textrm{d}x, \end{aligned}$$

(D3)

and thus,

$$\begin{aligned} Q_F = \frac{\partial p_1^*}{\partial Z^*}\frac{1}{\mu _1}\left( -\frac{1}{6}H^3 L + \frac{H^4}{2}\int _{-\delta \alpha }^{\delta \alpha } {\hat{w}}_1(x,0) \textrm{d}x\right) . \end{aligned}$$

(D4)

This flux is to be compared with that associated with a “comparison flow”: that of the channel flow with a Navier-slip condition with Navier-slip parameter $\lambda ^*$ on a flat boundary taken at the level of the interface. The comparison flow field $w^*_\lambda (x^*,y^*)$ satisfies

$$\begin{aligned}&\mu _1 \nabla ^{*2} w^*_\lambda (x^*,y^*) = \frac{\partial p_1^*}{\partial Z^*},{} & {} \qquad (x^*,y^*)\in D^*_{1}, \end{aligned}$$

(D5)

$$\begin{aligned}&w^*_\lambda = \lambda ^* \frac{\partial w^*_\lambda }{\partial \varvec{n}},{} & {} \quad -L\le x^* \le L,\quad y^* = 0, \end{aligned}$$

(D6)

$$\begin{aligned}&w^*_\lambda = 0,{} & {} \quad -L\le x^* \le L,\quad y^* = H, \end{aligned}$$

(D7)

$$\begin{aligned}&\frac{\partial w^*_\lambda }{\partial x^*} = 0,{} & {} \quad x^* = \pm L, \end{aligned}$$

(D8)

where $\varvec{n}$ denotes the normal pointing into the liquid in this case. Here $\lambda$ is the effective slip length of the channel. This problem is solved explicitly by

$$\begin{aligned} w^*_\lambda = \frac{\partial p_1^*}{\partial Z^*}\frac{1}{\mu _1}\left[ \frac{y^*(y^*-H)}{2} + \frac{\lambda ^* H}{2(\lambda ^* + H)}(y^*-H)\right] . \end{aligned}$$

(D9)

The total flux produced by $w^*_\lambda$ is then calculated as follows:

$$\begin{aligned} Q_\lambda = \int _{D^*}w^*_\lambda (x^*,y^*) \textrm{d}x^*\textrm{d}y^* = \frac{\partial p_1^*}{\partial Z^*}\frac{1}{\mu _1}\left( -\frac{1}{6}H^3L - \frac{\lambda ^* H^3 L }{2(\lambda ^*+H)}\right) . \end{aligned}$$

(D10)

By equating $Q_F$ to $Q_\lambda$, the effective slip length can be written in terms of the integral of ${{\hat{w}}}_1(x,0)$ on the interface as follows:

$$\begin{aligned} \lambda ^* = -\frac{H^2 \int _{-\delta \alpha }^{\delta \alpha } {\hat{w}}_1(x,0)\textrm{d}x}{L + H\int _{-\delta \alpha }^{\delta \alpha } {\hat{w}}_1(x,0)\textrm{d}x}. \end{aligned}$$

(D11)

Appendix E: Reciprocity

This appendix explains how to derive (B9) and (B10). By Gauss’s divergence theorem,

$$\begin{aligned} \int _{D_2}(w_{P,2}\nabla ^2 w_{P,2} + \nabla w_{P,2}\cdot \nabla w_{P,2})\textrm{d}x \, \textrm{d}y = \int _{\partial D_2} w_{P,2}\frac{\partial w_{P,2}}{\partial \varvec{n}}\textrm{d}s. \end{aligned}$$

(E1)

The right-hand side becomes

$$\begin{aligned} \int _{\partial D_2} w_{P,2}\frac{\partial w_{P,2}}{\partial \varvec{n}}\textrm{d}s = \frac{\delta \alpha }{2\tan \pi \phi }\int _{-\delta \alpha }^{\delta \alpha } \frac{1}{4}(\delta ^2\alpha ^2 - x^2)\textrm{d}x = \frac{\delta ^4\alpha ^4}{6\tan \pi \phi }. \end{aligned}$$

(E2)

By direct calculation, it can be shown that

$$\begin{aligned} \int _{D_2} \nabla w_{P,2}\cdot \nabla w_{P,2} \textrm{d}x \, \textrm{d}y&= \frac{1}{4}\int _{D_2}\left\{ x^2+\left( y - \frac{\delta \alpha }{\tan \pi \phi }\right) ^2 \right\} \textrm{d}x \, \textrm{d}y \end{aligned}$$

(E3)

$$\begin{aligned}&=\frac{\delta ^2\alpha ^2}{4\sin ^2\pi \phi }\int _{D_2}\textrm{d}x \, \textrm{d}y -\int _{D_2}w_{P,2}\textrm{d}x \, \textrm{d}y \end{aligned}$$

(E4)

$$\begin{aligned}&=\frac{\delta ^4\alpha ^4}{4\sin ^2\pi \phi }\left( \frac{\pi \phi }{\sin ^2\pi \phi }-\frac{1}{\tan \pi \phi }\right) -\int _{D_2}w_{P,2}\textrm{d}x \, \textrm{d}y. \end{aligned}$$

(E5)

Since $\nabla ^2 w_{P,2} = -1$, Eq. (E1) becomes

$$\begin{aligned} -\int _{D_2}w_{P,2} \textrm{d}x \, \textrm{d}y +\frac{\delta ^4\alpha ^4}{4\sin ^2\pi \phi }\left( \frac{\pi \phi }{\sin ^2\pi \phi }-\frac{1}{\tan \pi \phi }\right) -\int _{D_2}w_{P,2}\textrm{d}x \, \textrm{d}y = \frac{\delta ^4\alpha ^4}{6\tan \pi \phi }. \end{aligned}$$

Expression (B9) then follows.

For $s_n$, it is convenient to define $P_n({\mathcal {F}}(z)) \equiv f_n (x,y) + \textrm{i}g_n (x,y)$. Consider

$$\begin{aligned} \int _{D_2} g_n(x,y)\textrm{d}x \, \textrm{d}y&= \int _{D_2}(w_{P,2}\nabla ^2 g_n - g_n\nabla ^2 w_{P,2})\textrm{d}x \, \textrm{d}y\nonumber \\&=\int _{\partial D_2}\left( w_{P,2}\frac{\partial g_{n}}{\partial \varvec{n}} - g_{n} \frac{\partial w_{P,2}}{\partial \varvec{n}}\right) \textrm{d}s\nonumber \\&=\frac{1}{4}\int _{-\delta \alpha }^{\delta \alpha } (\delta ^2\alpha ^2 - x^2)\frac{\partial f_n}{\partial x}(x,0)\textrm{d}x - \frac{\delta \alpha }{2\tan \pi \phi }\int _{-\delta \alpha }^{\delta \alpha } g_n(x,0)\textrm{d}x\nonumber \\&= \frac{1}{2}\int _{-\delta \alpha }^{\delta \alpha } x f_n(x,0) \textrm{d}x - \frac{\delta \alpha }{2\tan \pi \phi }\int _{-\delta \alpha }^{\delta \alpha } g_n(x,0)\textrm{d}x, \end{aligned}$$

(E6)

where the Cauchy–Riemann equations have been used in the third equality. Because $g_n(x,0) = \textrm{Im}[P_n({\mathcal {F}}(z))] = \cos ((2n-1)\pi x/2\delta \alpha )$, the second term of (E6) can be calculated leading to the equation for $s_n$.