Longitudinal flow in superhydrophobic channels with partially invaded grooves

Abstract

Analytical expressions are derived for the longitudinal flow in a superhydrophobic microchannel where flat menisci in the Cassie state have partially invaded the grooves between no-slip blades. Using these solutions, the effective slip lengths are computed and compared with recent analytical results for unbounded shear flow over the same class of surfaces. Expressions for the first-order corrections to these effective slip lengths when the menisci are weakly curved are also derived. A mathematical connection to superhydrophobic channel flows where the flat menisci are still pinned to the tops of the pillars is also made, resulting in novel analytical expressions for those solutions too.

1 Introduction

Superhydrophobic surfaces, or SHS, can dramatically reduce flow resistance in the manipulation of small volumes of fluid in microchannel devices [1, 2]. At small scales, surface tension allows interfaces or menisci to span the gaps between microstructural protrusions that prevent fluid from fully penetrating interstitial regions. This leads to trapped gas pockets and enhanced slip over the spanning menisci. This so-called Cassie state can prove difficult to maintain and requires careful pressure control in many situations to prevent reversion to a fully wetted, or Wenzel, state. The use of textured groove sidewalls with reentrant and doubly reentrant pillar designs has been proposed in recent work [3,4,5,6] as a means to improve the robustness of the Cassie state. In many of these configurations, the menisci have depinned from the tops of the pillars and have partially invaded the grooves between pillars.

The quantification of the slip properties of superhydrophobic surfaces has been an area of much recent activity. Philip [7] provides explicit solutions to several mixed boundary value problems relevant to the mixture of no-slip and no-shear surfaces, which provide a good model of flow over superhydrophobic surfaces. Philip’s solutions are relevant when flat interfaces are flush with interspersed flat no-slip surfaces, a feature shared with later studies [8]. Sbragaglia and Prosperetti [9] examined how weak meniscus curvature affects slip by solving the relevant mixed boundary value problems. Their study was reappraised and extended by Crowdy [10] who showed that their slip length corrections can be found instead using integral identities, or “reciprocal theorems,” together with Philip’s exact solutions for flat menisci. In practice, this meniscus curvature is caused by pressure differences between the trapped gas and the working fluid.

As discussed above, another circumstance that can often occur is the depinning of the menisci from the top of the grating [5, 11]. This could be due to pressure fluctuations or mass transfer out of the cavities, among other reasons (see [12, 13] for more details). This causes the menisci to descend into the grooves and partially wet the cavities, a scenario that has received much less attention in the theoretical literature. Lee et al. [2] have pointed out that meniscus depinning and cavity invasion are significantly more deleterious to slip than mere curving of the menisci without depinning [14]. Several authors have carried out numerical studies to quantify slip for partially filled cavities [15,16,17]. Crowdy [18, 19] has derived several analytical results that quantify the effective slip for semi-infinite shear over grooved surfaces when the menisci have partially invaded the cavities.

The purpose of the present paper is to extend the recent work of [19], which involves semi-infinite shear over a single superhydrophobic surface, to the case of a bounded channel flow between two superhydrophobic surfaces making up the “top” and “bottom” of the channel, where fluid flows longitudinally parallel to the grooves. Figure 1 shows a schematic.

Fig. 1

A bounded channel flow between two superhydrophobic surfaces making up the top and bottom of the channel where the menisci have invaded the grooves

A new theoretical method is presented for obtaining the velocity field and the effective slip length for the flow in such a superhydrophobic channel. The main result of this paper is to show that a parametric solution for the flow $(0,0,w_F(x,y))$ driven by a constant pressure gradient ${\mathcal {S}}$ over flat menisci that have partially invaded the grooves as shown in Fig. 1 is

$$\begin{aligned} \begin{aligned} w_F(x,y)&= {\mathcal {S}}\left\{ x\left( L - \frac{x}{2}\right) + \frac{L(H+{G})}{\pi ^2}\textrm{Im} \oint _{|\zeta '|=1} \frac{\omega (\zeta ',\theta _1(\infty ))}{\omega (\zeta ',\theta _2(\infty ))} \, d\log \omega (\zeta ',\zeta ) \right\} , \\ z&= x+ \textrm{i} y = {\mathcal {Z}}(\zeta ) = -\frac{H+{G}}{\pi }\log \frac{\omega (\zeta ,\theta _1(\infty ))}{\omega (\zeta ,\theta _2(\infty ))}, \end{aligned} \end{aligned}$$

(1)

where the variable $\zeta$ sits in an appropriate circular domain $D_\zeta$ shown in Fig. 3, and $\omega (.,.)$ is a readily computable special function, known as the prime function [20], naturally associated with $D_\zeta$. The function $z={{{\mathcal {Z}}}}(\zeta )$ is a conformal mapping that transplants $D_\zeta$ to a period window of the flow as indicated in Fig. 3. Formula (1) is almost explicit, but not quite: given the geometric parameters L, H, and G characterizing the surface geometry, two non-linear equations must be solved numerically for two parameters, denoted by $\delta$ and q shown in Fig. 3. These furnish the center and radius, respectively, of the circular boundaries of $D_\zeta$, and are needed to define two functions $\lbrace \theta _j(.) |j=1,2 \rbrace$, which are simple Möbius maps as given in (30). Having derived the above expression for the flow, its features and slip properties are easily calculated. As $G/L\rightarrow \infty$, the calculated normalized slip lengths agree well with explicit formulas for the slip lengths of a semi-infinite shear flow where the menisci between the walls have invaded the grooves [19].

The structure of the paper is as follows. Section 2 sets out the problem statement and shows how it can be reduced to finding a single harmonic function in a typical period window. Section 3 discusses how to define an effective slip length associated with the flow; such diagnostics are used by applied scientists to quantify the slipperiness of the surface [1, 2]. The main tools needed to construct the flow solution, namely a conformal mapping from a circular preimage domain in a parametric $\zeta$ plane and an associated special function called the prime function [20], are described in Sect. 4. Then, in Sect. 5, those tools are used to construct the solution reported in (1). With the solution at hand, Sect. 6 gives a characterization of the flows and a calculation of the associated effective slip lengths discussed in Sect. 3. In Sect. 7 it is shown that, given the flow solution over partially invaded grooves where the menisci are flat, integral expressions for the first-order corrections to the slip lengths for weakly curved menisci can be written down. Finally, an intriguing mathematical observation is made in Sect. 8, connecting the problem considered here to a similar longitudinal channel flow over a symmetric superhydrophobic surface where the menisci are still pinned at the tops of the pillars and the pillars have variable width. An analytical solution to the latter problem has been given by [21], and the observations of Sect. 8 make a connection between the analysis of this paper and that earlier work.

2 Channel flow with partially invaded menisci

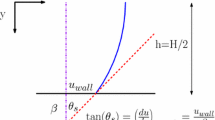
The challenge is to calculate the longitudinal flow $(0,0,w_F(x,y))$ in a typical period window of the superhydrophobic channel shown in Fig. 2. The origin in the cross-sectional (x, y) plane is taken at the intersection of the centerlines shown in Fig. 3. The period of the geometry in the x-direction is 2L, and the distance of displacement of the flat meniscus below to tips of the sidewalls is H. The height of the channel, or distance between the sidewall gratings, is 2G as shown in Figs. 3 and 9. We define $\Omega$ as the whole period window bounded by partially invaded grooves as shown in Figs. 3 and 4.

Fig. 2

(i) A superhydrophobic channel flow with flat menisci. (ii) A superhydrophobic channel flow with weakly curved menisci

Following the approach taken in [19, 21, 22], we assume that the fluid satisfies a no-slip condition on the walls and a no-shear condition on each meniscus. At first, it is assumed that the menisci are flat. Steady flow in the Z-direction along the channel is driven by a constant pressure gradient $\partial p/\partial Z$, where p is the pressure of the liquid. Let D denote the half-period window of the channel shown in Fig. 3. Then $w_F(x,y)$ satisfies the following boundary value problem:

$$\begin{aligned} \nabla ^2 w_F&= -{\mathcal {S}},{} & {} \qquad \ (x,y) \in D,\end{aligned}$$

(2)

$$\begin{aligned} \displaystyle \frac{\partial w_F}{\partial y}&= 0,{} & {} \qquad \ 0\le x\le L,\ y = \pm (H+{G}), \end{aligned}$$

(3)

$$\begin{aligned} \displaystyle \frac{\partial w_F}{\partial x}&= 0,{} & {} \qquad \ x=0,\ 0\le |y|\le {G}, \end{aligned}$$

(4)

$$\begin{aligned} \displaystyle \frac{\partial w_F}{\partial x}&= 0,{} & {} \qquad \ x=L,\ 0\le |y|\le H+{G}, \end{aligned}$$

(5)

$$\begin{aligned} w_F&= 0,{} & {} \qquad \ x=0,\ {G}\le |y|\le H+{G}. \end{aligned}$$

(6)

The boundary conditions (4) and (5) follow from the reflectional symmetry of the period window region.

Fig. 3

Conformal map from the upper-half unit disc with a circular hole to a half-period of the channel flow

It is convenient to define a new variable ${\hat{w}}(x,y)$ via

$$\begin{aligned} w_F = w_P + {\mathcal {S}}\hat{w},\qquad w_P(x,y) \equiv {\mathcal {S}}x\left( L - \frac{x}{2}\right) . \end{aligned}$$

(7)

The corresponding boundary value problem for $\hat{w}$ is then

$$\begin{aligned} \nabla ^2 \hat{w}&= 0,{} & {} \qquad \ (x,y) \in D,~\end{aligned}$$

(8)

$$\begin{aligned} \displaystyle \frac{\partial \hat{w}}{\partial y}&= 0,{} & {} \qquad \ 0\le x\le L,\ y = \pm (H+{G}),\end{aligned}$$

(9)

$$\begin{aligned} \displaystyle \frac{\partial \hat{w}}{\partial x}&= -L,{} & {} \qquad \ x=0,\ 0\le |y|\le {G}, \end{aligned}$$

(10)

$$\begin{aligned} \displaystyle \frac{\partial \hat{w}}{\partial x}&= 0,{} & {} \qquad \ x=L,\ 0\le |y|\le H+{G},\end{aligned}$$

(11)

$$\begin{aligned} \hat{w}&= 0,{} & {} \qquad \ x=0,\ {G}\le |y|\le H+{G}. \end{aligned}$$

(12)

Since $\hat{w}(x,y)$ is a harmonic function in D we aim to determine its analytic extension $h(z)\equiv \chi + \textrm{i}\hat{w}$, where $\chi$ is the harmonic conjugate of ${\hat{w}}$.

Use of the Cauchy–Riemann equations and (10) implies that

$$\begin{aligned} \frac{\partial \chi }{\partial y} = L, \qquad \textrm{or} \qquad \chi =Ly+c_1, \qquad \ x=0,\ 0\le |y|\le {G}. \end{aligned}$$

(13)

Similar arguments can be used to show that since $\partial \hat{w}/\partial x=0$ on $x=L,\ 0\le |y|\le H+{G}$ and since $\partial \hat{w}/\partial y=0$ on $0\le x\le L,\ y = \pm (H+{G})$, then

$$\begin{aligned} \chi = c_2, \qquad x=L,\ 0\le |y|\le H+{G}, \end{aligned}$$

(14)

and

$$\begin{aligned} \chi = c_\pm , \qquad 0\le x\le L,\ y = \pm (H+{G}), \end{aligned}$$

(15)

where $c_2,c_\pm \in {\mathbb {R}}$. Since $\chi$ is defined up to a constant, we set $c_2=0$ without loss of generality. The continuity of $\chi$ around the boundary of D then requires that $c_\pm =c_2=0$. An integral relation also reveals that $c_1=0$. To see this, consider the upper-left quadrant of $\Omega$, denoted by $D':=\{(x,y):x\in [0,L],y\in [0,H+{G}]\}$. Due to the symmetry of the flow about $y=0$, $\partial \hat{w}/\partial y=0$ on the lower boundary of $D'$, i.e., $\{(x,y):x\in [0,L],y=0\}$. Thus

$$\begin{aligned} 0=\int _{D'}\nabla ^2\hat{w} \, dA=\oint _{\partial D'}\frac{\partial \hat{w}}{\partial n} \, ds=\int _{{G}}^{H+{G}}\frac{\partial \hat{w}}{\partial x} \, dy-L{G}. \end{aligned}$$

(16)

Use of the Cauchy–Riemann equations gives

$$\begin{aligned} \begin{aligned} 0=-\int _{{G}}^{H+{G}}\frac{\partial \chi }{\partial y} \, dy-L{G}&=\chi ({G})-\chi (H+{G})-L{G} \\&=(L{G}+c_1) - c_2 -L{G}=c_1, \end{aligned} \end{aligned}$$

(17)

where we have used the fact that $c_2=0$. It follows from (13) that

$$\begin{aligned} \chi = L y, \qquad x=0, ~0 \le y \le G. \end{aligned}$$

(18)

3 Calculation of the slip lengths

The formula (1) for the velocity profile will be derived in Sects. 4 and 5. Once found, the effective slip lengths associated with the flow can readily be determined. We now discuss the calculation of these quantities.

We follow the approach expounded in [22] where reciprocity arguments are proposed to determine the volume flux associated with flows over superhydrophobic surfaces of this kind.

For

$$\begin{aligned} Q_F\equiv \int _{\Omega }w_F \, dA=\int _{\Omega }(w_P+{\mathcal {S}}\hat{w})\, dA=\frac{4}{3}{\mathcal {S}}(H+{G})L^3 + {\mathcal {S}}\int _{\Omega }\hat{w}\,dA, \end{aligned}$$

(19)

where the first term has been retrieved by elementary surface integration, and the second term will be evaluated using Green’s second identity. Noting that

$$\begin{aligned} \int _{\Omega }\left( w_P\nabla ^2\hat{w}-\hat{w}\nabla ^2w_P\right) dA=\oint _{\partial \Omega }\left( w_P\frac{\partial \hat{w}}{\partial n}-\hat{w}\frac{\partial w_P}{\partial n}\right) ds, \end{aligned}$$

(20)

the partial differential equations satisfied by, and symmetry in $y=0$, of $w_F$ and $w_P$ reduce this to

(21)

and thus

$$\begin{aligned} Q_F=\frac{4}{3}{\mathcal {S}}(H+{G})L^3+4{\mathcal {S}}L\int _0^{{G}}\hat{w}(0,y)\,\mathrm{{dy}}. \end{aligned}$$

(22)

Fig. 4

The definition of the effective slip length for a channel flow. The flow is compared to a Navier-slip flow with walls taken at the level of the invaded menisci

Next, we compare this flux with that of the Navier-slip problem. This is the standard procedure for calculating slip lengths in channels used in [21, 23]. The comparison flow that we have chosen imposes a Navier-slip condition on a flat boundary taken at the level of the menisci as shown in Fig. 4. We set the origin as the center of a period window. The flow field $w_{\lambda }(x,y)$ in the period window $\Omega _{\lambda }$ satisfies

$$\begin{aligned} \nabla ^2 w_{\lambda }&= -{\mathcal {S}},{} & {} \qquad \ (x,y) \in \Omega _{\lambda },\end{aligned}$$

(23)

$$\begin{aligned} w_{\lambda }&= \lambda \displaystyle \frac{\partial w_\lambda }{\partial n},{} & {} \qquad \ 0\le |x|\le L,\ y = \pm {(H+G)},\end{aligned}$$

(24)

$$\begin{aligned} \displaystyle \frac{\partial w_{\lambda }}{\partial x}&= 0,{} & {} \qquad \ x=\pm L,\ 0\le |y|\le {H+G}, \end{aligned}$$

(25)

where n denotes the normal pointing into the liquid in this case. Here, $\lambda$ is the slip length in question. This problem is solved by

$$\begin{aligned} w_{\lambda }(x,y)=w_{P,\lambda }(x,y)+\lambda {\mathcal {S}}(H+G),\qquad w_{P,\lambda }(x,y) \equiv \frac{{\mathcal {S}}}{2}[(H+G)^2-y^2] \end{aligned}$$

(26)

which gives the flux

$$\begin{aligned} Q_{\lambda }\equiv \int _{\Omega _{\lambda }}w_{\lambda }\,dA=\frac{4}{3}{\mathcal {S}} (H+G)^3L+4\lambda {\mathcal {S}}(H+G)^2L. \end{aligned}$$

(27)

Comparing (27) and (22) then yields

$$\begin{aligned} \lambda = \frac{L^2}{3(H+{G})}-\frac{H+{G}}{3} + \frac{1}{(H+{G})^2}\int _0^{{G}}\hat{w}(0,y)\,\mathrm{{dy}}. \end{aligned}$$

(28)

4 Conformal mapping and the prime function

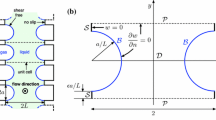
Let $D_\zeta$ be the circular domain in a parametric complex $\zeta$ plane interior to the unit circle, denoted by $C_0$, but exterior to two circles $C_1$ and $C_2$ each of radius q and having centers at $\pm \delta$, where $\delta$ is purely imaginary as shown in Fig. 3. It will be convenient later to denote by $C_0^+$ the semicircular portion of $C_0$ that is in the upper-half $\zeta$ plane, and by $C_0^-$ the semicircle in the lower-half $\zeta$ plane.

Now introduce the holomorphic conformal mapping function

$$\begin{aligned} {\mathcal {Z}}(\zeta ) = -\frac{H+{G}}{\pi }\log \left( \frac{\omega (\zeta ,\theta _1(\infty ))}{\omega (\zeta ,\theta _2(\infty ))} \right) , \end{aligned}$$

(29)

where

$$\begin{aligned} \theta _1(\zeta )\equiv \delta +\frac{q^2 \zeta }{1-\overline{\delta }\zeta },\qquad \theta _2(\zeta )\equiv -\delta +\frac{q^2 \zeta }{1+\overline{\delta }\zeta } = \overline{\theta _1}(\zeta ), \end{aligned}$$

(30)

and where overbars denote the Schwarz conjugate of an analytic function, which is defined by $\overline{\theta _1}(\zeta ) \equiv \overline{\theta _1(\overline{\zeta })}$. The function $\omega (\cdot ,\cdot )$ is the so-called (Schottky–Klein) prime function [20] on the triply connected domain $D_\zeta$. A detailed exposition of the diverse properties of the prime function associated with multiply connected domains has recently been given in [20]. The function (29) provides the one-to-one conformal map, $z={\mathcal {Z}}(\zeta )$, from the upper half of D. Figure 3 shows the correspondence between D and $D_\zeta$ schematically. The semicircle $C_0^+$ in the $\zeta$-plane is mapped to the line $|y|\le {G}$ on the imaginary axis in the z-plane, and the inner circle $C_1$ is mapped to middle line $x=L,\ |y|\le H+{G}$ of the periodic channel.

Because $D_\zeta$ is reflectionally symmetric about the real axis, its associated prime function has the special property

$$\begin{aligned} \overline{\omega }(z,\zeta ) = \omega (z,\zeta ),~ \end{aligned}$$

(31)

where we use the notation $\overline{\omega }(z,\zeta ) \equiv \overline{\omega (\overline{z},\overline{\zeta })}$; see [20] for more details. A consequence of this, together with (30), is that

$$\begin{aligned} \overline{{{\mathcal {Z}}}}(\zeta ) = -{{{\mathcal {Z}}}}(\zeta ). \end{aligned}$$

(32)

5 A Schwarz problem

Armed with this conformal mapping it will now be shown that the composed analytic function

$$\begin{aligned} {\mathcal {H}}(\zeta ) \equiv h({\mathcal {Z}}(\zeta )),\qquad \zeta \equiv \xi + \textrm{i}\eta \end{aligned}$$

(33)

is the solution to a classical problem in complex analysis known as the Schwarz problem in the triply connected circular domain $D_\zeta$ [20, 24].

Owing to the fact that we expect h(z) to have the same values on $\ y = \pm (H+{G})$ for any $0\le x\le L$, we seek a function ${\mathcal {H}}(\zeta )$ that is continuous across $\Gamma _\pm$ and, consequently, analytic in the upper half of $D_\zeta$. On $\overline{\zeta }=\zeta$, we know from (12) that

$$\begin{aligned} \hat{w}(x,y) = \textrm{Im}{[{\mathcal {H}}(\zeta )]} = 0, \end{aligned}$$

(34)

implying that the Schwarz conjugate function of ${{{\mathcal {H}}}}(\zeta )$ defined by $\overline{{\mathcal {H}}}(\zeta ) \equiv \overline{{\mathcal {H}}(\overline{\zeta })}$ coincides with ${{{\mathcal {H}}}}(\zeta )$, that is,

$$\begin{aligned} \overline{{\mathcal {H}}}(\zeta ) = {\mathcal {H}}(\zeta ). \end{aligned}$$

(35)

By the Schwarz reflection principle [25], since ${\mathcal {H}}(\zeta )$ is known to be analytic in the upper half of $D_\zeta$ we infer that ${\mathcal {H}}(\zeta )$ is analytic in the lower half too, that is, in the whole of $D_\zeta$.

If $\zeta \in C_0^{+}$ it follows from (18) that

$$\begin{aligned} \textrm{Re}{[{\mathcal {H}}(\zeta )]} = L\textrm{Im}{[{\mathcal {Z}}(\zeta )]}, \qquad \zeta \in C_0^{+}. \end{aligned}$$

(36)

Suppose now that $\zeta \in C_0^{-}$, then clearly ${\overline{\zeta }} \in C_0^+$. Furthermore,

$$\begin{aligned} \textrm{Re}{[{\mathcal {H}}(\zeta )]} = \textrm{Re}{[\overline{{\mathcal {H}}(\zeta )}]}=\textrm{Re}{[{\mathcal {H}}(\overline{\zeta })]}=L\textrm{Im}{[{\mathcal {Z}}(\overline{\zeta })]} = -L\textrm{Im}{[\overline{{\mathcal {Z}}({\overline{\zeta }})}]} = L\textrm{Im}{[{\mathcal {Z}}(\zeta )]}, \end{aligned}$$

(37)

where the first and fourth equalities follow from trivial properties of complex quantities, the second and last equalities follow from (35) and (32), respectively, and the third equality follows from (18) since ${\overline{\zeta }} \in C_0^+$.

A similar argument can be used to show that because $\textrm{Re}{[{\mathcal {H}}(\zeta )]}$ vanishes on $C_1$ due to (14), then it also vanishes on $C_2$.

We therefore arrive at a boundary value problem for the function ${\mathcal {H}}(\zeta )$, analytic in $D_\zeta$, with boundary values satisfying

$$\begin{aligned} \textrm{Re}{[{\mathcal {H}}(\zeta )]} = \left\{ \begin{array}{lll} \displaystyle L\textrm{Im}{[{\mathcal {Z}}(\zeta )]}, &{} \zeta \in C_0,\\ \displaystyle 0, &{} \zeta \in C_1,\ C_2. \end{array}\right. \end{aligned}$$

(38)

This is a standard Schwarz problem in $D_\zeta$: the problem of finding an analytic function in $D_\zeta$ given its real part everywhere on the domain boundary. Significantly, an explicit integral formula for its solution in a multiply connected circular domain like $D_\zeta$ has been given by [24]; see also Chapter 13 of [20]. This integral formula for the solution itself depends on the prime function of the domain $D_\zeta$. From the results in [20, 24] it can be inferred that, in this case, the solution for ${\mathcal {H}}(\zeta )$ is given by the simple formula

$$\begin{aligned} {\mathcal {H}}(\zeta )= & {} -\frac{L}{\pi }\oint _{C_0}{\mathcal {Z}}(\zeta ')\,d\log \omega (\zeta ',\zeta ). \end{aligned}$$

(39)

Note that ${\mathcal {H}}(\zeta )$ is not only analytic in $D_\zeta$ but also single-valued. More details are given in Appendix 1. The final expression for $\hat{w}(x,y)$ is

$$\begin{aligned} \hat{w}(x,y)= \textrm{Im}\left[ {{{\mathcal {H}}}}(\zeta )\right] = \frac{L(H+{G})}{\pi ^2}\textrm{Im}\left[ \oint _{C_0}\frac{\omega (\zeta ',\theta _1(\infty ))}{\omega (\zeta ',\theta _2(\infty ))} \, d\log \omega (\zeta ',\zeta )\right] . \end{aligned}$$

(40)

Combining (7) and (40) furnishes the explicit integral formula (1).

6 Characterization of the solutions

Analytical formulas have been derived for the solution of the flow problem in terms of the prime function. To study the flow, plot the velocity contours and calculate effective slip lengths, it is necessary to be able to evaluate the prime function $\omega (.,.)$ and there are (at least) two ways to do this.

The most numerically efficient method is to make use of freely available MATLAB codes that compute $\omega (.,.)$ for any user-specified circular domain akin to $D_\zeta$ [20, 26, 27]. These codes are based on a numerical algorithm described in detail in [27], and which extends an earlier algorithm proposed by Crowdy and Marshall [28].

For a triply connected domain, however, it is also known (see Chapter 14 of [20]) that the infinite product representation

$$\begin{aligned} \omega (z,\zeta ) = (z-\zeta )\prod _{\theta \in \Theta ''}\frac{(\theta (z)-\zeta )(\theta (\zeta )-z)}{(\theta (z)-z)(\theta (\zeta )-\zeta )}, \end{aligned}$$

(41)

is convergent; here each function $\theta$ lies in the set of Möbius maps $\Theta ''$ which denotes all elements of the free Schottky group generated by the basic Möbius maps $\lbrace \theta _j, \theta _j^{-1}: j=1,2 \rbrace$, except for the identity and excluding all inverses [20, 27, 28]. For numerical purposes of evaluation it is necessary to truncate this product, and the natural way to do so is to include all Möbius maps up to a chosen level: see [28] for more details. Use of this infinite product is perfectly feasible for most channel geometries. However, maintaining a required degree of accuracy requires truncation at increasingly high levels as the radii of $C_1$ and $C_2$ get larger, resulting in the convergence of the product becoming unacceptably slow. In such cases, use of the MATLAB code from [26] is preferred and advised.

The parameters $\delta$ and q are determined uniquely, for a given channel geometry, by solving the two equations

$$\begin{aligned} {{{\mathcal {Z}}}}(1) = \textrm{i} {G}, \qquad {{{\mathcal {Z}}}}(\delta +q\textrm{i})= L, \end{aligned}$$

(42)

subject to the constraints $|\delta |+q<1$, $|\delta |>0$, and $q>0$. Equations (42) are readily solved using any non-linear solver such as Newton’s method.

The half-period L has been used to non-dimensionalize lengths so that H/L and G/L are the relevant non-dimensional geometrical parameters. Figures 5 and 6 show typical velocity contour plots of $w_F(x,y)$. In Fig. 5, H/L is varied while fixing $G/L = 0.8$; in Fig. 6, the invasion depth G/L is varied while fixing $H/L = 0.8$.

The effective slip length $\lambda$ discussed in Sect. 3 has also been calculated. The left panel of Fig. 7 shows how the normalized slip length $\lambda /2L$ behaves for different values of G/L when the invasion depth H/L is varied. For the limiting case of a channel of infinite height, i.e., $G/L \rightarrow \infty$, the problem becomes equivalent to that studied by Crowdy [19] who derived the analytical result

$$\begin{aligned} \lambda _{\infty }= \frac{2L}{\pi }\log \textrm{cosech}\left( \frac{\pi H}{2L}\right) . \end{aligned}$$

(43)

The cross-dot line in Fig. 7 shows the slip length as given by this formula, which agrees well with the results of the new formulation when $G/L=8.5$.

Fig. 5

Contours of the velocity field $w_F(x,y)$. L and G are fixed to 1 and 0.8 in all figures, respectively. (a) $H=0.4$, (b) $H=0.8$, (c) $H=1.2$

Fig. 6

Contours of the velocity field $w_F(x,y)$. L and H are fixed to 1 and 0.8, respectively, in all figures. (a) $G=0.4$, (b) $G=0.8$, (c) $G=1.2$

Fig. 7

(Left) Normalized slip lengths $\lambda /2L$ for four different ratios of channel height G and period length L. The cross-dot line corresponds to the slip lengths, where G tends to infinity, calculated explicitly by [19]. (Right) Critical invasion depth $({H}/{L})_{\textrm{crit}}$ for increasing G/L

There is a value of H/L which yields a “zero slip length.” A similar observation was made by Crowdy [19] for the case of semi-infinite flow over a single surface. The reason for the vanishing slip length at this “critical invasion depth” is clear: since the slip length is measured relative to an effective slip flow in a channel taken at the level of the invaded menisci, the more the no-slip blades protrude into the flow, the more they will provide increased resistance. Thus, at a sufficiently large groove invasion depth, or equivalently, when the blades have protruded sufficiently far into the flow, any slip advantage afforded by the no-shear nature of the menisci will eventually be canceled out by the resistance offered by the protruding no-slip blades. The (non-dimensional) critical invasion depth, $(H/L)_{\textrm{crit}}$ say, is determined as a function of G/L by the criterion

$$\begin{aligned} \lambda =\lambda ((H/L)_{\textrm{crit}},{G}/L) = 0. \end{aligned}$$

(44)

The right panel of Fig. 7 shows the behavior of this critical invasion depth. As ${G}/L\rightarrow \infty$, it tends to $(2/\pi )\log (1+\sqrt{2})$, the value found by Crowdy [19]. Interestingly, as G/L tends to 0 (by definition, we must have ${G}>0$) the critical invasion depth tends to unity. When G/L tends to 0, the blades touch and form continuous no-slip walls. The menisci are shear-free so the flow resembles a channel flow in a vertical channel. Therefore, the comparison problem in a horizontal channel has the same mass flux when $\lambda =0$ and $H=L$ since these two flows are just rotations of each other by $90^{\textrm{o}}$. By taking the limit ${G/L}\rightarrow 0$ in equation (28) the slip length for this flow is obtained:

$$\begin{aligned} \lambda = \frac{L^2 - H^2}{3H}, \end{aligned}$$

(45)

which means $\lambda =0$ when $H/L=1$.

7 Slip correction for weakly curved menisci

If the menisci are weakly curved, we expect the slip length to be modified according to a regular perturbation expansion

$$\begin{aligned} \lambda _\theta = \lambda + \lambda _1 \theta +{\mathcal {O}}(\theta ^2), \end{aligned}$$

(46)

where, in order to make contact with other studies [9], the coefficient of the first-order slip correction $\lambda _1$ is decomposed as $\lambda _1 = \lambda _{11} + \lambda _{12}$, where $\lambda _{11}$ and $\lambda _{12}$ are defined in appendix 1.

Figure 8 shows graphs of $\lambda _1$. For large G/L, the slip length agrees well with analogous explicit integral formulas for the first-order correction to the slip length given recently in [19] for semi-infinite shear over a single surface. An interesting feature is that, for large G/L, $\lambda _1$ is monotonically decreasing, but this behavior is different for smaller values of G/L. At some critical value of G/L (close to unity) the slip length correction becomes negative as H/L increases. This observation means that increasing the curvature of the meniscus does not enhance slip when G/L is small, i.e., for shallow channels.

Fig. 8

The behavior of $\lambda _{1}$. $\lambda _{1}/2L$ agrees well with the infinite-height case when $G/L=20.0$

8 Connection with another SHS problem

To motivate his study of semi-infinite shear flow over a single surface of blades where the menisci have partially invaded the grooves, Crowdy [19] includes a figure similar to that shown in Fig. 9 which shows three different superhydrophobic surface (SHS) channel flows. Figure 9a shows the most commonly considered case: longitudinal channel flow over a 2L-periodic symmetric channel where menisci are flat, of length 2c, and flush with the tops of the no-slip pillars. The pillars therefore have width $2(L-c)$. As $c \rightarrow L$ the pillars become infinitely thin (“blades”) as shown in Fig. 9b. This flow scenario is singular because there is no solid surface left to retard the flow against the imposed pressure gradient. This manifests itself in the effective slip length associated with the flow in Fig. 9a becoming infinite as $c \rightarrow L$. A “continuation” of this singular state, discussed by Crowdy [19], is shown in Fig. 9c and shows the menisci descending by distance H into the grooves between infinitely thin walls. The analytical formulas (C9) and (43) refer to slip lengths associated with the flow shown in Fig. 9c in the limit ${G}/L \rightarrow \infty$ (which can be viewed as the problem of semi-infinite shear over a single SHS).

Remarkably, it turns out that there is a mathematical connection between (the physically distinct) SHS flows shown in Fig. 9a and c.

This is significant because it renders the new analytical solution (1) doubly useful.

The observation is that if we take the upper-half window in problem (a) and rotate it by $90^{\textrm{o}}$, then we obtain the period window relevant to problem (c) and, moreover, the boundary conditions associated with the two problems (a) and (c) can be seen to be of the same type on each boundary portion (i.e., either no-slip or the normal derivative vanishing). Indeed, it can be shown that the flow field in problem (a) can be deduced from the solution of problem (c) by using the following transformations:

$$\begin{aligned} x\mapsto y,\ y\mapsto x, \ L\mapsto {G},\ H+{G}\mapsto L,\ {G} \mapsto c. \end{aligned}$$

(47)

This mathematical transformation means that we have essentially solved two physically distinct problems at once. Figure 10 shows the transformations (47) graphically. We can see that both flows in the period window satisfy the same type of boundary conditions.

Fig. 9

Superhydrophobic channel flows. (a) Symmetric channel flow between two superhydrophobic surfaces with menisci spanning the grooves between thick walls. (b) The critical case when the walls become infinitely thin, i.e., $c\rightarrow L$; the solution here is known to be singular [19]. (c) The problem solved in this paper: symmetric channel flow where the menisci have partially invaded the grooves between infinitely thin blades

Fig. 10

(i) Superhydrophobic channel flow in problem (c). (ii) Superhydrophobic channel flow in problem (a). The boundary condition on the black portion is no-slip, while on the red portion it is no-shear. By the transformation (47), both flows in the period window match

This observation also means that we have produced a new representation of the solution to problem (a) found by Marshall [21] who used a very different approach. Marshall also adopted use of the prime function technology but he performed the analysis in a doubly connected annulus rather than the triply connected domain $D_\zeta$ used here. Conversely, the observation means that, in principle, the partially invaded meniscus problem (c) could have been solved by adapting Marshall’s solution of problem (a). Notwithstanding this observation, we believe that the conciseness of the new formula (1) has its own attractions and is interesting in its own right. Furthermore, use of the triply connected preimage domain of this paper has “uniformized” a square-root singularity that appears in the analysis when a doubly connected annulus is used instead. The approach proposed by Marshall involves the incomplete elliptic integral of the first kind, which has square-root singularities at the edges of the menisci. Such integrable singularities are eliminated safely in our approach. Elimination of square-root singularities can be desirable for numerical purposes since it obviates the need to deal with branch points and branch cuts associated with those singularities.

To corroborate this observation, Fig. 11 shows the slip length for problem (a), and the coefficient of the first-order correction for small meniscus curvature, as calculated by adapting our approach and making use of the transformation (47). The circle-dot lines correspond to the results obtained using Marshall’s alternative approach [21]; the cross-dot lines are the slip lengths for the flow in a periodic infinite channel, initially found in [7]:

$$\begin{aligned} \lambda _{\text {(a)},\infty } = \frac{2L}{\pi }\log \textrm{sec}\left( \frac{\pi c}{2L}\right) . \end{aligned}$$

(48)

Following [21], the slip length in problem (a) is

$$\begin{aligned} \lambda _{\mathrm{(a)}} = \frac{1}{L{G}}\int _{0}^{c}{\tilde{w}}(x,0)\,\mathrm{{dx}} = \frac{1}{L{G}}\int _{0}^{{G}}\hat{w}(0,y)\,\mathrm{{dy}}, \end{aligned}$$

(49)

where the flow in problem (a) is $w_{(a)}=w_{P}+\tilde{{w}}$, and where the transformation (47) is used in the second equality. Comparing equation (49) with (28) shows that $\lambda$ has an additional term and a different coefficient in front of the integral term, which results in the slip lengths having entirely different behavior as seen in Fig. 11. This is of course not surprising because, while the two flows might be related mathematically, they are nevertheless completely different flows.

It is interesting that, compared to problem (a), the channel height G in problem (c) needs to be much larger in order for the channel-flow slip length $\lambda$ to be well approximated by the semi-infinite flow result $\lambda _\infty$.

Fig. 11

Slip length and normalized coefficient of the first-order correction for weak meniscus curvature for problem (a). Solid lines show the quantities calculated using the new approach of this paper; results using Marshall’s approach [21] are shown as circle dots. The cross dots correspond to the slip length from formula (48)

9 Summary

This paper has shown how to use the prime function associated with a triply connected circular domain [20] to find compact representations of longitudinal channel flows over superhydrophobic surfaces where the menisci have depinned from the pillar tops and partially invaded the grooves. The solutions are explicit once two parameters, $\delta$ and q, have been found by solving two non-linear equations given the geometry of the surface. The slip properties of the surfaces have been quantified based on the use of these new formulas. It has also been indicated how previously derived solutions due to Marshall [21] for a different flow in a superhydrophobic channel can be derived by a simple transformation of our formula.

Given that a single period of any of these channel flows is simply connected, it is perhaps surprising that we have been able to make use of mathematical technology devised for solving problems in multiply (in this case, triply) connected geometries [20]. However, the key point is that the boundary of the simply connected flow region has different boundary conditions on distinct portions of this (single) boundary—it is a mixed-type boundary value problem—which makes it advantageous, as we have shown here and as also discussed in detail in [20], to identify the different portions of a boundary on which a particular boundary condition holds (e.g., a Dirichlet-type, or a Neumann-type condition) with distinct boundaries of a domain of higher connectivity. At first sight, this may seem like adding complication to the problem. However, with the aid of the prime function, and as the monograph [20] aims to show, it is no more difficult to solve problems in a triply connected domain as in a simply connected one. Moreover, transferring the problem to a higher connected domain can allow any boundary-point singularities resulting from mixed-type boundary conditions on a single boundary to be uniformized, that is, essentially removed. Notice that there are no explicit boundary-point singularities (e.g., branch points) appearing in the final formula (1).

We believe the compact form of the flow solution (1) is important since many applications of superhydrophobic surfaces involve additional physical effects, such as heat [23] and mass transfer, or thermocapillary or other surfactant effects [29, 30], making it useful to have available concise representations of the basic flow. Finally, for the convenience of readers wishing to make use of the solutions described herein, the authors are preparing downloadable MATLAB codes based on the theoretical work in this paper [26].

Appendices

Appendix A: The conformal map (29)

It is useful to give some background on the origin of the mapping (29). In Sect. 6.8 of [20], Crowdy discusses the so-called annular slit mappings associated with a multiply connected circular domain, one of which is

$$\begin{aligned} e^{2 \pi \textrm{i} ({{{\mathcal {G}}}}_1(\zeta ,a) -{{{\mathcal {G}}}}_2(\zeta ,a))}, \end{aligned}$$

(A1)

where a is some point inside $D_\zeta$, and $\lbrace \mathcal{G}_j(\zeta ,a) |j=1,2 \rbrace$ are (analytic extensions) of two of the modified Green’s functions associated with $D_\zeta$. Such a mapping transplants the two circles $C_1$ and $C_2$ to the concentric circular boundaries of a bounded annulus in an image plane, with $D_\zeta$ mapping to the annular region between these two image circles and with the circle $C_0$ being transplanted to a concentric circular slit of finite length inside this annulus. Therefore, on taking a logarithm of (A1), one produces the conformal mapping (29) of precisely the kind needed in the present application: a rectangle with a horizontal slit, or, on multiplying by a pure imaginary constant, a vertical slit. Furthermore, in Sects. 4.9 and 4.10 of [20], it is indicated how ${{{\mathcal {G}}}}_j(\zeta ,a)$ may be written in terms of the prime function, namely,

$$\begin{aligned} {{{\mathcal {G}}}}_j(\zeta ,a) = {1 \over 2 \pi \textrm{i}} \log \left( {\omega (\zeta ,a) \over \omega (\zeta , \theta _j(1/{\overline{a}}))} \right) + c_j(a), \end{aligned}$$

(A2)

where $c_j(a)$ is independent of $\zeta$. Actually, the representations (A2) were first derived in the context of adding circulation around airfoils in the study of aerodynamic lift on wings [31]. In deriving (29) we have taken a multiple of a logarithm of (A1) and used (A2) for $j=1, 2$ with the special choice $a=0$. As a final remark, we point out that (29) can also be identified with (a multiple of) the function $v_1(\zeta )-v_2(\zeta )$, where $\lbrace v_j(\zeta ) |j=1,2 \rbrace$ is a set of important functions associated with $D_\zeta$, and is introduced in Sect. 2.5 of [20].

Appendix B : Solution of Schwarz problem

The boundary value problem (38) for ${\mathcal {H}}(\zeta )$ is a standard Schwarz problem in a triply connected domain. The explicit general solution to such a problem has been given, in terms of the prime function, by Crowdy [24]. More precisely, a function $f(\zeta )$ that is analytic in $D_\zeta$ is uniquely determined up to an imaginary constant by the Schwarz integral formula:

$$\begin{aligned} f(\zeta )&= \frac{1}{2\pi \textrm{i}}\oint _{\partial D_\zeta }\textrm{Re}{[f(\zeta ')]}(d\log \omega (\zeta ',\zeta )+d\log \overline{\omega }(\overline{\zeta '},1/\zeta ))\nonumber \\&-\sum _{k=1}^2 A_k\textrm{i}v_k(\zeta ) + \textrm{i}c_0,\end{aligned}$$

(B3)

$$\begin{aligned} A_k&= \int _{C_0}\textrm{Re}[f(\zeta )]d\hat{v}_k - \sum _{j=1}^2 \int _{C_j}\textrm{Re}[f(\zeta )]d\hat{v}_k, \qquad \ k=1,2, \end{aligned}$$

(B4)

where $\lbrace v_j(\zeta ) |j=1,2 \rbrace$ are analytic functions in $D_\zeta$, with each $v_j$ having a logarithmic branch cut between $C_0$ and $C_j$. Each $\hat{v}_j$ is a linear combination of $\lbrace v_k(\zeta ) |k=1,2 \rbrace$, and $c_0$ is a real constant [20, 24]. See more details in Chapter 13 of [20]. For the particular problem in (38) it can be shown using properties of the prime function (and confirmed numerically) that, for this problem, $A_1=A_2=c_0=0$. This means, in particular, that ${{{\mathcal {H}}}}(\zeta )$ is single-valued in $D_\zeta$, a feature that is consistent with earlier arguments in Sect. 5 (indeed, alternatively we could have stated that the boundary value problem for the single-valued analytic function ${{{\mathcal {H}}}}(\zeta )$ is a modified Schwarz problem in $D_\zeta$, and then confirmed that the boundary data satisfy compatibility conditions necessary for such a single-valued function to exist [20, 24]). Consequently, (38) can be simplified to the compact expression

$$\begin{aligned} {\mathcal {H}}(\zeta ) =-\frac{L}{\pi }\oint _{C_0}{\mathcal {Z}}(\zeta ')\,d\log \omega (\zeta ',\zeta ), \end{aligned}$$

(B5)

where we have used the fact that $\overline{\zeta '} = 1/\zeta '$ on $C_0$ and the prime function property $\overline{\omega }(\zeta '^{-1},\zeta ^{-1})=- \omega (\zeta ',\zeta )/\zeta \zeta '$ (see Sect. 4.7 of [20]).

Appendix C: Two definitions of the effective slip length

Fig. 12

The two definitions of the effective slip length for a channel flow. In case (I) the flow is compared to a Navier-slip flow with walls taken level with the tops of the pillars; in case (II) it is compared to a Navier-slip flow with walls taken at the level of the invaded menisci

It is worth pointing out that there is arbitrariness in the choice of defining the slip length as already observed in Crowdy [19]. For example, consider two definitions of the effective slip length for a channel flow denoted by $\lambda _{\mathrm{(I)}}$ and $\lambda _{\mathrm{(II)}}$ shown in Fig. 12. In (I) the baseline is placed at the top of the grooves, while in (II) the baseline is at the same level as the meniscus. Case (II) is equivalent to the right panel of Fig. 4, i.e., $\lambda _{\mathrm{(II)}}=\lambda$. For case (I) we can use the same technique as Sect. 3 and obtain a formula for the slip length:

$$\begin{aligned} \lambda _{\mathrm{(I)}}= \frac{(H+{G})L^2}{3{G}^2} -\frac{{G}}{3} + \frac{1}{{G}^2}\int _0^{{G}}\hat{w}(0,y)\,dy. \end{aligned}$$

(C6)

There is a mathematical relation between $\lambda _{\mathrm{(I)}}$ and $\lambda _{\mathrm{(II)}}$. Multiplying $\lambda _{(\mathrm I)}$ by ${G}^2$ and $\lambda _{(\mathrm II)}$ by $(H+{G})^2$, we find

$$\begin{aligned} \lambda _{\mathrm{(I)}} = \left( 1+\frac{H}{{G}}\right) ^2 \lambda _{\mathrm{(II)}} + H\left( 1+\frac{H}{{G}}\right) + \frac{H^3}{3{G}^2}. \end{aligned}$$

(C7)

This expression can be seen as a generalization of equation (3.8) derived by Crowdy [19], who calculated the slip length for shear flow over a single surface with partially invaded grooves. Note that for ${G/L}\rightarrow \infty$, we obtain the asymptotic formula

$$\begin{aligned} \lambda _{\mathrm{(I)}} = \lambda _{(\mathrm II)} + H, \end{aligned}$$

(C8)

which is exactly the relation derived in [19]. For the limiting case of a channel of infinite height, i.e., $G/L \rightarrow \infty$, $\lambda _{\mathrm{(I)}}$ becomes the analytical result derived by Crowdy [19]:

$$\begin{aligned} \lambda _{\mathrm{(I)},\infty } = \frac{2L}{\pi }\log \left( 1+\textrm{coth}\left( \frac{\pi H}{2L}\right) \right) . \end{aligned}$$

(C9)

Appendix D: Weakly curved menisci

We follow the approach of Crowdy [22] who first proposed combining perturbation analysis with the use of integral “reciprocal identities” to find the leading order corrections to the flat-state slip length. Marshall [21] followed the approach of [22] in his analysis of the superhydrophobic channel problem (with non-invaded grooves) shown in Fig. 9a.

Each meniscus is assumed to be a circular arc with a protrusion angle denoted by $\theta$. In our case, the meniscus curves slightly downwards, hence $\theta$ is assumed to be small and negative. We write the solution for the flow field $w_\theta (x,y)$ as a series expansion in $\theta \ll 1$:

$$\begin{aligned} w_\theta (x,y) = w_F(x,y) + \theta w_1(x,y) + {\mathcal {O}}(\theta ^2). \end{aligned}$$

(D10)

Since the curved meniscus is a circular arc with protrusion angle $\theta$, the meniscus can be approximated by the quadratic curve $y=\theta Y(x)+{\mathcal {O}}(\theta ^2)$, where $Y(x)=(L^2-x^2)/2L$ [22]. The normal derivative of $w_\theta$ on the curved meniscus is

(D11)

Green’s second identity states that

$$\begin{aligned} \int _{\Omega _\theta }(w_F\nabla ^2 w_\theta - w_\theta \nabla ^2 w_F)dS = \int _{\partial \Omega _\theta }\left( w_F\frac{\partial w_\theta }{\partial n} - w_\theta \frac{\partial w_F}{\partial n} \right) ds, \end{aligned}$$

(D12)

and thus the volume flux in $\Omega _\theta$, denoted by $Q_\theta$, is given by

$$\begin{aligned} Q_\theta = Q_F +\theta (Q_{11}+Q_{12}) + {\mathcal {O}}(\theta ^2), \end{aligned}$$

(D13)

where

(D14)

(D15)

By equating $Q_\theta$ and $Q_{\lambda }$, we obtain

(D16)

where $\lambda _1 = \lambda _{11} + \lambda _{12}$, and

(D17)

(D18)